Research on the Optimal Control of Working Oil Pressure of DCT Clutch Based on Linear Quadratics Form
Abstract
1. Introduction
2. The Structure and Working Principle of DCT
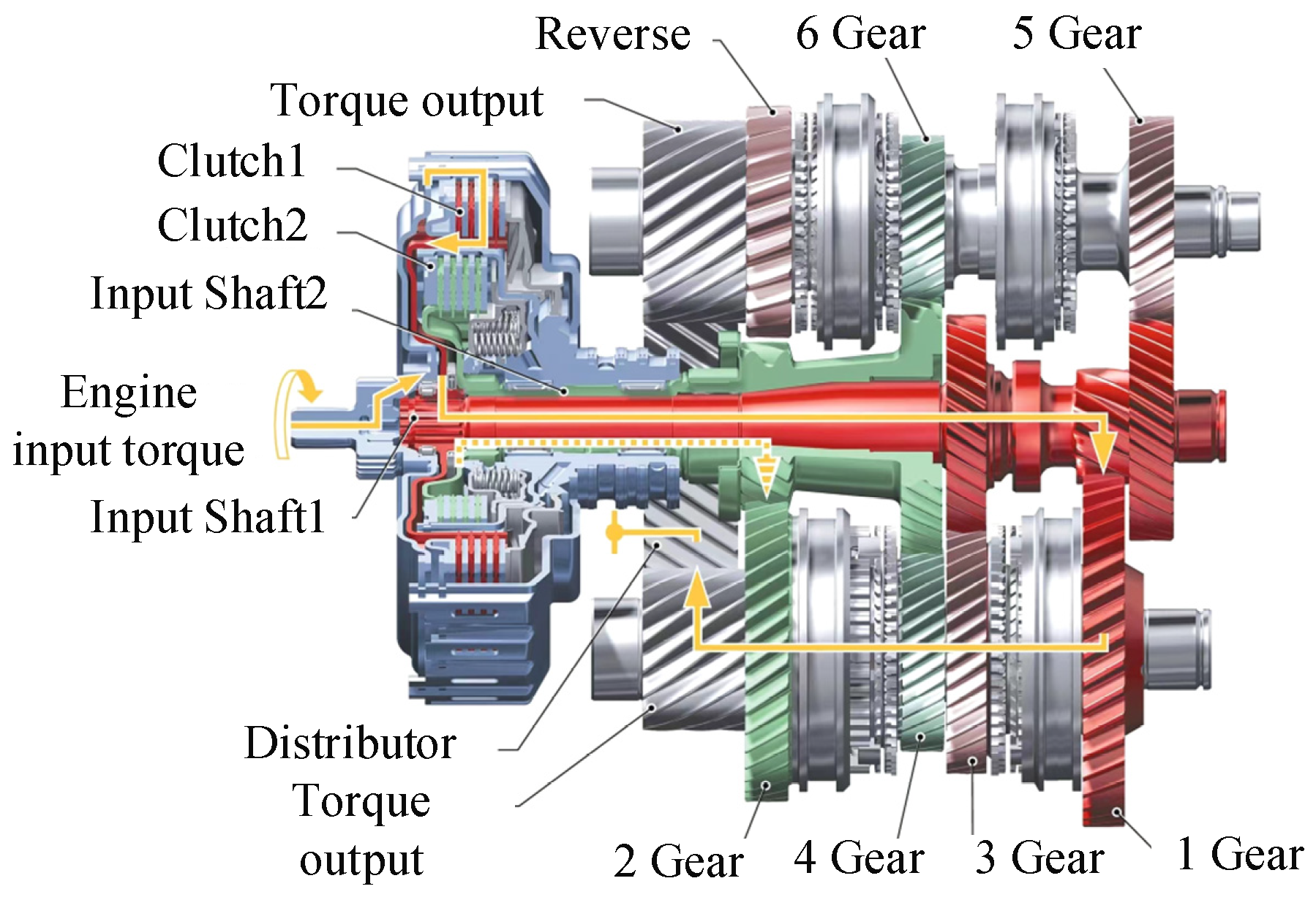
2.1. The Overall Structure of Wet Clutch
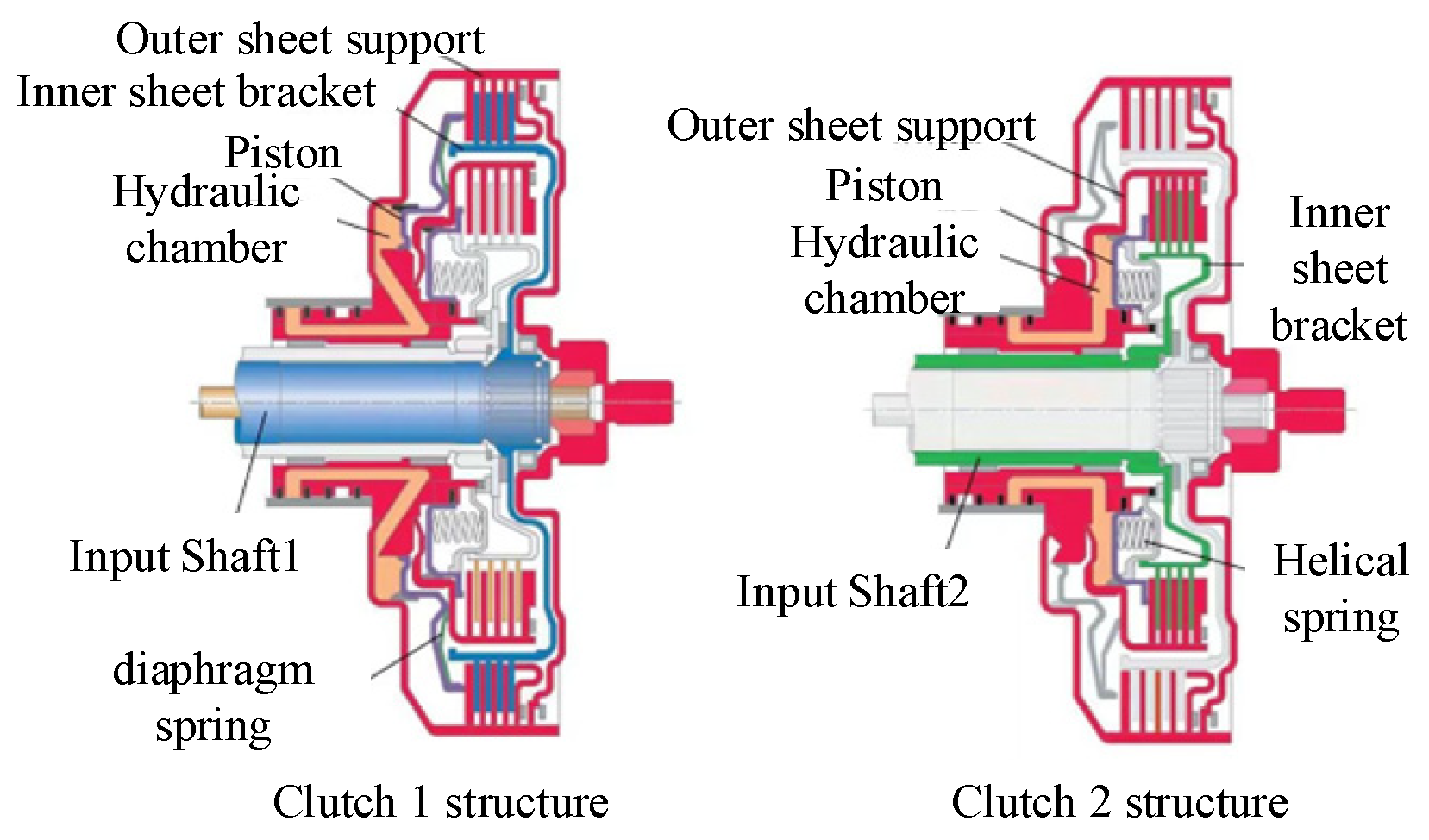
2.2. Clutch System
2.3. The Working Principle of DCT
3. Shift Quality Evaluation Index
3.1. Impact Degree
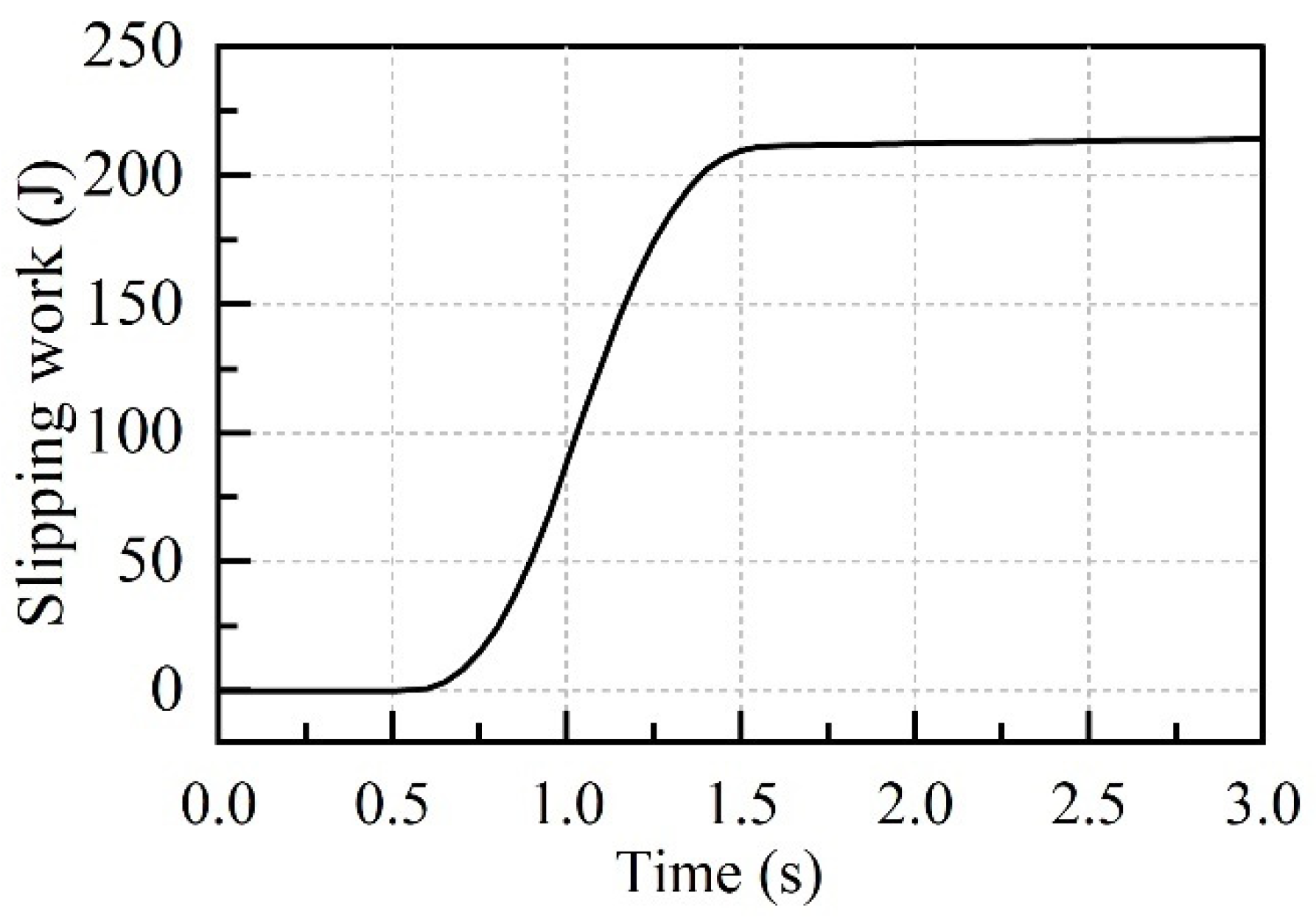
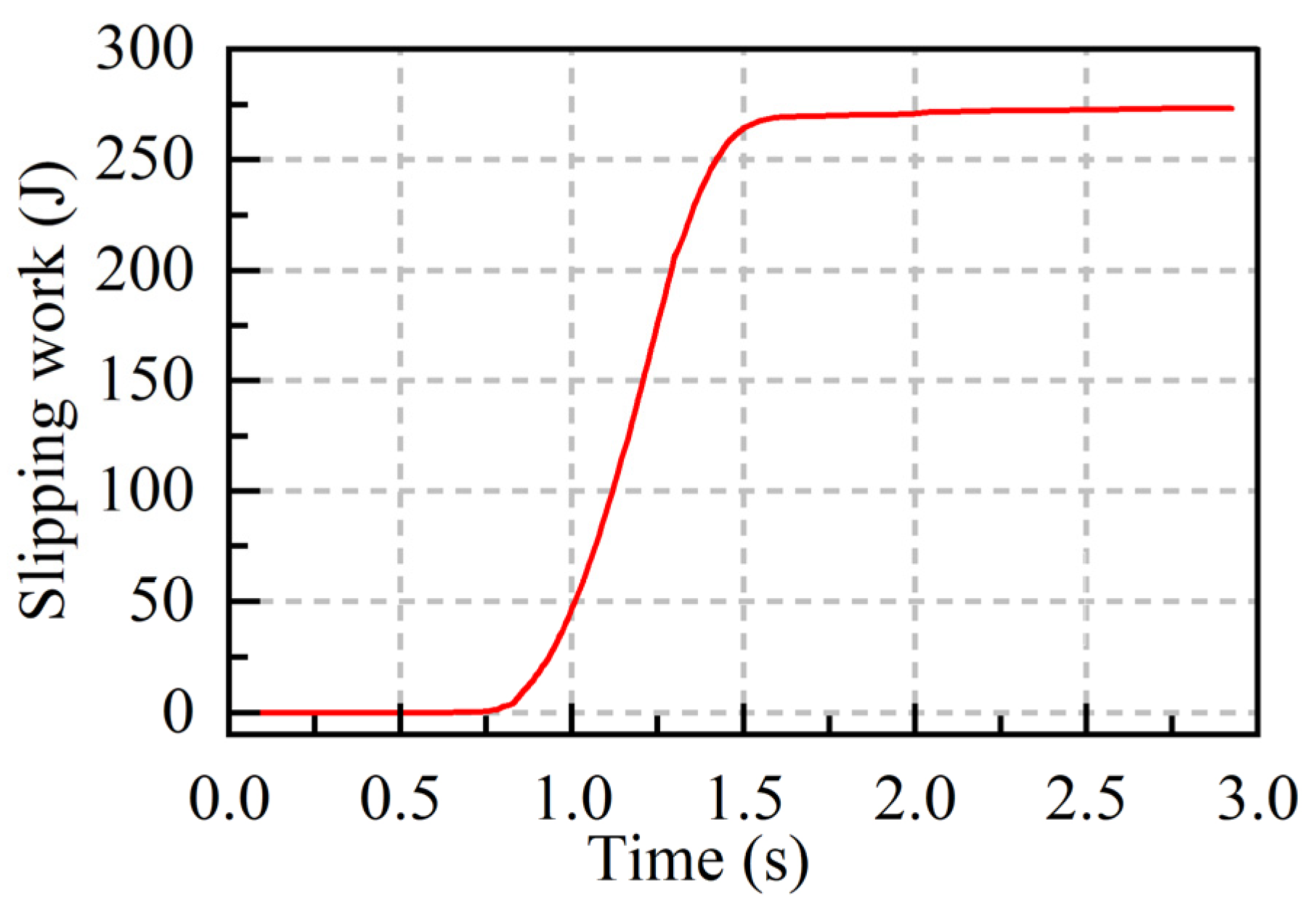
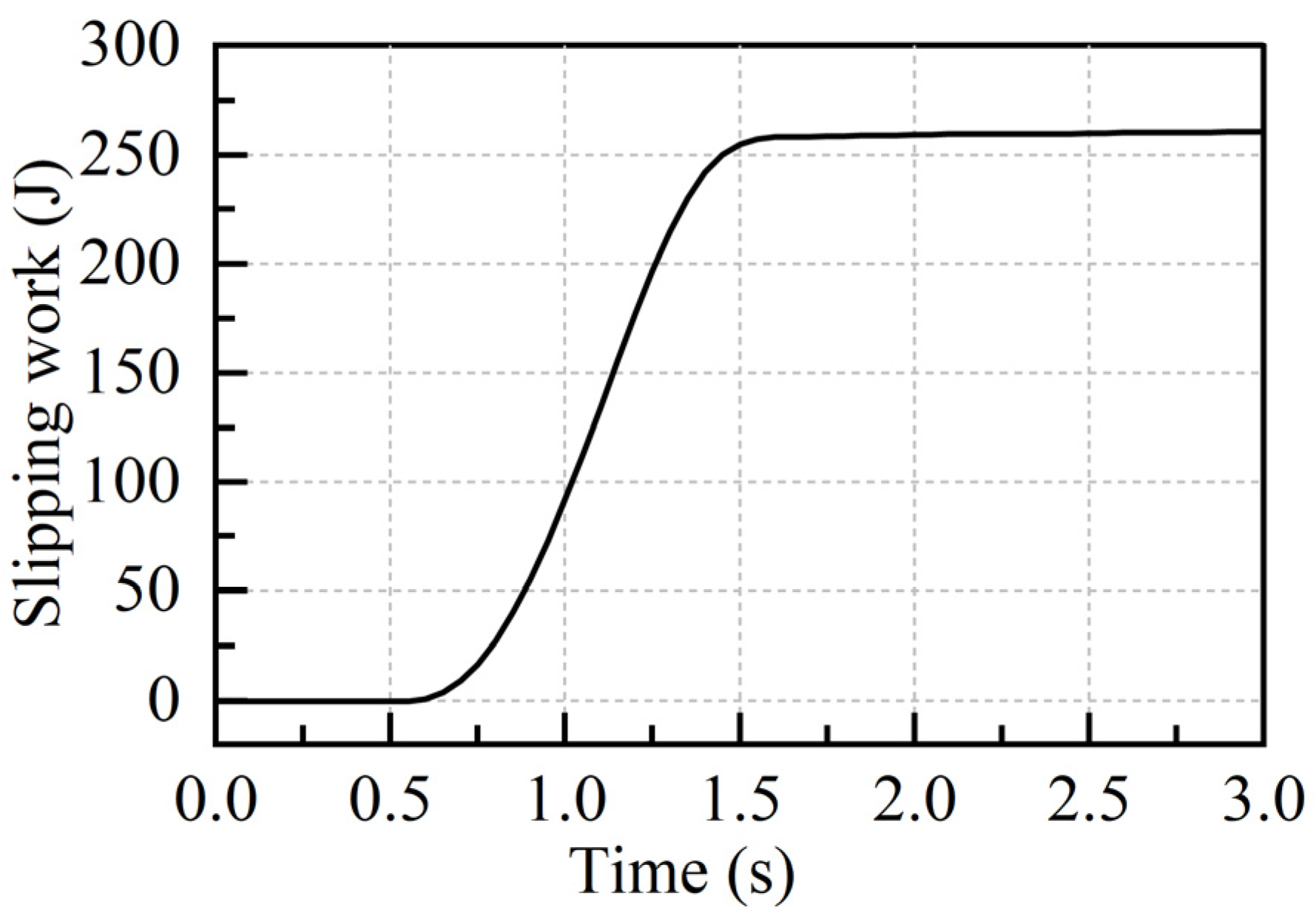
3.2. Slipping Work
4. Design of Oil Pressure Control Trajectory During DCT Shifting
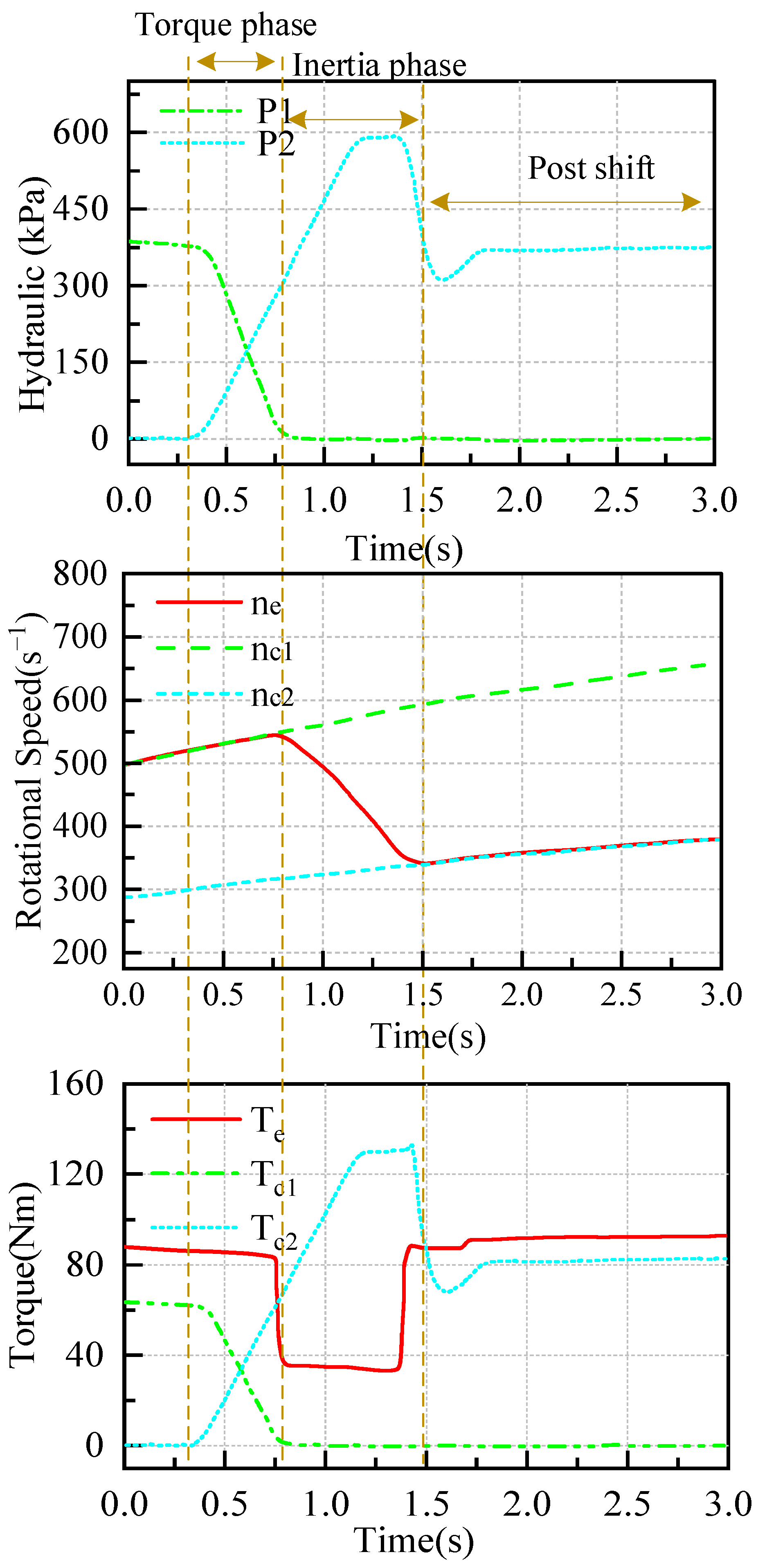
4.1. Torque Phase and Inertial Phase
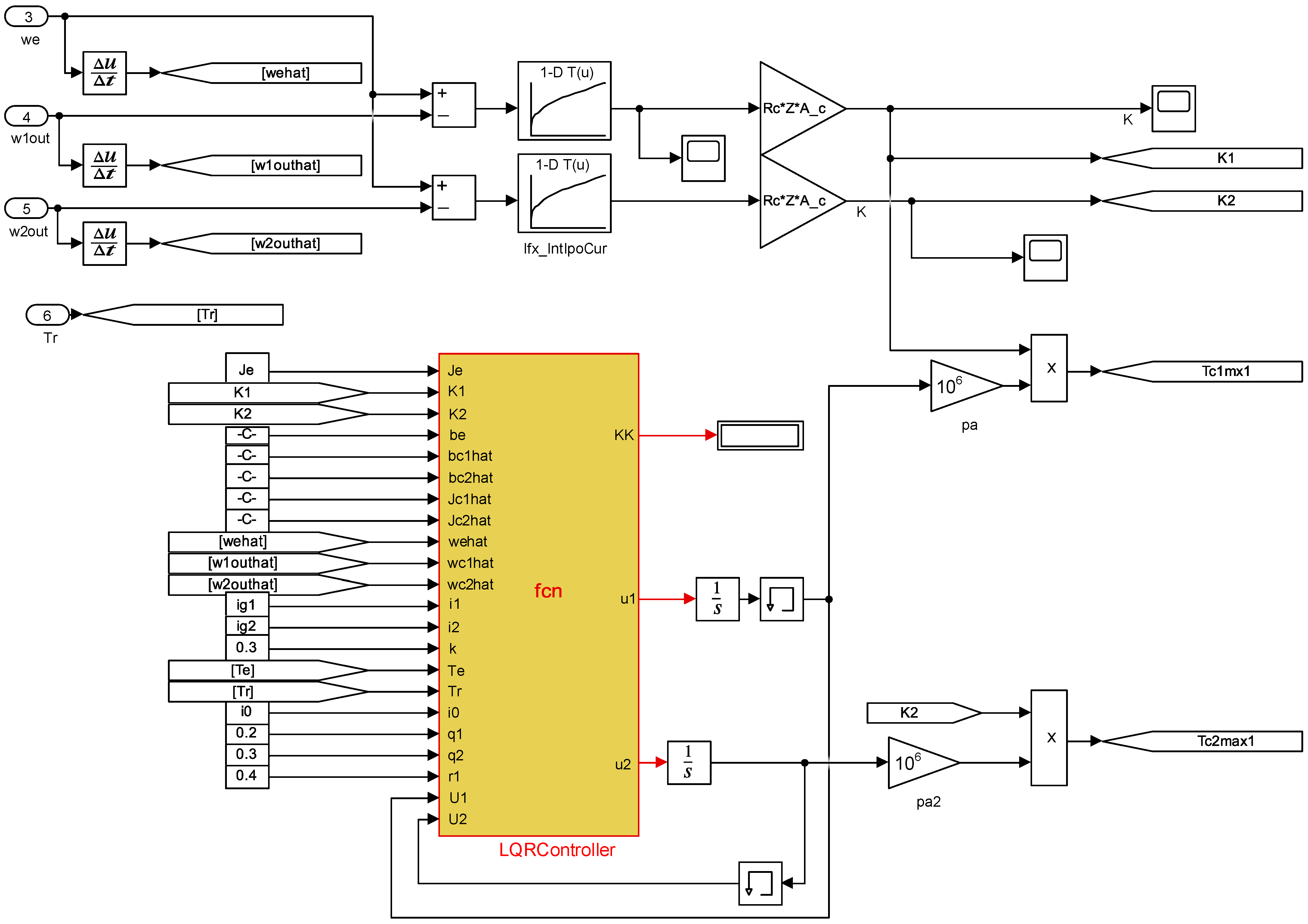
4.2. Optimization Problem Solving
5. Simulation Results and Analysis
5.1. Comparison of Simulation Results Under Different Operating Conditions
5.2. Comparison of Simulation Results Under Different Control Strategies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, X. Hydraulic Control System Analysis and Simulation Research of Wet Double Clutch Automatic Transmission. Ph.D. Thesis, Jilin University, Changchun, China, 2017. [Google Scholar]
- Zhang, Y. Master of Simulation Research and Analysis of Hydraulic Control System for Wet Dual-Clutch Automatic Transmission. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Zhou, B. Research on Micro-Slip Control Method of Wet Dual-Clutch Transmission. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2018. [Google Scholar]
- Liu, Y. Doctor of Integrated Matching Control for Dual-Clutch Transmission System of Passenger Car. Ph.D. Thesis, Chongqing University, Chongqing, China, 2010. [Google Scholar]
- Liu, Y. Shift Quality Simulation of Dual-Clutch Automatic Transmission. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2017. [Google Scholar]
- Li, Y.T.; Zhao, Z.G.; Zhang, T. Simulation study of DCT transmission dual-clutch pressure optimal control method. China Mech. Eng. 2010, 12, 1496–1501. [Google Scholar]
- Fu, S.H.; Gu, J.H.; Li, Z.; Mao, E.R.; Du, Y.F.; Zhu, Z.X. Pressure control method for wet clutch of power shift transmission based on MFAPC. J. Agric. Mach. 2020, 12, 367–376. [Google Scholar]
- Wang, Q.; Meng, B.W.; Jia, W.J.; He, H.R. Research on optimal control of AMT vehicle starting clutch based on variational method. Shanxi Electron. Technol. 2019, 05, 75–78. [Google Scholar]
- Zhao, K.G.; Ning, W.L.; Ye, J. Optimal coordinated control strategy for AMT vehicle start based on minimum principle. J. Chongqing Univ. Technol. (Nat. Sci.) 2021, 2, 17–25. [Google Scholar]
- Wang, C.; Qin, D.T.; Wu, B.Z.; Fang, H.S.; Cheng, K. Simulation and analysis of wet clutch engagement characteristics. J. Chongqing Univ. 2020, 10, 38–51. [Google Scholar]
- MGoetz, M.C.; Crolla, D.A. Dynamics and control of gearshifts on twin-clutch transmissions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 8, 951–963. [Google Scholar]
- Van Berkel, K.; Veldpaus, F.; Hofman, T.; Vroemen, B.; Steinbuch, M. Fast and Smooth Clutch Engagement Control for a Mechanical Hybrid Powertrain. IEEE Trans. Control. Syst. Technol.: A Publ. IEEE Control. Syst. Soc. 2014, 4, 1241–1254. [Google Scholar] [CrossRef]
- Walker, P.D.; Zhang, N.; Tamba, R. Control of gear shifts in dual-clutch transmission powertrains. Mech. Syst. Signal Process. 2010, 6, 1923–1936. [Google Scholar] [CrossRef]
- Liang, J.; Walker, P.D.; Ruan, J.; Yang, H.; Wu, J.; Zhang, N. Gearshift and brake distribution control for regenerative braking in electric vehicles with dual-clutch transmission. Mech. Mach. Theory 2019, 133, 1–22. [Google Scholar] [CrossRef]
- Kulkarni, M.; Shim, T.Y.; Zhang, Y. Shift dynamics and control of dual-clutch transmissions. Mech. Mach. Theory 2006, 2, 168–182. [Google Scholar] [CrossRef]
- Davis, G.; Donin, R.; Findlay, M.; Harman, P.; Ingram, M.; David, K. Optimisation of gear shift quality: By Means of Simulation. ATZ Worldw. 2004, 7–8, 23–26. [Google Scholar] [CrossRef]
- Jaecheol, C.; Yongseok, L.; Woojung, K.; Siyoul, J. Wet Single Clutch Engagement Behaviors in the Dual-Clutch Transmission System. Int. J. Automot. Technol. 2017, 19, 463–472. [Google Scholar]
- Byeon, S.J.; Kim, S.J.; Park, J.K.; Park, Y.J.; Lee, J.W. Parameter Study for Establishing a Synchronizer Control Strategy in Tractor Dual-Clutch Transmission. Agriculture 2024, 14, 218. [Google Scholar] [CrossRef]
- Hao, H.; Ma, H. Optimizing Gearshift Control of Wet Dual Clutch Transmission. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 936–947. [Google Scholar]
- Xiang, Y.; Li, R.; Brach, C.; Liu, X.; Geimer, M. A Novel Algorithm for Hydrostatic-Mechanical Mobile Machines with a Dual-Clutch Transmission. Energies 2022, 15, 2095. [Google Scholar] [CrossRef]
- Chen, Y.T.; Cheng, Z.; Qian, Y. Research on Wet Clutch Switching Quality in the Shifting Stage of an Agricultural Tractor Transmission System. Agriculture 2022, 12, 1174. [Google Scholar] [CrossRef]
- Li, Y.; Bao, D.; Tang, W. LQR control of a flexible ball screw feed system with a generalized extended state observer. J. Jiangsu Univ. (Nat. Sci. Ed.) 2019, 40, 446–450+457. [Google Scholar]
- Zhang, Z.; Wu, X.; Yang, C.; Zou, B. Research on precise control methods for clutch torque in the shifting process of wet DCT. J. Chongqing Univ. Technol. (Nat. Sci. Ed.) 2023, 37, 8–18. [Google Scholar]
- Zhao, D.; Cui, G.; Li, D. Shift quality of the transmission system in engineering vehicles. J. Jiangsu Univ. (Nat. Sci. Ed.) 2008, 5, 386–389. [Google Scholar]
- Hu, F.; Sun, D.; Qin, D.; Chen, R.; Luo, Y. Modeling and Simulation of the Joint Starting Mode of DCT Dual Clutch. J. Jiangsu Univ. (Nat. Sci. Ed.) 2010, 31, 19–25. [Google Scholar]
- Jia, Y.T.; Tian, J.Y.; Gu, Y.H.; Xia, C.G. Minimization of shift friction work and jerk of DCT for electric vehicles. J. Guangxi Univ. (Nat. Sci. Ed.) 2019, 5, 1355–1362. [Google Scholar]












| Clutch Number | Inside Diameter (mm) | Outside Diameter (mm) | Friction Surface |
|---|---|---|---|
| C1 | 191 | 210 | 2 |
| C2 | 143 | 169 | 2 |
| Character | Interpretation | Parameter Value | Unit |
|---|---|---|---|
| Jce | The input equivalent moment of inertia | 0.20 | (kg·m2) |
| Jc1 | Input shaft 1 equivalent moment of inertia | 0.043 | (kg·m2) |
| Jc2 | Input shaft 2 equivalent moment of inertia | 0.045 | (kg·m2) |
| Jo | Equivalent rotational inertia of drive shaft | 0.04 | (kg·m2) |
| Jv | Vehicle equivalent rotational inertia | 149.94 | (kg·m2) |
| ig1 | A gear speed ratio | 4.83 | |
| ig2 | Two gear speed ratio | 3.25 | |
| m | Complete vehicle quality | 1600 | (kg) |
| f | Coefficient of rolling resistance | 0.015 | (/) |
| CD | Coefficient of air resistance | 0.0293 | (/) |
| Wheel rolling radius | 0.30 | (m) | |
| ηT | Mechanical transmission efficiency | 92 | (%) |
| A | Vehicle windward area | 2.095 | (m2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Zhang, H.; Yang, X.; Xu, X.; Sun, X. Research on the Optimal Control of Working Oil Pressure of DCT Clutch Based on Linear Quadratics Form. Machines 2024, 12, 903. https://doi.org/10.3390/machines12120903
Shi G, Zhang H, Yang X, Xu X, Sun X. Research on the Optimal Control of Working Oil Pressure of DCT Clutch Based on Linear Quadratics Form. Machines. 2024; 12(12):903. https://doi.org/10.3390/machines12120903
Chicago/Turabian StyleShi, Guifa, Houzhong Zhang, Xiangtian Yang, Xing Xu, and Xiaoqiang Sun. 2024. "Research on the Optimal Control of Working Oil Pressure of DCT Clutch Based on Linear Quadratics Form" Machines 12, no. 12: 903. https://doi.org/10.3390/machines12120903
APA StyleShi, G., Zhang, H., Yang, X., Xu, X., & Sun, X. (2024). Research on the Optimal Control of Working Oil Pressure of DCT Clutch Based on Linear Quadratics Form. Machines, 12(12), 903. https://doi.org/10.3390/machines12120903




