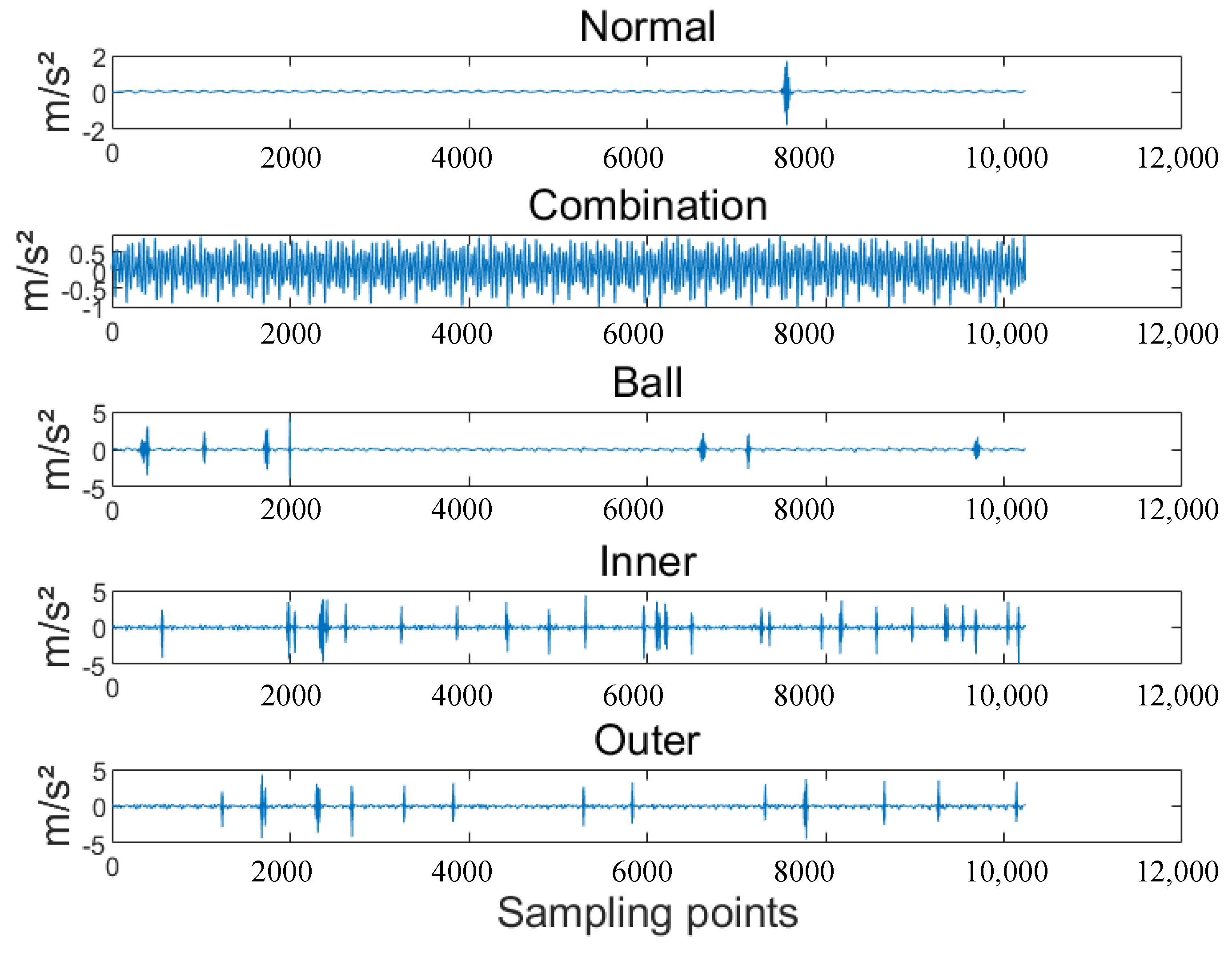
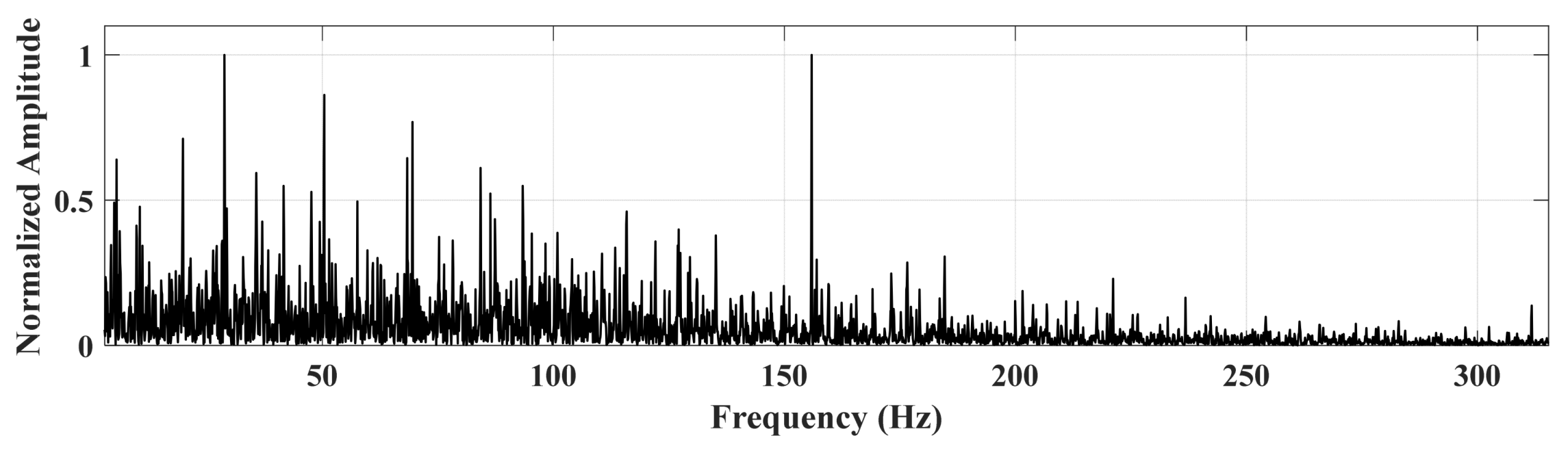
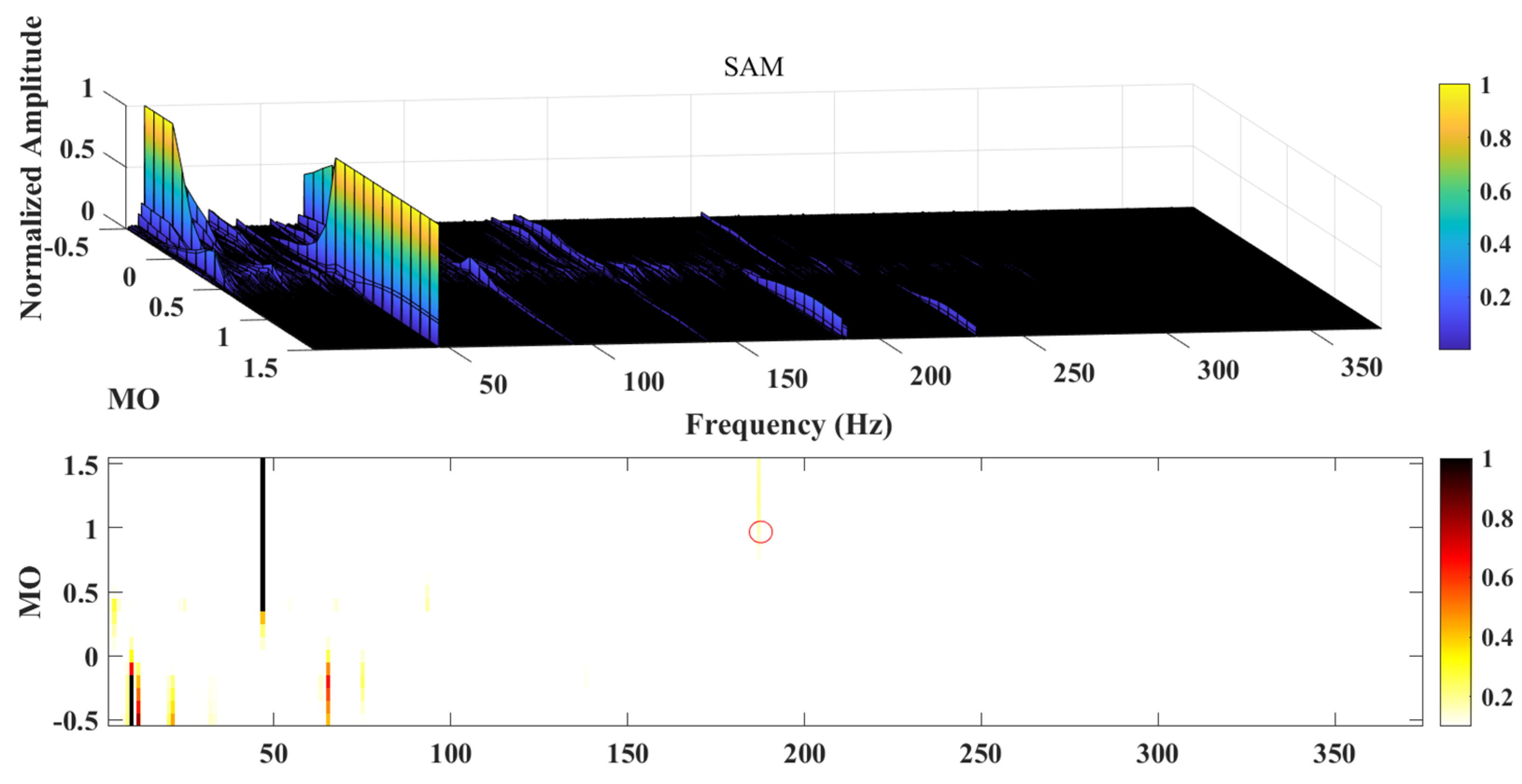
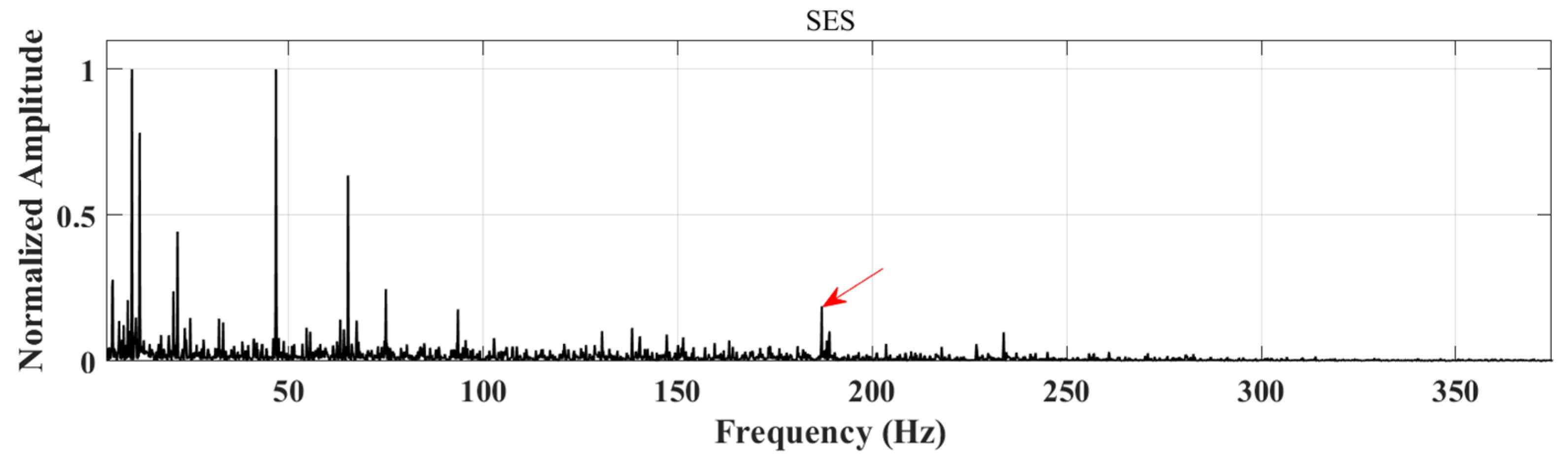
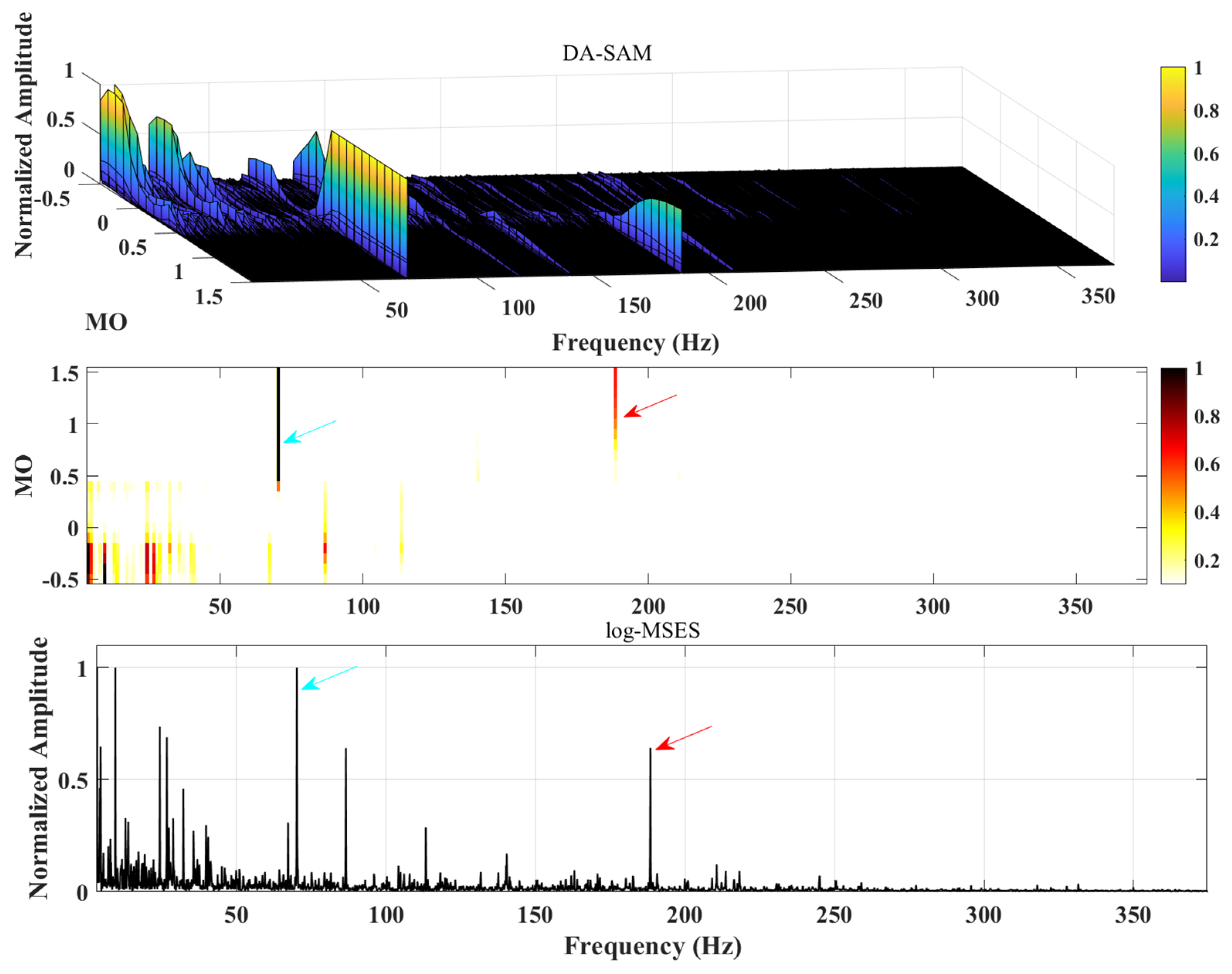
1. Introduction
Rolling bearings are widely used in rotating machinery and are one of the parts most prone to failure. Their working environment is relatively complex and harsh. Once a failure occurs, it will cause major safety accidents and even casualties. According to the statistics, in rotating machinery failure cases, 40–45% are caused by rolling bearing failure [
1]. Therefore, the importance of fault detection in rolling bearings is self-evident [
2]. It is precisely because of the complexity of its working conditions that the interference of various noises brings great difficulties to the detection of faults, and it is difficult to identify faults in the early stages; therefore, identifying weak faults under complex conditions is a top priority.
Among the currently known fault diagnosis techniques, the resonance demodulation technique [
3] is undoubtedly one of the most classic methods, also known as envelope analysis. The corresponding fault information can be obtained by band-pass filtering the resonance band with a high signal-to-noise ratio and then demodulating it using the Hilbert transform [
4,
5]. However, the selection of the resonance band is a relatively empirical process and is difficult in practical engineering applications. Therefore, in order to overcome this problem, Antoni et al. proposed fast spectral kurtosis [
6,
7,
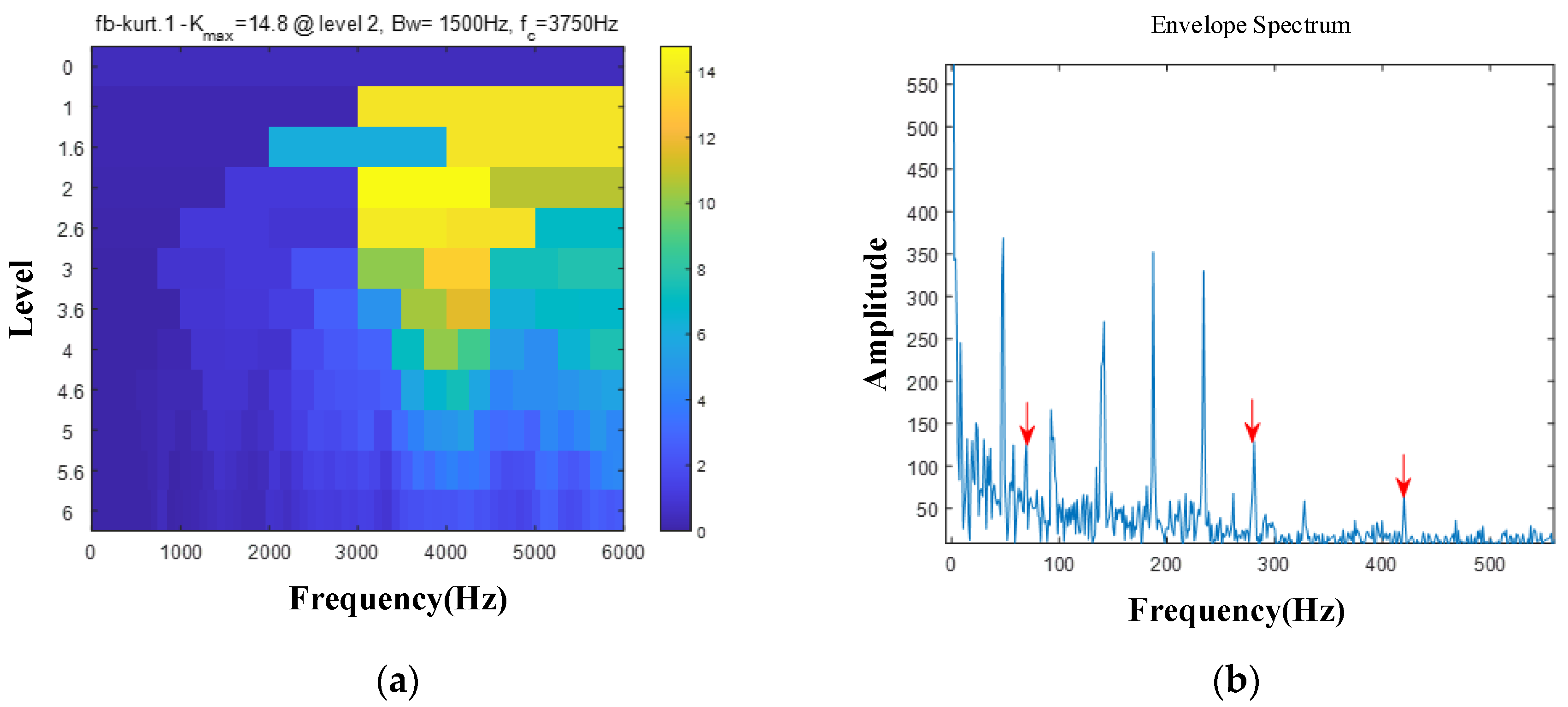
8], which calculates the kurtosis value of narrowband filtered signals, uses the dichotomy and trisection methods to divide the frequency band, and selects the frequency band with the largest kurtosis value for demodulation. However, with the deepening of research, the shortcomings of this method have gradually been exposed, and its kurtosis index is susceptible to noise and random pulses [
9]. In order to solve this problem, scholars have proposed a large number of improvement methods, such as Protrugram [
10], Infogram [
11], enhanced Kurtogram [
12], improved Kurtogram [
13] and Autogram [
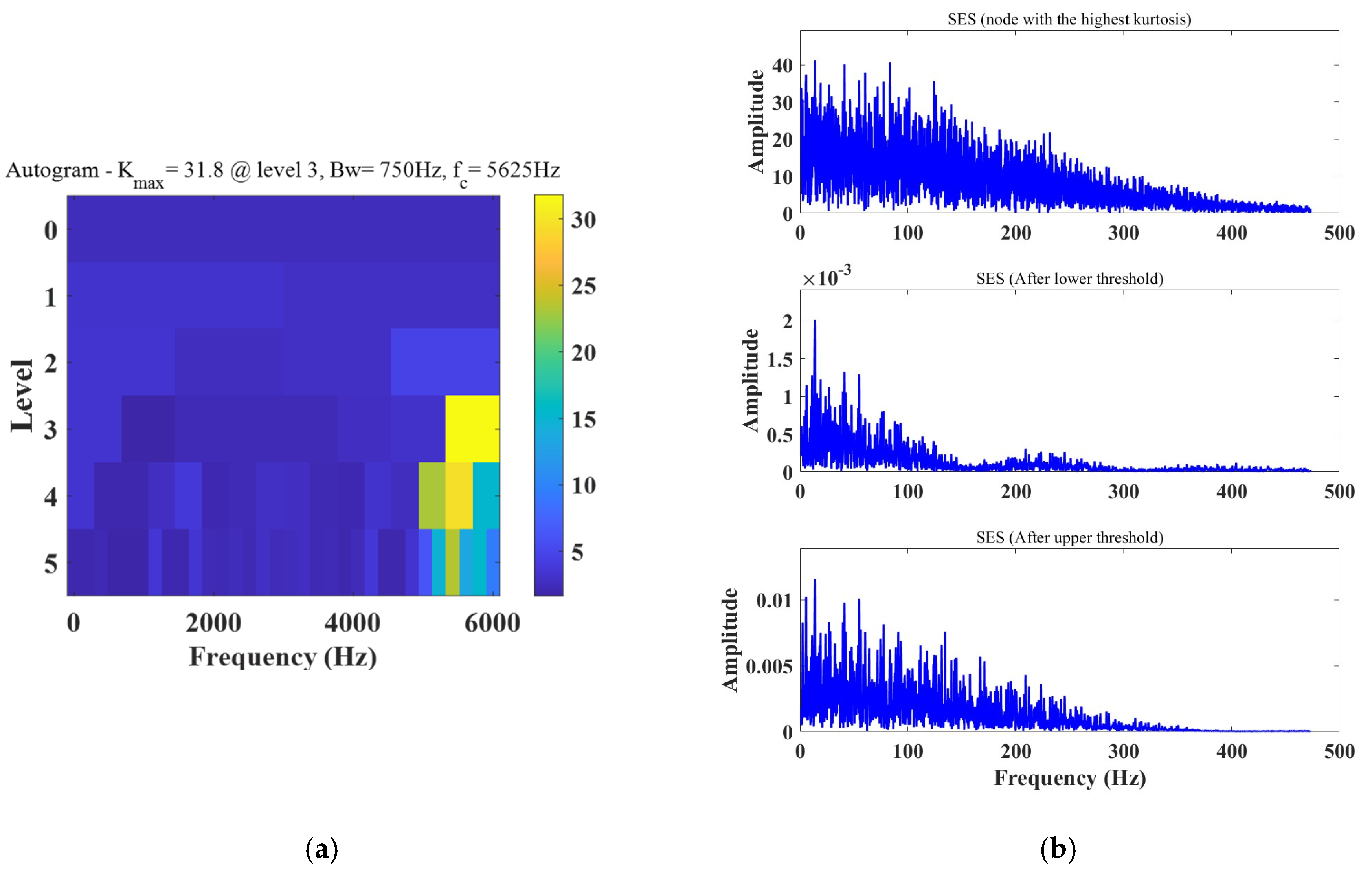
14], and Antoni et al. [
15] discussed a fast calculation method of Spectral Correlation (SC), all of which have achieved good results. In addition, other kurtosis methods based on the period index have been proposed [
16,
17,
18,
19,
20]. These methods can specify the frequency band in which the periodic component is located, and all suppress noise and irrelevant pulses to a certain extent. At present, finding the best demodulation band is still an arduous task. Various kurtosis diagram methods can only extract one best band, and much important information may be lost due to the impact signal generated by the fault. If the working conditions are complex, fault characteristic information cannot be effectively extracted.
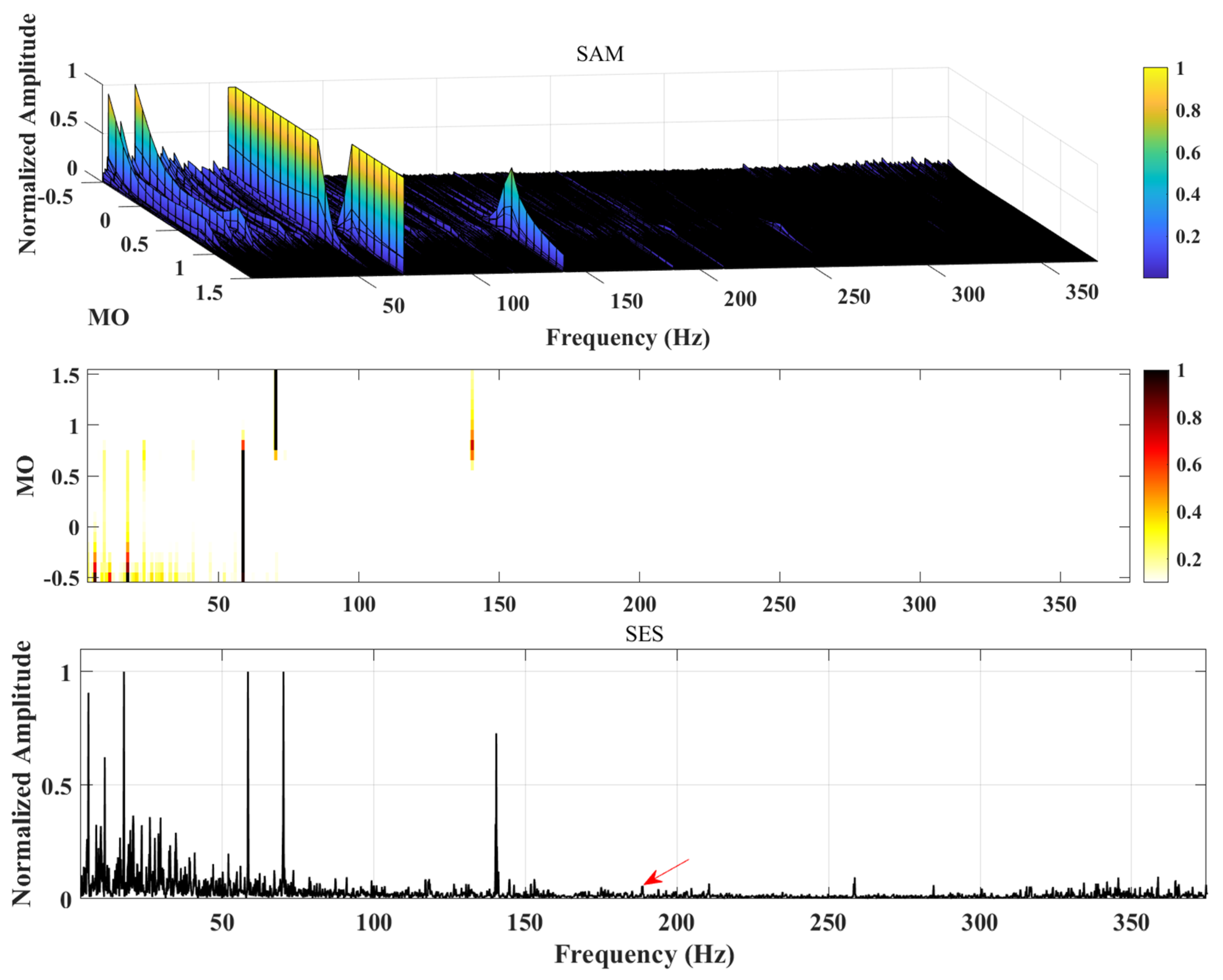
So, in order to solve the above problems, Moshrefzadeh [
21] proposed a new nonlinear filtering method, namely spectral amplitude modulation (Spectral Amplitude Modulation (SAM)), which performs Fourier transformation on the acquired vibration signal to obtain its amplitude spectrum and phase spectrum, and then assigns different weight indices to its phase spectrum (Magnitude order (MO)); the resulting edit spectrum is then inverse Fourier transformed to obtain a series of modified signals. Finally, the square spectrum of the modified signal is Fourier transformed to obtain the square envelope spectrum to view the fault characteristic information. SAM is not only efficient, but also simple to calculate, and has achieved remarkable results in the field of fault diagnosis. However, because it amplifies both fault components and interference components, its effectiveness is greatly reduced. In this regard, Qin et al. [
22] studied how to use the improved empirical wavelet transform (EWT) to diagnose complex weak faults in rolling bearings; Chen et al. [
23] studied a blind signal deconvolution method guided by generalized statistical indicators for fault diagnosis of railway vehicle axle box bearings; Shi et al. [
24] studied a new adaptive multi-parameter unsaturated bistable stochastic resonance (AMUBSR) system for weak signal enhancement in mechanical fault diagnosis; Han et al. [
25] studied a bearing fault diagnosis method based on clustering and frequency domain sparse representation; and Chen et al. [
26] studied the probability distribution and typical sparsity measures of the generalized envelope based on the Hilbert transform and their application in mechanical condition monitoring.
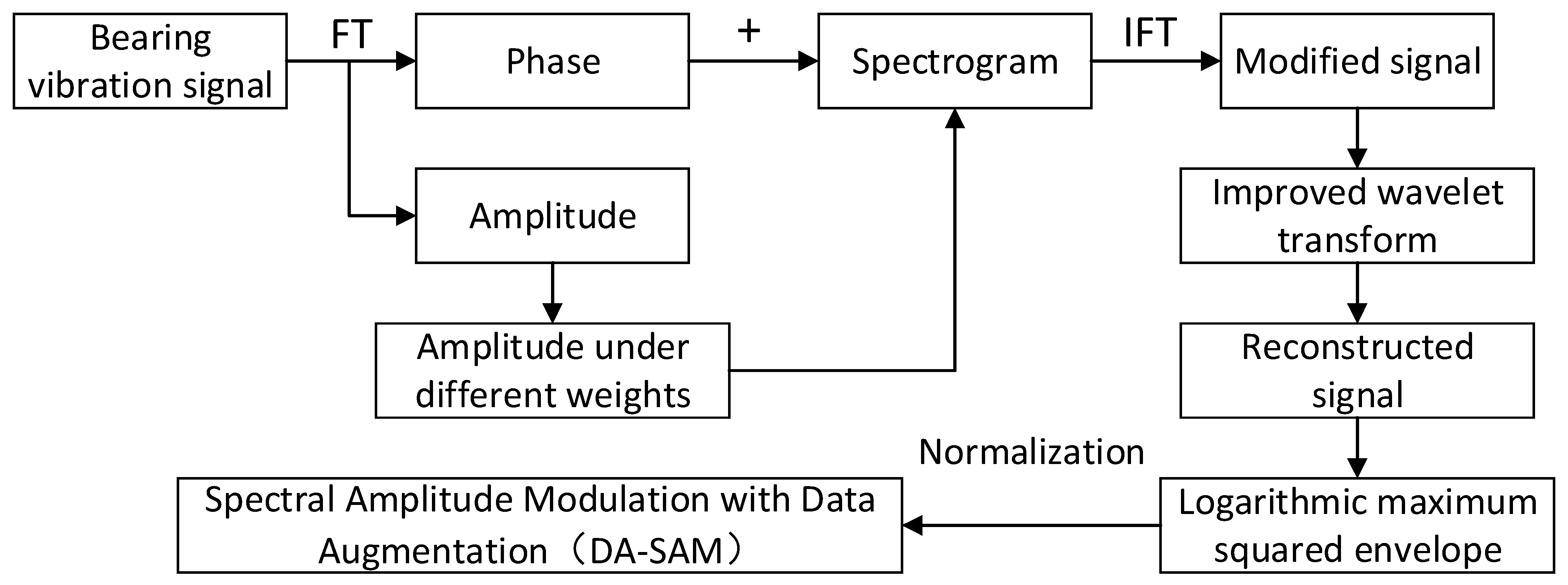
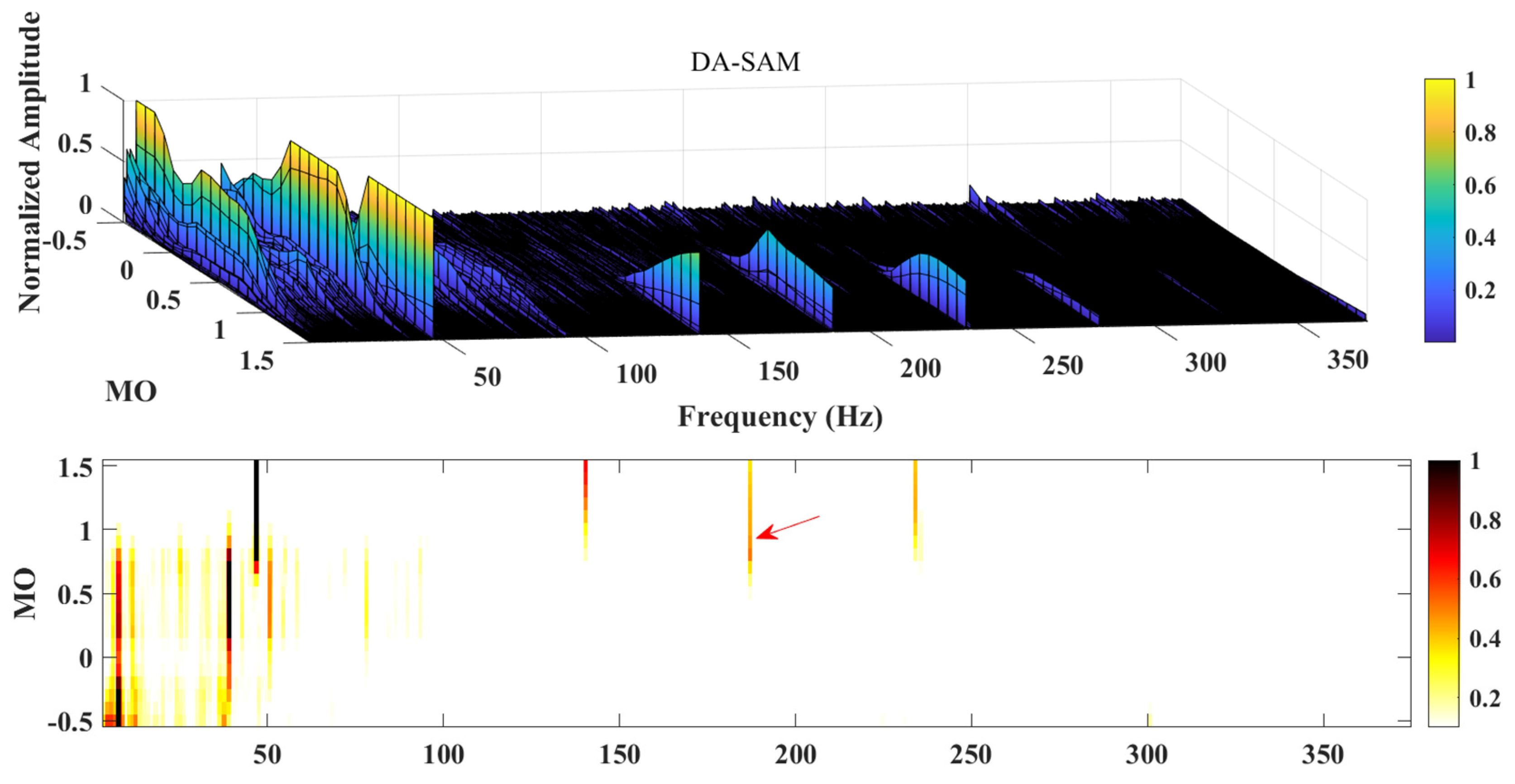
Although the above work has achieved excellent results, the application of SAM in practical projects still faces some challenges. First, while SAM enhances the weight of fault components, noise components with similar amplitudes also increase, which will lead to invalid SAM diagnosis results; second, in a strong interference environment, the interference component may be the dominant component of the signal. Although the signal has been modified, it is still possible to drown fault information in interference. Based on this, a data-enhanced spectral amplitude modulation method (DA-SAM) is proposed. In this research, first, the signal is transferred from the time domain to the frequency domain through Fourier transform to obtain the amplitude and phase, and the amplitude is assigned different weight indices to obtain the modified amplitude; then, the obtained modified amplitude is combined with its original phase to obtain the modified signal, and the improved wavelet transform is used to further reduce noise and reconstruct; finally, its logarithmic maximum square envelope spectrum is generated to complete the DA-SAM diagnosis. The feasibility and superiority of this study compared with some of the classic methods are verified.
2. Spectral Amplitude Modulation
SAM, as a nonlinear filtering method [
27], extracts frequency components of different energies in the signal by setting different MOs and does not need to input any parameters in advance, thereby realizing bearing fault diagnosis.
First, define
as the original input signal, transform the vibration signal from the time domain to the frequency domain through Fourier transform, and obtain its phase Φ
and amplitude
, as follows:
(1) where
is the imaginary unit and
FT is the Fourier transform. The phase is unchanged and different weight indices are assigned to the amplitude spectrum to adjust the amplitude in different frequency bands; then, the original phase is combined with the modulated amplitude to obtain the edited spectrum, and finally inverse Fourier transform is performed to obtain the corrected signal. This nonlinear filtering process is as follows:
In Equation (2),
represents the corrected signal under different weight exponents, and
IFT stands for the inverse Fourier transform. The recommended range for
is
with a step size of 0.1. The advantage of this approach is that it allows for fault diagnosis in different situations by adjusting the value of
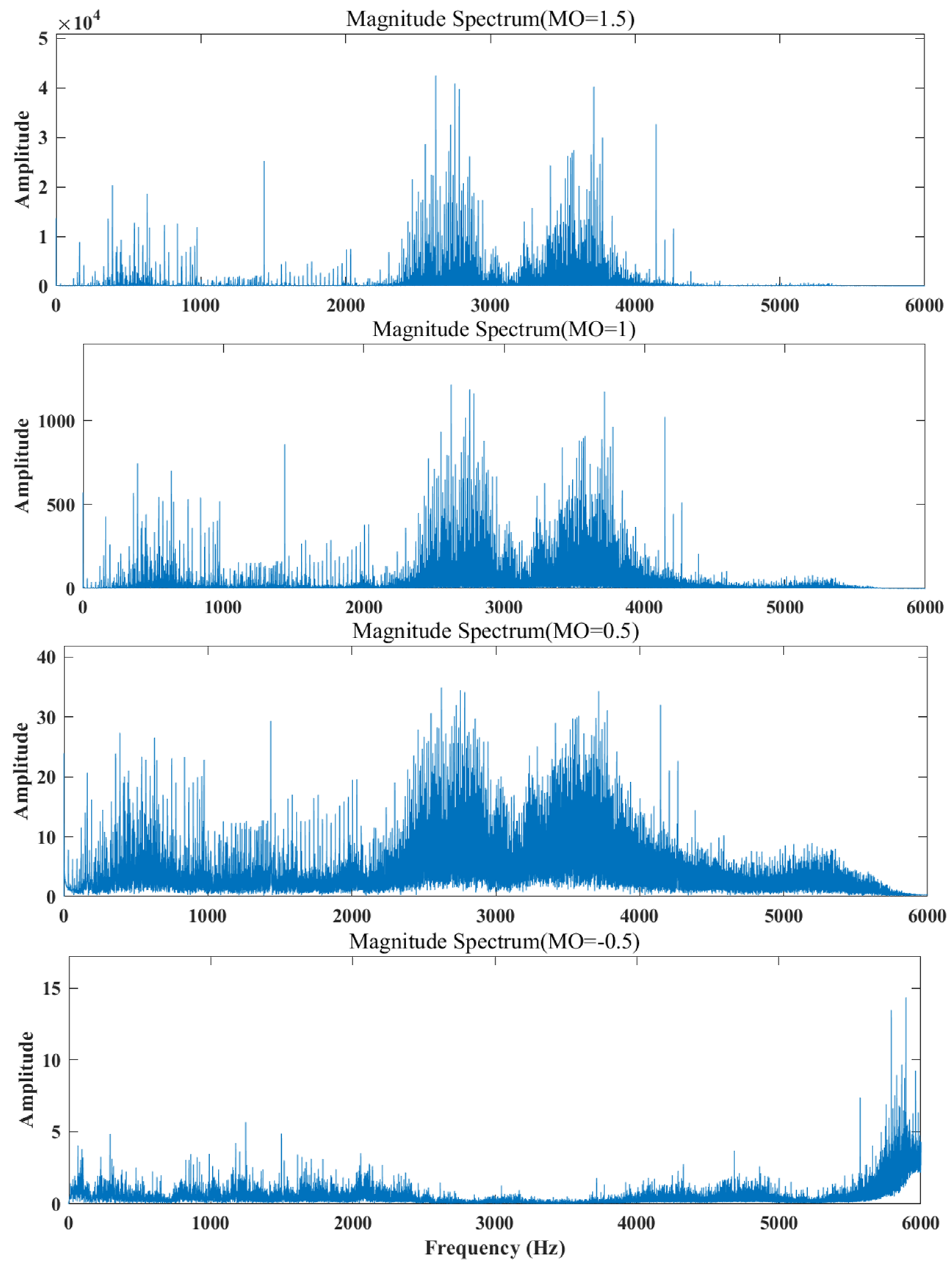
, effectively shielding interference components. The effects of different
values on the signal can be categorized into three main types: When
, the parts of the original signal with relatively small amplitudes are amplified, which is most suitable when the noise interference is low. When
, this range weakens the components with larger amplitudes while enhancing those with smaller amplitudes, while still retaining the relative levels of all components. When
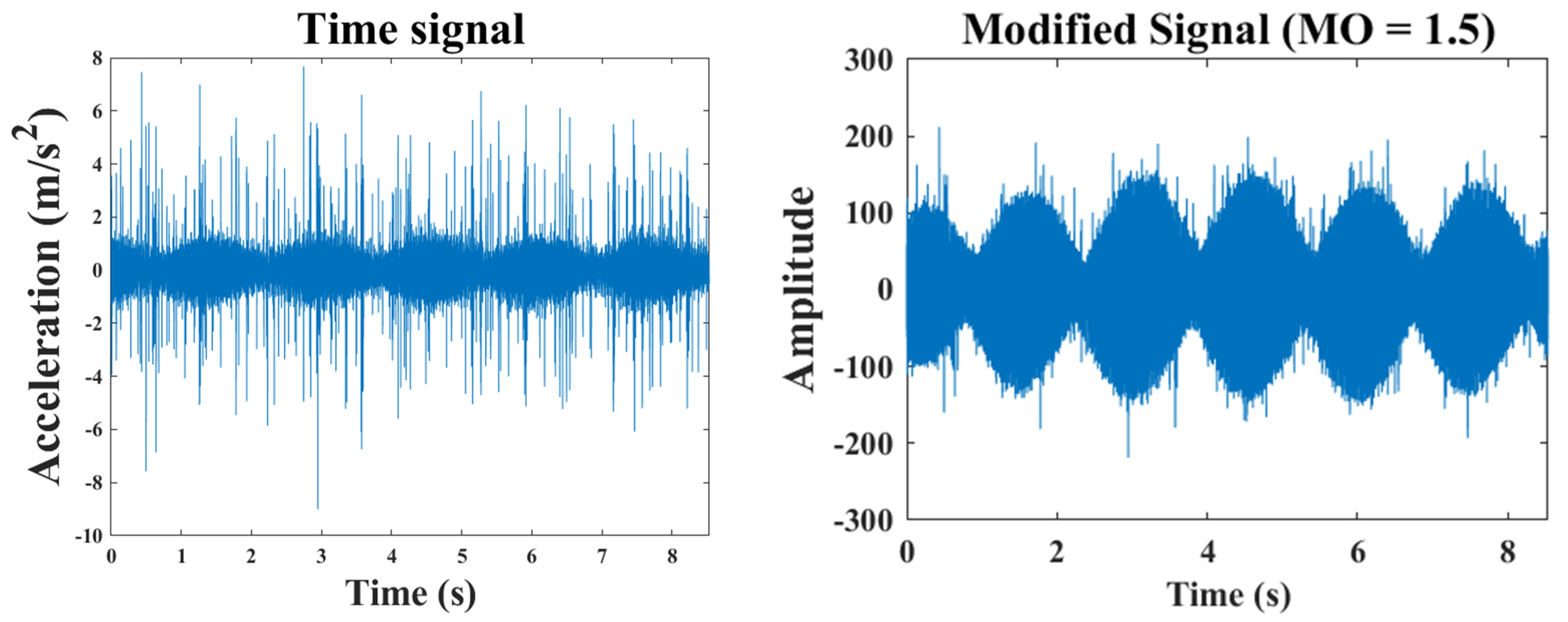
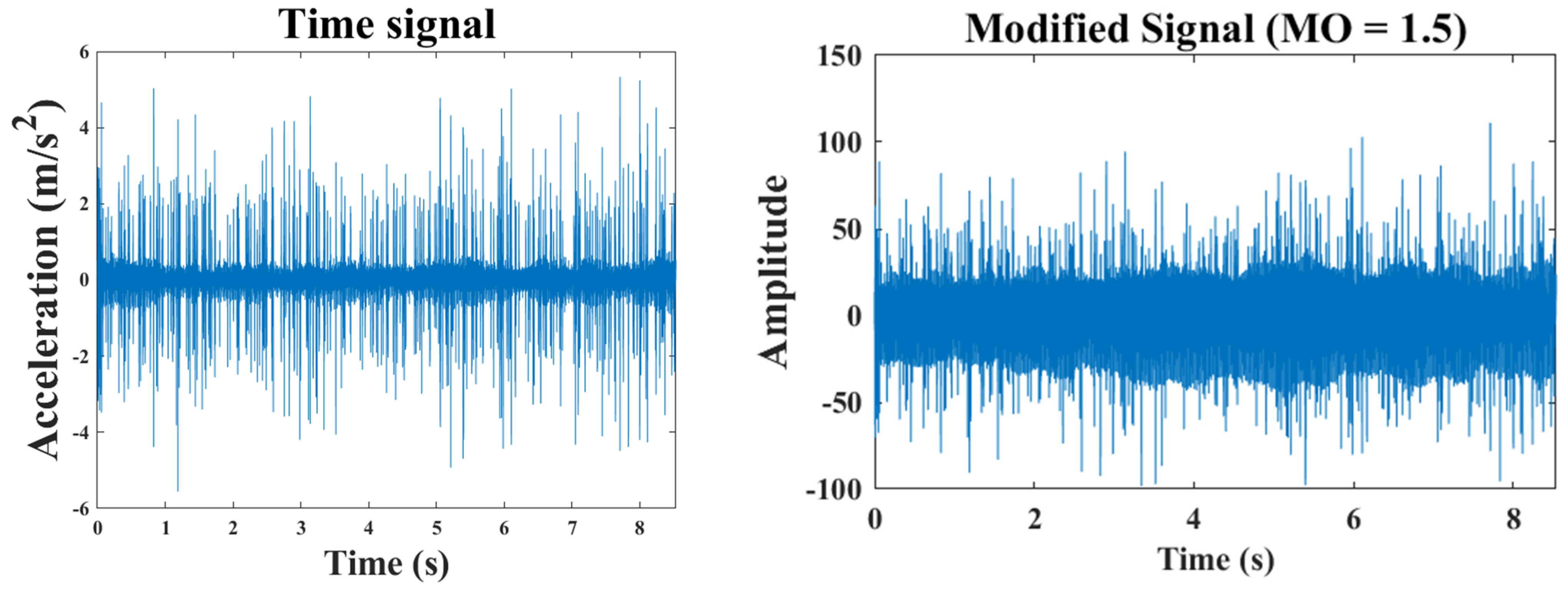
, this range is most suitable for cases with significant amplitude disturbances. The effects are illustrated in
Figure 1.
After obtaining the corrected signal, the Hilbert transform is then used to calculate its analytic signal, as shown in the following equation:
In Equation (3),
represents the analytic signal,
denotes the Hilbert transform, and finally, the Fourier transform is performed to obtain the squared envelope spectrum, as shown in the following equation:
4. Enhanced Spectral Amplitude Modulation Method
The method mentioned in this article solves the above shortcomings and improves the SAM method. It processes the modified signal by replacing FT with IWT. IWT can provide time–frequency-localized information about the signal, which means that it can reveal the changes in frequency components in the signal with time, making it very suitable for analyzing non-stationary signals. By selecting different wavelet bases and adjusting the scale of the transformation, IWT can adapt to different types of signals and data, making its application in different fields more flexible and extensive. Moreover, IWT performs well in denoising. It can effectively distinguish between abrupt parts and noise in the signal, thereby realizing the removal of non-stationary signals. Although its computational complexity may be higher than that of Fourier transform, it is implemented through fast algorithms, making it of high practical value in practical applications.
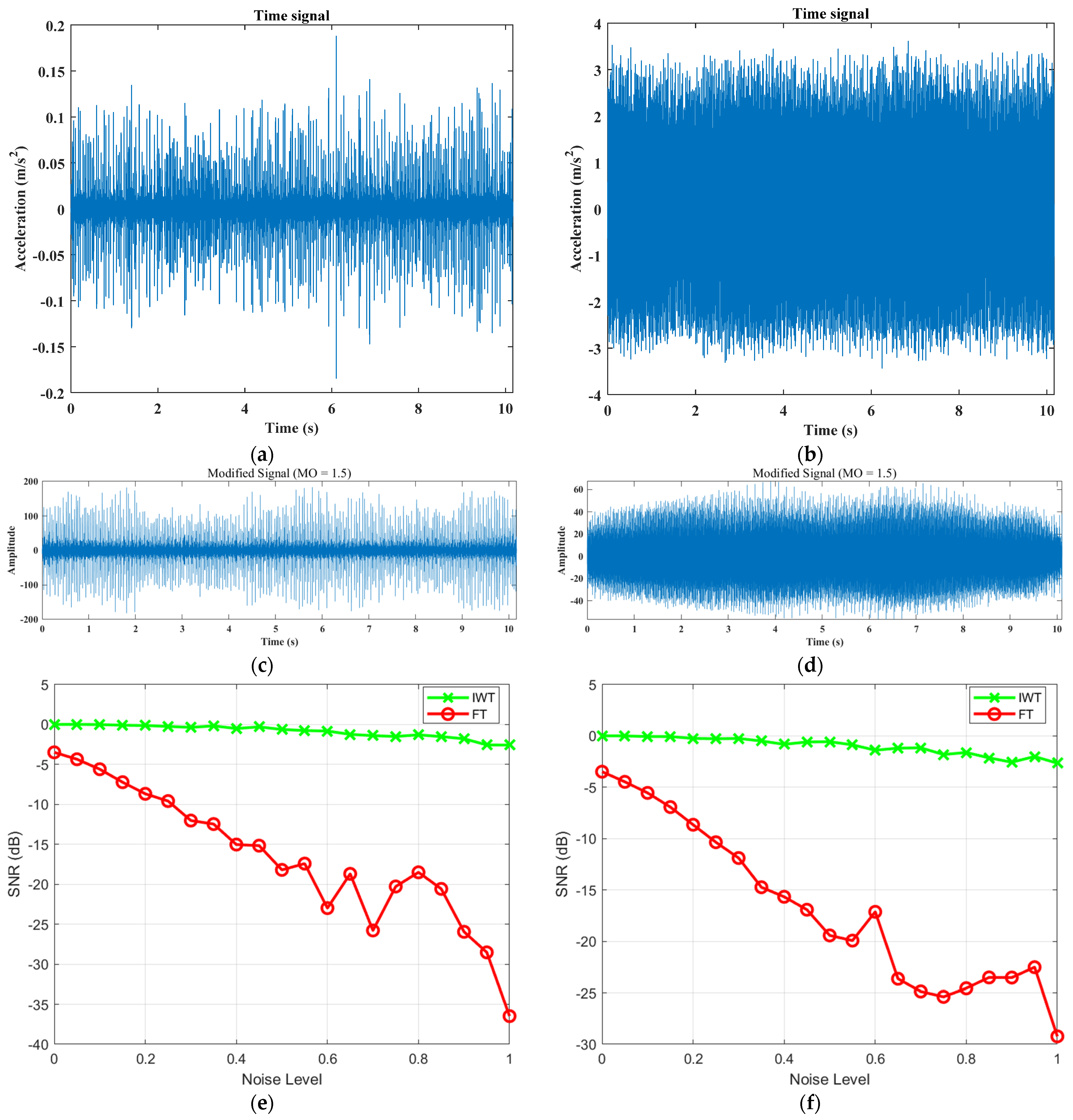
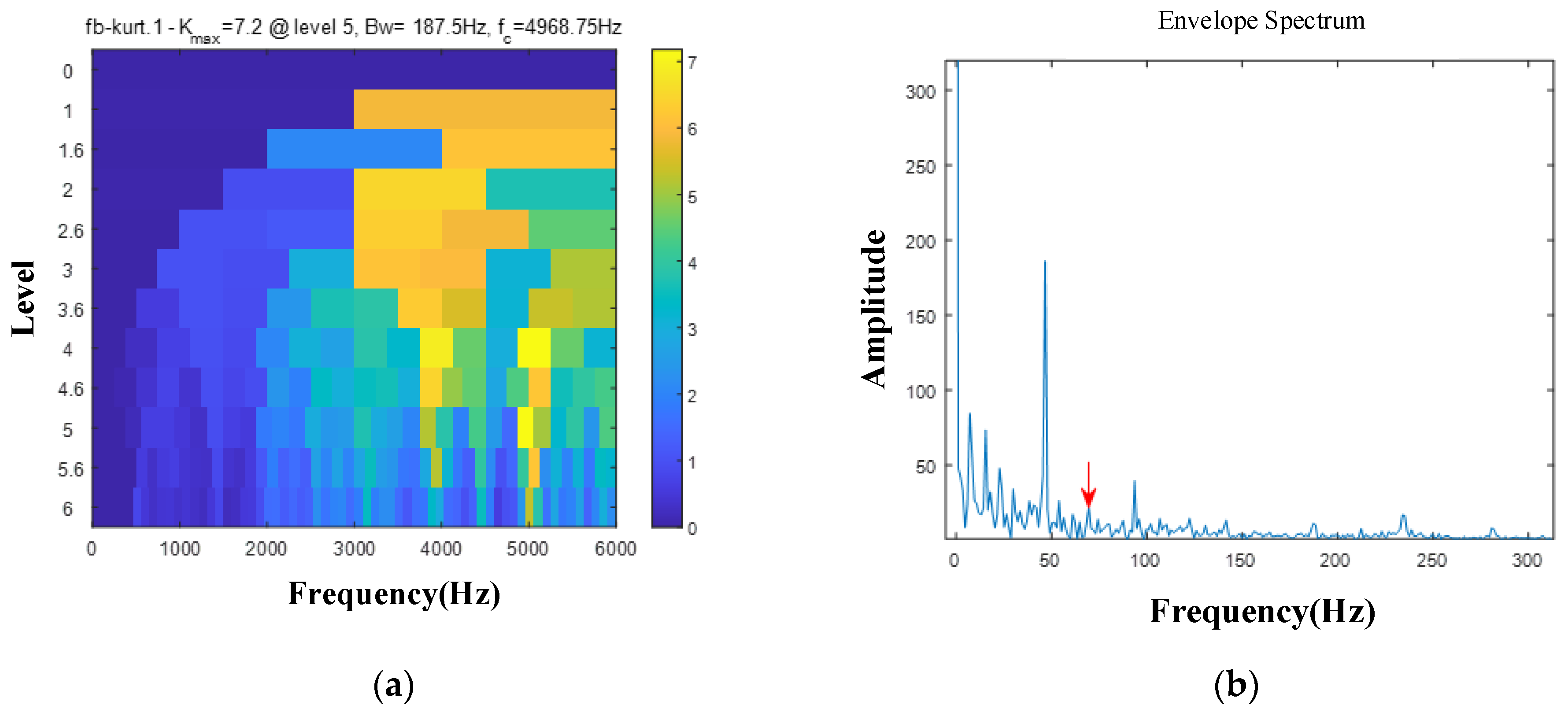
In order to further verify the superiority of IWT over FT, the signal-to-noise ratio (SNR) obtained between the two was compared with the increasing noise intensity. The noise intensity is set to [0, 1] and the step size is 0.05. Two sections of corrected fault signals with strong noise are used for testing, as shown in
Figure 2c,d. In the figure, (e) and (f) show a comparison of the signal-to-noise ratio of the two signals processed by FT and IWT, respectively. It can clearly be seen that the signal-to-noise ratio after IWT processing is significantly higher than that of FT and is stable. The above results once again prove the feasibility of the proposed method.
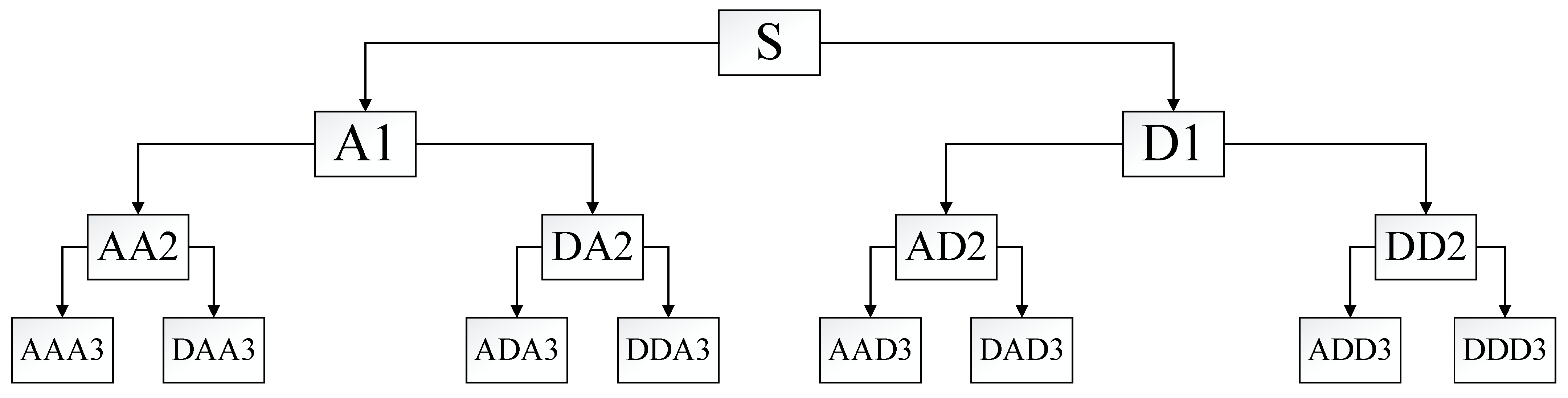
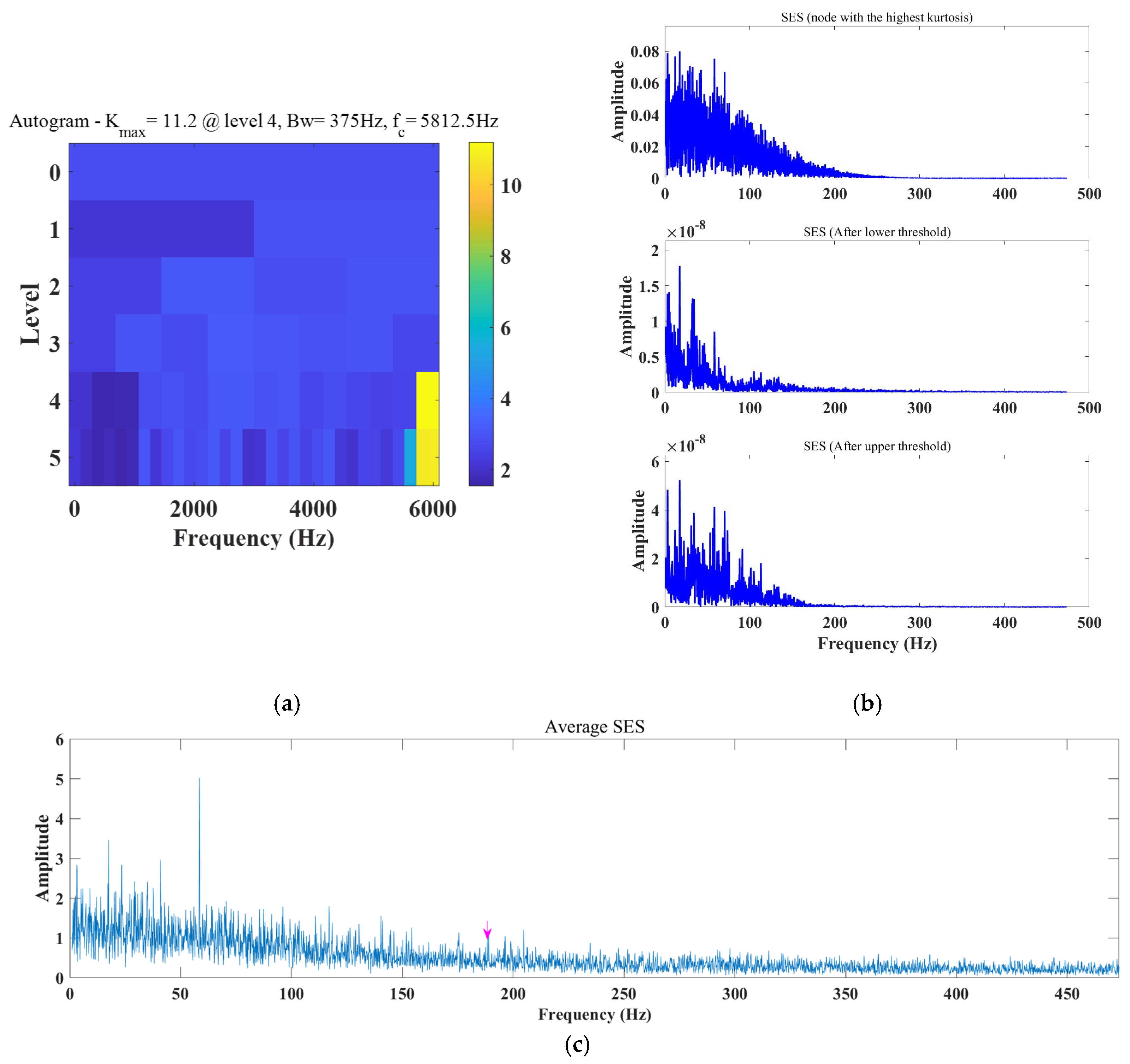
Therefore, this paper performs improved wavelet transform [
28] processing on the square envelope of the corrected signal, and uses a tree structure embedding algorithm to decompose and calculate the noisy signal layer by layer, as shown in
Figure 3 (where S is the original signal, and A1 and D1 are high-frequency and low-frequency signals, respectively. Subsequently, the decomposed frequency band will be divided into high and low halves to match with the signal spectrum, thereby obtaining a more refined decomposition). The noise signal is decomposed by selecting the appropriate number of layers and wavelet bases, and then selecting the appropriate threshold to quantify each layer system; finally, the denoised signal is obtained by reconstructing the wavelet coefficients.
The expression for the improved wavelet threshold function is as follows:
In (5),
represents the wavelet coefficients of the vibration signal at the
level of decomposition, while
is the threshold for the wavelet coefficients at each level. When
, in order to simulate a real environment, a decaying sine function is used for denoising; when
, the noise is relatively large, so an exponential denoising method is employed.
is the adjustment factor for the threshold function, obtained by calculating the mean and standard deviation of the wavelet coefficients, and then determining the range by adding or subtracting a multiple of the standard deviation from the mean, with a range of
, and
is a constant equal to 0.02. In Equation (6),
is the average value of the wavelet coefficients,
is the standard deviation of the wavelet coefficients, and
is a constant used to determine how many standard deviations deviate from the average value to determine the range of
.
Let
be the vibration signal and perform wavelet decomposition, then the threshold calculation formula [
29] corresponding to each layer of wavelet coefficients is:
In (7),
represents the standard deviation of the noise for the
wavelet coefficient;
is the length of the signal. The definition [
30] of
is as follows:
In (8), the threshold decreases as the decomposition scale increases, which aligns with the characteristic that the wavelet coefficients of the vibration signal diminish with larger decomposition scales, resulting in improved denoising effects.
Next, the modified signal
is reconstructed. First, select an appropriate wavelet basis function
and scale function
, which define the characteristics of the improved wavelet transform. Secondly, at each scale
, the signal
is decomposed into approximation coefficients
and detail coefficients
:
where
is the translation coefficient;
and
are defined as follows:
Subsequently, signal
is reconstructed from the IWT coefficients:
is the maximum scale of decomposition, and is the reconstructed modified signal.
Finally, the square envelope spectrum of the reconstructed signal is obtained, as shown in the following equation:
Since the human eye is more sensitive to changes on the logarithmic scale, in order to more clearly display the energy distribution on different frequency components, the obtained square envelope is subjected to further processing to obtain the logarithmic maximum square envelope spectrum:
First, obtain the frequency domain representation by performing a fast Fourier transform (FFT) on the square envelope signal:
where
represents the square envelope signal and
represents the FFT.
Then, take the logarithm of the FFT result to obtain the logarithmic square envelope spectrum:
where
represents the log-squared envelope spectrum.
Finally, find the maximum value in the log-squared envelope spectrum, and the corresponding frequency is the maximum log-squared envelope spectrum.
where
represents the maximum log-squared envelope spectrum.
After the above processing, not only are the characteristics of the fault signal highlighted and the fault feature information enhanced, but the periodic impact components are also further amplified, significantly improving the resolution of the modulation results. Moreover, the proposed method retains the advantages of the original method, which is simple and efficient, making it applicable for bearing fault diagnosis in high-noise environments. The specific process of the DA-SAM method is as follows:
Step 1: Perform a Fourier transform on the bearing vibration signal to obtain the magnitude and phase of the original signal.
Step 2: Keep the phase information unchanged and assign different weight exponents to the magnitude to obtain , where .
Step 3: Combine the spectral amplitudes under different modes () with the original phase to obtain the edited spectrum. Then, an inverse Fourier transform is performed on this edited spectrum to obtain a series of corrected signals.
Step 4: Process the square envelope of the modified signal with improved wavelet transform to further reduce the noise interference.
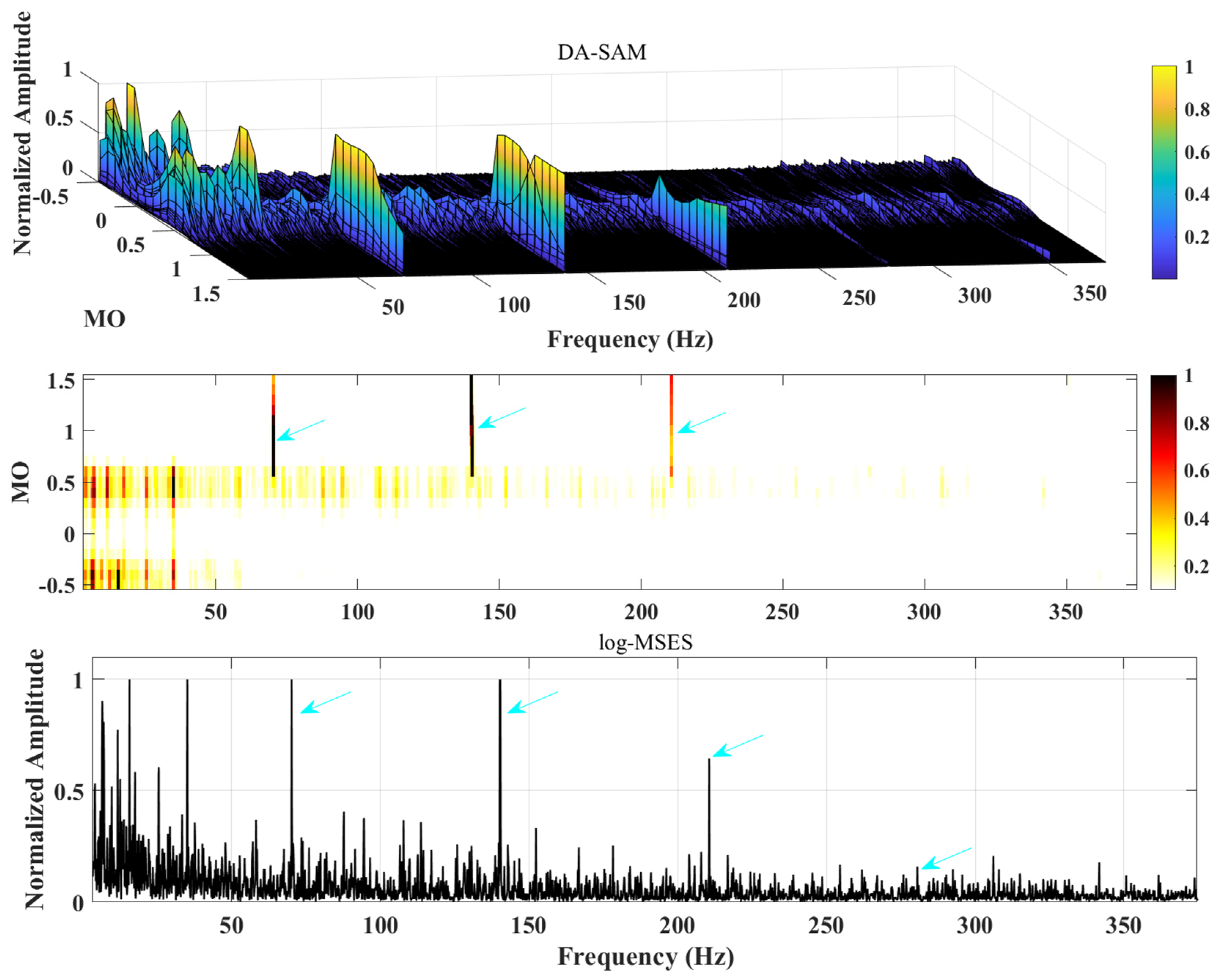
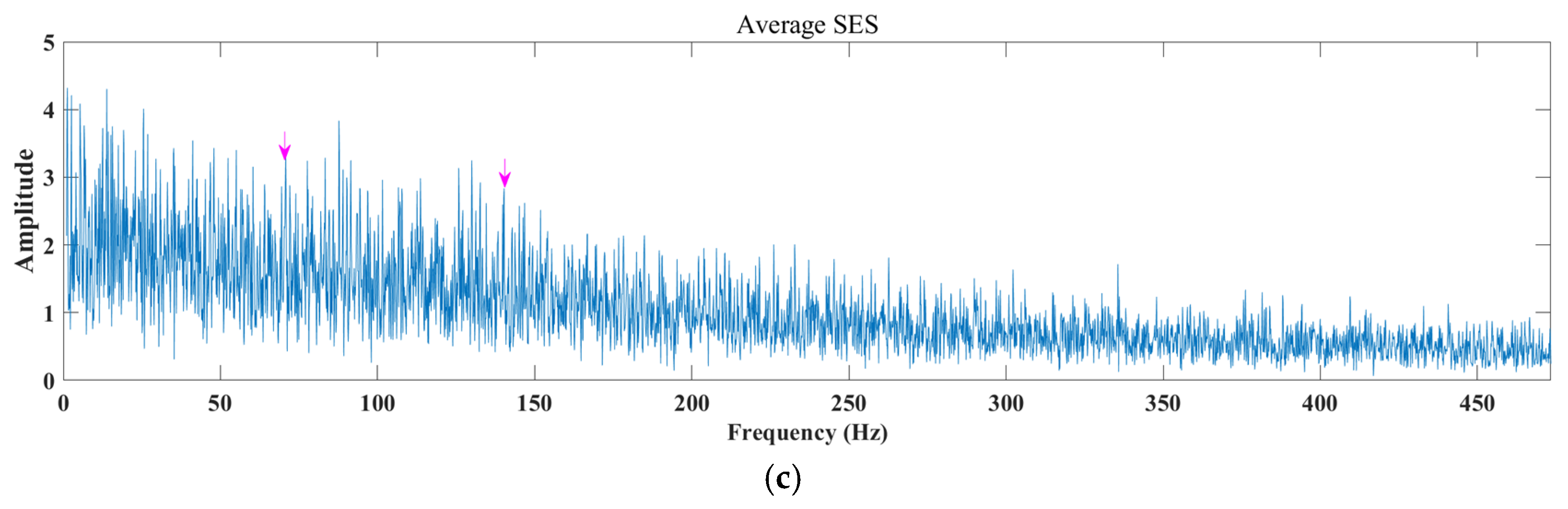
Step 5: Calculate the logarithmic maximum square envelope spectrum of the noise-reduced signal, perform normalization processing (eliminate the influence of signal amplitude), and obtain data-enhanced spectral amplitude modulation; calculate the fault frequency through the given data to complete the diagnosis.
In this study, it is necessary to explain the reasons for the normalization process. First, normalization can eliminate dimensional differences between different features and ensure that the data are within the same scale range, which is crucial for the comparison and analysis of features; second, the normalized data can improve the adaptability of the algorithm, allowing the algorithm to effectively process data of different magnitudes; third, in complex interference environments, normalization can help reduce irrelevant random noise interference generated by the nonlinear filtering process, thereby improving the identification effect of fault features; fourth, normalization can make fault features more obvious in the data, helping to highlight fault-related components and improve the accuracy of fault diagnosis. To sum up, normalization processing is crucial to the research in this paper. If normalization is not carried out, dimensional differences in different features may cause some features to dominate the analysis, thereby concealing different important fault information and even causing the algorithm’s performance to degrade; and under different exponential weights, unnormalized data may cause a large number of interference frequency components to be amplified, thereby reducing the effectiveness of identifying fault features, and may also lead to deviations in the feature extraction process and affect subsequent fault diagnosis and analysis.