State-of-the-Art Flocking Strategies for the Collective Motion of Multi-Robots
Abstract
1. Introduction
1.1. Related Surveys
1.2. Motivation
1.3. Methodology and Paper Contributions
- Laws of flocking and swarm or cluster flocking are evaluated.
- Flocking control methods founded on schemes, structures, and classic and state-of-the-art strategies are aggregated and reviewed.
- Applications of multi-robot systems with flocking control and their significance in various domains are explored.
- The challenges of implementing flocking control and multi-robot systems are identified.
- The problem statement of flocking is defined and a solution to the flocking problem is presented in terms of formation control, obstacle avoidance, and approaching targets.
1.4. Paper Organization
2. Preliminaries of Flocking Control
2.1. Laws of Flocking
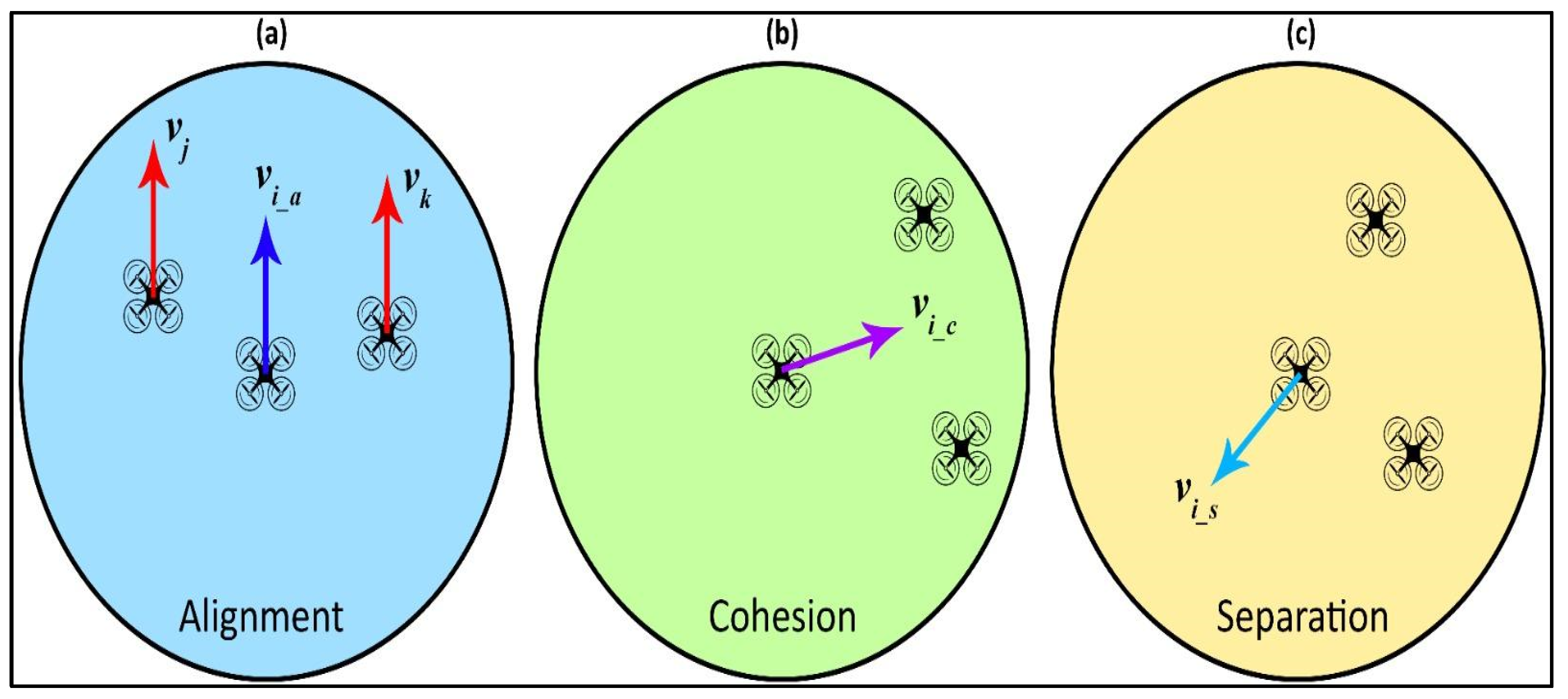
2.2. Cluster Flocking and Swarming
2.3. Flocking Phenomenon in Multi-Robot Systems
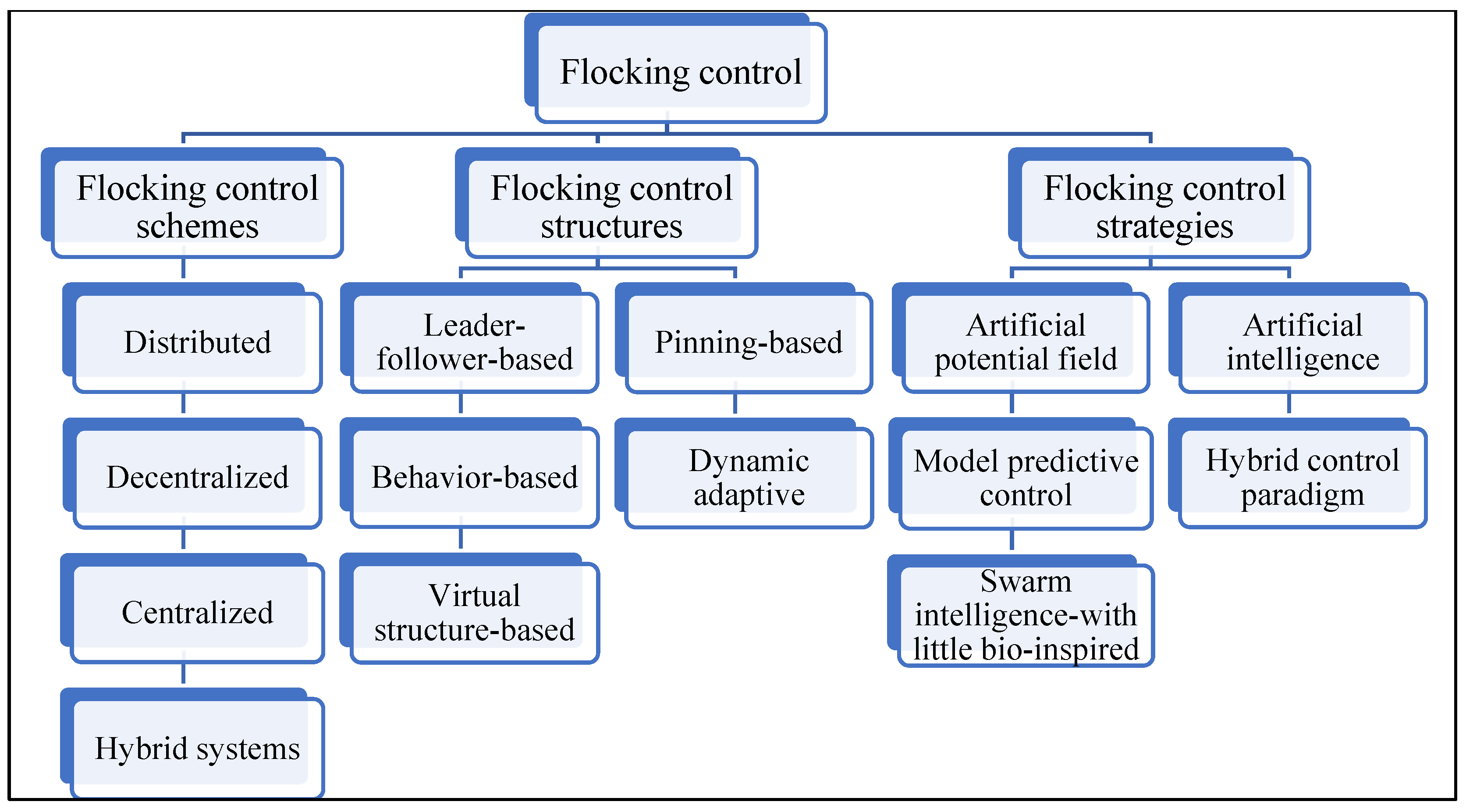
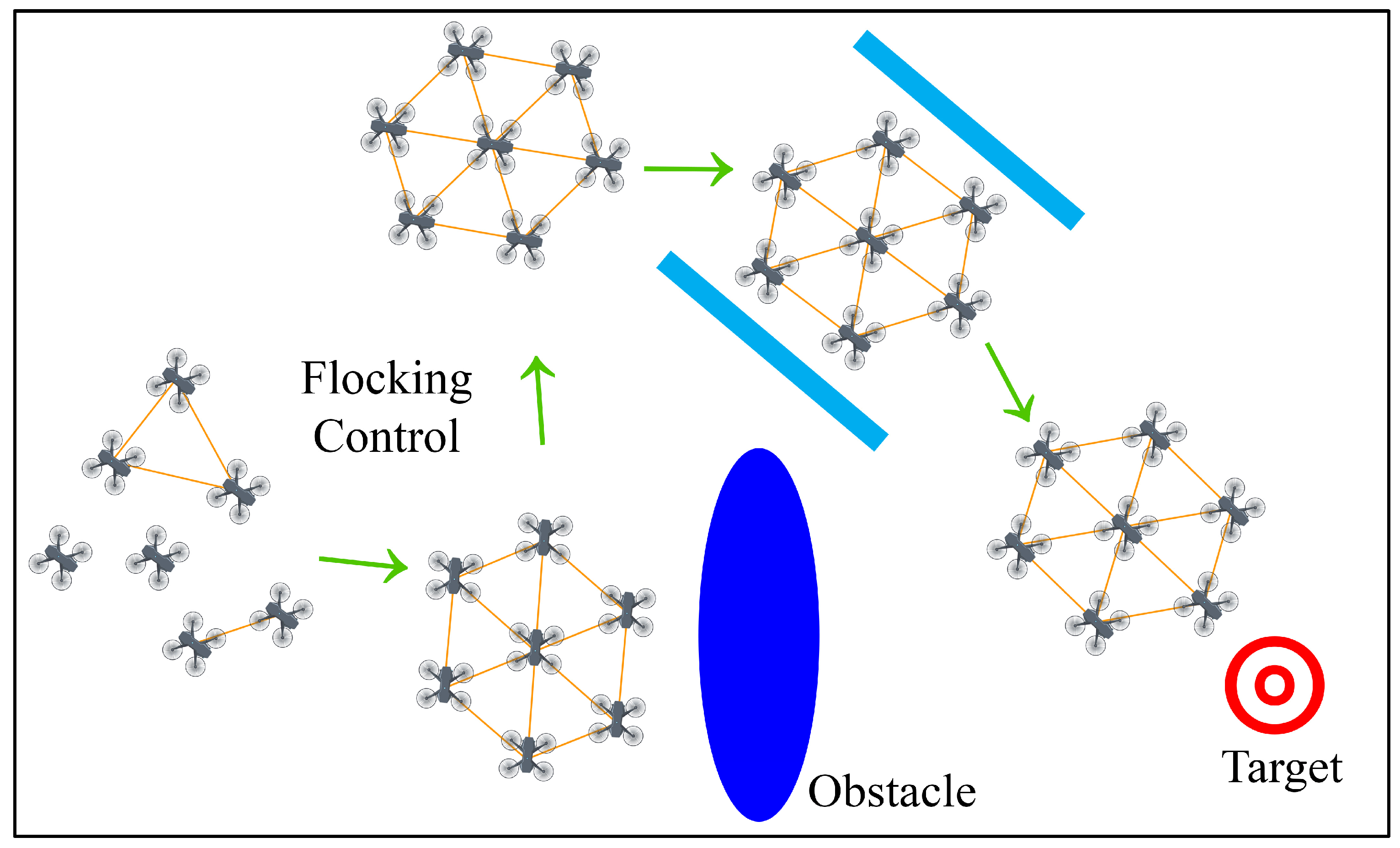
3. Flocking Control
3.1. Flocking Control Schemes
3.2. Flocking Control Structures
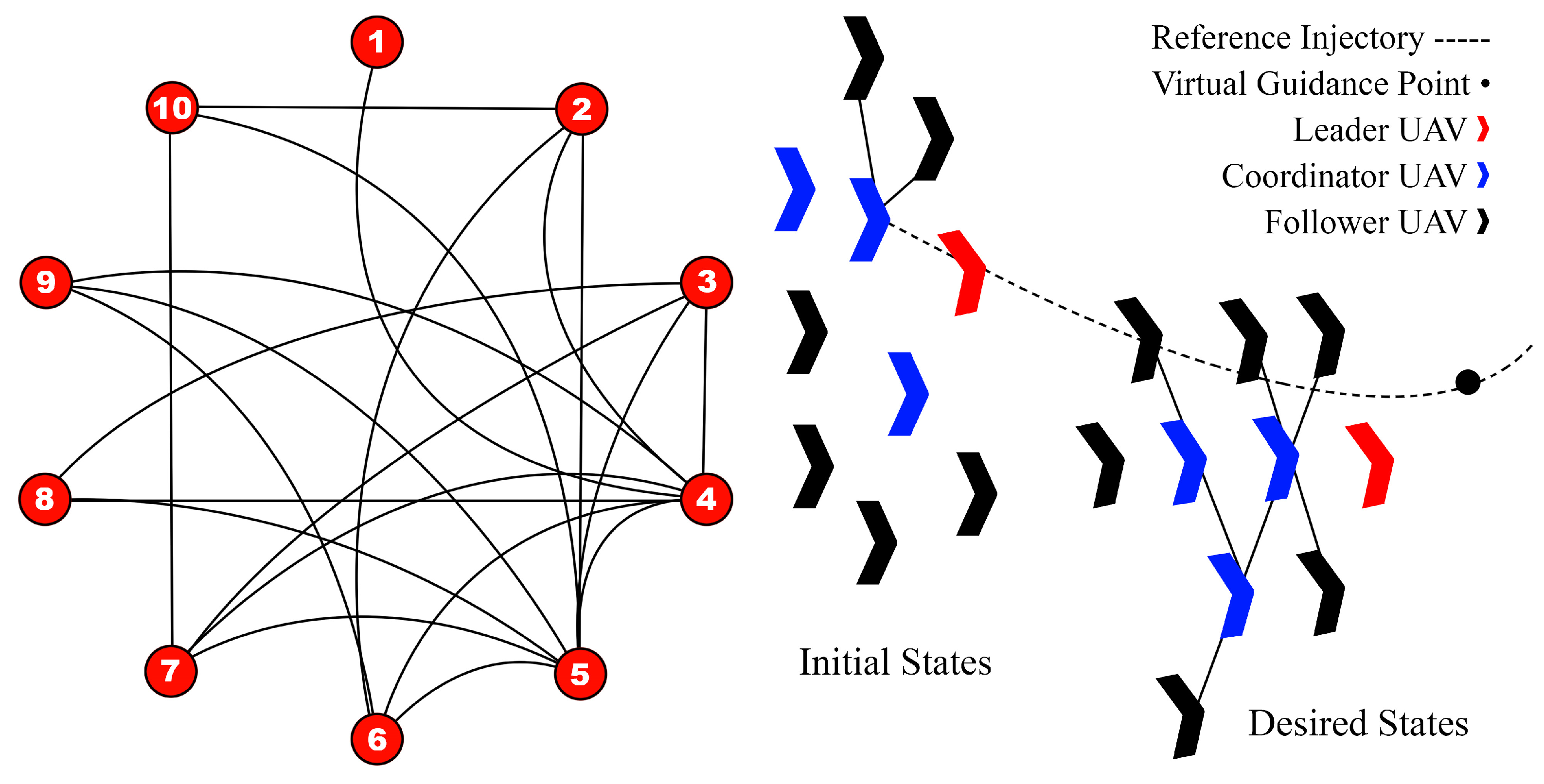
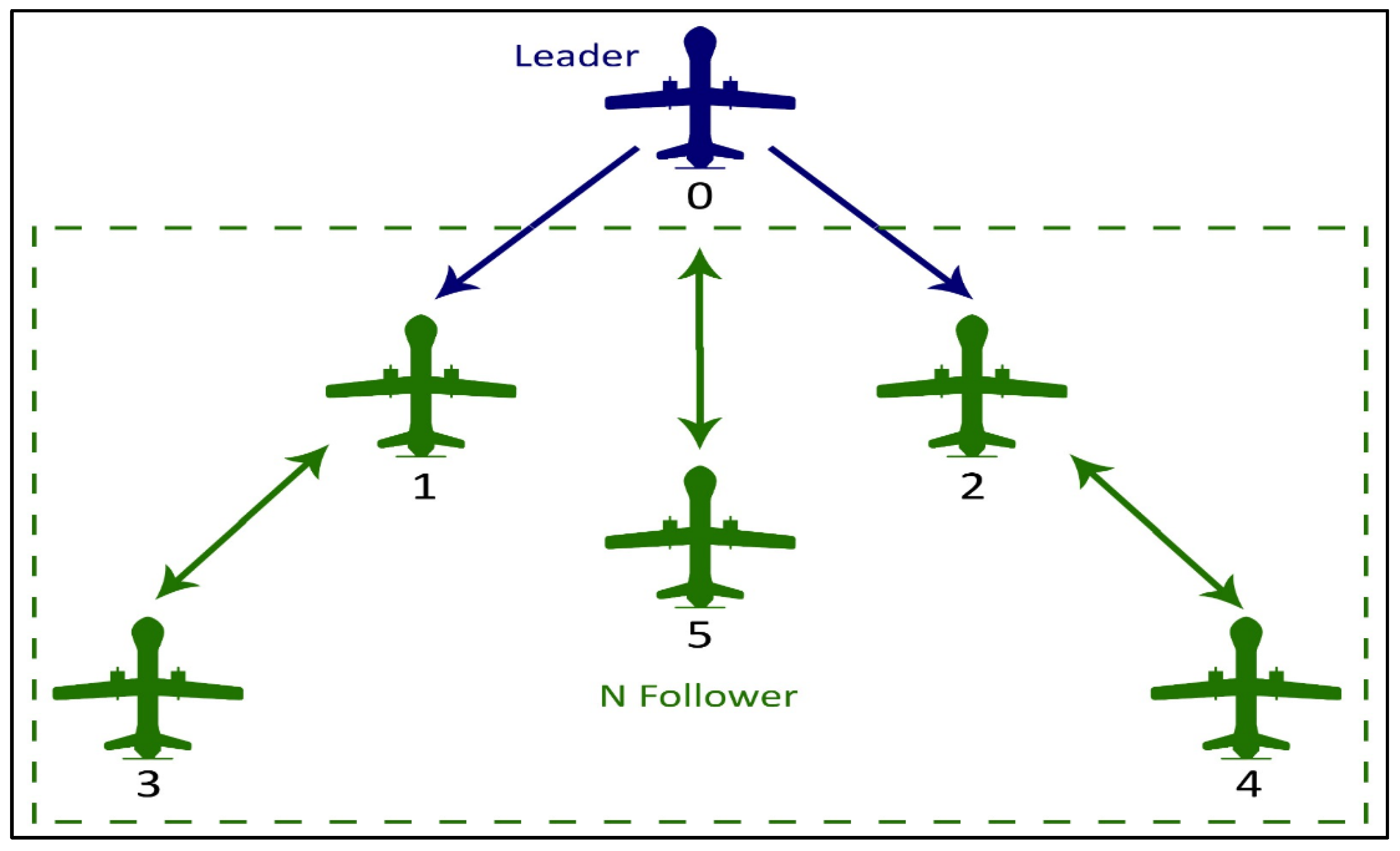
3.2.1. Leader–Follower-Based Flocking Structure
3.2.2. Behavior-Based Flocking Structure
3.2.3. Virtual Structure-Based Flocking Design
3.2.4. Pinning-Based Flocking Structure
3.2.5. Dynamic Adaptive Flocking Structure
3.3. Flocking Control Strategies
3.3.1. Artificial Potential Field Method
3.3.2. Model Predictive Control
3.3.3. Swarm Intelligence with Little Bio-Inspired Approaches
3.3.4. Artificial Intelligence
3.3.5. Hybrid Control Paradigms
| Reference | Multi-Agent System | Focus | Flocking Scheme | Flocking Structure and Strategy | Advantages | Limitations |
|---|---|---|---|---|---|---|
| De Sá and Neto [7] | UAVs | Collision avoidance | Centralized and decentralized | Virtual structure with leader |
|
|
| Konda et al. [31] | Multi-robot flocks | Predator avoidance | Distributed | FA-MARL |
|
|
| Ban et al. [32] | Robot swarm | Collision and obstacle avoidance | Distributed | Self-organized flocking with a leader–follower approach |
|
|
| Beaver and Malikopoulos [33] | Multi-robot cluster | Energy-reducing cluster flocking | Decentralized | Behavior-based and constraint-driven paradigm |
|
|
| Zheng et al. [34] | Mobile robot flocks | Flocking with privacy | Decentralized | GA-data-driven adversarial discriminator and leader–follower structure |
|
|
| Fu et al. [44] | UAV swarm | Formation maintenance and reconstruction | Distributed | Virtual leader and APF |
|
|
| Lin et al. [46] | AUV flock-based UWNs | Path planning | Centralized | APF |
|
|
| Van Der Helm et al. [51] | MAV swarms | Indoor leader–follower flight | Distributed | Leader–follower control |
|
|
| Li et al. [53] | Multi-agent flocks | Communication barriers affecting cohesion | Distributed | Leader–follower structure and local feedback mechanism |
|
|
| Wang et al. [54] | UAV flock | Obstacle avoidance | Distributed | Boid model behavior-based approach, improved APF, and detect velocity obstacles approach |
|
|
| Soma et al. [55] | Robot swarm | Shape formation and maintenance | Decentralized | Wall-following behavior-based and leader–follower approach |
|
|
| Bautista and de Marina [56] | Robot swarm | Circular formation | Distributed | Tornado schooling fish behavior-based approach |
|
|
| Kang et al. [57] | UAV swarm | Optimal configuration with intricate maneuver execution | Distributed | Reynold principle and virtual APF-based leader control |
|
|
| Liu et al. [59] | Multi-agent flocks | Optimal selection of pinning nodes | Distributed | Pinning control with virtual leader |
|
|
| Ren et al. [61] | Multi-agent system | Collision avoidance | - | Virtual leader–follower Cucker–Smale model with pinning control |
|
|
| Qu et al. [94] | Multi-agent flocks | Flock-guidance | Distributed | Fuzzy-RL and leader–follower structure |
|
|
4. Applications of Flocking Robots
4.1. Military Discipline
4.2. Agricultural Field
4.3. Manufacturing Sector
4.4. Logistics and Transportation Area
4.5. Healthcare and Medicine Domain
5. Challenges Influencing Robot Flocking
5.1. Challenges of Flocking-Based Formation
5.2. Dilemmas of Mobility Aspects
5.3. Lack of Safe, Reliable, and Long-Range Communication
5.4. Issues of Task Allocation and Localization
5.5. Unreliability for Real-World Applications
6. Flocking Problems and Solutions
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hénard, A.; Rivière, J.; Peillard, E.; Kubicki, S.; Coppin, G. A unifying method-based classification of robot swarm spatial self-organisation behaviours. Adapt. Behav. 2023, 31, 577–599. [Google Scholar] [CrossRef]
- Coppola, M.; McGuire, K.N.; De Wagter, C.; De Croon, G.C. A survey on swarming with micro air vehicles: Fundamental challenges and constraints. Front. Robot. AI 2020, 7, 18. [Google Scholar] [CrossRef] [PubMed]
- Ávila-Martínez, E.J.; Barajas-Ramírez, J.G. Flocking motion in swarms with limited sensing radius and heterogeneous input constraints. J. Frankl. Inst. 2021, 358, 2346–2366. [Google Scholar] [CrossRef]
- Pliego-Jiménez, J.; Martínez-Clark, R.; Cruz-Hernández, C.; Avilés-Velázquez, J.D.; Flores-Resendiz, J.F. Flocking and formation control for a group of nonholonomic wheeled mobile robots. Cogent Eng. 2023, 10, 2167566. [Google Scholar] [CrossRef]
- Beaver, L.E.; Malikopoulos, A.A. An overview on optimal flocking. Annu. Rev. Control 2021, 51, 88–99. [Google Scholar] [CrossRef]
- Bhatia, D. Constrained Dynamics Approach for Motion Synchronization and Consensus. The University of Texas at Arlington, ProQuest. Available online: https://www.proquest.com/openview/478332ef06ee5824bd9f5a7e409270c9/1?pq-origsite=gscholar&cbl=18750 (accessed on 20 July 2024).
- De Sá, D.F.S.; Neto, J.V.D.F. Multi-Agent Collision Avoidance System Based on Centralization and Decentralization Control for UAV Applications. IEEE Access 2023, 11, 7031–7042. [Google Scholar] [CrossRef]
- Azoulay, R.; Haddad, Y.; Reches, S. Machine learning methods for UAV flocks management-a survey. IEEE Access 2021, 9, 139146–139175. [Google Scholar] [CrossRef]
- Hacene, N.; Mendil, B. Behavior-based autonomous navigation and formation control of mobile robots in unknown cluttered dynamic environments with dynamic target tracking. Int. J. Autom. Comput. 2021, 18, 766–786. [Google Scholar] [CrossRef]
- Shi, P.; Yan, B. A survey on intelligent control for multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 161–175. [Google Scholar] [CrossRef]
- Wang, M.; Zeng, B.; Wang, Q. Research on motion planning based on flocking control and reinforcement learning for multi-robot systems. Machines 2021, 9, 77. [Google Scholar] [CrossRef]
- Anjos, J.C.D.; Matteussi, K.J.; Orlandi, F.C.; Barbosa, J.L.; Silva, J.S.; Bittencourt, L.F.; Geyer, C.F. A survey on collaborative learning for intelligent autonomous systems. ACM Comput. Surv. 2023, 56, 1–37. [Google Scholar] [CrossRef]
- Martínez, F.H. Review of flocking organization strategies for robot swarms. Tekhnê 2021, 18, 13–20. [Google Scholar]
- Ge, K.; Cheng, J. Review on flocking control. In International Conference on Multimedia Technology and Enhanced Learning; Springer International Publishing: Cham, Switzerland, April 2020. [Google Scholar]
- Sargolzaei, A.; Abbaspour, A.; Crane, C.D. Control of cooperative unmanned aerial vehicles: Review of applications, challenges, and algorithms. In Optimization, Learning, and Control for Interdependent Complex Networks. Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; pp. 229–255. [Google Scholar]
- Ali, Z.A.; Israr, A.; Hasan, R. Survey of Methods Applied in Cooperative Motion Planning of Multiple Robots. In Motion Panning of Dynamic Agents; Intechopen: London, UK, 2023. [Google Scholar]
- Bai, Y.; Zhao, H.; Zhang, X.; Chang, Z.; Jäntti, R.; Yang, K. Towards autonomous multi-UAV wireless network: A survey of reinforcement learning-based approaches. IEEE Commun. Surv. Tutor. 2023, 25, 3038–3067. [Google Scholar] [CrossRef]
- Orr, J.; Dutta, A. Multi-agent deep reinforcement learning for multi-robot applications: A survey. Sensors 2023, 23, 3625. [Google Scholar] [CrossRef]
- Shao, J.; Zheng, W.X.; Shi, L.; Cheng, Y. Leader–follower flocking for discrete-time Cucker–Smale models with lossy links and general weight functions. IEEE Trans. Autom. Control 2020, 66, 4945–4951. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987. [Google Scholar]
- Tanner, H.G. Flocking with obstacle avoidance in switching networks of interconnected vehicles. In Proceedings of the IEEE International Conference on Robotics and Automation, Proceedings. ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control. 2007, 51, 401–420. [Google Scholar] [CrossRef]
- Cucker, F.; Smale, S. Emergent behavior in flocks. IEEE Trans. Autom. Control. 2007, 52, 852–862. [Google Scholar] [CrossRef]
- Lee, D.; Spong, M.W. Stable flocking of multiple inertial agents on balanced graphs. IEEE Trans. Autom. Control. 2007, 52, 1469–1475. [Google Scholar] [CrossRef]
- Hoang, D.N.; Tran, D.M.; Tran, T.S.; Pham, H.A. An adaptive weighting mechanism for Reynolds rules-based flocking control scheme. PeerJ Comput. Sci. 2021, 7, 388–406. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, B. Flocking control of mobile robots with obstacle avoidance based on simulated annealing algorithm. Math. Probl. Eng. 2020, 2020, 7357464–7357473. [Google Scholar] [CrossRef]
- Wang, F.; Huang, J.; Low, K.H.; Nie, Z.; Hu, T. AGDS: Adaptive goal-directed strategy for swarm drones flying through unknown environments. Complex Intell. Syst. 2023, 9, 2065–2080. [Google Scholar] [CrossRef]
- Shrit, O.; Filliat, D.; Sebag, M. Iterative Learning for Model Reactive Control: Application to autonomous multi-agent control. In Proceedings of the 7th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 4–6 February 2021; pp. 140–146. [Google Scholar]
- Pyke, L.M.; Stark, C.R. Dynamic pathfinding for a swarm intelligence based UAV control model using particle swarm optimisation. Front. Appl. Math. Stat. 2021, 7, 744955. [Google Scholar] [CrossRef]
- Konda, R.; La, H.M.; Zhang, J. Decentralized function approximated q-learning in multi-robot systems for predator avoidance. IEEE Robot. Autom. Lett. 2020, 5, 6342–6349. [Google Scholar] [CrossRef]
- Ban, Z.; Hu, J.; Lennox, B.; Arvin, F. Self-organised collision-free flocking mechanism in heterogeneous robot swarms. Mob. Netw. Appl. 2021, 26, 2461–2471. [Google Scholar] [CrossRef]
- Beaver, L.E.; Malikopoulos, A.A. Beyond reynolds: A constraint-driven approach to cluster flocking. In Proceedings of the 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; pp. 208–213. [Google Scholar]
- Zheng, H.; Panerati, J.; Beltrame, G.; Prorok, A. An adversarial approach to private flocking in mobile robot teams. IEEE Robot. Autom. Lett. 2020, 5, 1009–1016. [Google Scholar] [CrossRef]
- Wu, J.; Yu, Y.; Ma, J.; Wu, J.; Han, G.; Shi, J.; Gao, L. Autonomous cooperative flocking for heterogeneous unmanned aerial vehicle group. IEEE Trans. Veh. Technol. 2021, 70, 12477–12490. [Google Scholar] [CrossRef]
- Xiao, J.; Yuan, G.; He, J.; Fang, K.; Wang, Z. Graph attention mechanism based reinforcement learning for multi-agent flocking control in communication-restricted environment. Inf. Sci. 2023, 620, 142–157. [Google Scholar] [CrossRef]
- Ma, L.; Bao, W.; Zhu, X.; Wu, M.; Wang, Y.; Ling, Y.; Zhou, W. O-flocking: Optimized flocking model on autonomous navigation for robotic swarm. In Proceedings of the Advances in Swarm Intelligence: 11th International Conference, ICSI, Belgrade, Serbia, 14–20 July 2020. [Google Scholar]
- Kamel, M.A.; Yu, X.; Zhang, Y. Real-time fault-tolerant formation control of multiple WMRs based on hybrid GA–PSO algorithm. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1263–1276. [Google Scholar] [CrossRef]
- Haldar, A.K.; Roy, D.; Maitra, M. Fault-tolerant V formation control of a leader-follower based multi-robot system in an unknown occluded environment. In Proceedings of the IEEE 3rd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 25–27 January 2024. [Google Scholar]
- Liu, W.; Gao, Z. A distributed flocking control strategy for UAV groups. Comput. Commun. 2020, 153, 95–101. [Google Scholar] [CrossRef]
- Huang, F.; Wu, P.; Li, X. Distributed flocking control of quad-rotor UAVs with obstacle avoidance under the parallel-triggered scheme. Int. J. Control Autom. Syst. 2021, 19, 1375–1383. [Google Scholar] [CrossRef]
- Yan, C.; Wang, C.; Xiang, X.; Low, K.H.; Wang, X.; Xu, X.; Shen, L. Collision-avoiding flocking with multiple fixed-wing UAVs in obstacle-cluttered environments: A task-specific curriculum-based MADRL approach. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 10894–10908. [Google Scholar] [CrossRef] [PubMed]
- Petráček, P.; Walter, V.; Báča, T.; Saska, M. Bio-inspired compact swarms of unmanned aerial vehicles without communication and external localization. Bioinspiration Biomim. 2020, 16, 026009. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Pan, J.; Wang, H.; Gao, X. A formation maintenance and reconstruction method of UAV swarm based on distributed control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Ribeiro, R.; Silvestre, D.; Silvestre, C. Decentralized control for multi-agent missions based on flocking rules. In Proceedings of the CONTROLO 2020: Proceedings of the 14th APCA International Conference on Automatic Control and Soft Computing, Bragança, Portugal, 1–3 July 2020; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Lin, C.; Han, G.; Du, J.; Bi, Y.; Shu, L.; Fan, K. A path planning scheme for AUV flock-based Internet-of-Underwater-Things systems to enable transparent and smart ocean. IEEE Internet Things J. 2020, 7, 9760–9772. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, X.; Yang, X.; Shang, Z.; Luo, X.; Guan, X. Joint design of channel estimation and flocking control for multi-AUV-based maritime transportation systems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14520–14535. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. A multi-objective pigeon-inspired optimization approach to UAV distributed flocking among obstacles. Inf. Sci. 2020, 509, 515–529. [Google Scholar] [CrossRef]
- Abdelkader, M.; Güler, S.; Jaleel, H.; Shamma, J.S. Aerial swarms: Recent applications and challenges. Curr. Robot. Rep. 2021, 2, 309–320. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Lv, M.; Zhang, B. Two-level hierarchical-interaction-based group formation control for MAV/UAVs. Aerospace 2022, 9, 510. [Google Scholar] [CrossRef]
- Van Der Helm, S.; Coppola, M.; McGuire, K.N.; De Croon, G.C. On-board range-based relative localization for micro air vehicles in indoor leader–follower flight. Auton. Robot. 2020, 44, 415–441. [Google Scholar] [CrossRef]
- Xu, D.; Guo, Y.; Yu, Z.; Wang, Z.; Lan, R.; Zhao, R.; Xie, X.; Long, H. PPO-Exp: Keeping fixed-wing UAV formation with deep reinforcement learning. Drones 2022, 7, 28. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Huang, T.Y.; Chen, X.B. An improved flocking control algorithm to solve the effect of individual communication barriers on flocking cohesion in multi-agent systems. Eng. Appl. Artif. Intell. 2024, 137, 109110. [Google Scholar] [CrossRef]
- Wang, C.; Du, J.; Ruan, L.; Lv, J.; Tian, S. Research on collision avoidance between UAV flocks using behavior-based approach. In China Satellite Navigation Conference Proceedings; Springer: Singapore, 2021. [Google Scholar]
- Soma, K.; Ravichander, A.; PM, V.N. Decentralized shape formation and force-based interactive formation control in robot swarms. arXiv 2023, arXiv:2309.01240. [Google Scholar]
- Bautista, J.; de Marina, H.G. Behavioral-based circular formation control for robot swarms. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar]
- Kang, C.; Xu, J.; Bian, Y. Affine Formation Maneuver Control for Multi-Agent Based on Optimal Flight System. Appl. Sci. 2024, 14, 2292. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, S.; Lei, L. A multi-UAV formation maintaining method based on formation reference point. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Liu, J.; Wu, Z.; Xin, Q.; Yu, M.; Liu, L. Topology uniformity pinning control for multi-agent flocking. Complex Intell. Syst. 2024, 10, 2013–2027. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, K.; Lü, Y.; Chen, L. Complex network–based pinning control of drone swarm. IFAC-Pap. 2022, 55, 207–212. [Google Scholar] [CrossRef]
- Ren, J.; Liu, Q.; Li, P. The Collision-Avoiding Flocking of a Cucker-Smale Model with Pinning Control and External Perturbation. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4853392 (accessed on 6 February 2024).
- Wang, X.; Li, X.; Lu, J. Control and flocking of networked systems via pinning. IEEE Circuits Syst. Mag. 2010, 10, 83–91. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, J.; Cai, Z.; Wang, Y.; Wu, K. Distributed coordinated control scheme of UAV swarm based on heterogeneous roles. Chin. J. Aeronaut. 2022, 35, 81–97. [Google Scholar] [CrossRef]
- Li, S.; Fang, X. A modified adaptive formation of UAV swarm by pigeon flock behavior within local visual field. Aerosp. Sci. Technol. 2021, 114, 106736. [Google Scholar] [CrossRef]
- Muslimov, T.Z.; Munasypov, R.A. Adaptive decentralized flocking control of multi-UAV circular formations based on vector fields and backstepping. ISA Trans. 2020, 107, 143–159. [Google Scholar] [CrossRef]
- Gao, C.; Ma, J.; Li, T.; Shen, Y. Hybrid swarm intelligent algorithm for multi-UAV formation reconfiguration. Complex Intell. Syst. 2023, 9, 1929–1962. [Google Scholar] [CrossRef]
- Zeng, Q.; Nait-Abdesselam, F. Multi-Agent Reinforcement Learning-Based Extended Boid Modeling for Drone Swarms. In Proceedings of the ICC 2024-IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024. [Google Scholar]
- Le Ménec, S. Swarm Guidance Based on Mean Field Game Concepts. Int. Game Theory Rev. 2024, 26, 2440008. [Google Scholar] [CrossRef]
- Liu, G.; Wen, N.; Long, F.; Zhang, R. A Formation Control and Obstacle Avoidance Method for Multiple Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 2346. [Google Scholar] [CrossRef]
- Han, G.; Qi, X.; Peng, Y.; Lin, C.; Zhang, Y.; Lu, Q. Early warning obstacle avoidance-enabled path planning for multi-AUV-based maritime transportation systems. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2656–2667. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.T.; Kim, H. Vmcs: Elaborating apf-based swarm intelligence for mission-oriented multi-uv control. IEEE Access 2020, 8, 223101–223113. [Google Scholar] [CrossRef]
- Li, J.; Fang, Y.; Cheng, H.; Wang, Z.; Wu, Z.; Zeng, M. Large-scale fixed-wing UAV swarm system control with collision avoidance and formation maneuver. IEEE Syst. J. 2022, 17, 744–755. [Google Scholar] [CrossRef]
- Nag, A.; Yamamoto, K. Distributed control for flock navigation using nonlinear model predictive control. Adv. Robot. 2024, 38, 619–631. [Google Scholar] [CrossRef]
- Önür, G.; Turgut, A.E.; Şahin, E. Predictive search model of flocking for quadcopter swarm in the presence of static and dynamic obstacles. Swarm Intell. 2024, 18, 187–213. [Google Scholar] [CrossRef]
- Hastedt, P.; Werner, H. Distributed model predictive flocking with obstacle avoidance and asymmetric interaction forces. In Proceedings of the American Control Conference (ACC), IEEE, San Diego, CA, USA, 31 May–2 June 2023. [Google Scholar]
- Vargas, S.; Becerra, H.M.; Hayet, J.B. MPC-based distributed formation control of multiple quadcopters with obstacle avoidance and connectivity maintenance. Control Eng. Pract. 2022, 121, 105054. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Pan, E.; Xu, W.; Xue, D. Autonomous Formation Flight Control of Large-Sized Flapping-Wing Flying Robots Based on Leader–Follower Strategy. J. Bionic Eng. 2023, 20, 2542–2558. [Google Scholar] [CrossRef]
- Kumar, A.; Misra, R.K.; Singh, D. Butterfly optimizer. In Proceedings of the IEEE Workshop on Computational Intelligence: Theories, Applications and Future Directions (WCI), Kanpur, India, 14–17 December 2015; pp. 1–6. [Google Scholar]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Eagle strategy using Lévy walk and firefly algorithms for stochastic optimization. In Recent Advances in Computational Optimization; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010; pp. 101–111. [Google Scholar]
- Alauddin, M. Mosquito flying optimization (MFO). In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 79–84. [Google Scholar]
- Rajabioun, R. Cuckoo optimization algorithm. Appl. Soft Comput. 2011, 11, 5508–5518. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, X.; Miao, Y. Starling-behavior-inspired flocking control of fixed-wing unmanned aerial vehicle swarm in complex environments with dynamic obstacles. Biomimetics 2022, 7, 214. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Maitra, M.; Bhattacharya, S. Adaptive formation-switching of a multi-robot system in an unknown occluded environment using BAT algorithm. Int. J. Intell. Robot. Appl. 2020, 4, 465–489. [Google Scholar] [CrossRef]
- Abichandani, P.; Speck, C.; Bucci, D.; Mcintyre, W.; Lobo, D. Implementation of decentralized reinforcement learning-based multi-quadrotor flocking. IEEE Access 2021, 9, 132491–132507. [Google Scholar] [CrossRef]
- Xiao, J.; Yuan, G.; Wang, Z. A multi-agent flocking collaborative control method for stochastic dynamic environment via graph attention autoencoder based reinforcement learning. Neurocomputing 2023, 549, 126379. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Fixed-Wing UAVs flocking in continuous spaces: A deep reinforcement learning approach. Robot. Auton. Syst. 2020, 131, 103594. [Google Scholar] [CrossRef]
- Gama, F.; Tolstaya, E.; Ribeiro, A. Graph neural networks for decentralized controllers. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 6–12 June 2021. [Google Scholar]
- Aydın, H.; Tunç, İ.; Söylemez, M.T. Fuzzy logic controller for leader-follower based navigation of mobile robots in a ROS-enabled environment. In Proceedings of the 13th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 25–27 November 2021. [Google Scholar]
- Nhu, T.; Hung, P.D.; Ngo, T.D. Fuzzy-based distributed behavioral control with wall-following strategy for swarm navigation in arbitrary-shaped environments. IEEE Access 2021, 9, 139176–139185. [Google Scholar] [CrossRef]
- Cavallaro, C.; Vizzari, G. A novel spatial–temporal analysis approach to pedestrian groups detection. Procedia Comput. Sci. 2022, 207, 2364–2373. [Google Scholar] [CrossRef]
- Wang, C.; Wang, D.; Gu, M.; Huang, H.; Wang, Z.; Yuan, Y.; Zhu, X.; Wei, W.; Fan, Z. Bioinspired environment exploration algorithm in swarm based on levy flight and improved artificial potential field. Drones 2022, 6, 122. [Google Scholar] [CrossRef]
- Zhou, Z.; Ouyang, C.; Hu, L.; Xie, Y.; Chen, Y.; Gan, Z. A framework for dynamical distributed flocking control in dense environments. Expert Syst. Appl. 2023, 241, 122694. [Google Scholar] [CrossRef]
- Qu, S.; Abouheaf, M.; Gueaieb, W.; Spinello, D. An adaptive fuzzy reinforcement learning cooperative approach for the autonomous control of flock systems. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Xiao, J.; Wang, Z.; He, J.; Yuan, G. A graph neural network based deep reinforcement learning algorithm for multi-agent leader-follower flocking. Inf. Sci. 2023, 641, 119074. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Ding, W.; Wang, Q.; Zhang, Z.; Jia, J. Bio-Inspired Fission–Fusion Control and Planning of Unmanned Aerial Vehicles Swarm Systems via Reinforcement Learning. Appl. Sci. 2024, 14, 1192. [Google Scholar] [CrossRef]
- UAS @ UCLA. The Evolution of Unmanned Aerial Vehicles: Navigating the Sky of Technology and Applications. Available online: https://uasatucla.org/ (accessed on 20 July 2024).
- Blue Falcon Aerial. Available online: https://www.bluefalconaerial.com/mastering-the-skies-the-power-of-drone-swarm-technology/ (accessed on 20 July 2024).
- Consortiq. Available online: https://consortiq.com/uas-resources/drone-swarm-delivery-system (accessed on 20 July 2024).
- Wei, H.; Chen, X.B. Flocking for multiple subgroups of multi-agents with different social distancing. IEEE Access 2020, 8, 164705–164716. [Google Scholar] [CrossRef]
- Amorim, T.; Nascimento, T.; Petracek, P.; De Masi, G.; Ferrante, E.; Saska, M. Self-organized uav flocking based on proximal control. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021. [Google Scholar]
- Bae, I.; Hong, J. Survey on the developments of unmanned marine vehicles: Intelligence and cooperation. Sensors 2023, 23, 4643. [Google Scholar] [CrossRef]
- Elmokadem, T.; Savkin, A.V. Computationally-efficient distributed algorithms of navigation of teams of autonomous UAVs for 3D coverage and flocking. Drones 2021, 5, 124. [Google Scholar] [CrossRef]
- Albiero, D.; Garcia, A.P.; Umezu, C.K.; de Paulo, R.L. Swarm Robots in Agriculture. arXiv 2021, arXiv:2103.0673. [Google Scholar]
- Sun, Y.; Cui, B.; Ji, F.; Wei, X.; Zhu, Y. The full-field path tracking of agricultural machinery based on PSO-enhanced fuzzy stanley model. Appl. Sci. 2022, 12, 7683. [Google Scholar] [CrossRef]
- Caruntu, C.F.; Pascal, C.M.; Maxim, A.; Pauca, O. Bio-inspired coordination and control of autonomous vehicles in future manufacturing and goods transportation. IFAC-Pap. 2020, 53, 10861–10866. [Google Scholar] [CrossRef]
- Koung, D.; Fantoni, I.; Kermorgant, O.; Belouaer, L. Consensus-based formation control and obstacle avoidance for nonholonomic multi-robot system. In Proceedings of the 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020. [Google Scholar]
- Sharma, K.; Doriya, R. Coordination of multi-robot path planning for warehouse application using smart approach for identifying destinations. Intell. Serv. Robot. 2021, 14, 313–325. [Google Scholar] [CrossRef]
- Divya Vani, G.; Karumuri, S.R.; Chinnaiah, M.C. Hardware Schemes for Autonomous Navigation of Cooperative-type Multi-robot in Indoor Environment. J. Inst. Eng. (India) Ser. B 2022, 103, 449–460. [Google Scholar] [CrossRef]
- Gopika, M.; Fathimathul, K.; Anagha, S.K.; Jomel, T.; Anandhi, V. Swarm robotics system for hospital management. IJCRT 2021, 9, g61–g66. [Google Scholar]
- Kharchenko, V.; Kliushnikov, I.; Rucinski, A.; Fesenko, H.; Illiashenko, O. UAV fleet as a dependable service for smart cities: Model-based assessment and application. Smart Cities 2022, 5, 1151–1178. [Google Scholar] [CrossRef]
- Qassab, M.; Ibrahim, Q. A portable health clinic (PHC) approach using self-organizing multi-UAV network to combat COVID-19 pandemic condition in hotspot areas. J. Mod. Technol. Eng. 2022, 7, 1. [Google Scholar]
- Zhu, P.; Dai, W.; Yao, W.; Ma, J.; Zeng, Z.; Lu, H. Multi-robot flocking control based on deep reinforcement learning. IEEE Access 2020, 8, 150397–150406. [Google Scholar] [CrossRef]
- Martinez, F.; Montiel, H.; Jacinto, E. A software framework for self-organized flocking system motion coordination research. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 1–8. [Google Scholar] [CrossRef]
- Shao, X.; Zhang, J.; Zhang, W. Distributed cooperative surrounding control for mobile robots with uncertainties and aperiodic sampling. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18951–18961. [Google Scholar] [CrossRef]


| Reference | Multi-Agent System | Applied Strategies | Application Area | Simulation/Experiment | Remarks |
|---|---|---|---|---|---|
| Wei and Chen [100] | Mobile agents | Semi-flocking and α-lattice flocking-based algorithms with multiple virtual leaders | Military | Simulation |
|
| Amorim et al. [101] | UAV swarm | Proximal control-based self-organized flocking | Military | Experiment |
|
| Elmokadem and Savkin [103] | Multi-UAV system | Voronoi partitions-based multi-region strategy | Agriculture | Simulation |
|
| Albiero et al. [104] | A swarm of small robot tractors | Swarm flocking | Agriculture | Simulation |
|
| Sun et al. [105] | Mobile vehicle and a combine harvester | PSO-FSM | Agriculture | Both |
|
| Caruntu et al. [106] | AXVs | Bio-inspired approaches | Manufacturing | Both |
|
| Koung et al. [107] | Multi-wheeled mobile robots | Consensus-based flocking with obstacle avoidance | Logistics and transportation | Both |
|
| Sharma and Doriya [108] | Multi-robot system | Smart distance metric-based approach | Logistics and transportation | Experiment |
|
| Divya Vani et al. [109] | Multi-robot system | Extended Dijkstra algorithm–Delaunay triangulation method and behavioral control with leadership-swapping methods | Logistics and transportation | Simulation |
|
| Kharchenko et al. [111] | UAV’s fleet | Queuing theory | Healthcare and medicine | Experiment |
|
| Qassab and Ibrahim [112] | UAV swam | Self-organizing with a leader–follower strategy | Healthcare and medicine | Simulation |
|
| Flocking Control | Categories | Opportunities | Weaknesses |
|---|---|---|---|
| Schemes | Distributed |
| |
| Decentralized |
|
| |
| Centralized |
|
| |
| Hybrid system |
|
| |
| Structures | Leader–follower |
|
|
| Behavior-based |
|
| |
| Virtual structure |
|
| |
| Pinning-based |
|
| |
| Dynamic adaptive structure |
| ||
| Strategies | APF |
|
|
| MPC |
|
| |
| SI with little bio-inspired |
|
| |
| AI techniques |
|
| |
| Hybrid control paradigms |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.A.; Alkhammash, E.H.; Hasan, R. State-of-the-Art Flocking Strategies for the Collective Motion of Multi-Robots. Machines 2024, 12, 739. https://doi.org/10.3390/machines12100739
Ali ZA, Alkhammash EH, Hasan R. State-of-the-Art Flocking Strategies for the Collective Motion of Multi-Robots. Machines. 2024; 12(10):739. https://doi.org/10.3390/machines12100739
Chicago/Turabian StyleAli, Zain Anwar, Eman H. Alkhammash, and Raza Hasan. 2024. "State-of-the-Art Flocking Strategies for the Collective Motion of Multi-Robots" Machines 12, no. 10: 739. https://doi.org/10.3390/machines12100739
APA StyleAli, Z. A., Alkhammash, E. H., & Hasan, R. (2024). State-of-the-Art Flocking Strategies for the Collective Motion of Multi-Robots. Machines, 12(10), 739. https://doi.org/10.3390/machines12100739