Compensation Function Observer-Based Backstepping Sliding-Mode Control of Uncertain Electro-Hydraulic Servo System

Abstract

Observer-based control is the most commonly used method in the control of electro-hydraulic servo system (EHSS) with uncertainties, but it suffers from the drawback of low accuracy under the influence of large external load forces and disturbances. To address this problem, this paper proposes a novel compensation function observer-based backstepping sliding-mode control (BSMC) approach to achieve high-accuracy tracking control. In particular, the model uncertainties, including nonlinearities, parameter perturbations and external disturbances are analyzed and treated together as a lumped disturbance. Then, a fourth-order compensation function observer (CFO) is constructed, which fully utilizes the system state information to accurately estimate the lumped disturbance. On this basis, the estimate of the lumped disturbance is incorporated into the design of a backstepping sliding-mode controller, allowing the control system to compensate for the disturbance effect. The stability of the closed-loop control system under the CFO and BSMC is rigorously proven through the use of the Lyapunov theory, which guarantees that all the tracking error signals converge exponentially to the origin. Comparative simulations are carried out to show the effectiveness and efficiency of the proposed approach, i.e., compared with PID and ESO-based BSMC methods, the tracking accuracy is respectively improved by $94.86\%$ and $88.19\%$ under the influence of large external load forces and disturbances.

1. Introduction

As a complex nonlinear mechatronic system, an electro-hydraulic servo system (EHSS) possesses many prominent merits such as fast response, strong load capacity, high power-to-weight ratio and so on [1,2,3]. Because of these advantages, EHSSs have been extensively used in modern industrial applications, such as digging robots [4,5,6], hydraulic press [7,8], mechanical arms [9,10], etc. Nevertheless, the EHSS in practical applications always suffers from various uncertainties. On one hand, the model parameters such as load mass, effective oil bulk modulus and leakage coefficient may significantly change with working conditions, temperature and equipment wear. On the other hand, the hydraulic system has strong nonlinearities in the flow and pressure dynamics of the control valve, oil compressibility and leakage. Furthermore, owing to the intricacy of the working environment, the EHSS is inevitably susceptible to unknown external load forces and disturbances. All these uncertainties could seriously deteriorate the system control performance, or even destroy the system. Therefore, the high-precision tracking control of an EHSS in the presence of uncertainties with advanced control methods still poses challenges for engineers.

Over the past several decades, there have been remarkable advancements on the control of EHSSs. The existing control methods can be classified into three categories: linear control [11,12,13,14,15,16], nonlinear control [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], and observer-based control [34,35,36,37,38,39,40,41].

The linear control algorithms, which are developed using conventional PID [11,12,13,14] or feedback linearization techniques [15,16], are simple and easy to implement in engineering. However, they only perform well under certain operating conditions, and fail to achieve satisfactory performance in the presence of aforementioned uncertainties, including parameter permutations, nonlinearities and disturbances. To enhance the control performance of EHSSs, extensive research has been conducted, and numerous advanced nonlinear control methods have been proposed, such as backstepping control, adaptive control, sliding-mode control and so on.

The backstepping technique is one of the most powerful tools in nonlinear control, in which the control laws are designed recursively by constructing a series of control Lyapunov functions. The distinctive feature of this approach lies in its well-defined step-by-step design procedure, and the system stability can be rigorously guaranteed by a Lyapunov stability theory. However, the control laws designed by this method depends on the accurate model of the system. To remove this obstacle, researchers often combine it with other advanced control methods such as adaptive control, fuzzy logic system (FLS)/neural network (NN) and sliding-mode control (SMC). For example, a desired compensation adaptive control framework was proposed in [17,18], where a projection-type adaptive law was designed to estimate the unknown parameters. In [19], an adaptive robust controller was developed by combining adaptive robust control with a discrete disturbance estimator, which can compensate for unknown parameters, nonlinearities and external disturbances. Unfortunately, the adaptive design process is usually required to be linearly parameterized with unknown constant parameters, which is not always satisfied for the complex EHSS. By employing FLS to approximate nonlinearities, parameter uncertainties and external disturbances, adaptive fuzzy backstepping controllers were presented in [20,21,22,23]. Similarly, taking advantage of the universal approximation ability of NN, adaptive backstepping NN control schemes have been extensively proposed in [24,25,26]. However, the control algorithms using FLS/NN are usually computationally expensive, since FLS relies heavily on the knowledge rules of expert and NN requires either online learning or offline training procedures to make the controller perform properly.

SMC is famous for its insensitivity to uncertainties in the manner of constructing a sliding-mode surface. Once the system states reach the surface, the controller has strong robustness against uncertainties. In view of this excellent feature, several control strategies that combine backstepping and SMC have been proposed in [27,28,29,30] to improve the robustness of EHSSs with backlash links, non-structural uncertainties or dead-zones. Furthermore, by incorporating NNs, adaptive NN sliding-mode control approaches were presented in [31,32,33] for EHSSs to achieve a high tracking accuracy.

Observer-based control has been proven to be a powerful technique to address uncertainties. The basic idea of this methodology is to design an observer to estimate the uncertainties and compensate for the effect in the control loop. Typical observers include high-gain observer (HGO), nonlinear disturbance observer (NDO), adaptive observer (AO), sliding-mode observer (SMO), and extended-state observer (ESO). Among them, ESO is the most classical disturbance estimation method, which regards the internal and external disturbance of the system as an extended system state variable [42,43]. In [39,40,41], three ESO-based sliding-mode controllers are proposed for an EHSS, in which ESO is used to estimate the lumped disturbance while the convergence of the system state is guaranteed by an SMC technique. In addition, by employing ESO with backstepping, a variety of control strategies such as ESO-based finite-time backstepping control [34,35], ESO-based adaptive backstepping control [36] and ESO-based backstepping robust control [37,38] have been proposed. Nevertheless, the ESO still has some drawbacks in the estimation accuracy and system convergence. It has been verified in [44] that the structure of ESO can be equivalent to a Type-I tracking system, which means a zero steady-state error convergence can only be achieved in the presence of constant disturbances.

According to the above literature review and analysis, it is evident that ESO-based control combined with SMC in the framework of backstepping is the most powerful and effective method for the control of EHSSs in the presence of complex nonlinearities and uncertainties. However, the dynamics and disturbances of EHSSs are dynamically changing, i.e., they are not constant. When employing the ESO-based backstepping sliding-mode control method, it faces challenging problems of low estimation accuracy and big estimation lag. Although increasing the ESO gains may improve the estimation accuracy, it would also amplify noises, leading to the so-called peaking phenomenon [45,46], or even system instability. Therefore, the improved backstepping SMC design based on the observer to handle this issue still needs further investigation. Recently, a novel compensation function observer (CFO) with a pure integral structure was proposed by Qi et al. in [44]. By introducing velocity information and using a first-order filter or integrator as a compensation function, the CFO becomes a Type-III system, which enable it to estimate constant, slope and acceleration disturbances or uncertainties with zero steady-state error. Due to these advantages, CFO was extensively applied to the attitude control of quadrotor aircraft [47,48], yielding favorable control outcomes. However, the application of CFO on EHSSs has not been reported.

Motivated by the above observations, this paper aims to directly deal with the problem of low accuracy in the estimation of large uncertainties when employing observer-based control techniques for uncertain EHSSs. A novel CFO-based backstepping sliding-mode control (CFO-BMSC) approach is proposed to enhance the tracking accuracy. The nonlinearities and disturbances of an EHSS are first analyzed, and the model equation is rearranged as an appropriate form, where all the uncertainties affecting the system including unknown frictions, parameter perturbations and external disturbances are collectively treated as a lumped disturbance. Then, inspired by the unique feature of compensation function, a fourth-order CFO is employed to estimate the lumped disturbance accurately, which is in turn incorporated into the control design to compensate for the effect of the disturbance. Furthermore, in the framework of backstepping, a sliding-mode controller is designed to stabilize all the tracking errors. The primary features and contributions of the proposed approach are underlined as follows:

(1)

Different from previous ESO-based methods (e.g., [34,35,37,39]), the CFO adopts a Type-III structure and fully utilizes system state information, which make it capable of estimating the disturbance with higher estimation accuracy. Detailed comparisons between the performance of ESO and CFO in the estimation of different disturbances are examined by extensive comparison simulations.

(2)

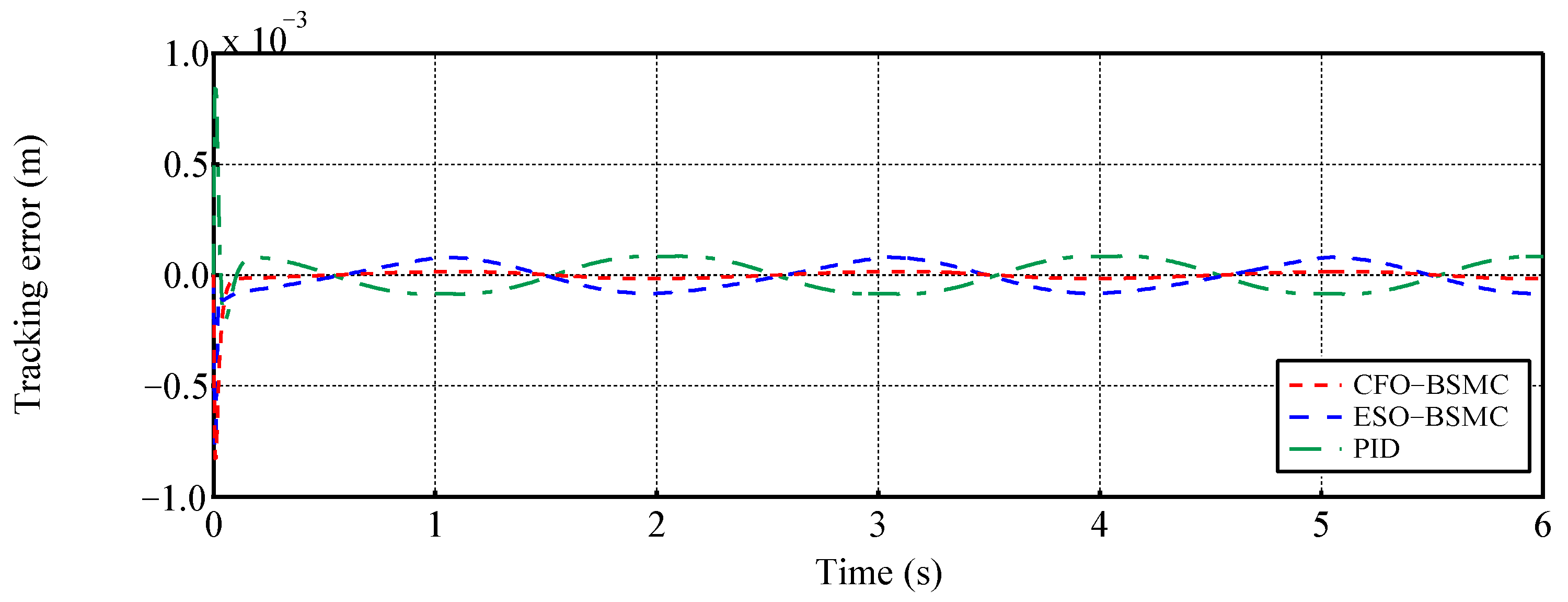
In comparison with conventional PID and ESO-based BSMC [12,46], the proposed CFO-BMSC tracks the reference trajectory with no phase lag under the influence of large external load forces and disturbances, and the tracking accuracy is increased by $94.86\%$ and $88.19\%$, respectively, obtaining better transient and steady-state tracking performances. To the best of our knowledge, this is the first attempt to incorporate CFO into the backstepping sliding-mode control of EHSSs.

(3)

The stability of the overall system including the CFO and BSMC is rigorously analyzed by the Lyapunov stability theory, which guarantees that the closed-loop control system is exponentially stable, and the tracking errors converge to the origin.

The remainder of this paper is organized as follows. The nonlinear mathematical model of the EHSS under study is given in Section 2. The control system design including compensation function observer, sliding-mode backstepping controller and the system stability analysis is presented in Section 3. Simulation results with comparisons are shown in Section 4, and conclusion remarks are finally given in Section 5.

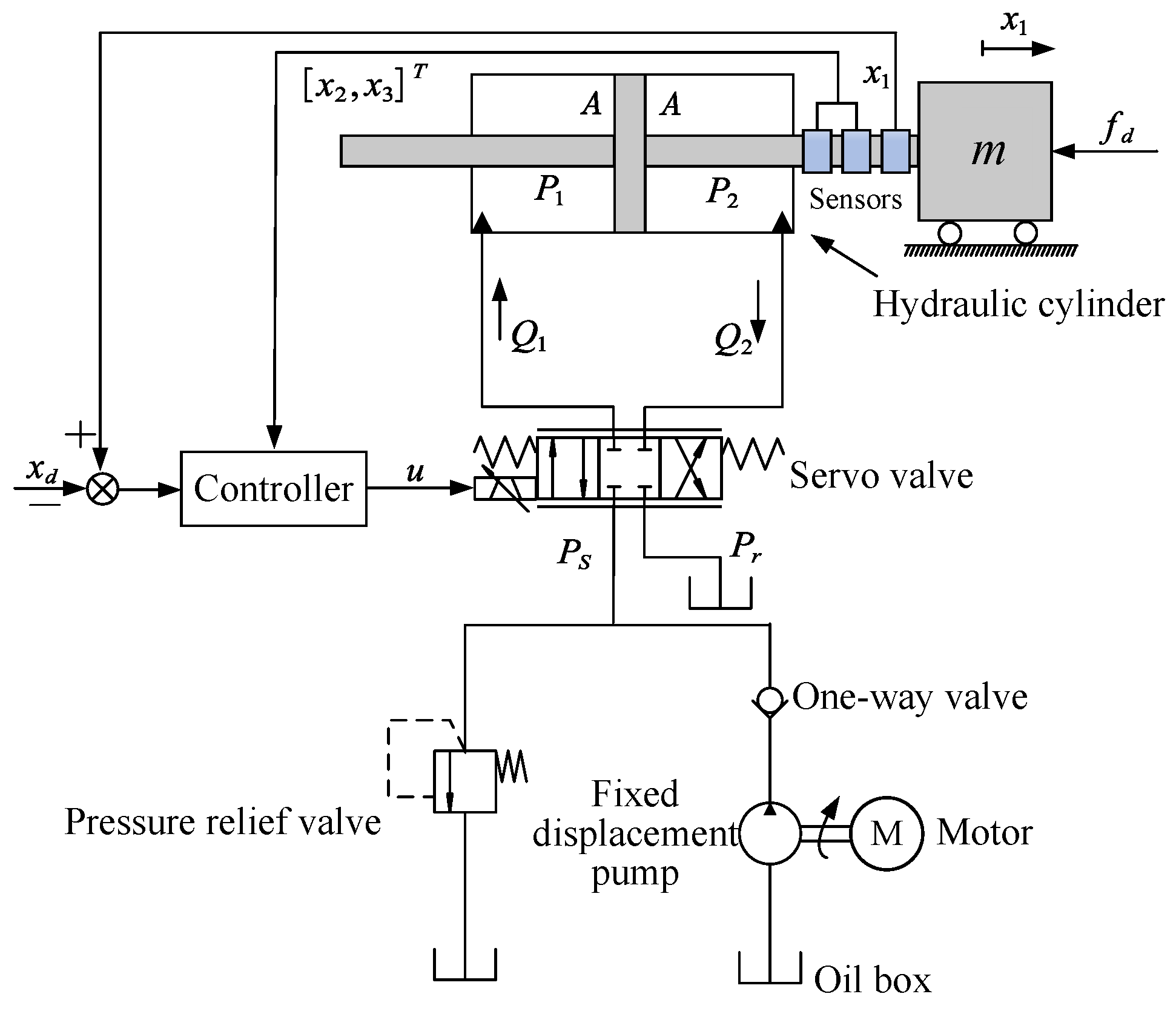
2. System Modeling and Problem Description

Figure 1 is the working principle diagram of the electro-hydraulic servo system (EHSS), which consists of an electro-hydraulic servo valve and a hydraulic cylinder. The load is controlled by an electro-hydraulic servo valve, which converts the received electrical signal into a hydraulic signal, and then drives the hydraulic cylinder. For the considered EHSS in Figure 1, m is the mass of the load, A is the ram area of the chamber, $x_p$ is the piston displacement, $x_v$ is the servo valve spool displacement, $f_d$ is the unmodeled friction and unknown disturbances in the systems, $P_1$ is the pressure inside the left chamber of the hydraulic cylinder, $P_2$ is the pressure inside the right chamber of the hydraulic cylinder, $Q_1$ is the supplied flow rate to the two chambers, $Q_2$ is the return flow rate to the two chambers, $P_s$ is the supply pressure and $P_r$ is the return pressure, which is almost zero [18].

According to Newton’s second law, the dynamic equation of the hydraulic cylinder is

$$P_{L}A=m{\ddot{x}}_p+B{\dot{x}}_p+f_d,$$

(1)

where $P_L$ is the load pressure in the hydraulic actuator, $P_L=P_1-P_2$ and B is the coefficient of the viscous friction force. Considering the effect of internal leakages, the load pressure dynamics can be defined as [18]

$${\dot{P}}_L={\displaystyle \frac{4{\beta }_e}{V_{\mathrm{t}}}}\left(Q_L-A{\dot{x}}_p-C_t{P}_L\right),$$

(2)

where ${\beta }_e$ is the effective oil bulk modulus; $Q_L$ is the load flow, $Q_L={\displaystyle \frac{1}{2}}\left(Q_1+Q_2\right)$; and $C_t$ is the coefficient of the total internal leakage of the hydraulic cylinder.

A high-performance servo valve with a natural frequency of 80 Hz is used, which is much higher than the frequency of the desired motion trajectories [19]. Thus, the relationship between the spool displacement and the control input is approximated as $x_v=k_{i}u$, where $k_i$ is a positive constant. The load flow can be obtained as [18]

$$Q_L=k_{t}u\sqrt{P_S-P_L\mathrm{sign}u},$$

(3)

where $k_t$ is the flow gain, $k_t=k_i{C}_d\omega \sqrt{{\displaystyle \frac{1}{\rho }}}$, $C_d$ is the flow coefficient, $\omega$ is the area gradient of the servo valve and $\rho$ is the oil density.

Define $x={\left[x_1,x_2,x_3\right]}^T={\left[x_p,{\dot{x}}_p,{\ddot{x}}_p\right]}^T$ as the state variables, and then, from (1)–(3), the state-space equation of the EHSS is expressed as [49]

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3,\hfill \\ {\dot{x}}_3=R_1{x}_2+R_{2}u+F,\hfill \end{array}\right.$$

(4)

where

$$\begin{array}{cc}\hfill & R_1=-{\displaystyle \frac{4A^2{\beta }_e}{m{V}_t}}+{\displaystyle \frac{B^2}{m^2}},\hfill \\ \hfill & R_2={\displaystyle \frac{4A{\beta }_e{k}_t}{m{V}_t}}\sqrt{P_S-P_L\mathrm{sign}u},\hfill \\ \hfill & F=\phi P_L-{\displaystyle \frac{B}{m}}{f}_d+{\dot{f}}_d,\hfill \\ \hfill & \phi =-{\displaystyle \frac{4A{\beta }_e{C}_t}{m{V}_t}}-{\displaystyle \frac{BA}{m^2}}.\hfill \end{array}$$

(5)

Note that $R_1$ and $R_2$ are certain constants, both of which are related to the system parameters. In practice, it is often difficult to obtain accurate system parameters, so there exist uncertain parts for $R_1$ and $R_2$, which can be denoted as $\Delta R_1$ and $\Delta R_2$. The term F includes unmodeled dynamics such as frictions and unknown external disturbances. In this paper, all the mentioned uncertainties are treated as a lumped disturbance $f_u$, which can be expressed as

$$f_u=\Delta R_1{x}_2+\Delta R_{2}u+F.$$

(6)

Thus, Equation (4) is rewritten as

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3,\hfill \\ {\dot{x}}_3=f_k+R_{2}u+f_u,\hfill \end{array}\right.$$

(7)

where $f_k=R_1{x}_2$ is the known nominal part of the EHSS model, and $f_u$ is the unknown lumped disturbance. In this paper, a CFO is designed to estimate $f_u$ in real time, and the estimate value is fed back to the controller to compensate for the effect of $f_u$ such that the output $x_1$ can track the desired trajectory $x_d$ quickly and accurately.

3. Control Design

In this section, an overview of the structure of the proposed control scheme is first presented and described. Then, a compensation function observer (CFO) is designed to accurately estimate the lumped disturbance in real time, on the basis of which a backstepping sliding-mode controller is designed to achieve the trajectory tracking control.

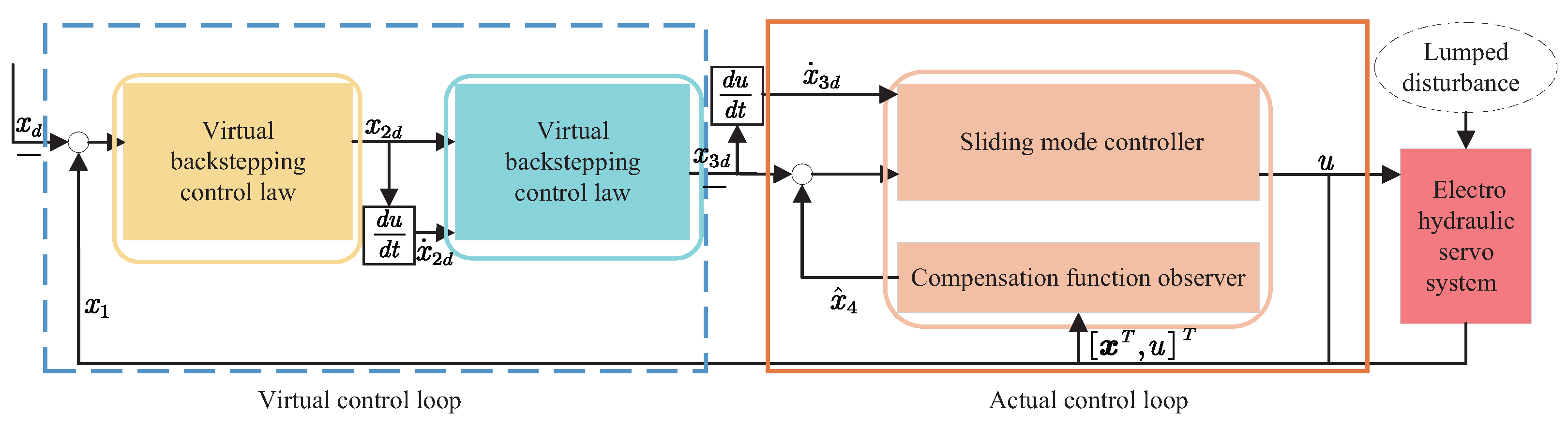
3.1. Structure of the Proposed Hierarchical Control Scheme

Figure 2 shows the structure of the proposed hierarchical backstepping sliding-mode control scheme based on CFO for the EHSS with uncertainties. By using the backstepping method for the EHSS model, the present control strategy is divided into two control loops, which are named as virtual control loop and actual control loop. In the virtual control loop, the goal is to design virtual control laws $x_{2d}$ and $x_{3d}$ to ensure that $x_1$ tracks $x_d$ ideally, while in the actual control loop, it aims to design a final control law to stabilize the tracking errors of intermediate variables. By taking the unknown lumped disturbance into consideration, a novel CFO is adopted in the actual loop to provide a real-time accurate estimate ${\widehat{x}}_4$ of the lumped disturbance.

3.2. Design of Compensation Function Observer

To estimate disturbances with high accuracy, a CFO was recently proposed in [44]. Before employing this kind of observer, expanding $f_u$ in (4) as a new state, i.e., $x_4=f_u$, yields

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2,\hfill \\ {\dot{x}}_2=x_3,\hfill \\ {\dot{x}}_3=f_k+R_{2}u+x_4,\hfill \\ {\dot{x}}_4=\dot{f_u}.\hfill \end{array}\right.$$

(8)

Then, for (8), a fourth-order CFO is designed as

$$\left\{\begin{array}{c}{\dot{z}}_1=z_2,\hfill \\ {\dot{z}}_2=z_3,\hfill \\ {\dot{z}}_3=f_k+R_{2}u+L{e}_c+z_4,\hfill \\ {\dot{z}}_4=\lambda L{e}_c,\hfill \\ \widehat{f_u}=L{e}_c+z_4,\hfill \end{array}\right.$$

(9)

where $z_i(i=1,2,3,4)$ are the states of the CFO, $L=\left[l_3,l_2,l_1\right]$ is the vector of positive gain parameters, $e_c={[e_{c1},e_{c2},e_{c3}]}^T={[x_1-z_1,x_2-z_2,x_3-z_3]}^T$, and $\lambda$ is a positive filtering factor. Note that $z_4$ is a compensation term corresponding to $x_4$ in (8), but $z_4\ne x_4$, which is the significant difference from ESO and why the observer is called the compensation function observer [47].

Define ${\widehat{x}}_i$ as the estimates of $x_i(i=1,2,3,4)$, and $e_{ci}=x_i-{\widehat{x}}_i$ are the estimation errors. Then, from (8) and (9), we obtain

$$\left\{\begin{array}{c}{\widehat{x}}_1=z_1,\hfill \\ {\widehat{x}}_2=z_2,\hfill \\ {\widehat{x}}_3=z_3,\hfill \\ {\widehat{x}}_4={\widehat{f}}_u=L{e}_c+z_4,\hfill \end{array}\right.$$

(10)

and

$$\left\{\begin{array}{c}{\dot{e}}_{c1}={\dot{x}}_1-{\dot{z}}_1=e_{c2},\hfill \\ {\dot{e}}_{c2}={\dot{x}}_2-{\dot{z}}_2=e_{c3},\hfill \\ {\dot{e}}_{c3}={\dot{x}}_3-{\dot{z}}_3=f_k+R_{2}u+x_4-(f_k+R_{2}u+L{e}_c+z_4)=e_{c4}.\hfill \end{array}\right.$$

(11)

Furthermore, the time derivative of (10) is obtained as

$$\left\{\begin{array}{c}{\dot{\widehat{x}}}_1={\widehat{x}}_2,\hfill \\ {\dot{\widehat{x}}}_2={\widehat{x}}_3,\hfill \\ {\dot{\widehat{x}}}_3=f_k+R_{2}u+{\widehat{x}}_4,\hfill \\ {\dot{\widehat{x}}}_4=\lambda l_3{e}_{c1}+(l_3+\lambda l_2)e_{c2}+(l_2+\lambda l_1)e_{c3}+l_1{e}_{c4}.\hfill \end{array}\right.$$

(12)

Subtracting (12) from (8) yields

$${\dot{E}}_c=A_c{E}_c+B\dot{f_u},$$

(13)

where $E_c={\left[e_c^T,e_{c4}\right]}^T$ and

$$A_c=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ -\lambda l_3& -l_3-\lambda l_2& -l_2-\lambda l_1& -l_1\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right].$$

(14)

Based on the above design procedure, the stability of the CFO and the convergence of the estimation errors are given in the following theorem.

Theorem 1. 

Consider the CFO designed in (9) for the EHSS with lumped unkown disturbance $f_u$. Suppose that $f_u$ is fourth-order infinitesimal if the gain parameters are chosen, satisfying

$$\left\{\begin{array}{c}\hfill l_1\left(\lambda l_1+l_2\right)-\lambda l_2-l_3>0,\\ \hfill l_1\left(\lambda l_1+l_2\right)\left(\lambda l_2+l_3\right)-{\left(l_3+\lambda l_2\right)}^2+\lambda l_1^2{l}_3>0,\end{array}\right.$$

(15)

Then, the CFO is exponentially stable and the steady-state estimation error of the lumped disturbance is zero.

Proof. 

From (14), the characteristic equation of $A_c$ is calculated as

$$s^4+l_1{s}^3+\left(l_2+\lambda l_1\right)s^2+\left(l_3+\lambda l_2\right)s+\lambda l_3=0,$$

(16)

and the Routh array of $A_c$ is calculated as follows:

$s^4$	1	$l_2+\lambda l_1$	$\lambda l_3$
$s^3$	$l_1$	$l_3+\lambda l_2$	0
$s^2$	$l_1\left(\lambda l_1+l_2\right)-\lambda l_2-l_3$	$\lambda l_3$
$s^1$	${\displaystyle \frac{l_1\left(\lambda l_1+l_2\right)\left(\lambda l_2+l_3\right)-{\left(l_3+\lambda l_2\right)}^2+\lambda l_1^2{l}_3}{l_1\left(\lambda l_1+l_2\right)-\lambda l_2-l_3}}$
$s^0$	$\lambda l_3$

According to the Routh–Hurwitz criterion, the system with $A_c$ is exponentially stable if all the elements in the first column of the Routh array are positive, i.e., the inequalities (9) hold. Furthermore, since $f_u$ is fourth-order infinitesimal, the fourth derivative $f_u$ is zero, i.e., ${\stackrel{⃜}{f}}_u=0$. Taking the time derivative of (13) three times yields

$${\stackrel{⃜}{E}}_c=A_c{\stackrel{⃛}{E}}_c+B\stackrel{⃜}{f_u}=A_c{\stackrel{⃛}{E}}_c.$$

(17)

Because of the stability of $A_c$, we obtain

$$\underset{t\to \infty }{lim}{\stackrel{⃛}{E}}_c=\underset{t\to \infty }{lim}[{\stackrel{⃛}{e}}_c,{\stackrel{⃛}{e}}_{c4}]=\underset{t\to \infty }{lim}[e_{c4},{\dot{e}}_{c4},{\ddot{e}}_{c4},{\stackrel{⃛}{e}}_{c4}]=0,$$

(18)

i.e.,

$$\underset{t\to \infty }{lim}{e}_{c4}=0.$$

(19)

Therefore, the steady-state estimation error of the lumped disturbance is zero.

This completes the proof of Theorem 1. □

Remark 1. 

It is worth noting that the CFO designed by Equation (9) has four gain parameters ($l_1,l_2,l_3,\lambda$), and the condition (15) is a little harsh for the parameter tuning of the CFO. However, a method of pole assignment can be employed to facilitate the search for parameters and ensure the stability of the system. The characteristic equation of the CFO can be rewritten as

$$s^4+l_1{s}^3+\left(l_2+\lambda l_1\right)s^2+\left(l_3+\lambda l_2\right)s+\lambda l_3={\left(s+\omega \right)}^2{\left(s+4\omega \right)}^2=0,$$

(20)

where $\omega >0$ is the bandwidth, and $-\omega ,-\omega ,-4\omega ,-4\omega$ are the poles of the CFO, having a relationship with the gain parameters as follows:

$$\left\{\begin{array}{c}{l}_1=10\omega ,\hfill \\ l_2+\lambda l_1=33{\omega }^2,\hfill \\ l_3+\lambda l_2=40{\omega }^3,\hfill \\ \lambda l_3=16{\omega }^4.\hfill \end{array}\right.$$

(21)

One solution of the above equations can be obtained as

$$l_1=10\omega ,l_2=25{\omega }^2,l_3=20{\omega }^3,\lambda ={\displaystyle \frac{4}{5}}\omega .$$

(22)

Since ω is the only adjustable parameter, the selection of the gain parameters is quite simple. Generally speaking, a big bandwidth obtains a better observation performance. However, it may amplify the influence of high-frequency noise to the system, and even worse, cause the instability of the control system. Therefore, the bandwidth should be suitably selected by a trial and error method.

3.3. Design of Backstepping Sliding-Mode Controller

Based on the CFO, the backstepping technique integrated with sliding-mode control is employed to design a controller to achieve the position tracking control objective.

Firstly, the tracking errors are defined as

$$\left\{\begin{array}{c}{e}_1=x_1-x_d,\\ e_2=x_2-x_{2d},\\ e_3=x_3-x_{3d},\end{array}\right.$$

(23)

where $x_d$ is the desired trajectory, and $x_{2d}$ and $x_{3d}$ are virtual control laws to be designed step by step as follows:

Step 1: To stabilize $e_1$, the first Lyapunov function is chosen as

$$V_1={\displaystyle \frac{1}{2}}{e}_1^2.$$

(24)

Based on (23), the derivative of $V_1$ is computed by

$${\dot{V}}_1=e_1{\dot{e}}_1=e_1\left({\dot{x}}_1-{\dot{x}}_d\right)=e_1\left(e_2+x_{2d}-{\dot{x}}_d\right).$$

(25)

To make ${\dot{V}}_1$ negative, the virtual control law $x_{2d}$ is chosen as

$$x_{2d}=-k_1{e}_1+{\dot{x}}_d,$$

(26)

where $k_1$ is a positive design parameter. Substituting (26) into (25) yields

$${\dot{V}}_1=-k_1{e}_1^2+e_1{e}_2.$$

(27)

Obviously, if $e_2=0$, then ${\dot{V}}_1⩽0$.

Step 2: Similarly, to stabilize $e_2$, the second Lyapunov function is chosen as

$$V_2=V_1+{\displaystyle \frac{1}{2}}{e}_2^2.$$

(28)

Based on (23) and (27), the derivative of $V_2$ is obtained as

$${\dot{V}}_2=-k_1{e}_1^2+e_1{e}_2+e_2\left(e_3+x_{3d}-{\dot{x}}_{2d}\right).$$

(29)

To make ${\dot{V}}_2$ negative, the virtual control law $x_{3d}$ is chosen as

$$x_{3d}=-k_2{e}_2-e_1+{\dot{x}}_{2d},$$

(30)

where $k_2$ is a positive design parameter. Then, substituting (30) into (29) yields

$${\dot{V}}_2=-k_1{e}_1^2-k_2{e}_2^2+e_2{e}_3.$$

(31)

If $e_3=0$, then ${\dot{V}}_2⩽0$.

Step 3: To design a final actual control law for u, a sliding-mode surface is chosen as

$$S=c_1{e}_1+c_2{e}_2+e_3,$$

(32)

where $c_1$ and $c_2$ are positive design parameters. Taking the time derivative of S and using (8) yields

$$\begin{array}{cc}\hfill \dot{S}=& c_1{\dot{e}}_1+c_2{\dot{e}}_2+{\dot{e}}_3\hfill \\ \hfill =& c_1\left(x_2-{\dot{x}}_d\right)+c_2\left(x_3+k_1\left(x_2-{\dot{x}}_d\right)-{\ddot{x}}_d\right)+f_k+R_{2}u+x_4-{\dot{x}}_{3d}\hfill \\ \hfill =& (c_1+c_2{k}_1)x_2+c_2{x}_3+x_4+X_d+f_k+R_{2}u\hfill \end{array}$$

(33)

where $X_d=-\left(c_1+c_2{k}_1\right){\dot{x}}_d-c_2{\ddot{x}}_d-{\dot{x}}_{3d}$ with

$${\dot{x}}_{3d}=-\left(k_1{k}_2+1\right)x_2-\left(k_1+k_2\right)x_3+\left(k_1{k}_2+1\right){\dot{x}}_d+\left(k_1+k_2\right){\ddot{x}}_d+{\stackrel{⃛}{x}}_d.$$

(34)

The final Lyapunov function is chosen as

$$V_3={\displaystyle \frac{1}{2}}{S}^2+V_2.$$

(35)

Based on (33), the derivative of $V_3$ is obtained as

$$\begin{array}{cc}\hfill {\dot{V}}_3=& S\dot{S}-k_1{e}_1^2-k_2{e}_2^2+e_2{e}_3\hfill \\ \hfill =& S\left[(c_1+c_2{k}_1)x_2+c_2{x}_3+x_4+X_d+f_k+R_{2}u\right]\hfill \\ \hfill & -k_1{e}_1^2-k_2{e}_2^2+e_2(S-c_1{e}_1-c_2{e}_2)\hfill \\ \hfill =& -k_1{e}_1^2-(k_2+c_2)e_2^2+e_{2}S-c_1{e}_1{e}_2\hfill \\ \hfill & +S\left[(c_1+c_2{k}_1)x_2+c_2{x}_3+x_4+X_d+f_k+R_{2}u\right].\hfill \end{array}$$

(36)

To make ${\dot{V}}_3$ negative, the actual control law u is designed as

$$\begin{array}{c}\hfill u=-{\displaystyle \frac{1}{R_2}}\left[\left(c_1+c_2{k}_1\right)x_2+c_2{x}_3+{\widehat{x}}_4+X_d+f_k+k_{3}S\right],\end{array}$$

(37)

where ${\widehat{x}}_4$ is the estimate of the lumped disturbance $f_u$ from the CFO in (9), and $k_3$ is a positive design parameter.

Summarizing the above results gives the following theorem for the stability of the closed-loop control system.

Theorem 2. 

Consider the EHSS with lumped disturbance described by (7). If the estimate of the lumped disturbance is employed from the CFO (9) and the design parameters are selected such that $k_1>{\displaystyle \frac{c_1}{2}}>0,k_2>{\displaystyle \frac{c_1+1}{2}}>0,k_3>{\displaystyle \frac{1}{2}}$, then the backstepping sliding-mode control laws (26), (30) and (37) guarantee that the closed-loop system is exponentially stable, and the tracking error signals converge to the origin.

Proof. 

Consider the final Lyapunov function $V_3$ in (35). Substituting (37) into (36) yields

$$\begin{array}{c}\hfill {\dot{V}}_3=-k_1{e}_1^2-k_2{e}_2^2-k_3{S}^2+e_{c4}S+e_{2}S-c_1{e}_1{e}_2.\end{array}$$

(38)

According to Theorem 1, the estimation error of CFO converges to zero, i.e.,

$$\underset{t\to \infty }{lim}{e}_{c4}=0.$$

(39)

In the sense of limiting, Equation (38) becomes

$$\begin{array}{cc}\hfill {\dot{V}}_3=& -k_1{e}_1^2-k_2{e}_2^2-k_3{S}^2+e_{2}S-c_1{e}_1{e}_2\hfill \\ \hfill \le & -k_1{e}_1^2-k_2{e}_2^2-k_3{S}^2+|e_{2}S|+|c_1{e}_1{e}_2|.\hfill \end{array}$$

(40)

Using Young’s inequality for the last two terms of (40) results in

$$\begin{array}{cc}\hfill & \left|e_{2}S\right|\le {\displaystyle \frac{1}{2}}{e}_2^2+{\displaystyle \frac{1}{2}}{S}^2,\left|c_1{e}_1{e}_2\right|\le {\displaystyle \frac{c_1}{2}}{e}_1^2+{\displaystyle \frac{c_1}{2}}{e}_2^2.\hfill \end{array}$$

(41)

Substituting (41) into (40) yields

$$\begin{array}{cc}\hfill {\dot{V}}_3\le & -k_1{e}_1^2-k_2{e}_2^2-k_3{S}^2+|e_{2}S|+|c_1{e}_1{e}_2|\hfill \\ \hfill \le & -\left(k_1-{\displaystyle \frac{c_1}{2}}\right)e_1^2-\left(k_2-{\displaystyle \frac{c_1+1}{2}}\right)e_2^2-\left(k_3-{\displaystyle \frac{1}{2}}\right)S^2.\hfill \end{array}$$

(42)

Rewriting inequality (42) in a compact form, we obtain

$${\dot{V}}_3\le -{\alpha }_0{V}_3,$$

(43)

where

$$\begin{array}{cc}\hfill & {\alpha }_0=min\left(k_1-{\displaystyle \frac{c_1}{2}},k_2-{\displaystyle \frac{c_1+1}{2}},k_3-{\displaystyle \frac{1}{2}}\right).\hfill \end{array}$$

(44)

Selecting the design parameters $k_1>{\displaystyle \frac{c_1}{2}}>0,k_2>{\displaystyle \frac{c_1+1}{2}}>0,k_3>{\displaystyle \frac{1}{2}}$ to ensure ${\alpha }_0>0$. Then, the solution of (43) is

$$V_3\left(t\right)\le V_3\left(0\right)e^{-{\alpha }_{0}t},$$

(45)

which means that $V_3\left(t\right)$ converges exponentially to zero, i.e., as $t\to \infty$, $e_i(i=1,2,3)\to 0$ and $S\to 0$. Therefore, the proposed CFO-based backstepping sliding-mode controller guarantees the stability of the closed-loop system of the EHSS, and the tracking errors converge to zeros.

This completes the proof of Theorem 2. □

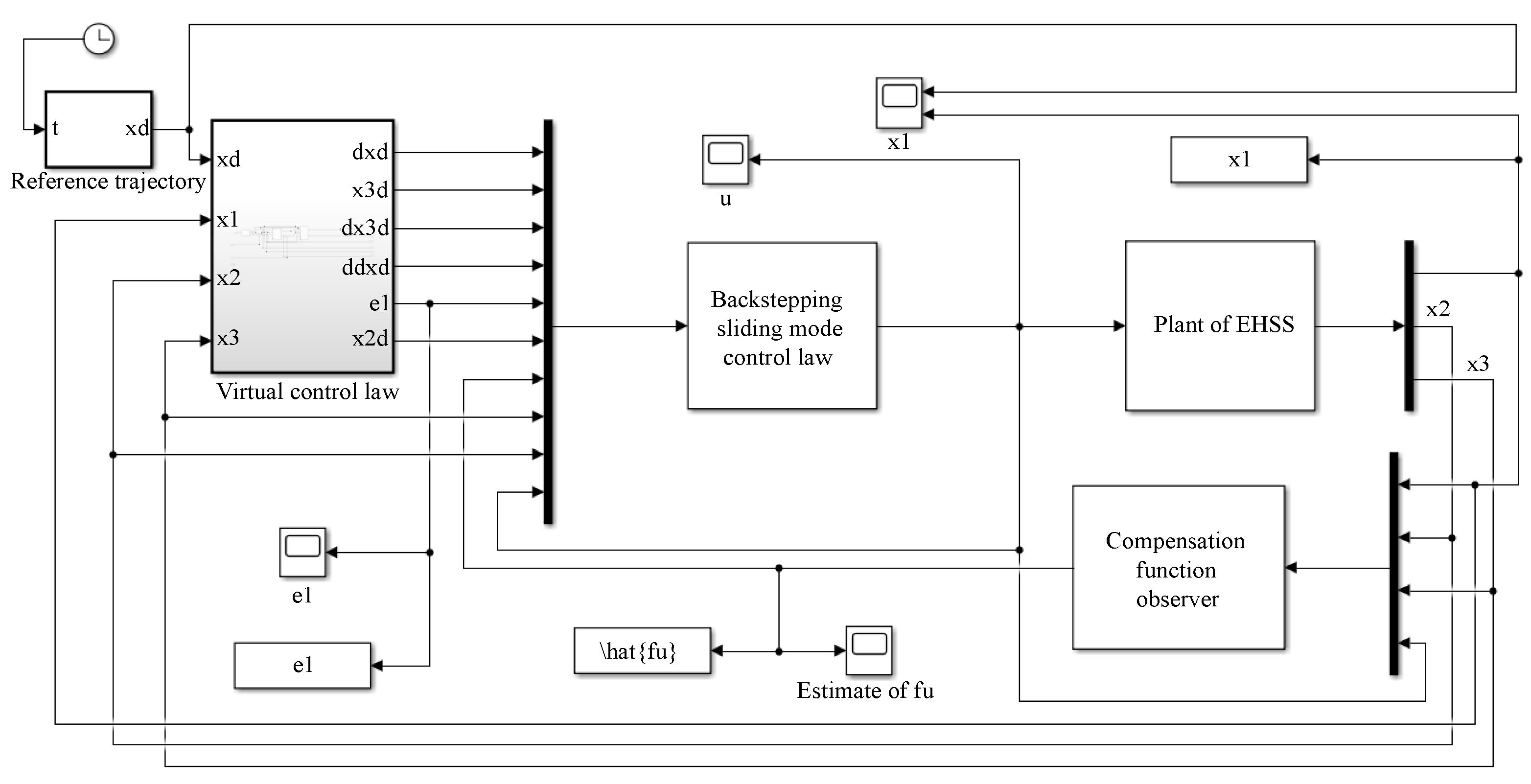
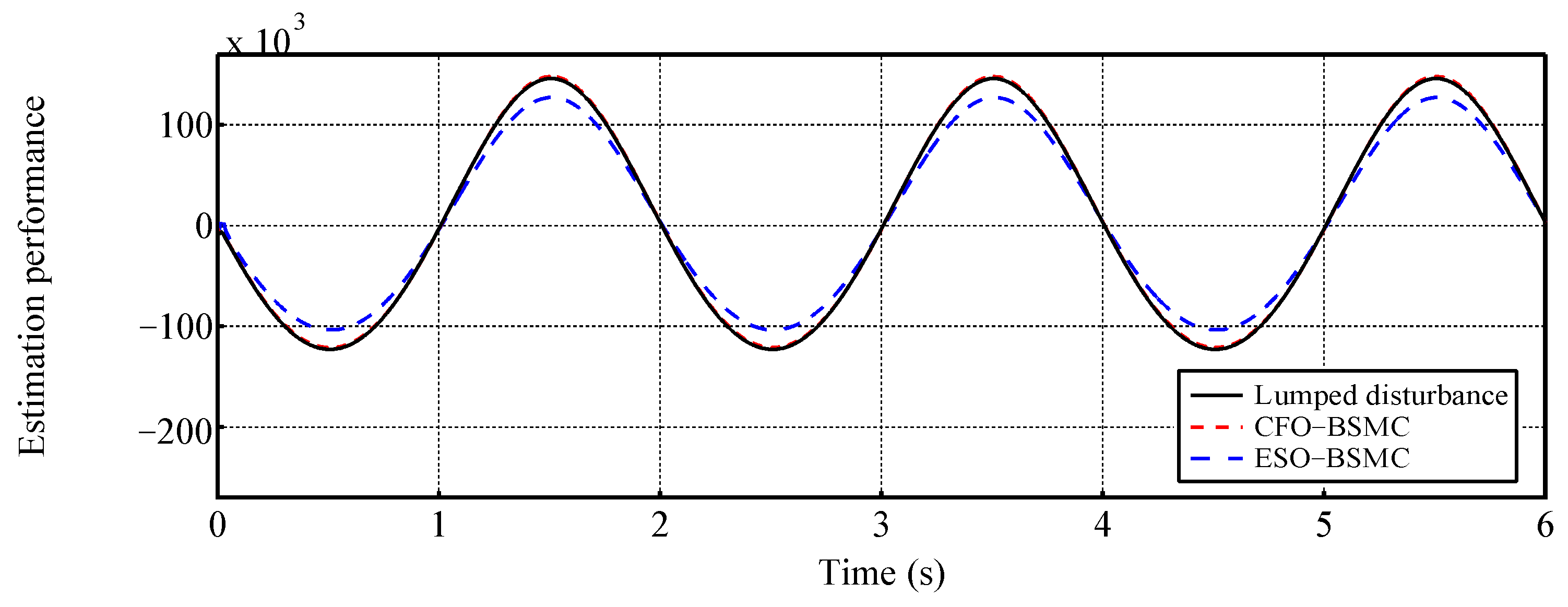
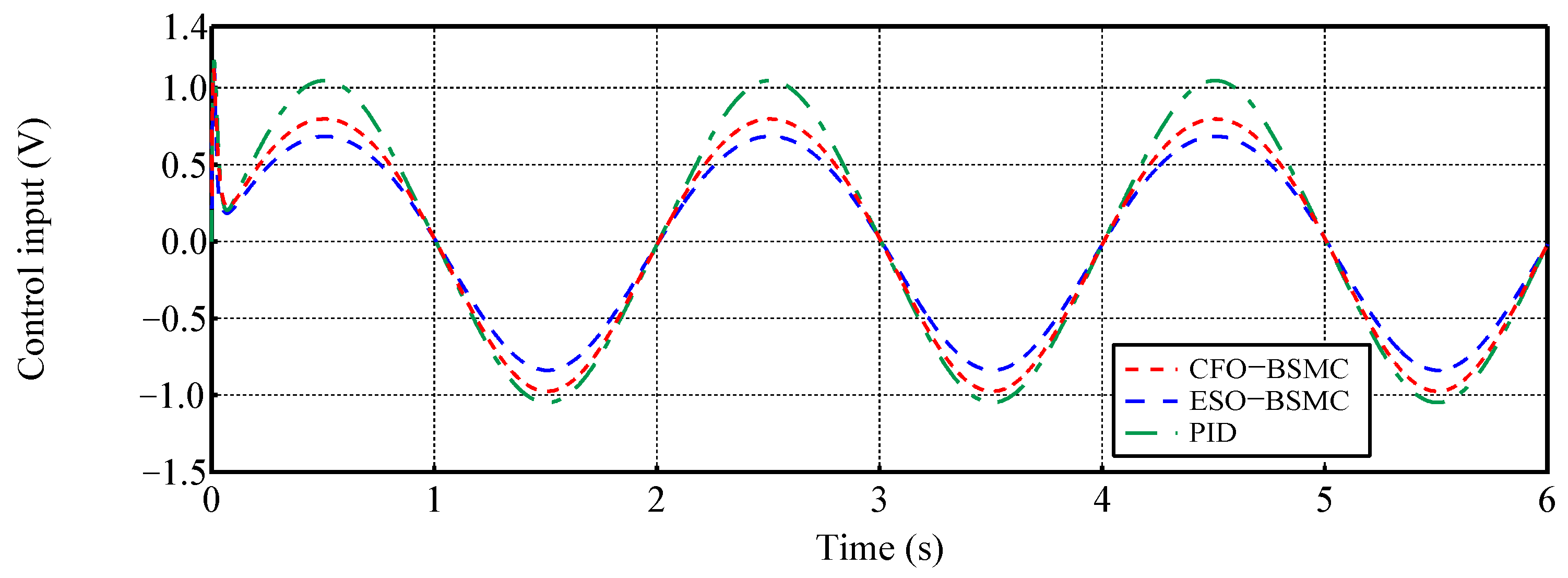
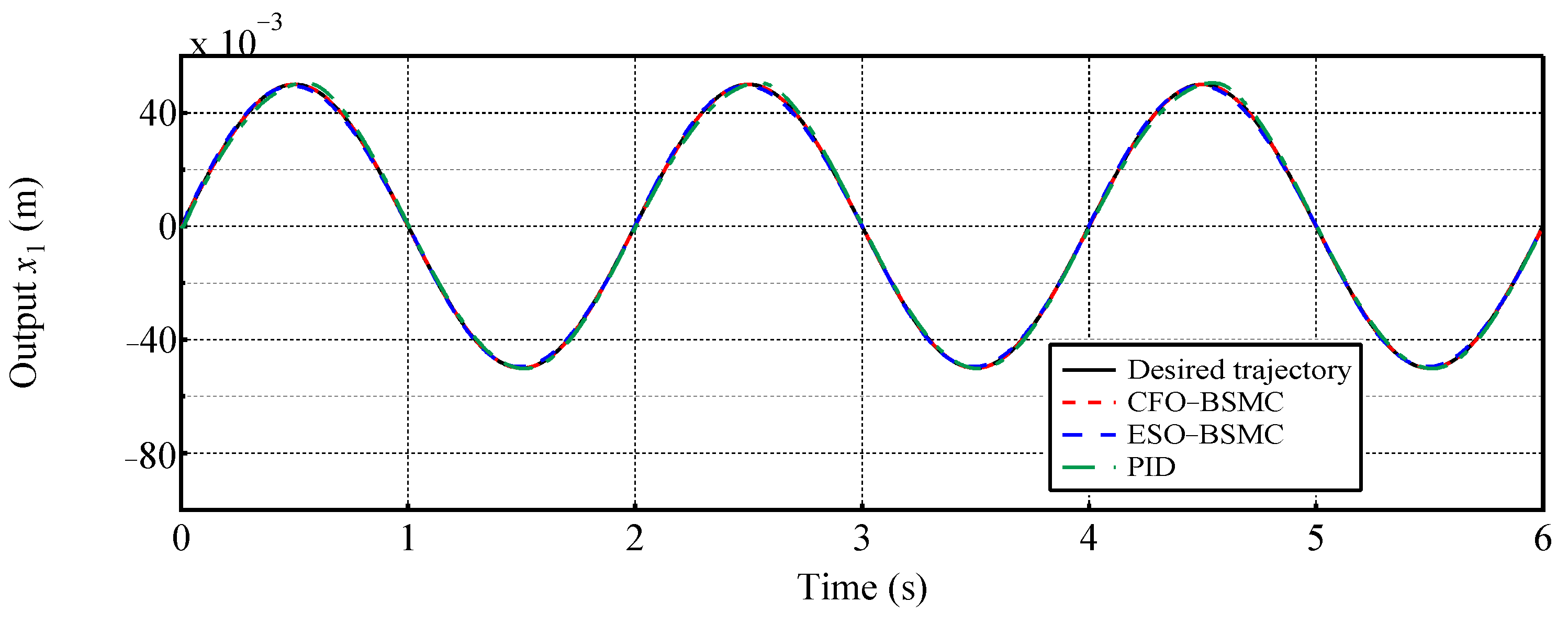
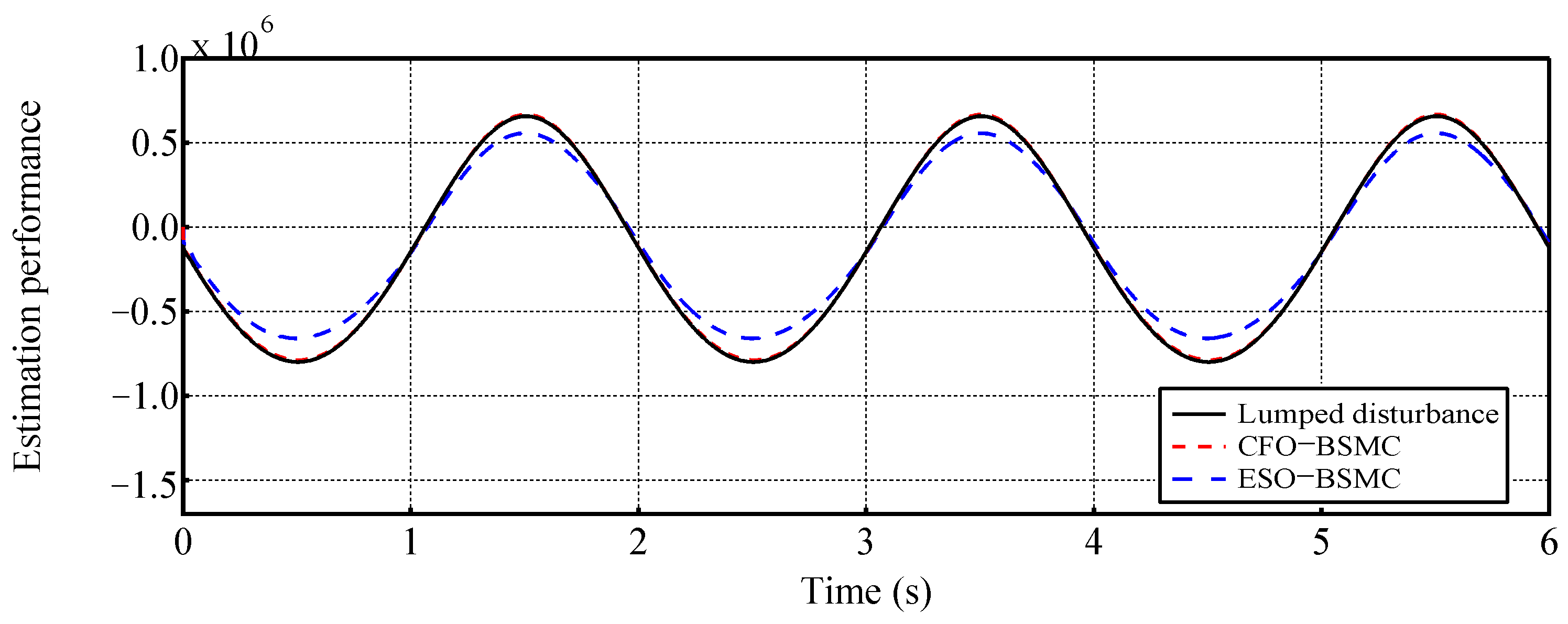
4. Simulation Results and Analysis

To evaluate the effectiveness and efficiency of the proposed control scheme for the EHSS, two different working cases are considered. The first case is to track an exponential trajectory with a relatively small $f_d$ disturbance, while the second case is to track a sinusoidal position trajectory with a large $f_d$ disturbance.

The simulations are conducted on a MATLAB/Simulink platform. As shown in Figure 3, the simulation model is composed of are four components, i.e., the plant of EHSS, compensation function observer (CFO), virtual control law (VCL) and backstepping sliding-mode control law (BSMC). The plant of EHSS, CFO and BSMC are modeled using S-Function, while VCL is built using the MATLAB Function. The physical parameters of the EHSS used in the simulation model are listed in

Table 1. Physical parameters of the electro-hydraulic servo system.

Parameters	Value	Parameters	Value
$m\left(\mathrm{kg}\right)$	30	$k_t\left({\mathrm{m}}^3/\mathrm{s}/\mathrm{V}/{\mathrm{Pa}}^{1/2}\right)$	$1\times {10}^{-8}$
$V_t\left({\mathrm{m}}^3\right)$	$2.398\times {10}^{-5}$	$P_s\left(\mathrm{MPa}\right)$	10
${\beta }_e\left(\mathrm{Pa}\right)$	$7\times {10}^8$	$C_t({\mathrm{m}}^3/\mathrm{s}/\mathrm{Pa})$	$3\times {10}^{-12}$
$A\left({\mathrm{m}}^2\right)$	$9.047\times {10}^{-4}$	$B(\mathrm{N}·\mathrm{s}·{\mathrm{m}}^{-1})$	$4\times {10}^3$

, and the system parameters such as the coefficient of the viscous friction force B and leakage coefficient of the system $C_t$ are assumed to be perturbed, which result in the uncertain parts $\Delta R_1$ and $\Delta R_2$ in (6) as $\Delta R_1=0.1R_{1}sin\left(\pi t\right)$ and $\Delta R_2=0.1R_{2}sin\left(\pi t\right)$. The system sample time is taken as $0.001$ s.

In addition, to illustrate the superiority of the proposed control approach, the following controllers are performed as comparison schemes.

(1) 

CFO-BSMC: This is the proposed backstepping sliding-mode controller based on CFO presented in Section 3. By trial and error, the parameters of the controller in (26), (30) and (37) are selected as $k_1=50,k_2=100,k_3=200,c_1=20$, $c_2$ = 2000. The bandwidth of the proposed CFO in Remark 1 is chosen as $\omega =1200$. Therefore, the gain parameters of the CFO are $l_1=1.2\times {10}^4,l_2=3.6\times {10}^7,l_3=3.456\times {10}^{10},\lambda =960$.

(2) 

ESO-BSMC: This is the backstepping sliding-mode controller based on the ESO proposed in [46]. To ensure a fair comparison, the parameters of the controller are chosen as the same as those in CFO-BSMC. In addition, the poles of the ESO are assigned as the same as CFO, having the characteristic equation $s^4+l_{e1}{s}^3+l_{e2}{s}^2+$$l_{e3}s+l_{e4}={\left(s+\omega \right)}^2{\left(s+4\omega \right)}^2=0$, where $l_{e1},l_{e2},l_{e3},l_{e4}$ are the gain parameters of the ESO. The bandwidth is also chosen as $\omega =1200$, which results in $l_{e1}=10\omega =1.2\times {10}^4,l_{e2}=33{\omega }^2=4.752\times {10}^7,l_{e3}=40{\omega }^3=6.912\times {10}^{10},l_{e4}=16{\omega }^4=3.31776\times {10}^{13}$. Note that the maximum gain of the ESO is 960 times that of the CFO.

(3) 

PID: This is the well-known proportional–integral–derivative (PID) controller, which has a wide range of application in the industry [12]. In order to obtain a group of optimal control gains for the PID, the auto-tuning technique in MATLAB is adopted, which results in $k_p=1062,k_i=35,002,k_d=0$.

4.1. Case 1: Tracking an Exponential Position Trajectory

In this case, the desired trajectory is selected as an exponential signal whose initial state is zero and steady state is 0.005 m, i.e., $x_d=0.005(1-e^{-50t})$ m, and a time-varying sinusoidal external disturbance $f_d=350sin\left(\pi t\right)$ N is imposed to the EHSS.

The simulation results of the EHSS under the three controllers are depicted in Figure 4, Figure 5, Figure 6 and Figure 7, which record tracking performance, the tracking errors, the estimation performance for the lumped disturbance, and the control input, respectively.

As seen from Figure 4, the proposed controller achieves superior tracking control performance over the other two controllers in the presence of parameter perturbations and time-varying sinusoidal disturbance. Specifically, by comparing the tracking error curves in Figure 5 during the transient and steady stages, it is evident that the tracking error of the PID controller fluctuates more seriously than that of CFO-BSMC. The reason for this is that the lumped disturbance can be estimated and compensated by both ESO and CFO. Furthermore, by examining the estimation curves of ESO and CFO in Figure 6, it is apparent that CFO obtains a higher estimation accuracy than ESO under the same bandwidth. Figure 7 exhibits that the control signals of the three controllers are smooth, continuous and bounded. This group of simulation results demonstrates the effectiveness and superiority of the proposed controller.

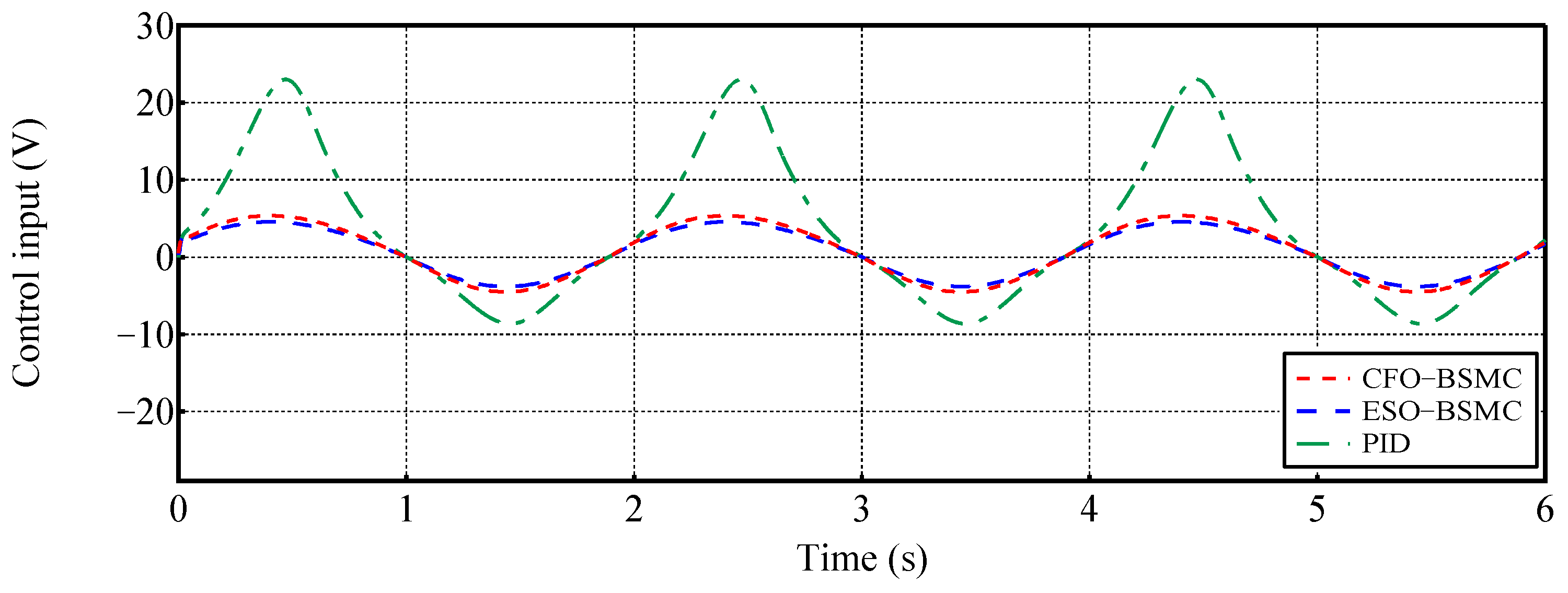
4.2. Case 2: Tracking a Sinusoidal Position Trajectory

To further test the tracking performance of the proposed controller, a smooth sinusoidal desired trajectory is employed as $x_d=0.05$ sin($\pi t$) m. In addition, a large external disturbance is injected into the system to examine the robustness of the proposed controller. The disturbance is given as $f_d=1000+5500sin\left(\pi t\right)$ N, which is composed of a large constant load force and a large time-varying sinusoidal disturbance.

The output tracking performance of the three controllers is presented in Figure 8. As can be seen, the three controllers are able to drive the output of the EHSS close to the desired trajectory. Furthermore, a comparative result of tracking errors is shown in Figure 9, which indicates that the proposed CFO-BSMC has the smallest tracking error, followed by ESO-BSMC, and the worst is the PID, which means the proposed controller achieves the best transient and steady-state tracking performance. Moreover, by comparing the estimation performances between CFO and ESO in Figure 10, it is evident that the ESO presents a phase lag in estimating the disturbance, while the proposed CFO can estimate the disturbance accurately. The smooth, continuous and bounded control signals are shown in Figure 11.

In order to quantitatively analyze the control performance of the three controllers, three performance indices are introduced as follows [17]:

(1) Mean absolute error:

$$E_{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|e_1\left(i\right)\right|.$$

(46)

(2) Root mean square error:

$$E_{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(\left|e_1\left(i\right)\right|-E_{MAE}\right)}^2}.$$

(47)

(3) Integrated time absolute error:

$$E_{ITAE}=\sum _{i=1}^{N}i{T}_s\left|e_1\left(i\right)\right|,$$

(48)

where $T_s$ is the simulation step.

The obtained comparison results of the performance indices under the three controllers are presented in

Table 2. Comparison results of performance indices under different control methods.

Control Methods	${\mathit{E}}_{\mathit{MAE}}\left(\mathbf{m}\right)$	${\mathit{E}}_{\mathit{RMSE}}\left(\mathbf{m}\right)$	${\mathit{E}}_{\mathit{ITAE}}\left(\mathbf{m}\right)$
PID [12]	$1.08500\times {10}^{-3}$	$3.41560\times {10}^{-7}$	$12.9343$
ESO-BSMC [46]	$4.72000\times {10}^{-4}$	$9.05394\times {10}^{-8}$	$8.61876$
CFO-BSMC (Proposed)	$5.57388\times {10}^{-5}$	$2.03874\times {10}^{-9}$	$1.71282$

. It is clearly seen that all the indices of the proposed CFO-BSMC are the smallest among the three controllers. More specifically, compared with PID and ESO-BSMC, the mean absolute error $E_{\mathrm{MAE}}$ of the proposed CFO-BSMC is increased by $94.86\%$ and $88.19\%$, and the the root mean square error $E_{RMSE}$ is improved by $99.4\%$ and $97.75\%$, respectively. These results verify that the proposed control approach achieves the best tracking accuracy. In addition, the integrated time absolute error $E_{\mathrm{ITAE}}$ is to weigh the tracking error by time, which represents the system insensitivity to initial error and sensitivity to the steady error. Obviously, the $E_{\mathrm{ITAE}}$ of the proposed controller is the smallest, which means the proposed controller performs the best robustness against external disturbances.

The simulation results in this group demonstrate that even in the presence of large external disturbances and system perturbations, the proposed control method can effectively estimate the lumped disturbance and compensate for its effect, achieving a high-precision tracking control for a sinusoidal trajectory.

5. Conclusions

In this paper, a novel CFO-based backstepping sliding-mode control method was proposed for the high-accuracy tracking control of an EHSS in the presence of lumped disturbance. A fourth-order CFO that fully utilized the system state information was designed to accurately estimate and compensate for the lumped disturbance, and a sliding-mode controller was developed by integrating the CFO into the backstepping design procedure. A rigorous stability analysis of the closed-loop control system was given by using Lyapunov’s theory. Comparative simulations demonstrated that it was capable of estimating the disturbance with a higher estimation accuracy, i.e, compared with PID- and ESO-based BSMC methods, the tracking accuracy improved by $94.86\%$ and $88.19\%$, respectively.

It is worth mentioning that due to the limitations of working conditions and hardware equipments, there always exist some constraints on the input or output in the practical application of EHSSs. In order to improve the practicality of the control method, it will be interesting to exploit a controller with the input or output constraint. In addition, we plan to build a semi-physical EHSS experimental platform to verify the control performance of the proposed approach. Furthermore, it is meaningful and significant to recalibrate the servo valves when the control system no longer works properly under the appearance of some wear in the servo valves. All these issues will be investigated in our future work.