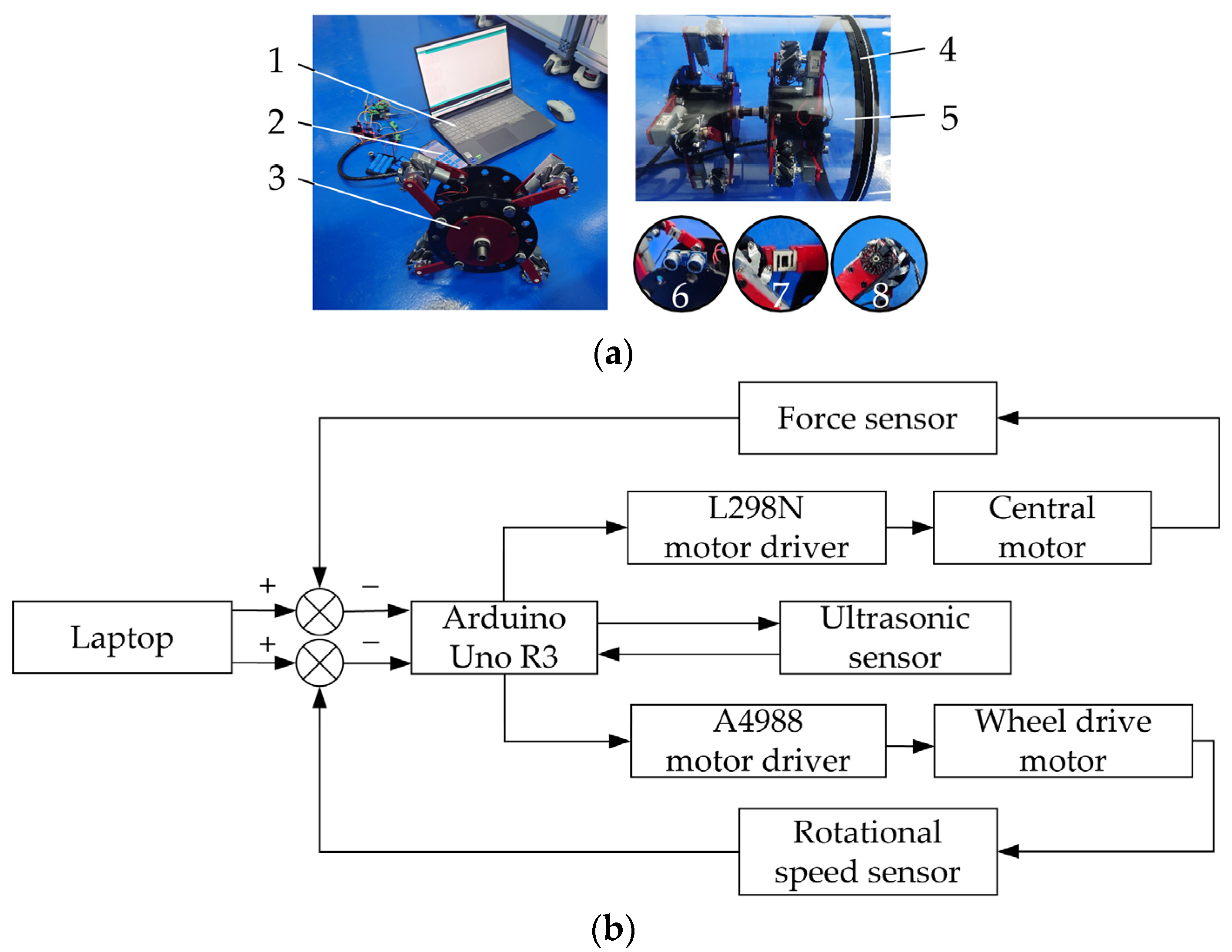
1. Introduction
Pipeline transportation is a method utilized for the long-distance conveyance of liquids and gases using pipelines. This mode of transport offers numerous advantages, including enhanced efficiency, cost-effectiveness, environmental sustainability, safety, and operational continuity [
1]. Pipeline transportation is acknowledged as one of the five principal modes of transport, alongside road, water, rail, and air transportation [
2]. The durability of pipelines depends on several factors, including the materials employed, design specifications, operational conditions, and maintenance protocols. Typically, the expected service life of steel pipes is around 30 years, while polyethylene pipes may surpass 50 years [
3]. Nevertheless, pipelines are susceptible to problems such as corrosion, wear, and degradation over time, making regular inspection and maintenance essential for ensuring their safe operation [
4]. Pipeline robots, which function as advanced tools for the inspection and maintenance of pipelines, are extensively employed in activities such as cleaning, inspection, repair, and welding [
5,
6]. The implementation of these measures is essential for extending the operational lifespan of pipelines and minimizing the risk of safety incidents.
A high-performance locomotion device is crucial for enhancing the passability and maneuverability of pipeline robots. Pipeline walking devices can be classified into several categories based on their operational modes, including support-wheel, track, and squirm types. The support-wheel type typically comprises a support module, a wall-press mechanism, and a driving wheel module. This configuration offers advantages such as a simple structure and high operational speed [
7]. The wall-press mechanism serves a dual purpose: it provides a reliable preload for the wheel drive and, when combined with the support module, enables the adaptation of pipeline robots to pipelines of varying diameters [
8]. By strategically arranging the spatial configuration of the walking wheels within the driving wheel module, various movement modes can be realized, including rectilinear [
9], rotational [
10], and helical [
11]. In contrast, the track-type walking device utilizes a track as its wheel module, which increases the contact area with the inner wall of the pipe compared to the support-wheel type. This design improves its efficacy in traversing pipes with slippery or rough inner surfaces [
12]. However, this type of walking device is characterized by a more complex structure due to the necessity of tensioning mechanisms within the tracks, while its motion is generally limited to a rectilinear mode [
13]. Squirm type walking devices, on the other hand, do not employ drive wheels; instead, they achieve bionic movement by adjusting the angles of their joints. Common variants include snake-type [
14] and inchworm-type devices [
15]. These walking devices demonstrate a high degree of freedom, which is dependent on the number of joints, thereby enabling a wide range of intricate movement patterns [
16]. This methodology is especially effective for managing irregular and intricate pipeline configurations; nonetheless, it is characterized by a relatively low operational speed.
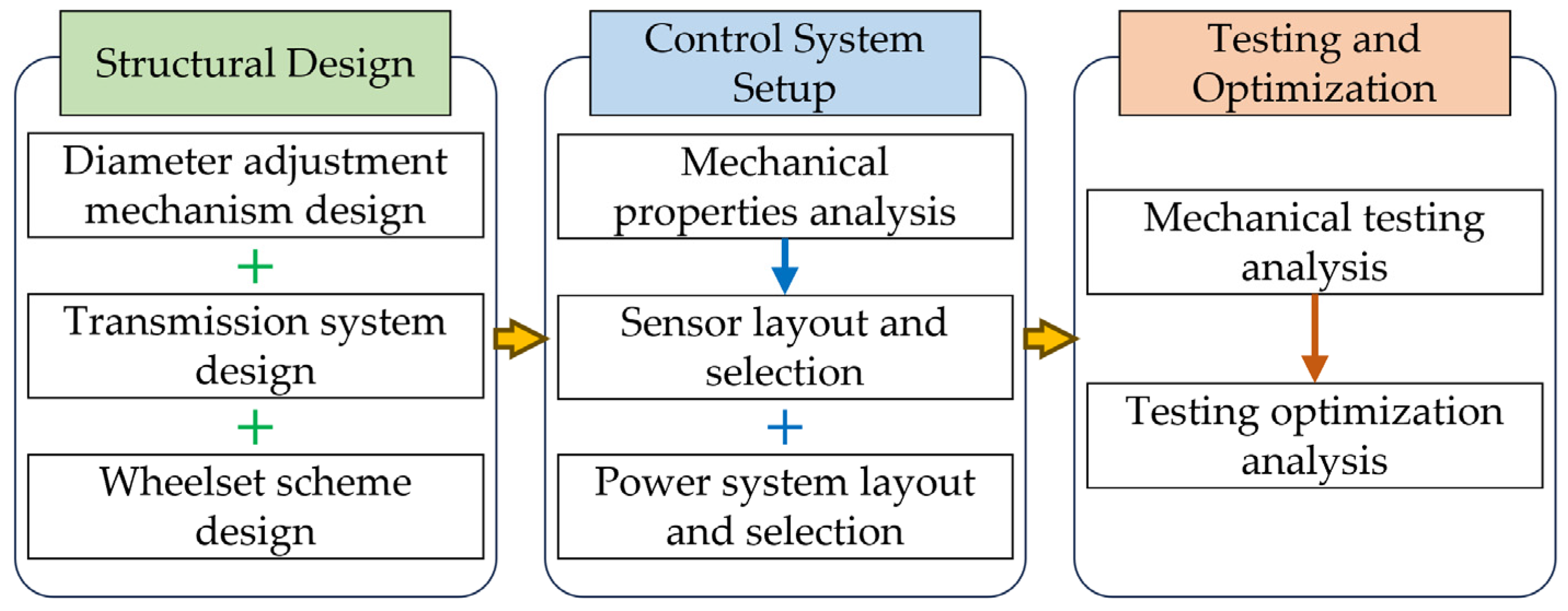
This paper provides a comprehensive comparison of the characteristics of various existing pipeline walking devices. To address the shortcomings of traditional support-wheel type devices—such as their singular mode of motion, limited capability to traverse obstacles, and insufficient adaptability to complex and irregular pipeline configurations—a modular walking device (MWD) is proposed, with research findings expected to support the development of efficient, fully mechanized pipeline detection technology.
The structure of this paper is organized as follows [
17,
18]: The second section presents a literature review and a proposed design scheme related to the diameter adjustment mechanism, drive module, and evaluation of work performance indicators. The third section introduces the design and analysis process of the WMD proposed in this study, including the design of the variable diameter module, drive module, walking module, and an analysis of mechanical fluctuations during movement. The fourth section examines the performance of the WMD during testing, with a primary focus on the force fluctuations in the walking wheel and the optimization of parameters based on orthogonal testing. Finally, the fifth section presents conclusions and recommendations for future research.
3. Structural Design and Analysis
3.1. Design and Analysis of the Variable Diameter Module
In order to clarify the influence of the primary component parameters of the variable diameter module on the outer diameter of the WMD, an investigation into its structure and key parameters was conducted. Given the circumferential symmetry of the variable diameter module, a representative structure was selected for modeling and analysis, as illustrated in
Figure 4.
Through structural analyses, it was established that the variable diameter ratio (
λ) of the MWD varies in relation to the parameters outlined below:
Note: k signifies the ratio between the length of wheel brackets l2 and the rotary radius of turntable bolted hole l1.
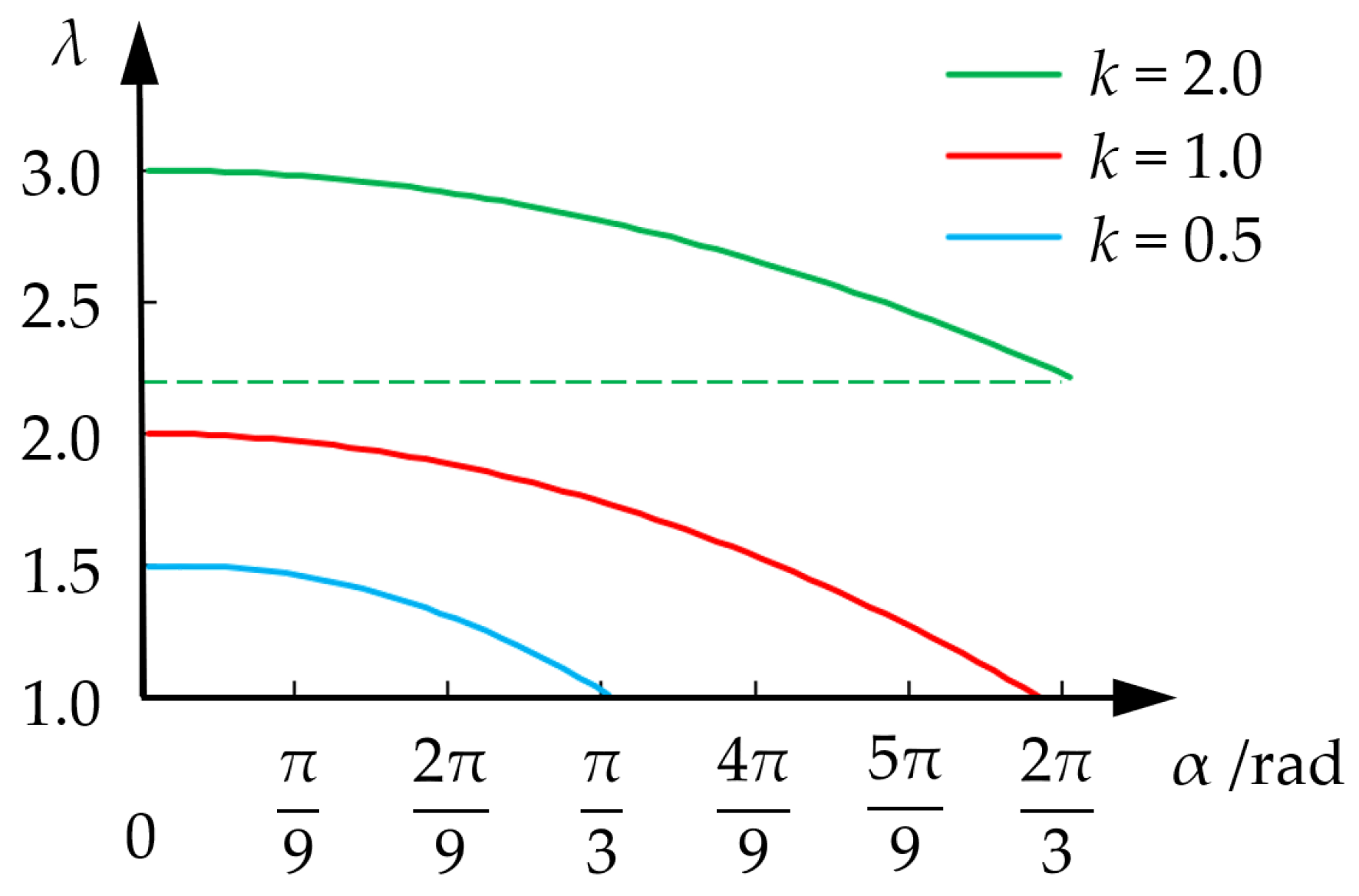
Figure 5 illustrates the relationship between the variable diameter law of MWD, with the phase angle of the turntable (
α) represented on the horizontal axis, while the variable diameter ratio (λ) is shown on the vertical axis. In light of structural limitations, it is essential that the outer diameter of MWD (
R) surpasses the rotary radius of the turntable’s bolted hole (
l). Consequently, this requirement stipulates that the variable diameter ratio (
λ) must exceed 1.
Taking into account the impact of variable diameter ratio parameters, it is possible to attain a more extensive range of variation within a specific range of turntable phase angles. When the ratio is set at k = 1.0, the variable diameter ratio (λ) is observed to range from 1.0 to 2.0, while the phase angle of the turntable (α) varies from 0 to 2.02 rad.
3.2. Design and Mechanical Analysis of Transmission System
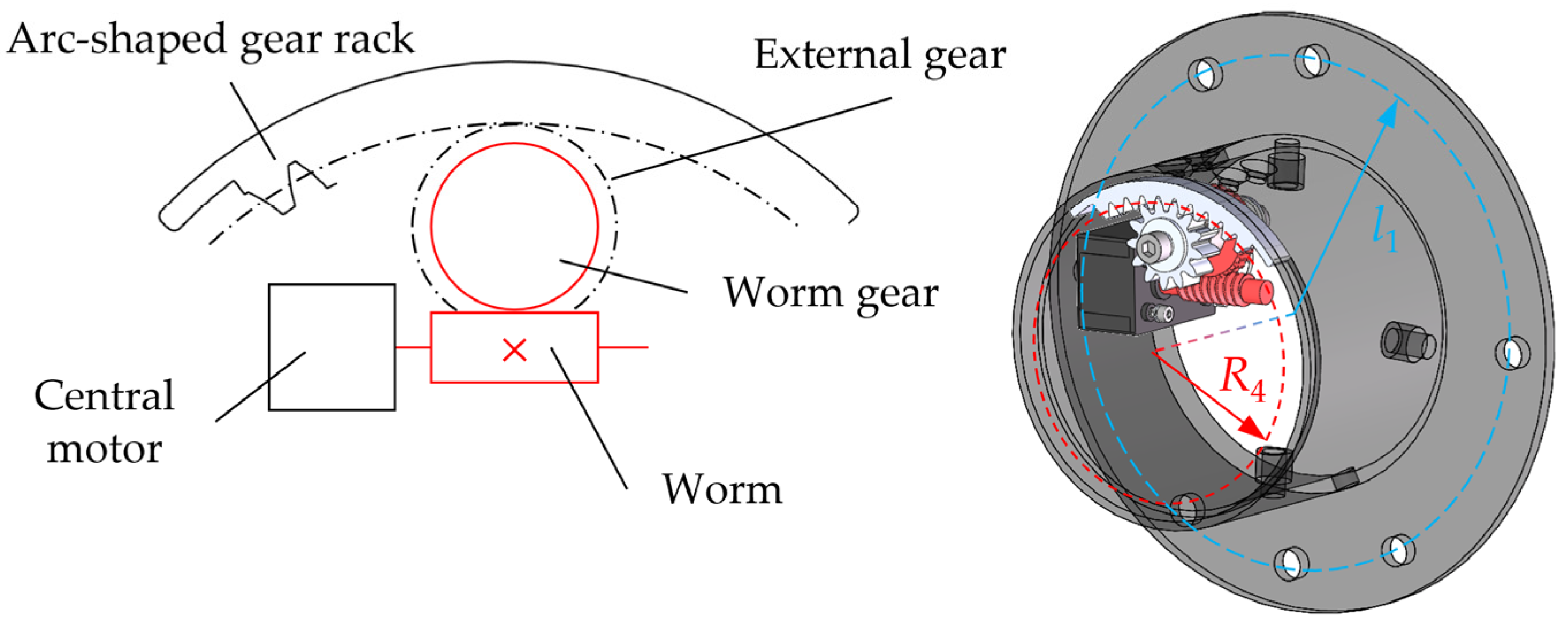
Design and mechanical analyses of the transmission system for the variable diameter module of the WMD were conducted. The schematic of the transmission system is illustrated in
Figure 6. Power for the diameter adjustment is supplied by a central motor, which drives the turntable’s rotation through a combination of a worm gear, worm, gear, and an arc-shaped gear rack, thereby facilitating the adjustment of the WMD’s outer diameter.
According to the range of the phase angle of the turntable (
α) variables, calculate the transmission ratio
i14 and the number of teeth
z4′ of the arc-shaped rack of the transmission system using Equation (2).
Note: R3 is the pitch circle radius of the external gear, mm; Z1 is the number of threads of the worm; Z2 is the number of teeth of the worm gear; m34 is the modulus of the external gear and the arc-shaped gear rack, mm.
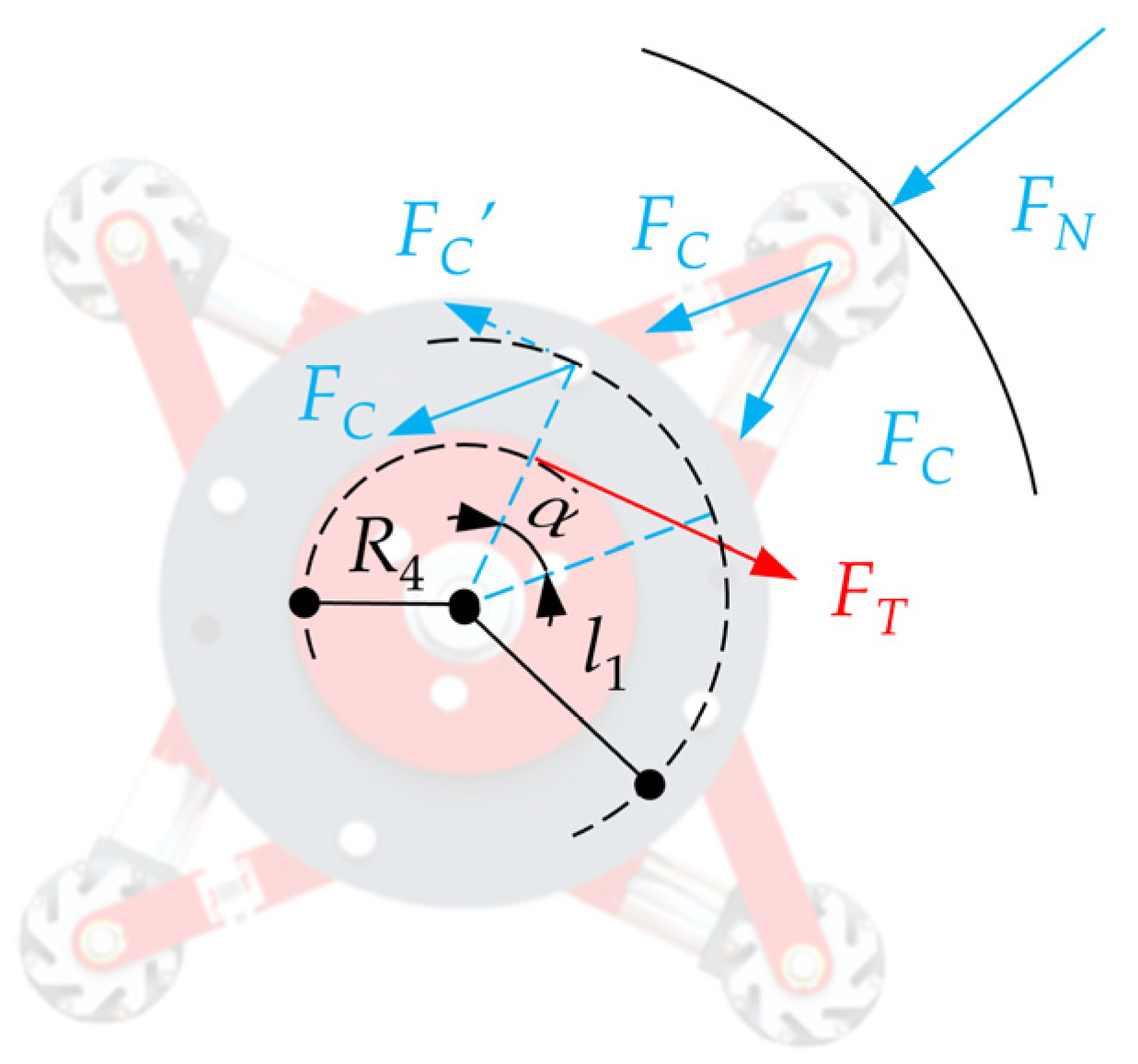
In order to effectively design the driving torque of the transmission system, a driving torque model for the WMD under external forces was developed. A schematic diagram illustrating the mechanical analysis is presented in
Figure 7. When the force exerted on the wheel by the inner wall of the pipeline is denoted as
FN, the force acting on the wheel bracket is represented as
FC. By decomposing the force transmitted to the turntable, derive the resistance in the tangential direction, denoted as
FC′. When the variable diameter module remains stable, the driving torque
TM of the transmission system is equivalent to the torque generated by the four tangential direction resistances. The relationship between force
FN and torque is established as shown in Equation (3).
By merging Equation (3), we find that the driving torque of the transmission system under external force satisfies the following condition:
3.3. Design and Analysis of the Walking Module
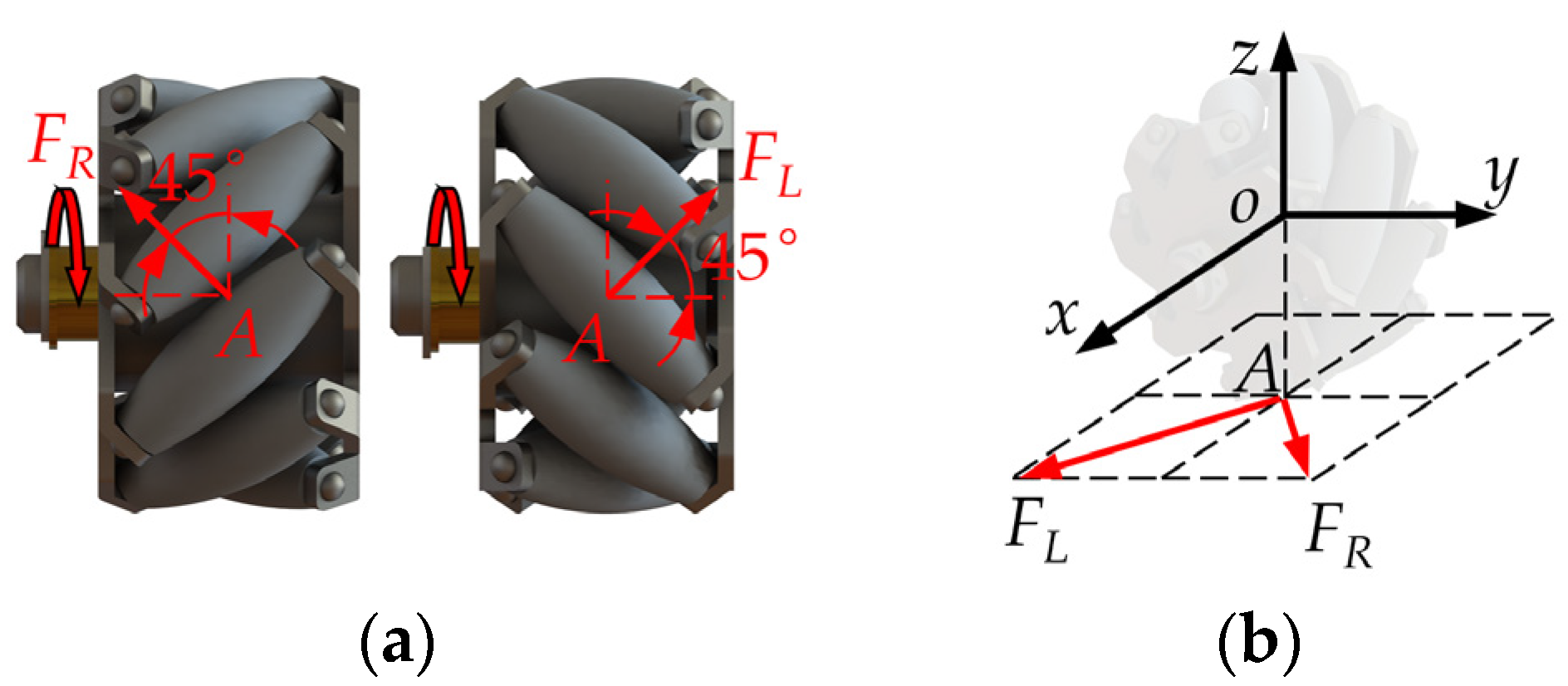
To enhance the diversity of motion modes for the MWD, a Mecanum wheel was selected as the primary component for wheeled locomotion [
32]. A Mecanum wheel is fundamentally composed of a central wheel and multiple passive rollers that are uniformly arranged at oblique angles around its perimeter [
33]. When the Mecanum wheel is in motion, the angle formed between the frictional force exerted by the passive rollers and the axis of the central wheel is 0.25
π rad, as illustrated in
Figure 8a. The mechanical properties of the wheels were modeled and analyzed using vector analysis [
34]. The centroid of the Mecanum wheel was designated as the origin of the coordinate system, with the
x-axis aligned with the direction of the wheel’s axis, the
z-axis oriented perpendicular to the ground, and the
y-axis established orthogonally to both the
x-axis and
z-axis in accordance with the right-hand rule. Point
A is defined as the contact point between the Mecanum wheel and the ground, as illustrated in
Figure 8b.
In examining the dynamics associated with Mecanum wheels, both the rotational direction and the configuration of the passive rollers were considered. The force vector
Fi generated during the operation of the Mecanum wheel is
Note: Ff is the friction force between wheel and contact surface, N; η is the rotational direction coefficient, which takes a value of 0 for forward rotation and 1 for reverse rotation; ζ is the configuration coefficient of passive rollers, which takes a value of 0 for right-handed and 1 for left-handed.
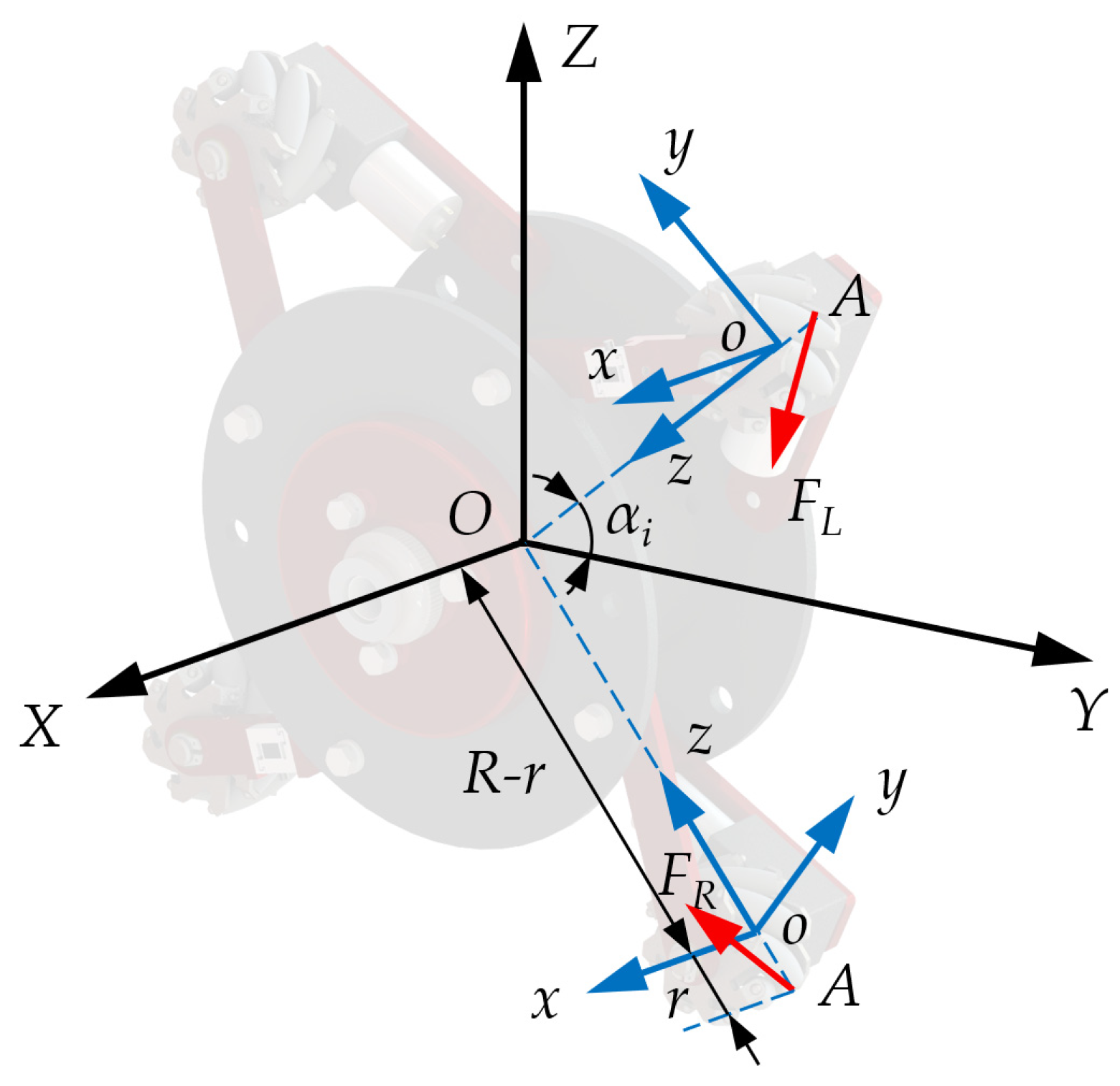
In the context of an MWD traversing a circular pipeline, the implementation of four sets of wheels, symmetrically arranged along the circumference, is essential for maintaining force equilibrium and facilitating various modes of motion. A model was formulated to analyze the rotational direction and configuration of passive rollers across various modes of motion. A spatial global Cartesian coordinate system was established, with the centroid of the MWD designated as the origin (
O). In this system, the pipeline axis is aligned with the
X-axis, the vertical direction corresponds to the
Z-axis, and a right-handed coordinate system orthogonal to both the
X-axis and
Z-axis is defined as the
Y-axis.
Figure 9 illustrates the relationship between the local position coordinates (
x,
y,
z) and the global position coordinates (
X,
Y,
Z) as the wheelset moves through the pipeline. The transformation equations that connect the local and global coordinate systems for each wheelset were derived using the rotation matrix, as presented in Equation (6).
where
Note: FX is the total force acting on all wheels along the X-axis, N; Fix and Fiy is the forces acting on each wheel along x-axis and y-axis, respectively, where i takes integer values from 1 to 4, N; TX is the moment of all wheels acting on X-axis, N·m.
In scenarios where
FX is not equal to zero and
TX is equal to zero, the MWD exhibits rectilinear motion. In contrast, when
FX is equal to zero and
TX is not equal to zero, the MWD exhibits a mode of rotational motion. Furthermore, when both
FX and
TX are not equal to zero, the MWD engages in a helical motion mode. Following this analysis, the rotational direction and configuration of the passive rollers associated with the four wheels were investigated, and the configuration scheme is summarized in
Table 3.
3.4. Analysis of Force Fluctuations on Wheel Sets during Motion
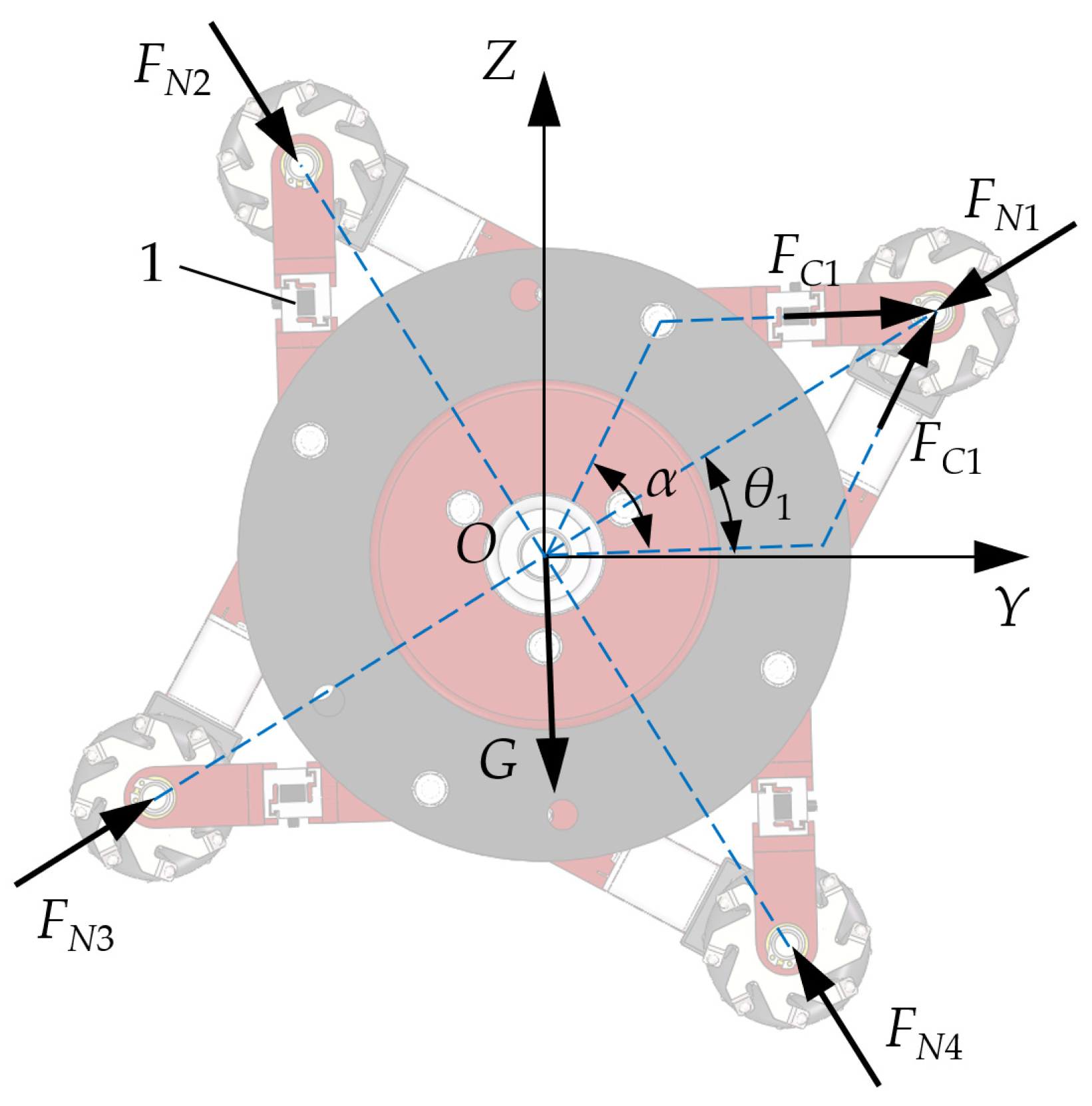
In order to mitigate the slipping of the walking wheel caused by fluctuations in the internal diameter of the pipeline, a force sensor was bolted to the wheel brackets. When the force detected by the bracket drops below a specified threshold, the external diameter of the MWD apparatus can be modified to regulate and control the force exerted between the walking wheel and the internal wall of the pipeline, as depicted in
Figure 10.
When the WMD performs rotational or helical motion within a circular pipeline, the positions of the four walking wheels continuously change in a periodic manner. Due to the influence of gravity, the support force on the lower walking wheel is not consistent with that on the upper walking wheel; specifically, the force exerted on the lower walking wheel consistently exceeds that of the upper wheel. This discrepancy leads to periodic changes in the forces acting on the wheel brackets, and the resulting instability complicates the establishment of thresholds. To clarify the fluctuation patterns of the forces in the wheel brackets, a mechanical analysis of the WMD’s motion was conducted, as illustrated in the following Equation:
where
Utilizing simultaneous Equations (8) and (9), the force relationships associated with the four walking wheels were derived, as expressed in Equation (10). The variation in force between opposing sides is influenced by gravitational force (
G) and the phase angle of motion (
θi), leading to periodic fluctuations. Nevertheless, the precise measurements of force variations within each bracket must still be determined through testing due to the restricted boundary conditions.
4. Testing Analysis and Optimization
4.1. Testing Conditions and Equipment
A prototype of the MWD was created for the purpose of testing assessment, during which its maneuverability and passability were evaluated through a range of testing methodologies. In alignment with the prototype’s outer diameter, a transparent acrylic pipeline was selected as the testing medium, featuring an inner diameter of 390 mm, a length of 2000 mm, and a wall thickness of 5 mm. An annular obstacle was deliberately positioned 1000 mm from the entrance of the pipeline, as depicted in
Figure 11.
4.2. Test Analysis of Dynamic Characteristics
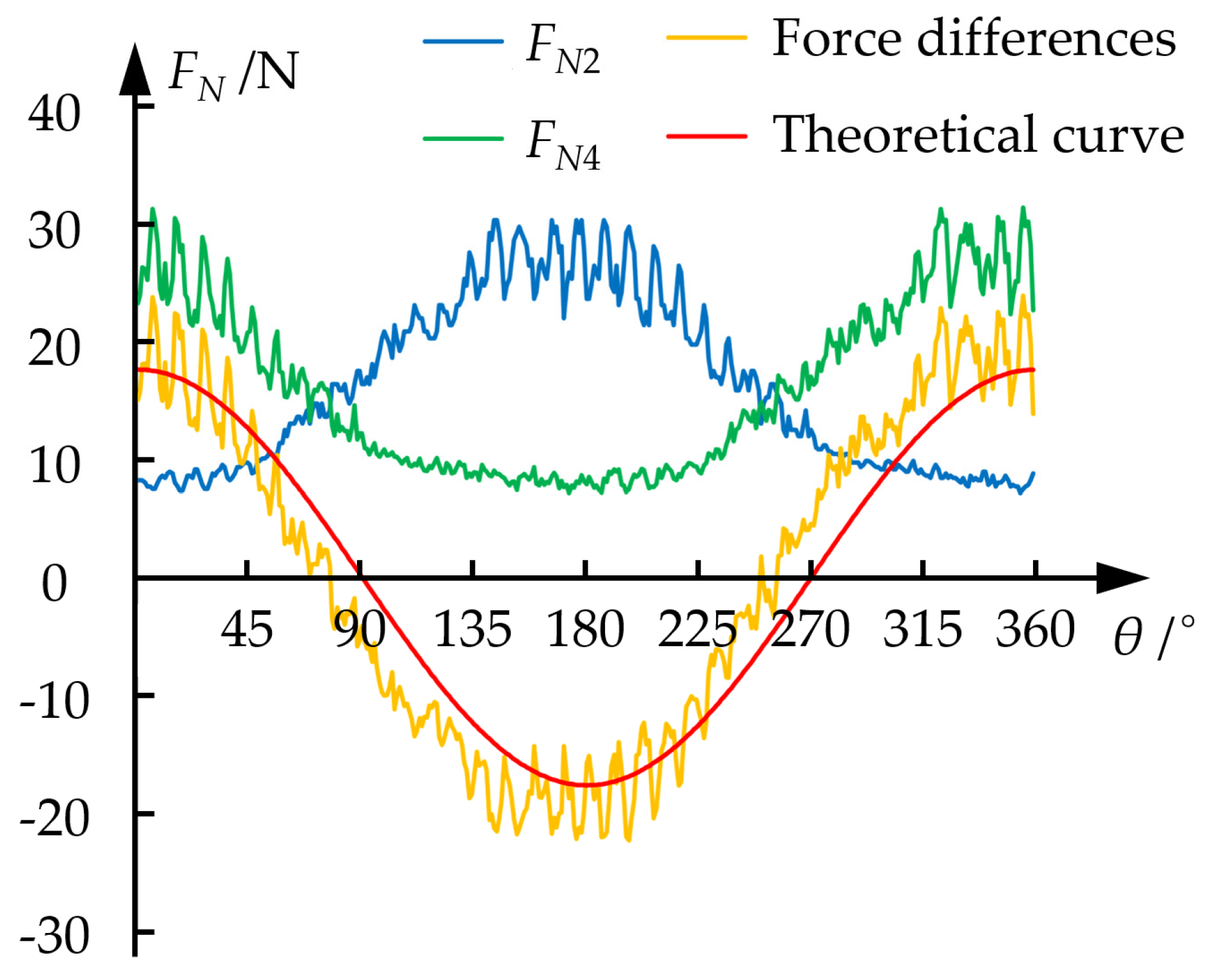
In order to assess the force fluctuations occurring between the walking wheel and the inner wall of the pipeline during movement, the MWD was configured to rotational mode, as detailed in
Table 3. Force fluctuations and the discrepancies between
FN2 and
FN4 were measured utilizing a force sensor. The data obtained from these force measurements facilitated the construction of a fluctuation curve. The theoretical differences between
FN2 and
FN4 were subsequently computed using Equation (10). The final results are illustrated in
Figure 12. The force sensor employed in this study was the ZNLBS-XII model, which possesses a capacity of 100 N and an accuracy of 0.03%.
The measurement results indicate that the force
FN2 exhibits an initial increase followed by a subsequent decrease within a single-phase period. Concurrently, the force value demonstrates varying degrees of jitter in relation to the motion phase angle, with the amplitude of the jitter positively correlated to the force magnitude. This phenomenon can be attributed to the interaction between the passive rollers of the Mecanum wheel and the pipeline wall during operation. As the passive rollers make intermittent contact with the wall, the force exerted on the wheel fluctuates. Elevated force values lead to increased deformation of the rubber rollers, which subsequently enhances the amplitude of the jitter. When the motion phase angle
θi is at 0, the force
FN2 is directed vertically downward and attains its maximum value. Conversely, the force
FN4 acts vertically upward and reaches its minimum value at this angle. The difference between
FN4 and
FN2 at this peak point signifies the gravitational influence on the MWD. At motion phase angles of
θi equal to 0.5
π or 1.5
π rad,
FN2, and
FN4 are horizontally aligned and possess equal magnitudes, resulting in their cancellation.
Figure 12 demonstrates that the measured difference curve between
FN2 and
FN4 closely aligns with the fluctuations of the theoretical curve. The congruence between mechanical analysis and empirical results substantiates their validity and serves as a robust reference for determining the force threshold.
4.3. Optimize Test Design and Method
The maneuverability and passability of the MWD are influenced by various parameters, including the radius of the walking wheel, its rotational speed, and the pre-tightening force applied. As illustrated in
Figure 4 and described in Equation (1), a reduction in the walking wheel radius results in an increased variable diameter ratio (
λ). Empirical observations and the existing literature [
35] indicate that a smaller radius diminishes grip, necessitating an increase in pre-tightening force to mitigate slip rates and improve maneuverability. Through practical production experience and preliminary testing, it was determined that a walking wheel radius of 30 mm is appropriate for a pipeline with a diameter of 390 mm. To investigate the factors influencing the maneuverability and passability of the MWD, an orthogonal test was conducted, examining three factors at three levels [
36,
37]. The factors analyzed included the rotational speed of the walking wheel (RS), the pre-tightening force of the wheel brackets (PF), and the height of the annular obstacle (OH). The slip rate and passing index were utilized as primary evaluation metrics. The RS was regulated by adjusting the reduction ratio of the driving motor. The selected motor model is the JGY-370 (manufactured by Shenzhen Chiming Motor Co., Ltd. in Shenzhen, China), which functions at a rated power of 4.8 W, a choice made in consideration of the structural dimensions. The output characteristics of the motor indicate an inverse relationship between driving torque and RS. A decrease in RS enhances the driving force of the MWD but concurrently diminishes work efficiency. Consequently, this study aims to achieve a balance between driving force and work efficiency while considering pre-test results. It establishes an RS range of 40 rpm to 100 rpm, which corresponds to a walking wheel torque range of 0.25 N·m to 0.59 N·m. The PF was adjusted by varying the external diameter of the MWD, with force measurements obtained using a force sensor and converted according to Equation (9). The PF signifies the minimum force exerted between the wheel and the pipeline wall during operation. As the MWD moves, the force applied to the pipeline wall exhibits periodic variations, as illustrated in
Figure 12. To ensure that the walking wheels maintain contact with the pipe wall, it is crucial to keep the PF above zero. However, excessive PF can increase the structural load on the MWD, and pre-test results indicate that high force levels can lead to significant fluctuations in sensor data, complicating the establishment of a force threshold. Therefore, the appropriate PF range was determined 10 N to 30 N. When the OH exceeds the walking wheel radius, it makes contact with the primary component of the MWD, thereby affecting the measurement of the test index. The walking wheel radius developed in this study is 30 mm, with a hub radius of 14 mm. Utilizing this information, the maximum allowable OH was established, and the corresponding test level was selected from
Table 4.
The slip rate of the MWD, denoted as
Y1, was determined by evaluating the actual rotational speed and linear walking speed of the walking wheel, utilizing Equation (11) [
38]. The actual rotational speed of the walking wheel was measured using the EE-SX671 type rotational speed sensor(manufactured by Omron Corporation in Osaka, Japan), which operates at a frequency of 1 kHz and has a measurement error of 0.8%. The speed of the WMD was determined by the HC-SR04 ultrasonic sensor (manufactured by Jinhua Longke Core Technology Co., Ltd. in Jinhua, China), which features a maximum measurement distance of 4 m, a measurement accuracy of ±3 mm, and a data reading interval of 0.05 s. The passability index,
Y2, was established according to the Performance test methods for service robots (GB/T38124-2019) [
39] set by the China Robot Standardization Group. A “perfect passage” is characterized by the MWD’s ability to navigate without making contact with any obstacles. A “smooth passage” occurs when the MWD traverses an obstacle without sustaining damage, with contact limited to the walking wheels. A “barely passage” is defined as the MWD crossing an obstacle without incurring damage, while making contact with surfaces other than the walking wheels. In contrast, a “failure passage” is indicated by either damage to the MWD or its inability to successfully navigate the obstacle. To quantify the test indicators, the four outcomes—perfect passage, smooth passage, barely passage, and failure passage—were assigned scores of 0, 1, 2, and 3, respectively. The results were aggregated following five iterations of the test.
Note: n is the actual rotational speed of the walking wheel, rpm; v is the linear speed of MWD, m/s.
4.4. Test Results and Range Analysis
The optimization principles of the testing indicators are outlined in Equation (12). Building on this, a range analysis of the testing results was conducted, and both the testing results and the range analysis are presented in
Table 5. The upper section of the table displays the arrangement of testing groups along with their corresponding average results, while the lower section presents the range analysis and optimization outcomes based on two test indicators.
The impact ranking for the slip rate variable Y1 was determined to be PF, RS, and OH. The optimal configuration recommended for this variable consists of an RS of 70 rpm, a PF of 20 N, and an OH of 10 mm. Meanwhile, the impact ranking for the passability index Y2 was identified as PF, OH, and RS, with the suggested parameters being an RS of 40 rpm, a PF of 30 N, and an OH of 5 mm. The optimization analysis conducted on the two indices collectively indicates that the PF factor achieves its optimal performance at the level PF3. The impact range value of the RS factor on the slip rate Y1 was found to be a mere 0.4; thus, the optimal level of the RS factor, as determined by index Y2, was identified as RS2. It is noteworthy that the OH factor, which signifies external environmental conditions, did not undergo any optimization process.
In conclusion, the range analysis suggests the following optimal combination of factors: an RS of 70 rpm in conjunction with a PF of 30 N.
4.5. Analysis of Variance of Test Results
The variance analysis of the test results was performed utilizing Design-Expert 8.0.6 software [
40,
41]. It was determined that the effects of OH on the slip rate
Y1 and RS on the passability index
Y2 were not statistically significant (
p > 0.05). Following the exclusion of these factors, a further analysis of variance was carried out, and the results are detailed in
Table 6. In the table, SS denotes the sum of squares of deviations for each corresponding item, DOF indicates the degrees of freedom for each item, MS represents the ratio of SS to DOF for each item, and
F values are the ratio of MS for each item to the MS for the error item. Finally,
p values are utilized to assess the significance of each item on the test indicators. A
p value of less than 0.01 signifies an extremely significant impact on the test indicators, while a
p value between 0.01 and 0.05 indicates a significant impact on the test indicators.
The slip rate Y1 exhibited a significant correlation with the RS (0.01 < p < 0.05), while the influence of the PF was found to be extremely significant (p < 0.01). This phenomenon can be attributed to the elastic deformation of the rubber passive rollers in the walking wheel when they come into contact with the pipeline. Such deformation increases the contact area with the pipeline, thereby enhancing the frictional driving force. An elevated RS accelerates these processes, resulting in a reduced contact duration between the rubber and the pipeline, which in turn diminishes the extent of deformation. Consequently, this reduction in driving force leads to an increase in the slip rate. In terms of the PF, increasing the force while maintaining a constant contact area can enhance the maximum static friction between the walking wheel and the pipeline. Conversely, an increase in PF may also amplify the elastic deformation of the rubber passive rollers. Additionally, the contact area between the walking wheel and the pipeline is a critical determinant of the slip rate Y1, thus underscoring the extremely significant impact of PF on the test index. The effects of both PF and OH on the passability index Y2 were found to be extremely significant (p < 0.01). When the MWD traverses an obstacle, the rear section must provide adequate support. Insufficient support compromises the coaxial alignment between the MWD and the pipeline, resulting in collisions between the lower walking wheel and obstacles, which ultimately reduces the passability index value. Therefore, both PF and OH exert a substantial influence on the test index.
In optimizing the test results to improve the maneuverability and passability of the MWD, the effects of multiple factors on slip rate Y1 and passability index Y2 were considered. The optimized parameters identified include an RS of 70 rpm and a PF of 30 N, consistent with the outcomes of the range analysis optimization.
4.6. Test Verification
To validate the optimization outcomes, a verification test was performed on the optimized device, which involved conducting five measurements of the slip rate to derive an average value. The results indicated that when the RS was set at 70 rpm and the PF at 30 N, the slip rate was recorded as 11.6 ± 1.5%. The findings from the passability verification test demonstrated that the MWD was capable of achieving smooth passage at OH of 5 mm and 10 mm. At an OH of 15 mm, one instance of barely passage was noted, while the remaining trials resulted in smooth passages. Furthermore, the motion mode of the MWD was assessed by adjusting the rotary direction of various wheelsets in accordance with
Table 3, leading to the acquisition of predicted results, which are illustrated in the subsequent
Figure 13.
5. Conclusions and Future Work
This study proposes an innovative modular walking device (MWD) designed for pipeline robots, based on several hypotheses: the ability to adapt to changes in the internal diameter of the pipeline, accommodate various pipeline shapes, and achieve multiple modes of movement.
(1) Regarding the adaptation to changes in the internal diameter of the pipeline, this study analyzes existing diameter adjustment mechanisms and proposes a laterally arranged scissor-hinge configuration that can effectively reduce the longitudinal length of the device.
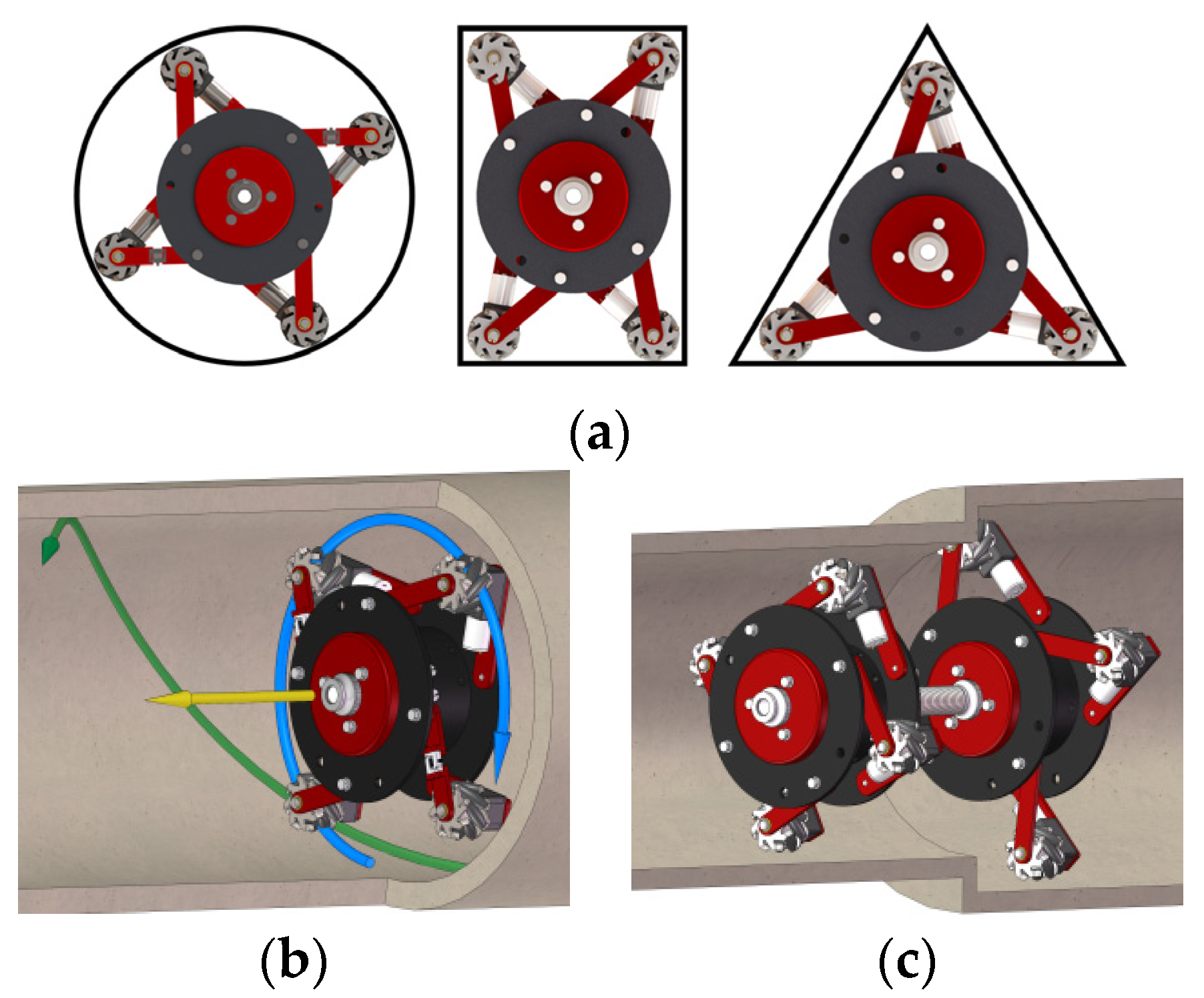
(2) In terms of accommodating various pipeline shapes, this study employs a modular design approach. By adjusting the position and number of walking modules, the device can adapt to a range of complex geometric shapes, including circular, rectangular, and triangular configurations. This feature is particularly important for operations involving irregularly shaped pipelines. Existing research often arranges walking devices uniformly to ensure stable force distribution within prototype pipelines; however, in specific scenarios—such as a circular pipeline becoming elliptical under external force—their applicability is compromised. This is where the modular design proposed in this study demonstrates its advantages.
(3) Regarding the capability to achieve multiple movement modes, the arrangement of Mecanum wheels analyzed in this study enables the MWD to transition seamlessly between linear, rotational, and helical movement modes within a circular pipeline by simply adjusting the rotation direction and speed of the wheels. Existing technologies often face structural limitations, resulting in the restriction to a single movement mode or necessitating additional mechanisms for mode adjustments. In contrast, the technology proposed in this study allows for rapid and straightforward transitions between various movement modes, which is particularly crucial in scenarios that require maneuvering around irregular protrusions or damaged pipelines, such as during industrial pipeline weld point inspections or damage assessments in compromised pipelines. In summary, the MWD proposed in this study can conveniently modify its movement mode to maintain stable forward motion when encountering significant depressions, damage, or complex protrusions.
To minimize the impact of environmental factors on testing results, this study conducted optimization tests in relatively controlled scenarios to evaluate the maneuverability and passability of the MWD. Future research will concentrate on more comprehensive testing and performance validation of the MWD in complex and variable real-world environments, ensuring its adaptability and stability across different industrial applications. By optimizing the design, control algorithms, and functional modules of the MWD, its performance in various specialized environments will be improved. This includes addressing the following aspects: (1) controlling and optimizing slip rates in slippery pipelines (e.g., oil transportation); (2) performing dynamic mechanical testing and stability optimization of force thresholds in rugged pipelines (e.g., construction pipelines); and (3) investigating the influence of dynamic loads generated by liquid flow on WMDs in pipelines containing liquid (e.g., drainage pipes). These areas represent the directions for the authors’ future research.