Form Deviation Uncertainty and Conformity Assessment on a Coordinate Measuring Machine
Abstract
1. Introduction
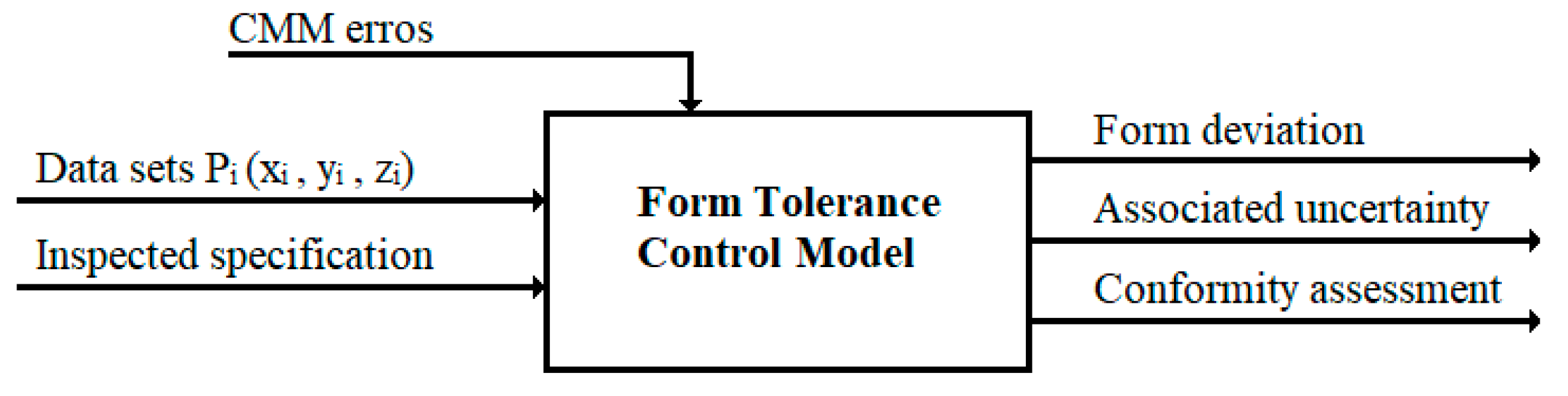
2. Materials and Methods
- Surface probing.
- Surface fitting.
- Form deviation evaluation.
- Estimation of the form deviation associated uncertainty.
- Declaration of conformity.
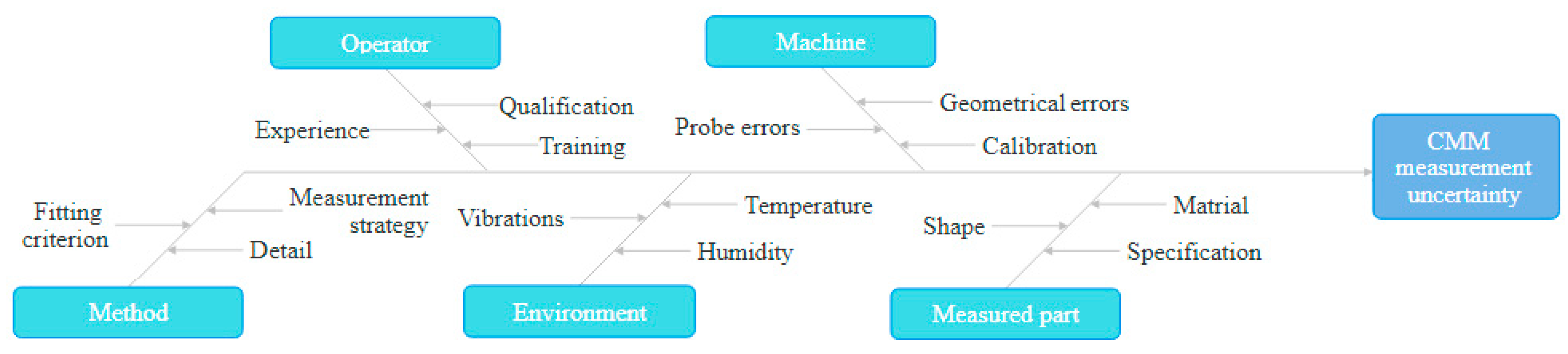
2.1. Machine Probing Uncertainty
2.2. Surface Fitting Parameters and Associated Variance–Covariance Matrix
- Line:
- Plane:
- Circle:
- Sphere:
- Cylinder:
- is the measurement uncertainty of the probed point.
- for points located in a critical area.
- for outliers.
2.3. Form Deviation Evaluation
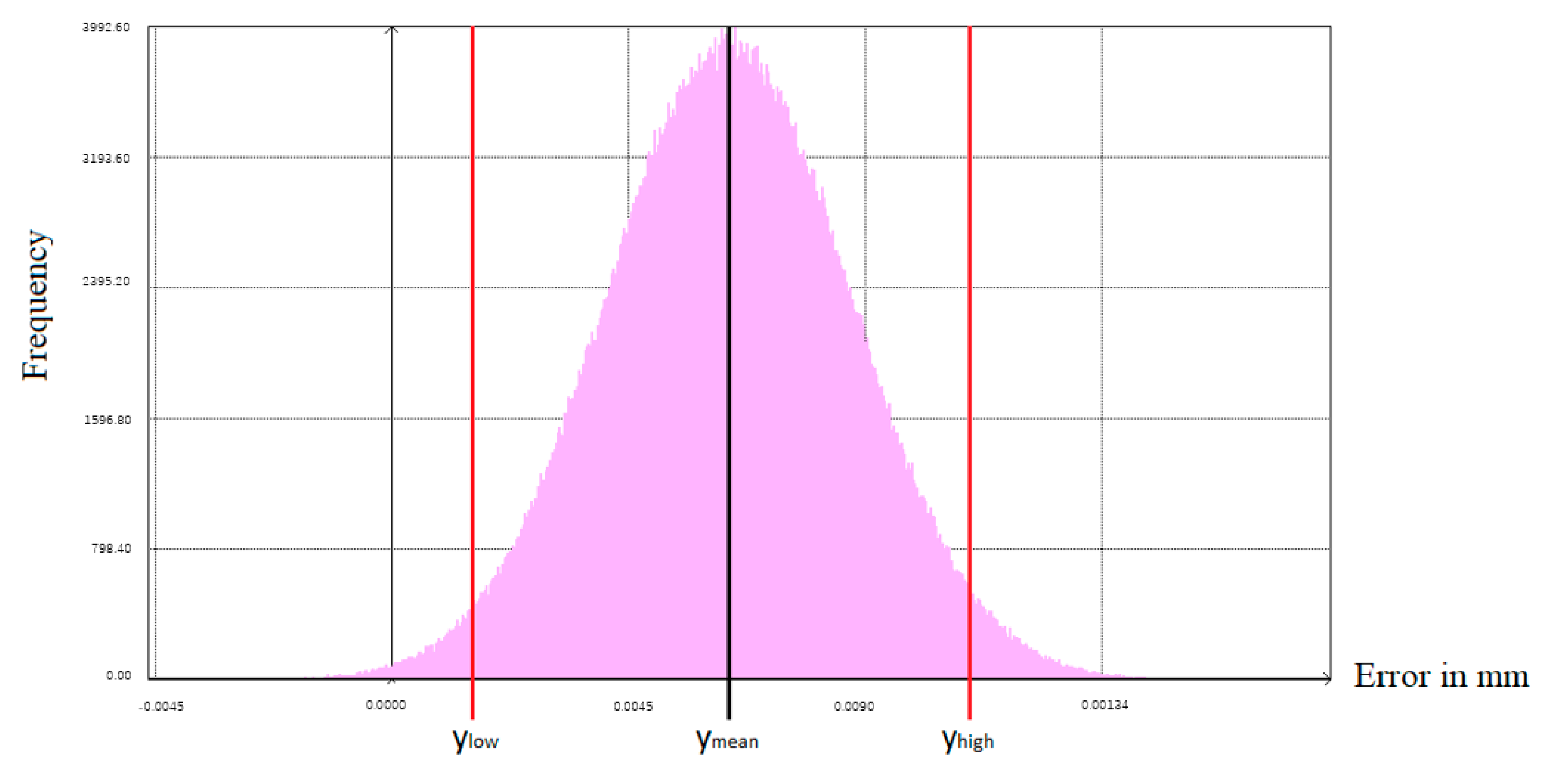
2.4. Estimation of Form Deviation Associated Uncertainty
2.5. Conformity Assessment
3. Proposed Algorithm
4. Results
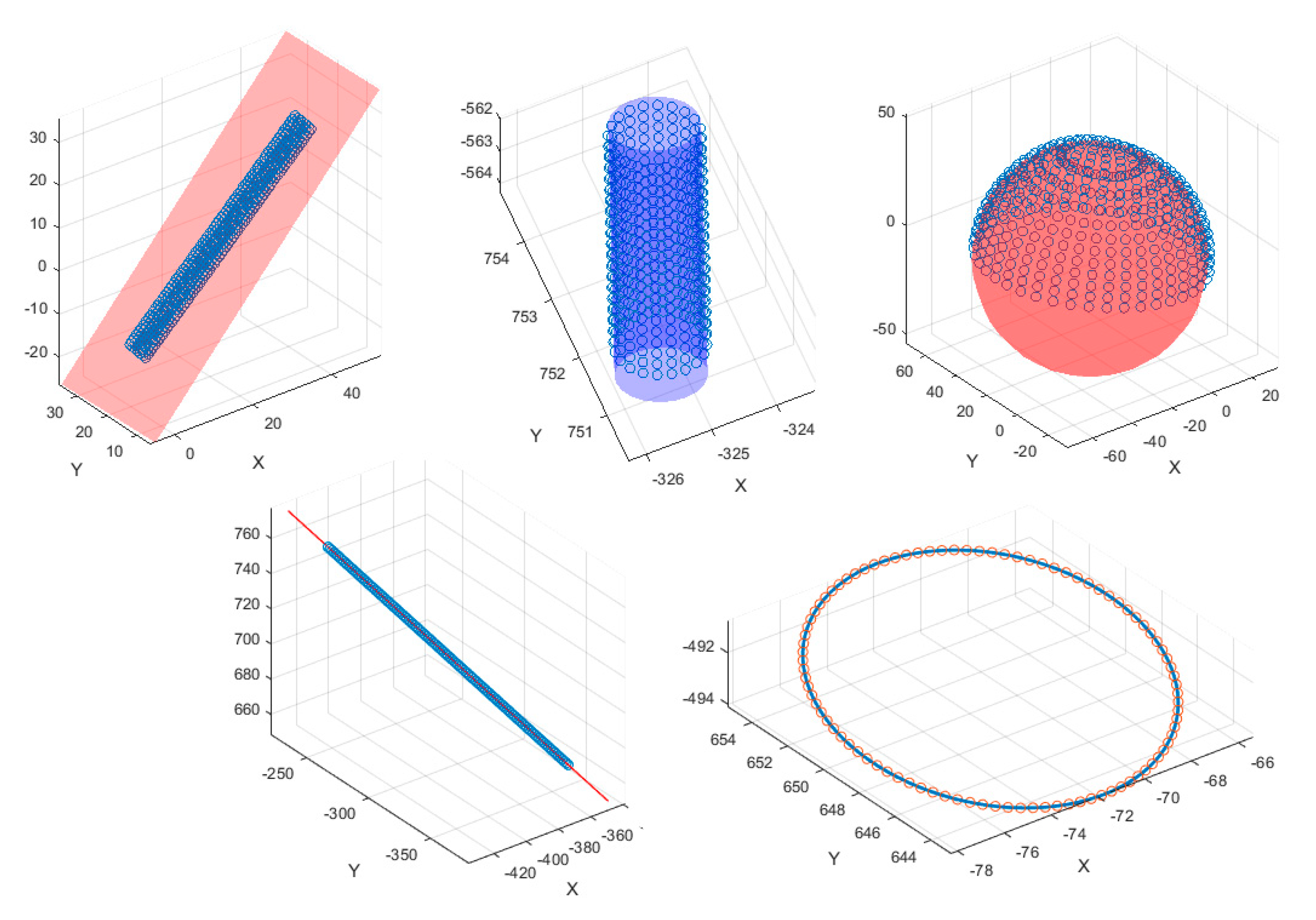
4.1. Straightness
- -
- Probing of the point dataset and surface fitting:
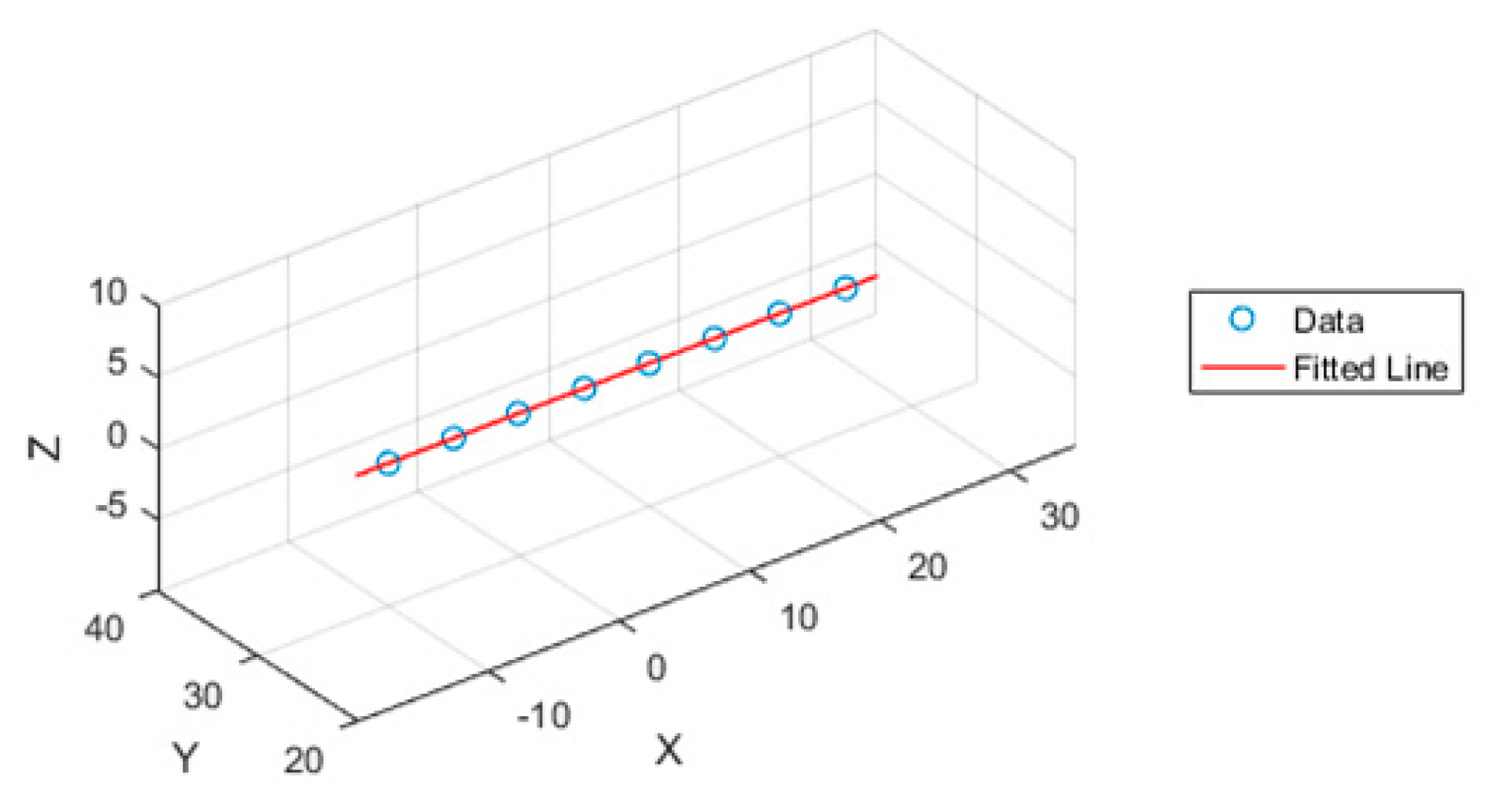
- -
- Determination of the two extreme points:
- -
- Calculation of the Jacobian, and construction of the variance–covariance matrix:
- -
- Estimation of straightness deviation and its associated uncertainty:
4.2. Flatness
- -
- Probing of the point dataset and surface fitting:
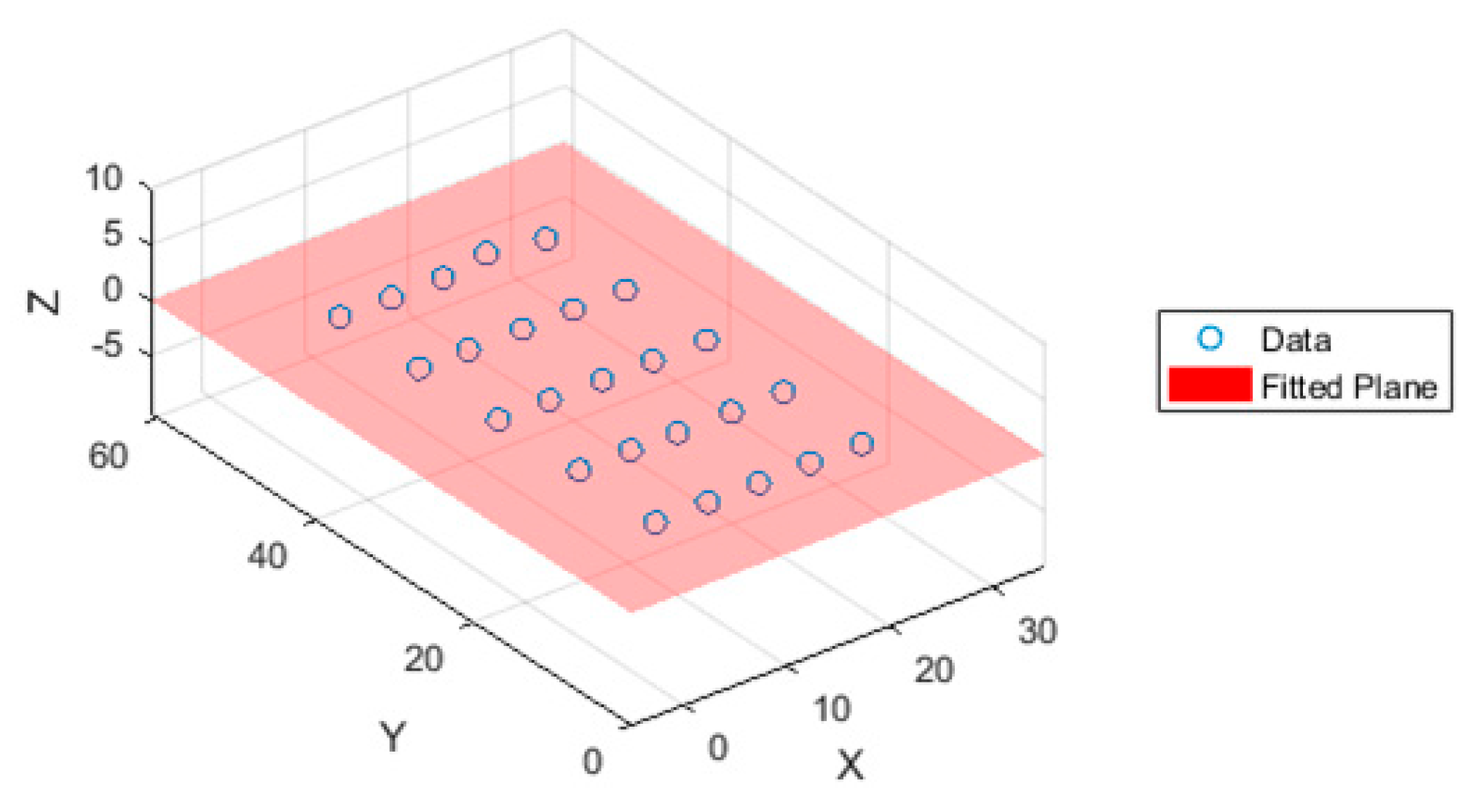
- -
- Determination of the two extreme points:
- -
- Calculation of the Jacobian and construction of the variance–covariance matrix:
- -
- Estimation of flatness deviation and its associated uncertainty:
4.3. Circularity
- -
- Probing of the point dataset and surface fitting:

- -
- Determination of the two extreme points:
- -
- Calculation of the Jacobian and construction of the variance–covariance matrix:
- -
- Estimation of circularity deviation and its associated uncertainty:
4.4. Sphericity
- -
- Probing of the point dataset and surface fitting:
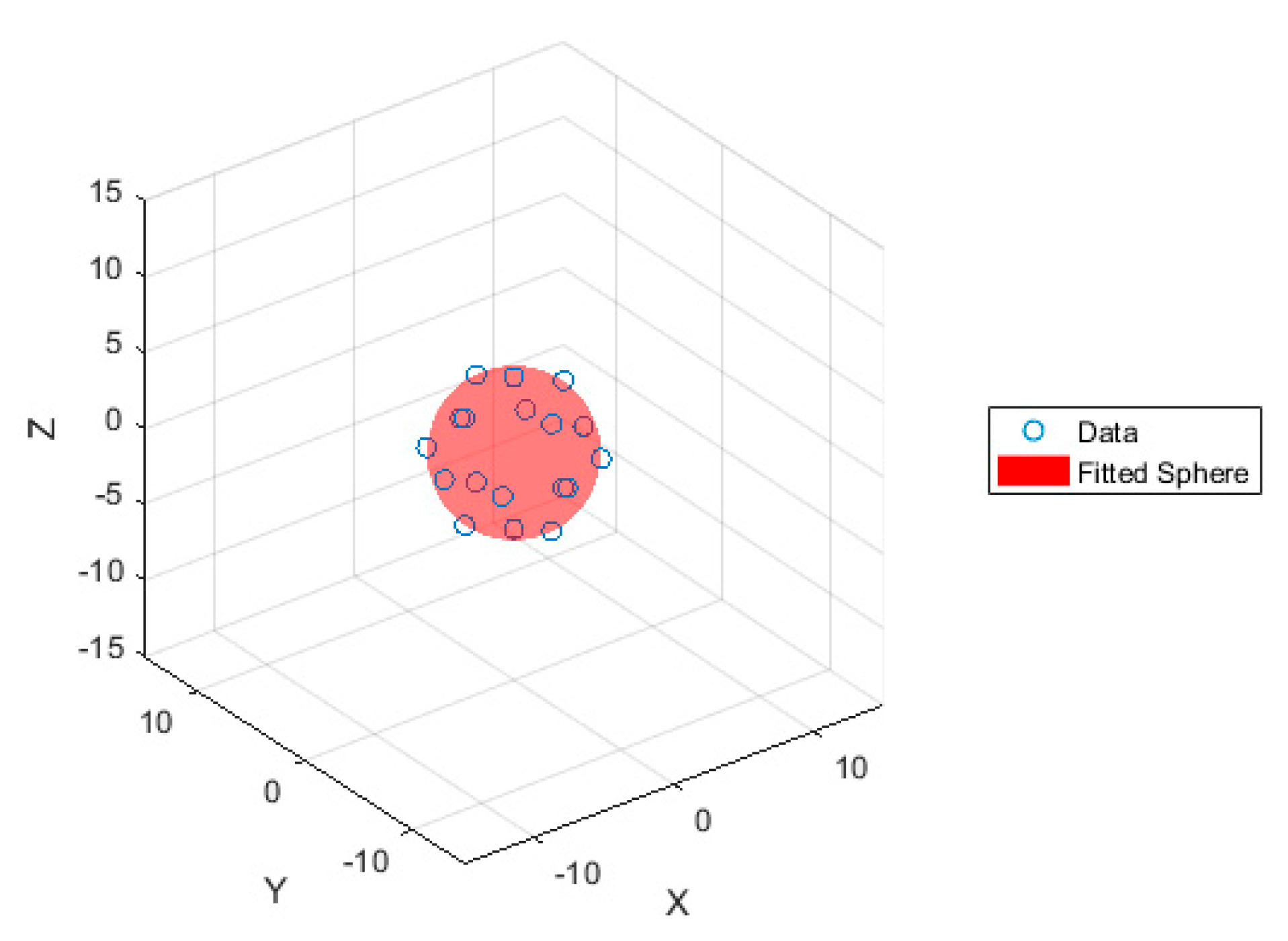
- -
- Determination of the two extreme points:
- -
- Calculation of the Jacobian and construction of the variance–covariance matrix:
- -
- Estimation of sphericity deviation and its associated uncertainty:
4.5. Cylindricity
- -
- Probing of the point dataset and surface fitting:
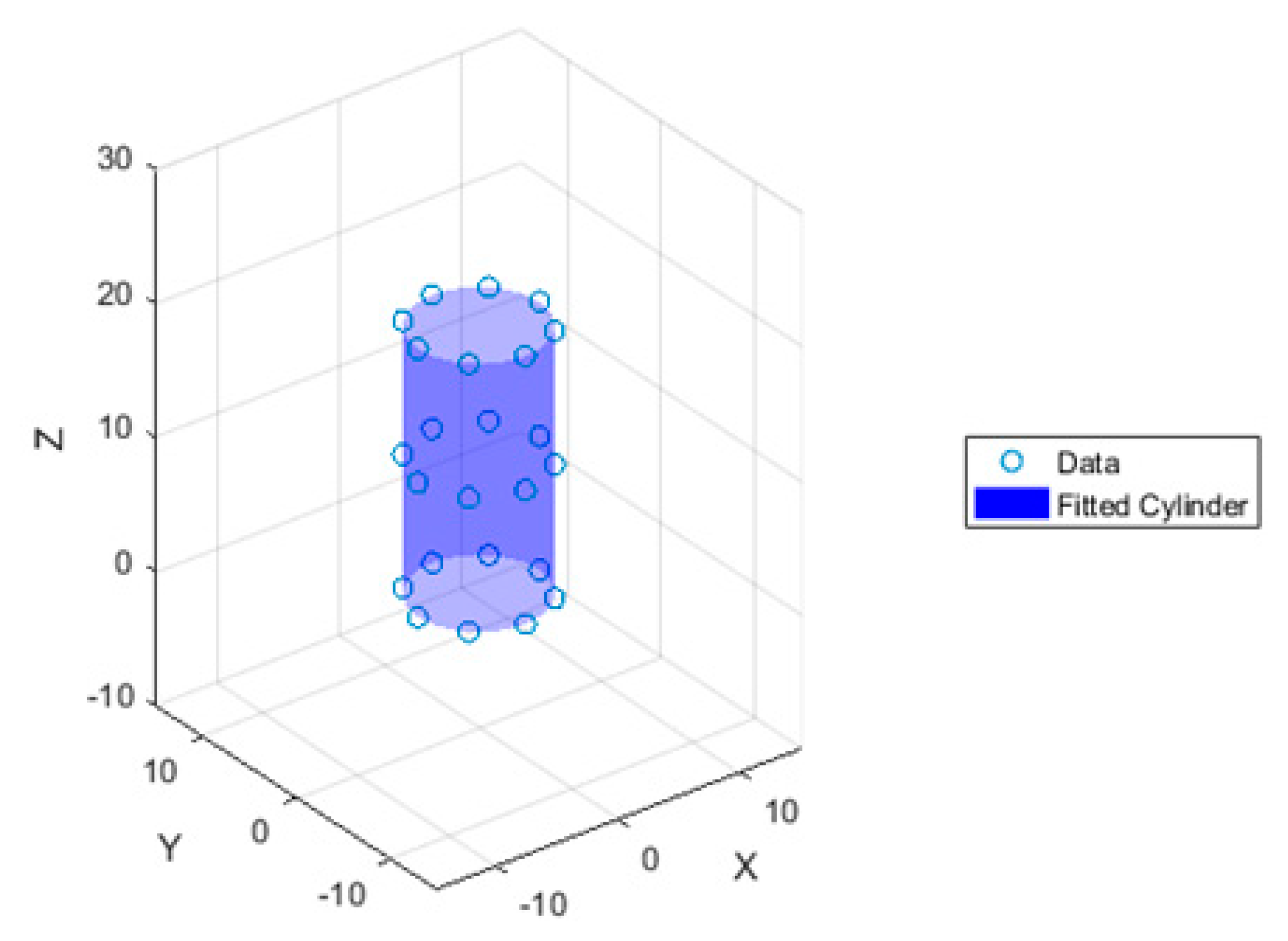
- -
- Determination of the two extreme points:
- -
- Calculation of the Jacobian and construction of the variance–covariance matrix:
- -
- Estimation of cylindricity deviation and its associated uncertainty:
5. Validation of the Proposed Model
5.1. Validation of the Surface Fitting Parameters Algorithm
5.2. Validation of the Form-Deviation-Associated Uncertainty Estimation Method (Monte Carlo Simulation)
5.3. Inter-Laboratory Comparison
6. Conclusions
- -
- Increasing the number of probed points , leading to a decrease in the residual variance , which has a direct impact on the covariance matrix , ultimately resulting in lower measurement uncertainty.
- -
- Ensuring better distribution of probed points on the controlled surface, which enhances the accuracy of the surface representation, reducing the likelihood of biases and gaps in the data that could lead to poor initial estimates for the fitting parameters.
- -
- Applying a low weighting factor (k < 1) to outliers. Significant errors can disproportionately affect the results when using the least squares method, as it tends to be particularly sensitive to outliers because it squares the errors, magnifying their impact on the overall fitting process.
- -
- Calibrating the machine, reducing probing speed, maintaining the temperature regulated at 20° ± 2 °C, choosing a stylus with short effective working length, etc., thus allowing for the minimization of the uncertainty associated with probing and consequently lowering the measurement uncertainty.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Line | Circle | ||||
|---|---|---|---|---|---|
| x | y | z | x | y | z |
| −9.9856 | 30.0019 | 0.0061 | 24.9996 | 15.0007 | 10.0001 |
| −4.9842 | 30.0 | 0.0077 | 23.5398 | 18.5305 | 10.0002 |
| −0.0347 | 30.0031 | 0.0072 | 20.0006 | 19.9997 | 9.9999 |
| 5.0178 | 29.9974 | 0.0063 | 16.4797 | 18.5391 | 10.0001 |
| 9.9783 | 30.0016 | 0.0058 | 14.9994 | 15.0001 | 9.9998 |
| 14.9966 | 30.0 | 0.0072 | 16.4694 | 11.4602 | 9.9998 |
| 19.9726 | 30.0024 | 0.0047 | 20.0004 | 10.0001 | 9.9999 |
| 25.0317 | 29.9998 | 0.0036 | 23.5396 | 11.4699 | 9.9999 |
| Plane | Cylinder | ||||
|---|---|---|---|---|---|
| x | y | z | x | y | z |
| 4.9219 | 9.972 | 0.0026 | 4.9994 | 0.0002 | −0.0003 |
| 5.2049 | 20.0021 | 0.0047 | 3.5351 | 3.545 | 0.0003 |
| 5.0133 | 30.011 | 0.0044 | −0.0001 | 5.0005 | −0.0004 |
| 4.9998 | 40.018 | 0.0049 | −3.5348 | 3.5349 | 0.0006 |
| 4.9629 | 50.0275 | 0.0065 | −5.0003 | −0.0003 | −0.0002 |
| 10.0416 | 10.0348 | 0.005 | −3.5351 | −3.5352 | −0.0006 |
| 10.2183 | 20.0059 | 0.0069 | 0.0 | −5.0001 | −0.0 |
| 10.006 | 30.02 | 0.005 | 3.535 | −3.5347 | 0.0 |
| 9.7648 | 39.9959 | 0.0086 | 5.0 | 0.0001 | 10.0 |
| 9.9785 | 50.0021 | 0.0076 | 3.5348 | 3.5348 | 10.0002 |
| 15.0064 | 9.9988 | 0.0083 | 0.0001 | 5.0002 | 10.001 |
| 14.7649 | 20.0022 | 0.0099 | −3.535 | 3.5348 | 9.9999 |
| 15.111 | 30.0036 | 0.0085 | −4.9999 | −0.0002 | 10.0004 |
| 15.02 | 40.0082 | 0.0097 | −3.5349 | −3.5352 | 9.9997 |
| 14.9722 | 50.0027 | 0.0065 | −0.0001 | −4.9999 | 10.0001 |
| 19.9854 | 10.0043 | 0.0054 | 3.5351 | −3.5351 | 9.9996 |
| 19.9845 | 20.0014 | 0.0091 | 5.0001 | −0.0002 | 20.0008 |
| 20.0342 | 30.06 | 0.0066 | 3.5352 | 3.5349 | 20.0005 |
| 20.0171 | 40.0035 | 0.0074 | −0.0 | 5.0004 | 19.9997 |
| 19.9783 | 50.9976 | 0.0074 | −3.5348 | 3.5347 | 19.9991 |
| 24.9961 | 10.0013 | 0.0061 | −5.0001 | −0.0004 | 20.0 |
| 25.0317 | 20.06 | 0.0057 | −3.5351 | −3.5354 | 20.0002 |
| 25.2187 | 30.0026 | 0.0077 | −0.0001 | −4.9996 | 20.0001 |
| 25.0159 | 39.9991 | 0.0042 | 3.5349 | −3.5352 | 19.9999 |
| 24.9788 | 50.0051 | 0.0037 |
| Sphere | ||
|---|---|---|
| x | y | z |
| 5.0022 | −0.0091 | −0.0041 |
| 3.5407 | 3.5373 | −0.0041 |
| −0.0041 | 5.0025 | 0.0003 |
| −3.5352 | 3.5328 | −0.0002 |
| −5.005 | −0.0056 | 0.002 |
| −3.5363 | −3.5327 | 0.0097 |
| −0.0066 | −5.0023 | 0.0042 |
| 3.5361 | −3.5401 | 0.0028 |
| 0.0032 | 5.0029 | 0.0017 |
| 0.0007 | 3.5275 | 3.5362 |
| −0.0009 | 0.0077 | 4.9918 |
| −0.0003 | −3.5393 | 3.5294 |
| −0.0061 | −4.995 | −0.004 |
| −0.0012 | −3.5358 | −3.528 |
| −0.0031 | −0.0038 | −5.0032 |
| −0.0033 | 3.5244 | −3.5393 |
| 5.004 | 0.0101 | 0.0015 |
| 3.536 | −0.0097 | 3.5311 |
| −0.0008 | −0.0066 | 5.0035 |
| −3.5337 | 0.0055 | 3.5396 |
| −5.0068 | −0.0011 | 0.0043 |
Appendix B
- Straightness:
- Flatness:
- Circularity:
- Cylindricity:
- Sphericity:
References
- ISO 17025:2017; General Requirements for the Competence of Testing and Calibration Laboratories. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 1101:2017; Geometrical Product Specifications (GPS) Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 10012:2003; Measurement Management Systems—Requirements for Measurement Processes and Measuring Equipment. International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 14253-2:2011; Geometrical Product Specifications (GPS)—Inspection by Measurement of Workpieces and Measuring Equipment—Part 2: Guide for the Estimation of Uncertainty in GPS Measurement, in Calibration of Measuring Equipment and in Product Verification. International Organization for Standardization: Geneva, Switzerland, 2011.
- Forbes, A. Uncertainty associated with form assessment in coordinate metrology. Int. J. Metrol. Qual. Eng. 2013, 4, 17–22. [Google Scholar] [CrossRef]
- Forbes, A. Measurement uncertainty and optimized conformance assessment. Measurement 2006, 39, 9. [Google Scholar] [CrossRef]
- Du, S.; Fei, L. Co-Kriging Method for Form Error Estimation Incorporating Condition Variable Measurements. J. Manuf. Sci. Eng. 2015, 138, 041003. [Google Scholar] [CrossRef]
- Habibi, N.; Jalid, A.; Salih, A.; Es-sadek, M.Z. Perpendicularity assessment and uncertainty estimation using coordinate measuring machine. Int. J. Metrol. Qual. Eng. 2023, 14, 12. [Google Scholar] [CrossRef]
- Habibi, N.; Jalid, A.; Salih, A.; Hanane, H. Estimation of parallelism measurement uncertainty according to the Geometrical Product Specifications standard using coordinate measuring machine. Int. J. Metrol. Qual. Eng. 2023, 14, 4. [Google Scholar] [CrossRef]
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. International Organization for Standardization: Geneva, Switzerland, 2008.
- JCGM 101:2008; Evaluation of Measurement Data Supplement 1 to the Guide to the Expression of Uncertainty in Measurement—Propagation of Distributions Using a Monte Carlo Method. International Organization for Standardization: Geneva, Switzerland, 2008.
- Jalid, A.; Hariri, S.; Senelaer, J.P. Estimation of form deviation and the associated uncertainty in coordinate metrology. Int. J. Qual. Reliab. Manag. 2015, 32, 456–471. [Google Scholar] [CrossRef]
- Jalid, A.; Hariri, S.; El Gharad, A.; Senelaer, J.P. Comparison of the GUM and Monte Carlo methods on the flatness uncertainty estimation in coordinate measuring machine. Int. J. Metrol. Qual. Eng. 2016, 7, 302. [Google Scholar] [CrossRef]
- Jalid, A.; Hariri, S.; Laghzale, N.E. Influence of sample size on flatness estimation and uncertainty in three-dimensional measurement. Int. J. Metrol. Qual. Eng. 2015, 6, 102. [Google Scholar] [CrossRef]
- Jakubiec, W.; Płowucha, W. First Coordinate Measurements Uncertainty Evaluation Software Fully Consistent with the GPS Philosophy. Procedia CIRP 2013, 10, 317–322. [Google Scholar] [CrossRef]
- Płowucha, W.; Jakubiec, W.; Wojtyła, M. Possibilities of CMM Software to Support Proper Geometrical Product Verification. Procedia CIRP 2016, 43, 303–308. [Google Scholar] [CrossRef][Green Version]
- Cui, C.; Fu, S.; Huang, F. Research on the uncertainties from different form error evaluation methods by CMM sampling. Int. J. Adv. Manuf. Technol. 2009, 43, 136–145. [Google Scholar] [CrossRef]
- Płowucha, W. Uncertainty of coordinate measurement of geometrical deviations. Procedia CIRP 2018, 75, 361–366. [Google Scholar] [CrossRef]
- Papananias, M.; Fletcher, S.; Longstaff, A.P.; Mengot, A.; Jonas, K.; Forbes, A.B. Modelling uncertainty associated with comparative coordinate measurement through analysis of variance techniques. In Proceedings of the 17th International Conference & Exhibition, Hannover, Germany, 29 May 2017; pp. 407–408. [Google Scholar]
- Li, H.; Chen, X.; Cheng, Y.; Liu, H.; Wang, H.; Cheng, Z.; Wang, H. Uncertainty Modeling and Evaluation of CMM Task Oriented Measurement Based on SVCMM. Meas. Sci. Rev. 2017, 17, 226–231. [Google Scholar] [CrossRef]
- Koucha, Y.; Forbes, A.; Yang, Q. A Bayesian conformity and risk assessment adapted to a form error model. Meas. Sens. 2021, 18, 100330. [Google Scholar] [CrossRef]
- Forbes, A. Uncertainty evaluation associated with fitting geometric surfaces to coordinate data. Metrologia 2006, 43, S282. [Google Scholar] [CrossRef]
- Forbes, A. Parameter Estimation Based on Least Squares Methods. In Modeling and Simulation in Science, Engineering and Technology; Springer: Cham, Switzerland, 2008. [Google Scholar] [CrossRef]
- Sheng, Y.; Wang, Y.; Liu, S.; Wang, C.; Xi, J. Large-Scale Measurement Layout Optimization Method Based on Laser Multilateration. Machines 2022, 10, 988. [Google Scholar] [CrossRef]
- Forbes, A. Approximate models of CMM behaviour and point cloud uncertainties. Meas. Sens. 2021, 18, 100304. [Google Scholar] [CrossRef]
- Wojtyła, M.; Rosner, P.; Płowucha, W.; Balsamo, A.; Piccato, A.; Forbes, A.B.; Savio, E. Determination Of Uncertainty Of Coordinate Measurements On The Basis Of The Formula For EL,MPE. Measurement 2023, 222, 113635. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, X.; Liu, Y. Path Planning for 5-Axis CMM Inspection Considering Path Reuse. Machines 2022, 10, 973. [Google Scholar] [CrossRef]
- ISO/IEC GUIDE 98–4; Uncertainty of Measurement Part 4: Role of Measurement Uncertainty in Conformity Assessment. International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO 10360-6:2001; Geometrical Product Specifications (GPS)—Acceptance and Reverification Tests for CMM Part 6: Estimation of Errors in Computing Gaussian Associated Features. International Organization for Standardization: Geneva, Switzerland, 2001.
- Available online: https://www.nist.gov (accessed on 8 April 2024).
- Available online: https://www.mccmaroc.com/ (accessed on 27 May 2024).
- ISO 13528:2015; Statistical Methods for Use in Proficiency Testing by Interlaboratory Comparison. International Organization for Standardization: Geneva, Switzerland, 2015.
- Takamasu, K. International Standard Development of Virtual CMM; Final Research Report; The University of Tokyo: Tokyo, Japan, 2002; p. 72. [Google Scholar]
- ISO 10360-2:2009; CMMs Used for Measuring Linear Dimensions. International Organization for Standardization: Geneva, Switzerland, 2009.
- Forbes, A. Least-Squares Best-Fit Geometric Elements; National Physical Laboratory: London, UK, 1989; Available online: https://eprintspublications.npl.co.uk/5050/ (accessed on 17 November 2023).
- Mikš, A.; Novák, J.; Novák, P. Linear method for evaluation of radius of spherical surface from discrete set of data points. Optik 2013, 124, 5473–5477. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory. In Numerical Analysis; Lecture Notes in Mathematics, 630, Watson, G.A., Eds.; Springer: Cham, Switzerland, 1977; pp. 105–116. [Google Scholar]
- Box, G.E.; Muller, M.E. A Note on the Generation of Random Normal Deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]

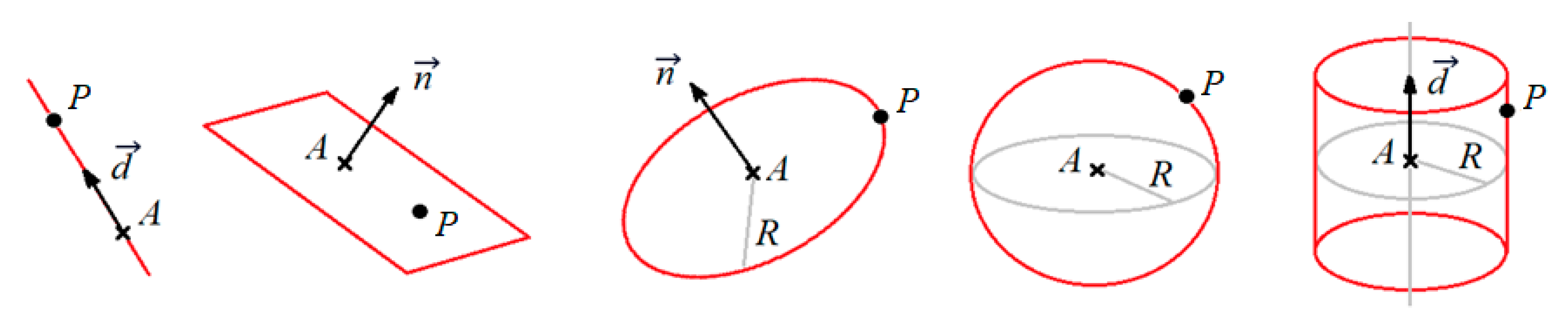




| Geometrical Elements | Point | Normal Vector | Radius R | Equation | ||
|---|---|---|---|---|---|---|
| Line |  | ∗ | ∗ | |||
| Plane |  | ∗ | ∗ | |||
| Circle |  | ∗ | ∗ | ∗ | ||
| Cylinder |  | ∗ | ∗ | ∗ | ||
| Sphere |  | ∗ | ∗ | |||
| Validation Method | Fitting Parameters | Form Deviation and Associated Uncertainty | Conformity Assessment |
|---|---|---|---|
| Inter-laboratory comparison | NIST | MCC | MCC |
| Numerical simulation | - | Monte Carlo | - |
| Element | Parameters | NIST | PCMT | Deviations |
|---|---|---|---|---|
| Line | (−387.257010, −301.481241, 712.848232) | (−387.257010, 3.01481241, 712.848232) | (0, 0, 0) | |
| (−0.356058, 0.751045, 0.556015) | (−0.356058, 0.751045, 0.556015) | (0, 0, 0) | ||
| Circle | (−71.807490, 649.102784, −492.439240) | (−71.807458, 649.102763, −492.439283) | (3.2 × 10−5, 2.1× 10−5, 4.3 × 10−5) | |
| (0.012021, −0.261410, 0.965152) | (0.012021, −0.261410, 0.965152) | (0, 0, 0) | ||
| R | 6.441995 | 6.441995 | 3 × 10−6 | |
| Plane | (23.199058, 20.545721, 4.654758) | (23.199058, 20.545721, 4.654758) | (0, 0, 0) | |
| (−0.737659, −0.015306, 0.674999) | (0.737659, 0.015306, −0.674999) | (0, 0, 0) | ||
| Sphere | (−24.376673, 15.038779, −5.784704) | (−24.376673, 15.038779, −5.784704) | (0, 0, 0) | |
| R | 47.462416 | 47.462416 | 0 | |
| Cylinder | (−324.756973, 752.733750, −563.110457) | (−324.756974, 752.733749, −563.110466) | (1 × 10−6, 1 × 10−6, 9 × 10−6) | |
| (−0.360737, −0.893967, 0.265877) | (0.360740, 0.8939637, −0.265885) | (3 × 10−6, 3 × 10−6, 8 × 10−6) | ||
| R | 1.323236 | 1.323231 | 5 × 10−6 |
| Geometrical Specification | Method | Form Deviation (in mm) | Associated Uncertainty (in mm) | Confidence Interval Limits (in mm) | Deviations (in mm) | ||
|---|---|---|---|---|---|---|---|
| Upper Bound | Lower Bound | ||||||
| Straightness | Gum | 0.010456 | 0.00334 | 3.429 × 10−4 | 3.562 × 10−4 | ||
| Monte Carlo | 0.0039 | 0.010798 | 0.002983 | ||||
| Flatness | Gum | 0.011237 | 0.002363 | 2.035 × 10−4 | 1.978 × 10−4 | ||
| Monte Carlo | 0.0046 | 0.011440 | 0.002165 | ||||
| Circularity | Gum | 0.014375 | 0.005424 | 2.245 × 10−4 | 2.555 × 10−4 | ||
| Monte Carlo | 0.0047 | 0.014599 | 0.005168 | ||||
| Sphericity | Gum | 0.018911 | 0.008889 | 1.826 × 10−4 | 8.256 × 10−5 | ||
| Monte Carlo | 0.0051 | 0.019093 | 0.008806 | ||||
| Cylindricity | Gum | 0.011581 | 0.002419 | 3.964 × 10−4 | 3.813 × 10−4 | ||
| Monte Carlo | 0.0049 | 0.011977 | 0.002037 | ||||
| Geometrical Specification | Tolerance (in mm) | Laboratory | Form Deviation (in mm) | Associated Uncertainty (in mm) | Normalized Error | Conformity Assessment |
|---|---|---|---|---|---|---|
| Straightness | PCMT | 0.247352 | NC | |||
| MCC | 0.0033 | NC | ||||
| Flatness | PCMT | 0.271245 | NC | |||
| MCC | 0.0053 | 0.0033 | C | |||
| Circularity | PCMT | 0.143876 | C | |||
| MCC | 0.0107 | 0.0033 | C | |||
| Sphericity | PCMT | 0.349955 | NC | |||
| MCC | 0.0118 | 0.0033 | C | |||
| Cylindricity | PCMT | 0.141693 | C | |||
| MCC | 0.0078 | 0.0033 | C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibi, N.; Jalid, A.; Salih, A. Form Deviation Uncertainty and Conformity Assessment on a Coordinate Measuring Machine. Machines 2024, 12, 704. https://doi.org/10.3390/machines12100704
Habibi N, Jalid A, Salih A. Form Deviation Uncertainty and Conformity Assessment on a Coordinate Measuring Machine. Machines. 2024; 12(10):704. https://doi.org/10.3390/machines12100704
Chicago/Turabian StyleHabibi, Nabil, Abdelilah Jalid, and Abdelouahab Salih. 2024. "Form Deviation Uncertainty and Conformity Assessment on a Coordinate Measuring Machine" Machines 12, no. 10: 704. https://doi.org/10.3390/machines12100704
APA StyleHabibi, N., Jalid, A., & Salih, A. (2024). Form Deviation Uncertainty and Conformity Assessment on a Coordinate Measuring Machine. Machines, 12(10), 704. https://doi.org/10.3390/machines12100704






