The Finite-Time Turnpike Property in Machine Learning

Abstract

The finite-time turnpike property describes the situation in an optimal control problem where an optimal trajectory reaches the desired state before the end of the time interval and remains there. We consider a machine learning problem with a neural ordinary differential equation that can be seen as a homogenization of a deep ResNet. We show that with the appropriate scaling of the quadratic control cost and the non-smooth tracking term, the optimal control problem has the finite-time turnpike property; that is, the desired state is reached within the time interval and the optimal state remains there until the terminal time T. The time $t_0$ where the optimal trajectories reach the desired state can serve as an additional design parameter. Since ResNets can be viewed as discretizations of neural odes, the choice of $t_0$ corresponds to the choice of the number of layers; that is, the depth of the neural network. The choice of $t_0$ allows us to achieve a compromise between the depth of the network and the size of the optimal system parameters, which we hope will be useful to determine the optimal depths for neural network architectures in the future.

1. Introduction

We study a system that is governed by a neural ODE that can be considered a continuous-time ResNet. Before we can outline the system, some notation is necessary.

The activation function $\sigma$ is assumed to be continuously differentiable and Lipschitz continuous with a Lipschitz constant that is less than or equal to 1, for example

$$\sigma \left(z\right)=\tanh \left(z\right),$$

or $\sigma \left(z\right)={\displaystyle \frac{1}{1+\exp (-z)}}$ where for $z\in {\mathbb{R}}^d$ the function $\sigma$ acts component-wise; that is, $\sigma \left(z\right)\in {\mathbb{R}}^d$ with the i-th component, e.g., ${\left(\sigma \left(z\right)\right)}_i=\tanh \left(z_i\right)$, ($i\in \{1,\cdots ,d\}$).

Let a real number $T>0$ and natural numbers d and p in $\{1,2,3,\cdots \}$ be given. For $i\in \{1,\cdots ,p\}$ and $t\in [0,T]$ almost everywhere, let $w_i\left(t\right)\in {\mathbb{R}}^d$ and $a_i\left(t\right)\in {\mathbb{R}}^d$ be given. The $w_i\left(t\right)$ are the columns of the matrix $W\left(t\right)\in {\mathbb{R}}^{d\times p}$ and the $a_i\left(t\right)$ are the columns of the matrix $A\left(t\right)\in {\mathbb{R}}^{d\times p}$. For $t\in [0,T]$, almost everywhere, let the bias vector $b\left(t\right)$ in ${\mathbb{R}}^p$ with the components $b_i\left(t\right)$ ($i\in \{1,\cdots ,p\})$ be given. In order to state the required regularity assumptions, we introduce the space

$X\left(T\right)=\left\{\mathrm{measurable} \mathrm{functions}\right(W\left(t\right),A\left(t\right),b\left(t\right)\left)\mathrm{defined} \mathrm{on}\right(0,T)$

          such that ${\int }_0^T{\parallel W\left(t\right)\parallel }^2+{\parallel A\left(t\right)\parallel }^2+{\parallel b\left(t\right)\parallel }^{2}dt<\infty \}.$

For parameters $(W,A,b)\in X\left(T\right)$, the system $\mathbf{S}$ is defined as follows:

$$\mathbf{S}\left\{\begin{array}{c}x\left(0\right)=x_0\in {\mathbb{R}}^d,\hfill \\ x^{\prime }\left(t\right)={\displaystyle \sum _{i=1}^p}\sigma (a_i{\left(t\right)}^{\top }x\left(t\right)+b_i\left(t\right))w_i\left(t\right)\hfill \end{array}\right.$$

(1)

(see for example [1,2]).

The motivation to study (1) is that a time-discrete version can be considered as a residual neural network (ResNet) that has been very useful in many applications; see [3] for identification problems with physics-informed neural ordinary differential equations, [4] for applications in image classification for the detection of colorectal cancer, and [5] for examples in image registration and classification problems. A time-discrete version can be obtained for example by an explicit Euler discretization of (1); see (28) in Section 4. The fact that ’ResNet, PolyNet, FractalNet and RevNet, can be interpreted as different numerical discretizations of differential equations’ has been discussed in detail in [6].

For the given time horizon $T>0$, we study an optimal control problem on the time interval $[0,T]$. The desired state is given by $x_T\in {\mathbb{R}}^d$; that is, $x_T$ denotes the desired output of the system. Let $t_0\in (0,T)$ be given. For the training of the system, we study the loss function with a tracking term

$$Q(W,A,b)={\int }_{t_0}^T|x\left(t\right)-x_T|+|x^{\prime }\left(t\right)|dt.$$

(2)

with the non-smooth norm $\left|z\right|={\sum }_{i=1}^d\left|z_i\right|$. For our result, the inclusion of the derivative $x^{\prime }$ in the definition of Q in (2) is essential, since due to this inclusion the loss function multiplied with the factor $\left({\displaystyle \frac{1}{T-t_0}}+1\right)$ is an upper bound for the maximum norm of $x-x_T$ on $[t_0,T]$; see the inequality (9) in Lemma 1. This allows us to prove the finite-time turnpike property in Theorem 1. We will explain the turnpike phenomenon below.

We define the control cost (regularization term)

$$R(W,A,b)={\int }_0^T\frac{1}{2}{\parallel W\left(t\right)\parallel }^2+\frac{1}{2}{\parallel A\left(t\right)\parallel }^2+\frac{1}{2}{\parallel b\left(t\right)\parallel }^{2}dt.$$

(3)

Here $\parallel W\left(t\right)\parallel$ denotes the Frobenius norm of $W\left(t\right)$.

Lemma 10 in [7] states that system (1) is exactly controllable; that is, the terminal condition

$$x\left(t_0\right)=z$$

(4)

can be satisfied for all $t_0>0$. To be precise, for all $t_0>0$ there exists a constant $C_e>0$, such that for all $z\in {\mathbb{R}}^d$ we can find a control $u_{exact}=(W_{exact},A_{exact},b_{exact})$, such that for the state $\tilde{x}$ that is generated by (1) with the initial condition $\tilde{x}\left(0\right)=x_0$, we have $\tilde{x}\left(t_0\right)=z$ and

$$\parallel u_{exact}{\parallel }_{L^2(0,t_0)}\le C_e\parallel z-x_0\parallel .$$

(5)

Also, the linearized system is exactly controllable in the sense that for all $t_0>0$ there exists a constant $C_e>0$, such that for all $z\in {\mathbb{R}}^d$ we can find a control $\delta u$, such that for the state $\delta x$ that is generated by the linearized system that is stated below with the initial condition $\delta x\left(0\right)=0$, we have $\delta x\left(t_0\right)=z$ and

$${\parallel \delta u\parallel }_{L^2(0,t_0)}\le C_e\parallel z\parallel .$$

(6)

The linearized system at a given $u=(W,A,b)$ for the variation $\delta x$ of the state that is generated by a variation $\delta u=(\delta W,\delta A,\delta b)$ of the control is

$$\delta x^{\prime }\left(t\right)=\sum _{i=1}^p\sigma (a_i{\left(t\right)}^{\top }x\left(t\right)+b_i\left(t\right))\delta w_i\left(t\right)+\sum _{i=1}^p{\sigma }^{\prime }(a_i{\left(t\right)}^{\top }x\left(t\right)+b_i\left(t\right))w_i\left(t\right)x{\left(t\right)}^{\top }\delta a_i\left(t\right)$$

$$+\sum _{i=1}^p{\sigma }^{\prime }(a_i{\left(t\right)}^{\top }x\left(t\right)+b_i\left(t\right))w_i\left(t\right)\delta b_i\left(t\right)+\sum _{i=1}^p{\sigma }^{\prime }(a_i{\left(t\right)}^{\top }x\left(t\right)+b_i\left(t\right))w_i\left(t\right)a_i{\left(t\right)}^{\top }\delta x\left(t\right)$$

with the initial condition $\delta x\left(0\right)=0$.

A universal approximation theorem for the corresponding time-discrete case with recurrent neural networks can be found in the seminal paper [8] by Cybenko; see also [9,10,11,12].

For a parameter $\gamma >0$, define

$$J(W,A,b)=\gamma Q(W,A,b)+R(W,A,b)$$

(7)

with Q as defined in (2) and R as defined in (3). We study the minimization (training) problem

$$\mathbf{P}(T,\gamma ):\underset{(W,A,b)\in X\left(T\right)}{\min }J(W,A,b)$$

Our main result is that if $\gamma$ is chosen sufficiently large, the optimal control problem $\mathbf{P}(T,\gamma )$ has the finite-time turnpike property; that is, the desired state is already reached within the time interval $[0,T]$ and remains there until the end of the time interval.

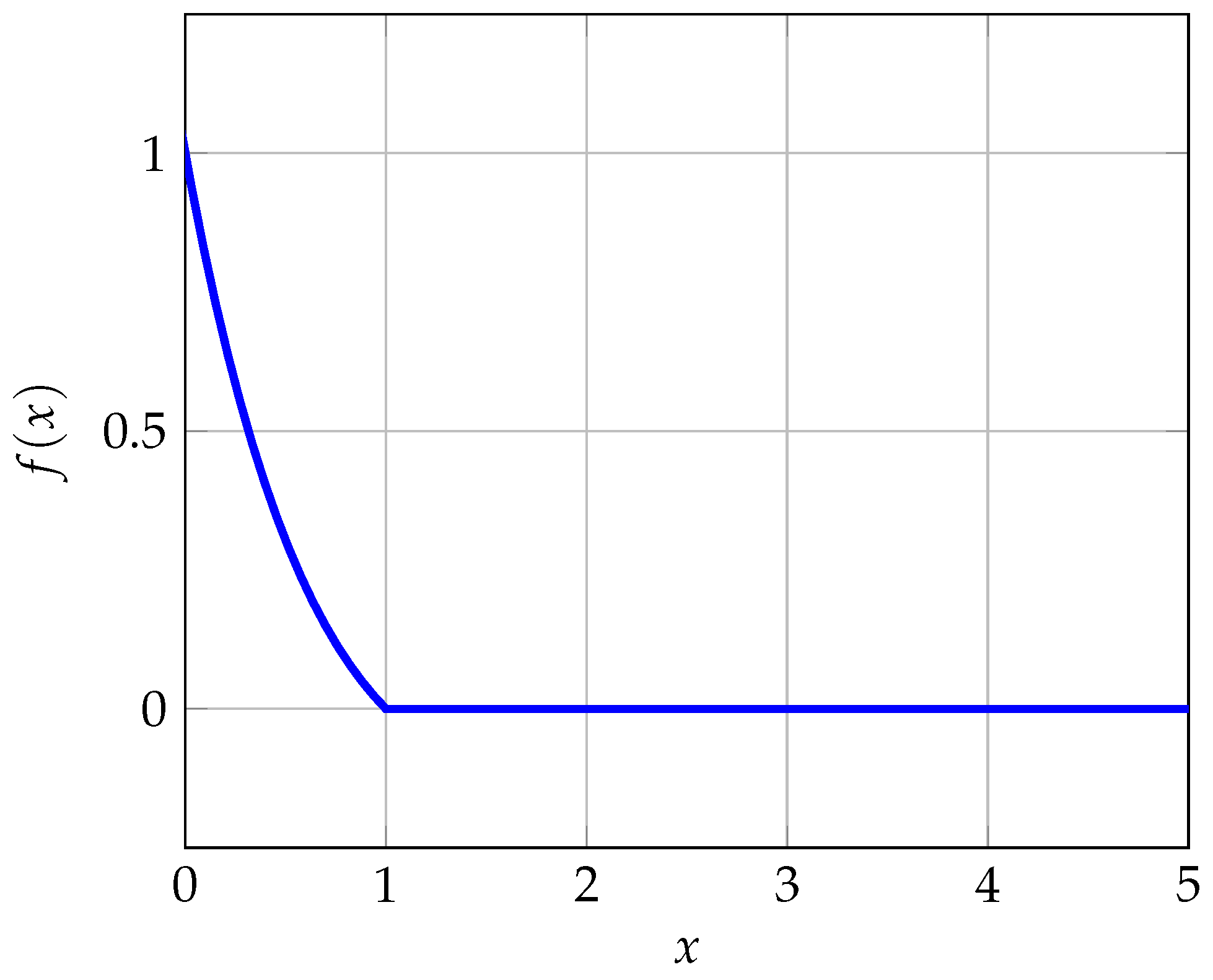
Figure 1 shows an example for the graph of the function $t\mapsto \left|x\right(t\left)\right|$ ($t\in [0,T]$), where x is an optimal trajectory that has the finite-time turnpike property. Our main result in Theorem 1 states that the optimal trajectories of $\mathbf{P}(T,\gamma )$ vanish on the interval $[t_0,T]$.

The finite-time turnpike property has been studied for example in [13,14,15]. In the first two references, the finite-time turnpike property is achieved by the non-smoothness of the objective functional. In this paper, we use a similar approach adapted to the framework of neural ordinary differential equations.

The finite-time turnpike property is an extremal case of the celebrated turnpike property that has originally been studied in economics. The turnpike analysis investigates how the solutions of dynamic optimal control problems with a time evolution are related to the solutions of the corresponding static problems where the time derivatives are set to zero and the initial conditions are cancelled. It turns out that, often for large time horizons on large parts of the time interval, the solution of the dynamic problems is very close to the solution of the corresponding static problem. For an overview about the turnpike property, see [16,17,18,19] and the numerous references therein.

In the case of the finite-time turnpike property, after a finite time, the solution of the dynamic problem coincides with the solution of the static problem. The exponential turnpike property for ResNets and beyond has been studied for example in [20], but not the finite-time turnpike property.

Our approach yields an optimization problem with a non-smooth objective functional without terminal constraints. For the numerical solution of this type of problem, a relaxation approach can be used; see, for example, [21]. Due to the finite-time turnpike property, we obtain learning problems without terminal conditions (that are easier to solve than problems with terminal constraints), where the optimal trajectories still attain the desired terminal states exactly.

Since the objective functional contains a tracking term of $L^1$-norm type, our problem is related to studies in compressed sensing, where this type of objective functional is used to enhance sparsity; see [22]. For a study about sparsity in Bregman machine learning, see [23].

In Section 3, we discuss the well-posedness of $\mathbf{P}(T,\gamma )$. We present a result about the existence of solutions of $\mathbf{P}(T,\gamma )$ for a fixed matrix A. This implies the existence of a solution for the problem where the feasible set contains only constant matrices A that are independent of t; see Remark 2.

In Section 4, numerical examples are presented that illustrate that the finite-time turnpike property is also visible in the time-discrete case.

2. The Finite-Time Turnpike Property

The following Theorem contains our main result, which states that the control cost entails the finite-time turnpike property.

Theorem 1.

For each sufficiently large $\gamma >0$ each optimal trajectory for $\mathit{P}(T,\gamma )$ satisfies

$$x\left(t\right)=x_T,t\in [t_0,T],$$

(8)

that is $\mathit{P}(T,\gamma )$ has the finite-time turnpike property. For $t\ge t_0$ for the optimal parameters, we have $W\left(t\right)=0$, $A\left(t\right)=0$ and $b\left(t\right)=0$. The optimal parameters remain unchanged if γ is further enlarged or if T is further enlarged.

Remark 1.

The condition in Theorem 1 that γ is sufficiently large is satisfied if inequality (19) holds, which is stated below. This requires a large size of γ if $t_0$ is chosen very close to T. In fact, as $t_0\in (0,T)$ approaches T, the lower bound for γ converges to infinity.

For the proof of Theorem 1, we need a result regarding the embedding of the continuous functions in the Sobolev space $W^{1,1}$ which are related to our learning problem due to the definition of Q in (2). Let

$$L^1(0,T)=\{f:[0,T]\to \mathbb{R},f\mathrm{is} \mathrm{measurable}, \mathrm{i}.\mathrm{e}.,{\int }_0^T\left|f\left(t\right)\right|dt<\infty \}.$$

Consider the embedding of the space of continuous functions in the space

$$W^{1,1}(0,T)=\{f\in L^1(0,T):f^{\prime }\in L^1(0,T)\}.$$

Lemma 1.

Let $t_0\in [0,T)$. For all $x\in W^{1,1}(t_0,T)$, we have the inequality

$$\underset{t\in [t_0,T]}{\max }\left|x\left(t\right)\right|\le \left({\displaystyle \frac{1}{T-t_0}}+1\right){\int }_{t_0}^T\left|x\left(t\right)\right|+\left|x^{\prime }\left(t\right)\right|dt.$$

(9)

Proof of Lemma 1.

For $t_1$, $t_2\in [t_0,T]$, we have

$$\begin{array}{ccc}\hfill |x\left(t_1\right)-x\left(t_2\right)|& =& \left|{\int }_{t_1}^{t_2}{x}^{\prime }\left(t\right)dt\right|\hfill \\ & \le & \left|{\int }_{t_1}^{t_2}\left|x^{\prime }\left(t\right)\right|dt\right|.\hfill \end{array}$$

Thus, x is continuous on $[t_0,T]$. Hence, there exists a point $t_{\ast }\in [t_0,T]$ with

$$|x\left(t_{\ast }\right)|=\underset{t\in [t_0,T]}{\min }|x\left(t\right)|\le {\displaystyle \frac{1}{T-t_0}}{\int }_{t_0}^T\left|x\left(t\right)\right|dt.$$

Thus, for all $\tau \in [t_0,T]$ the following inequality holds:

$$\begin{array}{ccc}\hfill \left|x\right(\tau \left)\right|& \le & |x\left(t_{\ast }\right)|+|x\left(t_{\ast }\right)-x\left(\tau \right)|\hfill \\ & \le & {\displaystyle \frac{1}{T-t_0}}{\int }_{t_0}^T\left|x\left(t\right)\right|dt+{\int }_{t_0}^T\left|x^{\prime }\left(t\right)\right|dt\hfill \\ & \le & \left({\displaystyle \frac{1}{T-t_0}}+1\right){\int }_{t_0}^T\left|x\left(t\right)\right|+\left|x^{\prime }\left(t\right)\right|dt.\hfill \end{array}$$

□

Now, we are prepared to detail the proof of Theorem 1.

Proof of Theorem 1.

• Case 1: If $x_0=x_T$, the parameters $u_{\ast }=(W_{\ast },A_{\ast },b_{\ast })=(0,0,0)$ generate the constant state $x\left(t\right)=x_T$. Hence, $u_{\ast }=0$ solves $\mathbf{P}(T,\gamma )$ and the assertion follows.
• Case 2: Now, we assume that $x_0\ne x_T$. For $u=(W,A,b)\in X\left(T\right)$, define the cost

  $$C_{(0,t_0)}\left(u\right)={\int }_0^{t_0}\frac{1}{2}{\parallel W\left(t\right)\parallel }^2+\frac{1}{2}{\parallel A\left(t\right)\parallel }^2+\frac{1}{2}{\parallel b\left(t\right)\parallel }^{2}dt.$$

  (10)

Consider the non-smooth tracking term $Q\left(u\right)$ as defined in (2). For $u\in X\left(T\right)$, define the objective functional

$$K_T\left(u\right)=C_{(0,t_0)}\left(u\right)+\gamma Q\left(u\right).$$

(11)

We consider the auxiliary problem

$$\mathbf{Q}\left(T\right):\underset{u\in X\left(T\right)}{\min }{K}_T\left(u\right).$$

We show that for each solution $u_{\ast }$ of $\mathbf{Q}\left(T\right)$, we have

$$Q\left(u_{\ast }\right)=0$$

by an indirect proof. Suppose that there exists a solution $u_{\ast }=(W_{\ast },A_{\ast },b_{\ast })$ of $\mathbf{Q}\left(T\right)$, such that $Q\left(u_{\ast }\right)>0$. Then, for the corresponding optimal state $x_{\ast }$ that is generated by system (1), we have $x_{\ast }\left(t_0\right)\ne x_T$; otherwise, (that is, if $x_{\ast }\left(t_0\right)=x_T$) we could proceed as follows: Switch off the control at $t_0$ and continue with the zero control $(0,0,0)$ for the $t\in (t_0,T]$ that generates the constant state $x_T$ on $(t_0,T]$. This approach would strictly improve the performance, since for the concatenated control $u_M\left(t\right)=u_{\ast }\left(t\right)$ for $t\in [0,t_0]$, $u_M\left(t\right)=0$ for $t\in (t_0,T]$, we have $C_{(t_0,T)}\left(u_M\right)=0$, $Q\left(u_M\right)=0$ and thus, $K_T\left(u_M\right)=C_{(0,t_0)}\left(u_{\ast }\right)<C_{(0,t_0)}\left(u_{\ast }\right)+\gamma Q(u\ast )=K_T\left(u_{\ast }\right)$ which is a contradiction, since $u_{\ast }$ is an optimal control for $\mathbf{Q}\left(T\right)$.

Define the auxiliary state

$$\tilde{x}\left(t_0\right)=x_T+{\displaystyle \frac{1}{Q\left(u_{\ast }\right)}}\left(x_{\ast }\left(t_0\right)-x_T\right).$$

(12)

The exact controllability of the linearized system implies that we can find a control $\tilde{v}\in L^2(0,t_0)$ that due to (6) and (12) satisfies the inequality

$$\parallel \tilde{v}{\parallel }_{L^2(0,t_0)}\le C_e\parallel \tilde{x}\left(t_0\right)-x_T\parallel =C_e{\displaystyle \frac{1}{Q\left(u_{\ast }\right)}}\parallel x_{\ast }\left(t_0\right)-x_T\parallel$$

(13)

that generates the state $\tilde{V}$ with $\tilde{V}(0,·)=0$ and $\tilde{V}\left(t_0\right)=\tilde{x}\left(t_0\right)-x_T$.

Due to (9), we have

$$\parallel x_{\ast }\left(t_0\right)-x_T\parallel \le \left({\displaystyle \frac{1}{T-t_0}}+1\right){\int }_{t_0}^T\left|x_{\ast }\left(t\right)-x_T\right|+\left|x_{\ast }^{\prime }\left(t\right)\right|dt$$

(14)

$$=\left({\displaystyle \frac{1}{T-t_0}}+1\right)Q\left(u_{\ast }\right).$$

Thus, (13) implies

$$\parallel \tilde{v}{\parallel }_{L^2(0,t_0)}\le C_e\left({\displaystyle \frac{1}{T-t_0}}+1\right).$$

For a step-size $\epsilon \in (0,Q\left(u_{\ast }\right))$, define

$$\lambda =1-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}\in (0,1).$$

(15)

Consider the control u that, for $t\in (0,t_0]$, is defined by the equation

$$u\left(t\right)=u_{\ast }\left(t\right)-\epsilon \tilde{v}\left(t\right)$$

(16)

and, for $t\in (t_0,T)$, we define $\tilde{v}=(\delta W,\delta A,\delta b)$ with

$$\delta W\left(t\right)=-{\displaystyle \frac{1}{Q\left(u_{\ast }\right)}}{W}_{\ast }\left(t\right),\delta A\left(t\right)=-{\displaystyle \frac{1}{Q\left(u_{\ast }\right)}}{A}_{\ast }\left(t\right),\delta b\left(t\right)=-{\displaystyle \frac{1}{Q\left(u_{\ast }\right)}}{b}_{\ast }\left(t\right).$$

We will show that if $\gamma >0$ is sufficiently large, $-\tilde{v}$ is a descent direction, in the sense that with a little step in the direction of $-\tilde{v}$, we can improve the performance of the control $u_{\ast }$. This can be seen as follows.

For the state $x=x_{\ast }+\delta x$ that is generated with the solution $\delta x$ of the linearized system with the initial condition $\delta x\left(0\right)=0$ and the control $-\epsilon \tilde{v}$, we have, at $t_0$,

$$\delta x\left(t_0\right)=-\epsilon (\tilde{x}\left(t_0\right)-x_T)=-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}(x_{\ast }\left(t_0\right)-x_T).$$

where the last step follows from (12).

On the following time interval $[t_0,T]$, for the corresponding state $x=x_{\ast }+\delta x$ that is generated with the solution $\delta x$ of the linearized system starting with

$$\delta x\left(t_0\right)=-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}\left(x_{\ast }\left(t_0\right)-x_T\right)$$

and the control $-\epsilon \tilde{v}$, we have

$$\delta x\left(t\right)=-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}\left(x_{\ast }\left(t\right)-x_T\right)+\mathcal{O}(\parallel \epsilon \tilde{v}{\parallel }^2).$$

For $t\in [t_0,T]$, due to the definition of $\lambda$ in (15), this yields

$$x\left(t\right)-x_T=\lambda (x_{\ast }\left(t\right)-x_T)+\mathcal{O}(\parallel \epsilon \tilde{v}{\parallel }^2).$$

Thus, for the tracking term with u defined in (16) we have the bound

$$Q\left(u\right)=\lambda Q\left(u_{\ast }\right)+\mathcal{O}\left({\epsilon }^2\right)=\left(1-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}\right)Q\left(u_{\ast }\right)+\mathcal{O}\left({\epsilon }^2\right).$$

For the control cost defined in (10), we have

$$C_{(0,t_0)}\left(u\right)={\langle u_{\ast }-\epsilon \tilde{v},u_{\ast }-\epsilon \tilde{v}\rangle }_{L^2(0,t_0)}=C_{(0,t_0)}\left(u_{\ast }\right)-2\epsilon {\langle u_{\ast },\tilde{v}\rangle }_{L^2(0,t_0)}+{\epsilon }^2{C}_{(0,t_0)}\left(\tilde{v}\right).$$

With $K_T$ as defined in (11), consider the function

$$p\left(\epsilon \right)=K_T(u_{\ast }-\epsilon \tilde{v})$$

$$=C_{(0,t_0)}\left(u_{\ast }\right)-2\epsilon {\langle u_{\ast },\tilde{v}\rangle }_{L^2(0,t_0)}+{\epsilon }^2{C}_{(0,t_0)}\left(\tilde{v}\right)+\gamma \left(1-{\displaystyle \frac{\epsilon }{Q\left(u_{\ast }\right)}}\right)Q\left(u_{\ast }\right)+\mathcal{O}\left({\epsilon }^2\right).$$

Then, we have

$$p^{\prime }\left(\epsilon \right)=-2{\langle u_{\ast },\tilde{v}\rangle }_{L^2(0,t_0)}+2\epsilon C_{(0,t_0)}\left(\tilde{v}\right)-\gamma +\mathcal{O}\left(\epsilon \right).$$

This yields

$$p^{\prime }\left(0\right)=-2{\langle u_{\ast },\tilde{v}\rangle }_{L^2(0,t_0)}-\gamma .$$

(17)

The exact controllability of (1) implies that there is a control $u_{exact}\in L^2(0,t_0)$ with (due to (5))

$$\parallel u_{exact}{\parallel }_{L^2(0,t_0)}\le C_e\parallel x_0-x_T\parallel$$

that generates the state $V_{exact}$ with $V_{exact}(0,·)=x_0$ and $V_{exact}(t_0,·)=x_T$. For $t>t_0$, let $u_{exact}\left(t\right)=0$. Since $u_{exact}$ is feasible for $\mathbf{Q}\left(T\right)$, this yields the inequality

$$C_{(t_0,T)}\left(u_{\ast }\right)\le K_T\left(u_{\ast }\right)\le K_T\left(u_{exact}\right)=\parallel u_{exact}{\parallel }_{L^2(0,t_0)}^2\le C_e^2{\parallel x_0-x_T\parallel }_{L^2(0,L)}^2.$$

Hence, we have

$$\left|{\langle u_{\ast },\tilde{v}\rangle }_{L^2(0,t_0)}\right|\le C_e\parallel x_0-x_T{\parallel }_{L^2(0,L)}\parallel \tilde{v}{\parallel }_{L^2(0,t_0)}\le {\parallel x_0-x_T\parallel }_{L^2(0,L)}{C}_e^2\left({\displaystyle \frac{1}{T-t_0}}+1\right).$$

(18)

Thus, if

$$\gamma >2\parallel x_0-x_T{\parallel }_{L^2(0,L)}{C}_e^2\left({\displaystyle \frac{1}{T-t_0}}+1\right),$$

(19)

due to (17) and (18), we have $p^{\prime }\left(0\right)\le -\gamma +2{\parallel x_0-x_T\parallel }_{L^2(0,L)}{C}_e^2\left({\displaystyle \frac{1}{T-t_0}}+1\right)<0$. This implies that for a $\epsilon >0$ sufficiently small, we have

$$K_T(u_{\ast }-\epsilon \tilde{v})<K_T\left(u_{\ast }\right),$$

which is a contradiction to the optimality of $u^{\ast }$.

Hence, for any optimal control of $\mathbf{Q}\left(T\right)$, we have

$$Q\left(u_{\ast }\right)=0.$$

(20)

With inequality (14), this implies that for each optimal state, we have

$$x_{\ast }\left(t_0\right)=x_T.$$

(21)

Now, we come back to the problem

$$\mathbf{P}(T,\gamma ):\underset{u}{\min }J\left(u\right)$$

with J defined in (7). Let $v_P\left(T\right)$ denote the optimal value of $\mathbf{P}(T,\gamma )$ and $v_Q\left(T\right)$ denote the optimal value of $\mathbf{Q}\left(T\right)$. Since $K_T\left(u\right)\le J\left(u\right)$, we have $v_Q\left(T\right)\le v_P\left(T\right).$

Moreover, any optimal control $u_{\ast }$ for $\mathbf{Q}\left(T\right)$ is feasible for $\mathbf{P}(T,\gamma )$. Since (21) holds, i.e., $x_{\ast }\left(t_0\right)=x_T$, we have $C_{(t_0,T)}\left(u_{\ast }\right)=0$. Hence, $v_P\left(T\right)\le J\left(u_{\ast }\right)=K_T\left(u_{\ast }\right)=v_Q\left(T\right)$, and thus $v_P\left(T\right)\le v_Q\left(T\right).$ Therefore, we have

$$v_P\left(T\right)=v_Q\left(T\right).$$

(22)

Equation (22) implies that the parameters that are optimal for $\mathbf{P}\left(T\right)$ are also optimal for $\mathbf{Q}\left(T\right)$. Hence, for each optimal state, we have (21) and (20), which implies (8) and the assertion follows. Thus, we have proved Theorem 1. □

3. The Existence of Solutions of P(T, γ) for Fixed A

For the sake of the completeness of the analysis, we also state an existence result. However, we can only prove the existence of a solution for the problem where the matrix A is fixed and not an optimization parameter for $\mathbf{P}(T,\gamma )$. Thus, for a given matrix-valued function $A\left(t\right)$, we consider the problem

$$\mathbf{P}(T,\gamma ,A):\underset{(·,A,·)\in X\left(T\right)}{\min }J(·,A,·)$$

In order to show the existence of a solution of $\mathbf{P}(T,\gamma ,A)$, we assume that there exists a number $M>0$, such that for $t\in [0,T]$, almost everywhere, we have ${\max }_{i\in \{1,\cdots ,p\}}\parallel \left(a_i\right)\left(t\right)\parallel \le M$. This is the case if the $a_i$ are elements of the function space $L^{\infty }(0,T)$; for example, if they are step functions over $(0,T)$.

Theorem 2.

Assume that ${\sup }_x\left|\sigma \left(x\right)\right|\le 1$ and the Lipschitz constant of σ is less than or equal to 1. Assume that $A\left(t\right)$ is given, such that we have

$$\mathrm{ess}\underset{i\in \{1,\cdots ,p\},s\in [0,T]}{\sup }\parallel \left(a_i\right)\left(s\right)\parallel <\infty .$$

Then, for each $T>0$ and $\gamma >0$, problem $\mathbf{P}(T,\gamma ,A)$ has a solution $W,b$, such that $(W,A,b)\in X\left(T\right)$.

If $A\left(t\right)=0$ for $t\ge t_0$, for sufficiently large γ, each solution of $\mathbf{P}(T,\gamma ,A)$ has the finite-time turnpike property stated in Theorem 1.

The proof of Theorem 2 uses Gronwall’s Lemma (see, for example, [24]). For the convenience of the reader, we state it here:

Lemma 2

(Gronwall’s Lemma). Let $L>0$, $U_0\ge 0$, $\epsilon \ge 0$ and an integrable function U on $[0,T]$ be given.

Assume that for $t\in [0,T]$, almost everywhere, the integral inequality

$$0\le U\left(t\right)\le U_0+{\int }_0^{t}LU\left(\tau \right)+\epsilon d\tau$$

(23)

hold. Then, for $t\in [0,T]$, almost everywhere, the function U satisfies the inequality

$$U\left(t\right)\le U_0{\mathrm{e}}^{Lt}+\epsilon {\displaystyle \frac{{\mathrm{e}}^{Lt}-1}{L}}.$$

(24)

Now, we present the proof of Theorem 2.

Proof of Theorem 2.

Consider a minimizing sequence ${\left(u_n\right)}_{n=1}^{\infty }$ with $u_n=(W_n,A,b_n)\in X\left(T\right)$ for all $n\in \{1,2,3,\cdots \}$. Define the norm

$$\parallel u_n{\parallel }_{X\left(T\right)}=\sqrt{{\int }_0^T\parallel W_n{\left(t\right)\parallel }^2+{\parallel A\left(t\right)\parallel }^2+{\parallel b_n\left(t\right)\parallel }^{2}dt}$$

and the corresponding inner product that gives a Hilbert space structure to $X\left(T\right)$. Due to the definition of J, there exists a number $M>0$, such that for all $n\in \{1,2,\cdots \}$ we have

$$\parallel u_n{\parallel }_{X\left(T\right)}\le M,$$

(25)

that is the sequence is bounded in $X\left(T\right)$.

Hence, there exists a weakly converging subsequence with a limit

$$u_{\ast }=(W_{\ast },A,b_{\ast })\in X\left(T\right).$$

Let $x_{\ast }$ denote the state generated by $u_{\ast }$. For the states $x_n$ generated by the $u_n$ as a solution of $\mathbf{S}$ defined in (1) we can assume, by increasing M if necessary, that we have

$$\underset{s\in [0,T],n\in \{1,2,3,\cdots \}}{\sup }\parallel x_n\left(s\right)\parallel \le M.$$

Due to Mazur’s Lemma (see for example [25,26]), there exists a subsequence of convex combinations that converges strongly. To be precise, there exist convex combinations

$$v_k=\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{u}_m,\mathrm{with} {\lambda }_m^{\left(k\right)}\ge 0,k\le m\le N\left(k\right) \mathrm{and} \sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}=1,$$

such that

$$\underset{k\to \infty }{\lim }{\parallel v_k-u_{\ast }\parallel }_{X\left(T\right)}=0.$$

This implies

$$\underset{k\to \infty }{\lim }{\int }_0^T\parallel W_n\left(t\right)-W_{\ast }\left(t\right)\parallel +\parallel b_n\left(t\right)-b_{\ast }\left(t\right)\parallel dt=0.$$

Since $\sigma$ is Lipschitz continuous with a Lipschitz constant that is less than or equal to 1, this implies for $i\in \{1,\cdots ,p\}$

$$\left|\sigma (\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}[\left(a_i\right){\left(t\right)}^{\top }{x}_m\left(t\right)+{\left(b_i\right)}_m\left(t\right))]-\sigma (\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)+{\left(b_i\right)}_{\ast }\left(t\right))\right|$$

$$\le \left|\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}[\left(a_i\right){\left(t\right)}^{\top }{x}_m\left(t\right)+{\left(b_i\right)}_m\left(t\right))\left)\right]-(\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)+{\left(b_i\right)}_{\ast }\left(t\right))\right|.$$

(26)

Thus, for $t\in [0,T]$, almost everywhere, we have

$$∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥$$

$$\le \sum _{i=1}^p{\int }_0^t∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)-{\left(w_i\right)}_{\ast }\left(s\right)∥\left|\sigma (\left(a_i\right){\left(s\right)}^{\top }{x}_{\ast }\left(s\right)+{\left(b_i\right)}_{\ast }\left(s\right))\right|$$

$$+∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)∥\left|\sigma (\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(s\right)}^{\top }{x}_m\left(s\right)+{\left(b_i\right)}_m\left(s\right)))-\sigma (\left(a_i\right){\left(s\right)}^{\top }{x}_{\ast }\left(s\right)+{\left(b_i\right)}_{\ast }\left(s\right))\right|ds.$$

Then, the fact that ${\sup }_x\left|\sigma \left(x\right)\right|\le 1$, the Cauchy–Schwarz inequality, (25) and (26) yield

$$∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥\le \sum _{i=1}^p{\int }_0^t∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)-{\left(w_i\right)}_{\ast }\left(s\right)∥ds$$

$$+\sqrt{{\int }_0^t{∥{\displaystyle \sum _{m=k}^{N\left(k\right)}}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)∥}^{2}ds}\sqrt{{\int }_0^t{\left|\sigma ({\displaystyle \sum _{m=k}^{N\left(k\right)}}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(s\right)}^{\top }{x}_m\left(s\right)+{\left(b_i\right)}_m\left(s\right)))-\sigma (\left(a_i\right){\left(s\right)}^{\top }{x}_{\ast }\left(s\right)+{\left(b_i\right)}_{\ast }\left(s\right))\right|}^{2}ds}$$

$$\le \sum _{i=1}^p{\int }_0^t∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)-{\left(w_i\right)}_{\ast }\left(s\right)∥ds$$

$$+M\sqrt{{\int }_0^t{\left|({\displaystyle \sum _{m=k}^{N\left(k\right)}}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(s\right)}^{\top }{x}_m\left(s\right)+{\left(b_i\right)}_m\left(s\right))-(\left(a_i\right){\left(s\right)}^{\top }{x}_{\ast }\left(s\right)+{\left(b_i\right)}_{\ast }\left(s\right))\right|}^{2}ds}$$

$$\le \sum _{i=1}^p{\int }_0^t∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(s\right)-{\left(w_i\right)}_{\ast }\left(s\right)∥ds$$

$$+M\sqrt{{\int }_0^t{\left|\left(a_i\right){\left(s\right)}^{\top }\left[{\displaystyle \sum _{m=k}^{N\left(k\right)}}{\lambda }_m^{\left(k\right)}{x}_m\left(s\right)-x_{\ast }\left(s\right)\right]\right|}^{2}ds}+M\sqrt{{\int }_0^t{\left|{\displaystyle \sum _{m=k}^{N\left(k\right)}}{\lambda }_m^{\left(k\right)}{\left(b_i\right)}_m\left(s\right)-{\left(b_i\right)}_{\ast }\left(s\right)\right|}^{2}ds.}$$

Due to Mazur’s Lemma, this yields the existence of a sequence ${\left({ϵ}_k\right)}_k$ with ${ϵ}_k\ge 0$ and ${\lim }_{k\to \infty }{ϵ}_k=0$, such that

$$∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥\le {\epsilon }_k+\sum _{i=1}^{p}M\sqrt{{\int }_0^t\mathrm{ess}\underset{s\in (0,T)}{\sup }{\parallel \left(a_i\right)\left(s\right)\parallel }^2{∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥}^{2}dt}.$$

Thus, by increasing the value of M if necessary, we obtain for $t\in [0,T]$, almost everywhere,

$$∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥\le {\epsilon }_k+\sum _{i=1}^{p}M\sqrt{\underset{0}{\overset{t}{\int }}{M}^2{∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(s\right)-x_{\ast }\left(s\right)∥}^{2}ds}.$$

Since $\left(\right|u|+{\left|v\right|)}^2\le {2\left|u\right|}^2+2{\left|v\right|}^2$ and

${\left({\displaystyle \sum _{i=1}^p}\sqrt{|z_i|}\right)}^2\le p{\displaystyle \sum _{i=1}^p}|z_i|$, this yields the integral inequality

$${∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥}^2\le 2{\left({\epsilon }_k\right)}^2+2p{M}^4\sum _{i=1}^p\underset{0}{\overset{t}{\int }}{∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(s\right)-x_{\ast }\left(s\right)∥}^{2}ds.$$

(27)

The integral inequality (27) has the form of (23) in Lemma 2. Hence, (24) from Gronwall’s Lemma yields for $t\in [0,T]$, almost everywhere,

$$∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥=\mathcal{O}\left({\epsilon }_k\right).$$

This yields

$$\underset{k\to \infty }{\lim }\underset{t\in \left[0T\right]}{\max }∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥=0.$$

For the time derivatives we obtain, again by increasing the value of M if necessary,

$${\int }_0^T∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m^{\prime }\left(t\right)-x_{\ast }^{\prime }\left(t\right)∥dt$$

$$\le \sum _{i=1}^p{\int }_0^T∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(t\right)-{\left(w_i\right)}_{\ast }\left(t\right)∥\left|\sigma (\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)+{\left(b_i\right)}_{\ast }\left(t\right))\right|$$

$$+∥{\sum }_{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(t\right)∥\left|\sigma ({\sum }_{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(t\right)}^{\top }{x}_m\left(t\right)+{\left(b_i\right)}_m\left(t\right)))-\sigma (\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)+{\left(b_i\right)}_{\ast }\left(t\right))\right|dt$$

$$\le \sum _{i=1}^p{\int }_0^T∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(t\right)-{\left(w_i\right)}_{\ast }\left(t\right)∥dt$$

$$+\sqrt{{\int }_0^T{∥{\sum }_{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(w_i\right)}_m\left(t\right)∥}^{2}dt}\sqrt{{\int }_0^T{\left|{\sum }_{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(t\right)}^{\top }{x}_m\left(t\right)+{\left(b_i\right)}_m\left(t\right)-\left(\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)+{\left(b_i\right)}_{\ast }\left(t\right)\right)\right|}^{2}dt}$$

$$\le {\epsilon }_k+\sum _{i=1}^{p}M\sqrt{{\int }_0^T{\left|\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}\left(a_i\right){\left(t\right)}^{\top }{x}_m\left(t\right)-\left(a_i\right){\left(t\right)}^{\top }{x}_{\ast }\left(t\right)\right|}^{2}dt}$$

$$+M\sqrt{{\int }_0^T{\left|\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{\left(b_i\right)}_m\left(t\right)-{\left(b_i\right)}_{\ast }\left(t\right)\right|}^{2}dt}$$

$$\le {\epsilon }_k(1+M)+M\sum _{i=1}^p\sqrt{{\int }_0^T{\left|{\left(a_i\right)}_m{\left(t\right)}^{\top }\left[\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)\right]\right|}^{2}dt}$$

$$\le {\epsilon }_k(1+M)+M\sum _{i=1}^p\sqrt{{\int }_0^T\parallel \left(a_i\right)\left(t\right){\parallel }^2{\parallel \sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\parallel }^{2}dt}$$

$$\le {\epsilon }_k(1+M)$$

$$+M\sum _{i=1}^p\mathrm{ess}\underset{s\in [0,T]}{\sup }\parallel \left(a_i\right)\left(s\right)\parallel \sqrt{{\int }_0^T{∥\sum _{m=k}^{N\left(k\right)}{\lambda }_m^{\left(k\right)}{x}_m\left(t\right)-x_{\ast }\left(t\right)∥}^{2}dt}$$

$$\le {\epsilon }_k(1+M)+M\sum _{i=1}^p\mathrm{ess}\underset{s\in [0,T]}{\sup }\parallel \left(a_i\right)\left(s\right)\parallel {\epsilon }_k=\mathcal{O}\left({\epsilon }_k\right).$$

Thus, we have

$$\underset{k\to \infty }{\lim \inf } Q\left(v_k\right)\ge Q\left(u_{\ast }\right)\mathrm{and}\underset{k\to \infty }{\lim \inf } R\left(v_k\right)\ge R\left(u_{\ast }\right).$$

This yields

$$\underset{k\to \infty }{\lim \inf } J\left(u_k\right)\ge J\left(u_{\ast }\right).$$

Hence, $u_{\ast }$ is a solution of $\mathbf{P}(T,\gamma ,A)$. This shows that solutions of $\mathbf{P}(T,\gamma ,A)$ exist.

The exact controllability properties that have been used for the construction in the proof of Theorem 1 still hold if the matrix A is fixed. Hence, also the assertion about the finite-time turnpike property follows. □

Remark 2.

The results in Theorem 1 can be adapted to the case where the feasible set only contains constant (that is, time-independent) matrices A and constant vectors b, since the exact controllability results that we have used in the proof still hold in this case. Since in this case A and b are in finite-dimensional spaces, Theorem 2 implies the existence of optimal parameters $(W,A,b)$. We consider a problem of this type in the numerical example that is presented in the next section.

4. Numerical Examples

To illustrate our findings, we present numerical experiments. Let a natural number $k_{\max }$ and $k_0\in \{1,\cdots ,k_{\max }\}$ be given. For $k\in \{1,2,\cdots ,k_{\max }\}$, we consider the time-discrete system

$${\mathbf{S}}_{dis}\left\{\begin{array}{c}x\left(0\right)=x_0\in {\mathbb{R}}^d,\hfill \\ x\left(k\right)=x(k-1)+{\displaystyle \sum _{i=1}^p}\sigma (a_i^{\top }x(k-1)+b_i)w_i\left(k\right)\hfill \end{array}\right.$$

(28)

Here, the $a_i\in {\mathbb{R}}^d$ and the real numbers $b_i$ are independent of the time step. Our results can be adapted to the case of a constant matrix A and a constant vector b, since the exact controllability results that we have used in the proofs still hold. Since in this case A and b are in finite-dimensional spaces, we also obtain the existence of optimal parameters in this case.

The matrices $W\left(k\right)$ depend on the current time step. To define the objective functional for the time-discrete case, let

$$Q_{dis}(W,A,b)=\sum _{k=k_0}^{k_{\max }}|x\left(k\right)-x_T|+\sum _{k=k_0}^{k_{\max }-1}|x(k+1)-x\left(k\right)|$$

where x is the solution of (28),

$$R_{dis}(W,A,b)=\frac{1}{2}{\parallel A\parallel }^2+\frac{1}{2}{\parallel b\parallel }^2+\sum _{k=1}^{k_{\max }}\frac{1}{2}{\parallel W\left(k\right)\parallel }^2$$

and

$$J_{dis}(W,A,b)=\gamma Q_{dis}(W,A,b)+R_{dis}(W,A,b).$$

(29)

We consider the minimization problem

$$\underset{W\left(k\right)\in {\mathbb{R}}^{d\times p}(k\in \{1,\cdots ,k_{\max }\}),A\in {\mathbb{R}}^{d\times p},b\in {\mathbb{R}}^p}{\min }{J}_{dis}(W,A,b).$$

For the numerical example we have chosen $d=p=3$, $k_{\max }=10$, $\gamma ={10}^5$, $x_0={(1,1,1)}^{\top }$ and $x_T=0$. For the training, we have used the global optimization toolbox in matlab.

Table 1. The evolution of the norm of the state along the approximations of the optimal trajectories. The structure of the numerical solutions shows the finite-time turnpike structure that is indicated in Theorem 1. Here, $\gamma ={10}^5$.

$\mathit{\gamma }={10}^5$	$\left|\mathit{x}\right(1\left)\right|$	$\left|\mathit{x}\right(2\left)\right|$	$\left|\mathit{x}\right(3\left)\right|$	$\left|\mathit{x}\right(3\left)\right|$	$\left|\mathit{x}\right(5\left)\right|$	$\left|\mathit{x}\right(6\left)\right|$	$\left|\mathit{x}\right(7\left)\right|$	$\left|\mathit{x}\right(8\left)\right|$	$\left|\mathit{x}\right(9\left)\right|$	$\left|\mathit{x}\right(10\left)\right|$
$k_0=1$	3	0	0	0	0	0	0	0	0	0
$k_0=2$	3	2.2178	0	0	0	0	0	0	0	0
$k_0=3$	3	3.2343	3.3124	0	0	0	0	0	0	0
$k_0=4$	3	2.3303	0.9089	0.7560	0	0	0	0	0	0
$k_0=5$	3	2.8638	2.6989	2.2098	0.0396	0	0	0	0	0
$k_0=6$	3	1.8557	1.0519	1.2795	1.1156	0.7379	0.0002	0	0	0

contains the evolution of the norms $\left|x\right(k\left)\right|$ ($k\in \{1,\cdots ,k_{\max }\}$) along the computed approximation of the optimal trajectories for different values of $k_0$. It clearly illustrates the finite-time turnpike behavior that is predicted by Theorem 1. The zeros in Table 1 represent numerical values of the order less than $5\times {10}^{-5}$.

For $\gamma ={10}^4$ and $k_0=5$, we have obtained the numerical result presented in

Table 2. For $\gamma ={10}^4$, the finite-time turnpike structure for $k_0=5$ is still visible.

$\mathit{\gamma }={10}^4$	$\left|\mathit{x}\right(1\left)\right|$	$\left|\mathit{x}\right(2\left)\right|$	$\left|\mathit{x}\right(3\left)\right|$	$\left|\mathit{x}\right(3\left)\right|$	$\left|\mathit{x}\right(5\left)\right|$	$\left|\mathit{x}\right(6\left)\right|$	$\left|\mathit{x}\right(7\left)\right|$	$\left|\mathit{x}\right(8\left)\right|$	$\left|\mathit{x}\right(9\left)\right|$	$\left|\mathit{x}\right(10\left)\right|$
$k_0=5$	3	3.2622	2.7861	2.0809	0.2694	$3\times {10}^{-8}$	$2\times {10}^{-8}$	$3\times {10}^{-8}$	$2\times {10}^{-8}$	$2\times {10}^{-8}$

. Also, for this smaller value of $\gamma$, the turnpike structure is still visible. Here, we have given the size of the small norms (that are the numerical approximations of zero) in more detail.

5. Conclusions

We have shown that with a suitable non-smooth loss function, each solution of a learning problem has the finite-time turnpike property, which means that it reaches the desired state exactly after a finite time. Since the finite time $t_0$ can be considered as a problem parameter, this situation allows us to choose $t_0$ in a convenient way. Thus, $t_0$ arises as an additional design parameter in the design of optimal neural networks, which corresponds to the number of layers. Since for $t\in [t_0,T]$ the optimal parameters are zero, System (1) has a constant state on $[t_0,T]$, and thus the time horizon can be cut off at $t_0$.

Therefore, the problem of finding the optimal number of layers in a neural network corresponds in the setting of neural ODEs to the problem of time-optimal control (see, for example, [27]), which is defined as follows. Let a number $\rho >0$ be given, which serves as problem parameter. The optimization problem involves

$$\mathit{finding} a \mathit{minimal} \mathit{value} \mathit{of} t_0$$

subject to (1), the terminal constraint $x\left(t_0\right)=x_T$ and for $u=(W,A,b)\in X\left(t_0\right)$ the inequality constraint $C_{(0,t_0)}\left(u\right)\le \rho$ holds.

Here, $C_{(0,t_0)}$ is as defined in (10). The solution of the time-optimal control problem is closely related to the solution of $\mathbf{P}(T,\gamma )$. This can be seen as follows. Let $\omega (T,\gamma )$ denote the optimal value of $\mathbf{P}(T,\gamma )$. Then, Theorem 1 implies that (if $\gamma$ is sufficiently large) for optimal parameters $u\left(t\right)$ that solve $\mathbf{P}(T,\gamma )$, we have $Q\left(u\right)=0$ and $C_{(0,t_0)}\left(u\right)=\omega (T,\gamma )$, and for the optimal state we have $x\left(t_0\right)=x_T$. Hence, we conclude that the optimal parameters for $\mathbf{P}(T,\gamma )$ also solve the time-optimal control problem with parameter $\rho =\omega (T,\gamma )$ and the optimal time is $t_0$.

This relation allows us to adapt the choice of $t_0$ to the desired value of $C_{(0,t_0)}\left(u\right)$. If $t_0$ is enlarged, this value can be decreased for the optimal parameters.

We have shown the existence of a solution of the nonlinear optimization problem for the case that one of the parameters, namely the matrix $A\left(t\right)$, is fixed. In order to show that a solution also exists with $A\left(t\right)$ as an additional (time-dependent) optimization parameter, we expect that an additional regularization term in the objective functional (for example ${\int }_0^T\parallel A^{\prime }\left(t\right){\parallel }^{2}dt)$ is necessary. This is a topic for future research.

We expect that the finite-time turnpike property also holds in the case $t_0=0$. However, the proof that is presented here does not apply to this case, so this is another topic for future research. As a possible application of our results, we have the numerical solution of shape inverse problems in mind, as described in [28]. Studying the finite-time turnpike phenomenon in a practical machine learning scenario will be of high value for future research.

Moreover, it would be interesting to combine the dynamics with an approach that allows for data assimilation, such as nudging induced neural networks (NINNs) that have been introduced recently in [29].