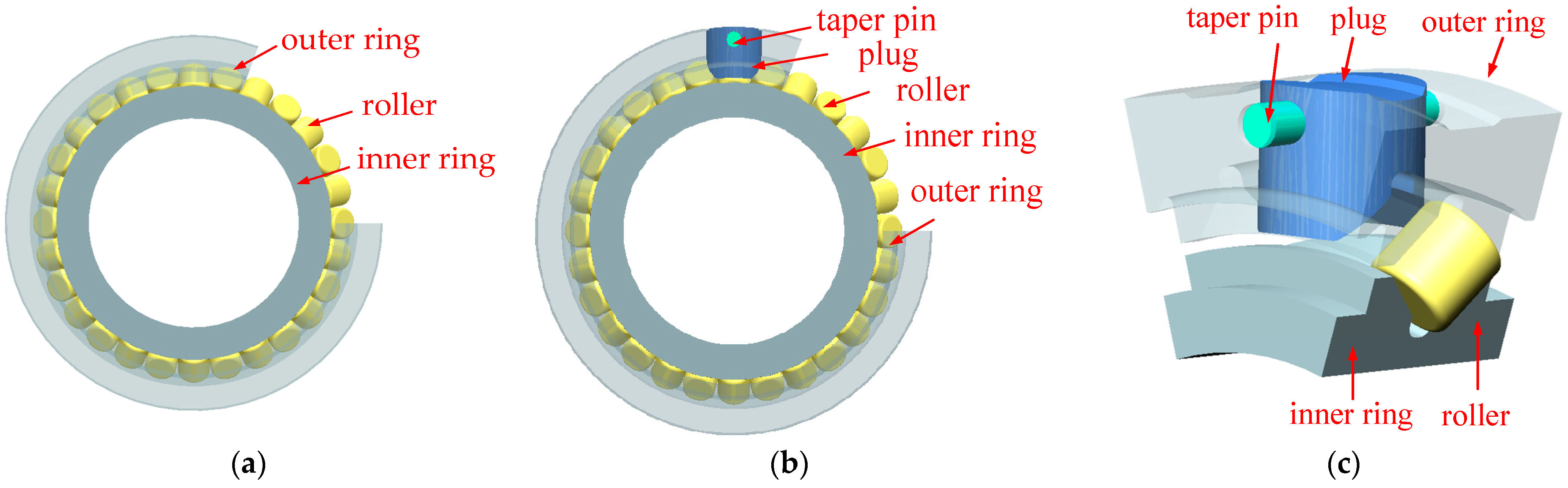
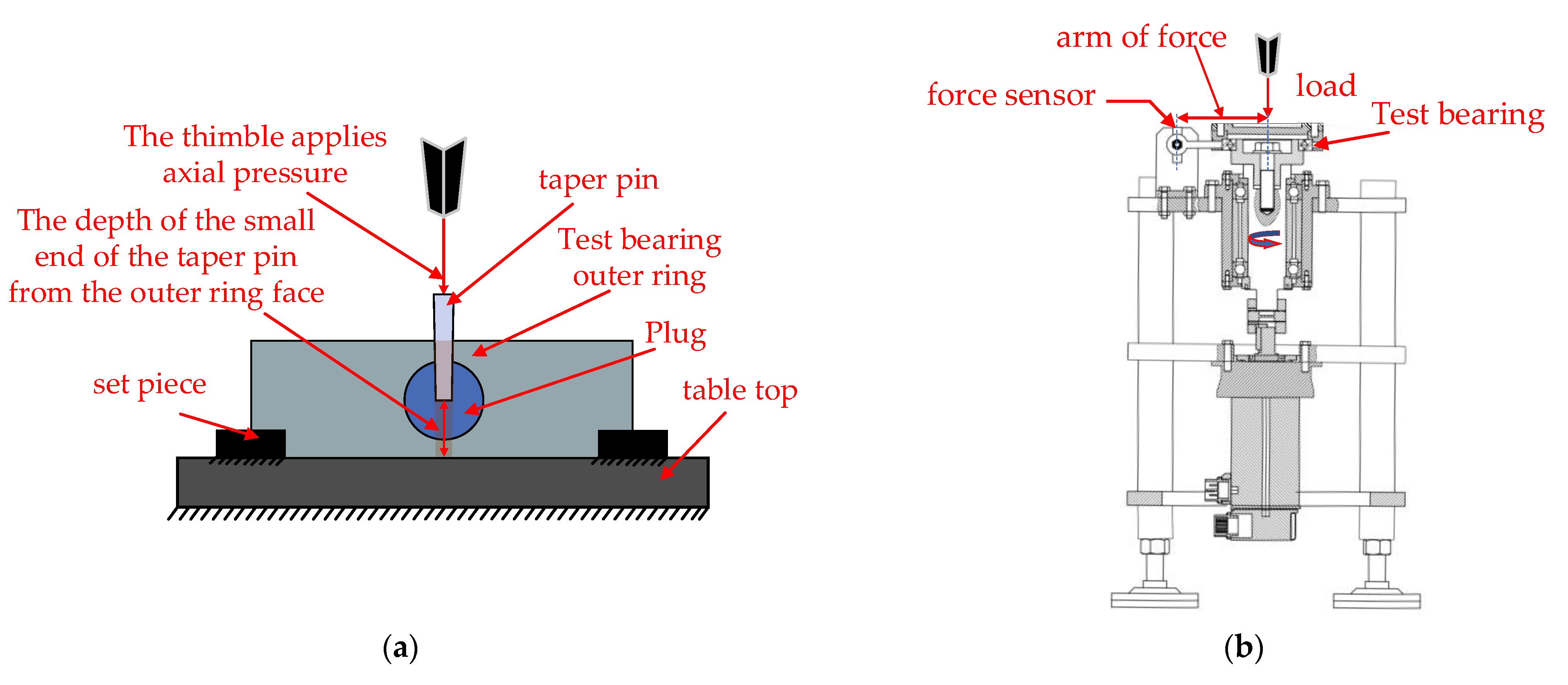
The cross roller bearing is a compact bearing featuring rollers that are alternately arranged at right angles between the inner and outer rings. This design enables it to withstand loads from multiple directions and offers characteristics such as high precision, high rigidity, and ease of installation. As a result, it is widely utilized in applications such as robot joints, rotating units, and machining center turntables, where a compact structure, high stiffness, and high rotational accuracy are essential [
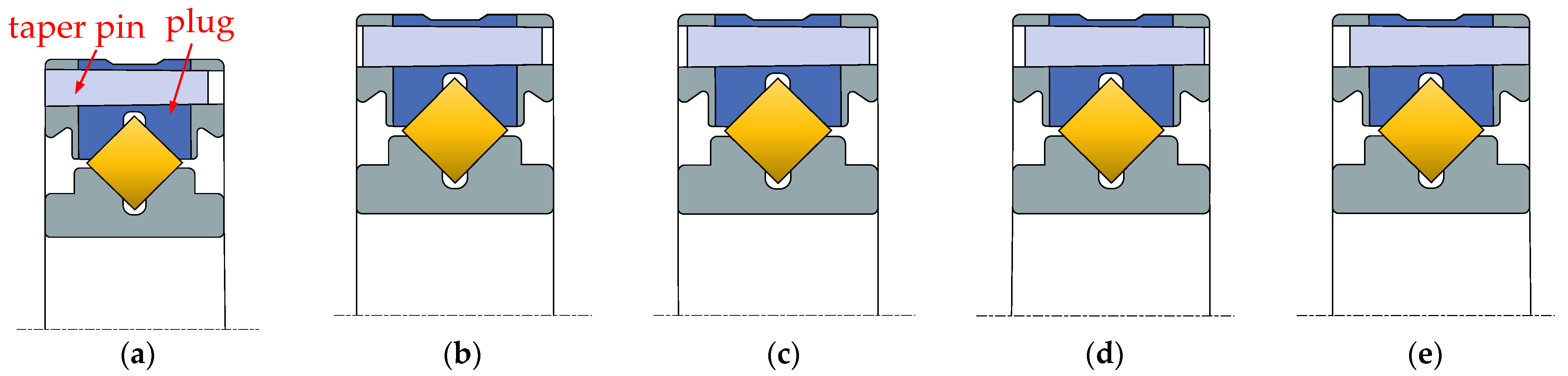
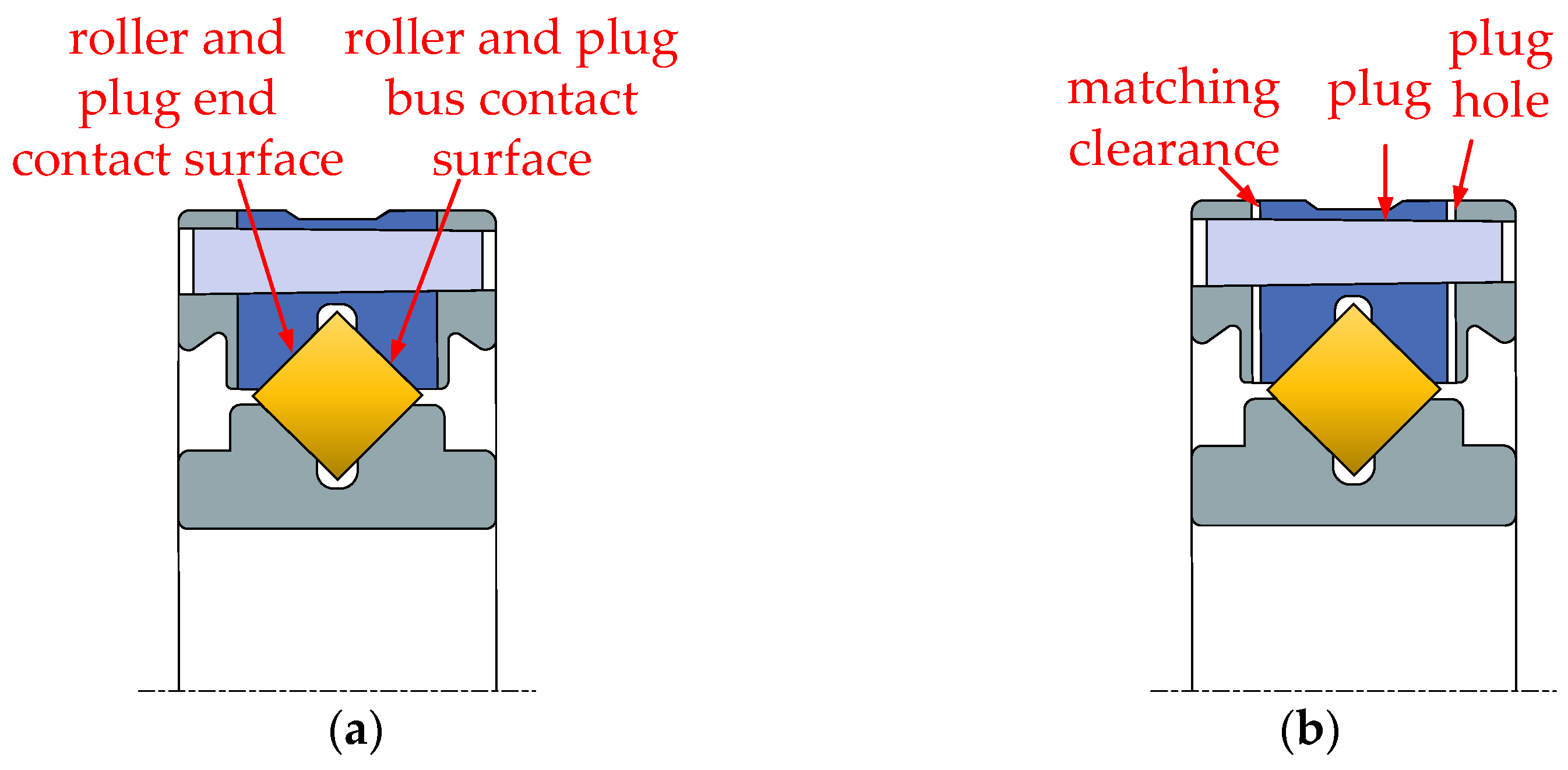
1]. Integrated cross roller bearings with inner and outer rings offer advantages over separate cross roller bearings, particularly in applications requiring higher rotational accuracy. However, the compact structure and high load capacity of internal and external integrated cross roller bearings necessitate the installation of as many rolling elements as possible by filling the holes, which are then sealed with plugs. The position of these plugs is critical to the overall structure of the bearing. Any significant deviation in the alignment of the plugging position during assembly can adversely affect the motion stability of the entire bearing. Consequently, post-assembly movement may be compromised, resulting in reduced flexibility and lower yield.
Currently, in the research on cross roller bearings, Seong-Ho Kang [
2] employed a calculation method based on Hertz theory to conduct theoretical investigations into the bearing stiffness of cross roller and four-point bearings. This method was utilized to analyze the maximum deflection and contact stress of the actuator assembly, and loading conditions for cross roller and four-point bearings of equivalent sizes. Luca Quagliato et al. [
3] applied Archard wear and Lemaitre damage models to simulate the wear phenomena associated with cross roller bearings. By utilizing wear and damage models, along with the results from accelerated life experiments, a reliable methodology can be established for predicting bearing life with minimal number of material property tests. Van-Canh Tong et al. [
4] considered a quasi-static five-degree-of-freedom model of cross roller bearings, taking into account the roundness deformation of rollers. They derived the inertial load resulting from the effect of rotational speed by factoring in the centrifugal force and gyroscopic moment of the rollers and validated the model’s accuracy through experimental verification. Van-Canh Tong et al. [
5] conducted an extensive simulation to investigate the stiffness characteristics of cross roller bearings under varying loads and boundary conditions, taking into account the effects of external load, axial preload, axial clearance, and angular misalignment. MV Prozhega et al. [
6] examined the friction torque and friction coefficient of cross roller bearings under different temperatures, cavity pressures, loads, and lubricant dosages, assessing the impact of various factors on the friction torque. Biao Deng et al. [
7] developed a partial finite element model of a turntable bearing in ABAQUS, analyzing the distribution characteristics of contact stress between the rolling elements and the raceway of the turntable bearing under axial and radial loads, and comparing the stress conditions of the raceway across different raceway structures. Li He et al. [
8] performed an experimental study on the friction characteristics and operational smoothness of ultrasonic suspension bearings. Hwang, So et al. [
9] employed two types of wear models, incorporating both linear and nonlinear mechanisms, to predict the wear of thrust bearings. Wu S et al. [
10] investigated the influence of the angle of the turntable and bearing stiffness on the system dynamics. Ruben Lostado R et al. [
11] proposed a method that integrates the finite element method with multi-response surface optimization to optimize the preload, radial load, and axial load of double-row tapered roller bearings. In the realm of finite element analysis, Yang, Y. et al. [
12] established a dynamic model of the rotor-bearing-cartridge system of rolling body bearings. They obtained and analyzed vibration signals from the bearing seat and cartridge, comparing the results of the bearing seat with itself, alongside both simulation and experimental outcomes. Tyagi, S. et al. [
13] established a finite element model for transient analysis of bearings, simulating and validating the vibration signals of ball bearings exhibiting faults. Taking into account the effects of centrifugal load and radial clearance, Tadina, M. et al. [
14] developed a numerical model of the bearing, assuming that the inner ring possesses only two degrees of freedom while the outer ring is deformable in the radial direction, and conducted finite element modeling. Kuncoro D. et al. [
15] employed the unlubricated Hertzian contact model to analyze the rotor, utilizing the finite element method as the foundation for a flexible rotor model to optimize the design of the auxiliary bearing in order to mitigate bearing instability. Shao, Y. et al. [
16] employ the finite element analysis (FEA) method to conduct simulation research based on a typical bearing assembly, examining its vibration characteristics from the perspective of small impacts and establishing a vibration response model. Common faults, such as outer ring defects, inner ring defects, and rolling ball defects are simulated, allowing for a comparison of their vibration responses under various fault conditions and different positions of the bearing seat. Schmidt, A.A. et al. [
17] utilize nonlinear, transient, three-dimensional finite element analysis (FEA) to simulate complex dynamic behavior in diverse contact situations, subsequently adjusting the mesh by implementing node displacement. This mesh refinement enhances the resolution of the results and facilitates convergence. Safian, A. et al. [
18] presents findings from a combination of lumped parameter and finite element models to simulate the strain signals of cylindrical roller bearings under both normal and defective conditions. The contact pressure is derived from the lumped parameter model and applied to the finite element model for transient analysis. A static two-dimensional finite element contact model and theoretical formulas are employed to verify the accuracy of the stress distribution generated by the model. Zeng, S. [
19] studied the transient response of active magnetic bearing rotor falling on spare bearing by numerical simulation and experiment, and compared the experimental results with the simulation results. Finally, the conclusion based on simulation and experiment is given.
Huang Jian et al. [
20] established a static model of cross roller bearings that accounts for raceway roundness. They derived a fatigue life calculation formula for cross roller bearings affected by raceway roundness errors and analyzed the impact of these errors on rotation accuracy, load distribution, and fatigue life. Oswald F.B. et al. [
21] proposed a method for enhancing roller shape, which subsequently improves bearing life and other properties. Deng B. et al. [
22] introduced a method for calculating the internal load distribution and contact stress of thrust angular contact ball turntable bearings using the finite element method. Pan Xingyu et al. [
23] developed a simulation model based on Romax to investigate how various working conditions affect the life of cross cylindrical roller bearings. He Dongkang et al. [
24] proposed a fault diagnosis method for cross roller bearings in industrial robots, utilizing maximum resolution singular value decomposition (MRSVD), singular value decomposition (SVD), and variable prediction model pattern recognition (VPMCD) to identify fault types. Hu Jingyuan et al. [
25] addressed the challenges of low assembly efficiency and accuracy in the production process of precision cross cylindrical roller bearings by enhancing bearing performance and production efficiency through stringent control of part accuracy, thereby ensuring the rotation accuracy of the finished bearings. Wang Kunping et al. [
26] introduced three common types of cross-cylindrical roller bearing structures and identified factors affecting the repeated positioning accuracy of these bearings from the perspectives of bearing design, processing technology, installation, and maintenance. They proposed corresponding improvement measures. He Peiyu et al. [
27] established a local finite element model to analyze the contact between rollers and raceways, investigating the damage conditions of cylindrical rollers in three-row roller type rotary table bearings under sliding, pure rolling, and sliding-rolling conditions. Their study also examined the effects of the friction coefficient, sliding displacement equivalent effect force, alternating stress, and contact stress. Building on the maximum load derived from finite element calculations, Huang Longyi et al. [
28] conducted a contact analysis of rollers and raceways, exploring the stress distribution at the contact points under various gap conditions. Qiao Shuxiang et al. [
29] addressed issues of abnormal bearing noise and excessive sound resulting from blockages in the angular contact ball turntable bearing’s position. They improved the design of the blocked position, ensuring coherence and consistency in the bearing raceway, which effectively enhanced the stability of the turntable bearing. Lastly, Zhijian Wang et al. [
30] developed a quasi-static model that accounts for inner ring dislocation and combined load to enhance the reliability of double-row cylindrical roller bearings.
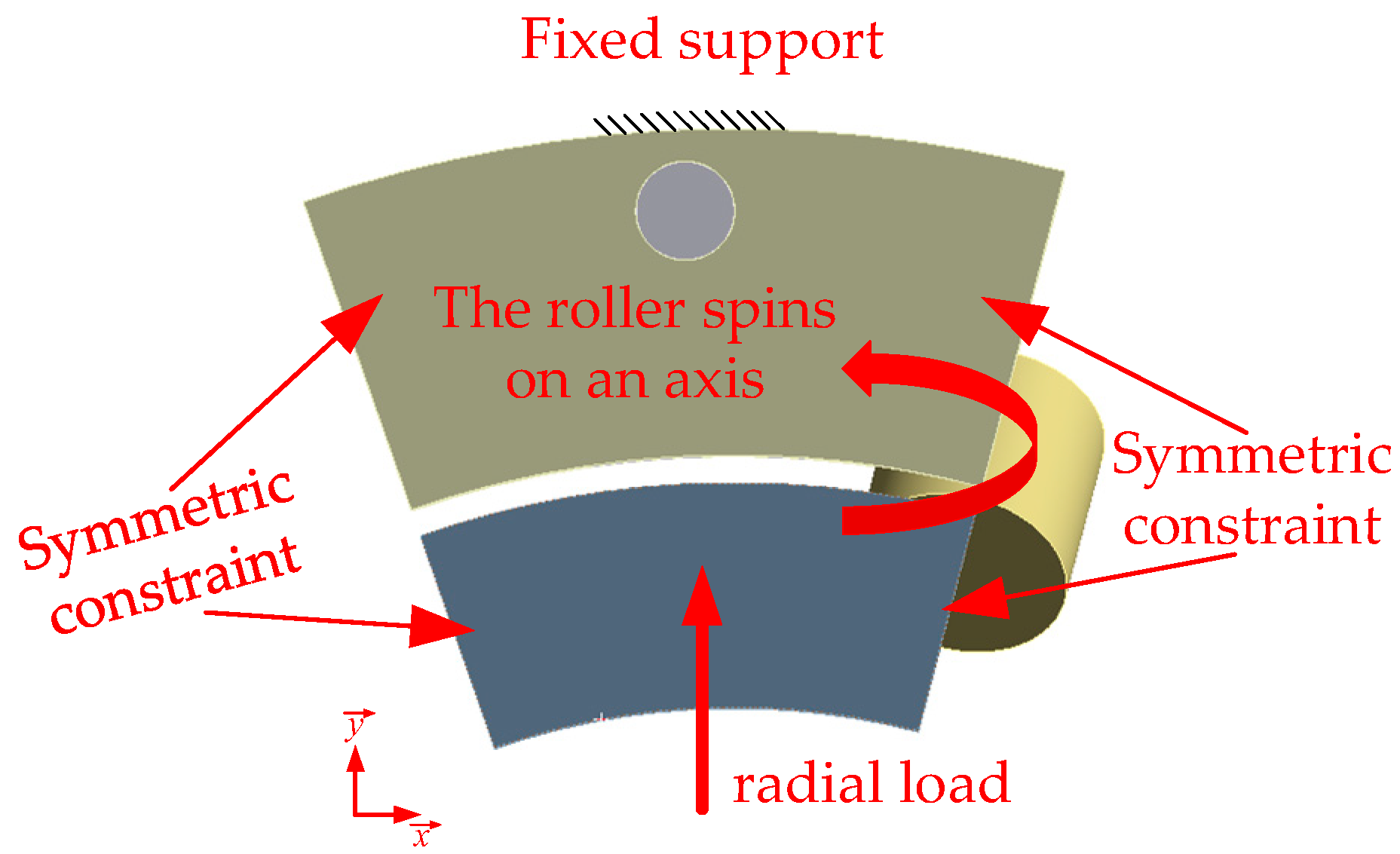
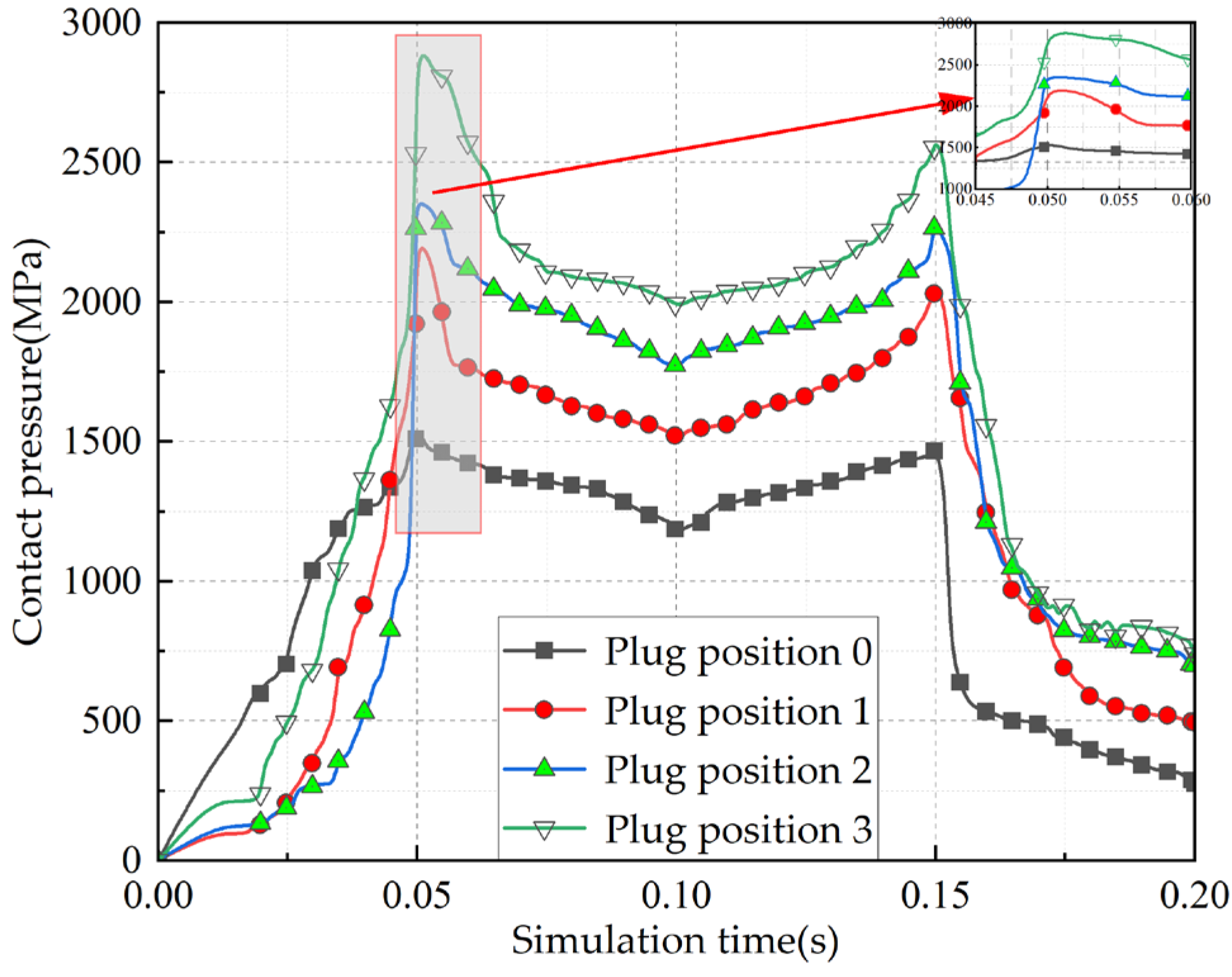
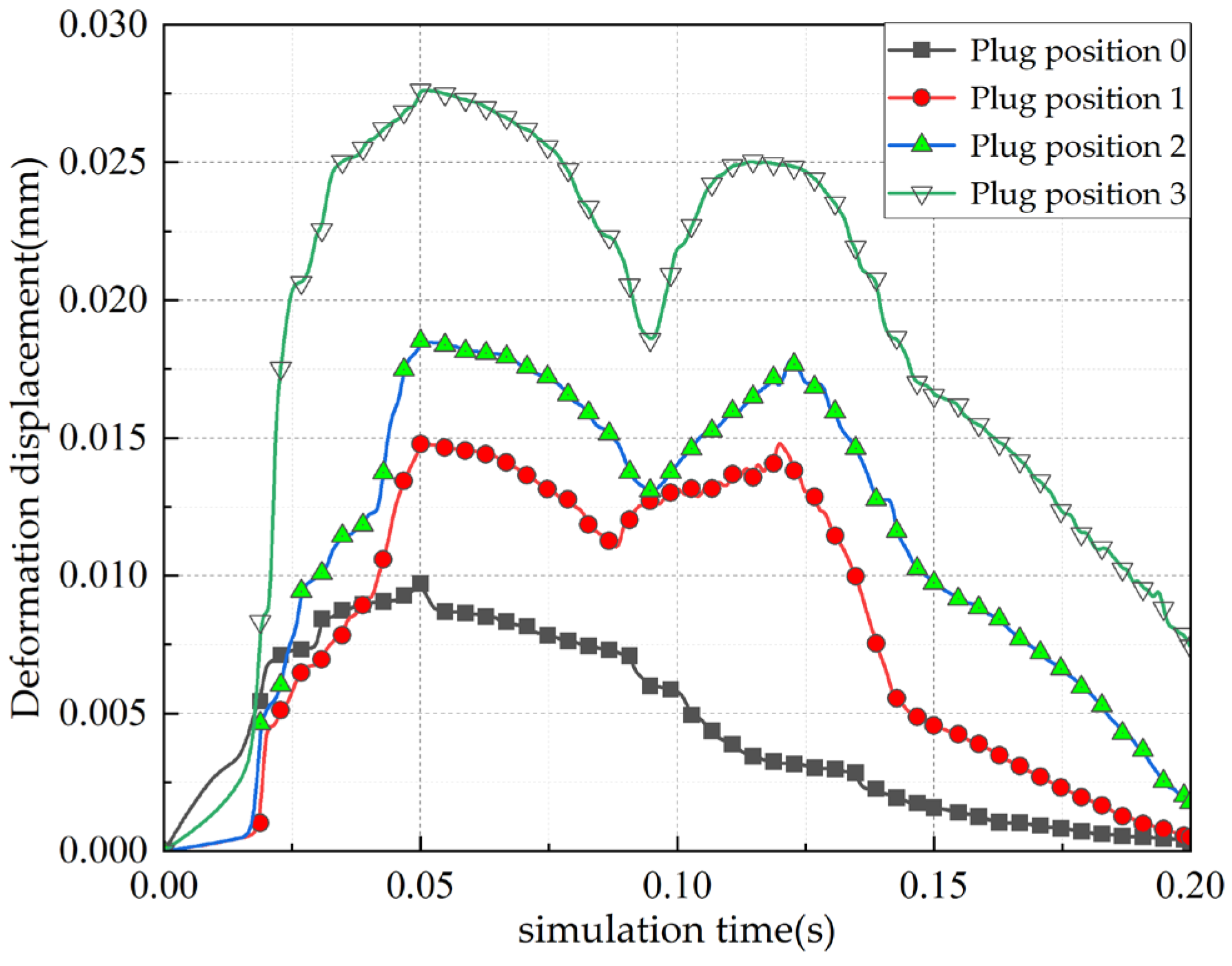
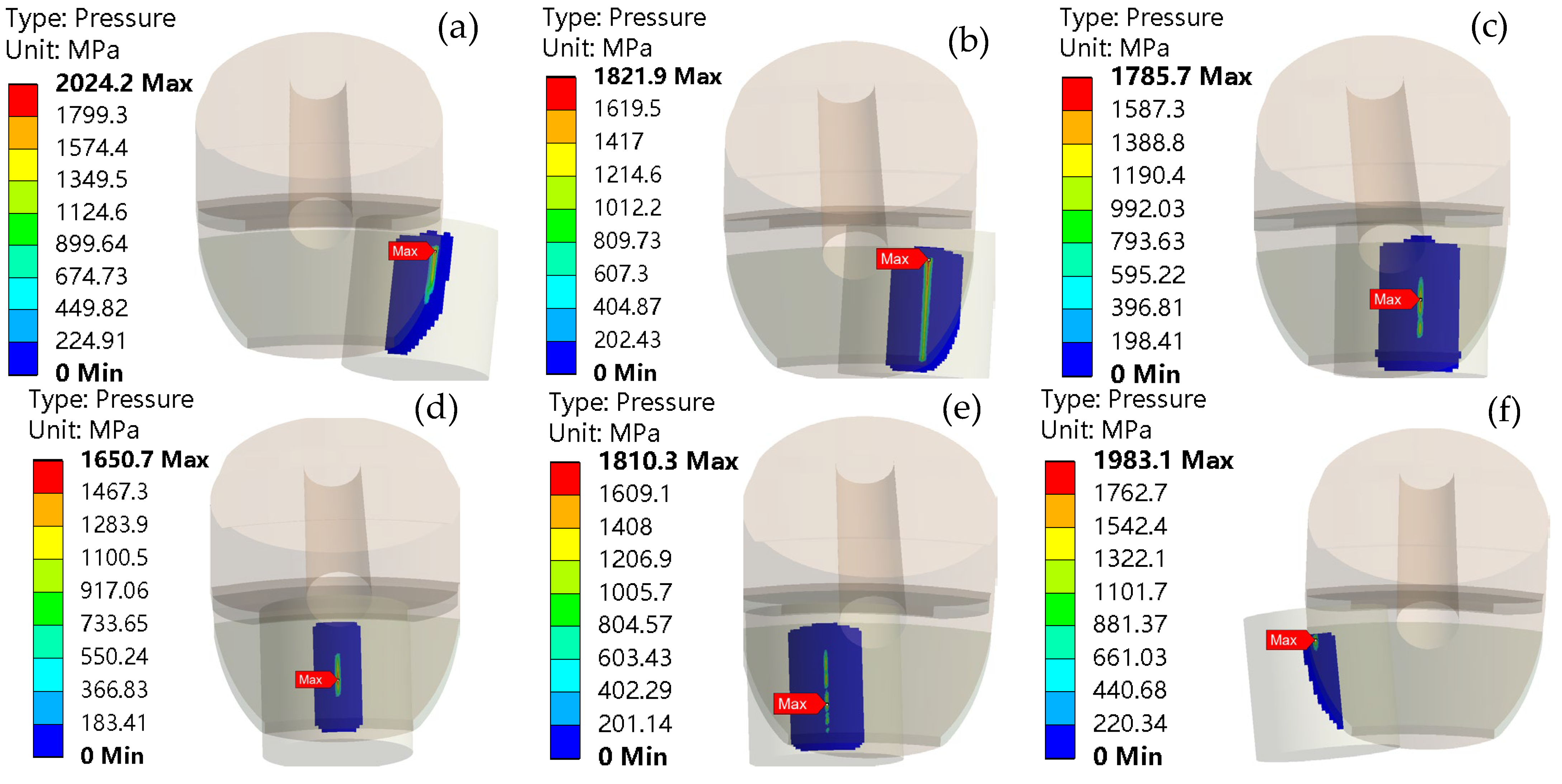
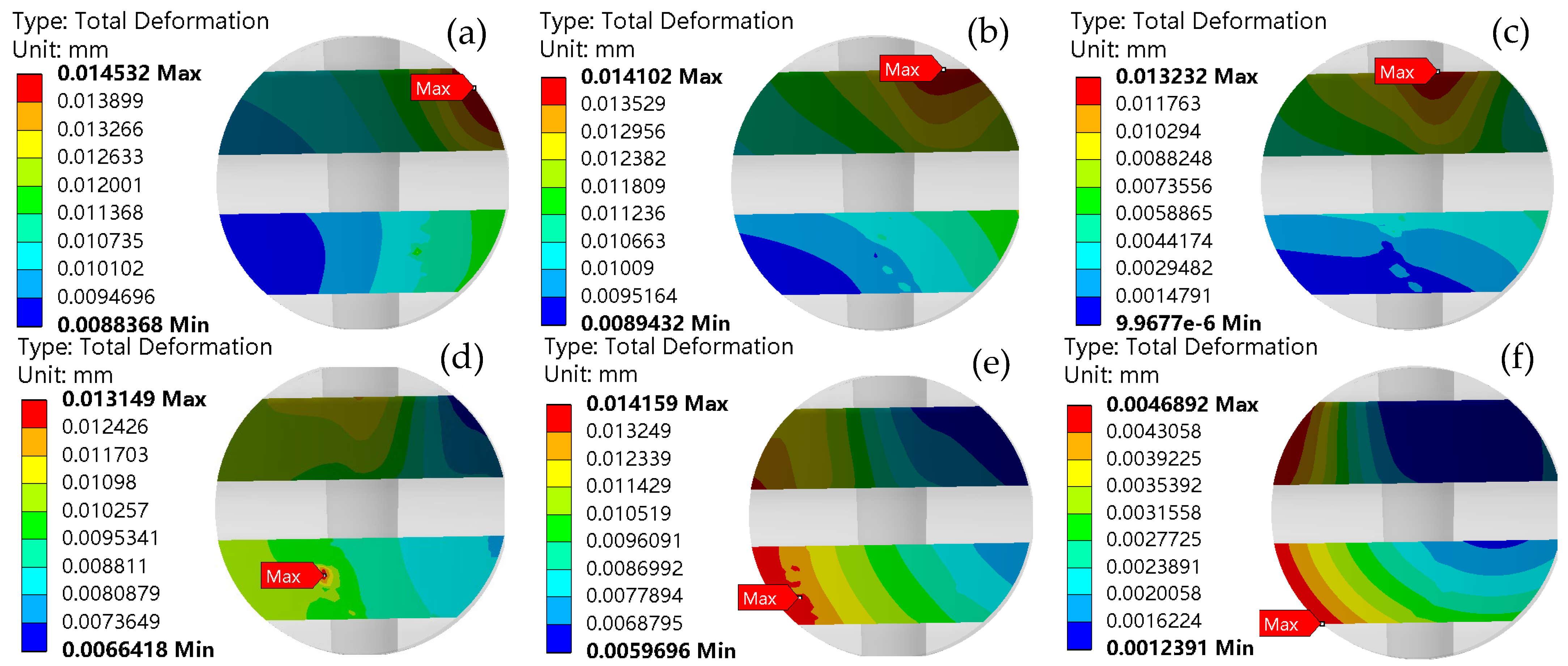
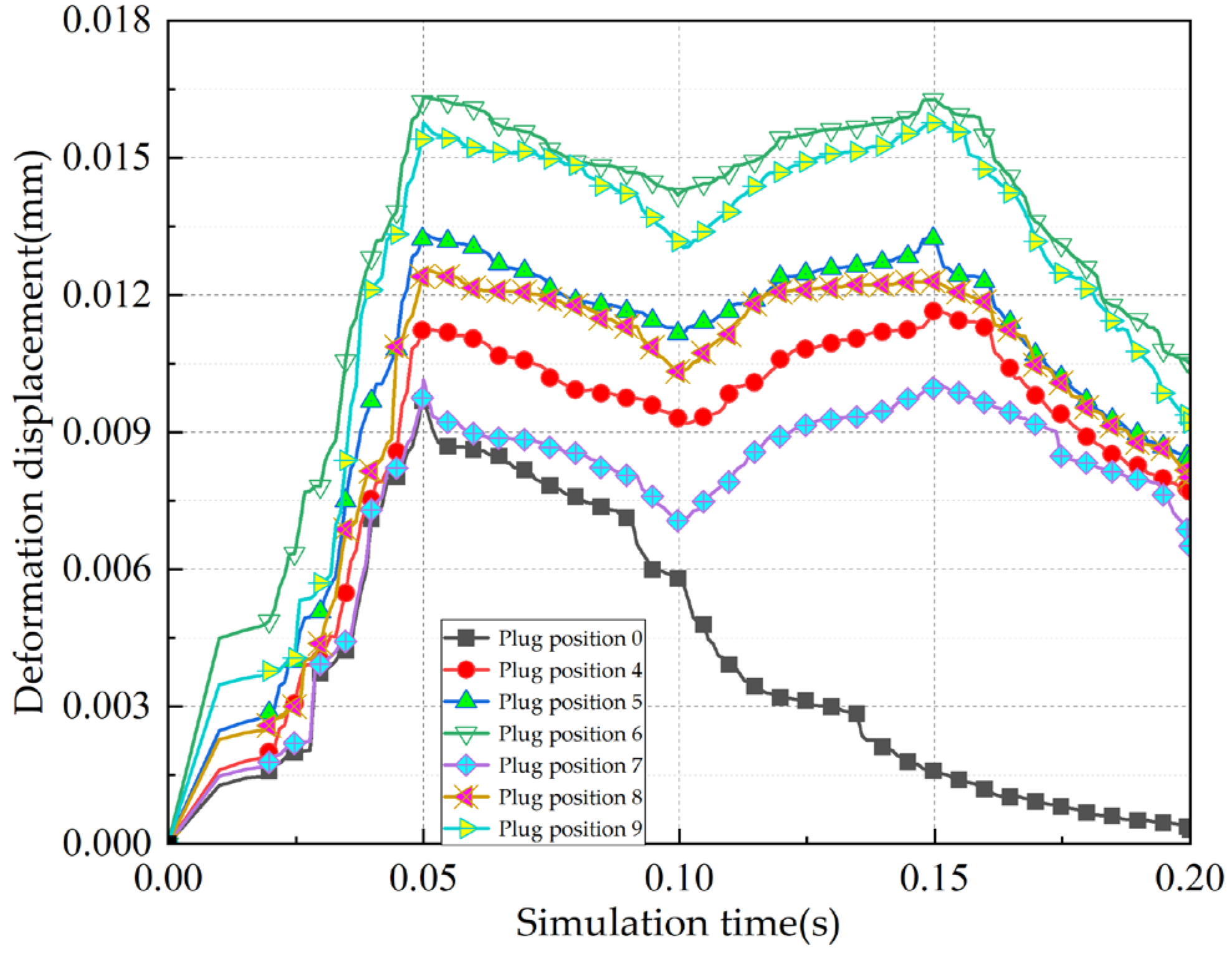
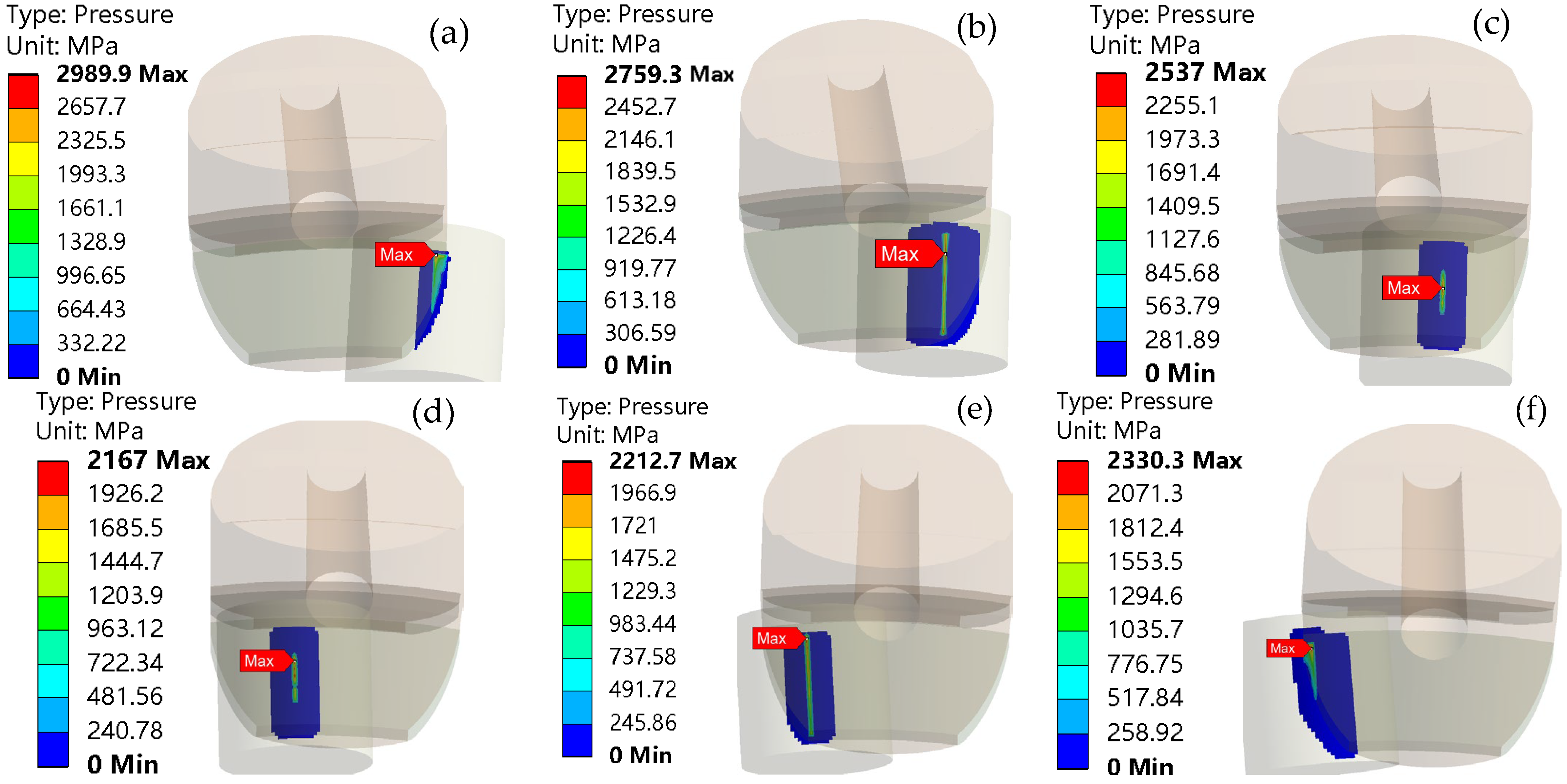
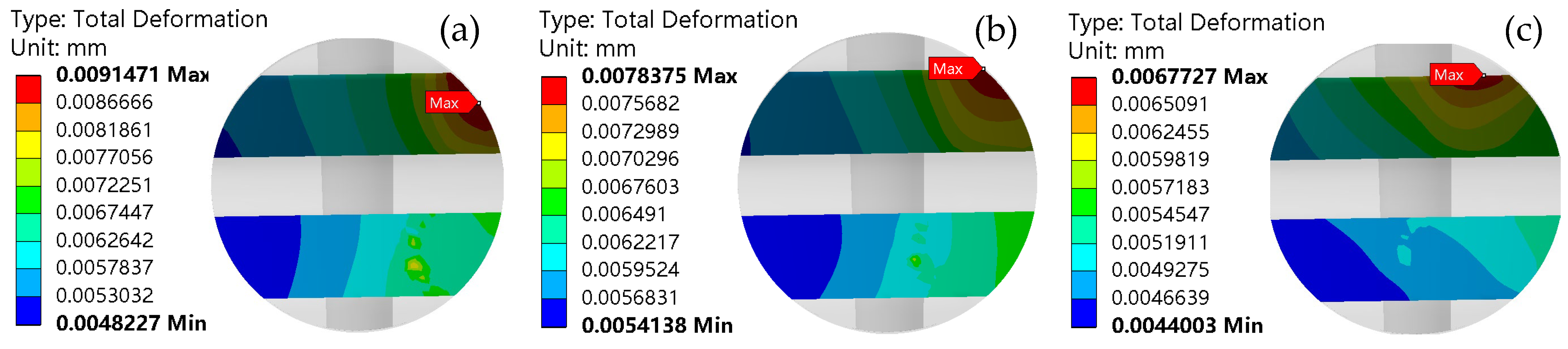
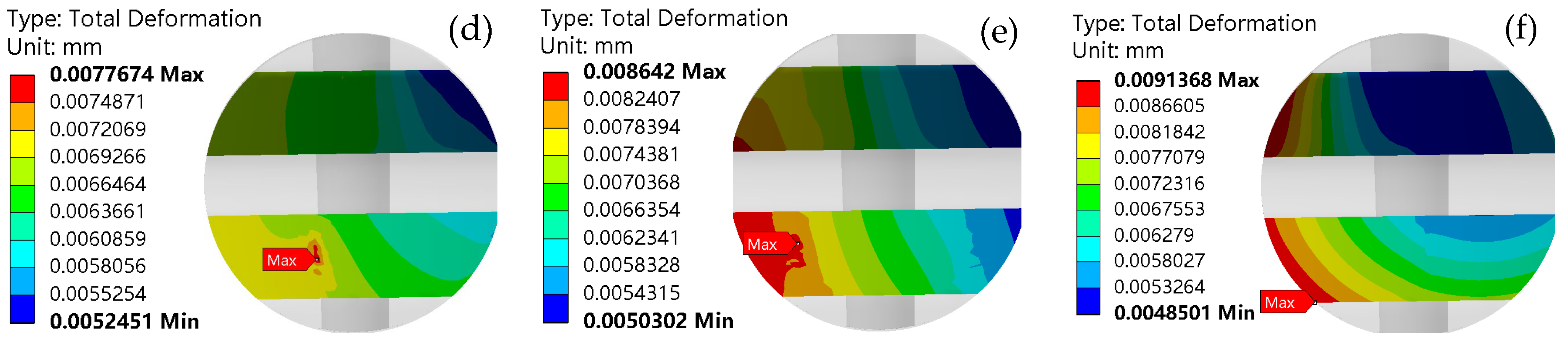
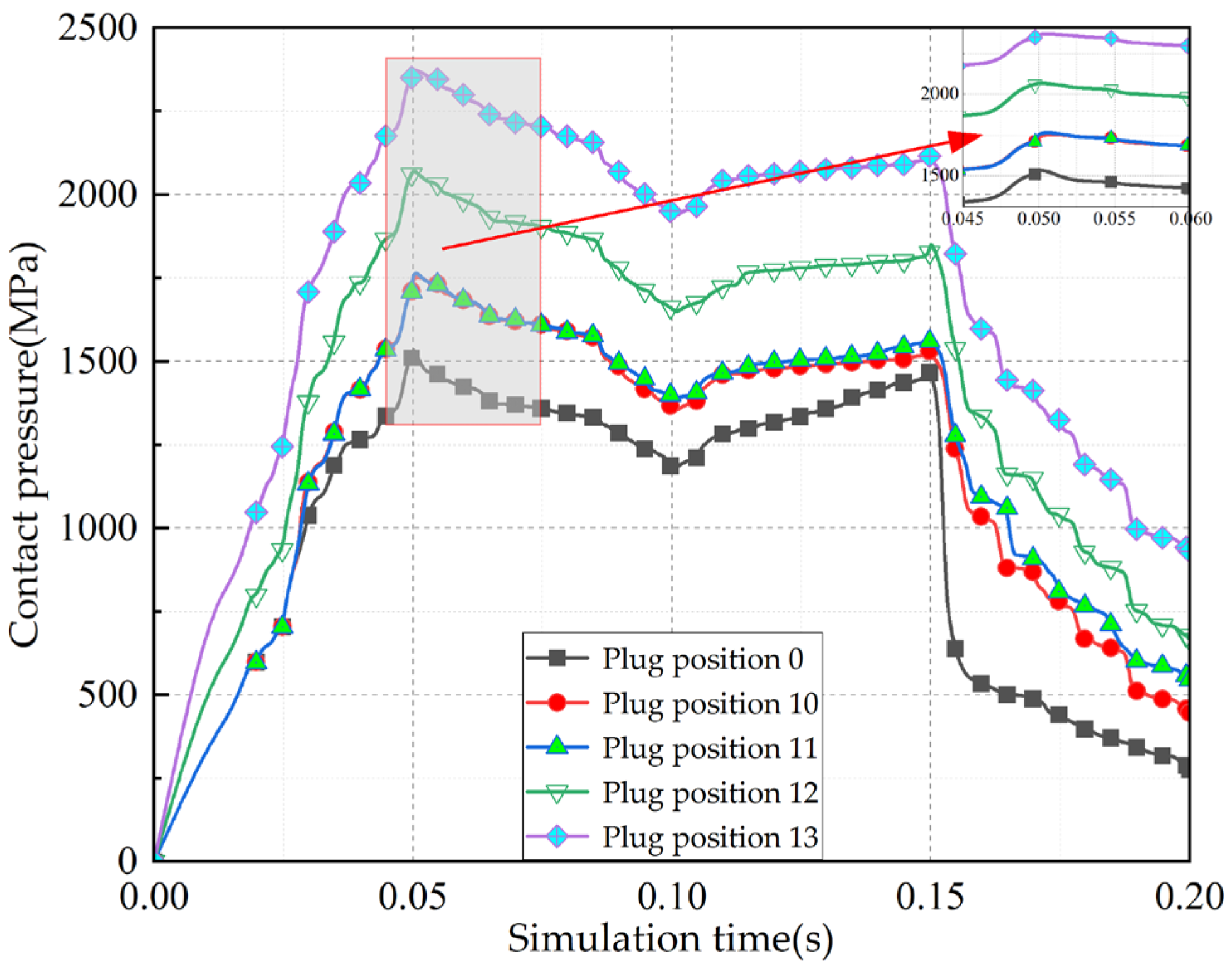
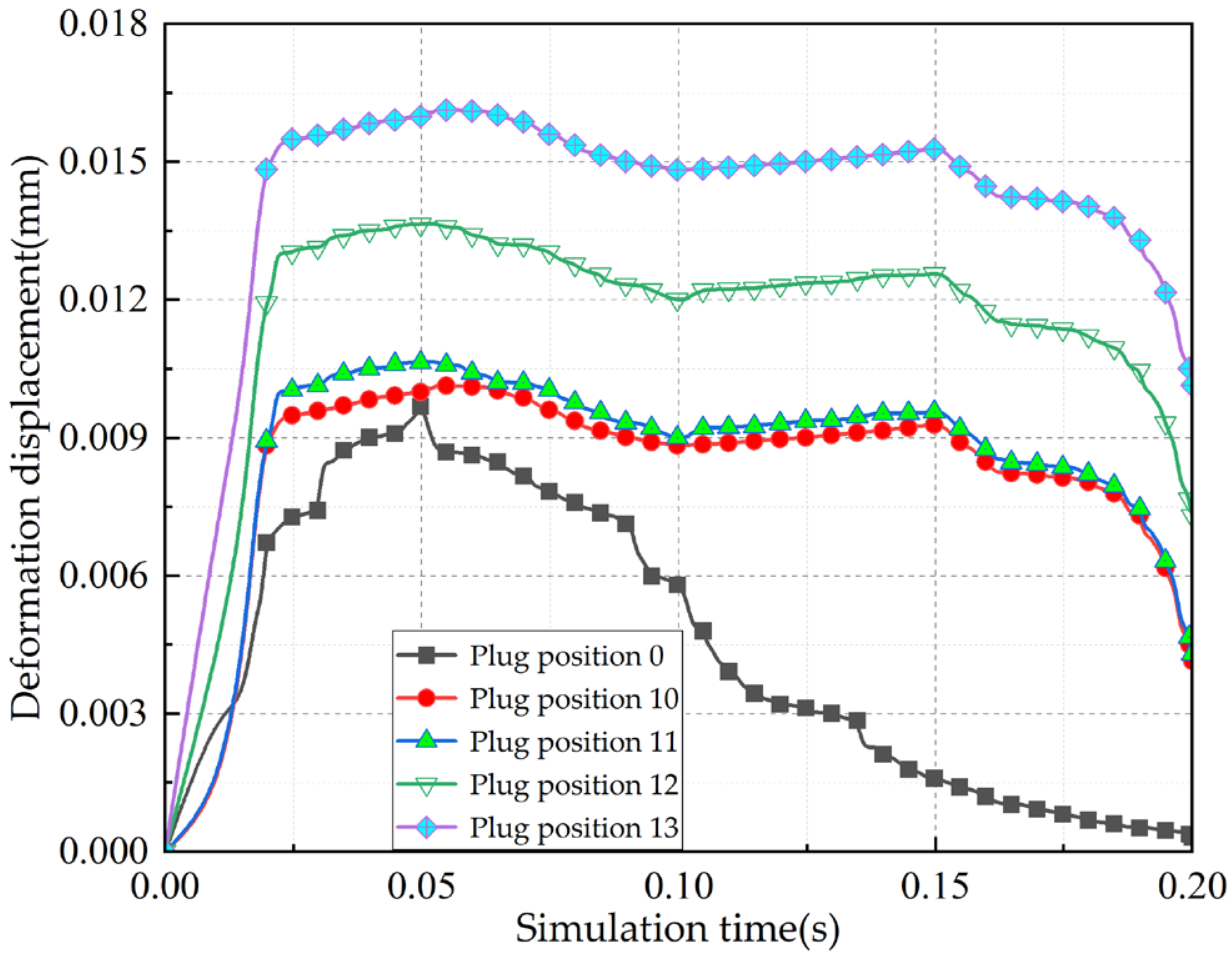
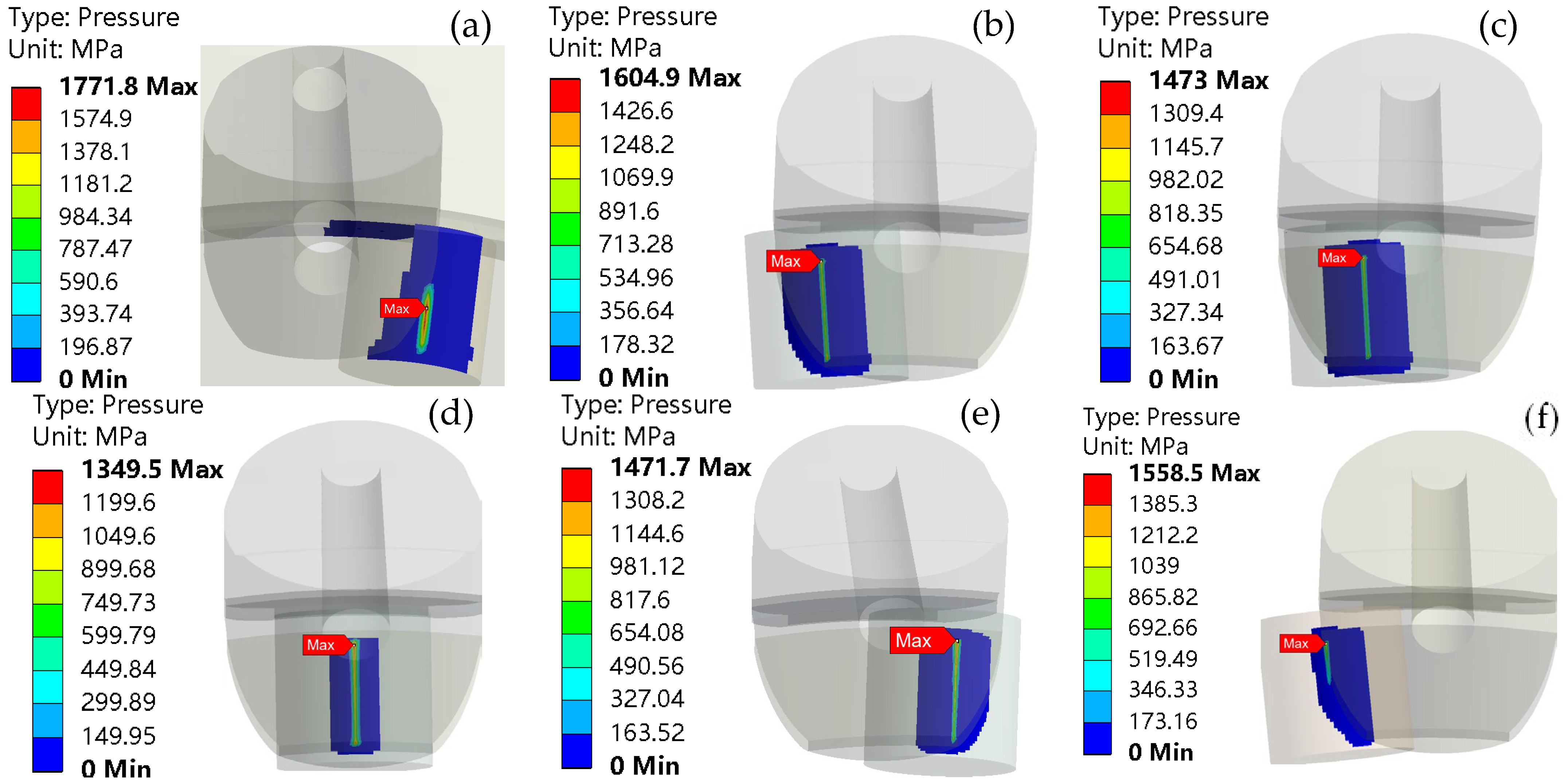
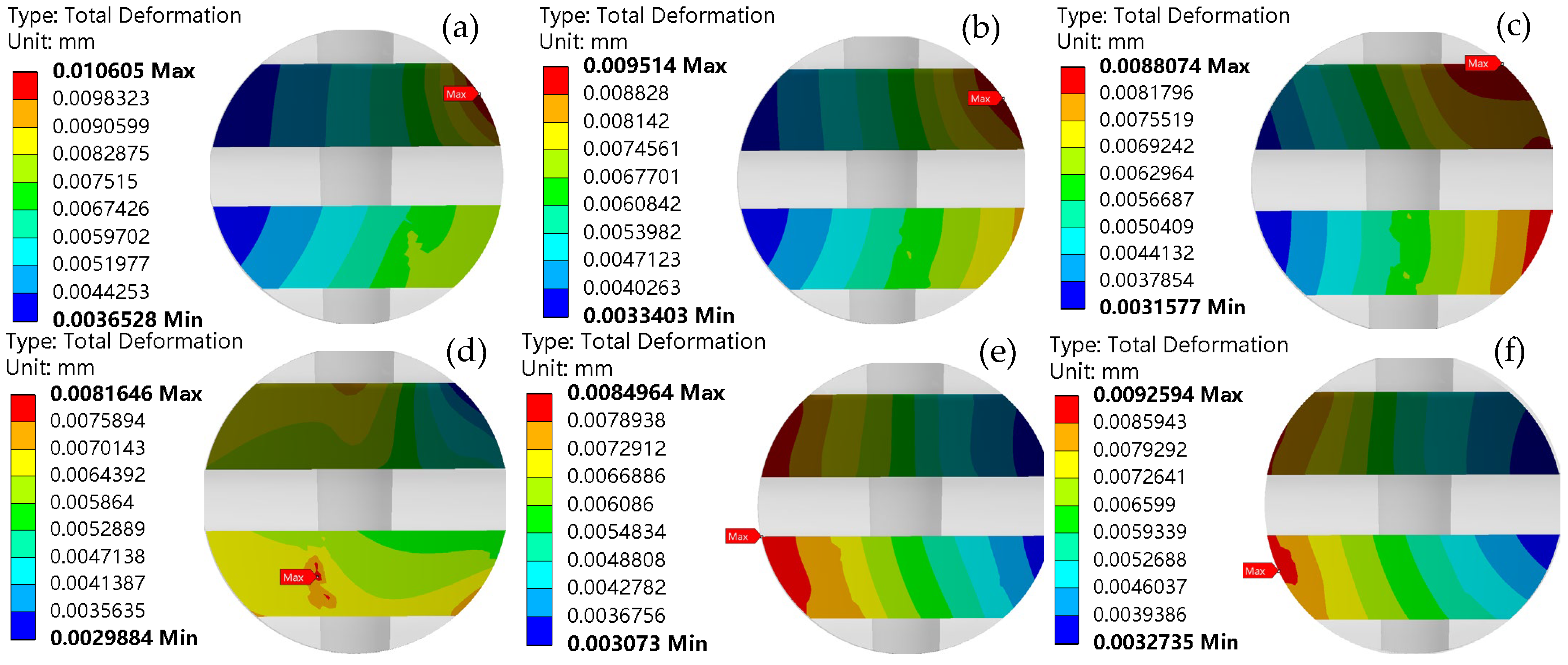
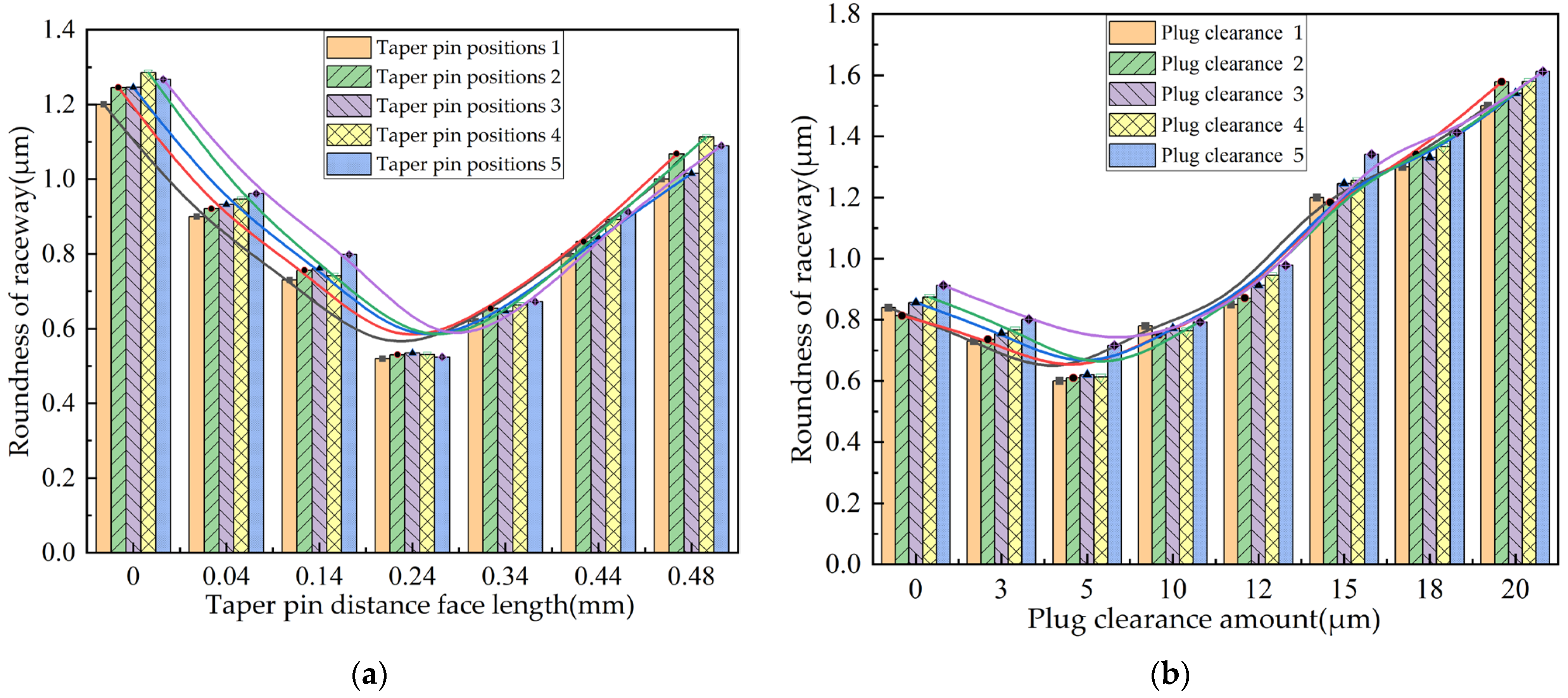
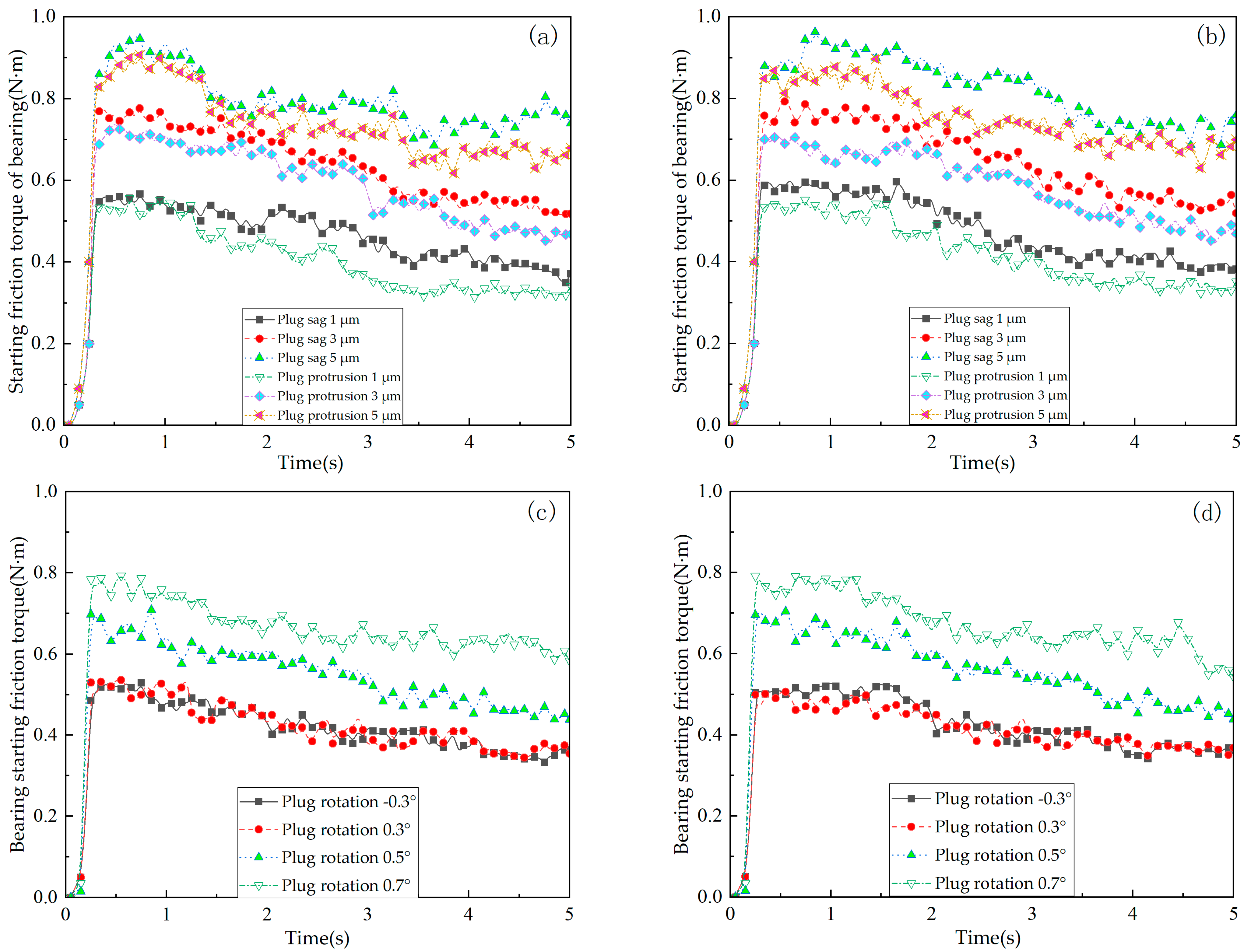
In summary, the life, load distribution, and fault identification of cross roller bearings have been comprehensively studied, with an analysis of the influence of various factors on bearing motion stability. However, the effects of the plugging position and fit on motion stability have not been addressed in the previous research. For internal and external integrated cross roller bearings, due to their compact structure and high load capacity requirements, it is essential to maximize the number of rolling elements by filling holes and ultimately sealing them with plugs. The plugging position of these bearings is a critical structural aspect. If there is a significant deviation in the plugging position or fit during assembly, it can greatly affect the motion stability of the entire bearing. Following assembly, the movement may often be unsmooth, leading to insufficient flexibility and reduced yield. To address the issue of poor movement in internal and external integrated cross roller bearings, this paper establishes a finite element explicit dynamic simulation model that incorporates the plugging position and fitting relationship. Through simulation, we obtain data on the contact pressure and deformation between the roller and the plug during the plugging process, and analyze how the plugging position and fitting relationship impact bearing motion stability. The findings of this research can provide valuable insights for selecting the optimal location and matching relationship of the plug-in cross roller bearings.