Current Status of Research on Fault Diagnosis Using Machine Learning for Gear Transmission Systems
Abstract
1. Introduction
2. Development of Fault Diagnosis of Gear Transmission System
3. Fault Diagnosis Method Based on Mathematical Signal Processing
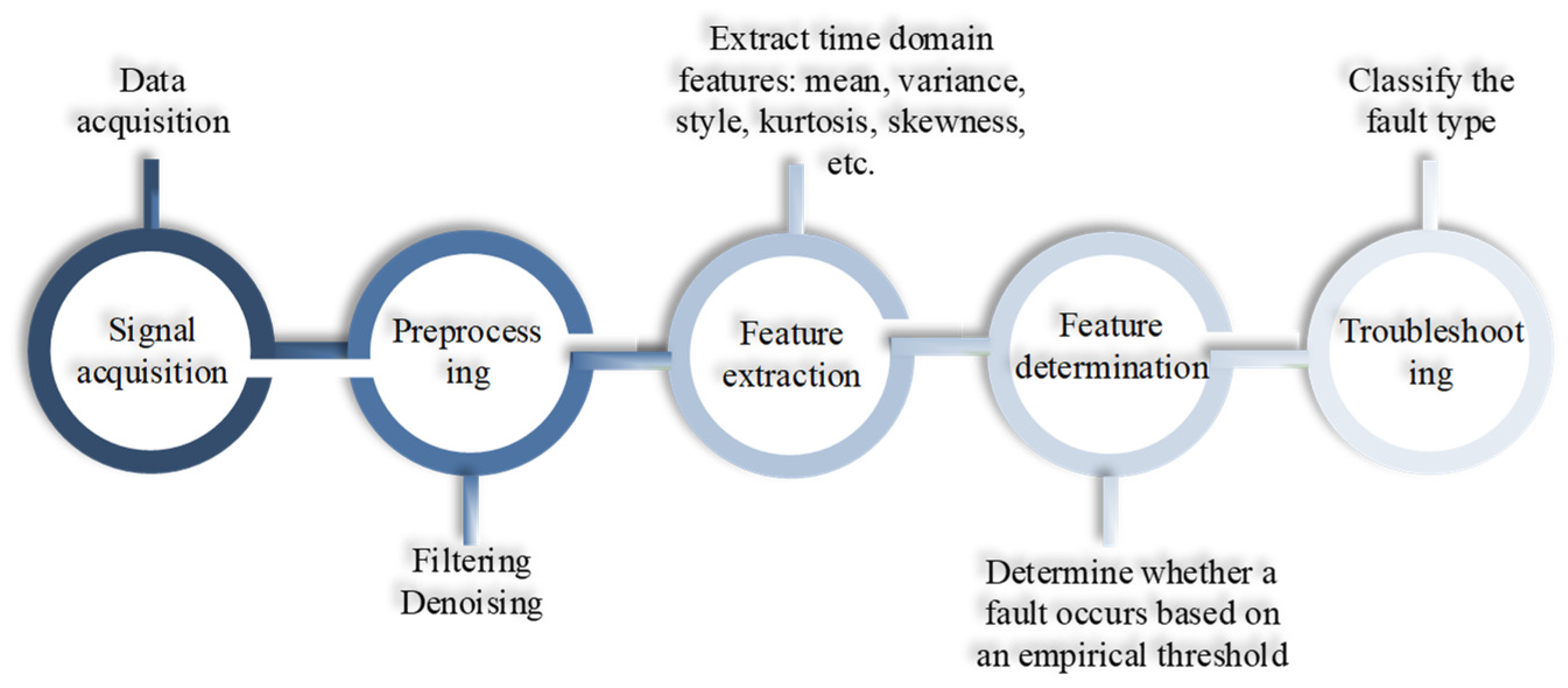
3.1. Time-Domain Analysis Method
3.2. Frequency-Domain Analysis Method
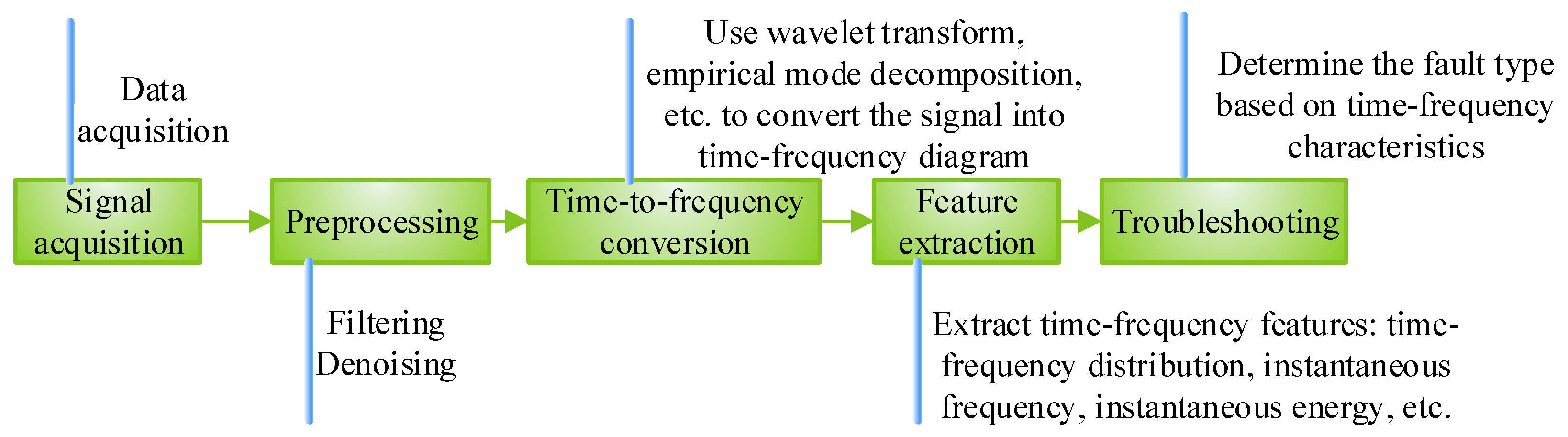
3.3. Time-Frequency-Domain Analysis Method
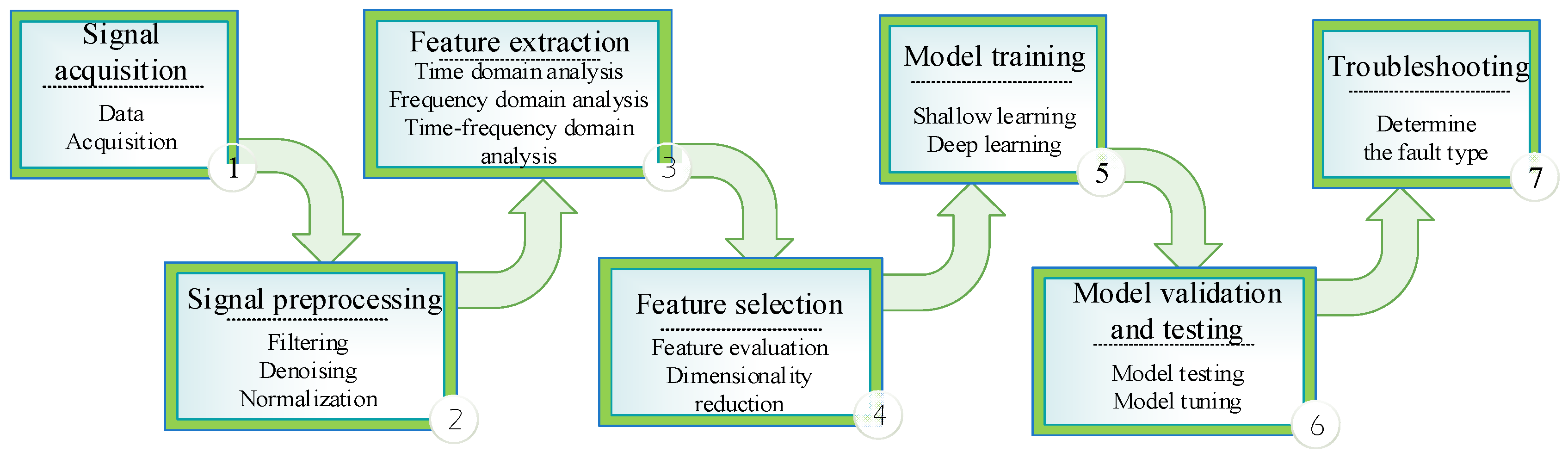
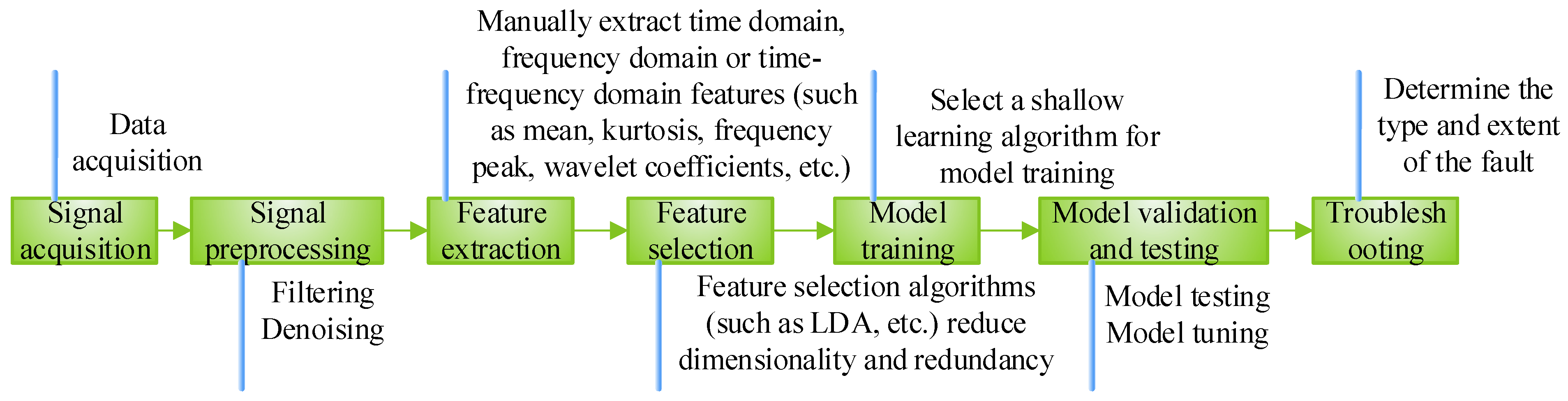
4. Fault Diagnosis Method Based on Intelligent Diagnosis
4.1. Diagnostic Methods Based on Shallow Learning
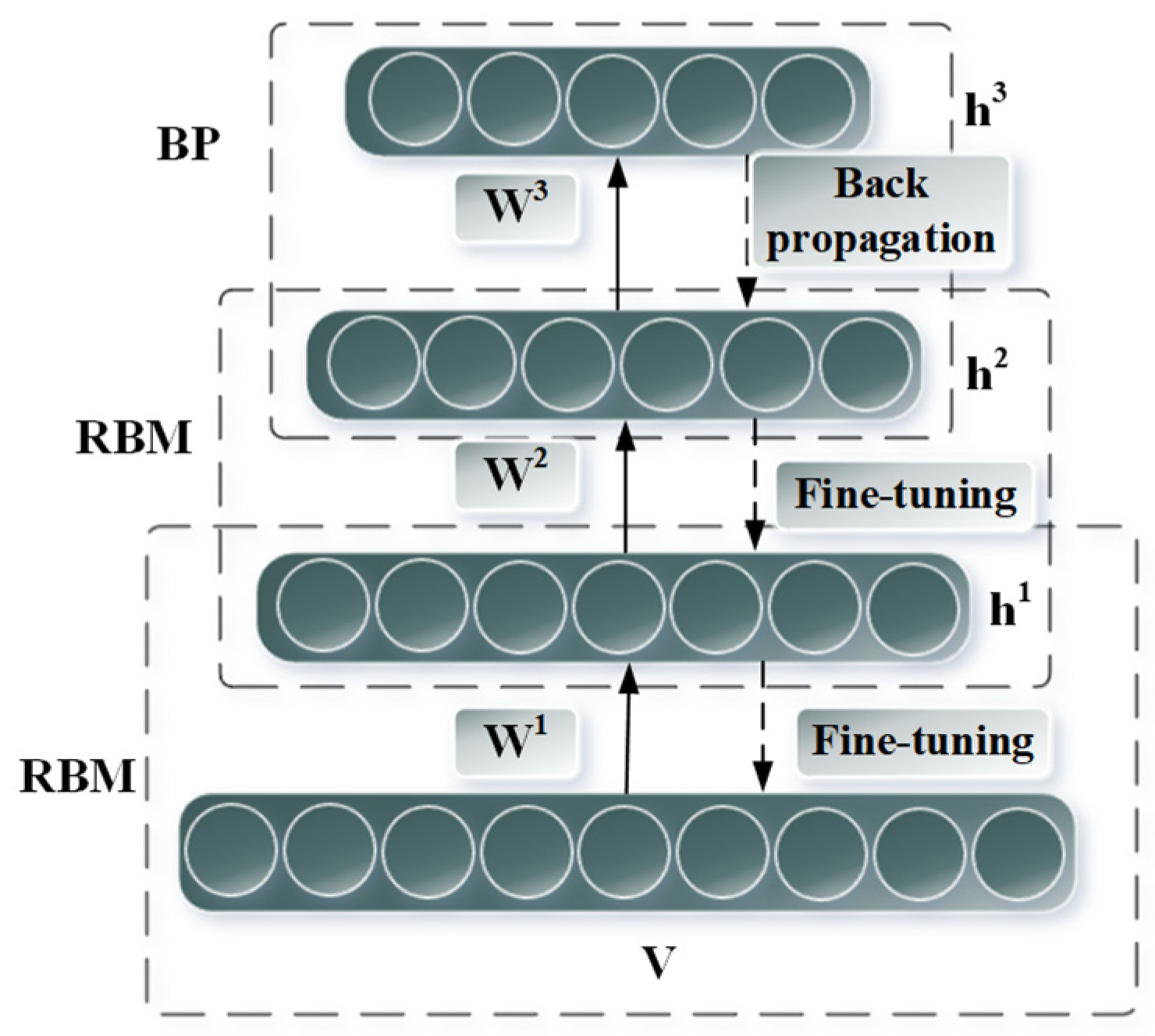
4.2. Diagnostic Methods Based on Deep Learning
4.3. Comparative Analysis of Shallow Learning and Deep Learning
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, K.; Li, W.H.; Zhu, X.Y. Practical Technology of Gear and Gearbox Fault Diagnosis; Machinery Industry Press: Beijing, China, 2005; pp. 156–179. [Google Scholar]
- Litvin, L.F.; Fuentes, A.; Gonzalez-Perez, I.; Carvenali, L.; Kawasaki, K.; Handschuh, R.F. Modified involute helical gears: Computerized design, simulation of meshing and stress analysis. Comput. Methods Appl. Mech. Eng. 2003, 192, 3619–3655. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. An Ease-Off Based Method for Loaded Tooth Contact Analysis of Hypoid Gears Having Local and Global Surface Deviations. J. Mech. Des. 2010, 132, 071004. [Google Scholar] [CrossRef]
- Fuentes-Aznar, A.; Gonzalez-Perez, I. Mathematical definition and computerized modeling of spherical involute and octoidal bevel gears generated by crown gear. Mech. Mach. Theory 2016, 106, 94–114. [Google Scholar] [CrossRef]
- Maksat, T.; Christos, S.; Dongming, W. A computationally robust solution to the contact problem of two rotating gear surfaces in space. Meccanica 2023, 58, 2455–2466. [Google Scholar]
- Hamza, T.; Zhaksylyk, G.; Andas, A.; Christos, S. Assessment of contact forces and stresses, torque ripple and efficiency of a cycloidal gear drive and its involute kinematical equivalent. Mech. Based Des. Struct. Mach. 2024, 52, 1304–1323. [Google Scholar]
- Chen, P.; Toyota, T.; He, Z. Automated Function Generation of Symptom Parameters and Application to Fault Diagnosis of Machinery Under Variable Operating Conditions. IEEE Trans. Syst. Man Cybern. Syst. 2001, 31, 775–781. [Google Scholar] [CrossRef]
- Chen, P.; Taniguchi, M.; Toyota, T.; He, Z. Fault diagnosis method for machinery in unsteady operating condition by instantaneous power spectrum and genetic programming. Mech. Syst. Signal Process. 2003, 19, 175–194. [Google Scholar] [CrossRef]
- Zhong, B.L.; Huang, R. Mechanical Fault Diagnosis, 3rd ed.; Machinery Industry Press: Beijing, China, 2007; pp. 141–161. [Google Scholar]
- Hua, W. Research on Vibration Fault Diagnosis of Low-Speed Heavy-Loaded Gears. Master’s Thesis, Henan Polytechnic University, Nanyang, China, 2007. [Google Scholar]
- Randall, R.B. New Method of Modeling Gear Faults. ASME J. Mech. Des. 1981, 104, 259–267. [Google Scholar] [CrossRef]
- McFadden, P.D.; Wang, W.J. Early detection of gear failure by vibration analysis—II. Interpretation of the time-frequency distribution using image processing techniques. Mech. Syst. Signal Process. 1993, 7, 205–215. [Google Scholar]
- Forrester, B.D. Gear Fault Detection using the Wigner-Ville Distribution. In Australian Vibration and Noise Conference 1990, Vibration and Noise-Measurement Prediction and Control; Preprints of Papers; Institution of Engineers: Barton, Australia, 1990. [Google Scholar]
- Yu, H.P.; Dong, W.F.; Liu, Y. Application of CAT technology in gearbox noise testing. China Test. 2009, 35, 90–93. [Google Scholar]
- Samanta, B. Gear fault detection using artificial neural networks and support vector machines with genetic algorithms. Mech. Syst. Signal Process. 2004, 18, 625–644. [Google Scholar] [CrossRef]
- Cheng, G.; Cheng, Y.; Shen, L.; Qiu, J.; Zhang, S. Gear fault identification based on Hilbert–Huang transform and SOM neural network. Measurement 2013, 46, 1137–1146. [Google Scholar] [CrossRef]
- Sanz, J.; Perera, R.; Huerta, C. Gear dynamics monitoring using discrete wavelet transformation and multi-layer perceptron neural networks. Appl. Soft Comput. J. 2012, 12, 2867–2878. [Google Scholar] [CrossRef]
- Hu, P.; Zhao, C.; Huang, J.; Song, T. Intelligent and Small Samples Gear Fault Detection Based on Wavelet Analysis and Improved CNN. Processes 2023, 11, 2969. [Google Scholar] [CrossRef]
- Bordoloi, D.; Tiwari, R. Optimization of support vector machine based multi-fault classification with evolutionary algorithms from time domain vibration data of gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2428–2439. [Google Scholar] [CrossRef]
- Bond, R.R. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications; John Wiley & Sons, Ltd.: New York, NY, USA, 2010; pp. 143–165. [Google Scholar]
- Simani, S.; Fantuzzi, C.; Patton, R.J. Model-Based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: Berlin/Heidelberg, Germany, 2003; pp. 61–113. [Google Scholar]
- Fu, Y.; Chen, X.; Liu, Y.; Son, C.; Yang, Y. Multi-Source Information Fusion Fault Diagnosis for Gearboxes Based on SDP and VGG. Appl. Sci. 2022, 12, 6323. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, T.; Xu, J.; Li, B. Keyless phase time domain synchronous averaging method for variable speed gearbox vibration signal monitoring. J. Xi’an Jiaotong Univ. 2012, 46, 111–114. [Google Scholar]
- Ha, M.J.; Youn, D.B.; Oh, H.; Han, B.; Jung, Y.; Park, J. Autocorrelation-based time synchronous averaging for condition monitoring of planetary gearboxes in wind turbines. Mech. Syst. Signal Process. 2016, 70–71, 161–175. [Google Scholar] [CrossRef]
- Yao, G.; Wang, Y.; Benbouzid, M.; Ait-Ahmed, M. A Hybrid Gearbox Fault Diagnosis Method Based on GWO-VMD and DE-KELM. Appl. Sci. 2021, 11, 4996. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. Application of Kurtosis-Based Deconvolution for Gear Fault Diagnosis. Mech. Syst. Signal Process. 2007, 22, 13–25. [Google Scholar]
- Liu, H.; Wang, X. Deconvolution Approach Using Maximum Correlation Kurtosis for Gearbox Fault Diagnosis. Mechanical Syst. Signal Process. 2009, 32, 13–15. [Google Scholar]
- Wu, Q.; Zhang, X. Enhanced Maximum Correlation Kurtosis Deconvolution Method for Gear Fault Detection. IEEE Trans. Instrum. Meas. 2011, 9, 73–95. [Google Scholar]
- Hua, W.; Luo, C.; Leng, J.; Wang, Z. Mine gearbox fault diagnosis based on multiwavelets and maximum correlated kurtosis deconvolution. J. Vibroeng. 2017, 19, 4185–4197. [Google Scholar] [CrossRef][Green Version]
- Chen, L.; Xu, Y. Multi-Scale Maximum Correlation Kurtosis Deconvolution for Fault Diagnosis of Gearbox. Mech. Syst. Signal Process. 2017, 42, 43–65. [Google Scholar]
- He, Q.; Guo, Y.G.; Wang, X.; Xie, P.; Jiang, G.; Li, J. Gearbox fault diagnosis based on signal resonance sparse decomposition and maximum correlation kurtosis deconvolution. China Mech. Eng. 2017, 28, 1528–1534. [Google Scholar]
- Hong, L.; Liu, X.; Zuo, H. Compound Fault Diagnosis of Rotating Machinery Based on Adaptive Maximum Correlated Kurtosis Deconvolution and Customized Multiwavelet Transform. Measurement 2019, 146, 87–100. [Google Scholar] [CrossRef]
- He, F.; Zheng, C.; Pang, C.; Zhao, C.; Yang, M.; Zhu, Y.; Luo, Z.; Luo, H.; Li, L.; Jiang, H. An Adaptive Deconvolution Method with Improve Enhanced Envelope Spectrum and Its Application for Bearing Fault Feature Extraction. Sensors 2024, 24, 951. [Google Scholar] [CrossRef]
- Wang, K.X.; Liu, R.C.; Sun, J.Z. Gear fault monitoring method based on electrostatic signal and short-time Fourier transform. Mech. Electr. Eng. 2023, 40, 1664–1672. [Google Scholar]
- Wu, H.; Lv, Y.; Yi, C.; Yuan, R. Synchronous compression algorithm with window expansion optimization and its application in instantaneous frequency estimation under variable speed conditions. China Mech. Eng. 2022, 33, 34–44. [Google Scholar]
- Bao, W.; Tu, X.; Li, F.; Dai, L.; Shen, Y.; Liu, Z.; Wang, X. Parameterized short-time Fourier transform and gearbox fault diagnosis. Vibration. Test Diagn. 2020, 40, 272–277. [Google Scholar]
- Zhang, Z.L. Research on Feature Detection of Time-Varying Non-Stationary Signals Based on Fractional Order Transform. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Jiao, L. Research on Non-Stationary Early Fault Diagnosis of Planetary Gears. Master’s Thesis, Beijing Information Science and Technology University, Beijing, China, 2021. [Google Scholar]
- Hu, R.; Pang, X.; She, C.; Liu, A.; Hu, S. Fault diagnosis of planetary gearbox under variable working conditions based on optimal window function Gabor transform. Wind Turbine Technol. 2021, 63, 79–90. [Google Scholar]
- Zhao, H.; Zhang, Z.; Mei, J.; Shen, H.; Chang, C. Early fault diagnosis of transmission gear based on FRFT and LSTM. J. Mil. Transp. Acad. 2020, 22, 36–41. [Google Scholar]
- Wang, H. Fractional S transform and its application in gearbox fault diagnosis. J. Electron. Meas. Instrum. 2019, 33, 133–139. [Google Scholar]
- Zhang, Z.; Mei, J.; Chang, C.; Zhao, H.; Shen, H. Feature extraction of early fault of gear based on FRFT target separation and MCKD feature enhancement. J. Mil. Transp. Acad. 2019, 21, 44–48. [Google Scholar]
- Guo, M.; Zhou, C.; Zheng, C.; Chen, P.; Hu, G. Variable working condition gear fault diagnosis method based on meta-learning technology. Mech. Electr. Eng. 2023, 40, 1682–1690. [Google Scholar]
- Yu, C.; Liang, R.; Ran, W.; Wang, Z. Gearbox fault diagnosis based on STFT and CNN. Mech. Manuf. Autom. 2022, 51, 152–154. [Google Scholar]
- Chen, X.; Liu, Q.J.; Wang, Z.Y. Research on transmission system fault diagnosis based on FFT and LLTSA. Mech. Electr. Eng. 2022, 39, 513–518. [Google Scholar]
- Zhen, C.; Tian, Y.; Ji, K.; Zhang, Z.; Huang, D. Gearbox oil temperature data prediction based on FFT and DNN. Comput. Mod. 2022, 4, 17. [Google Scholar]
- Zhu, Q.; He, H.; Li, F.; Li, Z.; Li, Z. Helicopter gearbox fault diagnosis method based on short-time Fourier transform and deep convolutional neural network. Fail. Anal. Prev. 2022, 17, 1–8. [Google Scholar]
- Zhang, L.; Xu, W.; Jing, L.; Tan, J. Rotating machinery fault diagnosis based on two-dimensional deep convolutional network. Mech. Strength 2020, 42, 1039–1044. [Google Scholar]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave Propagation and Sampling Theory-Part I: Complex Signal and Scattering in Multilayered Media. Geophysics 2013, 47, 203–221. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Ideal Spatial Adaptation by Wavelet Shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Parey, A.; Singh, A. Gearbox Fault Diagnosis Using Acoustic Signals, Continuous Wavelet Transform and Adaptive Neuro-Fuzzy Inference System. Appl. Acoust. 2019, 147, 133–140. [Google Scholar] [CrossRef]
- Liang, P.; Deng, C.; Wu, J.; Yang, Z.; Zhu, J.; Zhang, Z. Compound Fault Diagnosis of Gearboxes Via Multi-label Convolutional Neural Network and Wavelet Transform. Comput. Ind. 2019, 113, 103–132. [Google Scholar] [CrossRef]
- Saravanan, N.; Ramachandran, I. Fault Diagnosis of Spur Bevel Gear Box Using Discrete Wavelet Features and Decision Tree Classification. Expert Syst. Appl. 2009, 36, 9564–9573. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, Y.X. Application of frequency modulation empirical mode decomposition in bearing fault diagnosis. J. Vib. Shock 2014, 33, 185–189. [Google Scholar]
- Park, S.; Kim, S.; Choi, J. Gear fault diagnosis using transmission error and ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2018, 108, 262–275. [Google Scholar] [CrossRef]
- Tang, B.P.; Jiang, Y.H.; Zhang, X.C. Rolling bearing fault feature extraction method based on morphological singular value decomposition and empirical mode decomposition. J. Mech. Eng. 2010, 46, 37–42. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, Q.; Huang, M.; Huang, M.; Yan, W. Particle swarm optimization-based empirical mode decomposition–kernel independent component analysis joint approach for diagnosing wind turbine gearbox with multiple faults. Trans. Inst. Meas. Control 2018, 40, 1836–1845. [Google Scholar] [CrossRef]
- Zhang, L.W.; Qi, F.; Lin, J.; Zhang, Z.C.; Yan, X.H.; Li, C. A nearly end-to-end deep learning approach to fault diagnosis of wind turbine gearboxes under nonstationary conditions. Eng. Appl. Artif. Intell. 2023, 119, 105735. [Google Scholar] [CrossRef]
- Li, Y.; Si, S.; Liu, Z.; Liang, X. Review of local mean decomposition and its application in fault diagnosis of rotating machinery. J. Syst. Eng. Electron. 2019, 30, 799–814. [Google Scholar]
- Niu, X.; Lu, L.; Wang, J.; Han, X.; Li, X. An improved empirical mode decomposition based on local integral mean and its application in signal processing. Math. Probl. Eng. 2021, 2021, 8891217. [Google Scholar] [CrossRef]
- Cheng, J.S.; Zheng, J.D.; Yang, Y. A new method for non-stationary signal analysis: Local characteristic scale decomposition method. J. Vib. Eng. 2012, 25, 215–220. [Google Scholar]
- Cheng, J.; Yang, Y.; Yang, Y. A rotating machinery fault diagnosis method based on local mean decomposition. Digit. Signal Process. 2012, 22, 356–366. [Google Scholar] [CrossRef]
- Pan, Y.; Hu, Z.; Chen, J.; Wang, H.; Hong, R. Improved Complete Ensemble Robust Local Mean Decomposition with Adaptive Noise for Slewing Bearings Performance Degradation Assessment. IEEE Access 2022, 10, 78677–78690. [Google Scholar] [CrossRef]
- Zhou, J.; Cheng, J.; Wu, X.; Wang, J.; Cheng, J.; Yang, Y. Completely adaptive projection multivariate local characteristic-scale decomposition and its application to gear fault diagnosis. Measurement 2022, 202, 111743. [Google Scholar] [CrossRef]
- Cui, W.; Xu, A.; Li, W.; Li, W.; Meng, F. Gear fault diagnosis based on local characteristic scale decomposition combined with local mean demodulation. China Mech. Eng. 2016, 27, 3332–3337. [Google Scholar]
- Goyal, D.; Choudhary, A.; Sandhu, J.K.; Srivastava, P.; Saxena, K.K. An intelligent self-adaptive bearing fault diagnosis approach based on improved local mean decomposition. Int. J. Interact. Des. Manuf. 2022, 1–11. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.J. Artificial neural network identification method for mechanical equipment fault diagnosis. Mech. Strength 1995, 17, 48–54. [Google Scholar]
- Liao, X.X.; Chang, L.; Shen, Y. Research on the stability of discrete Hopfield neural network. Chin. J. Autom. 1999, 25, 721–727. [Google Scholar]
- Jin, S.; Cui, W.; Jin, Z.; Wang, Y. AF-DHNN: Fuzzy Clustering and Inference-Based Node Fault Diagnosis Method for Fire Detection. Sensors 2015, 15, 17366–17396. [Google Scholar] [CrossRef]
- Skowron, M.; Wolkiewicz, M.; Orlowska, K.T.; Kowalski, C.T. Effectiveness of Selected Neural Network Structures Based on Axial Flux Analysis in Stator and Rotor Winding Incipient Fault Detection of Inverter-fed Induction Motors. Energies 2019, 12, 2392. [Google Scholar] [CrossRef]
- Lang, S.C. Research on Ship Power Grid Fault Diagnosis Based on Hopfield Neural Network. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2019. [Google Scholar]
- Lin, T.; Yang, X.; Cai, R.; Zhang, L.; Liu, G. Elman neural network wind turbine fault diagnosis based on improved artificial bee colony algorithm. Renew. Energy 2019, 37, 612–617. [Google Scholar]
- Aydmj, T.; Duin, R. Pump failure determination using support vector data descriptions. Lect. Notes Comput. Sci. 1999, 8, 415–425. [Google Scholar]
- Tang, B.; Song, T.; Li, F.; Deng, L. Fault diagnosis for a wind turbine transmission system based on manifold learning and Shannon wavelet support vector machine. Renew. Energy 2014, 62, 1–9. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Li, S.; Li, X.; Ma, L. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mech. Mach. Theory 2015, 90, 219–229. [Google Scholar] [CrossRef]
- Martin, D.I.; Morinigo, S.D.; Duque, P.O.; Romero-Troncoso, R.D.J. Early fault detection in induction motors using AdaBoost with imbalanced small data and optimized sampling. IEEE Trans. Ind. Appl. 2016, 53, 3066–3075. [Google Scholar] [CrossRef]
- Ren, Z.; Huang, H.; Hu, Y. Research on gear fault diagnosis based on improved support vector machine. Mech. Des. Manuf. 2022, 4, 122–125. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. Physiology 1962, 160, 106–154. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, L.; Zhang, C.; Zhao, Q. Gearbox health status identification based on deep convolutional neural network. Comput. Simul. 2024, 41, 455–459. [Google Scholar]
- Zhang, Y.; Zhao, X.; Hui, Y.; Chen, P. SA-DACNN gearbox fault diagnosis method based on multi-sensor data fusion. Control Decis. 2024, 45, 60–71. [Google Scholar]
- Huang, K.; Wu, B.; Zhang, Z. Intelligent diagnosis method of planetary gear based on integrated convolutional neural network. Mech. Des. Manuf. 2024, 1, 170–174. [Google Scholar]
- Zhou, Q.; Li, Y.; Tian, Y.; Jiang, L. A novel method based on nonlinear auto-regression neural network and convolutional neural network for imbalanced fault diagnosis of rotating machinery. Measurement 2020, 161, 107880. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, J.; Hoseini, R. Vibration Signal Modeling of a Planetary Gear Set for Tooth Crack Detection. Eng. Fail. Anal. 2015, 48, 185–200. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, P.F. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Yin, J.T.; Zhao, W.T. Fault diagnosis network design for vehicle on-board equipment of high-speed railway: A deep learning approach. Eng. Appl. Artif. Intell. 2016, 56, 250–259. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Jiang, S.; Wang, T.; Yuan, L.; Li, B. Transformer fault diagnosis method based on self-powered RFID sensor tag, DBN, and MKSVM. IEEE Sens. J. 2019, 19, 8202–8214. [Google Scholar] [CrossRef]
- Yan, L.; Dong, X.; Zhang, Y.; Wang, T.; Gao, Q. Gas turbine gas path fault diagnosis method based on deep belief network. J. Eng. Thermophys. 2020, 41, 840–844. [Google Scholar]
- Zheng, X.; Guo, C.; Yao, B.; Feng, H. Aviation sensor fault diagnosis method based on deep learning. Comput. Eng. 2017, 43, 281–287. [Google Scholar]



| Method | Advantage | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| Time-domain statistics analysis | The calculation is simple, easy to understand and implement | Insensitive to non-Gaussian signals and susceptible to noise interference | Early fault detection, low noise environment |
| Time-domain waveform analysis | Intuitive, find obvious fault characteristics | Relying on experience and observation, it is difficult to analyze complex signals | Obvious fault feature detection, simple gear transmission system |
| Envelope analysis | Effectively extract impact signals suitable for fault feature extraction | Requires appropriate filter design, high computational complexity | Early gear fault detection |
| Shock pulse method | Sensitive to early faults and capture short-term impact signals | Requires high sampling rate equipment, noise sensitive | Early fault diagnosis of gears, local defects on tooth surface |
| Time-domain synchronous averaging | Suppress random noise and improve signal-to-noise ratio, especially suitable for extracting periodic impact signals | Requires precise synchronization signal, sensitive to speed fluctuations, and has complex processing | Gearbox periodic fault diagnosis, noisy environment |
| Maximum correlation kurtosis deconvolution | Significantly enhances impact signals, is sensitive to early faults, and extracts weak fault signals | The calculation complexity is high, parameter selection requires experience, and adaptability to strong noise environments needs to be studied. | Early fault diagnosis, weak impact signal extraction |
| Method | Advantage | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| Envelope demodulation analysis | Effectively extract and amplify impact signals, sensitive to early faults | The filter design is complex, parameter selection requires experience, and it is sensitive to strong noise environments. | Early fault detection, gear fault with obvious impact signal |
| Resonance demodulation analysis | Enhance weak fault signals, improve signal-to-noise ratio, and be sensitive to early faults | Requires accurate resonant frequency, complex filter design | Weak fault signal detection, tooth surface cracks, and wear |
| STFT | Provides time-frequency information, suitable for non-stationary signals | The time-frequency resolution is limited, and the window length selection needs to be balanced | Detection of non-stationary signals |
| Fast Fourier Transform | Fast calculation speed, suitable for real-time processing | Insensitive to non-stationary signals and difficult to process transient signals | Suitable for stable working state, real-time monitoring, and fault diagnosis |
| FRFT | Sensitive to linear frequency modulation signals, provides time-domain and frequency-domain information, suitable for complex signals | The calculation complexity is high, the selection of fractional order parameters requires experience, and the interpretation of results is complicated | Complex and non-stationary signal detection |
| Method | Advantage | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| Wavelet transform | Sensitive to non-stationary signals and transient faults, strong in multi-scale analysis capabilities | The computational complexity is high, the selection of wavelet basis and scale requires experience, and the interpretation of results is complex | Non-stationary signals and transient fault detection |
| Hilbert-Huang Transform | Applicable to nonlinear and non-stationary signals, providing high-precision time-frequency information | High computational complexity, susceptible to noise, and complex interpretation of results | Complex fault signal detection and analysis |
| EMD | Strong adaptability, suitable for nonlinear and non-stationary signals | Susceptible to noise and boundary effects, the decomposition process may produce mode aliasing | Analysis of complex signals, such as various types of gear faults |
| LMD | Effectively handle non-stationary signals, sensitive to transient faults, and the decomposition results have good physical meaning | High computational complexity, susceptible to noise, and interpretation of results requires experience | Non-stationary signals and transient fault detection, such as shock and sudden faults in gear systems |
| Method | Advantage | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| ANN | Strong nonlinear mapping capability, suitable for processing complex high-dimensional data and multi-classification problems | The training is complex, the computation is large, it is easy to fall into the local optimal solution, and a large amount of training data is required | Large-scale data, complex nonlinear problems, such as image classification, etc. |
| SVM | High-dimensional space performs well, is suitable for small sample data, and has a strong generalization ability | Inefficient for large-scale data and sensitive to parameter selection | Small sample, high-dimensional feature data, binary classification problem |
| K-nearest neighbor | Simple and intuitive, no training process required, suitable for multi-classification problems | High computational complexity, not applicable to large-scale data, sensitive to noise and unbalanced data | Datasets with smaller sample sizes and fewer features |
| Decision Tree | Easy to understand and interpret, handles multi-classification problems and nonlinear relationships | Prone to overfitting, sensitive to noise and changes in data distribution | Datasets with clear structures and complex feature relationships |
| Linear discriminant analysis | Suitable for high-dimensional data dimensionality reduction and classification, high computational efficiency, simple model | Assuming data is normally distributed and the covariance matrix is the same, poor performance for nonlinear data | Linearly separable data, dimensionality reduction, and classification combined application |
| Method | Advantage | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| CNN | Good image and two-dimensional data processing effect, strong feature extraction ability | The input data preprocessing and normalization requirements are high, and the training resource requirements are large | Image data, time-frequency images, two-dimensional signal data |
| DBN | Automatically learn hierarchical feature representation, suitable for feature extraction of complex data | The training is complex, requires layer-by-layer training, and is sensitive to the choice of hyperparameters | Feature learning, data preprocessing |
| Recursive neural network | Processing of sequence data and time series analysis, capturing temporal dependencies | Training is unstable, and gradient disappearance and explosion problems are serious | Time series data, dynamic data analysis |
| Long short-term memory network | Capture long-term dependencies and perform well in processing long-sequence data | High computational complexity and long training time | Long-sequence time data analysis and fault prediction |
| Autoencoder | Feature dimensionality reduction, data compression, anomaly detection, unsupervised learning | There are many model structures and parameter choices, and the training process requires a lot of data | Feature learning, anomaly detection, data dimensionality reduction |
| Generative adversarial network | Generate high-quality samples suitable for data augmentation and anomaly detection | The training is complex and unstable, and the quality of the generated samples needs to be fine-tuned | Data enhancement, abnormal sample generation, generative model |
| Graph neural network | Processing structured graph data, considering node relationships and graph structure information | Graph structure construction and node feature selection require high computational complexity | Structured data, relationship network analysis |
| Comparison Dimensions | Shallow Learning | Deep Learning | |
|---|---|---|---|
| Model complexity and feature extraction | Advantages: | The model is simple, and the training and inference time is short. | The model is complex, and features are learned automatically; It has strong expressive power for complex data. |
| Limitations: | Reliance on manual feature extraction | Training relies on a large amount of computing resources and data. | |
| Data requirements | Advantages: | Suitable for scenarios with less data; Does not rely on a large amount of labeled data. | Excels in data-rich situations. |
| Limitations: | Difficulty handling complex, nonlinear data. | Large-scale data is required. | |
| Explanation and generalization | Advantages: | High transparency and easy to interpret. | Strong generalization ability. |
| Limitations: | The generalization ability is weak, and it is difficult to handle complex nonlinear problems. | Poor interpretability, easily regarded as a “black box” model. | |
| Training cost | Advantages: | The training and inference costs are low; Suitable for scenarios with limited resources and high real-time requirements. | It has powerful representation learning capabilities. |
| Limitations: | For high-dimensional data, training and parameter adjustment are more complicated. | The training cost is high and the inference speed is slow; It requires a lot of computing resources. | |
| Applicable scenarios | Small datasets, tasks with clear features; Industrial applications that require strong interpretability. | Large data sets, complex pattern recognition tasks; Automated fault detection with sufficient computing resources. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Fang, Y.; Xu, Y.; Xu, H.; Ma, G.; Peng, N. Current Status of Research on Fault Diagnosis Using Machine Learning for Gear Transmission Systems. Machines 2024, 12, 679. https://doi.org/10.3390/machines12100679
Fu X, Fang Y, Xu Y, Xu H, Ma G, Peng N. Current Status of Research on Fault Diagnosis Using Machine Learning for Gear Transmission Systems. Machines. 2024; 12(10):679. https://doi.org/10.3390/machines12100679
Chicago/Turabian StyleFu, Xuezhong, Yuanxin Fang, Yingqiang Xu, Haijun Xu, Guo Ma, and Nanjiang Peng. 2024. "Current Status of Research on Fault Diagnosis Using Machine Learning for Gear Transmission Systems" Machines 12, no. 10: 679. https://doi.org/10.3390/machines12100679
APA StyleFu, X., Fang, Y., Xu, Y., Xu, H., Ma, G., & Peng, N. (2024). Current Status of Research on Fault Diagnosis Using Machine Learning for Gear Transmission Systems. Machines, 12(10), 679. https://doi.org/10.3390/machines12100679






