A Multi-Objective Trajectory Planning Method of the Dual-Arm Robot for Cabin Docking Based on the Modified Cuckoo Search Algorithm
Abstract
1. Introduction
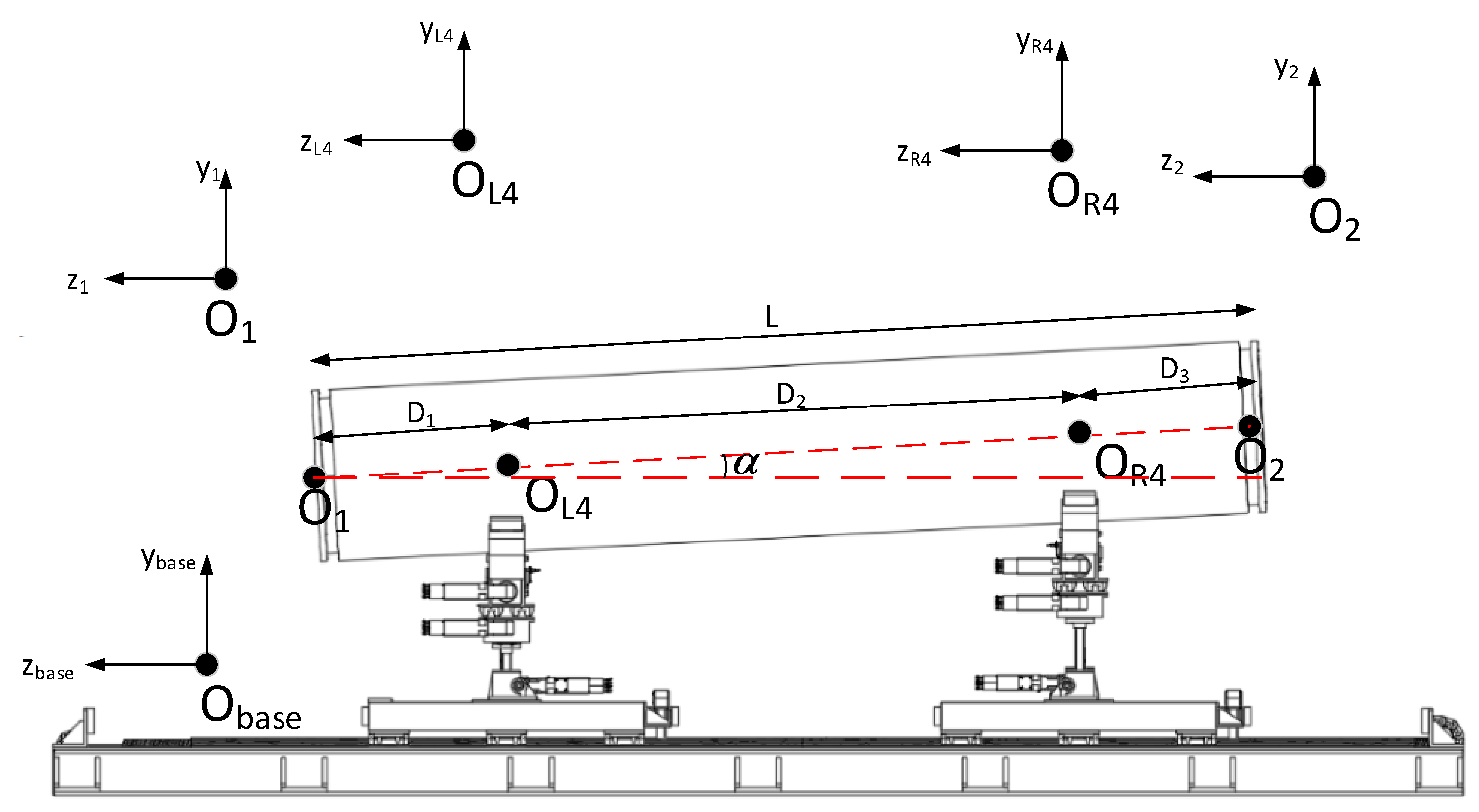
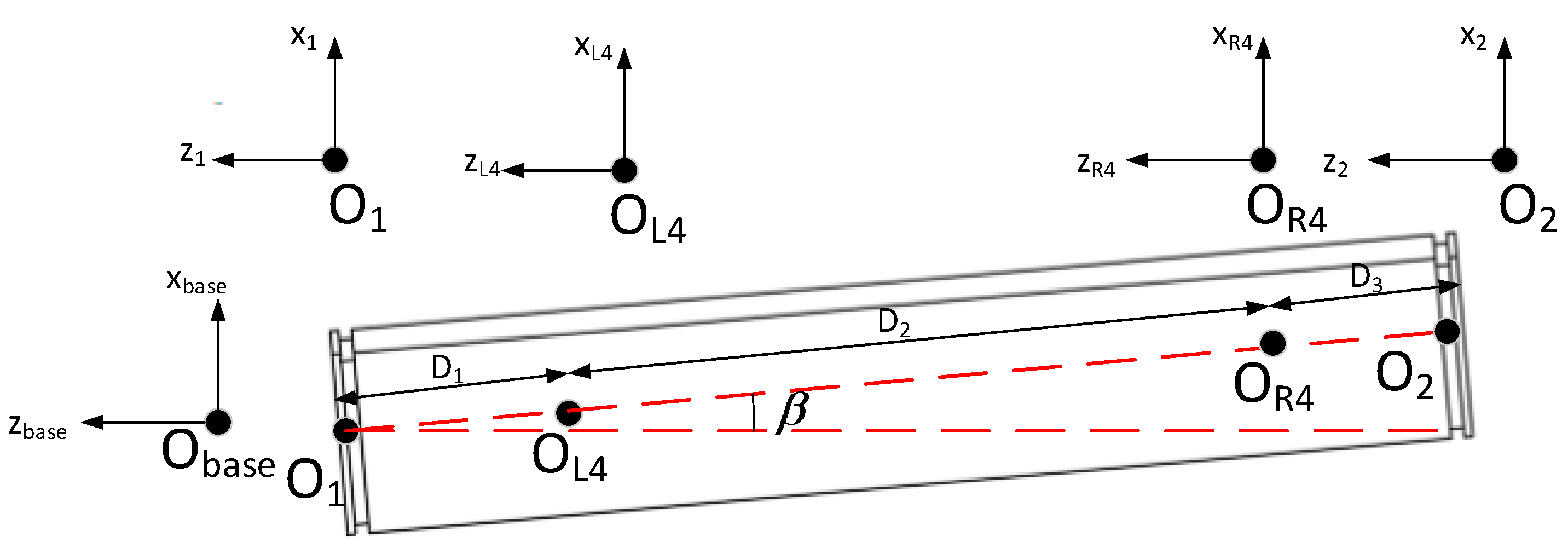
2. Kinematic Analysis of Cabin Docking Dual-Arm Robot
2.1. Forward Kinematic Model
2.2. Inverse Kinematics Model
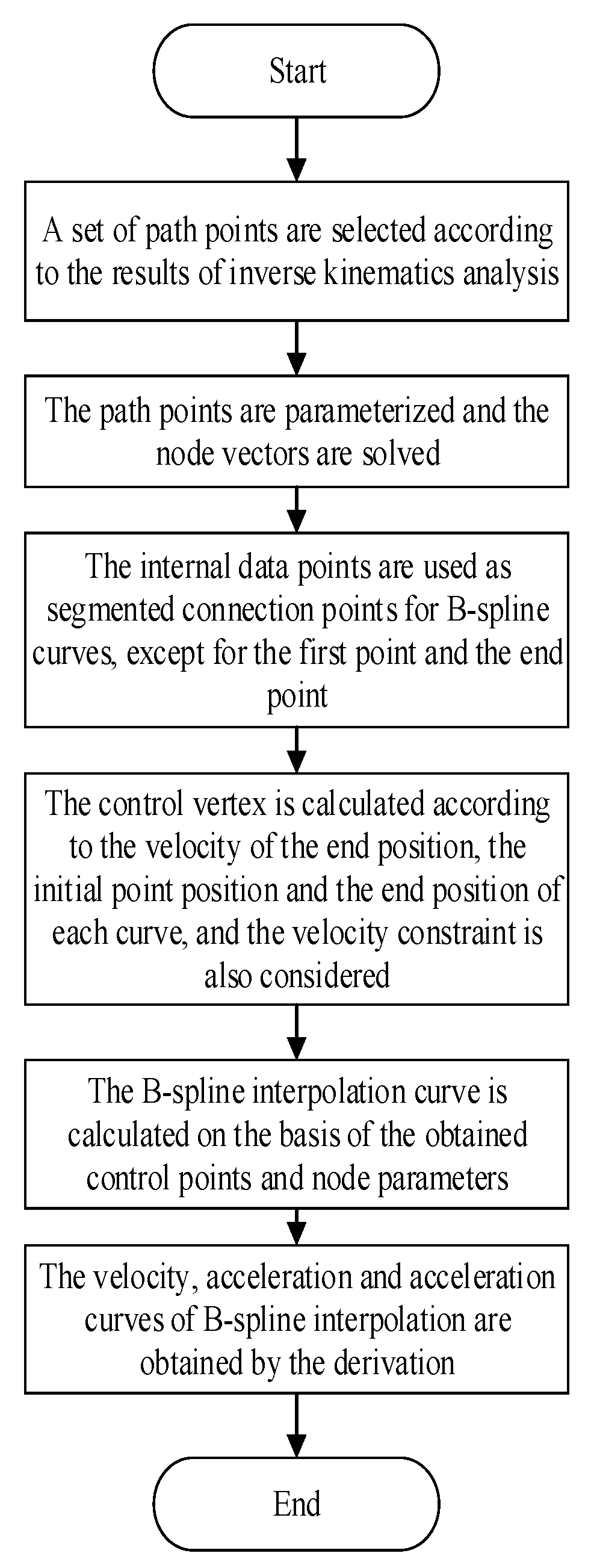
3. Trajectory Planning Method Based on B-Spline Interpolation
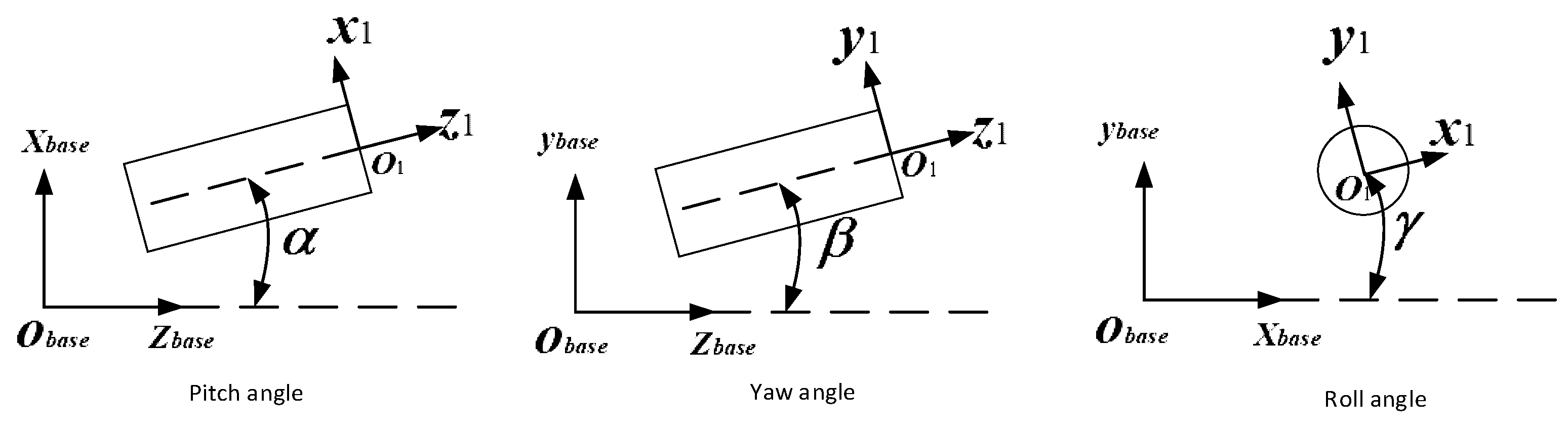
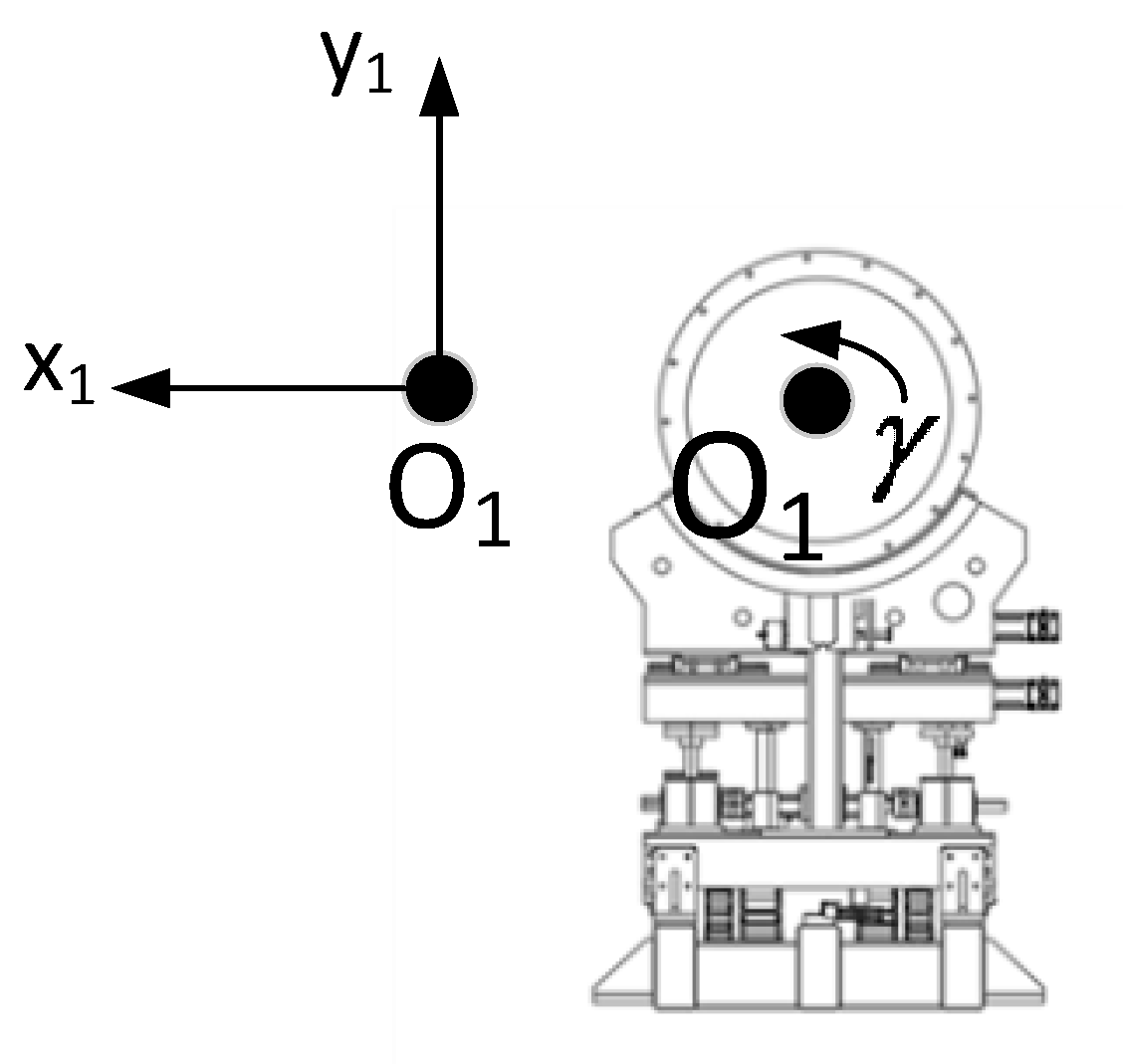
3.1. Trajectory Planning Scheme
- (1)
- Initial equilibrium position
- (2)
- 0° pitch angle
- (3)
- 0° yaw angle
- (4)
- 0° roll angle
3.2. B-Spline Curve Construction
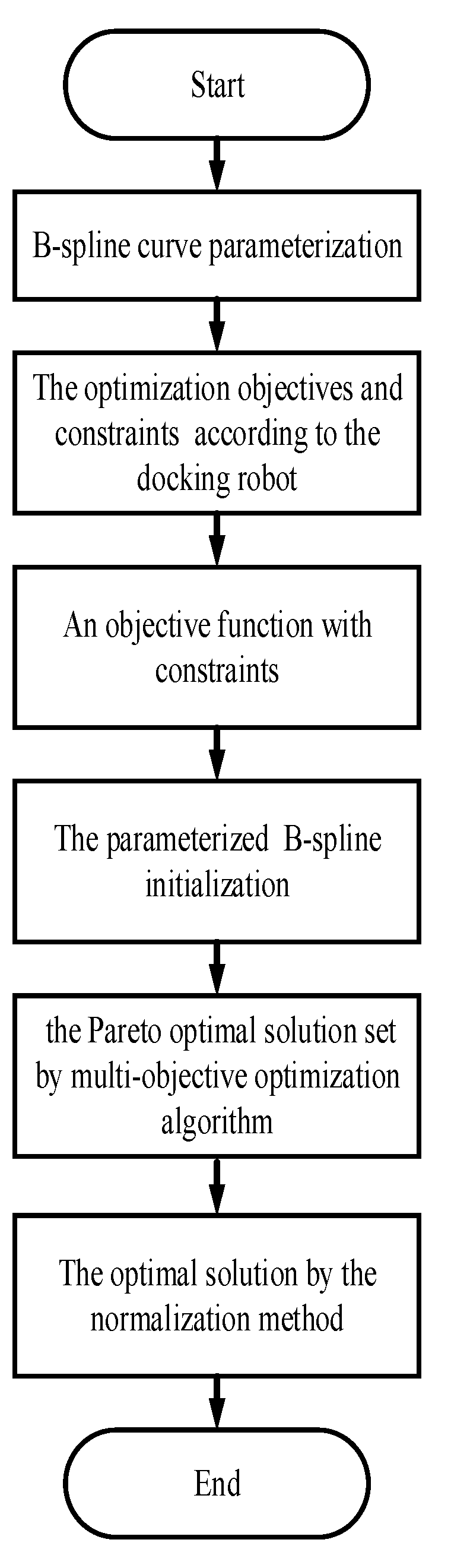
4. The Modified Multi-Objective Cuckoo Search Algorithm
4.1. The Objective Function and Comprehensive Optimal Solution
4.2. Traditional Multi-Objective Cuckoo Search Algorithm
4.3. Modified Multi-Objective Cuckoo Search Algorithm
4.3.1. Improvement of Initial Population Generation Method
4.3.2. Improvement of Step Size in Cuckoo Algorithm
4.4. Flowchart of Trajectory Optimization Algorithm
5. Simulation Analysis
5.1. Parameter Configuration
5.2. Results and Discussion
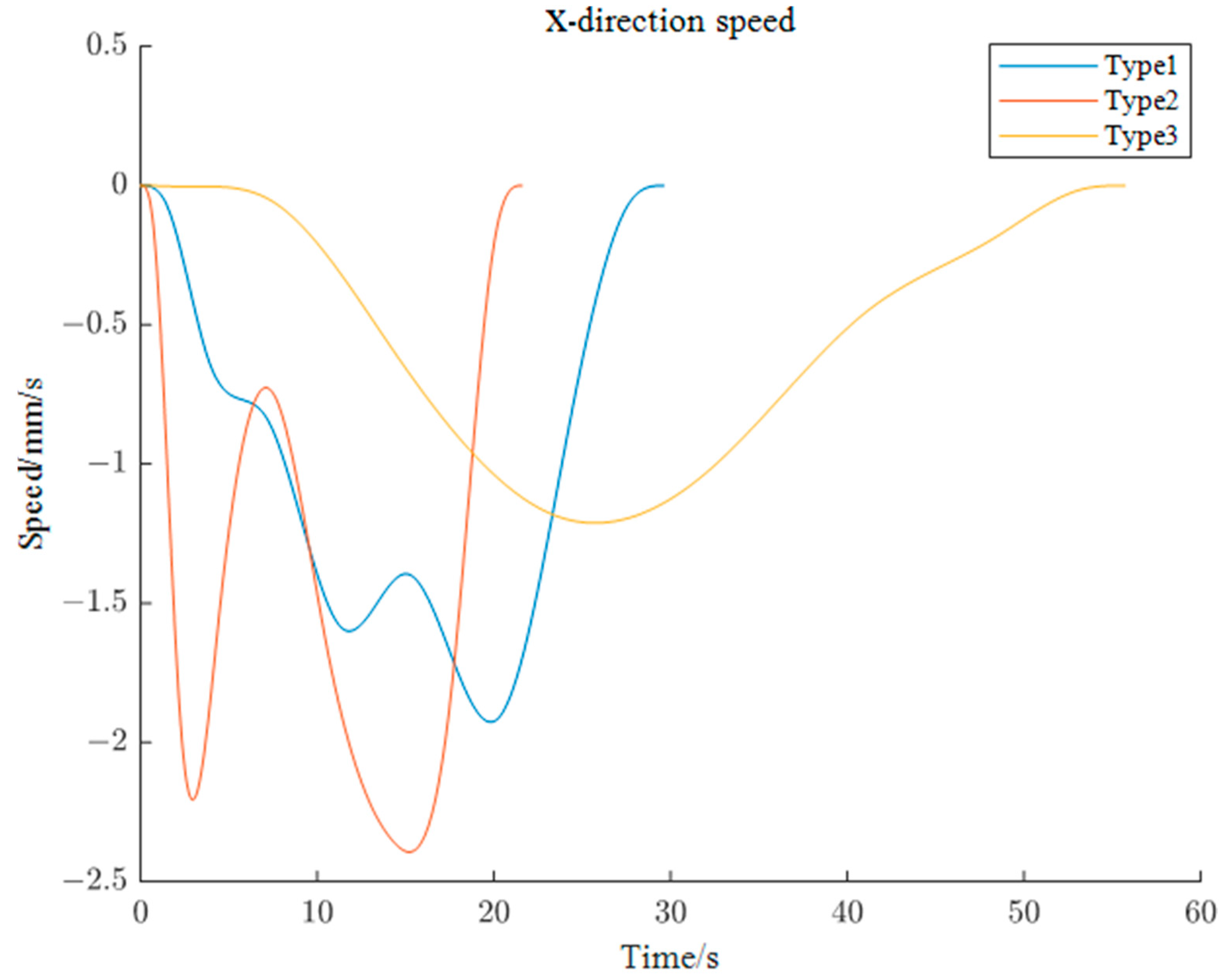
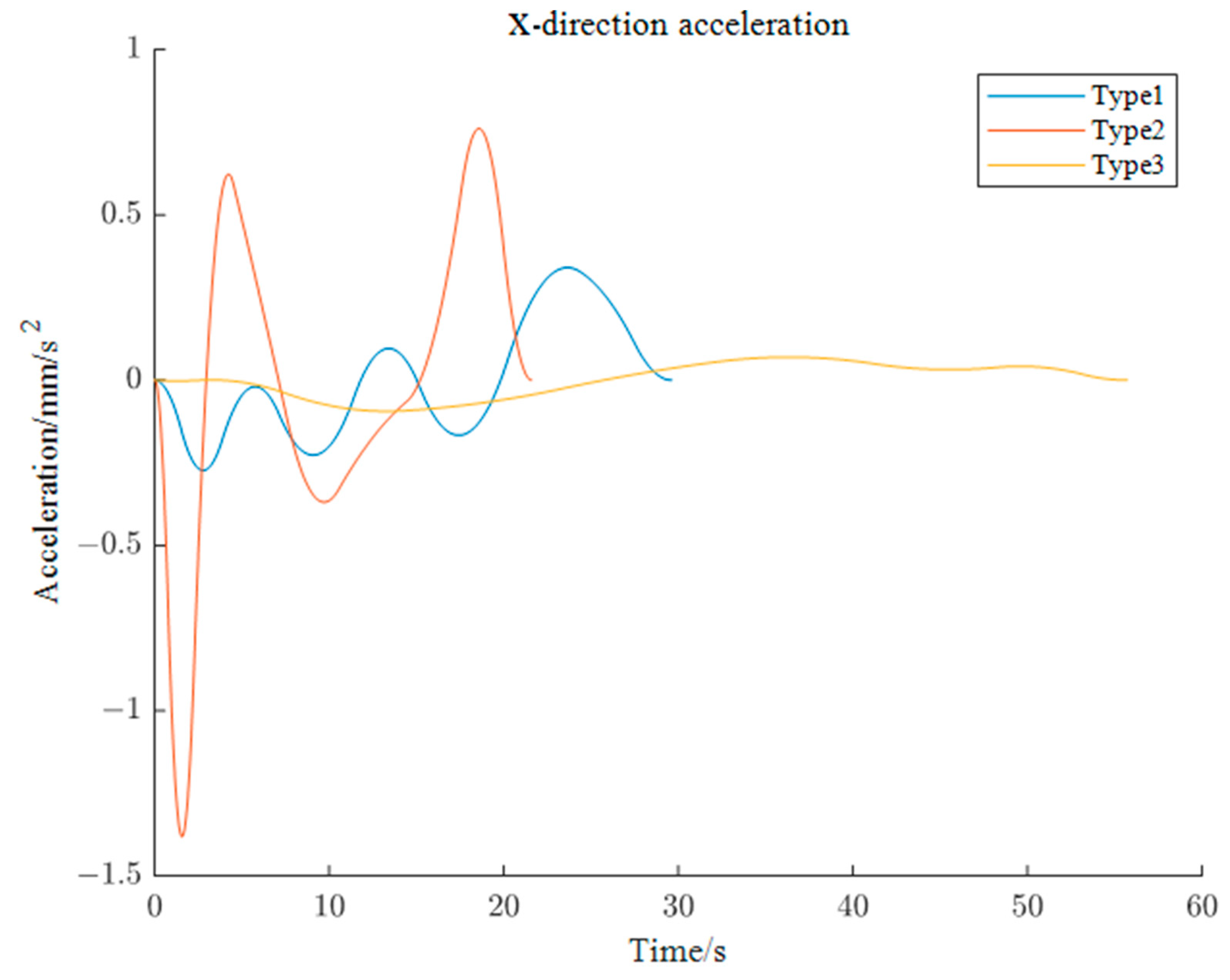
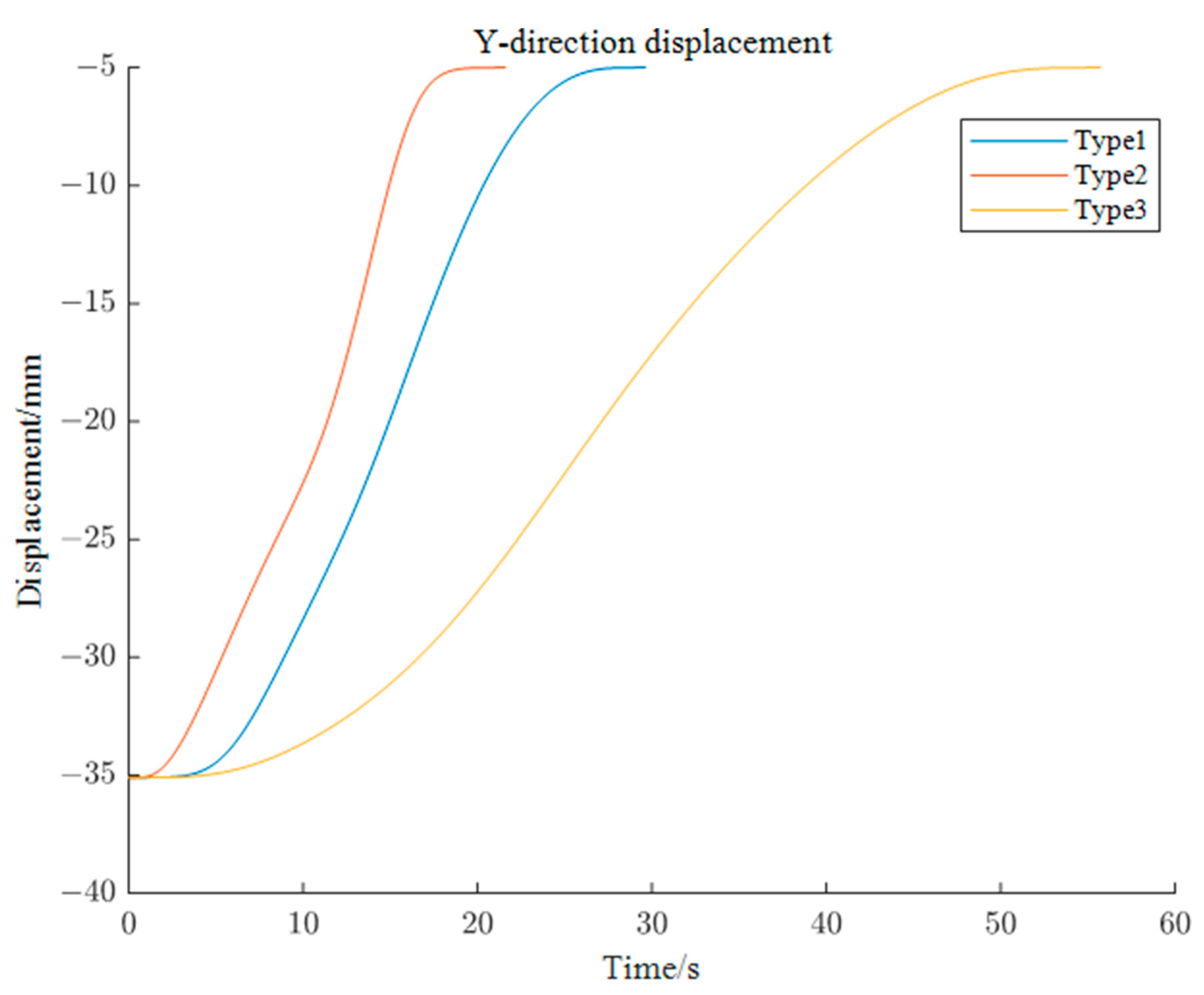
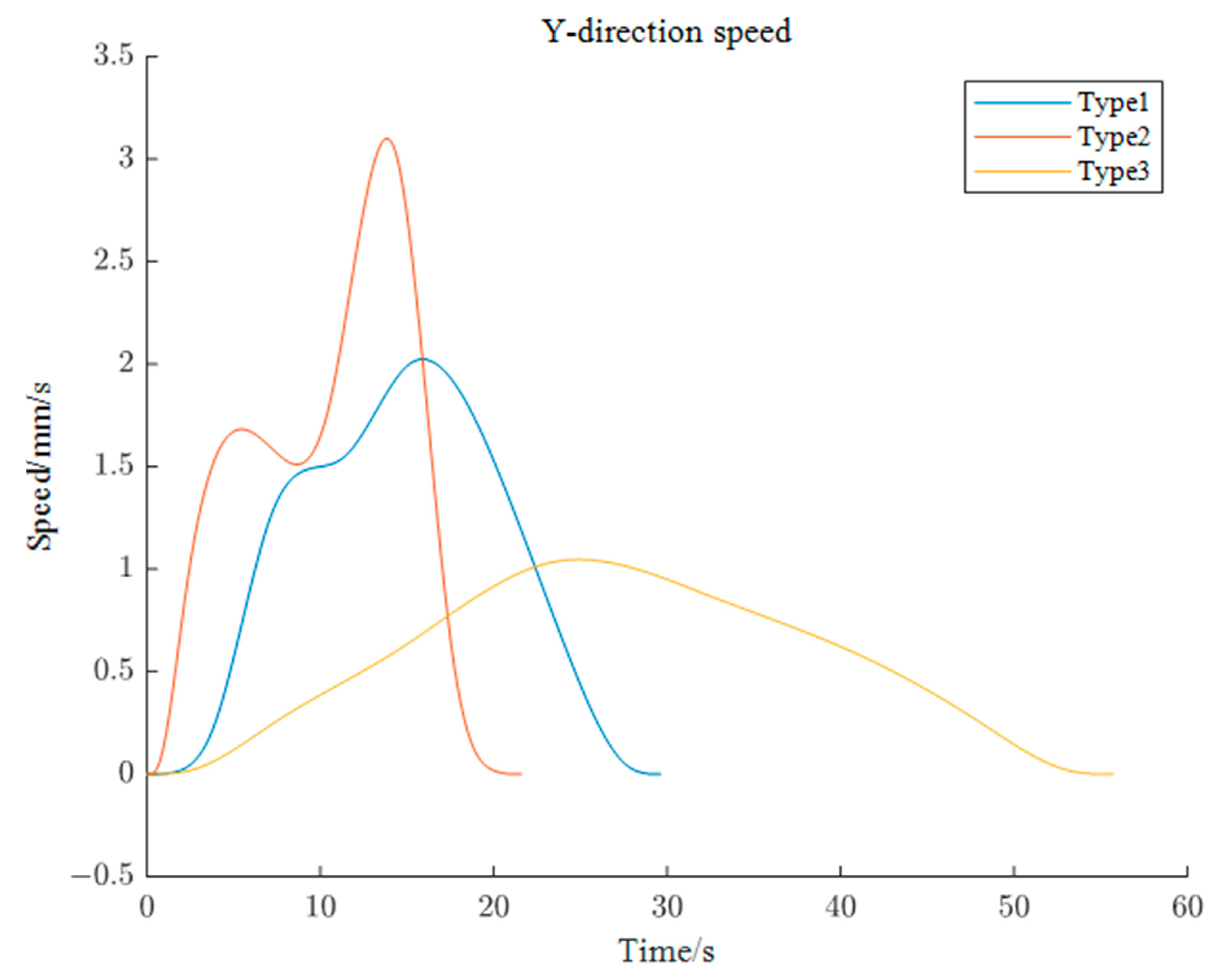
5.2.1. Simulation of X-axis End Motion Trajectory of Left Robotic Arm
5.2.2. Simulation of Y-axis End Motion Trajectory of Left Robotic Arm
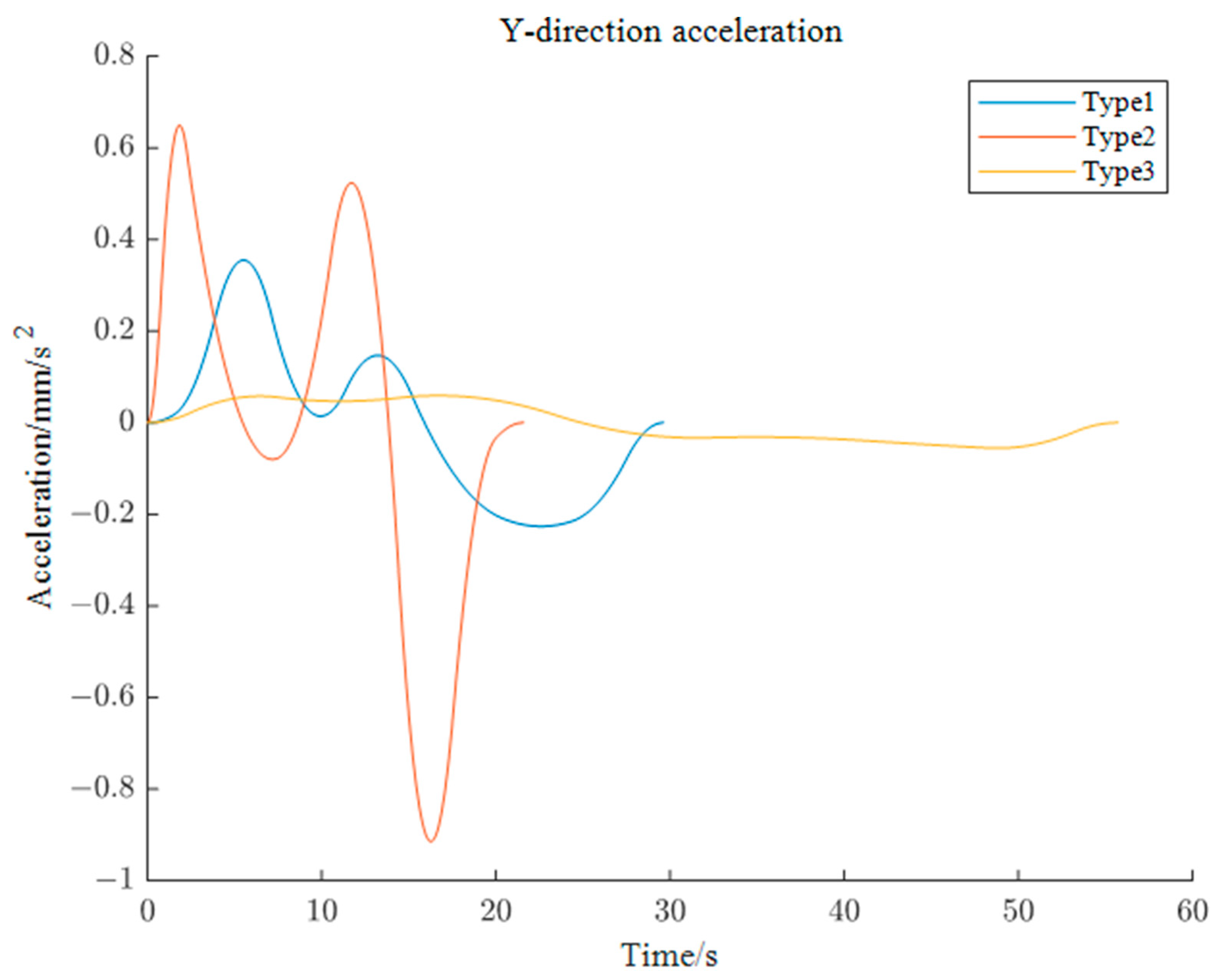
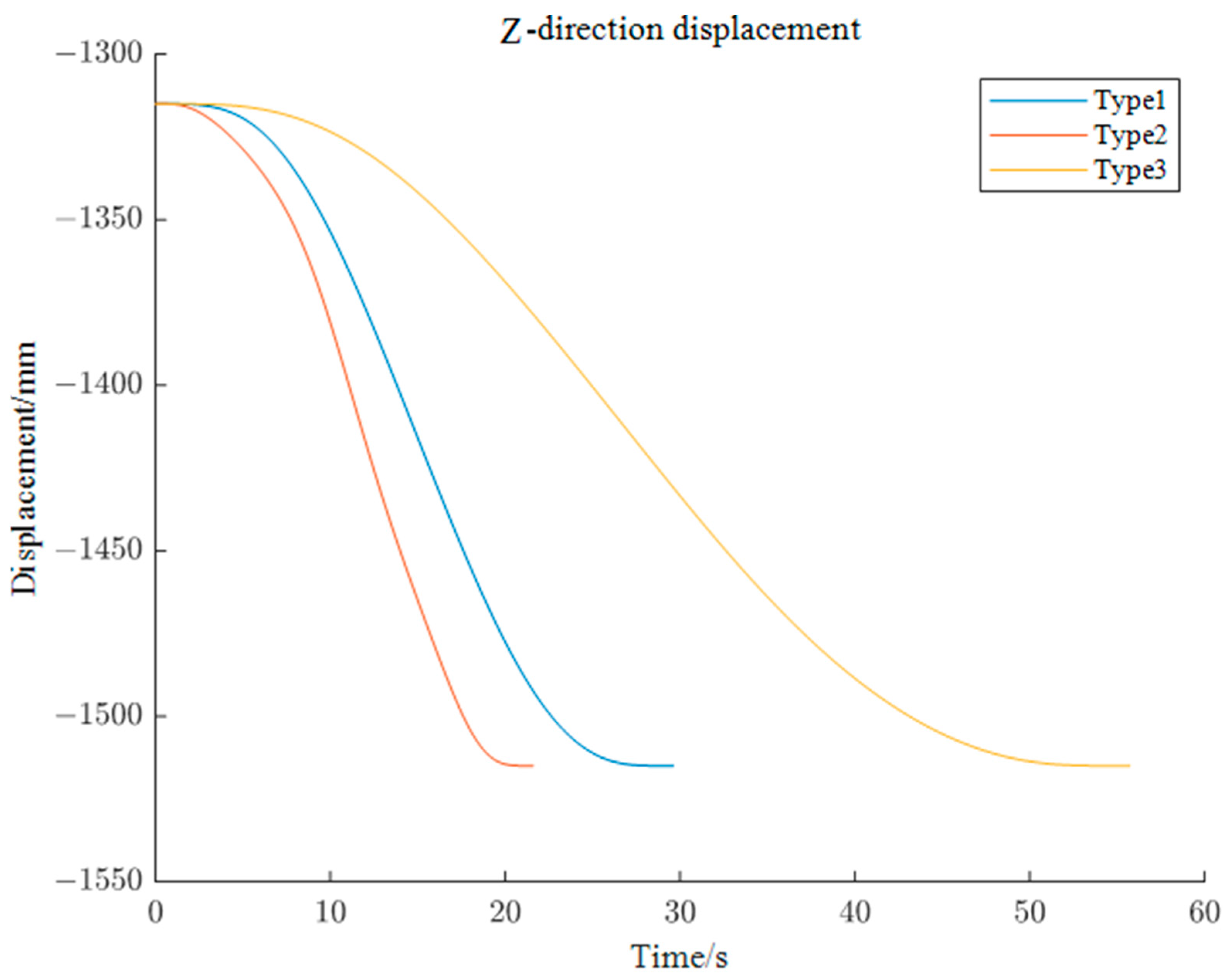
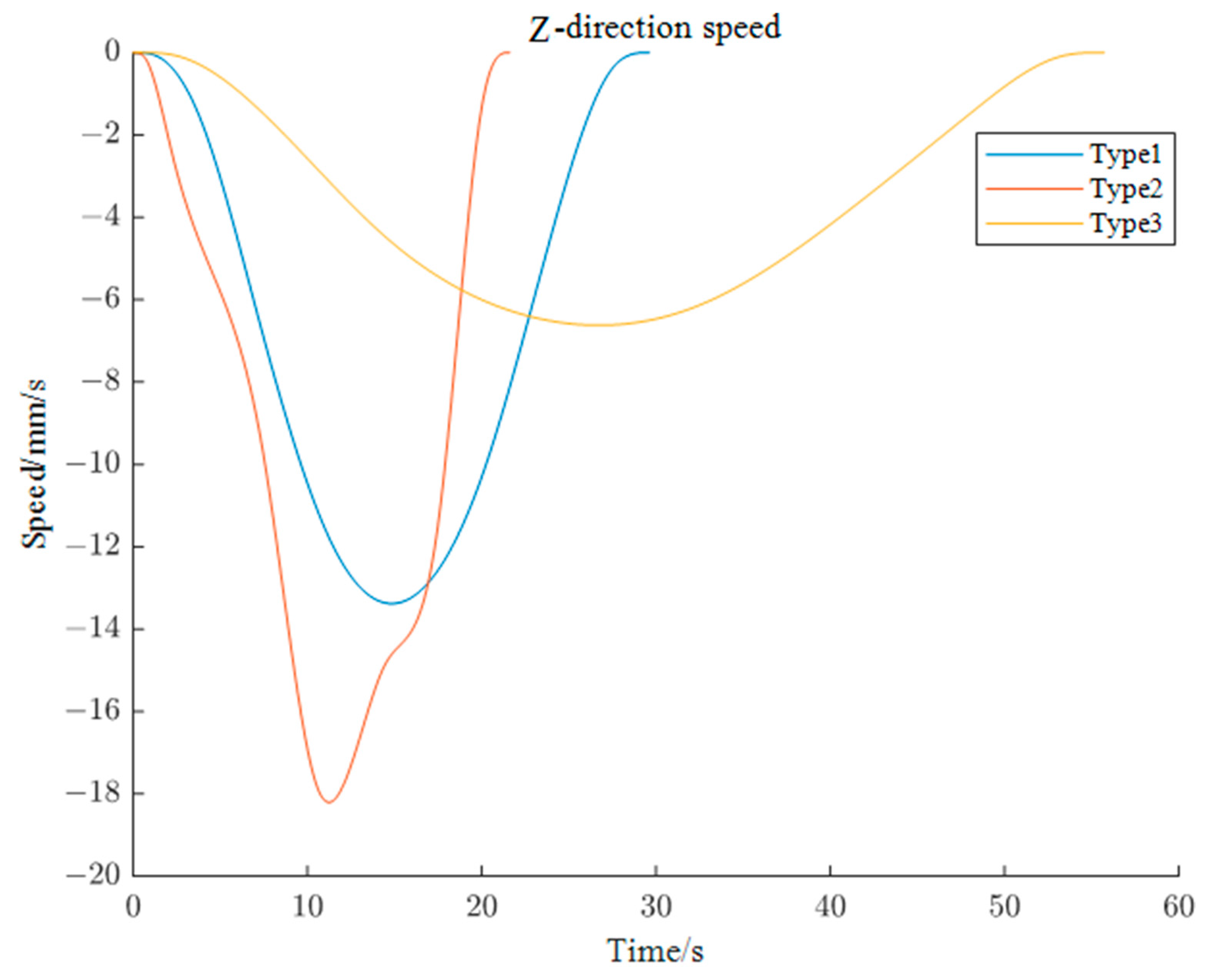
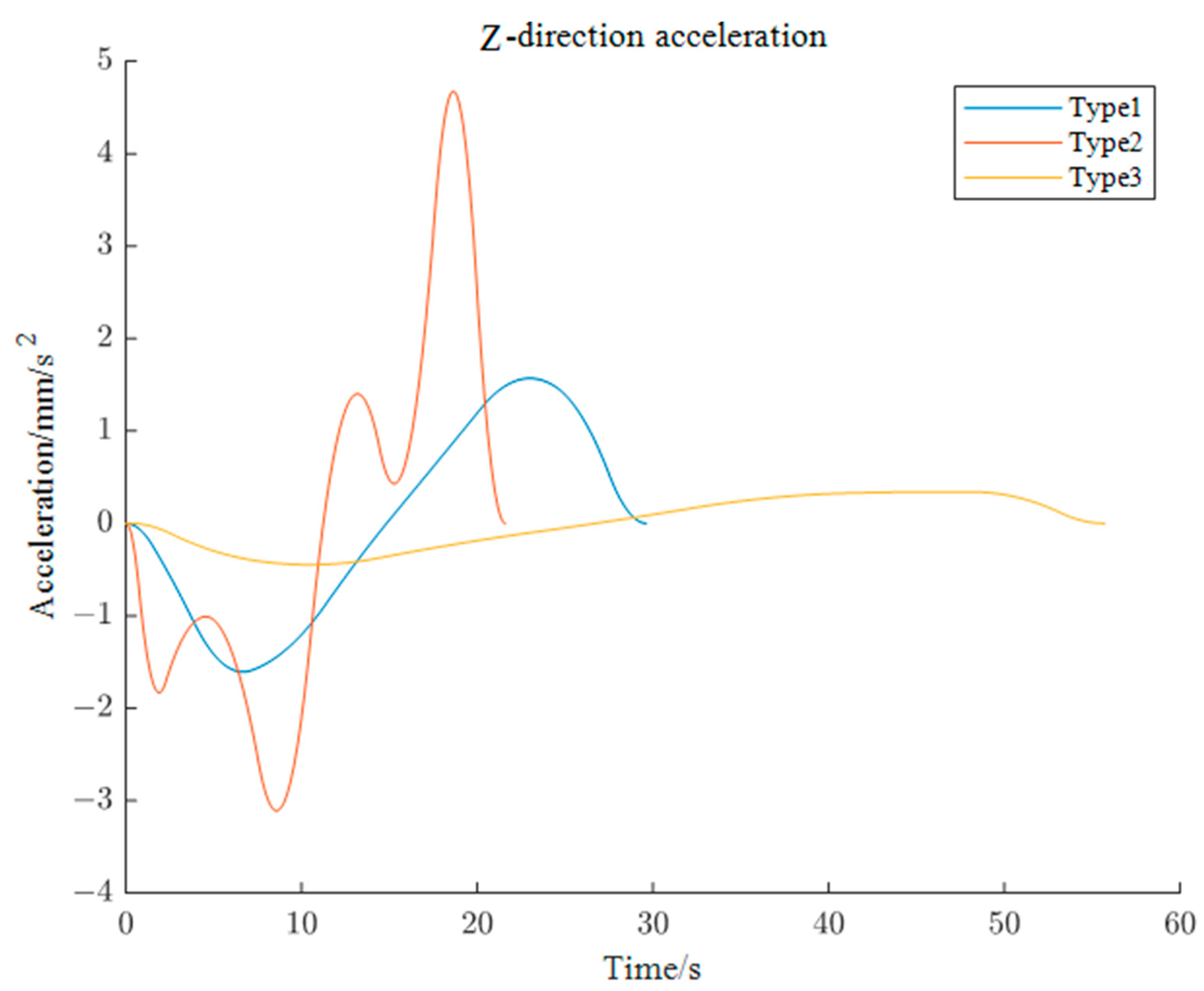
5.2.3. Simulation of Z-axis End Motion Trajectory of Left Robotic Arm
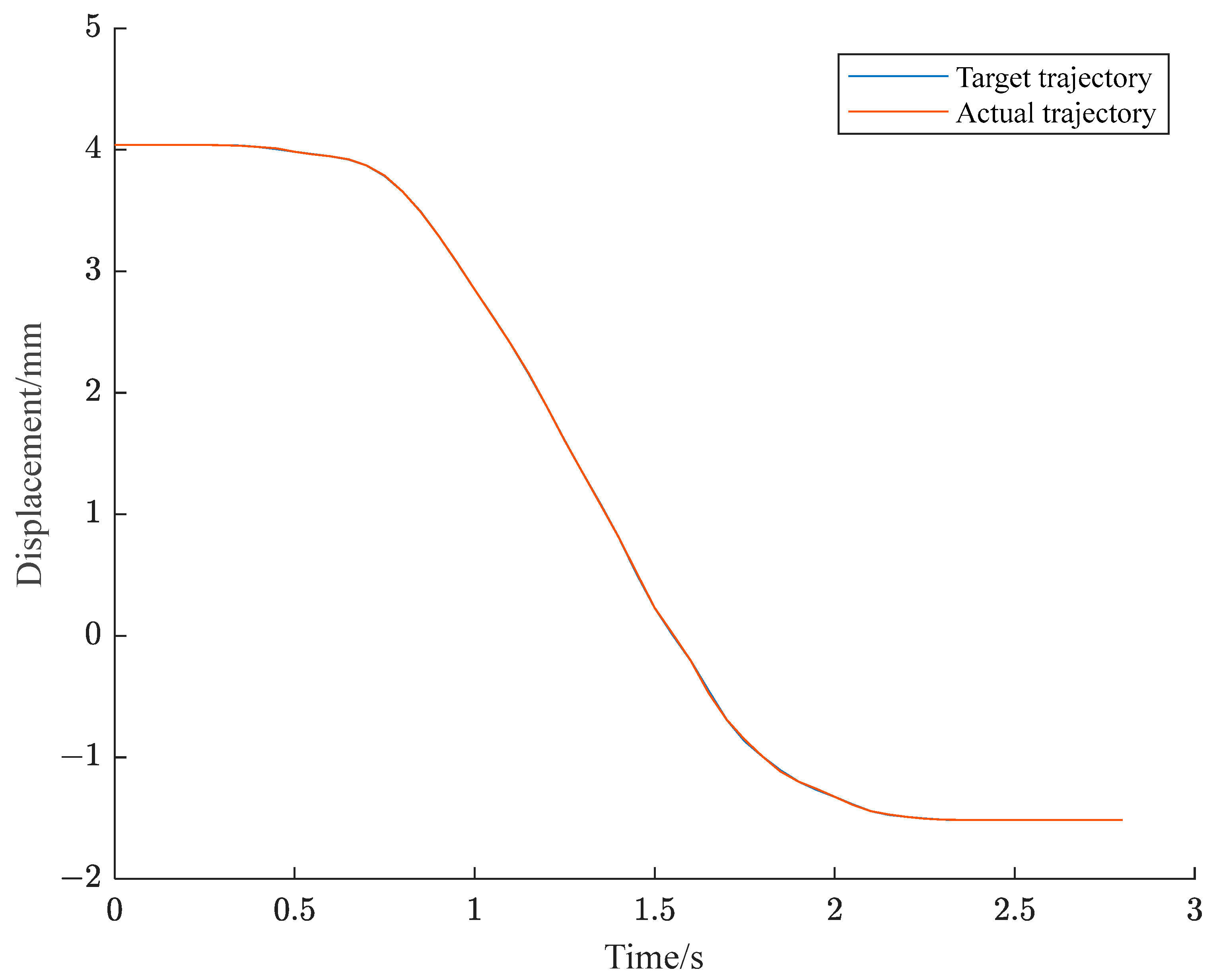
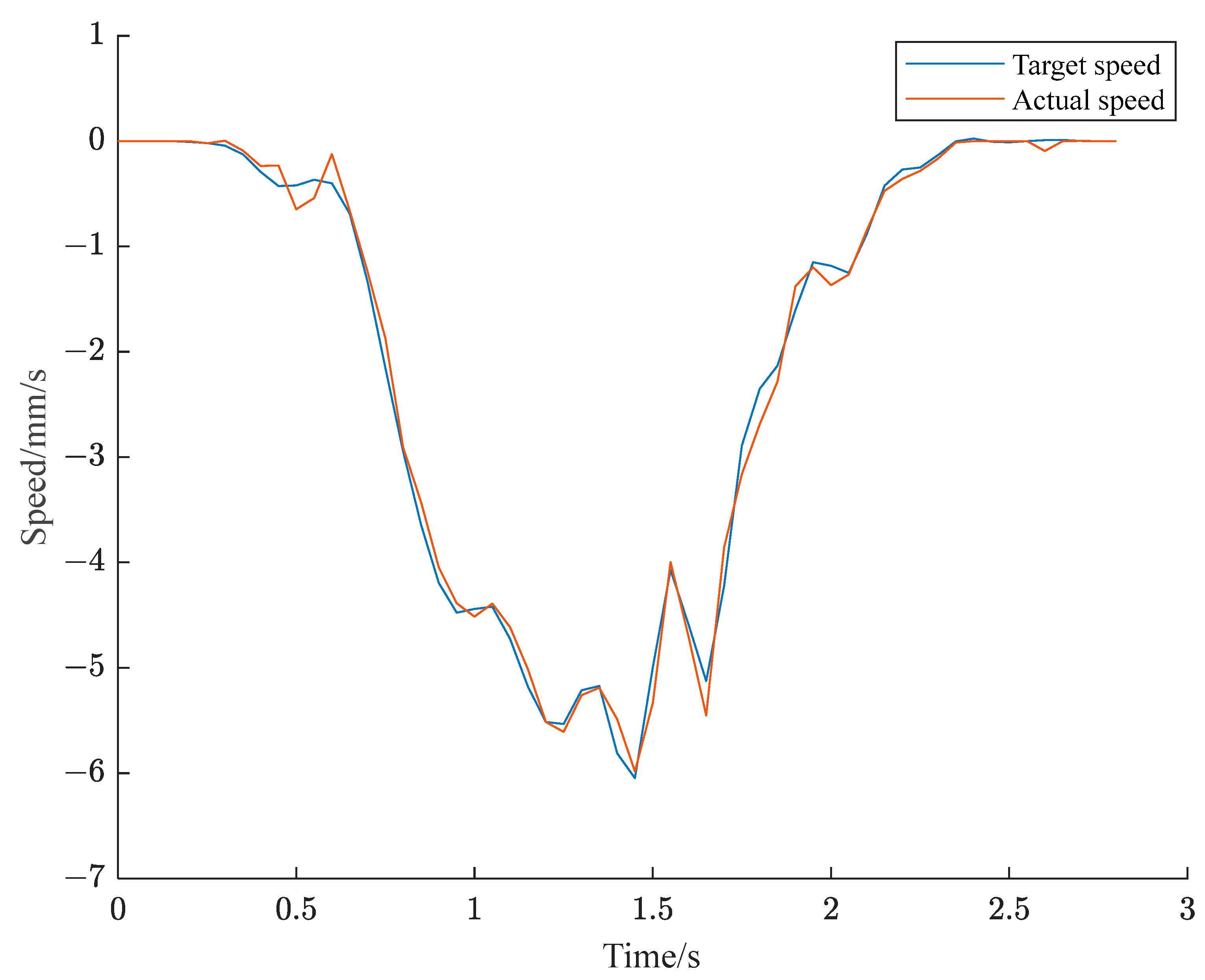
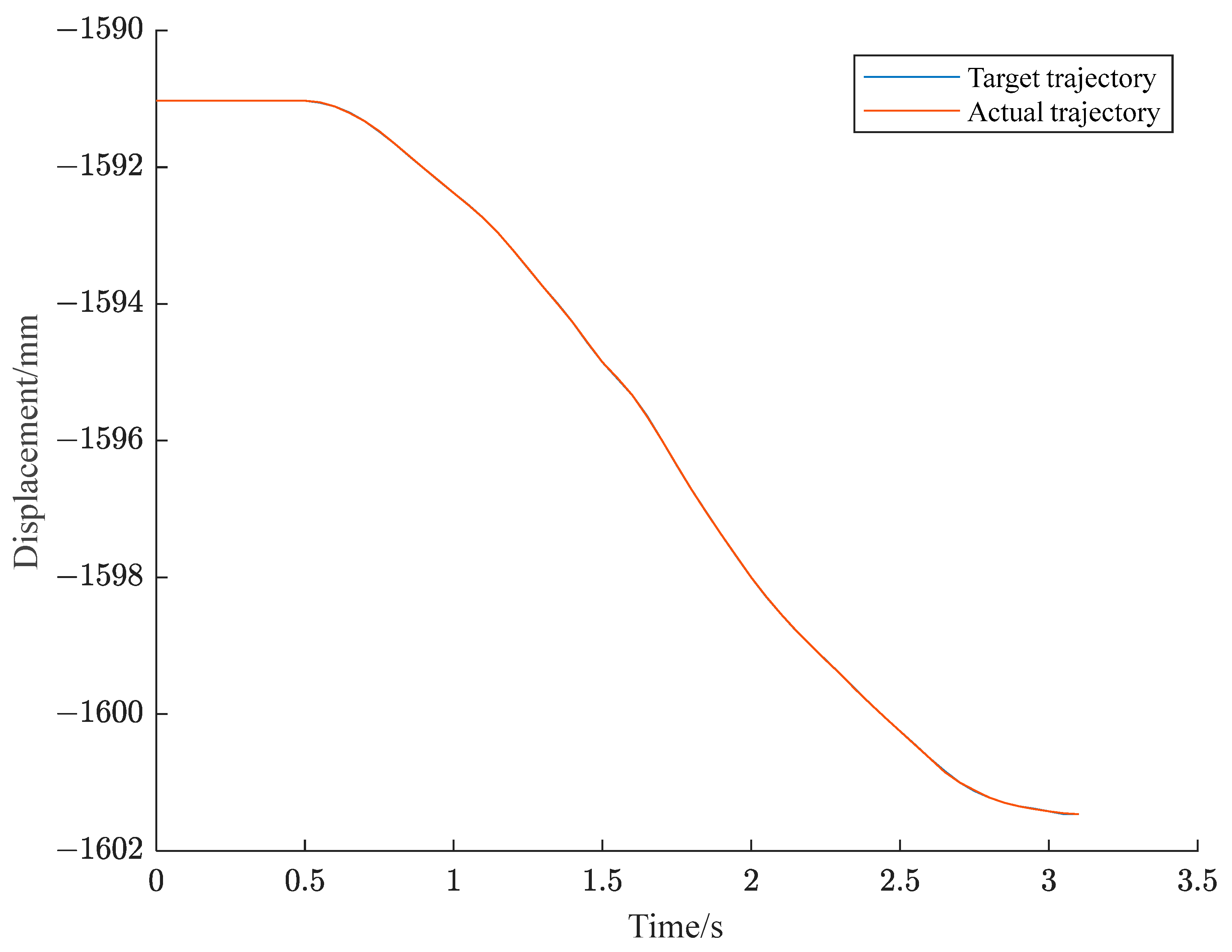
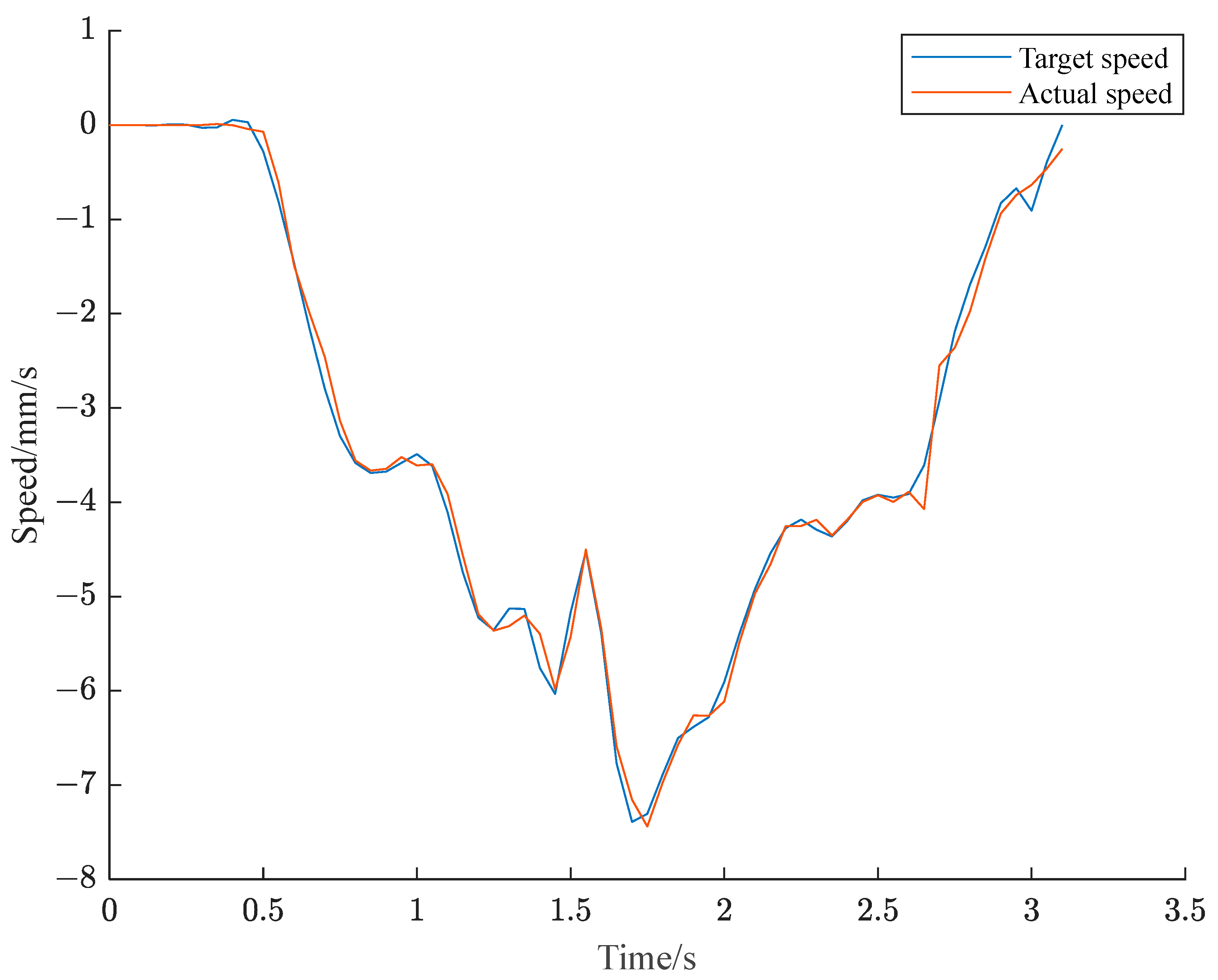
6. Experimental Confirmation
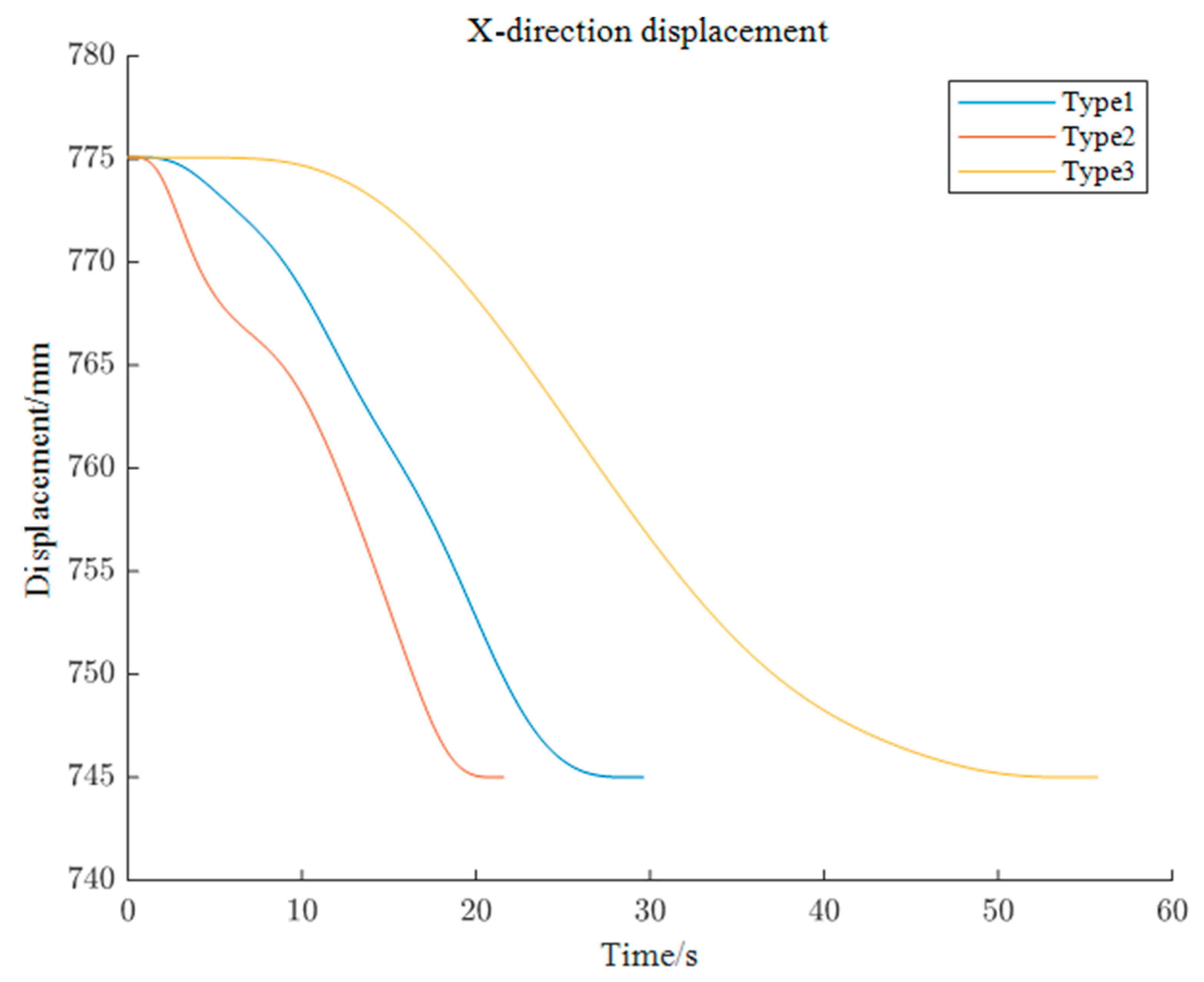
6.1. X-axis Trajectory Planning
6.2. Z-axis Trajectory Planning
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rüscher, O.; Mayländer, H. Automated alignment and marry-up of aircraft fuselage sections with a final assembly line. SAE Trans. 2001, 110, 173–178. [Google Scholar] [CrossRef]
- Bond, J. Mission critical: Precision in the air and on the ground. Mod. Mater. Handl. 2013, 68, 48–50. [Google Scholar]
- Kim, J.-J.; Lee, J.-J. Trajectory optimization with particle swarm optimization for manipulator motion planning. IEEE Trans. Ind. Inform. 2015, 11, 620–631. [Google Scholar] [CrossRef]
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2003, 14, 455–470. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Huang, J.; Zhao, B.; Quan, L. Smooth point-to-point trajectory planning for industrial robots with kinematical constraints based on high-order polynomial curve. Mech. Mach. Theory 2019, 139, 284–293. [Google Scholar] [CrossRef]
- Wang, S.; Wu, S.; Kang, C.; Li, X. Trajectory planning of a parallel manipulator based on kinematic transmission property. Intel. Serv. Robot. 2015, 8, 129–139. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Zhao, X.; Li, Y. Smooth trajectory planning for a parallel manipulator with joint friction and jerk constraints. Int. J. Control Autom. Syst. 2016, 14, 1022–1036. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Li, S.; Ren, J.; Wang, Q.; Cheng, Q.; Li, W. An Optimized Trajectory Planning for Welding Robot. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012009. [Google Scholar] [CrossRef]
- Gasparetto, A.; Zanotto, V. A technique for time-jerk optimal planning of robot trajectories. Robot. Comput. Integr. Manuf. 2007, 24, 415–426. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wang, J.; Feng, Y.; Liu, Y. A multi-objective trajectory planning method based on the improved immune clonal selection algorithm. Robot. Comput. Integr. Manuf. 2019, 59, 431–442. [Google Scholar] [CrossRef]
- Lan, J.; Xie, Y.; Liu, G.; Cao, M. A Multi-Objective Trajectory Planning Method for Collaborative Robot. Electronics 2020, 9, 859. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Shuai, K.; Zhu, W.; Chen, B.; Chen, K. Multi-objective Trajectory Planning Method based on the Improved Elitist Non-dominated Sorting Genetic Algorithm. Chin. J. Mech. Eng. 2022, 35, 81–95. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Xing, K.; She, B.; Liu, Y.; Chen, T.; Hu, G.; Wu, Q. Mixed Gaussian stochastic inversion based on a hybrid of cuckoo algorithm and Markov chain Monte Carlo. Chin. J. Geophys. 2021, 64, 2540–2553. [Google Scholar] [CrossRef]
- Jiang, Y.; Shuai, L.; Wu, Q.; Cao, Y. Optimization of resonant parameters of bidirectional DC electronic transformer based on cuckoo algorithm. Acta Energiae Solaris Sin. 2021, 42, 485–494. [Google Scholar] [CrossRef]
- Huang, B.Y.; Zhang, Y.X.; Zhao, L. Research on Fault Diagnosis Method of Rolling Bearings Based on Cuckoo Search Algorithm and Maximum Second Order Cyclostationary Blind Deconvolution. J. Mech. Eng. 2021, 57, 99–107. [Google Scholar] [CrossRef]
- Lai, Y.W.; Zhang, J. Urban Bus Scheduling Optimization Based on Simulated Anneal-adaptive Cuckoo Search Algorithm. J. Transp. Syst. Eng. Inf. Technol. 2021, 21, 183–189. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Multiobjective Cuckoo Search for Design Optimization; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Niknam, T.; Zare, M.; Gharibzadeh, M.; Azizipanah-Abarghooee, R. Multi-objective short-term scheduling of thermoelectric power systems using a novel multi-objective improved cuckoo optimization algorithm. Iet Gener. Transm. Distrib. 2014, 13, 1546–1550. [Google Scholar] [CrossRef]
- Wang, H.; Sheng, B.; Lu, Q.; Luo, R.; Fu, G. A Multi-Objective Cuckoo Search Algorithm Based on the Record Matrix for a Mixed-Model Assembly Line Car-Sequencing Problem. IEEE Access 2020, 8, 76453–76470. [Google Scholar] [CrossRef]
- Singh, G.; Banga, V.K. Kinematics and trajectory planning analysis based on hybrid optimization algorithms for an industrial robotic manipulators. Soft Comput. 2022, 26, 11339–11372. [Google Scholar] [CrossRef]
- De Boor, C. On Calculation with B-spline. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Cox, M.G. The numerical evaluation of B-spline. J. Inst. Maths. Appl. 1972, 10, 134–149. [Google Scholar] [CrossRef]
- Kahagalage, S.; Turan, H.H.; Jalalvand, F.; El Sawah, S. A novel graph-theoretical clustering approach to find a reduced set with extreme solutions of Pareto optimal solutions for multi-objective optimization problems. J. Glob. Optim. 2023, 86, 467–494. [Google Scholar] [CrossRef]
- Zhang, X.S.; Liu, J.; Luo, S.B. An improved multi-objective cuckoo search algorithm for airfoil aerodynamic optimization design. Acta Aeronaut. Astronaut. Sin. 2019, 40, 122500. (In Chinese) [Google Scholar] [CrossRef]
- Wang, L.P.; Ren, Y.; Qiu, Q.C.; Qiu, F.Y. Survey on Performance Indicators for Multi-objective Evolutionary Algorithms. Chin. J. Comput. 2021, 44, 1590–1619. (In Chinese) [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. On measuring multi-objective evolutionary algorithm performance. In Proceedings of the 2000 Congress on Evolutionary Comutation, La Jolla, CA, USA, 16–19 July 2000; Volume 204, p. 211. [Google Scholar]
- Van Veldhuizen, D.A. Lamont G B. Evolutionary computation and convergence to a Pareto front. In Proceeding of the Late-breaking Paper at the Genetic Programming 1998 Conference, Madison, WI, USA, 22–25 July 1998; pp. 221–228. [Google Scholar]
- Schoxtt, J.R. Fault-Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization. Master’s Thesis, Air Force Institute of Technology, Wright-Patterson AFB, OH, USA, 1995. [Google Scholar]
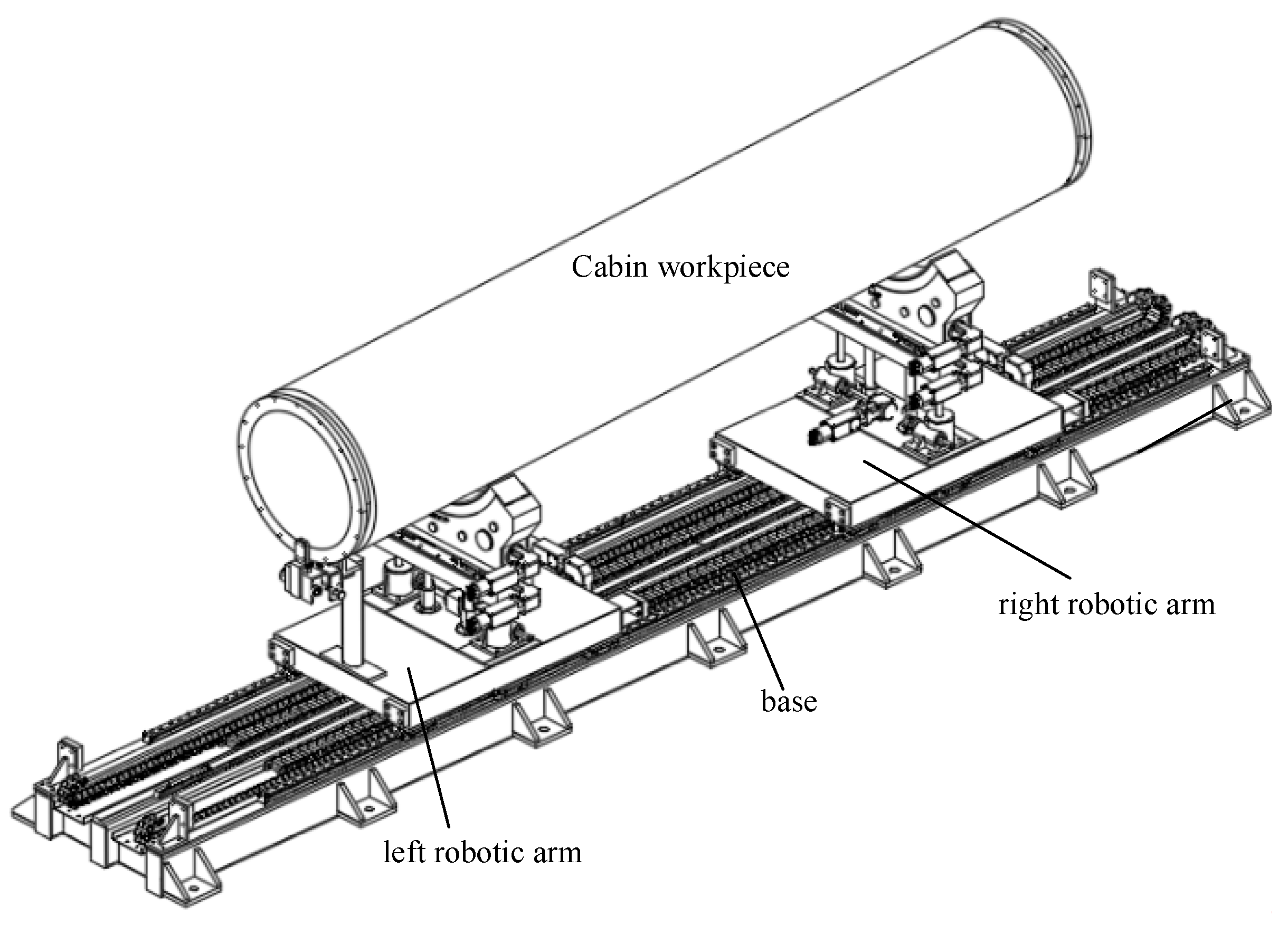
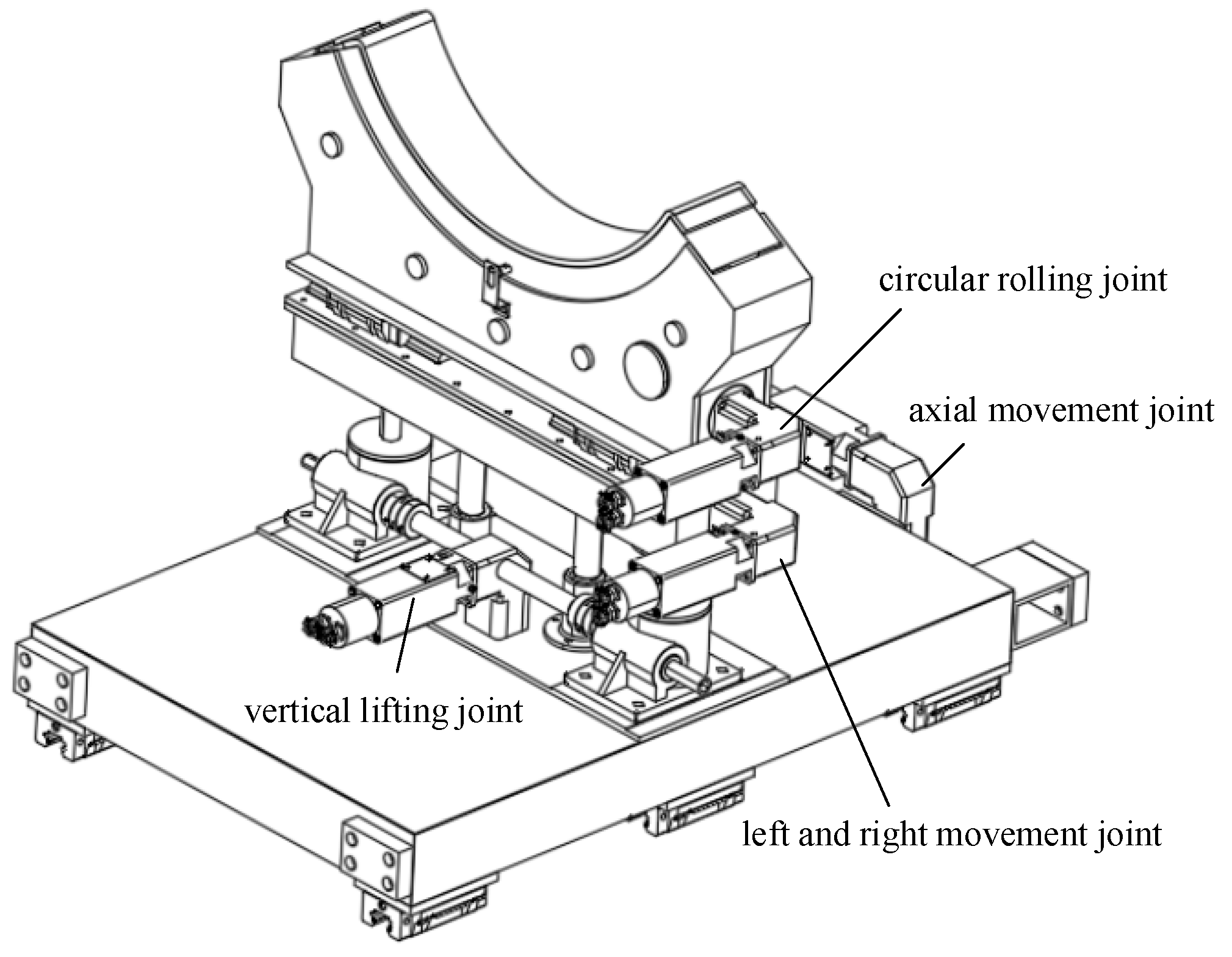
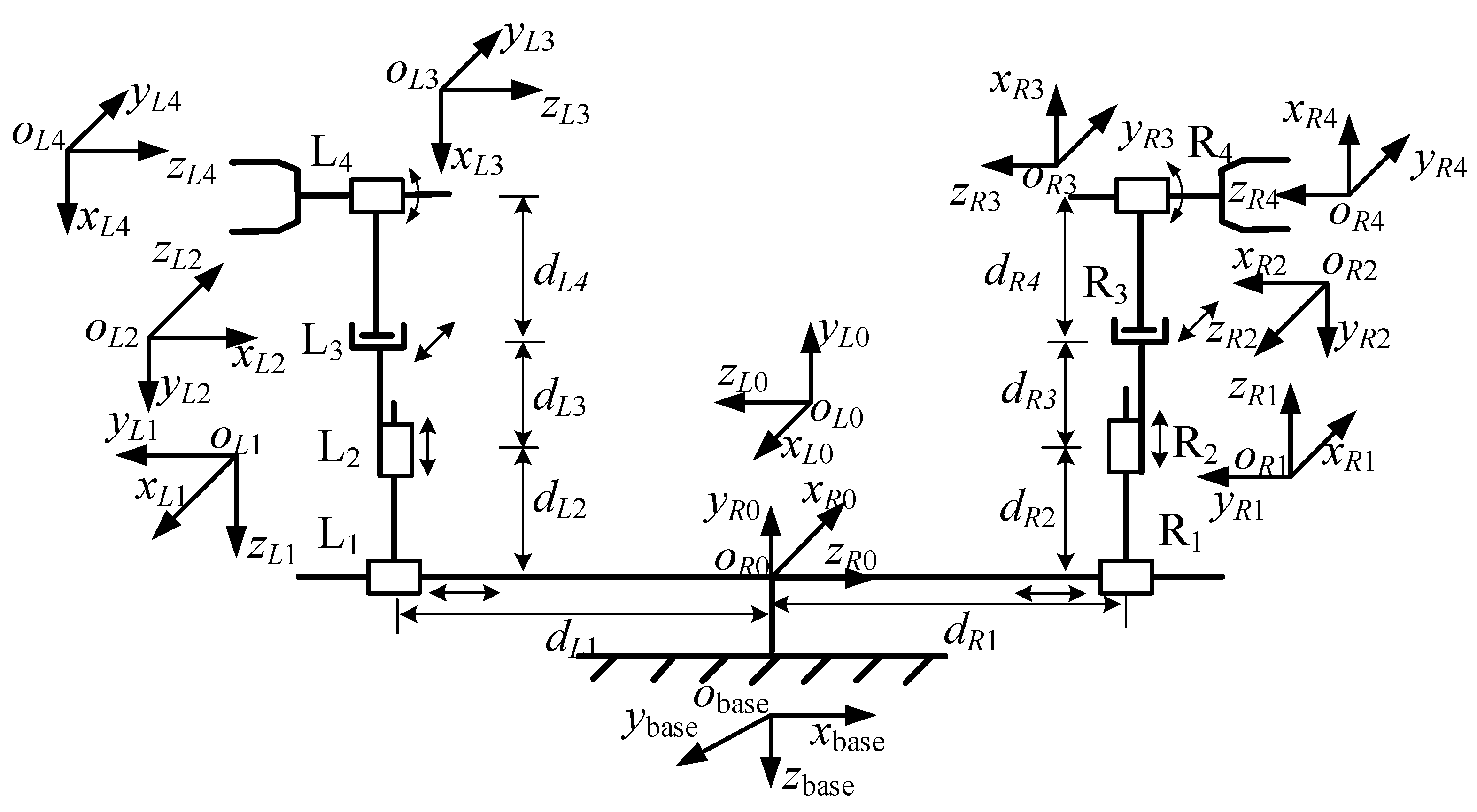
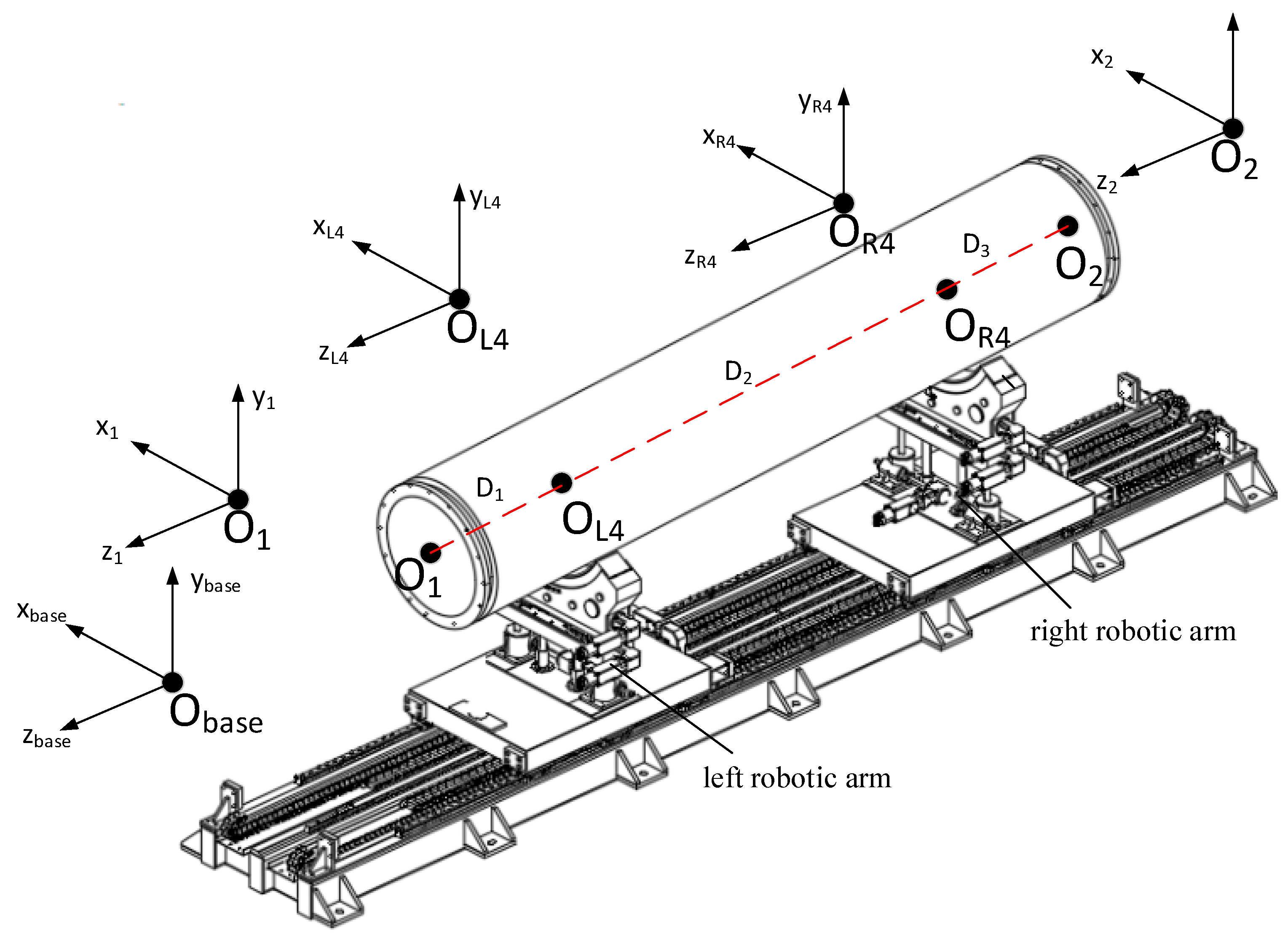


| Link | Joint Angle θi | Link Offset di | Link Length ai | Link Angle αi |
|---|---|---|---|---|
| Base-L0 | π/2 | 0 | 0 | −π/2 |
| L1 | 0 | dL1 | 0 | π/2 |
| L2 | −π/2 | dL2 | 0 | π/2 |
| L3 | π/2 | dL3 | dL | π/2 |
| L4 | θL | dL4 | 0 | 0 |
| Base-R0 | π/2 | 0 | 0 | π/2 |
| R1 | 0 | dR1 | 0 | −π/2 |
| R2 | π/2 | dR2 | 0 | −π/2 |
| R3 | −π/2 | dR3 | dR | −π/2 |
| R4 | θR | dR4 | 0 | 0 |
| Number | Parameter | Value |
|---|---|---|
| 1 | Roll angle range | ±15° |
| 2 | Z-axis direction travel range | ±600 mm |
| 3 | Y-axis direction travel range | ±50 mm |
| 4 | X-axis direction travel range | ±50 mm |
| 5 | Roll angle speed range | 0~6.8°/s |
| 6 | Z-axis direction speed range | 0~400 mm/s |
| 7 | Y-axis direction speed range | 0~25 mm/s |
| 8 | X-axis direction speed range | 0~2.5 mm/s |
| 9 | Roll angle acceleration range | 0~240°/s2 |
| 10 | Z-axis direction acceleration range | 0~100 mm/s2 |
| 11 | Y-axis direction acceleration range | 0~100 mm/s2 |
| 12 | X-axis direction acceleration range | 0~100 mm/s2 |
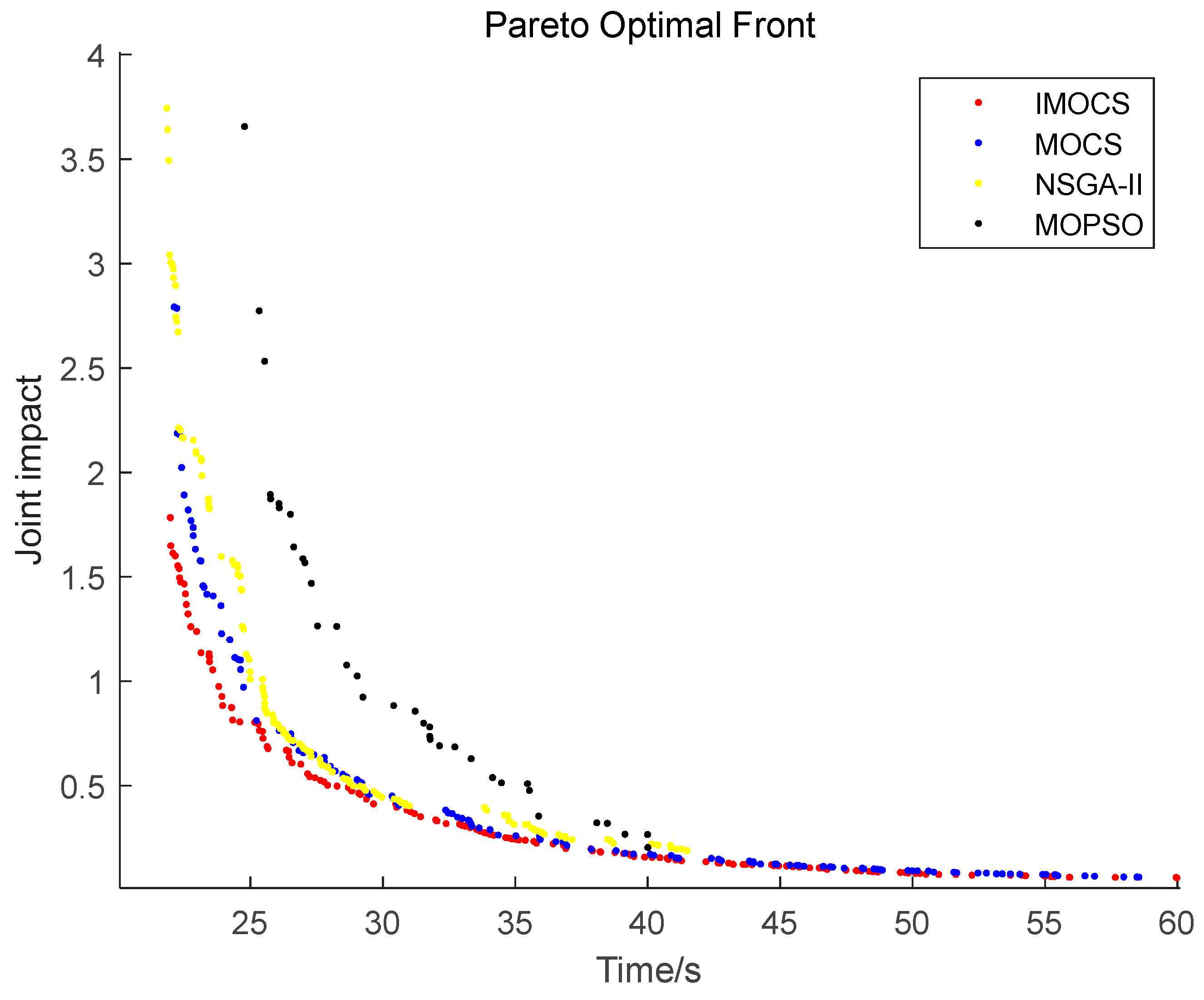
| Serial Number | Total Time | Joint Impact |
|---|---|---|
| 1 | 21.5743 | 3.9448 |
| 2 | 23.4057 | 1.5797 |
| 3 | 24.7217 | 1.0077 |
| 4 | 27.5831 | 0.6339 |
| 5 | 31.9816 | 0.3965 |
| 6 | 34.3913 | 0.3104 |
| 7 | 38.1978 | 0.2363 |
| 8 | 42.6796 | 0.1724 |
| 9 | 44.9217 | 0.1483 |
| 10 | 51.1223 | 0.1025 |
| 11 | 59.5678 | 0.0753 |
| Type | w1 | w2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Pan, F. A Multi-Objective Trajectory Planning Method of the Dual-Arm Robot for Cabin Docking Based on the Modified Cuckoo Search Algorithm. Machines 2024, 12, 64. https://doi.org/10.3390/machines12010064
Liu R, Pan F. A Multi-Objective Trajectory Planning Method of the Dual-Arm Robot for Cabin Docking Based on the Modified Cuckoo Search Algorithm. Machines. 2024; 12(1):64. https://doi.org/10.3390/machines12010064
Chicago/Turabian StyleLiu, Ronghua, and Feng Pan. 2024. "A Multi-Objective Trajectory Planning Method of the Dual-Arm Robot for Cabin Docking Based on the Modified Cuckoo Search Algorithm" Machines 12, no. 1: 64. https://doi.org/10.3390/machines12010064
APA StyleLiu, R., & Pan, F. (2024). A Multi-Objective Trajectory Planning Method of the Dual-Arm Robot for Cabin Docking Based on the Modified Cuckoo Search Algorithm. Machines, 12(1), 64. https://doi.org/10.3390/machines12010064





