Abstract
In this paper, an observer-based state feedback control strategy for trajectory tracking of a magnetic microrobot navigating within a 3D blood vessel is proposed. The desired trajectory to be followed by the microrobot is generated by an operator using a joystick device. To deal with the significant effect of both external disturbances and parametric uncertainties, often encountered in biological environments, a state feedback stabilization, that enforces the output tracking despite any environmental disturbances, is developed. Then, for the purpose of implementation, a state observer is developed to recover the whole state from the measured position of the microrobot. The state feedback and observer gains are determined separately by solving a set of linear matrix inequalities derived in the framework of Lyapunov stability theory. Simulation runs are performed to demonstrate the performance of the proposed control strategy.
1. Introduction
Nowadays, research works in the field of microrobotics have successfully biomedical resulted in applications that can, for example, unclog arteries and provide targeted drug delivery [1,2,3]. Indeed, micro-manipulation using microrobots provides a variety of flexible techniques for many biomedical applications, namely diagnosis, micro-surgery monitoring, and targeted drug delivery [4,5,6,7], to name a few. The use of a magnetic microrobot, actuated by an electromagnetic actuation (EMA) device, has received considerable attention, since microrobots are characterized by offering precise locomotion and possess the property of controllability. Various magnetic manipulations [1,2,3], which are non-contact actuation mechanisms, are widely used to actuate a vascular microrobot, both in in-vitro and in in-vivo experiments.
The propulsion principle of the magnetic microrobot in the blood vessel is accomplished by an EMA device that generates a magnetic force, which forces the microrobot to track a desired trajectory, as illustrated in Figure 1. In practice, it is well-known that when there are no actuation constraints, the coils are often overheated. This leads to an increase in the microrobot’s environmental temperature resulting in side effects, such as the disruption of blood viscosity and the deterioration of the coil wires. The last effect significantly impacts the performance of the EMA system, and, consequently, the motion of the microrobot.
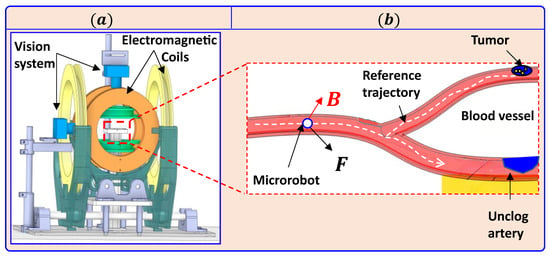
Figure 1.
Magnetic manipulation for drug delivery and unclogging arteries by means of a magnetic microrobot actuated by an electromagnetic actuation (EMA) device. (a) The prototype of the (EMA) device used for magnetic field generation within the 3D workspace. (b) Blood vessel and the microrobot.
The open-loop control approach used in microrobot navigation lacks precision and entails long-term operation, which poses significant physical challenges in various applications, such as drug delivery, minimally invasive surgery, detection, and detoxification [8]. To overcome these difficulties, and enhance both the efficiency and accuracy of microrobot navigation, the implementation of closed-loop control solutions is necessary. Closed-loop controllers enable precise navigation in dynamic and disturbed environments, and facilitate the execution of complex medical tasks. Control of magnetic microrobots is an active research area in the medical field, and considerable attention is devoted to the development of efficient closed-loop feedback controllers [9].
In-vivo medical applications require the manipulation of microrobots that move in a three-dimensional (3D) space. To the best of the authors’ knowledge, most closed-loop control approaches reported in the literature have primarily focused on two-dimensional (2D) space navigation. Remarkably few studies have been conducted to develop microrobot navigation control techniques for the performance of three-dimensional (3D) manipulation [10]. A 3D method for vascular navigation of microrobots, based on a model predictive controller, was proposed by [11]. In [12], an MRI-based generalized predictive controller (GPC) for a ferromagnetic microrobot, that navigates along a three-dimensional (3D) trajectory subject to a pulsatile flow disturbance, was proposed. A comparative study of the 3D tracking performance of an adaptive controller with that of a PID controller was conducted by [13]. A visual-based automatic controller, that enforces the input-to-state stability (ISS) of a microrobot moving within 2D and 3D fluidic environments, was investigated by [14,15], respectively. The linear quadratic (LQ) control of magnetic microbeads was investigated and successfully implemented by [16]. A 2D navigation control strategy, which combines backstepping control, sliding mode control, and disturbance compensation-based extended state observer, is proposed by [1]. Ghanbari et al. [17,18] proposed a time delay estimation (TDE) controller, to compensate for uncertainties and unknown dynamics, to control the 3D translational motion of a magnetic microrobot.
Most of reported studies have tended to show the effectiveness of automatic control of the microrobots. Nevertheless, they have largely overlooked the importance of constraints on the magnetic actuators and have disregarded the robustness issue and the environmental disturbances. In this study, a 3D control strategy that relies on the interaction between the operator and a joystick device to define the navigation path of the microrobot navigating in the blood vessel is proposed. Thus, an observer-based state feedback control strategy that forces the microrobot to track the desired trajectory, generated by an operator via a joystick, is developed.
The motivations and contributions of this paper are summarized by the following points:
- A 3D control strategy for a microrobot that effectively rejects environmental disturbances and accurately tracks a reference trajectory is proposed,
- A 3D observer is developed to estimate the whole state of the microrobot with a desired decay rate performance,
- A joystick device is utilized to translate the operator’s movements into a desired trajectory to be imposed for the microrobot.
The rest of the paper is organized as follows. Section 2 describes the mathematical model of a three-dimensional (3D) microrobot navigating within a cylindrical blood vessel, and path planning using a joystick device is developed. The proposed 3D observer-based state feedback control strategy is presented in Section 3. Simulation results and a comparative study that show the effectiveness of the proposed control strategy are reported in Section 4. Section 5 concludes the paper.
2. Modeling and Path Planning
2.1. Magnetic Microrobot Modeling
Consider the three-dimensional (3D) motion, of a spherical microrobot of radius r and density , that moves within a blood vessel (Figure 2). The vector denotes the position vector of the microrobot with x, y, and z are the coordinates of the directions of the microrobot along the , and axes, respectively. denotes the velocity vector with , , and are the microrobot velocities along the , and . During the navigation in a 3D-fluid environment, the microrobot is subject to the forces depicted in Figure 2, namely the following [19]: the gravitational force , the electrostatic force , the contact force , the Van der Waals force , the hydrodynamic force and the actuation magnetic force .
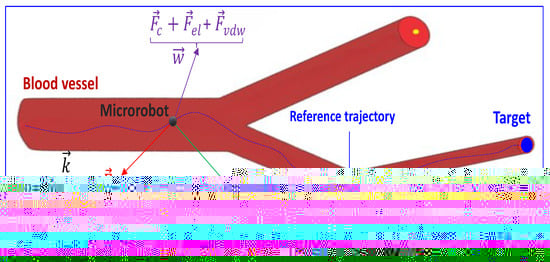
Figure 2.
Forces acting in a magnetic microrobot navigating within a blood vessel.
Most studies on the control of a microrobot have been conducted under the assumption that the microrobot navigates in the middle of the blood vessel [20,21]. In this case, it is assumed that the forces , and are negligible compared to and forces, and, consequently, their effects are insignificant and can be neglected. However, in practice, this assumption is not justified, which often results in poor performance [22].
To address this issue, a control scheme that copes with these disturbance forces and uncertainties is proposed in this work. Hence, by taking into account the effect of the different forces, the application of Newton’s law of motion yields the ordinary differential equation that describes the dynamic behavior of the microrobot navigating within a blood vessel, as follows [1,21]:
where m is the mass of the microrobot, , , and are unknown forces assumed to be external disturbances along the directions of the , and axes, and represents the vector of uncertainties. The dynamic model (1) can be rewritten as follows:
with
where g is the gravitational force.
Remark 1.
In the cases of i and j-axes, .
Assumption 1.
The external disturbances w is bounded.
Assumption 2.
The microrobot navigates in regions away from the heart.
Assumption 2 means that the microrobot operates under conditions of low Reynolds number; hence, according to Martel [23], the blood velocity is negligible.
The actuation magnetic force is given as follows:
where M and are the magnetization and the magnetic volume of the microrobot, respectively. The manipulated variable u is the vector of magnetic gradient fields, along the , and axes, which represent the manipulated variables or controls, that is,
where is the magnetic field vector.
Under Assumption 2, the drag force that opposes the motion of the microrobot is defined by the following Stokes’ law [20]:
where is the fluid viscosity.
Taking into account Equations (4) and (6), the dynamic model of microrobot (2) takes the following form:
with
Remark 2.
The microrobot model (7) can be seen as consisting of three decoupled subsystems. Each subsystem describes the dynamical behavior along a given axis. These subsystems have the same form, except along the z axis, which is affected by the force of gravity . Thus, for the controller and observer design, we considered the dynamical subsystem along the axis. The results along the axes and follow in the same way.
The dynamics of the microrobot along the axis is obtained by projecting Equation (7) onto i-axis, which yields the following dynamical model:
By introducing the state vector , the model (9) can be written under the following state space form:
with
Note that, in this work, the actual position x is accessible for measurement by a vision system. Let us now introduce the following dynamical errors:
where and are the desired position and velocity along the i-axis, respectively. The aim was to design a controller that forces the microrobot to track a desired trajectory and to reject the effect of the external disturbances.
Let us express the model (10) in terms of dynamical errors and . Hence, by taking and , the following model results:
with being the auxiliary control, and the actual magnetic field gradient to be applied is given as follows:
2.2. Path Planning with Joystick Device
Trajectory planning is a crucial element for the autonomy of microrobots within the human body. Although many works have been published on the control of microrobots, trajectory planning still remains a challenging problem [24]. The trajectory planning solution for a microrobot navigating within a blood vessel was investigated in the framework of optimal control by [24]. In [11], pre-defined path planning, based on detection of the microrobot’s position in a blood vessel, was extracted by Frangi vessel filtering from preoperative images. Global trajectory planning of the microrobot using the breadth first search (BFS) algorithm is proposed in [1]. A review of different solutions adopted for microrobot trajectory planning can be found in the study by [9]. However, the navigation of a microrobot in a complex environment, most notably in the vascular system, faces difficulties. In particular, the environment around the bifurcation can be complex and the prediction of the microrobot direction of motion is difficult by means of classical planning algorithms [1]. In this situation, it is necessary to design a local trajectory planner around this bifurcation.
The Joystick Falcon developed by Novint (see Figure 3) is a three-dimensional force feedback controller already exploited in several scientific applications [25]. The haptic interfaces that use the Joystick Falcon can be used in different modes [26,27]: force–position, force–force and four-channels modes.
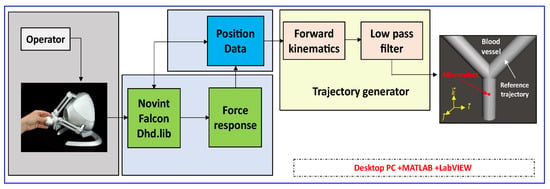
Figure 3.
Path planning for microrobot using the joystick.
In this work, the position–position mode is proposed to generate, in an intuitive way, and with the assistance of an operator, the 3D path-navigation of the microrobot. The joystick interface is developed under LabVIEW software number: 788492-35 at National Instruments-USA. Figure 3 summarizes the experimental setup of the Novint Falcon joystick device and the interaction with the operator.
3. Proposed Control Strategy
In this section, a control strategy (Figure 4) that combines a robust state-feedback controller and a Luenberger observer with a performance decay rate is proposed. The reference trajectory , to be followed by the microrobot, and the first and second derivatives are generated using the joystick device.
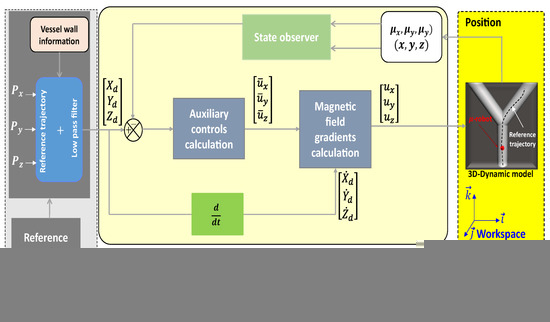
Figure 4.
Proposed control strategy for 3D navigation of a microrobot within a blood vessel.
In practice, to implement the control law (15), we need to estimate the micorobot’s velocity along the i-axis. For this purpose, a Luenberger observer, with a decay rate, was designed, based on a Lyapunov analysis, to reconstruct the states vector , that is, to achieve in closed-loop:
The observer is given as follows:
where represent the estimate state vector.
Combining (16), (18) and (19), one obtains the following dynamic model of the estimation error :
Recall that our objective was to design the auxiliary control so that the tracking error tends towards zero, that is,
Hence, the objective can be seen as the stabilization problem for the error-tracking model (16) of the microrobot, which can be solved using the following state-feedback:
Substituting (22) into (16), the following closed-loop system results:
where is the state feedback gain matrix to be designed so that the resulting closed-loop system is stable. The estimation error model (20) and the tracking error model (23) can be combined into the following augmented model:
Hence, by using the separation principle [28], the state feedback gains and the observer gains can be designed independently using the LMI-based design approach [29].
3.1. LMI-Based Design Approach
3.1.1. Observer Design
The gains of the state observer (18) and (19) are determined using the result of Theorem 1.
Theorem 1.
The estimation error (20) is asymptotically stable, with the decay rate performance , if there exist matrices and , such that the following LMI holds:
where is the decay rate performance of the state estimation error, and:
To analyze the convergence of the estimation error , the Lyapunov stability theory is used.
Proof of Theorem 1.
Let us consider the following Lyapunov function:
where is a symmetric positive definite matrix. The derivative of the function (27) with respect to t is:
The equilibrium point of the state estimation error model (20) is asymptotically stable if the derivative of the Lyapunov function (28) along the trajectories of the (20) is strictly negative, that is:
Now, to ensure a sufficiently rapid convergence toward zero, an exponential decay rate can be imposed by replacing the stability condition (29) with the following one:
Now, by combining Equations (28) and (30), the following LMI results [30]:
Then, if there exist matrices and , for which the LMI (31) holds, then the equilibrium point of the system (20) is asymptotically stable with a decay rate , and the observer gain (18) and (19) is given by:
□
3.1.2. State Feedback Design
To stabilize the system (16) and to reject the external disturbance , we propose modifying the state feedback (22) by adding an integral action [31]. Hence, the control law takes the following form:
with and being the new gain matrix and the new state with . Thus, the tracking error model (16) can be written in terms of , as follows:
with
Due to the effects of these external disturbances the closed-loop system’s performance deteriorates. Consequently, the rejection of their effects, to enhance the control performance, is crucial. Thus, to efficiently eliminate the effect of , we considered the following tracking performance criteria associated with the augmented tracking error (34) and (35) [32]:
where is a prescribed attenuation level [33]. The following theorem provides the conditions under which the proposed state feedback (33) can accomplish the control objective, even in the presence of the external disturbances . The convergence analysis of the tracking error is carried out using the Lyapunov stability theory.
Theorem 2.
Consider the error tracking model (34) and (35), for which the Assumption 1 holds. If, for a given value of , there exist a symmetric positive definite matrix and a gain matrix solution to the following LMI:
the state feedback controller (33) enforces the output tracking, while rejecting the external disturbances.
Proof of Theorem 2.
Let us consider the following Lyapunov function
with . The evaluation of the time derivative of provides:
The asymptotic stability is achieved if the following condition holds:
Now, by combining (37) and (41), the following asymptotical stability condition follows:
or, equivalently,
and by substituting (34) into (42), we obtain the following LMI:
where . Equation (44) can be rewritten in the following matrix form:
or, equivalently,
which implies that
and, using the Shur’s complement [34], Equation (46) reduces to
Then, the multiplication of both sides of the matrix in (48) by diag yields:
and the condition (38) follows from Equation (49) by taking and . □
As mentioned in the introduction, the manipulation of the magnetic field leads to coil overheating. So, to mitigate its impact, it is recommended to restrict the total expended energy by imposing the following constraint on the manipulated variable:
where is the maximum magnitude of the control variable .
At the injection location, the microrobot is at rest; that is, its velocity is null. Consequently, at , the initial condition is known. In this case, the constraint on the manipulated variable (50) can be enforced if there exist matrices and such that the following LMIs are fulfilled [30] Lemma 2:
Consequently, if there exist matrices and verifying the conditions (49), (51) and (52), the equilibrium point () of the system (34) is asymptotically stable and ensures the rejection of environmental disturbances. The state feedback gain is given by:
3.2. Stability Analysis
In this part, the closed-loop stability of the observer-based robust controller proposed is investigated. As mentioned in Section 3, the separation principle applies in our case. Indeed, from Equation (24), it is clear that the tuning of both observer (18), (19) and controller (33), that is, the determination of matrices (32) and (53), can be done separately. Now, from Equation (24), we obtain in closed loop the model, in terms of the tracking error , as follows:
According to Theorem 1, the estimation error is asymptotically stable with a decay rate performance if the matrix is determined so that the condition (25) is fulfilled. Hence, the convergence of the observer is ensured, i.e., the estimation error as . Consequently, from (54), the is a stable matrix, and, hence, is ; that is, according to (22), we have as .
Note that the state feedback controller (33) provides the auxiliary control , along the x axis. Following the same reasoning along the axes y and z, we obtain the auxiliary controls and . From a practical standpoint, the actual control to be applied to the microrobot is the magnetic field gradient, that is, the control u. Thus, the 3D observer-based magnetic controller of the microrobot navigating in a blood vessel takes the following form:
Figure 4 summarizes the proposed control strategy for the automatic navigation of a microrobot within a blood vessel.
4. Simulation and Results
In this section, the performance of the proposed control strategy, is evaluated through numerical simulations. The parameters of the magnetic microrobot are given in Table 1.

Table 1.
Microrobot parameters values.
4.1. Comparative Study
The aim of the first simulation run was to compare the proposed control strategy with the generalized predictive controller proposed by [12]. For the sake of comparison, we considered a microrobot navigating within a 1D blood vessel, and the measurements were corrupted with a white Gaussian noise, as in [12]. For both control strategies, the desired trajectory was predefined in advance. The parameters of both control strategies were tuned such that the maximum magnetic force did not exceed the maximum tolerated value of N. For the proposed control strategy, this constraint on was verified for . The gain matrix of the state feedback (33) along the -axis (1D blood vessel) was .
The results of the conducted comparison are depicted in Figure 5. It can be observed that both control strategies forced the microrobot to track the desired 1D trajectory, while effectively rejecting the disturbances. However, it is noticeable that the proposed control strategy yielded better performance compared to the generalized predictive controller, which was corroborated by the position tracking errors, provided in Figure 6. Indeed, the proposed control strategy provided a fast convergence to the desired trajectory without overshoots, compared to the generalized predictive controller that was characterized by a slow convergence and significant overshoots.
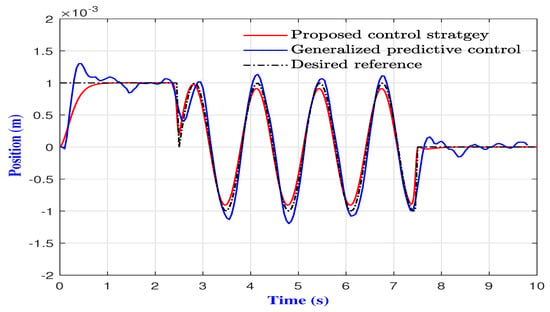
Figure 5.
Position tracking problem in the case of 1D blood vessel.
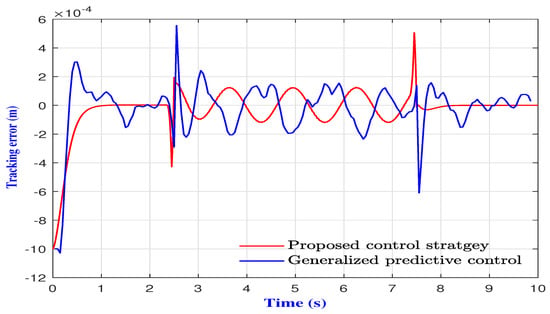
Figure 6.
Position tracking error.
4.2. Simulation with Joystick Device
The second simulation run consisted of evaluating the proposed control strategy in the case of a 3D blood vessel depicted in Figure 7. The vessel geometry considered in this work consisted of multiple combinations of Y-shaped bifurcations. Thus, the phantom was a miniaturized model and the internal diameters were about mm. In this simulation, the desired trajectory was generated by the joystick device, which demonstrated the interaction between the operator and the controller via the joystick. The initial conditions of the microrobot and the observer are given in Table 2.
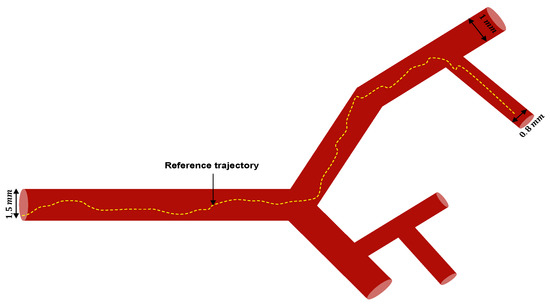
Figure 7.
Three-Dimensional blood vessel phantom with various branches and inclinations.

Table 2.
Initial conditions for the system and the observer.
The simulation parameters are summarized in Table 3.

Table 3.
Controller and observer parameter values.
The state feedback gain matrix (53) and the observer gain matrix (32) are determined by solving, using the YALMIP solver [35], the set of LMIs given by (38) and (25), respectively, which yields the following gain matrices:
In the simulation run, the external disturbances were defined as follows:
where , and are the uncertainties along the i, j and k-axes, respectively. In the simulation run, random variables were used to model these uncertainties.
The simulation results obtained are given by Figure 8 and Figure 9, which show that the proposed control strategy achieved a fast and asymptotic convergence without overshoots. Clearly, the proposed control strategy forced the microrobot to track the desired 3D trajectory despite the environmental disturbances. This was confirmed both by the position and the velocity tracking errors (Figure 10 and Figure 11).
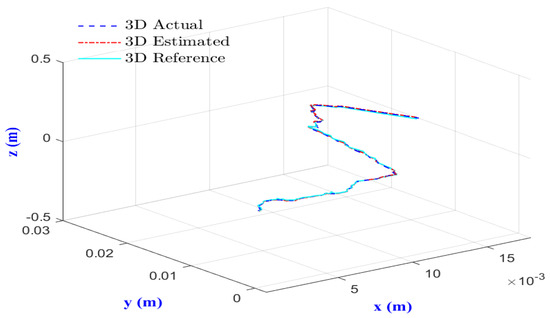
Figure 8.
3D Position tracking.
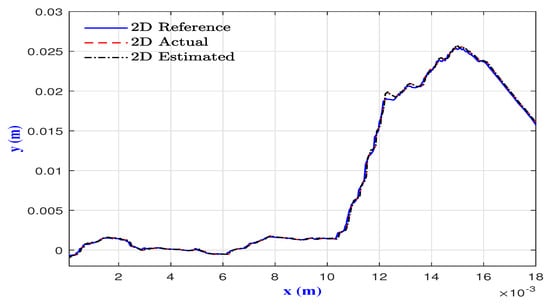
Figure 9.
2D position tracking.
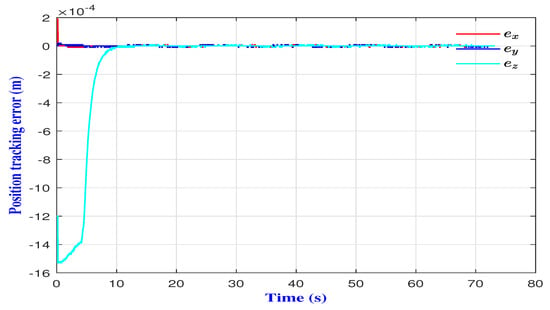
Figure 10.
Position tracking errors.
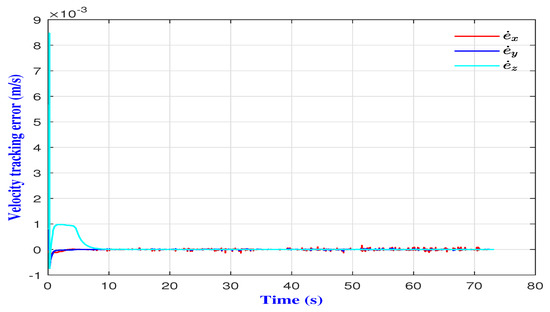
Figure 11.
Velocity tracking errors.
The obtained results also indicated the effectiveness of the Luenberger observer in recovering the microrobot state, even in the presence of environmental disturbances. Figure 12 and Figure 13 show the ability of the Luenberger observer to recover the microrobot actual states with an imposed decay rate. Figure 14 represents the magnetic field gradients delivered along , and -axes.
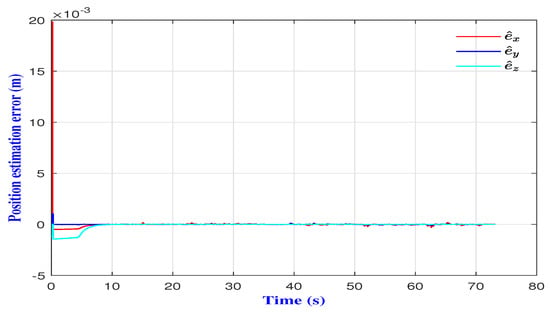
Figure 12.
Position estimation errors.
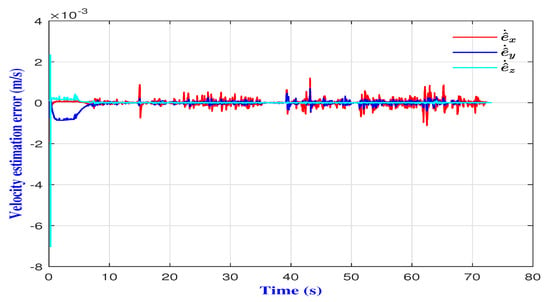
Figure 13.
Velocity estimation errors.
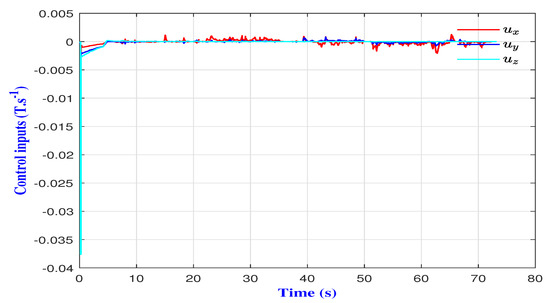
Figure 14.
Magnetic field gradient (controls).
5. Conclusions and Future Work
In this paper, new trajectory-tracking of a magnetic microrobot navigating within a 3D blood vessel is proposed. The objective consists in steering the microrobot from an initial position to a target position by tracking a desired reference trajectory generated by the joystick device interacting with the operator. To achieve this objective, a state feedback. that both stabilizes the tracking error model and rejects the external disturbances, is developed. Then, for implementation purposes, a state observer is developed to recover the whole state of the microrobot using accessible measurements. Thus, the combined state-feedback and observer yields the control strategy termed observer-based magnetic control. The tracking and disturbance rejection effectiveness of the proposed control strategy was demonstrated by means of simulation runs. It was shown that the proposed control strategy yielded better performances, in both the 1D and 3D blood vessel cases, and outperformed the generalized predictive control in the case of a 1D blood vessel.
These interesting simulation results motivate the implementation of the proposed control strategy on a dedicated platform in future works.
Author Contributions
Conceptualization, all authors; methodology, all authors; software, M.L.; formal analysis, all authors; investigation, M.L.; resources, K.B.; data curation, M.L.; writing original draft preparation, all authors; writing review and editing, all authors; visualization, all authors; supervision, E.-H.G. and A.M. and K.B.; project administration, K.B.; funding acquisition, K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Franco-Algerian Tassili Program (number: 43790QB).
Data Availability Statement
Data are available from the corresponding author on request.
Conflicts of Interest
The authors declared no potential conflict of interest with respect to the research, authorship, and/or publication of this article.
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | Two-dimensional space |
| 3D | Three-dimensional space |
| EMA | Electromagnetic Actuation |
| LQ | Linear Quadratic |
| GPC | generalized predictive Controller |
| ISS | Input-to-State Stability |
| MRI | Magnetic Resonance Imaging |
References
- Meng, K.; Jia, Y.; Yang, H.; Niu, F.; Wang, Y.; Sun, D. Motion planning and robust control for the endovascular navigation of a microrobot. IEEE Trans. Ind. Inform. 2019, 16, 4557–4566. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, L. Magnetic actuation systems for miniature robots: A review. Adv. Intell. Syst. 2020, 2, 2000082. [Google Scholar] [CrossRef]
- Yu, C.; Kim, J.; Choi, H.; Choi, J.; Jeong, S.; Cha, K.; Park, J.O.; Park, S. Novel electromagnetic actuation system for three-dimensional locomotion and drilling of intravascular microrobot. Sens. Actuators A Phys. 2010, 161, 297–304. [Google Scholar] [CrossRef]
- Larbi, M.; Guechi, E.H.; Chah, A.; Maidi, A.; Belharet, K. Sliding Mode Observer of a Two-Agent Microrobotic System. In Proceedings of the 2022 5th International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 22–25 March 2022; pp. 268–273. [Google Scholar]
- Koleoso, M.; Feng, X.; Xue, Y.; Li, Q.; Munshi, T.; Chen, X. Micro/nanoscale magnetic robots for biomedical applications. Mater. Today Bio 2020, 8, 100085. [Google Scholar] [CrossRef]
- Li, J.; Yu, J. Biodegradable Microrobots and Their Biomedical Applications: A Review. Nanomaterials 2023, 13, 1590. [Google Scholar] [CrossRef]
- Jamil, M.F.; Pokharel, M.; Park, K. Light-Controlled Microbots in Biomedical Application: A Review. Appl. Sci. 2022, 12, 11013. [Google Scholar] [CrossRef]
- Tottori, S.; Zhang, L.; Qiu, F.; Krawczyk, K.K.; Franco-Obregón, A.; Nelson, B.J. Magnetic helical micromachines: Fabrication, controlled swimming, and cargo transport. Adv. Mater. 2012, 24, 811–816. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Yang, Z.; Ferreira, A.; Zhang, L. Control and autonomy of microrobots: Recent progress and perspective. Adv. Intell. Syst. 2022, 4, 2100279. [Google Scholar] [CrossRef]
- Dong, D.; Xing, L.; Zheng, L.; Jia, Y.; Sun, D. Automated 3-d electromagnetic manipulation of microrobot with a path planner and a cascaded controller. IEEE Trans. Control Syst. Technol. 2021, 30, 2672–2680. [Google Scholar] [CrossRef]
- Belharet, K.; Folio, D.; Ferreira, A. Three-dimensional controlled motion of a microrobot using magnetic gradients. Adv. Robot. 2011, 25, 1069–1083. [Google Scholar] [CrossRef]
- Belharet, K.; Folio, D.; Ferreira, A. Endovascular navigation of a ferromagnetic microrobot using MRI-based predictive control. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2804–2809. [Google Scholar]
- Khamesee, M.B.; Kato, N.; Nomura, Y.; Nakamura, T. Design and control of a microrobotic system using magnetic levitation. IEEE/ASME Trans. Mechatron. 2002, 7, 1–14. [Google Scholar] [CrossRef]
- Ma, W.; Xu, M.; Zhong, Z.; Li, X.; Huan, Z. Closed-loop control for trajectory tracking of a microparticle based on input-to-state stability through an electromagnetic manipulation system. IEEE Access 2020, 8, 46537–46545. [Google Scholar] [CrossRef]
- Ma, W.; Li, J.; Niu, F.; Ji, H.; Sun, D. Robust control to manipulate a microparticle with electromagnetic coil system. IEEE Trans. Ind. Electron. 2017, 64, 8566–8577. [Google Scholar] [CrossRef]
- Mellal, L.; Folio, D.; Belharet, K.; Ferreira, A. Optimal control of multiple magnetic microbeads navigating in microfluidic channels. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1921–1926. [Google Scholar]
- Ghanbari, A.; Chang, P.H.; Nelson, B.J.; Choi, H. Electromagnetic steering of a magnetic cylindrical microrobot using optical feedback closed-loop control. Int. J. Optomechatron. 2014, 8, 129–145. [Google Scholar] [CrossRef]
- Ghanbari, A.; Chang, P.H.; Nelson, B.J.; Choi, H. Magnetic actuation of a cylindrical microrobot using time-delay-estimation closed-loop control: Modeling and experiments. Smart Mater. Struct. 2014, 23, 035013. [Google Scholar] [CrossRef]
- Belharet, K.; Folio, D.; Ferreira, A. 3D MRI-based predictive control of a ferromagnetic microrobot navigating in blood vessels. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 808–813. [Google Scholar]
- Belharet, K.; Folio, D.; Ferreira, A. Control of a magnetic microrobot navigating in microfluidic arterial bifurcations through pulsatile and viscous flow. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2559–2564. [Google Scholar]
- Arcese, L.; Fruchard, M.; Ferreira, A. Endovascular magnetically guided robots: Navigation modeling and optimization. IEEE Trans. Biomed. Eng. 2011, 59, 977–987. [Google Scholar] [CrossRef]
- Sadelli, L.; Fruchard, M.; Ferreira, A. 2D observer-based control of a vascular microrobot. IEEE Trans. Autom. Control 2016, 62, 2194–2206. [Google Scholar] [CrossRef]
- Martel, S. Nanorobots for Endovascular Target Interventions in Future Medical Practice. Curr. Adv. Med. Appl. Nanotechnol. 2012, 85. [Google Scholar]
- Huan, Z.; Ma, W.; Wang, J.; Wu, F. Path planning and optimization for microrobot in a vessel-mimic environment. Front. Neurorobotics 2022, 16, 923348. [Google Scholar] [CrossRef]
- Renon, P.; Yang, C.; Ma, H.; Cui, R. Haptic interaction between human and virtual icub robot using novint falcon with chai3d and matlab. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 6045–6050. [Google Scholar]
- Trucios, L.E.; Tavakoli, M.; Adams, K. Adaptive tracking control for task-based robot trajectory planning. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 4256–4260. [Google Scholar]
- Montero, D.; Páez, M.; Salinas, S. Teleoperation Prototype Using Novint Falcon Haptic Interfaces. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 201, Bucaramanga, Colombia, 26–28 October 2016. [Google Scholar]
- Tuan, H.D.; Apkarian, P.; Narikiyo, T.; Yamamoto, Y. Parameterized linear matrix inequality techniques in fuzzy control system design. IEEE Trans. Fuzzy Syst. 2001, 9, 324–332. [Google Scholar] [CrossRef]
- Yoneyama, J.; Nishikawa, M.; Katayama, H.; Ichikawa, A. Design of output feedback controllers for Takagi–Sugeno fuzzy systems. Fuzzy Sets Syst. 2001, 121, 127–148. [Google Scholar] [CrossRef]
- Wang, H.O.; Tanaka, K. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- David, I.; Robles, G. PID control dynamics of a Robotic arm manipulator with two degrees of Freedom. Control. Process. Robot. 2012, 3–7. [Google Scholar]
- Uang, H.J.; Huang, G. A robust fuzzy model following observer-based control design for nonlinear system. In Proceedings of the 2004 IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; Volume 1, pp. 171–176. [Google Scholar]
- Chen, B.S.; Lee, C.H.; Chang, Y.C. H∞ tracking design of uncertain nonlinear SISO systems: Adaptive fuzzy approach. IEEE Trans. Fuzzy Syst. 1996, 4, 32–43. [Google Scholar] [CrossRef]
- Zhang, F. The Schur Complement and Its Applications; Springer: New York, NY, USA, 2006. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in Matlab. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).