Parallel Pointing Systems Suitable for Robotic Total Stations: Selection, Dimensional Synthesis, and Accuracy Analysis

Abstract

Robotic Total Stations (RTS) are fully automated theodolites with electronic distance measurement (EDM) that include a number of additional tools (e.g., camera, laser rangefinder, onboard computer, and tracking software, etc.) enabling them to work autonomously. The added tools make RTSs able to track mobile targets on civil structures thus opening to the use of RTSs in structural monitoring. Unfortunately, the available RTSs are able to track a target up to a motion rate of 3 Hz. Reducing mobile masses is a viable design strategy for extending this frequency border. Such a strategy is pursued in this study by proposing the use of parallel pointing systems (PPS) as basic mechanical architectures for RTSs. The literature on PPSs is reviewed and the applicable PPS architectures are selected. Successively, the selected architectures are sized according to RTSs’ functional requirements, and the positioning precision of the sized mechanisms is evaluated. The result of this study is that there are three PPS architectures suitable for RTSs, whose detailed comparison is also presented.

1. Introduction

A theodolite [1] is an instrument that measures two angles, named pan and tilt angles, which locate the orientation of a line pointing at a target. It consists of a telescope connected to a frame (base) by the means of a universal (U) joint, which allows its rotation around a vertical axis (pan rotation) and a horizontal axis (tilt rotation), and a set of graduated circles that make the two angles accurately measurable. The base is levelled before the angle measurement and provides the reference horizontal plane. The telescope is equipped with a crosshair that enables the operator to point at a particular target; the axis of the telescope is the line whose pan and tilt angles are measured. Land surveying, construction, and mapping are the applicative fields of theodolites, where they establish points, lay out boundaries, and determine the heights and positions of objects or other features on the Earth’s surface.

Theodolites evolved into total stations, which also feature a laser rangefinder and an onboard computer that calculates the position of the target point with respect to the instrument. The added tools allow the operator (usually a surveyor) to point at a target, record the measured angles and distance, and repeat the two previous operations for many target points without moving the instrument to create a detailed 3D map of the site. Successively, total stations evolved into robotic total stations (RTS) that include a number of additional tools (e.g., actuators for controlling their motion, camera, tracking software, etc.), enabling them to work autonomously by following a loaded measurement program or remote controller.

The added tools [2,3,4,5,6] make RTSs also able to track mobile targets on civil structures, thus making possible their use in structural monitoring [7,8,9,10,11,12,13,14]. Indeed, they have been employed either together with other instruments, as GPS [7,8], or alone to measure the natural frequencies of road bridges [9,10], railway bridges [11,12], and pedestrian bridges [13,14] excited by the transit of people or vehicles, that is, when the oscillation amplitude has the order of centimeters and the oscillation frequency is lower than 1 Hz. In civil structures, the frequency border of 1 Hz is sufficient for many applicative cases; nevertheless, extending this border up to 5 Hz, or better, to 10 Hz, would greatly extend this field of application.

Despite the fact that recently presented RTSs (see

Table 1. Selection and data sheets of commercial robotic total stations (RTS).

Image
Manufacturer	Leica	Sokkia	Trimble	Topcon	GeoMax	Carlson	Hilti	Stonex
Model	Leica Nova TS60	iX-1201	S9 HP	MS05AXII	Zoom95	STReAM360	POS 180	R180
Angular accuracy	0.5″ (0.15 mgon)	1″ (0.3 mgon)	0.5″ (0.15 mgon)	0.5″ (0.15 mgon)	1″ (0.3 mgon)	1″ (0.3 mgon)	3″	0.5″
Distance accuracy	0.6 mm + 1 ppm	1 mm + 2 ppm	0.8 mm + 1 ppm	0.8 mm + 1 ppm	1 mm + 1.5 ppm	1 mm + 1.5 ppm	--	1 mm + 1 ppm
Maximum panrotation speed	180°/s	150°/s	115°/s	85°/s	90°/s	--	90°/s	180°/s
Motorization	Piezo Drives	Direct Drives	MagDrive servo	DC motor drives	Hybrid Drives	Hybrid Drives	--	Tdrive
Weight	7.7 kg	5.8 kg	5.85 kg	6.8 kg	5.3 kg	5.3 kg	--	9.3 kg
Other data	Camera’s frame rate: Up to 20 fps	Max auto tracking speed: 20°/s	Tracking rate: 10 Hz	--	--	Tracking speed: 90 km/h at 100 m	--	--

) are equipped with 360° reflector prisms [15] and have doubled their recording rate [16], extending this frequency border over 3 Hz still is a goal to reach [17]. Since RTSs’ angle/distance measurements come after the telescope collimation toward the target point and the collimation is a mechanical operation, extending this frequency limitation is intimately related to increasing the dynamic performance of the mechanism that moves the telescope.

Increasing the dynamic performances of any mechanical system unavoidably passes through a reduction in the mobile masses. Table 1 shows that the total mass of commercial RTSs ranges roughly from 5 kg to 9.5 kg and that most of their mass is loaded on mobile parts, even though the telescope, which is the component to move, usually weighs less than 0.5 kg. In short, until now, the automation of total stations has been implemented by simply adding actuators in the two revolute (R) pairs of the U-joint, which connects the telescope to the base, without redesigning the mechanical system for reducing all the mobile masses.

Moving the electrically supplied parts (e.g., actuators, Wi-Fi antenna, and display, etc.) together with their batteries onto the base is the design strategy to implement for greatly reducing the mobile masses. The vast majority of these components (e.g., Wi-Fi antenna, onboard computer, and display) are moveable onto the base without changing the mechanism that moves the telescope; whereas, moving the actuators onto the base needs to change such a mechanism from a serial architecture to a parallel architecture1. Replacing a serial architecture with a parallel one also brings other advantages. Indeed, parallel architectures, in general, are stiffer and more precise than their serial counterpart. Parallel architectures that orientate a line with respect to their base are named parallel pointing systems (PPS).

This paper reviews the PPS architectures proposed in the literature and selects those that are more suitable for RTSs with reference to RTSs’ functional requirements. Successively, it addresses the dimensional synthesis and accuracy analysis of the selected architectures. The result of this study is that there are three PPS types that are more suitable for RTSs. The pros and cons of these three PPS architectures are also discussed.

The paper is organized as follows. Section 2 reviews the literature on PPSs, defines the functional requirements for a PPS to be used in an RTS, and selects the most suitable ones. Section 3 addresses the position analysis and dimensional synthesis of the PPSs selected in the previous section, using the RTS’s functional requirements identified in the same section. Finally, Section 4 discusses the results, also evaluating their accuracy, and Section 5 draws conclusions.

2. Selection of PPS Architectures for RTS

The literature on the type synthesis2 of parallel architectures is practically complete. Indeed, type synthesis methods based on graph theory [18,19,20,21,22,23], screw theory [24,25,26,27,28,29,30] group theory [31,32,33,34,35,36,37,38], and evolutionary morphology [39], among others, have been proposed together with a long list of parallel-architecture types that satisfy many motion requirements. In this literature, the most extended lists of PPS architectures are reported in [37], [38] (Chap. 12), [39] (Vol. 4). Over these lists, papers (e.g., [40,41]) and patents (e.g., [42]) on specific PPS architectures have been presented, too.

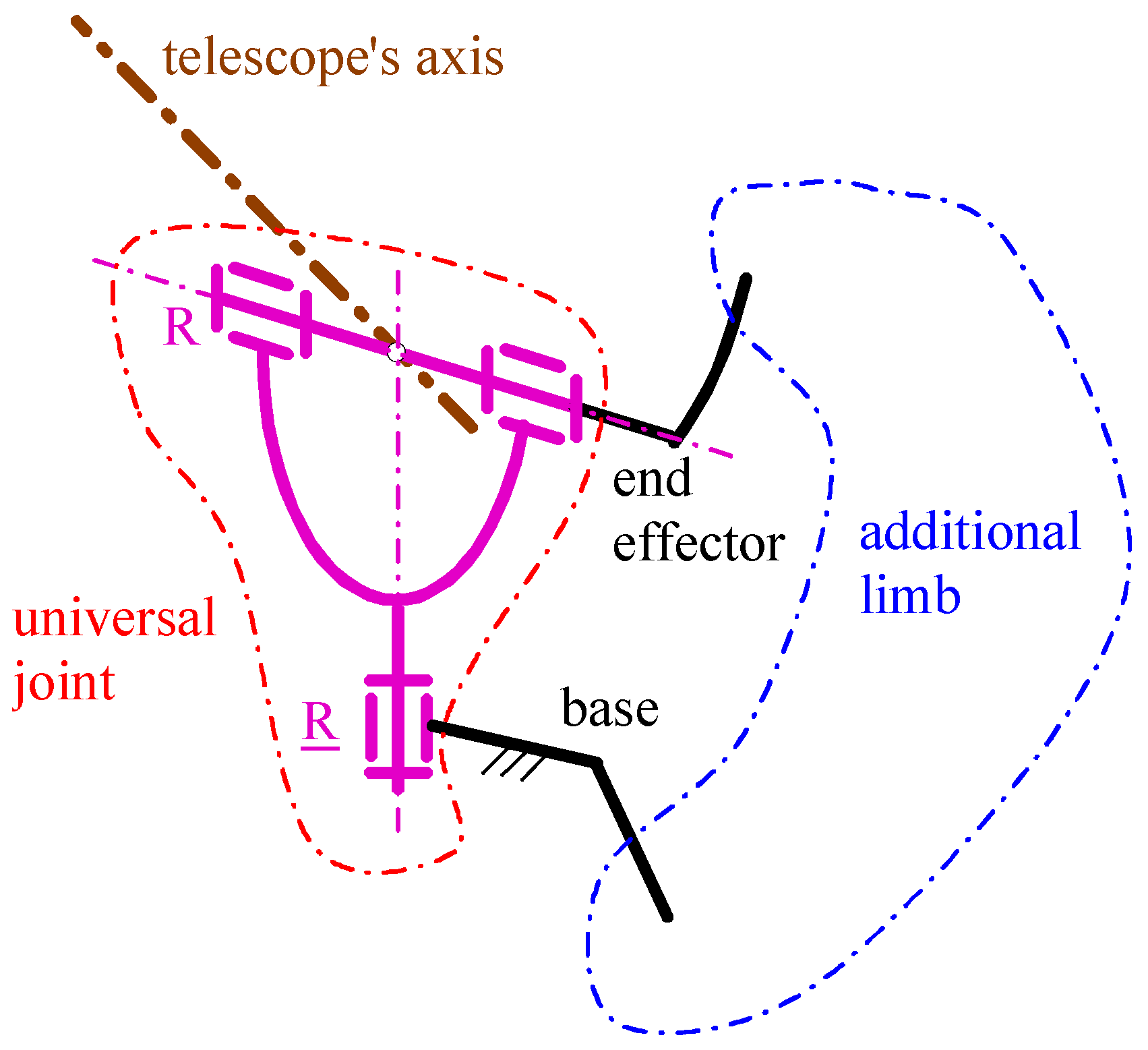
PPSs are two degrees-of-freedom (DOF) closed-chain mechanisms. All the PPS architectures proposed in the literature exhibit a U-joint that directly connects the end effector to the base. Such a U-joint is either fully passive (i.e., the two R pairs of the U-joint are both non-actuated) or partially active (i.e., one out of the two R pairs of the U-joint is actuated). It is fully passive in PPS architectures (e.g., [40,41]) that have two more limbs connecting the end effector to the base: these two additional limbs contain the two actuators (one per limb). These two-looped architectures pay their higher stiffness with a workspace reduction; they are suitable for applications (e.g., orientating satellite antennas or solar panels, etc.) where the end effector is heavy and the requested orientation workspace is limited.

Differently, the U joint is partially active in PPS architectures (e.g., [42]) that contain only one additional limb, which carries the second actuator. Since the telescope of an RTS is not a heavy object and it needs an ample orientation workspace, these single-looped architectures with a partially active U-joint must be chosen for RTSs. In particular, in the U joint, the R pair adjacent to the base, that is, the one with a vertical axis (see the images in Table 1), which makes the telescope perform the pan rotation, must be actuated. Moreover, in the additional limb, the first joint (i.e., the one adjacent to the base) must be actuated so that the remaining part of the limb can play only the role of a mechanical transmission that controls the motion of the non-actuated R pair of the U joint (i.e., the one that makes the telescope perform the tilt rotation). Figure 1 shows a generic PPS architecture that satisfies these requirements.

According to the Grübler–Kutzbach mobility criterion [43] and Euler’s formula [44], a two-DOF single-looped spatial mechanism, like the PPS architectures selected for RTSs, must satisfy the following condition to be non-overconstrained:

$$\begin{array}{l}2=6(m-1)-{\displaystyle \sum _{i=1,5}(6-i)c_i}\\ m={\displaystyle \sum _{i=1,5}{c}_i}\end{array}\}\Rightarrow {\displaystyle \sum _{i=1,5}i\hspace{0.17em}{c}_i}=8$$

(1)

where m is the number of links and c_i is the number of joints with i DOFs. Since the U joint yields a term equal to 2 in the summation on the left-hand side of Equation (1), the following relationships hold for the additional limb of a non-overconstrained PPS:

$$\{\begin{array}{l}{\displaystyle \sum _{i=1,5}i\hspace{0.17em}{c}_{i,limb}}=6\\ {\displaystyle \sum _{i=1,5}{c}_{i,limb}}={\displaystyle \sum _{i=1,5}{c}_i}-1\\ m_{limb}=m-2={\displaystyle \sum _{i=1,5}{c}_{i,limb}}-1\end{array}$$

(2)

where m_limb is the number of links of the additional limb and c_i,limb is the number of joints with i DOFs of the additional limb.

Choosing non-overconstrained PPS architectures is preferable since they do not require the imposition of tight tolerances on the unavoidable geometric errors that come out during manufacturing. Nevertheless, reducing the number of links and joints under the values provided by Equation (2) is also interesting when the introduced overconstraint is as “easy” to obtain as, for instance, it is for some planar or spherical kinematic chains. Moreover, PPS architectures that do not contain passive (i.e., non-actuated) prismatic (P) pairs must be preferred.

The above-defined requirements, together with the fact that the pan rotation must be a complete rotation in an RTS (i.e., the additional limb must not limit the pan rotation), lead one to select the PPS architectures shown in Figure 2, Figure 3 and Figure 4 with five, six, and seven links, respectively. Such architectures are deduced from the three main families of single-looped PPS architectures without passive P pairs reported in [37], [38] (Chap. 12), [39] (Vol. 4) by imposing that the additional limb must not limit the pan rotation and that its number of links and joints must be as small as possible.

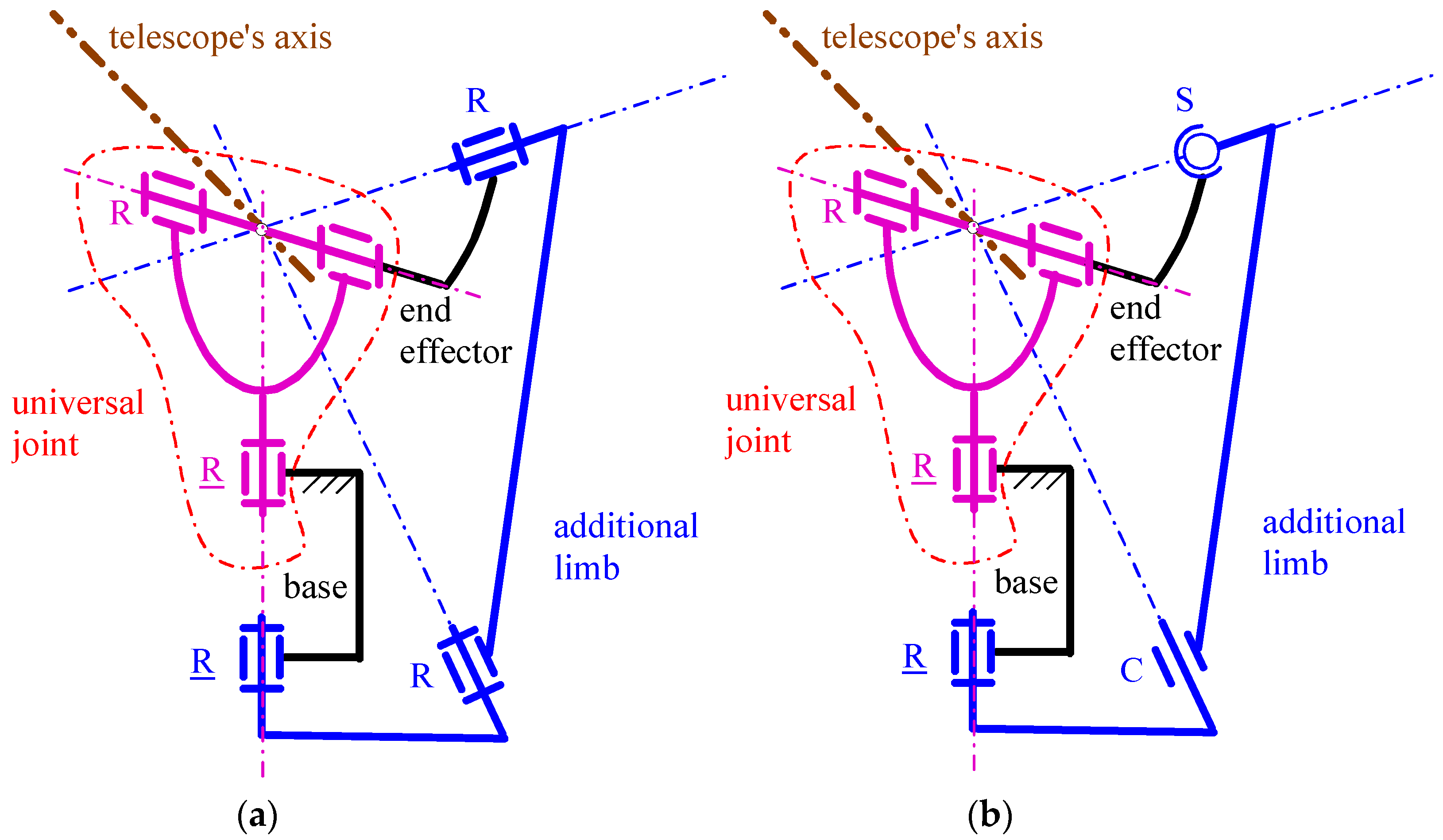
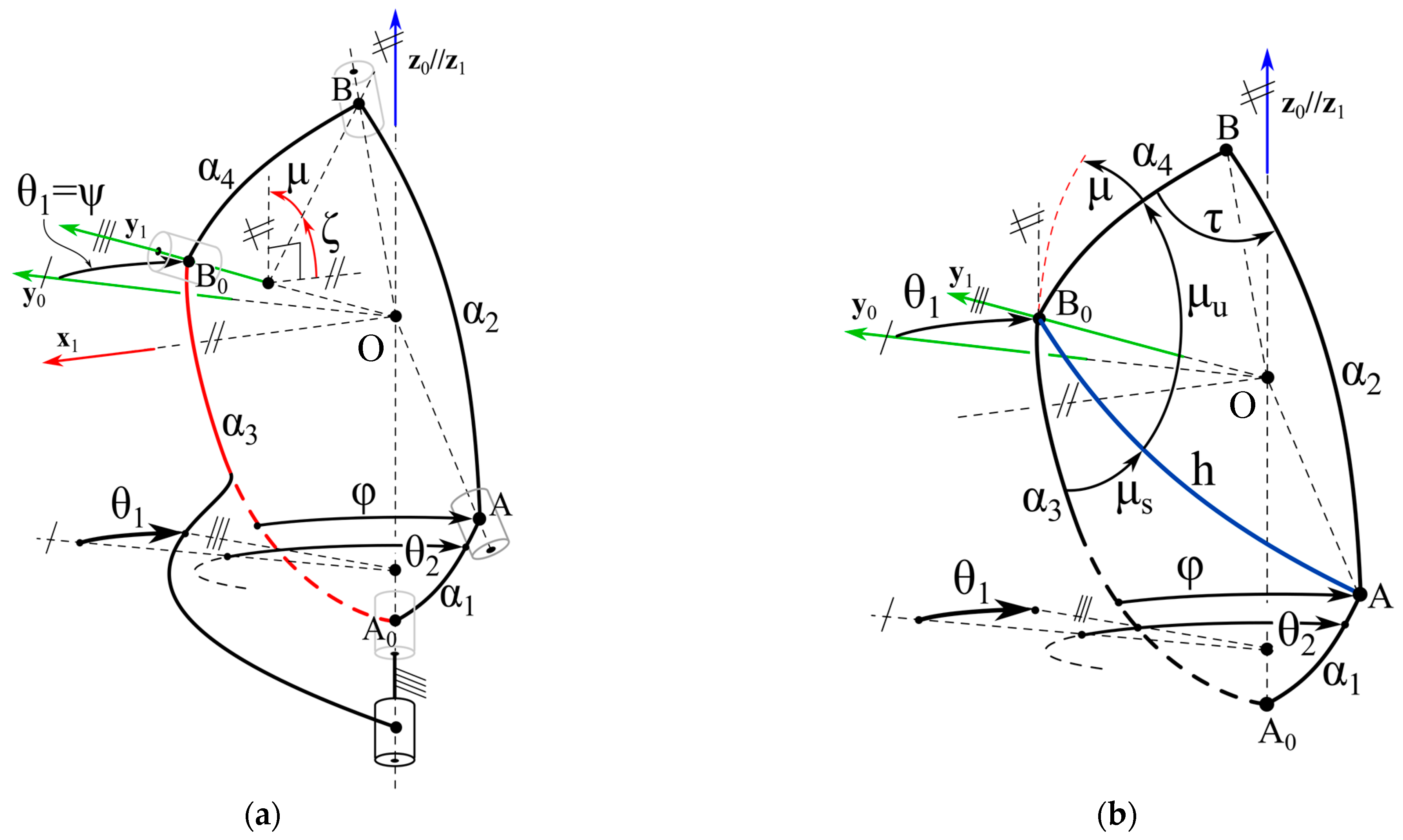
The PPS of Figure 2a, hereafter named the “spherical PPS”, is obtained from the general scheme of Figure 1 by choosing an additional limb of the RRR type (the underscore indicates an actuated joint). The peculiarities of this RRR limb are the following: (a.1) the axes of the three R pairs are so oriented that they all pass through the center of the partially active U joint (i.e., the purple RR limb in the figure), and (a.2) the axis of the actuated R-pair, adjacent to the base, coincides with the pan-rotation axis. The resulting single-looped architecture is a particular spherical five-bar linkage of the RR-RRR type that has the spherical motion center coincident with the U-joint center. Condition (a.2) is the one that allows the telescope to perform a complete pan rotation. This spherical five-bar linkage is overconstrained (i.e., it does not satisfy Equation (1)); nevertheless, its overconstraint can be easily removed by replacing, in the RRR limb, the intermediate R-pair with a cylindrical (C) pair and the R-pair adjacent to the end effector with a spherical (S) pair, as shown in Figure 2b. Doing so, the additional limb becomes of the RCS type.

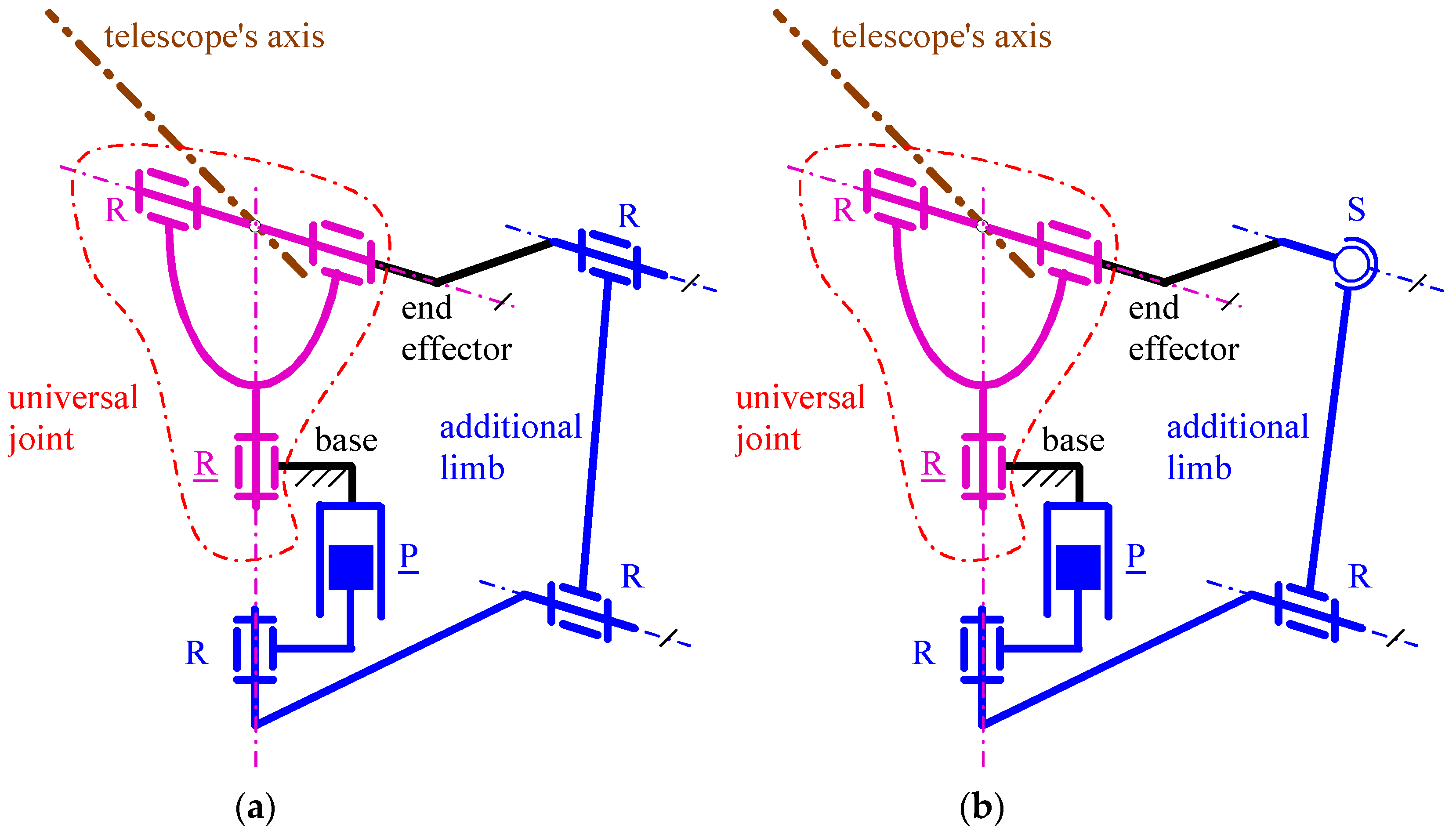
The PPS of Figure 3a, hereafter named the “1st decoupled PPS”, is obtained from the general scheme of Figure 1 by choosing an additional limb of the PRRR type. The peculiarities of this PRRR limb are the following: (b.1) the axis of the first R-pair, adjacent to the actuated P pair, coincides with the pan-rotation axis, (b.2) the sliding direction of the actuated P pair is parallel to the pan-rotation axis, and (b.3) the axes of the second and the third R pairs are both parallel to the tilt-rotation axis. The resulting single-looped architecture is a particular six-bar linkage of the RR-PRRR type that, when the actuated P pair (the actuated R pair) is locked, keeps the tilt (the pan) angle fixed (i.e., the pan and tilt rotations are independently moveable). This six-bar linkage is overconstrained (i.e., it does not satisfy Equation (1)); nevertheless, its overconstraint can be easily removed by replacing, in the PRRR limb, the R-pair adjacent to the end effector with an S pair, as shown in Figure 3b. Doing so, the additional limb becomes of the PRRS type.

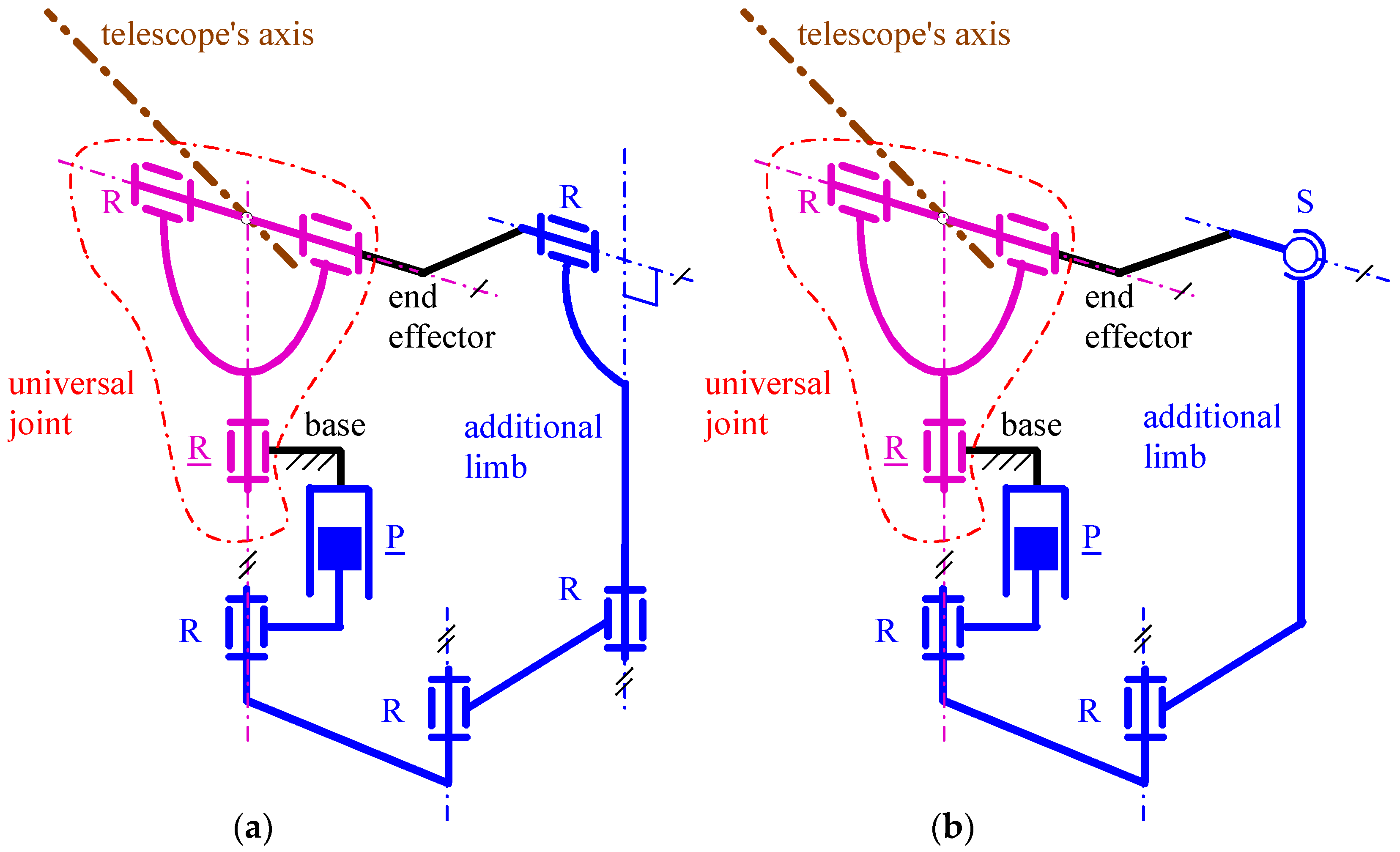
The PPS of Figure 4a, hereafter named the “2nd decoupled PPS”, is obtained from the general scheme of Figure 1 by choosing an additional limb of PRRRR type. The peculiarities of this PRRRR limb are the following: (c.1) the axis of the first R-pair, adjacent to the actuated P pair, coincides with the pan-rotation axis, (c.2) the sliding direction of the P pair and the axes of the second and third R pairs are all parallel to the pan-rotation axis, and (c.3) the axis of the fourth R pair, adjacent to the end effector, is parallel to the tilt-rotation axis. The resulting single-looped architecture is a particular seven-bar linkage of the RR-PRRRR type that, when the actuated P pair (the actuated R pair) is locked, keeps the tilt (the pan) angle fixed (i.e., the pan and tilt rotations are independently moveable). This seven-bar linkage is overconstrained (i.e., it does not satisfy Equation (1)); nevertheless, its overconstraint can be easily removed by replacing, in the PRRRR limb, the last two R-pairs with an S pair, as shown in Figure 4b. Doing so, the additional limb becomes of the PRRS type and the resulting linkage has only six links.

After having selected the PPS architectures suitable for RTSs, the dimensional synthesis of these architectures must be completed by imposing that:

(i) the tilt angle can cover a variation range (at least 90 degrees) suitable to make the telescope axis assume any direction inside the upper hemisphere;

(ii) the additional limb guarantees a sufficiently good transmission angle at any PPS configuration.

The next section, firstly, will deduce the kinematic relationships necessary to control the motion of the selected PPS architectures; then, it will exploit the deduced relationships to complete the dimensional synthesis of the selected PPS architectures by imposing the above-defined additional design requirements.

3. Kinematic Analysis and Dimensional Synthesis

In order to evaluate and compare the selected PPS architectures, the analytic relationships necessary to solve their kinematic analysis problems, which are involved in their motion control, must be deduced. Moreover, their dimensional synthesis must be completed for the determination of the geometric constants’ values that make the PPS satisfy the above-defined design requirements (i) and (ii).

In the following part of this section, these analytic/numeric computations are implemented for each of the three PPS architectures identified in the previous section. In doing so, a variation range of 120° is chosen for the tilt angle when imposing design requirements (i) and (ii). Hereafter, ψ, ζ, and θ₁ denote, respectively, the pan angle, the tilt angle, and the actuated-joint variable of the partially active U joint that directly connects the end effector to the base, which is the rotation angle of the R pair adjacent to the base (see Figure 1). Moreover, without losing generality, no phase difference is assumed between ψ and θ₁, that is, for all the selected PPSs (see Figure 1), the following relationship holds:

$$\mathsf{\psi }={\mathsf{\theta }}_1$$

(3)

Eventually, the kinematic analyses of the overconstrained mechanisms (i.e., Figure 2a, Figure 3a and Figure 4a) and their non-overconstrained counterparts (i.e., Figure 2b, Figure 3b and Figure 4b) coincide with one another if no geometric error occurs. As a consequence, since the evaluation of geometric error effects is out of the scope of this work, the kinematic analyses that follow will refer to the nominal geometry and, for the sake of simplicity, all the notations will be defined by using the overconstrained or non-overconstrained architectures according to convenience.

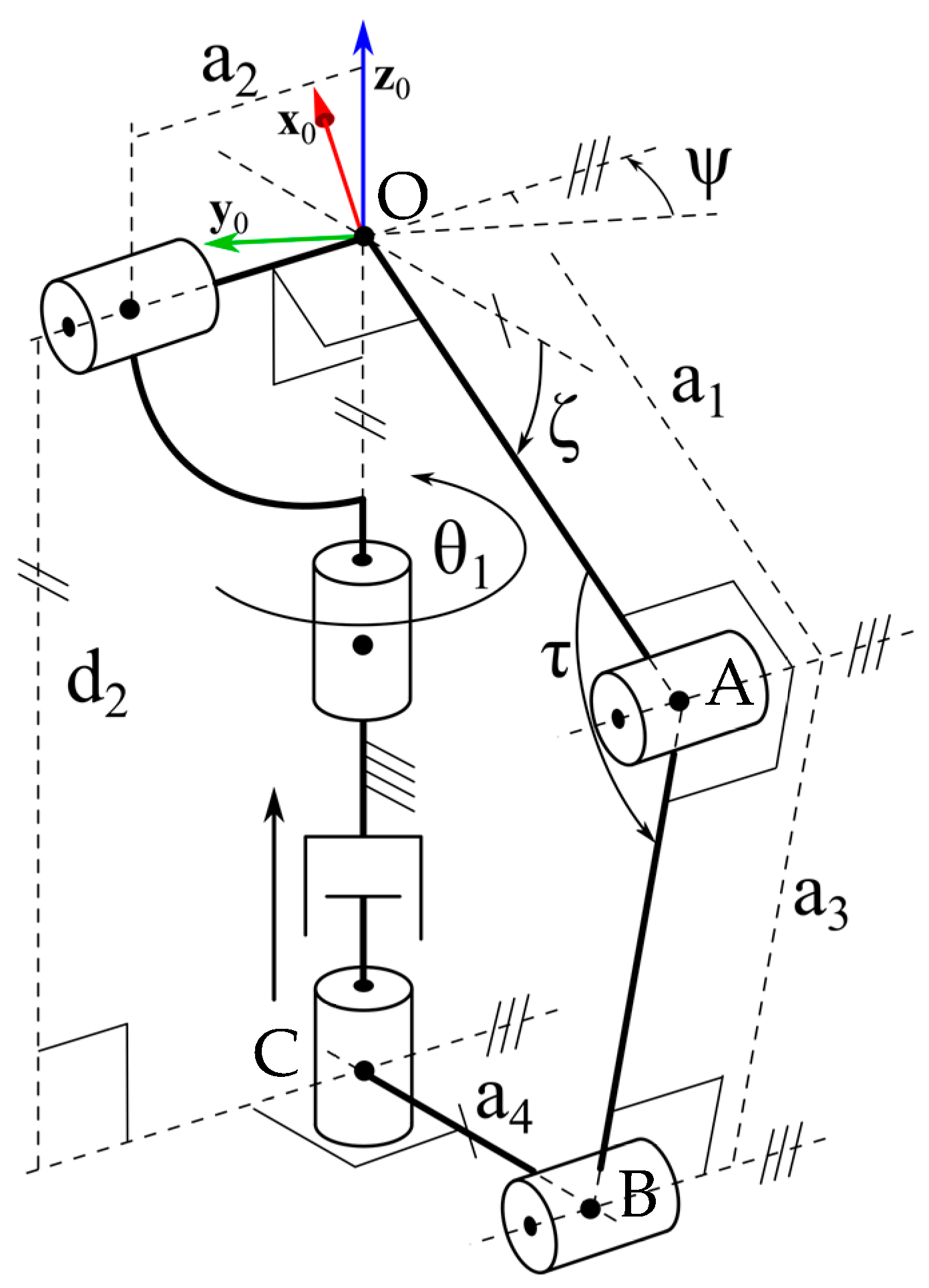
3.1. Spherical PPS

Figure 5a illustrates the adopted notations for the kinematic analysis and dimensional synthesis of the PPSs shown in Figure 2a. With reference to Figure 5a, Ox₀y₀z₀ (Ox₁y₁z₁) is a Cartesian reference system fixed to the base (to the cross link of the U joint (see Figure 2a) with the origin, O, coincident with the center of the U joint, the z₀-coordinate axis (z₁-coordinate axis) coincident with the pan rotation axis, and the y₀-coordinate axis as a phase reference for measuring the pan rotation (the y₁-coordinate axis is coincident with the tilt rotation axis). The x₀y₀-coordinate plane, coincident with the x₁y₁-coordinate plane, is the horizontal plane of the theodolite, which is also the phase reference for measuring the tilt angle, ζ, whereas the two mutually orthogonal axes of the two R pairs constituting the U joint lie on the y₁z₁-coordinate plane. Angle α_i, for i = 0, …,4, is the constant angle between the axes of the R pairs at the endings of link i. In particular, links 0 and 3 are the base and the cross link of the U joint, respectively; as a consequence, α₀ and α₃ are equal to 0° and 90°, respectively, whereas α₁, α₂, and α₄ must be sized by imposing design requirements (i) and (ii). Eventually, angle θ₂ is the joint variable of the first R pair, adjacent to the base, of the additional limb of the RRR type, and angle φ is equal to (θ₂ − θ₁).

When the pan rotation, ψ (=θ₁ (Equation (3))), is locked, the spherical five-bar linkage becomes the spherical four-bar linkage shown in Figure 5b, which has link 1 as an input link with φ (=(θ₂ − θ₁)) as the input variable and link 4 as the output link with the tilt angle, ζ, as the output variable. Such a spherical four-bar linkage is the same for any value of ψ. As a consequence, the kinematic model of this spherical four-bar linkage, together with Equation (3), provides the kinematic model of this spherical PPS.

With reference to Figure 5b, τ is the transmission angle [45] of this spherical four-bar linkage and h is the convex angle between segments OB₀ and OA. Moreover, the following relationships hold:

$$\zeta +\mathsf{\mu }=\frac{\mathsf{\pi }}{2};{\mathsf{\mu }}_s+{\mathsf{\mu }}_u+\mathsf{\mu }=\mathsf{\pi };{\mathsf{\mu }}_s+{\mathsf{\mu }}_u=\frac{\mathsf{\pi }}{2}+\zeta .$$

(4)

The cosine law for spherical triangles [45], when applied to the spherical triangles ΔA₀B₀A and ΔAB₀B of Figure 5b, which share side h, yields:

$$\cos {\mathsf{\alpha }}_2=\cos \hspace{0.17em}h\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}h\sin {\mathsf{\alpha }}_4\cos {\mathsf{\mu }}_u$$

(5a)

$$\cos \hspace{0.17em}h=\cos {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_3+\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_3\cos \mathsf{\phi }$$

(5b)

$$\cos {\mathsf{\alpha }}_1=\cos h\cos {\mathsf{\alpha }}_3+\sin h\sin {\mathsf{\alpha }}_3\cos {\mathsf{\mu }}_s$$

(5c)

whereas the application of the sine law for spherical triangles [45] to the spherical triangle ΔA₀B₀A gives:

$$\frac{\sin h}{\sin \mathsf{\phi }}=\frac{\sin {\mathsf{\alpha }}_1}{\sin {\mathsf{\mu }}_s}\Rightarrow \sin h\sin {\mathsf{\mu }}_s=\sin {\mathsf{\alpha }}_1\sin \mathsf{\phi }$$

(6)

By taking into account the value of α₃ (=π/2), the introduction of Equation (5b) into Equation (5a) transforms it as follows:

$$\cos {\mathsf{\alpha }}_2=\sin {\alpha }_1\cos \mathsf{\phi }\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}h\sin {\mathsf{\alpha }}_4\cos {\mathsf{\mu }}_u$$

(7)

which, after having introduced the expressions of μ_u coming from Equation (4) and cosμ_s and sinμ_s coming from Equations (5c) and (6), respectively, yields

$$\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\sin \mathsf{\phi }\hspace{0.17em}\cos \zeta -\cos {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\sin \zeta +\sin {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_4\cos \mathsf{\phi }-\cos {\mathsf{\alpha }}_2=0$$

(8)

Equation (8) is the closure equation of the spherical four-bar linkage of Figure 5b. Over ζ (i.e., the output variable) and φ (=(θ₂ − θ₁), i.e., the input variable), it contains only the geometric constants of the linkage (i.e., α₁, α₂, and α₄). If the geometric constants are known (as happens when a control algorithm must be implemented), it can be used to compute ζ as a function of φ (direct position analysis (DPA)), or, vice versa, φ as a function of ζ (inverse position analysis (IPA)). Differently, if the function ζ = ζ(φ) is fully or partly known (i.e., design requirements are assigned), it can be used to compute the linkage’s geometric constants α₁, α₂, and α₄ (dimensional synthesis).

3.1.1. Position Analysis of the Spherical PPS

The computation of ζ for the assigned values of the geometric constants and φ (i.e., the solution of the DPA) is implementable by rewriting Equation (8) as follows:

$$m_1\sin \zeta +m_2\hspace{0.17em}\cos \zeta +m_3=0$$

(9)

where:

$$\{\begin{array}{l}{m}_1=-\cos {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\\ m_2=\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\sin \mathsf{\phi }\\ m_3=\sin {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_4\cos \mathsf{\phi }-\cos {\mathsf{\alpha }}_2\end{array}$$

(10)

and then, by solving the quadratic equation obtained from Equation (9) through the half-tangent substitution (i.e., the change of variable sinx = 2t/(1 + t²) and cosx = (1 − t²)/(1 + t²) where t = tan(x/2)). Doing so, the following closed-form solution is obtained:

$${\zeta }_i=2\hspace{0.17em}\mathrm{atan}2\left(-m_1+{(-1)}^i\sqrt{m_1{}^2+m_2{}^2-m_3{}^2},\hspace{1em}{m}_3-m_2\right)\hspace{1em}\hspace{1em}i=0,1$$

(11)

Analogously, the computation of φ for the assigned values of the geometric constants and ζ (i.e., the solution of the IPA) is implementable by rewriting Equation (8) as follows:

$$n_1\sin \mathsf{\phi }+n_2\hspace{0.17em}\cos \mathsf{\phi }+n_3=0$$

(12)

where:

$$\{\begin{array}{l}{n}_1=\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\hspace{0.17em}\cos \zeta \\ n_2=\sin {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_4\\ n_3=-\cos {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_4\sin \zeta -\cos {\mathsf{\alpha }}_2\end{array}$$

(13)

and then, by solving the quadratic equation obtained from Equation (12) through the half-tangent substitution. Doing so, the following closed-form solution is obtained:

$${\mathsf{\phi }}_i=2\hspace{0.17em}\mathrm{atan}2\left(-n_1+{(-1)}^i\sqrt{n_1{}^2+n_2{}^2-n_3{}^2},\hspace{1em}{n}_3-n_2\right)\Rightarrow {\theta }_{2,i}={\mathsf{\phi }}_i+\mathsf{\psi }\hspace{1em}\hspace{1em}i=0,1$$

(14)

3.1.2. Dimensional Synthesis of the Spherical PPS

Here, design requirement (i) with Δζ = ζ_max − ζ_min = 120° must be imposed by taking into account that a crank-rocker four-bar has to be preferred and that design requirement (ii) must be satisfied, too. In order to have a crank-rocker four-bar, the Grashof rule [45] must be satisfied, that is, the following additional conditions must be imposed:

$$\{\begin{array}{l}{\mathsf{\alpha }}_1={\mathsf{\alpha }}_{\min }=\min ({\mathsf{\alpha }}_1,{\mathsf{\alpha }}_2,{\mathsf{\alpha }}_3,{\mathsf{\alpha }}_4)\\ {\mathsf{\alpha }}_{\min }+{\mathsf{\alpha }}_{\max }\le \frac{1}{2}{\displaystyle \sum _{i=1,4}{\mathsf{\alpha }}_i}\end{array}$$

(15)

where α_max = max(α₁, α₂, α₃, α₄).

The two extreme positions of link 4 (i.e., the rocker) correspond to the minimum, ζ_min, and the maximum, ζ_max, values of ζ and occur [45] when links 1 and 2 are flattened, that is, when the three segments OA₀, OA, and OB lie on the same plane. The application of the cosine law to the spherical triangle ΔBA₀B₀ at the occurrence of such a condition leads one to write the two equations:

$$\cos ({\mathsf{\alpha }}_1+{\mathsf{\alpha }}_2)=\cos \hspace{0.17em}{\mathsf{\alpha }}_3\cos {\mathsf{\alpha }}_4-\sin \hspace{0.17em}{\mathsf{\alpha }}_3\sin {\mathsf{\alpha }}_4\sin ({\mathsf{\zeta }}_{\min }+\frac{2}{3}\mathsf{\pi })\stackrel{\begin{array}{c}{\mathsf{\alpha }}_3=\frac{\mathsf{\pi }}{2}\\ \downarrow \end{array}}{=}-\sin {\mathsf{\alpha }}_4\sin ({\mathsf{\zeta }}_{\min }+\frac{2}{3}\mathsf{\pi })$$

(16a)

$$\cos ({\mathsf{\alpha }}_2-{\mathsf{\alpha }}_1)=\cos \hspace{0.17em}{\mathsf{\alpha }}_3\cos {\mathsf{\alpha }}_4-\sin \hspace{0.17em}{\mathsf{\alpha }}_3\sin {\mathsf{\alpha }}_4\sin {\mathsf{\zeta }}_{\min }\stackrel{\begin{array}{c}{\mathsf{\alpha }}_3=\frac{\mathsf{\pi }}{2}\\ \downarrow \end{array}}{=}-\sin {\mathsf{\alpha }}_4\sin {\mathsf{\zeta }}_{\min }$$

(16b)

which, by expanding the left-hand sides, can be transformed as follows:

$$\begin{array}{l}[\begin{array}{l}\cos {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_2-\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_2=\hspace{0.17em}\\ =-\sin {\mathsf{\alpha }}_4\sin ({\mathsf{\zeta }}_{\min }+\frac{2}{3}\mathsf{\pi })\end{array}\\ [\begin{array}{l}\cos {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_2+\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_2=\\ =-\sin {\mathsf{\alpha }}_4\sin {\mathsf{\zeta }}_{\min }\end{array}\end{array}\}\Rightarrow \{\begin{array}{l}\sin {\mathsf{\zeta }}_{\min }=-\frac{\cos {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_2+\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_2}{\sin {\mathsf{\alpha }}_4}\\ \cos {\mathsf{\zeta }}_{\min }=\frac{\cos {\mathsf{\alpha }}_1\cos {\mathsf{\alpha }}_2\left[\cos \left(\frac{2}{3}\mathsf{\pi }\right)-1\right]+\sin {\mathsf{\alpha }}_1\sin {\mathsf{\alpha }}_2\left[1+\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]}{\sin \left(\frac{2}{3}\mathsf{\pi }\right)\sin {\mathsf{\alpha }}_4}\end{array}$$

(17)

where the trigonometric identity $\sin ({\mathsf{\zeta }}_{\min }+\frac{2}{3}\mathsf{\pi })=\sin {\mathsf{\zeta }}_{\min }\cos \left(\frac{2}{3}\mathsf{\pi }\right)+\cos {\mathsf{\zeta }}_{\min }\sin \left(\frac{2}{3}\mathsf{\pi }\right)$ has also been introduced. Eventually, the introduction of Equation (17) into the trigonometric identity sin²ζ_min + cos²ζ_min = 1 yields:

$$2{\cos }^2{\mathsf{\alpha }}_1{\cos }^2{\mathsf{\alpha }}_2\left[1-\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]+2{\sin }^2{\mathsf{\alpha }}_1{\sin }^2{\mathsf{\alpha }}_2\left[1+\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]={\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right){\sin }^2{\mathsf{\alpha }}_4$$

(18)

The transmission angle, τ, reaches its minimum, τ_min, and maximum, τ_max, values when links 1 and 3 are flattened [45], that is, when the three segments OA₀, OA, and OB₀ lie on the same plane. The application of the cosine law to the spherical triangle ΔAB₀B at the occurrence of such a condition leads one to write the two equations:

$$\cos ({\mathsf{\alpha }}_3+{\mathsf{\alpha }}_1)=\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\max }$$

(19a)

$$\cos ({\mathsf{\alpha }}_3-{\mathsf{\alpha }}_1)=\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min }$$

(19b)

which, since ${\mathsf{\alpha }}_3=\frac{\mathsf{\pi }}{2}$, become:

$$-\sin {\mathsf{\alpha }}_1=\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\max }$$

(20a)

$$\sin {\mathsf{\alpha }}_1=\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min }$$

(20b)

If the values of τ_min and τ_max are assigned so that design requirement (ii) is satisfied, Equations (18) and (20) become a system of three trigonometric equations in three unknowns (i.e., α₁, α₂, and α₄), whose solution provides the sought-after sizes that satisfy both the design requirements. If the found solution also satisfies condition (15), it can be accepted; otherwise, the system must be solved again with new assigned values of τ_min and τ_max until all the conditions are satisfied.

The replacement of Equation (20a) with the sum of Equation (20a,b) and the introduction of Equation (20b) into Equation (18) after replacing cos²α₁ with the trigonometric identity cos²α₁ = 1 − sin²α₁ transform the system to solve as follows:

$$[\begin{array}{l}2{(\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min })}^2\left[{\sin }^2{\mathsf{\alpha }}_2-{\cos }^2{\mathsf{\alpha }}_2+\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]+\\ +2{\cos }^2{\mathsf{\alpha }}_2\left[1-\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]={\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right){\sin }^2{\mathsf{\alpha }}_4\end{array}$$

(21a)

$$\begin{array}{l}2\cos \hspace{0.17em}{\mathsf{\alpha }}_2\cos {\mathsf{\alpha }}_4+q\sin \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4=0\\ with\\ q=(\cos {\mathsf{\tau }}_{\max }+\cos {\mathsf{\tau }}_{\min })\end{array}\}\stackrel{\begin{array}{l}if\hspace{0.17em}{\mathsf{\alpha }}_2\ne \frac{\mathsf{\pi }}{2}\\ \hspace{1em}\hspace{1em}\downarrow \end{array}}{\hspace{0.17em}\hspace{0.17em}\Rightarrow }\tan \hspace{0.17em}{\mathsf{\alpha }}_2=-\frac{2\cos {\mathsf{\alpha }}_4}{q\sin {\mathsf{\alpha }}_4}$$

(21b)

$$\sin {\mathsf{\alpha }}_1=\cos \hspace{0.17em}{\mathsf{\alpha }}_2(\cos {\mathsf{\alpha }}_4+\tan \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min })=\pm \frac{\cos {\mathsf{\alpha }}_4+\tan \hspace{0.17em}{\mathsf{\alpha }}_2\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min }}{\sqrt{1+{\tan }^2\hspace{0.17em}{\mathsf{\alpha }}_2}}$$

(21c)

where Equation (21c) is Equation (20b) transformed by taking into account the trigonometric identity $\cos x=\pm 1/\sqrt{1+{\tan }^{2}x}$. It is worth stressing that the value α₂ = π/2, excluded in the deduction of Equation (21b), leads the determination of acceptable values of α₄ (i.e., α₄ ∈ [0, π]) only if simultaneously q = $(\cos {\mathsf{\tau }}_{\max }+\cos {\mathsf{\tau }}_{\min })=0$. In this case, such a condition makes Equation (21b) identically satisfied and transforms Equation (20b) as follows $\sin {\mathsf{\alpha }}_1=\sin {\mathsf{\alpha }}_4\cos {\mathsf{\tau }}_{\min }$, whose substitution into Equation (18) yields the following condition on τ_min: $2{\cos }^2{\mathsf{\tau }}_{\min }\left[1+\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]={\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right)$, that is, cosτ_min = −cosτ_max = $\sqrt{3}/2$. Such formulas make one determine τ_min = 30°, τ_max = 150°, and, as possible values for α₁ and α₄ that also satisfy condition (15), α₁ = 46.7805° = 0.81647 rad and α₄ = 57.29578° = 1 rad. Eventually, the introduction of α₂ = π/2 into Equation (17) yields $\sin {\zeta }_{\min }=-\sin {\mathsf{\alpha }}_1/\sin {\mathsf{\alpha }}_4\equiv -\cos {\mathsf{\tau }}_{\min }$, which provides ζ_min = −60° and ζ_max = ζ_min + 120° = 60° for τ_min = 30°.

The introduction of Equation (21b) into Equation (21a,c), where cosα₂ and sinα₂ have been replaced through the trigonometric identities $\cos x=\pm 1/\sqrt{1+{\tan }^{2}x}$ and $\sin x=\pm \tan x/\sqrt{1+{\tan }^{2}x}$, transforms system (21) into the final form:

$$\tan \hspace{0.17em}{\mathsf{\alpha }}_2=-\frac{2\cos {\mathsf{\alpha }}_4}{q\sin {\mathsf{\alpha }}_4}$$

(22a)

$$\sin {\mathsf{\alpha }}_1=\pm \frac{r\left|\sin {\mathsf{\alpha }}_4\right|\cos {\mathsf{\alpha }}_4}{\sqrt{q^2{\sin }^2{\mathsf{\alpha }}_4+4{\cos }^2{\mathsf{\alpha }}_4}}$$

(22b)

$$\frac{2q^2}{q^2{\sin }^2{\mathsf{\alpha }}_4+4{\cos }^2{\mathsf{\alpha }}_4}\left\{\left[1-\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]+{\cos }^2{\mathsf{\alpha }}_4{\left(\frac{r}{q}\right)}^2\left[1+\cos \left(\frac{2}{3}\mathsf{\pi }\right)-\frac{2q^2{\sin }^2{\mathsf{\alpha }}_4}{q^2{\sin }^2{\mathsf{\alpha }}_4+4{\cos }^2{\mathsf{\alpha }}_4}\right]\right\}={\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right)$$

(22c)

with $r=(\cos {\mathsf{\tau }}_{\max }-\cos {\mathsf{\tau }}_{\min })$.

The introduction of the trigonometric identity sin²α₄ = 1 − cos²α₄ into Equation (22c), together with the variable change p = cos²α₄, transforms it into the following quadratic equation:

$$g_2{p}^2+2g_{1}p+g_0=0$$

(23)

with:

$$\{\begin{array}{l}{g}_0=q^4\left\{2\left[1-\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]-{\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right)\right\}\\ g_1=q^2\left\{[4-q^2]\left[1-\cos \left(\frac{2}{3}\mathsf{\pi }\right)-{\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right)\right]+r^2\left[\cos \left(\frac{2}{3}\mathsf{\pi }\right)-1\right]\right\}\\ g_2=2r^2\left\{4\left[1+\cos \left(\frac{2}{3}\mathsf{\pi }\right)\right]-\left[\cos \left(\frac{2}{3}\mathsf{\pi }\right)-1\right]q^2\right\}-{\sin }^2\left(\frac{2}{3}\mathsf{\pi }\right){[4-q^2]}^2\end{array}$$

(24)

whose solutions are:

$$p_i=\frac{-g_1+{(-1)}^i\sqrt{g_1{}^2-g_0{g}_2}}{g_2}\Rightarrow {(\cos {\mathsf{\alpha }}_4)}_{ij}={(-1)}^j\sqrt{p_i}\hspace{1em}\hspace{1em}i,j=0,1$$

(25)

The values of α₄ obtained from Equation (25) as a function of τ_min and τ_max, when back substituted into Equation (22a,b), provide the corresponding values of α₁ and α₂. Eventually, the back substitution of the so-obtained triplets (α₁, α₂, α₄) into Equation (17) yields the corresponding values of ζ_min. Equation (25) yields, at most, four real values for cosα₄ and as many values of α₄ in the range of [0, π] rad. Successively, Equation (22a) (Equation (22b)) associates one value of tanα₂ (two values of sinα₁), which corresponds to two values of α₂ (of α₁) in the range of [0, π] rad, to each computed value of α₄. In conclusion, system (22) can have up to eight values of (α₁, α₂, α₄), with α₁, α₂, and α₄ belonging to the range of ]0, π[ rad that solve it and are selectable as possible sides of the studied spherical four bar.

This procedure has been implemented by using many values of τ_min and τ_max, but it has not led to the identification of values of α₁, α₂, α₄, and ζ_min that correspond to the values of τ_min and τ_max better than the ones found above for the case α₂ = 90° = π/2 rad (i.e., τ_min = 30°, τ_max = 150°). As a consequence, those values (i.e., τ_min = 30°, τ_max = 150°, α₂ = 90° = π/2 rad, α₁ = 46.7805° = 0.81647 rad, α₄ = 57.29578° = 1 rad, and ζ_min = −ζ_max = −60° = −1.0472 rad) are adopted as the optimal solution of the dimensional synthesis.

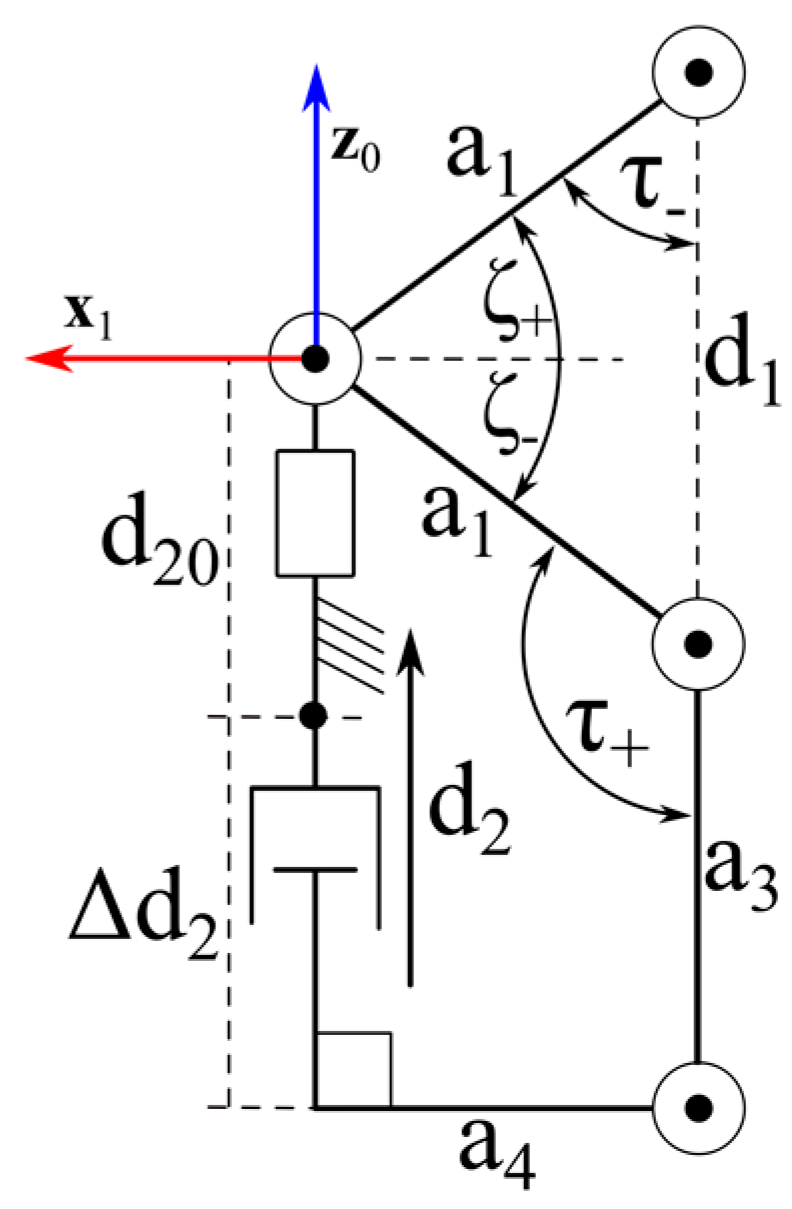
3.2. First Decoupled PPS

Figure 6 illustrates the adopted notations for the kinematic analysis and dimensional synthesis of the PPS shown in Figure 3a. With reference to Figure 6, d₂ is the actuated-joint variable of the P pair; τ is the transmission angle; and a₁, a₃, and a₄ are the distances between the two ending R-pair axes of links 1, 3, and 4, respectively, and they are the geometric constants of this PPS.

When the pan rotation is locked, the additional limb becomes a single-DOF planar linkage of type PRRR, whose motion plane is the plane perpendicular to the tilt-rotation axis that passes through the pan-rotation axis. In this plane, the adopted notations make it possible to write the following two relationships:

$${\mathrm{d}}_2={\mathrm{a}}_3\sin (\mathsf{\tau }+\zeta )-{\mathrm{a}}_1\sin \zeta$$

(26a)

$${\mathrm{a}}_1\cos \zeta ={\mathrm{a}}_4+{\mathrm{a}}_3\cos (\mathsf{\tau }+\zeta )$$

(26b)

Equation (26a,b) immediately allow for the determination of the explicit expressions of $\sin (\mathsf{\tau }+\zeta )$ and $\cos (\mathsf{\tau }+\zeta )$, respectively, whose introduction into the trigonometric identity ${\cos }^2(\mathsf{\tau }+\zeta )+{\sin }^2(\mathsf{\tau }+\zeta )=1$ yields the closure equation:

$${\mathrm{a}}_3{}^2={({\mathrm{d}}_2+{\mathrm{a}}_1\sin \zeta )}^2+{({\mathrm{a}}_1\cos \zeta -{\mathrm{a}}_4)}^2\hspace{0.17em}\Rightarrow \hspace{0.17em}{\mathrm{a}}_3{}^2={\mathrm{d}}_2{}^2+{\mathrm{a}}_4{}^2+{\mathrm{a}}_1{}^2+2{\mathrm{a}}_1{(\mathrm{d}}_2\sin \zeta -{\mathrm{a}}_4\cos \zeta )$$

(27)

3.2.1. Position Analysis of the 1st Decoupled PPS

The computation of ζ for assigned values of the geometric constants and d₂ (i.e., the solution of the DPA) is implementable by rewriting Equation (27) as follows:

$$k_1\sin \zeta +k_2\hspace{0.17em}\cos \zeta +k_3=0$$

(28)

where:

$$\{\begin{array}{l}{k}_1=2{\mathrm{a}}_1{\mathrm{d}}_2\\ k_2=-2{\mathrm{a}}_1{\mathrm{a}}_4\\ k_3={\mathrm{d}}_2{}^2+{\mathrm{a}}_4{}^2+{\mathrm{a}}_1{}^2-{\mathrm{a}}_3{}^2\end{array}$$

(29)

and then, by solving the quadratic equation obtained from Equation (28) through the half-tangent substitution. Doing so, the following closed-form solution is obtained:

$${\zeta }_i=2\hspace{0.17em}\mathrm{atan}2\left(-k_1+{(-1)}^i\sqrt{k_1{}^2+k_2{}^2-k_3{}^2},\hspace{1em}{k}_3-k_2\right)\hspace{1em}\hspace{1em}i=0,1$$

(30)

Differently, the computation of d₂ for assigned values of the geometric constants and ζ (i.e., the solution of the IPA) is implementable by simply noting that Equation (27) is a quadratic equation in d₂, whose solution is:

$${\mathrm{d}}_{2,i}=-{\mathrm{a}}_1\sin \zeta +{(-1)}^i\sqrt{{\mathrm{a}}_1{}^2{\sin }^2\zeta -{\mathrm{a}}_4{}^2-{\mathrm{a}}_1{}^2+{\mathrm{a}}_3{}^2+2{\mathrm{a}}_1{\mathrm{a}}_4\cos \zeta }\hspace{1em}\hspace{1em}i=0,1$$

(31)

3.2.2. Dimensional Synthesis of the 1st Decoupled PPS

With reference to Figure 6, the transmission angle is computable as a function of the actuated-joint variable, d₂, as follows:

$$\begin{array}{l}[\begin{array}{l}{\Vert B-O\Vert }^2=[(B-A)+(A-O)]\times [(B-A)+(A-O)]=\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}={\Vert B-A\Vert }^2+{\Vert A-O\Vert }^2+2(B-A)\times (A-O)\end{array}\\ \\ {\Vert B-O\Vert }^2={\mathrm{d}}_2{}^2+{\mathrm{a}}_4{}^2;\hspace{1em}{\Vert B-A\Vert }^2={\mathrm{a}}_3{}^2;\hspace{1em}{\Vert A-O\Vert }^2={\mathrm{a}}_1{}^2\\ (B-A)\times (A-O)=2{\mathrm{a}}_1{\mathrm{a}}_3\cos (\mathsf{\pi }-\mathsf{\tau })=-2{\mathrm{a}}_1{\mathrm{a}}_3\cos \mathsf{\tau }\end{array}\}\Rightarrow [\begin{array}{l}\cos \mathsf{\tau }=\frac{{\mathrm{a}}_1{}^2+{\mathrm{a}}_3{}^2-{\mathrm{a}}_4{}^2-{\mathrm{d}}_2{}^2}{2{\mathrm{a}}_1{\mathrm{a}}_3}=\\ \hspace{1em}=\frac{1+{\left(\frac{{\mathrm{a}}_3}{{\mathrm{a}}_1}\right)}^2-{\left(\frac{{\mathrm{a}}_4}{{\mathrm{a}}_1}\right)}^2-{\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_1}\right)}^2}{2\left(\frac{{\mathrm{a}}_3}{{\mathrm{a}}_1}\right)}\end{array}$$

(32)

The same figure reveals that τ_max (ζ_min) and τ_min (ζ_max) correspond to the maximum, d_2,max, and minimum, d_2,min, values of d₂, respectively. Accordingly, if ζ_max = 60° and ζ_min = −60° (considering that design requirements (i) with Δζ = ζ_max − ζ_min = 120° must be imposed) are chosen, the introduction of (τ_max, ζ_min), and then, of (τ_min, ζ_max), into Equation (26b) yields the following two relationships:

$$\left(\frac{{\mathrm{a}}_4}{{\mathrm{a}}_1}\right)+\left(\frac{{\mathrm{a}}_3}{{\mathrm{a}}_1}\right)\cos \left({\mathsf{\tau }}_{\max }-\frac{\mathsf{\pi }}{3}\right)=\cos \left(\frac{\mathsf{\pi }}{3}\right)$$

(33a)

$$\left(\frac{{\mathrm{a}}_4}{{\mathrm{a}}_1}\right)+\left(\frac{{\mathrm{a}}_3}{{\mathrm{a}}_1}\right)\cos \left({\mathsf{\tau }}_{\min }+\frac{\mathsf{\pi }}{3}\right)=\cos \left(\frac{\mathsf{\pi }}{3}\right)$$

(33b)

which are compatible if and only if the following relationship holds:

$$\cos \left({\mathsf{\tau }}_{\max }-\frac{\mathsf{\pi }}{3}\right)=\cos \left({\mathsf{\tau }}_{\min }+\frac{\mathsf{\pi }}{3}\right)\Rightarrow {\mathsf{\tau }}_{\max }-\frac{\mathsf{\pi }}{3}=\pm \left({\mathsf{\tau }}_{\min }+\frac{\mathsf{\pi }}{3}\right)\Rightarrow \{\begin{array}{l}{\mathsf{\tau }}_{\max }-{\mathsf{\tau }}_{\min }=\frac{2\mathsf{\pi }}{3}\\ or\\ {\mathsf{\tau }}_{\max }+{\mathsf{\tau }}_{\min }=0\begin{array}{c}\\ \end{array}\end{array}$$

(34)

Since 90° is the best transmission angle and the variation range of τ should be centered on this value, the condition ${\mathsf{\tau }}_{\max }+{\mathsf{\tau }}_{\min }=0$ is not valid, whereas the other condition can be satisfied by choosing ${\mathsf{\tau }}_{\max }=150°(=90°+60°)$ and ${\mathsf{\tau }}_{\min }=30°(=90°-60°)$, which, when introduced into Equation (33), yield the condition a₄ = 0.5a₁ (see Figure 7). Moreover, Equation (26a) yields (see Figure 7):

$$\begin{array}{l}{\mathrm{d}}_{2,\max }={\mathrm{a}}_3\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })-{\mathrm{a}}_1\sin {\zeta }_{\min }\\ {\mathrm{d}}_{2,\min }={\mathrm{a}}_3\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })-{\mathrm{a}}_1\sin {\zeta }_{\max }\end{array}\}\Rightarrow \{\begin{array}{l}[\begin{array}{l}\mathsf{\Delta }{\mathrm{d}}_2={\mathrm{d}}_{2,\max }-{\mathrm{d}}_{2,\min }=\\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}={\mathrm{a}}_3[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })-\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })]+\\ \hspace{1em}\hspace{1em}\hspace{0.17em}+{\mathrm{a}}_1(\sin {\zeta }_{\max }-\sin {\zeta }_{\min })\end{array}\\ [\begin{array}{l}{2\mathrm{d}}_{2,\mathrm{average}}={\mathrm{d}}_{2,\max }+{\mathrm{d}}_{2,\min }=\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}={\mathrm{a}}_3[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })+\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })]+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\mathrm{a}}_1(\sin {\zeta }_{\max }+\sin {\zeta }_{\min })\end{array}\end{array}$$

(35)

System (35) leads one to determine the following explicit formulas:

$$\{\begin{array}{l}{\mathrm{a}}_1=\frac{{2\mathrm{d}}_{2,\mathrm{average}}[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })-\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })]-\mathsf{\Delta }{\mathrm{d}}_2[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })+\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })]}{\mathsf{\Delta }}\\ {\mathrm{a}}_3=-\frac{\mathsf{\Delta }{\mathrm{d}}_2(\sin {\zeta }_{\max }+\sin {\zeta }_{\min })+{2\mathrm{d}}_{2,\mathrm{average}}(\sin {\zeta }_{\max }-\sin {\zeta }_{\min })}{\mathsf{\Delta }}\end{array}$$

(36)

with:

$$[\begin{array}{l}\mathsf{\Delta }=-\{[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })-\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })](\sin {\zeta }_{\max }+\sin {\zeta }_{\min })+\\ \hspace{1em}\hspace{1em}+(\sin {\zeta }_{\max }-\sin {\zeta }_{\min })[\sin ({\mathsf{\tau }}_{\max }+{\zeta }_{\min })+\sin ({\mathsf{\tau }}_{\min }+{\zeta }_{\max })]\}\end{array}$$

(37)

which, for the above-determined values of τ_max, ζ_min, τ_min, and ζ_max, yields:

$${\mathrm{a}}_1=\frac{\mathsf{\Delta }{\mathrm{d}}_2}{\sqrt{3}};{\mathrm{a}}_3=2{\mathrm{d}}_{2,\mathrm{average}}=2{\mathrm{d}}_{2,\min }+\mathsf{\Delta }{\mathrm{d}}_2\stackrel{\begin{array}{l}\mathsf{\Delta }{\mathrm{d}}_2={\mathrm{a}}_1\sqrt{3}\\ \hspace{1em}\hspace{1em}\downarrow \end{array}}{=}{\mathrm{a}}_1\sqrt{3}(\frac{{2\mathrm{d}}_{2,\min }}{\mathsf{\Delta }{\mathrm{d}}_2}+1)$$

(38)

where the values of ${\mathrm{d}}_{2,\min }$ and $\mathsf{\Delta }{\mathrm{d}}_2$ depend on how the actuated P-pair is sized (in Figure 7, d_2,min = d₂₀ and Δd₂ = d₁ = 2a₁ sinζ₊). Formula (38), together with the above-deduced relationship a₄ = 0.5a₁, provides the sizes of the 1st decoupled PPS for the chosen values of τ_max, ζ_min, τ_min, and ζ_max.

3.3. Second Decoupled PPS

Figure 8 illustrates the adopted notations for the kinematic analysis and dimensional synthesis of the PPS shown in Figure 4b. With reference to Figure 8, d₂ is the actuated-joint variable of the P pair and τ is the transmission angle. The lengths a₂, a₃, and a₄ are the distances of the S-pair center (point A in Figure 8), respectively, from the tilt-rotation axis, from the plane perpendicular to the pan-rotation axis that passes through point C, and from the axis of the second R pair of the RRS limb. Eventually, a₅ is the distance between the axes of the two R pairs of the RRS limb.

The following relationships hold among the above-defined geometric parameters:

$${\mathrm{d}}_2={\mathrm{a}}_3-{\mathrm{a}}_2\sin \zeta$$

(39a)

$$\mathsf{\tau }=\frac{\mathsf{\pi }}{2}-\zeta$$

(39b)

3.3.1. Position Analysis of the 2nd Decoupled PPS

Equation (39a) immediately provides the unique IPA solution (i.e., the determination of d₂ for assigned values of the geometric constants and ζ); whereas, for the DPA (i.e., the computation of ζ for assigned values of the geometric constants and d₂), it straightforwardly gives the following solution formula:

$$\zeta =\arcsin \left(\frac{{\mathrm{a}}_3-{\mathrm{d}}_2}{{\mathrm{a}}_2}\right)$$

(40)

which provides a unique solution for ζ ∈ [−90°, 90°].

3.3.2. Dimensional Synthesis of the 2nd Decoupled PPS

Equation (39b) states a linear relationship between the transmission angle, τ, and the tilt angle, ζ, that does not depend on the geometric constants of the PPS and gives the best transmission angle (i.e., 90°) for ζ = 0. Therefore, the best choice is ζ_max = −ζ_min = 60°, which gives ${\mathsf{\tau }}_{\max }=150°(=90°+60°)$ and ${\mathsf{\tau }}_{\min }=30°(=90°-60°)$. Moreover, since the geometric constants are not involved in Equation (39b), they can be freely chosen, provided that the following geometric constraints are satisfied (see Figure 8 and Equation (39a)):

$$\mathsf{\Delta }{\mathrm{d}}_2={\mathrm{d}}_{2,\max }-{\mathrm{d}}_{2,\min }={\mathrm{a}}_2(\sin {\zeta }_{\max }-\sin {\zeta }_{\min })\stackrel{\begin{array}{c}{\zeta }_{\max }=-{\zeta }_{\min }=60°\\ \downarrow \end{array}}{=}{\mathrm{a}}_2\sqrt{3}$$

(41a)

$${\mathrm{d}}_{2,\mathrm{average}}=\frac{{\mathrm{d}}_{2,\max }+{\mathrm{d}}_{2,\min }}{2}={\mathrm{a}}_3-{\mathrm{a}}_2\frac{\sin {\zeta }_{\max }+\sin {\zeta }_{\min }}{2}\stackrel{\begin{array}{c}{\zeta }_{\max }=-{\zeta }_{\min }=60°\\ \downarrow \end{array}}{=}{\mathrm{a}}_3$$

(41b)

$$\sqrt{{\Vert A_0-O\Vert }^2+{\mathrm{a}}_2{}^2}\le {\mathrm{a}}_4+{\mathrm{a}}_5$$

(41c)

where the values of ${\mathrm{d}}_{2,\mathrm{average}}$ and $\mathsf{\Delta }{\mathrm{d}}_2$ depend on how the actuated P-pair is sized.

4. Discussion and Accuracy Analysis

The above-reported kinematic analyses show that all three PPS architectures have closed-form solutions to their IPA and DPA, even though the formulas of the spherical PPS are slightly more cumbersome than those of the other two PPSs. Since the complexity of the formulas is not a problem when a motion control software uses them, the three selected architectures are equivalent from the motion control point of view. Of course, the fact that the spherical PPS has slightly coupled kinematics, which need the motion of both the actuators to keep the tilt angle fixed when only the pan angle has to change, requires a motion control software slightly more complex than that of the other two PPSs. Indeed, the “complexity” simply reduces to satisfying the condition that φ (=(θ₂ − θ₁)) be constant (see, Figure 5).

The above-reported dimensional synthesis determined the same optimal values of ζ_min, ζ_max, τ_min, and τ_max (i.e., ζ_max = −ζ_min = 60°, τ_min = 30°, and τ_max = 150°) for all of the three PPSs. Thus, even though the extreme values of the transmission angle are too far from its optimal value (i.e., τ = 90°), this drawback is common to all of them, and, in practice, is acceptable, since the telescope is light and does not carry heavy loads.

In order to complete the comparison among the selected PPSs, the relationships and sizes determined in the previous section must be used to evaluate the positioning precision (accuracy) of the additional limbs. Such an evaluation consists of estimating how a possible error in the actuated-joint variable of the additional limb affects the tilt angle, and it is implementable as follows.

For the spherical PPS, the differentiation of Equation (8) yields:

$$d\zeta =\frac{\sin {\mathsf{\alpha }}_1(\sin {\mathsf{\alpha }}_4\cos \mathsf{\phi }\hspace{0.17em}\cos \mathsf{\zeta }\hspace{0.17em}-\cos {\mathsf{\alpha }}_4\sin \mathsf{\phi })}{\sin {\mathsf{\alpha }}_4(\sin {\mathsf{\alpha }}_1\sin \mathsf{\phi }\hspace{0.17em}\sin \mathsf{\zeta }\hspace{0.17em}+\cos {\mathsf{\alpha }}_1\cos \mathsf{\zeta })}\hspace{0.17em}d\mathsf{\phi }$$

(42)

where, in the coefficient that multiplies dφ, ζ is related to φ through Equation (11), whereas the values of α₁ and α₄ are the optimal ones determined in the above-reported dimensional synthesis (i.e., α₁ = 46.7805° = 0.81647 rad and α₄ = 57.29578° = 1 rad). By replacing the differentials dζ and dφ with the joint-variable errors Δζ and Δφ, respectively, in Equation (42), and then, by taking the maximum absolute value of the coefficient that multiplies dφ in Equation (42), Equation (42) leads to the determination of the following limitation on |Δζ|:

$$\left|\mathsf{\Delta }\zeta \right|\le 1.7321\hspace{0.17em}\left|\mathsf{\Delta }\mathsf{\phi }\right|$$

(43)

which proves that, for the spherical PPS, |Δζ| has the same order of magnitude as |Δφ|.

For the 1st decoupled PPS, the differentiation of Equation (27) yields:

$$\hspace{0.17em}d\mathsf{\zeta }=-\frac{\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_1}\right)+\sin \mathsf{\zeta }}{\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_1}\right)\cos \mathsf{\zeta }\hspace{0.17em}+\left(\frac{{\mathrm{a}}_4}{{\mathrm{a}}_1}\right)\sin \mathsf{\zeta }}d\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_1}\right)$$

(44)

where, in the coefficient that multiplies d(d₂/a₁), (d₂/a₁) is related to ζ through Equation (31), whereas the values of a₁ and a₄ are the optimal ones determined in the above-reported dimensional synthesis (i.e., a₄ = 0.5a₁, ${\mathrm{a}}_1\sqrt{3}=\mathsf{\Delta }{\mathrm{d}}_2$). By replacing the differentials dζ and d(d₂/a₁) with the joint-variable errors Δζ and Δ(d₂/a₁), respectively, in Equation (44), and then, taking the maximum absolute value of the coefficient that multiplies d(d₂/a₁), for ζ ∈ [−60°, 60°], $\mathsf{\Delta }{\mathrm{d}}_2=\sqrt{3}$, and d_2,min = 0.5a₁, in Equation (44), Equation (44) leads to the determination of the following limitation on |Δζ|:

$$\left|\mathsf{\Delta }\mathsf{\zeta }\right|\le 2\hspace{0.17em}\left|\mathsf{\Delta }\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_1}\right)\right|$$

(45)

which proves that, for the 1st decoupled PPS, |Δζ| has the same order of magnitude as |Δ(d₂/a₁)|.

For the 2nd decoupled PPS, the differentiation of Equation (39a) yields:

$$\hspace{0.17em}d\mathsf{\zeta }=-\frac{1}{\cos \mathsf{\zeta }}d\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_2}\right)$$

(46)

where, in the coefficient that multiplies d(d₂/a₂), ζ is related to (d₂/a₂) through Equation (39a). By replacing the differentials dζ and d(d₂/a₂) with the joint-variable errors Δζ and Δ(d₂/a₂), respectively, in Equation (46), and then, taking the maximum absolute value of the coefficient that multiplies d(d₂/a₂), for ζ ∈ [−60°, 60°], in Equation (46), Equation (46) leads to the determination of the following limitation on |Δζ|:

$$\left|\mathsf{\Delta }\mathsf{\zeta }\right|\le 2\hspace{0.17em}\left|\mathsf{\Delta }\left(\frac{{\mathrm{d}}_2}{{\mathrm{a}}_2}\right)\right|$$

(47)

which proves that the 2nd decoupled PPS has the same accuracy as the 1st decoupled PPS with |Δζ| that has the same order of magnitude as |Δ(d₂/a₂)|.

The comparison of inequalities (45)–(47) shows that the three selected PPSs have essentially the same accuracy, with the spherical PPS being slightly better. In short, the kinematic analysis, the dimensional synthesis, and the accuracy analysis do not make any out of the three PPSs prevail over the remaining two. As a consequence, the fact that the spherical PPS has the minimum number of links and can actuate the tilt angle by using a continuous rotation as the input motion leads one to the conclusion that it should be preferred. 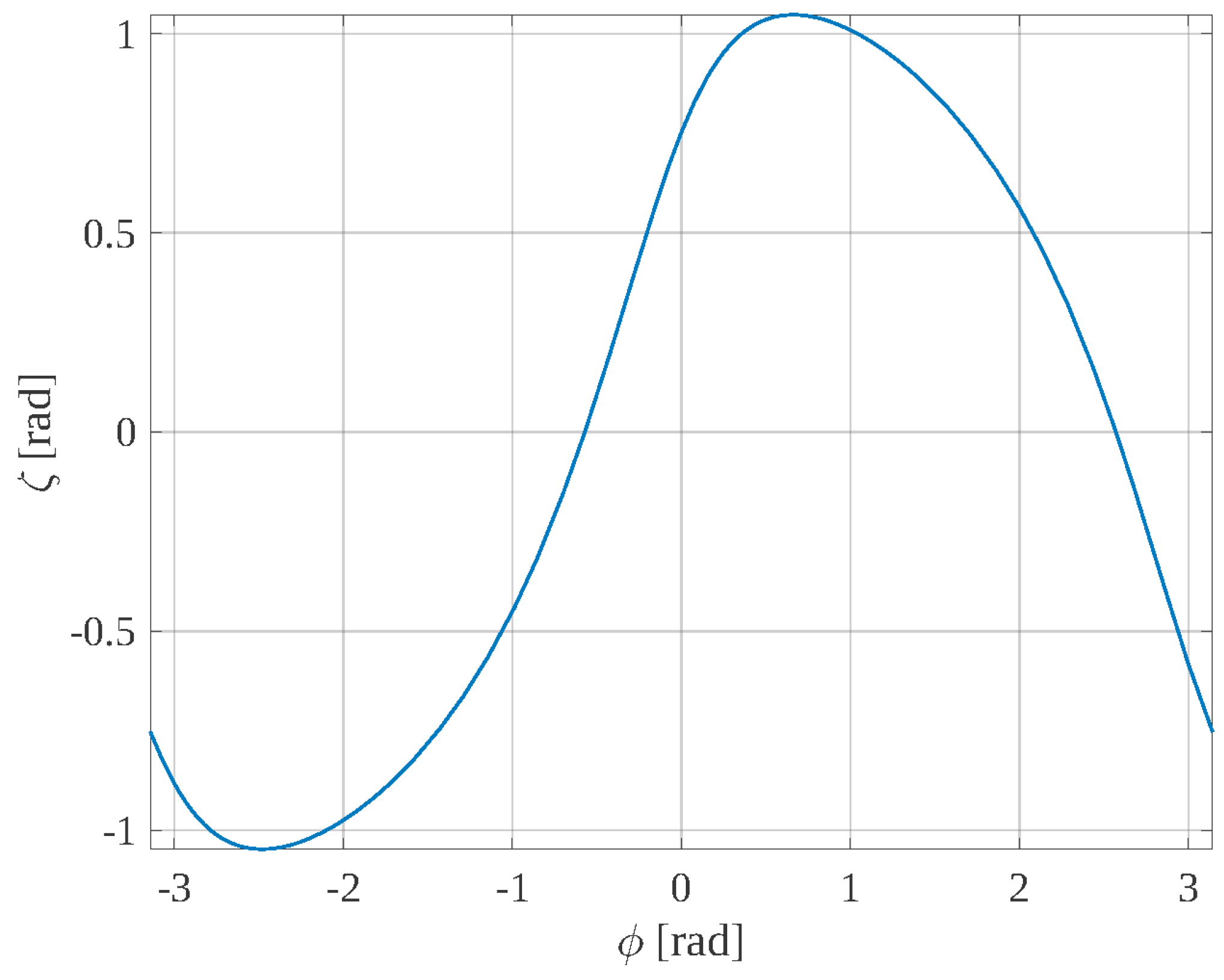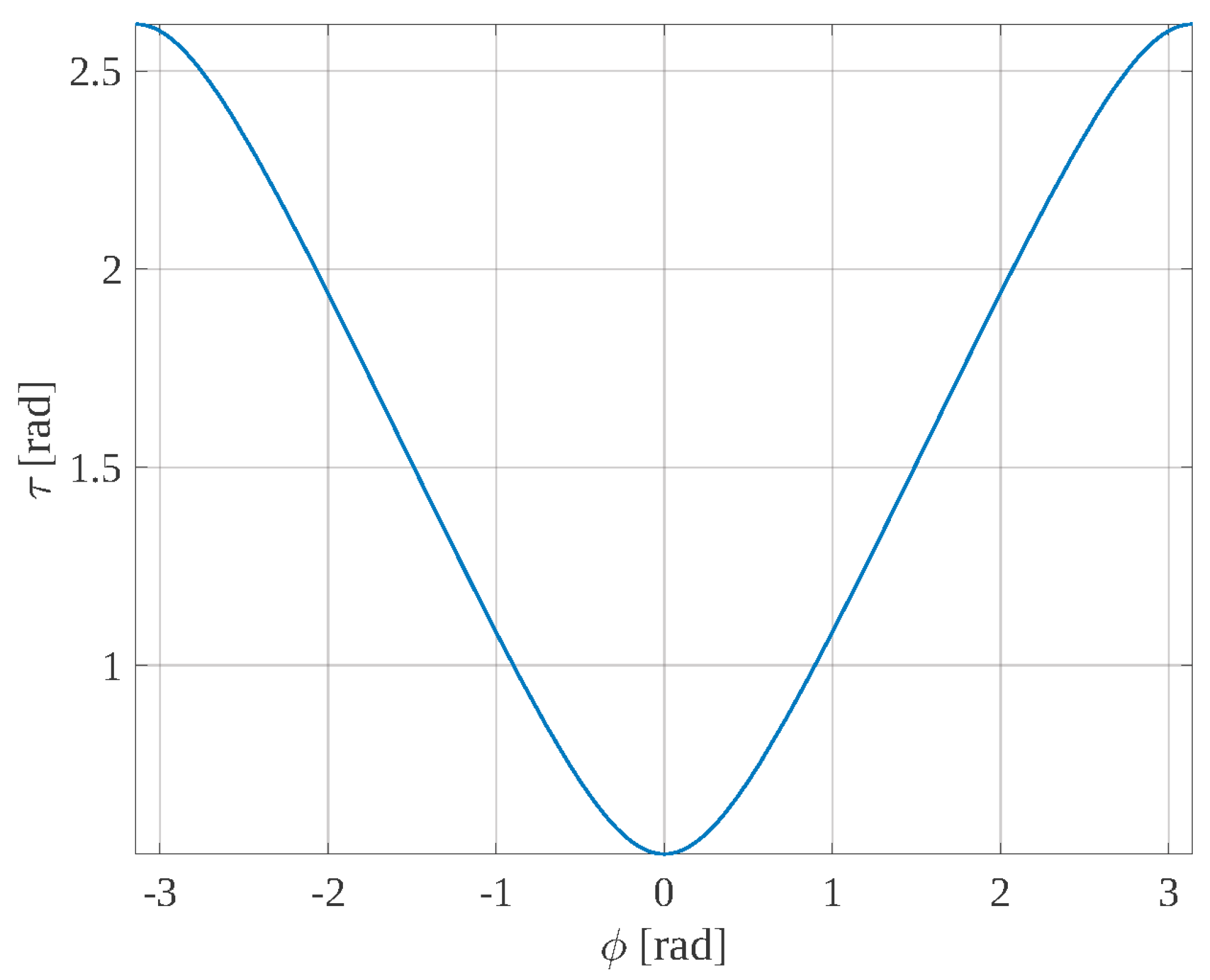Figure 9 shows the 3D CAD model of an RTS actuated through the spherical PPS with the above-determined sizes (i.e., α₂ = 90° = π/2 rad, α₁ = 46.7805° = 0.81647 rad, and α₄ = 57.29578° = 1 rad (see Figure 5)), whereas Figure 10 and Figure 11 show the tilt angle, ζ, and the transmission angle, τ, respectively, as a function of φ (=θ₂ − θ₁) for the same PPS. Eventually, the video “video_RTS.mp4” that shows the motion of the 3D CAD model (only tilt rotation followed by only pan rotation and, then, combined pan and tilt rotations) is downloadable from the supplementary materials that accompany this paper.

5. Conclusions

The literature on parallel pointing systems (PPS) has been reviewed to identify PPS architectures suitable for actuating robotic total stations (RTS). This review has led to the selection of three PPS architectures, named “Spherical PPS”, “1st Decoupled PPS”, and “2nd Decoupled PPS”.

The kinematic analysis, the dimensional synthesis, and the accuracy analysis of the selected PPS architectures have been addressed in detail in order to compare them. These studies have yielded the following conclusions: all of them (i) have simple motion control algorithms based on closed-form formulas, (ii) can be sized so that the telescope of the RTS can collimate toward any target on the upper hemisphere, and (iii) have a good accuracy.

Even though the three PPSs have comparable performances, the fact that the “Spherical PPS” has the minimum number of links and can actuate the tilt angle by using a continuous rotation as the input motion makes it prevail over the remaining two.