Experimental Validation of Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Permanent Magnet Synchronous Motor Drives
Abstract
1. Introduction
- Instead of employing two or three observers to estimate line currents, the proposed method utilizes only one observer to generate the three-phase stator currents.
- The proposed method is designed to enable fault detection, isolation, and reconfiguration in scenarios where two or three current sensors experience consecutive interruptions. As a result, the system can continue operating with the desired performance, even in the absence of any current sensor.
- This technique allows for adaptive reorganization in case the faulty sensors are restored or replaced. This adaptability ensures that the control system can maintain its maximum performance by leveraging the complementary nature of the other sensors.
- The study considers three different types of sensor failure: complete sensor outage, gain drop, and start-up with DC-offset fault. These specific failures have not been adequately addressed in the existing literature, and their inclusion serves to validate the accuracy of estimation and fault detection.
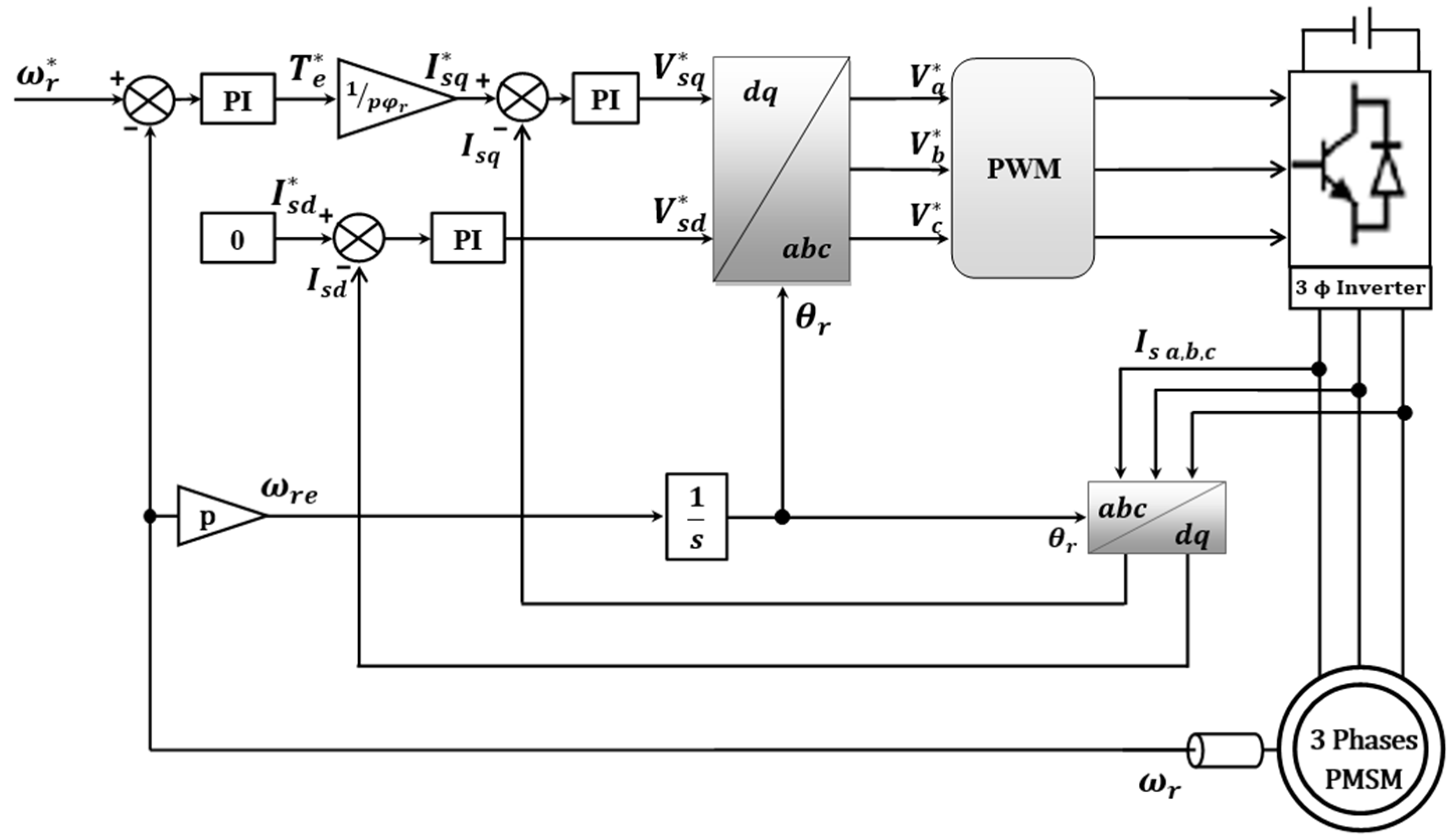
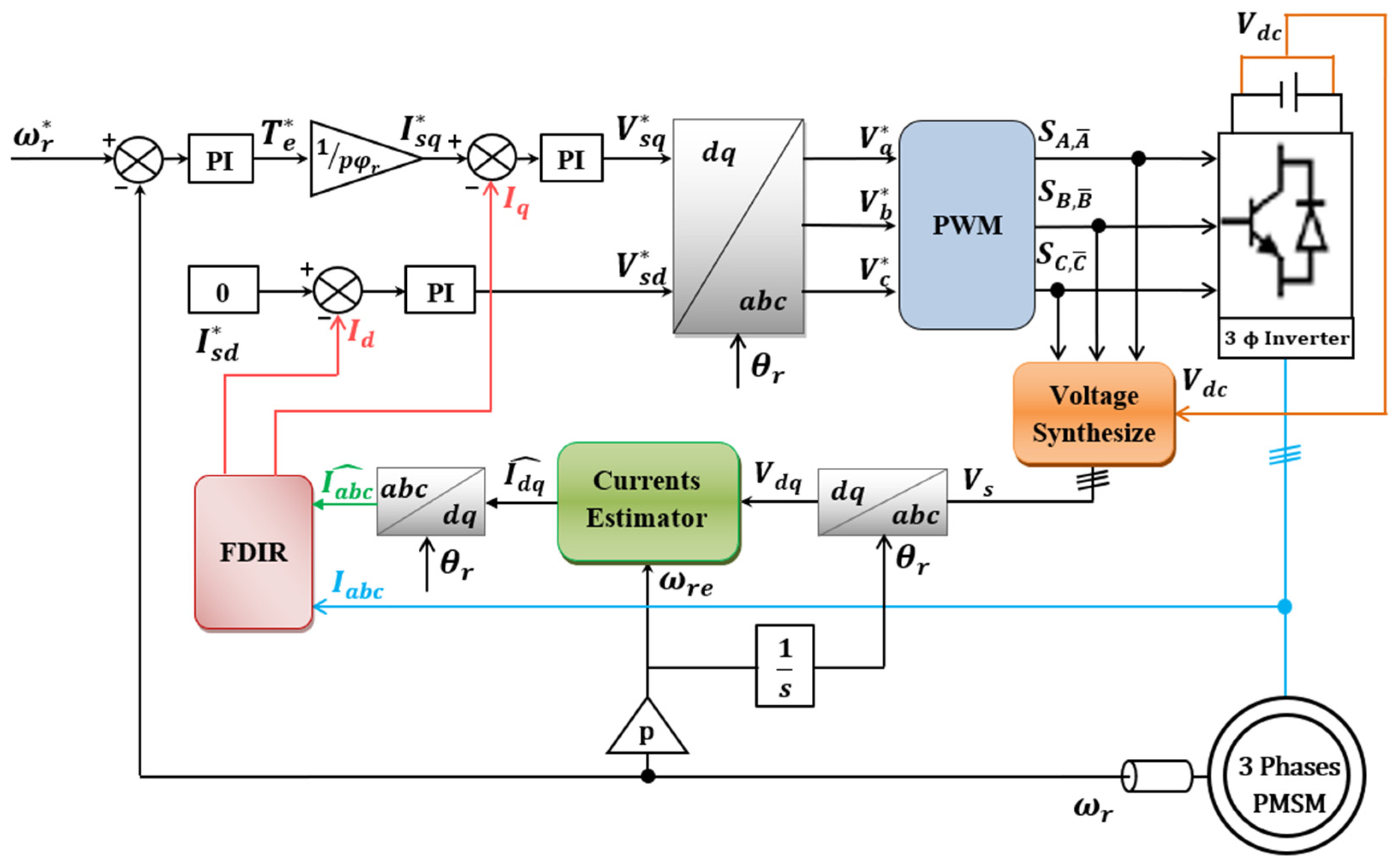
2. Permanent Magnet Synchronous Motor Model and Its Control
3. Current Sensor Fault-Tolerant Control
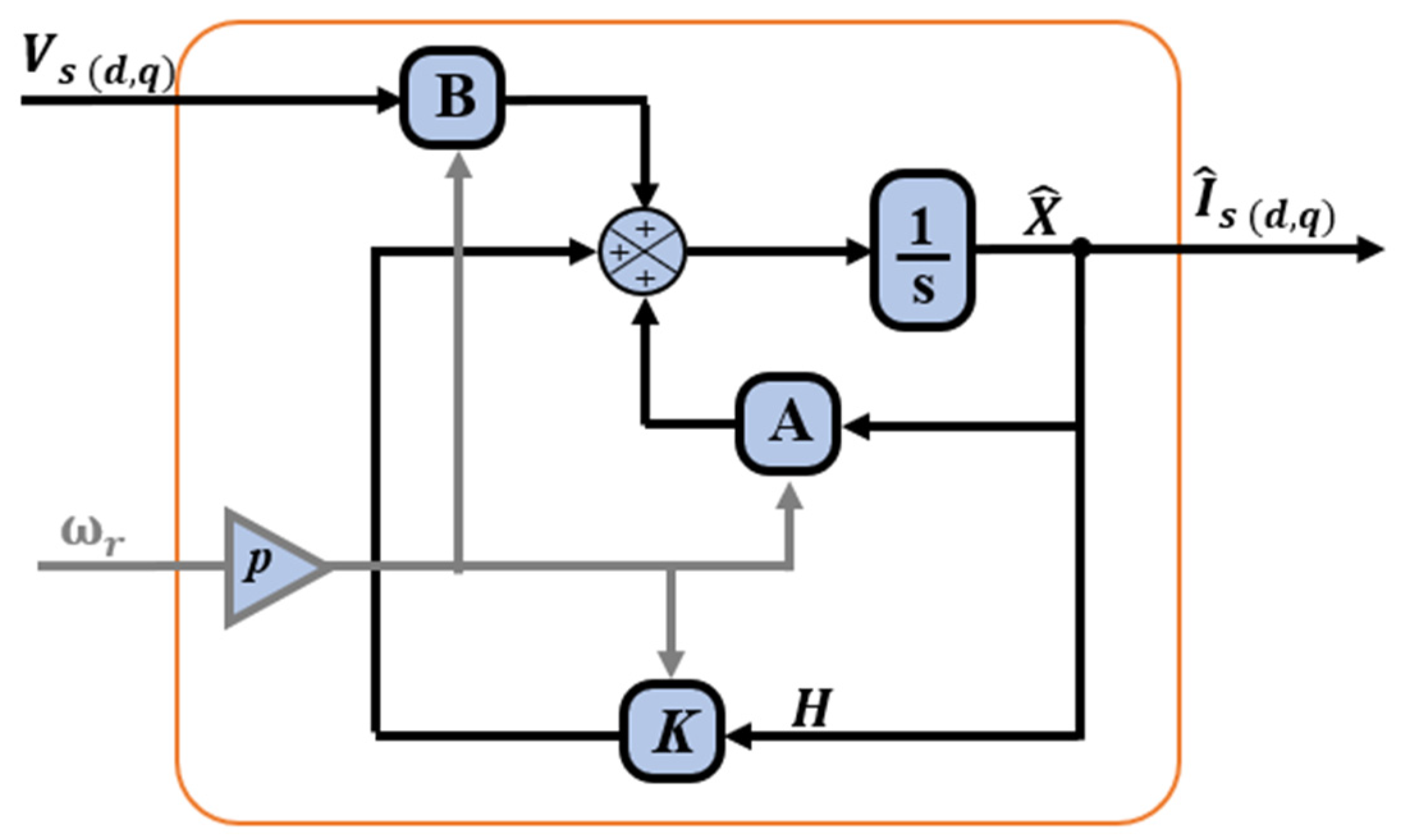
3.1. Stator Current Estimation
3.2. Fault Detection, Isolation, and Reconfiguration
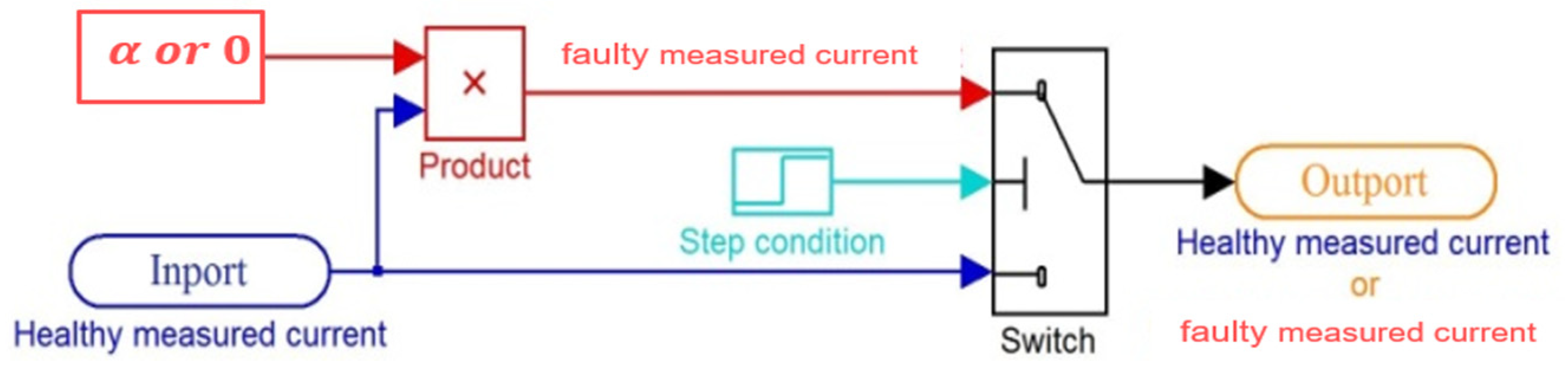
3.3. Considered Defects and Their Modelization
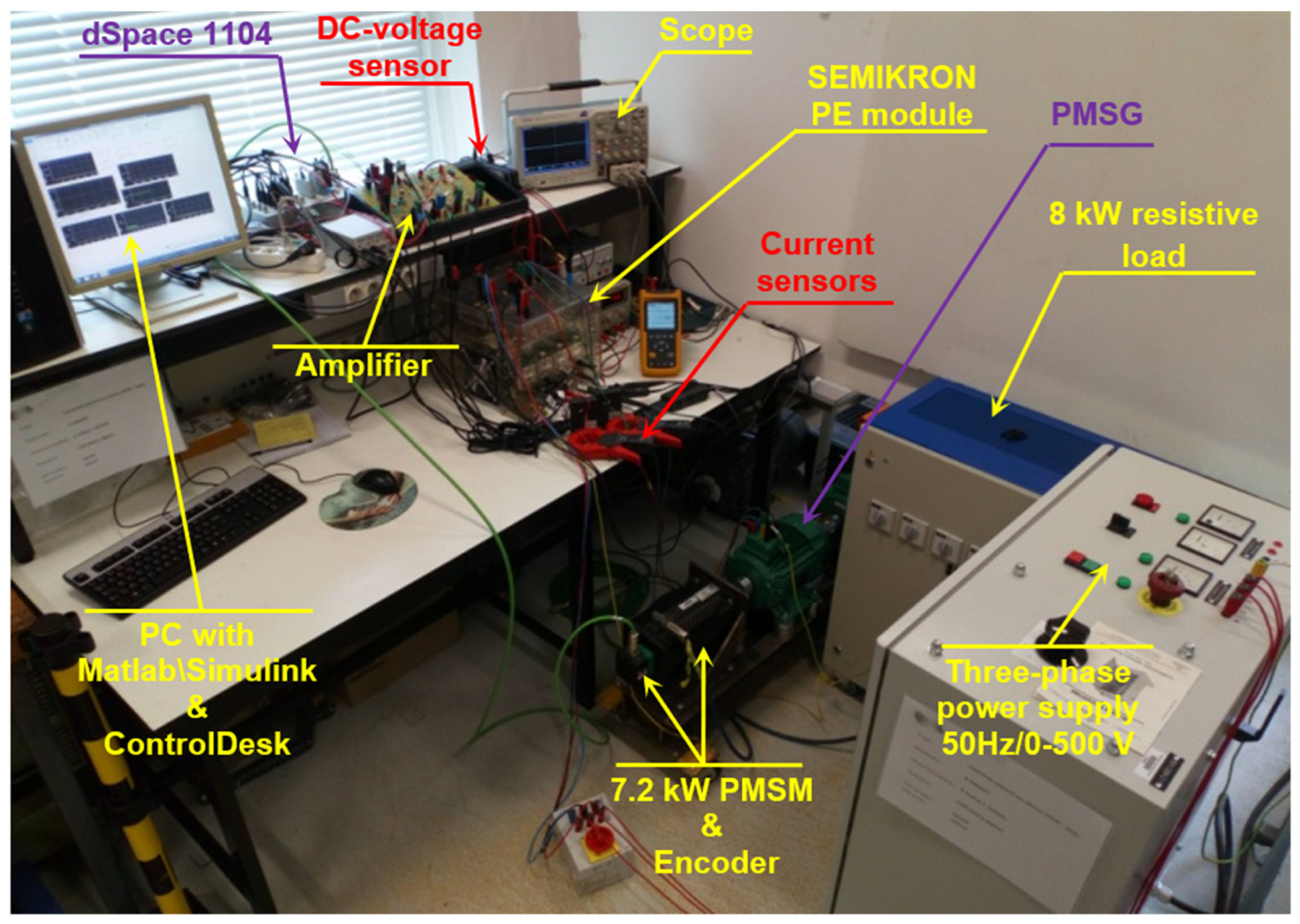
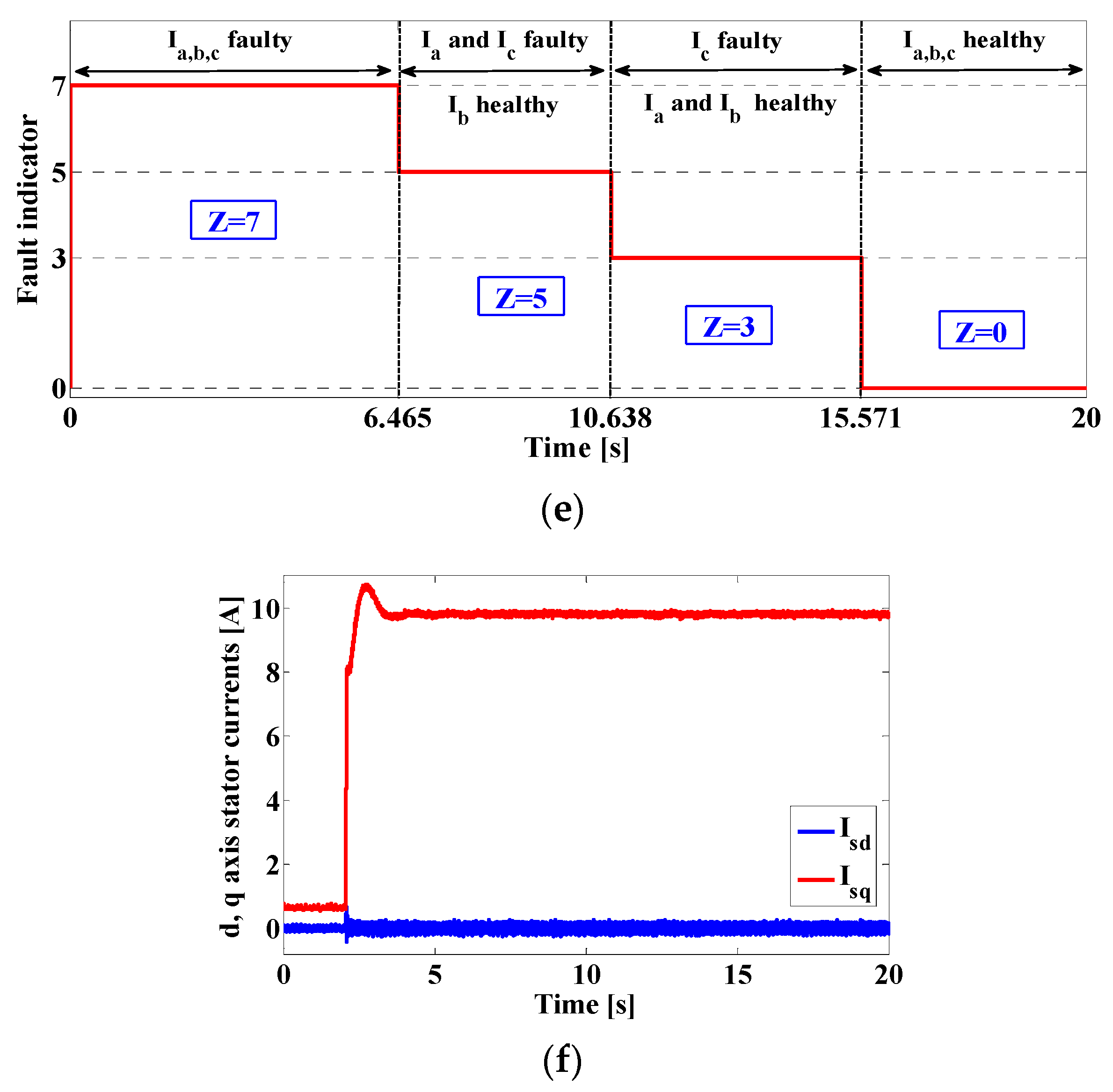
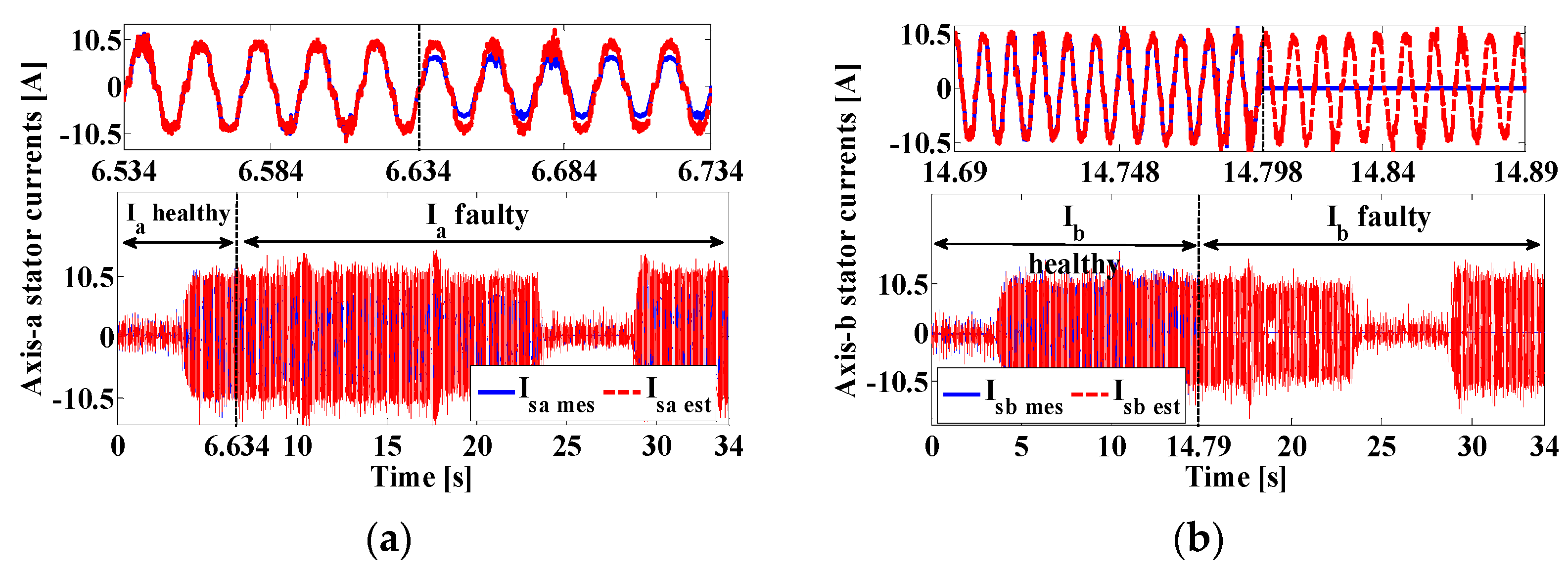
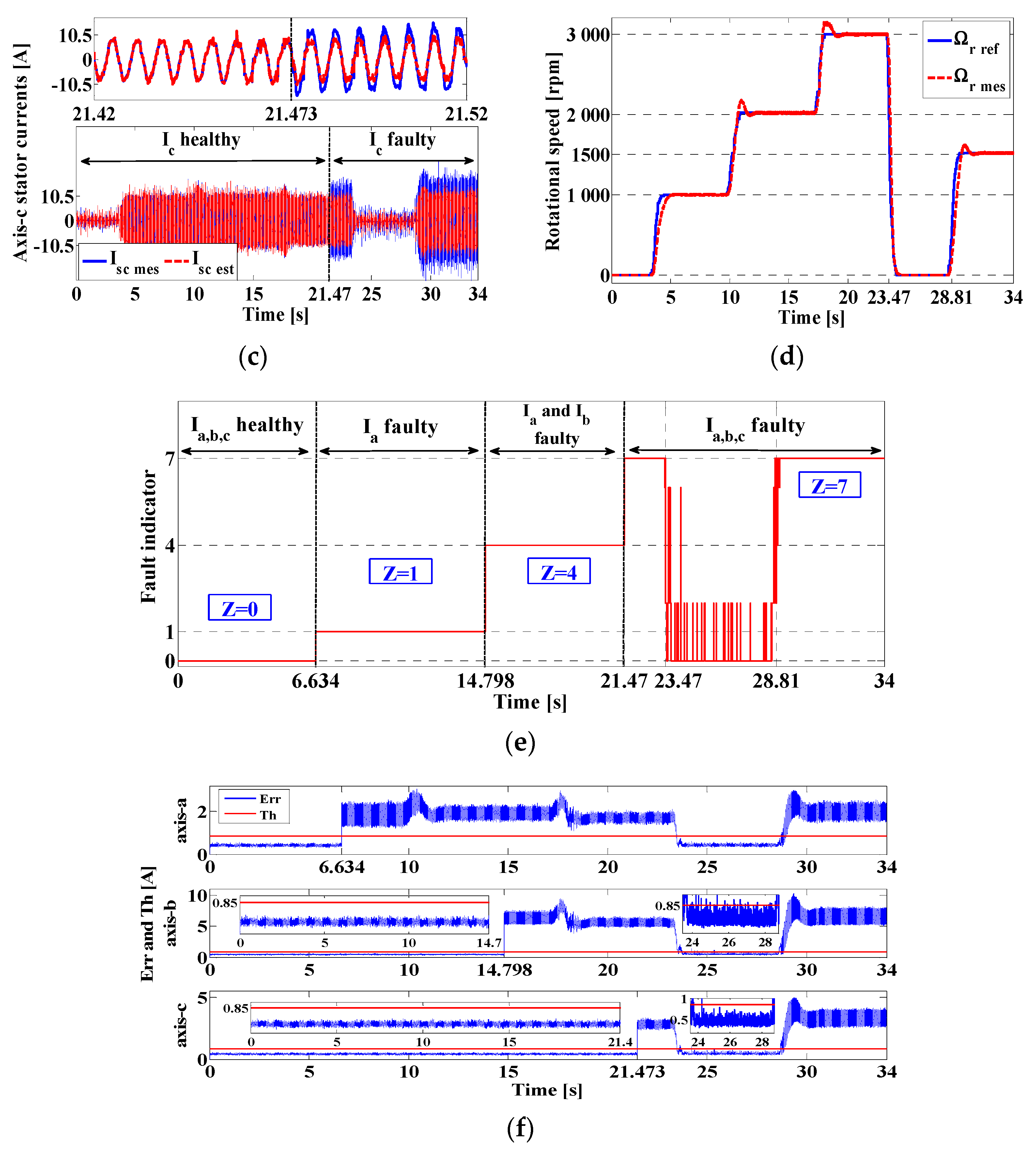
4. Results and Discussion
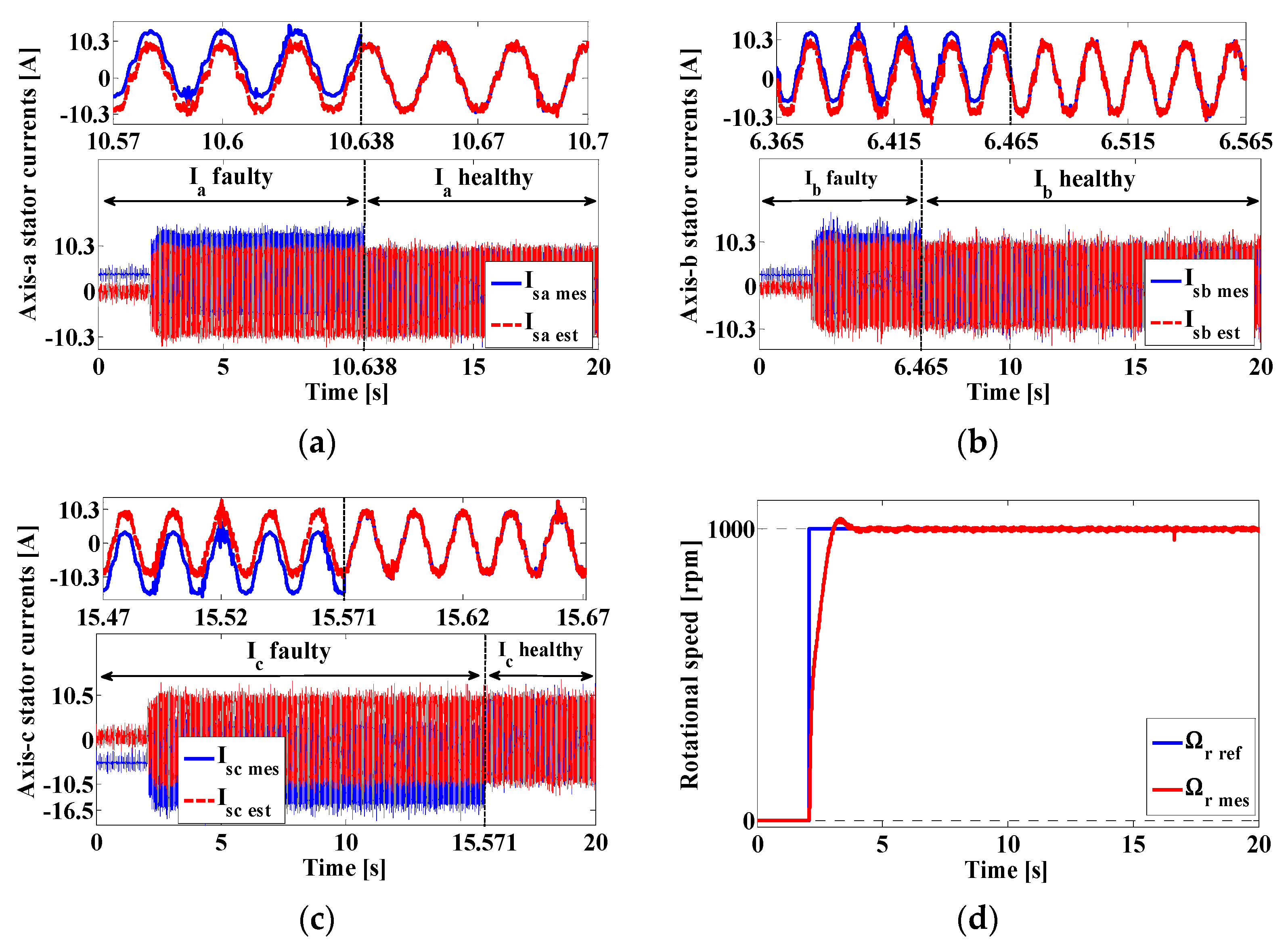
4.1. First Scenario: Gain Faults in Sensor-b and Sensor-c
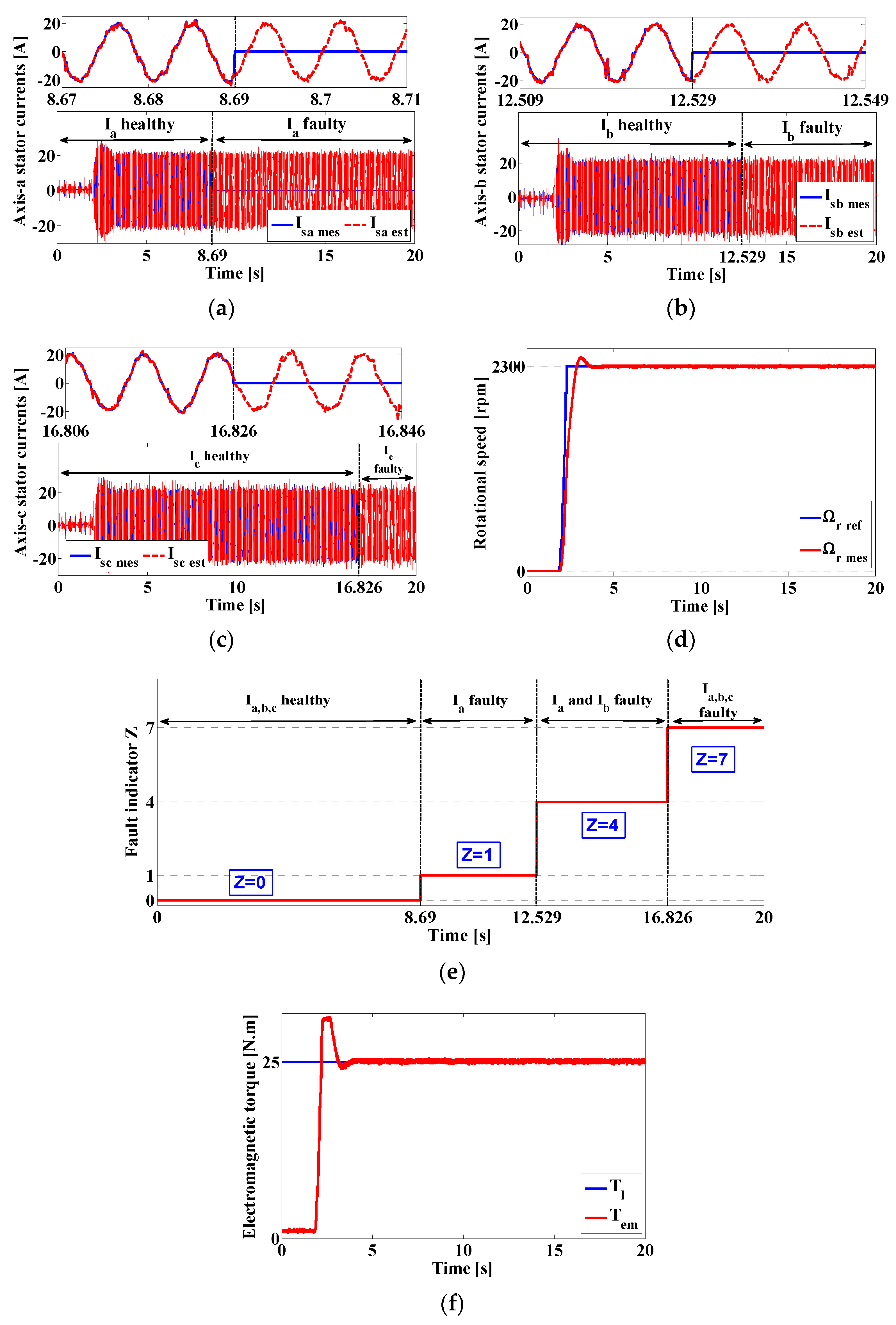
4.2. Second Scenario: Complete Outage of the Three Current Sensors
4.3. Third Scenario: Start-Up with a DC-Offset Fault in the Three Current Sensors
4.4. Fourth Scenario: Sensor Failure under Variable Speed Conditions
4.5. Fifth Scenario: Sensor Failure under Variable Load Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Nomenclature | |
| Inverter input voltage [V] | |
| d-q axis stator voltages [A] | |
| d-q axis stator currents [A] | |
| d-q axis estimated stator currents [A] | |
| Direct and quadrature inductances [H] | |
| Electromagnetic and load torques [N.m] | |
| Reference and measured rotational speeds [rad/s] | |
| Electrical measured rotational speed | |
| Reference and measured rotational speeds [rpm] | |
| Rotor position [rad] | |
| Rotor magnet flux [Wb] | |
| Number of pole pairs | |
| (a,b,c) axis measured stator currents [A] | |
| (a,b,c) axis estimated stator currents [A] | |
Appendix B
| PMSM Specifications | Parameters | ||
| Nominal power [kW] | 7.4 | [Ω] | 0.7 |
| Nominal voltage [V] | 400 | [H] | 0.007 |
| Nominal current [A] | 14.7 | [H] | 0.007 |
| Frequency [Hz] | 150 | [Wb] | 0.225 |
| Number of pole pairs | 3 | [Kg.m2] | 0.000629 |
| Nominal speed [rpm] | 3000 | F [N.m.s.rad−1] | 0.0003025 |
| Nominal torque [N.m] | 23.4 | ||
References
- Benbouzid, M.E.H.; Diallo, D.; Zeraoulia, M. Advanced Fault-Tolerant Control of Induction-Motor Drives for EV/HEV Traction Applications: From Conventional to Modern and Intelligent Control Techniques. IEEE Trans. Commun. 2007, 56, 519–528. [Google Scholar] [CrossRef]
- Azzoug, Y.; Sahraoui, M.; Pusca, R.; Ameid, T.; Romary, R.; Cardoso, A.J.M. A Variable speed control of permanent magnet synchronous motor without current sensors. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1523–1528. [Google Scholar]
- Lee, K.-S.; Ryu, J.-S. Instrument Fault Detection and Compensation Scheme for Direct Torque Controlled Induction Motor Drives. IEE Proc. Control Theory Appl. 2003, 150, 376–382. [Google Scholar] [CrossRef]
- Skowron, M.; Teler, K.; Adamczyk, M.; Orlowska-Kowalska, T. Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach. Energies 2022, 15, 6646. [Google Scholar] [CrossRef]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A Survey of Fault Detection, Isolation, and Reconfiguration Methods. IEEE Trans. Control Syst. Technol. 2010, 18, 636–653. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Espinoza-Trejo, D.R.; Palacios, E. Fault-Tolerant Control in Variable Speed Drives: A Survey. IET Electr. Power Appl. 2008, 2, 121–134. [Google Scholar] [CrossRef]
- Cristian, F.; Dancey, B.; Dehn, J. Fault-Tolerance in Air Traffic Control Systems. ACM Trans. Comput. Syst. 1996, 14, 265–286. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, M.C.; Seong, P.H.; Kang, H.G.; Jang, S.C. Evaluation of Error Detection Coverage and Fault-Tolerance of Digital Plant Protection System in Nuclear Power Plants. Ann. Nucl. Energy 2006, 33, 544–554. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Gong, W.; Zhao, W. A New Fault-Tolerant Permanent-Magnet Machine for Electric Vehicle Applications. IEEE Trans. Magn. 2011, 47, 4183–4186. [Google Scholar] [CrossRef]
- Bennett, J.W.; Atkinson, G.J.; Mecrow, B.C.; Atkinson, D.J. Fault-Tolerant Design Considerations and Control Strategies for Aerospace Drives. IEEE Trans. Ind. Electron. 2012, 59, 2049–2058. [Google Scholar] [CrossRef]
- Aouzellag, H.; Ghedamsi, K.; Aouzellag, D. Energy Management and Fault Tolerant Control Strategies for Fuel Cell/Ultra-Capacitor Hybrid Electric Vehicles to Enhance Autonomy, Efficiency and Life Time of the Fuel Cell System. Int. J. Hydrogen Energy 2015, 40, 7204–7213. [Google Scholar] [CrossRef]
- Wang, M.; Deng, J.; Pattinson, C.; Richardson, S. A Fuzzy controller for fault tolerant control of nuclear reactor. In Proceedings of the 2017 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 14–16 December 2017; pp. 387–390. [Google Scholar]
- Habibi, H.; Howard, I.; Simani, S. Reliability Improvement of Wind Turbine Power Generation Using Model-Based Fault Detection and Fault Tolerant Control: A Review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Rahman, S.U.; Xia, C. Rotor Speed and Position Estimation Analysis of Interior PMSM Machines in Low and Medium-High Speed Regions Adopting an Improved Flux Observer for Electric Vehicle Applications. Machines 2023, 11, 574. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Fault-Tolerant Predictive Current Control of Six-Phase PMSMs with a Single Isolated Neutral Configuration. Machines 2022, 10, 1152. [Google Scholar] [CrossRef]
- Li, L.; Zhou, W.; Bi, X.; Shi, X. Speed Estimation of PMSM Based on a Super-Twisting Slide Mode Observer. Machines 2022, 10, 681. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, W.; Sun, X.-M. Current-Constrained Adaptive Robust Control for Uncertain PMSM Drive Systems: Theory and Experimentation. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Guezmil, A.; Berriri, H.; Pusca, R.; Sakly, A.; Romary, R.; Mimouni, M.F. Experimental Investigation of Passive Fault Tolerant Control for Induction Machine Using Sliding Mode Approach. Asian J. Control 2019, 21, 520–532. [Google Scholar] [CrossRef]
- Raval, S.; Patel, H.R.; Patel, S.; Shah, V.A. Passive fault-tolerant control scheme for nonlinear level control system with parameter uncertainty and actuator fault. In Proceedings of the North American Fuzzy Information Processing Society Annual Conference, Halifax, NS, Canada, 31 May–3 June 2022; pp. 229–242. [Google Scholar]
- Manohar, M.; Das, S. Current sensor fault-tolerant control of induction motor driven electric vehicle using flux-linkage observer. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 884–889. [Google Scholar]
- Adamczyk, M.; Orlowska-Kowalska, T. Current sensors fault detection and tolerant control for induction motor drive. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 888–892. [Google Scholar]
- Chakraborty, C.; Verma, V. Speed and Current Sensor Fault Detection and Isolation Technique for Induction Motor Drive Using Axes Transformation. IEEE Trans. Ind. Electron. 2015, 62, 1943–1954. [Google Scholar] [CrossRef]
- Rothenhagen, K.; Fuchs, F.W. Current Sensor Fault Detection, Isolation, and Reconfiguration for Doubly Fed Induction Generators. IEEE Trans. Ind. Electron. 2009, 56, 4239–4245. [Google Scholar] [CrossRef]
- Sanchez, O.D.; Martinez-Soltero, G.; Alvarez, J.G.; Alanis, A.Y. Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors. Machines 2022, 10, 1198. [Google Scholar] [CrossRef]
- Foo, G.H.B.; Zhang, X.; Vilathgamuwa, D.M. A Sensor Fault Detection and Isolation Method in Interior Permanent-Magnet Synchronous Motor Drives Based on an Extended Kalman Filter. IEEE Trans. Ind. Electron. 2013, 60, 3485–3495. [Google Scholar] [CrossRef]
- Wang, G.; Hao, X.; Zhao, N.; Zhang, G.; Xu, D. Current Sensor Fault-Tolerant Control Strategy for Encoderless PMSM Drives Based on Single Sliding Mode Observer. IEEE Trans. Transp. Electrif. 2020, 6, 679–689. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Z.; Xu, D.; Zhou, T.; Xu, R. Speed and Current Sensor Fault Detection and Isolation Based on Adaptive Observers for IM Drives. J. Power Electron. 2014, 14, 967–979. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Wang, B.; Huang, X.; Xu, D. Current Sensor Fault Diagnosis and Tolerant Control for VSI-Based Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 4238–4248. [Google Scholar] [CrossRef]
- Aguilera, F.; de la Barrera, P.M.; De Angelo, C.H. Speed and Current Sensor Fault-Tolerant Induction Motor Drive for Electric Vehicles Based on Virtual Sensors. Electr. Eng. 2022, 104, 3157–3171. [Google Scholar] [CrossRef]
- Sepe, R.B.; Fahimi, B.; Morrison, C.; Miller, J.M. Fault tolerant operation of induction motor drives with automatic controller reconfiguration. In Proceedings of the IEMDC 2001 IEEE International Electric Machines and Drives Conference (Cat. No.01EX485), Cambridge, MA, USA, 17–20 June 2001; pp. 156–162. [Google Scholar]
- Diallo, D.; Benbouzid, M.E.H.; Makouf, A. A Fault-Tolerant Control Architecture for Induction Motor Drives in Automotive Applications. IEEE Trans. Veh. Technol. 2004, 53, 1847–1855. [Google Scholar] [CrossRef]
- Tabbache, B.; Benbouzid, M.; Kheloui, A.; Bourgeot, J.-M. DSP-Based Sensor Fault Detection and Post Fault-Tolerant Control of an Induction Motor-Based Electric Vehicle. Int. J. Veh. Technol. 2012, 2012, 608381. [Google Scholar] [CrossRef]
- Tabbache, B.; Rizoug, N.; Benbouzid, M.E.H.; Kheloui, A. A Control Reconfiguration Strategy for Post-Sensor FTC in Induction Motor-Based EVs. IEEE Trans. Veh. Technol. 2013, 62, 965–971. [Google Scholar] [CrossRef][Green Version]
- Kuchar, M.; Palacky, P.; Simonik, P.; Strossa, J. Self-Tuning Observer for Sensor Fault-Tolerant Control of Induction Motor Drive. Energies 2021, 14, 2564. [Google Scholar] [CrossRef]
- Berriri, H.; Naouar, M.W.; Slama-Belkhodja, I. Easy and Fast Sensor Fault Detection and Isolation Algorithm for Electrical Drives. IEEE Trans. Power Electron. 2012, 27, 490–499. [Google Scholar] [CrossRef]
- Azzoug, Y.; Sahraoui, M.; Pusca, R.; Ameid, T.; Romary, R.; Marques Cardoso, A.J. Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Induction Motor Drives. Electr. Eng. 2021, 103, 881–898. [Google Scholar] [CrossRef]
- Luenberger, D. An Introduction to Observers. IEEE Trans. Autom. Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Azzoug, Y.; Sahraoui, M.; Pusca, R.; Ameid, T.; Romary, R.; Cardoso, A.J.M. High-Performance Vector Control without AC Phase Current Sensors for Induction Motor Drives: Simulation and Real-Time Implementation. ISA Trans. 2021, 109, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Azzoug, Y.; Menacer, A.; Ameid, T.; Ammar, A. Performance improvement of sensorless vector control for induction motor drives using fuzzy-logic Luenberger observer: Experimental investigation. In Proceedings of the 2019 International Conference on Applied Automation and Industrial Diagnostics (ICAAID), Elazig, Turkey, 25–27 September 2019; pp. 1–6. [Google Scholar]
- Volpato Filho, C.J.; Scalcon, F.P.; Gabbi, T.S.; Vieira, R.P. Adaptive Observer for sensorless permanent magnet synchronous machines with online pole placement. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]

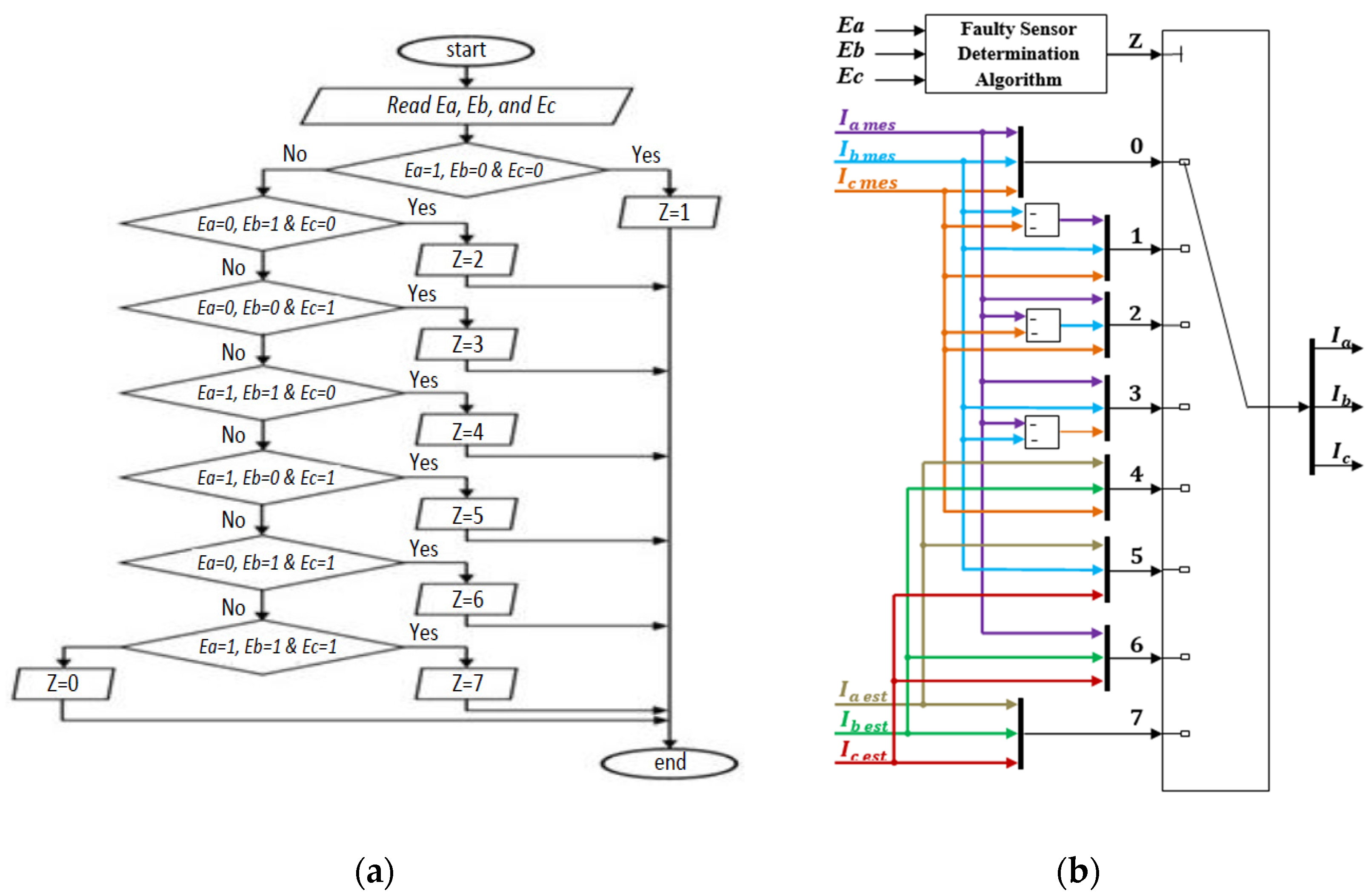



| Sensor-a | Sensor-b | Sensor-c | Z | Selected Currents in the Faulty State | ||
|---|---|---|---|---|---|---|
| Phase-a | Phase-b | Phase-c | ||||
| Faulty | Healthy | Healthy | 1 | |||
| Healthy | Faulty | Healthy | 2 | |||
| Healthy | Healthy | Faulty | 3 | |||
| Faulty | Faulty | Healthy | 4 | |||
| Faulty | Healthy | Faulty | 5 | |||
| Healthy | Faulty | Faulty | 6 | |||
| Faulty | Faulty | Faulty | 7 | |||
| Healthy | Healthy | Healthy | 0 | |||
| Fault | Mathematical Expression |
|---|---|
| Gain | |
| Complete outage | |
| DC-offset |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzoug, Y.; Pusca, R.; Sahraoui, M.; Ameid, T.; Romary, R. Experimental Validation of Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Permanent Magnet Synchronous Motor Drives. Machines 2023, 11, 873. https://doi.org/10.3390/machines11090873
Azzoug Y, Pusca R, Sahraoui M, Ameid T, Romary R. Experimental Validation of Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Permanent Magnet Synchronous Motor Drives. Machines. 2023; 11(9):873. https://doi.org/10.3390/machines11090873
Chicago/Turabian StyleAzzoug, Younes, Remus Pusca, Mohamed Sahraoui, Tarek Ameid, and Raphael Romary. 2023. "Experimental Validation of Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Permanent Magnet Synchronous Motor Drives" Machines 11, no. 9: 873. https://doi.org/10.3390/machines11090873
APA StyleAzzoug, Y., Pusca, R., Sahraoui, M., Ameid, T., & Romary, R. (2023). Experimental Validation of Current Sensors Fault Detection and Tolerant Control Strategy for Three-Phase Permanent Magnet Synchronous Motor Drives. Machines, 11(9), 873. https://doi.org/10.3390/machines11090873





