Improved Rapid-Expanding-Random-Tree-Based Trajectory Planning on Drill ARM of Anchor Drilling Robots

Abstract

Permanent highway support in deep coal mines now depends on the anchor drilling robot’s drill arm. The drilling arm’s trajectory planning using the conventional RRT (rapid-expanding random tree) algorithm is inefficient and has crooked, rough paths. To improve the accuracy of path planning, we propose an improved RRT algorithm. Firstly, the kinematic model of the drill arm of the drill and anchor robot was established, and the improved DH solution parameters and the positive solution of the drill arm kinematics were solved. The end effector’s attainable working space was calculated using the Monte Carlo approach. Additionally, to address the problem of the slow running speed of the RRT algorithm, an artificial potential field factor was introduced to construct virtual force fields at obstacle and target points and calculate the potential field map for the entire reachable workspace to improve the speed of the sampling points close to the target point. At the same time, the greedy approach and the three-time B-sample curve-fitting method were used simultaneously to remove unnecessary points and carry out smooth path processing in order to improve the quality of the drill arm trajectory. This was carried out in order to solve the issue of rough pathways generated by the RRT algorithm. Finally, 50 time-sampling comparison experiments were conducted on 2D and 3D maps. The experimental results showed that the improved RRT algorithm improved the average sampling speed by 20% and reduced the average path length by 14% compared with the RRT algorithm, which verified the feasibility and effectiveness of this improved RRT algorithm. The improved RRT algorithm generates more efficient and smoother paths, which can improve the intelligence of the support process by integrating and automating drilling and anchoring and providing reliable support for coal mine intelligence.

1. Introduction

Coal mine intelligence is the core of the high-quality development of the coal industry and provides technical support and the necessary road for the coal industry [1,2,3]. However, due to the limited degree of automation of coal mine roadway comprehensive excavation workforce equipment, China’s coal mines generally have low digging efficiency and high safety risks [4,5,6]. Moreover, at the present stage, the permanent support of the roadway mainly relies on manual operation, and the number of support workers accounts for more than 70% of the number of workers in the digging face. The drilling and anchoring robot is an important piece of equipment for the realization of intelligent, integrated coal mine excavation. With the drill arm as the main motion device of the anchor drilling robot, optimizing the trajectory of the arm is all about reducing the time of the entire drilling operation [7,8]. Therefore, studying the drilling arm trajectory planning algorithm for coal mine anchor drilling robots has significant practical implications for enhancing support speed and effectiveness, ensuring staff safety, and enhancing the effectiveness of digging in the comprehensive excavation face [9].

For the reachable workspace and trajectory planning algorithm of robotic arms, many scholars at home and abroad have carried out extensive and in-depth research and practice [10,11,12]. Long [13] can be categorized into joint-space trajectory planning and Cartesian-space trajectory planning based on the planning space used for trajectory planning. For ease of use, joint-space trajectory planning is commonly used in robots today. The performance of trajectory planning algorithms for robotic arms in underground coal mines directly affects the motion efficiency of the robotic arms [14]. Some classical trajectory planning methods have been proposed by scholars at home and abroad. The main ones are the genetic algorithm, the artificial potential field method, the particle swarm algorithm, the rapid-expanding random tree (RRT) method, etc. [15,16,17]. Wang [18] proposed an improved RRT* algorithm suitable for solving narrow channel problems to improve the performance of RRT*. The improved algorithm takes less than half the time required by the existing algorithm to find the optimal path from the start node to the target node.

Tang [19] proposed an adaptive particle swarm algorithm with perturbation that can be planned for time, capacity, and leapfrog optimal trajectories while satisfying joint constraints, but the problem of local minima is not taken into account. Kivelä, T et al. [20] proposed a path planning method for autonomous avoidance of dynamic obstacles that is able to achieve the completion of dynamic path planning when obstacles enter suddenly. Deng [21] proposed a two-population genetic optimal-time trajectory planning algorithm based on a chaotic local search for the trajectory planning problem of industrial robots aiming at the shortest running time. It has been verified that the proposed algorithm enables smooth and time-optimal trajectories of the robot end effector. However, a multi-degree-of-freedom robotic arm was not considered. Vandeweghe [22] proposes a sampling-based path planning algorithm that extends the rapid-expanding random tree (RRT) algorithm to cope with goals specified in the configuration space of goals specified in a subspace of the manipulator. Solutions to high-dimensional manipulation problems can be efficiently generated. An improved RRT algorithm based on target bias and the expansion point selection mechanism was proposed by Wei-Hua Bai et al. [23], and the results show that the improved algorithm can guide the tree growth direction, avoid falling into local minima while improving the convergence speed of the algorithm, and improve the efficiency of motion planning of the robotic arm in the simulation. However, the feasibility of the algorithm in a moving obstacle environment was not considered. In response to the target unreachability and local minimum problems of the traditional artificial potential field (APF) method in the obstacle-avoidance path planning process of the robotic arm. Hou [24] proposed an improved APF algorithm that introduces the hopping point search algorithm to find the optimal hopping point as the next iteration point and, at the same time, sets the forced neighbors as the virtual target points to guide the robotic arm to get rid of the dangerous area. However, the effectiveness of the algorithm in three dimensions is not considered. Khan et al. [25] proposed a model-free control framework based on a weighted Jacobi random-tree intelligent algorithm for the path planning method for rigid–flexible robotic arms that is robust enough to handle uncertainties in the robotic arm and make the computation of path planning more efficient. However, this model-free control framework does not consider the working space of the robotic arm. Tie Zhang et al. [26] proposed a practical time-optimal smoothing trajectory planning algorithm and applied it to a robot manipulator arm. In addition, the proposed algorithm utilizes an input-shaping algorithm instead of adding acceleration constraints to the trajectory optimization model to achieve a smooth trajectory. Experimental results on a six-degree-of-freedom industrial robot show the effectiveness of the proposed algorithm. However, the case of local minima is not considered. Wang Lei [27] and others proposed a new algorithm for solving the trajectory planning of robots, especially robot manipulator arms, based on heuristic optimization algorithms: the Trajectory-Planning Beetle Swarm Optimization (TPBSO) algorithm. Two specific robotic-arm trajectory planning problems are proposed as practical applications of the algorithm, namely point-to-point planning and fixed-geometric-path planning, but with low computational complexity.

In summary, the above-mentioned scholars have studied the use of various intelligent algorithms for trajectory planning solutions instead of traditional mathematical calculation methods. Different intelligent algorithms have different strengths and weaknesses and are constantly evolving to suit different scenarios. However, none of the trajectory planning algorithms applicable to multi-degree-of-freedom robotic arms in high-dimensional spaces have been considered comprehensively. Therefore, based on the research of the group, this paper proposes a trajectory planning and path optimization method based on an improved RRT algorithm in the reachable working space of the drilling arm, with the aim of improving the intelligence of roadway support. In the Section 2, the general scheme for the trajectory planning of the drill arm of the anchor drilling robot is described. 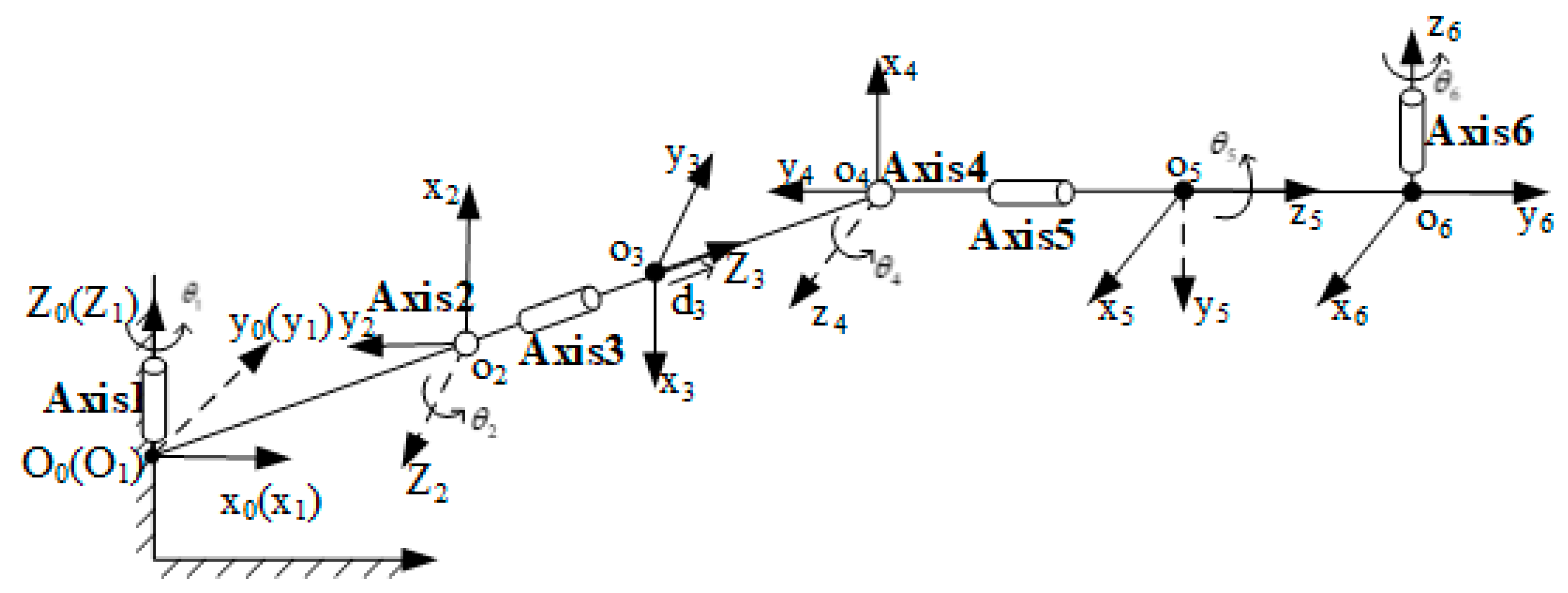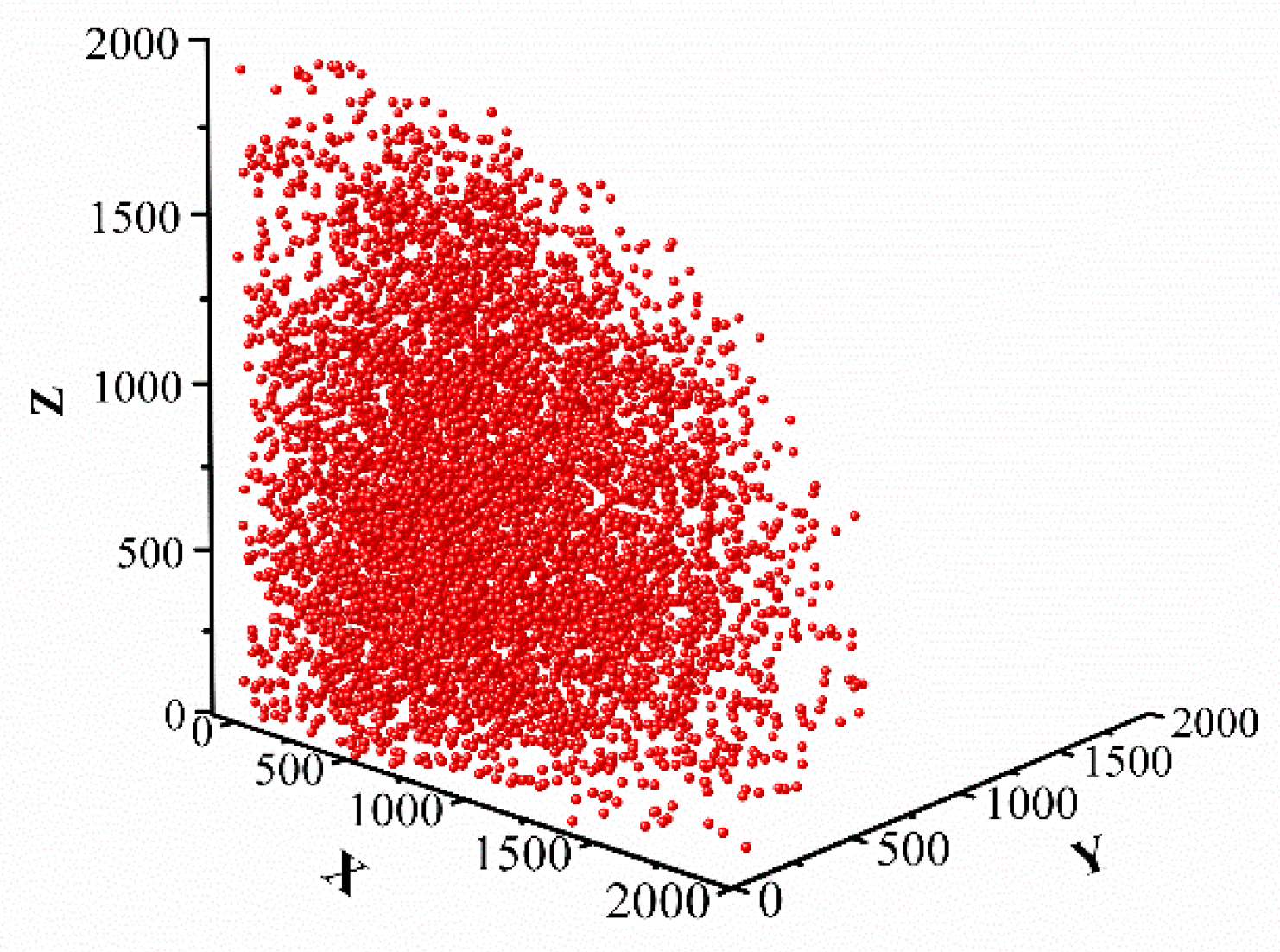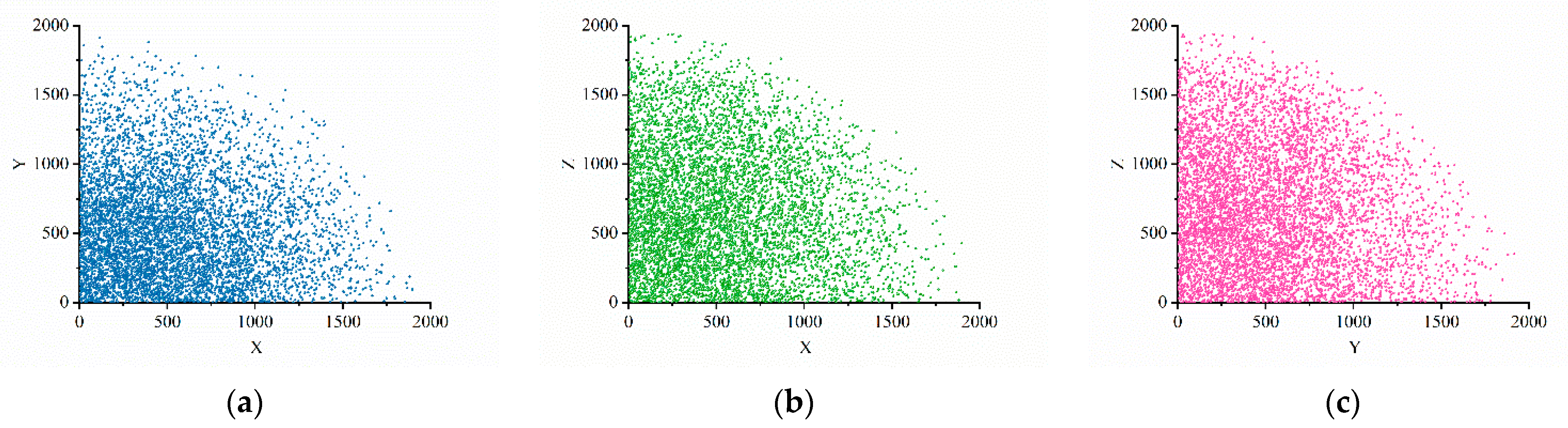In the Section 3, the six-degree-of-freedom drilling arm of the drilling and anchoring robot is analyzed according to the modified DH (M-DH) solution method, the overall link coordinate system of the drilling arm is established, and the M-DH parameters of the drilling arm are finally determined according to the link coordinate system. A Monte Carlo random sampling method is used to calculate the reachable working space of the drill arm, and subsequent planning of the drill arm trajectory is carried out within the reachable working space. In the Section 4, the principles and procedures of the RRT algorithm, the artificial potential field method, and the three-time B-sample curve fitting are described. In the Section 5, simulation experiments are conducted in 2D and 3D maps to analyze and compare the difference in time consumption and path length between the RRT algorithm and the improved RRT algorithm. The results show that the improved RRT algorithm can effectively optimize the base path, improve path planning efficiency, enhance path smoothing, and shorten the path length. In the Section 6, the feasibility and superiority of the improved RRT algorithm are summarized.

2. Overall Program for the Trajectory Planning of the Anchor Drilling Robot Drill Arm

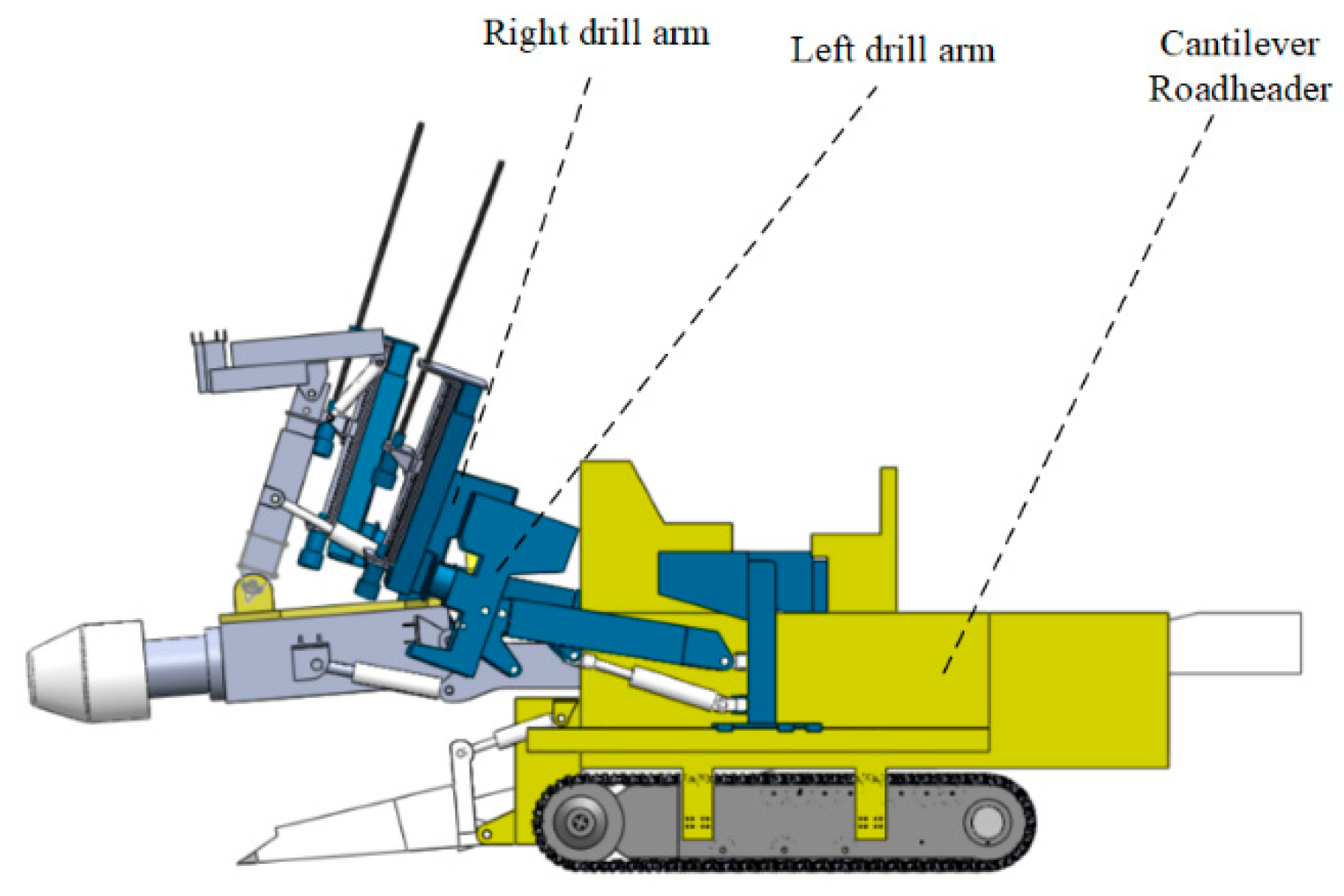
In this paper, the drilling arm of a drilling anchor robot is used as the object of study. Anchor drilling robots are essentially two six-degree-of-freedom robotic arms integrated into the body of a cantilevered road header. The basic structure of the anchor drilling robot is shown in Figure 1. The cantilevered road header section is mainly used to cut the coal mine roadway, while the six-degree-of-freedom robotic arm section uses the drilling rig as its actuator to support the roadway.

The drilling arm mainly consists of the drilling machine, the swing mechanism, the telescopic mechanism, the cantilever mechanism, the slide seat mechanism, and the slide rail mechanism, as shown in Figure 2.

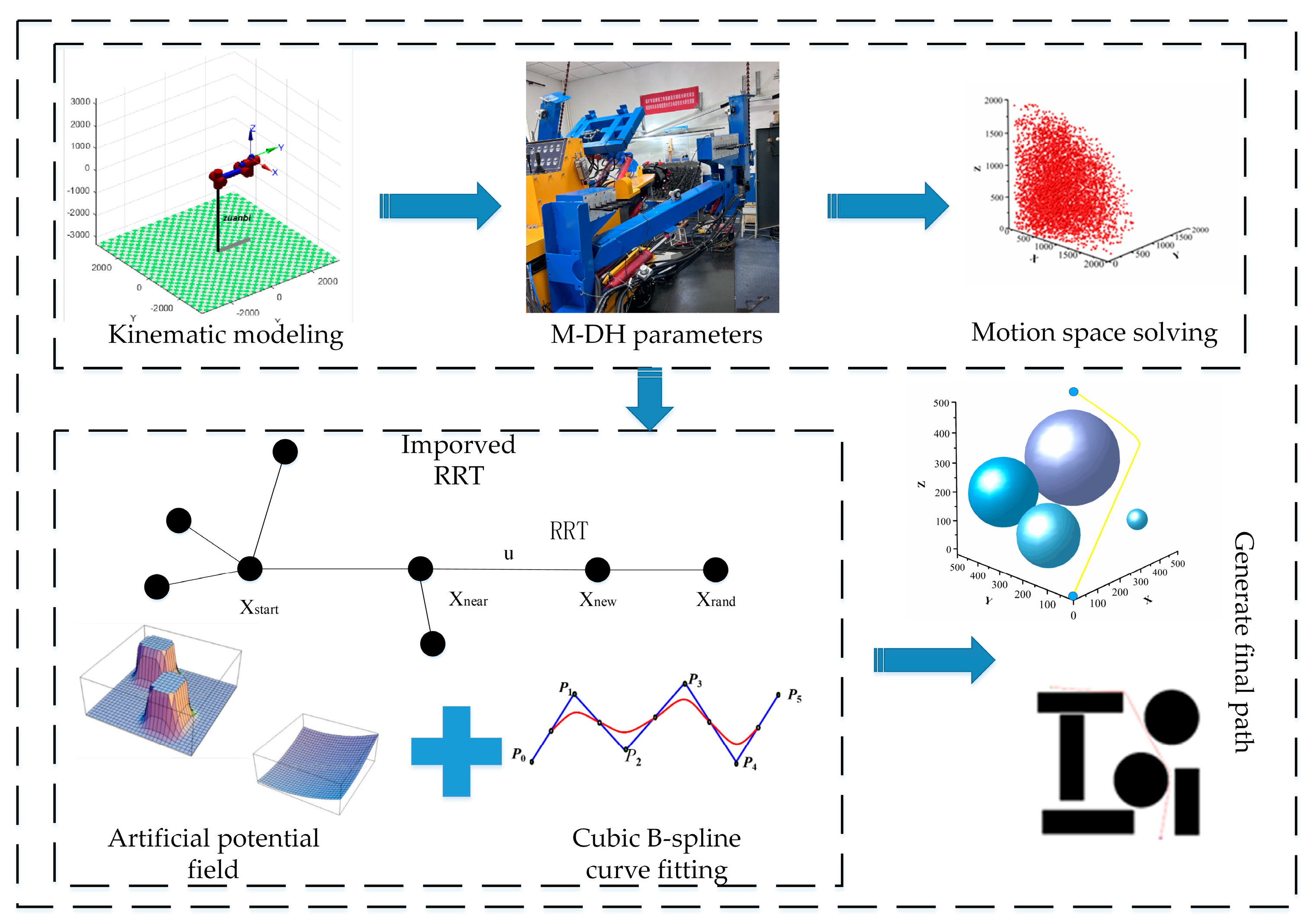
The working space of the anchor drilling robot is limited by the space in the underground coal mine tunnel, and at the same time, the environment in the working space is complex and variable during the drilling arm support process. Therefore, the trajectory planning process requires that information about the workspace environment and information about the feasible domain of the robotic arm be specified as the basis for planning, and the planning path must have real-time collision detection and dynamic planning capabilities to cope with the dynamically changing working environment. Therefore, the overall program of the drilling arm trajectory planning method of the drilling anchor robot based on the improved RRT algorithm in this paper is shown in Figure 3.

Firstly, the kinematic model of the drilling arm is established; it is kinematically positive, and the DH solving parameters are solved, solving the drilling anchor module motion space using the Monte Carlo method and verifying that it meets the roadway support requirements. Secondly, a trajectory planning algorithm based on Rapidly Expanding Random Trees (RRTs, rapid-expanding random trees), by avoiding the need to model the space by performing collision detection on sampled points in the state space, is capable of efficiently solving path planning problems with high-dimensional spaces and complex constraints; it is also suitable for solving trajectory planning for multi-degree-of-freedom robots in complex and dynamic environments. The introduction of an artificial potential field factor into the algorithm can greatly improve search efficiency. At the same time, the path quality is improved by removing redundant points and smoothing and optimizing the path using a greedy algorithm and cubic B-sample curve fitting. This results in the realization of autonomous trajectory planning for the drilling arm of an underground coal mine anchor drilling robot.

3. Kinematic Analysis of the Drilling Arm for the Anchor Drilling Robots

3.1. Kinematic Modeling of the Drill Arm for Anchor Drilling Robots

The kinematic modeling of the drilling arm is an important basis and prerequisite for the study of the achievable working space and trajectory planning of the drilling arm. The six-degree-of-freedom drilling arm of the drilling anchor robot was analyzed according to the modified DH (M-DH) solution [28]. Firstly, the drilling arm was reduced to a link and a joint, and the M-DH joint i was fixed to the i-coordinate system, i.e., the coordinate system was built on the input of the link. The origin of each joint’s coordinate system and XYZ axis separately, according to the principle of establishing a modified DH link coordinate system, was determined. Then, the coordinate system of the whole link of the drilling arm was established, and the geometric parameters of the arm were added. The complete link coordinate system obtained is shown in Figure 4.

The M-DH parameters of the drilling arm were finally determined according to the link coordinate system, as shown in

Table 1. The drill arm improved the DH parameters.

i	ai−1 (mm)	αi−1 (rad)	di (mm)	θi (rad)
1	0	0	0	θ1
2	0	pi/2	0	pi/2 + θ2
3	0	pi/2	1200 + d3	pi
4	0	pi/2	0	pi + θ4
5	200	pi/2	400	pi/2 + θ5
6	0	pi/2	200 + d6	0

, where a_i−1 indicates the length of the connecting rod, α_i−1 indicates the torsion angle of the connecting rod, θ_i denotes the joint variable, and d_i indicates the connecting rod offset.

3.2. Analysis of the Positive Kinematics of the Drilling Arm of the Anchor Drilling Robot

The positive kinematics of the robot involve obtaining the positional attitude of the end effector with known relative position relationships (joint angles) of the connecting rods. The order of their products is as follows:

$${}^{i-1}T_i=Rot(x_i,{\alpha }_{i-1})\times Trans(x_i,{\alpha }_{i-1})\times Rot(z_i,{\theta }_i)\times Trans(z_i,d_i)$$

(1)

The generic chi-square transformation matrix between adjacent coordinate systems under the modified DH (M-DH) parameters is:

$${}^{i-1}T_i=\left[\begin{array}{cccc}\cos {\theta }_i& -\sin {\theta }_i& 0& a_{i-1}\\ \sin {\theta }_i\cos {\partial }_{i-1}& \cos {\theta }_i\cos {\partial }_{i-1}& -\sin {\partial }_{i-1}& -\sin {\partial }_{i-1}{d}_{{}_i}\\ \sin {\theta }_i\sin {\partial }_{i-1}& \cos {\theta }_i\sin {\partial }_{i-1}& \cos {\partial }_{i-1}& \cos {\partial }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]$$

(2)

The MD-H parameters in Table 1 are brought into the respective generic chi-square transformation matrices to obtain the ${}^{0}T_1$, ${}^{1}T_2$, ${}^{2}T_3$, ${}^{3}T_4$, ${}^{4}T_5$, and ${}^{5}T_6$ matrices, as follows:

$${}^{0}T_1=\left[\begin{array}{cccc}\cos {\theta }_1& -\sin {\theta }_1& 0& 0\\ \sin {\theta }_1& \cos {\theta }_1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(3)

$${}^{1}T_2=\left[\begin{array}{cccc}-\sin {\theta }_2& -\cos {\theta }_2& 0& 0\\ 0& 0& -1& 0\\ \cos {\theta }_2& -\sin {\theta }_2& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(4)

$${}^{2}T_3=\left[\begin{array}{cccc}-1& 0& 0& 0\\ 0& 0& -1& -(1200+d_3)\\ 0& -1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(5)

$${}^{3}T_4=\left[\begin{array}{cccc}-\cos {\theta }_4& \sin {\theta }_4& 0& 0\\ 0& 0& -1& 0\\ -\sin {\theta }_4& -\cos {\theta }_4& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(6)

$${}^{4}T_5=\left[\begin{array}{cccc}-\sin {\theta }_5& -\cos {\theta }_5& 0& 200\\ 0& 0& -1& -400\\ \cos {\theta }_5& -\sin {\theta }_5& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(7)

$${}^{5}T_6=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& -1& -(200+d_6)\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(8)

The total chi-square change matrix of the end coordinate system of the arm with respect to the base coordinate system is obtained by multiplying the chi-square change matrix sequentially:

$${}^{0}T_6={}^{0}T_1\times {}^{1}T_2\times {}^{2}T_3\times {}^{3}T_4\times {}^{4}T_5\times {}^{5}T_6=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]$$

(9)

In the formula, a and o represent the proximity vector and the direction vector, respectively; n represents the normal vector; and p represents the position vector. The unit orthogonal vectors n, o, and a describe the attitude of the drilling rig relative to the base coordinate system of the drill arm, and p describes the position of the drilling rig relative to the base coordinate system of the drill arm. According to the above analysis, the corresponding values of each variable are substituted into Formula (9), and the spatial pose of the drilling rig relative to the base coordinate system of the drilling arm can be obtained. The spatial pose relative to the body coordinate system of the drilling and anchoring robot can be obtained by coordinate system transformation.

3.3. Reachable Workspace of Drill Arm for Anchor Drilling Robots

The accessible working space of a robot is the overall volume of space swept by its end effector when the robot performs all possible actions. The reachable working space is limited by the geometry of the robot and the mechanical limits on each joint.

The reachable working space of the drilling anchor robot end effector (drill rig) is an important parameter reflecting the performance of the drilling anchor robot support. This paper uses Monte Carlo random sampling to calculate the reachable working space of the drill arm, with each joint’s angle being randomly selected within the joint’s range. The simulation model of the arm is constructed by first assigning values to the arm-related parameters in the Robotic Toolbox according to the defined kinematic parameters of the arm. Next, 30,000 random joint variables are generated and sequentially substituted into the positive kinematic equations for the solution. Finally, the points representing each reachable position of the end effector (drill rig) are marked in 3D space, creating a dot matrix that represents the reachable working space of the drill arm. The subsequent trajectory planning of the drilling arm will be carried out in the accessible working space. The results of the simulation of the reachable workspace of the drill arm end effector (drill rig) are shown in Figure 5. Figure 6 shows the projection of the drilling arm movement space in the XOY, XOZ, and YOZ planes. The results show that the reachable working space of the drill rig in the drill arm coordinate system spans x [0, 2193.2], y [0, 2177.3], and z [0, 2203.3] (in mm).

4. Drill Arm Trajectory Planning Based on Improved RRT

4.1. RRT Algorithm

The traditional path planning algorithms are the artificial potential field method, the fuzzy rule method, the genetic algorithm, the neural network, and the ant colony optimization algorithm, among others. However, each of these methods requires the modeling of an obstacle in a defined space; the computational complexity is exponentially related to the robot’s degrees of freedom, so it is not suitable for solving the planning of multi-degree-of-freedom robots in complex environments. In the complex, dusty, and poorly illuminated environment of coal mines underground, a path planning algorithm based on Rapidly Expanding Random Trees (RRTs, rapid-expanding random trees) is characterized by its ability to search high-dimensional spaces quickly and efficiently by randomly sampling points in the state space and directing the search to blank regions to find a planned path from the start point to the goal point, which is suitable for solving the path planning of multi-degree-of-freedom robots in complex and dynamic environments; the algorithm has high coverage and a wide search range. The RRT algorithm generates a random tree through incremental, step-by-step iterations. The RRT algorithm node expansion process is shown in Figure 7.

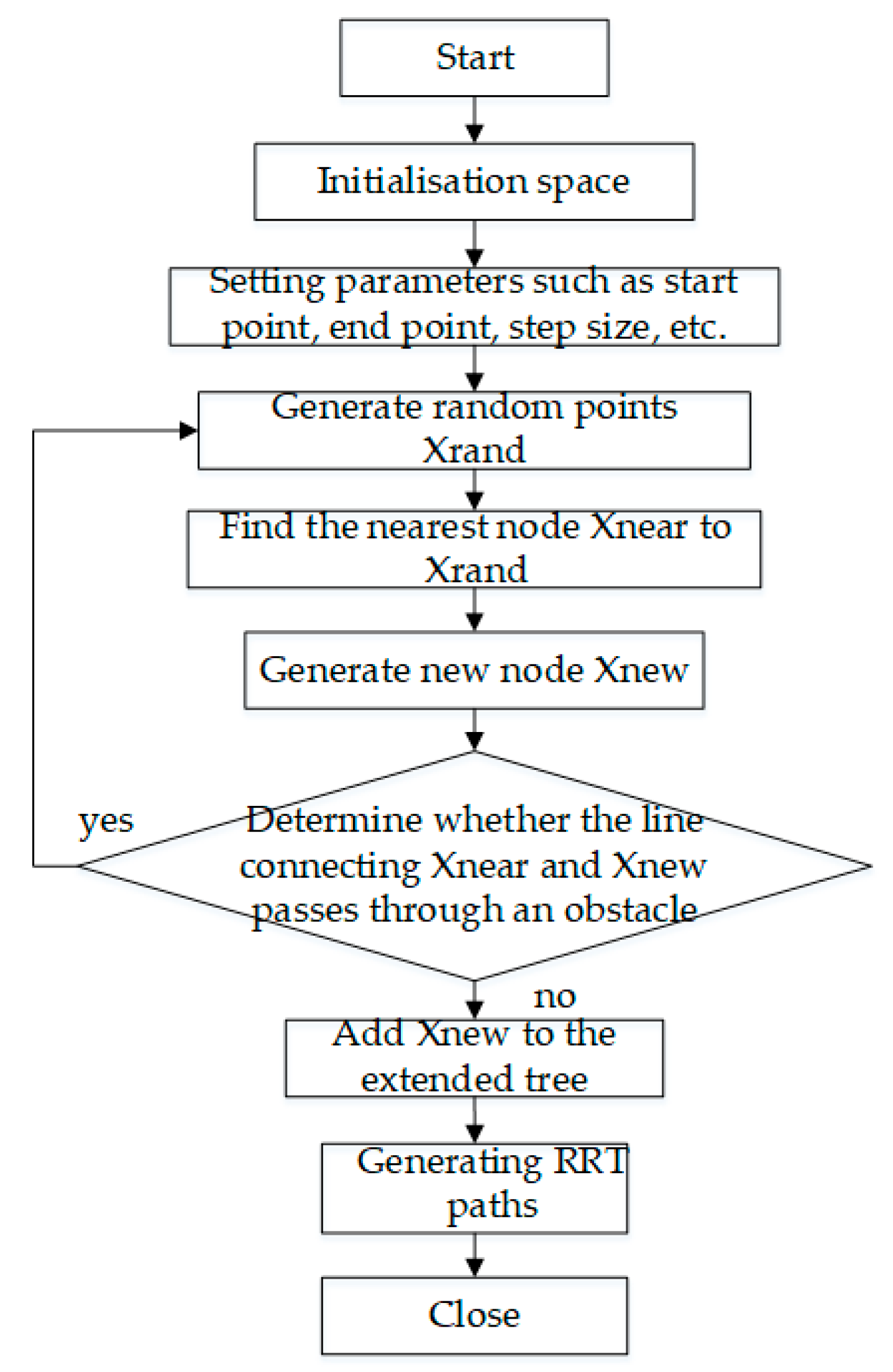
The specific steps of the RRT algorithm are shown in Figure 8.

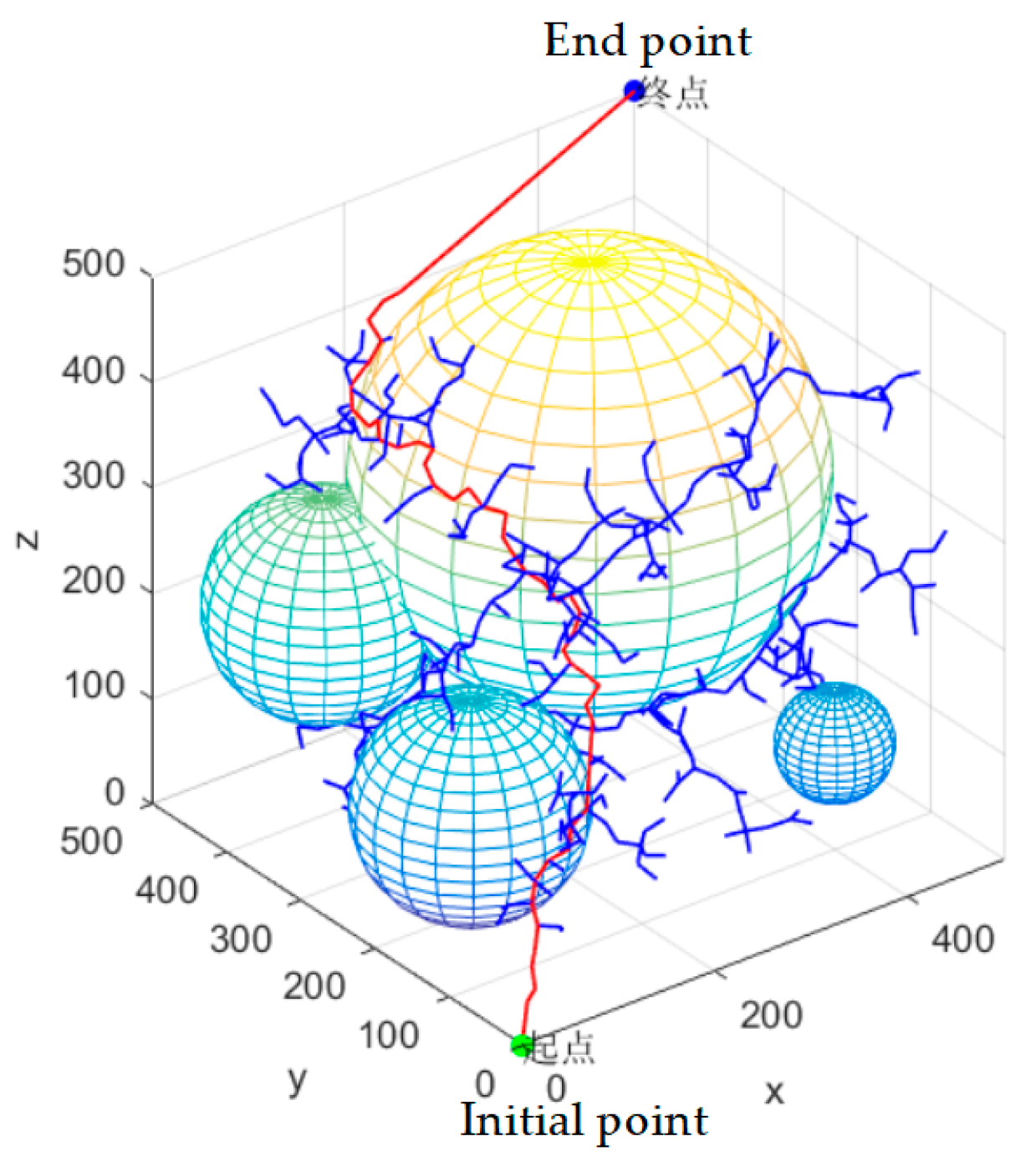
In the first step, the whole space is initialized, defining parameters such as the initial point, the end point, the number of sampling points, and the step size U between points. In the second step, a random point Xrand is generated in the space. In the third step, find the nearest point Xnear this random point in the set of points in the known tree. In the fourth step, intercept the point Xnew from Xnear in the direction of the line from Xnear to Xrand in step U. In the fifth step, determine if there is an obstacle between Xnear and Xnew, and if so, discard the point. In the sixth step, add new points to the tree collection. Cycle through steps two to six. Loop end condition: there is a new point within the set neighborhood of the end point.

In summary, the RRT algorithm generates random trees through incremental, step-by-step iterations and uses them to search for paths in high-dimensional spaces, avoiding spatially complex modeling and reducing computational costs. It is therefore suitable for solving the path planning problem of multi-degree-of-freedom robots in complex environments.

4.2. Improved RRT Algorithm

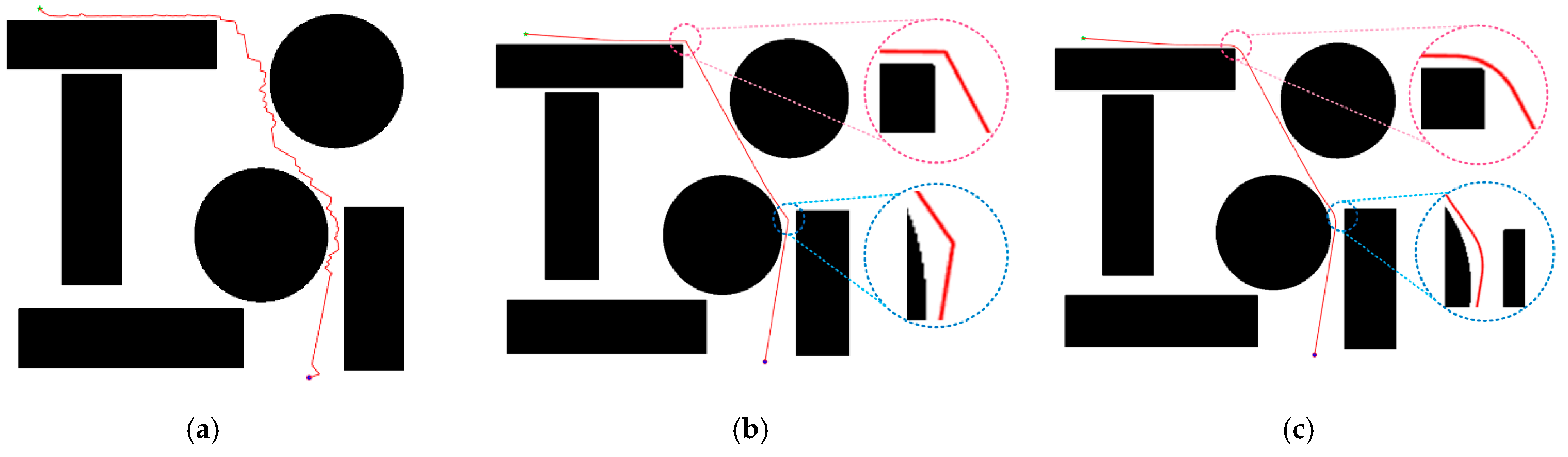
The algorithm flow shows that the RRT algorithm aims to find a path from the start point to the end point, starting from the beginning and keeping searching towards the end. But there are some drawbacks: The paths searched are not optimal and are inefficiently sampled throughout the space. The drawbacks of the RRT algorithm are especially obvious in the three-dimensional, spatially complex environment of the coal mines underground. The RRT algorithm can obtain a path from the start point to the end point in the complex environment of coal mines underground, but the path obtained has problems such as not being smooth and having a long generation time. This leads to low efficiency and poor path quality. In order to solve the above problems, an improved RRT algorithm is proposed.

4.2.1. Artificial Potential Field Method

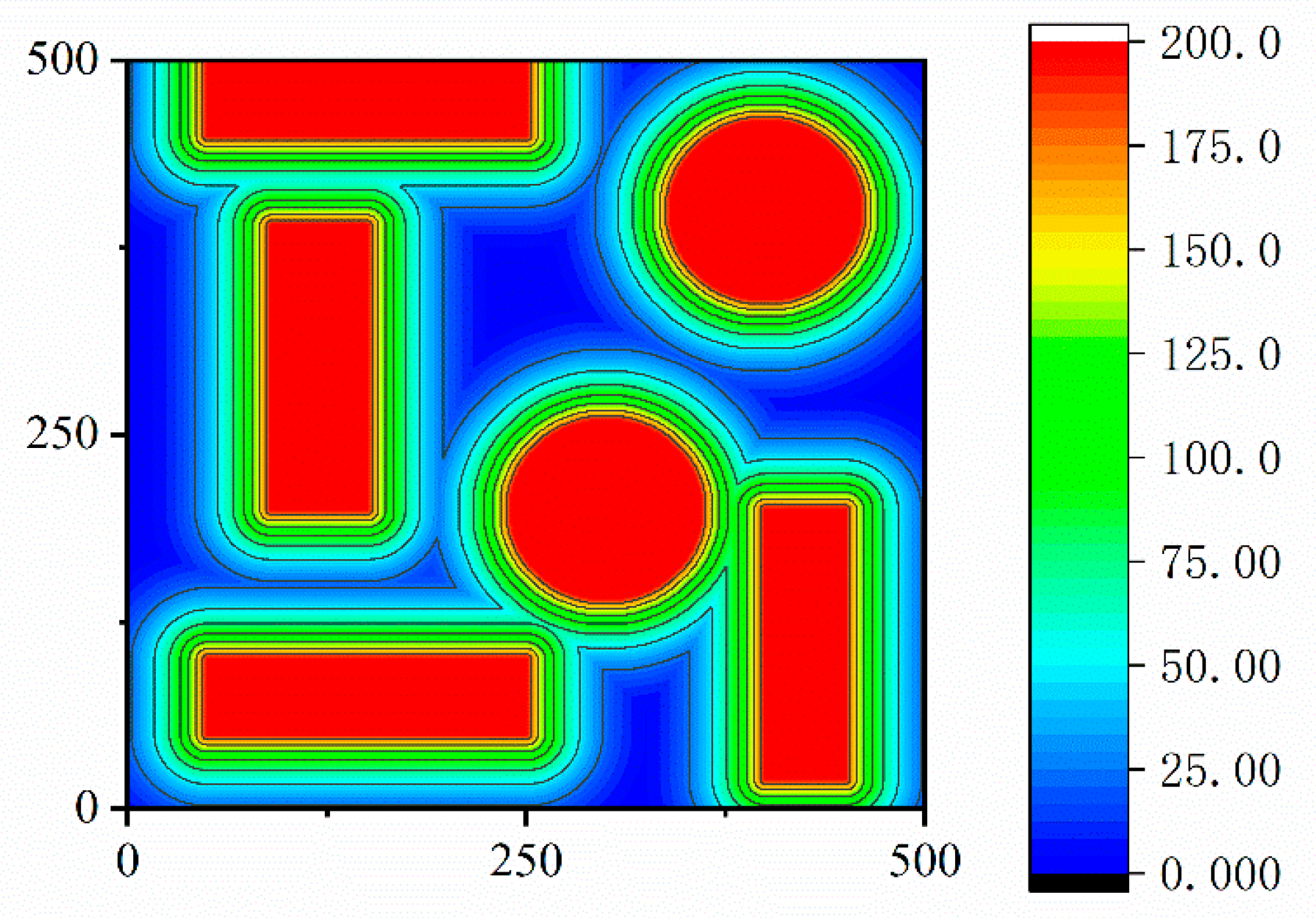
Firstly, to improve the efficiency of sampling and path generation, an artificial potential field factor is introduced. The potential field map is calculated for the entire known map by considering the target point location as the lowest point of the potential and the obstacles as the highest point of the potential. The gravitational potential field is mainly related to the distance between the end effector (drilling rig) and the drill hole at the target point. The greater the distance, the greater the potential energy value of the end effector (drilling rig). The smaller the distance, the smaller the potential energy value of the end effector (drilling rig), and the greater the potential energy value of the end effector (drilling rig):

$$U_{att}(q)=\frac{1}{2}\eta {\rho }^2(q,q_g)$$

(10)

$$F_{att}(q)=-\nabla U_{att}(q)=-\eta \rho (q,q_g)$$

(11)

where $\eta$ is a scale factor indicator and $\rho (q,q_g)$ is the distance between the current state of the end effector (drilling rig) and the target. The factor that determines the obstacle’s repulsive potential field is the distance between the end effector (drilling rig) and the obstacle. When the end effector (drilling rig) does not enter the area of influence of the obstacle, it is subjected to a potential energy value of zero. The greater the distance between the end effector (drilling rig) and the obstacle after it enters the area of influence of the obstacle, the smaller the potential energy value of the end effector (drilling rig). The greater the potential energy value of the end effector (drilling rig) after it enters the area of influence of the obstacle, the smaller the distance and the greater the value of potential energy to which the end effector (drilling rig) is subjected. The potential field function of the repulsive potential field is given by:

$$U_{req}(q)=\left\{\begin{array}{cc}\frac{1}{2}k(\frac{1}{\rho (q,q_0)}-\frac{1}{{\rho }_0}),& 0\le \rho (q,q_0)\le {\rho }_0\\ 0,& \rho (q,q_0)\ge {\rho }_0\end{array}\right.$$

(12)

The corresponding repulsive force is the negative gradient force of the repulsive potential field:

$$F_{req}(q)=\left\{\begin{array}{cc}k(\frac{1}{\rho (q,q_0)}-\frac{1}{q_0})\frac{1}{{\rho }^2(q,q_0)},& 0\le \rho (q,q_0)\le {\rho }_0\\ 0,& \rho (q,q_0)\ge {\rho }_0\end{array}\right.$$

(13)

where $\rho (q,q_0)$ represents the distance between the object and the obstacle and ${\rho }_0$ represents the radius of influence of each obstacle. Based on the gravitational field function and the repulsive field function defined above, a composite field can be obtained for the entire running space; the size of the combined potential field is the sum of the repulsive and gravitational potential fields. Therefore, the total function of the combined potential field is:

$$U(q)=U_{att}(q)+U_{req}(q)$$

(14)

The combined force applied is:

$$F(q)=-\nabla U(q)=F_{att}(q)+F_{req}(q)$$

(15)

The combined forces of gravity and repulsion guide the drill arm closer to the target point. The force analysis of the end effector is shown in Figure 9.

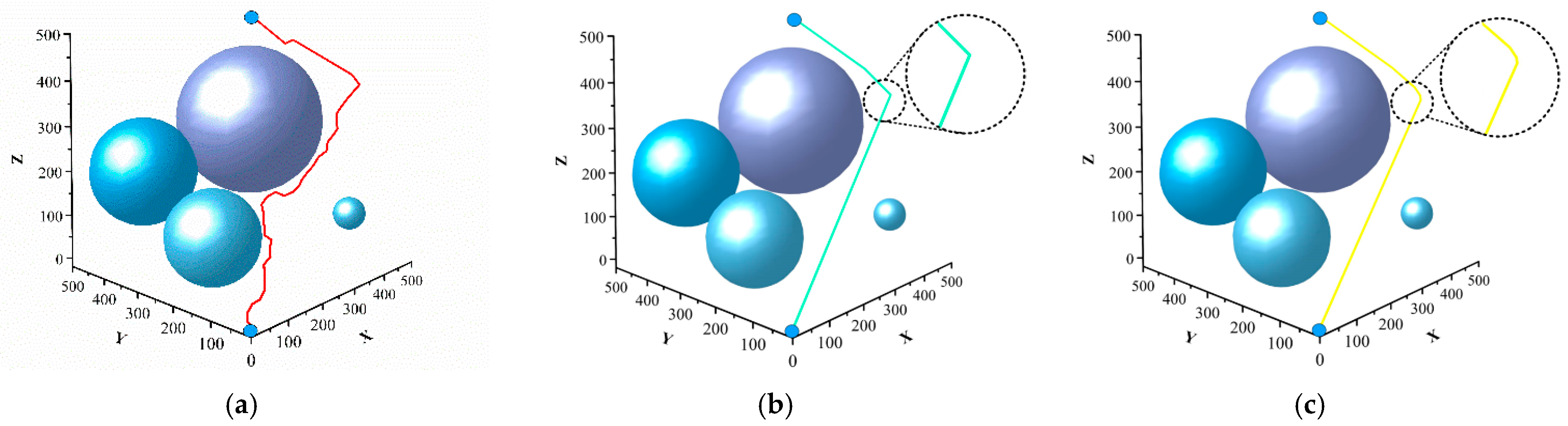
Secondly, in order to solve the problem of unsmooth paths and poor quality, a greedy algorithm is introduced to remove redundant points from the paths, and three-time B-splines are used to post-process the smooth paths.

4.2.2. Redundant Point Rejection Based on Greedy Algorithm

The basic idea of the greedy algorithm is to develop a mathematical model to describe the problem, divide the problem to be solved into subproblems, solve each subproblem to obtain a locally optimal solution to the subproblem, and synthesize the locally optimal solutions of the subproblems into one solution of the original solution problem. The specific steps are as follows:

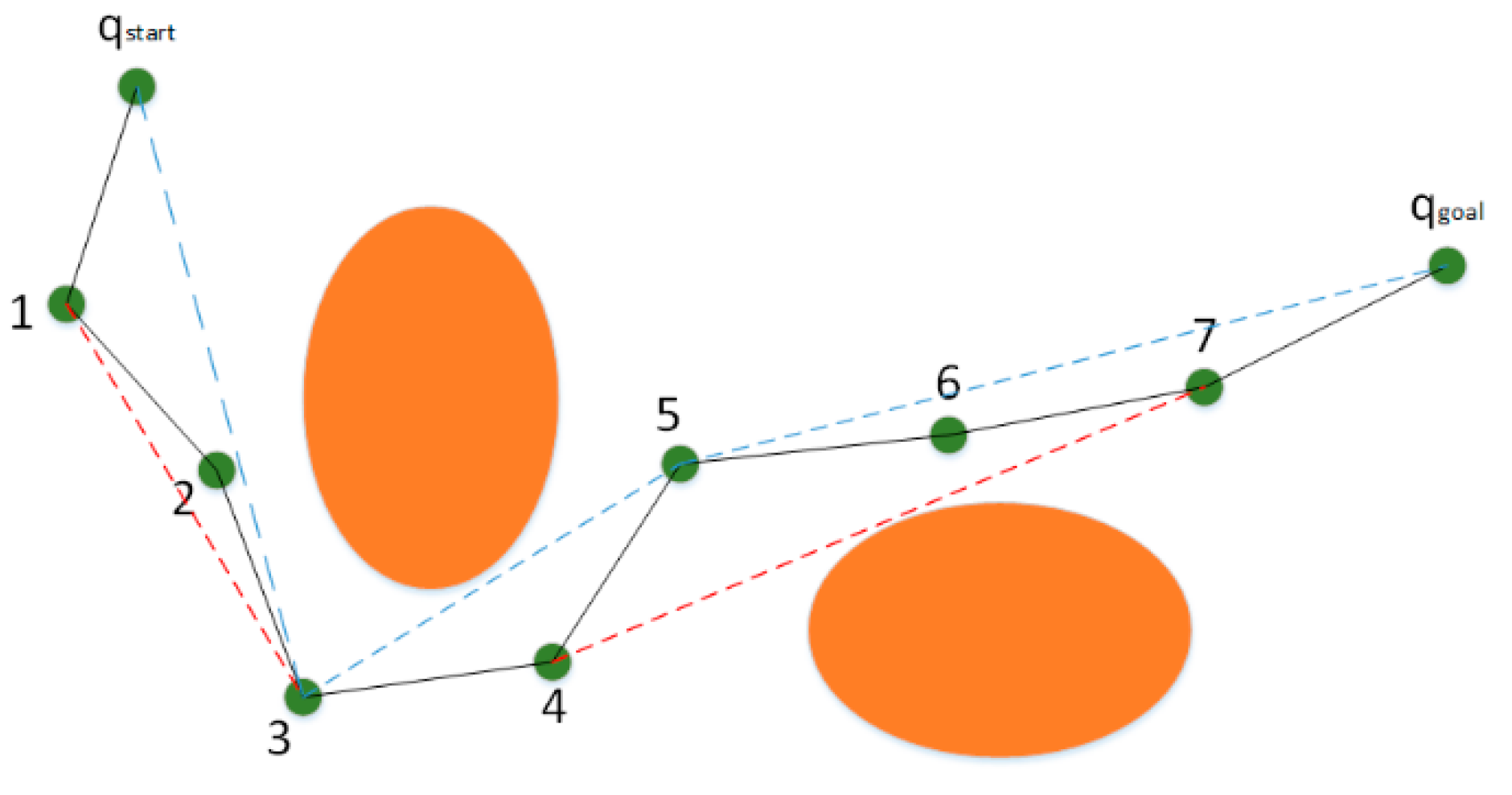
Firstly, the path starts at Xstart. Set a step size X to divide the path into segments according to the step size X. The X1 point is obtained by taking the distance of step X from the starting point. Connect the points Xstart and X1, and if there is no obstacle between them, then discard the X1 point. Then, connect Xstart with X2 and continue to repeat the above judgment operation. As shown in Figure 10, the path between Xstart and X4 can be optimized as a segment. If there is an obstacle between the two, it means that the small section of the path is already the optimal path. Next, using X4 as a starting point, connect X4 to X5 and continue with the optimization steps. Finally, continue the cycle until all of the several points into which the path is divided have been run. The path obtained at this point will be shorter and more efficient than the initial path obtained by the RRT algorithm. The greedy algorithm removes the redundant points of the path as shown in Figure 10. Among them, the orange circle represents the obstacle, 1–7 points represent the sampling point, the black line represents the original sampling path, and the blue and red lines represent two paths after removing redundant points from different angles.

4.2.3. Smoothing Paths Based on Cubic B-Splines

B-spline curves are a class of curves developed on the basis of Bezier curves that overcome the inconvenience caused by the overall controllability of the Bezier curve. Three planar discrete points determine a quadratic B-spline curve, and four planar discrete points determine a cubic B-spline curve. Bezier curves are irregular curves that require the construction of a mixture of interpolating polynomials between the start and endpoints; usually, an nth-degree polynomial is defined by n + 1 vertices and then given a position vector P(i-0,1,2,...n) of n + 1 points in space. The interpolation formula for the coordinates of the points on the Bezier parametric curve is:

$$P(t)={\displaystyle {\sum }_{i=0}^n{P}_i}{F}_{i,k}(t)$$

(16)

where $P_i$ is the characteristic point of the control curve and $F_{i,k}(t)$ is the K-order B-spline basis function. The basis functions in the cubic B-spline curve equation are:

$$F_{i,k}(t)=\frac{1}{k!}{\displaystyle {\sum }_{m=0}^{k-i}{(-1)}^m}(\begin{array}{c}m\\ k+1\end{array}){(t+k-m-j)}^k$$

(17)

where $(\begin{array}{c}m\\ k+1\end{array})$ denotes the factorial. Therefore, the cubic B-spline curve equation is:

$$P(t)=P_0\times F_{0,3}(t)+P_1\times F_{1,3}(t)+P_2\times F_{2,3}(t)+P_3\times F_{3,3}(t)$$

(18)

Three planar discrete points determine a quadratic B-spline curve, and four planar discrete points determine a cubic B-spline curve.

The matrix form of the parametric expression for the cubic B-spline curve is given by:

$$P(t)=\left[\begin{array}{cccc}{t}^3& t^2& t^1& 1\end{array}\right]\left[\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 3& 0\\ -3& 0& 3& 0\\ 1& 4& 1& 0\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\end{array}\right]\left(0\le t\le 1\right)$$

(19)

Let the four discrete points be $P_0$, $P_1$, $P_2$, and $P_3$. Let the midpoint be $M_1=\frac{1}{2}(P_0+P_2)$, $M_2=\frac{1}{2}(P_1+P_3)$. The starting point S of the curve is on the center line $P_1{M}_1$ of the $△P_0{P}_1{P}_2$, $\frac{1}{3}{P}_1{M}_1$ points from $P_1$. The starting point E of the curve is on the center line $P_2{M}_2$ of the $△P_1{P}_2{P}_3$, $\frac{1}{3}{P}_2{M}_2$ points from $P_2$. The tangent to the start of the curve is parallel to $P_0{P}_2$, and the tangent to the end is parallel to $P_1{P}_3$. The principle of cubic B-spline fitting is shown in Figure 11.

Introducing an artificial potential field factor into the map while optimizing the paths derived from the basic RRT algorithm based on the above greedy algorithm and cubic B-splines can increase the speed of path generation, reduce the length of the paths, and smooth the paths.

The artificial potential field factor and cubic B-spline curve fitting are introduced into the RRT algorithm. The next chapter introduces simulations and comparative analyses in the debugging software and prototype to verify the effectiveness of the improved algorithm.

5. Algorithm Experiment and Analysis

5.1. Comparison of Simulation and Analysis of RRT Algorithm and Improved RRT Algorithm in 3D Space

The working space of the drilling arm of the anchor drilling robot is a three-dimensional space, so it is also necessary to carry out simulation and comparison experiments in a three-dimensional space to verify the effectiveness of the improved algorithm. The 3D map is created in the workspace of the drilling arm, with a map range of 500 mm × 500 mm × 500 mm. Random obstacles are set inside the map, and random sampling points are all within the map range. The coordinates of the start point are (0,0,0), and the coordinates of the target point are (500,500,500). The 3D spatial map is shown in Figure 12.

Firstly, the gravitational and repulsive potential fields are set up in the 3D spatial map, and the combined potential field is synthesized as shown in Figure 13.

A total of 50 experiments in 3D spatial maps for the RRT algorithm and the improved RRT algorithm were performed. Both algorithms take the expansion step as u. The maximum number of samples taken during the sampling period is x. The coordinates of the start point are (0,0,0), and the coordinates of the target point are (500,500,500). The 3D spatial simulation results are shown in Figure 14.

Figure 15a depicts the initial path generated using the RRT algorithm. From this, it can be observed that the initial path is highly tortuous. Meanwhile, Figure 15b displays the path after optimization using the greedy algorithm. Upon comparison, it is evident that the redundant points within the path have been eliminated, resulting in a significant reduction in the path length. Figure 15c illustrates the path further optimized after the removal of the redundant points by the greedy algorithm. It is noteworthy that, following this enhancement, the inflection points of the path appear smoother. Such a design is intended to prevent potential damage to the end effector due to excessive bends during the path’s traversal.

After 50 experiments, the comparison between the RRT algorithm and the improved RRT algorithm in terms of time consumption and path length in 3D maps were shown in Figure 16.

5.2. Comparison of Simulation and Analysis of RRT Algorithm and Improved RRT Algorithm in 2D Space

In order to verify the effectiveness and superiority of the improved RRT algorithm, this paper presents simulation comparison experiments on the trajectory planning of a six-degree-of-freedom drilling arm of a drilling anchor robot in a reachable workspace. Firstly, the simulation is carried out on a two-dimensional map; the map is 500 × 500 in size, with random obstacles set up inside it. The random sampling points are all within the map, and the start and target points are customizable. The 2D map is shown in Figure 17.

Firstly, the gravitational and repulsive potential fields are set up in the map and synthesized into a combined potential field; the obstacle is the potential high point and the potential low point at the target point, as shown in Figure 18.

In this paper, 50 random sampling experiments are carried out for the basic RRT and the improved RRT algorithms in 2D maps. Both algorithms take the expansion step as u, the maximum number of samples during the sampling period is x, and the start and target points are customizable. This experiment defines the starting point as (20,480) and the target point as (350,10). The 2D simulation results are shown in Figure 19.

Figure 20a shows the initial path generated using the RRT algorithm in a 2D environment. From it, it is also observed that this initial path exhibits a high degree of curvature. Meanwhile, Figure 20b demonstrates the path after applying the greedy algorithm for optimization. By comparison, we clearly see that the redundant points in the path have been removed, resulting in a significant reduction in the path length. Figure 20c, on the other hand, depicts the path that is further optimized based on the removal of the redundant points by the greedy algorithm. The turning points of the path appear smoother, which is designed to avoid end effector damage due to excessive turning during path conduction.

As shown in the figure above, it is evident in the 2D and 3D map simulations that the improved RRT algorithm can effectively optimize the base path, improve the path planning efficiency, enhance the path smoothness, and shorten the path length. For the results of the 50 experiments, the data collection of the path time and length of the RRT algorithm and the improved RRT algorithm under different maps was carried out, and the results are shown below.

After 50 experiments, the comparison between the RRT algorithm and the improved RRT algorithm in terms of time consumption and path length in 2D maps were shown in Figure 21.In terms of time consumption, the RRT algorithm has a long sampling time, poor stability, and average trajectory planning times of 114.2303 s (2D) and 4.0277 s (3D). The average path planning times of the improved RRT algorithm are 91.325174 s (2D) and 3.0588 s (3D). The average path planning time improved by 20.05% (2D) and 24.06% (3D). Improving the RRT algorithm can effectively improve sampling efficiency and reduce the time spent on trajectory planning. In terms of trajectory planning path length, the average path lengths of the basic RRT algorithm are 1207.9428 mm (2D) and 973.3125 mm (3D). The average path lengths after the removal of the redundant points by the greedy algorithm are 1032.1995 mm (2D) and 871.5103 mm (3D). The lengths of the path after three-time B-spline smoothing are 1008.0407 mm (2D) and 863.3197 mm (3D); the average path lengths were reduced by 16.55% (2D) and 11.30% (3D). It can be clearly seen that path optimization by greedy algorithms and cubic B-splines is effective and leads to higher-quality paths.

5.3. Prototype Platform Experimental Verification

The feasibility and effectiveness of the present improved algorithm were verified using a prototype anchor drilling robot platform. Simulating the process of anchor drilling and robotic anchoring and drilling in underground coal mines, the end effector drilling machine of the drilling arm needs to autonomously plan a drilling path from the starting point to the steel strip hole. The main structure of the platform is described in Figure 22.

To set up the RRT algorithm and improved RRT algorithm trajectory planning experiments, set up the same starting point and ending point for the second hole of the steel strip, which can be accomplished by writing algorithms and control programs in the prototype’s host computer. The final RRT and improved RRT algorithm trajectories were obtained as shown in Figure 23 and Figure 24, respectively.

Meanwhile, 10 validation experiments were conducted on the prototype platform to collect data on the path time and length of the RRT and improved RRT algorithm trajectories, and the results are shown in Figure 25.

Figure 23 illustrates the process under the guidance of the RRT algorithm, where the end effector (drilling rig) progressively moves from the preset starting position to the steel tape hole (target position). Figure 23 displays the final, complete path for this process.

Figure 24 presents the trajectory when the end effector (drilling rig) moves step by step from the preset starting position to the steel tape hole (target position) after the enhancement of the RRT algorithm. Figure 24 shows the complete path of this optimized process. Upon careful observation, it is evident that the improved path, compared to the original one, is shorter in length and smoother in trajectory.

It can be seen that the improved RRT algorithm trajectory is better than the RRT algorithm trajectory in terms of both time and path, which verifies the feasibility and effectiveness of the algorithm in this paper.

6. Conclusions

When establishing the kinematic model of a drilling arm, the kinematic analysis of the intelligent drilling and anchor robot is the basis for optimal design and motion control, allowing the kinematic positive solution and M-DH solution parameters to be solved. The Monte Carlo method is used to solve the motion space of the drilling and anchor module to verify that it meets the requirements of roadway support.

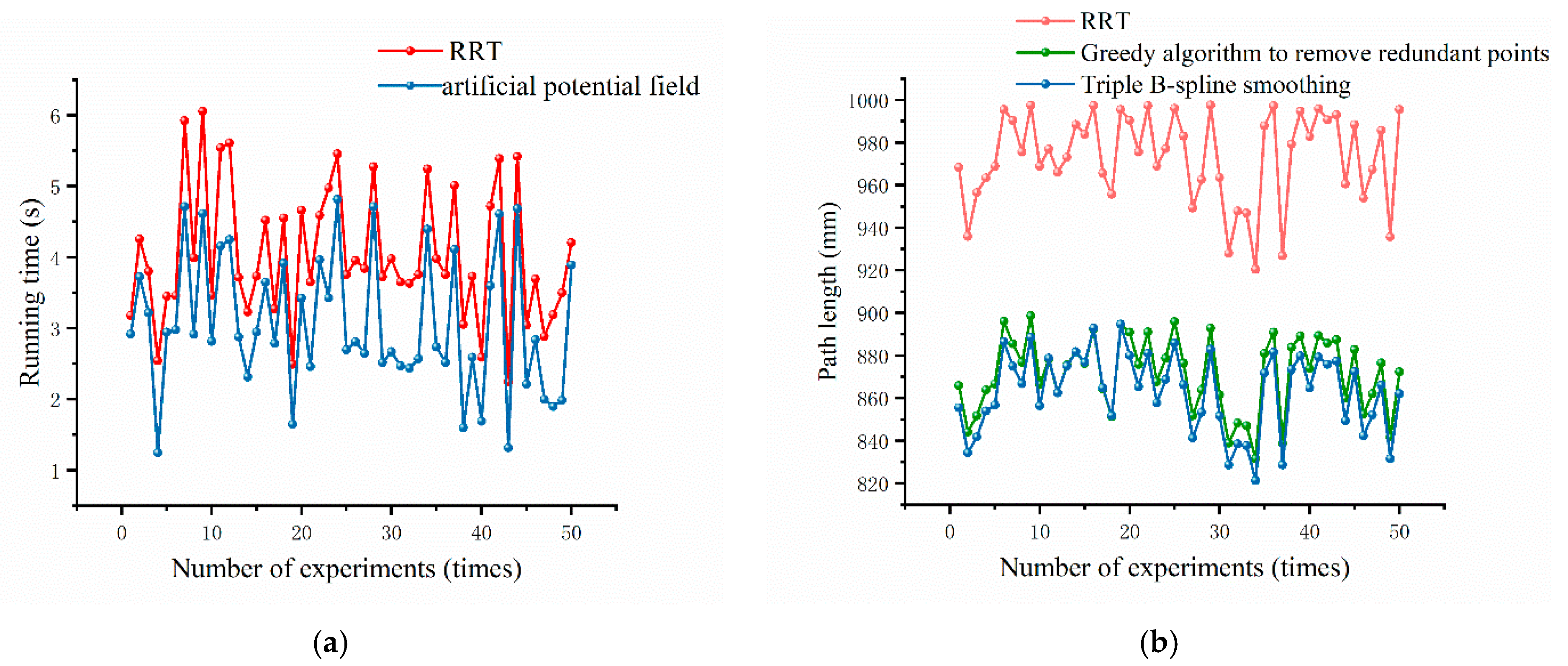
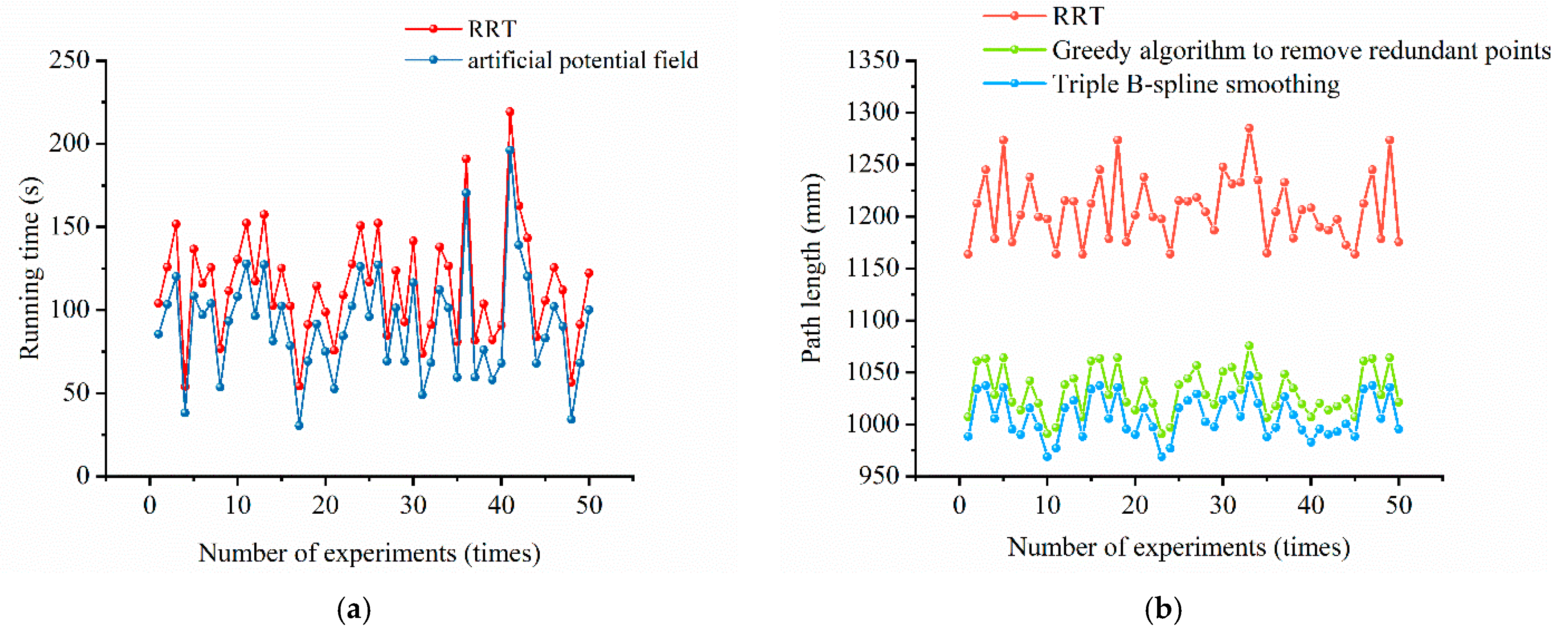
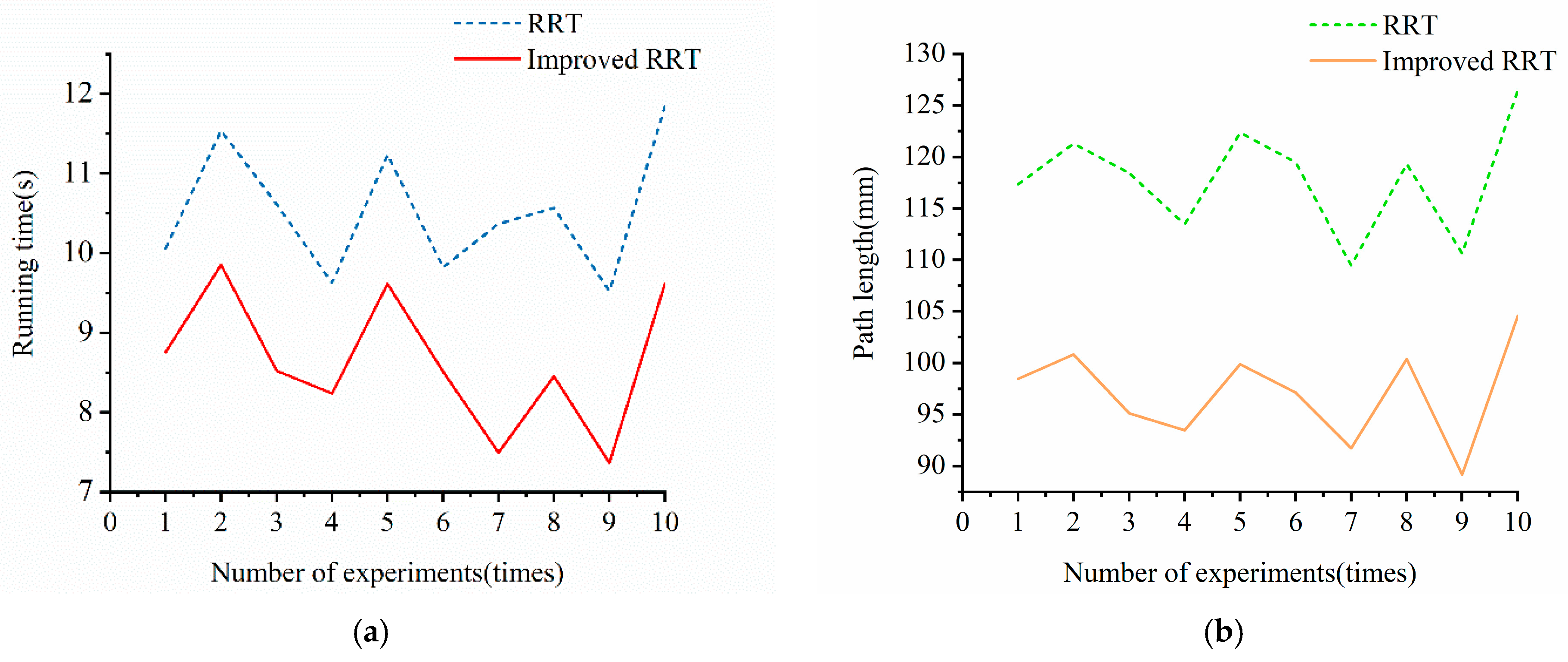
By introducing an artificial potential field factor, treating the target point location as the lowest point of potential energy and obstacles as the highest point of potential energy, and calculating the potential field map of the whole known map, the average speed of sampling and path generation is improved by 22%.

Aiming at the roughness of the path generated by the basic RRT algorithm, the greedy algorithm and the cubic B-spline are used to optimize the original path. The greedy algorithm is used to remove the redundant points, and the cubic B-spline is used to smooth the path; the average length of the path is reduced by 14% so as to improve the quality of the trajectory.

Through the comprehensive subjective and objective analysis of the kinematic modeling of the drilling and anchoring robot and the performance of the improved RRT algorithm, it is concluded that the improved RRT algorithm proposed in this paper for the trajectory planning of the drilling arm of the drilling and anchoring robot has strong robustness and real-time performance. The results show that the algorithm can provide high-quality and reliable information support for the tasks of trajectory planning and control of the drilling and anchoring robot.