Research on Lateral Maneuverability of a Supercavitating Vehicle Based on RBFNN Adaptive Sliding Mode Control with Rolling Restriction and Planing Force Avoidance
Abstract
:1. Introduction
- (1)
- Compared with previous studies on supercavitating vehicles, this paper constructs the 6-DOF kinematic and dynamic equations of a supercavitating vehicle in a comprehensive way, considering the cavity memory effects, the mass changes caused by fuel consumption, and frictional resistance during navigation.
- (2)
- A parallel control scheme is proposed based on the sliding mode control method. In this control scheme, longitudinal stability and lateral motion control are realized simultaneously. The dynamic controller is designed to avoid the nonlinear and discontinuous planing force. The adaptive RBFNN is adopted to estimate external disturbances and uncertainties in the dynamic models and compensate for the dynamic control law, which improves the system’s robustness.
- (3)
- Fin deflection angles and control efforts are the key factors influencing the lateral maneuverability of a supercavitating vehicle. A control allocation solver based on the least squares method is proposed to solve the control input of each actuator in real time with roll restriction as a constraint. To the best of the authors’ knowledge, no literature has proposed this kind of method in the field of supercavitating vehicles.
2. Supercavitating Vehicle Model
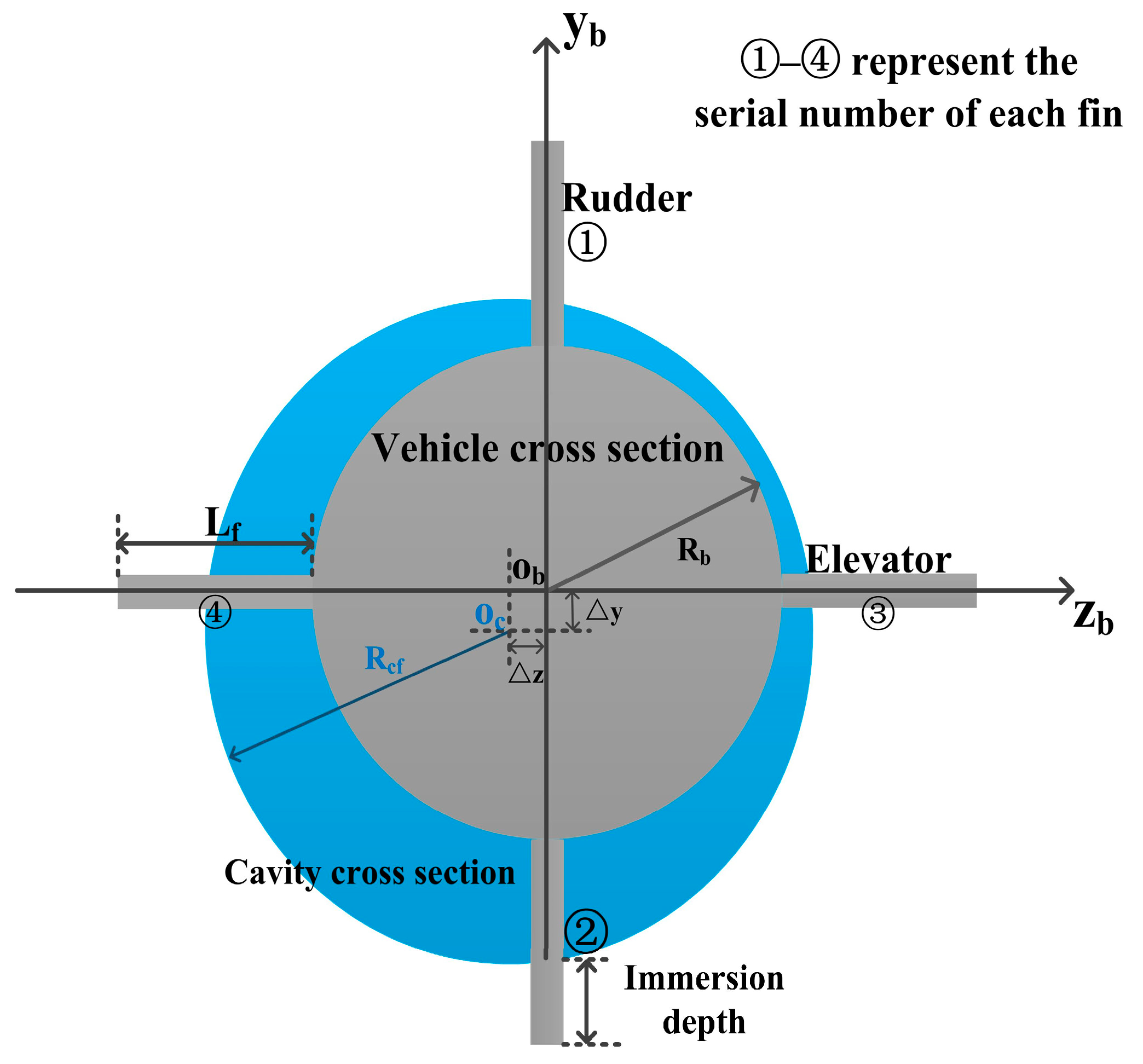
2.1. Geometry of the Supercavitating Vehicle
2.2. Supercavitating Vehicle Reference Frames
2.3. Dynamic and Kinematic Models
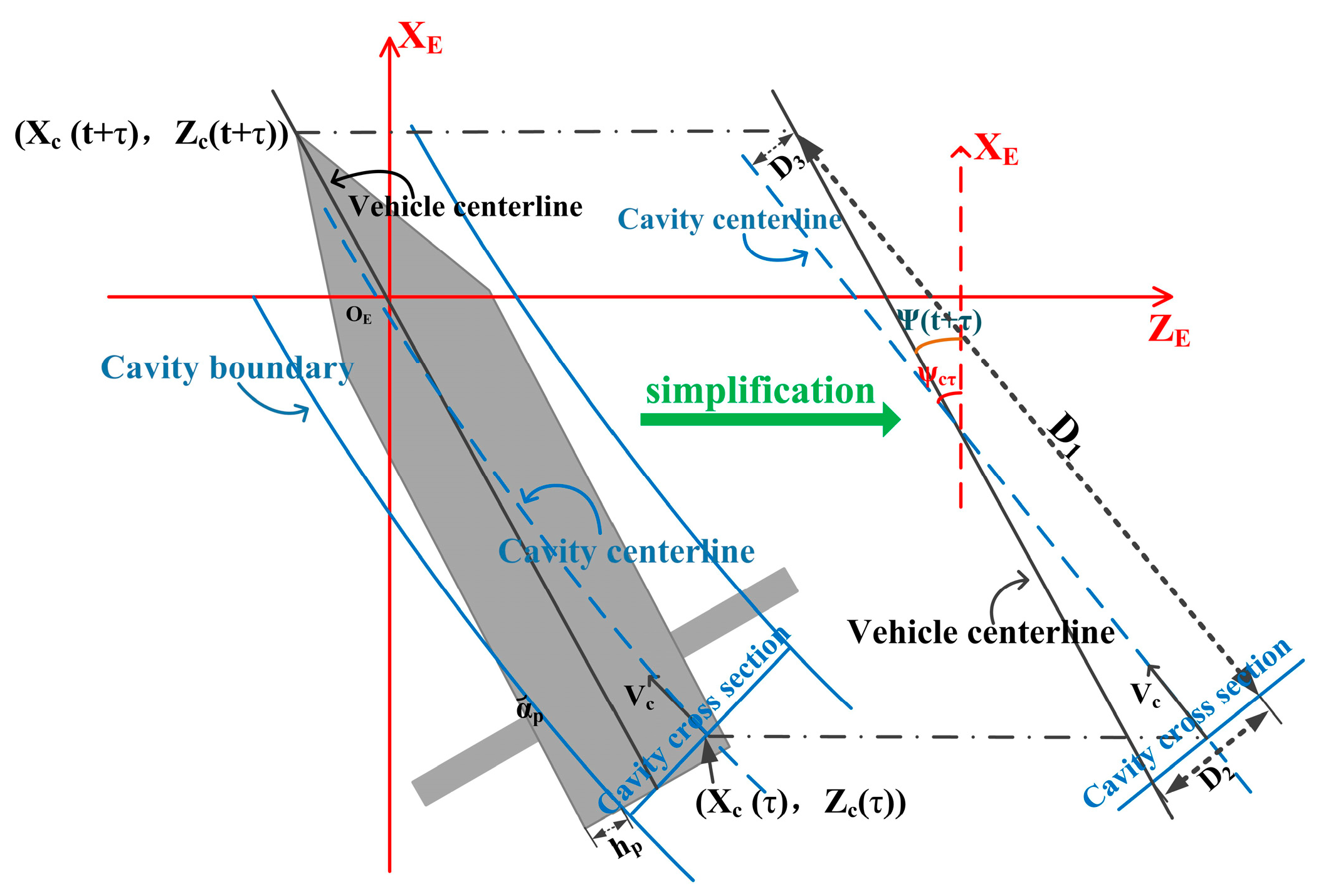
2.4. Supercavity Model
2.5. Analysis and Formulation of Forces Acting on the Vehicle
2.5.1. Planing Force
2.5.2. Fin Forces
2.5.3. Frictional Drag
2.5.4. Cavitator Force
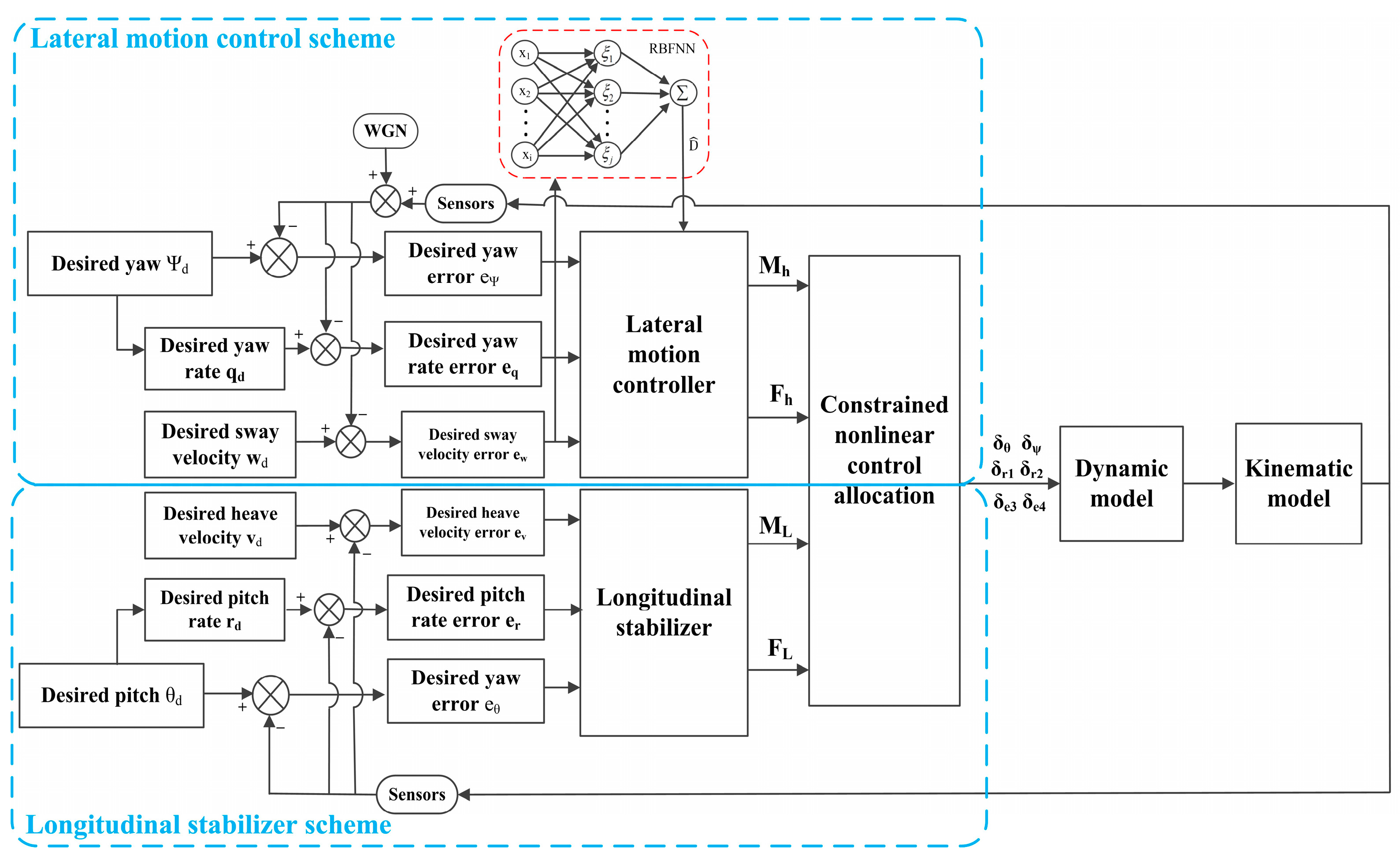
3. Controller Design
3.1. Lateral Motion Controller Design
3.2. Longitudinal Stabilizer Design
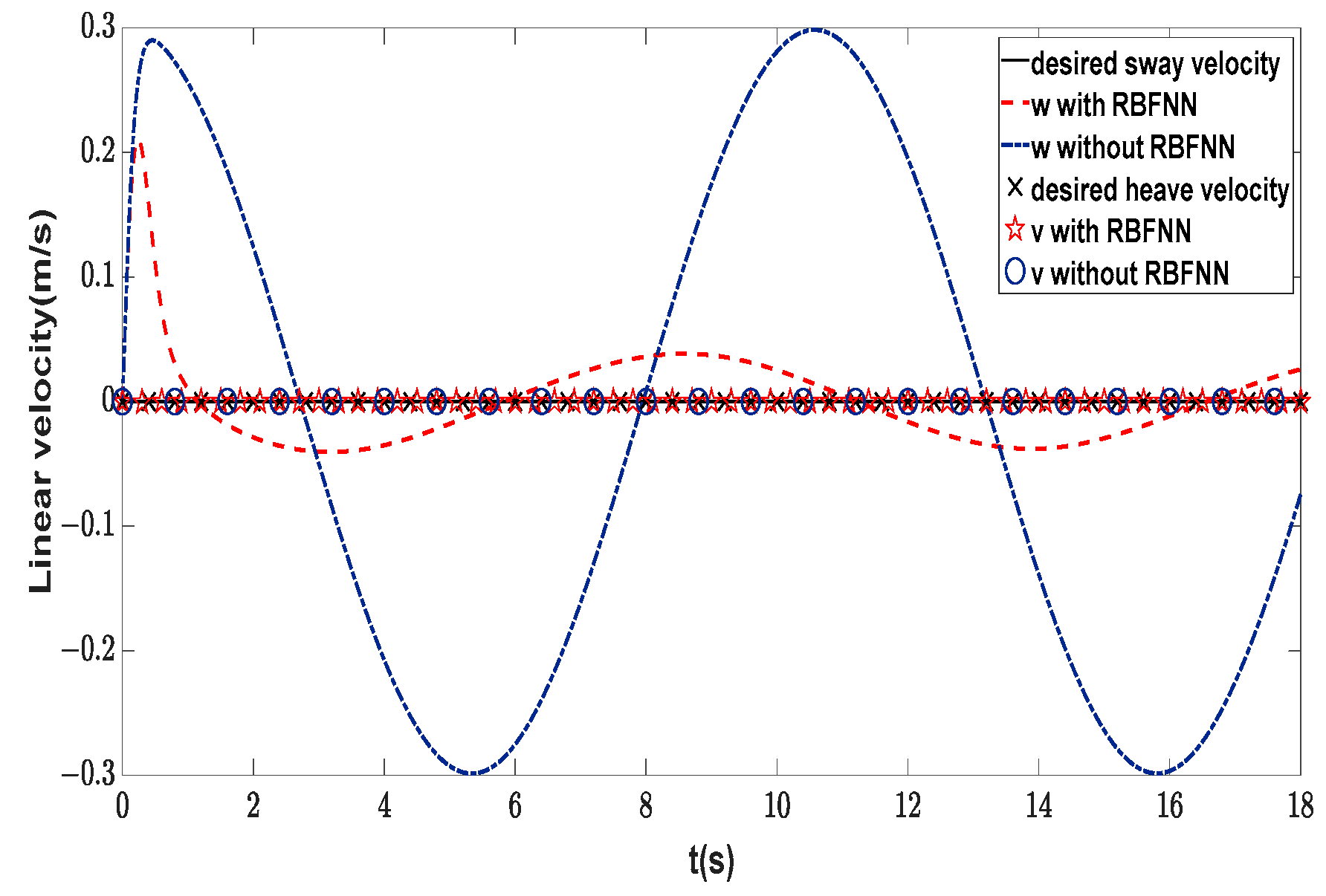
3.3. Adaptive RBFNN Approximator Design
3.4. Control Allocation
4. Numerical Simulation and Discussion
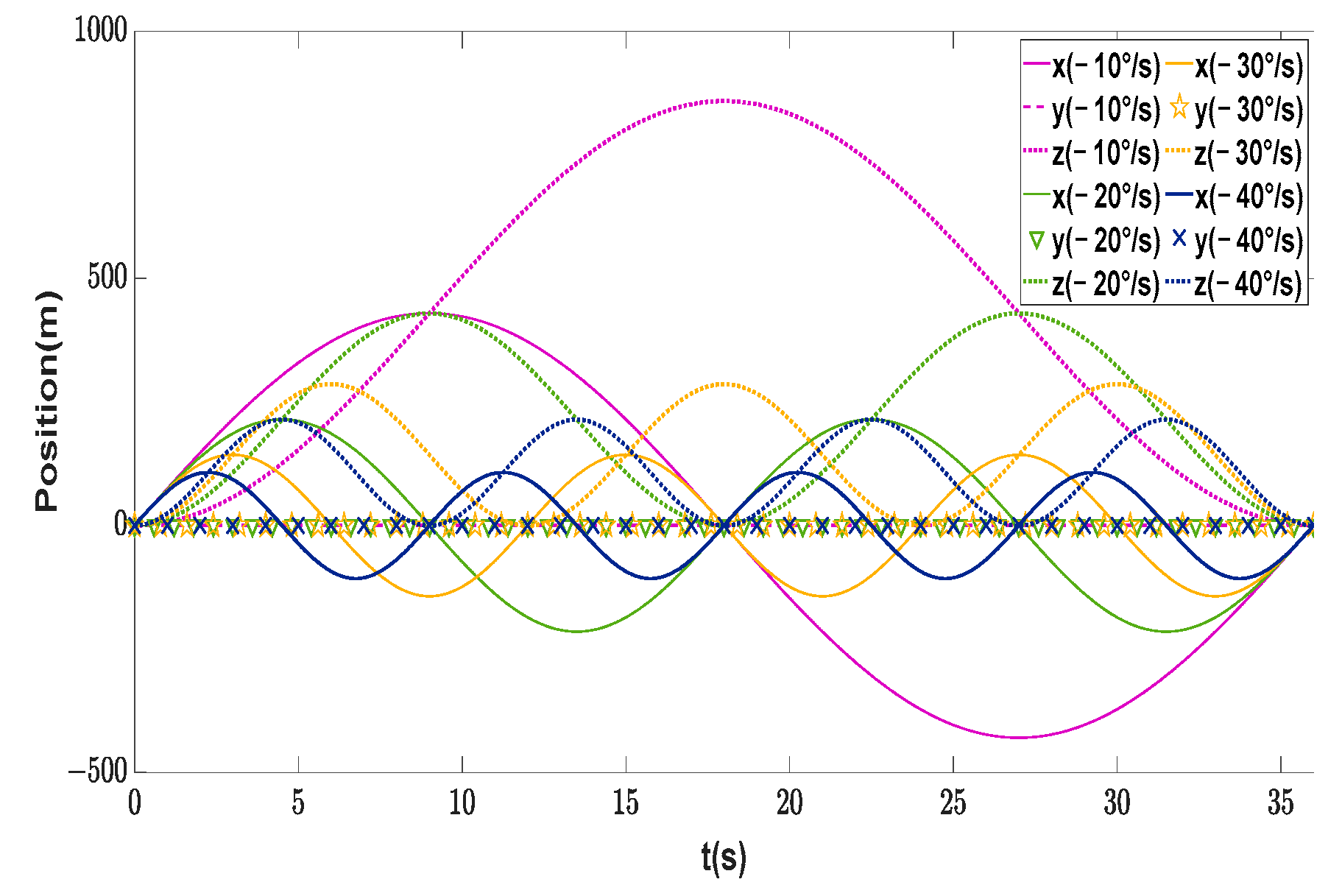
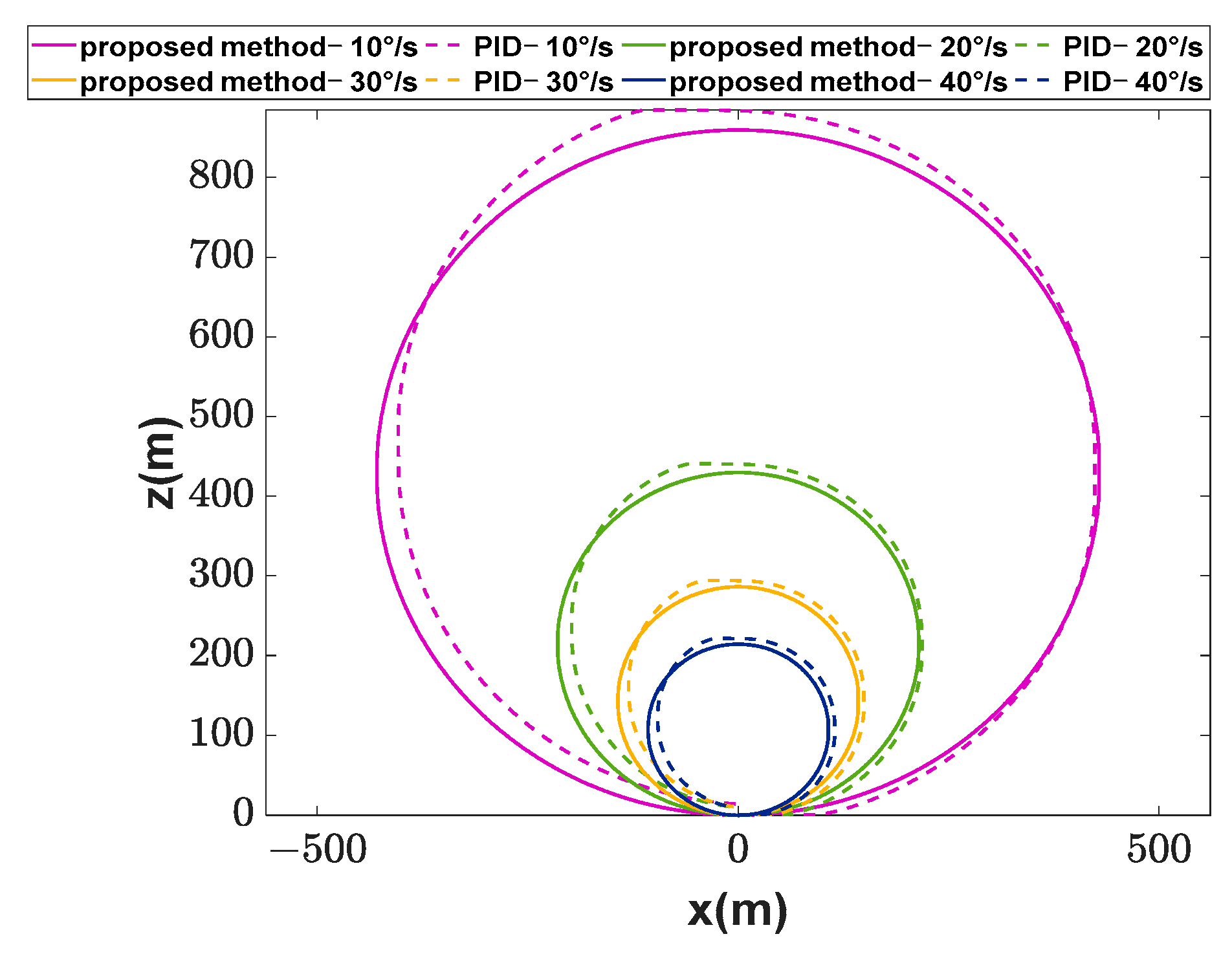
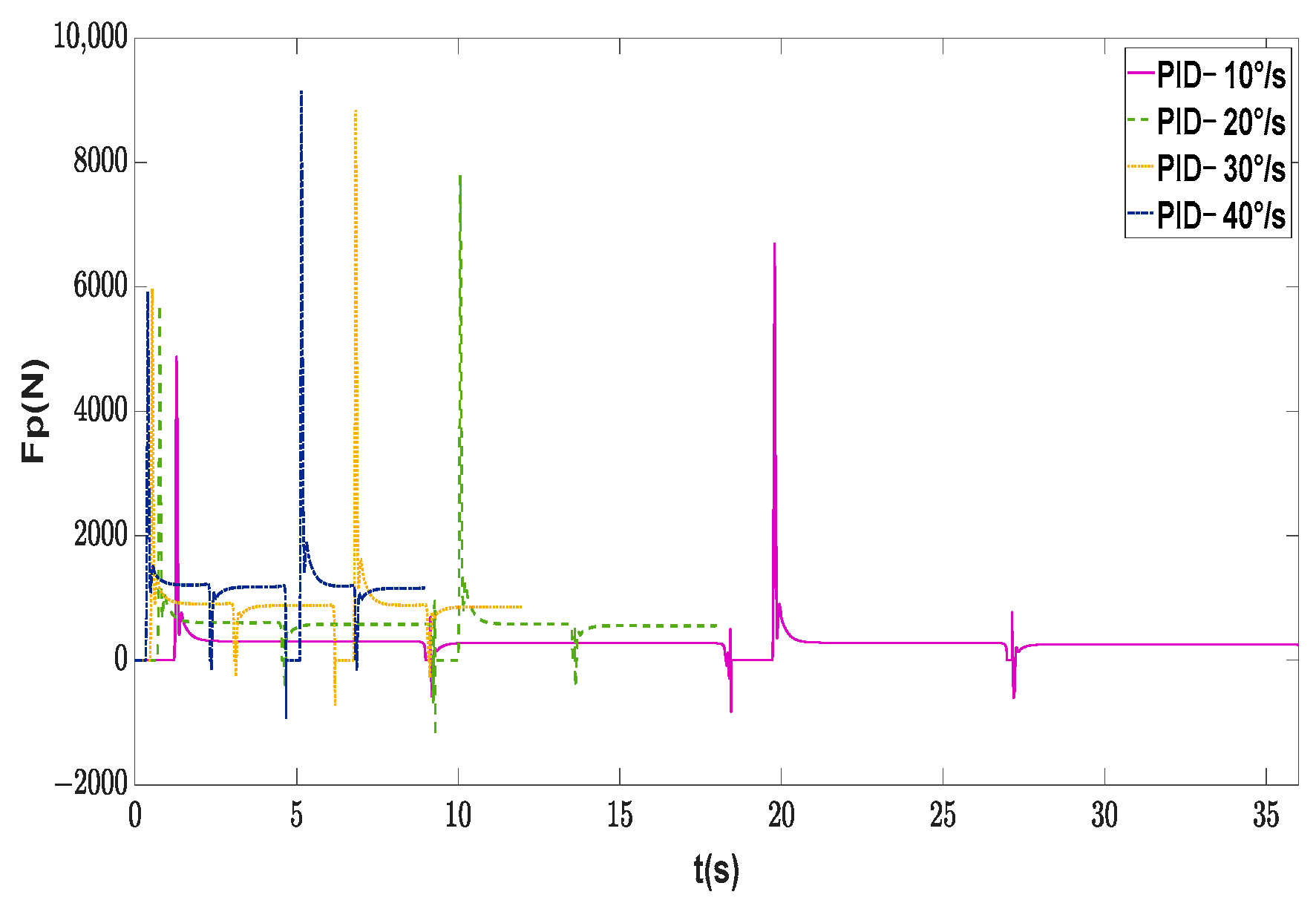
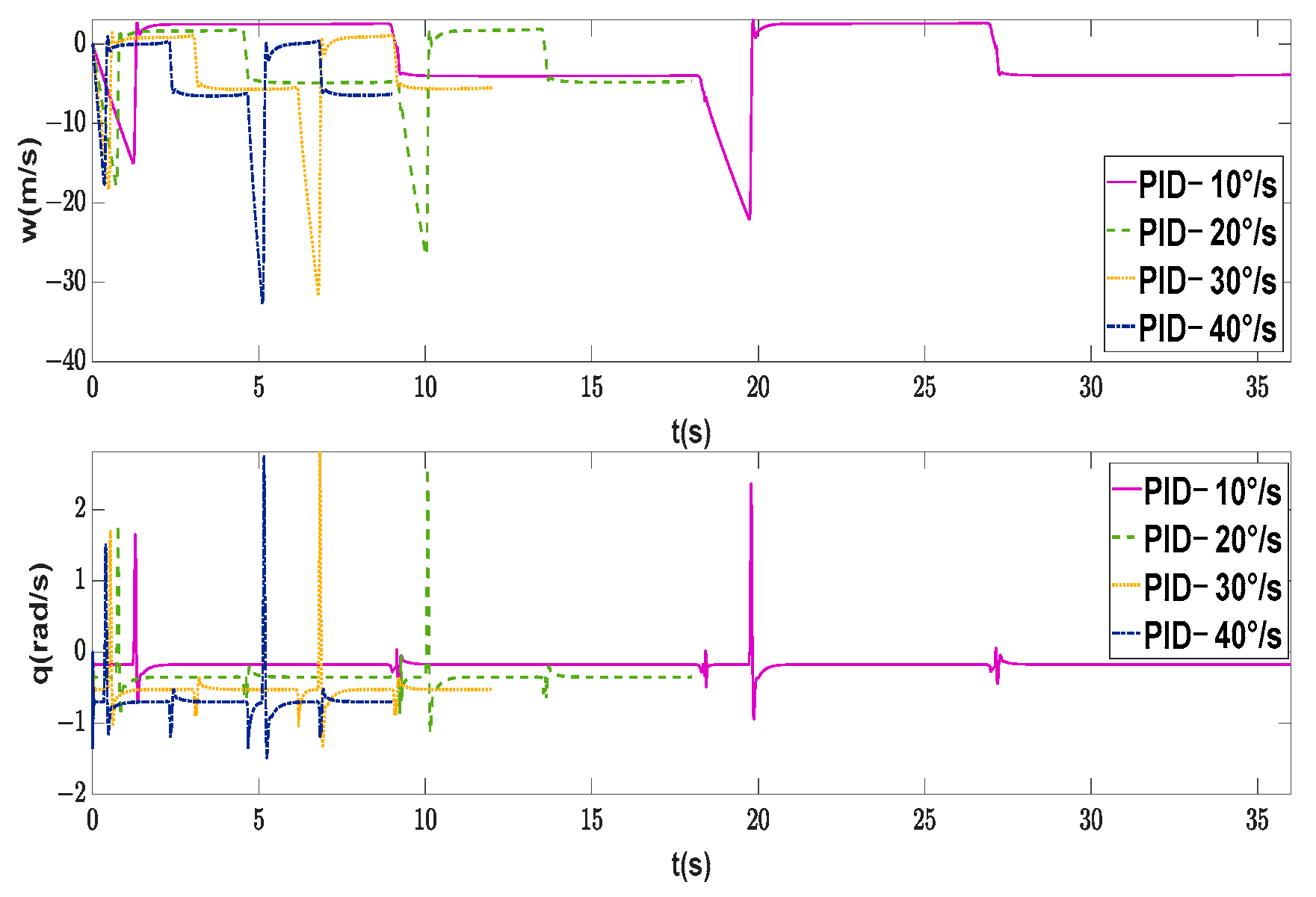
4.1. Research on Maneuverability without External Disturbances
4.2. Verification of Maximum Maneuverability with External Disturbances
4.3. Piecewise Trajectory Following Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiang, X.; Yu, C.; Zhang, Q. Robust fuzzy 3D path following for autonomous underwater vehicle subject to uncertainties. Comput. Oper. Res. 2017, 84, 165–177. [Google Scholar] [CrossRef]
- Ruzzene, M.; Kamada, R.; Bottasso, C.; Scorcelletti, F. Trajectory Optimization Strategies for Supercavitating Underwater Vehicles. J. Vib. Control. 2008, 14, 611–644. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Wang, X. Longitudinal dynamics modeling and MPC strategy for high-speed supercavitating vehicles. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 5947–5950. [Google Scholar]
- Dzielski, J.; Kurdila, A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions. J. Vib. Control. 2003, 9, 791–804. [Google Scholar] [CrossRef]
- Lin, G.; Balachandran, B.; Abed, E.H. Dynamics and Control of Supercavitating Vehicles. J. Dyn. Syst. Meas. Control. 2008, 130, 021003. [Google Scholar] [CrossRef]
- Sanabria, D.E.; Balas, G.J.; Arndt, R.E. Planing avoidance control for supercavitating vehicles. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4979–4984. [Google Scholar] [CrossRef]
- Han, Y.; Xu, Z.; Guan, L. Predictive Control of a Supercavitating Vehicle Based on Time-Delay Characteristics. IEEE Access 2020, 9, 13499–13512. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, S.; Wang, X.; Jing, L. A Cascade Approach for Stability Control of Supercavitating Vehicle. In Proceedings of the Global Oceans 2020: Singapore—US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, S.; Kim, N. Control method for ventilated supercavitating vehicle considering planing avoidance and stability. J. Eng. Marit. Environ. 2019, 233, 957–968. [Google Scholar] [CrossRef]
- Zou, W.; Wang, B. Longitudinal maneuvering motions of the supercavitating vehicle. Eur. J. Mech.-B/Fluids 2020, 81, 105–113. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, M.; Zhang, J.; Chen, Z. Depth and Attitude Coordinated Control for Supercavitating Vehicle Avoiding Planing Force. Machines 2022, 10, 433. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Ye, X.; Liu, Y. Sliding mode controller design for supercavitating vehicles. Ocean Eng. 2019, 184, 173–183. [Google Scholar] [CrossRef]
- Yang, G.; Lu, F.; Wu, L.; Xu, J. Design of Particle Swarm Optimization Adaptive Sliding Mode Controller Based on an Extended State Observer for the Longitudinal Motion of a Supercavitating Vehicle with Input Saturation. J. Sensors 2023, 2023, 2938089. [Google Scholar] [CrossRef]
- Wu, S.N.; Sun, X.Y.; Sun, Z.W.; Wu, X.D. Sliding-mode control for staring-mode spacecraft using a disturbance observer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 215–224. [Google Scholar] [CrossRef]
- Liu, E.; Yan, Y.; Yang, Y. Neural network approximation-based backstepping sliding mode control for spacecraft with input saturation and dynamics uncertainty. Acta Astronaut. 2022, 191, 1–10. [Google Scholar] [CrossRef]
- Fan, B.; Zhang, Y.; Chen, Y.; Meng, L. Intelligent vehicle lateral control based on radial basis function neural network sliding mode controller. CAAI Trans. Intell. Technol. 2022, 7, 455–468. [Google Scholar] [CrossRef]
- Esmaeili, N.; Kazemi, R.; Oreh, S.H.T. An adaptive sliding mode controller for the lateral control of articulated long vehicles. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 487–515. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
- Wang, W.; Xia, Y.; Chen, Y.; Xu, G.; Chen, Z.; Xu, K. Motion control methods for X-rudder underwater vehicles: Model based sliding Mode and non-model based iterative sliding mode. Ocean Eng. 2020, 216, 108054. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Huang, Z.; Wang, W.; Xu, G.; Li, Y. Adaptive energy-efficient tracking control of a X rudder AUV with actuator dynamics and rolling restriction. Appl. Ocean Res. 2022, 118, 102994. [Google Scholar] [CrossRef]
- Miao, J.; Wang, S.; Tomovic, M.M.; Zhao, Z. Compound line-of-sight nonlinear path following control of underactuated marine vehicles exposed to wind, waves, and ocean currents. Nonlinear Dyn. 2017, 89, 2441–2459. [Google Scholar] [CrossRef]
- Jinghua, W.; Yang, L.; Guohua, C.; Yongyong, Z.; Jiafeng, Z. Design of RBF Adaptive Sliding Mode Controller for A Supercavitating Vehicle. IEEE Access 2021, 9, 39873–39883. [Google Scholar] [CrossRef]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. Adaptive-neural-network-based robust lateral motion control for autonomous vehicle at driving limits. Control. Eng. Pract. 2018, 76, 41–53. [Google Scholar] [CrossRef]
- Wei, M.; Chen, G. Adaptive RBF neural network sliding mode control for ship course control system. In Proceedings of the 2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2011; pp. 27–30. [Google Scholar]
- Wang, X.; Deng, Z.; Peng, H.; Wang, L.; Wang, Y.; Tao, L.; Lu, C.; Peng, Z. Autonomous docking trajectory optimization for unmanned surface vehicle: A hierarchical method. Ocean Eng. 2023, 279, 114156. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Su, X.; Peng, H.; Wang, L.; Lu, C.; Wang, C. Autonomous dispatch trajectory planning on flight deck: A search-resampling-optimization framework. Eng. Appl. Artif. Intell. 2023, 119, 105792. [Google Scholar] [CrossRef]
- Vanek, B.; Bokor, J.; Balas, G.J.; Arndt, R.E. Longitudinal Motion Control of a High-Speed Supercavitation Vehicle. J. Vib. Control 2007, 13, 159–184. [Google Scholar] [CrossRef]
- Bai, T.; Bi, X. Studies on lateral motion control of supercavitating vehicle. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 6–7 January 2011; pp. 377–380. [Google Scholar]
- Vanek, B.; Balas, G.J.; Arndt, R.E. Linear, parameter-varying control of a supercavitating vehicle. Control. Eng. Pract. 2010, 18, 1003–1012. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Wang, W.; Xu, G.; Xiang, X.; Li, Y. Optimal robust trajectory tracking control of a X-rudder AUV with velocity sensor failures and uncertainties. Ocean Eng. 2020, 198, 106949. [Google Scholar] [CrossRef]
- Logvinovich, G.V. Hydrodynamics of Flows with Free Boundaries; Shanghai Jiao Tong University Press: Shanghai, China, 2012; pp. 97–126. ISBN 978-73-1308-814-7. [Google Scholar]
- Xinhua, Z.; Yao, S.; Zengkun, Q.; Minyan, H. Catastrophe characteristics and control of pitching supercavitating vehicles at fixed depths. Ocean Eng. 2016, 112, 185–194. [Google Scholar] [CrossRef]
- Han, Y.; Xu, Z.; Guo, H. Robust predictive control of a supercavitating vehicle based on time-delay characteristics and parameter uncertainty. Ocean Eng. 2021, 237, 109627. [Google Scholar] [CrossRef]
- Doan, P.T.; Bui, P.D.H.; Vu, M.T.; Thanh, H.L.N.N.; Hossain, S. Stability Analysis of a Fractional-Order High-Speed Supercavitating Vehicle Model with Delay. Machines 2021, 9, 129. [Google Scholar] [CrossRef]
- Zhang, Y.-W.; Yuan, X.-L.; Deng, F. Fluid Dynamics of Supercavitating Underwater Vehicles; National Defense Industry Press: Beijing, China, 2014; p. 167. [Google Scholar]
- Li, Y.; Zhang, Y. The influence of cavity shape on maneuverability rotational movement of supercavitating vehicle. J. Vib. Shock. 2014, 33, 165–170. [Google Scholar]
- Nguyen, V. Dynamics and Control of Non-Smooth Systems with Applications to Supercavitating Vehicles; University of Maryland: College Park, MD, USA, 2011. [Google Scholar]
- Zhang, K.; Li, P.; Wang, Z.; Yan, K.; Chen, W.; Xu, L.H. Experimental study of planning force on supercavitating vehicle tail. J. Ship Mech. 2020, 24, 8–17. [Google Scholar]
- Gao, H. Research on the Integration of Guidance and Control of Underwater High Speed Vehicle; Harbin Engineering University: Harbin, China, 2017. [Google Scholar]
- Kim, S.; Kim, N. Integrated dynamics modeling for supercavitating vehicle systems. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 346–363. [Google Scholar] [CrossRef]
- Kim, S.; Kim, N. Neural network-based adaptive control for a supercavitating vehicle in transition phase. J. Mar. Sci. Technol. 2015, 20, 454–466. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Pang, A. Supercaviting Vehicle Control; Harbin Institute of Technology: Harbin, China, 2017. [Google Scholar]
- El Hajjami, L.; Mellouli, E.M.; Berrada, M. Neural network based sliding mode lateral control for autonomous vehicle. In Proceedings of the 2020 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 16–19 April 2020; pp. 1–6. [Google Scholar]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Jia, L.Y.; Zhu, Z.Y. Improved fractional-order integral sliding mode control for AUV based on RBF neural network. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 1–3 December 2018. [Google Scholar]
- Sarhadi, P.; Noei, A.R.; Khosravi, A. Adaptive integral feedback controller for pitch and yaw channels of an AUV with actuator saturations. ISA Trans. 2016, 65, 284–295. [Google Scholar] [CrossRef]
- Walker, K.L.; Gabl, R.; Aracri, S.; Cao, Y.; Stokes, A.A.; Kiprakis, A.; Giorgio-Serchi, F. Experimental Validation of Wave Induced Disturbances for Predictive Station Keeping of a Remotely Operated Vehicle. IEEE Robot. Autom. Lett. 2021, 6, 5421–5428. [Google Scholar] [CrossRef]
- Gabl, R.; Davey, T.; Cao, Y.; Li, Q.; Li, B.; Walker, K.L.; Giorgio-Serchi, F.; Aracri, S.; Kiprakis, A.; Stokes, A.A.; et al. Hydrodynamic loads on a restrained ROV under waves and current. Ocean Eng. 2021, 234, 109279. [Google Scholar] [CrossRef]


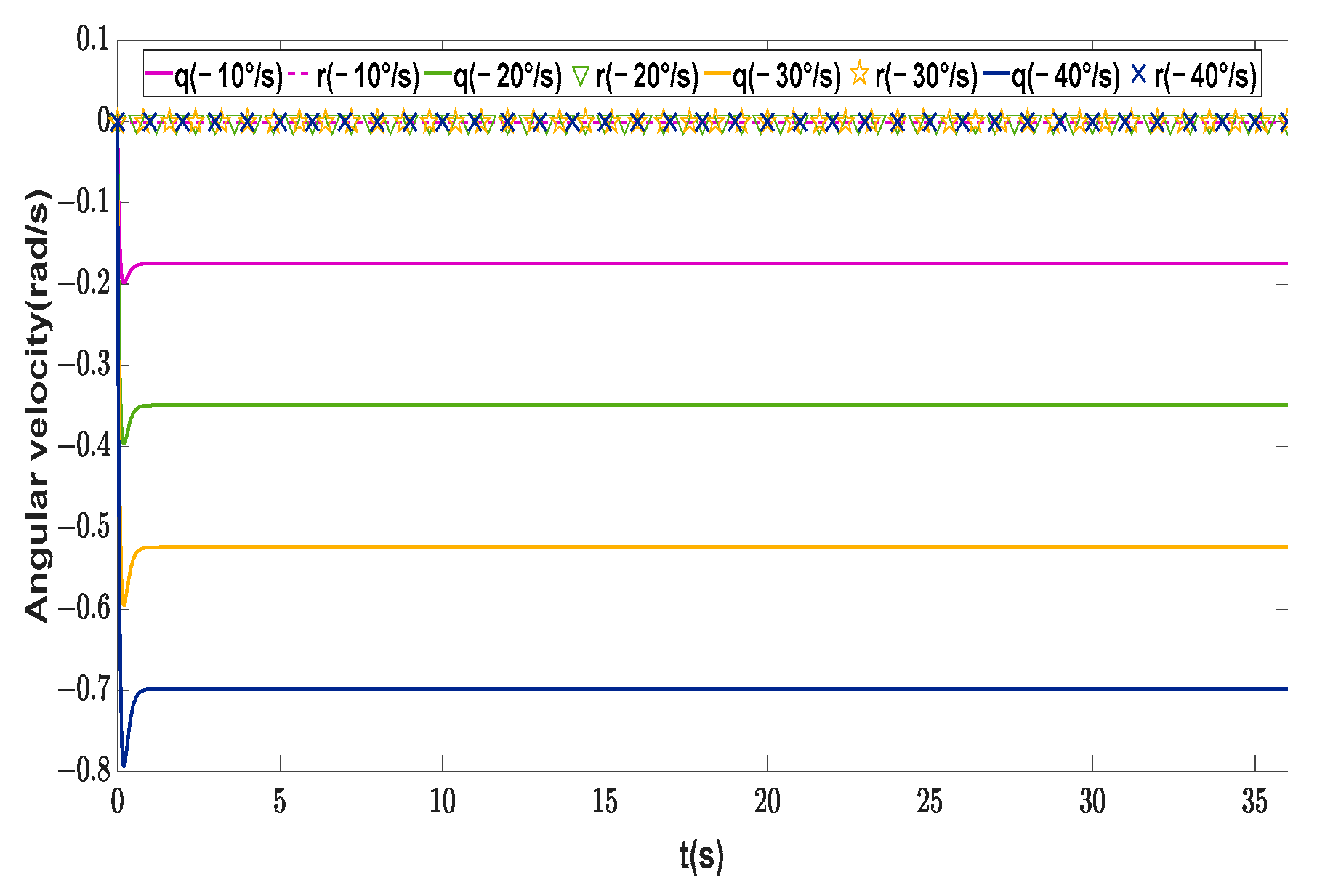
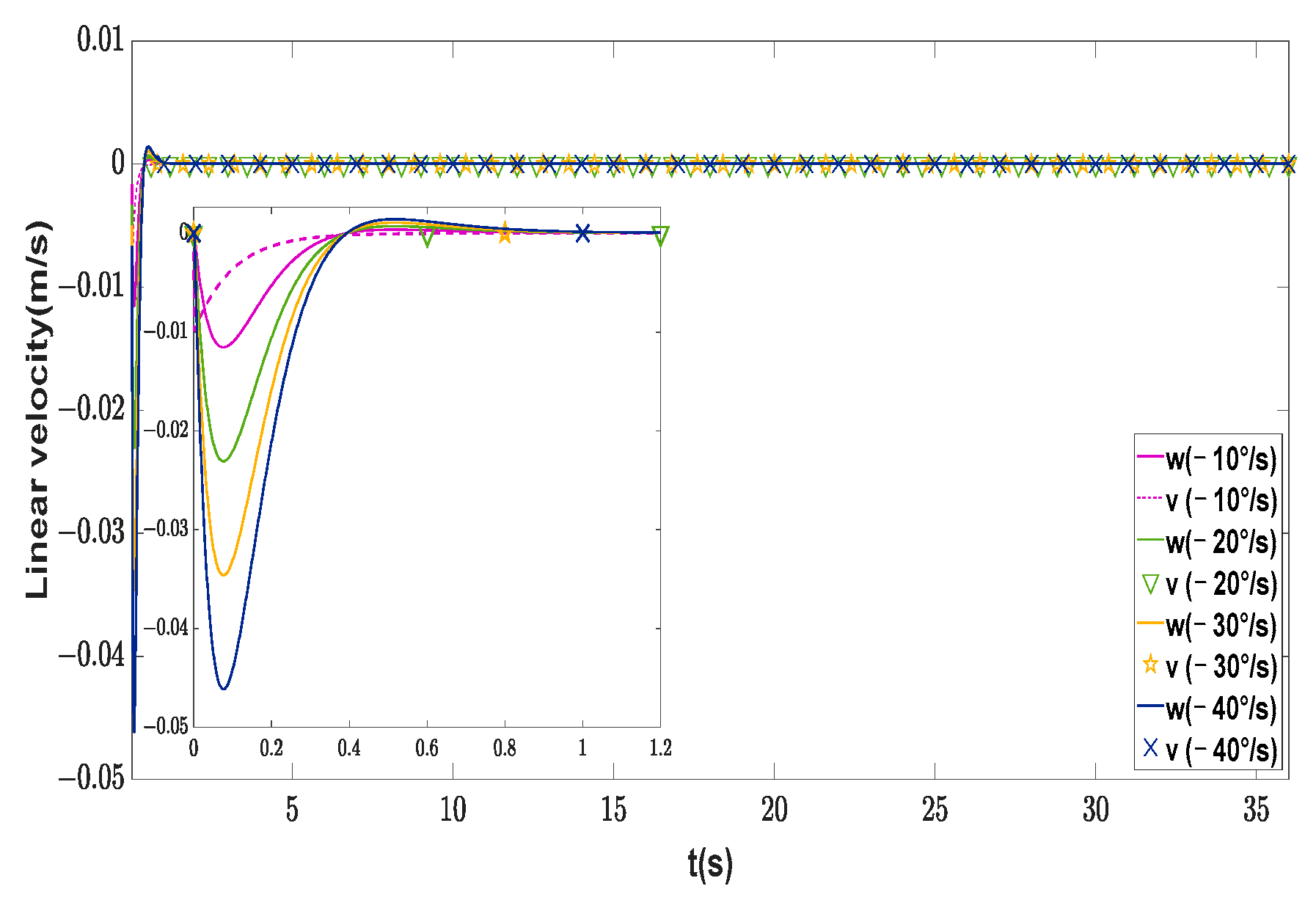
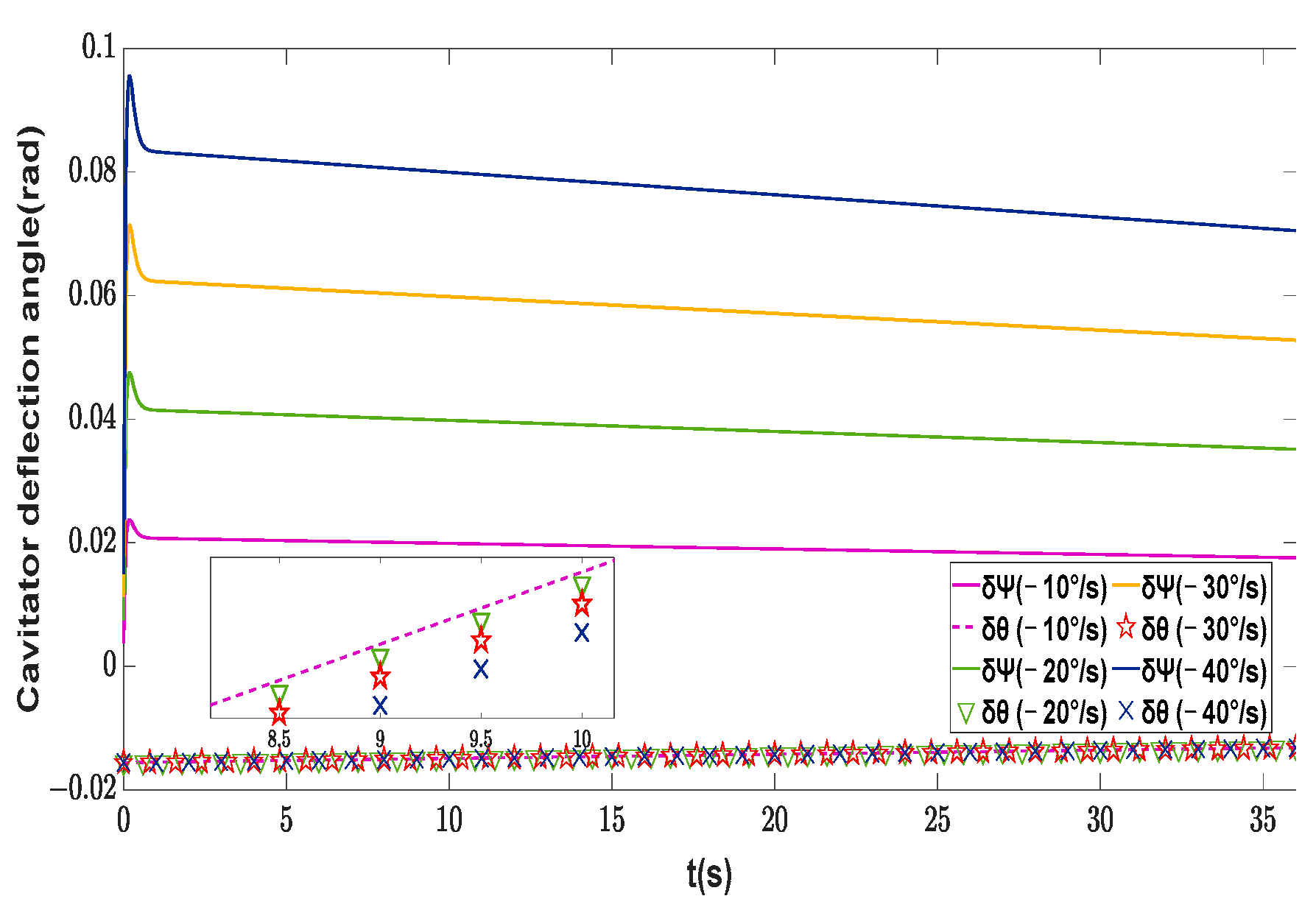
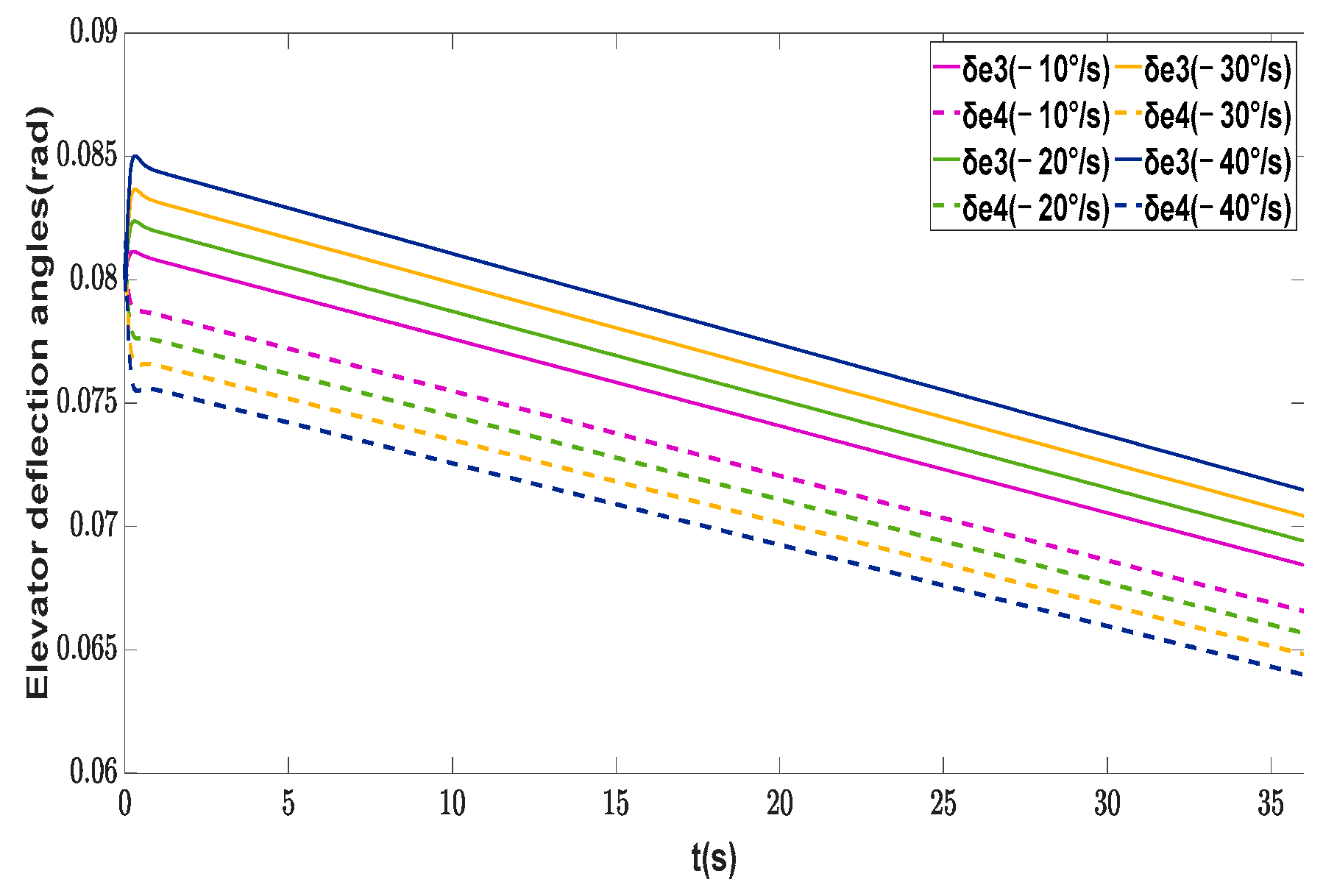
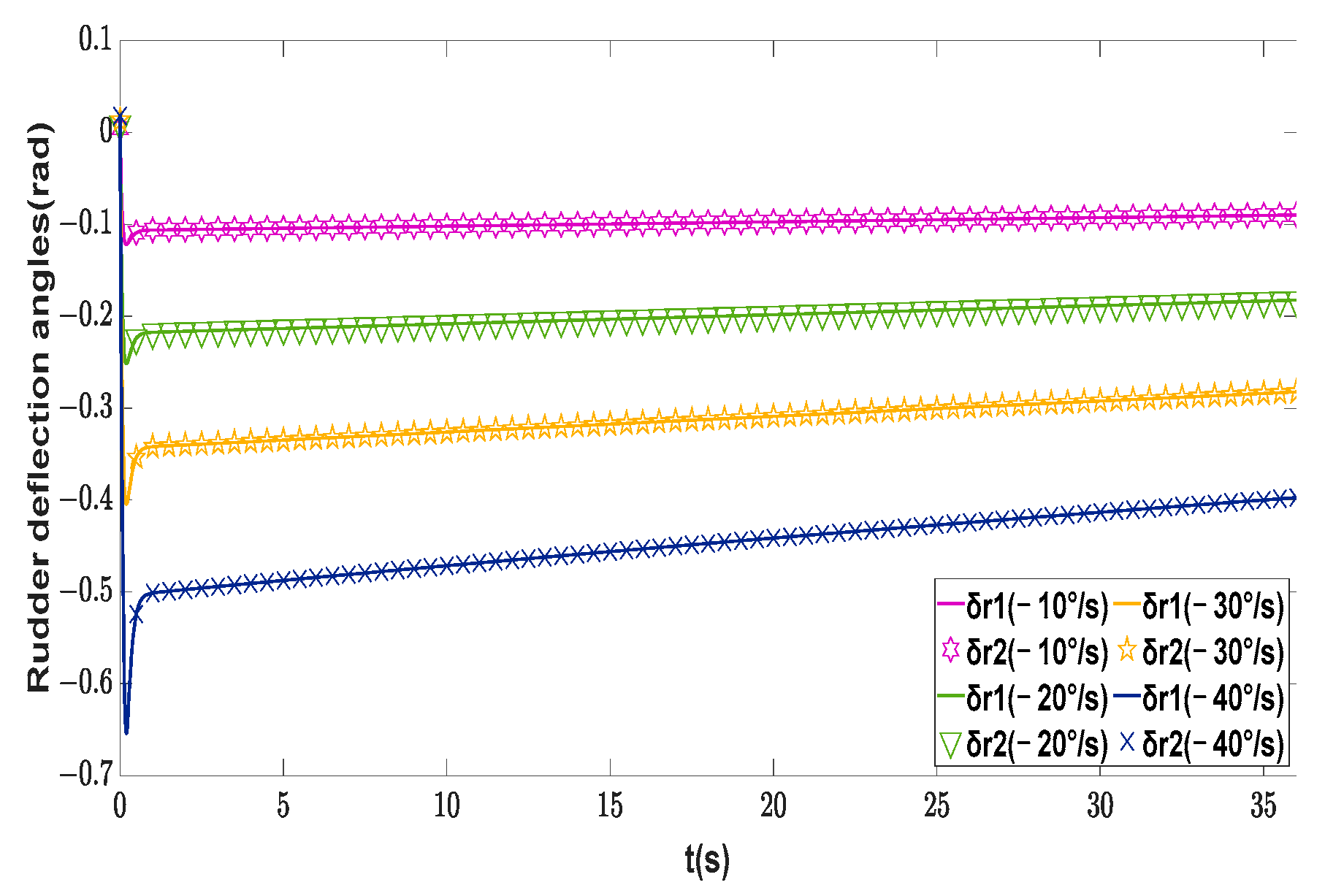
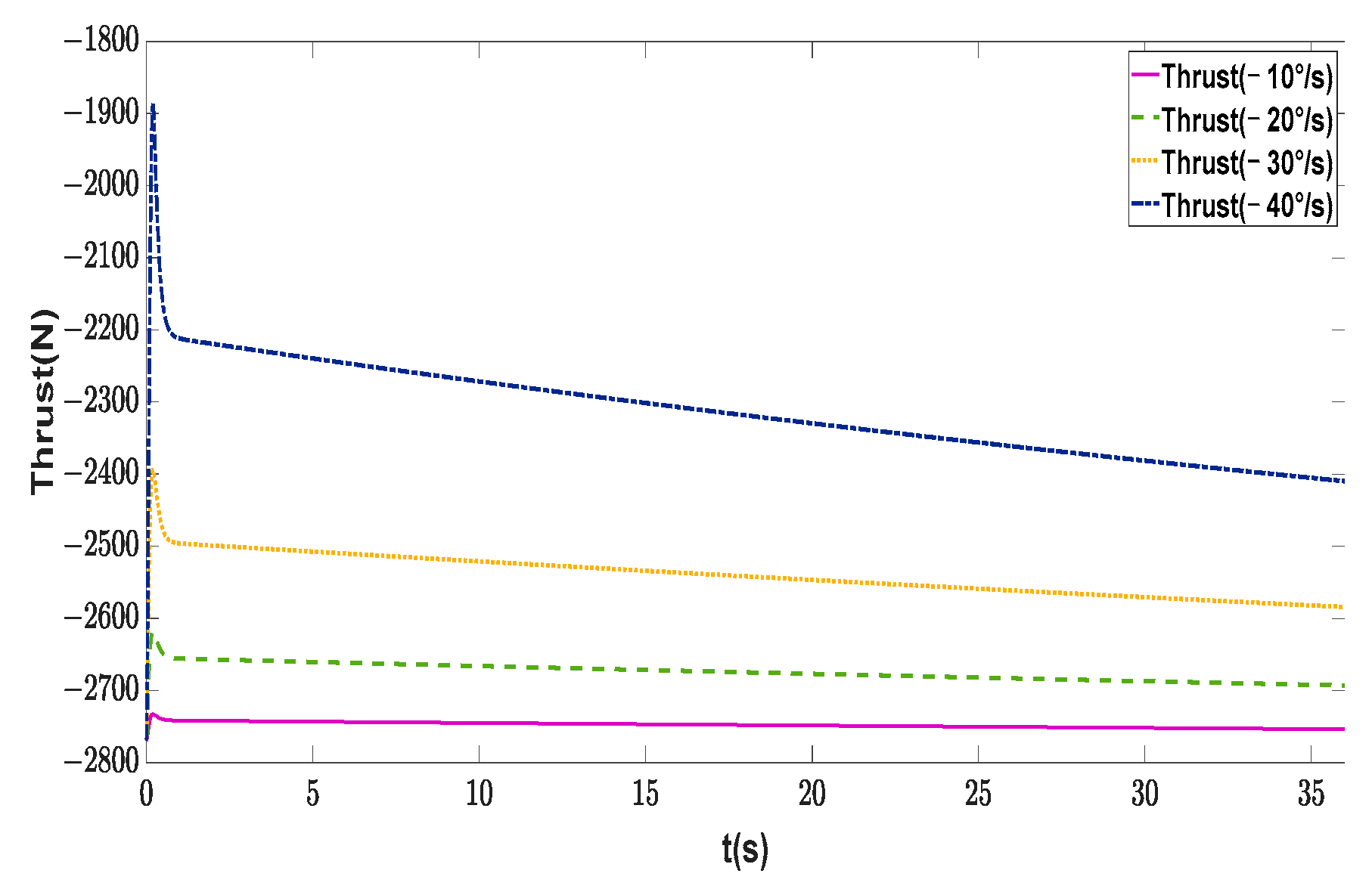
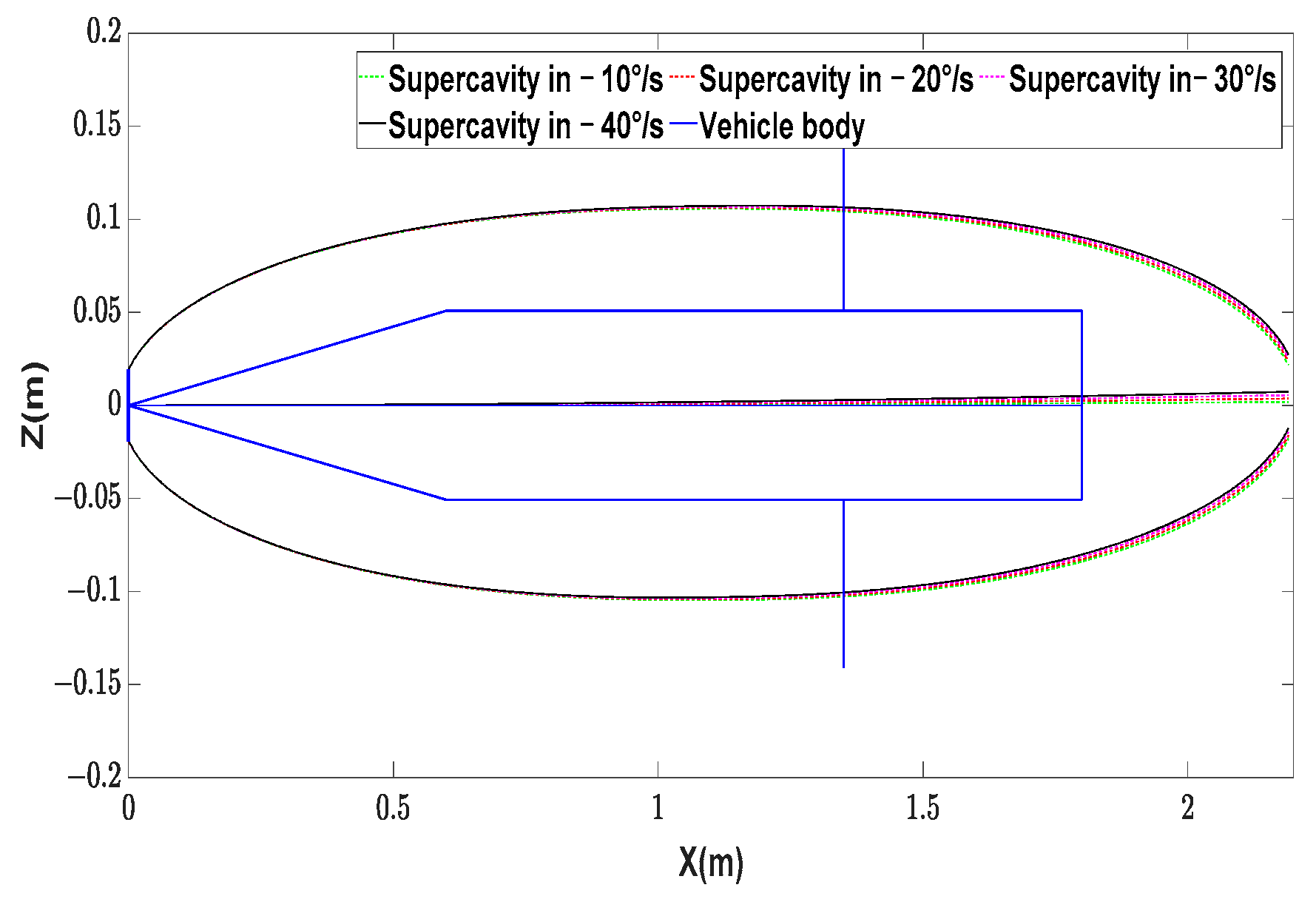
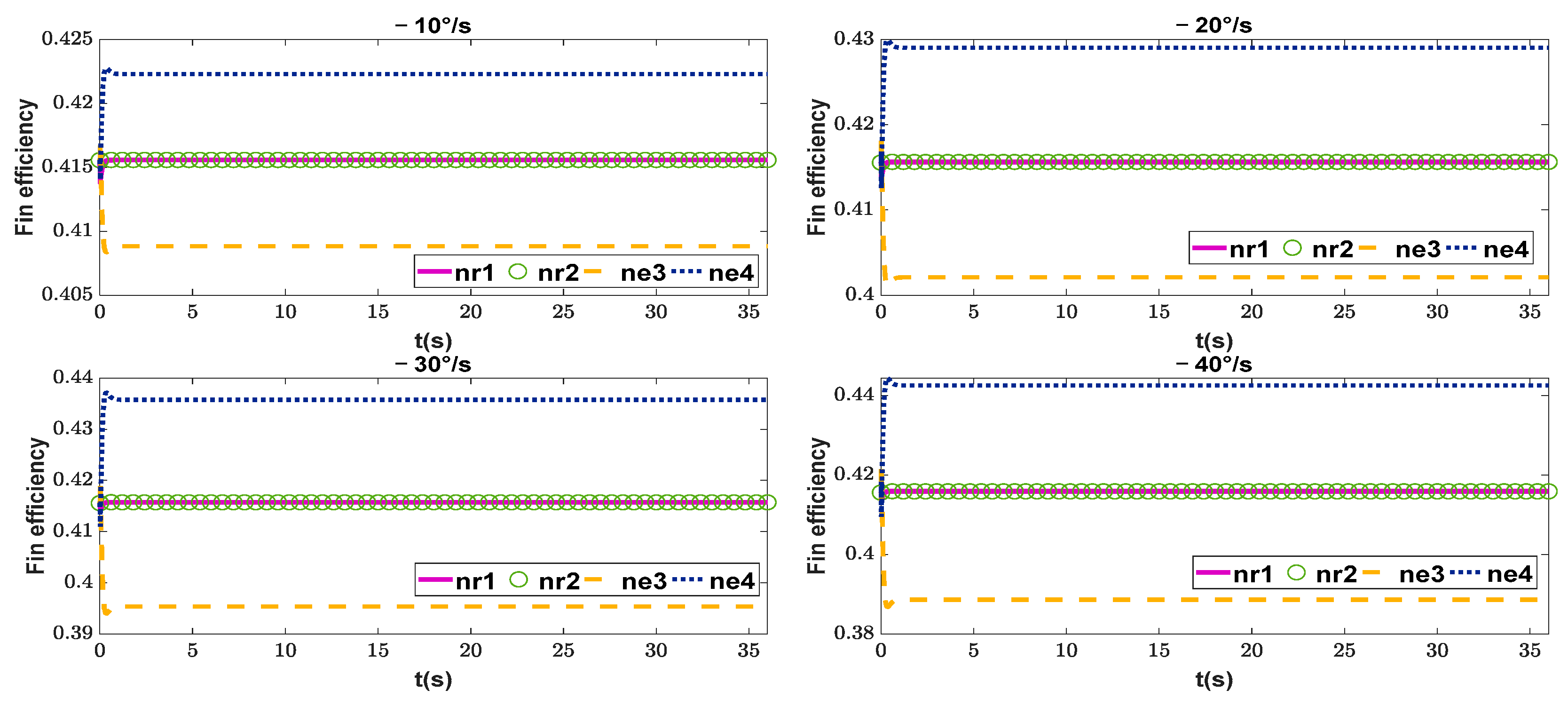
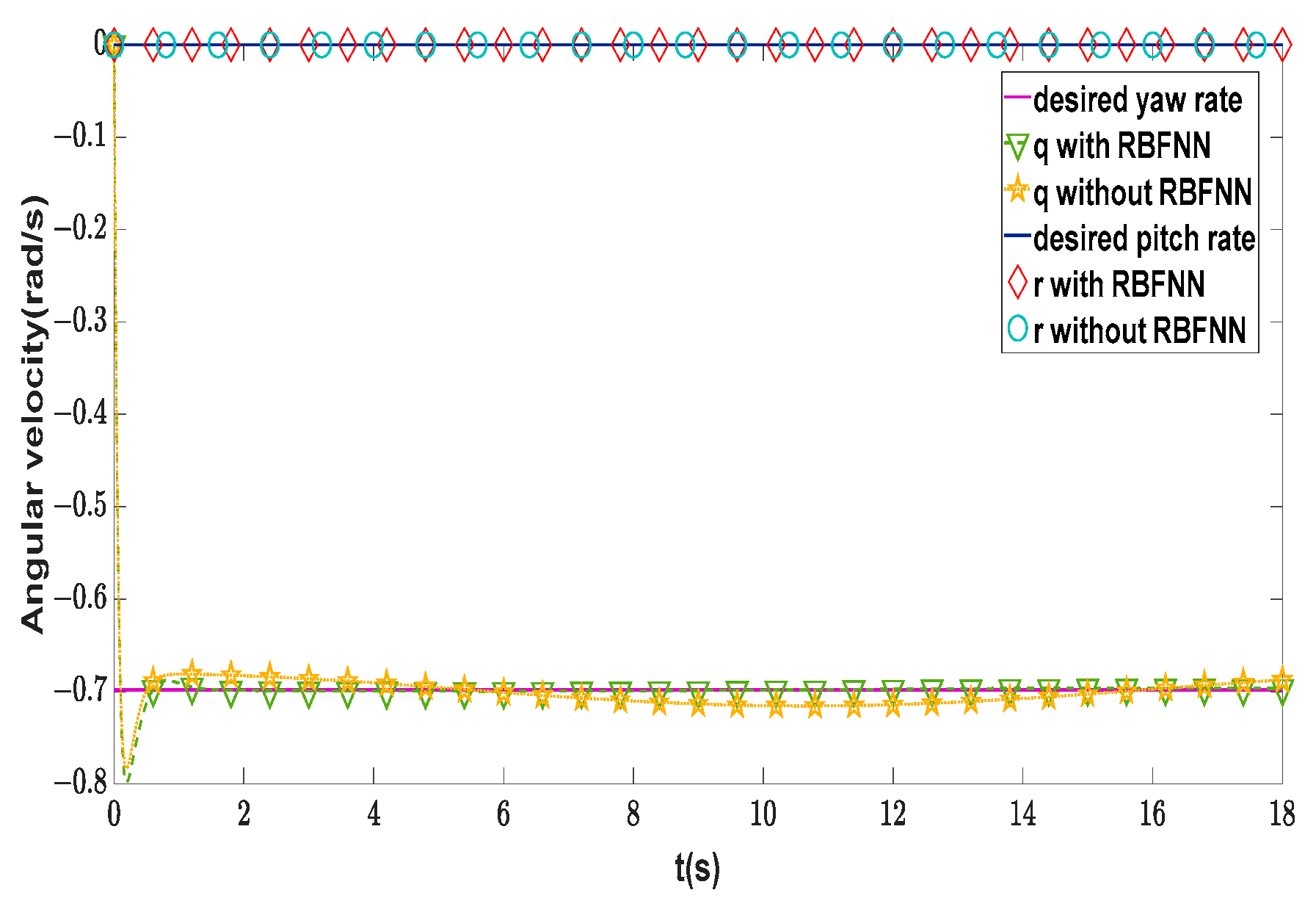
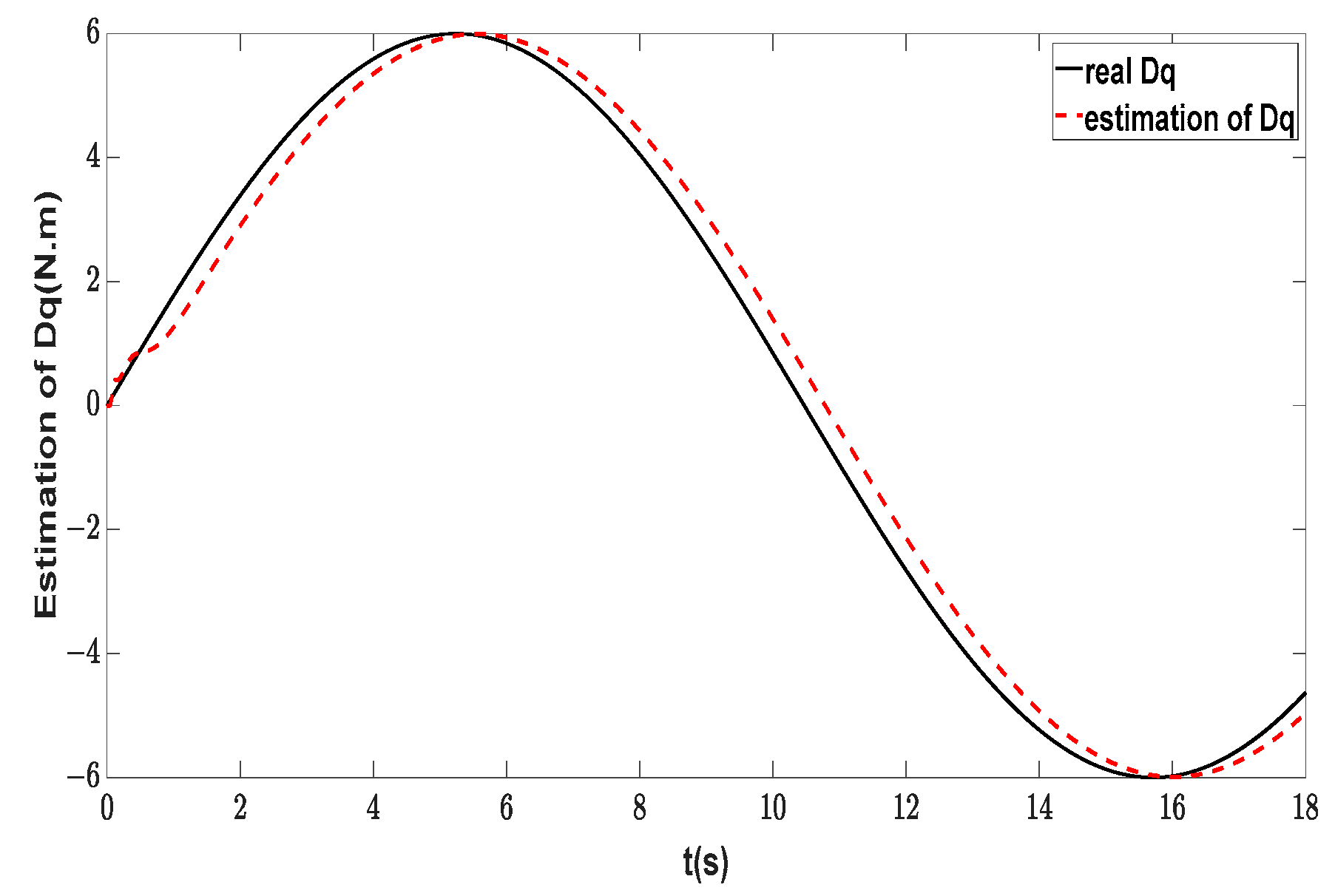
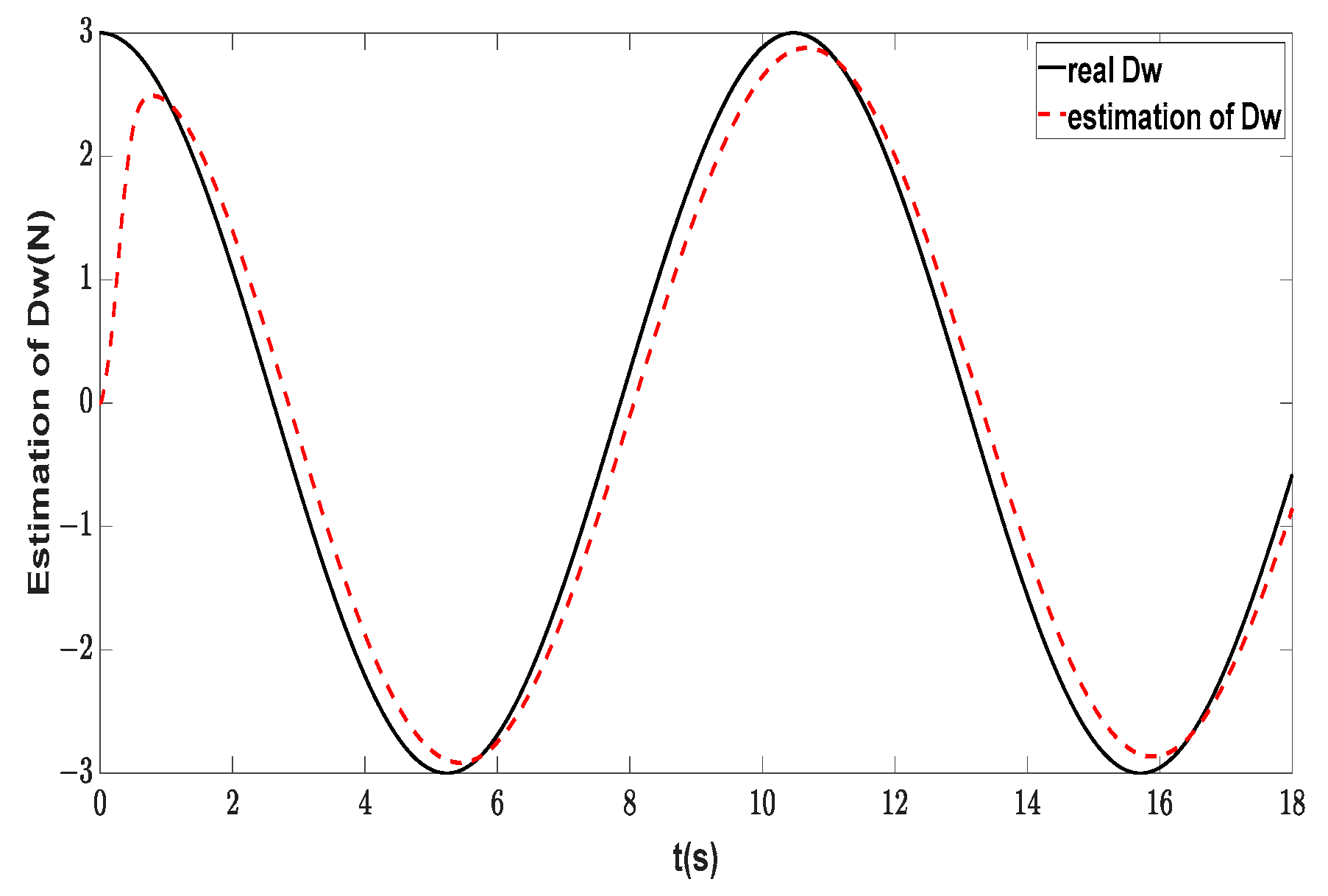
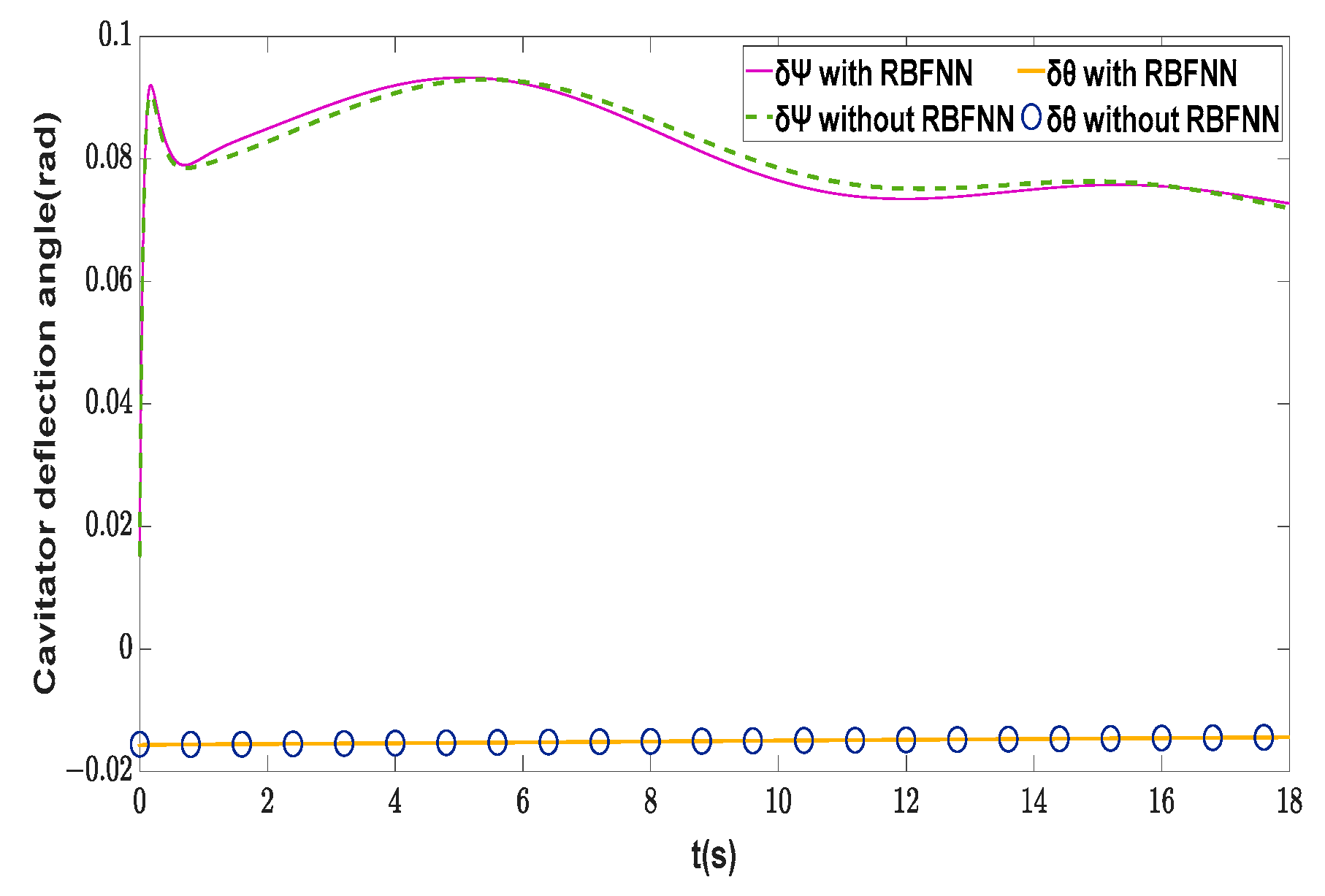
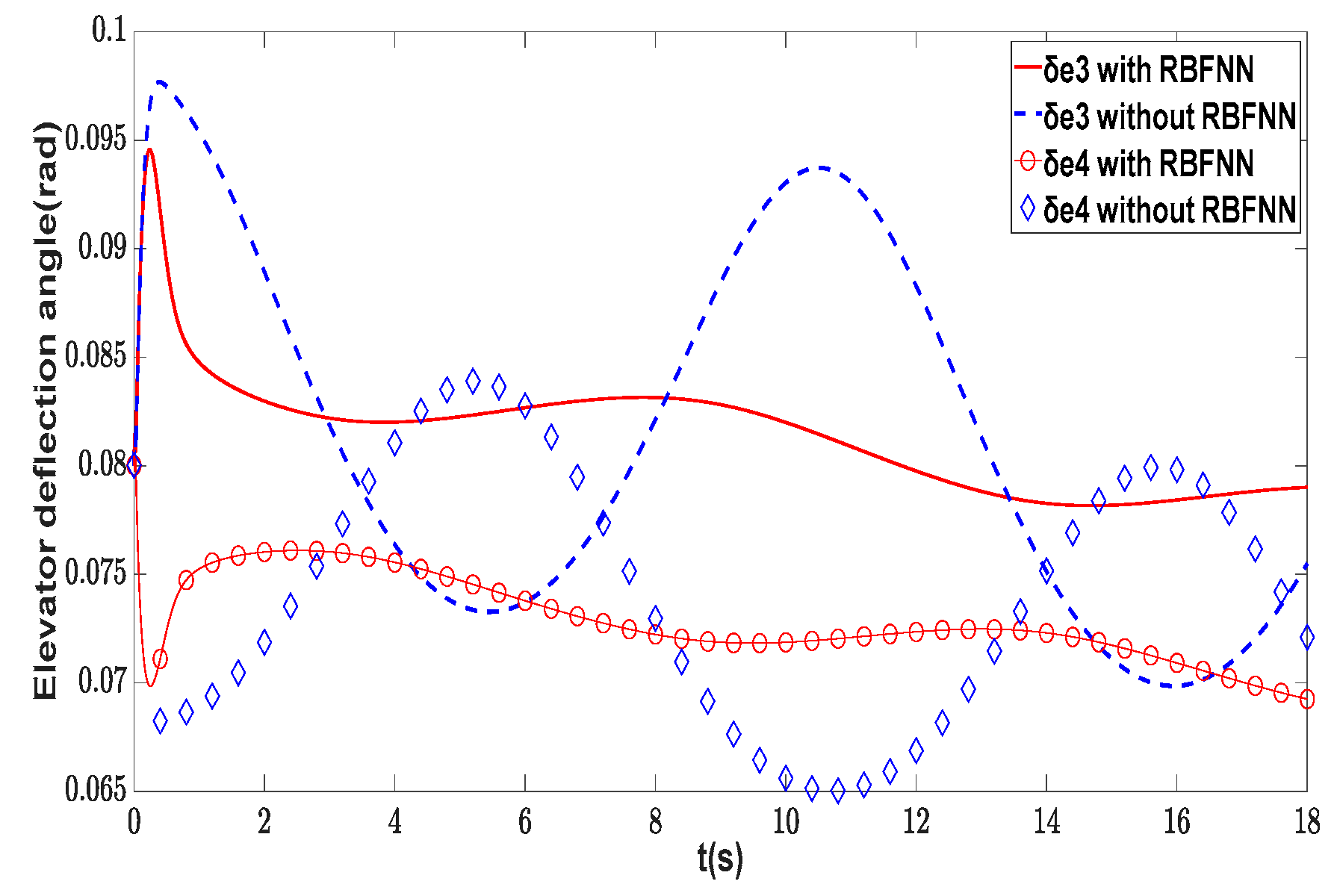
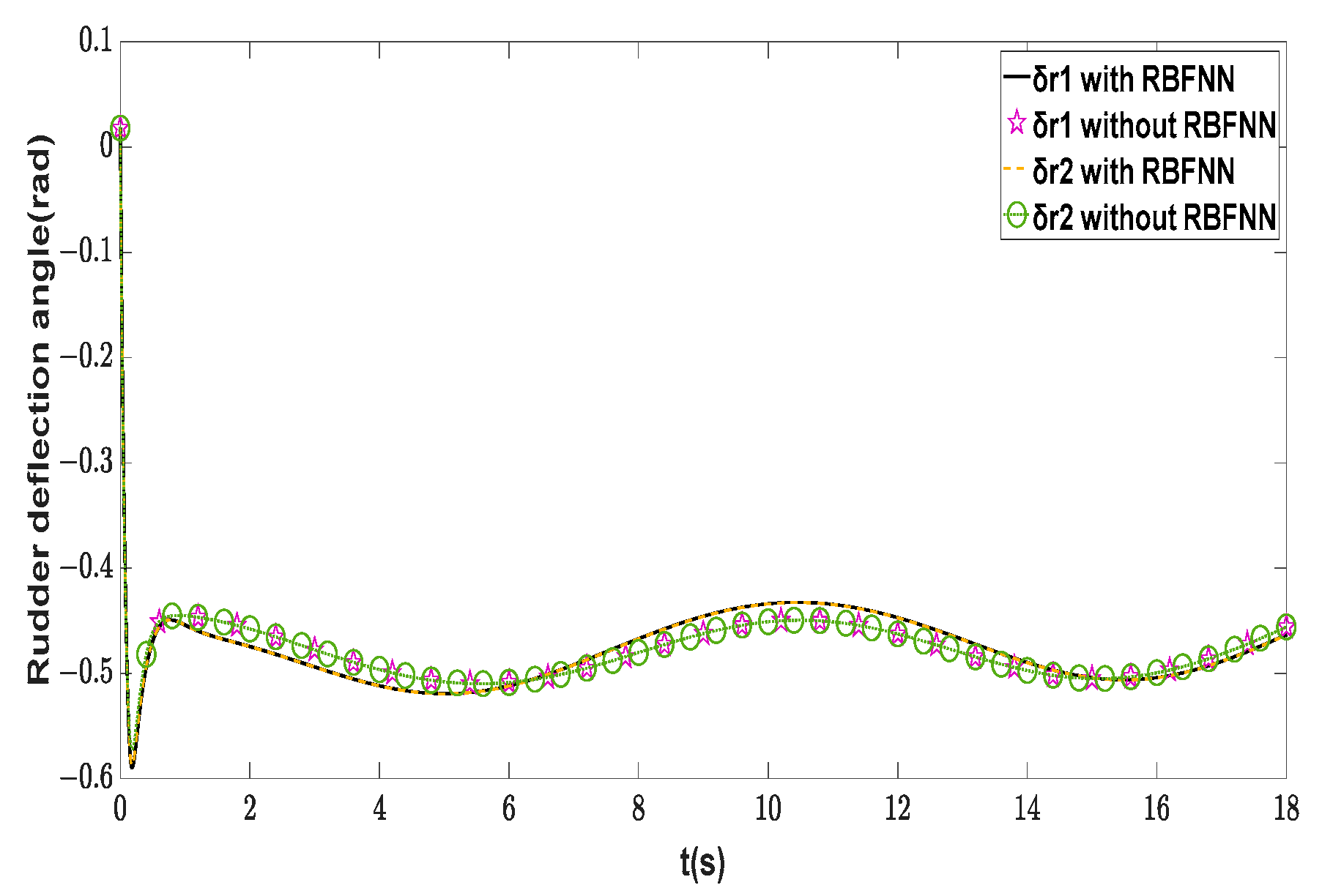
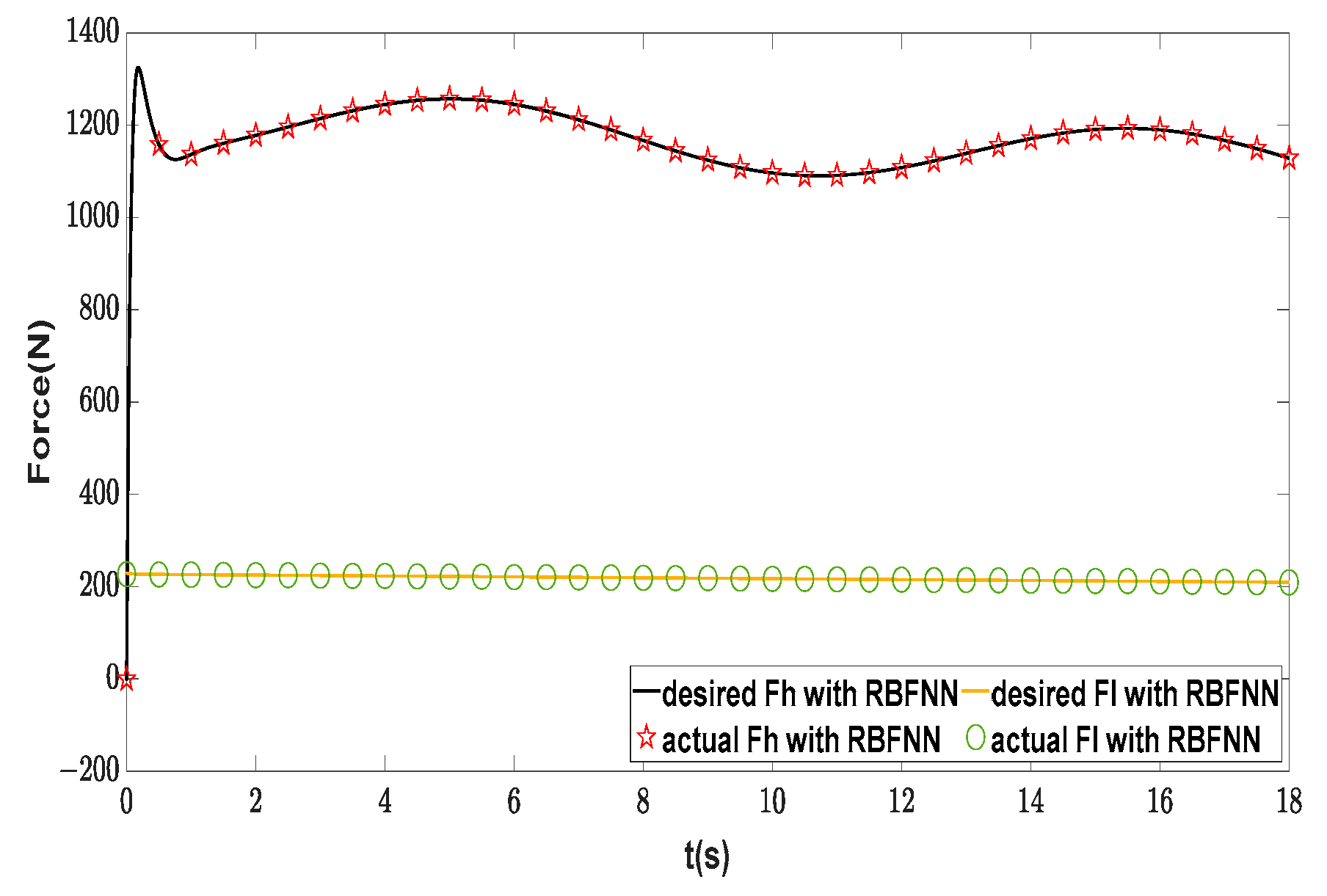
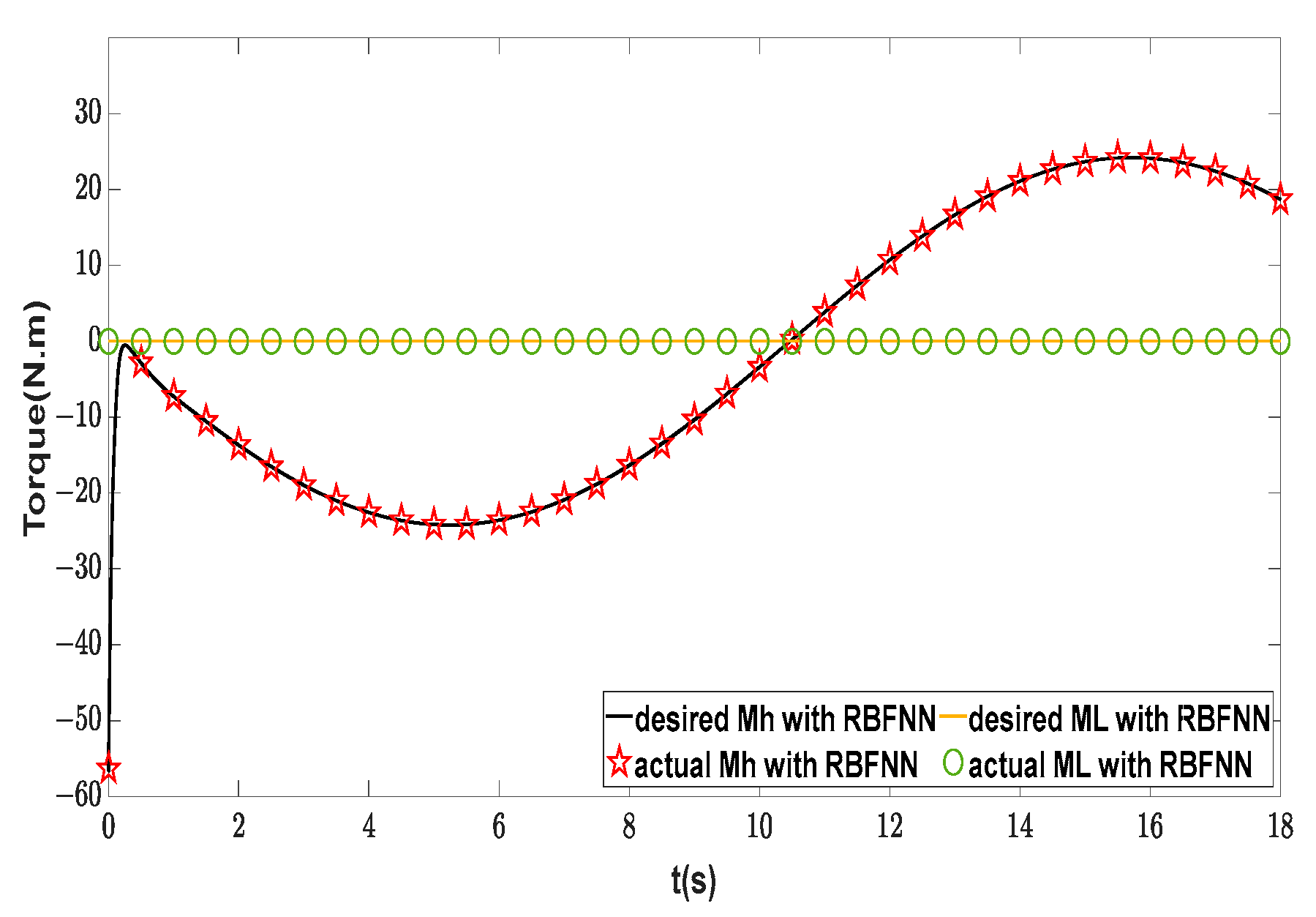
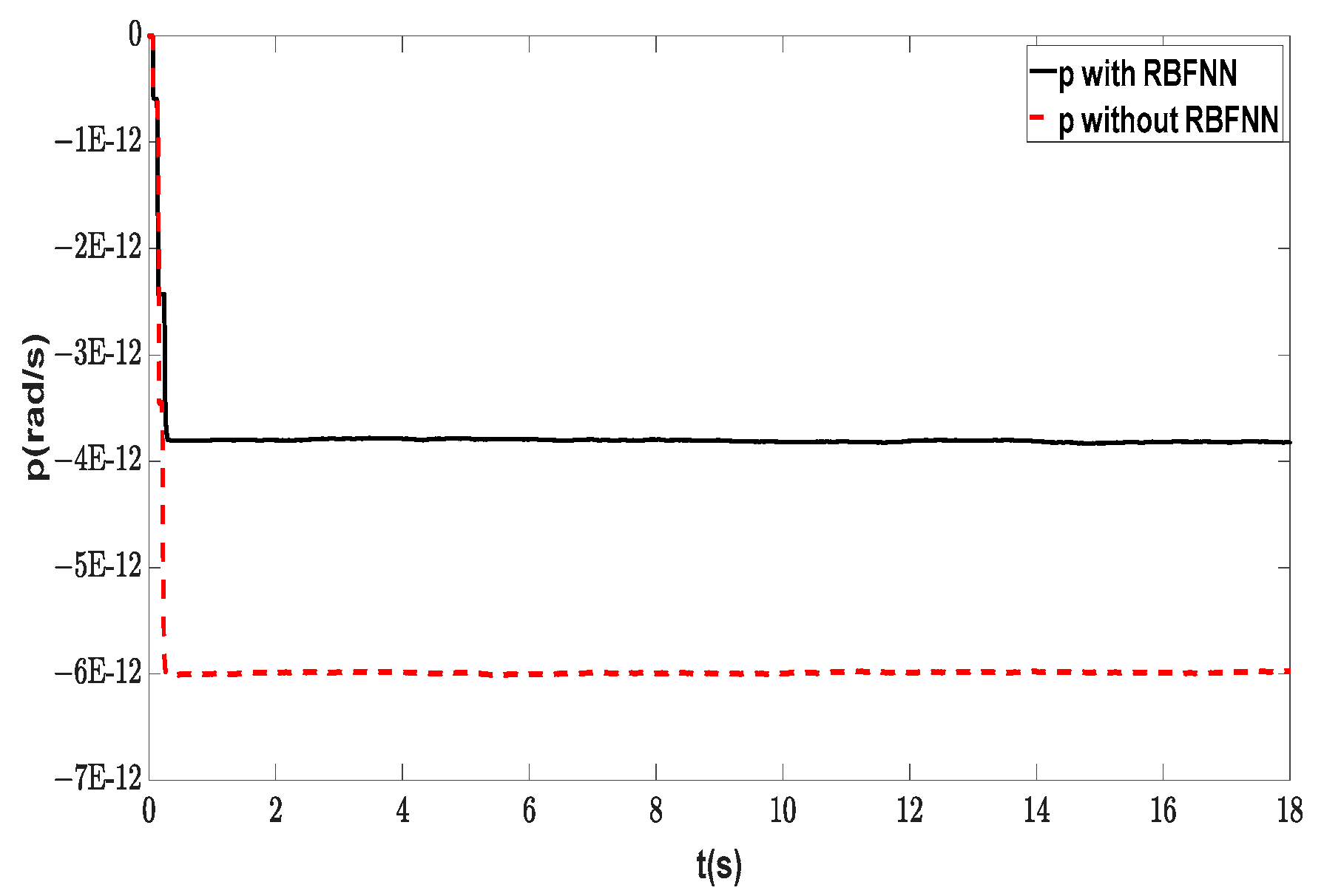
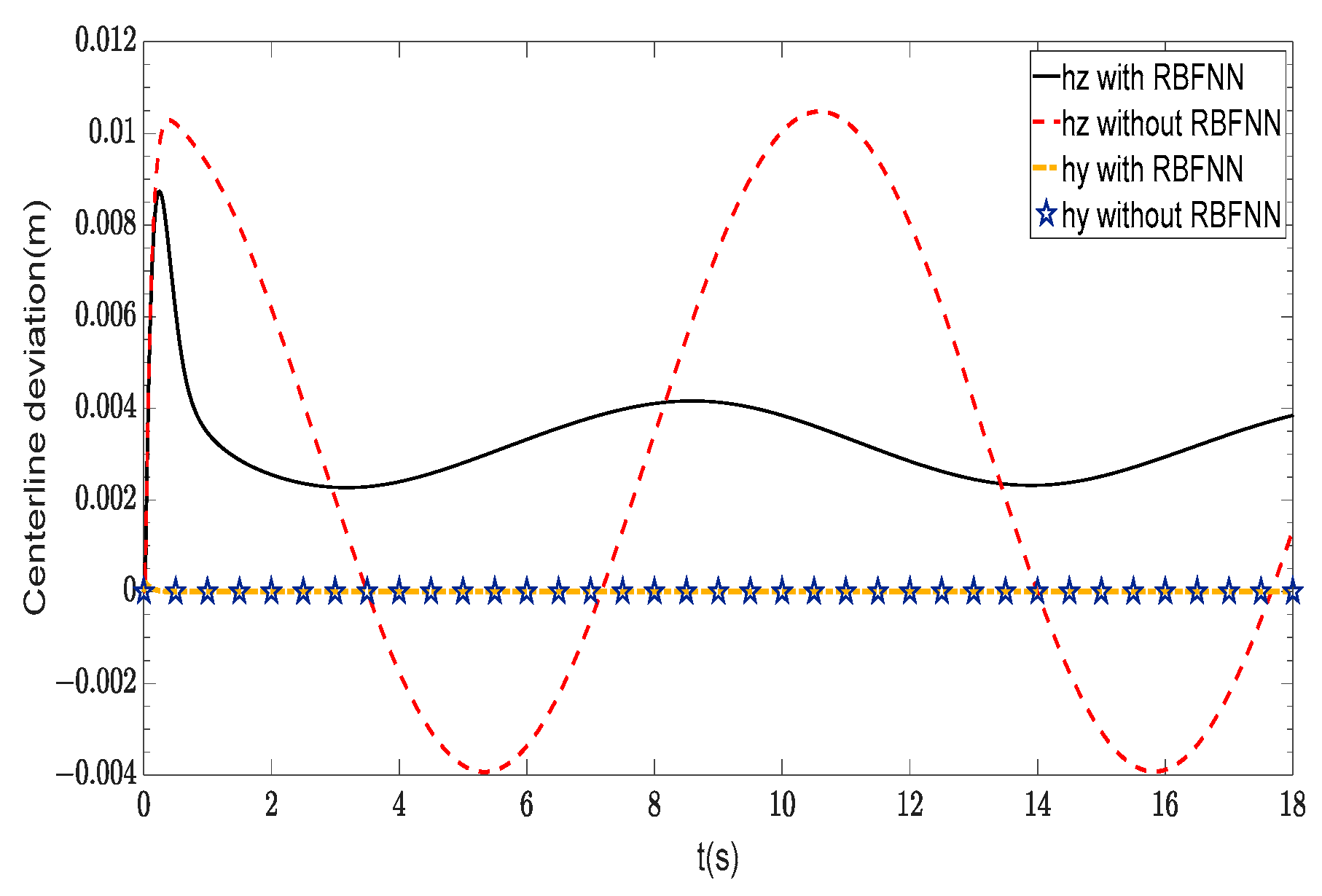
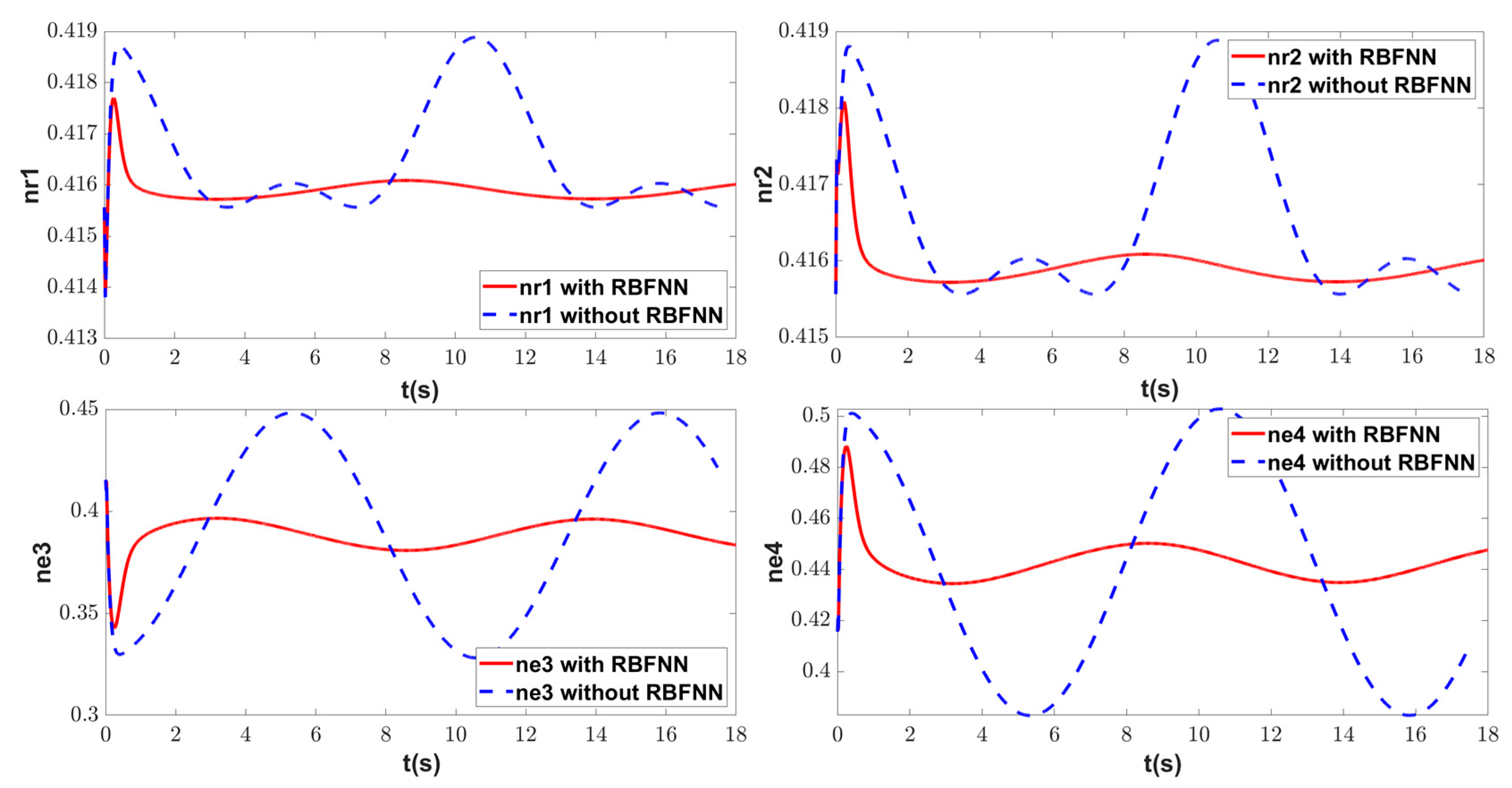


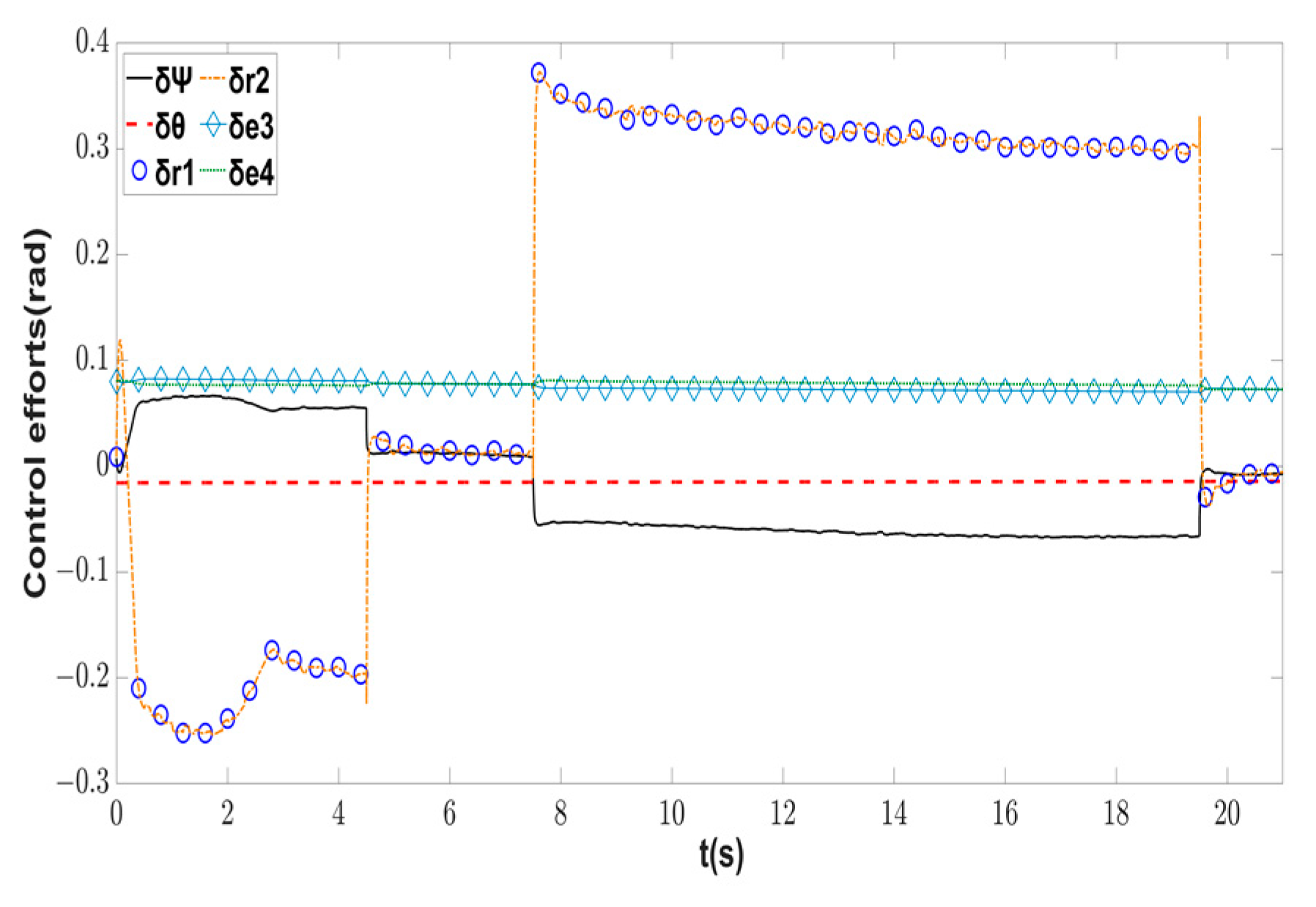

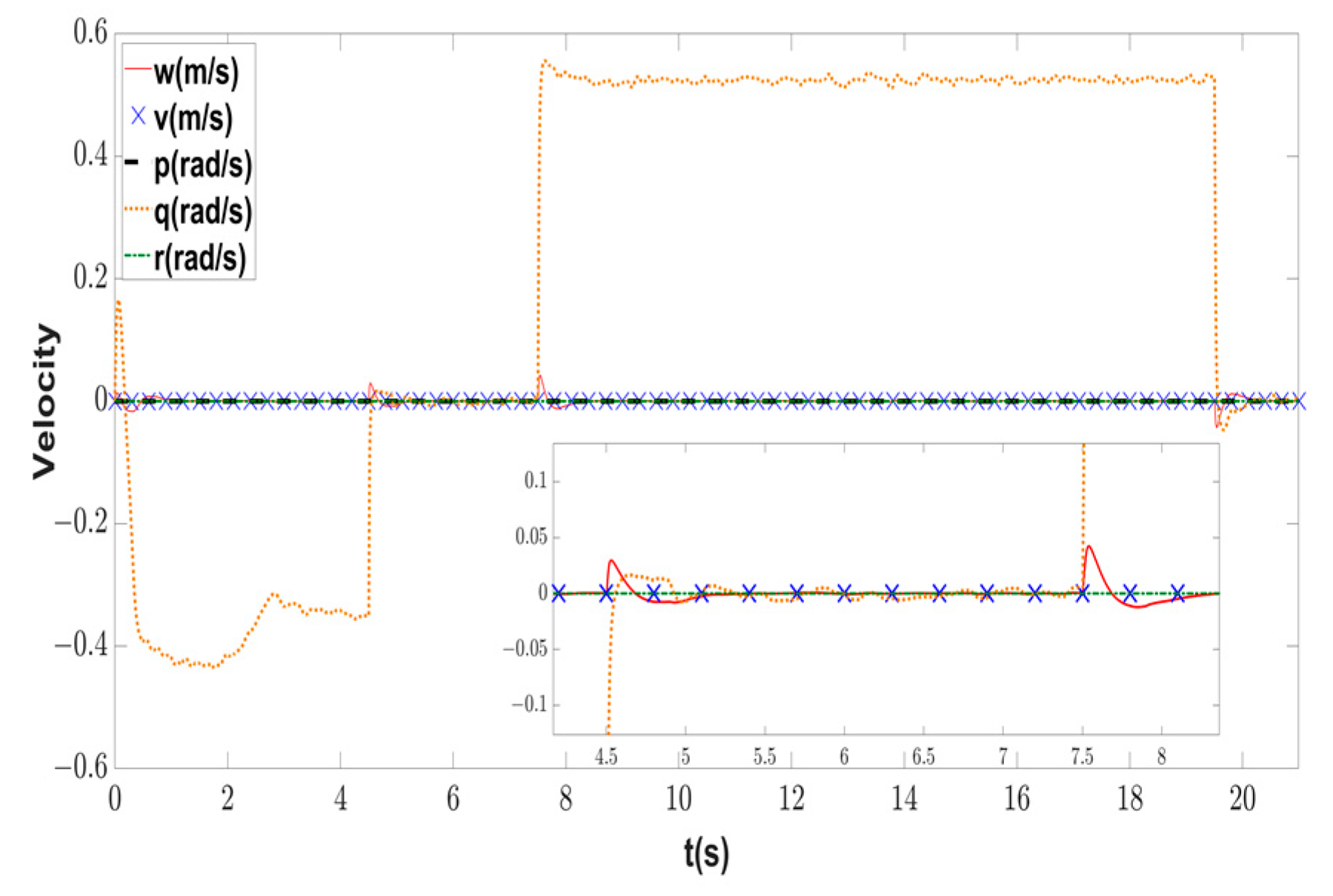
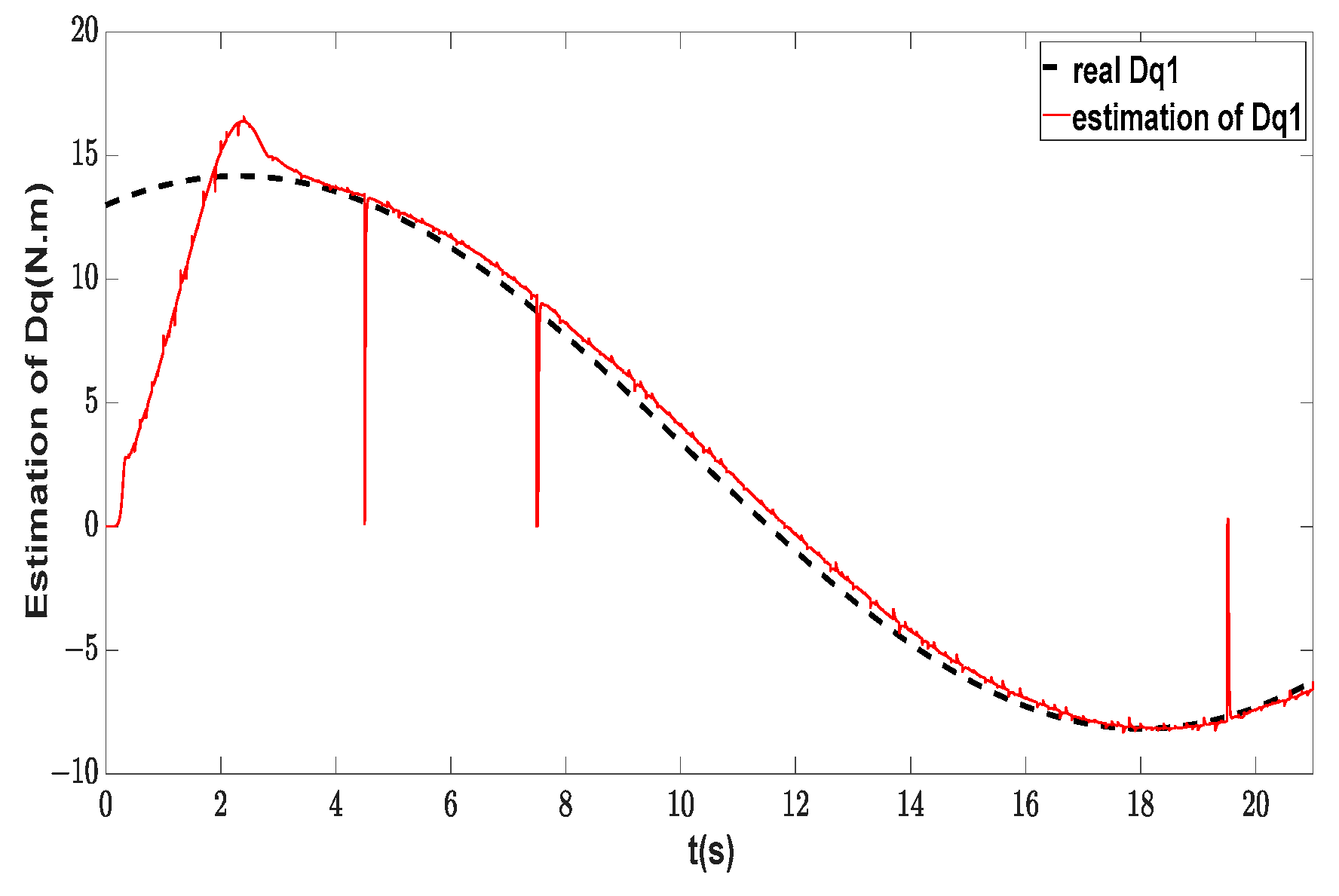
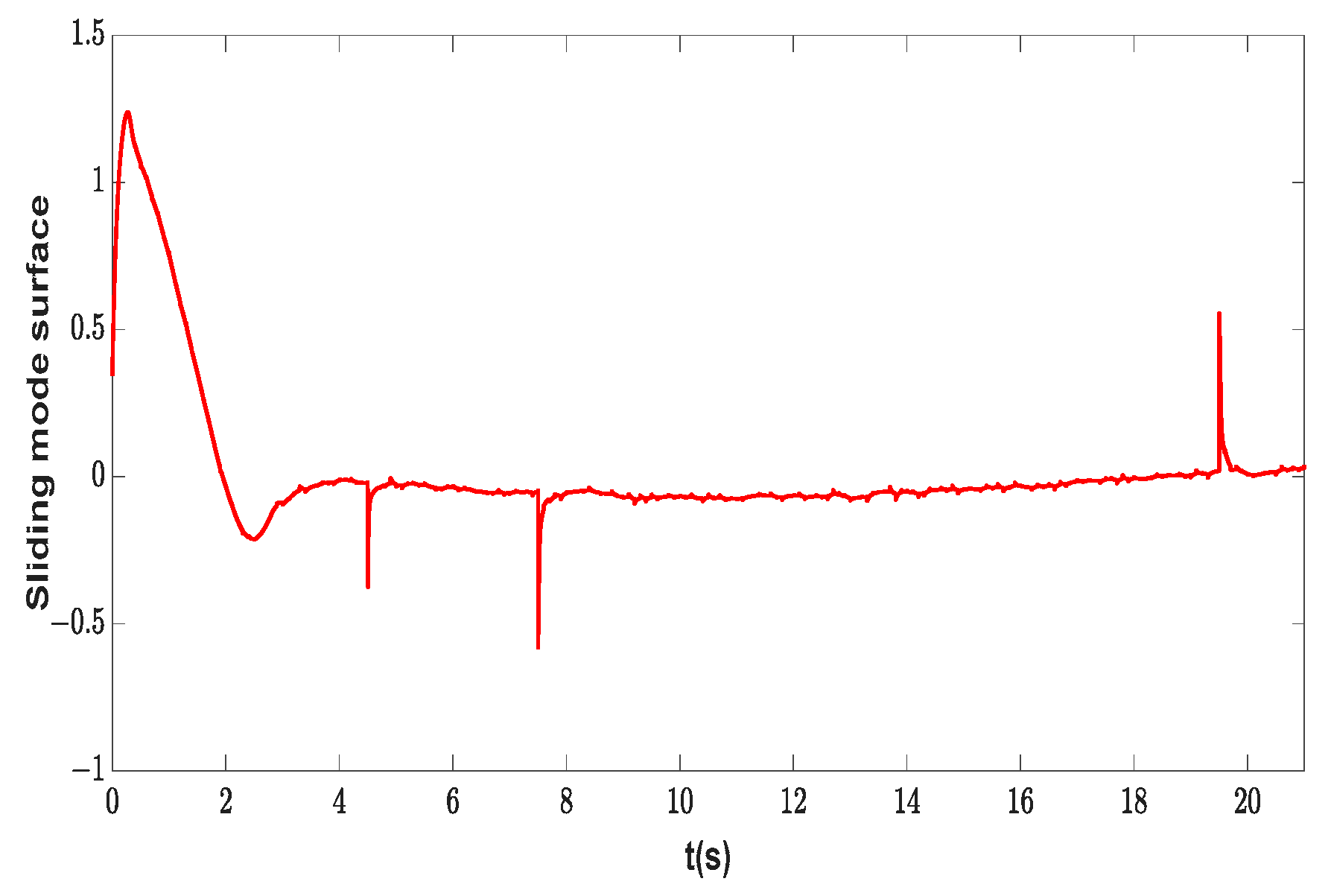
| Symbol | Description | Value | Unit |
|---|---|---|---|
| m | Original vehicle mass | 23.1545 | kg |
| Rate of vehicle mass change | −0.1 | kg/s | |
| Length of the vehicle | 1.8 | m | |
| Fin area | 0.0011 | m2 | |
| Span of the fin | 0.09 | m | |
| Chord of the fin | 0.0122 | m | |
| Radius of the body | 0.0508 | m | |
| Cavitator area | 0.0011 | m2 | |
| Radius of the cavitator | 0.0191 | n | |
| Density of the vehicle | 2040 | kg/m3 | |
| Sea-water density | 1020 | kg/m3 | |
| Similarity ratio of hydrodynamic coefficients | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Lu, F.; Xu, J. Research on Lateral Maneuverability of a Supercavitating Vehicle Based on RBFNN Adaptive Sliding Mode Control with Rolling Restriction and Planing Force Avoidance. Machines 2023, 11, 845. https://doi.org/10.3390/machines11080845
Yang G, Lu F, Xu J. Research on Lateral Maneuverability of a Supercavitating Vehicle Based on RBFNN Adaptive Sliding Mode Control with Rolling Restriction and Planing Force Avoidance. Machines. 2023; 11(8):845. https://doi.org/10.3390/machines11080845
Chicago/Turabian StyleYang, Guang, Faxing Lu, and Junfei Xu. 2023. "Research on Lateral Maneuverability of a Supercavitating Vehicle Based on RBFNN Adaptive Sliding Mode Control with Rolling Restriction and Planing Force Avoidance" Machines 11, no. 8: 845. https://doi.org/10.3390/machines11080845
APA StyleYang, G., Lu, F., & Xu, J. (2023). Research on Lateral Maneuverability of a Supercavitating Vehicle Based on RBFNN Adaptive Sliding Mode Control with Rolling Restriction and Planing Force Avoidance. Machines, 11(8), 845. https://doi.org/10.3390/machines11080845







