PT-Informer: A Deep Learning Framework for Nuclear Steam Turbine Fault Diagnosis and Prediction
Abstract
:1. Introduction
2. Theories and Methods
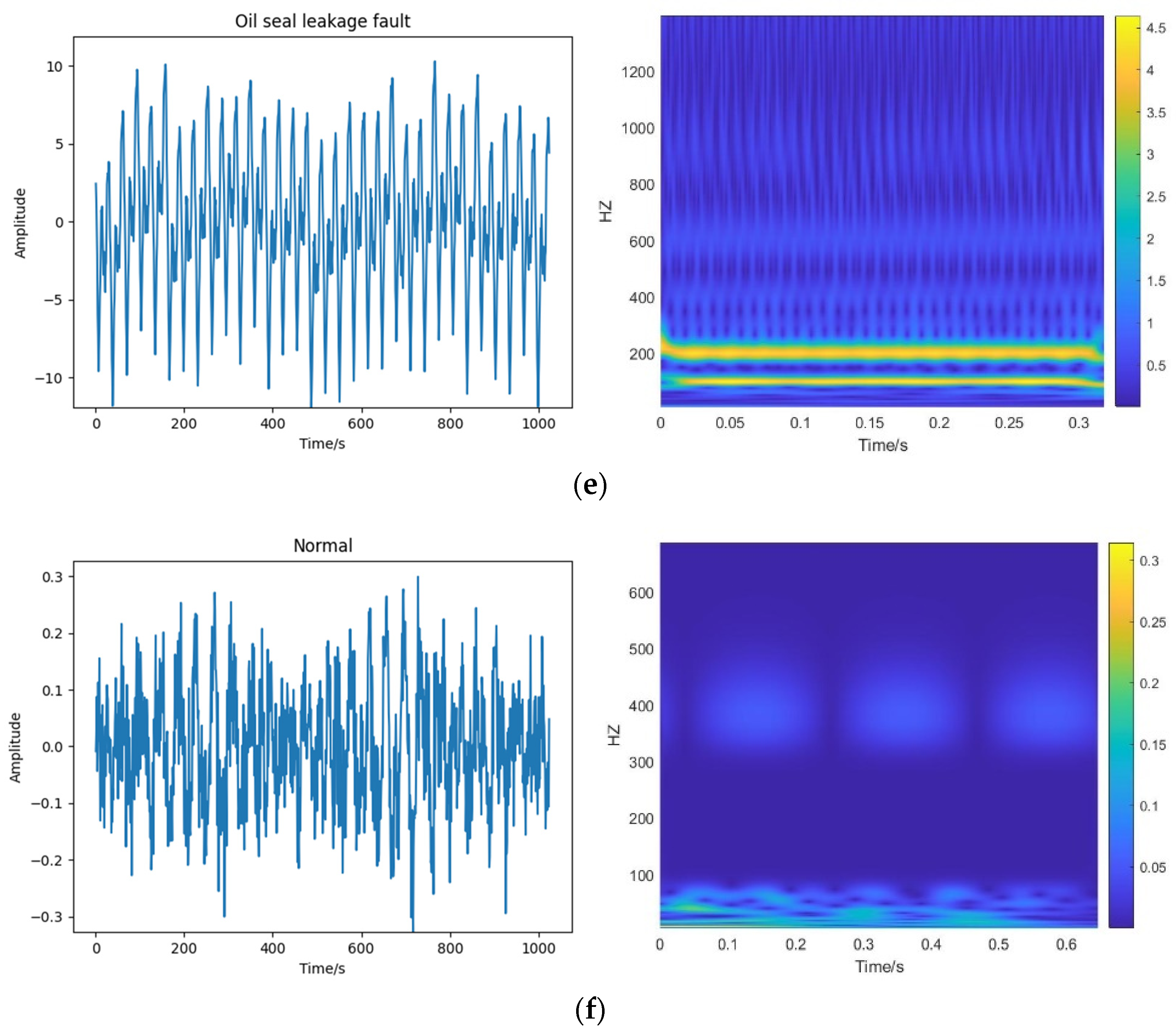
2.1. Feature Extraction with Wavelet Analysis
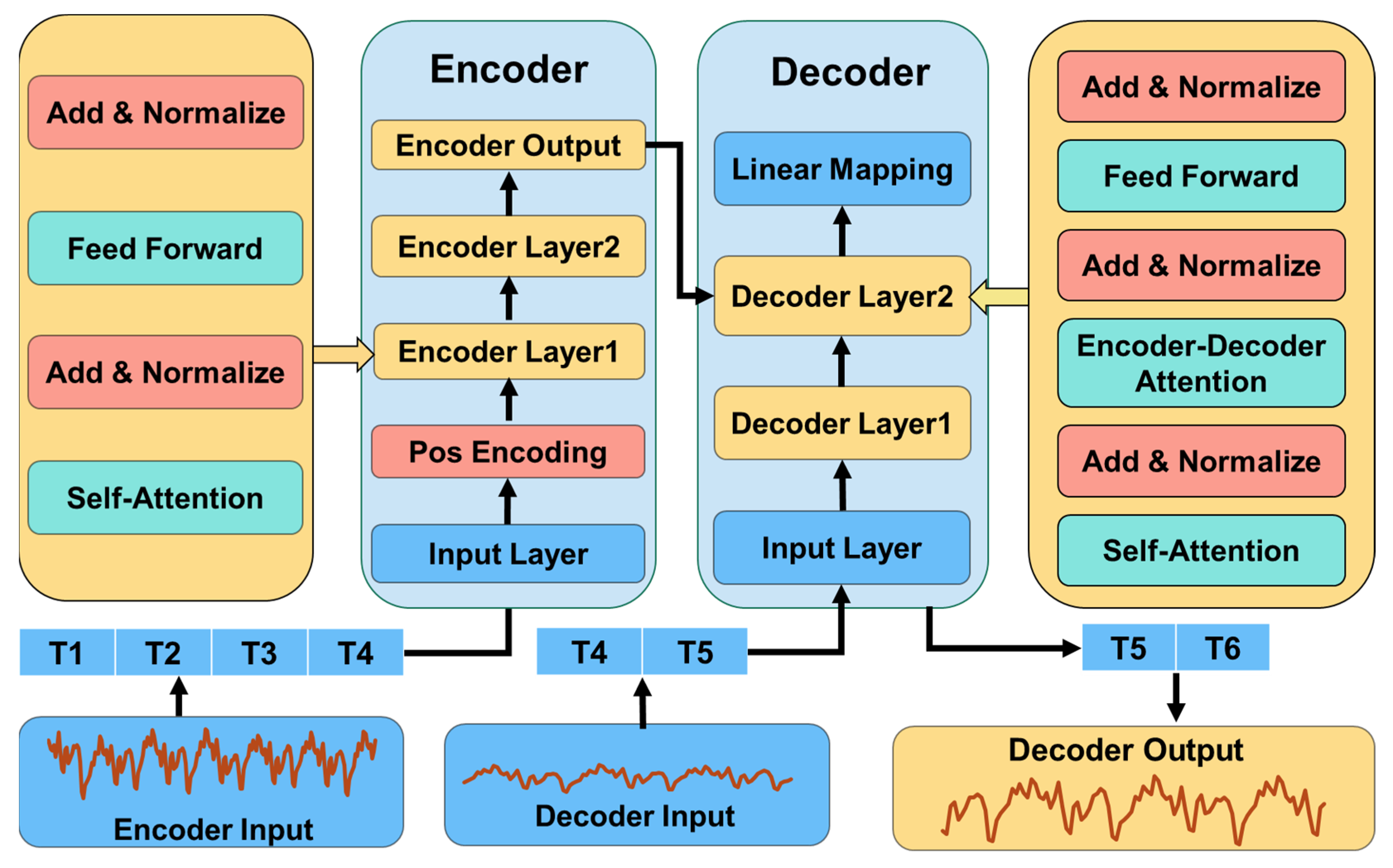
2.2. Prediction with Informer
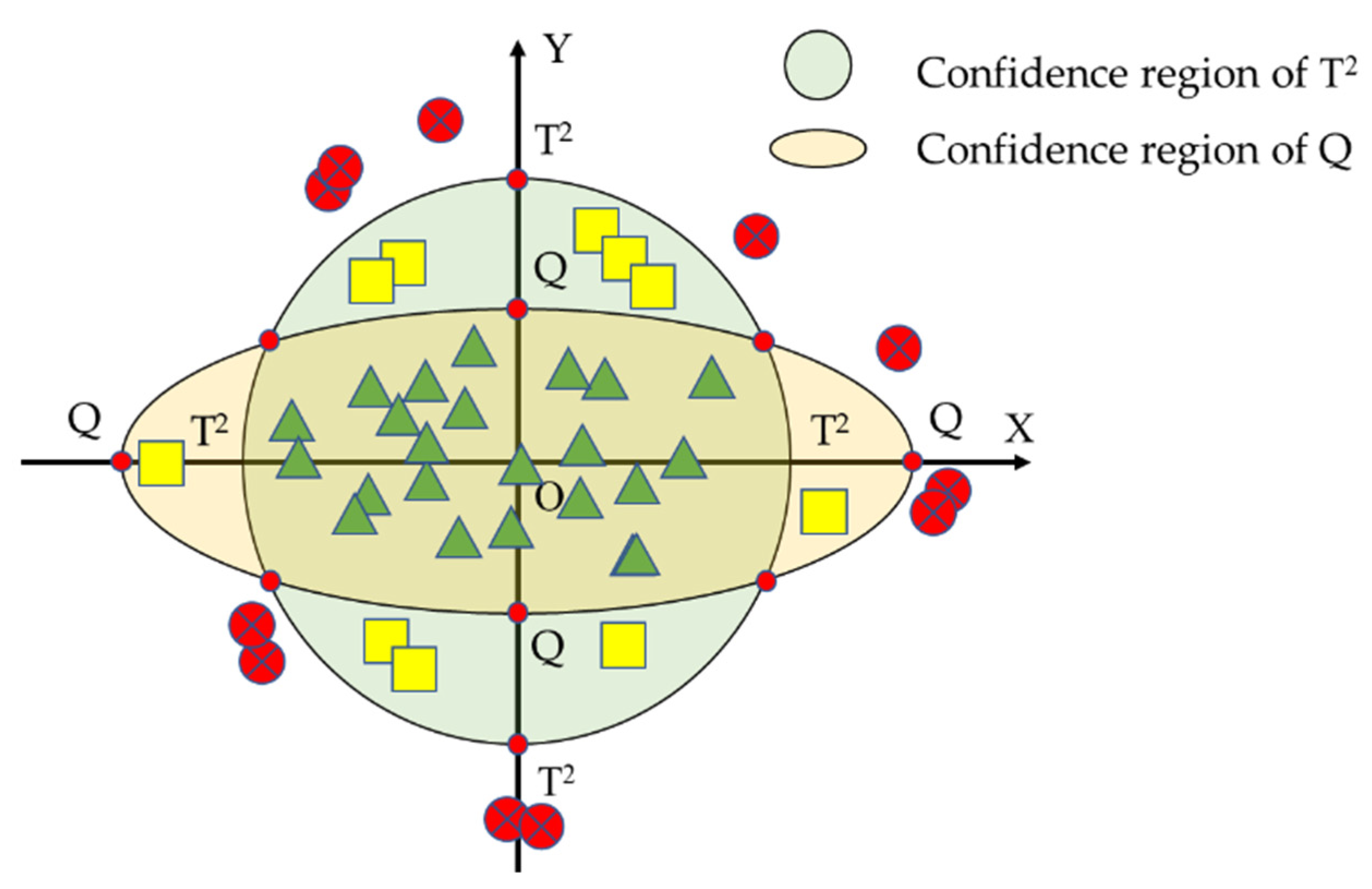
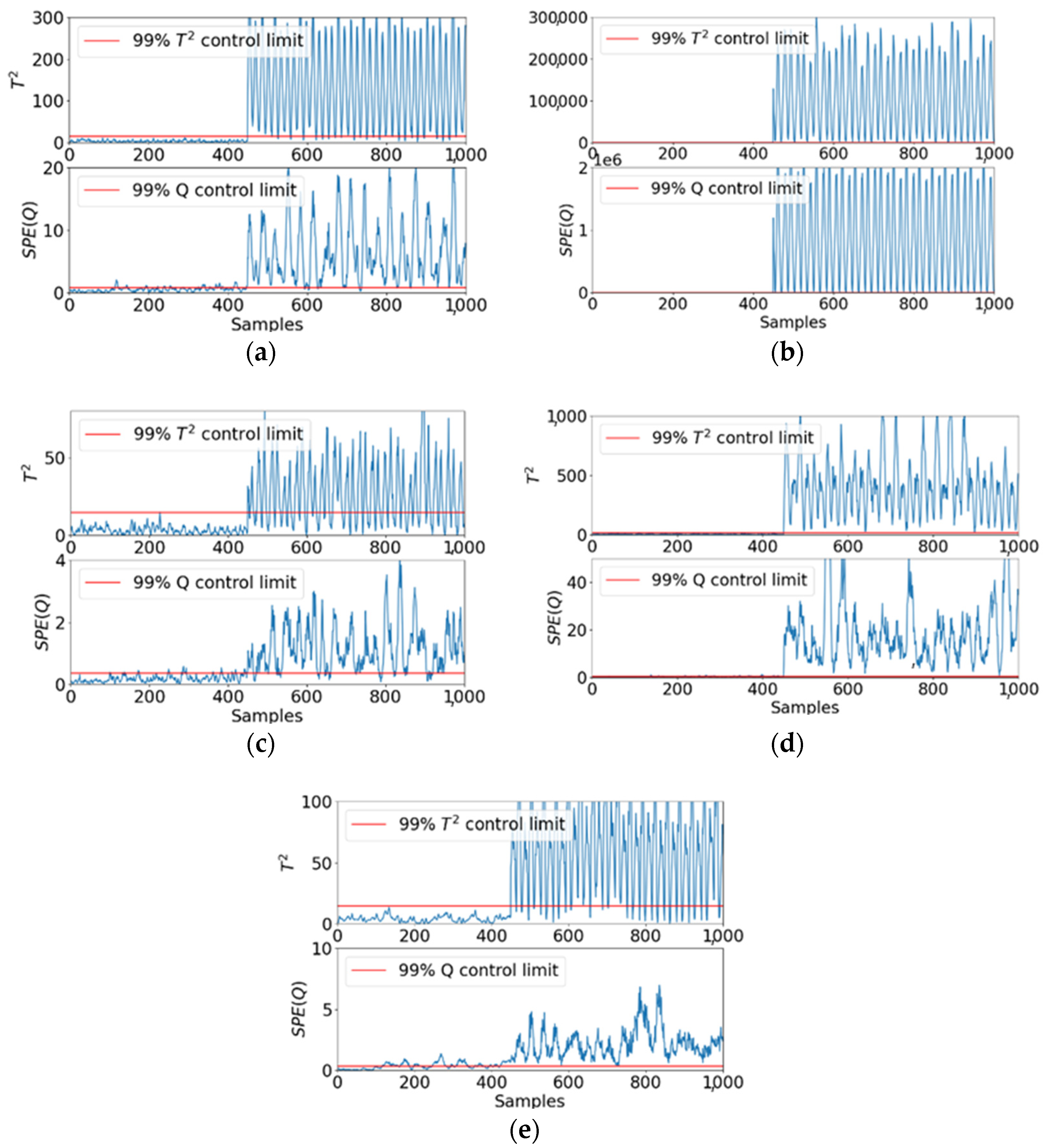
2.3. Fault Detection with PCA
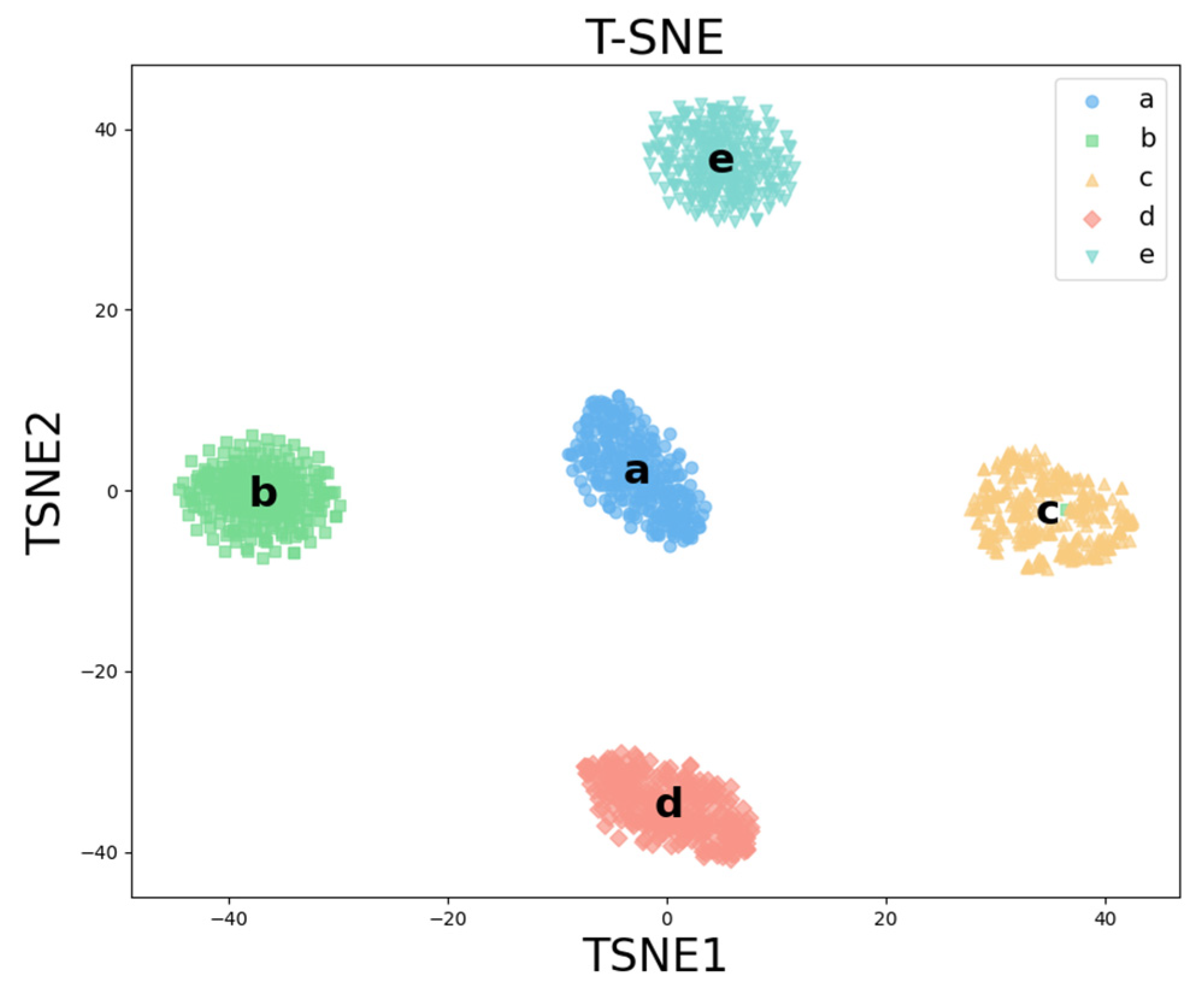
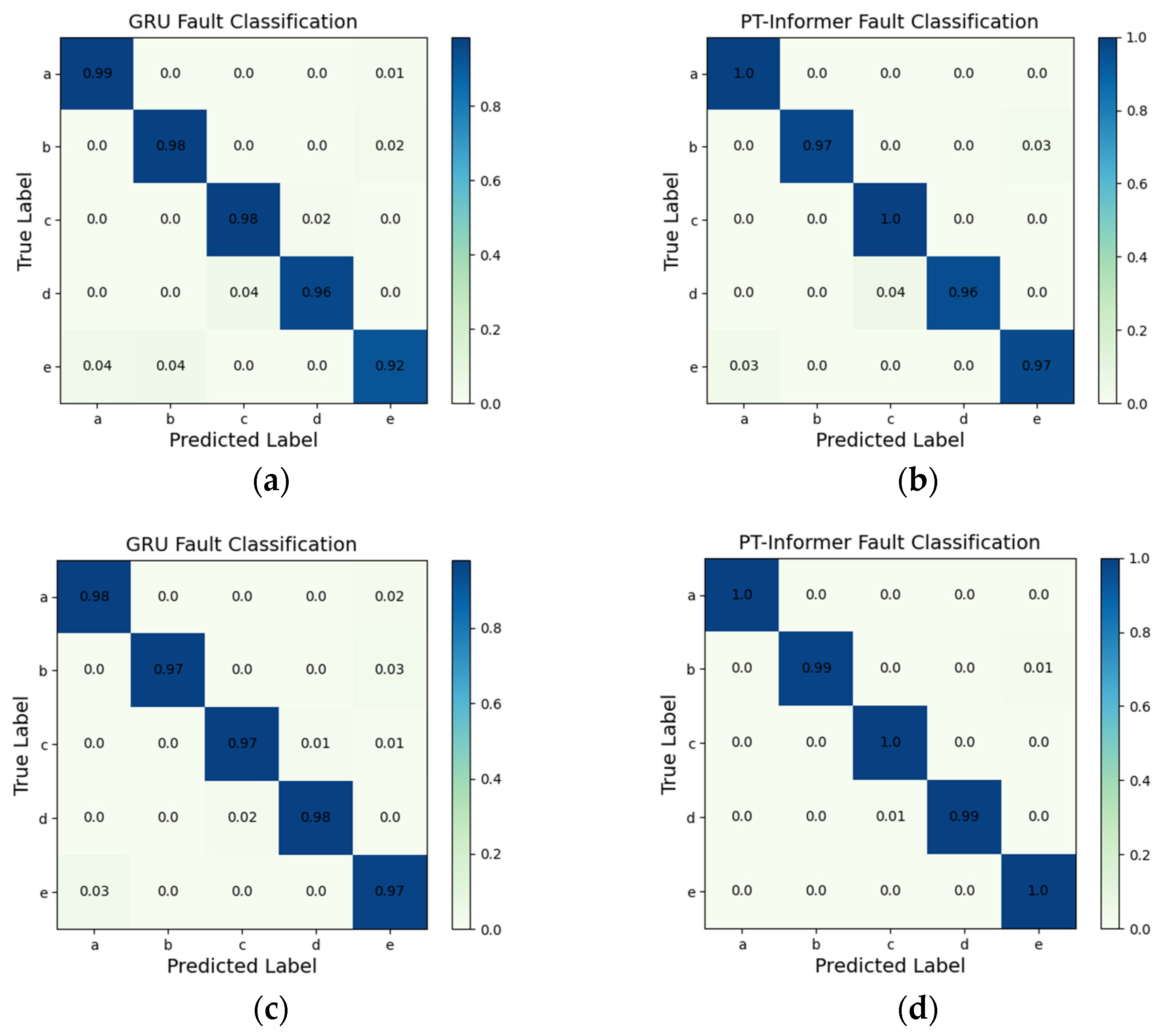
2.4. Fault Classification with t-SNE
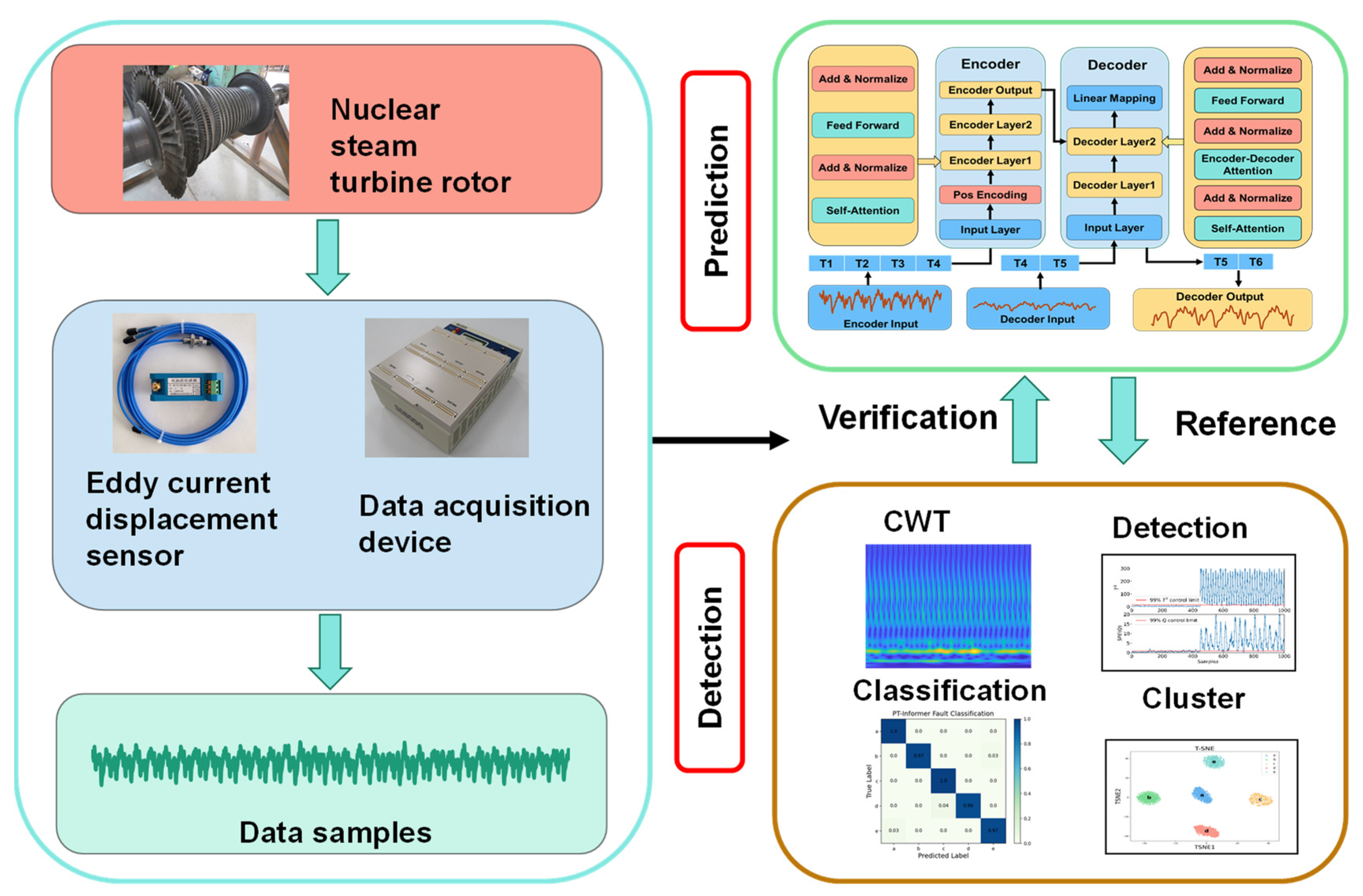
3. Experiments
3.1. Experiment Setup
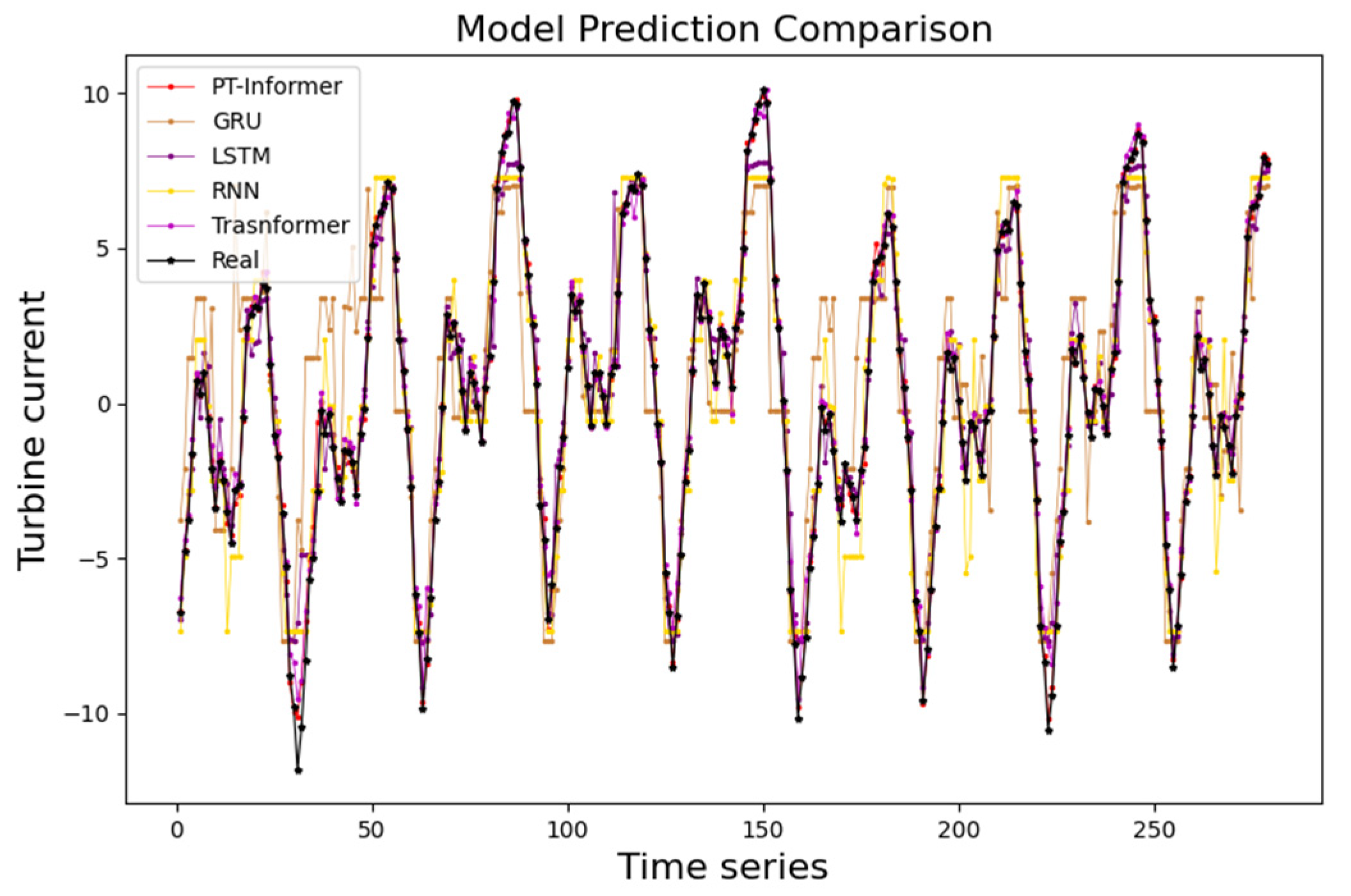
3.2. Fault Prediction Results
3.3. Data Preprocessing
3.4. Fault Detection Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, B.; Li, Z. Towards world’s low carbon development: The role of clean energy. Appl. Energy 2022, 307, 118160. [Google Scholar] [CrossRef]
- Yang, X.; Song, Y.; Wang, G.; Wang, W. A comprehensive review on the development of sustainable energy strategy and implementation in China. IEEE Trans. Sustain. Energy 2010, 1, 57–65. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, M.; Zhu, Y.; Zhang, K.; Li, Q. A Review of Fault Diagnosis, Status Prediction, and Evaluation Technology for Wind Turbines. Energies 2023, 16, 1125. [Google Scholar] [CrossRef]
- Tanuma, T. Introduction to steam turbines for power plants. In Advances in Steam Turbines for Modern Power Plants; Woodhead Publishing: Cambridge, UK, 2022; pp. 3–10. [Google Scholar]
- Li, S.; Li, J. Condition monitoring and diagnosis of power equipment: Review and prospective. High Volt. 2017, 2, 82–91. [Google Scholar] [CrossRef]
- Salahshoor, K.; Kordestani, M.; Khoshro, M.S. Fault detection and diagnosis of an industrial steam turbine using fusion of SVM (support vector machine) and ANFIS (adaptive neuro-fuzzy inference system) classifiers. Energy 2010, 35, 5472–5482. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. A comprehensive review on convolutional neural network in machine fault diagnosis. Neurocomputing 2020, 417, 36–63. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Fenton, W.G.; McGinnity, T.M.; Maguire, L.P. Fault diagnosis of electronic systems using intelligent techniques: A review. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2001, 31, 269–281. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Han, B.; Wang, J.; Zhang, Z.; Bao, H. Dynamic Simulation Model-Driven Fault Diagnosis Method for Bearing under Missing Fault-Type Samples. Appl. Sci. 2023, 13, 2857. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K. Data-driven prognostic scheme for bearings based on a novel health indicator and gated recurrent unit network. IEEE Trans. Ind. Inform. 2022, 19, 1301–1311. [Google Scholar] [CrossRef]
- Wu, C.; Li, X.; Guo, Y.; Wang, J.; Ren, Z.; Wang, M.; Yang, Z. Natural language processing for smart construction: Current status and future directions. Autom. Constr. 2022, 134, 104059. [Google Scholar] [CrossRef]
- An, Z.; Cheng, L.; Guo, Y.; Ren, M.; Feng, W.; Sun, B.; Ling, J.; Chen, H.; Chen, W.; Luo, Y.; et al. A Novel Principal Component Analysis-Informer Model for Fault Prediction of Nuclear Valves. Machines 2022, 10, 240. [Google Scholar] [CrossRef]
- Inyang, U.I.; Petrunin, I.; Jennions, I. Diagnosis of multiple faults in rotating machinery using ensemble learning. Sensors 2023, 23, 1005. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S.-S.; Fu, S.; Lin, L. A novel gas turbine fault diagnosis method based on transfer learning with CNN. Measurement 2019, 137, 435–453. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Michau, G.; Hu, Y.; Palmé, T.; Fink, O. Feature learning for fault detection in high-dimensional condition monitoring signals. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2020, 234, 104–115. [Google Scholar] [CrossRef]
- Fast, M.; Assadi, M.; De, S. Development and multi-utility of an ANN model for an industrial gas turbine. Appl. Energy 2009, 86, 9–17. [Google Scholar] [CrossRef]
- Asgari, H.; Chen, X.; Menhaj, M.B.; Sainudiin, R. Artificial neural network–based system identification for a single-shaft gas turbine. J. Eng. Gas Turbines Power 2013, 135, 092601. [Google Scholar] [CrossRef]
- Barad, S.G.; Ramaiah, P.V.; Giridhar, R.K.; Krishnaiah, G. Neural network approach for a combined performance and mechanical health monitoring of a gas turbine engine. Mech. Syst. Signal Process. 2012, 27, 729–742. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Ma, J. Rolling bearing fault diagnosis based on STFT-deep learning and sound signals. Shock Vib. 2016, 2016, 6127479. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.-Y.; Qin, W.-L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Ul-Haq Gilani, S.I.; Baheta, A.T.; Li, Y.-G. Performance-based fault diagnosis of a gas turbine engine using an integrated support vector machine and artificial neural network method. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 786–802. [Google Scholar] [CrossRef]
- Zhao, M.; Fu, X.; Zhang, Y.; Meng, L.; Tang, B. Highly imbalanced fault diagnosis of mechanical systems based on wavelet packet distortion and convolutional neural networks. Adv. Eng. Inform. 2022, 51, 101535. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer networks for trajectory forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 10335–10342. [Google Scholar]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, S.; Xiao, X.; Ding, Q.; Zhao, P.; Wei, Y.; Huang, J. Adversarial sparse transformer for time series forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17105–17115. [Google Scholar]
- Cai, L.; Janowicz, K.; Mai, G.; Yan, B.; Zhu, R. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Trans. GIS 2020, 24, 736–755. [Google Scholar] [CrossRef]
- Xu, M.; Dai, W.; Liu, C.; Gao, X.; Lin, W.; Qi, G.-J.; Xiong, H. Spatial-temporal transformer networks for traffic flow forecasting. arXiv 2020, arXiv:2001.02908. [Google Scholar]
- Wang, Z.; Zhang, Q.; Xiong, J.; Xiao, M.; Sun, G.; He, J. Fault diagnosis of a rolling bearing using wavelet packet denoising and random forests. IEEE Sens. J. 2017, 17, 5581–5588. [Google Scholar] [CrossRef]
- Chaouch, H.; Charfeddine, S.; Ben Aoun, S.; Jerbi, H.; Leiva, V. Multiscale monitoring using machine learning methods: New methodology and an industrial application to a photovoltaic system. Mathematics 2022, 10, 890. [Google Scholar] [CrossRef]
- Tao, H.; Cheng, L.; Qiu, J.; Stojanovic, V. Few shot cross equipment fault diagnosis method based on parameter optimization and feature mertic. Meas. Sci. Technol. 2022, 33, 115005. [Google Scholar] [CrossRef]
- He, X.; Wang, Z.; Li, Y.; Khazhina, S.; Du, W.; Wang, J.; Wang, W. Joint decision-making of parallel machine scheduling restricted in job-machine release time and preventive maintenance with remaining useful life constraints. Reliab. Eng. Syst. Saf. 2022, 222, 108429. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, P.; Yang, X.; Hu, A.; Su, H. Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism. Measurement 2021, 175, 109094. [Google Scholar] [CrossRef]
- Cheng, L.; An, Z.; Guo, Y.; Ren, M.; Yang, Z.; McLoone, S. MMFSL: A novel multi-modal few-shot learning framework for fault diagnosis of industrial bearings. IEEE Trans. Instrum. Meas. 2023; early access. [Google Scholar] [CrossRef]


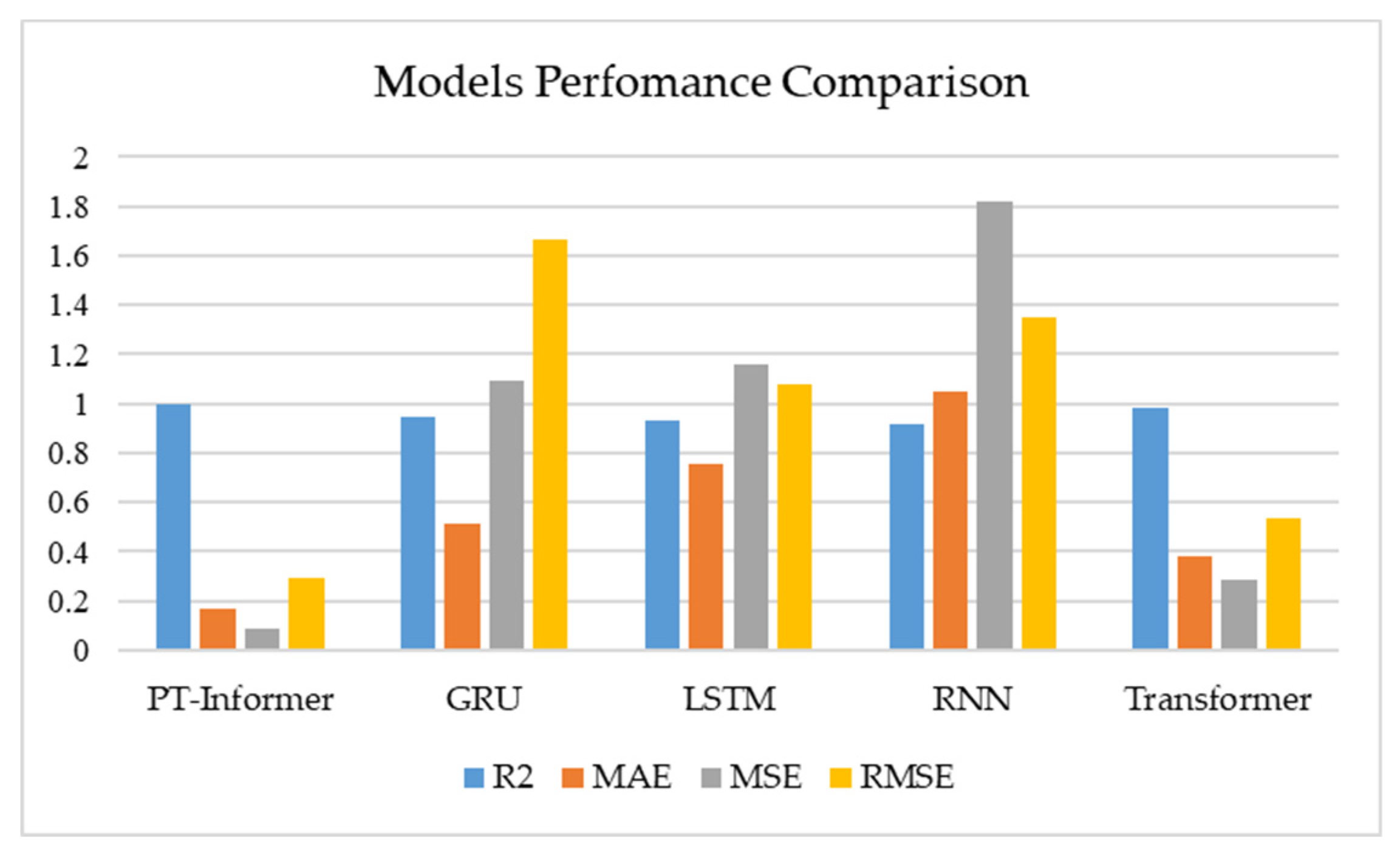


| Methods | PT-Informer | GRU | LSTM | RNN | Transformer |
|---|---|---|---|---|---|
| R2 | 0.9960291244 | 0.9491238937 | 0.9339795604 | 0.9144744538 | 0.9855304990 |
| MAE | 0.1707754554 | 0.5170966758 | 0.7587701152 | 1.0483688931 | 0.3807402089 |
| MSE | 0.0853712703 | 1.0954833102 | 1.1624907156 | 1.8177715859 | 0.2835630504 |
| RMSE | 0.2921836243 | 1.6637348423 | 1.0781886271 | 1.3482475981 | 0.5325063853 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; An, Z.; Yang, Z.; Zhang, Y.; Chen, H.; Chen, W.; Luo, Y.; Guo, Y. PT-Informer: A Deep Learning Framework for Nuclear Steam Turbine Fault Diagnosis and Prediction. Machines 2023, 11, 846. https://doi.org/10.3390/machines11080846
Zhou J, An Z, Yang Z, Zhang Y, Chen H, Chen W, Luo Y, Guo Y. PT-Informer: A Deep Learning Framework for Nuclear Steam Turbine Fault Diagnosis and Prediction. Machines. 2023; 11(8):846. https://doi.org/10.3390/machines11080846
Chicago/Turabian StyleZhou, Jiajing, Zhao An, Zhile Yang, Yanhui Zhang, Huanlin Chen, Weihua Chen, Yalin Luo, and Yuanjun Guo. 2023. "PT-Informer: A Deep Learning Framework for Nuclear Steam Turbine Fault Diagnosis and Prediction" Machines 11, no. 8: 846. https://doi.org/10.3390/machines11080846
APA StyleZhou, J., An, Z., Yang, Z., Zhang, Y., Chen, H., Chen, W., Luo, Y., & Guo, Y. (2023). PT-Informer: A Deep Learning Framework for Nuclear Steam Turbine Fault Diagnosis and Prediction. Machines, 11(8), 846. https://doi.org/10.3390/machines11080846







