Contactless Method for Measurement of Surface Roughness Based on a Chromatic Confocal Sensor
Abstract
1. Introduction
2. Literature Review
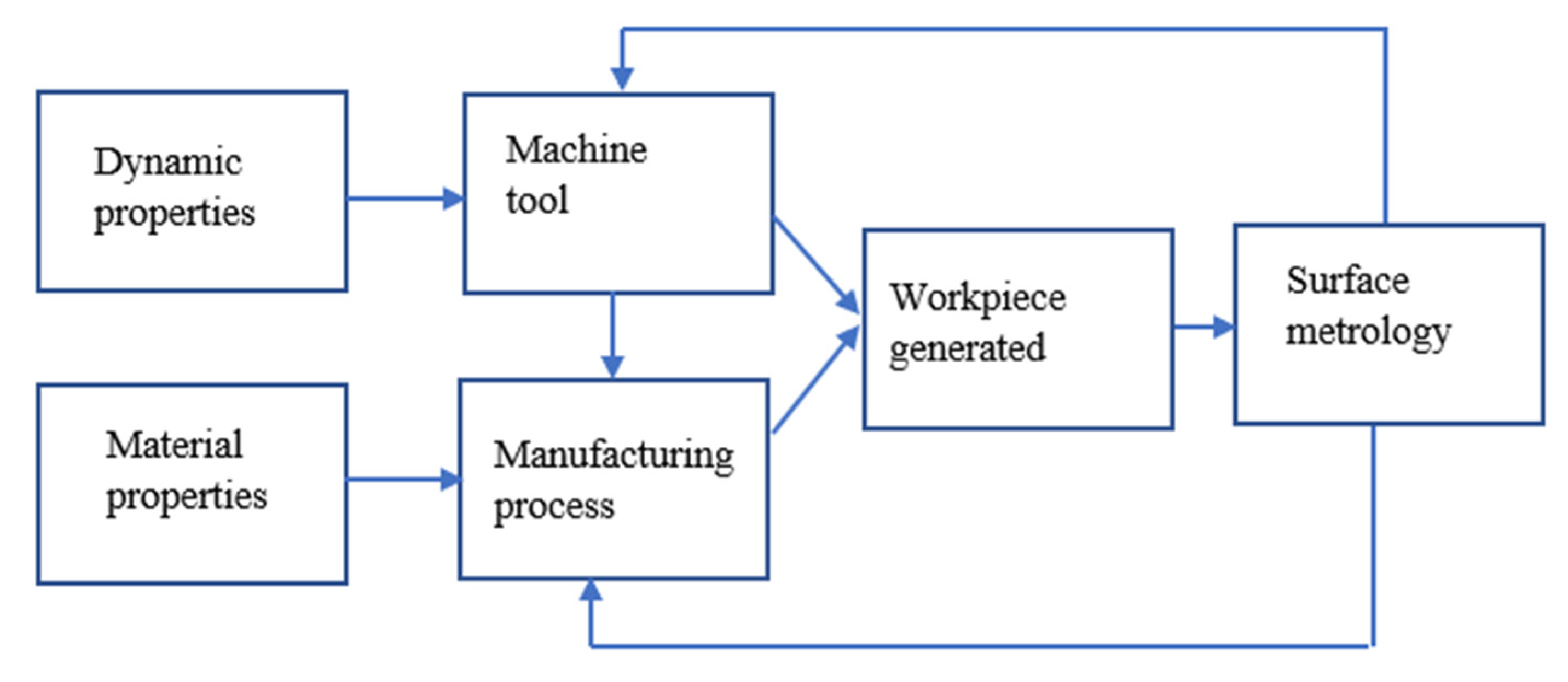
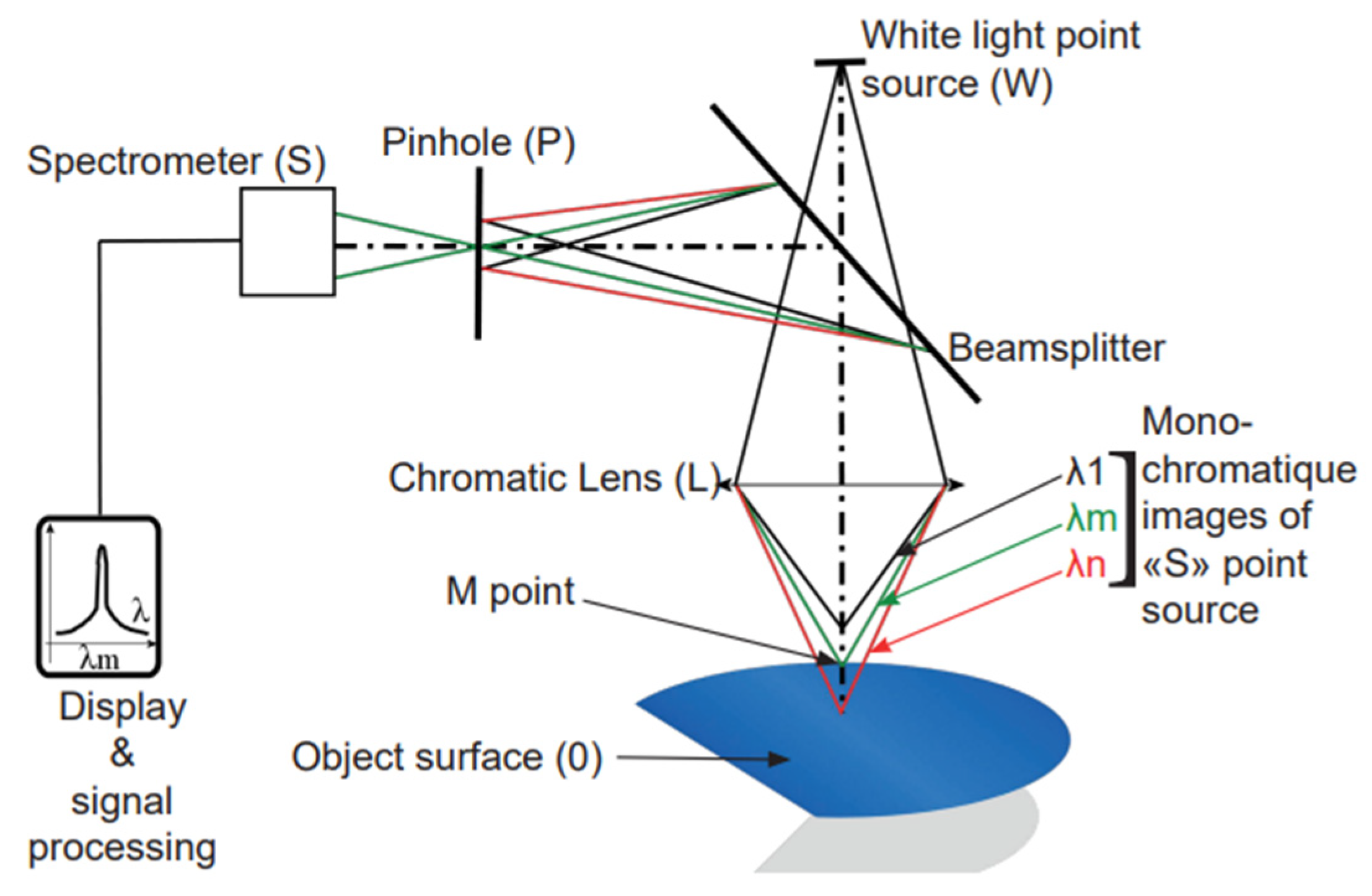
- Samples are recommended to be measured at certain settings for cutoff, evaluation length, and stylus travel.
- The measuring system has a trace length limit of 12.7 mm.
- To obtain a profile of the measured surface, it is necessary to use the data-stitching algorithm, since they are limited in length to 0.8 mm.
- It is not indicated whether the profile type (periodic, non-periodic) was taken into account when choosing the settings and whether the profile type affects the relative measurement error.
- -
- Carry out a comparative analysis of the results of contact and non-contact methods for measuring surface irregularities of a metal specimen with a known process roughness. Set the relative error of the non-contact method compared to the contact method.
- -
- Conduct comparative studies on metal samples—metal surface roughness standard set, obtained by mechanical processing and with two types of profiles: periodic and non-periodic. Set the relative error of the non-contact method compared to the contact method in a wide range of surface roughness parameters.
- -
- Investigate the influence of speed on the measurement uncertainty for the selected range of the roughness parameter under study, taking into account the noise arising from the drive unit and the sample state.
- -
- Set the roughness range of surfaces obtained by machining methods, taking into account the possible noise from the surface gradient, the drive noise, etc.
- -
- Identify the scope and the settings of the chromatic confocal laser sensor for the purpose of determining the roughness parameters.
- -
- Study the profilogram as a signal in the time and frequency domains, which will provide additional functions for monitoring the process (operation). Study the autocorrelation function and the power spectrum density for periodic and aperiodic profiles.
3. Materials and Methods
3.1. Stylus Measurement
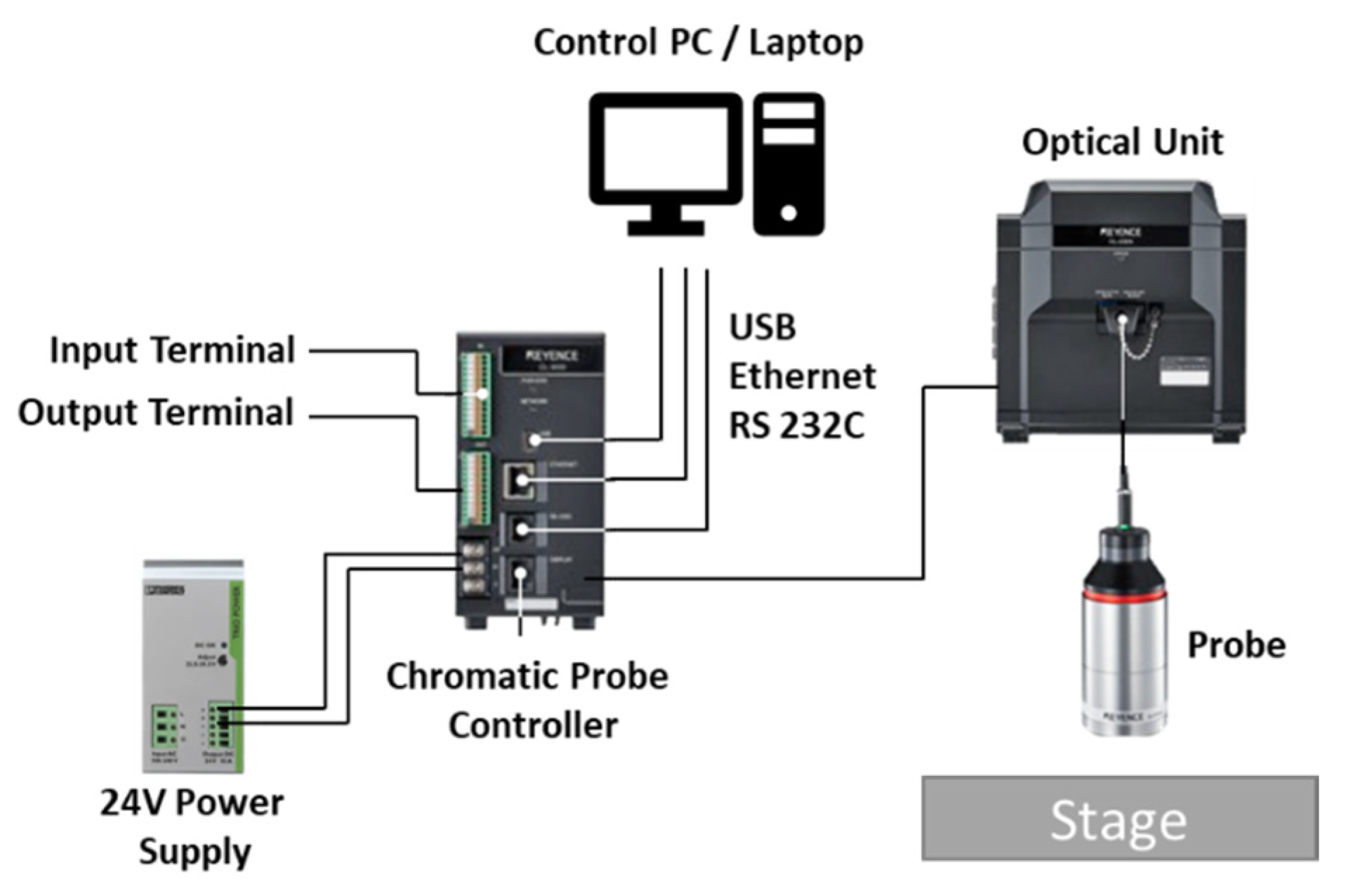
3.2. Laser Confocal Measurement Method
4. Results
4.1. Comparison of Stylus and Confocal Measurement Methods
- When changing the stylus speed, the sample standard deviation of the Ra parameter varied from 0 to 0.012 µm, while the Rz parameter varied from 0 to 0.462 µm. Moreover, the largest values referred to the maximum probe movement speed of 1 mm/s.
- The margin of error for the Ra parameter varied from 0 to 0.014 µm, and for the Rz parameter it varied from 0 to 1.147 µm. Moreover, the largest value referred to the maximum probe movement speed of 1 mm/s.
- When the probe movement speed increased from V = 0.05 mm/s to V = 1 mm/s, the sample standard deviation and margin of error parameters for the Ra parameter remained constant, while for the Rz parameter they were variable values. In this case, the average Ra values were averaged over three measurements of the roughness parameters measured at the same place in each track, then averaged over three tracks.
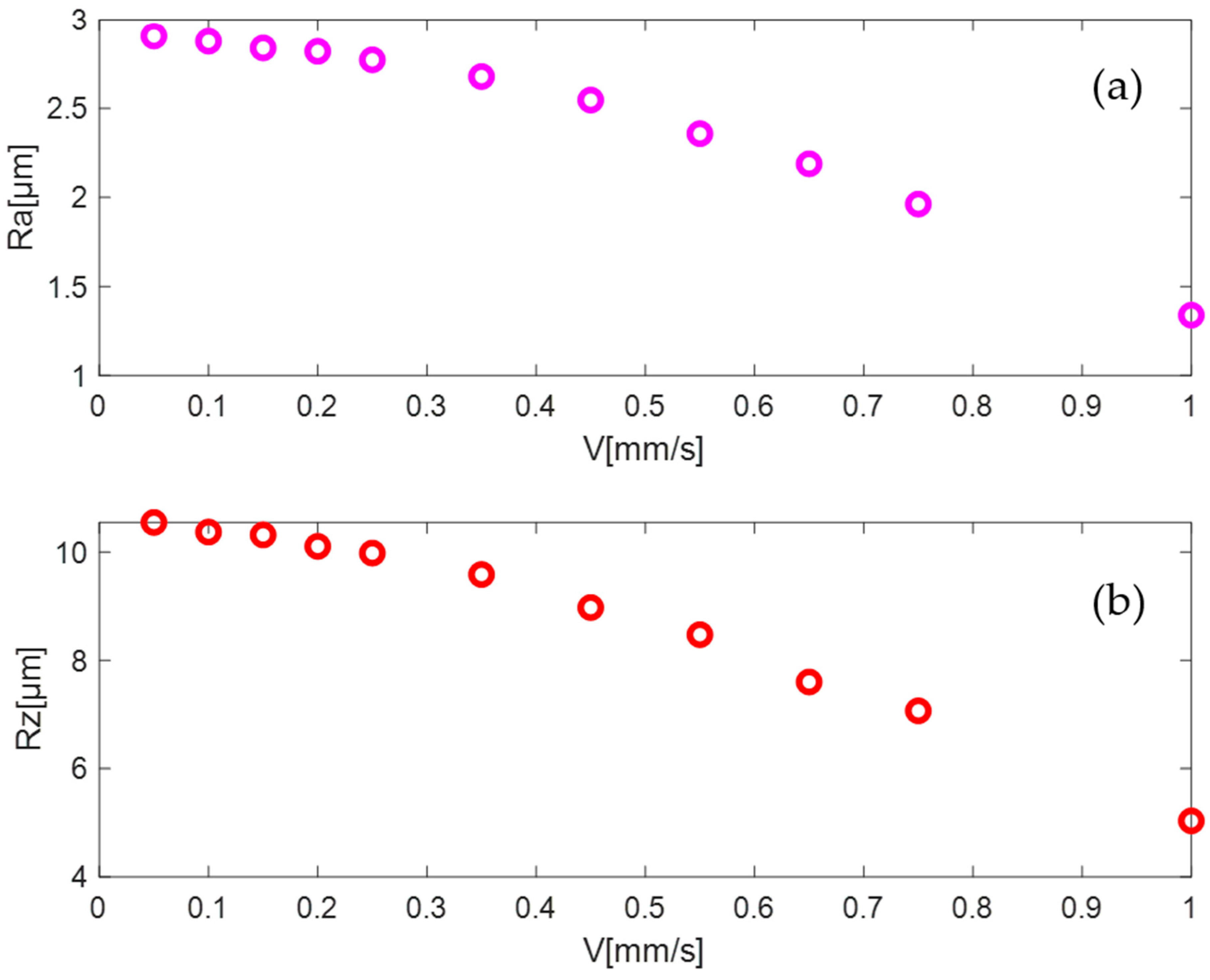
- The probe movement speed had little effect on the parameters Ra and Rz. For example, when the probe speed increased from 0.05 mm/s to 1 mm/s, the parameter Ra changed by 0.43%, and Rz by 0.2%. Therefore, it is possible to set the maximum speed of the probe when measuring.
- When the speed of the measuring head increased, the average values of the parameters Ra and Rz decreased. In this case, the average values were averaged over three measurements of the roughness parameters measured at the same place in each track, then averaged over three tracks.
- When the speed of the measuring head increased from V = 0.05 mm/s to V = 0.15 mm/s, the sample standard deviation and margin of error for the Rz were less than those for the Ra parameter. When the speed of the probe increased from V = 0.20 mm/s to V = 1 mm/s, the opposite trend was observed.
- When changing the speed of the measuring head, the sample standard deviation of Ra varied from 0 to 0.145 µm, while for Rz from 0.013 to 0.939 µm.
- The margin of error for Ra varied from 0.002 to 0.181 µm, and that for Rz from 0.031 to 0.707 µm.
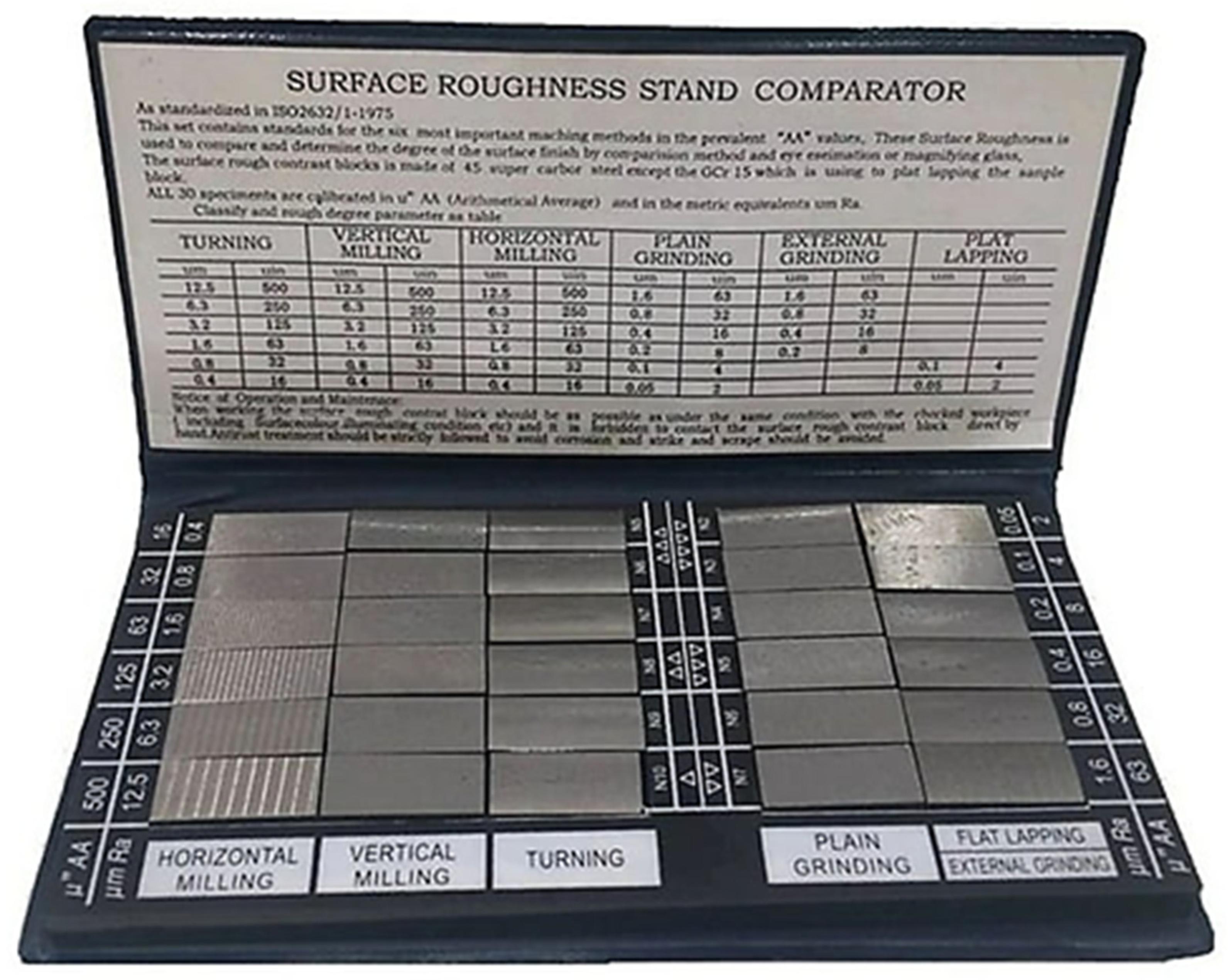
4.2. Roughness Measurement of Sample Roughness Set
4.3. Correlation Analysis and Frequency Analysis for Development of the Estimated Functions—Power Spectrum Density and Autocorrelation Function
4.3.1. Correlation Analysis
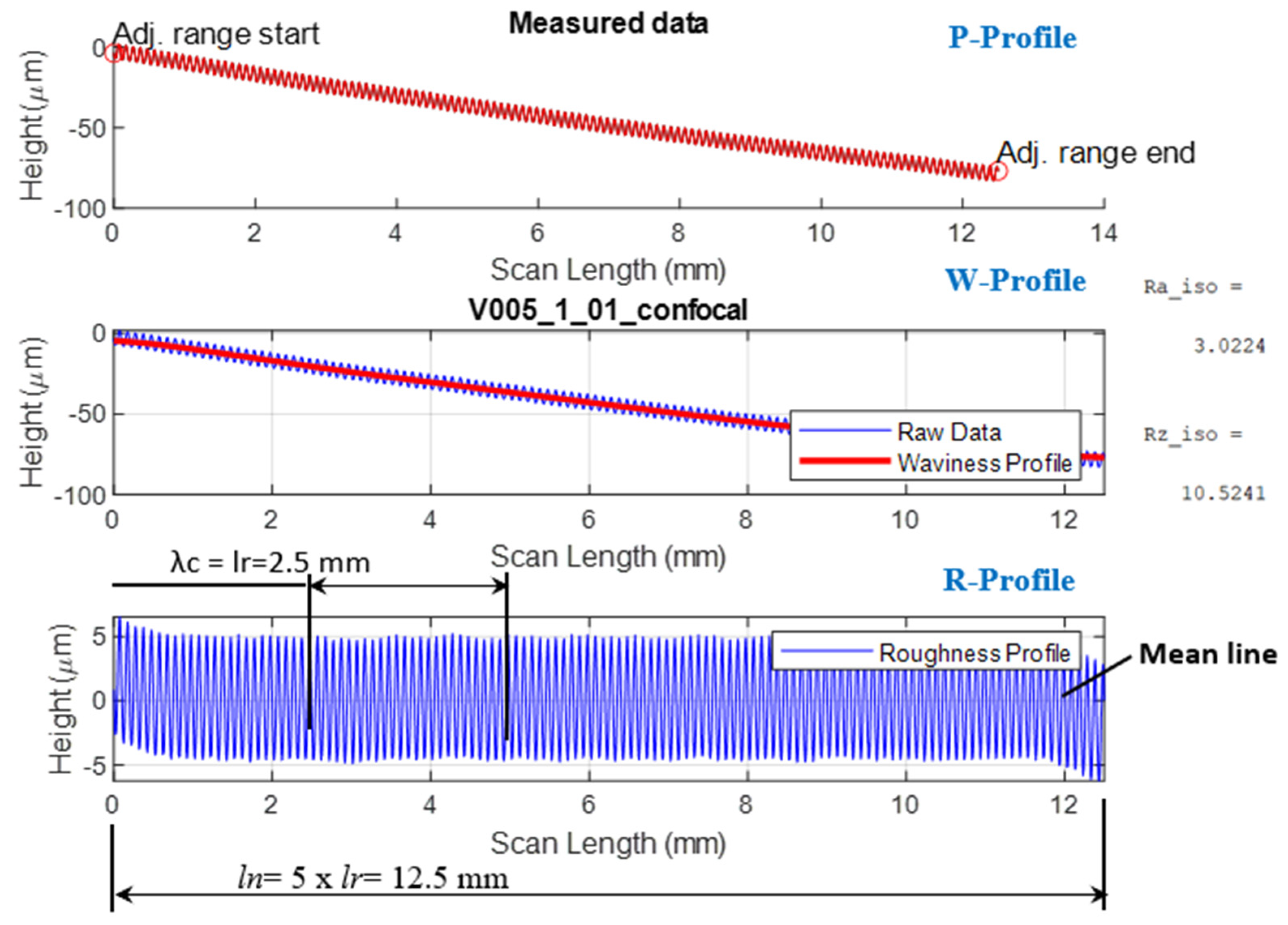
- The profilogram of the surface is considered as a realization of a stationary random process on the length of the profilogram , i.e., a random process with the constant expected value equal to zero.
- The real surface profile is represented as the sum of two components: deterministic (periodic, regular) and random (non-deterministic, aperiodic, irregular). In this case, the deterministic component , in contrast to the random component, is a polyharmonic oscillation consisting of the sum of simple harmonics, and the random component is a random stationary function with zero mathematical expectation and variance . The mathematical model, for example of a profilogram signal, has the form [38]:



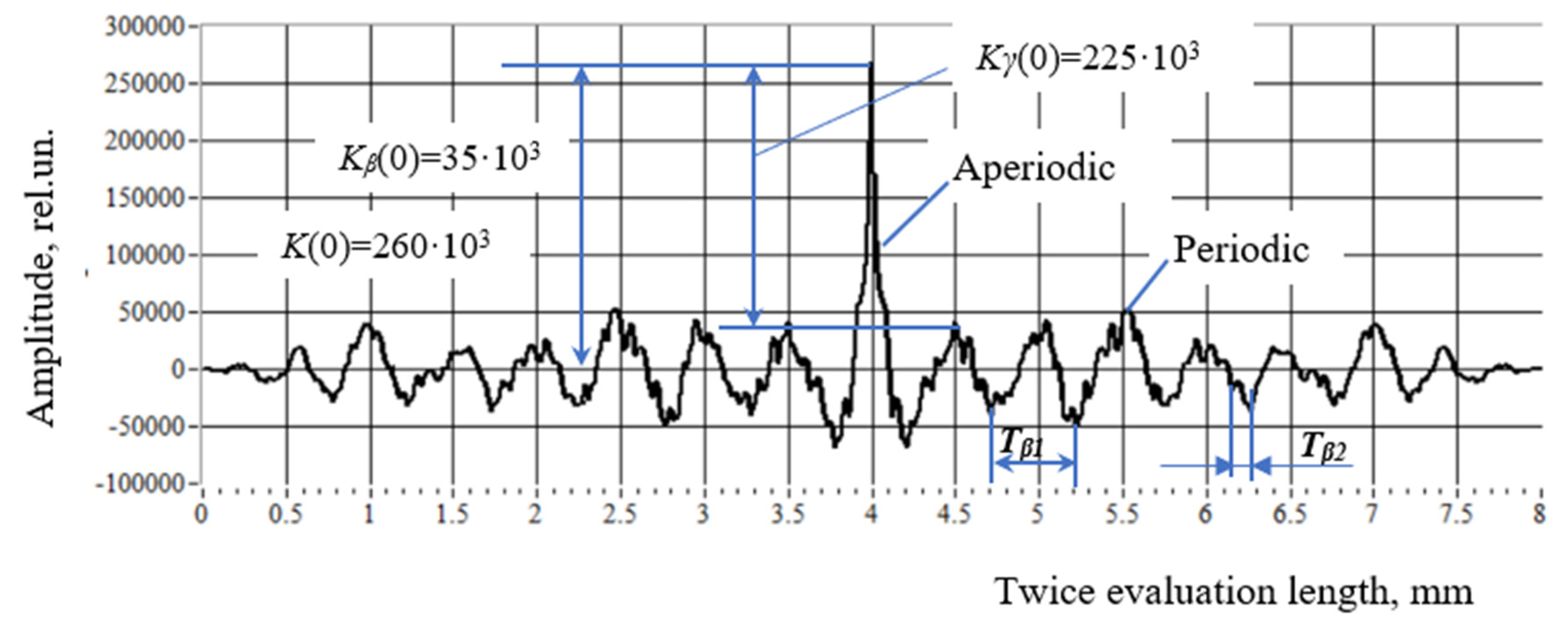
- 3.
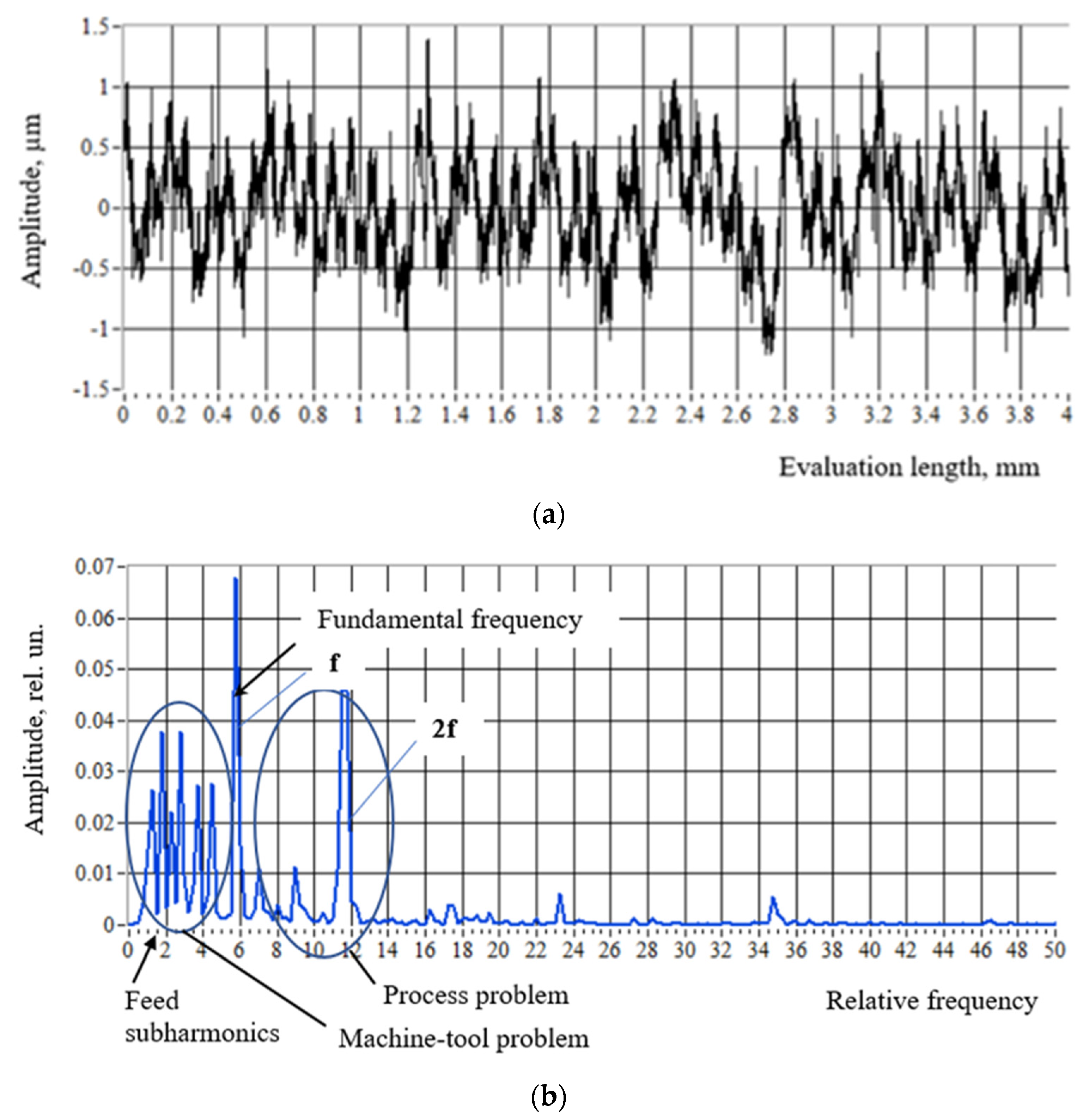
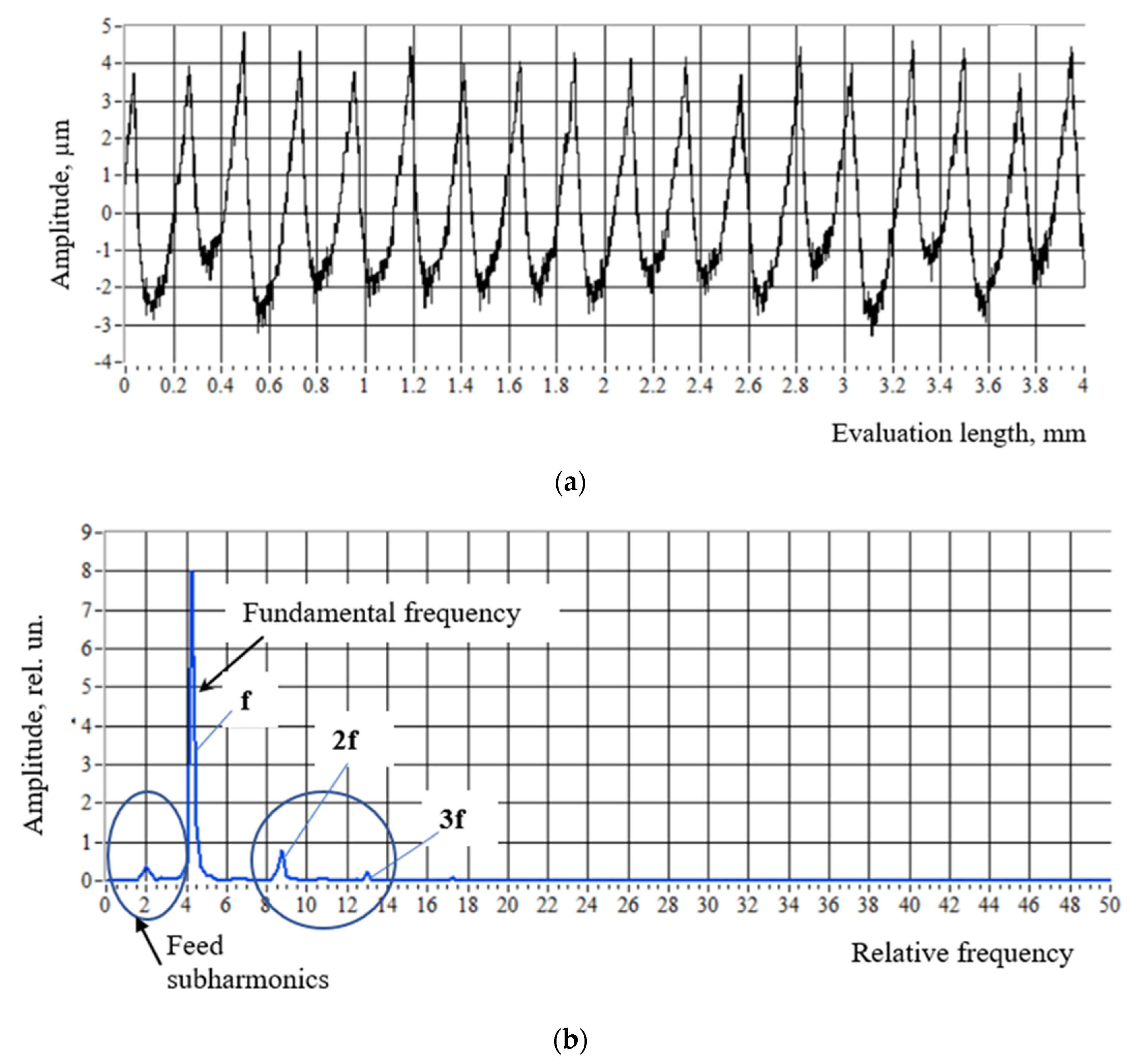
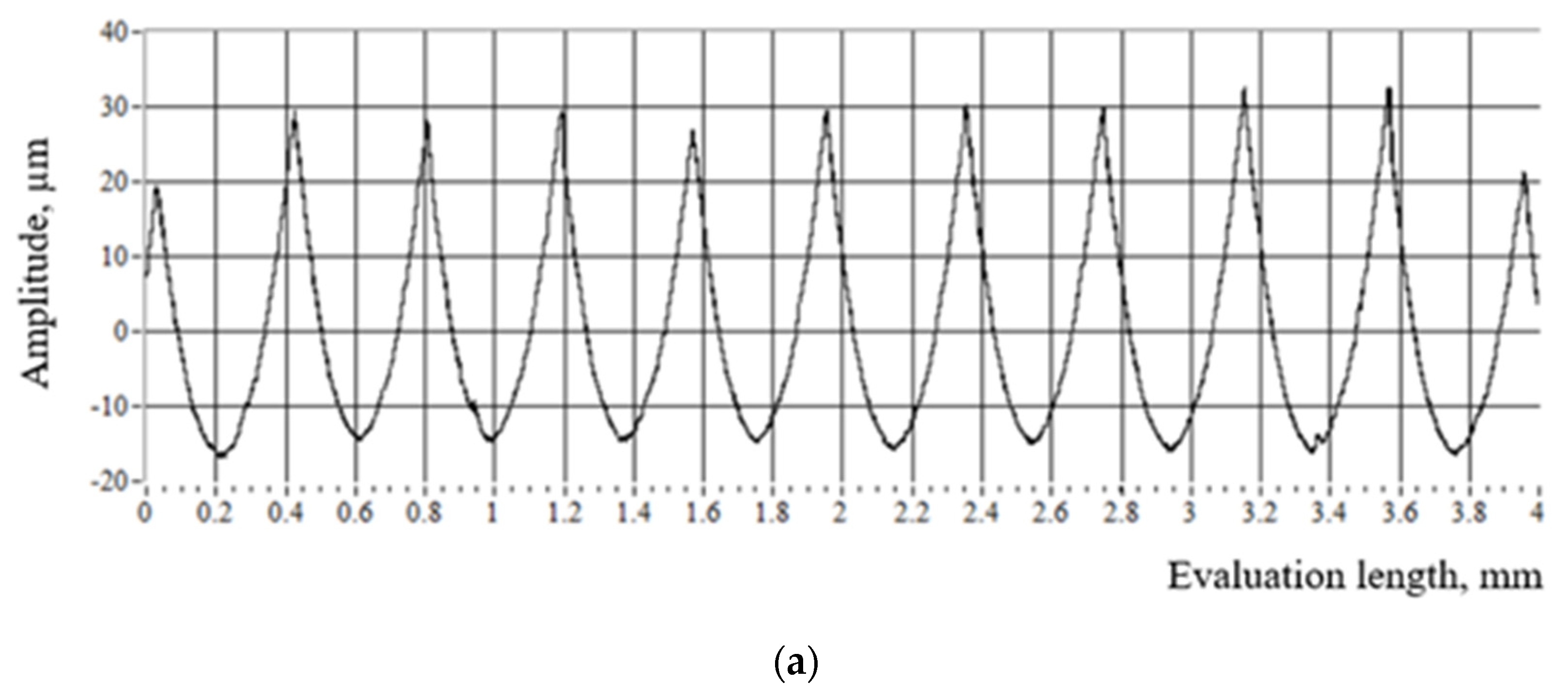
- The wave step (0.25 mm) of the initial total signal for sample No. 1 (Figure 15) coincided with the wave step of the autocorrelation function for the same sample, i.e., mm (Figure 16). At the same time, for sample No. 2 (Figure 17), the deterministic component of the signal associated with its periodicity was not expressed—it was hidden and characterized by variable steps = 0.5 mm and = 0.1 mm (Figure 18).
- With an increase of the nominal roughness from Ra 0.4 to Ra 12.5 (in this case, the actual values changed from 0.363 µm to 11.23 µm, measured by SJ-400) for samples after the turning operation, the proportion of the deterministic component in the total signal increased.
- Of the cutting modes, the feed and cutting speed had the most significant influence. Turning formed a periodic profile on the sample surface by changing the tool feed.
- 3.
- With an increase of the nominal roughness from Ra 0.4 to Ra 1.6 (in this case, the actual values changed from 0.42 µm to 1.48 µm, measured SJ-400) for samples after the grinding operation, the ratio between the deterministic and random components was almost constant.
- 4.
- Grinding is a stochastic process, during which the surface roughness was formed by randomly arranged abrasive grains. Consequently, an aperiodic profile was formed on the surface of the sample. Therefore, the random component was larger than the deterministic one, and the ratio between them practically remained constant.
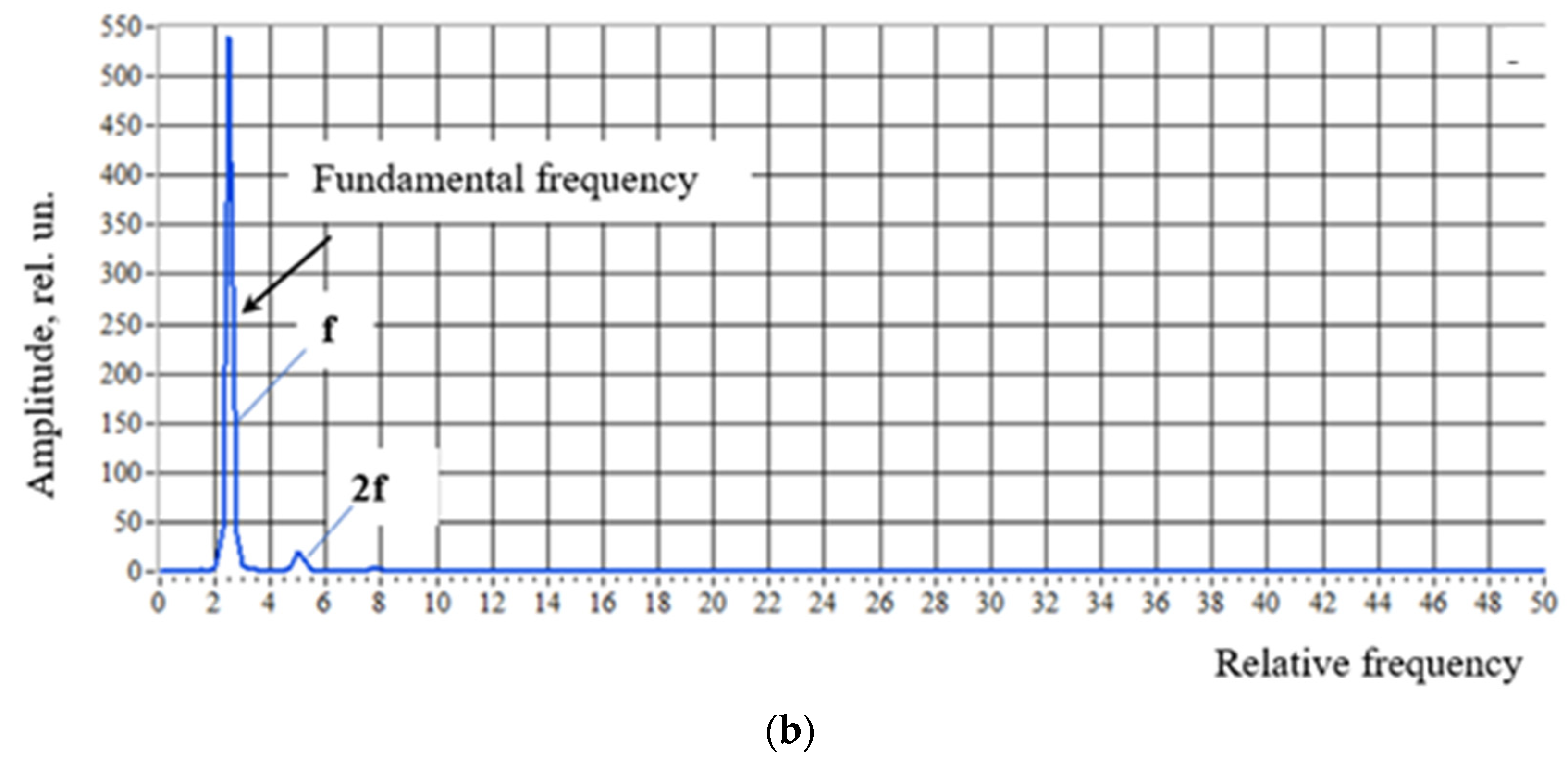
4.3.2. Frequency Analysis
- -
- To develop a frequency profile analysis technique based on the fast Fourier transform (FFT) and the formation of power spectrum density.
- -
- To consider the possibility of using the power spectrum density spectrogram to analyze the situation during turning. This setting can be effective as it provides a significant signal gain over the noise introduced into the system. This approach can be used to develop software for process-monitoring systems.
5. Conclusions
- A measuring system based on a chromatic confocal sensor was developed that allows measuring surface roughness with the ability to select settings, such as: the speed of the measuring head, the evaluation length, the traverse length, the cutoff, the number of tracks on the sample surface, and the distance between the measured tracks.
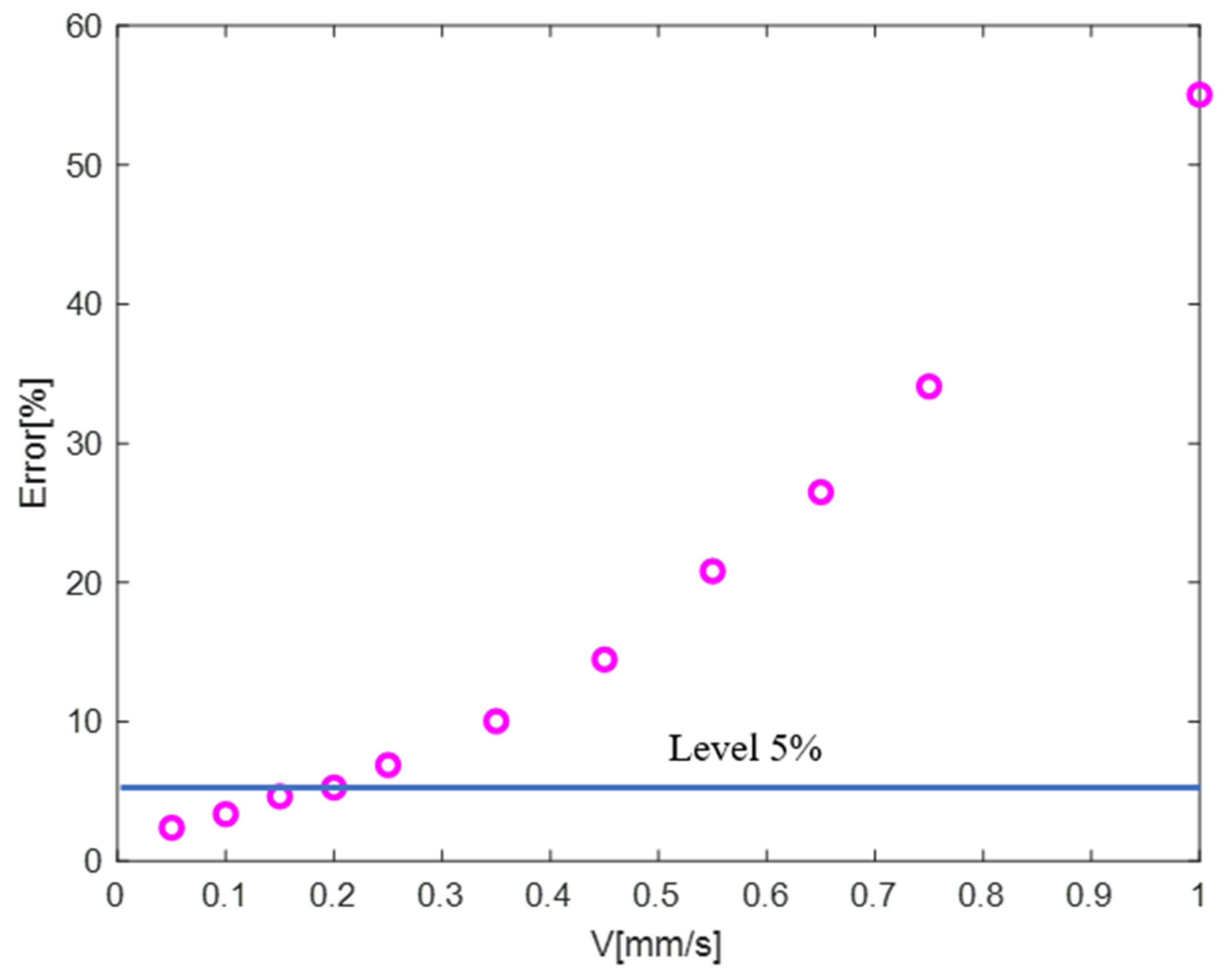
- When operation testing of the developed measuring system was conducted on a standard metal sample with a known roughness, it was found that with an increase of the speed of the measuring head, the error in the estimates of Ra and Rz increased. An error level of 5% corresponded to the probe movement speed of V = 0.2 mm/s.
- The roughness parameters of metal samples are invariant to the speed of the tip of the stylus profilometer, Portable Surface Roughness Tester Surftest SJ-400. As the handpiece speed increased from 0.05 mm/s to 1 mm/s, Ra changed by 0.43% and Rz by 0.2%. Therefore, the maximum speed of the probe can be set during the measurement.
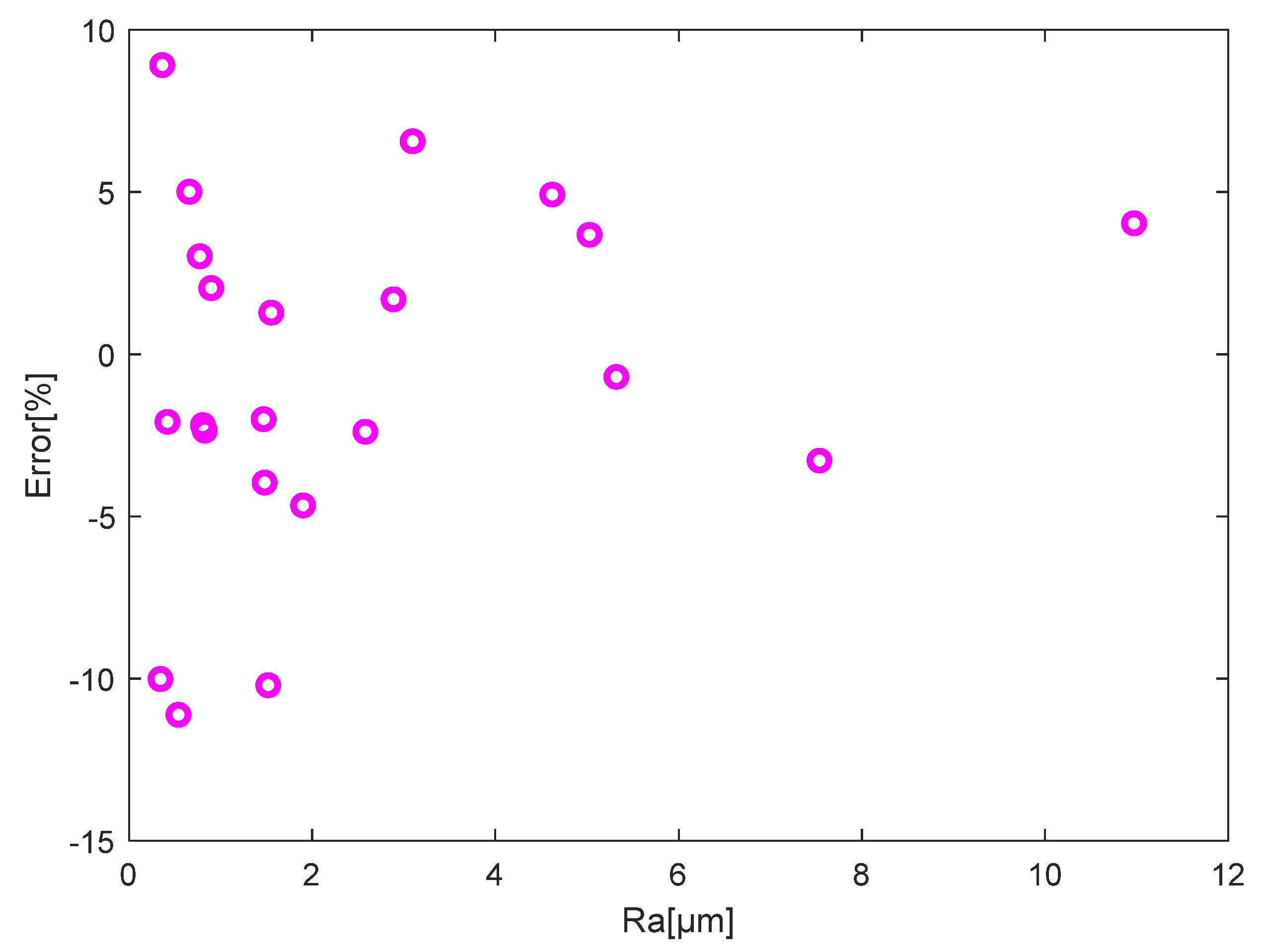
- When testing the operation of the developed measuring system using the surface roughness comparator standards composite set, the assembled measuring system based on the chromatic confocal sensor showed its performance in assessing the roughness parameter Ra from 0.4 µm to more than 12 µm, which covers a common range of milling, turning, and grinding. In this range of measurement, relative errors can be controlled within 10%. Moreover, in the Ra range from 2 µm to 12 µm, the error was 5%.
- Under these laboratory conditions, in the studied range of scanning speeds for a given range of changes in the roughness parameters of samples obtained by mechanical processing methods, the measurement uncertainty was not detected.
- Frequency analysis and correlation analysis of profilograms were carried out. Within the framework of correlation analysis, a method for separating the deterministic and random components of the processed signal of the surface profile was developed and tested on examples. The method allowed identifying the hidden periodicity of the profile. Relationships between the deterministic and random components were established based on the example of samples processed by turning and grinding.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Measuring Speed, mm/s | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | ||||||||||||
| Number of Tracks | Number of Tests | Average | Sample Standard Deviation, µm | Margin of Error, µm | ||||||||
| 1 | 2 | 3 | ||||||||||
| Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra | Rz | Ra | Rz | |
| 1 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 0 | 0.115 | 0 | 0.287 |
| 2 | 2.98 | 9.60 | 2.98 | 9.60 | 2.98 | 9.60 | 2.98 | 9.60 | 0 | 0 | 0 | 0 |
| 3 | 2.98 | 9.50 | 2.99 | 10.10 | 2.99 | 9.70 | 2.99 | 9.77 | 0.006 | 0.306 | 0.014 | 0.759 |
| 2.983 | 9.62 | 0.006 | 0.137 | 0.014 | 0.339 | |||||||
| 0.1 | ||||||||||||
| 1 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 0 | 0 | 0 | 0 |
| 2 | 2.98 | 9.70 | 2.98 | 9.60 | 2.98 | 9.60 | 2.98 | 9.63 | 0 | 0.058 | 0 | 0.143 |
| 3 | 2.99 | 9.50 | 3.00 | 10.10 | 2.99 | 9.50 | 2.99 | 9.70 | 0.006 | 0.346 | 0.014 | 0.861 |
| 2.983 | 9.61 | 0.006 | 0.101 | 0.014 | 0.252 | |||||||
| 0.5 | ||||||||||||
| 1 | 2.98 | 9.50 | 2.97 | 9.50 | 2.97 | 9.50 | 2.97 | 9.50 | 0 | 0 | 0 | 0 |
| 2 | 2.98 | 9.70 | 2.98 | 9.60 | 2.98 | 10.1 | 2.98 | 9.80 | 0 | 0.265 | 0 | 0.657 |
| 3 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 0 | 0 | 0 | 0 |
| 2.977 | 9.60 | 0.006 | 0.173 | 0.014 | 0.430 | |||||||
| 1.0 | ||||||||||||
| 1 | 2.97 | 9.50 | 2.99 | 10.30 | 2.97 | 9.50 | 2.98 | 9.77 | 0.012 | 0.462 | 0.029 | 1.147 |
| 2 | 2.97 | 10.50 | 2.97 | 9.70 | 2.97 | 9.70 | 2.97 | 9.97 | 0 | 0.462 | 0 | 1.147 |
| 3 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 2.98 | 9.50 | 0 | 0 | 0 | 0 |
| 2.97 | 9.60 | 0.006 | 0.236 | 0.014 | 0.586 | |||||||
| Formulas for the margin of error for comparing the results (SR-Test, SJ-400) and the impact speed (SR-Test): Sample standard deviation is: where is the parameter current value, is the sample mean, and is the sample size. The margin of error is: —t-score. In our case, = 3, and = 4.303, at a confidence level of 95%, which means that: 0.95 = 1 − α The significance level α = 1 − 0.95 = 0.05, and the degrees of freedom − 1 = 3 − 1 = 2. | ||||||||||||
| Measuring Speed, mm/s | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | ||||||||||||
| Number of Tracks | Number of Tests | Average | Sample Standard Deviation, µm | Margin of Error, µm | ||||||||
| 1 | 2 | 3 | ||||||||||
| Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra, µm | Rz, µm | Ra | Rz | Ra | Rz | |
| 1 | 3.022 | 10.524 | 3.030 | 10.613 | 3.006 | 10.525 | 3.019 | 10.554 | 0.012 | 0.051 | 0.030 | 0.126 |
| 2 | 2.768 | 10.621 | 2.769 | 10.602 | 2.771 | 10.583 | 2.769 | 10.603 | 0.002 | 0.019 | 0.003 | 0.046 |
| 3 | 2.931 | 10.411 | 2.930 | 10.479 | 2.934 | 10.597 | 2.932 | 10.496 | 0.002 | 0.939 | 0.006 | 0.233 |
| 2.907 | 10.550 | 0.127 | 0.053 | 0.315 | 0.133 | |||||||
| 0.1 | ||||||||||||
| 1 | 2.930 | 10.373 | 2.969 | 10.331 | 2.973 | 10.260 | 2.957 | 10.321 | 0.024 | 0.057 | 0.059 | 0.142 |
| 2 | 2.767 | 10.409 | 2.755 | 10.457 | 2.788 | 10.288 | 2.769 | 10.385 | 0.017 | 0.087 | 0.042 | 0.216 |
| 3 | 2.915 | 10.422 | 2.912 | 10.414 | 2.896 | 10.398 | 2.908 | 10.411 | 0.011 | 0.013 | 0.026 | 0.031 |
| 2.878 | 10.372 | 0.097 | 0.046 | 0.240 | 0.115 | |||||||
| 0.15 | ||||||||||||
| 1 | 2.897 | 10.263 | 2.958 | 10.314 | 2.951 | 10.487 | 2.935 | 10.354 | 0.033 | 0.117 | 0.083 | 0.291 |
| 2 | 2.737 | 10.283 | 2.739 | 10.342 | 2.752 | 10.282 | 2.743 | 10.302 | 0.008 | 0.034 | 0.019 | 0.084 |
| 3 | 2.848 | 10.303 | 2.846 | 10.261 | 2.837 | 10.341 | 2.844 | 10.302 | 0.006 | 0.04 | 0.014 | 0.099 |
| 2.840 | 10.319 | 0.116 | 0.030 | 0.288 | 0.076 | |||||||
| 0.20 | ||||||||||||
| 1 | 2.891 | 10.326 | 2.891 | 10.236 | 2.870 | 10.145 | 2.884 | 10.235 | 0.012 | 0.091 | 0.030 | 0.226 |
| 2 | 2.707 | 10.168 | 2.745 | 9.954 | 2.810 | 9.729 | 2.754 | 9.950 | 0.052 | 0.219 | 0.129 | 0.546 |
| 3 | 2.811 | 10.160 | 2.832 | 10.106 | 2.827 | 10.138 | 2.823 | 10.135 | 0.011 | 0.028 | 0.028 | 0.068 |
| 2.821 | 10.107 | 0.078 | 0.144 | 0.194 | 0.359 | |||||||
| 0.25 | ||||||||||||
| 1 | 2.815 | 10.156 | 2.861 | 10.189 | 2.803 | 10.079 | 2.826 | 10.141 | 0.031 | 0.056 | 0.076 | 0.139 |
| 2 | 2.734 | 9.839 | 2.708 | 9.953 | 2.742 | 9.560 | 2.728 | 9.784 | 0.018 | 0.202 | 0.044 | 0.502 |
| 3 | 2.772 | 9.989 | 2.764 | 10.047 | 2.760 | 10.034 | 2.765 | 10.023 | 0.006 | 0.030 | 0.014 | 0.076 |
| 2.773 | 9.983 | 0.065 | 0.182 | 0.161 | 0.452 | |||||||
| 0.35 | ||||||||||||
| 1 | 2.665 | 9.794 | 2.740 | 9.955 | 2.692 | 9.751 | 2.699 | 9.833 | 0.094 | 0.268 | 0.038 | 0.108 |
| 2 | 2.690 | 9.196 | 2.714 | 9.588 | 2.603 | 9.335 | 2.669 | 9.373 | 0.145 | 0.493 | 0.058 | 0.199 |
| 3 | 2.649 | 9.651 | 2.716 | 9.487 | 2.648 | 9.530 | 2.671 | 9.556 | 0.098 | 0.210 | 0.039 | 0.085 |
| 2.679 | 9.587 | 0.024 | 0.232 | 0.059 | 0.576 | |||||||
| 0.45 | ||||||||||||
| 1 | 2.544 | 9.219 | 2.593 | 9.538 | 2.603 | 8.989 | 2.579 | 9.249 | 0.032 | 0.275 | 0.078 | 0.684 |
| 2 | 2.490 | 8.749 | 2.579 | 8.885 | 2.452 | 8.815 | 2.507 | 8.816 | 0.066 | 0.068 | 0.163 | 0.168 |
| 3 | 2.599 | 8.738 | 2.545 | 8.764 | 2.517 | 9.089 | 2.554 | 8.863 | 0.042 | 0.196 | 0.103 | 0.487 |
| 2.547 | 8.976 | 0.040 | 0.237 | 0.100 | 0.589 | |||||||
| 0.55 | ||||||||||||
| 1 | 2.372 | 8.718 | 2.456 | 8.682 | 2.352 | 8.656 | 2.393 | 8.686 | 0.055 | 0.032 | 0.136 | 0.078 |
| 2 | 2.300 | 8.188 | 2.345 | 8.163 | 2.364 | 8.497 | 2.336 | 8.282 | 0.033 | 0.186 | 0.081 | 0.462 |
| 3 | 2.348 | 8.549 | 2.358 | 8.338 | 2.330 | 8.476 | 2.346 | 8.454 | 0.0142 | 0.107 | 0.035 | 0.266 |
| 2.358 | 8.474 | 0.043 | 0.202 | 0.106 | 0.502 | |||||||
| 0.65 | ||||||||||||
| 1 | 2.149 | 7.974 | 2.226 | 7.405 | 2.291 | 7.686 | 2.222 | 7.688 | 0.071 | 0.285 | 0.176 | 0.707 |
| 2 | 2.249 | 7.668 | 2.122 | 7.469 | 2.129 | 7.428 | 2.167 | 7.522 | 0.071 | 0.128 | 0.178 | 0.319 |
| 3 | 2.177 | 7.454 | 2.149 | 7.651 | 2.216 | 7.668 | 2.181 | 7.591 | 0.033 | 0.119 | 0.083 | 0.297 |
| 2.189 | 7.600 | 0.039 | 0.083 | 0.098 | 0.208 | |||||||
| 0.75 | ||||||||||||
| 1 | 1.938 | 7.074 | 1.918 | 7.306 | 1.933 | 7.179 | 1.929 | 7.187 | 0.011 | 0.116 | 0.027 | 0.288 |
| 2 | 1.919 | 7.179 | 1.941 | 7.013 | 2.055 | 7.086 | 1.972 | 7.093 | 0.073 | 0.083 | 0.181 | 0.207 |
| 3 | 1.993 | 7.091 | 1.977 | 6.665 | 1.991 | 7.000 | 1.987 | 6.919 | 0.008 | 0.224 | 0.021 | 0.557 |
| 1.963 | 7.066 | 0.041 | 0.136 | 0.101 | 0.337 | |||||||
| 1 | ||||||||||||
| 1 | 1.412 | 4.961 | 1.325 | 5.144 | 1.337 | 5.064 | 1.358 | 5.056 | 0.047 | 0.092 | 0.117 | 0.228 |
| 2 | 1.317 | 4.743 | 1.305 | 5.056 | 1.313 | 5.017 | 1.312 | 4.939 | 0.006 | 0.170 | 0.015 | 0.423 |
| 3 | 1.354 | 5.358 | 1.348 | 5.281 | 1.336 | 4.711 | 1.346 | 5.117 | 0.009 | 0.354 | 0.023 | 0.878 |
| 1.339 | 5.037 | 0.024 | 0.090 | 0.058 | 0.224 | |||||||
References
- Cheng, F.; Fu, S.W.; Leong, Y.S. Research on optical measurement for additive manufacturing surfaces. Proc. SPIE 2017, 10250, 102501F. [Google Scholar] [CrossRef]
- Lishchenko, N.; Pitel’, J.; Larshin, V. Online Monitoring of Surface Quality for Diagnostic Features in 3D Printing. Machines 2022, 10, 541. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T. Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination. Metals 2020, 10, 69. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Surface metrology. Meas. Sci. Technol. 1997, 8, 955–972. [Google Scholar] [CrossRef]
- Fu, S.; Kor, W.S.; Cheng, F.; Seah, L.K. In-situ measurement of surface roughness using chromatic confocal sensor. Procedia CIRP 2020, 94, 780–784. [Google Scholar] [CrossRef]
- Bellinger, R. Measuring Surface Roughness: The Benefits of Laser Confocal Microscopy. Available online: https://www.photonics.com/Articles/Measuring_Surface_Roughness_The_Benefits_of/a58301 (accessed on 10 February 2023).
- Young, S.S. Laser Sensors for Displacement, Distance and Position. Sensors 2019, 19, 1924. [Google Scholar] [CrossRef]
- Mathia, T.; Pawlus, P.; Wieczorowski, M. Recent trends in surface metrology. Wear 2011, 271, 494–508. [Google Scholar] [CrossRef]
- Blateyron, F. Chromatic Confocal Microscopy. In Optical Measurement of Surface Topography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 71–166. [Google Scholar] [CrossRef]
- Chromatic Confocal Reference Guide. Available online: https://www.marposs.com/media/16330/d-1/t-file/STIL-Brochure_EN.pdf (accessed on 10 February 2023).
- Basics of Optical Surface Topography—Technology from Polytec. Available online: https://www.polytec.com/eu/surface-metrology/technology/chromatic-confocal-technology (accessed on 17 July 2015).
- Xu, X.M.; Hu, H. Interferometry Development of Non-contact Surface Roughness Measurement in Last Decades. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009. [Google Scholar] [CrossRef]
- Seppä, J.; Niemelä, K.; Lassila, A. Metrological characterization methods for confocal chromatic line sensors and optical topography sensors. Meas. Sci. Technol. 2018, 29, 054008. [Google Scholar] [CrossRef]
- Wagner, M.; Isaacson, A.; Michaud, M.; Bell, M. A comparison of surface roughness measurement methods for gear tooth working surfaces. In Proceedings of the AGMA American Gear Manufacturers Association 2019 Fall Technical Meeting, FTM 2019, Detroit, MI, USA, 14 October 2019. [Google Scholar]
- Poon, C.Y.; Bhushan, B. Comparison of surface roughness measurements by stylus profiler, AFM and non-contact optical profiler. Wear 1995, 190, 76–88. [Google Scholar] [CrossRef]
- Mital’, G.; Dobránsky, J.; Ružbarský, J.; Olejárová, Š. Application of laser profilometry to evaluation of the surface of the workpiece machined by abrasive water jet technology. Appl. Sci. 2019, 9, 2134. [Google Scholar] [CrossRef]
- Mital’, G. Contactless measurement and evaluation machined surface roughness using laser profilometry. Transf. Inovácií 2021, 43, 19–24. Available online: https://www.sjf.tuke.sk/transferinovacii/pages/archiv/transfer/43-2021/pdf/019-024.pdf (accessed on 10 February 2023).
- Fu, S.; Cheng, F.; Tjahjowidodo, T.; Zhou, Y.; Butler, D.A. A Non-Contact Measuring System for In-Situ Surface Characterization Based on Laser Confocal Microscopy. Sensors 2019, 18, 2657. [Google Scholar] [CrossRef] [PubMed]
- Rishikesan, V.; Samuel, G.L. Evaluation of Surface Profile Parameters of a Machined Surface Using Confocal Displacement Sensor. Procedia Mater. Sci. 2014, 5, 1385–1391. [Google Scholar] [CrossRef][Green Version]
- Advantages of Optical Sensors in CMMs. Available online: https://www.controlsdrivesautomation.com/optical-sensor-advantages-in-CMMs (accessed on 17 July 2023).
- Confocal Chromatic Sensors Enable New Measurement Perspectives. Available online: https://electronics360.globalspec.com/article/13005/confocal-chromatic-sensors-enable-new-measurement-perspectives (accessed on 17 July 2023).
- Ma, Y.D.; Xiao, Y.C.; Wang, Q.Q.; Yao, K.; Wang, X.R.; Zhou, Y.P.; Liu, Y.C.; Sun, Y.; Duan, J. Applications of Chromatic Confocal Technology in Precision Geometric Measurement of Workpieces. J. Phys. 2022, 2460, 012077. [Google Scholar] [CrossRef]
- Confocal Displacement Sensor CL-3000 Series. Available online: http://gts-adriatic.rs/wp-content/uploads/2018/12/AS_100320_CL-3000_C_611I32_US_1108-1.pdf (accessed on 17 January 2023).
- Nano Point Scanner. Available online: https://hirox-europe.com/products/nps-confocal-whitelight-system/ (accessed on 10 February 2023).
- Vakili, A.; Xiong, D.; Rajadhyaksha, M.; DiMarzio, C.A. High brightness LED in confocal microscopy. Three-Dimens. Multidimens. Microsc. Image Acquis. Process. XXII 2015, 9330, 933006. [Google Scholar] [CrossRef]
- LMI Technologies. Available online: https://lmi3d.com/line-confocal-imaging (accessed on 18 July 2023).
- Ye, L.; Qian, J.; Haitjema, H.; Reynaerts, D. On-machine chromatic confocal measurement for micro-EDM drilling and milling. Precis. Eng. 2022, 76, 110–123. [Google Scholar] [CrossRef]
- Ye, L.; Qian, J.; Haitjema, H.; Reynaerts, D. Uncertainty Evaluation of an On-Machine Chromatic Confocal Measurement System. Measurement 2023, 216, 112995. [Google Scholar] [CrossRef]
- Nagy, A. Influence of measurement settings on areal roughness with confocal chromatic sensor on face-milled surface. Cut. Tools Technol. Syst. 2020, 93, 65–75. [Google Scholar] [CrossRef]
- Aich, U.; Banerjee, S. Characterizing topography of EDM generated surface by time series and autocorrelation function. Tribol. Int. 2017, 111, 73–90. [Google Scholar] [CrossRef]
- Podulka, P. Resolving Selected Problems in Surface Topography Analysis by Application of the Autocorrelation Function. Coatings 2023, 13, 74. [Google Scholar] [CrossRef]
- Roughness Measuring Systems from Jenoptik—Surface Texture Parameters in Practice. Available online: http://www.jenoptik.com/en-roughness-measurement-and-contour-measurement (accessed on 17 July 2015).
- Surftest SJ-400. Available online: http://www.gagesite.com/documents/SJ-401.pdf (accessed on 17 July 2022).
- Semiconductor Wafer and Glass Substrates Inspection. Available online: https://www.keyence.com/ss/products/measure/sealing/examples/semiconductor.jsp (accessed on 17 January 2023).
- ISO 4287:1997; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 1997. Available online: https://www.iso.org/standard/10132.html (accessed on 30 May 2023).
- ISO 4288:1996; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. ISO: Geneva, Switzerland, 1996. Available online: https://www.iso.org/standard/2096.html (accessed on 30 May 2023).
- Quick Guide to Surface Roughness Measurement. Available online: https://www.mitutoyo.com/webfoo/wp-content/uploads/1984_Surf_Roughness_PG.pdf (accessed on 30 May 2023).
- Larshin, V.; Lishchenko, N.; Pitel’, J. Detecting systematic and random component of surface roughness. Her. Adv. Inf. Technol. 2020, 3, 61–71. [Google Scholar] [CrossRef]
- AutoCorrelationVI. Available online: https://www.ni.com/docs/en-US/bundle/labview/page/lvanls/autocorrelation.html (accessed on 17 July 2022).



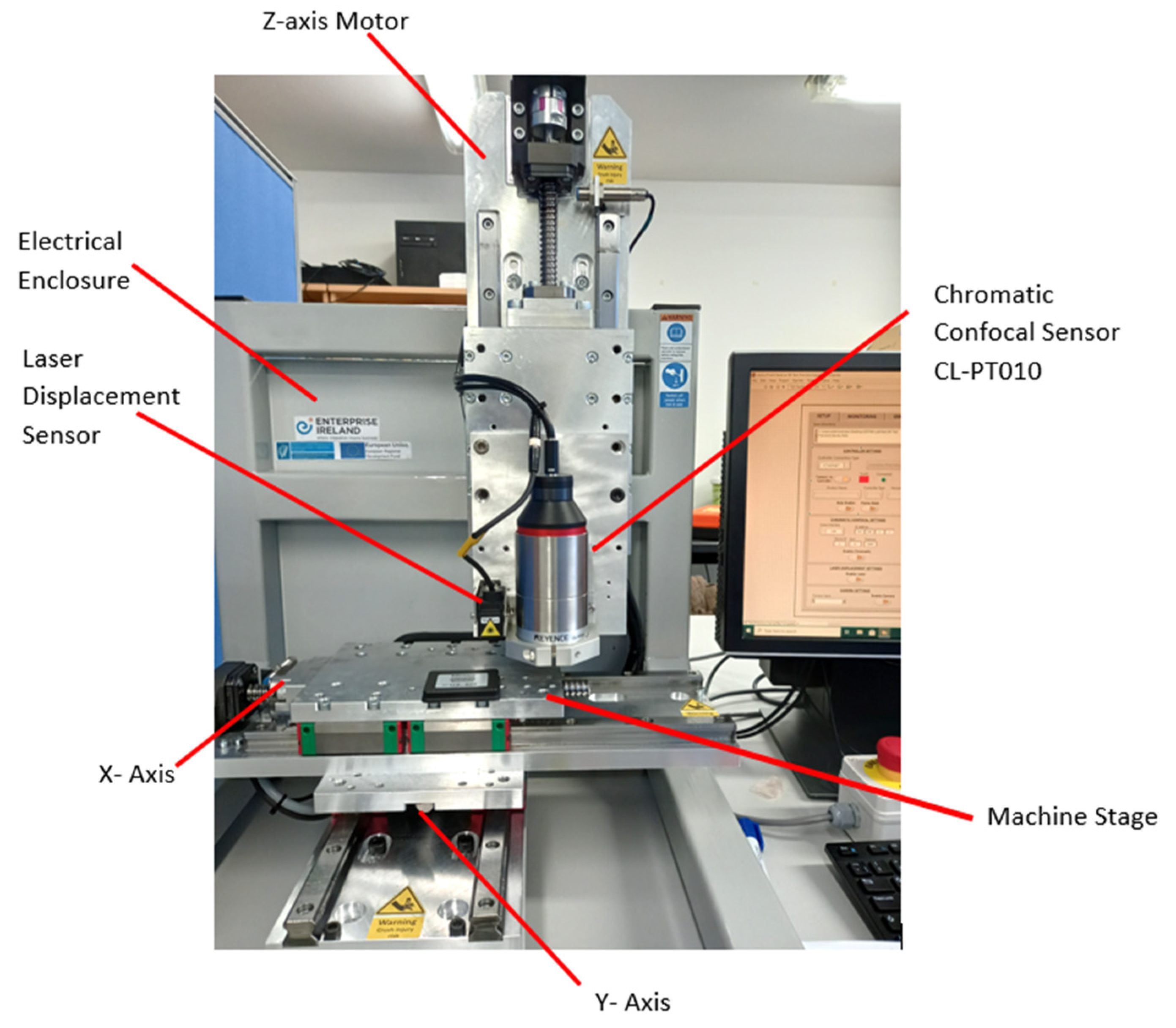


| Parameter | Value |
|---|---|
| Measuring range Z-axis | 800 µm, 80 µm, 8 µm |
| X-axis | 25 mm |
| Cutoff length | 0.08, 0.25, 0.8, 2.5, 8 mm |
| Measuring speed | 0.05, 0.1, 0.5, 1 mm/s |
| Measuring force | 0.75 mN |
| Minimum resolution | 0.000125 µm (8 µm range) |
| Arbitrary length | 0.1 to 25 mm |
| Digital filter | 2CR, PC75, Gauss |
| Specification | Value | |
|---|---|---|
| Reference distance | 10 mm | |
| Reference measurement range | Measurement range | ±0.3 mm |
| Linearity | ±0.22 µm | |
| High-precision measurement range | Measurement range | ±0.15 mm |
| Linearity | ||
| Resolution | 0.25 µm | |
| Spot diameter | 3.5 µm |
| Machining Method | Ra, µm | SJ-400, Contact Method | Chromatic Confocal Sensor, Non-Contact Method | Error, % |
|---|---|---|---|---|
| Vertical milling | 12.5 6.3 3.2 1.6 0.8 0.4 | 10.97 4.62 2.89 1.47 0.66 0.34 | 11.41 4.85 2.94 1.44 0.69 0.31 | 4.04 4.92 1.70 −2.00 5.01 −10.01 |
| Turning | 12.5 6.3 3.2 1.6 0.8 0.4 | 11.23 5.03 2.58 1.55 0.77 0.36 | 11.61 5.21 2.52 1.57 0.79 0.39 | 0.75 3.68 −2.39 1.28 3.02 8.91 |
| Horizontal milling | 12.5 6.3 3.2 1.6 0.8 | 7.54 5.32 3.10 1.90 0.89 | 7.29 5.28 3.30 1.81 0.91 | −3.28 −0.69 6.57 −4.66 2.04 |
| Plane grinding | 1.6 0.8 0.4 0.2 0.1 0.05 | 1.48 0.83 0.42 0.15 0.12 0.08 | 1.42 0.81 0.41 0.23 0.17 0.15 | −3.95 −2.35 −2.08 54.78 38.59 87.38 |
| External grinding | 1.6 0.8 0.4 0.2 | 1.52 0.81 0.54 0.19 | 1.20 1.79 0.48 0.28 | −21.16 −2.19 −11.11 47.04 |
| Lapping | 0.1 0.05 | 0.1 0.06 | 0.18 0.14 | 79.67 130.61 |
| Machining Operation | |||||
|---|---|---|---|---|---|
| Ra, µm | Turning | Ra, µm | Plane Grinding | ||
| Deterministic Component, % | Random Component, % | Deterministic Component, % | Random Component, % | ||
| 0.4 | 28.6 | 71.4 | 0.4 | 15 | 85 |
| 0.8 | 55 | 45 | 0.8 | 22 | 78 |
| 1.6 | 80 | 20 | 1.6 | 15 | 85 |
| 3.2 | 85 | 15 | |||
| 6.3 | 89.7 | 10.3 | |||
| 12.5 | 89.3 | 10.7 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lishchenko, N.; O’Donnell, G.E.; Culleton, M. Contactless Method for Measurement of Surface Roughness Based on a Chromatic Confocal Sensor. Machines 2023, 11, 836. https://doi.org/10.3390/machines11080836
Lishchenko N, O’Donnell GE, Culleton M. Contactless Method for Measurement of Surface Roughness Based on a Chromatic Confocal Sensor. Machines. 2023; 11(8):836. https://doi.org/10.3390/machines11080836
Chicago/Turabian StyleLishchenko, Natalia, Garret E. O’Donnell, and Mark Culleton. 2023. "Contactless Method for Measurement of Surface Roughness Based on a Chromatic Confocal Sensor" Machines 11, no. 8: 836. https://doi.org/10.3390/machines11080836
APA StyleLishchenko, N., O’Donnell, G. E., & Culleton, M. (2023). Contactless Method for Measurement of Surface Roughness Based on a Chromatic Confocal Sensor. Machines, 11(8), 836. https://doi.org/10.3390/machines11080836








