A Knowledge Discovery Process Extended to Experimental Data for the Identification of Motor Misalignment Patterns
Abstract
1. Introduction
2. Materials and Methods
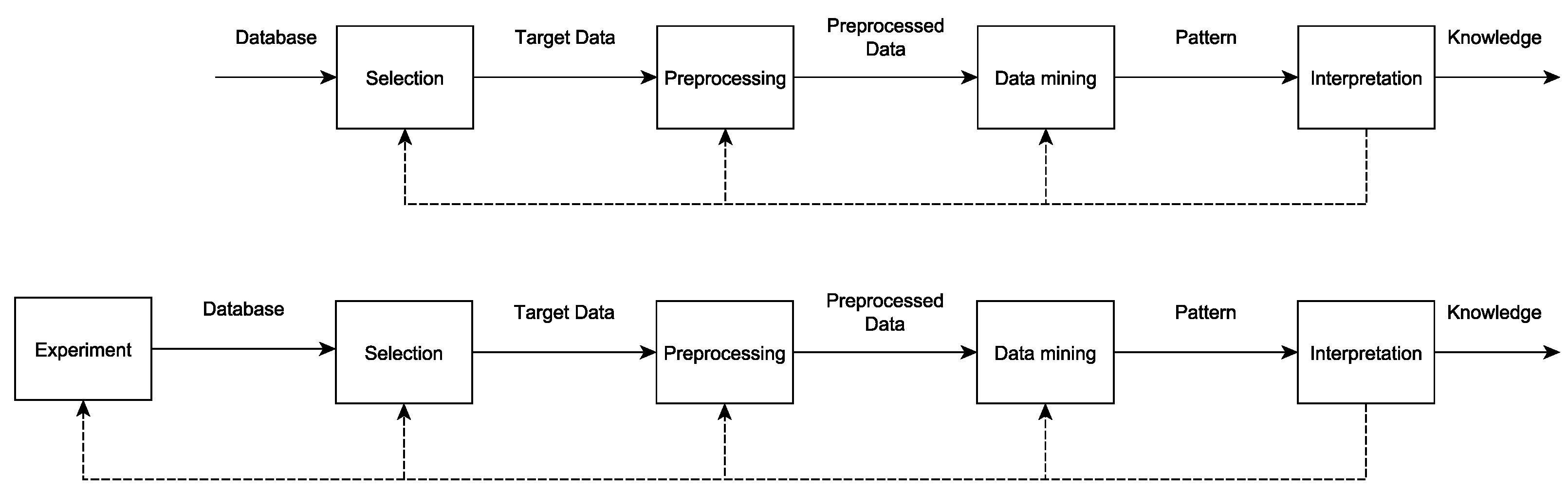
2.1. Knowledge Discovery
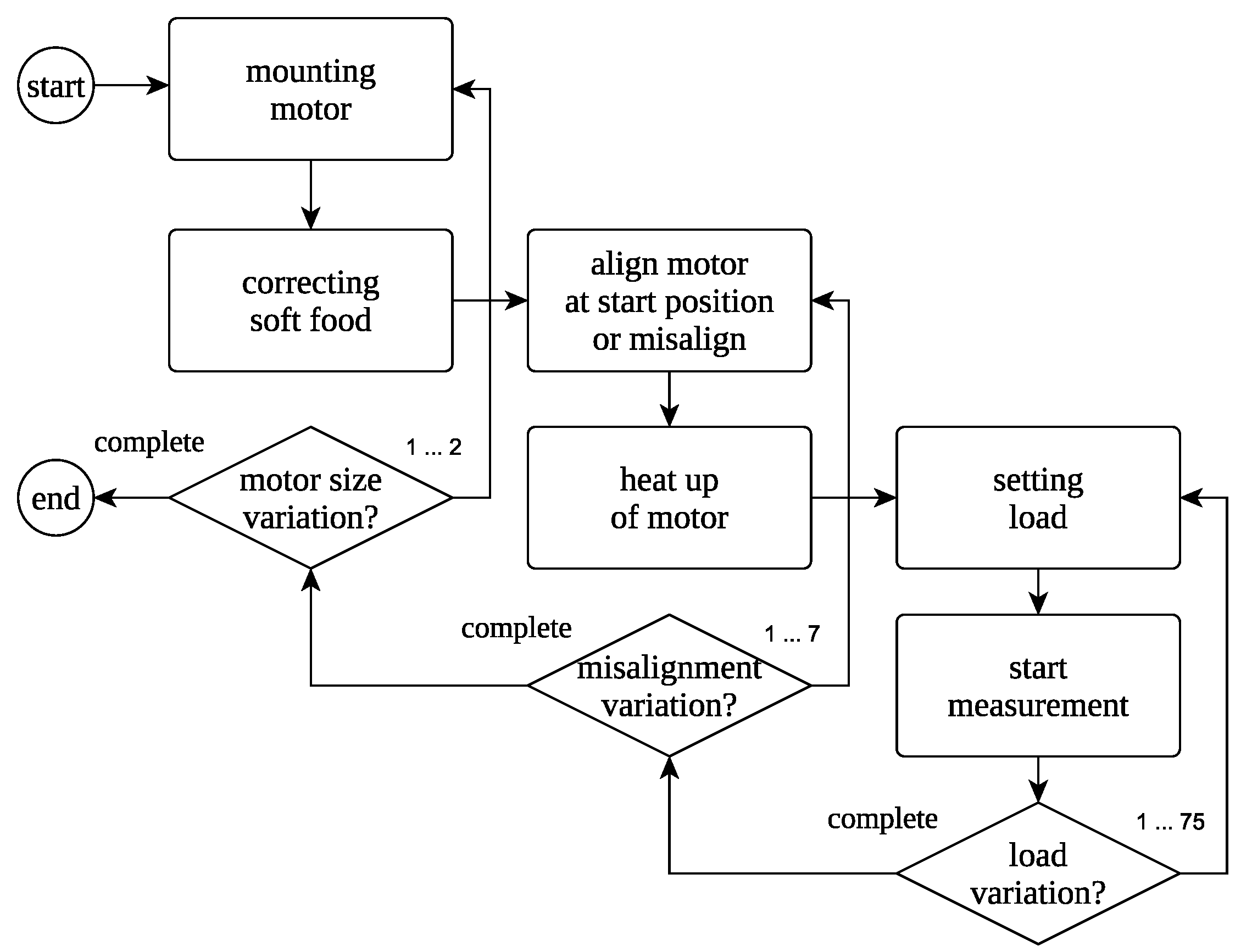
2.2. Experiment
2.2.1. Experimental Set-Up
- Measurement of signals for data processing
- Offline acquisition of misalignment for quality management
- Online acquisition of process signals for quality management
2.2.2. Scope of the Experiment
- Motor size (kW): 1.1 and 7.5
- Load (% of rated power): 100–92, 90–82, 80–72
- Misalignment (mm): aligned = 0.02 (PM, AM), 0.05 (PM), 0.08 (PM), 0.11 (PM), 0.05 (AM), 0.08 (AM), 0.11 (AM).
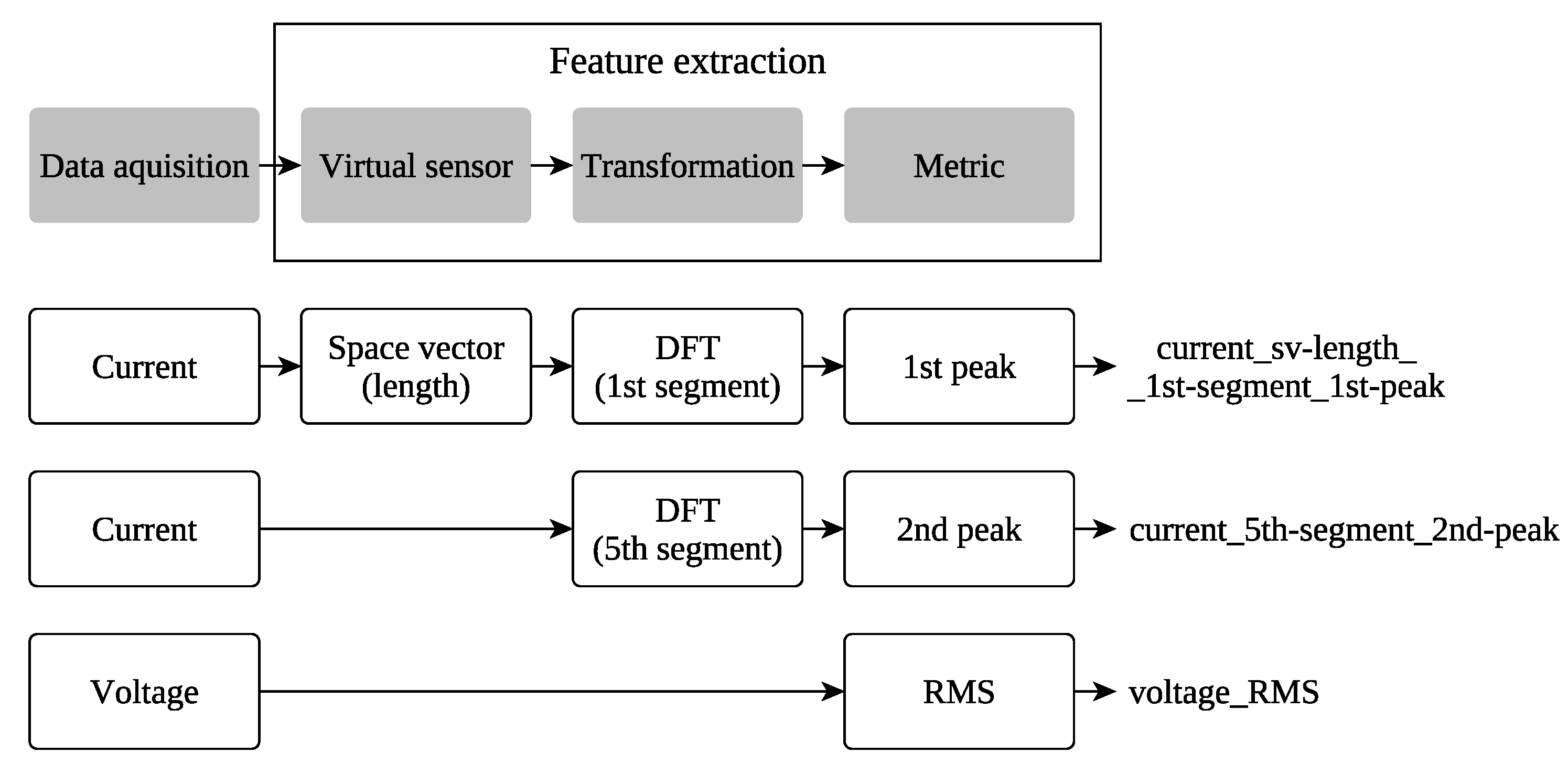
2.3. Feature Extraction and Preprocessing
- 1.
- Time-domain features extractor
- 2.
- Space vector time-domain features extractor
- 3.
- Frequency-domain features extractor
- 4.
- Space vector frequency-domain features extractor
- 5.
- MCSA features extractor.
- Length of the space vector
- Angle of the space vector
- Fluctuation of the space vector length
- Fluctuation of the space vector angle [30].
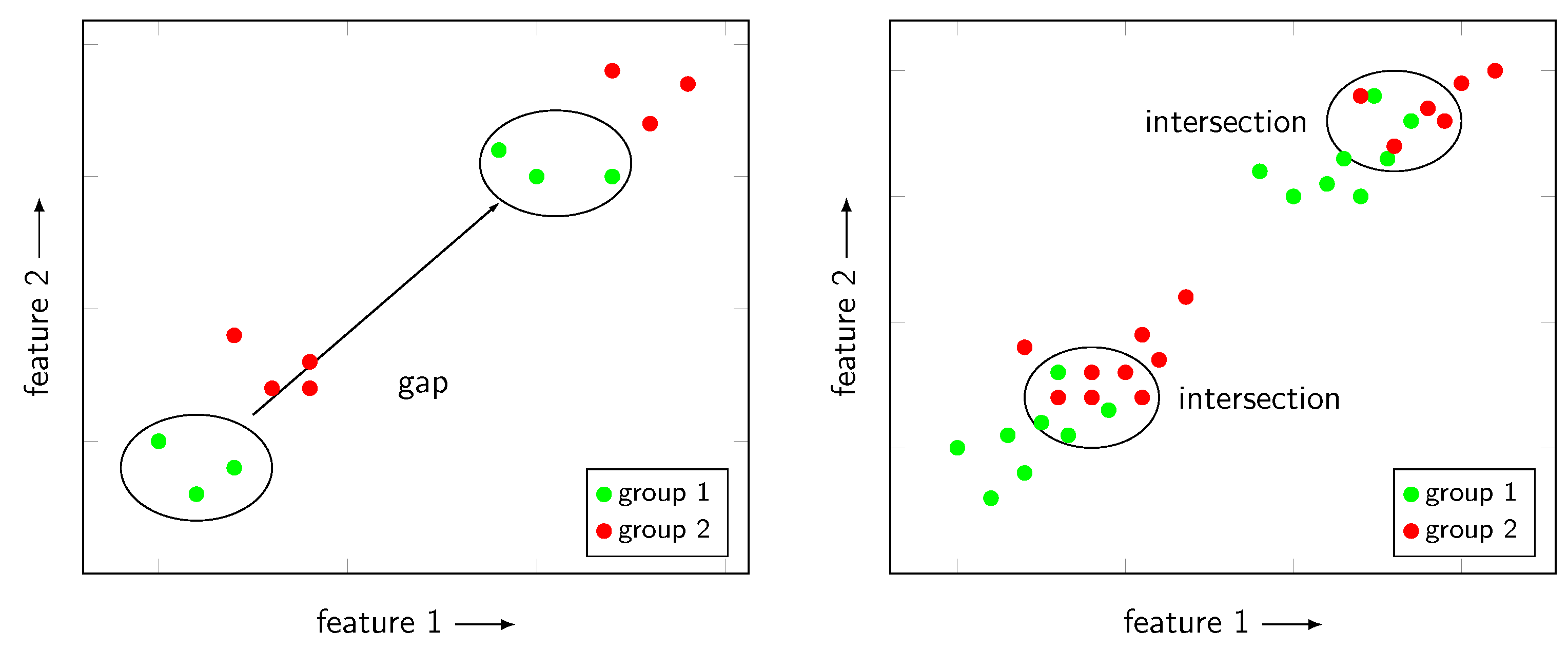
2.4. Feature Selection
- Target: parallel misalignment, angular misalignment
- Restriction: DUT 1, DUT 2 (motor size)
- Disturbance: load.
3. Results
3.1. Parallel Misalignment
3.2. Angular Misalignment
4. Discussion and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IM | Induction Motor |
| MCSA | Motor Current Signature Analysis |
| KDD | Knowledge Discovery in Database |
| DM | Data Mining |
| DUT | Device Under Test |
| PM | Parallel Misalignment |
| AM | Angular Misalignment |
Appendix A
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 1 | |||||||||
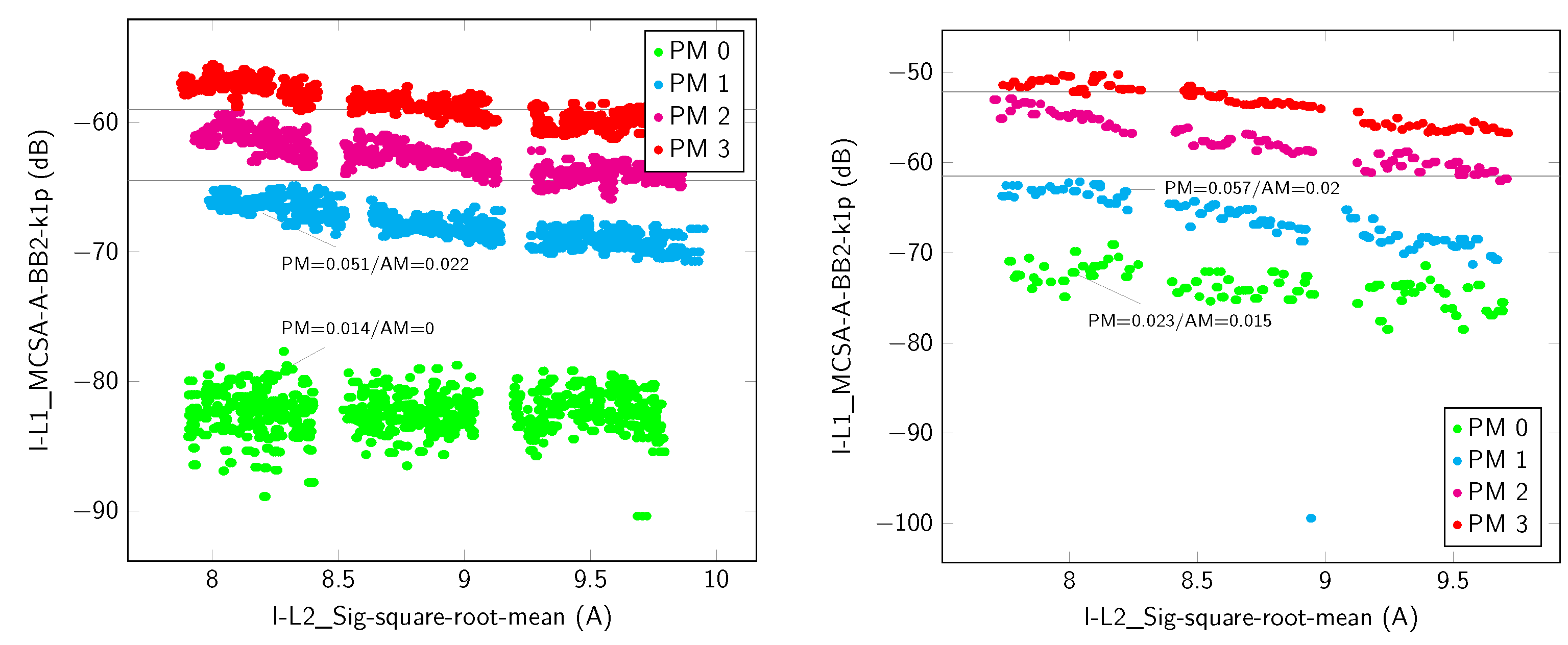
| MCSA () | BB2 (k1+) | −0.087 | 0.962 | 0.619 | −0.23 | 0.929 | 0.808 | ||
| Signal () | SRM | 0.96 | 0.011 | 0.045 | 0.962 | 0.002 | 0.009 | ||
| complete vector | 0 | 0.17 | / | / | / | / | / | / | |
| Selection 2 | |||||||||
| MCSA () | ECC1 (k1-) | −0.087 | 0.962 | 0.619 | −0.23 | 0.929 | 0.808 | ||
| Signal () | SRM | 0.962 | −0.007 | 0.003 | 0.962 | 0.01 | 0.007 | ||
| complete vector | 0 | 0.17 | / | / | / | / | / | / | |
| Selection 3 | |||||||||
| MCSA () | ECC2 (k1-) | −0.087 | 0.962 | 0.619 | −0.23 | 0.929 | 0.808 | ||
| Signal () | RV | 0.962 | −0.008 | 0.003 | 0.962 | 0.015 | 0.011 | ||
| complete vector | 0 | 0.17 | / | / | / | / | / | / | |
| Selection 4 | |||||||||
| MCSA () | BB2 (k1+) | −0.094 | 0.965 | 0.61 | −0.237 | 0.956 | 0.828 | ||
| Signal () | SRM | 0.958 | 0.033 | 0.01 | 0.962 | −0.005 | −0.001 | ||
| complete vector | 0 | 0 | / | / | / | / | / | / | |
| Selection 5 | |||||||||
| MCSA () | ECC1 (k1-) | −0.094 | 0.965 | 0.61 | −0.237 | 0.956 | 0.828 | ||
| Signal () | RV | 0.958 | 0.035 | 0.013 | 0.962 | −0.005 | −0.001 | ||
| complete vector | 0 | 0 | / | / | / | / | / | / | |
| Selection 6 | |||||||||
| MCSA () | ECC2 (k1-) | −0.094 | 0.965 | 0.61 | −0.237 | 0.956 | 0.828 | ||
| Signal () | MS | 0.958 | 0.036 | 0.016 | 0.961 | −0.006 | −0.003 | ||
| complete vector | 0 | 0 | / | / | / | / | / | / | |
| Selection 7 | |||||||||
| MCSA () | BB2 (k1+) | −0.098 | 0.968 | 0.59 | −0.249 | 0.953 | 0.838 | ||
| Signal () | RMS | 0.962 | −0.01 | 0.001 | 0.962 | 0.02 | 0.014 | ||
| complete vector | 0 | 0 | / | / | / | / | / | / | |
| Selection 8 | |||||||||
| MCSA () | ECC1 (k1-) | −0.098 | 0.968 | 0.591 | −0.249 | 0.953 | 0.838 | ||
| Signal () | MS | 0.961 | −0.01 | 0.001 | 0.961 | 0.02 | 0.015 | ||
| complete vector | 0 | 0 | / | / | / | / | / | / | |
| Selection 9 | |||||||||
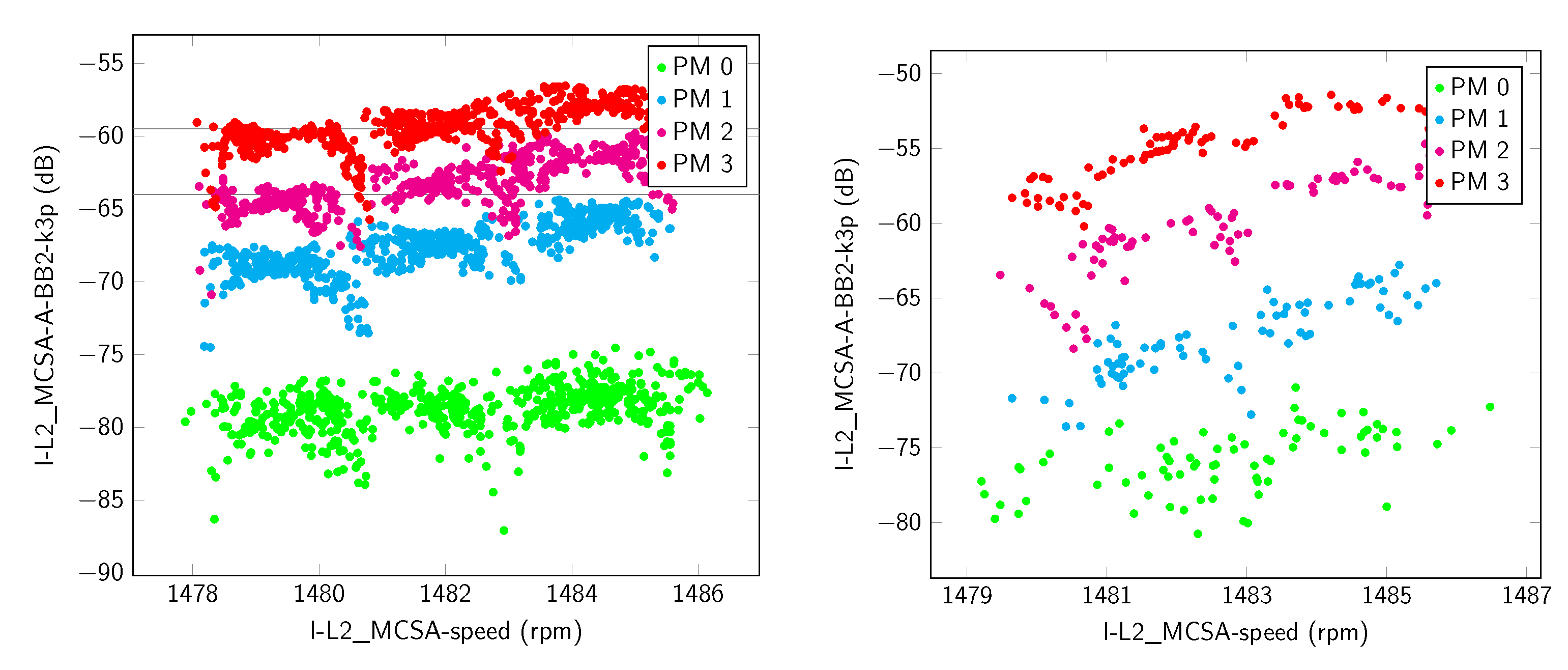
| MCSA () | ECC1 (k1+) | −0.139 | 0.96 | 0.576 | −0.254 | 0.947 | 0.826 | ||
| Space Vector (r) | SF | −0.254 | −0.396 | −0.432 | −0.063 | −0.619 | −0.433 | ||
| complete vector | 0.742 | 6.13 | / | / | / | / | / | / | |
| Selection 10 | |||||||||
| MCSA () | BB2 (k3+) | −0.139 | 0.96 | 0.576 | −0.254 | 0.947 | 0.826 | ||
| MCSA () | n | −0.939 | −0.07 | −0.065 | −0.91 | −0.092 | −0.127 | ||
| complete vector | 1.075 | 0.3 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 11 | |||||||||
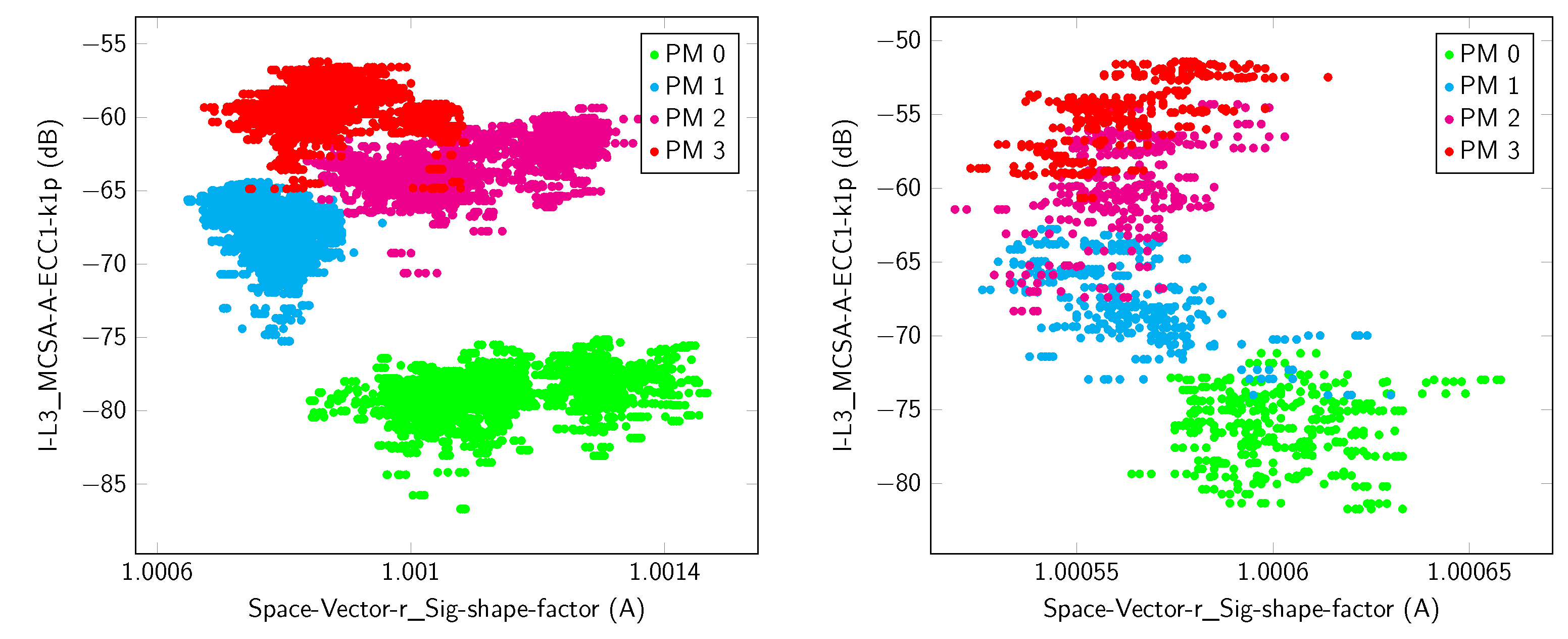
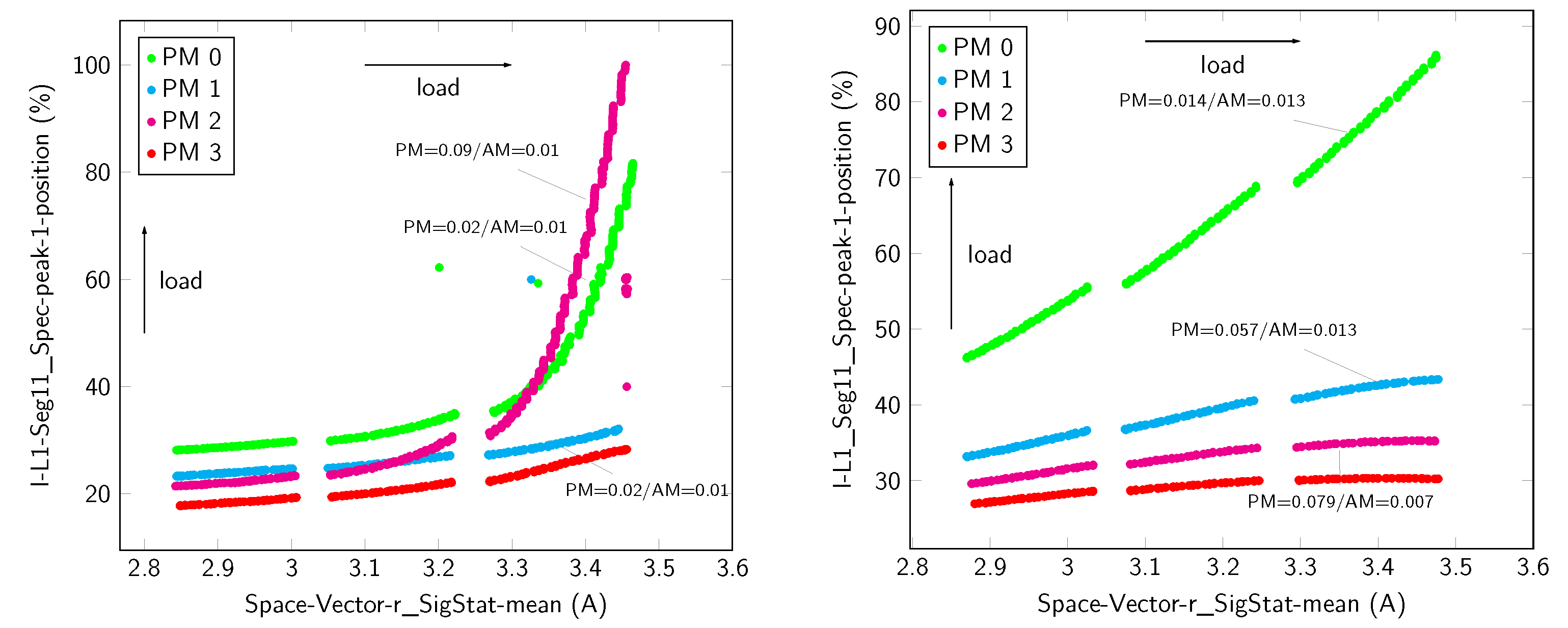
| SV (r) | mean | 0.961 | 0 | 0 | 0.962 | 0.011 | −0.001 | ||
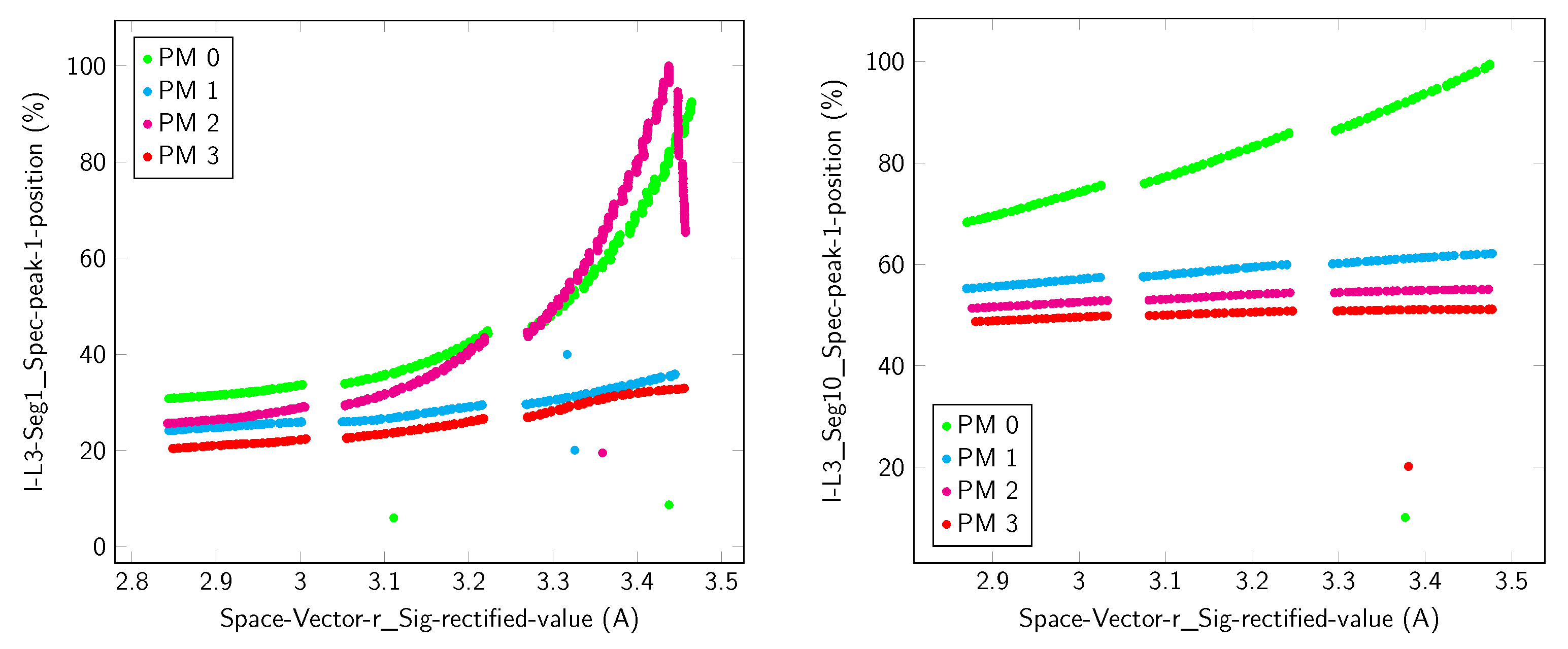
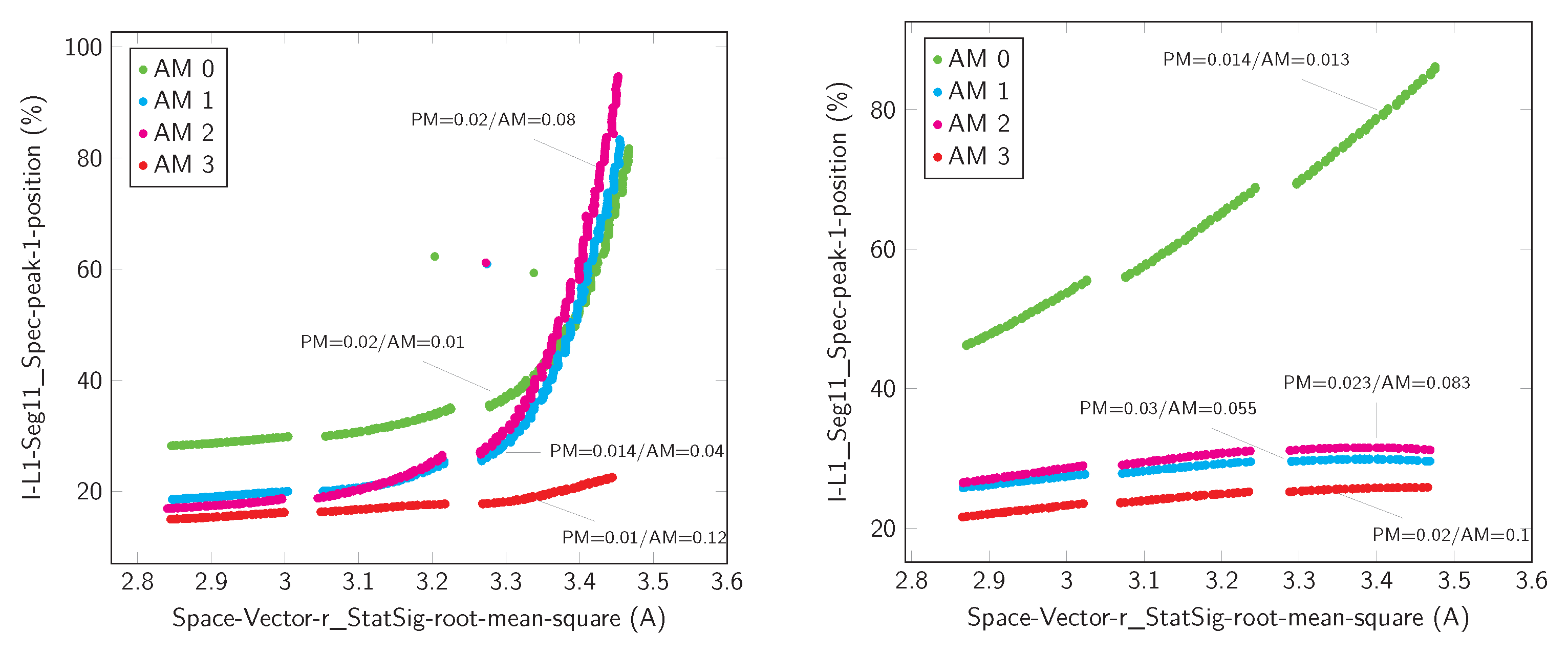
| Spectrum (, Seg. 11) | peak position | 0.52 | −0.299 | 0 | 0.284 | −0.883 | 0.499 | ||
| complete vector | 0.217 | 0 | / | / | / | / | / | / | |
| Selection 12 | |||||||||
| SV r | RV | 0.961 | 0 | 0 | 0.962 | 0.011 | −0.007 | ||
| Spectrum (, Seg. 10) | peak position | 0.577 | −0.26 | 0 | 0.225 | −0.897 | 0.511 | ||
| complete vector | 0.383 | 0 | / | / | / | / | / | / | |
| Selection 13 | |||||||||
| SV (r) | SRM | 0.961 | 0.001 | 0 | 0.962 | 0.011 | −0.007 | ||
| Spectrum (, Seg. 9) | peak position | 0.441 | −0.381 | 0 | −0.293 | 0.035 | 0.005 | ||
| complete vector | 1.6 | 1.03 | / | / | / | / | / | / | |
| Selection 14 | |||||||||
| SV (r) | RMS | 0.961 | 0 | 0 | 0.962 | 0.011 | −0.007 | ||
| Spectrum (, Seg. 10) | 2. peak position | 0.509 | −0.244 | 0 | 0.052 | −0.669 | 0.387 | ||
| complete vector | 3.625 | 2.3 | / | / | / | / | / | / | |
| Selection 15 | |||||||||
| SV (r) | MS | 0.96 | −0.001 | 0 | 0.691 | 0.01 | 0.007 | ||
| Spectrum (, Seg. 10) | peak position | −0.179 | 0.435 | 0 | 0.101 | −0.442 | 0.327 | ||
| complete vector | 3.908 | 19.7 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 16 | |||||||||
| Space vector (r) | RMS | 0.961 | 0.008 | −0.018 | 0.962 | −0.009 | −0.015 | ||
| Spectrum (, Seg. 11) | peak pos. | 0.56 | 0.412 | −0.425 | 0.222 | −0.677 | −0.846 | ||
| complete vector | 0.642 | 0 | / | / | / | / | / | / | |
| Selection 17 | |||||||||
| Space vector (r) | MS | 0.96 | 0.009 | −0.018 | 0.961 | −0.009 | −0.015 | ||
| Spectrum (, Seg. 10) | peak pos. | 0.63 | 0.405 | −0.398 | 0.17 | −0.681 | −0.863 | ||
| complete vector | 1.175 | 12.77 | / | / | / | / | / | / | |
| Selection 18 | |||||||||
| Space vector (r) | SS | 0.96 | 0.009 | −0.018 | 0.961 | −0.009 | −0.015 | ||
| Spectrum (, Seg. 9 ) | peak pos. | 0.475 | 0.384 | −0.459 | −0.327 | 0.015 | −0.078 | ||
| complete vector | 2.867 | 1.5 | / | / | / | / | / | / | |
| Selection 19 | |||||||||
| Space vector (r) | RSS | 0.961 | 0.008 | −0.0178 | 0.962 | −0.009 | −0.015 | ||
| Spectrum (, Seg. 10) | 2. peak pos. | 0.553 | 0.354 | −0.346 | 0.048 | −0.548 | −0.683 | ||
| complete vector | 4.583 | 16.23 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 20 | |||||||||
| Signal () | N6M | −0.166 | −0.94 | −0.737 | 0.866 | 0.043 | 0.014 | ||
| Signal () | SF | 0.4 | 0.846 | 0.842 | 0.682 | −0.45 | 0.472 | ||
| complete vector | 3.325 | 14.9 | / | / | / | / | / | / | |
| Selection 21 | |||||||||
| Space vector (r) | SRM | 0.962 | 0.005 | 0.003 | 0.962 | 0.005 | −0.004 | ||
| Space vector (LF) | MS | 0.958 | −0.03 | −0.023 | 0.956 | 0 | 0.004 | ||
| complete vector | 4.592 | 39.13 | / | / | / | / | / | / | |
| Selection 22 | |||||||||
| Space vector (r) | mean | 0.962 | 0.004 | 0.002 | 0.962 | 0.005 | −0.004 | ||
| Space vector (LF) | SS | 0.958 | −0.03 | −0.023 | 0.956 | 0 | 0.004 | ||
| complete vector | 4.617 | 39.23 | / | / | / | / | / | / | |
| Selection 23 | |||||||||
| Space vector (r) | RV | 0.962 | 0.004 | 0.002 | 0.962 | 0.005 | −0.004 | ||
| Space vector (LF) | Var | 0.958 | −0.03 | −0.023 | 0.956 | 0 | 0.004 | ||
| complete vector | 4.625 | 39.23 | / | / | / | / | / | / | |
| Selection 24 | |||||||||
| Space vector (r) | RMS | 0.962 | 0.001 | 0 | 0.962 | 0.005 | −0.004 | ||
| Space vector (LF) | RMS | 0.962 | −0.03 | −0.023 | 0.961 | 0 | 0.004 | ||
| complete vector | 4.683 | 39.37 | / | / | / | / | / | / | |
| Selection 25 | |||||||||
| Space vector (r) | MS | 0.961 | 0.001 | 0 | 0.961 | 0.005 | −0.004 | ||
| Space vector (LF) | RSS | 0.962 | −0.03 | −0.023 | 0.961 | 0 | 0.004 | ||
| complete vector | 4.542 | 39.53 | / | / | / | / | / | / | |
| Selection 26 | |||||||||
| Space vector (r) | SS | 0.961 | 0.001 | 0 | 0.961 | 0.005 | −0.004 | ||
| Space vector (LF) | SD | 0.962 | −0.03 | −0.023 | 0.961 | 0 | 0.004 | ||
| complete vector | 4.642 | 39.53 | / | / | / | / | / | / | |
Appendix B
References
- Haroun, S.; Seghir, A.N.; Hamdani, S.; Touati, S. AR model of the torque signal for mechanical induction motor faults detection and diagnosis. In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar] [CrossRef]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. Knowledge Discovery and Data Mining: Towards a Unifying Framework. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Ali, A.; Abdelhadi, A. Condition-Based Monitoring and Maintenance: State of the Art Review. Appl. Sci. 2022, 12, 688. [Google Scholar] [CrossRef]
- Verma, A.K.; Sarangi, S.; Kolekar, M.H. Shaft Misalignment Detection using Stator Current Monitoring. Int. J. Adv. Comput. Res. 2013, 3, 305–309. [Google Scholar]
- Popaleny, P.; Antonino-Daviu, J. Electric Motors Condition Monitoring Using Currents and Vibrations Analyses. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar] [CrossRef]
- Kumar, C.; Krishnan, G.; Sarangi, S. Experimental investigation on misalignment fault detection in induction motors using current and vibration signature analysis. In Proceedings of the 2015 International Conference on Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZE), Greater Noida, India, 25–27 February 2015. [Google Scholar] [CrossRef]
- Obaid, R.; Habetler, T. Effect of load on detecting mechanical faults in small induction motors. In Proceedings of the 4th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, 2003. SDEMPED 2003, Atlanta, GA, USA, 24–26 August 2003. [Google Scholar] [CrossRef]
- Tahir, M.M.; Hussain, A.; Badshah, S.; Khan, A.Q.; Iqbal, N. Classification of unbalance and misalignment faults in rotor using multi-axis time domain features. In Proceedings of the 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 18–19 October 2016. [Google Scholar] [CrossRef]
- Bossio, J.M.; Bossio, G.R.; Angelo, C.H.D. Angular misalignment in induction motors with flexible coupling. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.; Popaleny, P. Detection of Induction Motor Coupling Unbalanced and Misalignment via Advanced Transient Current Signature Analysis. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar] [CrossRef]
- Haroun, S.; Seghir, A.N.; Touati, S.; Hamdani, S. Misalignment fault detection and diagnosis using AR model of torque signal. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015. [Google Scholar] [CrossRef]
- Tran, M.Q.; Liu, M.K.; Tran, Q.V.; Nguyen, T.K. Effective Fault Diagnosis Based on Wavelet and Convolutional Attention Neural Network for Induction Motors. IEEE Trans. Instrum. Meas. 2021, 71, 1–13. [Google Scholar] [CrossRef]
- Kumar, P.; Hati, A.S. Convolutional neural network with batch normalisation for fault detection in squirrel cage induction motor. IET Electr. Power Appl. 2021, 15, 39–50. [Google Scholar] [CrossRef]
- Shao, S.Y.; Sun, W.J.; Yan, R.Q.; Wang, P.; Gao, R.X. A Deep Learning Approach for Fault Diagnosis of Induction Motors in Manufacturing. Chin. J. Mech. Eng. 2017, 30, 1347–1356. [Google Scholar] [CrossRef]
- Okwuosa, C.N.; Akpudo, U.E.; Hur, J.W. A Cost-Efficient MCSA-Based Fault Diagnostic Framework for SCIM at Low-Load Conditions. Algorithms 2022, 15, 212. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.W. Towards bearing failure prognostics: A practical comparison between data-driven methods for industrial applications. J. Mech. Sci. Technol. 2020, 34, 4161–4172. [Google Scholar] [CrossRef]
- Calabrese, F.; Regattieri, A.; Bortolini, M.; Galizia, F.G.; Visentini, L. Feature-Based Multi-Class Classification and Novelty Detection for Fault Diagnosis of Industrial Machinery. Appl. Sci. 2021, 11, 9580. [Google Scholar] [CrossRef]
- Sinha, A.K.; Hati, A.S.; Benbouzid, M.; Chakrabarti, P. ANN-Based Pattern Recognition for Induction Motor Broken Rotor Bar Monitoring under Supply Frequency Regulation. Machines 2021, 9, 87. [Google Scholar] [CrossRef]
- Hasan, M.J.; Sohaib, M.; Kim, J.M. A Multitask-Aided Transfer Learning-Based Diagnostic Framework for Bearings under Inconsistent Working Conditions. Sensors 2020, 20, 7205. [Google Scholar] [CrossRef] [PubMed]
- Bold, S.; Urschel, S. Feature Identification for Diagnosing Misalignment under the Influence of Parameter Variation. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar] [CrossRef]
- Ltifi, H.; Ayed, M.B.; Alimi, A.M.; Lepreux, S. Survey of information visualization techniques for exploitation in KDD. In Proceedings of the 2009 IEEE/ACS International Conference on Computer Systems and Applications, Rabat, Morocco, 10–13 May 2009. [Google Scholar] [CrossRef]
- McDonald, R.; Kovalerchuk, B. Lossless Visual Knowledge Discovery in High Dimensional Data with Elliptic Paired Coordinates. In Proceedings of the 2020 24th International Conference Information Visualisation (IV), Melbourne, Australia, 7–11 September 2020. [Google Scholar] [CrossRef]
- Dymora, P.; Mazurek, M.; Bomba, S. A Comparative Analysis of Selected Predictive Algorithms in Control of Machine Processes. Energies 2022, 15, 1895. [Google Scholar] [CrossRef]
- Mahoto, N.A.; Shaikh, A.; Reshan, M.S.A.; Memon, M.A.; Sulaiman, A. Knowledge Discovery from Healthcare Electronic Records for Sustainable Environment. Sustainability 2021, 13, 8900. [Google Scholar] [CrossRef]
- Visalakshi, S.; Radha, V. A literature review of feature selection techniques and applications: Review of feature selection in data mining. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2014. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, Y. Feature selection for high-dimensional data in astronomy. Adv. Space Res. 2008, 41, 1960–1964. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Crone, S.F.; Kourentzes, N. Feature selection for time series prediction—A combined filter and wrapper approach for neural networks. Neurocomputing 2010, 73, 1923–1936. [Google Scholar] [CrossRef]
- Piatetsky-shapiro, G.; Matheus, C.J. The Interestingness of Deviations. In Proceedings of the Workshop on Knowledge Discovery in Databases, Seattle, WA, USA, 31 July–1 August 1994. [Google Scholar]
- Kostic-Perovic, D.; Arkan, M.; Unsworth, P. Induction motor fault detection by space vector angular fluctuation. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No.00CH37129), Rome, Italy, 8–12 October 2000. [Google Scholar] [CrossRef]


| Device/Sensor | Type | Specification |
|---|---|---|
| Oscilloscope | RTE1034 | 4-channel, 350 MHz, 5 |
| Current transducer | IT 200-S | A |
| Shunt | 19/SH5/BNC/0.05 | |
| Differential probe | RT-ZD01 | 1000 V (RMS) |
| Torque measurement shaft | 4503A50L | Nm ( Nm) |
| Temperature sensor | LM35DT | / |
| Alignment system | XT660 | / |
| Power analyzer | WT3000 | 4-channel |
| Type | Threshold | |
|---|---|---|
| Acceptable (mm) | Excellent (mm) | |
| Parallel | 0.09 | 0.06 |
| Angular | 0.07 | 0.05 |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 1 | |||||||||
| MCSA () | BB2 (k1+) | −0.087 | 0.962 | 0.619 | −0.23 | 0.929 | 0.808 | ||
| Signal () | SRM | 0.96 | 0.011 | 0.045 | 0.962 | 0.002 | 0.009 | ||
| complete vector | 0 | 0.17 | / | / | / | / | / | / | |
| Selection 9 | |||||||||
| MCSA () | ECC1 (k1+) | −0.139 | 0.96 | 0.576 | −0.254 | 0.947 | 0.826 | ||
| Space Vector (r) | SF | −0.254 | −0.396 | −0.432 | −0.063 | −0.619 | −0.433 | ||
| complete vector | 0.742 | 6.13 | / | / | / | / | / | / | |
| Selection 10 | |||||||||
| MCSA () | BB2 (k3+) | −0.139 | 0.96 | 0.576 | −0.254 | 0.947 | 0.826 | ||
| MCSA () | n | −0.939 | −0.07 | −0.065 | −0.91 | −0.092 | −0.127 | ||
| complete vector | 1.075 | 0.3 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 1 | |||||||||
| SV (r) | mean | 0.961 | 0 | 0 | 0.962 | 0.011 | −0.001 | ||
| Spectrum (, Seg. 11) | peak position | 0.52 | −0.299 | 0 | 0.284 | −0.883 | 0.499 | ||
| complete vector | 0.217 | 0 | / | / | / | / | / | / | |
| Selection 2 | |||||||||
| SV r | RV | 0.961 | 0 | 0 | 0.962 | 0.011 | −0.007 | ||
| Spectrum (, Seg. 10) | peak position | 0.577 | −0.26 | 0 | 0.225 | −0.897 | 0.511 | ||
| complete vector | 0.383 | 0 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 2 | |||||||||
| Space vector (r) | SRM | 0.962 | 0.005 | 0.003 | 0.962 | 0.005 | −0.004 | ||
| Space vector (LF) | MS | 0.958 | −0.03 | −0.023 | 0.956 | 0 | 0.004 | ||
| complete vector | 4.592 | 39.13 | / | / | / | / | / | / | |
| Feature Extractor | Metric | Error Rate (%) | Correlation (1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis | Test | Analysis | Test | ||||||
| Load | PM | AM | Load | PM | AM | ||||
| Selection 1 | |||||||||
| Space vector (r) | RMS | 0.961 | 0.008 | −0.018 | 0.962 | −0.009 | −0.015 | ||
| Spectrum (, Seg. 11) | peak pos. | 0.56 | 0.412 | −0.425 | 0.222 | −0.677 | −0.846 | ||
| complete vector | 0.642 | 0 | / | / | / | / | / | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bold, S.; Urschel, S. A Knowledge Discovery Process Extended to Experimental Data for the Identification of Motor Misalignment Patterns. Machines 2023, 11, 827. https://doi.org/10.3390/machines11080827
Bold S, Urschel S. A Knowledge Discovery Process Extended to Experimental Data for the Identification of Motor Misalignment Patterns. Machines. 2023; 11(8):827. https://doi.org/10.3390/machines11080827
Chicago/Turabian StyleBold, Sebastian, and Sven Urschel. 2023. "A Knowledge Discovery Process Extended to Experimental Data for the Identification of Motor Misalignment Patterns" Machines 11, no. 8: 827. https://doi.org/10.3390/machines11080827
APA StyleBold, S., & Urschel, S. (2023). A Knowledge Discovery Process Extended to Experimental Data for the Identification of Motor Misalignment Patterns. Machines, 11(8), 827. https://doi.org/10.3390/machines11080827








