Improving Efficiency and Power Output of Switched Reluctance Generators through Optimum Operating Parameters
Abstract
1. Introduction
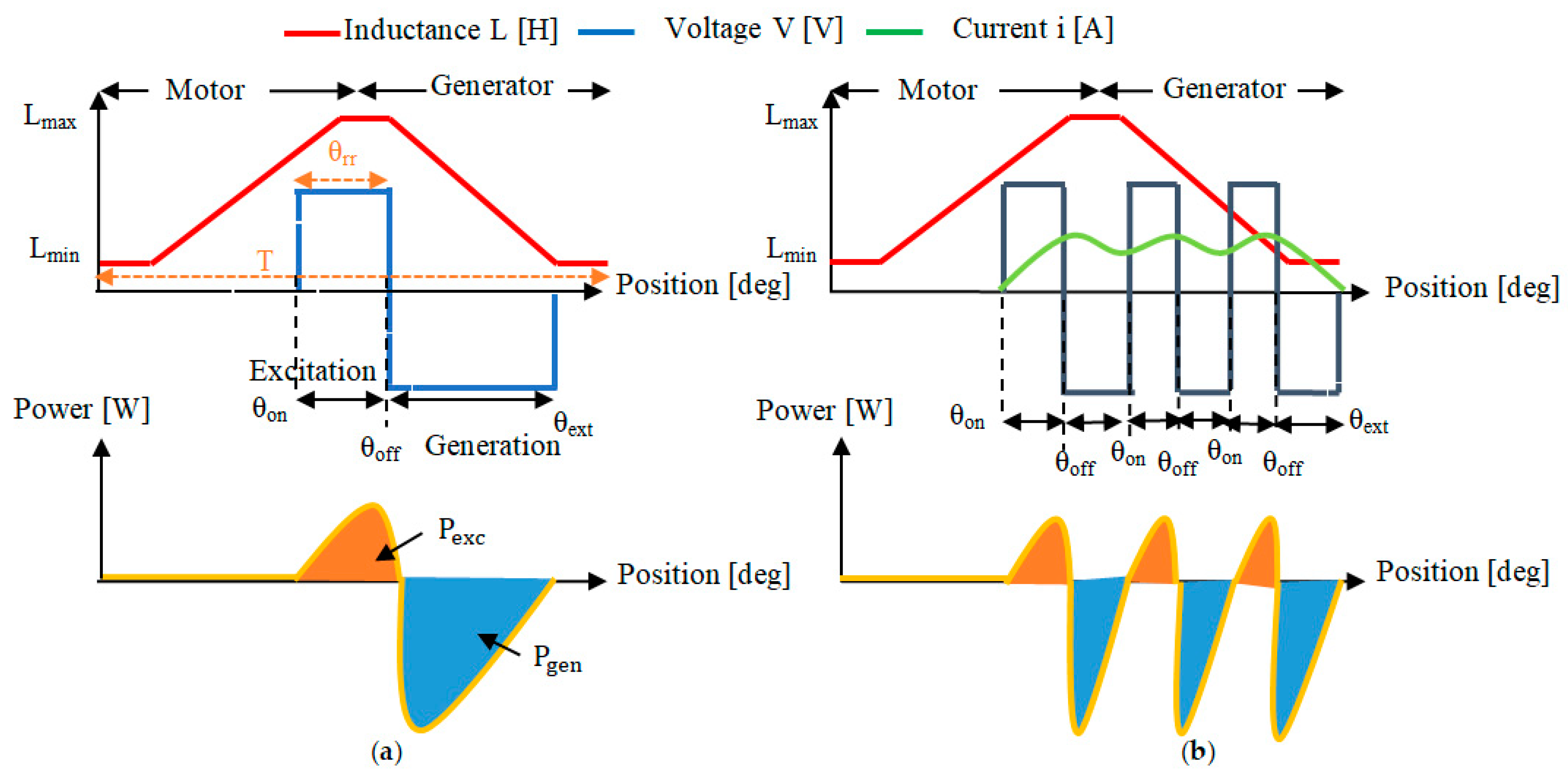
2. SRG Power
- Motor mode: (Te > 0) corresponds to the increasing stage of the inductance ((dL/dθm) > 0);
- Generator mode: (Te < 0) corresponds to the decreasing stage of the inductance ((dL/dθm) < 0).
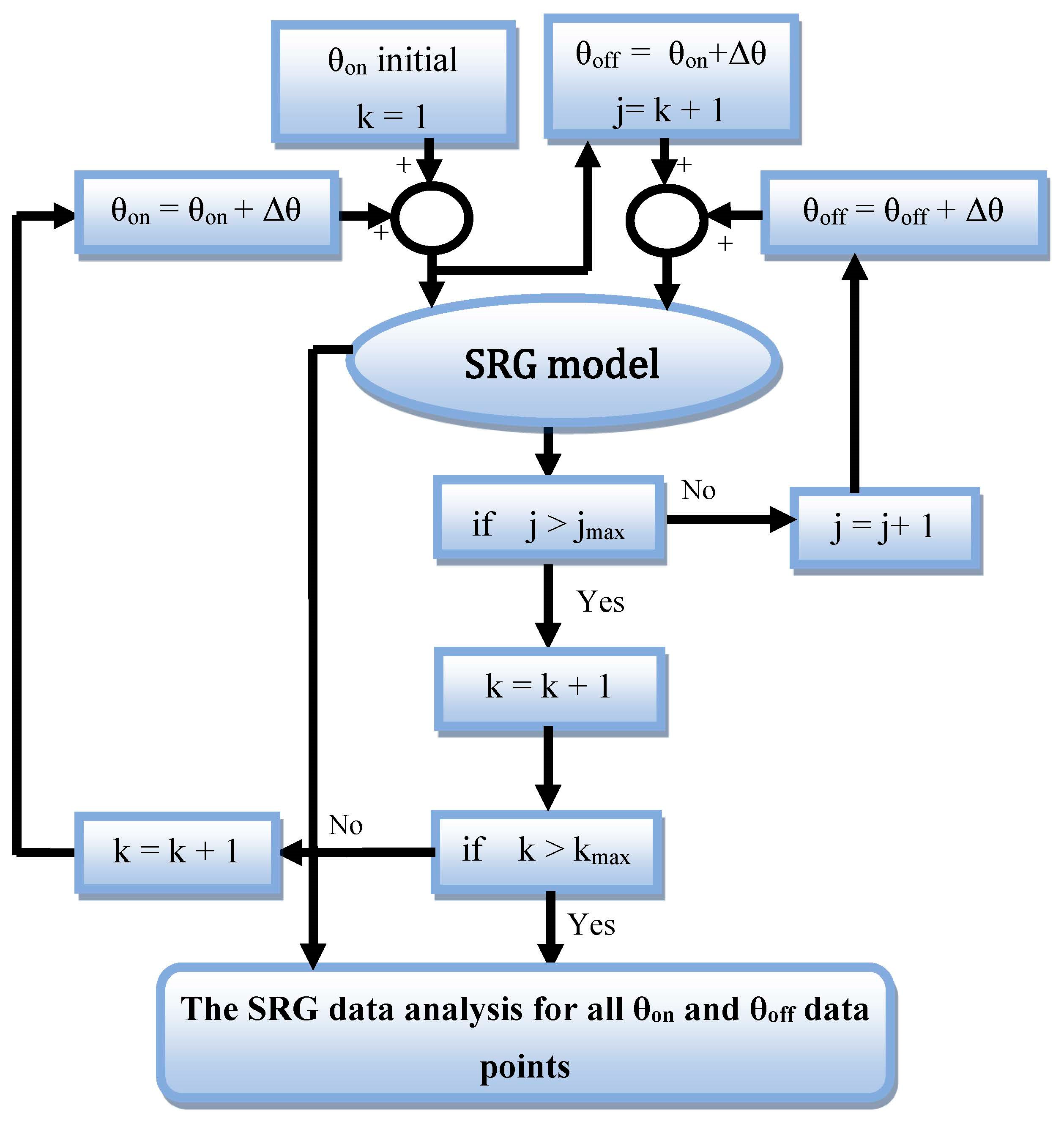
3. Data Extraction of the SRG Characteristics
4. SRG Data for Power Performance
5. SRG Power Efficiency
6. MPPT Algorithm for the SRG
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Characteristics | Values |
|---|---|
| SRM Ns/Nr | 12/8 |
| Polar arc of the stator βs | 15.28 [deg] |
| Polar arc of the rotor βr | 15.48 [deg] |
| Stator outer radius | 69.50 mm |
| Inside radius of stator cylinder head | 57.50 mm |
| Inside radius of stator | 37.50 mm |
| Rotor outer radius | 37.00 mm |
| Rotor cylinder head outer radius | 24.50 mm |
| Shaft radius | 12.50 mm |
| Active length | 110.00 mm |
| Number of series on turns/phase | 50.00 |
References
- Kumar, B.; Sandhu, K.S.; Sharma, R. Comparative analysis of control schemes for dfig-based wind energy system. J. Inst. Eng. India Ser. B. 2021, 103, 1–20. [Google Scholar] [CrossRef]
- Sunan, E.; Kucuk, F.; Goto, H.; Guo, H.J.; Ichinokura, O. Three-phase full-bridge converter controlled permanent magnet reluctance generator for small-scale wind energy conversion systems. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kowloon, Hong Kong, China, 7–10 December 2014. [Google Scholar]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Adetokun, B.B. Optimal capacitance selection for a wind-driven self-excited reluctance generator under varying wind speed and load conditions. Appl. Energy 2017, 190, 339–353. [Google Scholar] [CrossRef]
- Mohanty, P.; Bhuvaneswari, G.; Balasubramanian, R.; Dhaliwal, N.K. MATLAB based modeling to study the performance of different MPPT techniques used for solar PV system under various operating conditions. Renew. Sustain. Energy Rev. 2014, 38, 581–593. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Deng, X. Control for power converter of small-scale switched reluctance wind power generator. IEEE Trans. Ind. Electron. 2020, 68, 3148–3158. [Google Scholar] [CrossRef]
- Dos Santos Barros, T.A.; dos Santos Neto, P.J.; Nascimento Filho, P.S.; Moreira, A.B.; Ruppert Filho, E. An approach for switched reluctance generator in a wind generation system with a wide range of operation speed. IEEE Trans. Power Electron. 2017, 32, 8277–8292. [Google Scholar] [CrossRef]
- Viajante, G.P.; Andrade, D.A.; Chaves, E.N.; Bernadelli, V.R.; Queiroz, C.A.; Freitas, M.A.A.; Gomes, L.C. A grid connection scheme of a switched reluctance generator for active power injection using P-resonant (P-RES) controller. Electr. Power Syst. Res. 2016, 141, 572–579. [Google Scholar] [CrossRef]
- Hasanien, H.M.; Muyeen, S.M. Speed control of grid-connected switched reluctance generator driven by variable speed wind turbine using adaptive neural network controller. Electr. Power Syst. Res. 2012, 84, 206–213. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, design optimization, and applications of switched reluctance machines—A review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Daldaban, F.; Buzpinar, M.A. Pulse injection-based sensorless switched reluctance motor driver model with machine learning algorithms. Electr. Eng. 2021, 103, 705–715. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Zhang, L.; Du, L.; Wang, Q. Magnetic field analysis and iron loss calculation of a special switched reluctance generator. J. Electr. Eng. Technol. 2019, 14, 1991–2003. [Google Scholar] [CrossRef]
- Kushwaha, A.; Kanagaraj, R. Peak-current estimation using simplified current-rise model of switched reluctance generator operating in single-pulse mode. Int. J. Electr. Power Energy Syst. 2020, 120, 105971. [Google Scholar] [CrossRef]
- Chirapo, K.A.C.; Oliveira, A.L.; Sguarezi Filho, A.J.; Pelizari, A.; Di Santo, S.G.; Costa, E.C.M. P+ res controller applied to the direct power control of switched reluctance generator. J. Control Autom. Electr. Syst. 2020, 31, 360–366. [Google Scholar] [CrossRef]
- Ćalasan, M.P.; Vujičić, V.P. A robust continuous conduction mode control strategy of switched reluctance generator for wind power plant applications. Electr. Eng. 2017, 99, 943–958. [Google Scholar] [CrossRef]
- Scalcon, F.P.; Fang, G.; Volpato Filho, C.J.; Gründling, H.A.; Vieira, R.P.; Nahid-Mobarakeh, B. A Review on Switched Reluctance Generators in Wind Power Applications: Fundamentals, Control and Future Trends. IEEE Access 2022, 8, 69412–69427. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C. Optimized direct instantaneous torque control for SRMs with efficiency improvement. IEEE Trans. Ind. Electron. 2020, 68, 2072–2082. [Google Scholar] [CrossRef]
- Deng, X.; Mecrow, B.; Wu, H.; Martin, R. Design and development of low torque ripple variable-speed drive system with six-phase switched reluctance motors. IEEE Trans. Energy Convers. 2017, 33, 420–429. [Google Scholar] [CrossRef]
- Labiod, C.; Kamel, S.; Belkacem, M.; Benchouia, M.T.; Benbouzid, M.E.H. Analyze of non-linearity effects of 8/6 switched reluctance machine by finite elements method. In Proceedings of the 2018 International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 17–18 December 2018. [Google Scholar]
- Srairi, K.; Feliachi, M. Numerical coupling models for analyzing dynamic behaviors of electromagnetic actuators. IEEE Trans. Magn. 1998, 34, 3608–3611. [Google Scholar] [CrossRef]
- Salah Boughezala, M.; Srairi, K.; Labiod, C.; Chemsa, A.; Benbouzid, M.E.H. A Novel Control Technique Based on Multi-Objective Intelligent Routing Algorithms for Optimum Performances of 12/8 Switched Reluctance Motor. Int. J. Energy Convers. (IRECON) 2021, 10, 1–11. [Google Scholar] [CrossRef]
- Torres, J.; Moreno-Torres, P.; Navarro, G.; Blanco, M.; Nájera, J.; Santos-Herran, M.; Lafoz, M. Asymmetrical Rotor Skewing Optimization in Switched Reluctance Machines Using Differential Evolutionary Algorithm. Energies 2021, 14, 3194. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, T.; Ding, W. Performance evaluation on a novel power converter with minimum number of switches for a six-phase switched reluctance motor. IEEE Trans. Ind. Electron. 2018, 66, 1693–1702. [Google Scholar] [CrossRef]
- Labiod, C.; Bahri, M.; Srairi, K.; Mahdad, B.; Benchouia, M.T.; Benbouzid, M.E.H. Static and dynamic analysis of non-linear magnetic characteristics in switched reluctance motors based on circuit-coupled time stepping finite element method. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 47–55. [Google Scholar] [CrossRef]
- Furukakoi, M.; Adewuyi, O.B.; Matayoshi, H.; Howlader, A.M.; Senjyu, T. Multi objective unit commitment with voltage stability and PV uncertainty. Appl. Energy 2018, 228, 618–623. [Google Scholar] [CrossRef]
- Zhong, Y.; Lin, J.; Wang, L.; Zhang, H. Discrete comprehensive learning particle swarm optimization algorithm with Metropolis acceptance criterion for traveling salesman problem. Swarm Evol. Comput. 2018, 42, 77–88. [Google Scholar] [CrossRef]
- Feng, L.; Sun, X.; Tian, X.; Diao, K. Direct torque control with variable flux for an SRM based on hybrid optimization algorithm. IEEE Trans. Power Electron. 2022, 37, 6688–6697. [Google Scholar] [CrossRef]
- Feng, L.; Sun, X.; Yang, Z.; Diao, K. Optimal Torque Sharing Function Control for Switched Reluctance Motors Based on Active Disturbance Rejection Controller. IEEE/ASME Trans. Mechatron. 2023. early access. [Google Scholar] [CrossRef]
- Zine, M.; Chemsa, A.; Labiod, C.; Ikhlef, M.; Srairi, K.; Benbouzid, M. Coupled Indirect Torque Control and Maximum Power Point Tracking Technique for Optimal Performance of 12/8 Switched Reluctance Generator-Based Wind Turbines. Machines 2022, 10, 1046. [Google Scholar] [CrossRef]
- Sridharan, S.; Prabhu, V.V.; Velmurugan, P. Efficient maximum power point tracking in grid connected switched reluctance generator in wind energy conversion system: An enhanced Mayfly Algorithm transient search optimization. Energy Sources Part A Recovery Util. Environ. Eff. 2021. early access. [Google Scholar] [CrossRef]
- Mapa, S.; Gurumoorthy, B. Maximum power extraction from a switched reluctance generator based wind power generating system using optimization techniques. Eng. Rep. 2022, 4, 1–14. [Google Scholar] [CrossRef]
- Araujo, W.R.; Reis, M.R.; Wainer, G.A.; Calixto, W.P. Efficiency enhancement of switched reluctance generator employing optimized control associated with tracking technique. Energies 2021, 14, 8388. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Z.; Cui, X. Research on novel direct instantaneous torque control strategy for switched reluctance motor. IEEE Access 2020, 8, 66910–66916. [Google Scholar] [CrossRef]
- Teekaraman, Y. Implementation of Control Variables to Exploit Output Power for SRGs in Single Pulse Mode Operation. Int. J. Eng. 2016, 29, 505–513. [Google Scholar]
- Sunan, E.; Kucuk, F.; Raza, K.S.; Goto, H.; Guo, H.; Ichinokura, O. Torque ripple minimization and maximum power point tracking of a permanent magnet reluctance generator for wind energy conversion system. J. Renew. Sustain. Energy 2013, 5, 013114. [Google Scholar] [CrossRef]
- Labiod, C.; Srairi, K.; Mahdad, B.; Benbouzid, M.E.H. A novel control technique for torque ripple minimization in switched reluctance motor through destructive interference. Electr. Eng. 2018, 100, 481–490. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, H.; Zhang, J. Regenerative braking control strategy for electric vehicles based on optimization of switched reluctance generator drive system. IEEE Access 2020, 8, 76671–76682. [Google Scholar] [CrossRef]
- Wanthong, N.; Ohyama, K. Effect of the excitation conditions on the power generation efficiency of a switched reluctance generator. In Proceedings of the 2021 7th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Pattaya, Thailand, 1–3 April 2021. [Google Scholar]
- Diko, M.; Rafajdus, P.; Makys, P.; Dubravka, P.; Szabo, L.; Ruba, M. A novel concept of short-flux path switched reluctance motor for electrical vehicles. Adv. Electr. Electron. Eng. 2015, 13, 206–211. [Google Scholar] [CrossRef]
- Dos Santos Neto, P.J.; dos Santos Barros, T.A.; de Paula, M.V.; de Souza, R.R.; Ruppert Filho, E. Design of computational experiment for performance optimization of a switched reluctance generator in wind systems. IEEE Trans. Energy Convers. 2017, 33, 406–419. [Google Scholar] [CrossRef]
- Choi, D.W.; Byun, S.I.; Cho, Y.H. A study on the maximum power control method of switched reluctance generator for wind turbine. IEEE Trans. Magn. 2013, 50, 1–4. [Google Scholar] [CrossRef]
- Hajiabadi, H.; Farshad, M.; Shamsinejad, M. Multi-objective optimization and online control of switched reluctance generator for wind power application. Int. J. Ind. Electron. Control Optim. 2021, 4, 33–45. [Google Scholar]
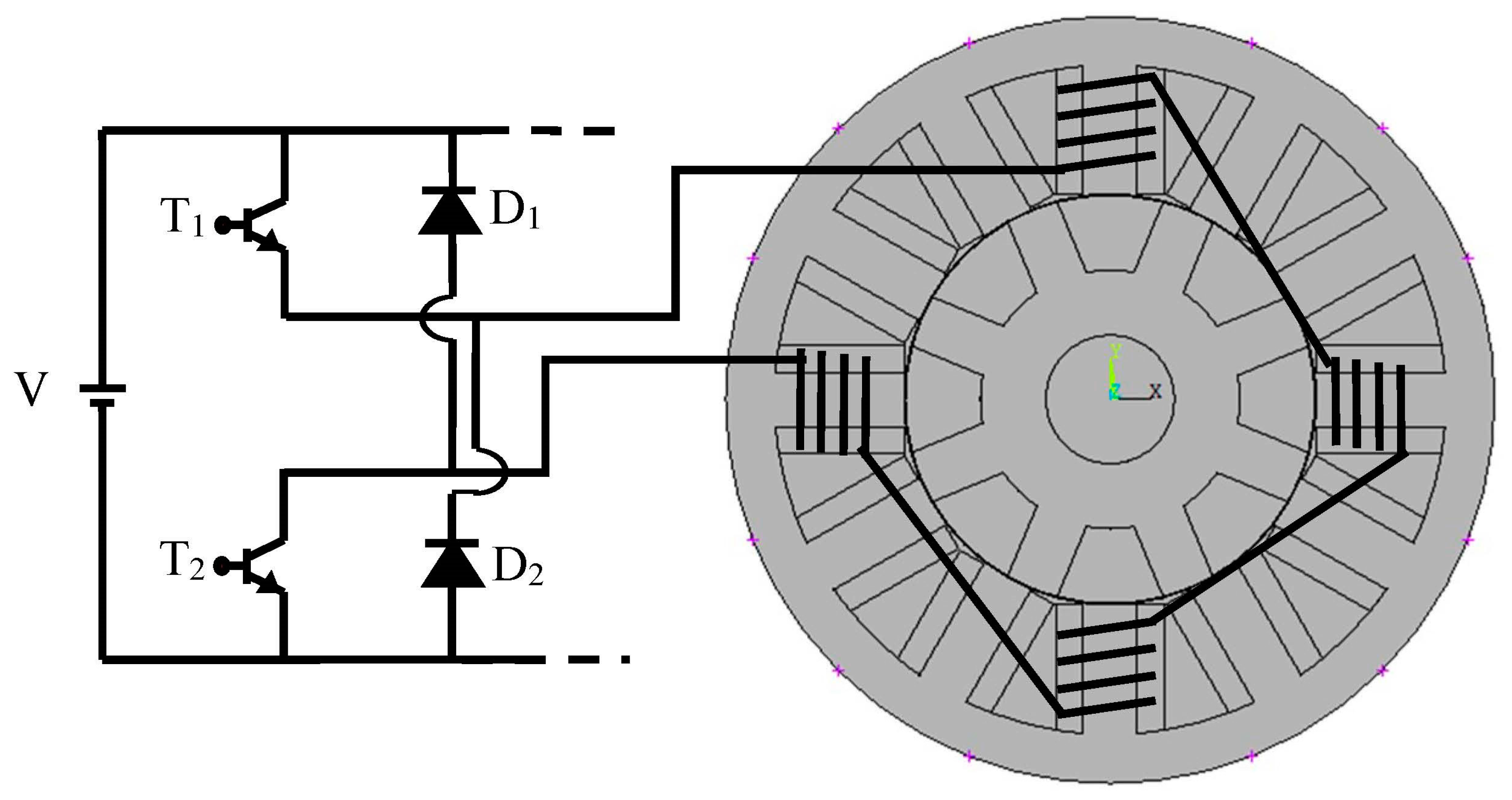

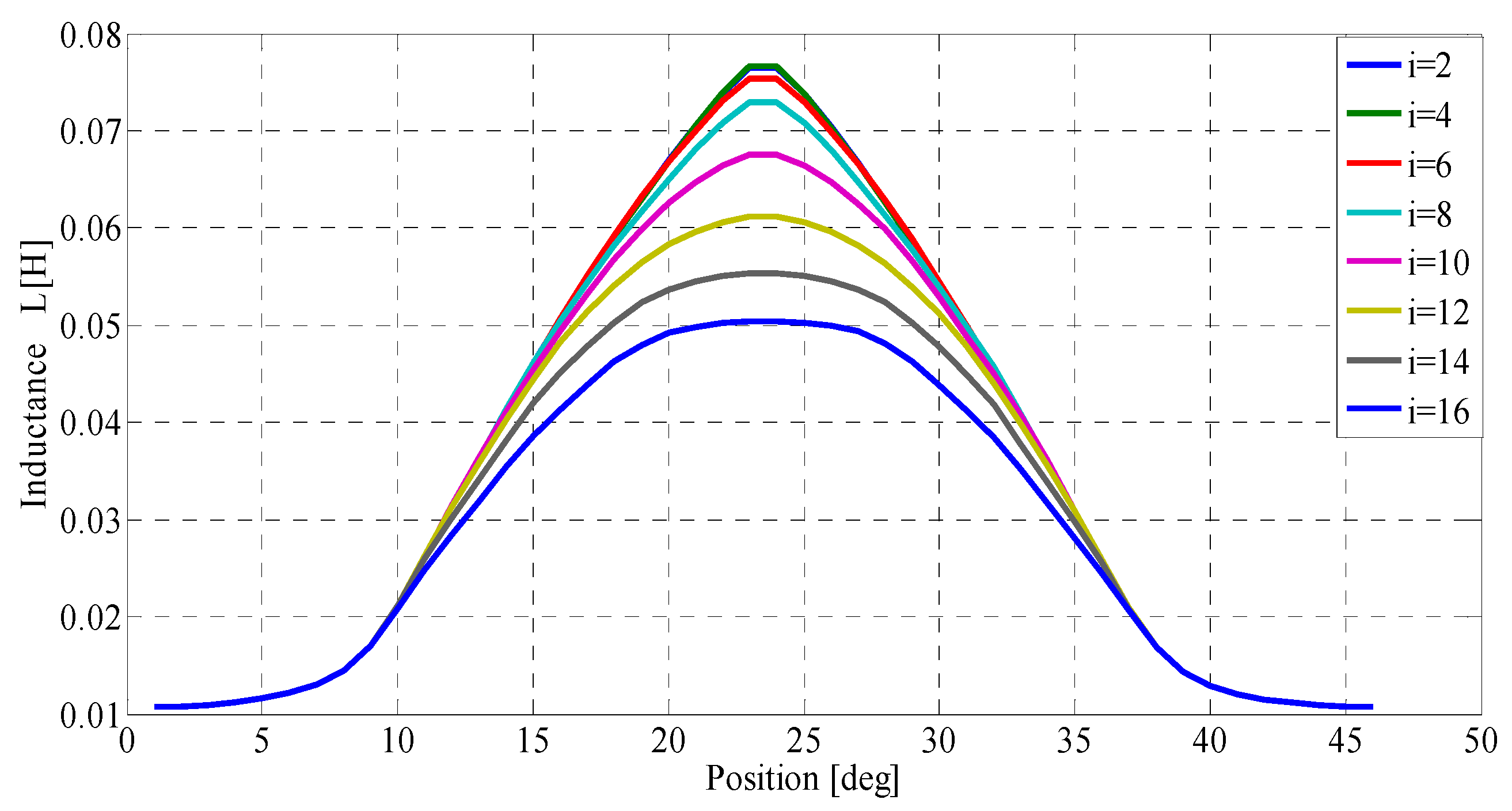

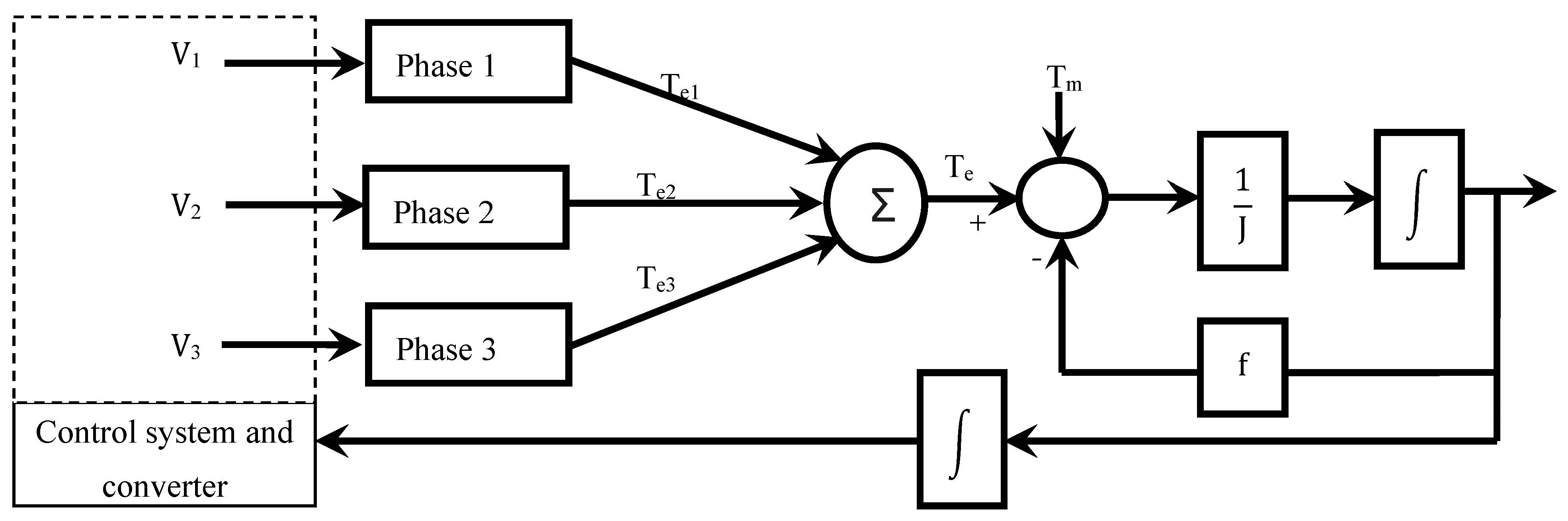
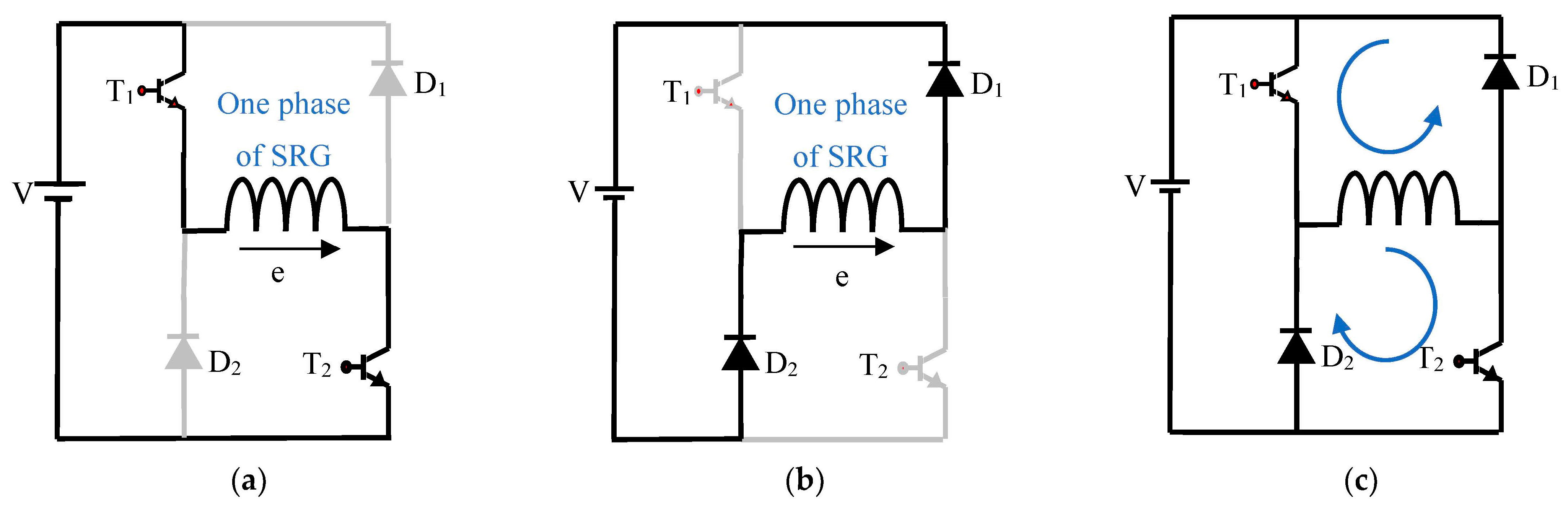
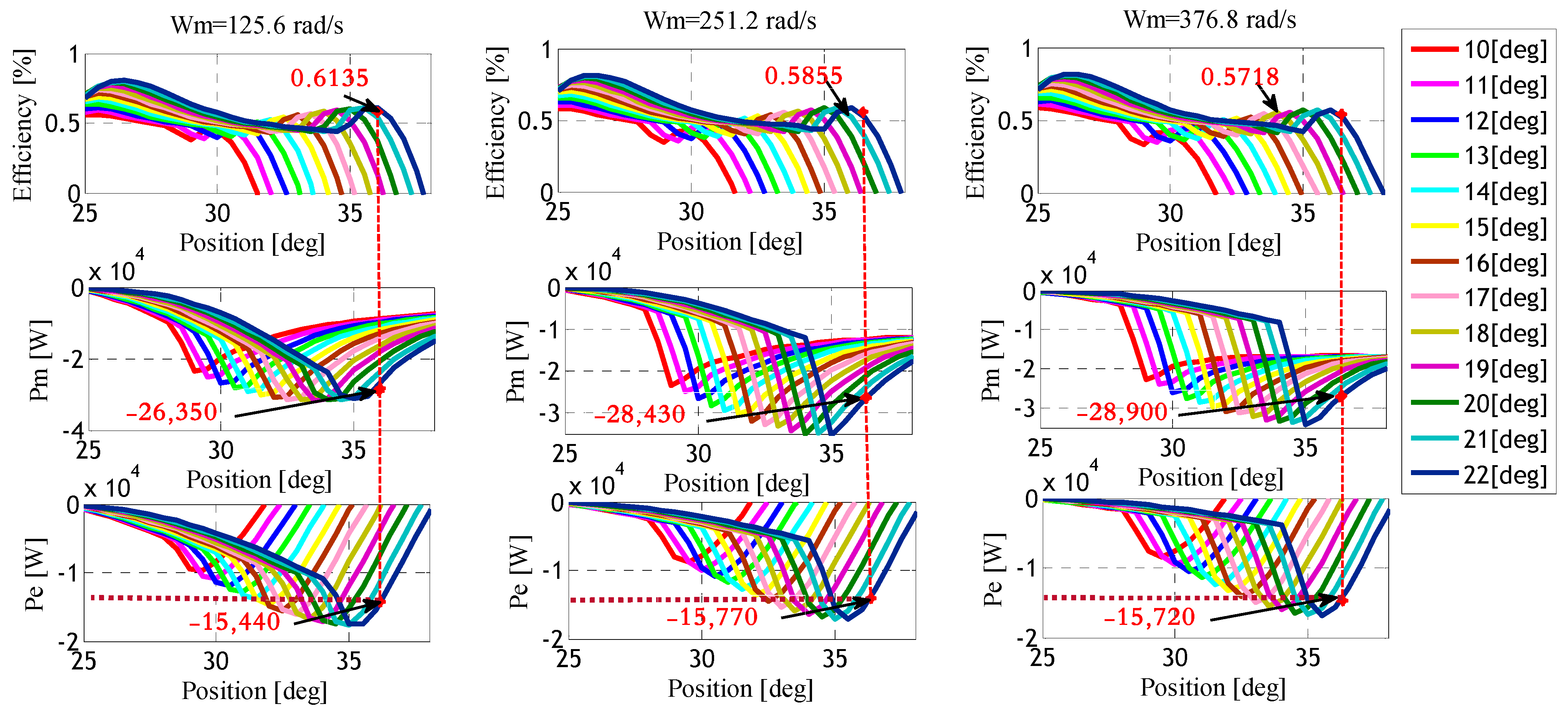
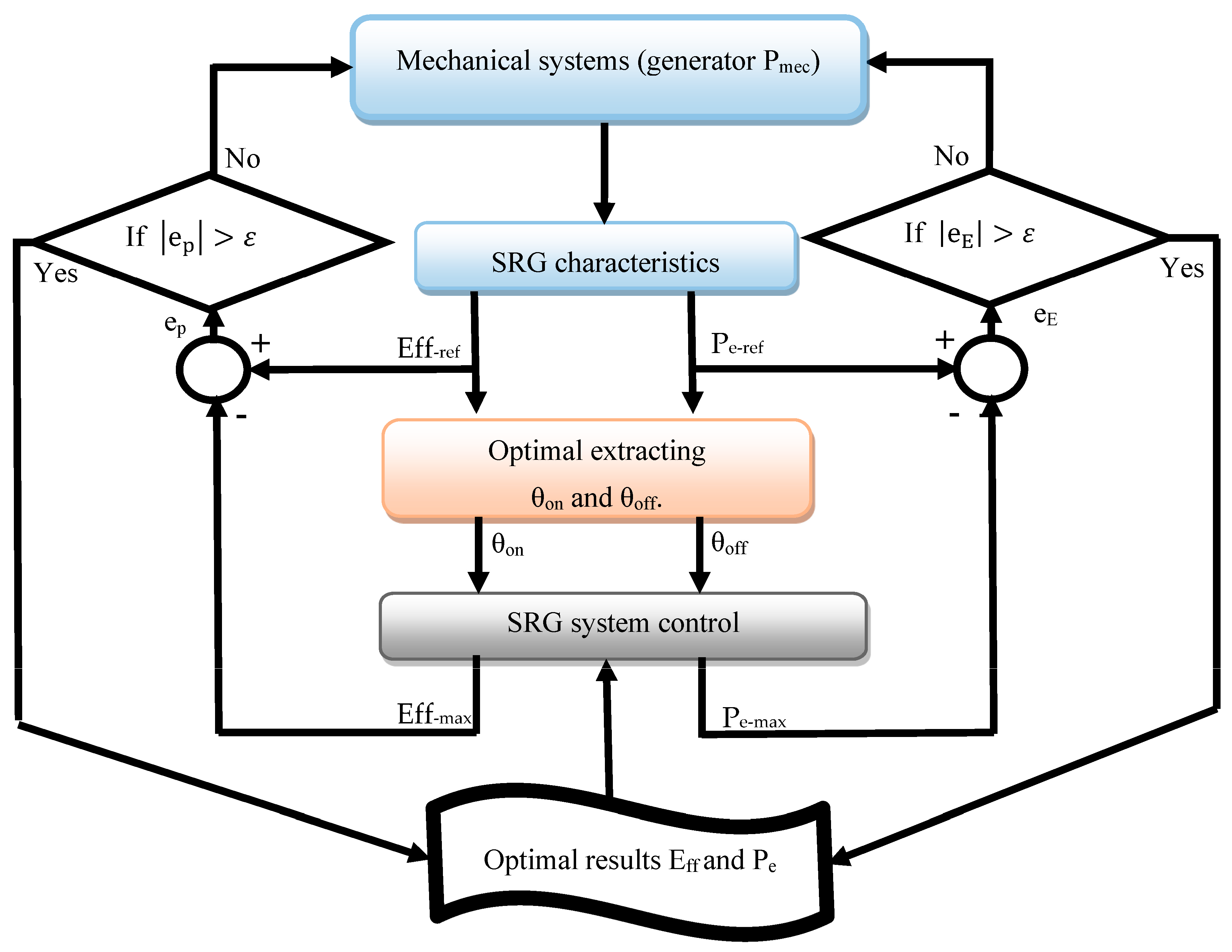
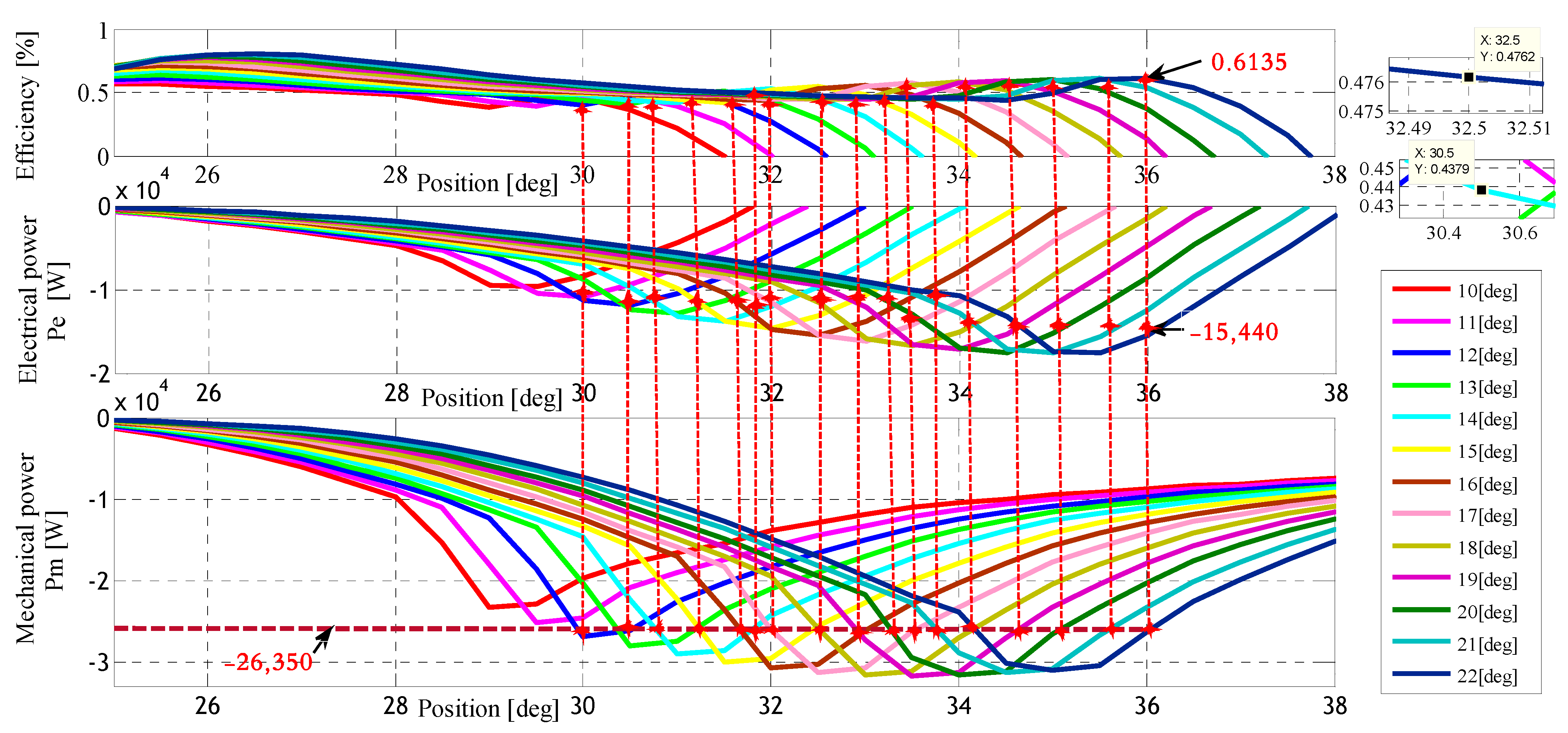
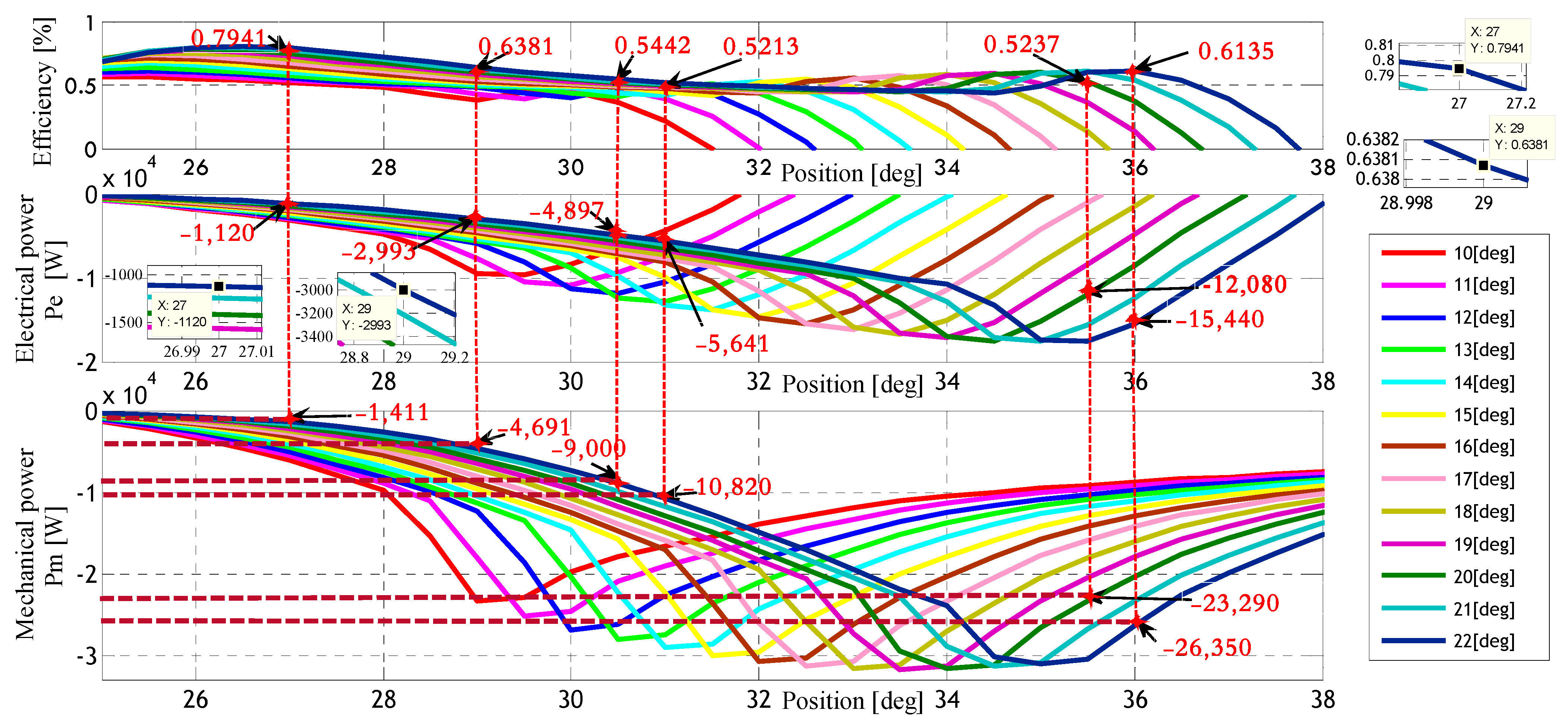
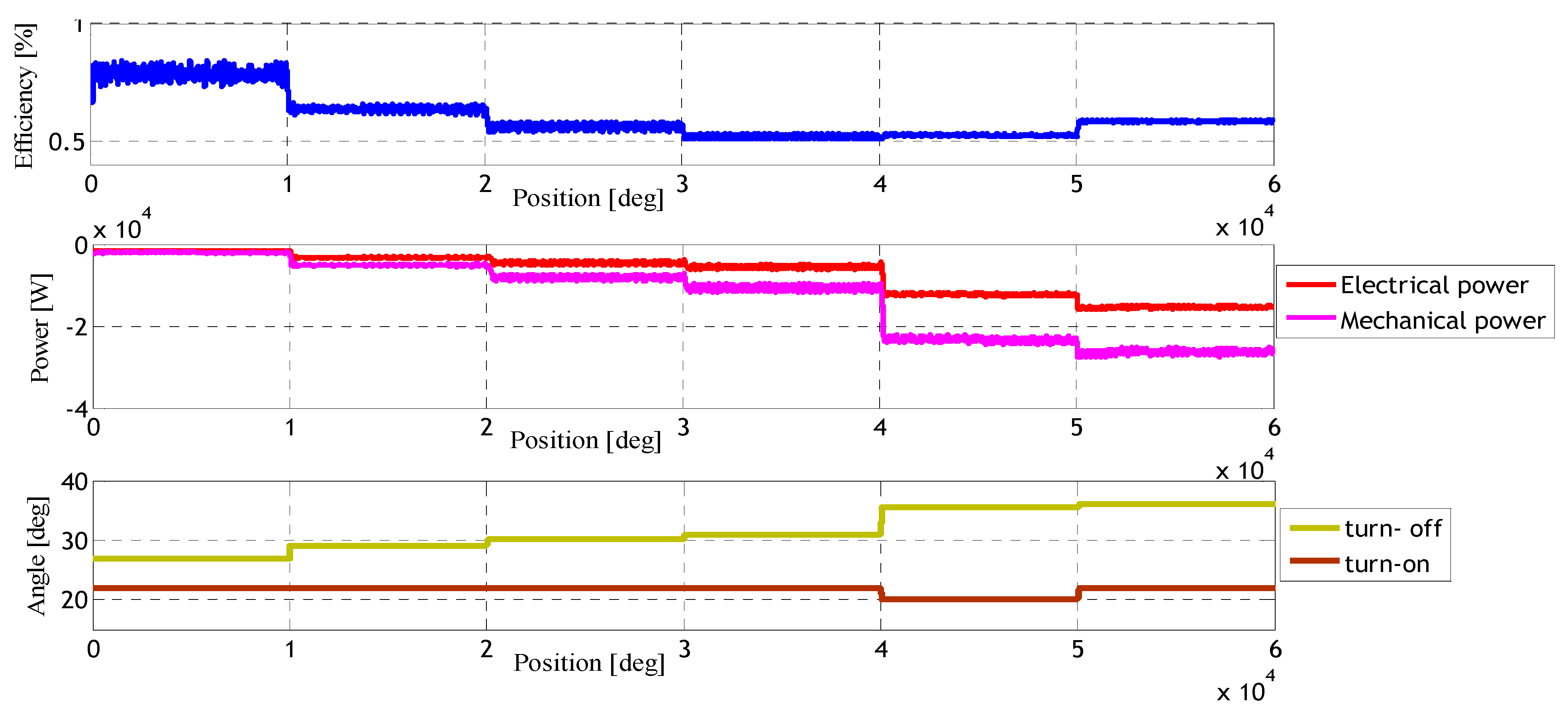
| Reference speed Wm [rad/s] | Efficiency Eff [%] | Mechanical Power Pm [W] | Electrical Power Pe [W] | θon [deg] | θoff [deg] |
|---|---|---|---|---|---|
| 125.60 | 61.35 | −26,350 | −15,440 | 22 | 36 |
| 251.20 | 58.55 | −28,430 | −15,770 | 22 | 36 |
| 378.80 | 57.18 | −28,900 | −15,720 | 22 | 36 |
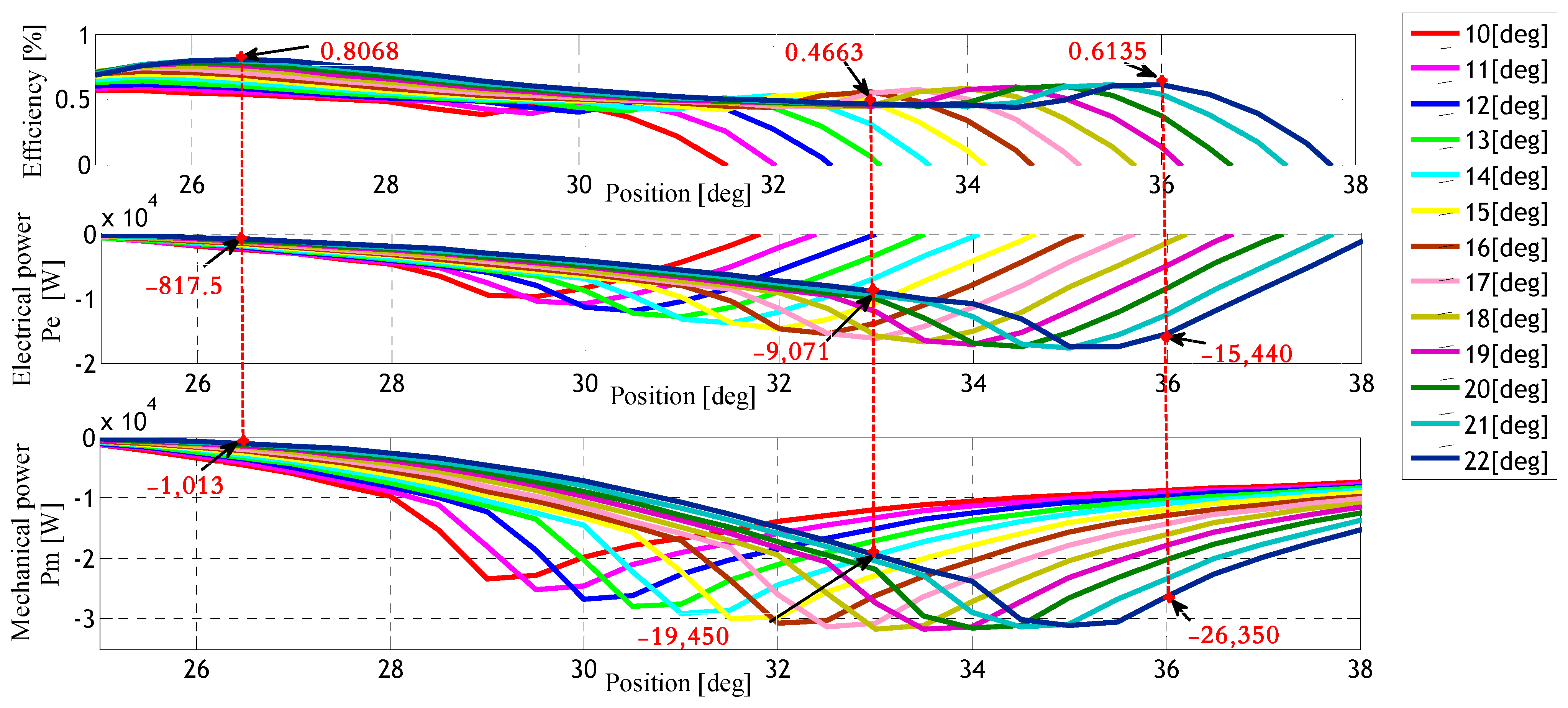
| Efficiency Eff [%] | Mechanical Power Pm [W] | Electrical Power Pe [W] | θon [deg] | θoff [deg] |
|---|---|---|---|---|
| 61.35 | −26,350 | −15,440.00 | 22 | 36.0 |
| 46.63 | −19,450 | −9071.00 | 22 | 33.0 |
| 80.68 | −1013 | −817.50 | 22 | 26.5 |
| Efficiency Eff [%] | Electrical Power Pe [W] | θon [deg] | θoff [deg] |
|---|---|---|---|
| 0.3958 | −11,380 | 12 | 30.00 |
| 0.4073 | −11,920 | 12 | 30.50 |
| 0.4387 | −11,560 | 14 | 30.75 |
| 0.4315 | −11,880 | 13 and 15 | 31.25 |
| 0.4387 | −12,080 | 16 | 31.70 |
| 0.5031 | −12,430 | 14 | 31.80 |
| 0.4762 | −11,540 | 17 | 32.00 |
| 0.4469 | −11,560 | 18 | 32.50 |
| 0.4387 | −11,920 | 19 | 32.75 |
| 0.5698 | −14,270 | 17 | 33.50 |
| 0.4387 | −11,560 | 21 | 33.75 |
| 0.5853 | −14,700 | 18 and 22 | 34.10 |
| 0.5849 | −14,720 | 19 | 34.60 |
| 0.5941 | −14,900 | 20 | 35.10 |
| 0.5698 | −14,720 | 21 | 35.60 |
| 0.6135 | −15,440 | 22 | 36.00 |
| Mechanical Power Pm [W] | θon [deg] | θoff [deg] | Efficiency Eff [%] | Electrical Power Pe [W] |
|---|---|---|---|---|
| −1411 | 22 | 27.00 | 0.7941 | −1120 |
| −4691 | 22 | 29.00 | 0.6381 | −2993 |
| −9000 | 22 | 30.25 | 0.5442 | −4897 |
| −10,820 | 22 | 31.00 | 0.5213 | −5641 |
| −23,290 | 20 | 35.50 | 0.5237 | −12,080 |
| −26,350 | 22 | 36.00 | 0.6135 | −15,440 |
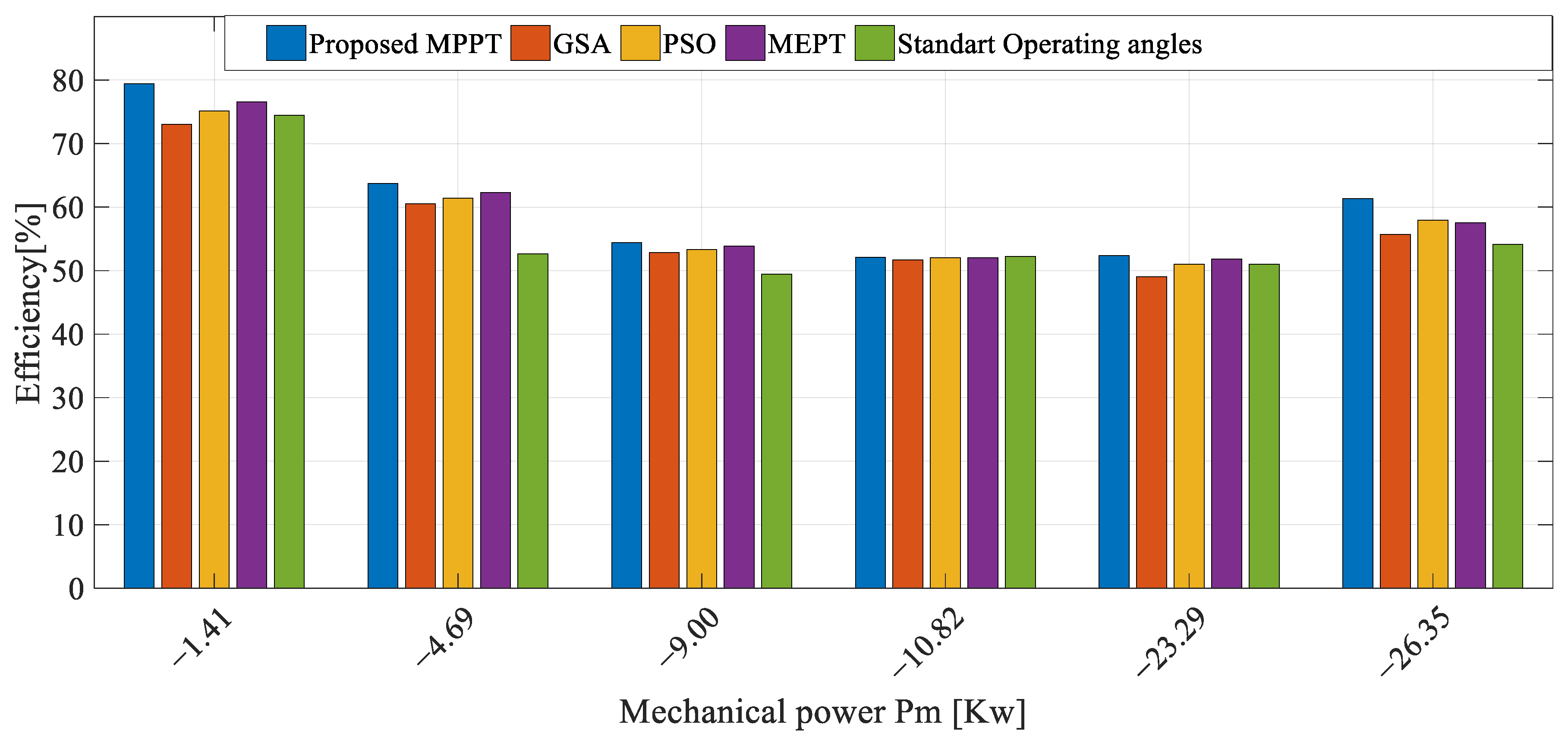
| Pm [KW] | −1.41 | −4.69 | −9.00 | −10.82 | −23.29 | −26.35 | |
| Proposed MPPT | (θon, θoff) | (22.0, 27.0) | (22.0, 29.0) | (22.0, 30.2) | (22.0, 31.0) | (20.0, 35.5) | (22, 36.0) |
| Eff [%] | 79.43 | 63.75 | 54.44 | 52.13 | 52.37 | 61.35 | |
| Pe [Kw] | −1.12 | −2.99 | −4.90 | −5.64 | −12.08 | −15.44 | |
| GSA [32] | (θon, θoff) | (17.0, 26.0) | (16.0, 27.7) | (16.0, 29.0) | (18.0, 30.0) | (17.0, 34.0) | (19.0, 34.6) |
| Eff [%] | 73.05 | 60.55 | 52.88 | 51.66 | 49.07 | 55.71 | |
| Pe [Kw] | −1.03 | −2.84 | −4.76 | −5.59 | −11.43 | −14.68 | |
| PSO [32] | (θon, θoff) | (18.0, 26.2) | (17.0, 27.9) | (17.0, 29.3) | (19.0, 30.3) | (19.0, 35.0) | (20.0, 35.0) |
| Eff [%] | 75.17 | 61.40 | 53.33 | 52 | 51 | 57.91 | |
| Pe [Kw] | −1.06 | −2.88 | −4.80 | −5.62 | −11.88 | −15.26 | |
| MEPT [31] | (θon, θoff) | (19.0, 26.4) | (18.0, 28.1) | (19.0, 29.8) | (20.0, 30.5) | (20.0, 30.5) | (21.0, 35.6) |
| Eff [%] | 76.59 | 62.26 | 53.88 | 52.03 | 51.86 | 57.57 | |
| Pe [Kw] | −1.08 | −2.92 | −4.85 | −5.63 | −12.08 | −15.17 | |
| Standard operating angles | (θon, θoff) | (20.0, 30.0) | (20.0, 30.0) | (20.0, 30.0) | (20.0, 30.0) | (20.0, 30.0) | (20.0, 30.0) |
| Eff [%] | 74.46 | 52.66 | 49.44 | 52.21 | 51 | 54.15 | |
| Pe [Kw] | −1.05 | −2.47 | −4.45 | −5.65 | −11.88 | −14.27 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zine, M.; Labiod, C.; Ikhlef, M.; Srairi, K.; Benbouzid, M. Improving Efficiency and Power Output of Switched Reluctance Generators through Optimum Operating Parameters. Machines 2023, 11, 816. https://doi.org/10.3390/machines11080816
Zine M, Labiod C, Ikhlef M, Srairi K, Benbouzid M. Improving Efficiency and Power Output of Switched Reluctance Generators through Optimum Operating Parameters. Machines. 2023; 11(8):816. https://doi.org/10.3390/machines11080816
Chicago/Turabian StyleZine, Mahmoud, Chouaib Labiod, Malika Ikhlef, Kamel Srairi, and Mohamed Benbouzid. 2023. "Improving Efficiency and Power Output of Switched Reluctance Generators through Optimum Operating Parameters" Machines 11, no. 8: 816. https://doi.org/10.3390/machines11080816
APA StyleZine, M., Labiod, C., Ikhlef, M., Srairi, K., & Benbouzid, M. (2023). Improving Efficiency and Power Output of Switched Reluctance Generators through Optimum Operating Parameters. Machines, 11(8), 816. https://doi.org/10.3390/machines11080816








