The Differential Entropy Generation Rate as a Unified Measure for Both the Stability and Efficiency of an Axial Compressor
Abstract
1. Introduction
2. Grid Independence Verification and Numerical Simulation Method Validation
2.1. Model and Grid Independence Verification
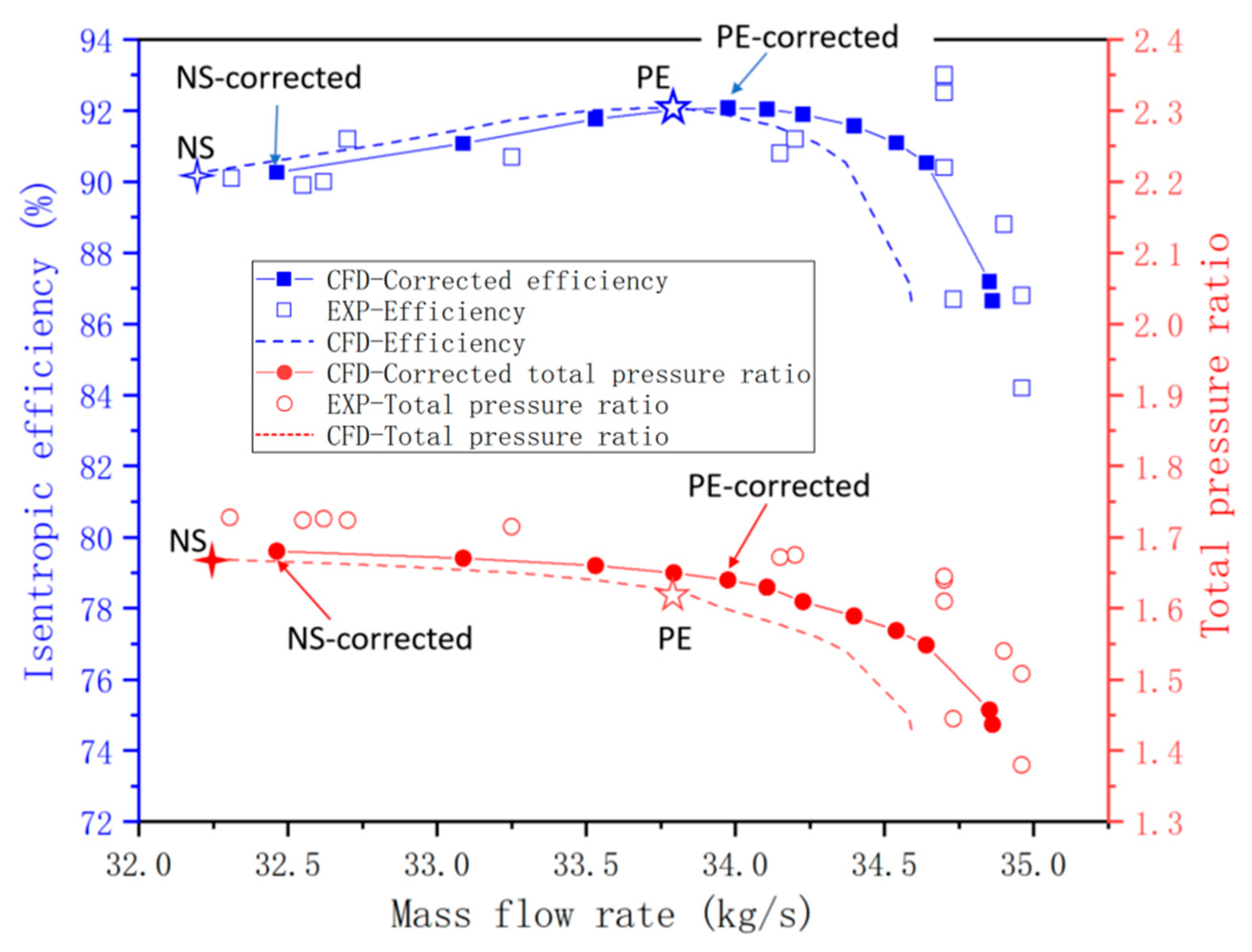
2.2. Validation of Numerical Simulation Method
3. Results and Discussions
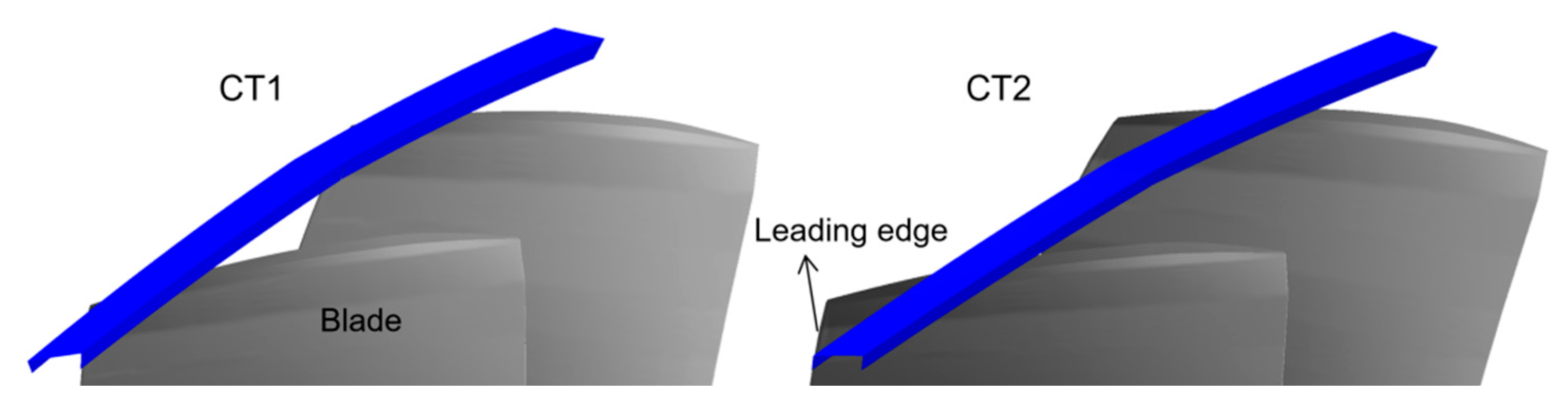
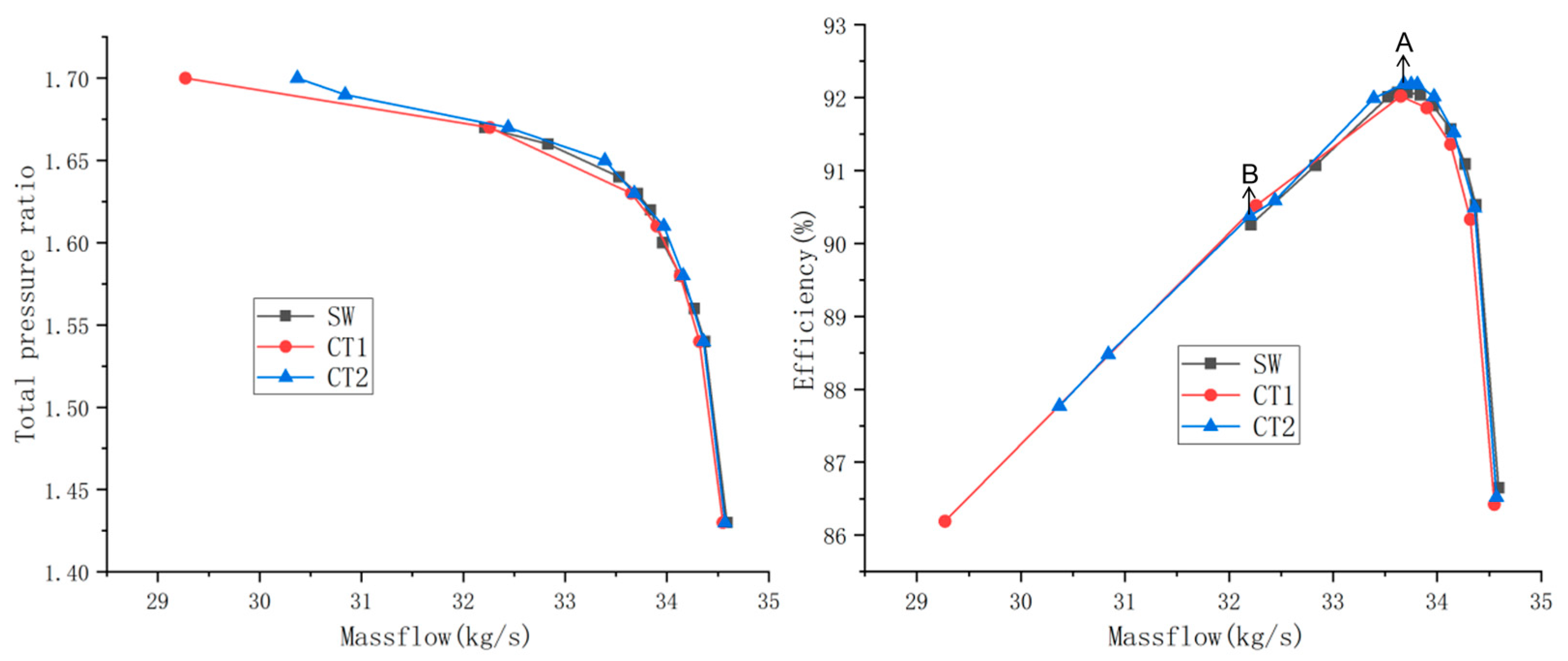
3.1. Casing Treatment Configuration and Comparison with a Solid Wall
3.2. Correlation between Entropy Generation and Peak Efficiency
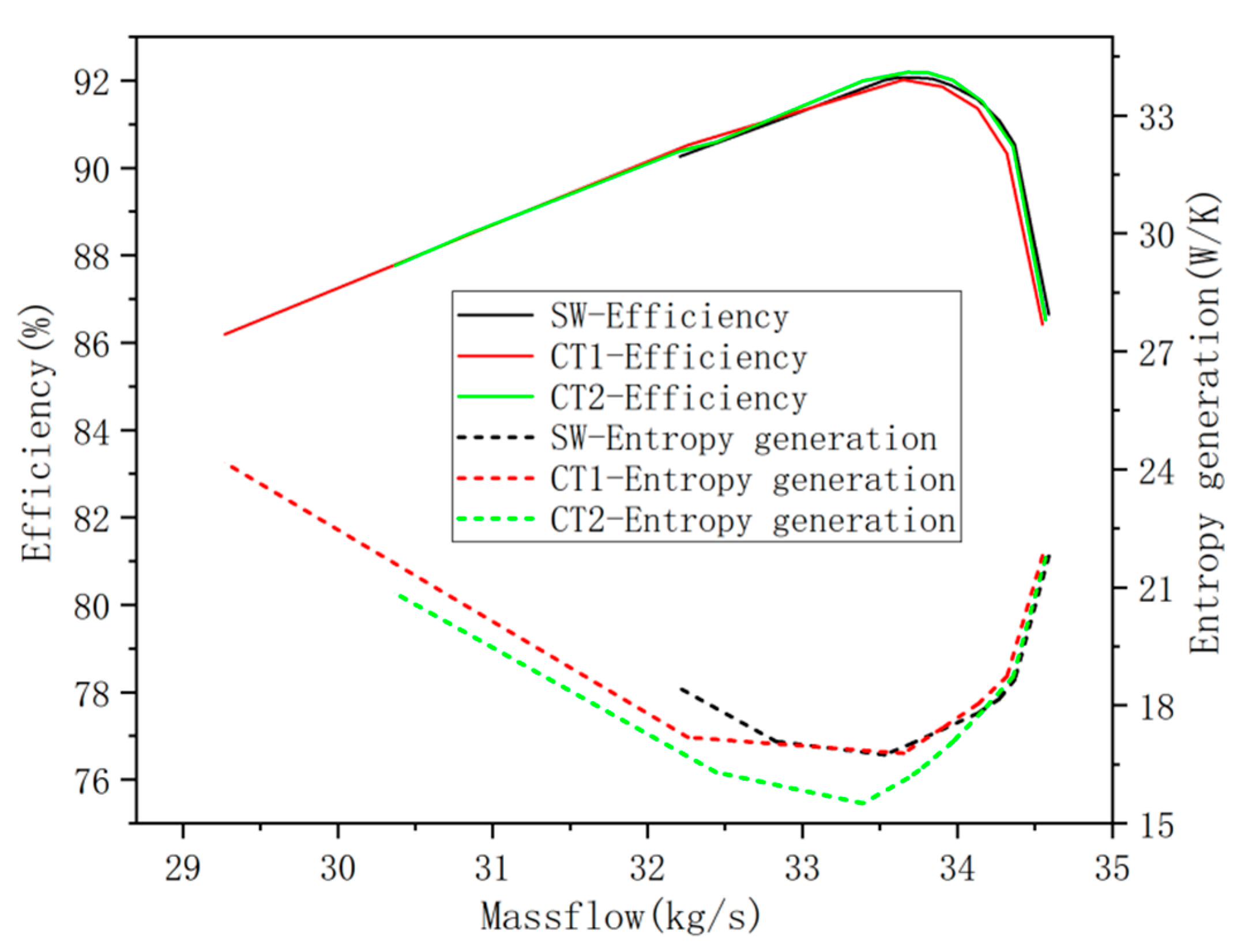
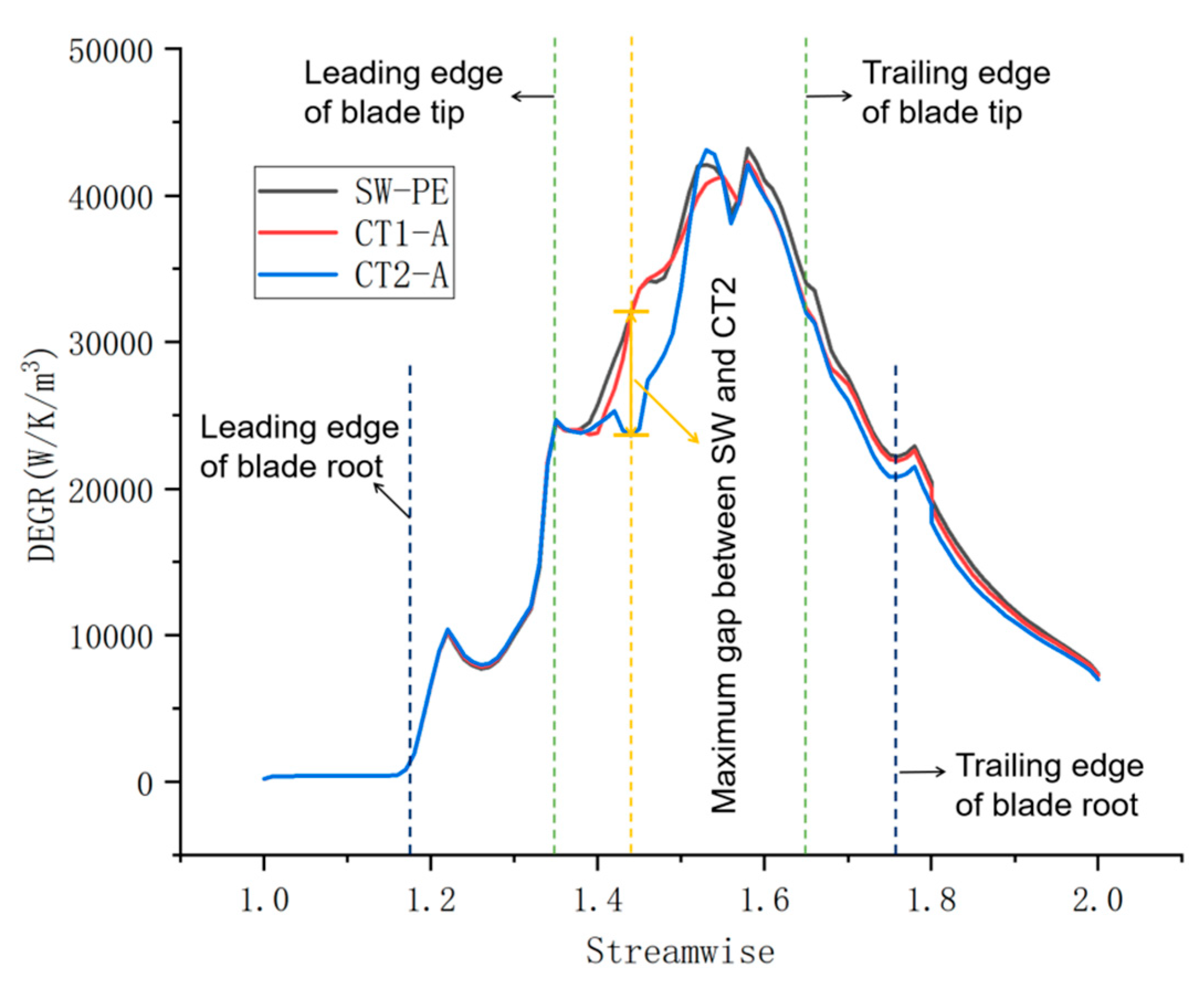
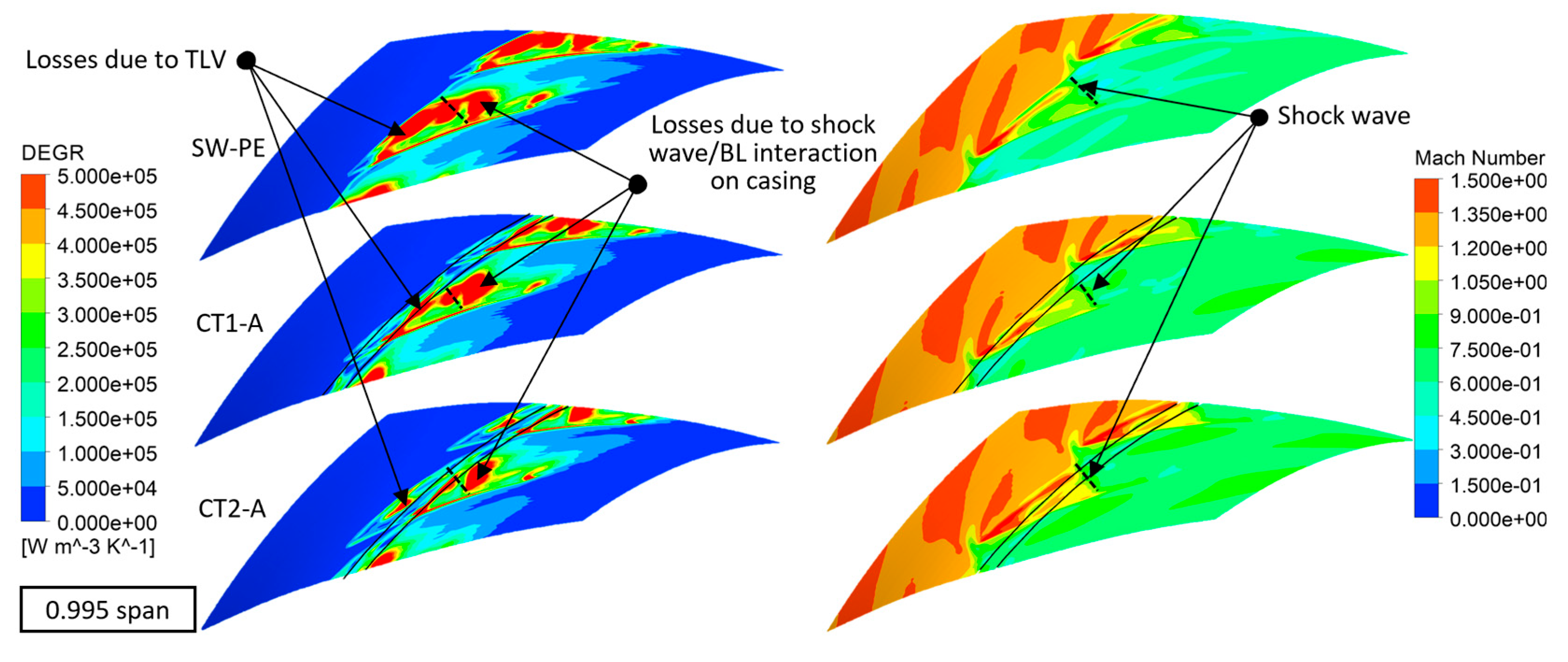
3.2.1. Correlation of Efficiency and DEGR and its Flow Mechanism
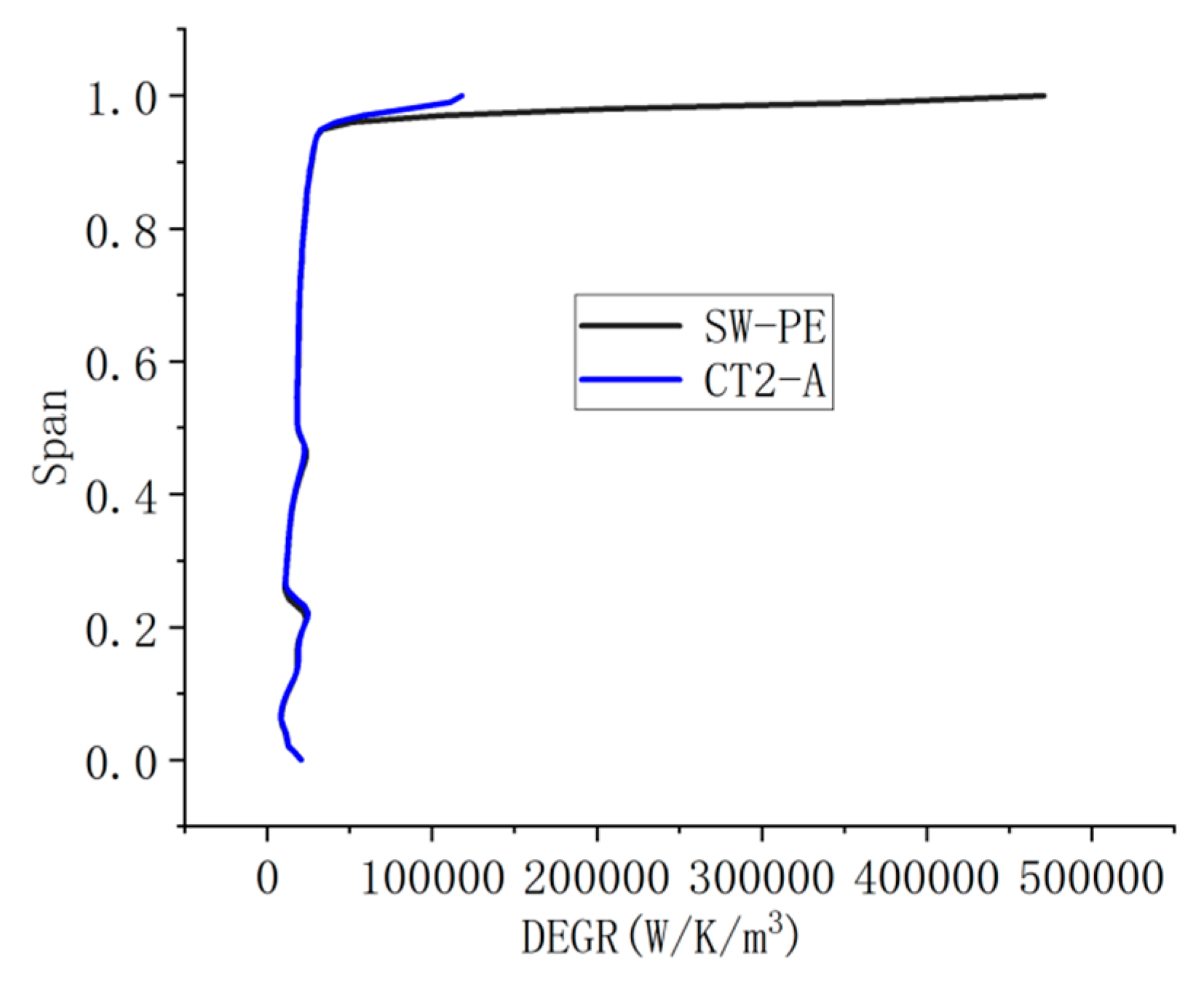
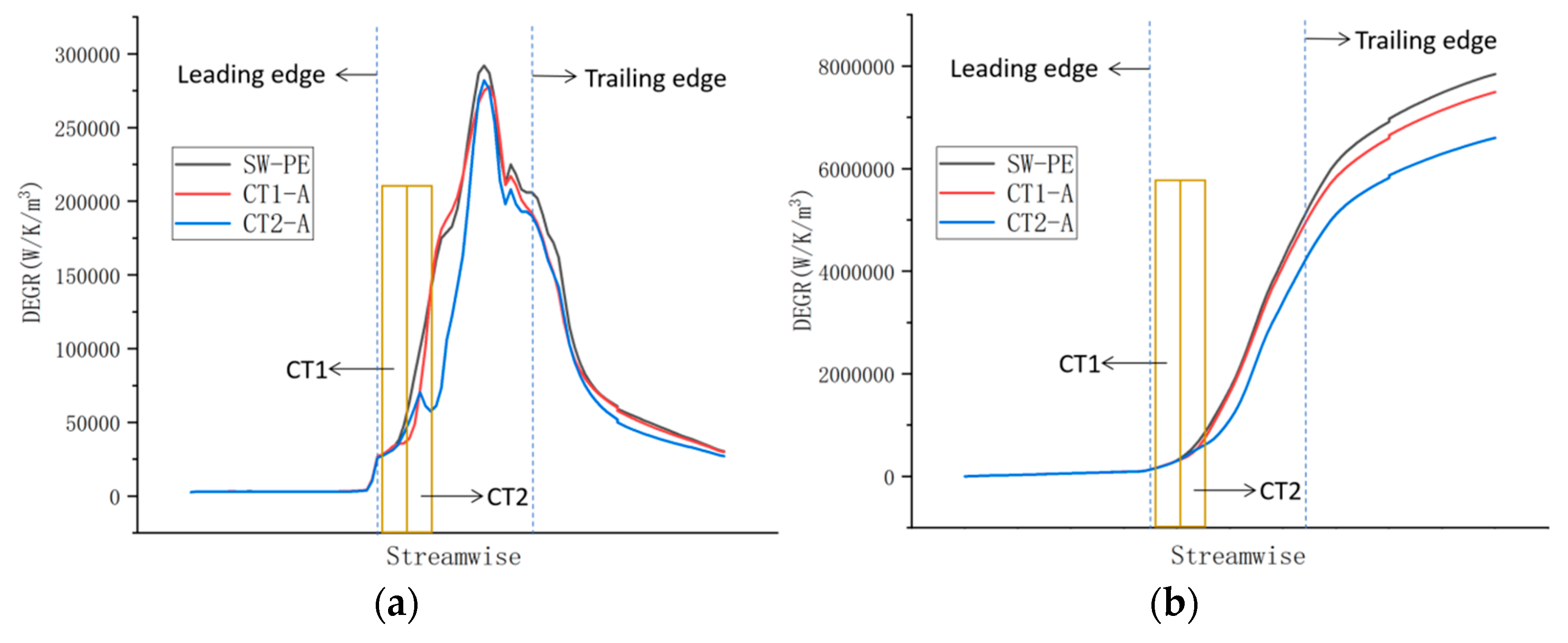
3.2.2. The Metric of the CTs Efficiency Change by DEGR
3.3. Correlation between the DEGR and the Stability
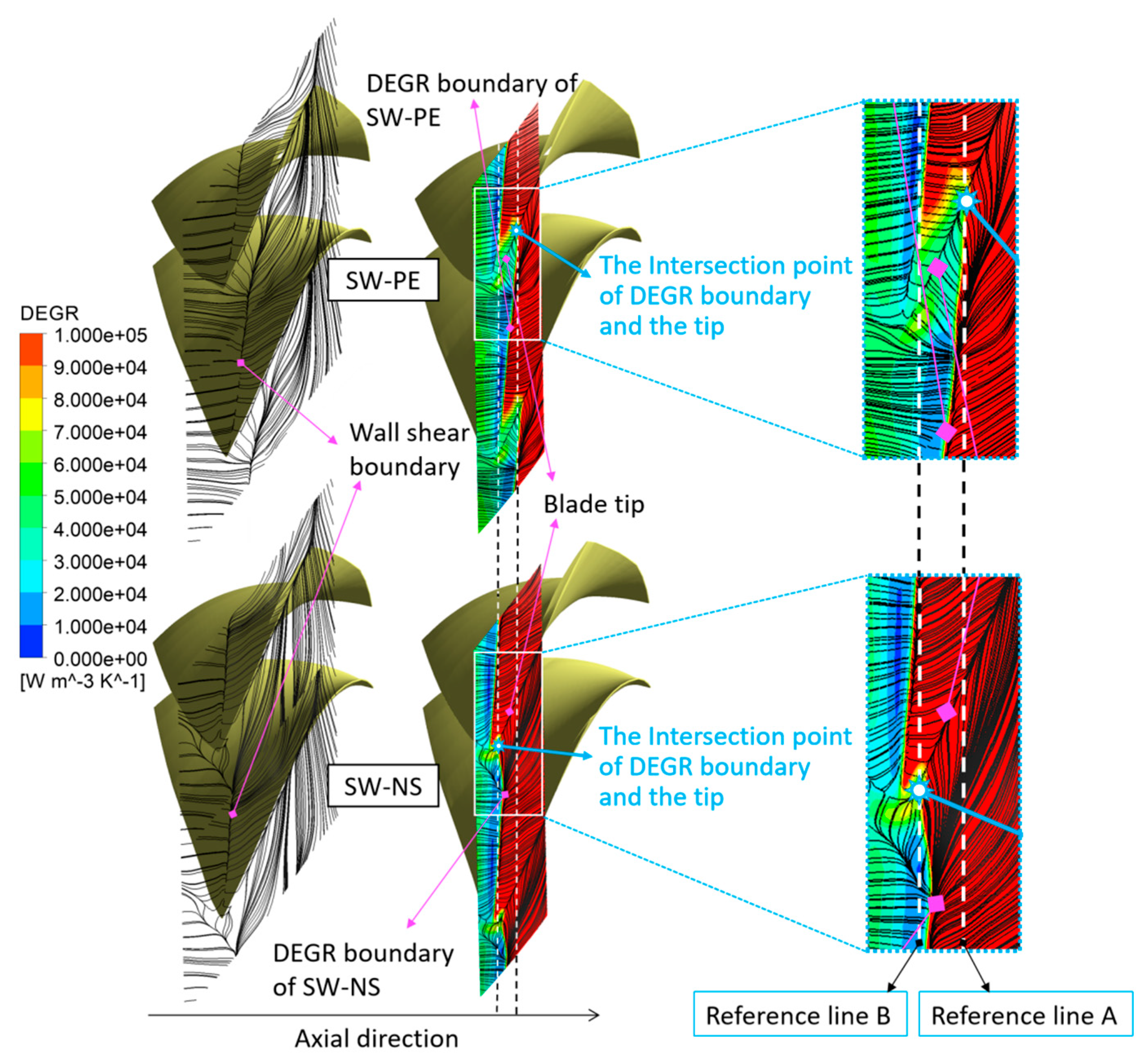
3.3.1. Connection between DEGR and the MF/LF Interface at the near Stall
3.3.2. The Metric of the CTs Stability Enhancement by DEGR
3.3.3. Flow Mechanism between the DEGR and Stability Enhancement
4. Conclusions
- (1)
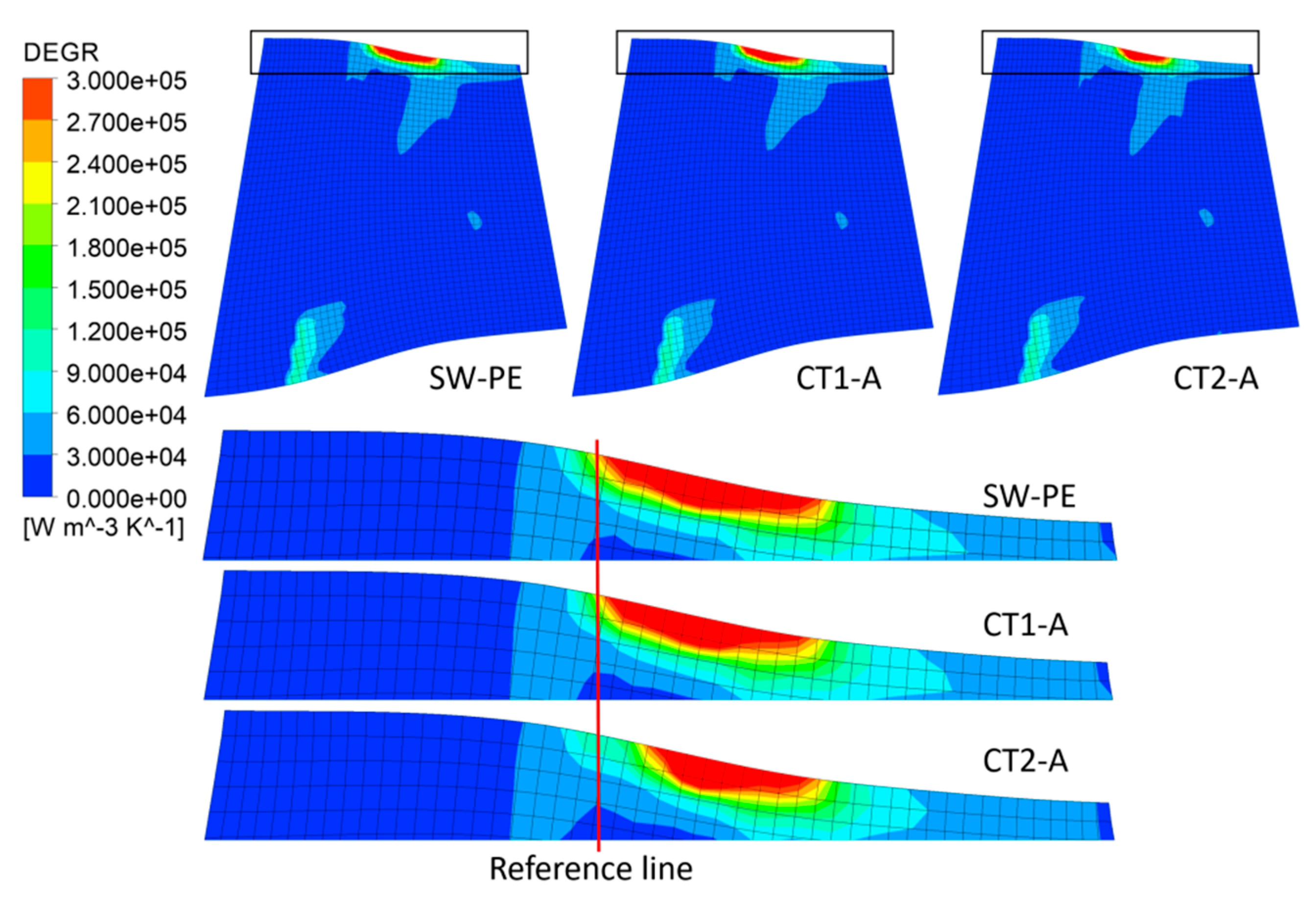
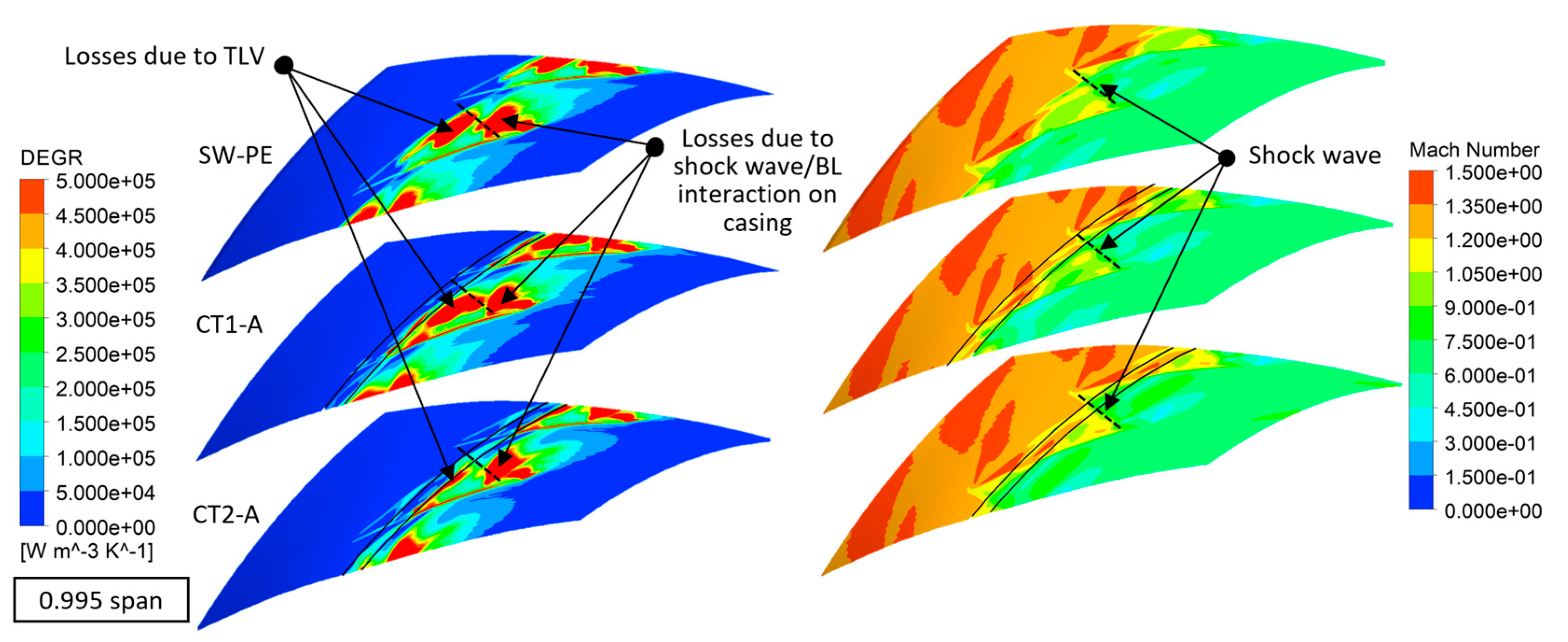
- The total entropy generation shows a reversed trend to isentropic efficiency as mass flow varies. In the PE operating condition, high DEGR regions are primarily concentrated near the blade tip. The influence of CTs on DEGR is also focused around the blade tip. CTs can enhance efficiency by suppressing the highest DEGR generated by complex flows around the blade tip.
- (2)
- The DEGR boundary aligns completely with the wall shear boundary at the near stall, which means that the DEGR boundary can represent the MF/LF interface. At the near stall, high DEGR regions are mainly concentrated near the blade tip, and the influence of CTs on DEGR is also focused around the blade tip. CTs can narrow down the range of high DEGR and push the DEGR boundary downstream. The flow mechanism shows that the CTs inhibit the TLV turning toward to the leading edge. In other words, CTs suppress the interface of MF/LF moving upstream, thereby delaying the onset of stall.
- (3)
- The method of how to utilize the DEGR to measure the efficiency and stability enhancement of CTs are proposed. Volumes within the 0.95–1 span were chosen for averaging the DEGR. The cumulative distribution of the DEGR along the axial direction provides a measure for efficiency improvement ability of CTs. The location of the DEGR along the axial direction provides a measure for the stability enhancement ability of CTs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Thermal diffusivity, (m2/s) | |
| t | Thermal diffusivity of the fluctuating temperature, (m2/s) |
| Dimensionless temperature, K | |
| Thermal conductivity, J s−1 m−1 K−1 | |
| Dynamic viscosity, kg m−1 s−1 | |
| Entropy production term, (WK/m3) | |
| Characteristic frequency, MHz | |
| Rotation speed, rpm | |
| Local pressure, N m−2 | |
| Entropy production rate by turbulent dissipation, (W/(m3 K)) | |
| Entropy production rate by viscous dissipation, (W/(m3 K)) | |
| Entropy production rate by heat transfer with gradients of the fluctuating temperature, (W/(m3 K)) | |
| Entropy production rate by heat transfer with mean temperature gradients, (W/(m3 K)) | |
| Bulk temperature, K | |
| u’ v’ w’ | Local fluctuating velocity component, m s−1 |
| Local average velocity component, m s−1 | |
| x y z | Coordinate vector component, m |
Abbreviations
| CT | Casing treatment |
| CT-A | Casing treatment’s A operating condition |
| CT-B | Casing treatment’s B operating condition |
| TLV | Tip leakage vortex |
| DEGR | Differential entropy generation rate |
| Solid wall | |
| EXP | Experimental data |
| NS | Near stall |
| NS-corrected | Corrected near stall |
| PE | Peak efficiency |
| PE-corrected | Corrected peak efficiency |
| R67 | NASA Rotor 67 |
| BL | Boundary leakage |
| MF/LF | Main flow/leakage flow |
| Subscripts | |
| gen | Generation rate |
| Turbulent dissipation | |
| Viscous dissipation | |
| Heat transfer with gradients of the fluctuating temperature | |
| Heat transfer with mean temperature gradients | |
| Reversible | |
| t | Relative total |
References
- Maher, N.H.; Ross, M.H.; Morris, S.C.; Priebe, S.; Jothiprasad, G.; Allan, D.; McNulty, G.; Macrorie, M.; Mallina, R. Experimental and computational investigation of an advanced casing treatment in a single-stage high-speed compressor. J. Turbomach. 2023, 145, 071003. [Google Scholar] [CrossRef]
- Yoon, S.; Cargill, P. Casing treatment: Its potential and limitations. J. Turbomach. 2023, 145, 041011. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mao, X.C.; Gao, L.M. Numerical investigation on the cross-stage self-recirculating casing treatment for a counter-rotating axial compressor. Aerosp. Sci. Technol. 2023, 135, 108161. [Google Scholar] [CrossRef]
- Hah, C. Stall margin improvement in a transonic compressor with a casing treatment: Flow mechanism. J. Turbomach. 2023, 145, 041004. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wang, H.; Dong, F.Y.; Jing, F.Y.; Chu, W.L. Mechanism study on the effect of self-circulating casing treatment with different circumferential coverage ratios on the axial compressor stability. Phys. Fluids 2023, 35, 056112. [Google Scholar]
- Lu, B.X.; Teng, J.F.; Zhu, M.M.; Qiang, X.Q. Design optimization of a transonic compressor blade with sweep and lean integrated with axial slot casing treatment. Aerosp. Sci. Technol. 2023, 136, 108225. [Google Scholar] [CrossRef]
- Zhang, H.G.; Chu, W.L.; Wu, Y.H.; Su, Z.L. Investigation of the flow mechanisms of affecting compressor performance with axial skewed slots casing treatment. Aerosp. Sci. Technol. 2010, 31, 555–561. [Google Scholar]
- Nan, X.; Ma, N.; Li, J.C.; Liu, L.; Lin, F. Evaluation of the effectiveness of typical casing treatments for a low-speed compressor by an integral method. Aerosp. Sci. Technol. 2016, 52, 234–242. [Google Scholar] [CrossRef]
- Nan, X.; Ma, N.; Lin, F.; Himeno, T.; Watanabe, T. A new approach of casing treatment design for high speed compressors running at partial speeds with low speed large scale test. Aerosp. Sci. Technol. 2018, 72, 104–113. [Google Scholar] [CrossRef]
- Liu, L.; Li, J.C.; Lin, F. The stall inceptions in an axial compressor with single circumferential groove casing treatment at different axial locations. Aerosp. Sci. Technol. 2016, 59, 145–154. [Google Scholar] [CrossRef]
- Du, J.; Gao, L.P.; Li, J.C.; Lin, F.; Chen, J.Y. Initial selection of groove location combination for multi-groove casing treatments. J. Mech. Sci. Technol. 2016, 30, 697–704. [Google Scholar] [CrossRef]
- Liu, L.; Nan, X.; Lin, F. Flow measurements near the open surfaces of single circumferential grooves in a low-speed axial compressor. Aerosp. Sci. Technol. 2018, 78, 531–541. [Google Scholar] [CrossRef]
- Fan, L.; Ning, F.F.; Liu, H.X. Quasi-steady flow model of slot-type casing treatments II: Design optimization of casing treatment for a transonic rotor. J. Aerosp. Power 2012, 27, 1278–1287. [Google Scholar]
- Wang, W.; Zhang, X.; Lu, J.L.; Luo, X.Q.; Chu, W.L. Coupling Method and Mechanism of stability enhancement for endwall stall in axial flow compressor. J. Propuls. Technol. 2020, 41, 544–552. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy generation in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Herwig, H.; Schmandt, B. How to determine losses in a flow field: A paradigm shift towards the second law analysis. J. Entropy 2014, 16, 2959–2989. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Losses due to conduit components: An optimization strategy and its application. J. Fluids Engineering 2016, 138, 031204. [Google Scholar] [CrossRef]
- Jin, Y.; Du, J.; Li, Z.Y.; Zhang, H.W. Second-law analysis of irreversible losses in gas turbines. J. Entropy 2017, 19, 470. [Google Scholar] [CrossRef]
- Geng, L.P.; Jin, Y.; Herwig, H. Can pulsation unsteadiness increase the convective heat transfer in a pipe flow? A systematic study. J. Numer. Heat Transf. Part B Fundam. 2020, 78, 160–174. [Google Scholar] [CrossRef]
- Li, Z.Y.; Du, J.; Jemcov, A.; Ottavy, X.; Lin, F. A study of loss mechanism in a linear compressor cascade at the corner stall condition. In Proceedings of the ASME Turbo Expo 2017: Turbine Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Zhang, Q.F.; Du, J.; Li, Z.H.; Li, J.C.; Zhang, H.W. Entropy generation analysis in a mixed-flow compressor with casing treatment. J. Therm. Sci. 2019, 28, 915–928. [Google Scholar] [CrossRef]
- Ma, J.Y.; Lin, F. Loss Analysis of a transonic rotor with a differential approach to entropy generation. Machines 2023, 11, 472. [Google Scholar] [CrossRef]
- Vo, H.D.; Tan, C.S.; Greitzer, E.M. Criteria for spike initiated rotating stall. J. Turbomach. 2008, 130, 011023. [Google Scholar] [CrossRef]
- Furukawa, M.; Inoue, M.; Saike, K.; Yamada, K. The role of tip leakage vortex breakdown in compressor rotor aerodynamics. J. Turbomach. 1999, 121, 469–480. [Google Scholar] [CrossRef]
- Yamada, K.; Funazaki, K.; Furukawa, M. The behavior of tip clearance flow at near-stall condition in a transonic axial compressor rotor. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea and Air, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Hah, C.; Rabe, D.C.; Wadia, A.R. Role of tip-leakage vortices and passage shock in stall inception in a swept transonic compressor rotor. In Proceedings of the ASME Turbo Expo 2004 Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Lin, F.; Zhang, J.X.; Chen, J.Y.; Nie, C.Q. Flow structure of short-length-scale disturbance in an axial-flow compressor. J. Propuls. Power 2008, 24, 1301–1308. [Google Scholar] [CrossRef]
- Strazisar, A.J.; Wood, J.R.; Hathaway, M.D.; Suder, K.L. Laser Anemometer Measurements in a Transonic Axial-Flow Fan Rotor; NASA Technical Paper; NASA: Washington, DC, USA, 1989; p. 2879. [Google Scholar]
- Bennington, M.A.; Ross, M.H.; Cameron, J.D.; Morris, S.C.; Du, J.; Lin, F.; Chen, J.Y. An experimental and computational investigation of tip clearance flow and its impact on stall inception. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Hou, J.X.; Liu, Y.W.; Zhong, L.Y.; Zhong, W.B.; Tang, Y.M. Effect of vorticity transport on flow structure in the tip region of axial compressors. Phys. Fluids 2022, 34, 055102. [Google Scholar] [CrossRef]
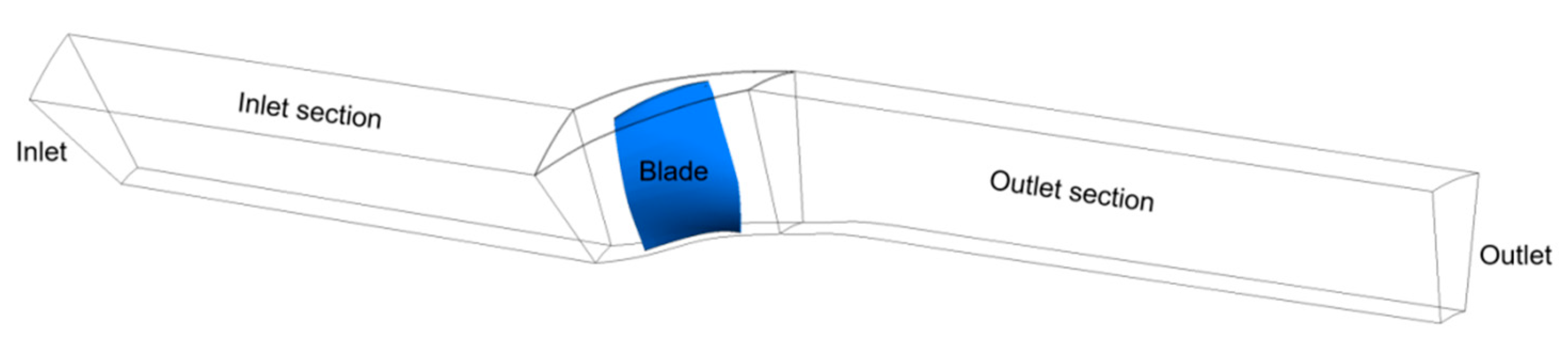
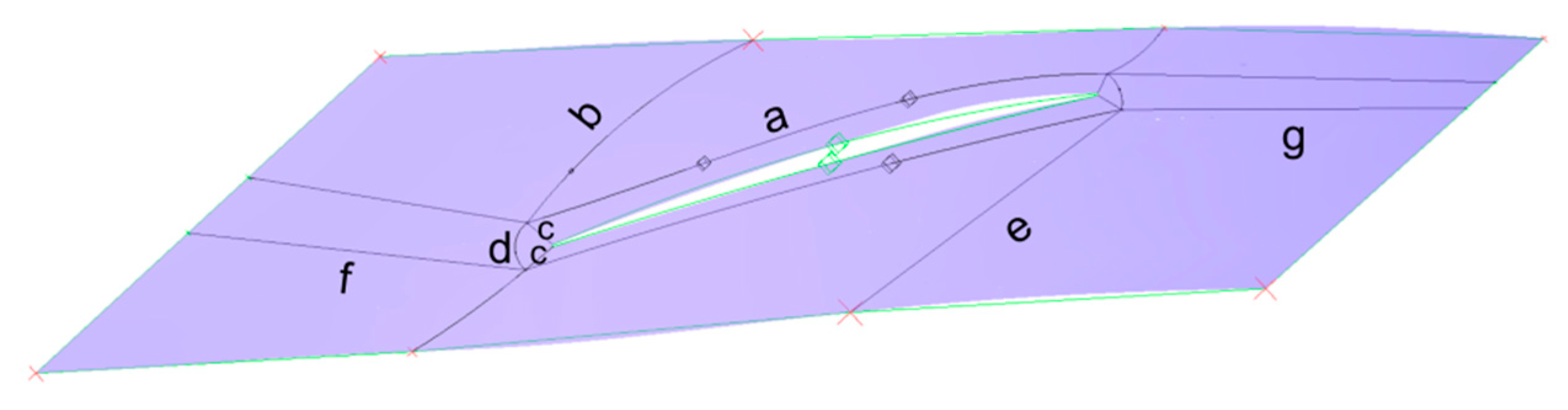
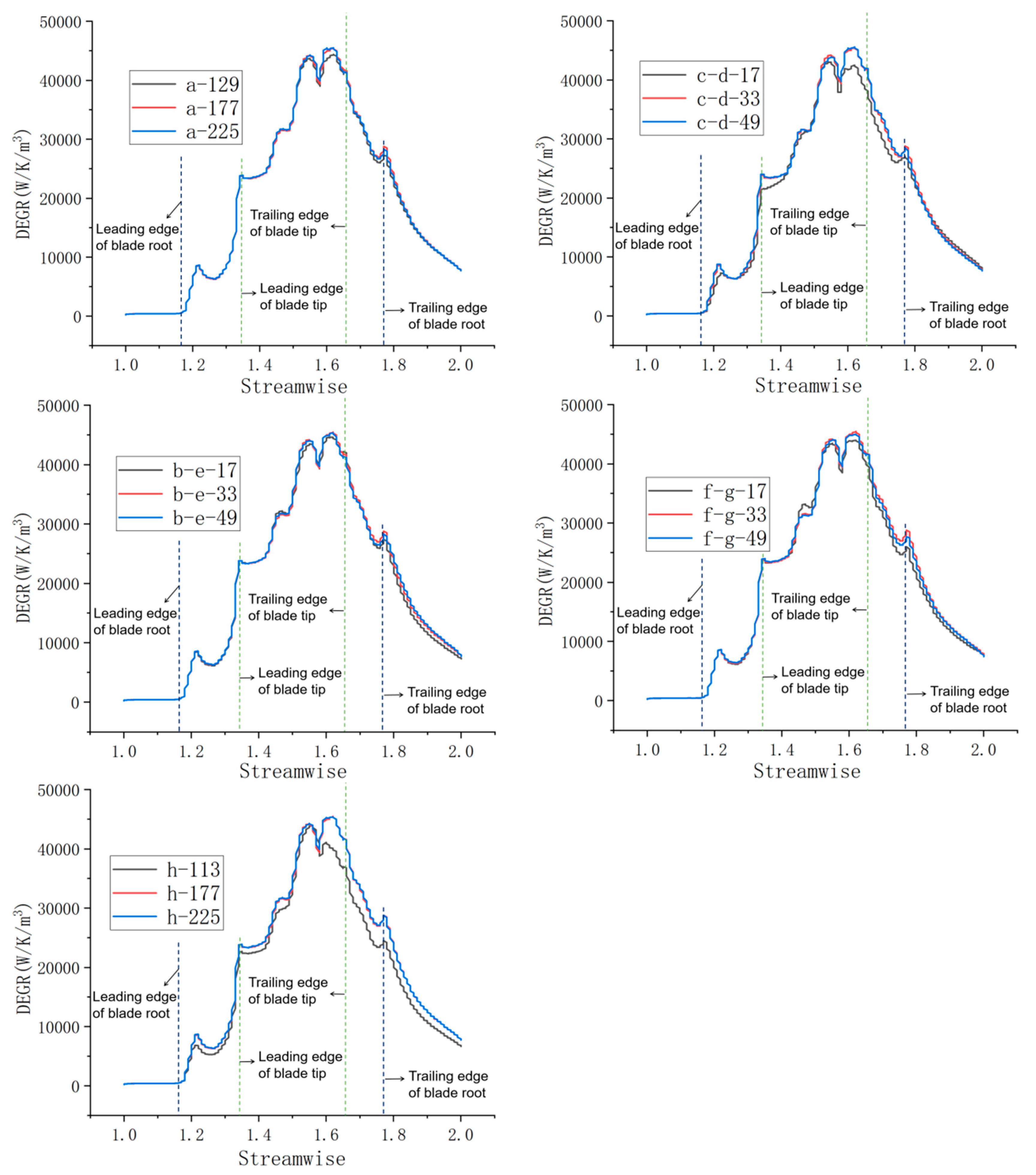



| a | Entropy Generation (W/K) | b and e | Entropy Generation (W/K) | c and d | Entropy Generation (W/K) | f and g | Entropy Generation (W/K) | h (Height) | Entropy Generation (W/K) |
|---|---|---|---|---|---|---|---|---|---|
| 129 | 17.54 | 17 | 16.21 | 17 | 17.07 | 17 | 17.25 | 113 | 16.21 |
| 177 | 17.79 | 33 | 17.79 | 33 | 17.79 | 33 | 17.79 | 177 | 17.79 |
| 225 | 17.78 | 49 | 17.85 | 49 | 17.81 | 49 | 17.67 | 225 | 17.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Lin, F. The Differential Entropy Generation Rate as a Unified Measure for Both the Stability and Efficiency of an Axial Compressor. Machines 2023, 11, 815. https://doi.org/10.3390/machines11080815
Ma J, Lin F. The Differential Entropy Generation Rate as a Unified Measure for Both the Stability and Efficiency of an Axial Compressor. Machines. 2023; 11(8):815. https://doi.org/10.3390/machines11080815
Chicago/Turabian StyleMa, Jingyuan, and Feng Lin. 2023. "The Differential Entropy Generation Rate as a Unified Measure for Both the Stability and Efficiency of an Axial Compressor" Machines 11, no. 8: 815. https://doi.org/10.3390/machines11080815
APA StyleMa, J., & Lin, F. (2023). The Differential Entropy Generation Rate as a Unified Measure for Both the Stability and Efficiency of an Axial Compressor. Machines, 11(8), 815. https://doi.org/10.3390/machines11080815





