Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert–Huang Transformation in Machining Stainless Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. Theoretical Foundations of VMD
2.1.2. VMD Parameter Selection Based on Grey Wolf Optimization Algorithm
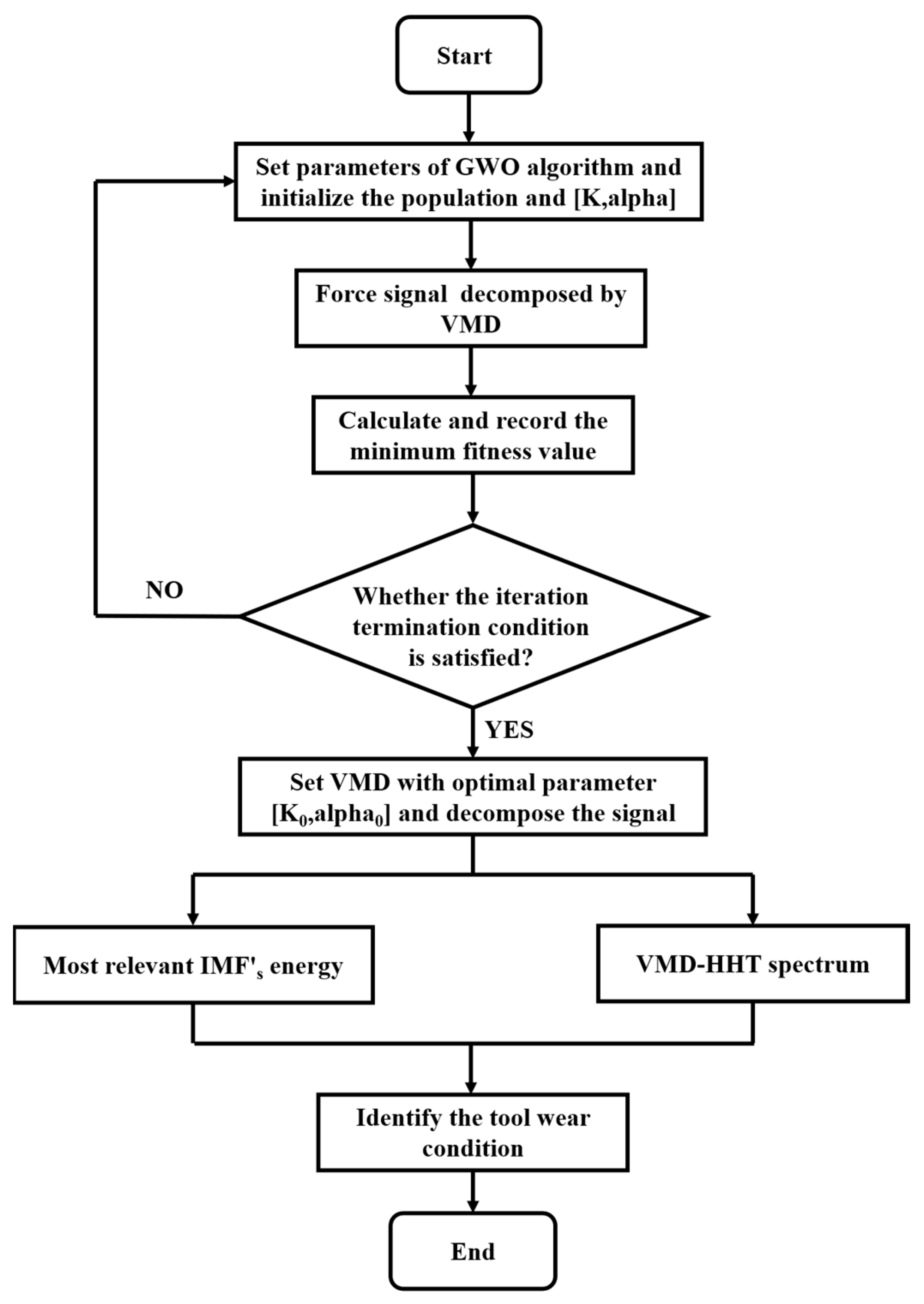
2.1.3. GWO Optimizes the VMD Parameter Flow
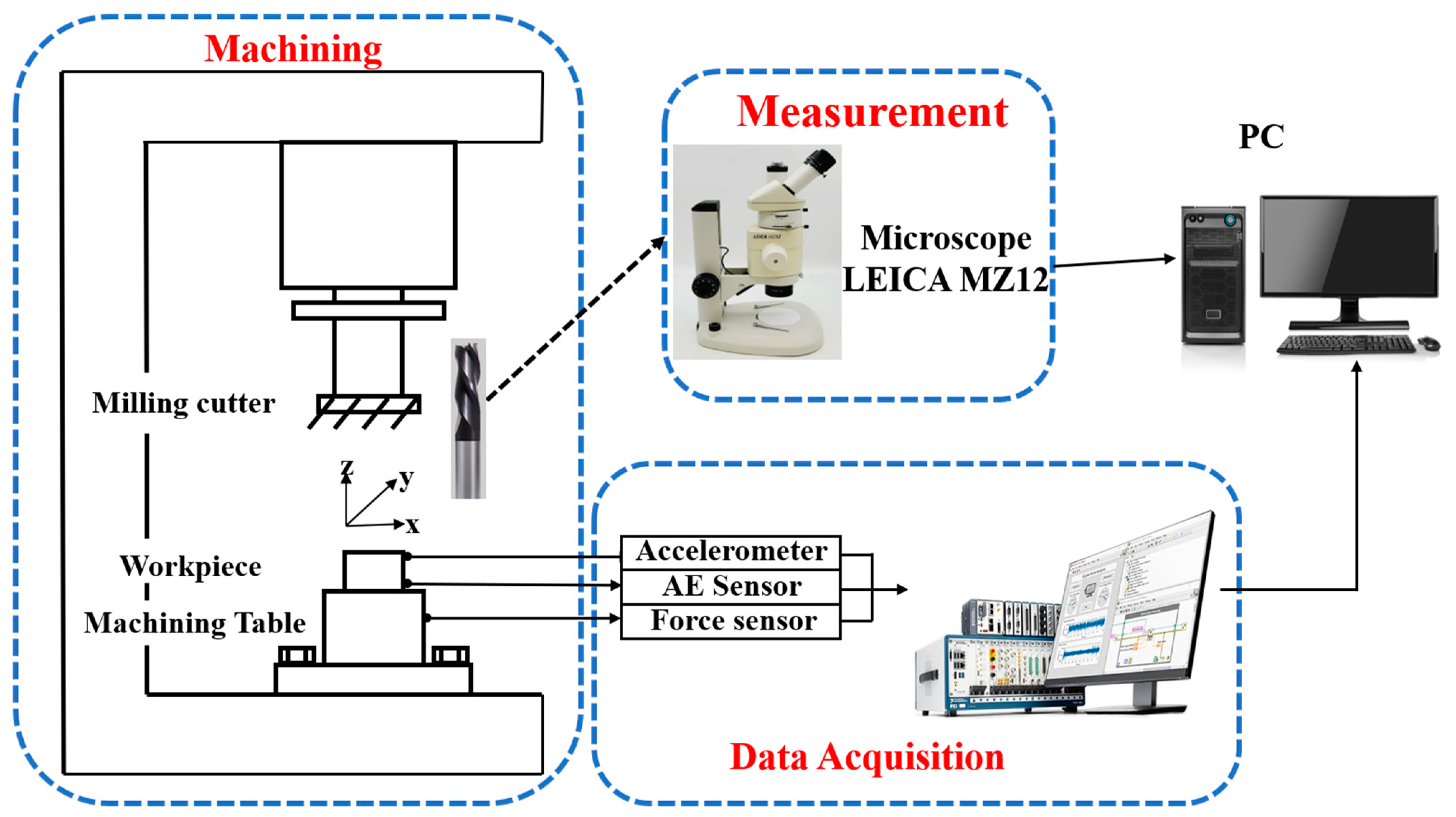
2.2. Materials and Experimental Description
3. Results
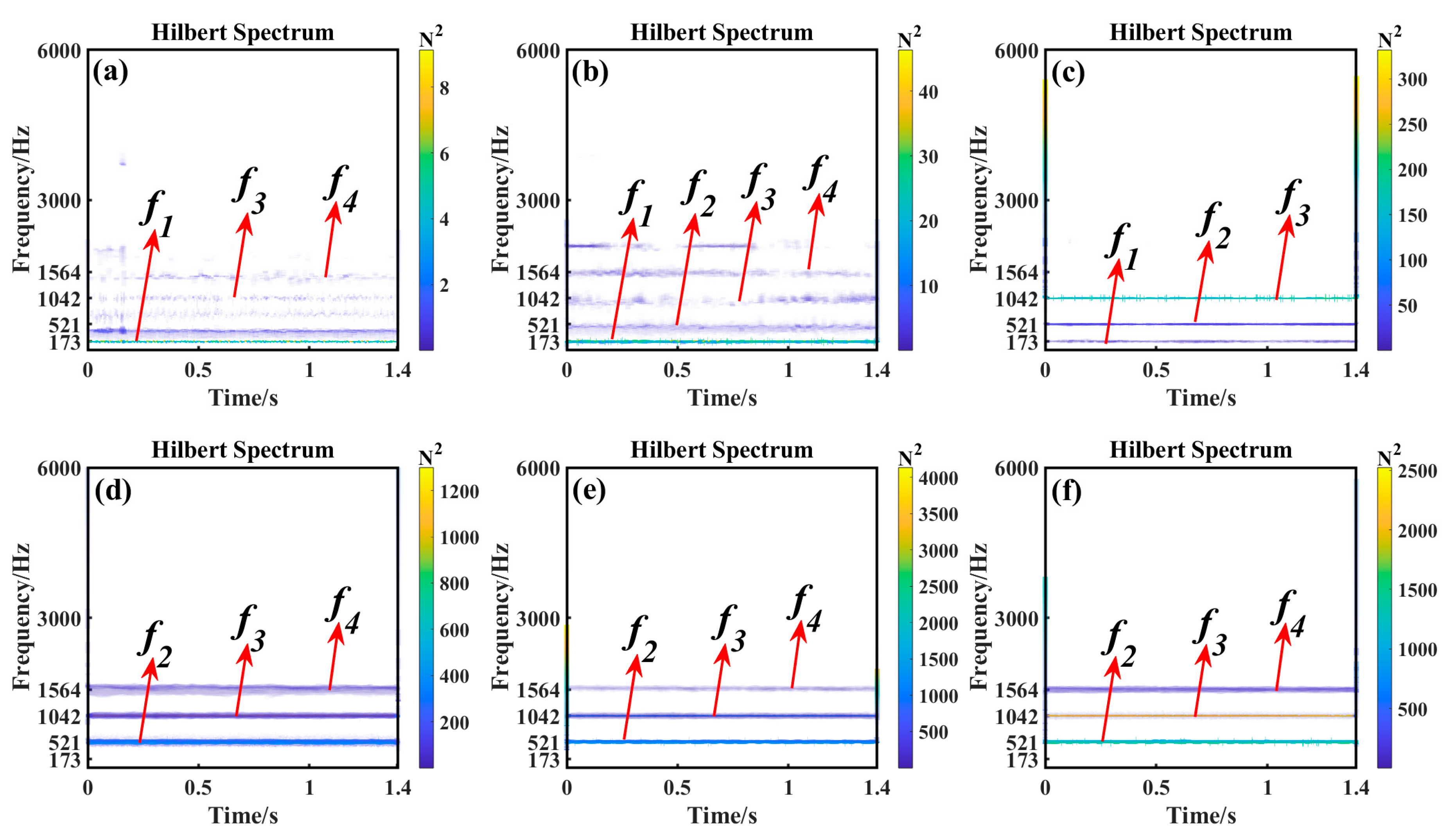
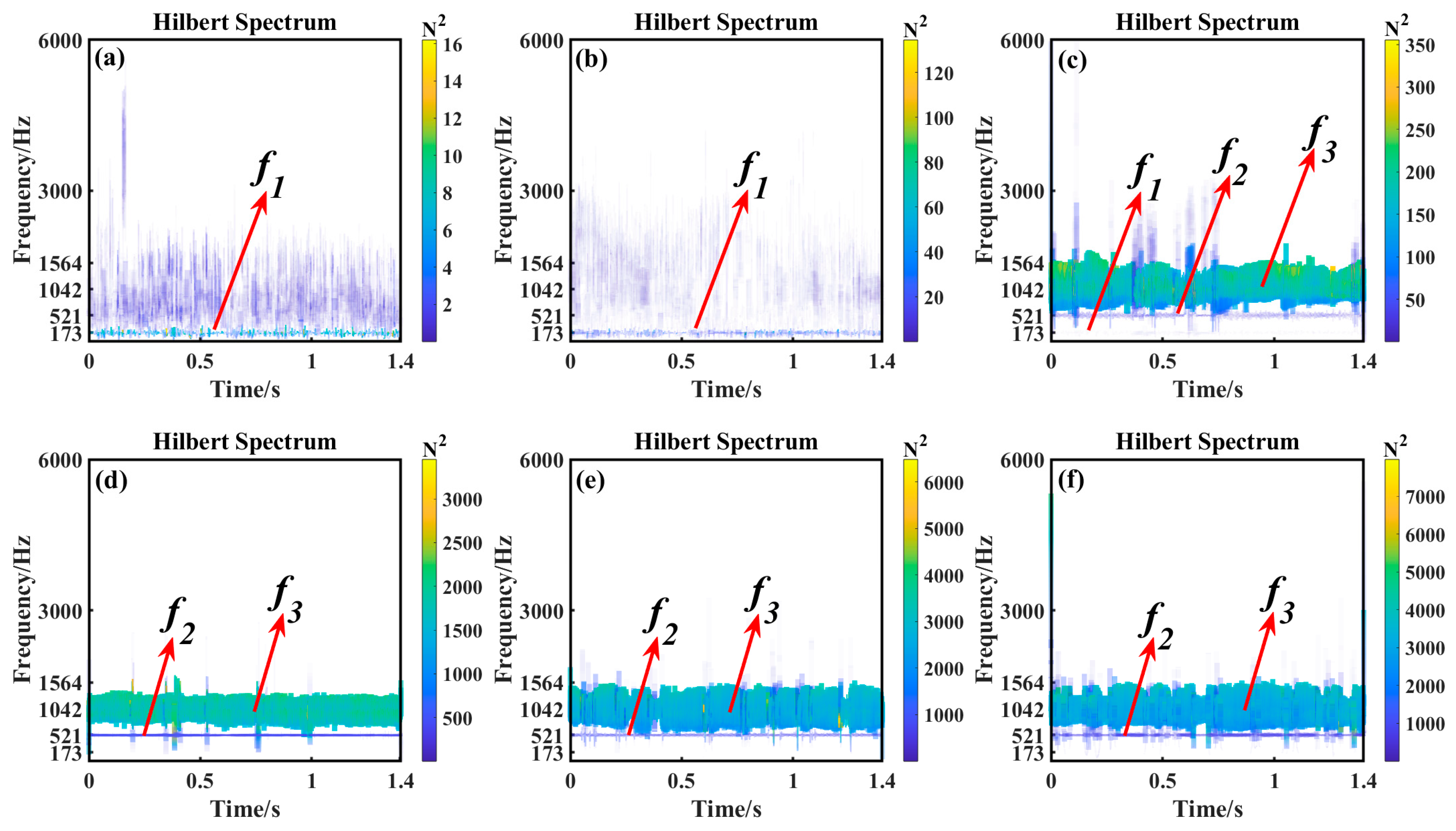
3.1. Simulation Signal Analysis
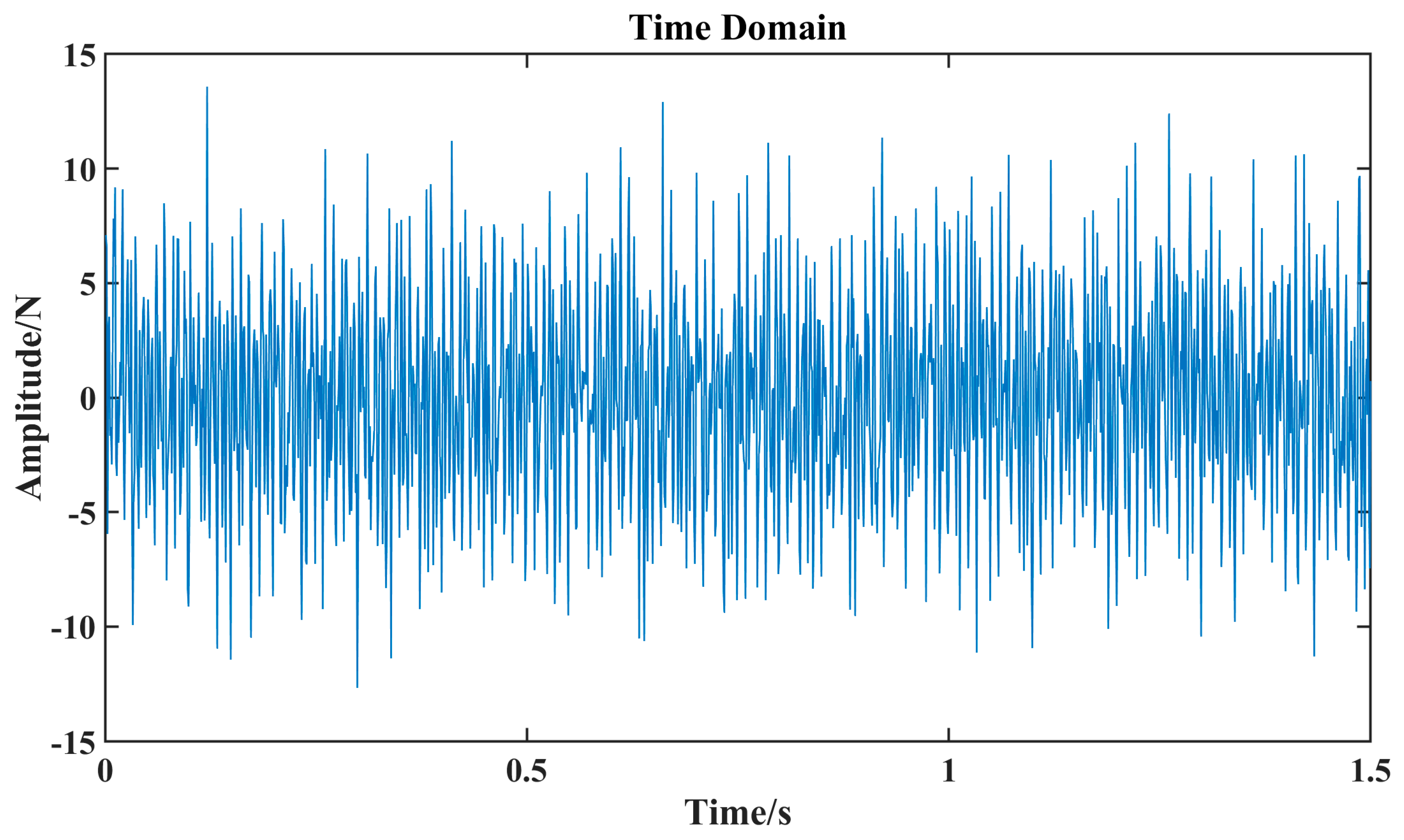
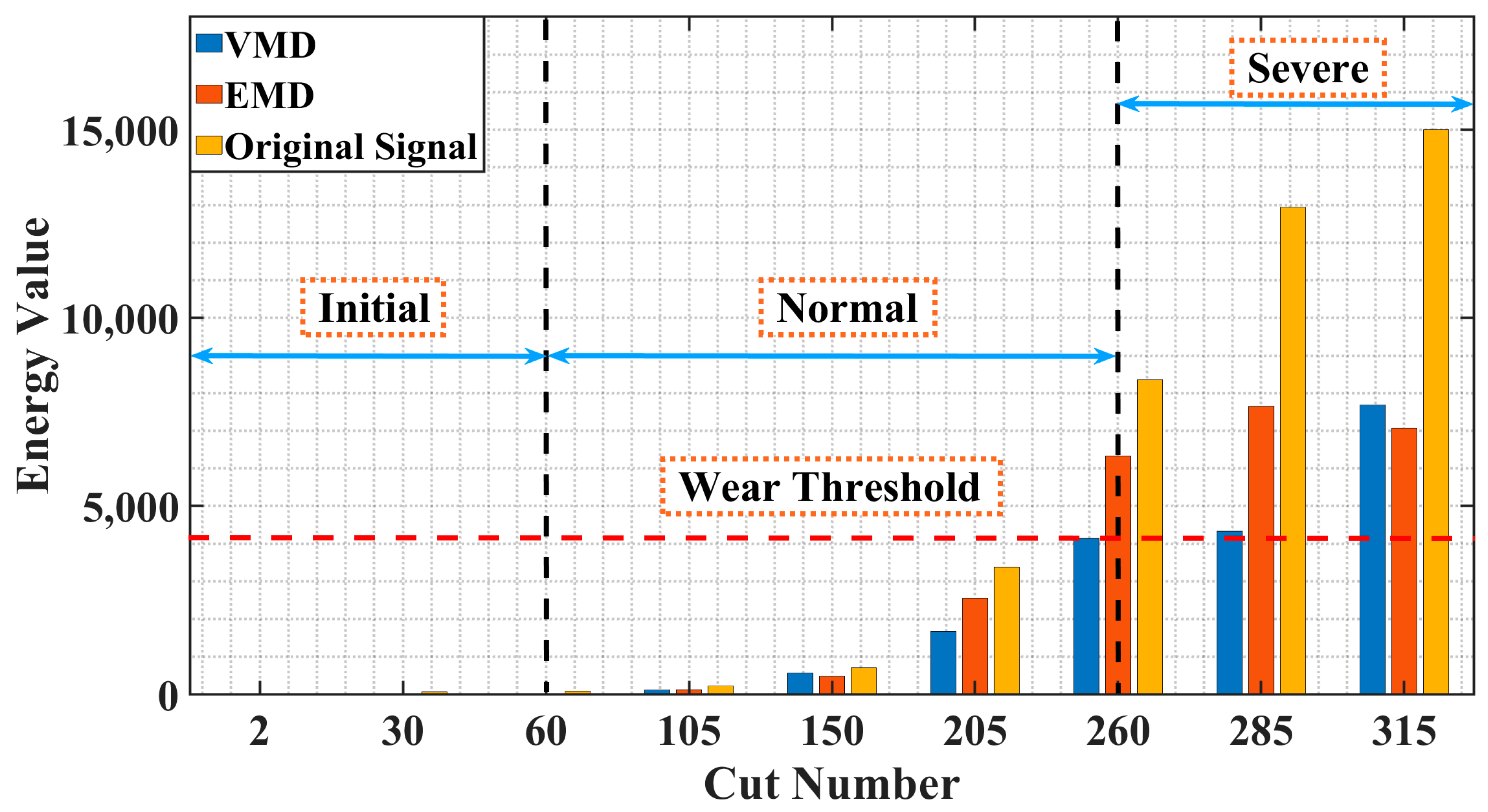
3.2. Force Signal Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Li, Y.; Hua, J.; Lu, N.; Mou, W. Real-time cutting tool state recognition approach based on machining features in NC machining process of complex structural parts. Int. J. Adv. Manuf. Technol. 2018, 97, 229–241. [Google Scholar] [CrossRef]
- Yi, S.; Li, G.; Ding, S.; Mo, J. Performance and mechanisms of graphene oxide suspended cutting fluid in the drilling of titanium alloy Ti-6Al-4V. J. Manuf. Process. 2017, 29, 182–193. [Google Scholar] [CrossRef]
- Li, G.; Munir, K.; Wen, C.; Li, Y.; Ding, S. Machinablility of titanium matrix composites (TMC) reinforced with multi-walled carbon nanotubes. J. Manuf. Process. 2020, 56, 131–146. [Google Scholar] [CrossRef]
- Li, G.; Yi, S.; Sun, S.; Ding, S. Wear mechanisms and performance of abrasively ground polycrystalline diamond tools of different diamond grains in machining titanium alloy. J. Manuf. Process. 2017, 29, 320–331. [Google Scholar] [CrossRef]
- Rahim, M.Z.; Li, G.; Ding, S.; Mo, J.; Brandt, M. Electrical discharge grinding versus abrasive grinding in polycrystalline diamond machining—Tool quality and performance analysis. Int. J. Adv. Manuf. Technol. 2015, 85, 263–277. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, D.; Wu, W.; Zou, K. Methods and Research for Multi-Component Cutting Force Sensing Devices and Approaches in Machining. Sensors 2016, 16, 1926. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, B.; Sun, W. A tool condition monitoring method based on two-layer angle kernel extreme learning machine and binary differential evolution for milling. Measurement 2020, 166, 108186. [Google Scholar] [CrossRef]
- Kong, D.; Chen, Y.; Li, N.; Duan, C.; Lu, L.; Chen, D. Relevance vector machine for tool wear prediction. Mech. Syst. Signal Process. 2019, 127, 573–594. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Y.; Huang, Z.; Chen, N.; Li, L.; Jiang, Y.; He, N. Research on the milling tool wear and life prediction by establishing an integrated predictive model. Measurement 2019, 145, 178–189. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, J.; Lei, J.; Li, X.; Tian, F. Tool wear predicting based on multi-domain feature fusion by deep convolutional neural network in milling operations. J. Intell. Manuf. 2019, 31, 953–966. [Google Scholar] [CrossRef]
- Antić, A.; Popović, B.; Krstanović, L.; Obradović, R.; Milošević, M. Novel texture-based descriptors for tool wear condition monitoring. Mech. Syst. Signal Process. 2018, 98, 1–15. [Google Scholar] [CrossRef]
- Rmili, W.; Ouahabi, A.; Serra, R.; Leroy, R. An automatic system based on vibratory analysis for cutting tool wear monitoring. Measurement 2016, 77, 117–123. [Google Scholar] [CrossRef]
- Wang, C.; Bao, Z.; Zhang, P.; Ming, W.; Chen, M. Tool wear evaluation under minimum quantity lubrication by clustering energy of acoustic emission burst signals. Measurement 2019, 138, 256–265. [Google Scholar] [CrossRef]
- Zhou, J.-H.; Pang, C.K.; Zhong, Z.-W.; Lewis, F.L. Tool Wear Monitoring Using Acoustic Emissions by Dominant-Feature Identification. IEEE Trans. Instrum. Meas. 2011, 60, 547–559. [Google Scholar] [CrossRef]
- Ren, Q.; Baron, L.; Balazinski, M.; Botez, R.; Bigras, P. Tool wear assessment based on type-2 fuzzy uncertainty estimation on acoustic emission. Appl. Soft Comput. 2015, 31, 14–24. [Google Scholar] [CrossRef]
- Saw, L.H.; Ho, L.W.; Yew, M.C.; Yusof, F.; Pambudi, N.A.; Ng, T.C.; Yew, M.K. Sensitivity analysis of drill wear and optimization using Adaptive Neuro fuzzy –genetic algorithm technique toward sustainable machining. J. Clean. Prod. 2018, 172, 3289–3298. [Google Scholar] [CrossRef]
- Bernini, L.; Albertelli, P.; Monno, M. Mill condition monitoring based on instantaneous identification of specific force coefficients under variable cutting conditions. Mech. Syst. Signal Process. 2023, 185, 109820. [Google Scholar] [CrossRef]
- Thirukkumaran, K.; Mukhopadhyay, C.K. Analysis of Acoustic Emission Signal to Characterization the Damage Mechanism During Drilling of Al-5%SiC Metal Matrix Composite. Silicon 2020, 13, 309–325. [Google Scholar] [CrossRef]
- del Olmo, A.; López de Lacalle, L.N.; Martínez de Pissón, G.; Pérez-Salinas, C.; Ealo, J.A.; Sastoque, L.; Fernandes, M.H. Tool wear monitoring of high-speed broaching process with carbide tools to reduce production errors. Mech. Syst. Signal Process. 2022, 172, 109003. [Google Scholar] [CrossRef]
- Gomes, M.C.; Brito, L.C.; Bacci da Silva, M.; Viana Duarte, M.A. Tool wear monitoring in micromilling using Support Vector Machine with vibration and sound sensors. Precis. Eng. 2021, 67, 137–151. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Jiang, H.; Wang, R.; Qiu, T.; Wang, X. Intelligent tool wear monitoring and multi-step prediction based on deep learning model. J. Manuf. Syst. 2022, 62, 286–300. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, K. A Switching Hidden Semi-Markov Model for Degradation Process and Its Application to Time-Varying Tool Wear Monitoring. IEEE Trans. Ind. Inform. 2021, 17, 2621–2631. [Google Scholar] [CrossRef]
- Kotsiopoulos, T.; Leontaris, L.; Dimitriou, N.; Ioannidis, D.; Oliveira, F.; Sacramento, J.; Amanatiadis, S.; Karagiannis, G.; Votis, K.; Tzovaras, D.; et al. Deep multi-sensorial data analysis for production monitoring in hard metal industry. Int. J. Adv. Manuf. Technol. 2020, 115, 823–836. [Google Scholar] [CrossRef]
- Papageorgiou, K.; Theodosiou, T.; Rapti, A.; Papageorgiou, E.I.; Dimitriou, N.; Tzovaras, D.; Margetis, G. A systematic review on machine learning methods for root cause analysis towards zero-defect manufacturing. Front. Manuf. Technol. 2022, 2, 972712. [Google Scholar] [CrossRef]
- Zhu, K.; Wong, Y.S.; Hong, G.S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results. Int. J. Mach. Tools Manuf. 2009, 49, 537–553. [Google Scholar] [CrossRef]
- Li, Z.; Liu, R.; Wu, D. Data-driven smart manufacturing: Tool wear monitoring with audio signals and machine learning. J. Manuf. Process. 2019, 48, 66–76. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, L.; Dun, Y. Tool wear monitoring of TC4 titanium alloy milling process based on multi-channel signal and time-dependent properties by using deep learning. J. Manuf. Syst. 2021, 61, 495–508. [Google Scholar] [CrossRef]
- Jauregui, J.C.; Resendiz, J.R.; Thenozhi, S.; Szalay, T.; Jacso, A.; Takacs, M. Frequency and Time-Frequency Analysis of Cutting Force and Vibration Signals for Tool Condition Monitoring. IEEE Access 2018, 6, 6400–6410. [Google Scholar] [CrossRef]
- Zhou, C.a.; Yang, B.; Guo, K.; Liu, J.; Sun, J.; Song, G.; Zhu, S.; Sun, C.; Jiang, Z. Vibration singularity analysis for milling tool condition monitoring. Int. J. Mech. Sci. 2020, 166, 105254. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, F.; Hu, M.; Zhang, L.; Liu, H.; Li, M. A novel denoising algorithm based on TVF-EMD and its application in fault classification of rotating machinery. Measurement 2021, 179, 109337. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, K.; Hwang, T.; Park, J.; Jeong, H.; Kim, T.; Youn, B.D. Motor-current-based electromagnetic interference de-noising method for rolling element bearing diagnosis using acoustic emission sensors. Measurement 2022, 193, 110912. [Google Scholar] [CrossRef]
- Kumar Shakya, A.; Singh, S. Design of novel Penta core PCF SPR RI sensor based on fusion of IMD and EMD techniques for analysis of water and transformer oil. Measurement 2022, 188, 110513. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Álvarez-Flórez, J.; Domínguez-Fernández, A. Acoustic emission analysis for the detection of appropriate cutting operations in honing processes. Mech. Syst. Signal Process. 2018, 99, 873–885. [Google Scholar] [CrossRef]
- Susanto, A.; Liu, C.-H.; Yamada, K.; Hwang, Y.-R.; Tanaka, R.; Sekiya, K. Application of Hilbert–Huang transform for vibration signal analysis in end-milling. Precis. Eng. 2018, 53, 263–277. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, Z.; Xie, C.; Huang, Y. Application of Hilbert–Huang Transform to acoustic emission signal for burn feature extraction in surface grinding process. Measurement 2014, 47, 14–21. [Google Scholar] [CrossRef]
- Mahata, S.; Shakya, P.; Babu, N.R. A robust condition monitoring methodology for grinding wheel wear identification using Hilbert Huang transform. Precis. Eng. 2021, 70, 77–91. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wei, W.; Li, L.; Shi, W.-f.; Liu, J.-p. Ultrasonic imaging recognition of coal-rock interface based on the improved variational mode decomposition. Measurement 2021, 170, 108728. [Google Scholar] [CrossRef]
- Su, W.; Lei, Z. Mold-level prediction based on long short-term memory model and multi-mode decomposition with mutual information entropy. Adv. Mech. Eng. 2019, 11, 1687814019894433. [Google Scholar] [CrossRef]
- Wei, X.; Liu, X.; Yue, C.; Wang, L.; Liang, S.Y.; Qin, Y. Tool wear state recognition based on feature selection method with whitening variational mode decomposition. Robot. Comput.-Integr. Manuf. 2022, 77, 102344. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, X.; Zhou, Q.; Wen, D.; Ran, X. Acoustic emission identification of wheel wear states in engineering ceramic grinding based on parameter-adaptive VMD. Ceram. Int. 2022, 49, 13618–13630. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, Z.; Wang, Y.; Chen, H. Machined surface defects monitoring through VMD of acoustic emission signals. J. Manuf. Process. 2022, 79, 587–599. [Google Scholar] [CrossRef]
- Bazi, R.; Benkedjouh, T.; Habbouche, H.; Rechak, S.; Zerhouni, N. A hybrid CNN-BiLSTM approach-based variational mode decomposition for tool wear monitoring. Int. J. Adv. Manuf. Technol. 2022, 119, 3803–3817. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Shi, P.; Yang, W. Precise feature extraction from wind turbine condition monitoring signals by using optimised variational mode decomposition. IET Renew. Power Gener. 2017, 11, 245–252. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M.; Xiang, L. Compound fault diagnosis of rotating machinery based on OVMD and a 1.5-dimension envelope spectrum. Meas. Sci. Technol. 2016, 27, 075002. [Google Scholar] [CrossRef]
- 2010 PHM Society Conference Data Challenge. Available online: https://phmsociety.org/phm_competition/2010-phm-society-conference-data-challenge/ (accessed on 1 March 2023).
- Peng, D.; Smith, W.A.; Randall, R.B.; Peng, Z. Use of mesh phasing to locate faulty planet gears. Mech. Syst. Signal Process. 2019, 116, 12–24. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Y.; Zhou, H.; Li, D.; Liu, H.; Qiao, H.; Wang, X. Timely online chatter detection in end milling process. Mech. Syst. Signal Process. 2016, 75, 668–688. [Google Scholar] [CrossRef]

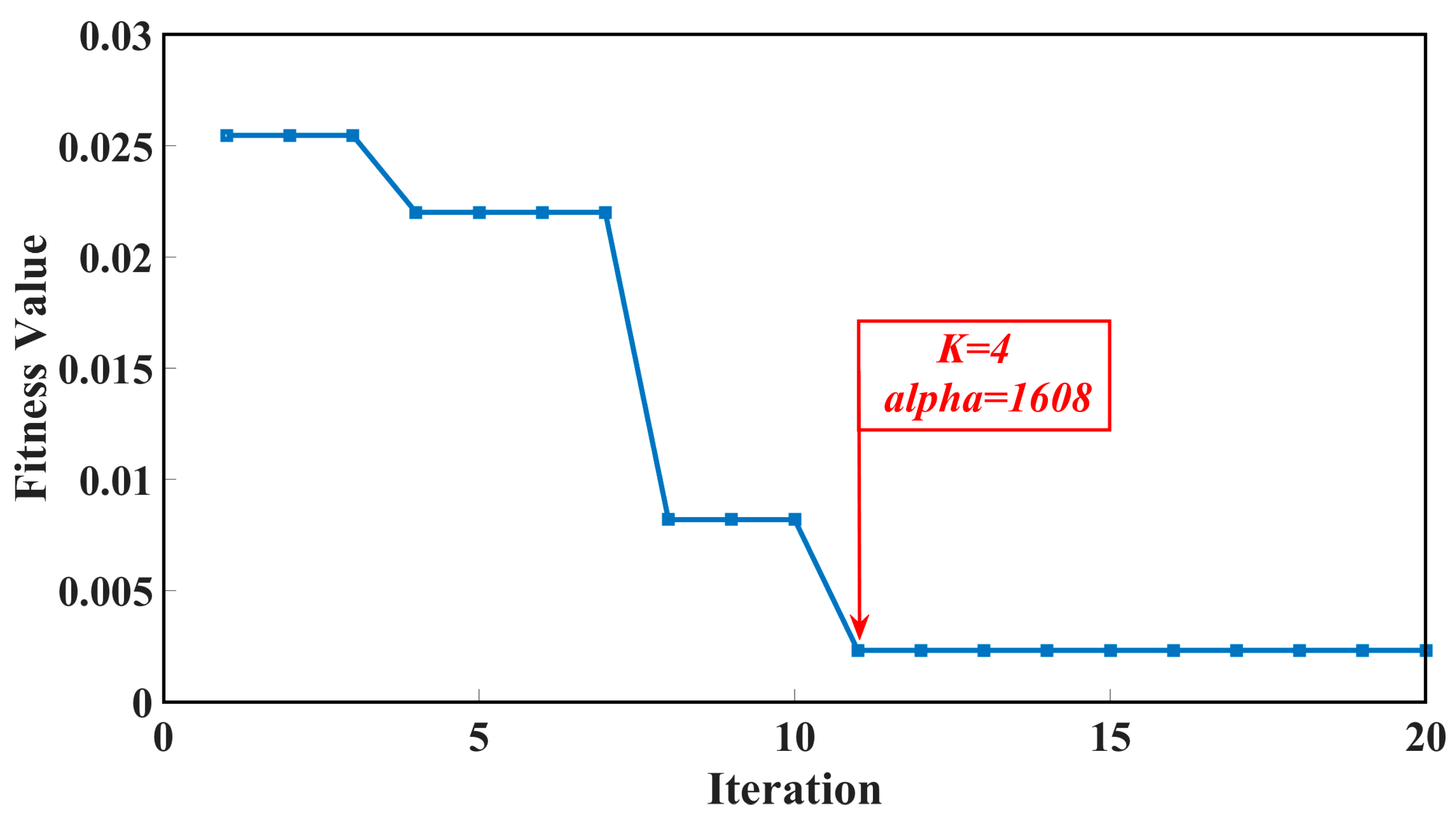

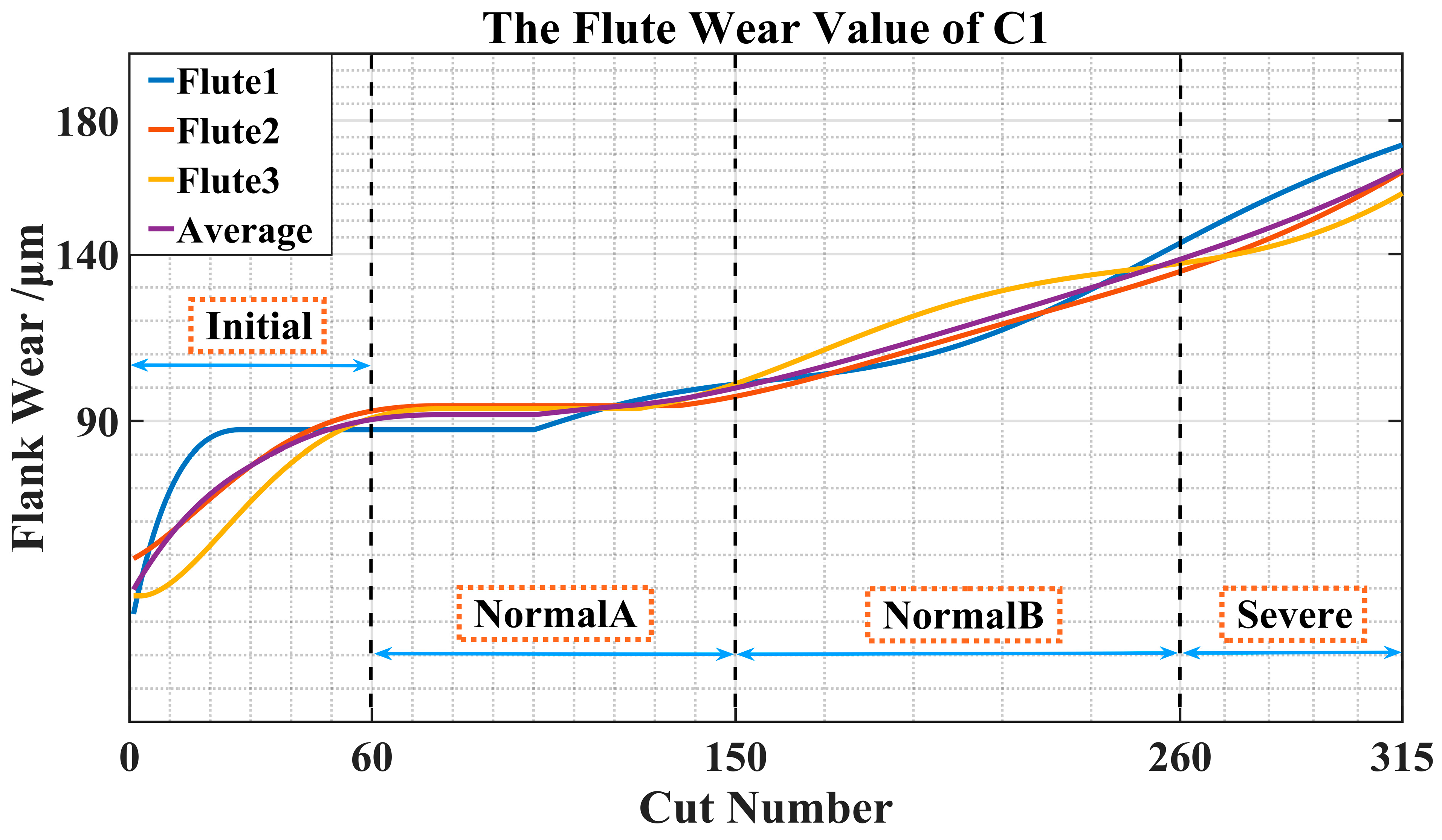
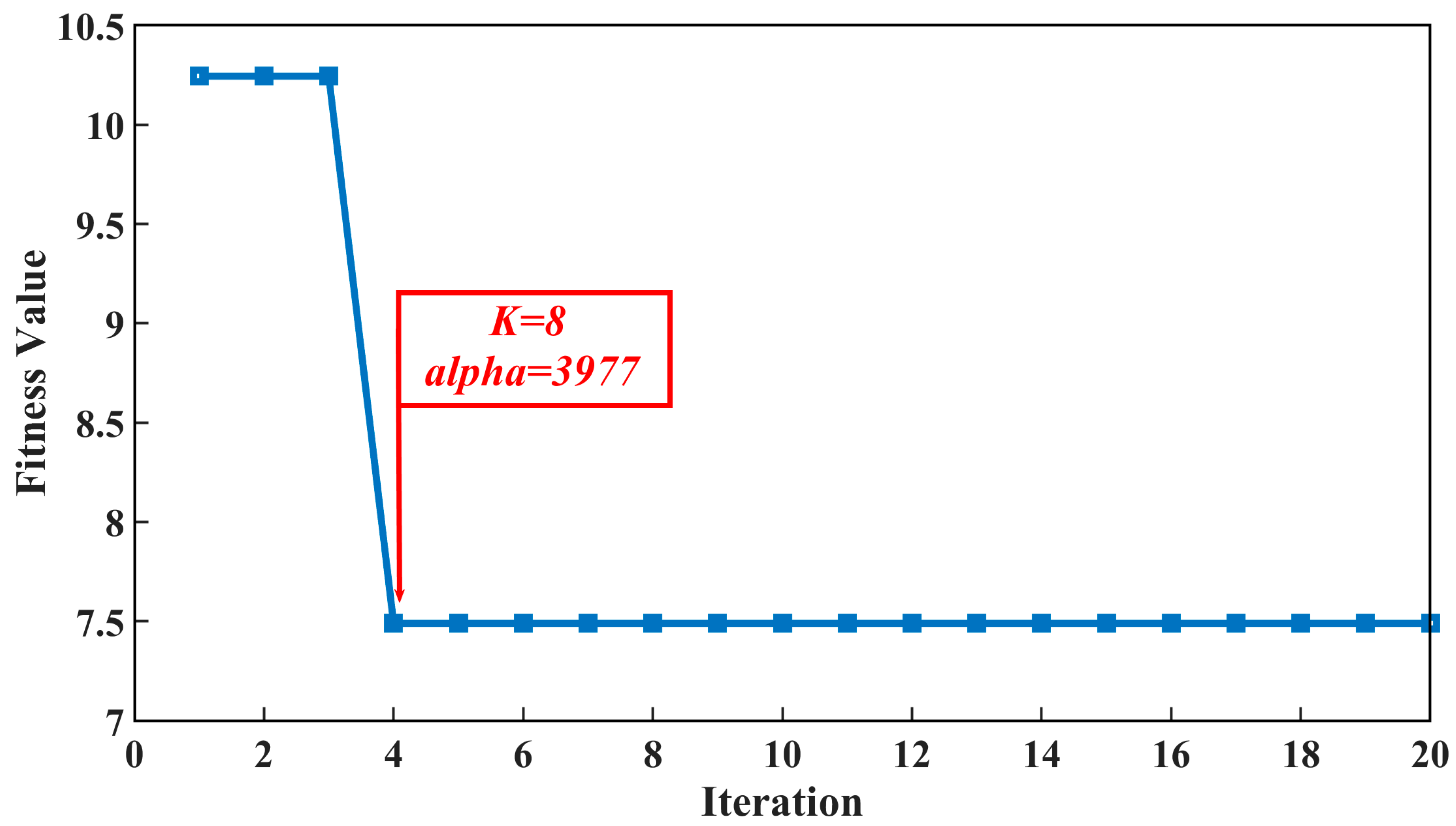

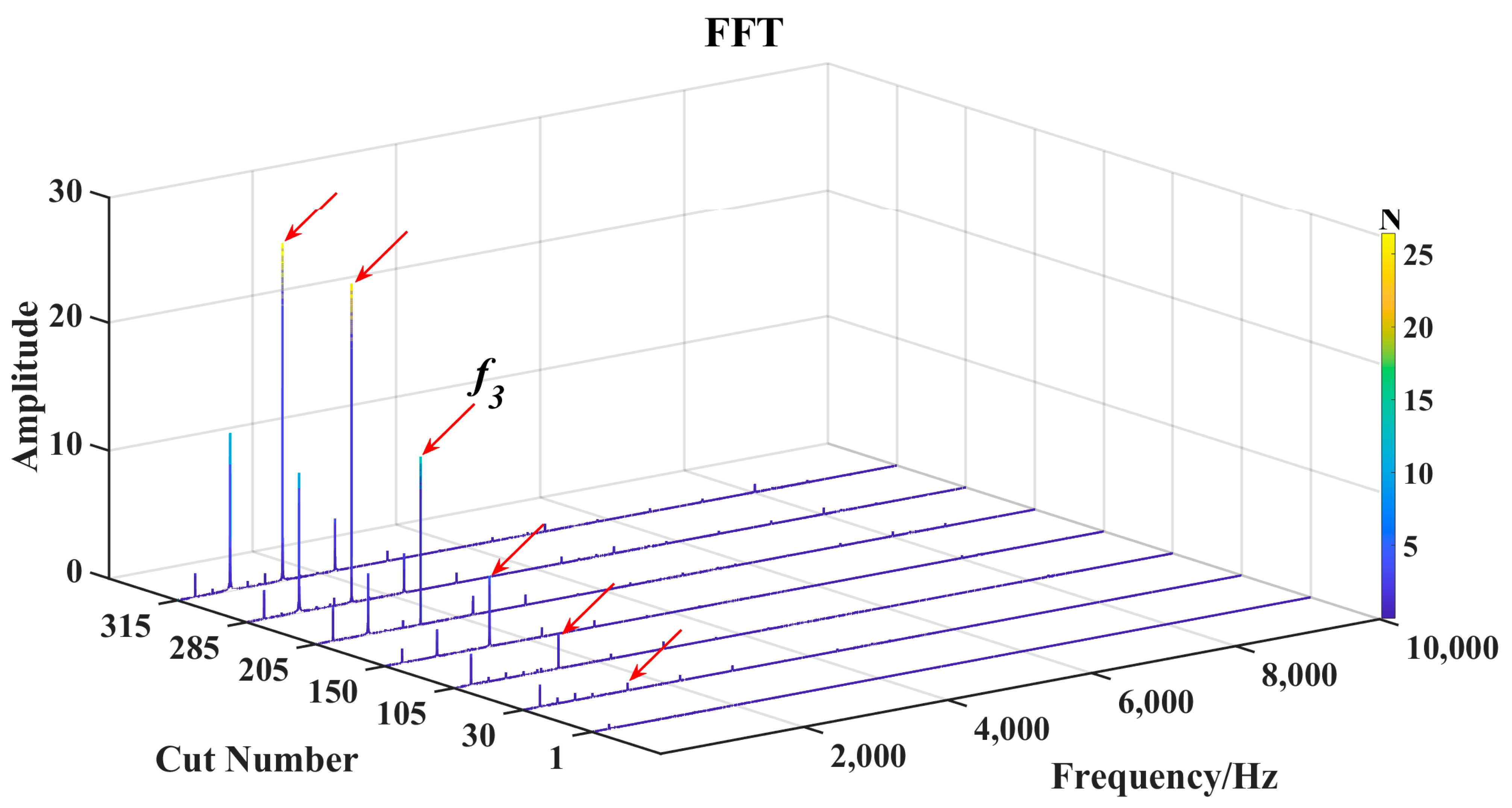
| Spindle Speed (r/min) | Feed Rate (mm/min) | Radial Cutting Depth (mm) | Axial Cutting Depth (mm) | Sampling Rate (kHz) |
|---|---|---|---|---|
| 10,400 | 1555 | 0.125 | 0.2 | 50 |
| Wear State | Label | VB Value (μm) | Times |
|---|---|---|---|
| Initial wear | 1 | 39.64~90.44 | 1~60 |
| Steady wear | 2 | 90.62~99.88 | 61~150 |
| 3 | 100.14~138.42 | 151~260 | |
| Severe wear | 4 | 138.82~165.17 | 261~315 |
| IMF | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|
| correlation coefficient | 0.1775 | 0.3721 | 0.8992 | 0.1045 | 0.1075 | 0.0383 | 0.0118 | 0.0093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, W.; He, G.; Yang, J.; Li, G.; Ding, S. Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert–Huang Transformation in Machining Stainless Steel. Machines 2023, 11, 806. https://doi.org/10.3390/machines11080806
Wei W, He G, Yang J, Li G, Ding S. Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert–Huang Transformation in Machining Stainless Steel. Machines. 2023; 11(8):806. https://doi.org/10.3390/machines11080806
Chicago/Turabian StyleWei, Wei, Guichao He, Jingyi Yang, Guangxian Li, and Songlin Ding. 2023. "Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert–Huang Transformation in Machining Stainless Steel" Machines 11, no. 8: 806. https://doi.org/10.3390/machines11080806
APA StyleWei, W., He, G., Yang, J., Li, G., & Ding, S. (2023). Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert–Huang Transformation in Machining Stainless Steel. Machines, 11(8), 806. https://doi.org/10.3390/machines11080806










