Design and Verification of Offline Robust Model Predictive Controller for Wheel Slip Control in ABS Brakes

Abstract

Wheel slip control is a critical aspect of vehicle safety systems, notably the antilock braking system (ABS). Designing a robust controller for the ABS faces the challenge of accommodating its strong nonlinear behavior across varying road conditions and parameters. To ensure optimal performance during braking and prevent skidding or lock-up, the ideal wheel slip value can be determined from the peak of the tire–road friction curve and maintained throughout the braking process. Among various control approaches, model predictive control (MPC) demonstrates superior performance and robustness. However, online MPC implementation encounters significant computational burdens and real-time limitations, particularly when dealing with larger problem sizes. To address these issues, this study introduces an offline robust model predictive control (RMPC) methodology. The proposed approach is based on the robust asymptotically stable invariant ellipsoid methodology, which employs linear matrix inequalities (LMIs) to calculate a collection of invariant state feedback laws associated with a sequence of nested invariant stable ellipsoids. Simulation results indicate a significant reduction in computational burden with the offline RMPC approach compared to online implementation, while effectively tracking the desired wheel slip reference values and system constraints. Moreover, the offline RMPC design aligns well with the online MPC design and verifies its effectiveness in practice.

1. Introduction

The rapid increase in demand for passenger and commercial vehicles has led to a higher likelihood of traffic accidents, making them one of the leading causes of un-natural deaths worldwide. Consequently, vehicle safety technologies have garnered significant attention from the automotive industry in recent decades, with a focus on improving vehicle active safety. Given that human error plays a major role in most accidents, the development of systems that can assist drivers in unfavorable driving conditions, such as low surface friction, high-speed maneuvers, sudden changes in road direction, and varying climate conditions, has become imperative. To this end, the main goal of all scientific studies in this area, such as [1,2], is to increase the safety of vehicles under different road and braking conditions.

The antilock braking system (ABS) is a crucial active safety system that regulates the longitudinal dynamics of a vehicle during severe braking. Under hard braking conditions, wheel lock-up may occur, resulting in a loss of vehicle steerability and an increase in stopping distance. As an active safety measure, ABS prevents wheel lock-up by modulating the braking pressure and maintaining the longitudinal wheel slip at its optimal and desired value, thereby minimizing stopping distance.

ABS typically consists of various components, including wheel speed sensors, an electronic control unit (ECU), and a brake pressure modulator. However, the design process is complicated by the presence of measurement noises, uncertainties, and nonlinearities. Furthermore, due to variations in road conditions, key characteristics such as braking pressure, wheel slip, and tire–road friction parameters exhibit wide-ranging variability and must be estimated. Consequently, numerous approaches have been proposed and implemented in recent years to effectively control ABS under these varying conditions and enhance its application. The majority of the literature focuses on wheel slip control, which serves as the primary variable that varies across different braking scenarios and road conditions. Therefore, in the design procedure of antilock braking system (ABS) control, the vehicle velocity and longitudinal wheel slip emerge as the two primary state variables. Conversely, the main challenges in ABS control design involve the nonlinear dynamics of the vehicle during the braking process, uncertainties arising from tire force saturation behavior, and variations in vehicle parameters and tire–road friction coefficients across different road conditions. Overcoming these challenges necessitates the development of a robust controller. Consequently, numerous approaches have been proposed to address this issue, including fuzzy logic controllers [3,4,5] and gain scheduling [6], among others. Some studies have combined different approaches to enhance performance [7,8,9,10,11], often augmenting the fuzzy controller approach with other conventional control techniques for wheel slip control in ABS. However, a notable disadvantage of these approaches is their high memory storage requirement.

In addition to these conventional methods, the widely recognized industrial proportional integral derivative (PID) controller has been integrated with other methodologies to control wheel slip in ABS design in some studies [12,13]. However, compared to other control strategies, PID controllers struggle with system nonlinearities and demonstrate suboptimal performance across different operating points. Sliding mode control (SMC) has been extensively employed in various research studies for ABS control [14,15,16,17,18,19,20]. Although SMC possesses robust characteristics for addressing system nonlinearities, its inherent drawbacks include high-frequency oscillation and chattering. Consequently, SMC has been combined with other approaches to overcome these limitations [21,22,23]. Within the domain of robust control methodologies, optimal H_∞ controllers have been designed to handle uncertainties in the presence of disturbances, noise, and changes in system parameters [24,25,26]. However, the design of an optimal H_∞ controller is numerically complex. Considering the limitations of the aforementioned approaches, model predictive control (MPC) has been proposed to enhance the design objectives in terms of robustness and performance [27,28,29,30]. During different research studies, several types of MPC approaches, such as economic MPC [30] and its application in large-scale processes, Ultra-local MPC [31], and Fast MPC [32] have been proposed, which can be efficiently solved online.

Among the various control approaches discussed earlier, model predictive control (MPC) shows promise in addressing the design objectives of ABS, including robustness and tracking performance. However, the computational burden associated with online MPC implementations is typically substantial, which can hinder real-time implementation, particularly in systems that require quick responses with minimal delays, such as braking systems. Consequently, despite being an advanced control methodology, MPC’s primary limitation lies in its significant computational requirements.

To overcome this limitation, Wan and Kothare [33] proposed an offline robust constrained MPC approach based on the concept of asymptotically stable ellipsoids using constrained linear matrix inequalities (LMIs). The controller’s design entails acquiring state feedback gains offline for a series of nested ellipsoids. During each sampling interval, the active ellipsoid encompassing the current state is identified. Utilizing linear interpolation between the corresponding state feedback gains associated with the active ellipsoid, the controller gain is determined. This innovative approach substantially reduces the computational burden, enabling more practical real-time implementation. Therefore, in this study, we propose the utilization of the offline robust MPC methodology as an alternative approach to address the aforementioned MPC limitation and facilitate its application for wheel slip control in ABS. This new approach effectively addresses the classic MPC limitations and enhances its capability for real-time implementation.

The main contributions of this study can be summarized as follows:

• Designing a novel offline robust MPC approach for wheel slip control, where the optimization is performed offline within a sequence of nested asymptotically stable ellipsoids. Unlike the conventional MPC methodology, which requires online optimization at each sampling time and is time-consuming, the proposed approach effectively handles the computational burden while providing a faster response;
• In the design of the offline robust MPC, the LMIs are derived to incorporate the system’s physical constraints, uncertainties, and parameter variations to ensure the stability of the controlled system.

By adopting this offline robust MPC approach, we aim to enhance the performance and applicability of ABS control, overcoming the computational challenges associated with online MPC implementations and facilitating real-time implementation.

The subsequent sections of this study are organized as follows: Section 2 provides an overview of the nonlinear dynamical equations governing the behavior of the wheel in the quarter-car model. In Section 3, the mathematical structure of the proposed offline RMPC approach is presented. Section 4 presents the simulation results and offers a comprehensive discussion of the obtained outcomes. Finally, Section 5 concludes the study by summarizing the main findings and implications.

2. System Modeling

2.1. Wheel Dynamics

A nonlinear full-vehicle model encompasses all the intricate dynamic characteristics of a vehicle, which can complicate controller design. As a result, a simplified nonlinear quarter vehicle model, which captures the essential features of the actual vehicle model, is often used as a foundational system model for wheel slip control in controller design [28]. Figure 1 illustrates this model. The dynamic equations governing the motion of the nonlinear quarter vehicle model are as follows:

$$F_x={-m}_t\dot{V}$$

(1)

$$I_w\dot{\omega }=R{F}_x-T_b$$

(2)

$$F_z=m_{t}g$$

(3)

where $F_x$ is the longitudinal tire force, $m_t$ is the total mass of the quarter vehicle, V is the vehicle body speed, $I_w$ is the wheel moment of inertia, $\omega$ is the wheel’s angular velocity, R is the wheel radius, and $T_b$ represents the braking torque. This torque is defined as $T_b=K_b{P}_b$, where $K_b$ is the braking coefficient, and $P_b$ is the brake pressure. During braking, braking torque produces traction between the tire and the road surface. This traction causes the tire to travel more distance than it would in normal tumbling, called wheel slip. Wheel slip is calculated mathematically as:

$$\lambda =\frac{V-R\omega }{\max (V,R\omega )}$$

(4)

The expression provided above defines the relative velocity between the longitudinal speed of the vehicle and the linear speed of the wheel. When the wheel is in braking mode, the longitudinal velocity of the vehicle (V) exceeds the linear speed of the wheel ((Rω) (V > Rω)), indicating braking action. In the case of a wheel rolling without slip, the slip value is zero. The parameter λ is introduced to represent the slip ratio or slip coefficient and takes values greater than zero (λ > 0). A value of λ = 1 corresponds to maximum traction between the tire and the road surface, indicating a locked-wheel situation. The slip ratio (λ) serves as a measure of the relative difference between the speeds of the wheel and the vehicle, providing insight into the wheel’s braking behavior.

The Burckhardt relative represents the tire–road friction coefficient, which nonlinearly depends on the wheel slip ($\lambda$) as expressed below:

$$\mu \left(\lambda \right)=c_1\left(1-e^{\left(-c_2\lambda \right)}\right)-c_3\lambda$$

(5)

where constants $c_1$, $c_2$, and $c_3$ depend on the road type and conditions, as well as wheel and vehicle operational conditions, which were calculated in [34]. These values are given in

Table 1. Burckhardt relative constant values for different road conditions.

Road Conditions	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$
Dry asphalt road	1.2801	23.99	0.52
Wet asphalt road	0.857	33.822	0.347
Snowy road	0.1946	94.129	0.0646
Icy road	0.05	306.39	0

for different road profiles. μ(λ) represents the friction coefficient, which depends on the specific characteristics of the tire and the road surface. Figure 2 demonstrates the μ(λ) curves for different road surface conditions. The friction coefficient (μ) is typically defined as a function of the wheel slip (λ), taking into account the nonlinear behavior of the tire and its interaction with the road.

According to Figure 1, the longitudinal friction force ($F_x$) is related to the tire normal load ($F_z$) and defined as a function of wheel slip and modeled as

$$F_x=\mu \left(\lambda \right)F_z$$

(6)

2.2. State-Space Representation of the System

As mentioned before, during braking, $V>R\omega$, and the wheel slip ($\lambda$) is described as:

$$\lambda =\frac{V-R\omega }{V }$$

(7)

In this study, the longitudinal vehicle velocity and the wheel slip ($\mathit{x}=\left[\begin{array}{cc}\lambda & V\end{array}\right]$) are considered the system’s state variables. Derivation of Equation (7), with substitution of Equations (1) and (2), results in:

$$\dot{\lambda }=-\frac{1}{V}\left(\frac{F_x}{m_t}\left(1-\lambda \right)+\frac{R^2{F}_x}{I_t}\right)+\frac{R}{V{I}_t}{T}_b$$

(8)

Rewriting Equations (1) and (8) with state variables of $\mathit{x}=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]$ provides the state-space representation of the dynamical equations of the nonlinear system. This nonlinear representation of the system can be written in the following form:

$$\dot{\mathit{x}}=f\left(\mathit{x}\right)+g\left(\mathit{x}\right)T_b$$

(9)

in which the $T_b$ represents the control input.

3. Control Design Scheme

3.1. Problem Formulation

To design the model predictive controller, the control law of the form $u\left(k+i|k\right)=F\left(k\right)x\left(k+i|k\right)$ leads to the following cost function minimization problem:

$$J\left(k\right)={{\displaystyle \sum }}_{i=0}^{\infty }\left({x\left(k+i|k\right)}^T\mathcal{L}x\left(k+i|k\right)+{u\left(k+i|k\right)}^T\mathcal{R}u\left(k+i|k\right)\right)$$

(10)

where $\mathcal{L}$ and $\mathcal{R}$ represent the weighting matrices of the system states and control input, respectively. The design procedure of the online RMPC and the proposed offline RMPC controllers using an LMI framework is described in this section. In this case, it is supposed that all states are available.

3.2. Online RMPC

The following theorem explains the LMI-based form of the online RMPC approach:

Theorem 1. 

For a linear time-varying system (LTV) such as [33]

$$x\left(k+1\right)=A\left(k\right)x\left(k\right)+Bu\left(k\right),$$

(11)

$$y\left(k\right)=Cx\left(k\right)$$

With a sampling time of k, there exists an upper bound ($\gamma$) on the objective cost function ($J_{\infty }\left(k\right)$($J_{\infty }\left(k\right)<\gamma$)) if and only if there exists a symmetric matrix ($Q\succ 0$) and Y that satisfy the following LMIs:

$$\left[\begin{array}{cc}1& {x\left(k|k\right)}^T\\ x\left(k|k\right)& Q\end{array}\right]\succcurlyeq 0, Q\succ 0$$

(12)

$$\left(\begin{array}{c}Q\\ A_{j}Q+B_{j}Y\\ \begin{array}{c}{\mathcal{L}}^{1/2}Q\\ {\mathcal{R}}^{1/2}Y\end{array}\end{array}\begin{array}{c}Q{A}_j^T+Y^T{B}_j^T\\ Q\\ \begin{array}{c}0\\ 0\end{array}\end{array}\begin{array}{c}Q{\mathcal{L}}^{1/2}\\ 0\\ \begin{array}{c}\gamma I\\ 0\end{array}\end{array}\begin{array}{c}{Y}^T{\mathcal{R}}^{1/2}\\ 0\\ \begin{array}{c}0\\ \gamma I\end{array}\end{array}\right)\succcurlyeq 0,j=1,\dots ,L$$

(13)

$$\left(\begin{array}{cc}X& Y\\ Y^T& Q\end{array}\right)\succcurlyeq 0,\mathit{with} X_{rr}\preccurlyeq u_{r,max}^2,r=1,2,\dots ,n_u$$

(14)

$$\left(\begin{array}{cc}Z& C(A_{j}Q+B_{j}Y)\\ {(A_{j}Q+B_{j}Y)}^T{C}^T& Q\end{array}\right)\succcurlyeq 0,Z_{rr}\preccurlyeq y_{r,max}^2,r=1,2,\dots ,n_y$$

(15)

The following linear objective minimization problem gives the robust and asymptotic solution for the closed-loop system:

$$\underset{\gamma ,\mathit{Q},\mathit{X},\mathit{Y},\mathit{Z}}{\mathit{min}}\gamma \mathit{subject} \mathit{to} \left(12\right)-(15)$$

(16)

After solving this minimization problem, $Q=\gamma {P\left(k\right)}^{-1}$ and $F\left(k\right)=Y{Q}^{-1}$ yield the state feedback matrix ($F\left(k\right)$) in the control law ($u\left(k+i|k\right)=F\left(k\right)x\left(k+i|k\right), i\ge 0$). Interested readers are referred to [35] to see the proof of the robustness check in the presence of parameter uncertainties. The online MPC structure is shown in Figure 3.

3.3. Offline RMPC

This section presents the algorithm for the offline RMPC approach, which is based on the concept of asymptotically stable invariant ellipsoids proposed in [33]. By applying Theorem 1 to a state located at a certain distance from the origin, a more constrained feedback matrix is obtained. In an asymptotically stable system, the state tends to converge to the origin. Therefore, according to [35], it is not necessary to maintain a far-reaching feedback matrix, as it imposes fewer constraints. The offline RMPC approach optimizes the distance between the state and the origin by adding nested asymptotically stable invariant ellipsoids. Among the sequence of ellipsoids, the smallest one that contains the state is selected offline. The distance of the state and the origin in the asymptotically stable invariant ellipsoid ($\epsilon =\left\{x\in {\mathfrak{R}}^{n_x}|x^T{Q}^{-1}x\le 1\right\}$) is defined as the weighted norm (${‖x‖}_{Q^{-1}}^2\triangleq x^T{Q}^{-1}x$). To extend the feedback matrix as a continuous real-time application, it is necessary to carry out a linear interpolation between corresponding state feedback gains. Algorithm 1 illustrates the offline RMPC structure.

Algorithm 1. Offline Robust MPC

In the uncertain system in Equation (11) for an initial feasible state $\left(x_1\right),$ generate the minimizers ${\gamma }_i, Q_i,X_i,Y_i, and Z_i$ (let $i=1$) offline from Equation (16); Employ N nested ellipsoids. Using Theorem 1 and an additional constraint $({‖x_{i+1}‖}_{{Q_i}^{-1}}^2<1)$ compute minimizers ${\gamma }_i, Q_i,X_i,Y_i,$ and $Z_i$ for N feasible arbitrary initial states $(x_i, i=2, \dots , N$; ignored at i = 1); Store $X_i,Y_i, Q_i^{-1},$ and $F_i(=Y_i{Q}_i^{-1})$ in a lookup table; Let $i=i+1$ go to step 1. In the lookup table obtained from steps 1 and 2, check the feasibility of the following inequality for each $i\ne N$:               $Q_i^{-1}-{\left(A_j+B_j{F}_{j+1}\right)}^T{Q}_i^{-1}\left(A_j+B_j{F}_{j+1}\right)\succ 0$                                                  (17) In the real-time implementation, given an initial state $\left(x\right(0\left)\right)$ satisfying ${‖x\left(0\right)‖}_{{Q_1}^{-1}}^2\le 1,$ perform an online bisection search over $Q_i^{-1}$ in the lookup table to find the largest index (i; or, equivalently, the smallest ellipsoid ${\epsilon }_i=\left\{x\in {\mathfrak{R}}^{n_x}|x^T{Q}_i^{-1}x\le 1\right\})$ such that ${‖x‖}_{{Q_i}^{-1}}^2\le 1;$ Apply the control law $(u\left(k\right)=F_{i}x\left(k\right));$ According to the equivalent ellipsoid, if $i\ne N,$ solve ${x\left(k\right)}^T({\alpha }_i{Q}_i^{-1}+\left(1-{\alpha }_i\right)Q_{i+1}^{-1}x\left(k\right))=1;$ $0\le {\alpha }_i\le 1$ is the solution, and the control law is               $f\left(x\right)=\left\{\begin{array}{c}{\alpha }_i{F}_i+\left(1-{\alpha }_i\right)F_{i+1}, if {‖x‖}_{{Q_i}^{-1}}^2\le 1. {‖x‖}_{{Q_i}^{-1}}^2>1. i\ne N\\ F_N i=N\end{array}\right.$              (18)

Based on Equation (18), it is evident that the feedback matrix (F) is a continuous function of state x. However, in real-time applications, the implementation of MPC typically involves a bisection search on a precomputed lookup table. This offline-generated table contains the optimal feedback matrices corresponding to different states. By performing a bisection search, the appropriate feedback matrix is selected from the table to generate the control force. This approach significantly reduces the computational burden associated with MPC, making it feasible for real-time implementation in fast process systems. Instead of performing complex computations to determine the feedback matrix at each sampling time, the use of a precomputed lookup table streamlines the control process and enables quicker decision making. Consequently, the real-time implementation of MPC is facilitated, allowing for efficient control of dynamic systems.

4. Offline RMPC Implementation for ABS

In this section, the offline RMPC approach is designed for the nonlinear model of ABS in different road conditions, and the simulation results are compared to those of the online MPC. The nonlinear quarter-car model described in Equations (7) and (8) is used for this application with the parameters given in

Table 2. Quarter-car model parameters.

Parameter	Value	Annotation
¼ sprung mass (m)	340	kg
Wheel radius (R)	0.33	m
Total wheel moment of inertia ($I_t$)	1.7	kg/m2
Maximum braking torque ($T_b$)	2000	Nm
Desired wheel slip ($\lambda$)	0.17	-
Gravitational acceleration	9.81	m/s2

. In the design procedure, it is supposed that all states are available. The main goal is to find the optimized control force at which the wheel slip can maintain its optimal value. The block diagram of the offline RMPC is illustrated in Figure 4.

As the $\mathcal{L}$ and $\mathcal{R}$ matrices are the weighting matrices in the cost function, they should be selected appropriately to optimize the performance of the system parameters to work properly on their given constraints. These matrices are specified as follows:

$$\mathcal{L}=\left[\begin{array}{cc}2& 0\\ 0& 1000\end{array}\right],\mathcal{R}=0.00001$$

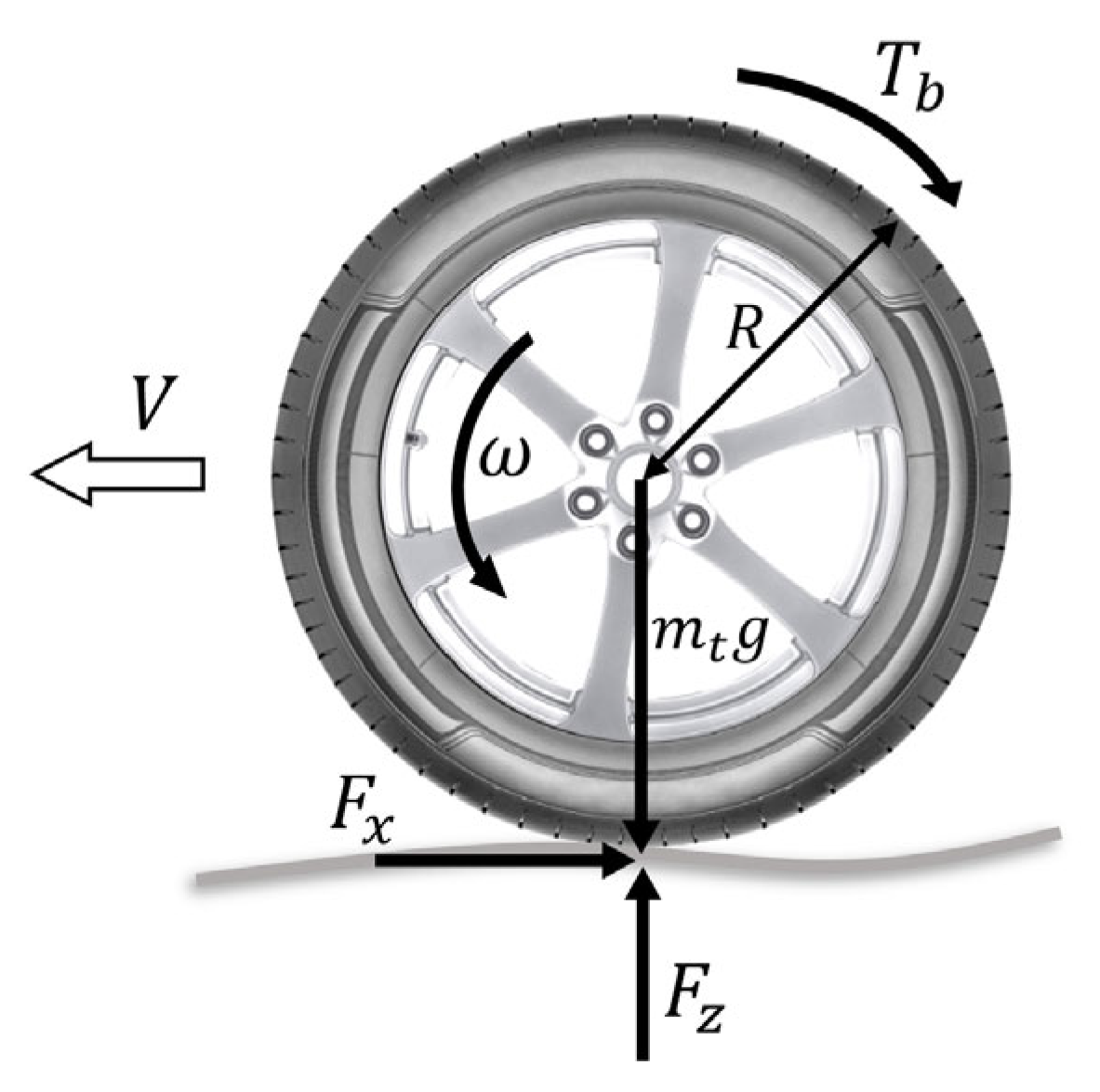
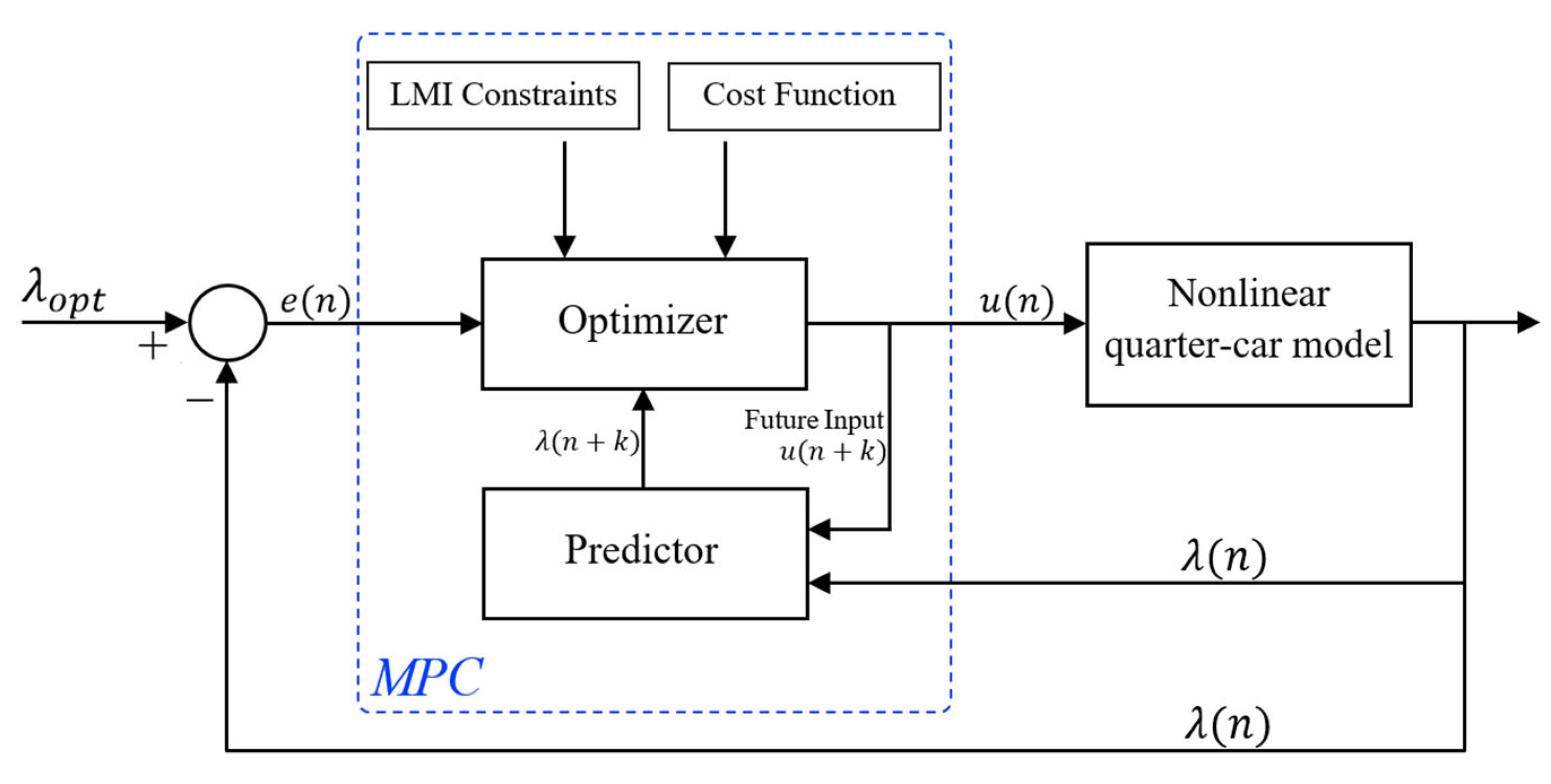
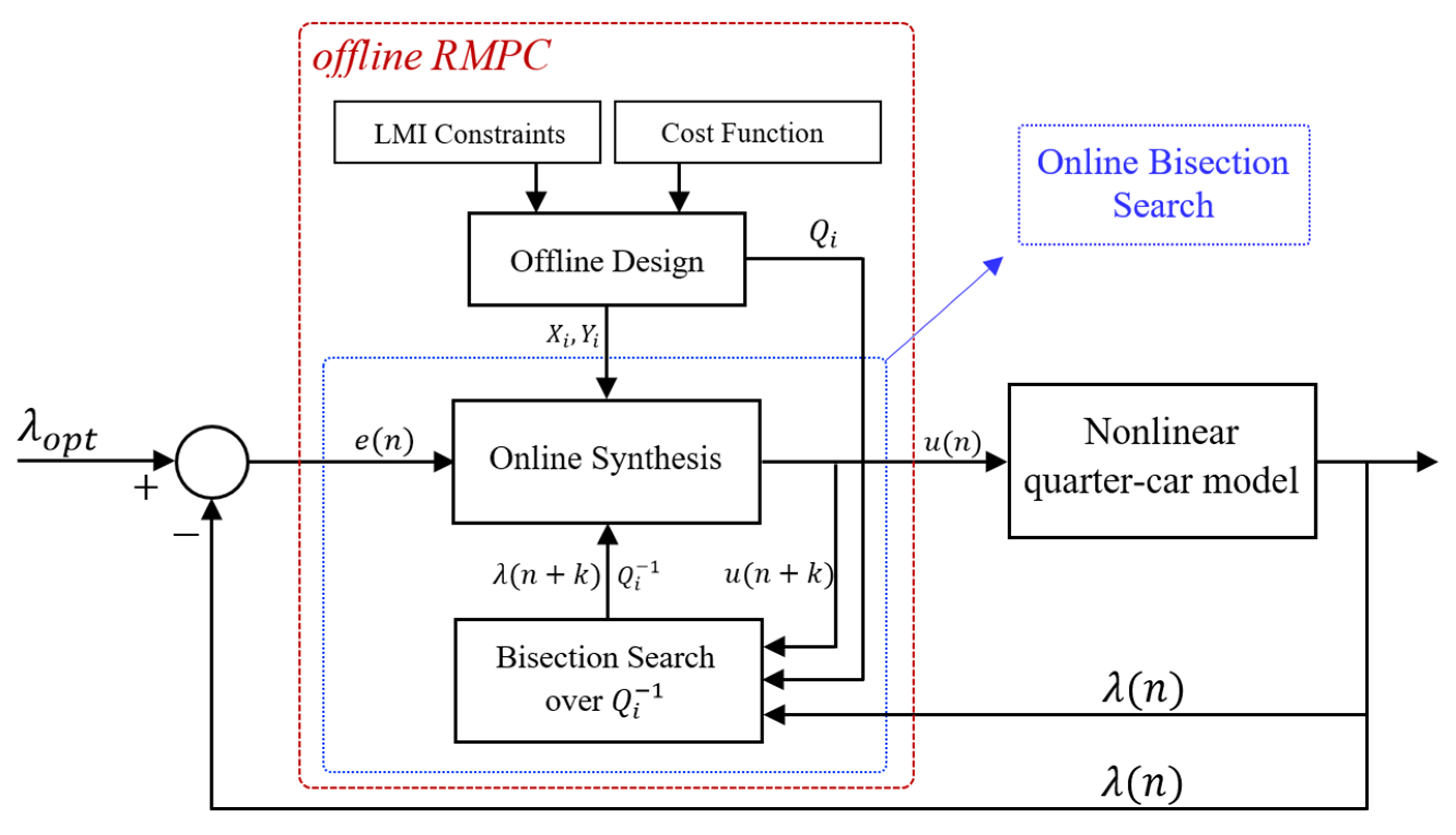
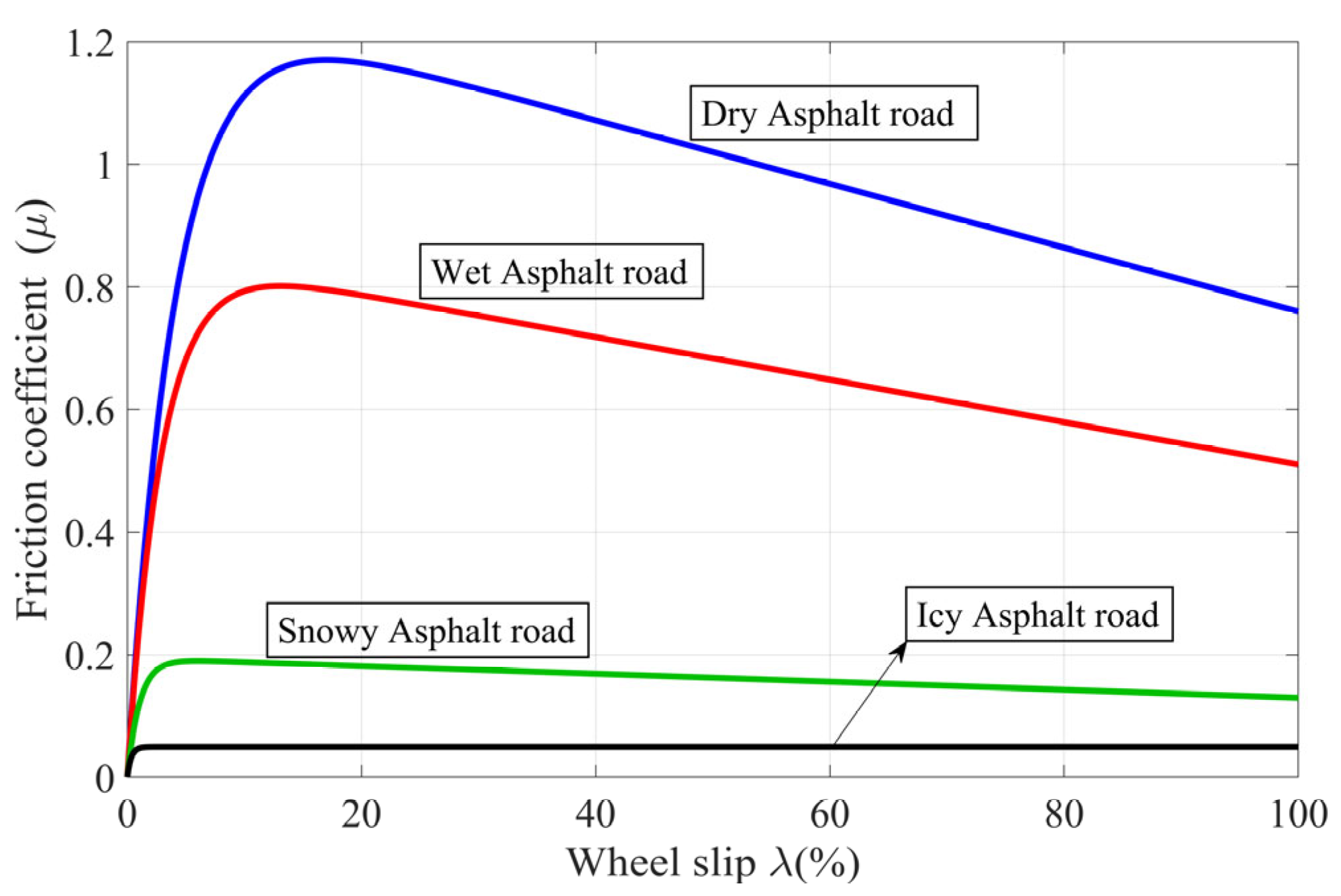
In the MPC approach, the design procedure is typically carried out using the linearized model of the system. However, it is important to note that the nonlinear ABS model does not possess a specific equilibrium point. Instead, there exists an equilibrium manifold within the stable region of the tire–road friction curves [36]. By considering the peak values of the tire–road friction curves depicted in Figure 2, it is possible to determine the optimal values of wheel slip for different road profiles. The stable performance region of the ABS is then identified to lie within the range of 0 < λ < ${\lambda }_{opt}$ (0 < μ < ${\mu }_{peak}$), where ${\lambda }_{opt}$ and ${\mu }_{peak}$ denote the optimal and peak values, respectively. For more in-depth information on this topic, interested readers are referred to [37]. A comprehensive listing of the optimal and peak values for various road profiles can be found in

Table 3. Friction and wheel slip optimal values for the Burckhardt friction model.

Road Type	${\mathit{\mu }}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$	${\mathit{\lambda }}_{\mathit{o}\mathit{p}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{l}}$
Dry asphalt	1.17	0.17
Wet asphalt	0.80	0.131
Snowy asphalt	0.19	0.06

.

4.1. Simulations and Results

To consider the design limitations and structural constraints arising from different road conditions, certain bounds are imposed on the states and inputs of the system. These bounds are summarized in

Table 4. Constraints on states and input according to the road conditions.

Road Type	${\mathit{T}}_{\mathit{b},\mathit{m}\mathit{a}\mathit{x}}$ (Nm)		${\mathit{V}}_{\mathit{x}}$ (m/s)	$\mathit{\lambda }$
	Lower Bound	Upper Bound	Upper Bound
Dry asphalt	0	1800	20	0.17
Wet asphalt	0	1100	20	0.131
Snowy asphalt	0	350	14	0.06

, providing explicit limits for the various variables involved in ABS control design. These constraints ensure that the system operates within safe and feasible ranges, taking into consideration factors such as vehicle dynamics, tire characteristics, and road conditions. By adhering to these bounds, the control algorithm can effectively regulate the system’s behavior and ensure stability and performance while accommodating the specific constraints imposed by the ABS application.

To design an offline RMPC for the dry road condition, the $x_1$ axis is chosen as a one-dimensional subspace and discretized to a sequence of 10 states as $x_1^{set}=\left[0.2, 0.17, 0.15, 0.12, 0.1, 0.08, 0.06, 0.03, 0.01, 0\right]$, which represent different wheel slips during braking until the vehicle velocity reaches its safe moment (${2~5 }^{\mathrm{m}/\mathrm{s}}$) in optimal wheel slip, at which point the ABS is cut off. The sequence of $Q_i^{-1}$ is obtained from the offline part of Algorithm 1. 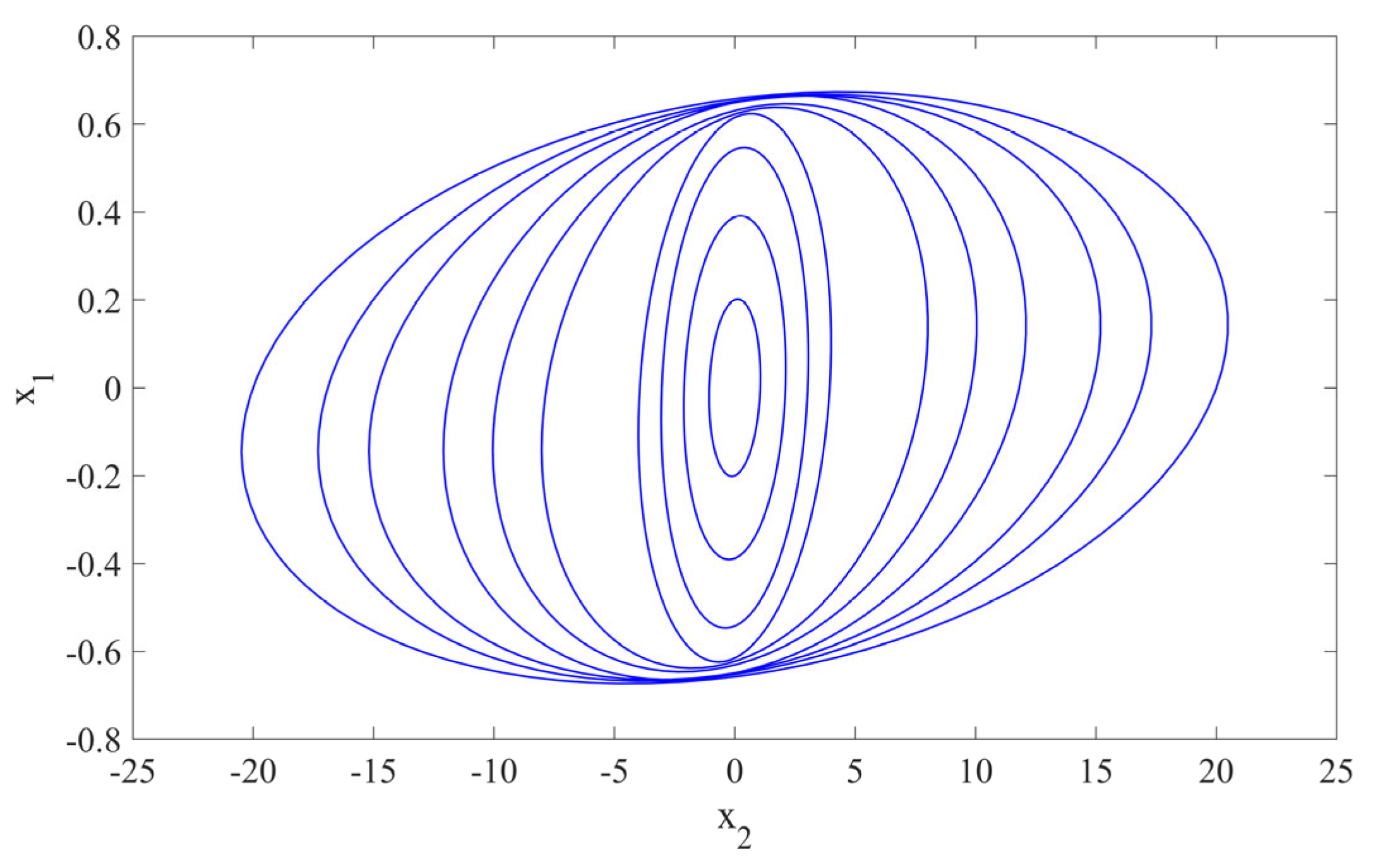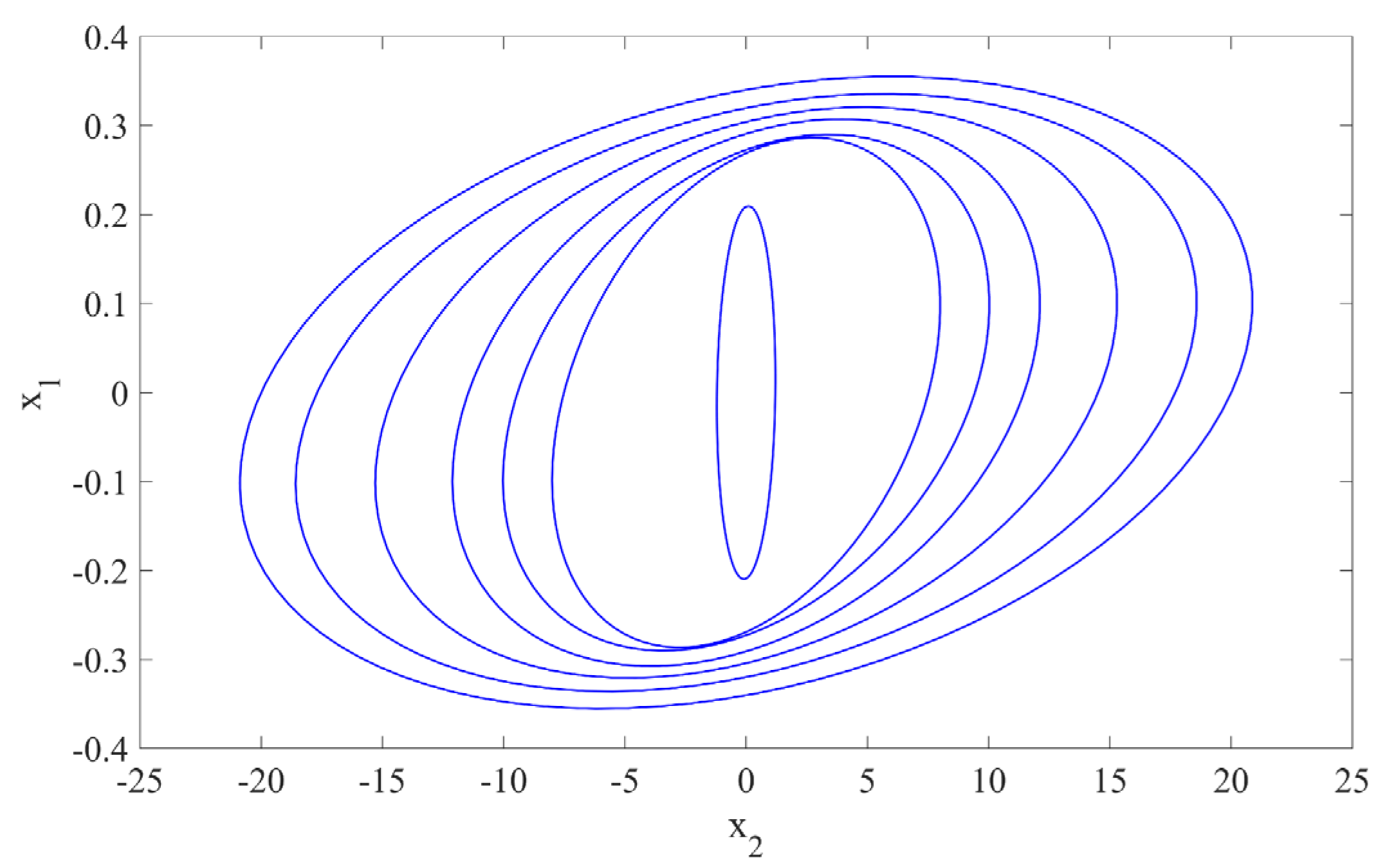Figure 5 illustrates the relevant nested ellipsoids defined by $Q_i^{-1}$ for ten discrete points.

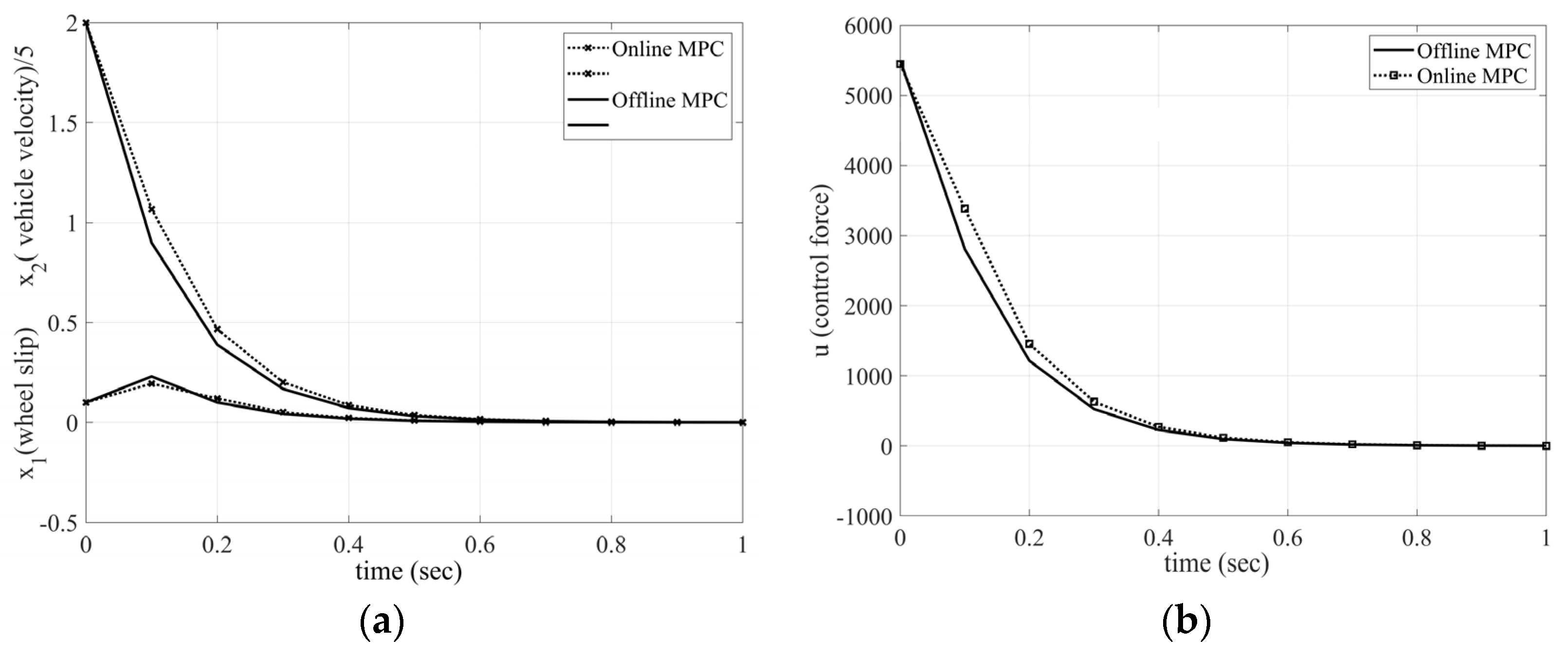
In the first step for verification of the proposed algorithm for an ABS control, the moment during braking is considered as an initially disturbed state, which is specified as $x\left(0\right)=\left[\begin{array}{c}0.1\\ 10\end{array}\right]$, in which the first element is wheel slip and the second element represents the vehicle speed. For the linearized system and discretization using a sampling time of 0.1, the control law and the closed-loop responses of the system are shown in Figure 6.

Based on the observations from Figure 6, it is evident that the offline RMPC algorithm operates effectively and exhibits comparable response and performance to the online MPC design when using the same control input. Moving forward, the simulation results of the nonlinear system will be discussed. In consideration of practical aspects, it is worth noting that during the braking process, the vehicle and wheel velocities eventually reach zero, resulting in the wheel slip tending towards infinity. At this point, certain manufacturers deactivate the ABS and transition it into a passive mode when the speed falls below a minimum limit. Consequently, the simulations are terminated when the vehicle velocity reaches 3 m/s, aligning with this industry practice.

The simulations are conducted in the MATLAB/Simulink environment, utilizing YALMIP’s MOSEK optimization solver toolbox [38], and the hardware platform consists of an Intel i7-10510U CPU with a clock speed of 4.3 GHz and 16 GB RAM. To clearly illustrate the performance of the proposed offline RMPC approach compared to the online method in the nonlinear system, a sampling time of 0.005 s is set. For the dry asphalt road, the initial speed of the vehicle and the wheel slip at the moment of braking are set to 20 m/s (72 km/h) and 0, respectively.

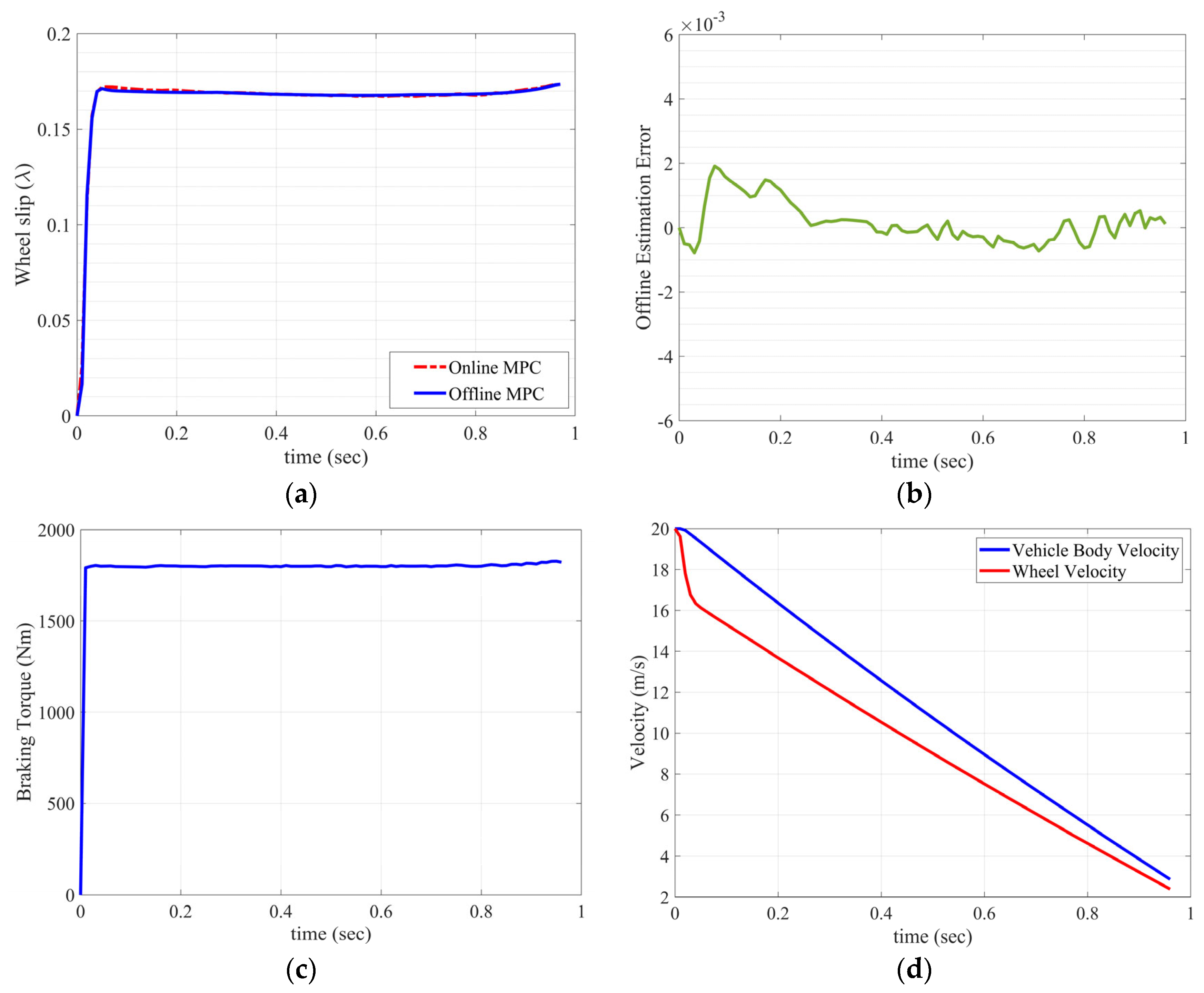
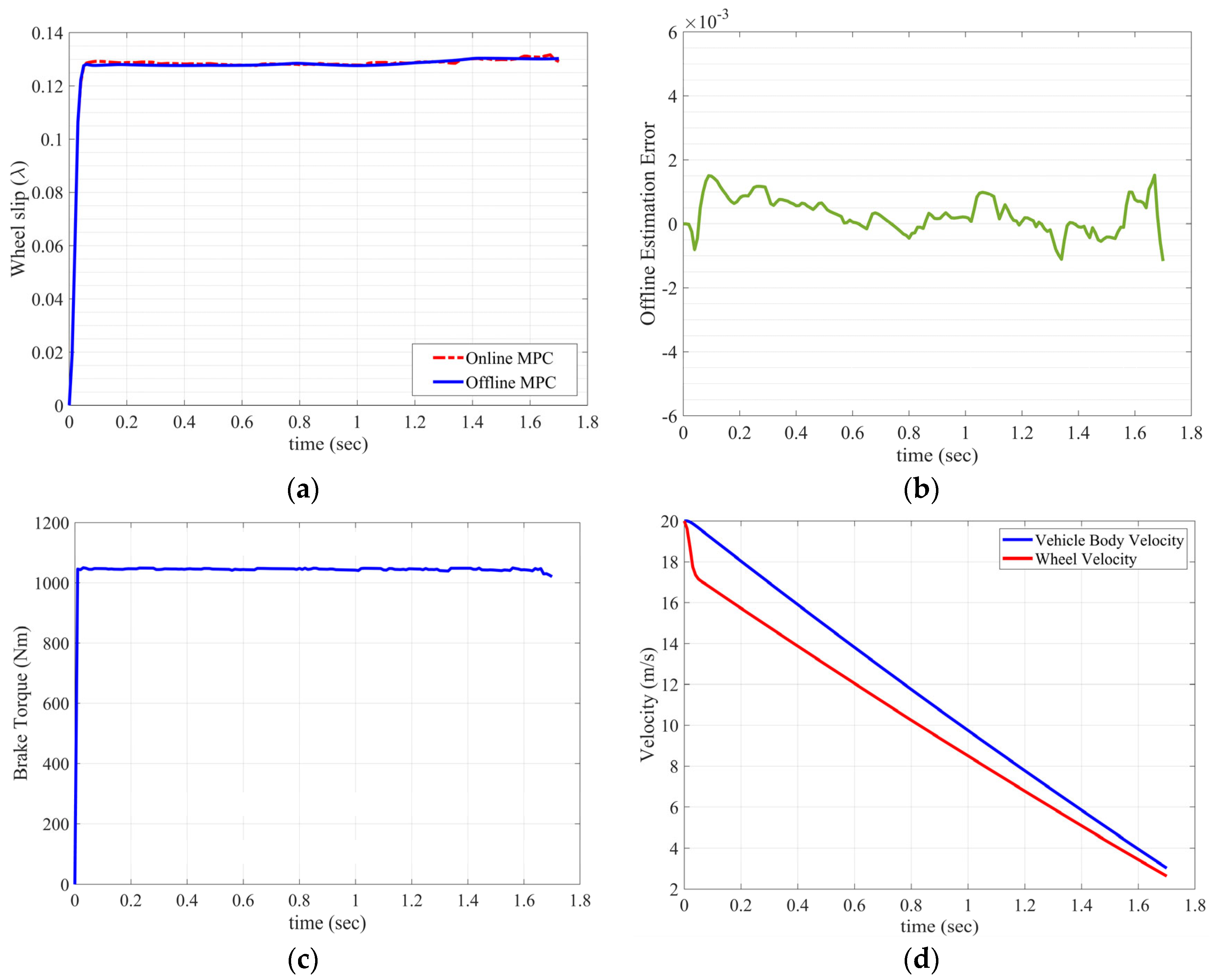
The main objective of the MPC feedback controller design is to regulate the tire–road friction around its peak value (${\mu }_{peak}=1.17$) while minimizing the tracking error of the wheel slip set point. In the first step, the online MPC controller is designed according to Equations (12)–(16). Subsequently, the offline RMPC is designed based on Algorithm 1. Figure 7 illustrates the simulation results of the proposed offline controller compared to the online controller.

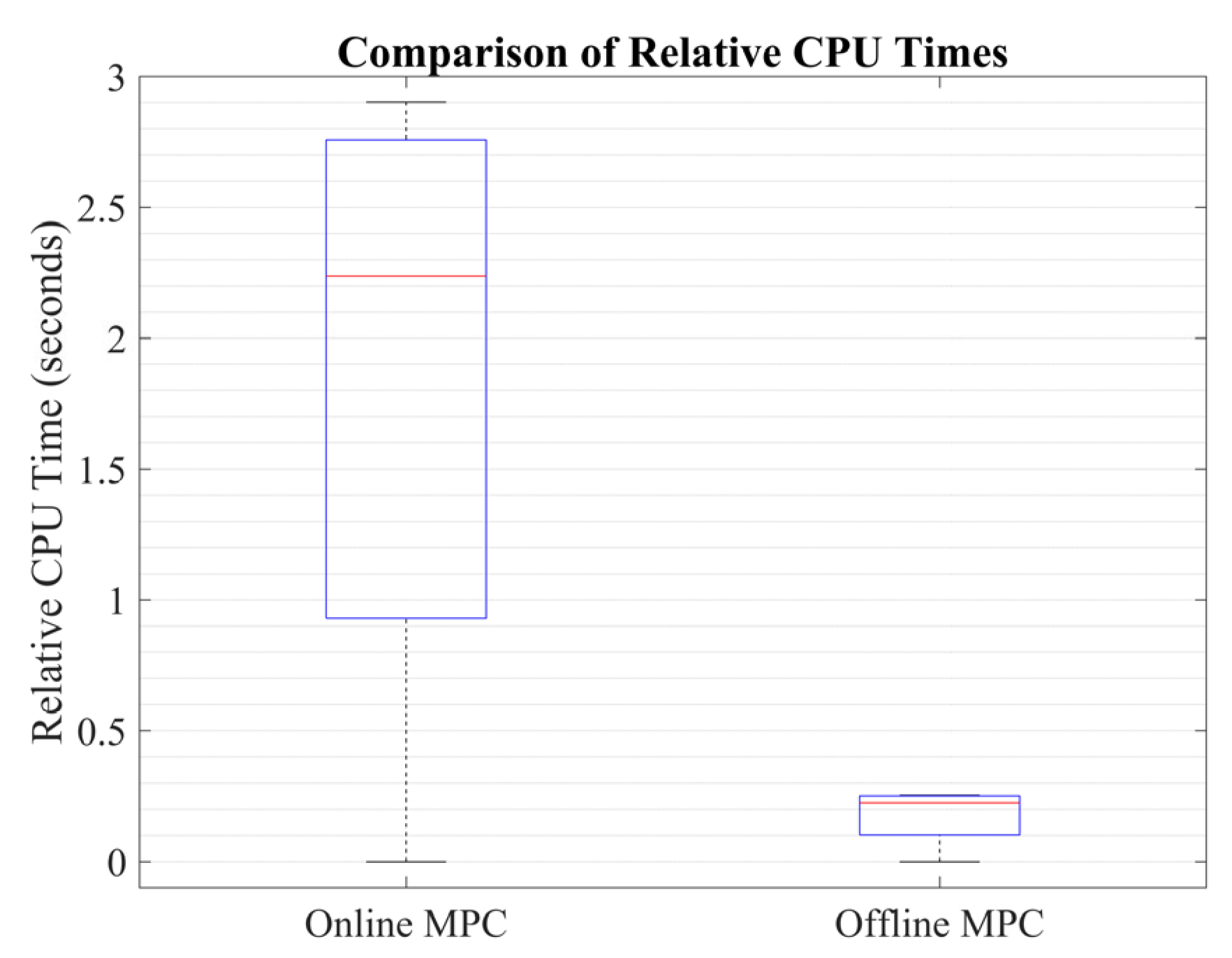
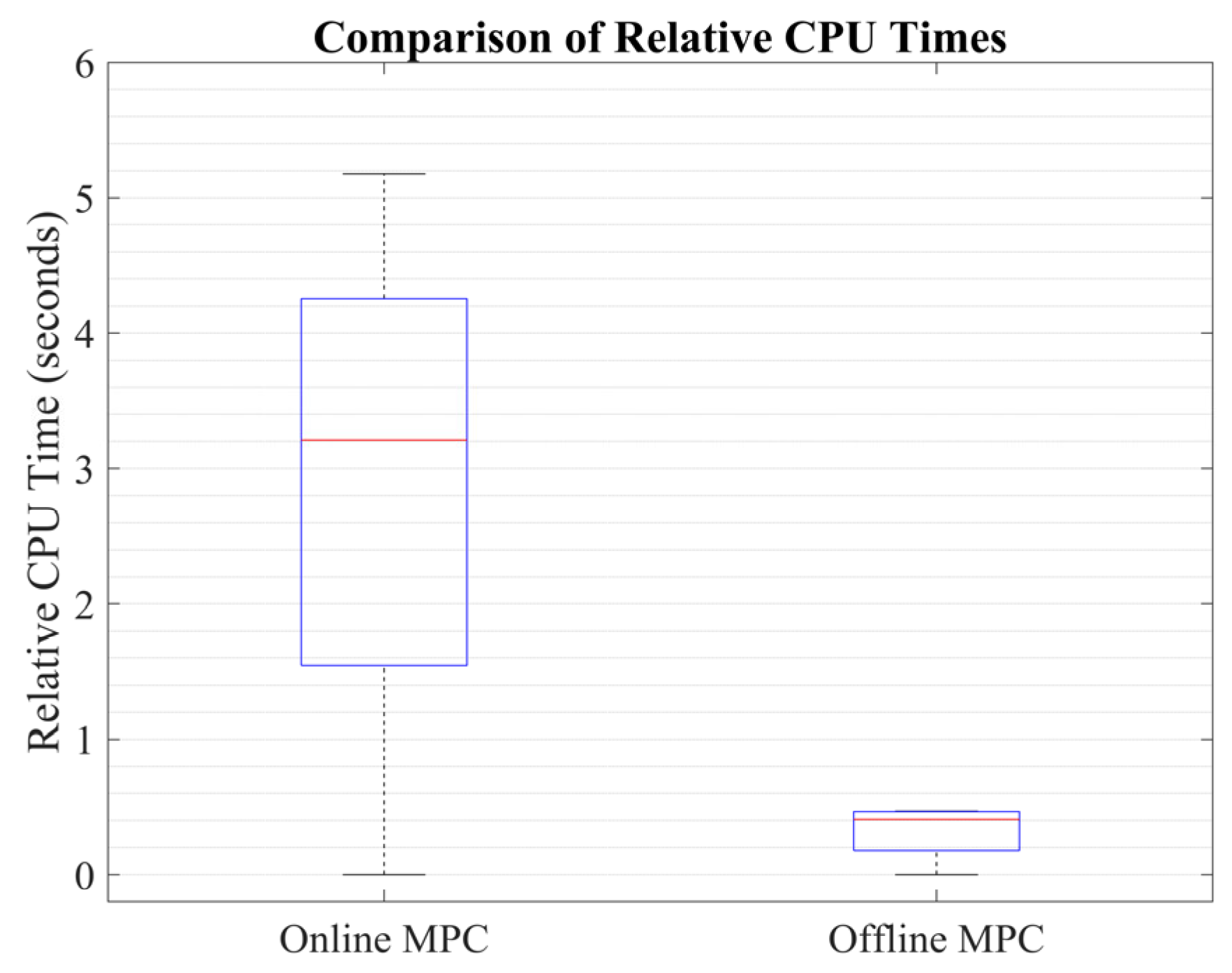
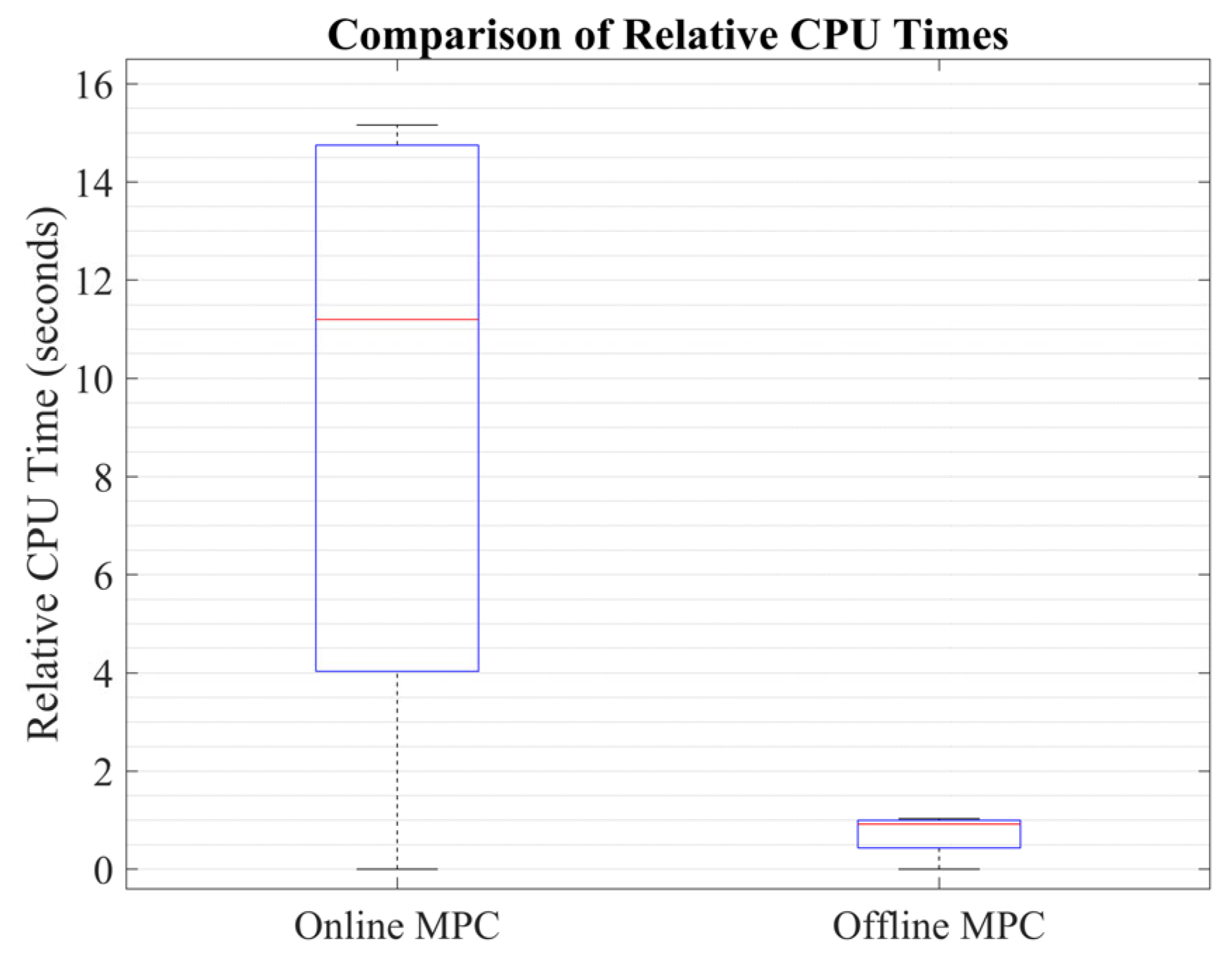
From Figure 7, it is evident that the online RMPC approach effectively tracks the design objectives and ensures the satisfaction of the design constraints. Moreover, the offline RMPC algorithm performs impressively by closely overlapping the results obtained from the online controller. The significant advantage of the offline RMPC is its reduced computational burden, requiring much less time for computation compared to the online approach. The offline RMPC is approximately 12 times faster than the online controller, as shown in Figure 8. The box–whisker plot visually represents the CPU time comparison between the online MPC and the proposed offline RMPC approach, further highlighting the computational efficiency of the offline method.

Using the algorithm described in the previous section, online and offline RMPC simulations are conducted for the wet asphalt road condition, similar to the dry asphalt condition. In the offline algorithm, the state variable ($x_1$) is discretized into a sequence of seven states, denoted as $x_1^{set}=\left[0.131, 0.11, 0.09, 0.06, 0.04, 0.02, 0\right]$. Figure 9 illustrates the relevant nested ellipsoids defined by $Q_i^{-1}$ for these discretized points.

It is important to note that in the wet asphalt road condition, the optimal value for the wheel slip is obtained as ${\lambda }_{opt}=0.131$ from the peak of the road–tire friction equation. Therefore, the discretization of the $x_1$ state is performed using seven sequences to capture the range of optimal values.

In the case of wet asphalt road conditions, the initial values for the vehicle velocity and wheel slip at the moment of braking are assumed to be the same as those in dry asphalt conditions, namely 20 m/s and 0, respectively. The controller’s design objective in this road condition is to maintain the wheel slip at its optimal value of 0.131, which corresponds to the maximum tire–road friction and ensures safe braking without skidding. Figure 10 depicts the simulation results of the ABS performance controlled with the MPC controller under these wet asphalt road conditions.

According to Figure 10, the simulation results show satisfactory performance for both controllers in the given braking moment and design constraints under wet road conditions. Similar to the previous scenario, the offline RMPC design closely aligns with the online approach and accurately tracks the reference wheel slip value, and the control input remains within its upper bound. Notably, the offline approach exhibits a significantly reduced computational burden, resulting in a much faster CPU time usage: approximately 11.5 times faster. Figure 11 illustrates the CPU time comparison between the two methods.

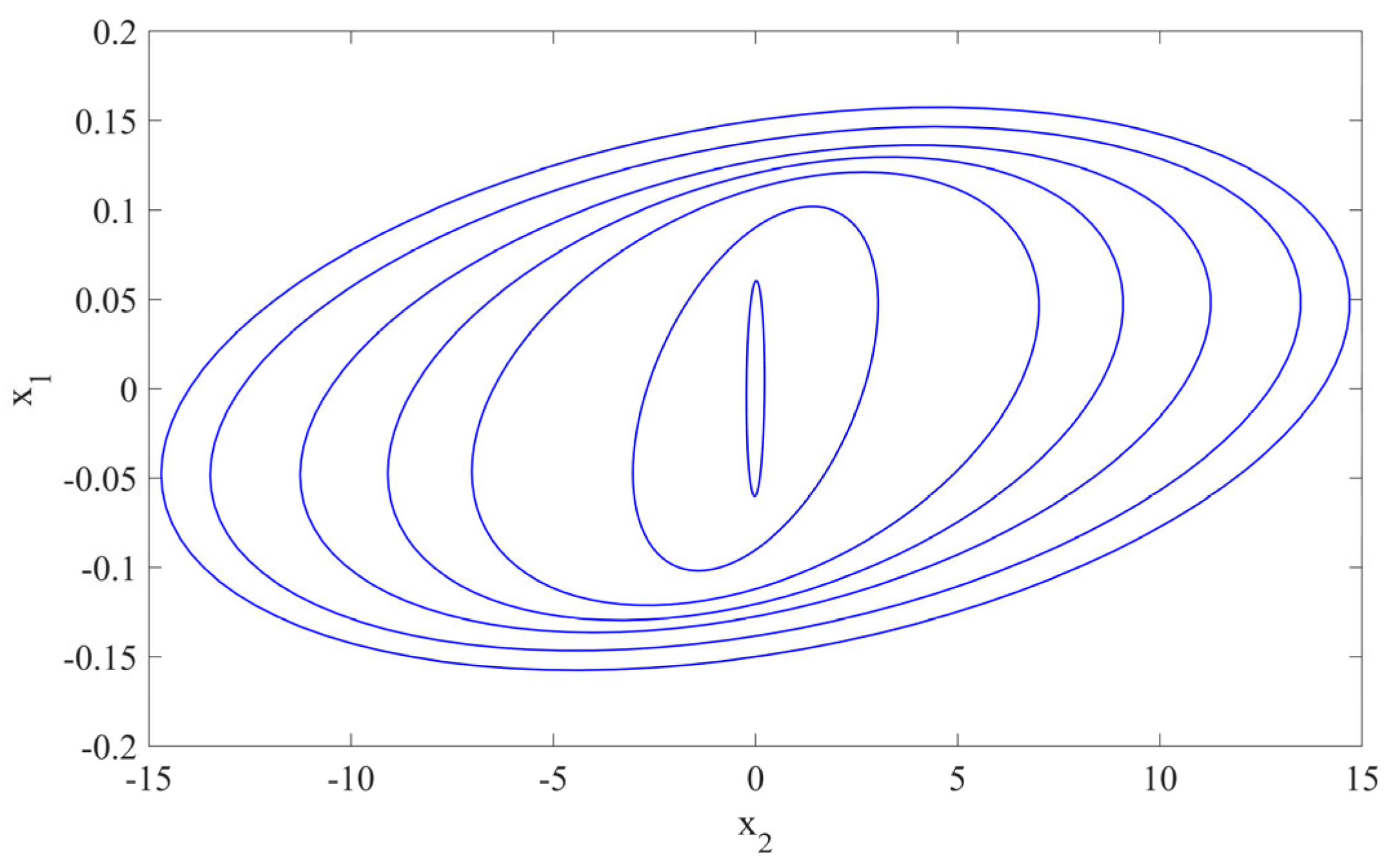
Snowy road conditions are used as another scenario to test the offline approach for the nonlinear ABS model. Due to reduced traction on snowy roads, vehicles are required to move at slower speeds. In this case, the vehicle’s speed during braking is set to 14 m/s (~50 Km/h). From Table 4, the optimal wheel slip value for these conditions is determined to be 0.06. The objective of the controller is to track and maintain this wheel slip value during braking, preventing the vehicle from skidding. The $x_1$ state is discretized to a sequence of seven states as $x_1^{set}=\left[0.06, 0.05, 0.04, 0.03, 0.02, 0.01, 0\right]$. Figure 12 represents the nested ellipsoids. Figure 13 illustrates the simulation results of online and offline RMPC designs.

Based on Figure 13, it can be observed that both the online and offline RMPC approaches effectively track the reference wheel slip and satisfy the design constraints within their bounds for all three road scenarios. However, the computational burden of the offline RMPC is significantly lower compared to the online design. The offline RMPC approach achieves this by performing the optimization offline and using a bisection search during real-time implementation, resulting in a faster CPU time. The CPU time of the offline RMPC is approximately 15 times faster than the online MPC approach, as depicted in Figure 14. This comparison of relative CPU times further highlights the efficiency of the offline RMPC in terms of computational speed and real-time implementation across different road scenarios.

In summary, for a more mathematical comparison, the CPU times of online and offline RMPC approaches are listed in

Table 5. Comparison between the online and offline MPC using relative CPU time (sec).

Road Condition	Relative CPU Time (sec)		Improvement (Time)
	Online MPC	Offline RMPC
Dry asphalt	2.90	0.25	11.60
Wet asphalt	5.19	0.45	11.53
Snowy asphalt	15.16	1.02	14.86

for different road condition scenarios.

Based on the analysis of Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, it can be concluded that the offline RMPC approach exhibits similar performance to the online MPC in controlling the nonlinear ABS model. It effectively addresses the main drawback of the online MPC design, which is the large computational burden. The offline RMPC significantly reduces the CPU time required for computation while maintaining consistent results with the online controller.

4.2. Results for Uncertain System Model

This subsection repeats the simulation study to assess the robustness of the proposed offline RMPC for varying sprung mass and wheel radius. The offline RMPC is derived using the proposed algorithm, ensuring efficacy under uncertainties. Simulation results test the controller with an uncertain tire model, considering a 10% change in sprung mass and wheel radius. This analysis evaluates the controller’s stability and performance across different vehicle configurations, enhancing its real-time applicability. Root mean square error (RMSE) values of the design objectives during parameter uncertainties for different road conditions are shown in

Table 6. RMS values of states’ error considering a 10% change in system parameters.

RMS Value	Dry Road	Wet Road	Snowy Road
$rms(\lambda -{\lambda }_{changes})$	0.0028	0.0023	8.9269 × 10−4
$\mathit{r}\mathit{m}\mathit{s}(\mathit{V}-{\mathit{V}}_{\mathit{changes}})$	0.0391	0.0364	0.0340

.

Based on the data presented in Table 6, the performance of the offline RMPC in the ABS is shown to be robust in the presence of parameter uncertainties. Despite the variations in system parameters, the offline RMPC effectively satisfies the imposed constraints. This underscores the offline RMPC’s ability to maintain stability and reliable control, even under conditions of uncertainty, making it a promising and suitable approach for practical implementation in ABS.

5. Conclusions

This study introduces a novel offline robust model predictive control (MPC) approach for controlling nonlinear ABS. The literature review reveals that MPC exhibits superior performance compared to alternative methods in terms of robustness and meeting system constraints for handling the substantial nonlinearity present in ABS. However, a major limitation of MPC is its heavy computational burden for online computation, often rendering it challenging or infeasible for real-time applications. To address this issue, the proposed offline RMPC approach is developed based on the robust asymptotically stable invariant ellipsoid methodology. It involves the offline calculation of a set of invariant state feedback laws corresponding to a sequence of nested invariant stable ellipsoids using linear matrix inequalities (LMIs) that incorporate design constraints. Simulation results demonstrate that by employing a bisection search over the nested ellipsoids, the offline algorithm’s computational burden is significantly reduced while maintaining substantial agreement with the results obtained by the classic MPC. This reduction in computational burden makes the proposed offline approach viable for real-time applications such as ABS systems, with minimal impact on system behavior. To showcase the performance of the proposed offline algorithm, three distinct road conditions are considered, and a comparison of CPU times is conducted between the classic online MPC and the proposed offline RMPC controllers under these scenarios. The simulation results reveal comparable responses between the offline RMPC algorithm and the online MPC, with response times that are 11–15 times faster and a significantly reduced computational burden. The robustness of the proposed offline method against parameter uncertainties is thoroughly tested in the final step, wherein a 10% variation in tire parameters is considered. The system’s state RMSE values serve as a clear demonstration of the novel offline RMPC’s robustness and performance under conditions of uncertainty, effectively meeting the design constraints.

As a future endeavor, the authors plan to extend the proposed ABS controller by integrating it with the electronic stability control (ESC) system within a full-car model. This extension aims to enhance the overall vehicle dynamic control and further improve the safety and stability of the vehicle. Furthermore, as part of a future study, the novel offline RMPC methodology will be subjected to real-time testing on an ABS system using a hardware-in-the-loop simulation on the dSPACE platform, which aims to assess the feasibility and performance of the proposed approach in enhancing ABS systems, contributing to automotive control strategy advancements.