Measuring Point Planning and Fitting Optimization of the Flange and Spigot Structures of Aeroengine Rotors
Abstract
1. Introduction
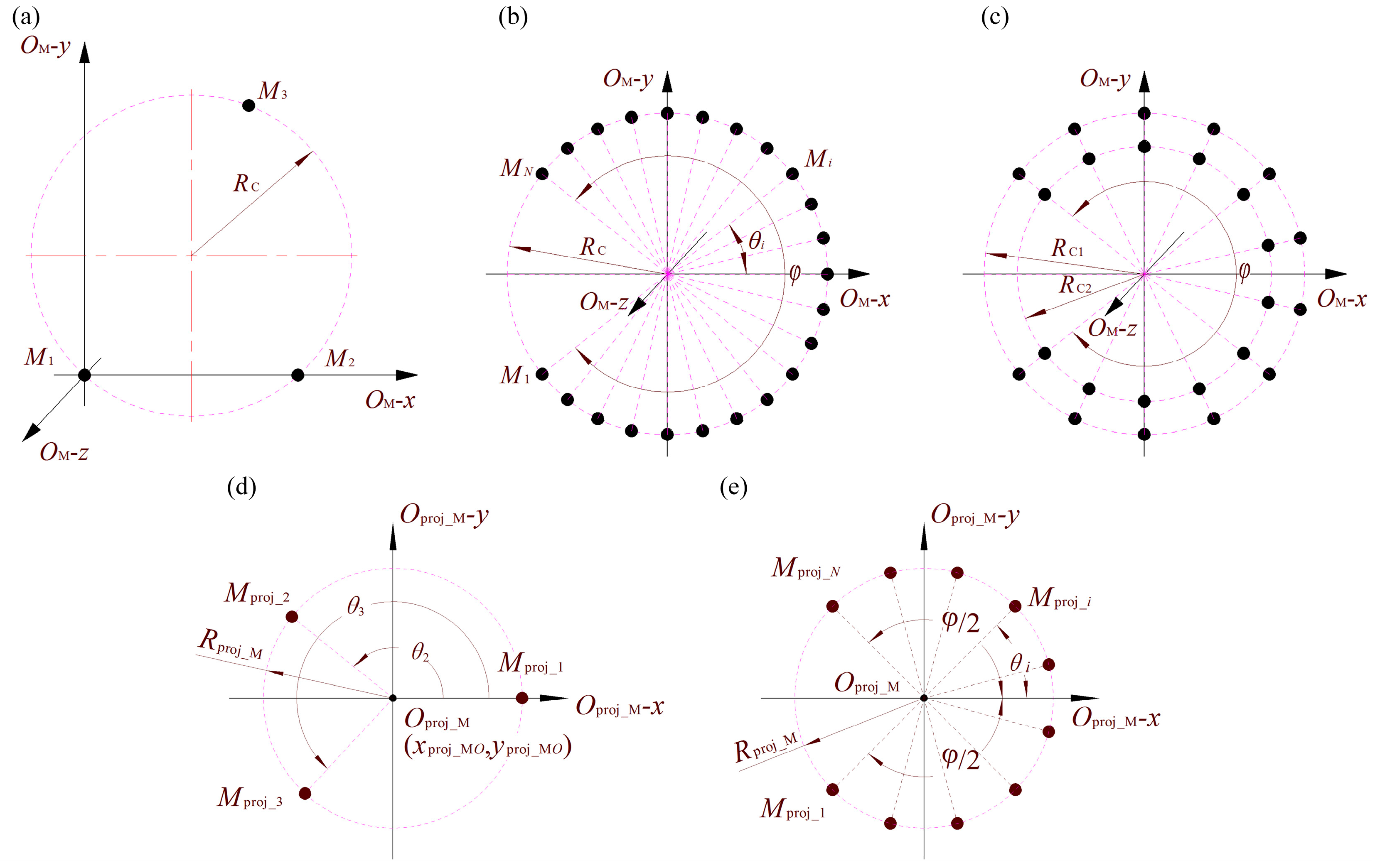
2. Measuring Point Planning Method
3. Optimization of Fitting Algorithm
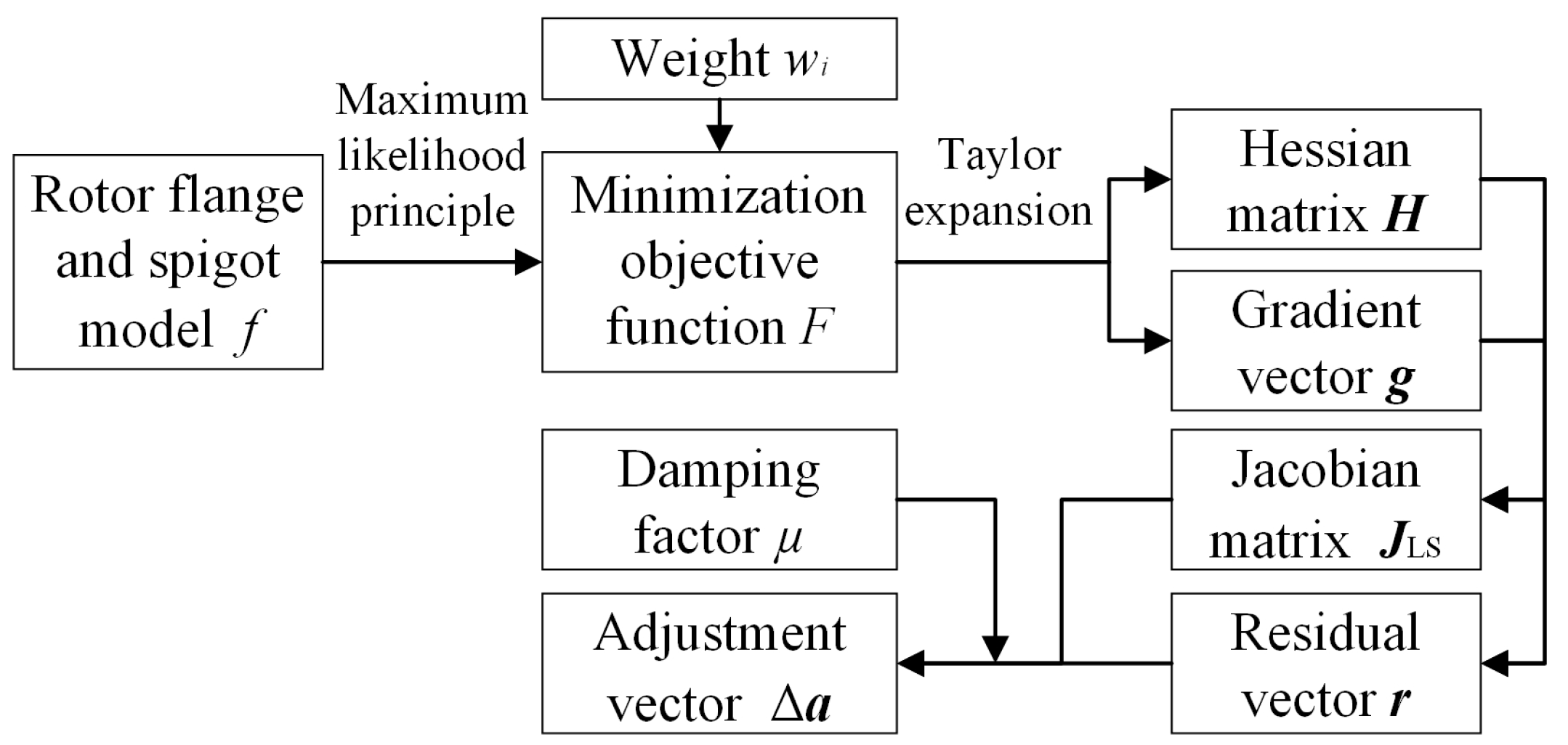
3.1. LS Principle and Gauss Newton Iterative Solution Method Considering Damping Factors
3.2. Optimized Fitting Method for Flange Annular End Face
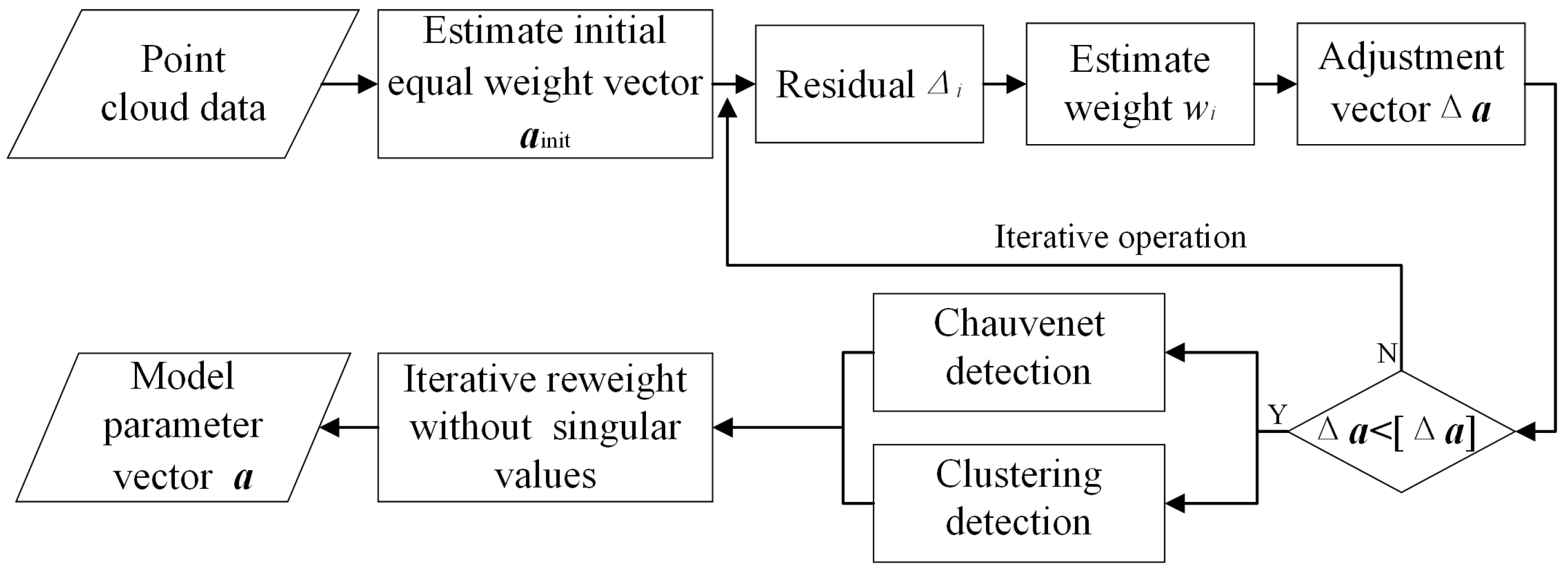
3.2.1. Iterative Estimation of Weights Based on Residuals
3.2.2. Standard Residual Singular Value Detection Based on the Chauvenet Criterion
3.2.3. Clustering Detection
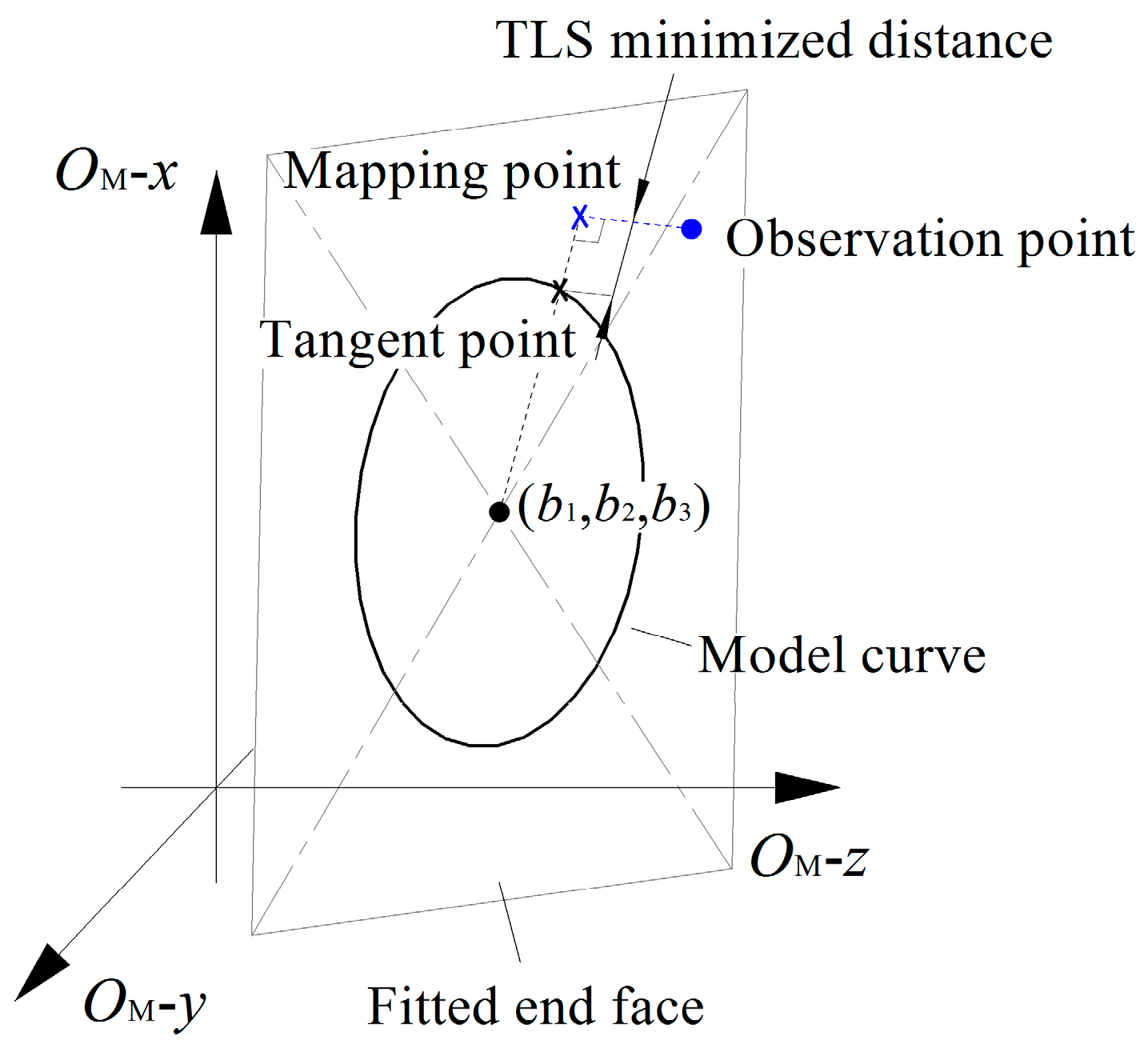
3.3. Optimized Fitting Method for Spigot Cylindrical Face
4. Measurement Experiment
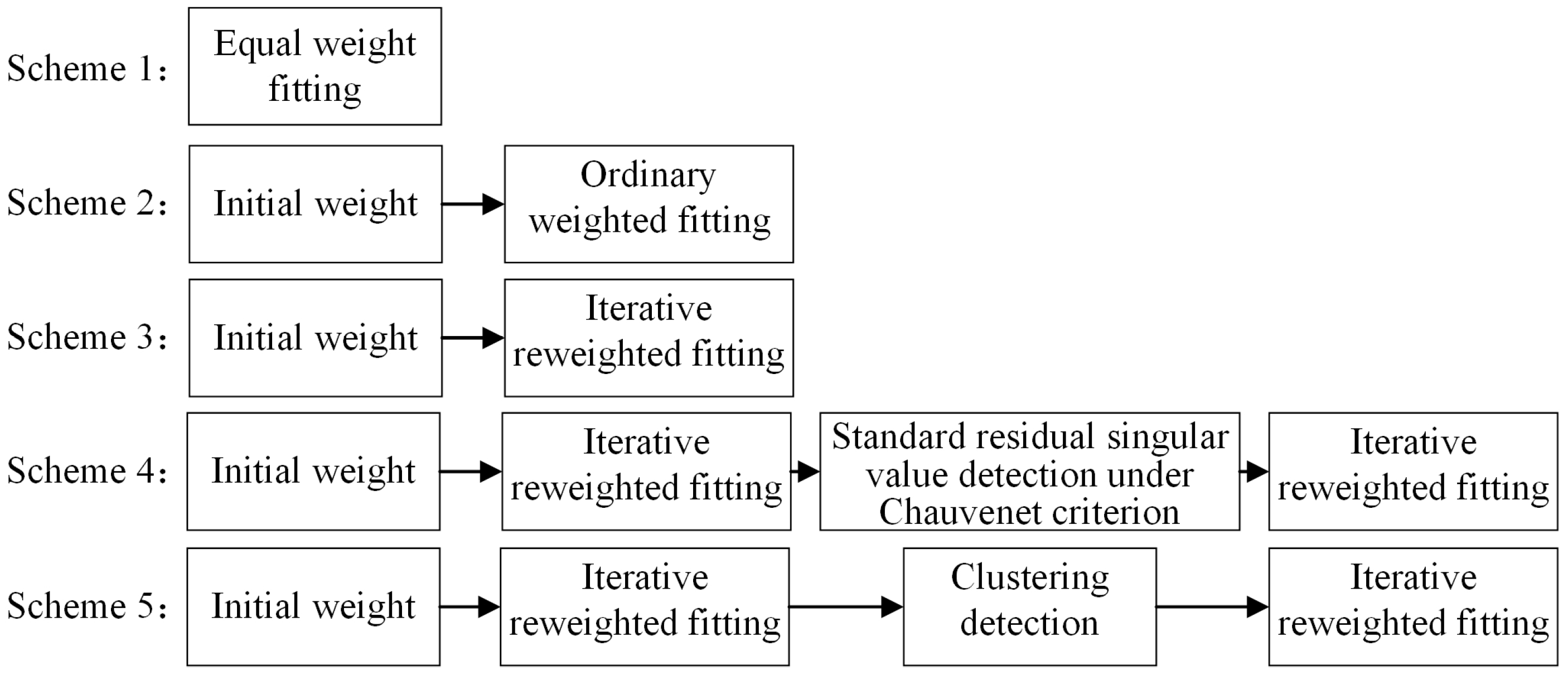
4.1. Measurement and Fitting Experiment of Flange end Face
4.2. Measurement and Fitting Experiment of the Spigot Cylindrical Face
5. Conclusions
- (1)
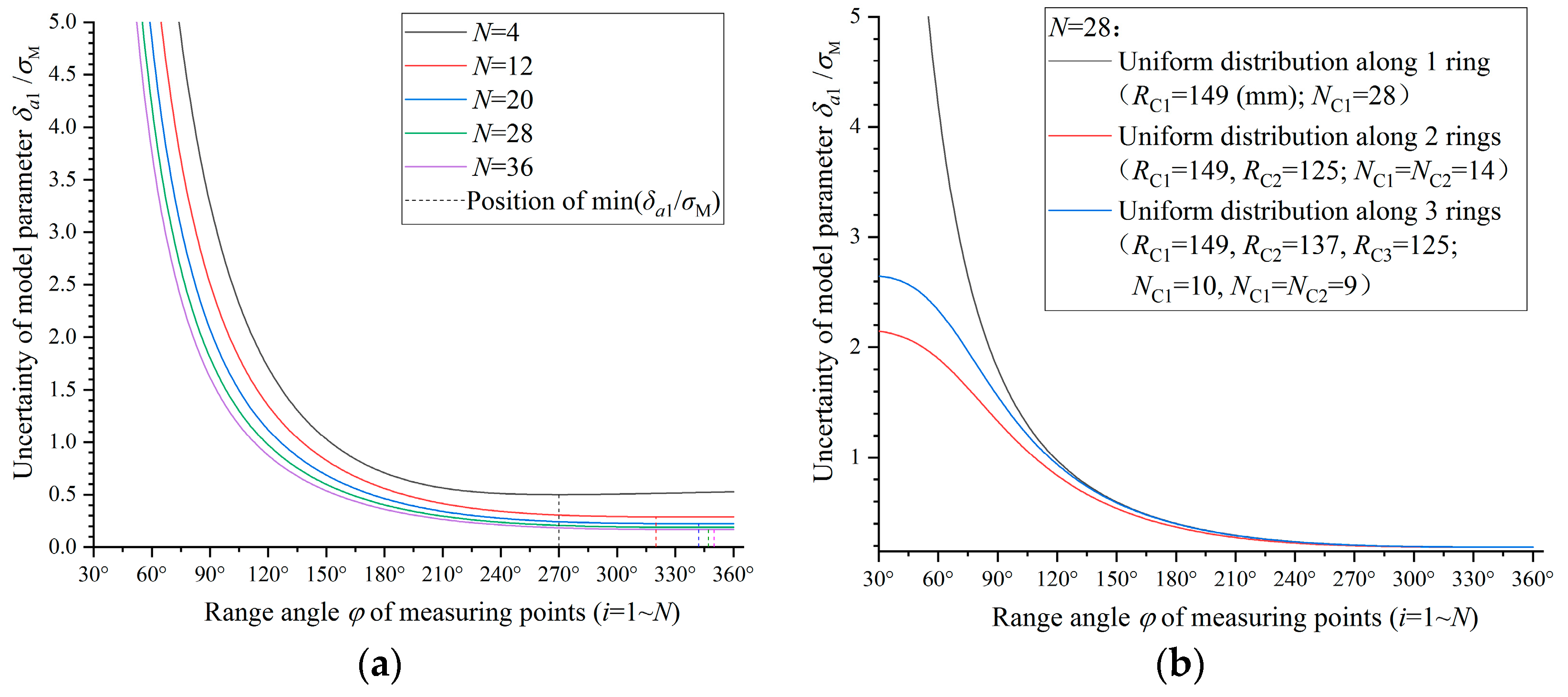
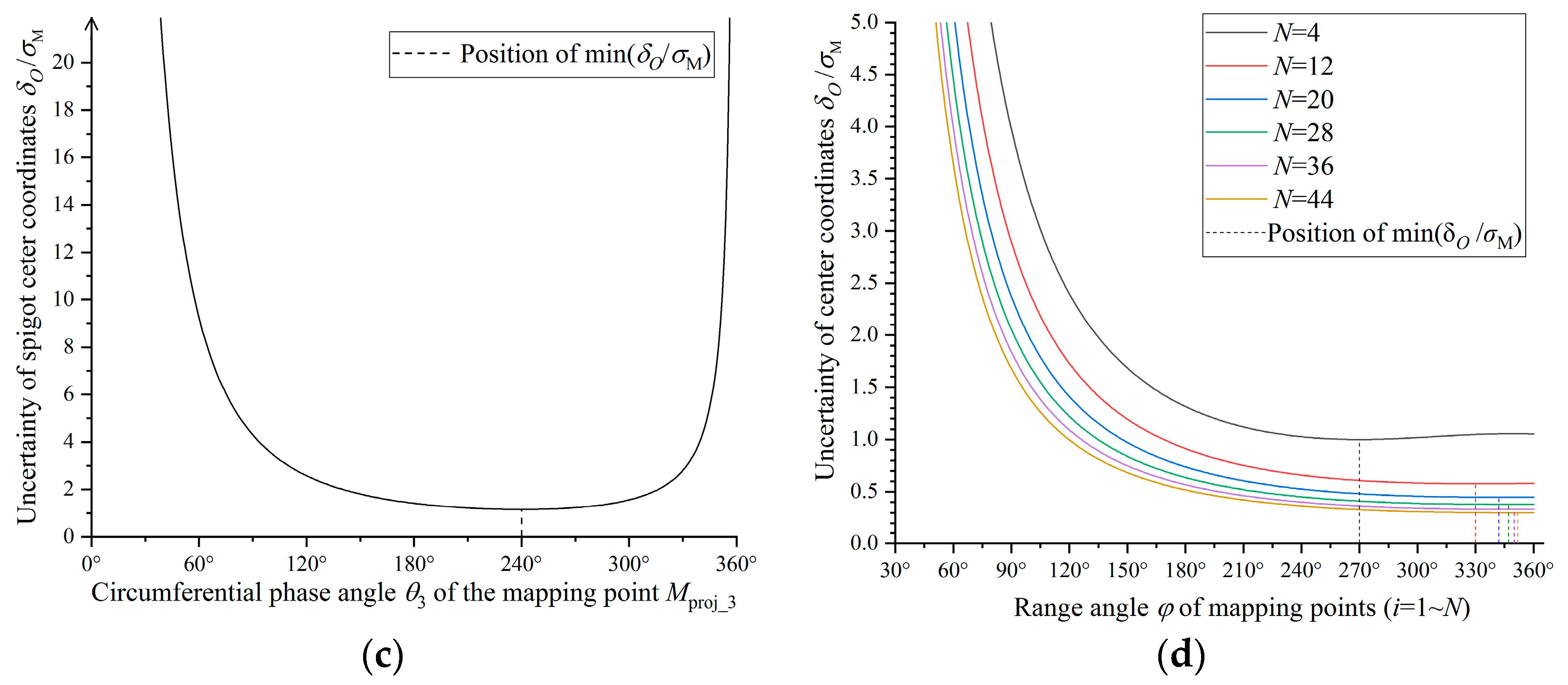
- The equation of model parameter uncertainty δa1 that affects the end face normal vector error angle and the equation of coordinate uncertainty δO of the spigot spatial circle center are derived. The effects of the circumferential phase angle θi, distribution range angle φ, total number of measuring points N, and multiple concentric measurement paths on uncertainty are analyzed. The measuring point planning schemes for flange annular end faces and spigot cylindrical faces of the LPT rotors of an aeroengine are proposed.
- (2)
- The LS minimization criterion and Gauss Newton iterative solution principle under Levenberg Marquardt damping factors are clarified. Based on this principle, an optimized iterative reweighting method with singular values removed is proposed for fitting the flange annular end face, including processes such as residual-based weight wi iterative estimation, standard residual singular value detection under Chauvenet criterion, and clustering detection. Additionally, a mapping point TLS method with practical geometric significance is proposed for fitting the circle center of the spigot.
- (3)
- Measurement and fitting experiments on a low-pressure turbine shaft are performed. Five fitting methods for the flange annular end face are compared. When the optimized iterative reweighting method is used with singular values removed, the goodness of fit gfit = 0.756, model parameter uncertainty δa1 = 0.026, and δa2 and δa3 < 4.3 × 10−5. Simultaneously, three fitting methods for the spigot cylindrical face are compared. When the mapping point iterative TLS fitting method is used, the goodness of fit gfit = 0.011 and the average orthogonal distance = 0.089 mm. The proposed fitting methods achieve better fitting accuracy results compared with the other traditional methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Liu, Y.; Zhang, M.; Sun, C.; Hu, M.; Chen, D.; Liu, Z.; Tan, J. A method to minimize stage-by-stage initial unbalance in the aero engine assembly of multistage rotors. Aerosp. Sci. Technol. 2019, 85, 270–276. [Google Scholar] [CrossRef]
- Yang, Z.; Hussain, T.; Popov, A.A.; McWilliam, S. Novel optimization technique for variation propagation control in an aero-engine assembly. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 100–111. [Google Scholar] [CrossRef]
- Nizametdinov, F.R.; Romashin, Y.S.; Berne, A.L.; Leontyev, M.K. Investigation of bending stiffness of gas turbine engine rotor flanged connection. J. Mech. 2020, 36, 729–736. [Google Scholar] [CrossRef]
- Zhou, T.; Gao, H.; Wang, X.; Li, L.; Chen, J.; Peng, C. Prediction method of aeroengine rotor assembly errors based on a novel multi-axis measuring and connecting mechanism. Machines 2022, 10, 387. [Google Scholar] [CrossRef]
- Ding, S.; He, Y.; Zheng, X. A probabilistic approach for three-dimensional variation analysis in aero-engine rotors assembly. Int. J. Aeronaut. Space 2021, 22, 1092–1105. [Google Scholar] [CrossRef]
- Hussain, T.; Yang, Z.; Popov, A.A.; McWilliam, S. Straight-build assembly optimization: A method to minimize stage-by-stage eccentricity error in the assembly of axisymmetric rigid components (two-dimensional case study). J. Manuf. Sci. Eng. 2011, 133, 031014. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Jin, S.; Ding, S.; Li, Z.; Yang, F.; Ma, X. Point-based solution using Jacobian-Torsor theory into partial parallel chains for revolving components assembly. J. Manuf. Syst. 2018, 46, 46–58. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Y.; Wang, C.; Hong, J. Interval analysis of rotor dynamic response based on Chebyshev polynomials. Chin. J. Aeronaut. 2020, 33, 2342–2356. [Google Scholar] [CrossRef]
- Satish, T.N.; Rao, A.N.V.; Nambiar, A.S.; Uma, G.; Umapathy, M.; Chandrashekhar, U.; Petley, V.U. Investigation into the development and testing of a simplex capacitance sensor for rotor tip clearance measurement in turbo machinery. Exp. Tech. 2018, 42, 575–592. [Google Scholar] [CrossRef]
- Jayaweera, N.; Webb, P.; Johnson, C. Measurement assisted robotic assembly of fabricated aero-engine components. Assem. Autom. 2010, 30, 56–65. [Google Scholar] [CrossRef]
- Wong, S.K.; Riseborough, E.; Duff, G.; Chan, K.K. Radar cross-section measurements of a full-scale aircraft duct/engine structure. IEEE Trans. Antennas Propag. 2006, 54, 2436–2441. [Google Scholar] [CrossRef]
- Garcia, I.; Przysowa, R.; Amorebieta, J.; Zubia, J. Tip-clearance measurement in the first stage of the compressor of an aircraft engine. Sensors 2016, 16, 1897. [Google Scholar] [CrossRef]
- Ristic, M.; Brujic, D.; Ainsworth, I. Measurement-based updating of turbine blade CAD models: A case study. Int. J. Comput. Integr. Manuf. 2004, 17, 352–363. [Google Scholar] [CrossRef]
- Burghardt, A.; Kurc, K.; Szybicki, D.; Muszynska, M.; Szczech, T. Robot-operated inspection of aircraft engine turbine rotor guide vane segment geometry. Teh. Vjesn. Tech. Gaz. 2017, 242, 345–348. [Google Scholar]
- Zhang, M.; Liu, Y.; Sun, C.; Wang, X.; Tan, J. Measurements error propagation and its sensitivity analysis in the aero-engine multistage rotor assembling process. Rev. Sci. Instrum. 2019, 90, 115003. [Google Scholar] [CrossRef]
- Sun, B.; Li, B. Laser displacement sensor in the application of aero-engine blade measurement. IEEE Sens. J. 2016, 16, 1377–1384. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, W.; Wu, Q.; Wang, Y.; Yu, B.; Yue, Y.; Zhang, J. A combined measurement method for large-size aerospace components. Sensors 2020, 20, 4843. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Sheng, B.; Chen, G.; Luo, R.; Sheng, G.; Lu, Y. A contact on-machine measurement points’ planning method based on similarity of 3-D process element. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Mao, Z.; Li, S.; Xu, Y.; Zeng, Q.; Zhu, K. A difference measurement points planning method for large-scale surface of aircraft. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1024–1031. [Google Scholar]
- Magdziak, M. Selection of the best model of distribution of measurement points in contact coordinate measurements of free-form surfaces of products. Sensors 2019, 19, 5346. [Google Scholar] [CrossRef] [PubMed]
- Piasecki, R. A generalization of the inhomogeneity measure for point distributions to the case of finite size objects. Phys. A 2008, 387, 5333–5341. [Google Scholar] [CrossRef]
- Calvo, R. Sphericity measurement through a new minimum zone algorithm with error compensation of point coordinates. Measurement 2019, 138, 291–304. [Google Scholar] [CrossRef]
- Seiler, A.; Grossmann, D.; Juettler, B. Spline surface fitting using normal data and norm-like functions. Comput. Aided Geom. Des. 2018, 64, 37–49. [Google Scholar] [CrossRef]
- Brujic, D.; Ainsworth, I.; Ristic, M. Fast and accurate NURBS fitting for reverse engineering. Int. J. Adv. Manuf. Technol. 2011, 54, 691–700. [Google Scholar] [CrossRef][Green Version]
- Gao, F.; Pan, Z.; Zhang, X.; Li, Y.; Duan, J. An adaptive sampling method for accurate measurement of aeroengine blades. Measurement 2021, 173, 108531. [Google Scholar]
- Magdziak, M. The influence of a number of points on results of measurements of a turbine blade. Aircr. Eng. Aerosp. Technol. 2017, 89, 953–959. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Sun, C.; Wang, X.; Tan, J. Precision measurement and evaluation of flatness error for the aero-engine rotor connection surface based on convex hull theory and an improved PSO algorithm. Meas. Sci. Technol. 2020, 31, 085006. [Google Scholar] [CrossRef]
- Zhu, L.; Luo, H.; Ding, H. Optimal design of measurement point layout for workpiece localization. J. Manuf. Sci. Eng. 2008, 131, 011006–01100613. [Google Scholar] [CrossRef]
- Ding, S.; Jin, S.; Li, Z.; Wei, Z.; Yang, F. Deviation propagation model and optimization of concentricity for aero-engine rotor assembly. J. Shanghai Jiao Tong Univ. 2018, 52, 54–62. [Google Scholar]
- Xie, Z.; Jiang, Z.; Zhu, H.; Li, Z.; Lei, L.; Kong, M.; Wang, D.; Zhang, B. Research on fitting method of thread middle axis based on 3D point cloud. Acta Metrol. Sin. 2020, 41, 918–925. [Google Scholar]
- Whitehouse, D.J. Some theoretical aspects of error separation techniques in surface metrology. J. Phys. E Sci. Instrum. 1976, 9, 531–536. [Google Scholar] [CrossRef]
- Jin, S.; Fan, D.; Chen, R.; Tian, M. Method and experimental study of machine vision measurement for the roundness of rotary parts. Mach. Des. Res. 2016, 32, 117–119, 124. [Google Scholar]
- Chetwynd, D.G. High-precision measurement of small balls. J. Phys. E Sci. Instrum. 1987, 20, 1179–1187. [Google Scholar] [CrossRef]
- Sun, C.; Wang, B.; Liu, Y.; Wang, X.; Li, C.; Wang, H.; Tan, J. Design of high accuracy cylindrical profile measurement model for low-pressure turbine shaft of aero engine. Aerosp. Sci. Technol. 2019, 95, 105442. [Google Scholar] [CrossRef]
- Sun, C.; Wang, L.; Tan, J.; Zhao, B.; Tang, Y. Design of roundness measurement model with multi-systematic error for cylindrical components with large radius. Rev. Sci. Instrum. 2016, 87, 025110. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Sun, C.; Wang, X.; Tan, J. A systematic error modeling and separation method for the special cylindrical profile measurement based on 2-dimension laser displacement sensor. Rev. Sci. Instrum. 2019, 90, 105006. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Yuan, B. Novel on-machine measurement system and method for flatness of large annular plane. Meas. Sci. Technol. 2020, 31, 015004. [Google Scholar] [CrossRef]
- Song, T.; Xi, F.J.; Guo, S.; Ming, Z.; Lin, Y. A comparison study of algorithms for surface normal determination based on point cloud data. Precis. Eng. 2015, 39, 47–55. [Google Scholar] [CrossRef]
- Nouira, H.; Bourdet, P. Evaluation of roundness error using a new method based on a small displacement screw. Meas. Sci. Technol. 2014, 25, 044012. [Google Scholar] [CrossRef]

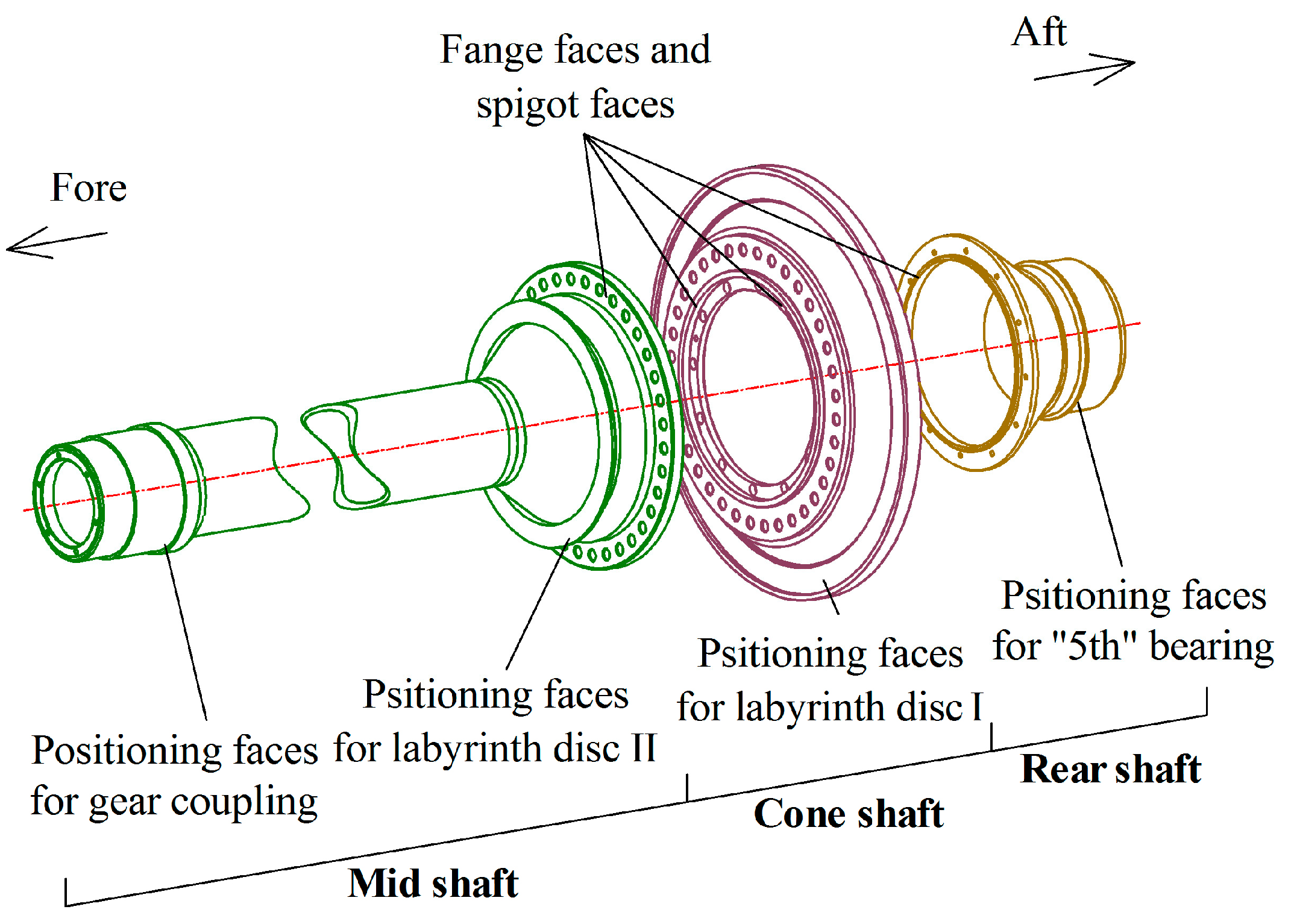


| End Faces | Fore Flange Face on the Rear Shaft/Aft Flange Face on the Cone Shaft | Fore Flange Face on the Cone Shaft/Aft Flange Face on the Mid Shaft | “Fifth” Bearing Positioning End Face on the Rear Shaft | Labyrinth Disc I Positioning End Face on the Cone Shaft | Labyrinth Disc II Positioning End Face on the Mid Shaft | Toothed Coupling Positioning End Face on the Mid Shaft |
|---|---|---|---|---|---|---|
| Total number of measuring points N | 22 | 28 | 14 | 38 | 22 | 12 |
| Distribution rings | 2 | 2 | 1 | 2 | 2 | 1 |
| Measuring path radius RC1 (mm) | 104 | 125 | 79 | 191 | 107 | 64 |
| Measuring path radius RC2 (mm) | 113 | 149 | - | 208 | 120 | - |
| Cylindrical Faces | Fore Spigot Face on the Rear Shaft/Aft Spigot Face on the Cone Shaft | Fore Spigot Face on the Cone Shaft/Aft Spigot Face on the Mid Shaft | “Fifth” Bearing Positioning Cylindrical Face on the Rear Shaft | Labyrinth Disc I Positioning Cylindrical Face on the Cone Shaft | Labyrinth Disc II Positioning Cylindrical Face on the Mid Shaft | Gear Coupling Positioning Cylindrical Face on the Mid Shaft |
|---|---|---|---|---|---|---|
| Total number of measuring points N | 30 | 36 | 22 | 50 | 36 | 18 |
| Spigot radius RS (mm) | 99 | 119 | 76 | 213 | 125 | 62 |
| Point Ordinal i | Coordinate (xMi, yMi, zMi) (mm) | Point Ordinal i | Coordinate (xMi, yMi, zMi) (mm) |
|---|---|---|---|
| 1 | (779.131, −28.201, 738.614) | 15 | (755.145, −27.781, 739.189) |
| 2 | (765.561, 36.669, 740.852) | 16 | (743.757, 26.638, 741.100) |
| 3 | (725.182, 89.201, 743.466) | 17 | (709.884, 70.707, 743.266) |
| 4 | (665.992, 118.993, 745.763) | 18 | (660.228, 95.703, 745.333) |
| 5 | (599.710, 120.149, 747.419) | 19 | (604.624, 96.671, 747.502) |
| 6 | (539.475, 92.431, 748.026) | 20 | (554.089, 73.419, 748.019) |
| 7 | (497.208, 41.339, 747.523) | 21 | (518.630, 30.555, 746.707) |
| 8 | (481.281, −23.014, 745.988) | 22 | (505.269, −23.431, 745.412) |
| 9 | (494.854, −87.879, 743.753) | 23 | (516.656, −77.848, 743.528) |
| 10 | (535.232, −140.412, 741.160) | 24 | (550.530, −121.921, 741.345) |
| 11 | (594.424, −170.208, 738.866) | 25 | (600.188, −146.915, 739.493) |
| 12 | (660.704, −171.360, 737.185) | 26 | (655.788, −147.884, 738.012) |
| 13 | (720.941, −143.646, 736.614) | 27 | (706.324, −124.632, 737.485) |
| 14 | (763.209, −92.552, 737.063) | 28 | (741.783, −81.770, 737.861) |
| Iterations | Initial Values of Model Parameters and Iterative Compensation Values |
|---|---|
| Equal weight | ainit = [758.7075, −0.0247, 0.0307] |
| First weighting | ∆a = [−0.2475, 0.0003, −0.0006] |
| Second iteration reweighting | ∆a = [−0.0677, 0.0001, −0.0001] |
| Third iteration reweighting | ∆a = [−0.0203, 0.0000, 0.0000] |
| Fourth iteration reweighting | ∆a = [0.0046, 0.0000, 0.0000] |
| Reweighting after removing singular values | ∆a = [0.0001, 0.0000, 0.0000] |
| Pre-Processing before Detection | Detection Method | Experiment No. | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Equal weight | Residual method | 2 | 1 | 0 | 2 | 0 |
| Clustering detection | 0 | 0 | 0 | 1 | 0 | |
| Iterative reweighting | Residual method | 2 | 1 | 1 | 2 | 0 |
| Clustering detection | 2 | 1 | 0 | 2 | 0 | |
| Fitting Scheme | Weighted Variance χ2 | Goodness of Fit gfit | Uncertainty δa1 | Uncertainty δa2 | Uncertainty δa3 |
|---|---|---|---|---|---|
| Equal weight | 1.355 | 0.054 | 0.289 | 4.45 × 10−4 | 4.45 × 10−4 |
| Initial equal weight + ordinary weighting | 8.592 | 0.344 | 0.066 | 9.66 × 10−5 | 1.09 × 10−4 |
| Initial equal weight + iterative reweighting | 23.244 | 0.930 | 0.028 | 4.35 × 10−5 | 4.56 × 10−5 |
| Iterative reweighting + singular point detection + reweighting | 18.895 | 0.756 | 0.026 | 4.09 × 10−5 | 4.26 × 10−5 |
| Point Ordinal i | Coordinate (xMi, yMi, zMi) (mm) | Point Ordinal i | Coordinate (xMi, yMi, zMi) (mm) |
|---|---|---|---|
| 1 | (749.407, −27.570, 735.914) | 19 | (510.816, −23.424, 741.800) |
| 2 | (747.988, −6.840, 736.496) | 20 | (512.268, −44.161, 741.056) |
| 3 | (742.961, 13.347, 737.306) | 21 | (517.289, −64.343, 740.337) |
| 4 | (734.499, 32.334, 738.070) | 22 | (525.729, −83.333, 739.604) |
| 5 | (722.886, 49.592, 738.795) | 23 | (537.342, −100.582, 738.873) |
| 6 | (708.472, 64.551, 739.561) | 24 | (551.787, −115.522, 738.089) |
| 7 | (691.649, 76.746, 740.451) | 25 | (568.603, −127.775, 737.305) |
| 8 | (672.951, 85.874, 741.211) | 26 | (587.287, −136.891, 736.484) |
| 9 | (652.969, 91.608, 741.744) | 27 | (607.274, −142.623, 735.869) |
| 10 | (632.299, 93.777, 742.380) | 28 | (627.966, −144.795, 735.212) |
| 11 | (611.534, 92.340, 742.795) | 29 | (648.684, −143.330, 734.757) |
| 12 | (591.375, 87.282, 743.212) | 30 | (668.887, −138.297, 734.422) |
| 13 | (572.349, 78.825, 743.408) | 31 | (687.876, −129.845, 734.323) |
| 14 | (555.123, 67.192, 743.357) | 32 | (705.121, −118.199, 734.216) |
| 15 | (540.129, 52.775, 743.428) | 33 | (720.110, −103.756, 734.224) |
| 16 | (527.913, 35.938, 743.246) | 34 | (732.342, −86.929, 734.493) |
| 17 | (518.756, 17.244, 742.812) | 35 | (741.472, −68.230, 734.762) |
| 18 | (513.015, −2.741, 742.426) | 36 | (747.227, −48.238, 735.204) |
| Fitting Scheme | Initial Values of Model Parameters and Iterative Compensation Values |
|---|---|
| Initial average method estimation | binit = [630.2059, −25.6046, 742.3183, 119.3481] |
| LS fitting | ∆b= [−0.1181, 0.1368, 0.0069, −0.0001] |
| First TLS fitting | ∆b = [−0.1057, 0.1260, 0.0063, 0.0000] |
| Second TLS fitting | ∆b = [0.1119, −0.1387, −0.0069, −0.0001] |
| Third TLS fitting | ∆b = [0.0880, −0.1004, −0.0051, 0.0000] |
| Fourth TLS fitting | ∆b = [0.0005, 0.0090, 0.0002, −0.0001] |
| Fitting Scheme | Average Orthogonal (mm) | Variance χ2 | Goodness of Fit gfit |
|---|---|---|---|
| LS fitting | 0.116 | 0.622 | 0.019 |
| Single TLS fitting | 0.105 | 0.517 | 0.016 |
| Iterative TLS fitting | 0.089 | 0.366 | 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Hu, L.; Jin, X.; Li, T.; Zhang, Y.; Chen, J.; Gao, H. Measuring Point Planning and Fitting Optimization of the Flange and Spigot Structures of Aeroengine Rotors. Machines 2023, 11, 786. https://doi.org/10.3390/machines11080786
Zhou T, Hu L, Jin X, Li T, Zhang Y, Chen J, Gao H. Measuring Point Planning and Fitting Optimization of the Flange and Spigot Structures of Aeroengine Rotors. Machines. 2023; 11(8):786. https://doi.org/10.3390/machines11080786
Chicago/Turabian StyleZhou, Tianyi, Lei Hu, Xiaoxiao Jin, Ting Li, Yan Zhang, Jianfeng Chen, and Hang Gao. 2023. "Measuring Point Planning and Fitting Optimization of the Flange and Spigot Structures of Aeroengine Rotors" Machines 11, no. 8: 786. https://doi.org/10.3390/machines11080786
APA StyleZhou, T., Hu, L., Jin, X., Li, T., Zhang, Y., Chen, J., & Gao, H. (2023). Measuring Point Planning and Fitting Optimization of the Flange and Spigot Structures of Aeroengine Rotors. Machines, 11(8), 786. https://doi.org/10.3390/machines11080786






