Abstract
One of the most discussed topics in toothbrush design is identifying the contact force exerted by the bristles on the teeth. Each bristle must generate a contact force to ensure tooth cleaning without damaging it. Numerical simulation is a very powerful tool for understanding the influence of design parameters (bristle shape and materials). This paper proposes a flexible multibody model to efficiently simulate the 3D compliance of a toothbrush. Each bristle is modeled using a discrete, flexible approach. The contact between the bristles and the target surface is established using the penalty contact method. An experimental test bench with a Universal Robot and a flat, transparent surface is set up. Validation is provided by comparing the reaction forces of the toothbrush with the reaction forces acquired by the load cells mounted on the end effector of the Robot. The results demonstrate the accuracy of estimating normal and tangential forces in various operating situations. The discrete flexible multibody technique has also demonstrated its viability in evaluating the displacement of the bristles when the toothbrush’s base body is put through a specified motion, even when it is exposed to a sudden change in direction. As a result, the model can be effectively utilized to assess how well various brush classes remove dental plaque. Therefore, the suggested model could provide guidance for holistic modeling and advancements in toothbrush design to boost their effectiveness for thorough cleaning.
1. Introduction
Oral hygiene is one of the most discussed topics in dentistry. Poor oral hygiene can lead to several oral diseases. In [], the World Health Organization highlights that the global situation regarding oral health is alarming and requires urgent action. Over the past 30 years, oral disease cases have increased by about 1 billion. The main reason for this increase is the lack of oral health care. One of the key factors in reducing cases of oral diseases is prevention. Good oral hygiene greatly lowers the chance of developing oral diseases. Therefore, the topic of cleaning teeth is a very important issue. The tools available for oral hygiene can be classified into toothbrushes (and toothpaste), dental floss, and periodic cleanings at professional dentists.
For many years, one of the most discussed dental topics has been the correct use of the toothbrush to clean the teeth. Proper use of the toothbrush allows you to perform a complete cleaning without damaging the tooth. In particular, three main factors can be identified that impact the effectiveness of brushing: the type of toothpaste used; toothbrush handling; and the shape and materials with which the toothbrush is characterized.
In the literature, several experimental or clinical trials have been carried out on the analysis of toothbrush wear. A study [] reported on the erosion generated from toothpaste slurries of different abrasive levels and toothbrushes of different filament diameters. A systematic review [] reports how the effects of bristle stiffness and bristle end shape influence tooth wear. The impact of toothbrushes with tapered and cross-angled soft bristle designs on dental plaque and gingival inflammation through a randomized and controlled clinical trial is discussed in []. An analysis of the wear of different toothbrushes that have bristles of different stiffness was experimentally verified in []. Analysis shows that as stiffness increases, wear increases despite the overall force applied by the toothbrush being kept constant.
Other experimental comparisons have been made on thin-bristled toothbrushes (ultrasoft toothbrushes) []. In this study, it is demonstrated that different types of ultra-soft toothbrushes have a different effect on the progression of erosive tooth wear as a function of the substrate (dentine or enamel).
As computing resources increase, numerical simulation becomes increasingly important for component design. For this reason, numerical simulation has become a very powerful tool for understanding the influence of design parameters (bristle shape and materials). In recent years, there have been a few attempts to synthesize the toothbrushing phenomenon through mathematical or numerical models. In particular, in 1990, Rawls et al. [] developed a mathematical model to predict the stiffness of toothbrushes. Despite this, several numerical or mathematical models have been developed to study the phenomenon of brushing machine tools.
For example, several studies on wire brushes can be found in the literature. Stango, adopting the classical beam theory in [], deduced equations for calculating the bending of the bristles acting on a flat surface. Heinrich extended Stango’s formulation for bristles acting on curved surfaces []. Subsequently, they validated the numerical results obtained with an experimental campaign [,]. Shia, belonging to the same research group, introduced the influence of friction in 1994 [], while four years later he developed the first 2D discrete model based on the Lagrange equations to calculate more precisely the contact forces exchanged between the bristles and the surface [].
In the same way, many studies on rotary cup brushes are present in the literature. Abded developed the firm finite element model (FEM) to analyze the brush characteristics of rotatory brushes [], while Venegas-Useche [] determined through a FEM the coefficients of friction between the bristles of a cutting brush of street sweepers and a concrete road surface, and in [] the effectiveness of gutter brushes in removing street sweep waste is verified through experiments.
In recent years, several numerical approaches based on multibody dynamics methodology have been introduced to simulate the tridimensional effects of flexible components. Uhlmann in [] proposes a three-dimensional dynamic contact analysis of abrasive filaments with a multibody system to analyze abrasive brushes. Ma [] developed a dynamic model to analyze satellite detumbling using a brush-type contactor based on flexible multibody dynamics. Liu [] adopted a flexible approach to create a dynamic model of a brush sampling mechanism. Ma [] introduced a flexible brush-type model to identify wear in soil removal machines and increase the machine’s lifetime. Recently, this approach has been introduced even in the simulation of toothbrushes. In [], a comparison of several multibody approaches to modeling toothbrush bristles elasto-kinematics is shown.
According to the authors’ knowledge, numerical models have not yet been developed for the dynamic simulation of toothbrushes capable of accurately identifying the three-dimensional displacement of the bristles and consequently evaluating the force exchanged with the teeth. The advantage of developing a numerical model lies not only in the possibility of being able to predict the overall behavior of the toothbrush but, above all, in the possibility of being able to evaluate the contribution of each bristle. In this way, it is possible to have a more detailed result that will surely give additional information for shape optimization processes.
This paper proposes a flexible multibody model to efficiently simulate the 3D compliance of a toothbrush. Compared to the classical finite element approach, the flexible multibody technique is lighter from a computational point of view and ensures the same degree of accuracy [,]. There are several approaches to introducing flexibility in multibody methods [,,]. This paper considers each bristle as a flexible beam; for this reason, they have been modeled according to discrete flexible theory. This method considers a flexible body as a series of rigid bodies connected by lumped stiffness entities. Contact between the teeth and the target surface, such as the contact between the tips of the bristles, is established using the penalty contact method (Section 2.2). The model validation is performed by adopting an ad hoc experimental bench test. It is fulfilled using a Universal Robot and a flat, transparent surface. Validation is provided by comparing the reaction forces of the toothbrush with the reaction forces acquired by the load cells mounted on the end-effector of the Robot. Several trajectories of the toothbrush have been measured to point out the tridimensional motion. The results demonstrate the accuracy of estimating normal and tangential forces.
The paper is organized as follows: the Section 2 reports a description of the methodology adopted to create the discrete flexible model; the Section 3 regards the description of the case study; the experimental setup is described in Section 4 and in Section 5, the obtained results and the relative discussion are reported. At last, conclusions are presented.
2. Numerical Model
The model developed and used to calculate the dynamic behavior of the toothbrush is based on two important features: the dynamics of flexible structures undergoing large deflection and contact mechanics formulation to evaluate the interaction between the bristles and the surface to be cleaned and the interaction effect among the bristles themselves. The objective of the dynamic model is to examine the bristles’ motion and forces on the bristles to determine their brushing performance. As a result, the approach concentrates on modeling the bristles and simplifies the toothbrush by simply taking into consideration its head and ignoring its flexible handle. Even if the flexibility of the handle plays an important role in the entire elasto-kinematics of the toothbrush, the aim of this analysis is to isolate the specific contribution of bristle flexibility from other contributions that may be either due to the handle or, for example, to the compliance of the hand of the user performing the brushing. It is important to highlight that a tilt of the toothbrush head is reflected in a different decomposition of the tangential and normal forces, but it does not influence the reliability of the model.
2.1. Discrete Flexible Model
The approach adopted for the simulation of bristle compliance is the discrete flexible multibody model (DFM). Considering this approach, each bristle is discretized into several rigid bodies connected in series through stiffness and damping matrices (Figure 1). Both inertial properties, stiffness, and damping matrix coefficients depend on the beam’s dimensions and material. Adjacent bodies interact due to stiffness matrices, which produce reaction forces and moment fields depending on the relative displacement between nodes’ coordinate reference systems. Each stiffness matrix can then be represented according to the Timoshenko beam theory [] as follows:
where
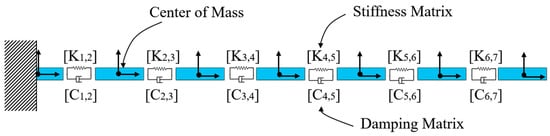
Figure 1.
Schematic representation of a discrete, flexible model of a bristle.
s is the shear area ratio, is the Young’s Modulus, is the shear modulus, is the section area, is the distance between adjacent nodes, and is the moment of inertia of the cross-section concerning the j-axis.
Moreover, each damping matrix can be defined as follows:
As a result, the forces and moments between the adjacent nodes can be expressed as:
where and are the vector of relative displacements (translational and rotational) and the relative velocity between the nodes’ generalized coordinates, respectively.
2.2. Contact Mechanics
The contact mechanics can be split into two phases: the detection phase and the restitution phase. In the detection phase, the bodies that come into contact are identified [], and the contact point(s) coordinates are assessed. This phase is subdivided into two separate sub-phases: a first sub-phase called pre-search and a second sub-phase called detailed search. In the first sub-phase, the overlapping of bounding boxes built around the geometric bodies in the simulation is verified. When two bounding boxes overlap, the second sub-phase is activated, reducing the integration time step and thus refining the accuracy of the contact point calculation. In this way, once the actual bodies come into contact, the restitution phase will be activated. The contact force computed in the restitution phase and applied at the contact point(s) is based on a penalty contact model. In this approach, the contact forces and the deformations are simulated with a set of spring-damper elements that represent the surface compliance of the contact bodies []. The original approach, developed from the Hertz theory [,], was recently revised and modified to be more suitable for integration into full multibody models [,]. The enhanced contact formulation [,] allows calculating the normal force through the relationship:
where:
, are the penetration and the penetration rate;
m1, m2, and m3 are the exponents of stiffness, damping, and the indentation factor, respectively;
k and c are the stiffness and damping coefficients, respectively.
Stick-Slip Friction Model
A stick-slip algorithm in a tangential contact force model [] is adopted to compute the friction force. The friction force is obtained as follows:
where and represent the friction force during the stiction and sliding phases. These terms can be evaluated as
where
: is the stiction deformation that represents the maximum value of the body deformation before the sliding phase [].
: is a parameter depending on the sliding (tangential) velocity
: the sliding velocity
: the dynamic/sliding friction coefficient
: the static/stiction friction coefficient
and represent the maximum value of the stiction deformation and the threshold velocity, respectively. Defining the terms and as the static friction force and the dynamic friction force expressed as: and , it is possible to introduce Table 1, which represents the state of the variables as a function of the assumed conditions.

Table 1.
Stick-slip parameters in cases of either stiction or sliding conditions.
The step function mentioned in Table 1 smooths the transition from stiction to slip conditions and is expressed as:
2.3. Dynamic Equation
Considering the Equations (5)–(7), the equations of motion of the generic -th rigid body node can be written as follows:
where
is the mass matrix, i.e., ;
is the vector of the generalized acceleration ;
and are the stiffness matrices of the elastic compliance between node and nodes and , respectively;
and are the damping matrices between node and nodes and , respectively;
and are the relative displacement between nodes and nodes and generalized coordinates, respectively.
and are the contact forces and their moments with respect to the rigid body node location.
As can be seen, the Equation (11) contains first the inertial term related to all the masses in the model; The second, third, fourth, and fifth terms represent the elastic and damping forces generated by the elastic and damping matrices that connect the DFM bodies; and finally, the external forces (normal and tangential) that depend on the contact among the spheres and between the spheres and the outer surface.
3. Case Study
With the aim of verifying the methodology, a case study in which the toothbrush is constrained to slip on a flat surface is performed. The main scope of these boundary conditions is to check the numerical model’s behavior in a systematic and reproducible scenario. The brush is initially positioned in contact with the flat surface. A motion of 3 mm along the bristles axis is applied so that the inflection of the bristles occurs. Subsequently, a circular motion is imposed on the toothbrush. A measure of the normal and tangential forces is provided to compare the numerical model with the experimental. The tridimensional model is created by adopting reverse engineering techniques. In particular, the process was performed using a Microscribe GX2 by Revware, a 3D coordinate measuring machine (CMM) for implementing a point-data measurement of the brush’s base. Data points were taken at high density to reflect the complex shape of the object. The data points were then imported into a CAD environment to build curves and surfaces, thus recreating the main body. On the other hand, the use of a caliber allowed for the reverse engineering of the bristle locations and dimensions. The defined CAD geometry of the toothbrush is reported in Figure 2b and compared with the real silicon sample in Figure 2a.

Figure 2.
(a) toothbrush test case; (b) toothbrush multibody model.
In this phase, a detailed model of the number and shape of the bristles is provided. The next step has been the building of the multibody model. Each bristle is modeled through the DFM approach, considering six rigid bodies with rectangular sections equally distributed along the bristle length. This choice is made because bristles have different lengths. Although the real bristles of the toothbrush are tapered towards the contact end, the section of the modeled bristles is selected constantly along their axis. Moreover, the outer bristles have different section dimensions with respect to the inner ones. Namely, the internal bristle section is 1.8 mm × 0.8 mm, while the external bristle section is 1.3 mm × 0.8 mm. The lumped stiffness matrix is computed using the Equation (1) E = 7 GPa.
Each bristle is provided with a dummy spherical body on the tip with a radius as 0.44 mm to establish smooth contact and reduce the computational burden. A bounding box having is considered for the pre-search contact phase. Thanks to the dummies bodies, it has been possible to establish a contact relationship among the dummies adjacent spherical bodies to reproduce the interaction among the bristles. For this kind of contact, friction is neglected. Moreover, to reproduce the contact between the bristles and the flat surface, the base surface is approximated with a multi-triangular mesh, while the action surface, the analytical relation of the sphere, is considered. In this contact group, a stick-slip contact is considered.
It is crucial to highlight that the auto-interaction among the bristles represents an important contribution to a generalization of the problem because when the direction of motion changes, the interaction between the bristles leads to a reduction of normal forces as they collide with each other, exerting less pressure on the flat surface. The parameters adopted for the contact spheres and the flat surface are reported in Table 2, while the contact parameters of interaction among the spheres are reported in Table 3. On the one hand, the contact parameters for the evaluation of the normal force (i.e., , , mi) are set to ensure a penetration lower than 5 µm in the non-indentation region, therefore ensuring reliable contact detection and evaluation while guaranteeing the lowest possible computational burden. On the other hand, considering the tangential force characterization, the friction coefficients were assumed as suggested in the literature for dry silicon rubber and acrylic contact [,,].

Table 2.
Contact properties of the interaction between the tip of the bristles (spheres) and the flat surface.

Table 3.
Contact parameters of the interaction among the tips of the bristles (spheres).
4. Experimental Setup
The experimental setup is based on the use of the Cobot UR5 [] to move the toothbrush as can be seen in Figure 3. The wrist of the cobot (collaborative robot) is equipped with load cells to assess the forces acting on the Tool Center Position (TCP). The toothbrush is clamped to the robot arm just above the bristles through a 3D-printed flange bolted to the cobot’s wrist. This arrangement allows for the neglect of handling compliance according to the numerical model. The brushing takes place on a flat plexiglass surface, firmly mounted to an aluminum support structure. Furthermore, a Logitech C920 HD Pro webcam is mounted on the aluminum structure, and it was used to monitor the deformation state of the brush bristles during the circular path.

Figure 3.
Picture of the experimental setup adopted.
Experimental results are determined with the UR5 algorithm explained below. Considering the system of references adopted in Figure 4,the circle path is obtained with the MoveL command, which moves the TCP center of the coordinate system linearly between two control points []. As shown in Figure 5, two MoveL commands are imposed in sequence: the first one from CP1 to CP2, and the second one from CP2 to CP3. In the first command, a fillet radius is set equal to r, so the TCP trajectory follows the continuous line. As a result, the TCP transits around the CP2, allowing the arm to not stop at that point. If the fillet radius is not set, the TCP trajectory follows the pointed line.
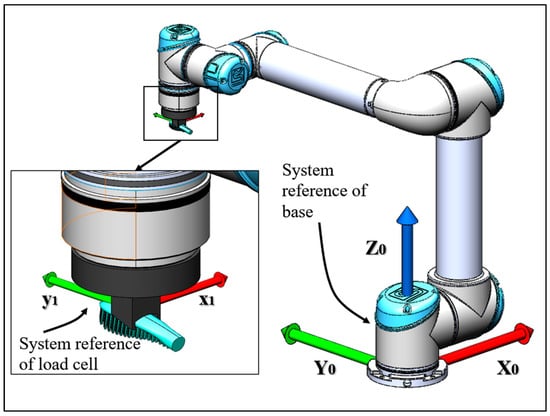
Figure 4.
Representation of the UR5 and its system of references.
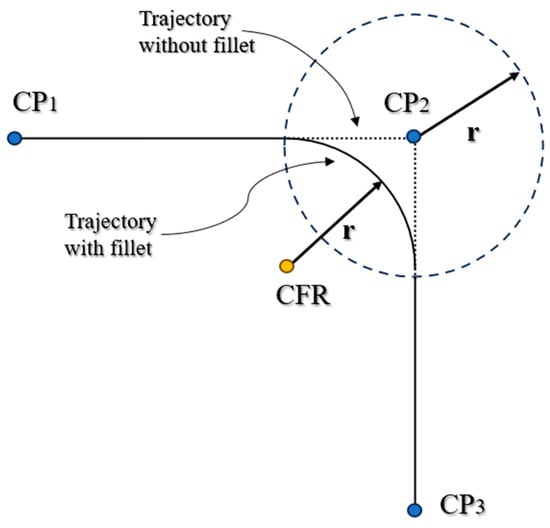
Figure 5.
Fillet radius path in the MoveL command.
Four control points, one for each quarter circumference, have been chosen to create a circular motion with the built-in MoveL command, 4. Between these points, the command is imposed with the fillet radius equal to the circle radius. On the other hand, in the first phase of the experiment, the toothbrush’s approach motion to the surface is obtained using the MoveJ command towards the starting point of the circular path. The MoveJ command performs movements calculated in the joint space of the robot arm. This type of motion results in a curved tool path to minimize the time it takes to travel the trajectory.
The resulting prescribed motion path on the brushing plane is shown in Figure 6. P0 is the starting point of the circle path, while the control points are P1, P2, P3, and P4 in order. Algorithm 1describes in detail the series of commands imposed on the Robot in order to make its tip describe the circular path. Furthermore, it must be highlighted that the Robot accomplishes four complete rotations and that the first movement imposed (from P0 to P1) is not exactly circular and therefore is not taken into account in the postprocess section.
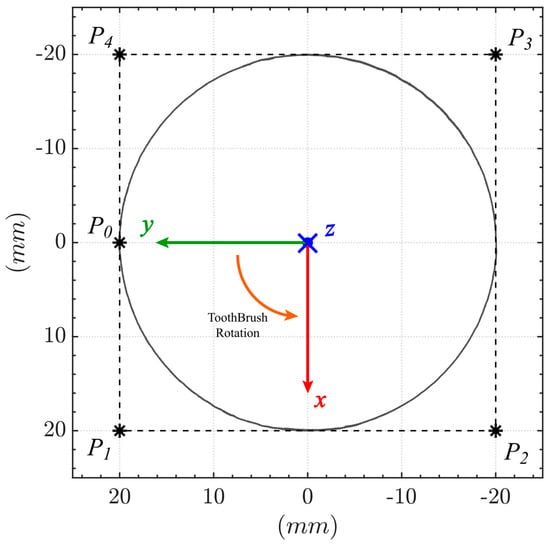

Figure 6.
UR5 circle path and control points.
| Algorithm 1: Description of the algorithm scripted to impose the robot tip’s circular trajectory. CIRCULAR PATH UR. | |
| Input: starting point (P0), blend radius (r), tool acceleration (a), tool speed (v) | |
| Control points definition: P1, P2, P3, and P4. | Each point has its 3D coordinate position and the euler angles value. |
| while (running = True): $ 1 “Robot Program” $ 2 “MoveL” $ 3 “P0” “breakAfter” movel(P0, a, v) $ 4 “Loop” while (running = True): $ 5 “MoveL” $ 6 “P1” “breakAfter” movel(P1, a, v, r) $ 7 “P2” “breakAfter” movel(P2, a, v, r) $ 8 “P3” “breakAfter” movel(P3, a, v, r) $ 9 “P4” “breakAfter” movel(P4, a, v, r) end end | |
| Functions MoveL Syntax: movel(pos, a, v, r) Parameters: pos: target position a: tool acceleration [m/s2] v: tool speed [m/s] r: blend radius [m] | |
5. Results and Discussions
5.1. Circular Motion
As previously disclosed, the tip of the Robot is programmed to follow a circular motion with a radius of 20 mm. The circular path analysis is also created with the multibody model previously described. The model has six motion constraints that bind the toothbrush base to follow the same circular trajectory as the experimental. Moreover, the trajectory that the Robot follows was checked in the postprocessing of the experimental results to be the same as the one imposed and shown in Figure 6, with the reference frame of the robot tool center point (TCP) highlighted.
The forces that the load cells measured in the experimental analysis during three circular rotations are shown in Figure 7 as solid lines. Furthermore, the reaction forces calculated with the multibody model in the motion constraints are aligned accordingly to the robot reference frame and are presented in the same figure as dotted lines.
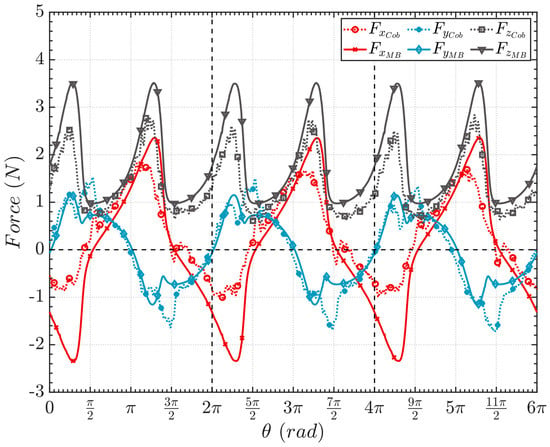
Figure 7.
Forces evaluated during the circular trajectory vs. the angle of rotation. The experimental results (dotted lines with markers) are compared with the model forces (solid lines with markers).
The comparison between the experimental and computational results, illustrated in Figure 7, shows good agreement. The forces obtained with the multibody model accurately follow the trend of the ones measured by the load cells in the robot.
During the prescribed circular motion, the toothbrush is subjected to two jamming phenomena. In other words, in the positions around 9/4 Π and 13/4 Π, the brush experiences a change from the main direction of motion along the y-axis to the x-axis. Thus, the tufts are constrained to rapidly invert their deformed shape in the opposite direction. This phenomenon is well described in Figure 8, where a series of photos of the bristles’ deformed shapes are shown for a set of positions. In particular, the pictures are taken from the experimental analysis around the positions previously stated. Furthermore, Figure 9 illustrates the deformed shapes calculated through the MB model in comparison to the pictures obtained in the experiment. The deformations of the bristles calculated at the selected angle positions effectively agree with the photos, thus confirming the validity of the model.
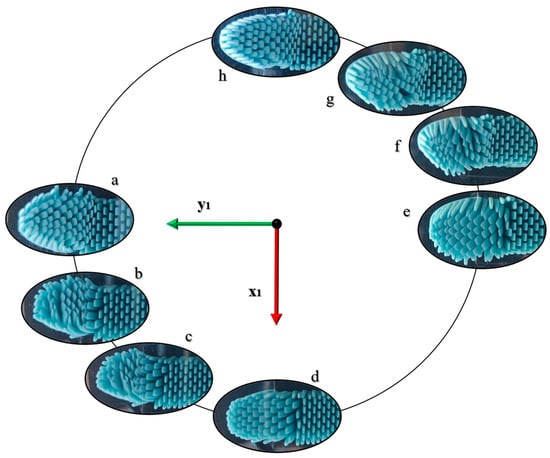
Figure 8.
Toothbrush’s bristles deformation detail. Series of pictures taken during the experiment that highlight the inversion phases in the lower left quarter (a–d) and upper right quarter (e–h).
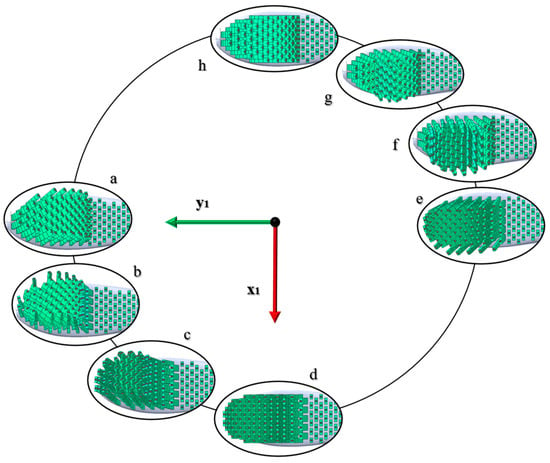
Figure 9.
Toothbrush’s bristles deformation detail. A series of screenshots from the MB model that highlight the inversion phases in the lower left quarter (a–d) and upper right quarter (e–h).
Without any loss of generality, the upper-right quarter is considered to describe the inversion phenomenon. The bristles in Figure 8e are deformed in parallel planes along the same direction. With the incoming change of the motion direction from the x-axis to the y-axis, the bristles indent and start inverting the direction of their deformed shapes (Figure 8f). During the inversion, the forces peak at the highest values and then decrease when the bristles return to being almost on parallel planes and in the opposite direction to the one imposed by the motion (Figure 8g,h). Mirror behavior occurs for Figure 8a–d.
From the results shown in Figure 7, the peak trend exists in both experimental and multibody calculated forces. On the other hand, a difference is depicted in the value of the force in the y-axis direction during the phase around the jamming angle of the lower left quarter.
This difference in the results should be attributed to the presence of compliance in the grasping system between the robot hand and the brush. In particular, during the experimental analysis, a loss of rigidity is detected mainly in one direction, which has a higher influence on the lower left transition than in the other. That is, when the toothbrush reaches the inversion position point (Figure 8b,g), the bristles are subjected to a rapid change in the deflection curvature sign, but instead of measuring a fast increase in the force value, the toothbrush tilts in its pitch direction. Therefore, the multibody model, where the brush position is constrained, calculates a force higher than the one obtained in the experiment.
Hence, to verify this hypothesis, an improved model is created with motion constraints that simulate the compliance that affects the experimental results.
5.2. Circular Motion with a Pitch Error
The novel case study is created to consider the compliance of the linking structure between the toothbrush and the robot hand, thus checking the effect of an imposed titling motion when the bristles reach a rapid change of deflection plane. This tilting is imposed in the pitch direction of the brush’s main body. In particular, a rotation is imposed with an incremental step between the angular positions of 2Π and 5/2Π, thus creating a peak at the center of this interval equal to 1 deg. The equation is expressed as:
where the step function definition is similar to the one already depicted in Equation (10) and is the compliance angle.
The results obtained through this new model are reported in Figure 10 and compared with the experimentally obtained forces. Taking into account the previously shown results (Figure 7) and comparing them with those in Figure 10, it is possible to observe the induced asymmetry of the force along the y-axis with respect to the x-axis. This feature also exists in the force obtained through the experimental analysis, which explains the uneven compliance previously discussed. The force calculated along the y direction changes the slope and reduces its maximum value, as shown in the positive part of the graph.
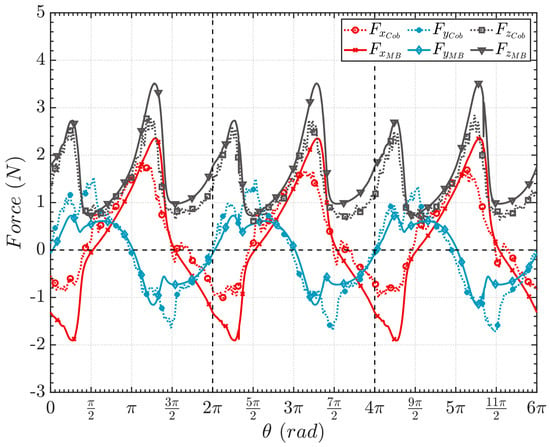
Figure 10.
Forces evaluated during the circular trajectory with the simulated compliance of the toothbrush’s grasping structure versus the angle of rotation. The experimental results (dotted lines with markers) are compared with the model forces (solid lines with markers).
Therefore, introducing the simulated compliance in the multibody model has allowed us to analyze and explain the asymmetry depicted in the y direction. It is possible to state that this rigidity loss could be the main cause of this behavior, while more unpredictable, less gradual, and bigger compliance should be needed to match the trend perfectly.
6. Conclusions
This paper proposes a flexible multibody model to efficiently simulate the 3D compliance of a toothbrush. The model is based on the discrete flexible model method adopted in the multibody dynamic approach. The method considers each bristle divided into several rigid bodies connected by stiffness and damping matrices. The contact between the bristles and the target surface is established using the penalty contact method, and the slip-stiction model of friction is considered. Moreover, the contact among the bristles is established using a penalty contact method without a friction component.
An experimental test bench adopting UR’s collaborative robot and a flat transparent surface are set up. The validation of the MB model is provided by comparing the reaction forces of the toothbrush with the reaction forces acquired by the load cells mounted on the end-effector of the Robot. In addition, the tilting behavior of the experimental toothbrush is detected and considered in the mathematical model. The results demonstrate the model’s accuracy in estimating both normal and tangential forces in several operating conditions.
Moreover, the discrete flexible multibody approach has been proven to be feasible in predicting the displacement of the bristles while the base body of the toothbrush is subjected to a prescribed motion. The positions of the deformed bristles are accurately calculated when the imposed movement is continuous and rectilinear and when the toothbrush is subjected to a rapid change in direction. Therefore, the model could be used properly to evaluate the ability of different toothbrush classes to perform cleaning operations.
Nevertheless, a more in-depth analysis is still necessary to examine the DFM tridimensional bristles’ behavior on a wider range of surfaces, such as bi-curvature or generally specified surfaces, and to assess the model’s performance. Future studies should investigate how sensitive the model is to contact shape and property, for instance, by incorporating additional spheres per bristle or accounting for different contact types. Additionally, considering various materials and geometries, the methodology can be extended to a wider range of toothbrushes. Moreover, the elasticity of the entire handle deserves further investigation.
Finally, the proposed model could offer hints towards holistic modeling and the improvement of toothbrush design to increase their efficiency in performing a complete cleaning without damaging the teeth. An indispensable property to ensure good oral hygiene, thus lowering the chance of developing oral diseases.
Author Contributions
Conceptualization, M.C., A.C., L.D., M.M. and P.P.V.; methodology, M.C., A.C., L.D. and P.P.V.; software, M.C., A.C. and L.D.; validation, M.C., A.C., L.D., M.M. and P.P.V.; formal analysis, M.C., A.C. and L.D.; investigation, M.C., M.M. and P.P.V.; resources, P.P.V.; data curation, M.C., A.C., L.D. and M.M.; writing—original draft preparation, M.C., A.C., L.D. and P.P.V.; writing—review and editing, M.C., A.C., L.D., M.M. and P.P.V.; visualization, M.C., A.C., L.D. and M.M.; supervision, M.C. and P.P.V.; project administration, M.C. and P.P.V.; funding acquisition, P.P.V.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the European Union—NextGenerationEU under the Italian National Center 1 on HPC—Spoke 6: “Multiscale Modelling and Engineering Applications”. MUR: CUP: E83C22003230001.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- WHO. Global Oral Health Status Report: Towards Universal Health Coverage for Oral Health by 2030; World Health Organization: Geneva, Switzerland, 2022.
- Wiegand, A.; Kuhn, M.; Sener, B.; Roos, M.; Attin, T. Abrasion of eroded dentin caused by toothpaste slurries of different abrasivity and toothbrushes of different filament diameter. J. Dent. 2009, 37, 480–484. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ranzan, N.; Muniz, F.W.M.G.; Rösing, C.K. Are bristle stiffness and bristle end-shape related to adverse effects on soft tissues during toothbrushing? A systematic review. Int. Dent. J. 2019, 69, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.-F.; Cacciato, R.; Whelehan, M.T.; Ning, L.; Malmstrom, H.S. Effects of toothbrushes with tapered and cross angled soft bristle design on dental plaque and gingival inflammation: A randomized and controlled clinical trial. J. Dent. 2007, 35, 614–622. [Google Scholar] [CrossRef] [PubMed]
- Souza, C.D.M.S.; Sakae, L.O.; Carneiro, P.M.A.; Esteves, R.A.; Scaramucci, T. Interplay between different manual toothbrushes and brushing loads on erosive tooth wear. J. Dent. 2021, 105, 103577. [Google Scholar] [CrossRef]
- Pereira, T.P.; Vieira, T.A.F.; Dos Santos, W.; Bezerra, S.J.C.; Sobral, M.Â.P.; Scaramucci, T. Influence of different ultra-soft toothbrushes on erosive tooth wea. J. Dent. 2023, 132, 104502. [Google Scholar] [CrossRef]
- Rawls, H.; Mkwayi-Tulloch, N.; Krull, M. A mathematical model for predicting toothbrush stiffness. Dent. Mater. 1990, 6, 111–117. [Google Scholar] [CrossRef]
- Stango, R.J.; Heinrich, S.M.; Shia, C.Y. Analysis of constrained filament deformation and stiffness properties of brushes. J. Eng. Ind. 1989, 111, 238–243. [Google Scholar] [CrossRef]
- Heinrich, S.M.; Stango, R.J.; Shia, C.Y. Effect of workpart curvature on the stiffness properties of circular filamentary brushes. J. Eng. Ind. 1991, 113, 276–282. [Google Scholar] [CrossRef]
- Stango, R.J.; Cariapa, V.; Prasad, A.; Liang, S.K. Measurement and analysis of brushing tool performance characteristics, part 1: Stiffness response. J. Manuf. Sci. Eng. 1991, 113, 283–289. [Google Scholar] [CrossRef]
- VCariapa, V.; Stango, R.J.; Liang, S.K.; Prasad, A. Measurement and Analysis of Brushing Tool Performance Characteristics, Part 2: Contact Zone Geometry. J. Manuf. Sci. Eng. 1991, 113, 290–296. [Google Scholar]
- Shia, C.-Y.; Stango, R.J. On the frictional response of a filamentary brush in contact with a curved workpart. Int. J. Mach. Tools Manuf. 1994, 34, 573–589. [Google Scholar] [CrossRef]
- Shia, C.-Y.; Stango, R.J.; Heinrich, S.M. Analysis of contact mechanics for a circular filamentary brush/workpart system. J. Manuf. Sci. Eng. 1998, 120, 715–721. [Google Scholar] [CrossRef]
- Wahab, M.A.; Parker, G.; Wang, C. Modelling rotary sweeping brushes and analyzing brush characteristic using finite element method. Finite Elements Anal. Des. 2007, 43, 521–532. [Google Scholar] [CrossRef]
- Useche, L.V.V.; Wahab, M.M.A.; Parker, G.A. Determination of friction coefficients for cutting brush—Road surface interaction through FEM. In Proceedings of the IEEE SoutheastCon 2010 (SoutheastCon), Concord, NC, USA, 18–21 March 2010. [Google Scholar]
- Useche, L.V.V.; Wahab, M.M.A.; Parker, G.A. Effectiveness of gutter brushes in removing street sweeping waste. J. Waste Manag. 2010, 30, 174–184. [Google Scholar] [CrossRef]
- Uhlmann, E.; Sommerfeld, C. Three-dimensional dynamic contact analysis of abrasive filaments with a multibody system. Procedia CIRP 2018, 72, 615–621. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Z.; Zou, H.; Liu, J. Dynamic modeling and analysis of satellite detumbling using a brush type contactor based on flexible multibody dynamics. Mech. Mach. Theory 2022, 170, 104675. [Google Scholar] [CrossRef]
- Lei, B.; Ma, Z.; Liu, J.; Liu, C. Dynamic modelling and analysis for a flexible brush sampling mechanism. Multibody Syst. Dyn. 2022, 56, 335–365. [Google Scholar] [CrossRef]
- Ma, S.; Xu, L.; Xu, S.; Tan, H.; Song, J.; Shen, C. Wear study on flexible brush-type soil removal component for removing soil used to protect grapevines against cold. Biosyst. Eng. 2023, 228, 88–104. [Google Scholar] [CrossRef]
- Cellupica, A.; D’Angelo, L.; Cirelli, M.; Mazur, M.; Valentini, P.P. Multibody approach to model toothbrush bristles elasto-kinematics. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Lisbon, Portugal, 24–28 July 2023. [Google Scholar]
- Valentini, P.P.; Pennestrì, E. Elasto-kinematic comparison of flexure hinges undergoing large displacement. Mech. Mach. Theory 2017, 110, 50–60. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Compliant four-bar linkage synthesis with second-order flexure hinge approximation. Mech. Mach. Theory 2018, 128, 225–233. [Google Scholar] [CrossRef]
- Verotti, M. A pseudo-rigid body model based on finite displacements and strain energy. Mech. Mach. Theory 2020, 149, 103811. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Second-order approximation pseudo-rigid model of leaf flexure hinge. Mech. Mach. Theory 2017, 116, 352–359. [Google Scholar] [CrossRef]
- Sorgonà, O.; Belfiore, N.; Giannini, O.; Verotti, M. Application of the ellipse of elasticity theory to the functional analysis of planar compliant mechanisms. Mech. Mach. Theory 2023, 184, 105308. [Google Scholar] [CrossRef]
- Hutchinson, J.R. Shear coefficients for Timoshenko beam theory. J. Appl. Mech. 2001, 68, 87–92. [Google Scholar] [CrossRef]
- Choi, J.; Ryu, H.S.; Kim, C.W.; Choi, J.H. An efficient and robust contact algorithm for a compliant contact force model between bodies of complex geometry. Multibody Syst. Dyn. 2010, 23, 99–120. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Young, W.C.; Budynas, R.G.; Sadegh, A.M. Roark’s Formulas for Stress and Strain; McGraw-Hill Education: New York, NY, USA, 2012. [Google Scholar]
- Popov, V.L. Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Flores, P.; Machado, M.; Silva, M.T.; Martins, J.M. On the continuous contact force models for soft materials in multibody dynamics. Multibody Syst. Dyn. 2011, 25, 357–375. [Google Scholar] [CrossRef]
- Autiero, M.; Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P.P. Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines. Machines 2022, 10, 966. [Google Scholar] [CrossRef]
- Choi, J.; Rhim, S.; Choi, J.H. A general purpose contact algorithm using a compliance contact force model for rigid and flexible bodies of complex geometry. Int. J. Non-Linear Mech. 2013, 53, 13–23. [Google Scholar] [CrossRef]
- Cha, H.; Choi, J.; Ryu, H.; Choi, J. Stick-slip algorithm in a tangential contact force model formulti-body system dynamics. J. Mech. Sci. Technol. 2011, 25, 1687–1694. [Google Scholar] [CrossRef]
- Dahl, P.R. Solid Friction Damping of Mechanical Vibrations. AIAA J. 1976, 14, 1675–1682. [Google Scholar] [CrossRef]
- Rabinowicz, E. Friction and Wear of Materials, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford Classic Texts in the Physical Sciences; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Fuller, D.D. Theory and Practice of Lubrication for Engineers, 2nd ed.; Wiley: Hoboken, NJ, USA, 1984. [Google Scholar]
- UR. User Manual Universal Robot; UR: Boston, MA, USA, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).