Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via a Sandwich Belt Conveyor—Part 2
Abstract
1. Introduction
2. Materials and Methods
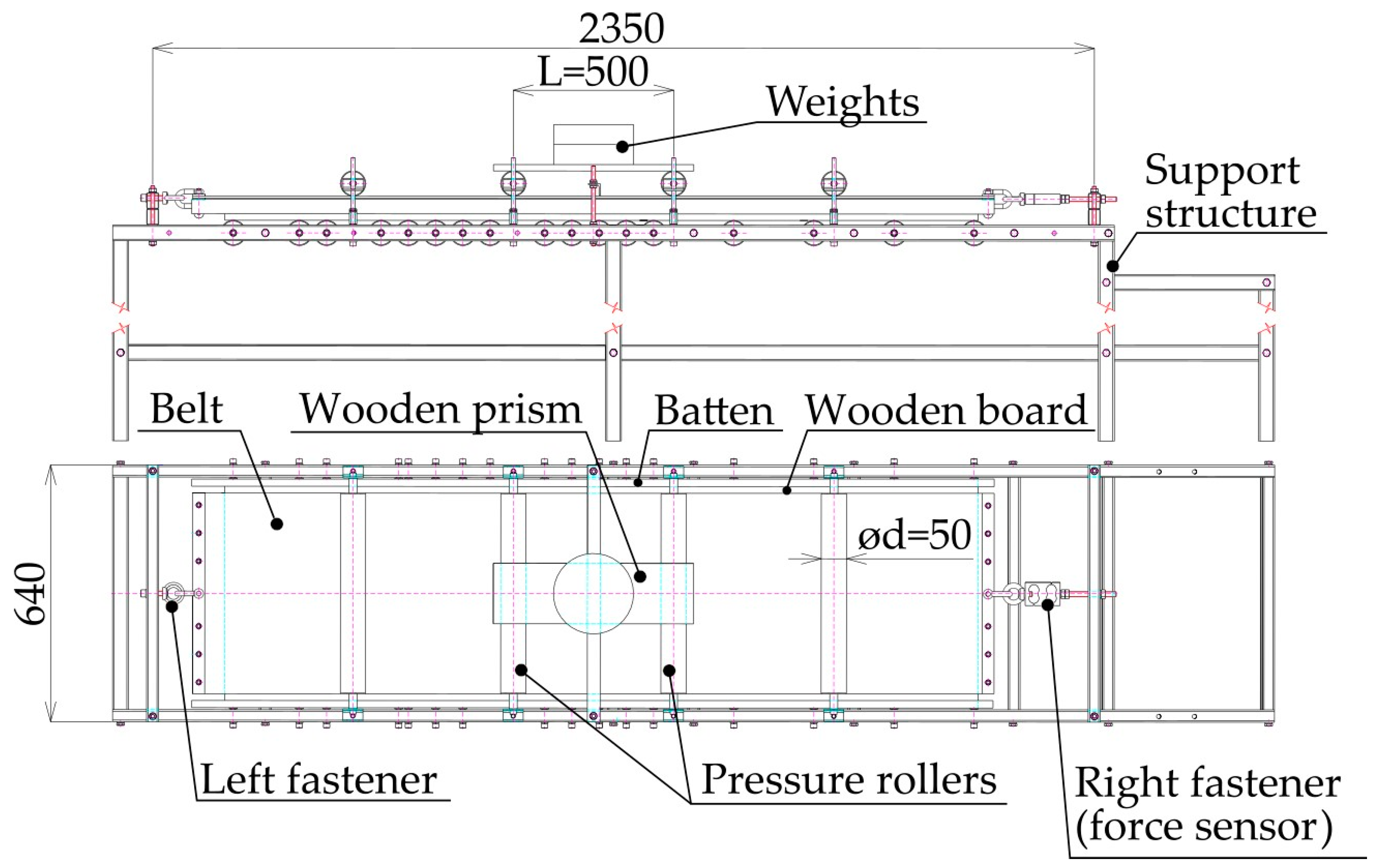
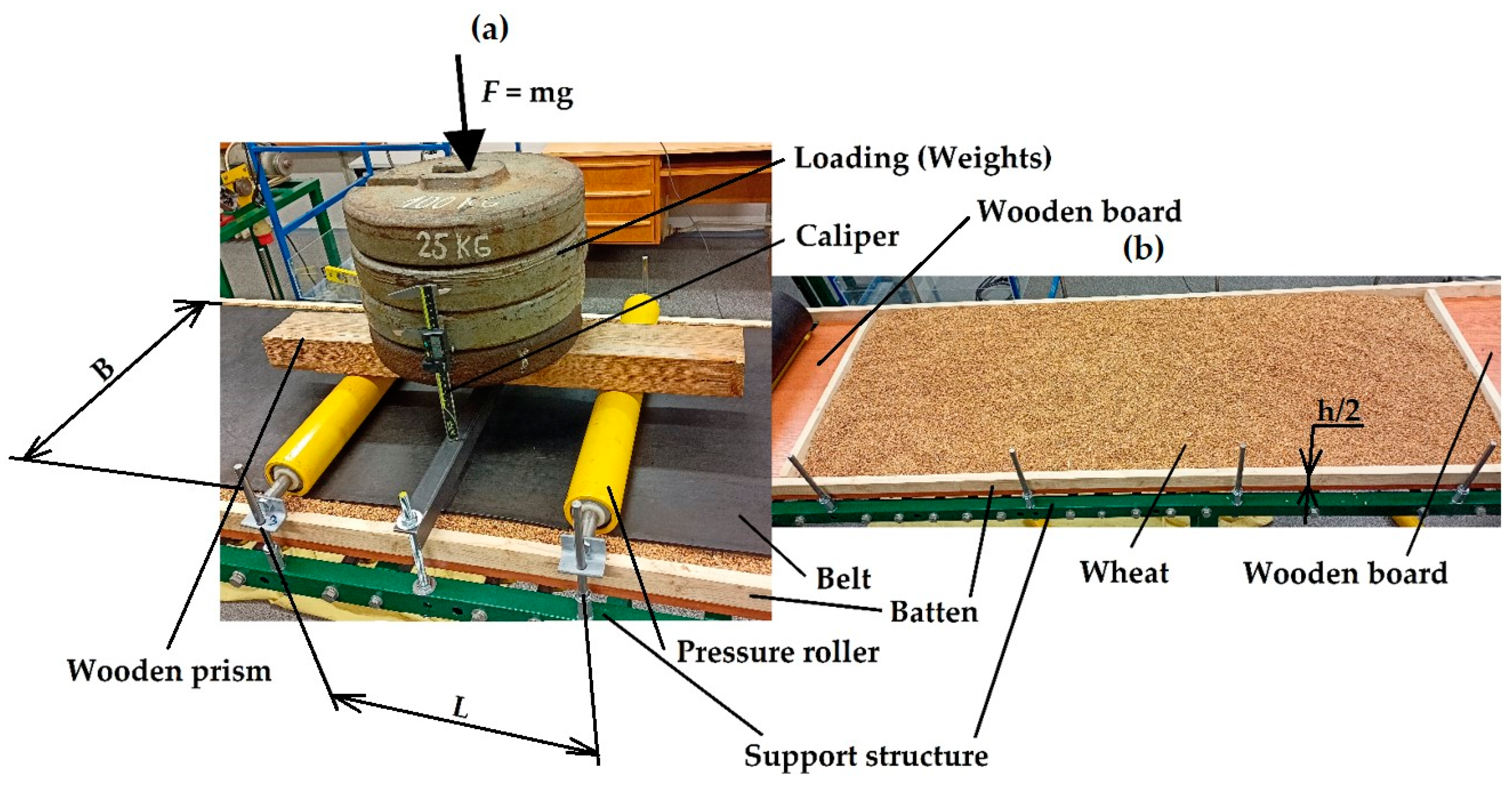
2.1. Experimental Measurement
2.2. Sandwich Conveyor Belt and Its Force Sensor
2.3. Wheat
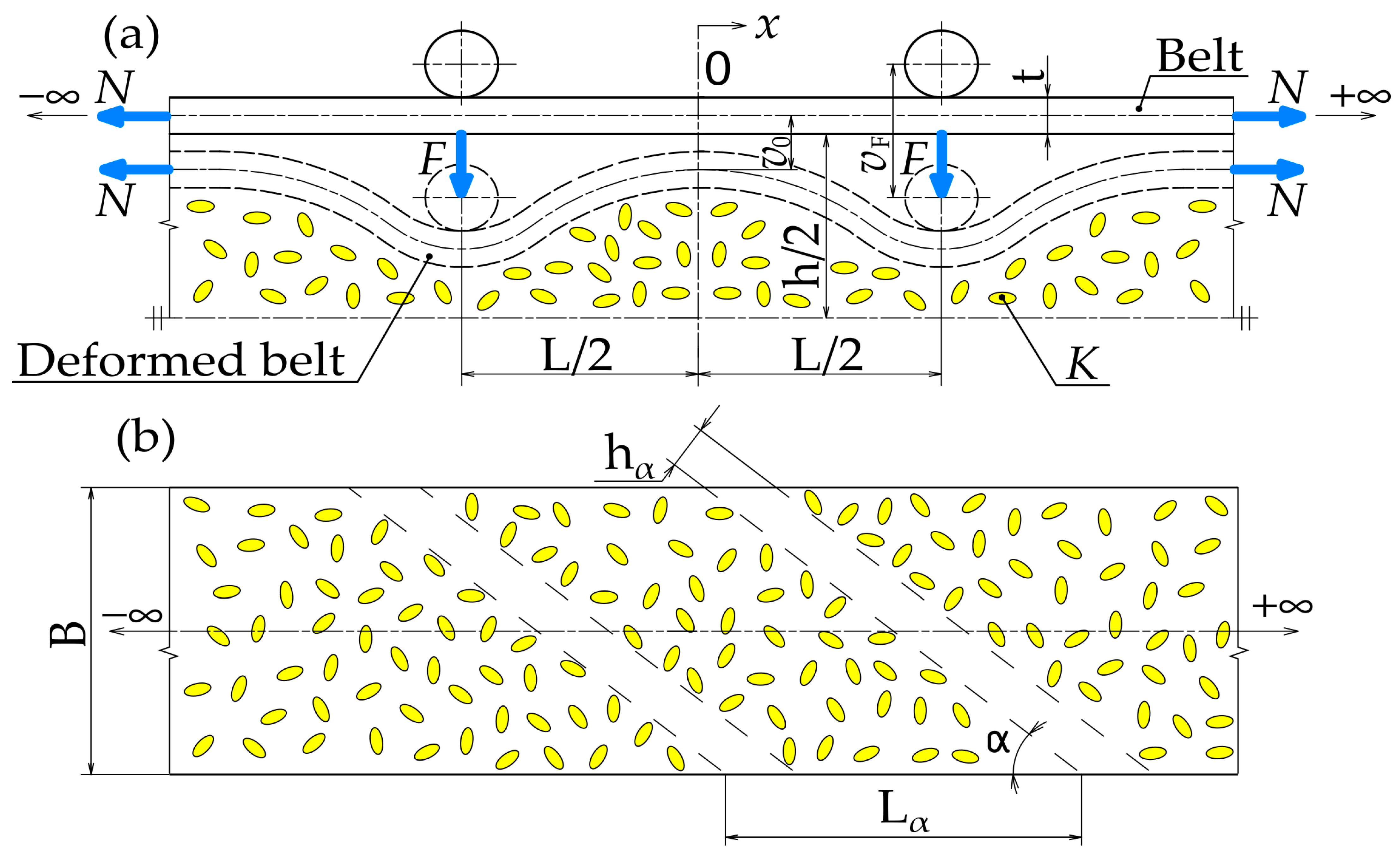
2.4. Analytical Approach
2.5. Numerical Approach
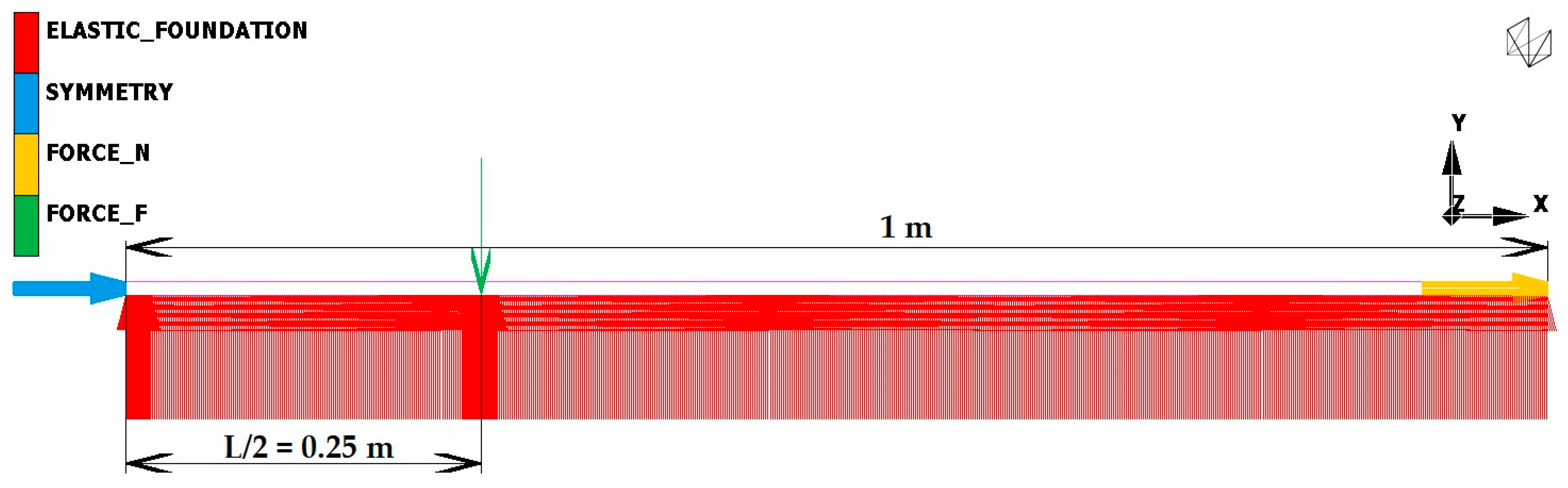
2.5.1. Finite Element Analysis
2.5.2. Finite Element Meshes and Their Boundary Conditions
2.6. Regression
2.7. Monte Carlo Method
3. Results
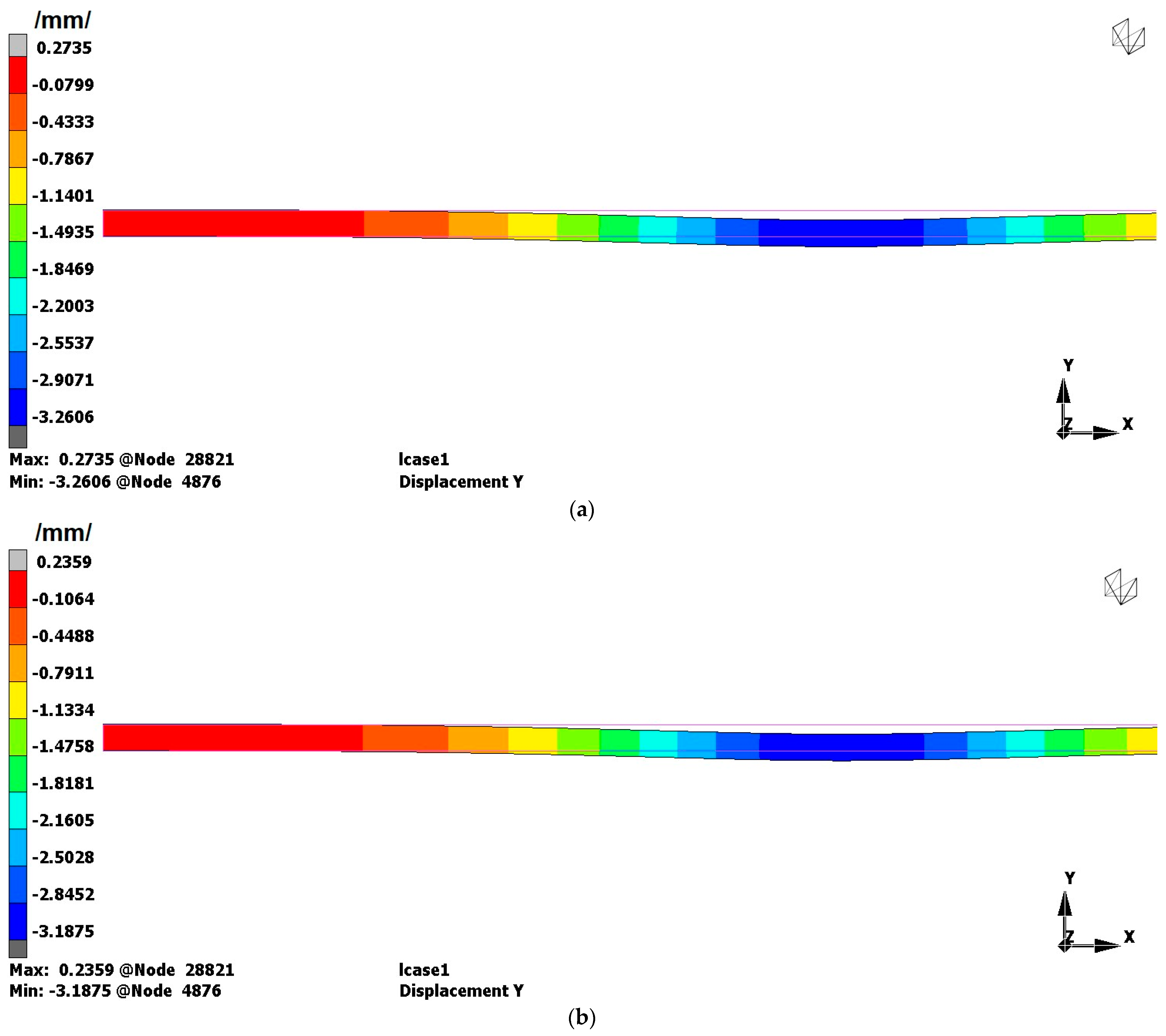
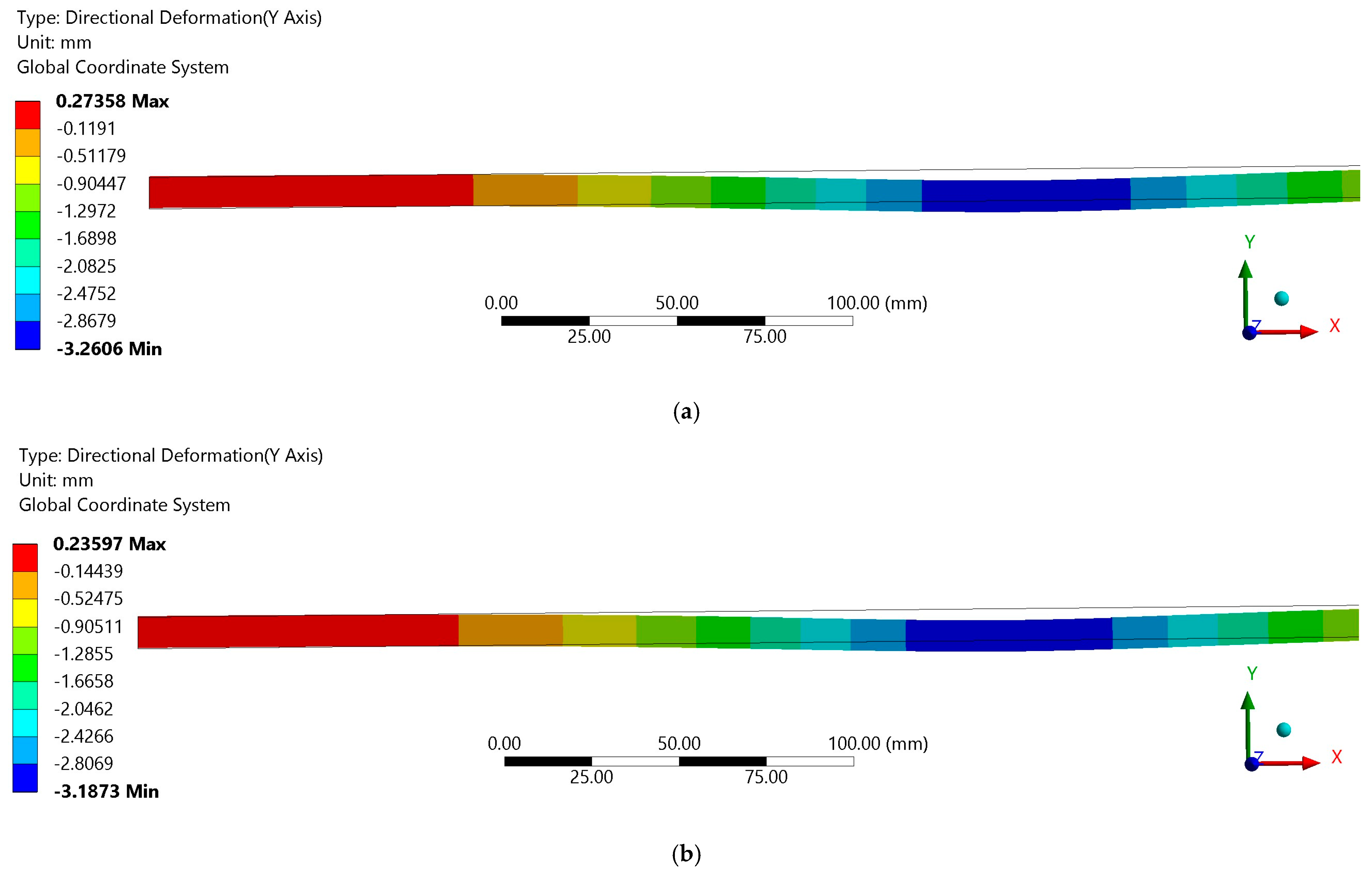
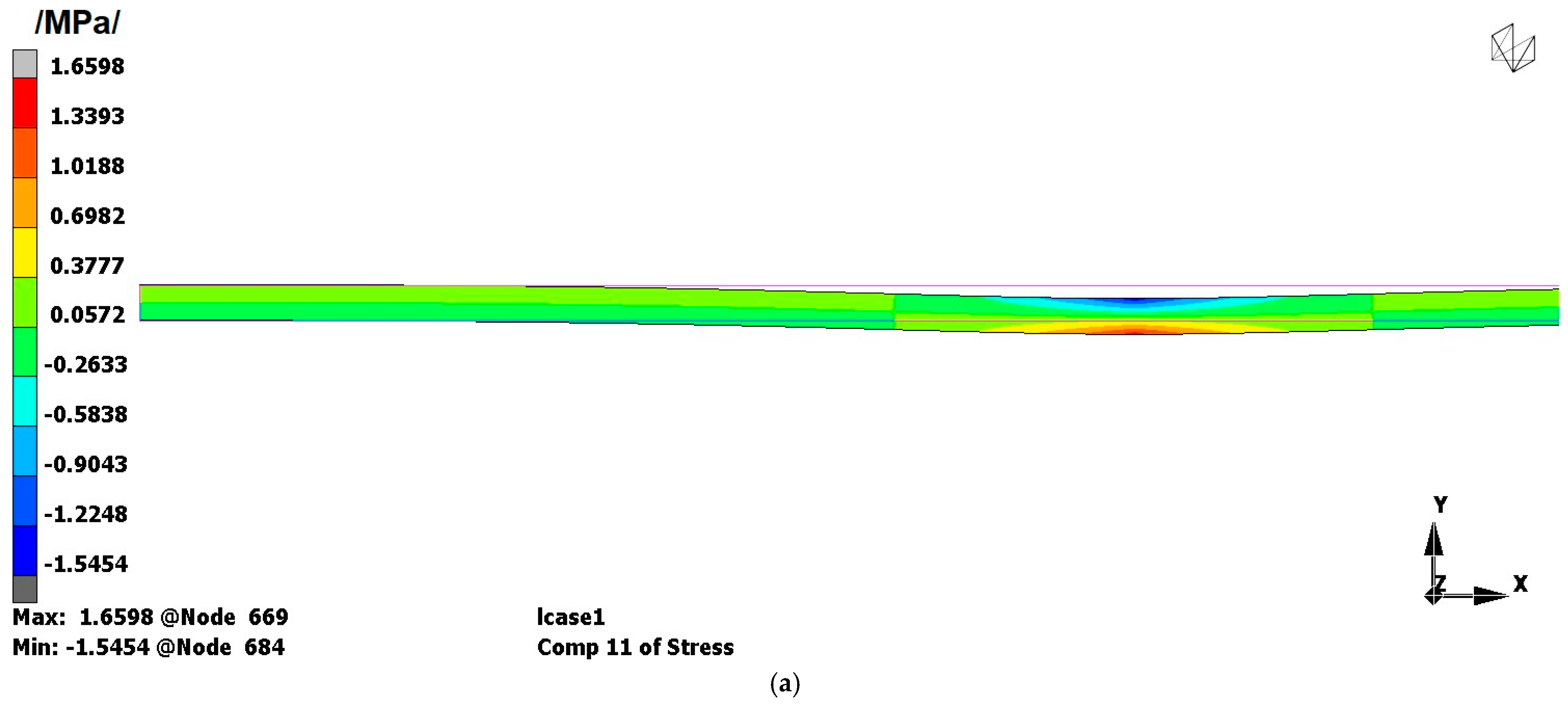
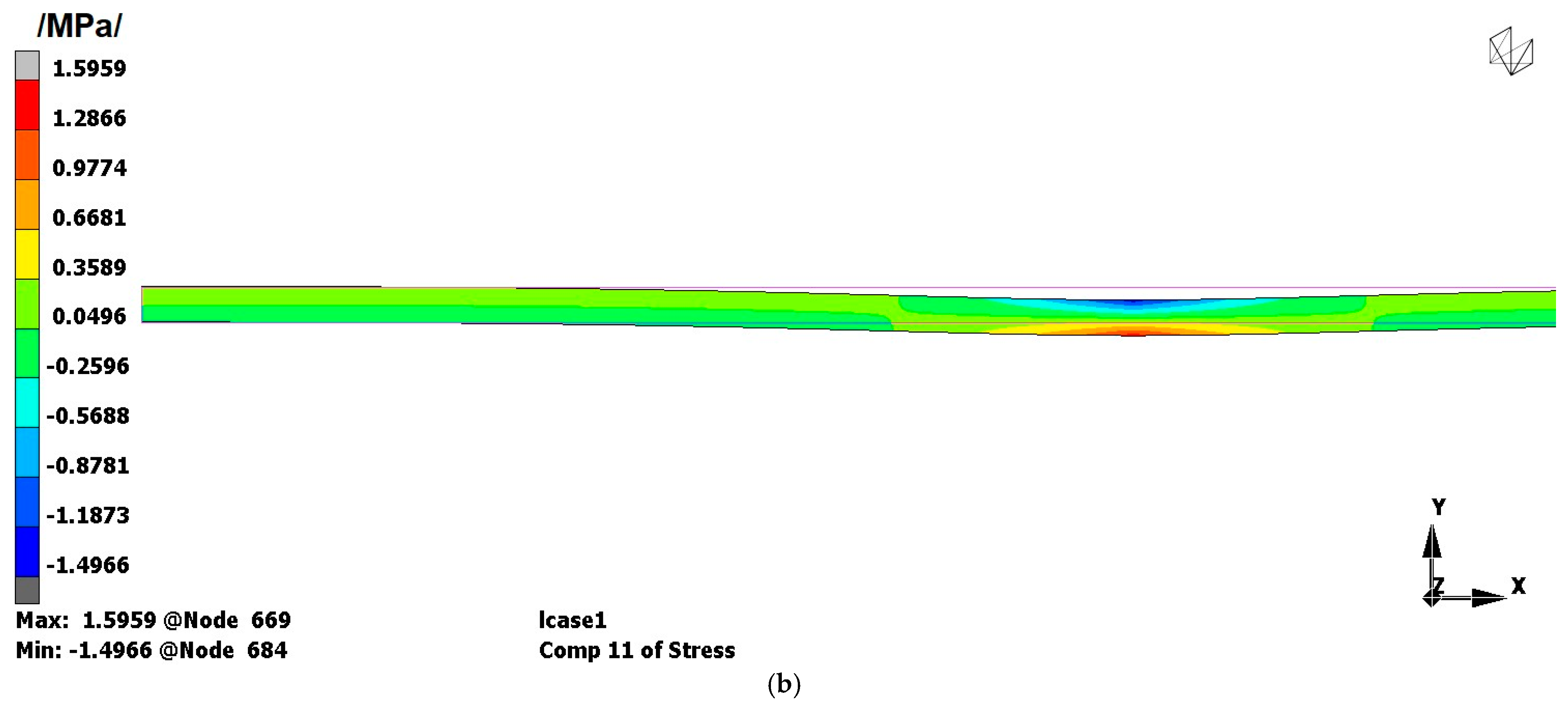
3.1. Finite Element Analyses—Results for a Uniform Layer of Wheat and Verification of the Results of [5]
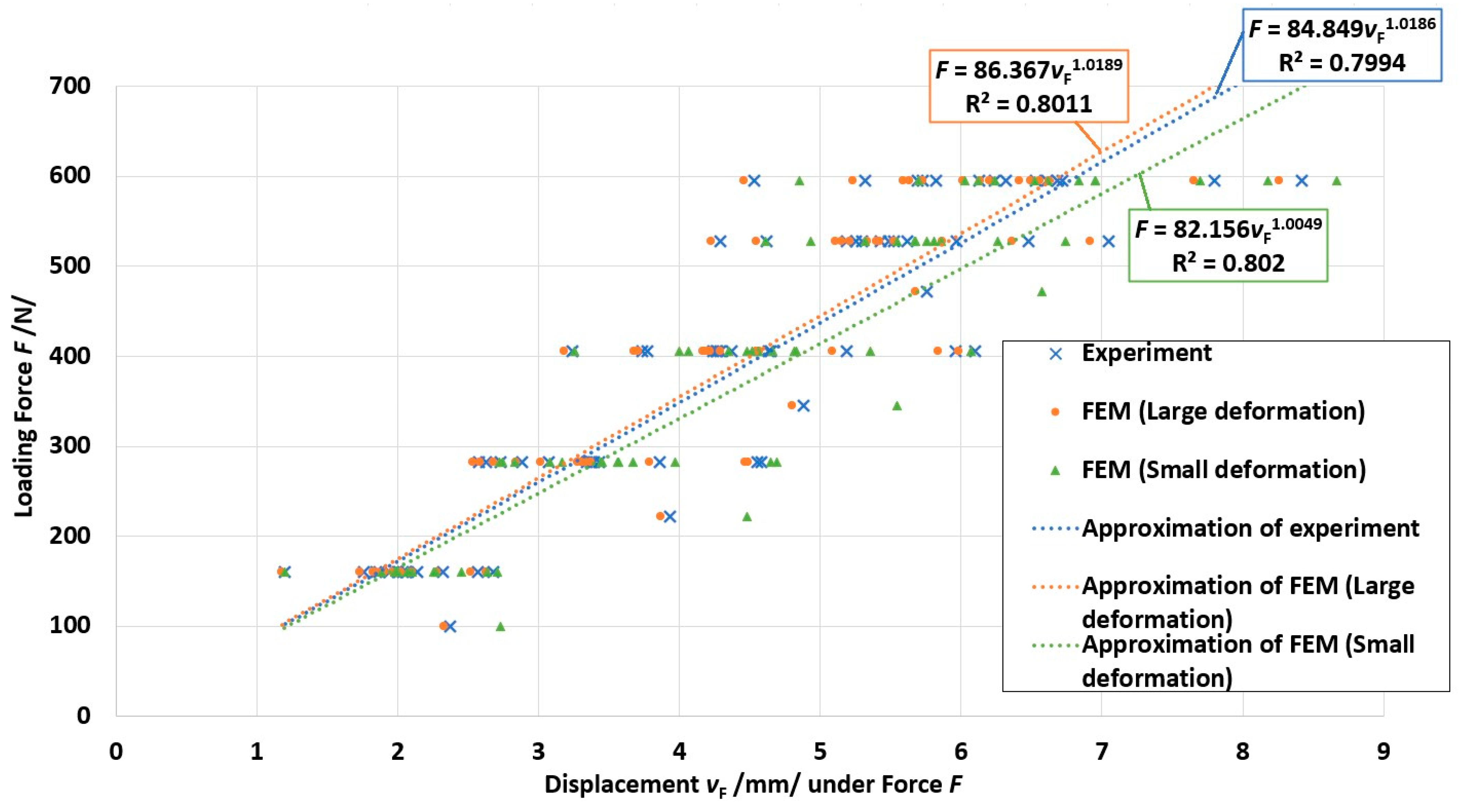
Comparison of the FEA and Analytical Results
3.2. Nonuniform Layer of Wheat
3.2.1. Approximation of Results
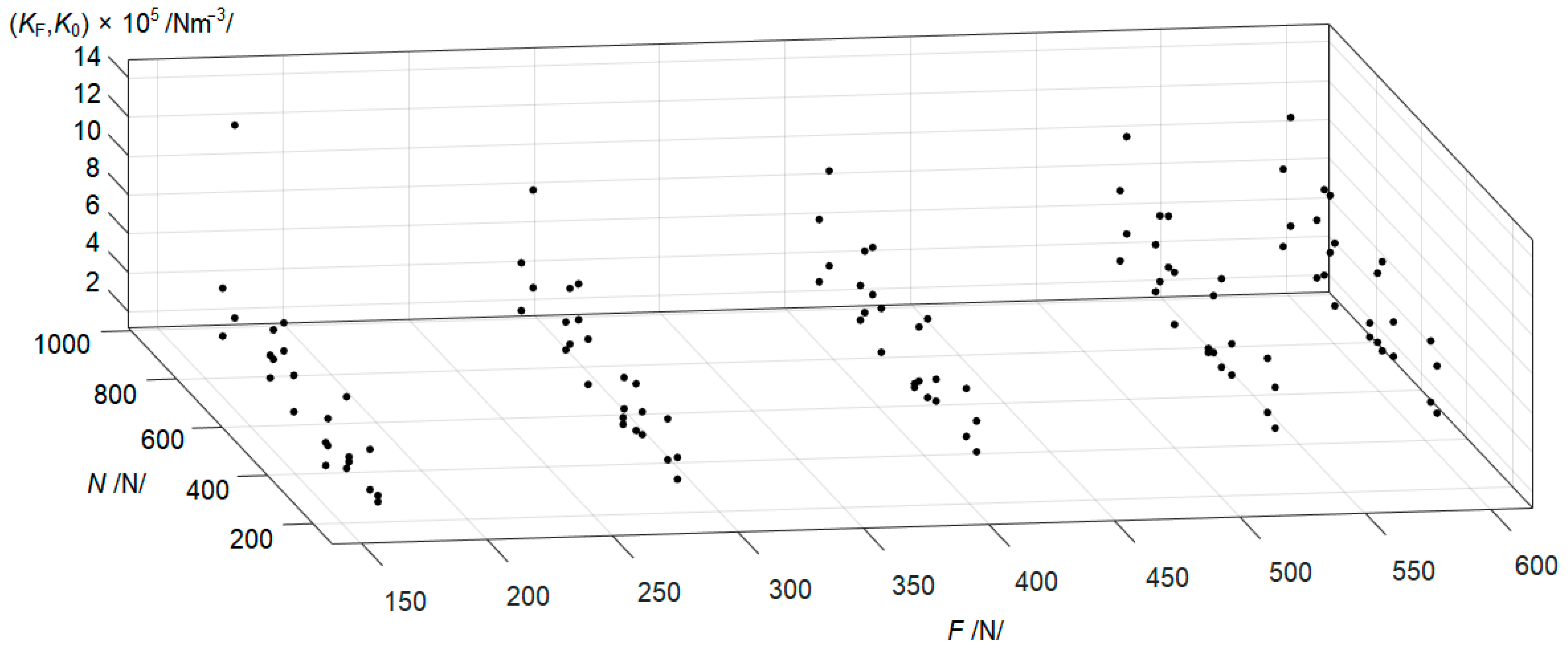
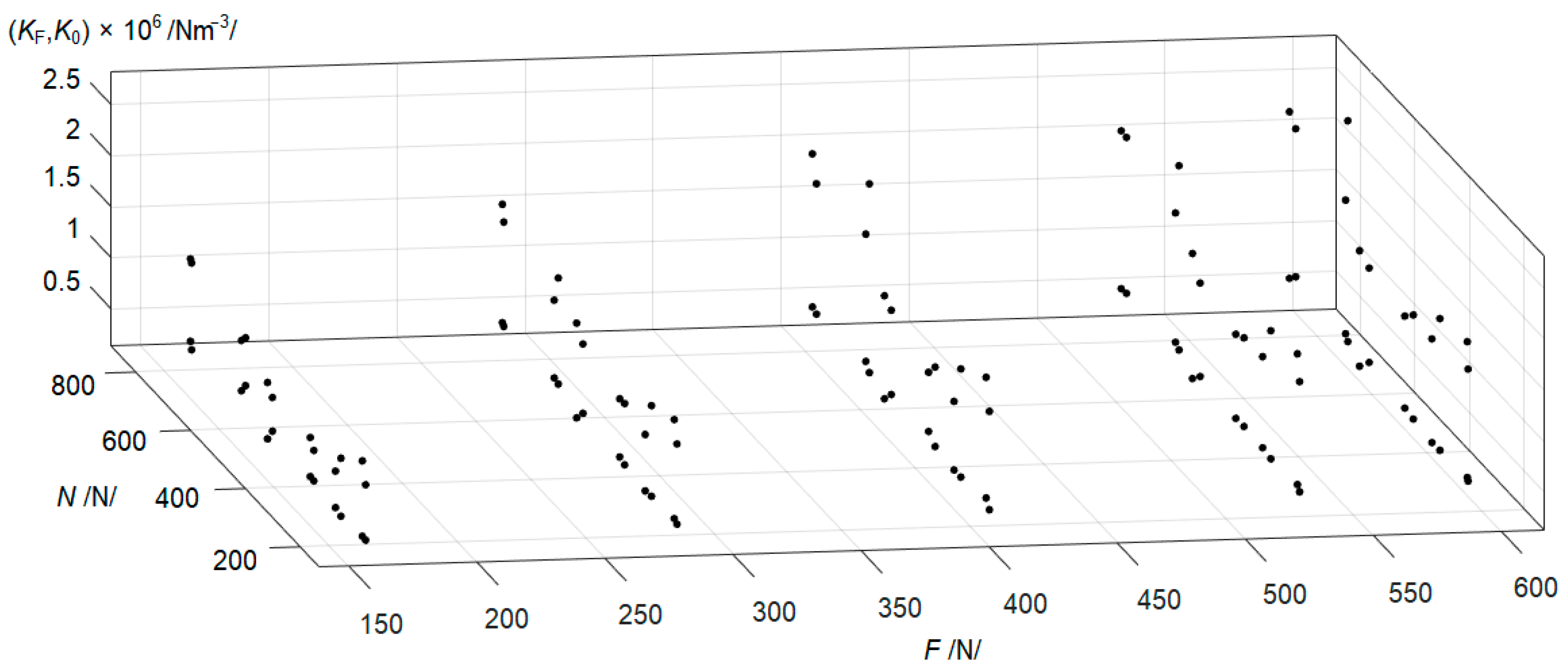
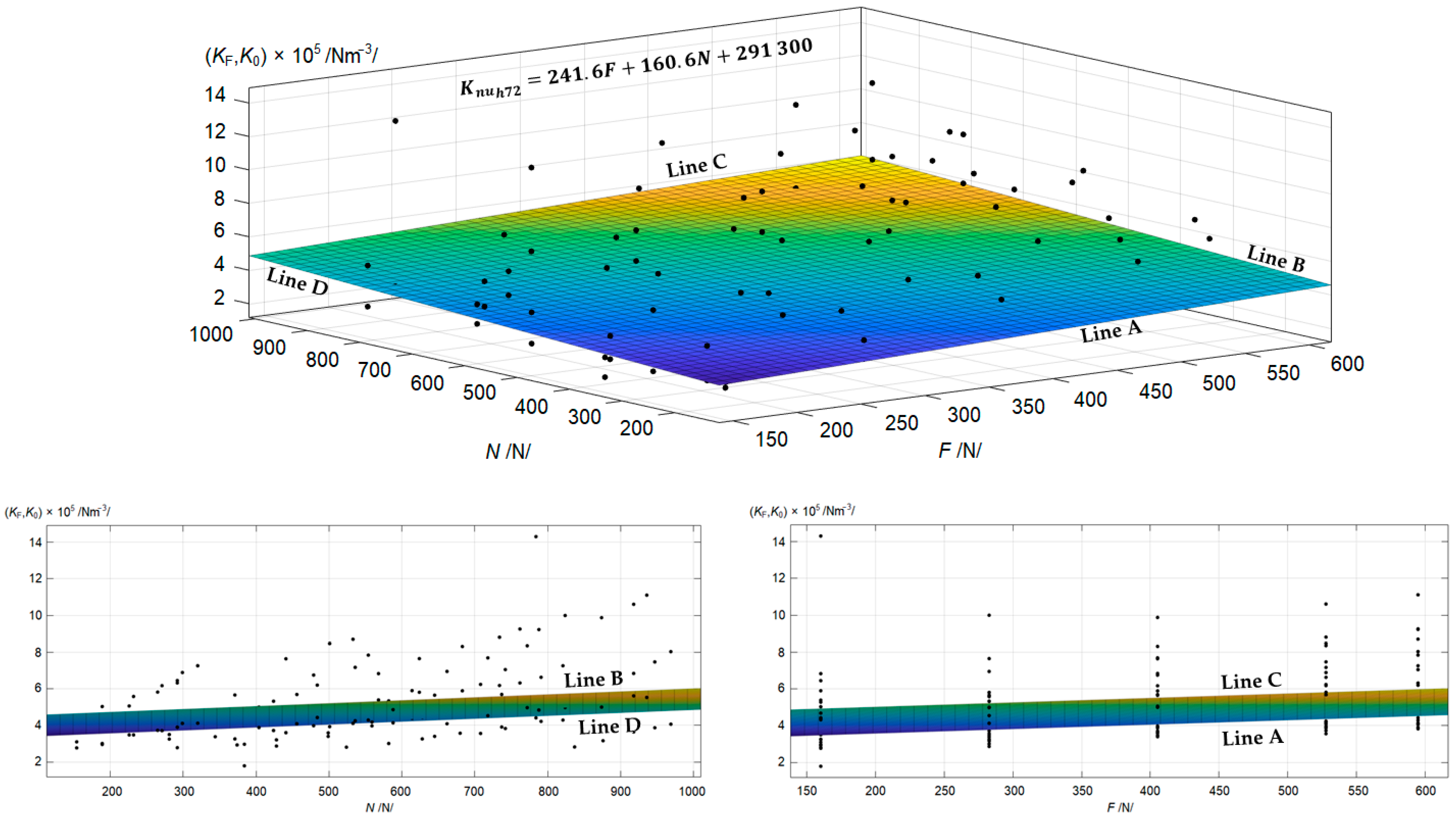
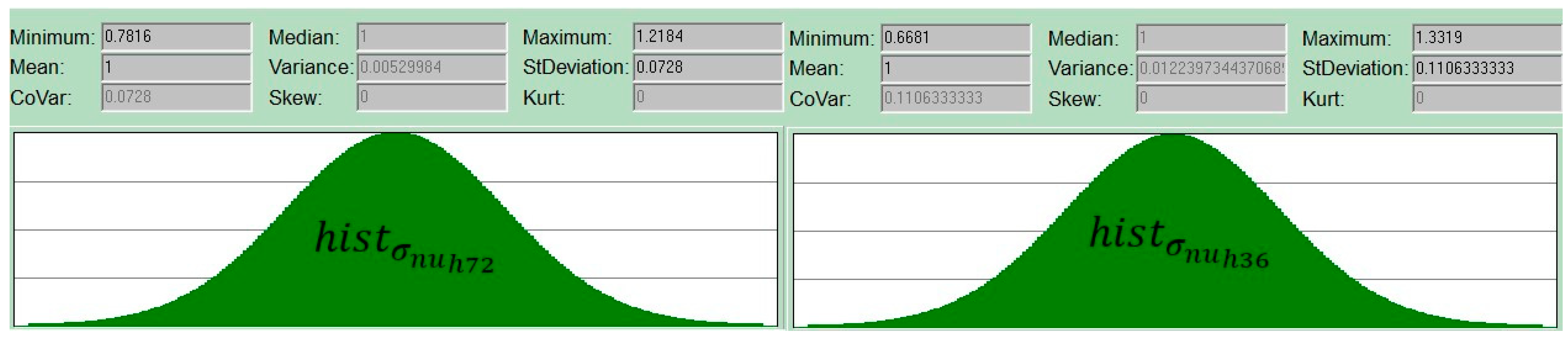
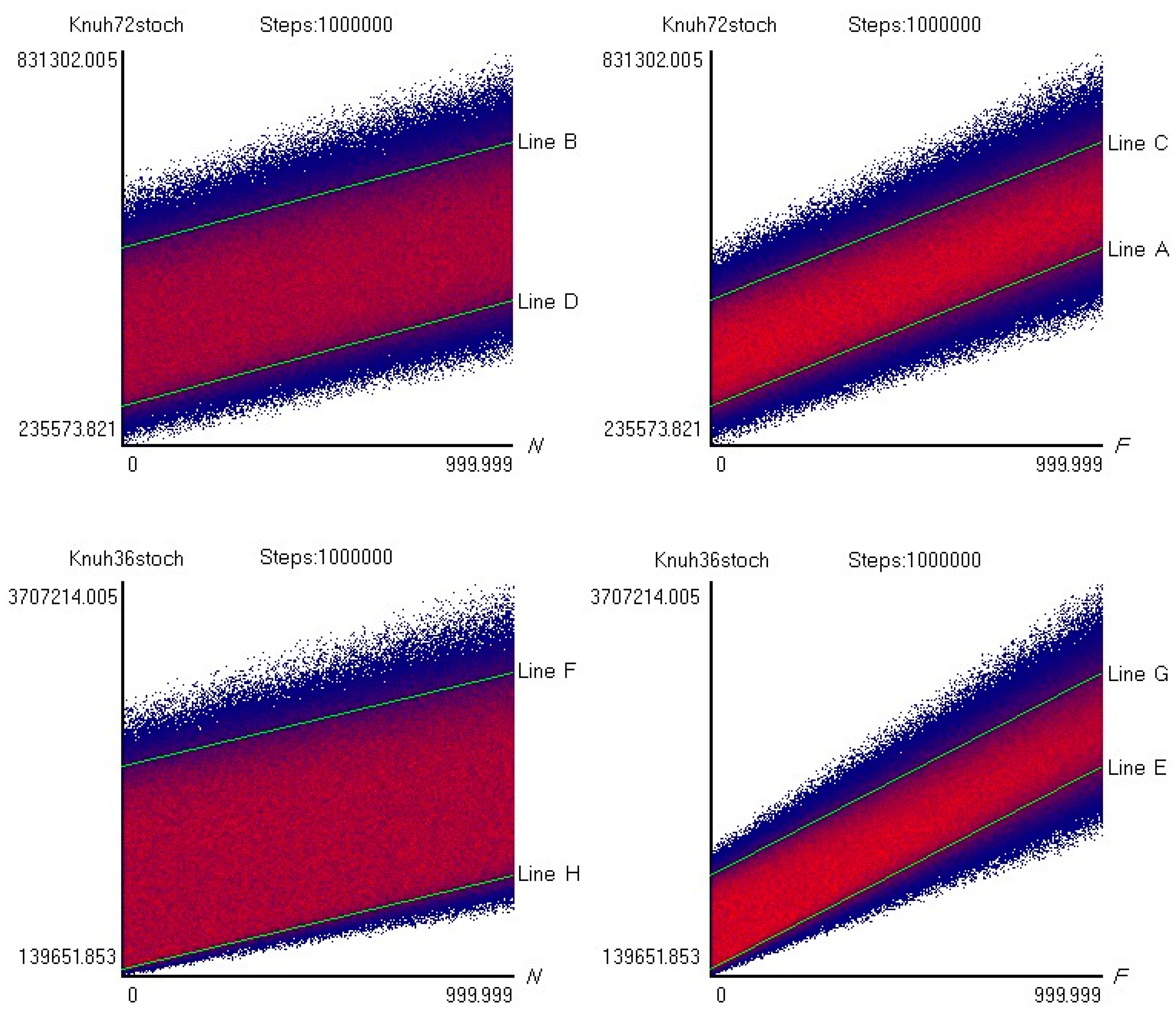
3.2.2. Stochastic Evaluation
4. Discussion
- Experiments were performed by using the laboratory test equipment in our department, i.e., a conveyor with a cover belt and pressure rollers, as shown in Figure 1, Figure 2, Figure 3 and Figure 4. The original measurements—specifically, those of the compression of the belt with wheat (Triticum aestivum)—were conducted for two thicknesses of loose material, namely, h = 72 mm and h = 36 mm, by using symmetric boundary conditions. The measurements were performed for uniformly distributed layers of wheat (see [5]) and nonuniformly distributed layers of wheat (presented in this article).
- Analytical models of a beam on a bilateral Winkler elastic foundation, according to the theory of the second order in mechanics, are suitable and simple enough for modeling the interaction between the belt and wheat. A relatively “simple” linear mechanics problem was then analytically solved. The cover belt was treated as a beam, the pressure rollers were replaced by point forces along the cross-section, and the interaction with the wheat was modeled as a bilateral Winkler elastic foundation.
- The finite element method confirmed the validity of the above-mentioned analytical approach. The application of the plane strain formulation was very close to our analytical model.
- The Winkler moduli of the elastic foundation were obtained from the measured data by using the Newton–Raphson method. The experiment and its evaluation showed that the Winkler modulus of elasticity was not constant, and it was influenced by several factors that were mentioned above, but the values were in the same range as those commonly reported in the literature for loose materials or elastic foundations; see, e.g., [12].
- Furthermore, the obtained results were statistically evaluated. The obtained regression plane functions were in the forms of and for the uniform distribution and of and for the nonuniform distribution of wheat. The functions were then stochastically processed in the form of defined histograms (truncated normal distribution). From the calculated values, a relatively large but natural degree of variability was found. A comparison of the median values for the moduli of the elastic foundation is presented in Figure 21.
- All approaches, i.e., experimental, analytical, numerical, and stochastic, complemented each other and were not contradictory. However, the analytical approach was easy to apply.
- Similarly, as mentioned in [5], in future work, some other characteristics could be added to the measurements; for example, a more proper and complicated model of an elastic foundation could be used for the evaluation of the interaction of the belt and loose material.
- These elastic foundation models are, e.g., the Hetényi model, which was firstly and marginally used by the authors in [10]; see also [23,24]. The differential equation for the Winkler model is prescribed via Equation (1), and the differential equation for the Hetényi (two-parameter) model is Equation (10):where /Nm−3/ and /Nm/ are the moduli of the Hetényi elastic bilateral foundation. Other two-parameter elastic foundation models can also be used, such as those of Pasternak, Filodenko-Borodic, Kerr, etc. [25,26,27]. Multi-parameter models are better suited for the behaviors of elastic foundations but are more complicated.
- Similarly, as cited in [5], the analytical model that used the beam theory and plane strain numerical FEM models could be transformed into a more complicated shell or 3D models, and other stochastic or dynamic (e.g., the start-up, steady-state, modal analysis, etc. (see, e.g., [28])) solutions can be used; see, e.g., [15,16,17,18,19,20,21,29,30,31,32,33,34,35].
- Similarly, as cited in [5], the methodology and the experimental equipment that were shown and used can also be used for different types of loose materials, e.g., seeds, sand, sawdust, gravel, industrial waste, etc., when designing belt conveyors and in material transport.
- The experiments were performed for multiple magnitudes of forces , their corresponding measured tensile forces different thicknesses h of layers of loose material, and different thicknesses of batten hα (the spacings defined in the wheat distribution). Thus, some uncertainties were considered in the calculations.
- The material properties of loose materials have greater variability (statistical dispersion) in mechanical properties than the material properties of rubber belts. However, even the material properties of belts have a statistical dispersion, which was neglected in the calculations. It was assumed that the material properties of belts could be considered constant in our initial approach.
- According to [36], a sensitivity analysis can be used for quantification. However, in this article, it was not performed. The reasons for this was that the main goal of this article was to assess sandwich belt conveyors, elastic foundations, and loose materials. The theory of probability/statistics was a secondary goal. Medians, means, and standard deviations were mainly used with the application of the Monte Carlo method.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| mm | Largest wheat grain length | |
| a | m−2 | Auxiliary variable in Matlab script |
| m−3 | Regression constant | |
| B | m | Belt width |
| b | m2 | Auxiliary variable in Matlab script |
| m−3 | Regression constant | |
| Nm−3 | Regression constant | |
| d | mm | Diameter of pressure rollers |
| rad | Slope (first derivative of deflection) of a beam | |
| m−1 | Second derivative of deflection of a beam | |
| m−3 | Fourth derivative of deflection of a beam | |
| E | Pa | Young’s modulus of a belt |
| 1 | Error between analytical and approximated values of Winkler moduli of elastic foundation | |
| % | Error of FEA | |
| e | 1 | Euler’s number |
| N | Loading force | |
| FEA | Finite element analysis | |
| FEM | Finite element method | |
| h | mm | Loose material (wheat) layer thickness |
| m | Thickness of batten (defined spacings in wheat distribution) | |
| 1 | Truncated normal histogram created from | |
| 1 | Truncated normal histogram created from | |
| m4 | Principal second moment of cross-sectional area of a belt | |
| Nm−3 | Winkler modulus of the elastic foundation | |
| Nm−3 | Winkler modulus of the foundation calculated from deflections | |
| Nm−3 | First Hetényi modulus of the foundation | |
| Nm | Second Hetényi modulus of the foundation | |
| Nm−3 | Analytical Winkler modulus of the foundation (i.e., and ) | |
| Nm−3 | Winkler modulus of the foundation calculated from deflections | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for uniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for h = 36 mm for uniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for h = 72 mm for uniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of foundation for h = 72 mm for the nonuniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for nonuniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for h = 36 mm for nonuniform distribution of wheat | |
| Nm−3 | Approximation function of the Winkler modulus of the foundation for h = 72 mm for nonuniform distribution of wheat | |
| Nm−3 | Stochastic function of the Winkler modulus of the foundation for nonuniform distribution of wheat with h = 36 mm | |
| Nm−3 | Stochastic function of the Winkler modulus of the foundation for nonuniform distribution of wheat with h = 72 mm | |
| Nm−3 | Stochastic function displayed with the Anthill software | |
| L | m | Span between pressure rollers |
| m | Span of the batten pattern | |
| Nm | Bending moment in the belt | |
| m | kg | Weight of loading |
| N | Tensile (axial) force in the belt | |
| R2 | 1 | Coefficient of determination |
| r | m−2 | Auxiliary variable in Matlab script |
| S | m−2 | Auxiliary variable in Matlab script |
| sw | Software | |
| N | Shearing force in the belt | |
| t | m | Thickness of the belt |
| m | Deflection of belt (beam) | |
| mm | Deflection of belt midway between the forces acquired from experiments | |
| mm | Deflection of belt under the force acquired from experiments | |
| mm | Deflection of belt under the force acquired from FEA | |
| x | X axis of the coordinate system | |
| m | General distance from the origin of coordinate system | |
| y | Y axis of the coordinate system | |
| α | ° | Angle |
| ψd | ° | Loose grain angle for wheat |
| m−1 | Parameter of the solution for the differential equation | |
| m−1 | Parameter of the solution for the differential equation | |
| m−1 | Parameter of the solution for the differential equation | |
| kgm−3 | Loose weight of wheat | |
| 1 | Standard deviation of the error for uniform wheat layer thickness of h = 36 mm | |
| 1 | Standard deviation of the error for uniform wheat layer thickness of h = 72 mm | |
| 1 | Standard deviation of the error for nonuniform wheat layer thickness of h = 36 mm | |
| 1 | Standard deviation of the error for nonuniform wheat layer thickness of h = 72 mm |
References
- Dos Santos, J.A. Sandwich Belt High Angle Conveyors Coal Mine to Prep Plant and Beyond–2016. In Proceedings of the XVIII International Coal Preparation Congress, Saint Petersburg, Russia, 28 June–1 July 2016; Litvinenko, V., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 111–117. [Google Scholar]
- Grujić, M.; Erdeljan, D. Advantages of High Angle Belt Conveyors (Hac) in Mining. Appl. Mech. Mater. 2014, 683, 73–77. [Google Scholar] [CrossRef]
- Hrabovský, L.; Blata, J.; Hrabec, L.; Fries, J. The Detection of Forces Acting on Conveyor Rollers of a Laboratory Device Simulating the Vertical Section of a Sandwich Belt Conveyor. Measurement 2023, 207, 112376. [Google Scholar] [CrossRef]
- Fedorko, G.; Molnár, V.; Vasiľ, M.; Salai, R. Proposal of Digital Twin for Testing and Measuring of Transport Belts for Pipe Conveyors within the Concept Industry 4.0. Measurement 2021, 174, 108978. [Google Scholar] [CrossRef]
- Frydrýšek, K.; Čepica, D.; Hrabovský, L.; Nikodým, M. Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via Sandwich Belt Conveyors. Machines 2023, 11, 327. [Google Scholar] [CrossRef]
- Ansys Workbench, Release 2022R2. Available online: www.ansys.com (accessed on 14 April 2023).
- Marc Mentat, Release 2022.3. Available online: https://simulatemore.mscsoftware.com/category/products/marc-mentat/ (accessed on 14 April 2023).
- MATLAB, 9.11.0.1769968 (R2021b). 2021. Available online: https://www.mathworks.com/products/matlab.html (accessed on 23 April 2023).
- Guštar, M.; Marek, P. Anthill. Version 10 Pro. Available online: http://www.noise.cz/sbra/software.html (accessed on 2 May 2023).
- Hrabovský, L.; Frydrýšek, K.; Čepica, D. Winkler and Hetenyi Elastic Foundation Applied in Belt Conveyors for Wheat Transport. In Proceedings of the Engineering Mechanics 2022, Milovy, Czech Republic, 15–18 May 2023; Volume 27/28th, pp. 149–152. [Google Scholar]
- Avramidis, I.E.; Morfidis, K. Bending of Beams on Three-Parameter. Solids Struct. 2006, 43, 357–375. [Google Scholar] [CrossRef]
- Frydrýšek, K.; Jančo, R.; Nikodým, M. Beams and Frames on Elastic Foundation 3; VŠB—Technical University of Ostrava: Ostrava, Czech Republic, 2010; ISBN 978-80-248-2257-0. [Google Scholar]
- Winkler, E. Die Lehre von der Elastizitat und Festigkeit (The Theory of Elasticity and Stiffness); H. Dominicus: Prague, Czech Republic, 1867. [Google Scholar]
- Hetényi, M. Beams on Elastic Foundation: Theory with Applications in the Fields of Civil and Mechanical Engineering; University of Michigan Press: Ann Arbor, MI, USA, 1946; ISBN 978-0-472-08445-6. [Google Scholar]
- Benaroya, H.; Han, S.M.; Nagurka, M. Probability Models in Engineering and Science; CRC Press: Boca Raton, FL, USA, 2005; ISBN 978-0-8247-2315-6. [Google Scholar]
- Kalos, M.H.; Whitlock, P.A. Monte Carlo Methods, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008; Available online: https://www.wiley.com/en-us/Monte+Carlo+Methods%2C+2nd+Edition-p-9783527407606 (accessed on 15 May 2023).
- Marek, P. Probabilistic Assessment of Structures Using Monte Carlo Simulation: Background, Exercises and Software, 2nd ed.; Institute of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic: Praha, Czech Republic, 2003; ISBN 80-86246-19-1. [Google Scholar]
- Čajka, R.; Vašková, J.; Vašek, J. Numerical Analyses of Subsoil-Structure Interaction in Original Non-Commercial Software Based on FEM. IOP Conf. Ser. Earth Environ. Sci. 2018, 143, 012003. [Google Scholar] [CrossRef]
- Vavrušová, K.; Mikolášek, D.; Lokaj, A.; Klajmonová, K.; Sucharda, O.; Pařenica, P. Determination of Carrying Capacity of Steel-Timber Joints with Steel Rods Glued-in Parallel to Grain. Wood Res. 2016, 61, 733–740. [Google Scholar]
- Famfulík, J.; Míková, J.; Lánská, M.; Richtář, M. A Stochastic Model of the Logistics Actions Required to Ensure the Availability of Spare Parts during Maintenance of Railway Vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 85–92. [Google Scholar] [CrossRef]
- Tvrdá, K. Probability and Sensitivity Analysis of Plate. Appl. Mech. Mater. 2014, 617, 193–196. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Texts in Applied Mathematics; Springer: New York, NY, USA, 2007; Volume 37, ISBN 978-1-4757-7394-1. [Google Scholar]
- Younesian, D.; Hosseinkhani, A.; Askari, H.; Esmailzadeh, E. Elastic and Viscoelastic Foundations: A Review on Linear and Nonlinear Vibration Modeling and Applications. Nonlinear Dyn. 2019, 97, 853–895. [Google Scholar] [CrossRef]
- Dillard, D.A.; Mukherjee, B.; Karnal, P.; Batra, R.C.; Frechette, J. A Review of Winkler’s Foundation and Its Profound Influence on Adhesion and Soft Matter Applications. Soft Matter 2018, 14, 3669–3683. [Google Scholar] [CrossRef] [PubMed]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants. Gos. Izd. Lit. Po Strait Arkh. 1954. Available online: https://cir.nii.ac.jp/crid/1573950399307292288 (accessed on 5 June 2023).
- Filonenko-Borodich, M.M. Some Approximate Theories of Elastic Foundation. Uch. Zap. Mosk. Gos. Univ. Mekh. 1940, 46, 3–18. [Google Scholar]
- Kerr, A.D. Elastic and Viscoelastic Foundation Models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Ungureanu, M.; Medan, N.; Ungureanu, N.S.; Pop, N.; Nadolny, K. Tribological Aspects Concerning the Study of Overhead Crane Brakes. Materials 2022, 15, 6549. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zhong, Y.; Li, M. Analytic Bending Solutions of Free Rectangular Thin Plates Resting on Elastic Foundations by a New Symplectic Superposition Method. Proc. R. Soc. Math. Phys. Eng. Sci. 2013, 469, 20120681. [Google Scholar] [CrossRef]
- Silva, A.R.D.; Silveira, R.A.M.; Gonçalves, P.B. Numerical Methods for Analysis of Plates on Tensionless Elastic Foundations. Int. J. Solids Struct. 2001, 38, 2083–2100. [Google Scholar] [CrossRef]
- Lokaj, A.; Vavrusova, K.; Rykalová, E. Application of Laboratory Tests Results of Dowel Joints in Cement-Splinter Boards VELOX into the Fully Probabilistic Methods (SBRA Method). Appl. Mech. Mater. 2012, 137, 95–99. [Google Scholar] [CrossRef]
- Murčinková, Z.; Šmeringaiová, A.; Halapi, M. Damping Properties of Composites with Short and Long Fibres by Impact Testing. AIP Conf. Proc. 2019, 2077, 020042. [Google Scholar] [CrossRef]
- Murčinková, Z.; Postawa, P.; Winczek, J. Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids. Polymers 2022, 14, 3060. [Google Scholar] [CrossRef]
- Haniszewski, T.; Margielewicz, J.; Gąska, D.; Opasiak, T. New Crane Bumper Design with An Energy Absorption Device System. Transp. Probl. 2022, 17, 5–16. [Google Scholar] [CrossRef]
- Lesňák, M.; Maršálek, P.; Horyl, P.; Pištora, J. Load-Bearing Capacity Modelling and Testing of Single-Stranded Wire Rope. Acta Montan. Slovaca 2020, 25, 192–200. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Ghasemi, H. Quantifying the uncertainties in modeling soft composites via a multiscale approach. Int. J. Solids Struct. 2022, 256, 111959. [Google Scholar] [CrossRef]








| Deflection under force /m/ | |
| Deflection midway between the forces /m/ | |
| Slope under force /rad/ | |
| Slope midway between the forces /rad/ | 0 |
| Bending moment under force /Nm/ | |
| Bending moment midway between the forces /Nm/ | |
| Shearing force under force /N/ | |
| Shearing force midway between the forces /N/ | 0 |
| Software | No. of Nodes | No. of Elements | Type of Element |
|---|---|---|---|
| Ansys 2022 R2 | 3761 | 1028 | PLANE183 |
| Marc 2022.3 | 15,281 | 4620 | 27, quad8 |
| Inputs from the Experiment | Outputs from the Analytical Solution | Outputs from FEA (Marc sw) | |||||
|---|---|---|---|---|---|---|---|
/N/ | /N/ | in [5] | |||||
| Small Deformation | Large Deformation | ||||||
| /mm/ | Error /%/ | /mm/ | Error /%/ | ||||
| 825 | 99.5 | 2.365 | 388,552 | 2.7296 | −15.17 | 2.3302 | 1.68 |
| 883 | 222.1 | 3.926 | 593,598 | 4.4795 | −13.98 | 3.8641 | 1.68 |
| 974 | 344.7 | 4.880 | 807,735 | 5.5479 | −13.69 | 4.8048 | 1.54 |
| 1100 | 472.3 | 5.761 | 983,020 | 6.5762 | −14.17 | 5.6736 | 1.50 |
| 1176 | 594.9 | 6.723 | 1,085,698 | 7.6954 | −14.51 | 6.6230 | 1.44 |
| 250 | 160.1 | 2.036 | 1,085,077 | 2.0717 | −1.55 | 1.9972 | 2.10 |
| 269 | 282.7 | 3.378 | 1,177,415 | 3.4425 | −1.85 | 3.3140 | 1.95 |
| 303 | 405.3 | 4.263 | 1,394,325 | 4.3518 | −2.15 | 4.1837 | 1.79 |
| 356 | 527.9 | 5.520 | 1,392,673 | 5.6731 | −2.77 | 5.4187 | 1.84 |
| 386 | 594.9 | 6.320 | 1,355,528 | 6.5231 | −3.21 | 6.2044 | 1.83 |
| 603 | 160.1 | 1.868 | 1,144,399 | 1.9925 | −6.55 | 1.8374 | 1.74 |
| 619 | 282.7 | 2.575 | 1,616,621 | 2.7194 | −5.40 | 2.5335 | 1.80 |
| 646 | 405.3 | 4.273 | 1,310,841 | 4.5576 | −6.74 | 4.2007 | 1.62 |
| 698 | 527.9 | 5.298 | 1,393,375 | 5.6719 | −7.02 | 5.2091 | 1.72 |
| 712 | 594.9 | 5.823 | 1,440,310 | 6.2357 | −7.14 | 5.7255 | 1.62 |
| 154 | 160.1 | 1.197 | 2,267,645 | 1.1953 | 0.39 | 1.1767 | 1.94 |
| 178 | 282.7 | 2.732 | 1,598,355 | 2.7413 | −0.41 | 2.6811 | 1.79 |
| 206 | 405.3 | 3.242 | 2,055,253 | 3.2564 | −0.51 | 3.1833 | 1.75 |
| 252 | 527.9 | 5.250 | 1,518,707 | 5.3179 | −1.29 | 5.1506 | 1.89 |
| 280 | 594.9 | 6.130 | 1,440,006 | 6.2354 | −1.72 | 6.0142 | 1.89 |
| 682 | 160.1 | 1.758 | 1,230,281 | 1.8846 | −7.08 | 1.7282 | 1.81 |
| 691 | 282.7 | 2.883 | 1,363,932 | 3.0831 | −7.05 | 2.8379 | 1.46 |
| 718 | 405.3 | 3.740 | 1,563,796 | 3.9961 | −6.85 | 3.6792 | 1.63 |
| 747 | 527.9 | 4.618 | 1,679,055 | 4.9353 | −6.82 | 4.5424 | 1.68 |
| 761 | 594.9 | 5.315 | 1,626,241 | 5.6957 | −7.06 | 5.2281 | 1.73 |
| 264 | 160.1 | 2.572 | 782,445 | 2.6372 | −2.61 | 2.5216 | 1.88 |
| 296 | 282.7 | 4.552 | 774,149 | 4.6928 | −3.14 | 4.4622 | 1.93 |
| 347 | 405.3 | 6.102 | 840,786 | 6.3313 | −3.79 | 5.9841 | 1.90 |
| 401 | 527.9 | 7.052 | 982,880 | 7.3488 | −4.24 | 6.9197 | 1.85 |
| 448 | 594.9 | 7.797 | 1,000,092 | 8.1758 | −4.82 | 7.6532 | 1.88 |
| 350 | 160.1 | 2.002 | 1,088,641 | 2.0669 | −3.35 | 1.9658 | 1.71 |
| 371 | 282.7 | 3.070 | 1,318,829 | 3.1644 | −3.07 | 3.0141 | 1.82 |
| 410 | 405.3 | 4.655 | 1,211,655 | 4.8315 | −3.90 | 4.5693 | 1.74 |
| 462 | 527.9 | 5.622 | 1,333,423 | 5.8601 | −4.27 | 5.5210 | 1.76 |
| 488 | 594.9 | 6.530 | 1,272,758 | 6.8367 | −4.70 | 6.4124 | 1.80 |
| 520 | 160.1 | 2.138 | 960,093 | 2.2689 | −6.02 | 2.1013 | 1.81 |
| 542 | 282.7 | 3.366 | 1,124,544 | 3.5628 | −5.72 | 3.3072 | 1.86 |
| 573 | 405.3 | 4.241 | 1,341,238 | 4.4803 | −5.67 | 4.1676 | 1.71 |
| 613 | 527.9 | 5.426 | 1,366,172 | 5.7556 | −6.00 | 5.3325 | 1.80 |
| 635 | 594.9 | 5.688 | 1,506,847 | 6.0290 | −5.96 | 5.5914 | 1.73 |
| 771 | 160.1 | 2.057 | 966,801 | 2.2579 | −9.61 | 2.0249 | 1.70 |
| 781 | 282.7 | 2.627 | 1,533,641 | 2.8289 | −7.56 | 2.5861 | 1.67 |
| 804 | 405.3 | 3.767 | 1,527,840 | 4.0664 | −7.86 | 3.7071 | 1.67 |
| 831 | 527.9 | 4.295 | 1,837,813 | 4.6133 | −7.54 | 4.2266 | 1.48 |
| 849 | 594.9 | 4.527 | 2,014,491 | 4.8536 | −7.14 | 4.4559 | 1.64 |
| 605 | 160.1 | 1.852 | 1,157,734 | 1.9755 | −6.78 | 1.8220 | 1.51 |
| 619 | 282.7 | 3.427 | 1,080,675 | 3.6697 | −6.99 | 3.3689 | 1.78 |
| 644 | 405.3 | 4.367 | 1,271,449 | 4.6622 | −6.69 | 4.2932 | 1.76 |
| 682 | 527.9 | 5.195 | 1,436,339 | 5.5450 | −6.84 | 5.1075 | 1.59 |
| 702 | 594.9 | 5.730 | 1,475,859 | 6.1233 | −6.86 | 5.6337 | 1.68 |
| 479 | 160.1 | 2.317 | 863,950 | 2.4528 | −5.72 | 2.2770 | 1.85 |
| 499 | 282.7 | 3.392 | 1,121,037 | 3.5714 | −5.35 | 3.3335 | 1.67 |
| 534 | 405.3 | 4.292 | 1,327,431 | 4.5153 | −5.25 | 4.2187 | 1.66 |
| 578 | 527.9 | 5.492 | 1,350,807 | 5.8048 | −5.73 | 5.3986 | 1.66 |
| 598 | 594.9 | 6.242 | 1,330,286 | 6.6163 | −6.03 | 6.1359 | 1.67 |
| 354 | 160.1 | 1.941 | 1,135,778 | 2.0033 | −3.26 | 1.9064 | 1.73 |
| 382 | 282.7 | 3.336 | 1,172,888 | 3.4531 | −3.39 | 3.2758 | 1.92 |
| 427 | 405.3 | 4.628 | 1,217,474 | 4.8148 | −3.99 | 4.5453 | 1.83 |
| 486 | 527.9 | 5.973 | 1,220,123 | 6.2609 | −4.87 | 5.8675 | 1.72 |
| 521 | 594.9 | 6.611 | 1,243,692 | 6.9558 | −5.23 | 6.4949 | 1.74 |
| 276 | 160.1 | 2.055 | 1,065,360 | 2.1004 | −1.96 | 2.0171 | 2.08 |
| 307 | 282.7 | 3.863 | 970,943 | 3.9717 | −2.89 | 3.7894 | 1.83 |
| 353 | 405.3 | 5.185 | 1,054,064 | 5.3580 | −3.24 | 5.0882 | 1.96 |
| 409 | 527.9 | 6.480 | 1,104,481 | 6.7410 | −4.03 | 6.3614 | 1.83 |
| 437 | 594.9 | 6.680 | 1,244,116 | 6.9537 | −4.10 | 6.5598 | 1.80 |
| 177 | 160.1 | 2.680 | 754,264 | 2.7091 | −1.09 | 2.6259 | 2.02 |
| 201 | 282.7 | 4.580 | 784,705 | 4.6463 | −1.45 | 4.4874 | 2.02 |
| 239 | 405.3 | 5.955 | 890,653 | 6.0680 | −1.81 | 5.8372 | 2.06 |
| 285 | 527.9 | 7.608 | 905,809 | 7.8057 | −2.57 | 7.4600 | 1.97 |
| 311 | 594.9 | 8.418 | 924,039 | 8.6679 | −2.94 | 8.2566 | 1.94 |
| Matlab Script | Description |
|---|---|
| function [KF,K0]=winkler(vF,v0,F,N) | Definition of function “winkler” with 4 inputs and 2 outputs |
| EJzt=6.318; B=0.4; L=0.5; | Definition of inputs, E*Jzt /Nm2/ and B, L /m/ |
| a=N/(4*EJzt); b=(8*EJzt)/F; | Definition of auxiliary variables a /m−2/ and b /m2/ to simplify equations and stated in Table 1 |
| syms r r=vpasolve(-b*vF*r*sqrt(r^2-a^2)+sqrt(r-a)+sqrt(r-a)*cos(sqrt(r-a)*L)*… exp(-sqrt(r+a)*L)+sqrt(r+a)*sin(sqrt(r-a)*L)*exp(-sqrt(r+a)*L)==0,r,500); KF=4*EJzt*r^2/B; | Auxiliary variable: ; Using the native Matlab function “vpasolve” (which uses the Newton–Raphson method) with an initial guess of to calculate for |
| syms s s=vpasolve(-(b/2)*v0*s*sqrt(s^2-a^2)+sqrt(s-a)*cos(sqrt(s-a)*L/2)*… exp(-sqrt(s+a)*L/2)+sqrt(s+a)*sin(sqrt(s-a)*L/2)*exp(-sqrt(s+a)*L/2)==0,s,50); K0=4*EJzt*s^2/B; | Auxiliary variable: ; Using the native Matlab function “vpasolve” with an initial guess of to calculate for |
| end | End of function |
| Inputs from the Experiment | Outputs | ||||
|---|---|---|---|---|---|
/N/ | /N/ | /mm/ | /Nm−3/ | ||
| 837 | 160.1 | 3.084 | 1.425 | 528,288 | 282,097 |
| 876 | 282.7 | 5.199 | 2.095 | 560,720 | 316,480 |
| 918 | 405.3 | 6.474 | 2.370 | 683,989 | 364,305 |
| 947 | 527.9 | 7.911 | 2.800 | 746,895 | 386,520 |
| 969 | 594.9 | 8.461 | 2.895 | 803,139 | 406,516 |
| 614 | 160.1 | 2.961 | 0.506 | 589,836 | 439,119 |
| 662 | 282.7 | 4.634 | 1.101 | 695,102 | 409,377 |
| 718 | 405.3 | 6.144 | 1.316 | 769,218 | 452,638 |
| 772 | 527.9 | 7.506 | 1.441 | 834,777 | 496,734 |
| 788 | 594.9 | 7.884 | 1.751 | 921,535 | 484,429 |
| 568 | 160.1 | 2.695 | 0.271 | 683,079 | 538,954 |
| 624 | 282.7 | 4.362 | 0.411 | 764,637 | 581,459 |
| 683 | 405.3 | 5.852 | 0.621 | 831,127 | 589,060 |
| 734 | 527.9 | 7.272 | 0.751 | 880,478 | 617,839 |
| 762 | 594.9 | 7.890 | 0.821 | 925,099 | 631,971 |
| 374 | 160.1 | 3.833 | 1.004 | 432,459 | 292,714 |
| 424 | 282.7 | 5.801 | 1.089 | 532,211 | 371,839 |
| 479 | 405.3 | 6.976 | 1.409 | 675,225 | 397,898 |
| 536 | 527.9 | 8.633 | 1.659 | 717,065 | 425,319 |
| 554 | 594.9 | 9.118 | 1.869 | 783,708 | 428,815 |
| 281 | 160.1 | 4.534 | 0.719 | 349,764 | 325,030 |
| 344 | 282.7 | 6.569 | 1.244 | 455,212 | 338,475 |
| 404 | 405.3 | 8.724 | 1.369 | 499,587 | 388,262 |
| 456 | 527.9 | 10.279 | 1.669 | 569,084 | 408,754 |
| 484 | 594.9 | 10.859 | 1.579 | 620,042 | 442,785 |
| 189 | 160.1 | 3.575 | 0.800 | 503,237 | 295,671 |
| 232 | 282.7 | 5.818 | 0.995 | 557,664 | 347,951 |
| 271 | 405.3 | 7.708 | 1.275 | 616,710 | 371,024 |
| 299 | 527.9 | 9.228 | 1.295 | 689,437 | 411,204 |
| 320 | 594.9 | 9.988 | 1.505 | 725,996 | 412,134 |
| 784 | 160.1 | 1.566 | 0.583 | 1,425,808 | 440,912 |
| 824 | 282.7 | 3.526 | 0.803 | 999,410 | 498,187 |
| 874 | 405.3 | 5.066 | 1.193 | 987,246 | 499,595 |
| 918 | 527.9 | 6.238 | 1.218 | 1,062,552 | 561,291 |
| 936 | 594.9 | 6.786 | 1.448 | 1,114,999 | 552,856 |
| 628 | 160.1 | 3.599 | 0.981 | 442,658 | 326,022 |
| 680 | 282.7 | 5.799 | 1.496 | 499,506 | 356,945 |
| 737 | 405.3 | 7.537 | 1.851 | 568,944 | 390,773 |
| 791 | 527.9 | 8.774 | 2.126 | 662,501 | 422,219 |
| 821 | 594.9 | 9.244 | 2.366 | 726,420 | 428,964 |
| 524 | 160.1 | 3.530 | 1.223 | 467,548 | 280,781 |
| 582 | 282.7 | 5.633 | 1.958 | 533,638 | 301,395 |
| 645 | 405.3 | 7.685 | 2.313 | 564,849 | 339,745 |
| 708 | 527.9 | 9.258 | 2.853 | 623,804 | 356,492 |
| 742 | 594.9 | 9.543 | 2.838 | 705,046 | 383,271 |
| 384 | 160.1 | 7.100 | 0.980 | 178,553 | 297,404 |
| 428 | 282.7 | 8.913 | 1.530 | 286,614 | 321,012 |
| 499 | 405.3 | 11.188 | 1.830 | 340,051 | 359,151 |
| 559 | 527.9 | 12.500 | 2.005 | 417,815 | 397,227 |
| 588 | 594.9 | 12.630 | 2.105 | 485,965 | 414,364 |
| 292 | 160.1 | 2.937 | 1.033 | 645,198 | 278,455 |
| 371 | 282.7 | 5.612 | 1.398 | 565,574 | 326,013 |
| 441 | 405.3 | 6.432 | 1.723 | 764,442 | 359,537 |
| 501 | 527.9 | 7.725 | 1.943 | 846,685 | 392,568 |
| 533 | 594.9 | 8.505 | 2.023 | 869,377 | 411,423 |
| 154 | 160.1 | 5.086 | 0.890 | 309,876 | 277,158 |
| 189 | 282.7 | 7.268 | 1.355 | 412,772 | 300,810 |
| 226 | 405.3 | 8.943 | 1.410 | 506,393 | 348,219 |
| 265 | 527.9 | 10.473 | 1.620 | 581,969 | 373,034 |
| 292 | 594.9 | 11.081 | 1.690 | 631,635 | 389,535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čepica, D.; Frydrýšek, K.; Hrabovský, L.; Nikodým, M. Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via a Sandwich Belt Conveyor—Part 2. Machines 2023, 11, 715. https://doi.org/10.3390/machines11070715
Čepica D, Frydrýšek K, Hrabovský L, Nikodým M. Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via a Sandwich Belt Conveyor—Part 2. Machines. 2023; 11(7):715. https://doi.org/10.3390/machines11070715
Chicago/Turabian StyleČepica, Daniel, Karel Frydrýšek, Leopold Hrabovský, and Marek Nikodým. 2023. "Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via a Sandwich Belt Conveyor—Part 2" Machines 11, no. 7: 715. https://doi.org/10.3390/machines11070715
APA StyleČepica, D., Frydrýšek, K., Hrabovský, L., & Nikodým, M. (2023). Experimental and Stochastic Application of an Elastic Foundation in Loose Material Transport via a Sandwich Belt Conveyor—Part 2. Machines, 11(7), 715. https://doi.org/10.3390/machines11070715







