A Review of Additive Manufacturing of Soft Magnetic Materials in Electrical Machines

Abstract

This paper presents a review of the main advantages and challenges of Additive Manufacturing (AM) applied in the production of soft magnetic components for electrical machines. Firstly, a general introduction about additive manufacturing is made, considering all of its possibilities of application, then the authors focused on the electrical machine application field, in particular the AM of soft ferromagnetic materials. The soft ferromagnetic materials are fundamental for the production of electrical machines, and currently, there are more and more requests for designed ad hoc geometries, which can be difficult to produce with conventional manufacturing technologies. With this purpose, AM can be used to produce the desired geometries.

1. Introduction

Currently, Additive Manufacturing (AM) has the potential to innovate the design and manufacturing of Electric Machines (EMs). Thanks to AM, new optimised geometries can be designed and manufactured with the purpose of improving the machine’s thermal, electromagnetic, and mechanical performance [1,2,3]. In addition, it is possible to reduce the waste of raw material compared to traditional manufacturing techniques.

Nevertheless, AM still has some limitations that make it unsuitable for today’s industrial production. Some of the most-relevant disadvantages are the limited maximum size of the part, long manufacturing times, and the need for post-processing and finishing machining, which increase the total cost of the whole processing. Recent scientific research has shown some promising results for the manufacturing of high-efficiency EMs.

The expression AM includes a wide variety of techniques that create a component by layer deposition using different types of materials (e.g., plastics or metals). Focusing on EM manufacturing, “Powder Bed Fusion” is the most-employed method: it melts or sinters particles of metal powder (e.g., aluminium and titanium alloys, electric steels, soft magnetic composites, etc.) using a laser (e.g., SHS, SLM, SLS, DMLS) or electron beam (e.g., EBM) [4,5].

The AM technologies mentioned before require an energy source, which leads to a very high thermal gradient, whose effects will be further explored in Section 3.

From the point of view of iron losses, additively manufactured rotors or stators exhibit much higher losses than laminated ones because of the solid construction, which causes an increment of the eddy currents induced in the part, as analysed in Section 4.

For these reasons, some scientific papers have focused on methods to reduce the iron losses; in [6], a multi-material printing method was proposed to overcome the iron loss drawback of AM rotors.

AM introduces inherent material anisotropy, which is particularly interesting for the winding design in the case of high-frequency applications and for grain-oriented magnetic synchronous reluctance rotors [7,8].

Overview of the Additive Manufacturing of EMs

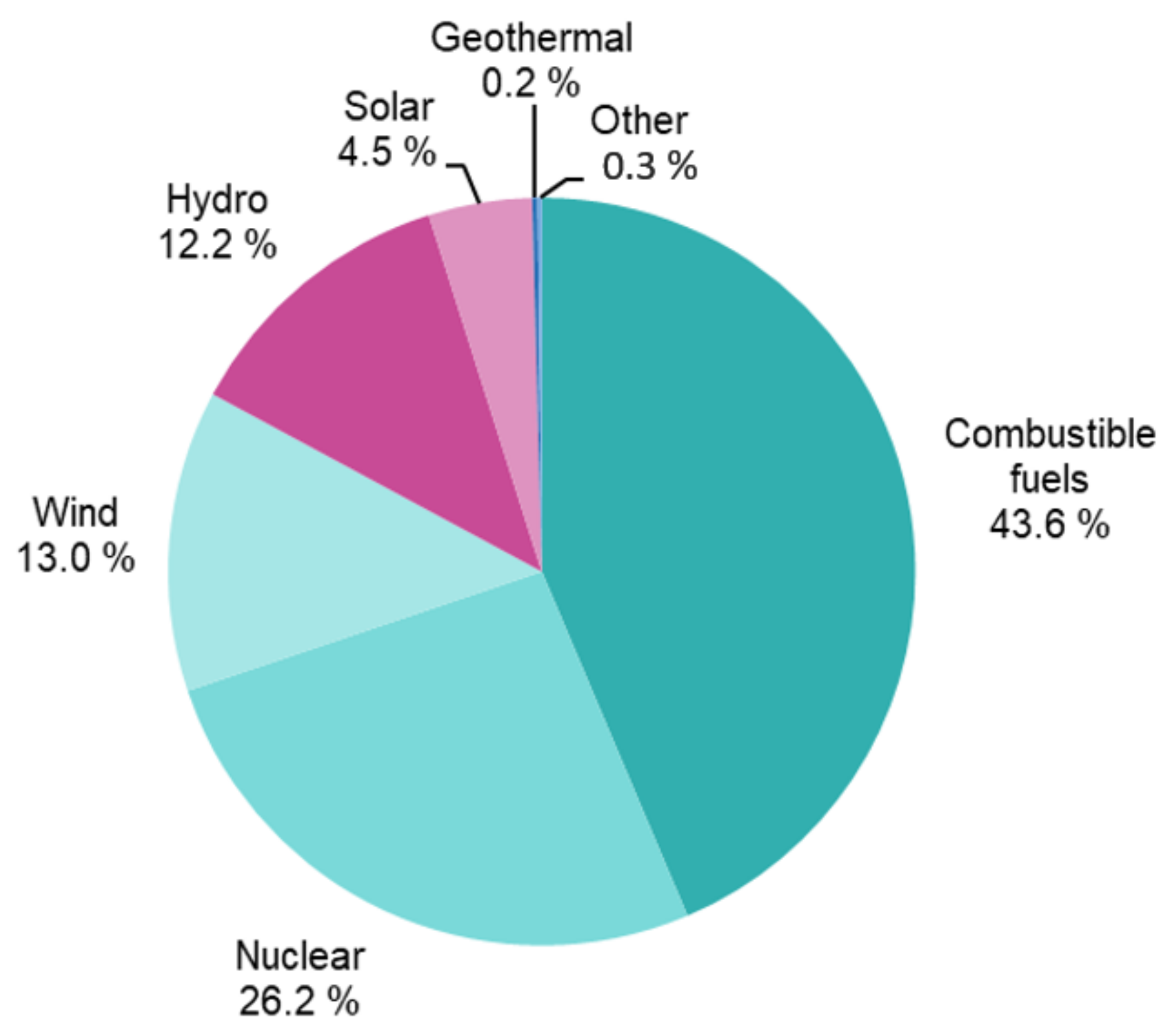
Electric motors come in virtually all sizes, ranging from mW up to MW. EMs, through electro-mechanical conversion, essentially produce all the electrical energy used on Earth. In fact, in 2019, only 4.5% of the total electricity harnessed in the EU came from the conversion of solar thermal energy to electricity by the photovoltaic effect, as shown in Figure 1 [9,10].

In addition, EMs for industrial applications, indicatively, take up 40% of the total available electricity and are expected to increase by 15% per year in the near future. The massive and increasing use of EMs is evident, so it is of paramount importance to continuously develop and innovate EMs.

In this regard, the new EU efficiency parameters required for all electric motors rated from 0.75 up to 1000 kW belonging to the IE4 class must be met. This task is really challenging because, in order to raise the efficiency by two percentage points from 92% to 94%, the machine energy losses should be reduced by 25% [11]. In fact, most motor losses result in heat rejected into the atmosphere, and reducing losses can significantly reduce the cooling loads of an industrial facility’s air conditioning system [6,12].

In light of this, the development of new materials integrated into modern Additive Manufacturing (AM) technologies is what could have the greatest impact on the performance of future EMs [13]. Other areas of research such as control, design, and optimisation allow for the refinement of the machine for implementation in the specific application, but it is the materials and manufacturing techniques that impose the practical limits of the machine itself [14].

As Naseer et al. pointed out [1], by innovating materials and component fabrication technologies, it would be possible to make EMs with a higher power density, increased efficiency, and a reduced weight/volume. In addition, the greater freedom in the design and construction of complex geometries would allow the integration of heat dissipation into the structural components of the EM itself with a consequent thermo-mechanical benefit.

The construction of high-performance metal components by means of AM techniques has reached high levels of maturity in a relatively short time and with even good production volumes while still being relatively high in cost, which limits its application to high-tech industries [15,16]. For example, GE Aviation [17] from 2015 to 2021 made by means of “Metal 3D-PRINTING” 100,000 pieces of its fuel nozzle.

More recently, Porsche Industry [18] has produced entirely by SLM its electrical drive housing. It is a prototype, but compared with a weight reduction of 40% compared with the same component made by conventional mechanical technologies, the mechanical properties are almost the same. In addition, the production cycle promises to be leaner.

AM allows a freedom of design and construction previously unknown for EMs by paving the way toward entirely new geometries no longer constrained by previous planar-symmetry parameters.

In 2013, Aguilera et al. [19] constructed nonmetallic structural components within which the active components, such as magnets and windings, can then be inserted.

The first “metal additive manufactured” rotors appeared in 2016 as demonstrated by the attempt made by selective laser melting (SLM) by Lammers et al. [20]. Due to the lack of specific materials, Lammers et al. chose H13, which was identified as the most-suitable AM material, and it was formed by adding alloying elements to carbon steel, to build their prototype to compare with a commercial target rotor in order to test its mechanical and electromagnetic properties in order to scientifically validate their method. The poor magnetic properties were attributable to the martensitic microstructure with the austenite parts of H13; however, by performing heat treatment in a furnace under an “argon atmosphere” at 780 °C for 20 min with subsequent slow cooling in the furnace, a significant improvement in the permeability of their prototype was possible. On the other hand, since the rotor was not structured with laminations, the energy losses due to eddy currents became dominant as the frequency increased. The mechanical advantages were obvious as they reduced the mass by 25% and the mass moment of inertia by 23%, which meant a restriction of the initial acceleration transient by 23%.

Starting from 2018, there has been a strong acceleration of research in the field of AM applied to EMs as evidenced by the appearance of an increasing number of papers on the subject devoted to the design and implementation of new geometries for “active” and “passive” components and the development of hard or soft magnetic materials specific to the AM techniques. In [21], the authors printed a full E-type transformer core, then they presented a comparison between its properties and the ones of commercial FeSi alloys, with a particular focus on iron loss generation. This aspect will be further analysed in Section 4.

This push for scientific research can be attributed, according to Wrobel et al. [4], to the 18% growth that the AM market, to be understood as “hardware, materials, software, manufactured parts” related to the aerospace, biomedical, automotive, etc., industries, has accomplished just in 2018, settling at USD 9.3 trillion and with even the future forecast to exceed USD 41 trillion in 2027.

AM offers the possibility to optimise the plunger geometry of reluctance tubular machines, as the authors accomplished in [22]. In Figure 2, the mock up prototype of the machine’s plunger pole is reported; thanks to additive manufacturing, it was possible to explore more geometries with a different number of flux barriers, with the purpose of maximising the performance of the machine.

In addition, thanks to AM, it is possible to optimise the geometry of electrical machines’ windings, with the purpose of maximising the slot-filling factor and obtaining a better current distribution in the slots, leading to a maximisation of the performance of the machine, as shown in [23,24,25]. Another important application of AM in electrical machines regards the cooling system, which can be optimised to reach the desired power dissipation, as shown in [26,27].

Taking a cursory look at the items selected and studied, it can be said that about half of them involve “Laser Powder Bed Fusion” (L-PBF), used in [28]. This is explained by virtue of the high manufacturing densities it provides. About one-fourth of the articles concern different extrusion methods that are well suited for the production of low-density parts and also of permanent magnets, by virtue of the advantages that the non-homogeneous structure can guarantee in PMs. Other AM techniques for metallic materials pioneered in the field of EMs are “Electron Beam Melting” (EBM), “Direct Energy Deposition”, and “Bitter Jetting” (BJ).

AM application in the EM field has reached different grades of maturity. Large-scale production using AM is possible for non-active assemblies for mechanical and thermal management. On the other hand, active parts such as windings, magnetic cores, and permanent magnets have a lower maturity. With AM, however, it is possible to design structures for these components that are impossible to realise through conventional manufacturing techniques [23].

The paper is structured in the following way. Firstly, an introduction about AM techniques and applications to different material is made, then the authors focus mainly on AM applied to electrical machines, considering soft magnetic materials’ application. Afterwards, the main causes of mechanical defects are investigated. To conclude, an overview of power losses generated by hysteresis and eddy current development is given.

2. AM Technologies

In general, the term “Additive Manufacturing” refers to those technologies of building layer upon layer from a 3D model in .STL format through seamless digital Computer-Aided Design (CAD) and Computer-Aided Manufacturing (CAM) integration; by varying the material used, the energy source and other macroparameters, different AM techniques can be specified. For the American Society for Testing and Standards (ASTM) [29], there are seven types of AM:

• Vat Photopolymerisation (VPP): the liquid photopolymer in a vat is selectively cured by light-activated polymerisation;
• Material Jetting (MJT): the droplets of the build material are selectively deposited;
• Binder Jetting (BJT): the liquid bonding agent is selectively deposited to join powder materials;
• Material Extrusion (MEX): the material is selectively dispensed through a nozzle or orifice;
• Powder Bed Fusion (PBF): the thermal energy selectively fuses regions of a powder bed;
• Sheet Lamination (SL): sheets of the material are bonded to form an object;
• Direct Energy Deposition (DED): focused thermal energy is used to fuse materials by melting as they are being deposited.

Variable subclasses can also be identified for each of the previous seven main classes based on the materials with which they operate.

2.1. AM for Polymers

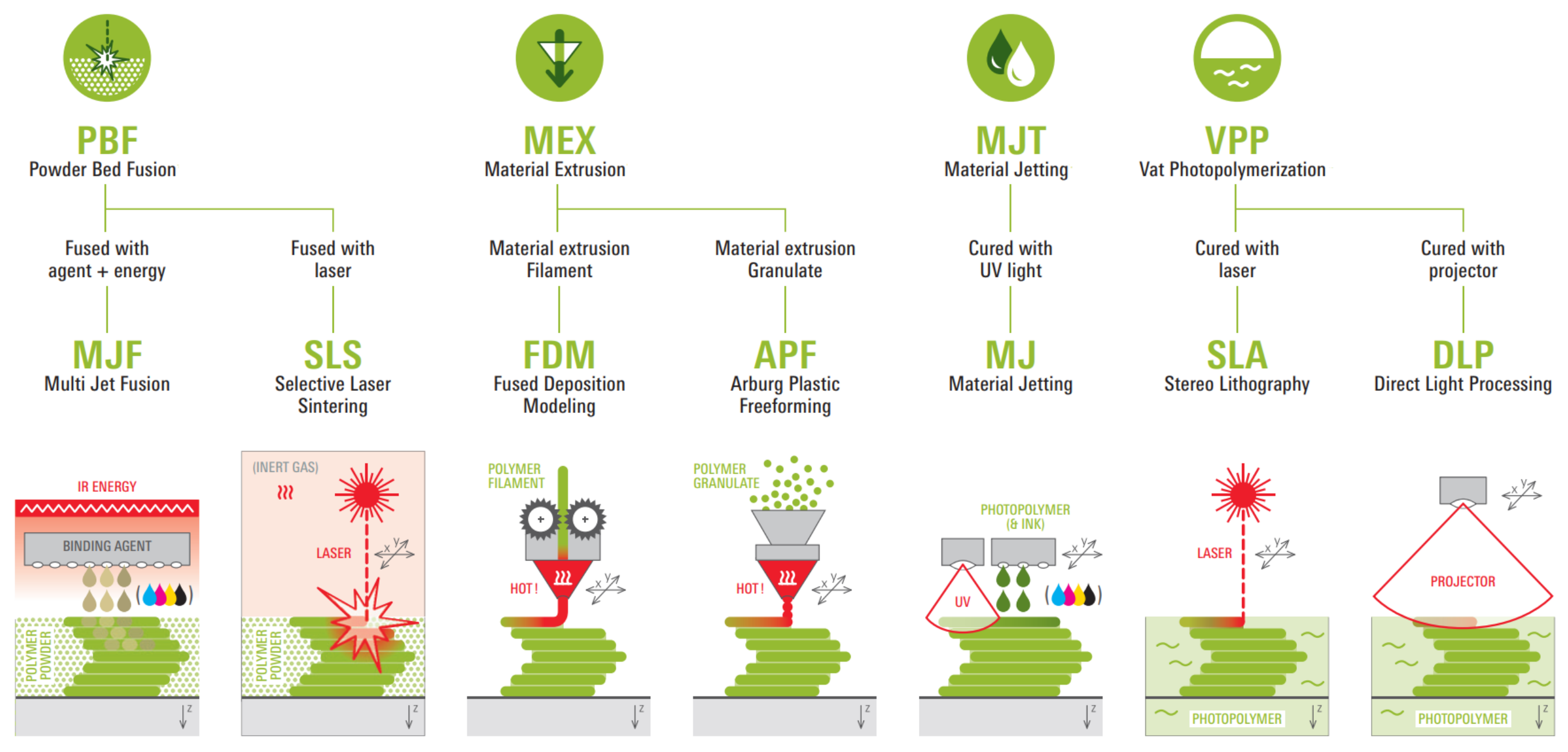
As can be seen in Figure 3, taken from [30], PBF applied to polymeric materials includes “Multi Jet Fusion” (MJF) and “Selective Laser Sintering” (SLS). In MJF, the process begins with a layer of polymer powder. Then, liquid droplets are applied to the powder layer, and thanks to an infrared source, the material is melted. SLS exploits a movable laser beam, which sinters the polymer powder locally layer-by-layer. The component is generated by solidifying its cross-section in each layer.

MEX applied to polymers includes the “Fused Deposition Modeling” (FDM), used in [31] and the “Arburg PLstic Freeforming” (APF). FDM uses a hot nozzle unit to plasticise a polymer filament. APF, instead of a wire-shaped plastic, uses a plastic granulate.

The “Material Jetting” for polymers (MJ) applies locally and layer-by-layer small droplets of a photopolymer through many nozzles and, instantly, cures the viscous photopolymer by means of UV light.

“Stero Lithography” (SLA) and “Direct Light Processing” (DLP) are two examples of VPP applied to polymers. SLA cures selectively the viscous photopolymer in layers by means of a movable laser beam. DLP polymerises the exposed photopolymer layer-by-layer using a projector.

In [32], an interesting application, which used 3D-printed polymers, was presented for lightweight silicon photovoltaics technology.

2.2. AM for Metals

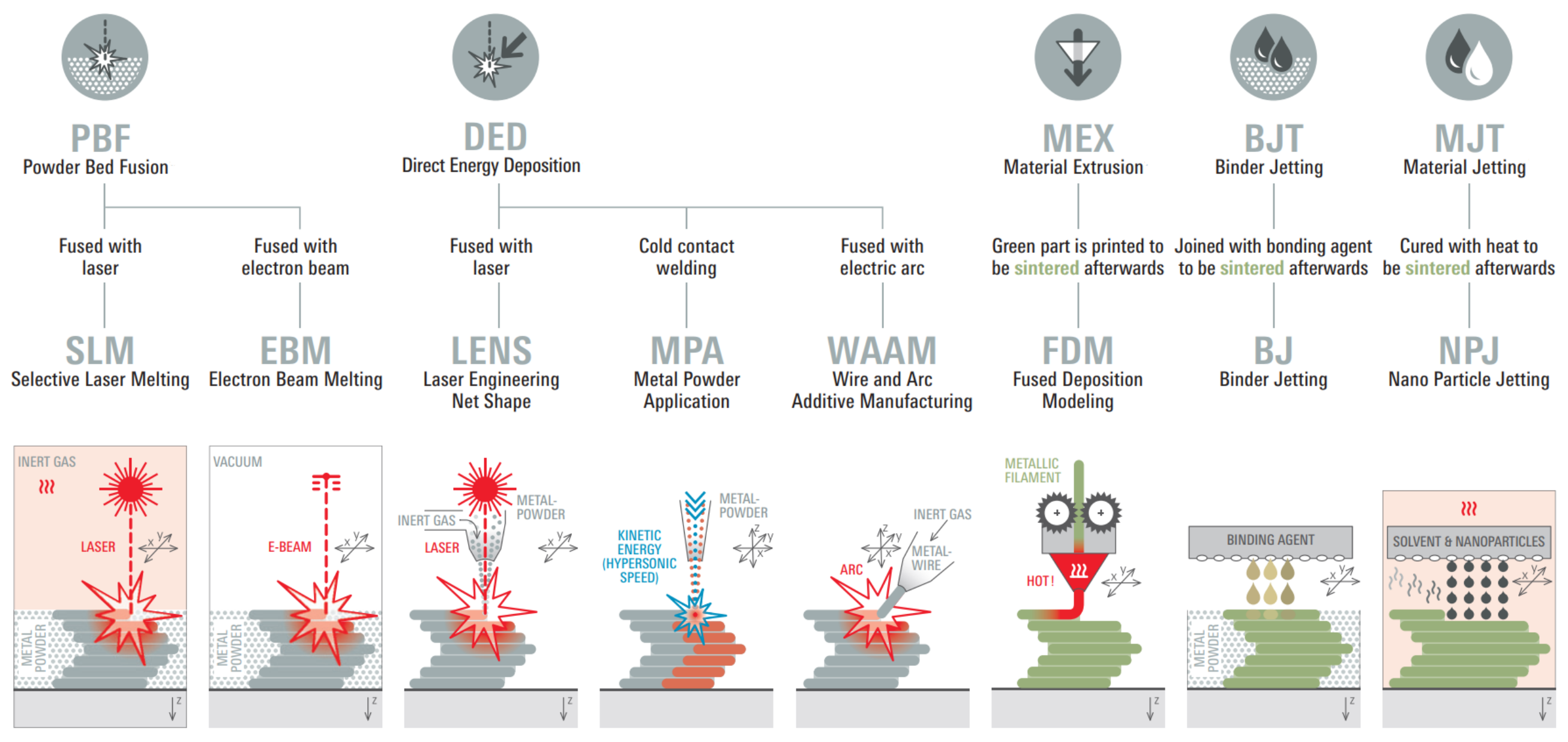
In Figure 4, there is a schematic recap of the AM technologies that could be applied to metals. Regarding PBF, it is possible to recognise “Selective Laser Melting” (SLM) and “Electron Beam Melting”. SLM melts locally layer-by-layer the selected metal powder by means of a movable laser beam, thus solidifying a cross-section of the component. Compared to sintering, there is a higher density of the component and a different microstructure due to the different process of consolidation, which leads to greater mechanical characteristics for the same material used. The main challenges of this technology were deeply analysed in [33]. EBM works in the same way, but instead of a laser, it uses an electron beam to melt locally layer-by-layer the selected metal powder; for this reason, EMB can be used with only a few metals (e.g., titanium, tungsten, Co-Cr, Inconel 718, etc.).

The “Laser Engineering Net Shape” (LENS) [34], the “Metal Powder Application” (MPA), and the “Wire and Arc Additive Manufacturing” (WAAM) are DED technologies. LENS applies and melts the metal material simultaneously by a laser beam. The solidification of the melt generates new layers.

The MPA, also called “Cold Spray”, applies the metallic powder with very high kinetic energy layer-by-layer; in this way, the component is close to the final shape, and it is also possible to combine more materials. The WAAM applies locally and layer-by-layer the melted metal wire by means of arc welding; in this way, it is possible to quickly produce near-net-shape metal components. MEX for metals is called “Fused Deposition Modeling” (FDM), and it plasticises a metallic filament by means of a hot nozzle unit and doses selectively the material layer-by-layer. “Binder Jetting” for metals (BJ) applies selectively tiny binder droplets onto the metal powder by means of many nozzles to stick it together layer-by-layer. In the end, the MJT applied to metals is called “Nano Particle Jetting” (NPJ). NPJ doses selectively and locally a solvent fluid containing nano-metal particles; when the solvent evaporates, the nano-particles bond together. The components made by FDM, BJ, and NPJ must be sintered afterwards.

2.3. AM for Other Materials

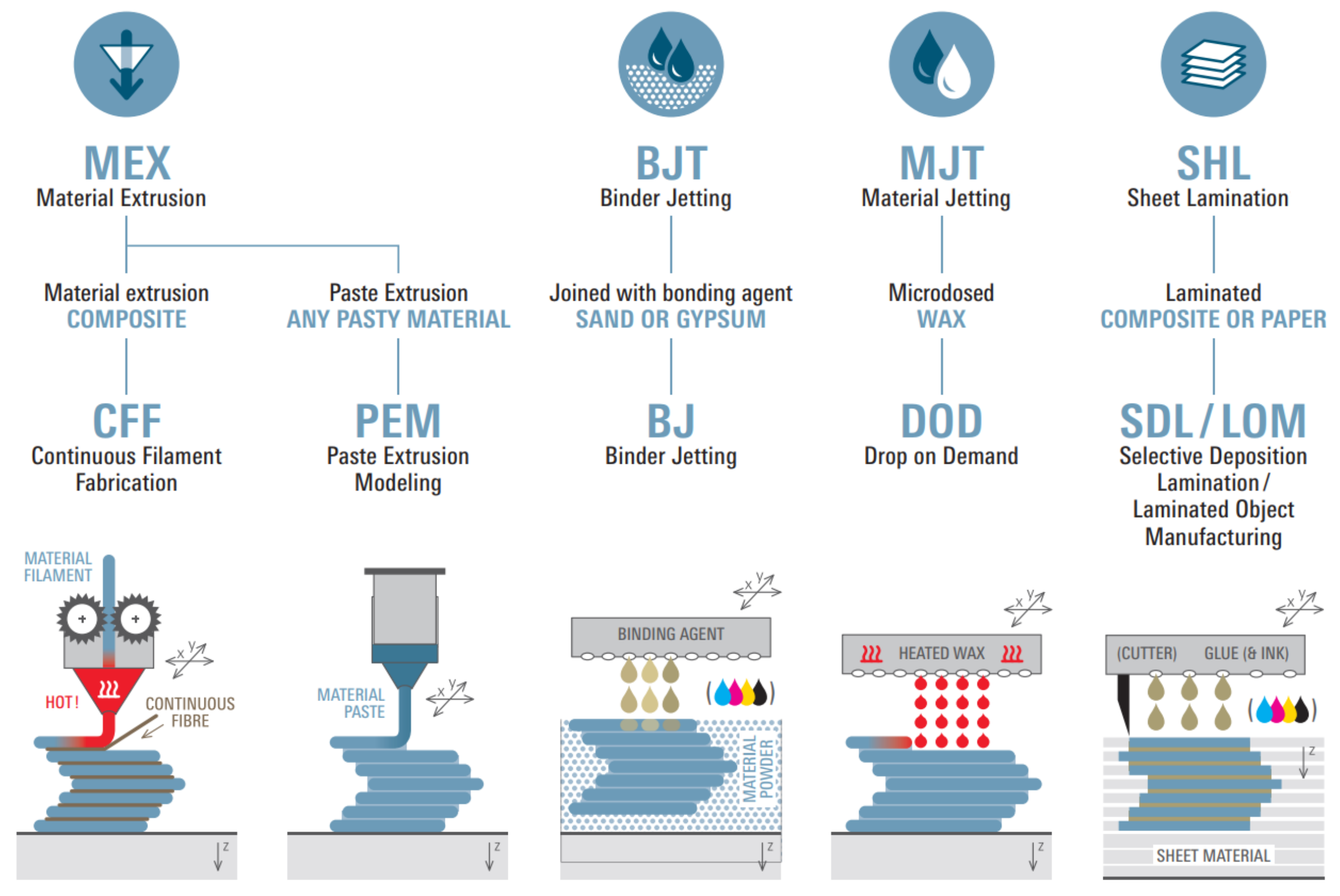
Looking at Figure 5, the technologies for other materials are rather similar to those we have already discussed in the previous “subsection”.

It is possible to add that MEX for a composite material is called “Continuous Filament Fabrication” (CFF) and uses a hot nozzle unit to plasticise selectively a wire-shaped plastic that is dosed layer-by-layer around continuously deposited reinforcing fibres. Another MEX technology is “Paste Extrusion Modeling” (PEM), which doses selectively layer-by-layer any pasty material by means of a piston nozzle.

BLT joins with a bonding agent sand or gypsum.

MJT is called “Drop on Demand” because it microdoses selectively, through many nozzles, heated wax droplets layer-by-layer.

SHL laminates composite or paper and is called “Selective Deposition Lamination” (SDL) or “Laminated Object Manufacturing” (LOM). Nozzles are devices that are designed to control the direction or characteristics of a fluid flow, usually to increase its velocity. In this application, they are used to guarantee a good level of precision to apply locally adhesive to the respective material layer. Each level can be stacked and laminated directly or subsequently, and then, the finished component can be cut out along the contour. Nozzles are devices that are designed to control the direction or characteristics of a fluid flow, usually to increase its velocity. In this application, they are used to guarantee a good level of precision to apply locally adhesive to the respective material layer. Each level can be stacked and laminated directly or subsequently, and then, the finished component can be cut out along the contour.

2.4. AM for EMs

Focusing on EM manufacturing, “Powder Bed Fusion” is the most-employed method: it melts or sinters particles of metal powder (e.g., aluminium and titanium alloys, electric steels, soft magnetic composites, etc.) using a laser or electron beam. It is possible to classify the following PBF techniques:

• Direct Metal Laser Sintering (DMLS);
• Electron Beam Melting (EBM);
• Selective Heat Sintering (SHS);
• Selective Laser Melting (SLM);
• Selective Laser Sintering (SLS).

After the previous general review of the AM technologies for metal, particular focus should be dedicated to the main ones among them that are used for fabricating permanent magnets, such as cold spray.

Cold spray, also called “Metal Powder Application”, has been recently applied to the fabrication of PMs. In a CS process, the fine magnetic particles, in a compressed gas stream, are hurled at high velocity, in general higher than 300 m/s, onto a substrate or backing plate; they deform plastically, so they can mechanically interlock and metallurgically bond, creating a layer.

The metallic powder remains in a solid state during the entire deposition process, and in this way, the thermal defects, e.g., oxidation and thermal stresses, are not seen in the PMs so made. Moreover, CS allows spraying on a metallic surface such as the rotor core. In this way, it is possible to obtain a complex near-net-shape geometry.

3. Origin of Mechanical Defects

There are different kinds of defects that can be originated from distinct factors. Some of them can be related to the powder, such as trapped gas or surface contamination and oxidation. Others can be related to the process, such as the lack of fusion porosity, the formation of columnar grains, or the surface finish and roughness [35]. It is also important to take into account the possibilities of defect generation after a post-processing treatment, such as annealing, which can cause thermally induced porosity. Limiting the arising of these kinds of defects is fundamental to obtain a part with the desired mechanical properties.

One important parameter to set in an additive manufacturing process is the laser energy input, which can significantly affect the mechanical properties of the material. In fact, increasing the energy input brings an improvement in powder melting and a reduction in melt-pool instabilities, so the part becomes more dense. Anyway, as said before, the increment of the energy input leads to spherical pores and crack generation, which cause difficulties for the part to reach full densification. When the energy input is high, the melt-pool shape changes from flat to protuberant, and conduction mode welding is replaced by key-hole welding. The surface vaporisation of the material brings the formation of a key-hole. In this process, the gas bubbles generated can remain trapped inside the melt-pool during the solidification process.

Thermal stresses are the main cause that brings the formation of cracks during the SLM process. In fact, since the SLM process’s working principle is based on the concentrated application of high energy in a short time on the same point, tensile residual stresses could be introduced in the part. Considering this and the low heat conductivity of the powder bed, a high thermal gradient is generated near the laser spot. In these conditions, differential thermal expansion are generated, so the heat-affected zone, which presents a reduction of the tendency to expand due to being inhibited by the surrounding material, could be plastically compressed. During cooling, tensile stresses are generated because of the upper layer’s tendency to contract.

3.1. Effects of Annealing

Annealing is the process of heating a metal or alloy to a temperature below its melting point in order to improve its mechanical characteristics. In [36], the authors investigated the effects of annealing on the properties of FeSi6.9 produced by SLM. Some sets of different samples were manufactured with different shapes: cubic, wall, and ring. Then, they were annealed in an argon atmosphere for 1 h at four different temperatures (400 °C, 700 °C, 900 °C, and 1150 °C) before furnace cooling. The authors noticed that, thanks to the annealing at 900 °C, the melt-pool boundary lines disappeared, probably because of the dissolution of silicon in the solid. At 1150 °C, the sample had a homogenised microstructure, which presented a non-uniform grain size, so the recrystallisation process had not finished yet.

The technique used to perform these analyses was Electron Backscatter Diffraction (EBSD), which is a Scanning Electron Microscopy (SEM) technique for material characterisation, in which the electron beam is scanned across the surface of a tilted crystalline sample; the diffracted electrons at each point form a pattern that can be detected and, then, analysed with appropriate hardware and software. The results obtained showed that annealing did not modify the $<001>$ texture induced by SLM in the Building Direction (BD), so it can be used to improve the material’s mechanical and magnetic properties without weakening the beneficial crystallographic texture induced by SLM. The properties obtained from the tests performed on the as-built and annealed ring samples are resumed in the following points with a comparison with a commercial grade of high-Si electrical steel. These results showed that:

• The permeability grew with the increase of the annealing temperature, reaching the value of the commercial sample. This happened thanks to the fact that stress relief and grain growth reduced the amount of lattice defects, which caused permeability reduction since they act as pinning sites for the magnetic domain walls.
• Induction $B_{10}$, which is the flux density at an applied field strength H = 1000 A/m, increased with annealing temperature; otherwise, $B_{50}$ was little affected by annealing, which means that the considered applied field was strong enough to overcome most of the manufacturing-induced obstacles to magnetisation.
• Hysteresis loss, expressed in terms of $H_c$, decreased with the increase of the annealing temperature.
• The remanence $B_r$ had a non-monotonic dependence on the annealing temperature. Its initial increase was due to the effect of the residual stress relief, but then, thanks to grain enlargement, the defect density decreased, hindering demagnetisation and leading to a reduction in Br at a high annealing temperature.
• The total power loss decreased with increasing annealing temperature, with a trend similar to the one of $H_c$. This suggested that the eddy current loss component did not increase significantly with grain growth.

With the SLM process, the material texture presented a small grain size, which caused a degradation of the magnetic properties of the printed material. Therefore, for practical application an annealing treatment is fundamental to promote grain enlargement.

3.2. Relationship between Laser Energy Input, Microstructures, and Magnetic Properties of Soft Ferromagnetic Materials

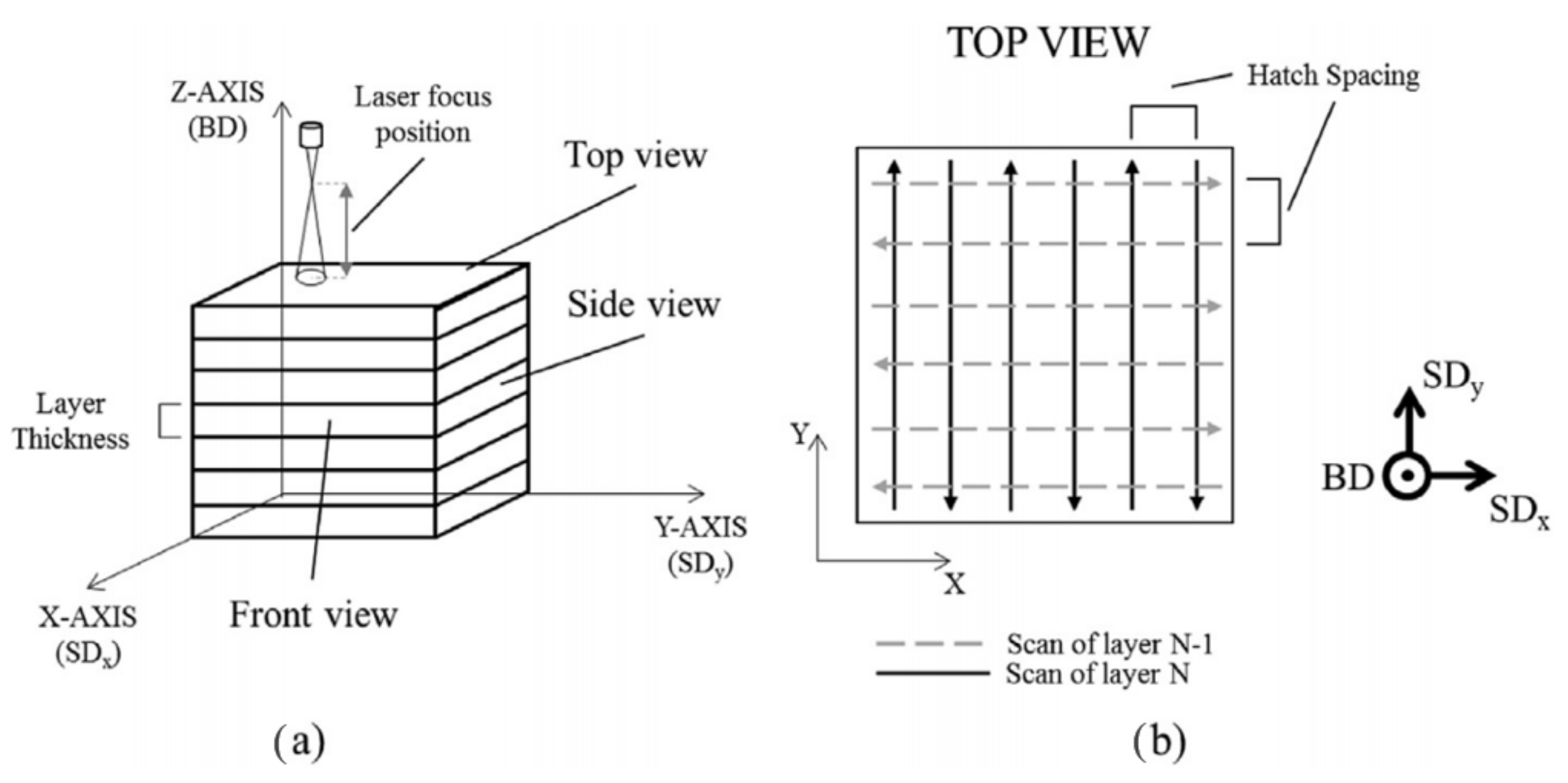
Laser energy input is an important parameter that must be defined in a proper way to obtain the desired performance from the material. With the purpose of defining a better way to produce a part, it is a good starting point to analyse the correlation between the construction parameters and the magnetic end mechanical properties of the generated material. The authors in [37] defined the main SLM parameters as recommended by the ReaLizer SLM-50 manufacturer, which is an industrial desktop 3D printer made by ReaLizer, for processing stainless steel powders (Figure 6); in this way, the thermal and optical properties of the material obtained are expected to be the closest to those of silicon steel. Varying the scan speed (v), the effect of energy input $E=\frac{P}{v}$ on the material properties can be studied. The energy input is a very important parameter that can affect much of the crystallographic structure of a component generated using AM, modifying its mechanical and magnetic properties. 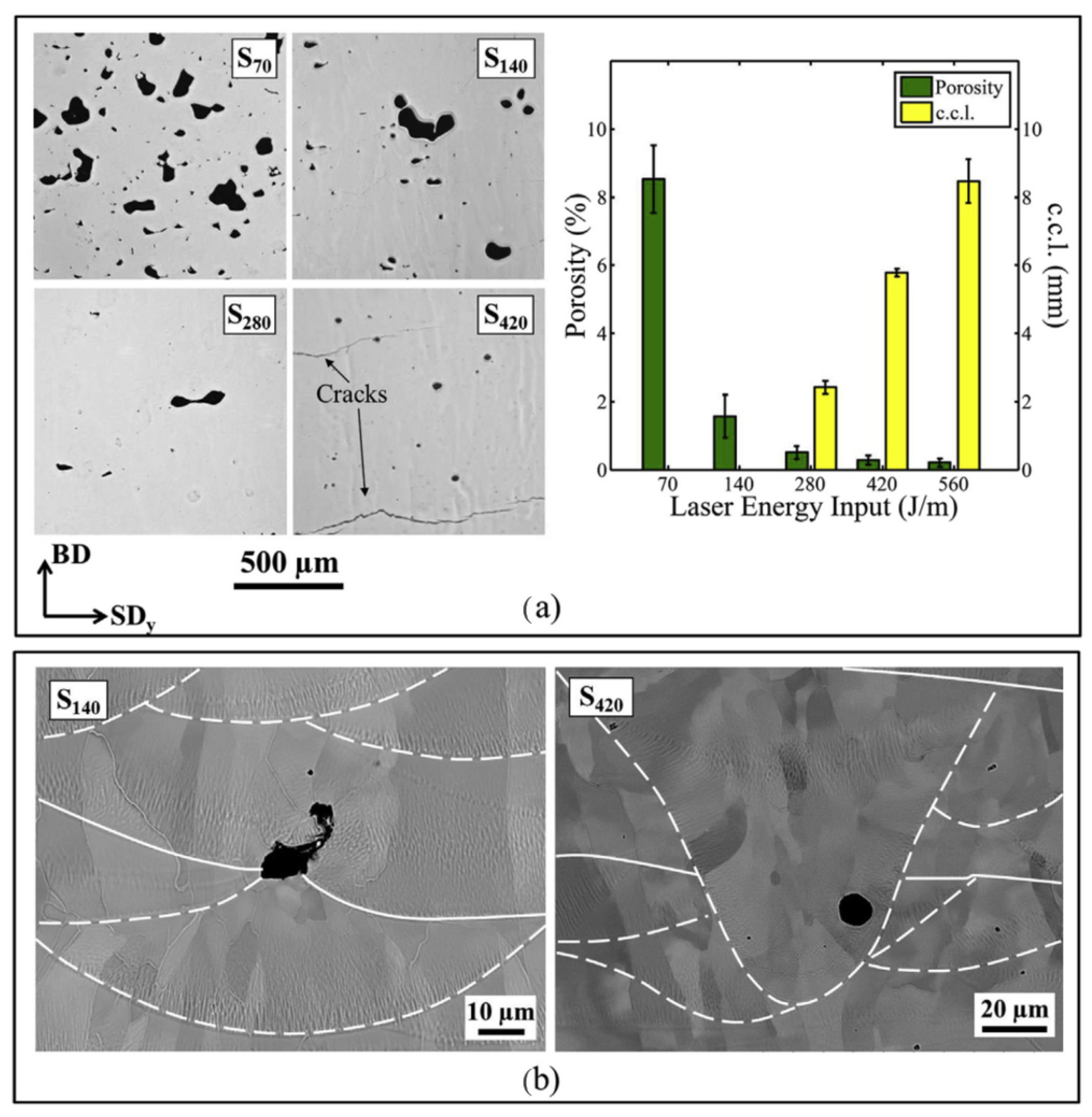In Figure 7a, the porosity and pore morphology obtained in the samples are reported, showing the effects of the laser energy input. According to the results reported, the samples obtained with laser energy input $E<280\frac{\mathrm{J}}{\mathrm{m}}$ were characterised by large pores with an irregular shape. Increasing the energy input, the pores presented a more regular shape, but crack generation was induced; in fact, considering $E\ge 420\frac{\mathrm{J}}{\mathrm{m}}$, small spherical pores came out and crack formation was promoted. As shown in Figure 7, the samples that ensured the best compromise between part densification and crack formation were $S_{140}$ and $S_{280}$. 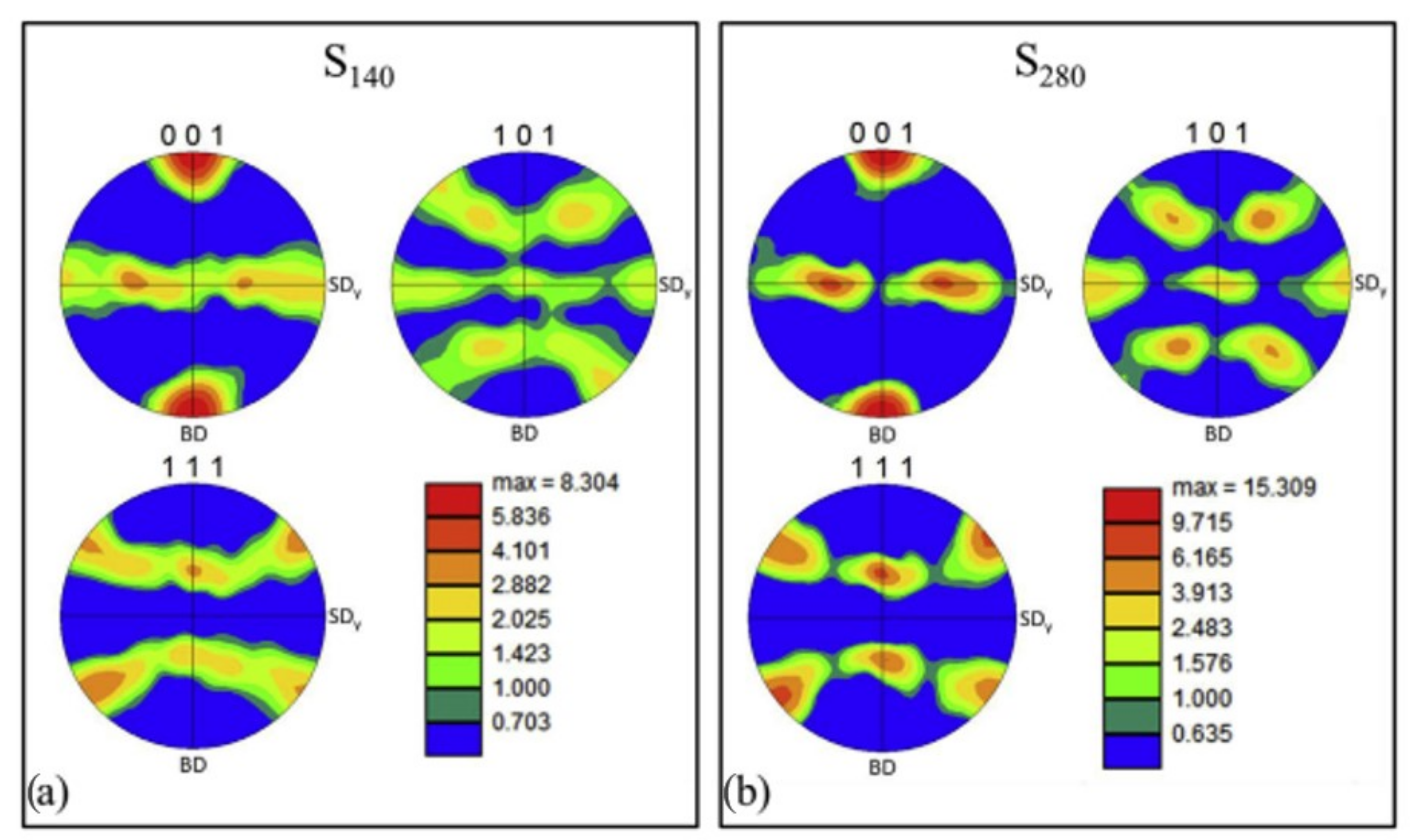Considering samples $S_{140}$ and $S_{280}$, in Figure 8, the results of the PFs are reported, which quantified the texture intensities for the three crystallographic direction families $<001>$, $<101>$, and $<111>$. Both samples had a $<001>$ texture along the Building Direction (BD). Increasing the energy input to $280\frac{\mathrm{J}}{\mathrm{m}}$, the fibre texture in sample $S_{140}$ became a cube texture. Therefore, the laser energy input largely affected the intensity of the texture, intensifying the crystallographic texture along the BD; this was due to the amount of partial remelting, which increased, and the improved smoothness of the deposited layers, which occurred when the energy input of the scanning laser was increased. Having a great quantity of optimally oriented grains will lead to stronger texture intensities.

Furthermore, augmenting the energy input from $140\frac{\mathrm{J}}{\mathrm{m}}$ to $280\frac{\mathrm{J}}{\mathrm{m}}$ modified the $<001>$ fibre texture into a cubic texture, as shown in Figure 8. As a consequence, deeper melt-pools were generated, leading to a shift of about 90° in the growth direction of the cellular dendritic solidification structure. In the scanning plane, some grains were produced with an elongated cross-section and oriented following the solidification front normal. The morphological orientation also prompted a crystallographic texture, and the EBSD results showed that, in the scanning plane, the $<001>$ crystallographic axes followed the morphological orientation of the grains (Figure 9).

The most-common soft magnetic material used for the manufacture of electrical machines is FeSi electrical steel [7]. In these alloys, there can be a different percentage of silicon, depending on the purpose of the specific application. Silicon is a substitutional element that increases the resistivity of the alloy and reduces the coercive field, so it leads to lower energy losses per (de)magnetisation cycle. Thanks to silicon’s properties, the FeSi alloy is a very good soft magnetic material for electrical machines, where it is responsible for carrying and amplifying the magnetic flux density B. One of the most-important properties for a soft magnetic material is the magnetic relative permeability $\mu$, which strongly depends on the crystal direction of the electrical steel; usually, in FeSi-based alloys, a preferential $<100>$ crystal orientation is obtained with a dedicated thermomechanical processing, which generates a textured material (known as grain-oriented electrical steel). The magnetic relative permeability is optimum along any of the crystal direction $<100>$. Compared to grain-non-oriented steels, grain-oriented ones present a magnetic relative permeability that is twice as high and much lower magnetic losses (about one order of magnitude). Anyway, until now, grain-oriented electrical steels have been mainly used in transformer applications, because the locked $<100>$ crystal direction cannot be optimal for the requested B path in applications that include a rotating field. To make these materials attractive for variable-direction magnetic flux applications, the author in [7] proposed a methodology to change the flux direction according to specific boundary conditions.

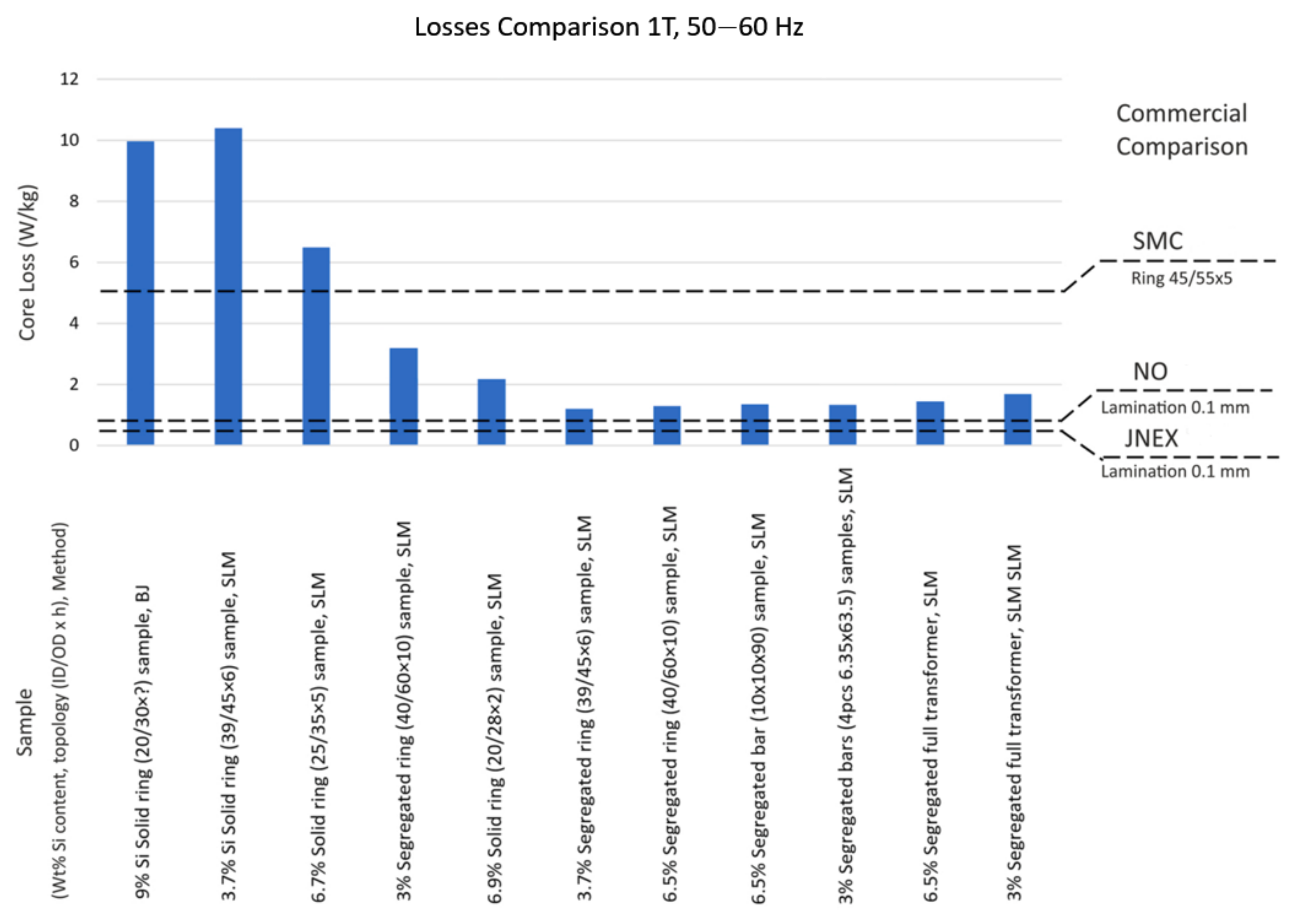
A material that can combine the best crystallographic texture and the optimised anisotropy synergy has high potential in terms of the machine’s performance. In Figure 10, a comparison of the total core losses of the printed samples and commercial materials is shown. The figure presents core losses measured at 50–60 Hz, at a magnetic polarisation of 1 T (10 kGauss), because of the overall lower polarisation that can be obtained from the printed samples. Since the total core losses depend on the geometry of the sample, the physical dimensions are considered through a normalised geometric parameter. Most measurements have been conducted on ring samples, which have an outer dimension that goes from 28 to 60 mm. For solid printed samples, core losses are significant, up to approximately 10 W/kg ($W_{10,50}$), but by refining the sample topologies, lower losses were obtained. The refined samples were built with the introduction of internal air gaps, both parallel and perpendicular to the build direction. In comparison, for typical commercial materials, the total core losses are significantly lower, for NO JNEX super core laminations 0.5 W/kg, for NO 3% FeSi laminations 0.8 W/kg, and for SMC 5 W/kg. The superiority of 3D-printed soft magnetic cores to SMC cores is evident per weight. In fact, considering the per-volume value, the conclusion made before would not be true, since in 3D-printed parts, air gaps were introduced with the purpose of reducing the eddy current component, but they increment the volume of the sample.

The authors in [39] made magnetic measurements of ring samples, and the results obtained are resumed below, as a function of the laser energy input. It can be noticed that:

• The maximum permeability was not affected by the first two values of the energy input, but it started decreasing when $E=420\frac{\mathrm{J}}{\mathrm{m}}$.
• The ${\mu }_{40}$, which is the relative magnetic permeability at an applied field strength H = 40 A/m, had a non-monotonous behaviour with the maximum value at $E=280\frac{\mathrm{J}}{\mathrm{m}}$.
• The $B_{50}$, which is the flux density at an applied field strength H = 5000 A/m, had a non-monotonous behaviour with the maximum value at $E=280\frac{\mathrm{J}}{textm}$.
• The remanence $B_r$ decreased slightly with the increment of the energy input.
• $H_c$ had a non-monotonous behaviour with the minimum value at $E=280\frac{\mathrm{J}}{\mathrm{m}}$.
• The total power losses had a non-monotonous trend with the minimum value at $E=280\frac{\mathrm{J}}{\mathrm{m}}$.

It is evident that, in soft magnetic materials, a compromise between a finer grain structure and large grains should be found. The first one leads to poorer quasistatic magnetisation properties and higher hysteresis losses; otherwise, larger grains cause the eddy losses to increase. In fact, eddy losses depend on the grain size, since their increment worsens superficial roughness, leading to undesired electrical shorting between walls. In addition, as stated in [40], the optimal grain size depends on the working conditions of the material, such as the frequency or working induction.

Manufacturing defects represent pinning sites, which led to an increment of the coercivity and hysteresis losses and a decreasing of permeability. If large enough, pores and cracks represent air gaps from which demagnetisation fields emanate, resulting in sheared B-H curves. As shown in [37], when the energy input is high, the sample porosity decreases, so cracks are generated in the part. The crystallographic texture can help to clarify the magnetic behaviour of the material treated at high-laser-energy inputs. As a consequence, the horizontal plane loses its isotropic character. The small grain size obtained with SLM is the factor limiting the magnetic performance of the printed material; for this reason, a grain enlargement obtained with a heat treatment, such as the annealing described before, becomes fundamental for practical applications.

4. Hysteresis and Eddy Current Losses

Considering high motor speed, the magnetic losses of electrical machines increase, so magnetic components generate more heat, which must be dissipated in the environment, causing an increment of the machine’s internal temperatures. Focusing on soft magnetic materials’ application in electrical machines [41,42], the losses generated inside them can be divided into:

• Hysteresis losses, which are directly related to the grain size, texture, and structural disorder in the material.
• Eddy current losses, which are generated from induction currents in the core and depend on the electric resistivity of the material.

Eddy currents’ development is promoted in the material when its size is larger than the skin depth, which can be found according to Equation (1).

$$\delta =\frac{1}{{\left(\pi f\sigma \mu \right)}^{0.5}}$$

(1)

where $\sigma$ is the electrical conductivity (S/m); f is the frequency (Hz); $\mu$ is the magnetic permeability (Vs/Am).

Gargalis et al. in [43] realised an electrical machine with an additively manufactured rotor and compared its performance with a conventionally laminated rotor, considering different operating conditions. In the low-speed region, the behaviour of the two machines was comparable, while at a high speed, core losses had a significant increment. The optimised geometry of the rotor led to the high efficiency and elevated performance of the machine, but when the speed increased, it was necessary to implement some strategies to reduce the losses generated.

In traditionally manufactured FeSi devices, laminated sheet metal is used; thanks to this configuration, eddy current development is limited and so are its associated power losses. The purpose of the authors in [44] was to understand the impact of additively manufactured geometries on power losses. As seen in previous sections, the grain structure greatly affects the magnetic performance of soft ferromagnetic materials, so geometries must be designed considering also grain structure development. Eddy current development should be modelled as a function of cross-sectional geometry and the heat conduction during the AM process.

From the schematics of the scan patterns used for additively manufactured thin-wall structures by Plotkowski et al., it can be noticed that the scan pattern is rotated by 67° between each layer. In order to increase the energy deposited per layer, a double scan was performed: this technique includes a second scan pattern, which performed a first scan on each layer equal to the first sample and a second scan oriented parallel to the sample edge (this procedure should be adopted for all layers). The solidification cooling rates can be decreased by increasing the energy stored per layer. Then, an annealing procedure at 1150 °C was performed, with the purpose of eliminating any residual porosity and to enable recrystallisation and grain growth to increase the magnetic performance. In [44], the authors could characterise the behaviour of the tested components by describing the total losses using the approximated equation reported in Equation (2), which comes from the Steinmetz law [45].

$$P_{cycle}=c_{hyst}\left(B\right)f+c_{eddy}\left(B\right)f^2$$

(2)

where $P_{cycle}$ is the total power loss per cycle, f is the frequency, $c_{hyst}$ is a coefficient associated with hysteresis (material) losses, and $c_{eddy}$ is a coefficient associated with eddy current losses.

The linear least-square fit performed on the data based on [44] is obtained using Equation (3).

$$E_{cycle}=c_{hyst}\left(B\right)+c_{eddy}\left(B\right)f$$

(3)

where $E_{cycle}$ is the total energy loss for a given cycle, which is equal to the integrated area of the hysteresis loop.

The linear trend described by Equation (3) represents the loss behaviour depending on the frequency, showing that this approach can be used to decompose the origins of the energy losses for this material. Using the coefficients $c_{hyst}$ and $c_{eddy}$ as quantitative indicators of the material and eddy current losses, the fraction of power losses due to the eddy current can be computed as follows.

$$F_{eddy}=\frac{c_{eddy}f}{c_{hyst}+c_{eddy}f}$$

(4)

Plotkowski et al. in [44] compared the ESBD of the bulk cross-sections, highlighting that the single-scan pattern showed a chaotic structure with many small grains, while in the double-scan pattern, an orientation of the $<100>$-type crystallographic direction was conserved with larger grains. The magnetic test results showed that the double-scan pattern had lower hysteresis loss coefficients, because of the increased strength of the fibre texture, which granted a more-convenient magnetising direction. Using Equation (4), the fraction of power losses due to the eddy current is computed; even if the double-scan pattern improves the material properties, it leads to very small improvements in the overall efficiency on the device value. In fact, conventionally, soft magnetic components are produced using laminated sheet metal to confine eddy current loops to the sheet thickness.

To obtain performance similar to the one obtained with laminated configurations, AM should be used to produce thin-wall structures. In this way, the arising of eddy currents in the material is restrained.

Plotkowski et al. in [44] realised samples of different shapes and thicknesses and performed an experimental comparison between the loss behaviour for the bulk, thin-wall, and mesh cross-section; the mesh and the bulk components showed a similar behaviour, but the mesh one was characterised by a lower saturation inductance.

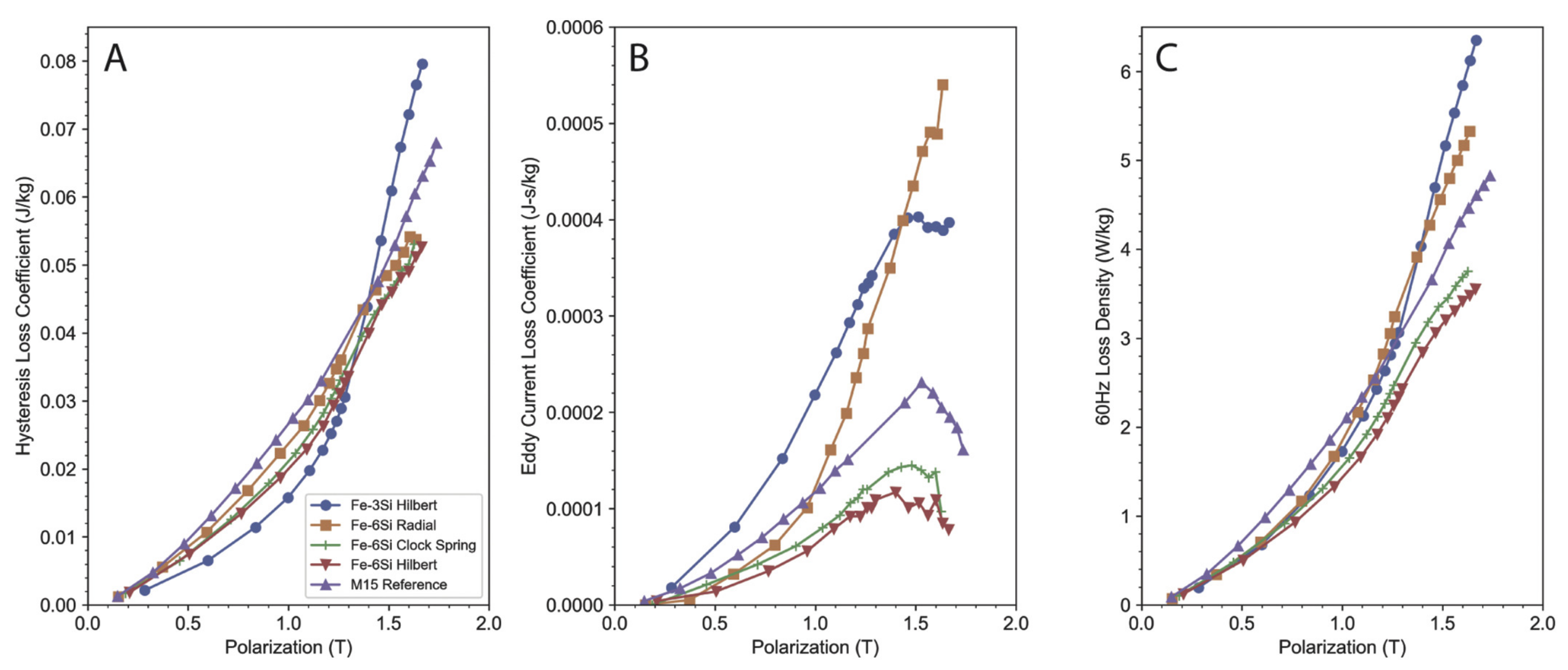
The structure that showed a lower level of performance was the mesh one; otherwise, the Hilbert structure sample showed a significant improvement, leading to lower values of the eddy current loss coefficient. A heat treatment was performed on the samples considered in [44], with the purpose of studying the trend of the loss behaviour after that. The treatment chosen in this case was hot isostatic pressing; after the treatment, a reduction of the hysteresis loss coefficients could be noticed and, at the same time, an increment of the eddy current loss coefficient, which was more evident in the thin-wall sample with 13 parallel plates. The Hilbert structures seemed to be the best ones, since they had the lowest eddy current and hysteresis loss coefficient. Regardless of the increase in eddy current losses, the heat treatment brought a net decrease in the power losses. Moreover, thanks to the heat treatment, also an increment in the effective permeability could be observed.

Heat-treated samples exhibited an increase in maximum effective permeability and a decrease in the total loss density at an applied field of 3000 A/m. As shown in the previous section, heat treatments bring grain growth, so confirming the evidence by showing an increment in permeability (leading to an increment in eddy current losses) and a reduction in the hysteresis losses, since materials with larger grains can be magnetised and demagnetised easily.

These factors bring a reduction of the skin depth, according to Equation (1). The results obtained suggest also that the influence of the geometry is greater than the effect of manufacturing an ideal composition, since the loss density showed an increment with the increase of the sample mass. In particular, the Hilbert structure sample showed a very good response to heat treatment, the sample having the lowest loss density and one of the best samples in terms of permeability.

In [46] also, the Hilbert structure was the one that showed the lowest losses compared with the other samples, and it was used to produce the prototype of a transformer core in AM. The test results showed performance comparable to the conventional non-oriented sheet, as shown in Figure 11.

Anyway, in particular for the FeSi6 alloy, fractures were induced in the AM core due to the high silicon content. It is also important to notice that 54% of this AM core was made of air, so the majority of the losses generated were due to this pure air insulation, represented in Figure 12.

In [47], the properties of additively manufactured electric steel powder cores with increased Si content, obtained by the definition of the best laser powder bed fusion printing conditions, were presented and compared with commercial FeSi alloys. The analysis showed promising results regarding the magnetic behaviour of FeSi6.5 samples.

In the following, the magnetic characterisation of other two FeSi alloys with different silicon content is presented.

4.1. Magnetic Characterisation of FeSi4

In [48], samples from FeSi4 powder were fabricated using SLM to perform the magnetic characterisation of the material and compare its properties with commercial samples.

The powder used to make the toroidal specimens by SLM was a gas-atomised pre-alloyed powder of FeSi with an average silicon content of 3.8–4.1% and 1.1–1.3% of chromium content, with a slightly low magnetic saturation magnetisation of the material. In order to achieve less than 2% porosity and avoid macroscopic defects, such as visible cracks, delaminations, or uneven growth, as photographed in Figure 13, the technique of “laser re-melting” was applied, which consisted of making two consecutive scans of the same layer before proceeding with the fresh powder and making the next layer. This study showed excellent DC magnetic properties, comparable to commercial soft ferromagnetic materials at low magnetisation. After the annealing, the hysteresis losses decreased, but the eddy currents increased greatly when the material went into the saturation region. These losses can be reduced by introducing some air gaps by realising a split material internal structure.

Two issues were found in the powder coating of the toroidal samples:

• Uneven growth (Figure 13a) due to powder balling, caused by uneven powder deposition, which was solved by brushing away the excess powder.
• Delaminations (Figure 13b), which were generated because of an excessive powder deposition on the printed part.

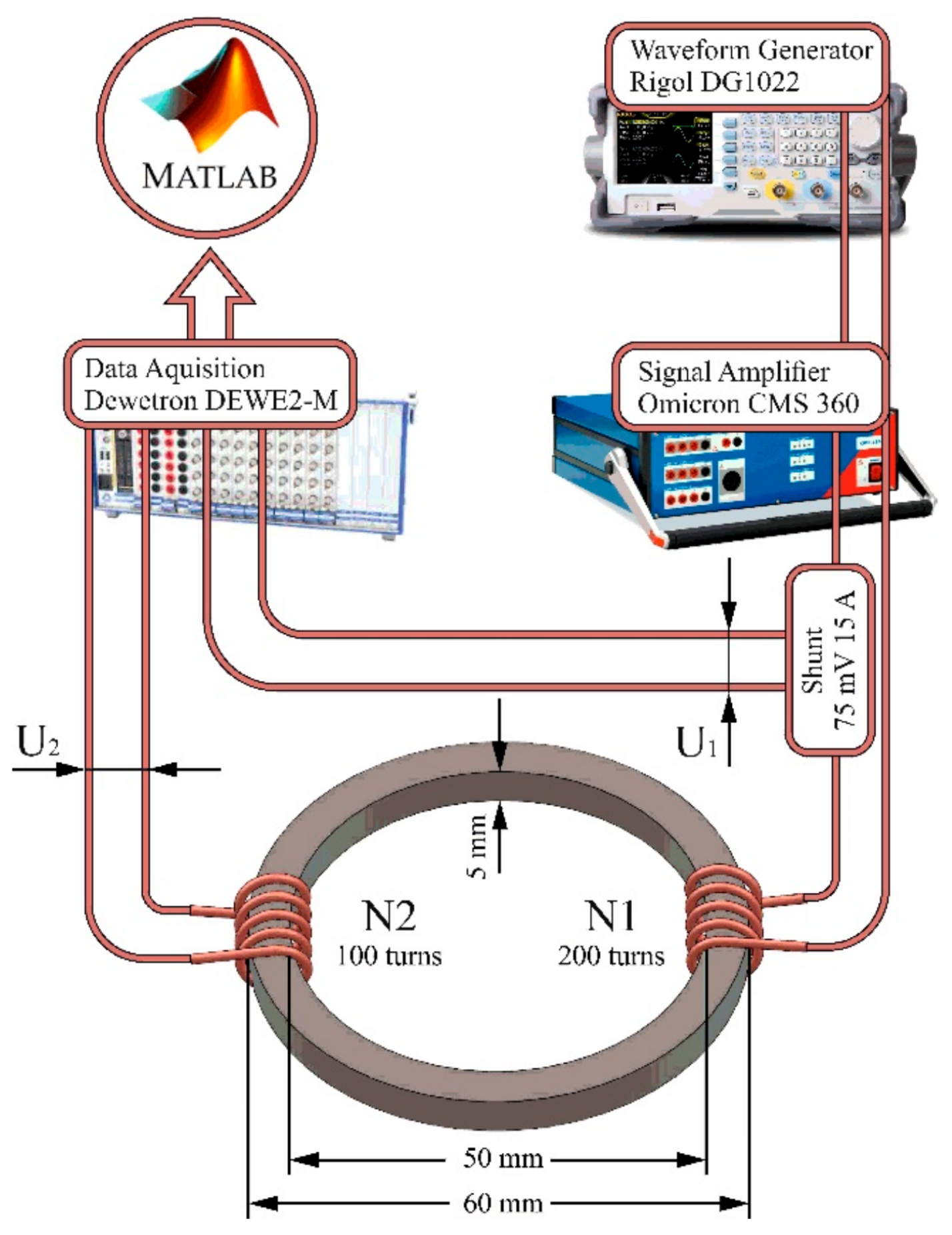
In [42], the ring method was used for the measurements of the printed material’s magnetic properties, considering different frequencies: 25 mHz (quasi-static), 1 Hz, 10 Hz, and 50 Hz in the magnetising range of 0.9–1.6 T. The setup was organised in a way similar to [48], and its schematic is reported in Figure 14.

$N_1$ is the number of turns of the primary coil; $N_2$ is the number of turns of the secondary coil; I is the instantaneous current value; e is the instantaneous induced electromotive force; $l_t$ is the toroid average length; S is the toroid cross-section area. The magnetic field and the average flux density can be found as follows:

$$H=\frac{N_{1}i}{l_t}$$

(5)

$$B=\frac{1}{N_{2}S}{\int }_{t}e\left(t\right)dt$$

(6)

After constructing the hysteresis curves for the measured data, the specific iron losses $P_s$ were calculated by subtracting the curve areas and can be expressed as:

$$P_s=\frac{1}{T\varrho }\left({\int }_0^T{H}_{1}d{B}_1-{\int }_0^T{H}_{2}d{B}_2\right)$$

(7)

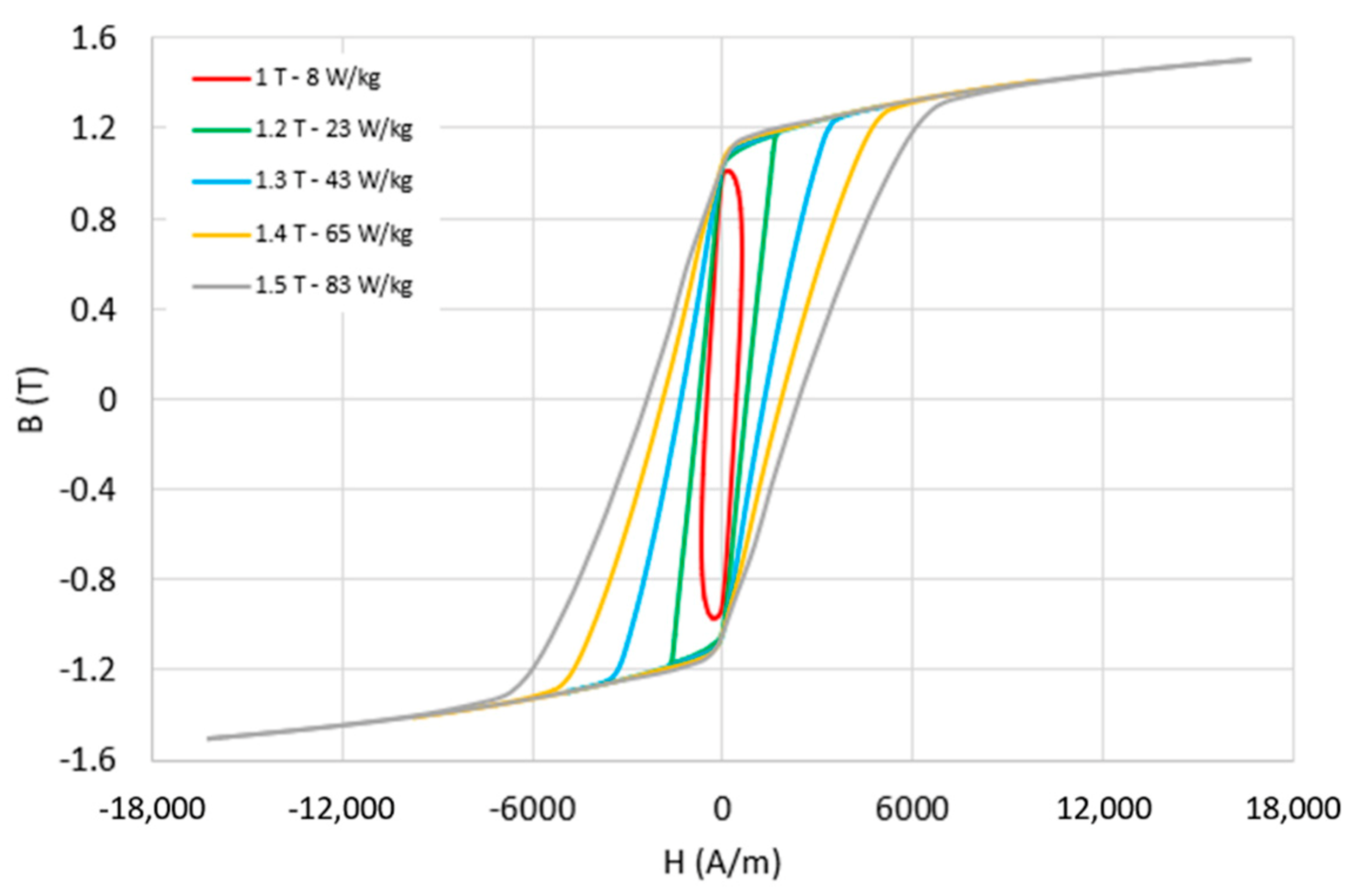
where $\varrho$ is the average density and T is the period. Quasi-static measurements of the sample are presented in Figure 15. The sample showed DC magnetic properties that were comparable to commercial and 3D-printed soft ferromagnetic materials from the literature. Anyway, it had a low value of saturation (1.3 T at $5000\frac{\mathrm{A}}{\mathrm{m}}$), while the commercial materials usually had 16 T–1.7 T at $5000\frac{\mathrm{A}}{\mathrm{m}}$. The reduction in saturation magnetisation came from the pinning effect of intragranular porosities on the large recrystallised grains.

A comparison between some parameters obtained in the study and SLM-fabricated FeSi6.7 and FeSi6.9 found in the literature is given in

Table 1. Parameters’ comparison.

Parameters	Component
	FeSi4	FeSi6.7–FeSi6.9
Relative permeability	21,500	25,000–31,000
Coercivity (A/m)	49	16
Total iron losses (W/kg)	7–9	0.5–0.7

.

AC measurements confirmed an increase in iron losses, which were dominated by eddy current losses. Besides, the losses augmented their value when the material saturated; in fact, the loss coefficient went from $8.17\frac{\mathrm{W}}{\mathrm{kg}}$ (at 1 T) to $83.7\frac{\mathrm{W}}{\mathrm{kg}}$ (at 1.5 T) with the increment of the saturation of the material for the ring sample after annealing, as shown in Figure 16.

4.2. Magnetic Characterisation of FeSi6.7

High-silicon FeSi alloys impose strict constraints concerning the AM production parameters. As shown in the previous sections and in [37] for a high laser energy input, cracks can occur, which negatively affect the magnetic and mechanical properties of the component. In order to obtain an optimised microstructure and good magnetic properties, the AM parameters must be properly defined, united with the post-annealing parameters. In [41], prototypes using FeSi6.7 were realised to perform the magnetic characterisation of the material.

Heat treatment such as annealing showed a positive effect on the hysteresis losses generated by the material. In fact, the hysteresis losses decreased with the increasing of the laser power only for the annealed material; on the other side, for the as-built sample, the opposite effect was encountered. This can be explained by the fact that, with higher laser power, the cooling rate decreased, leading to a larger average grain size and, consequently, lower losses. Anyway, a good balance between laser power and optimised magnetic performance should be found, since with a too-high laser power, the material tended to generate residual stresses, and therefore, crack formation was enhanced.

The maximum permeability reached by the FeSi6.7 was 31,000 at $H=24\frac{\mathrm{A}}{\mathrm{m}}$ for the optimised sample. This value is much higher than the one reported in the literature for FeSi6.9 (24,000) [36]. The core losses were also studied, and they can be separated into hysteresis losses $P_h$ and eddy current losses $P_e$; both of them increase with the increment of the frequency. It is evident that, to obtain good performance in high-frequency applications, the eddy current losses must be reduced significantly.

Then, the DC hysteresis loop of the additively manufactured FeSi6.7 (optimised) was compared with common commercial electrical steel and SMC material. The additively manufactured sample showed the lowest value of coercivity ($H_c=16\frac{\mathrm{A}}{\mathrm{m}}$), the highest maximum permeability (31,000), and the largest remanence ($J_r=1.26T$). Therefore, the DC properties of additively manufactured FeSi6.7 can compete with conventional electrical steel.

4.3. Adding Boron to FeSi Alloys

It is known that high iron loss due to eddy currents affects the additive manufactured bulk iron cores. Pham et al. [49] already showed that adding boron for the binder jet printing of FeSi reduces the hysteresis losses, so S.N. Foster et al. [50] found a non-linear relation between the boron particle size and the magnetic properties.

For their studies, S.N. Foster et al., used three binder-jetting-printed samples with the same identical boron content, but with different boron particle sizes:

• Boron particle size of Sample 1: 0.1 μm;
• Boron particle size of Sample 2: 0.5 μm;
• Boron particle size of Sample 3: 1.0 μm.

The experimental results of the quasi-static at 1Hz testing for DC characterisation showed that the maximum relative permeability ${\mu }_{r,max}$ and the magnetic flux density $B_5$, $B_{25}$, and $B_{100}$ (at 500, 2500, and 10,000 A/m, respectively) were almost the same even if the particle size changed; otherwise, the intrinsic coercivity $H_c$ and the correspondent hysteresis losses per cycle, $P_h/f$, changed non-linearly with the boron particle size changing.

The core loss density was maximum for the sample with the biggest boron particle size for all frequencies and for all magnetic flux density. Furthermore, decreasing the boron particle size is possible to reduce the core losses, even if there is not a linear correspondence between the specific core losses reducing and the boron particle size.

S.N. Foster et al. simulated also a 48-slot/eight-pole interior permanent magnet machine with the BJP core made of, alternatively, the three materials studied, and the 2D FEA simulation confirmed what the experimental tests showed. Indeed, the combined hysteresis loss as a function of the speed decreased with the growing of the boron particle size, while the combined eddy current loss as a function of the speed increased with the growing of the boron particle size.

In the end, comparing the simulated iron loss at the maximum torque in the speed range, the IPM machine with smallest boron particle size showed the lowest iron loss and the highest efficiency.

5. Conclusions

In this paper, we gave a general presentation of the state-of-the-art of the soft magnetic materials used in EM applications. Post-processing treatments such as annealing are very important since they give the material better mechanical and magnetic properties. In fact, the crystallographic structure and grain dimensions of the material, which are highly influenced by post-processing treatments and the AM input parameters, are fundamental to obtain the best material properties in terms of mechanical resistance and magnetic performance. In the last section of the paper, the problem of eddy currents’ development and hysteresis losses was explored, and the magnetic characterisation of some common alloys was proposed. The main problem in losses’ generation is due to the fact that the AM material is generated as a block, so eddy current development is favoured. The main solutions found in the literature propose finding an optimal laminated structure that can lead to a reduction of the power losses’ generation in the material by exploiting the main advantage of AM, which is the possibility to produce optimised geometries. To conclude, AM is a promising technique for EM fabrication since it allows obtaining optimised geometries for particular motors, and by focusing on the study of the losses’ development, also a good compromise can be found that can limit their generation inside the material.