Investigation on the Design of Double-Stage Scissor Lifts Based on Parametric Dimension Technique
Abstract
1. Introduction
- The parametric dimension technique is proposed to analyze both the geometry and loads of the double-stage scissors lift as functions that depends on the design parameters. This means that instead of using finite element analysis, the loads on joints and geometries of the system can be determined through functions, which can reduce the time required for model construction and simulation;
- Working Model software is applied to evaluate the accuracy of the proposed method;
- Based on the evaluation of the design parameters, designers simply determine a suitable configuration of the double-stage scissors lift, which meets the working requirements of the system, i.e., optimal lifting height, maximum load, the type of lift object, and stability of the system.
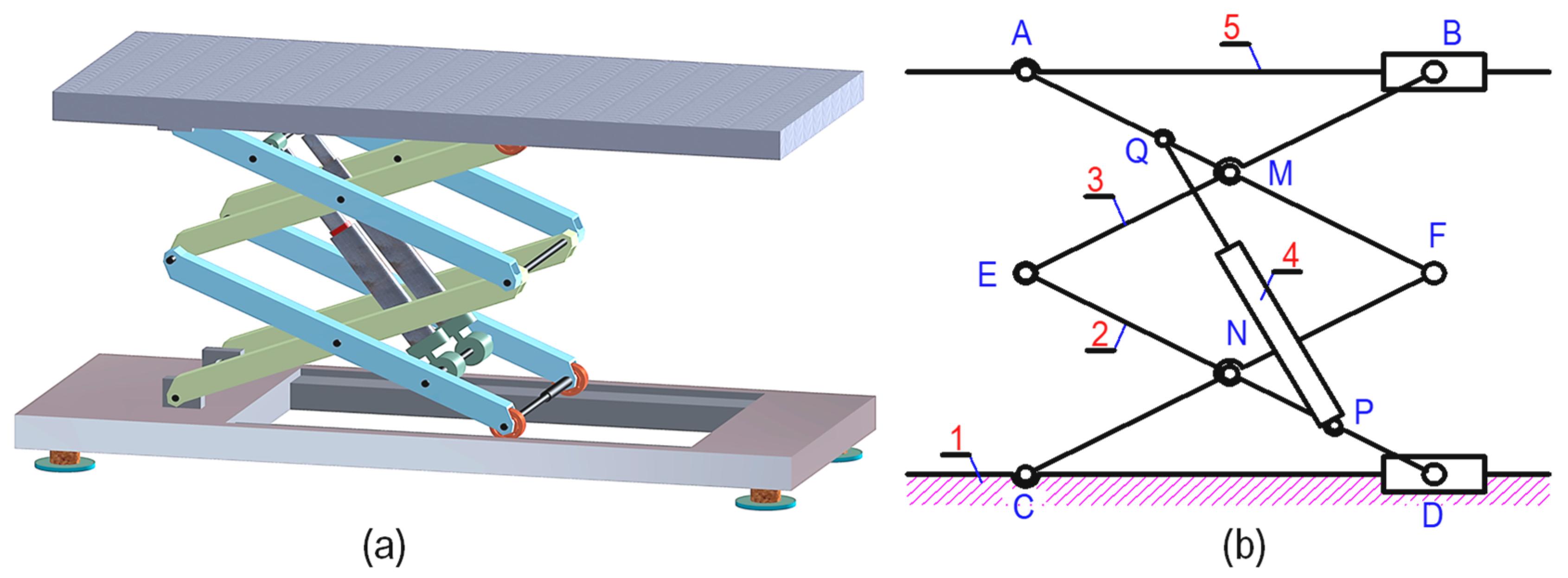
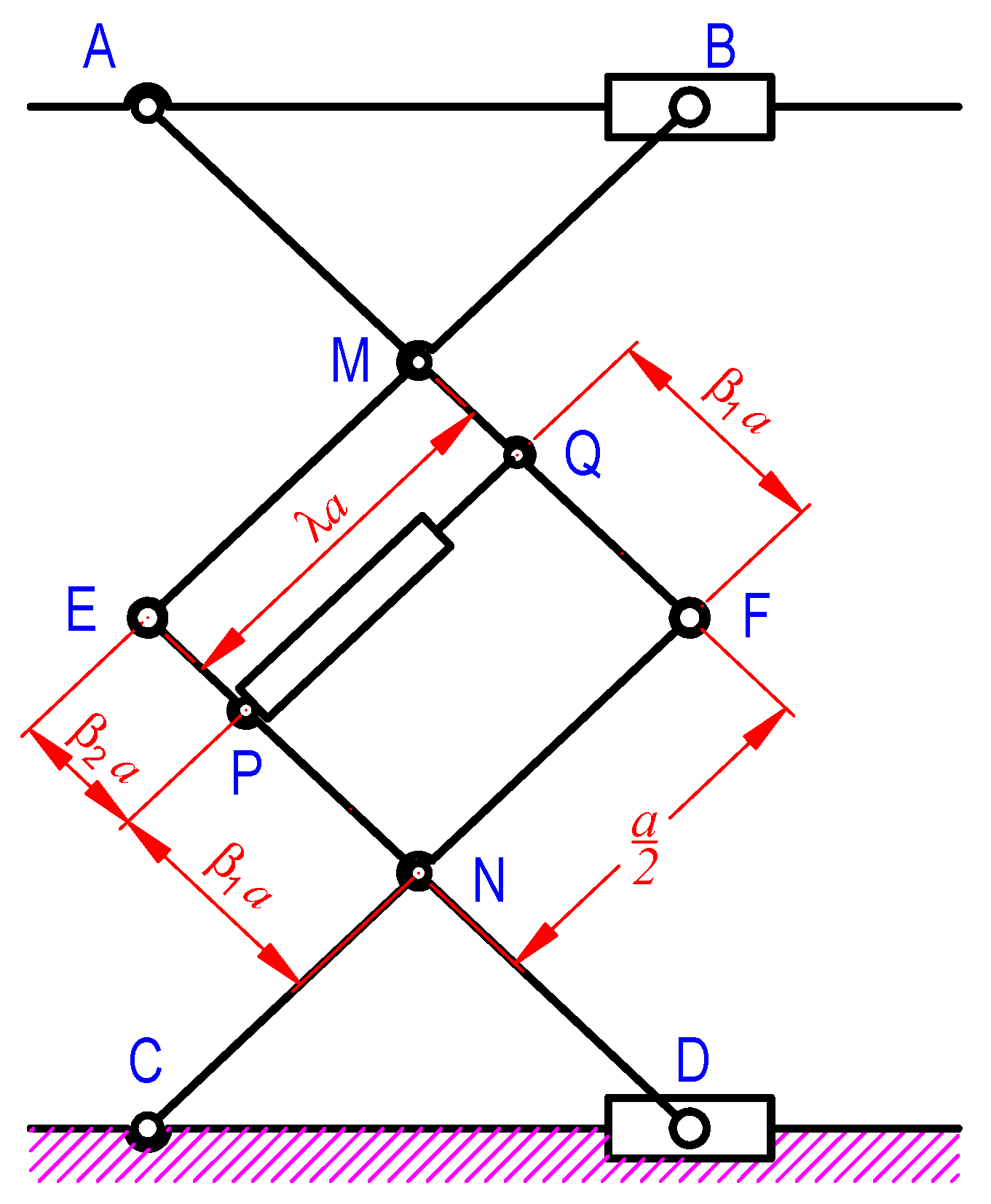
2. Mathematical Model for Double-Stage Scissor Lift Analysis
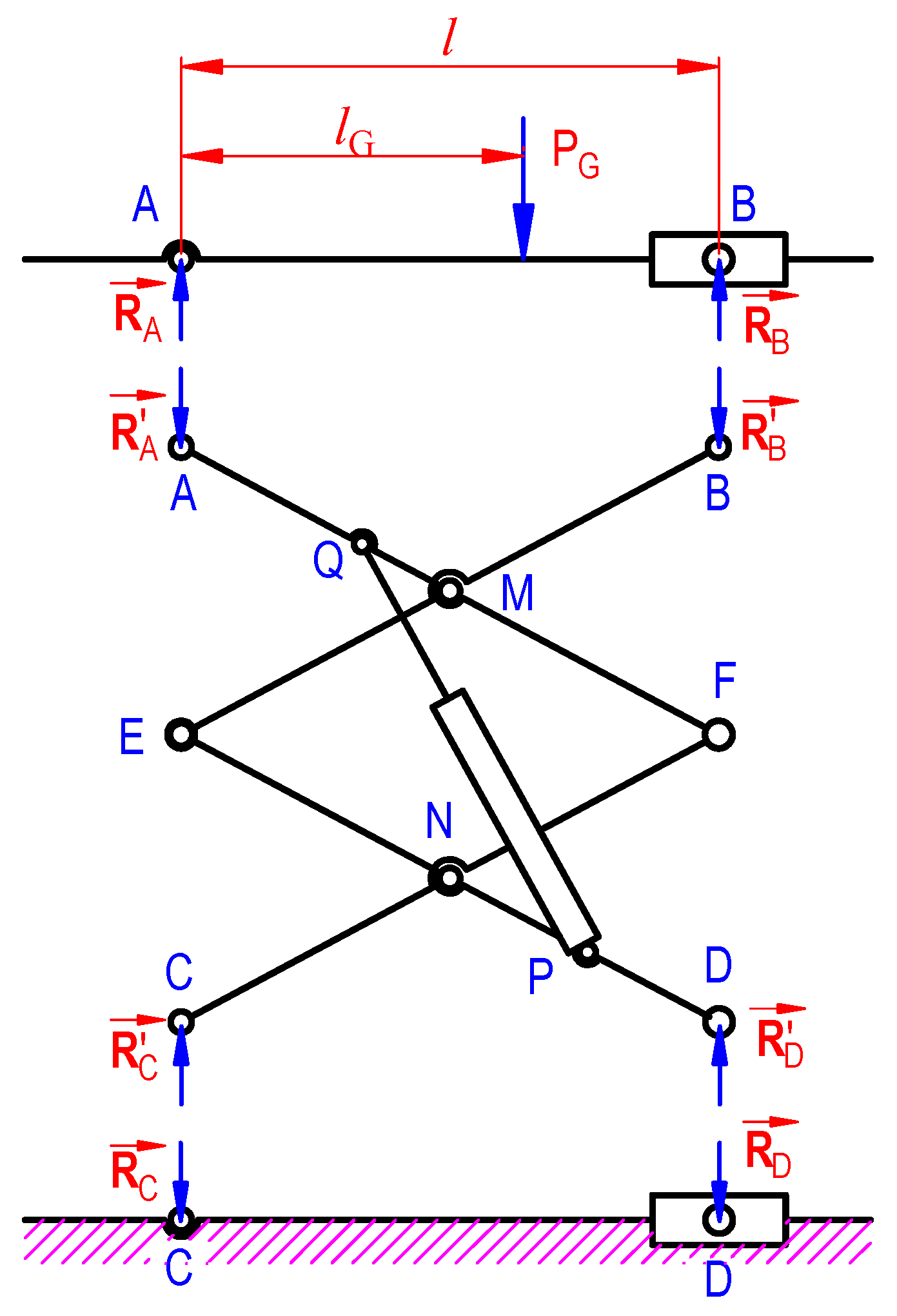
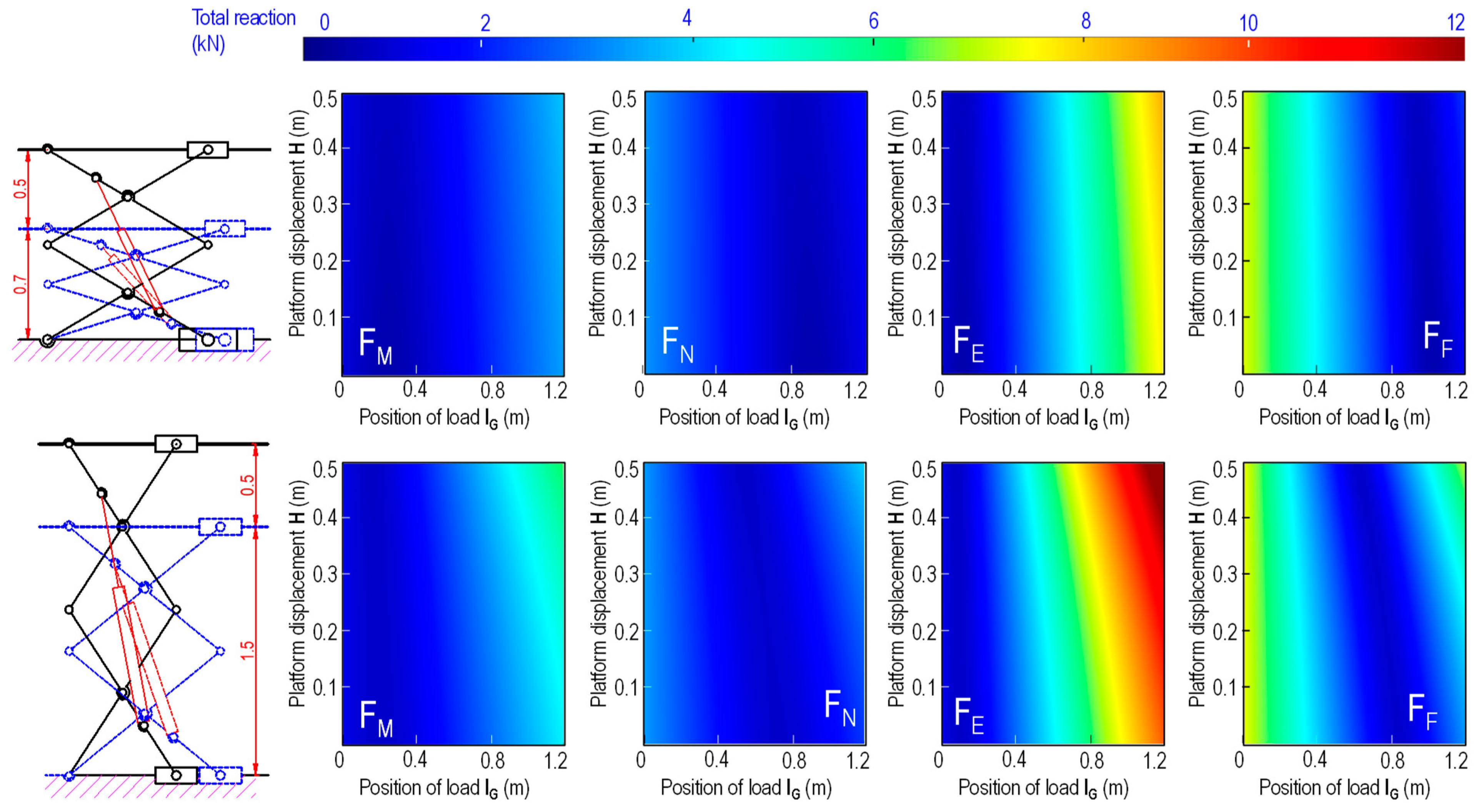
3. Computation of Loads
4. Numerical Simulation of the Model
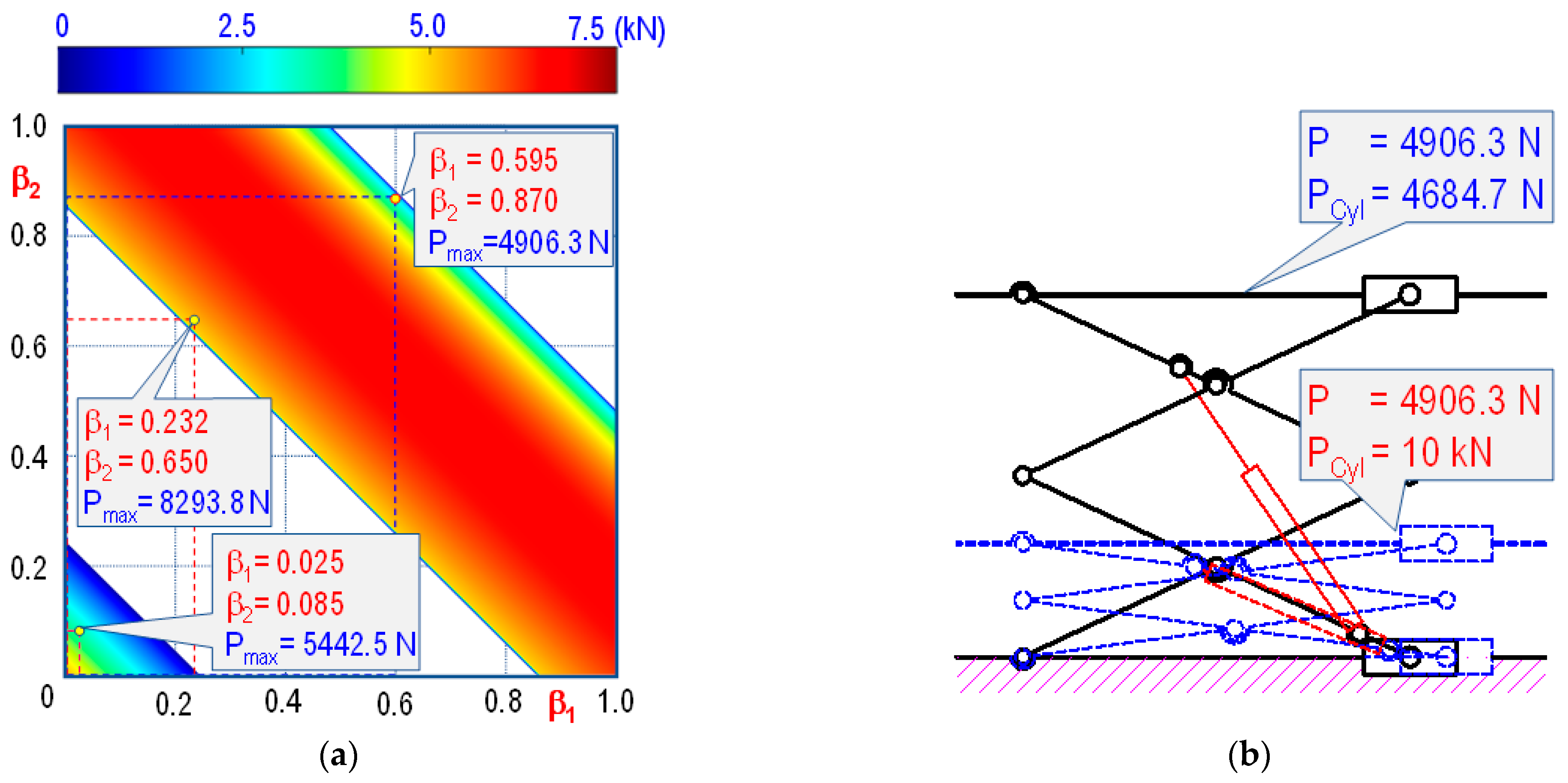
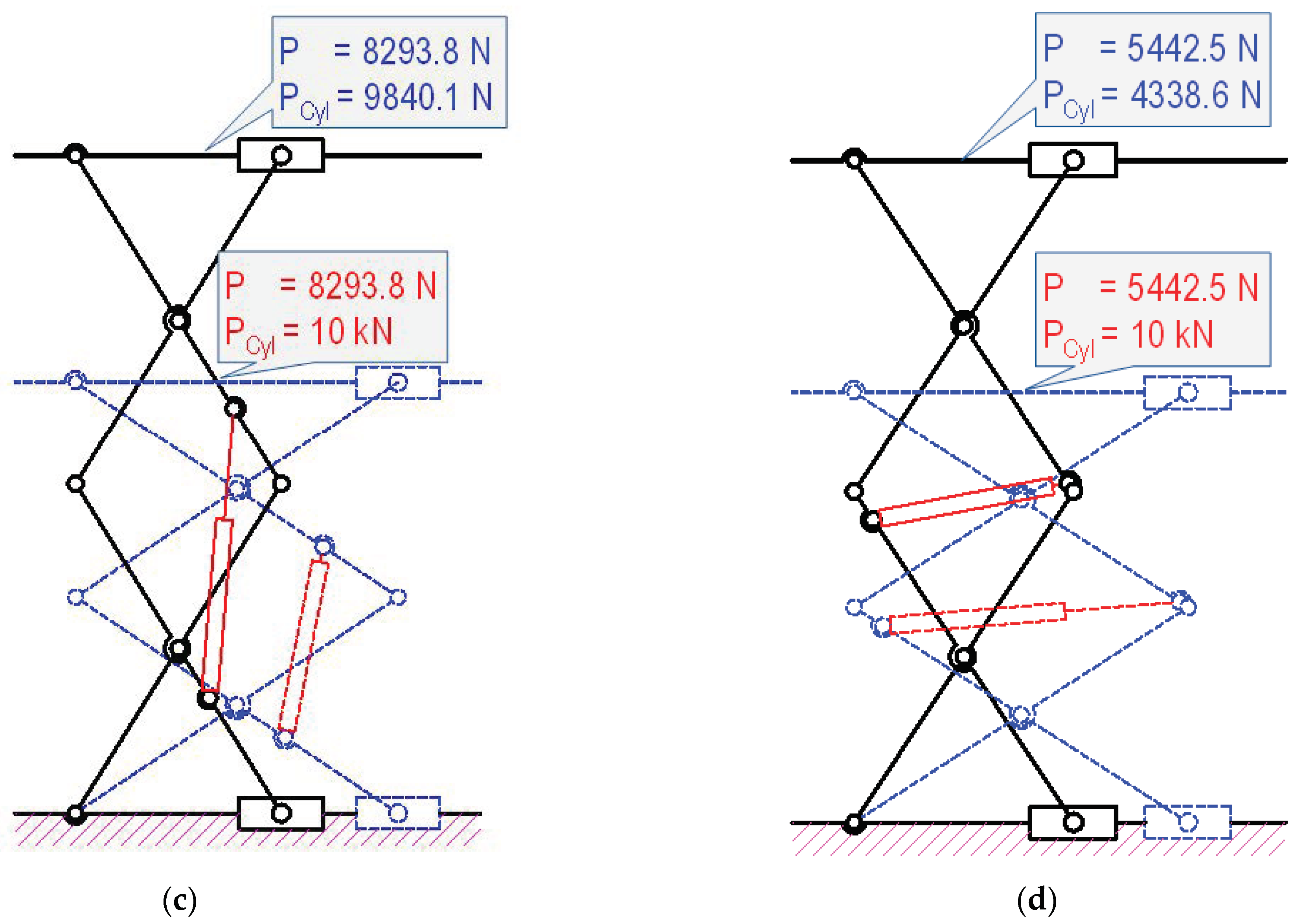
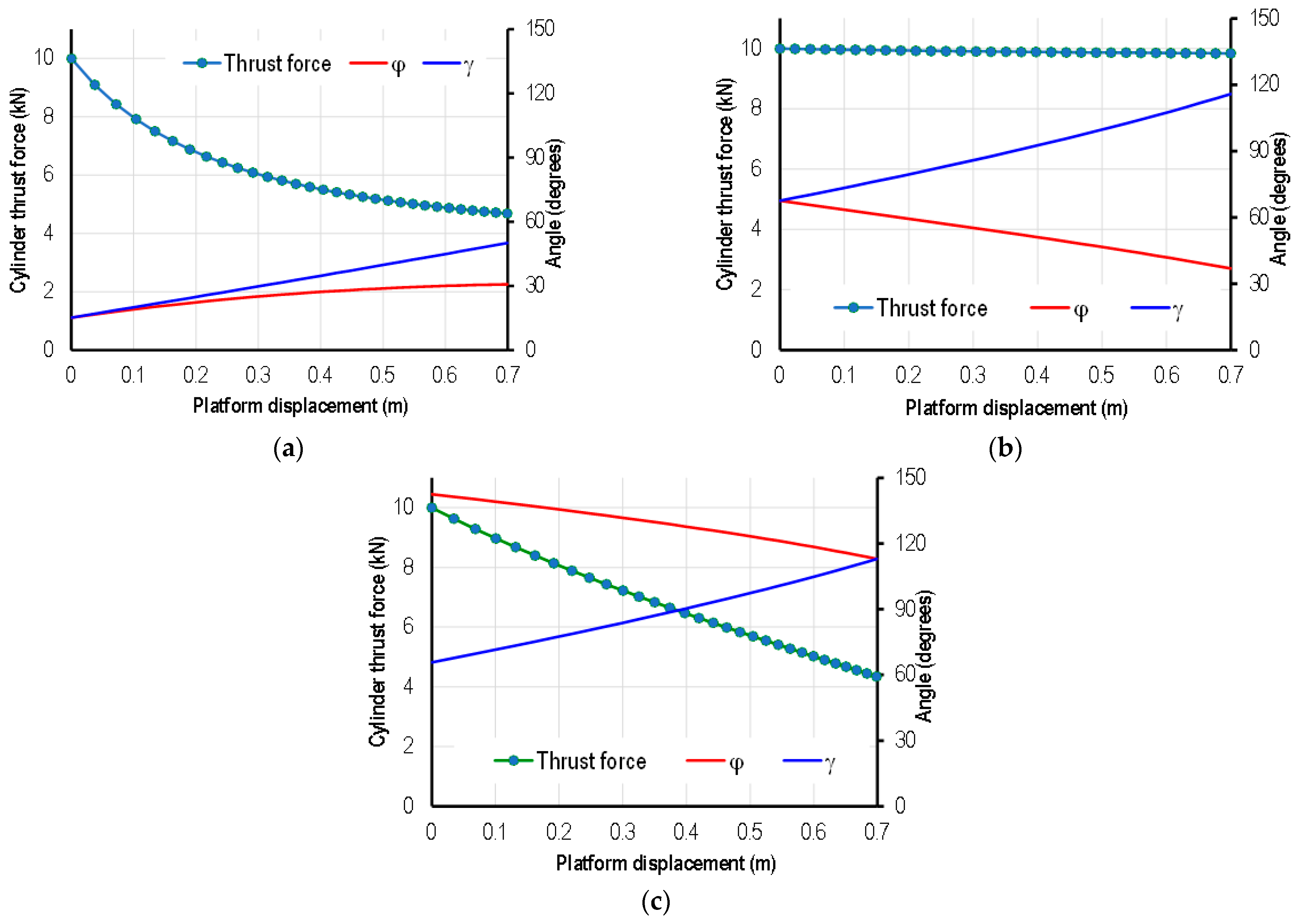
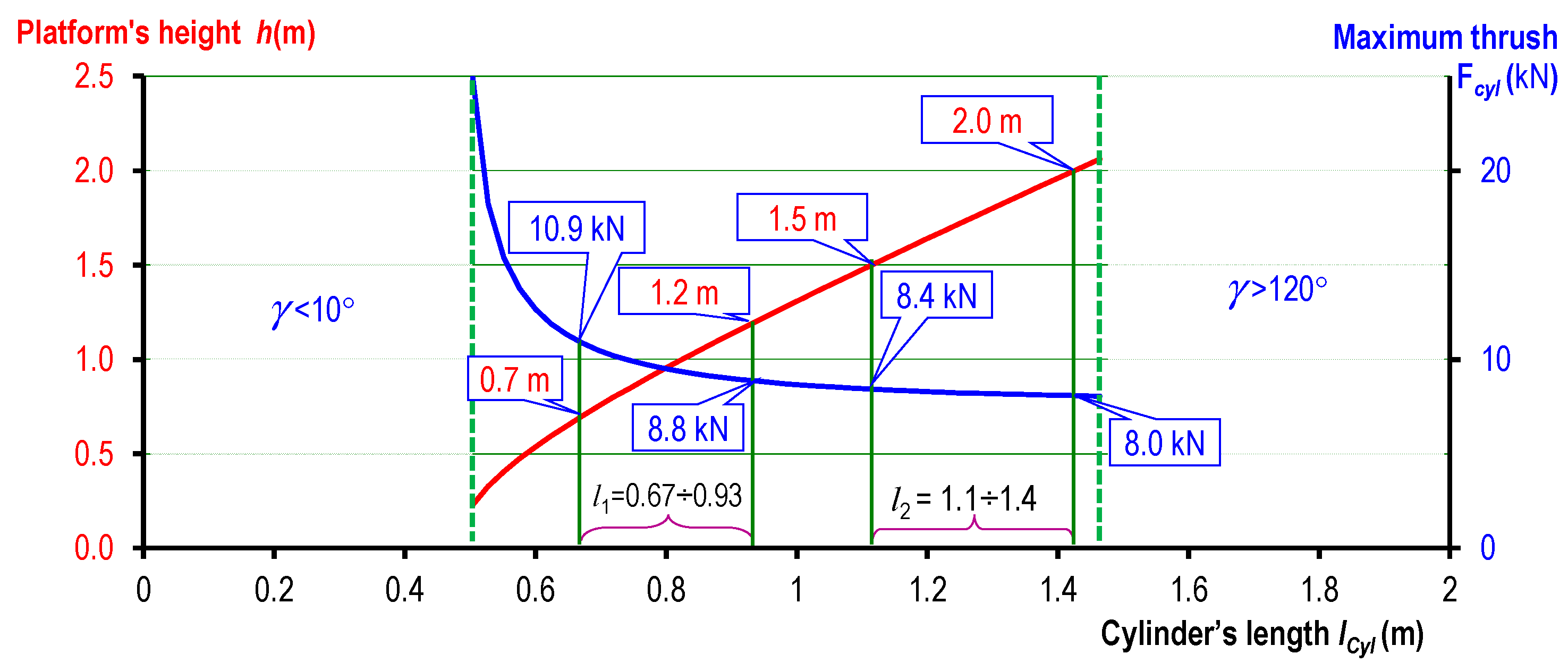
5. Application Examples
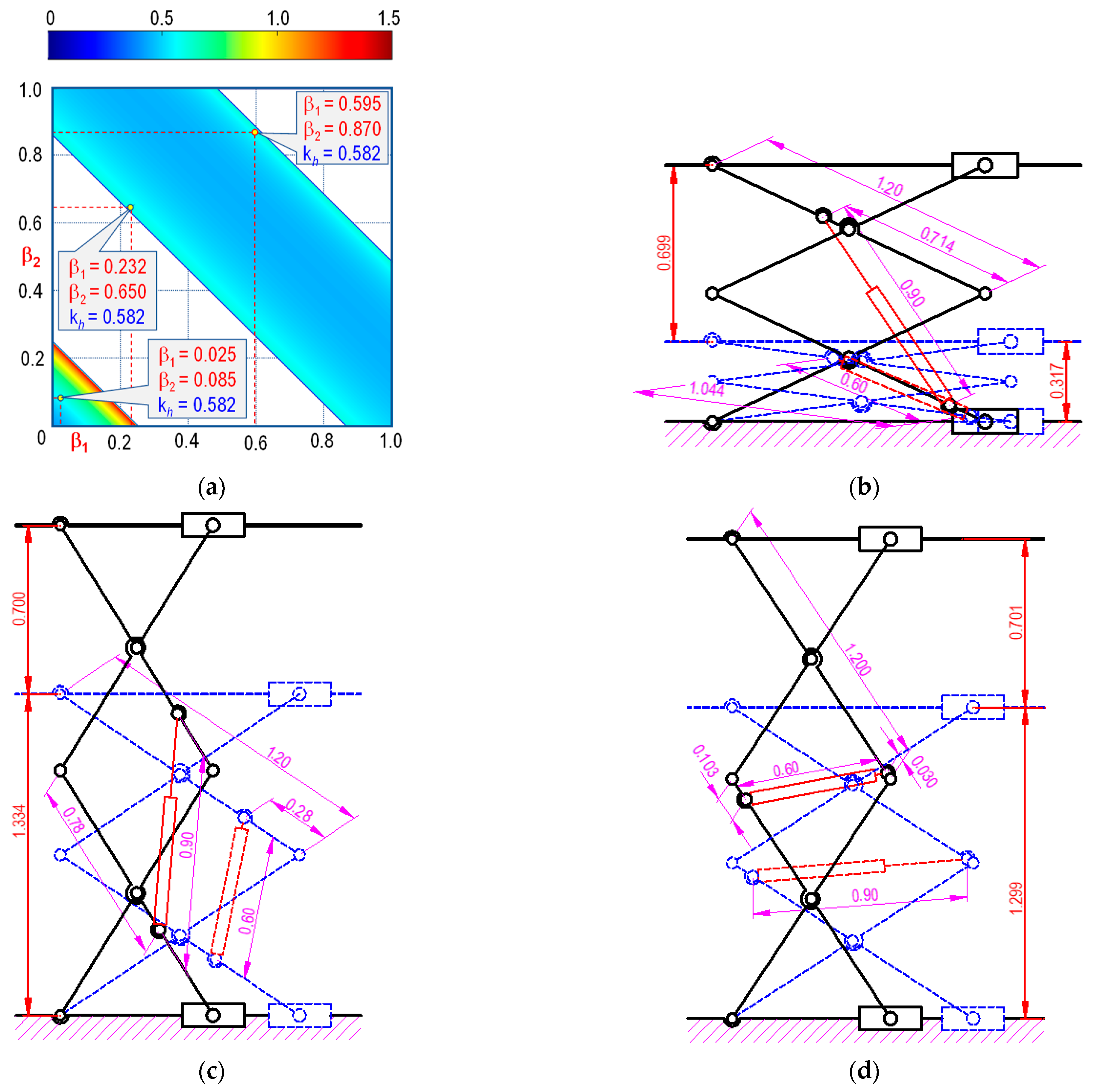
5.1. Designing Double-Stage Scissor Lifts with Optimal Lifting Height and Maximum Load
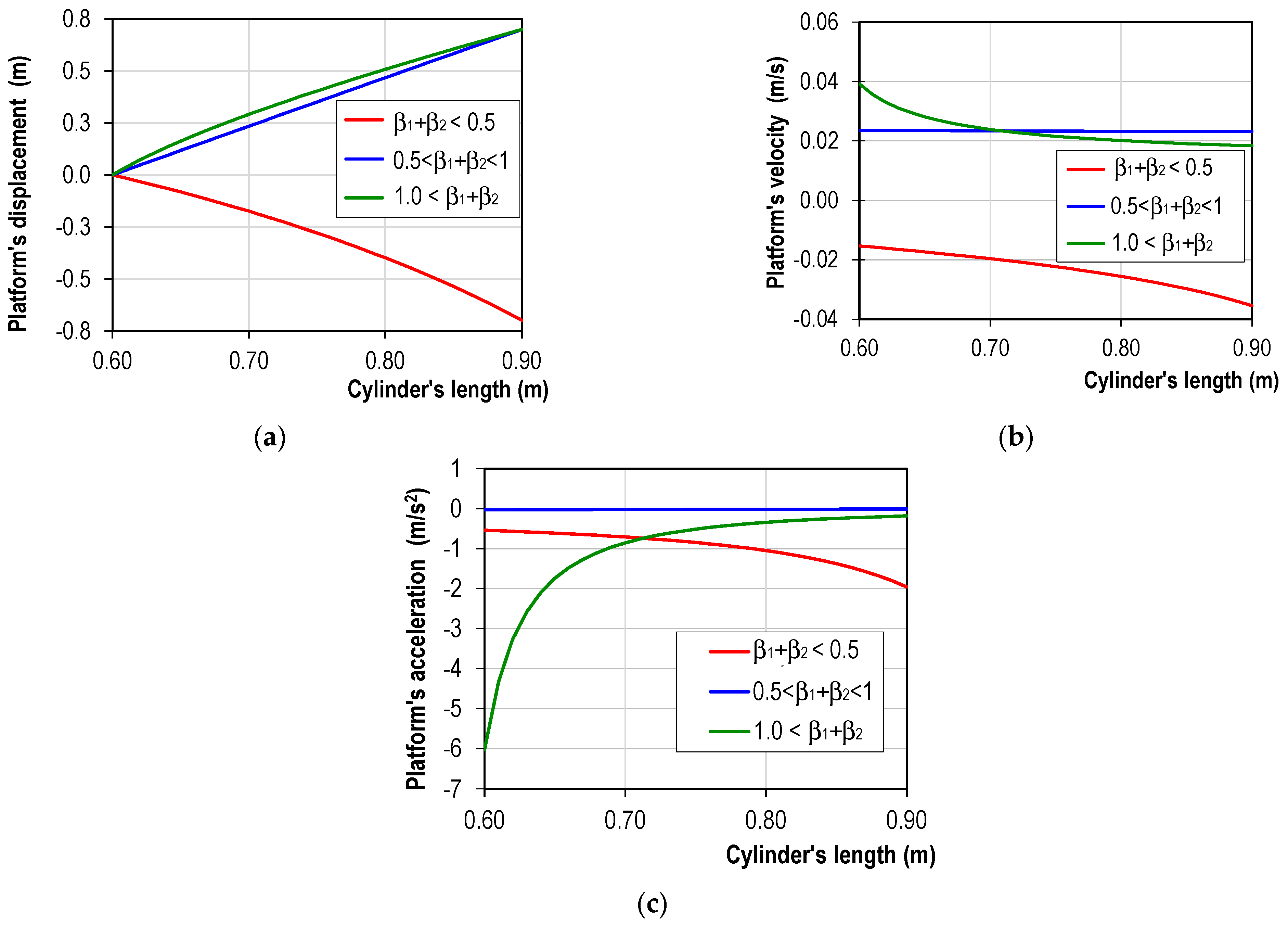
5.2. Designing Double-Stage Scissor Lifts for Selecting the Appropriate Cylinder
6. Conclusions
- -
- By assigning dimensional parameters for the arrangement of cylinders, the information of the system (platform’s height, stability of platforms, and reaction on joints) can be accurately calculated. This allows the selection of components without the need to construct 3D models for complicate inspections or experiments;
- -
- From design requirements, the appropriate information of the lift system can be efficiently and robustly constructed. Designers can select the cylinder to assembly in the given position, or choose the orientation for cylinders that satisfy the operation of platform;
- -
- From the obtained reactions and information of the designed lift, the detailed structure of the system can be optimized, which reduces the manufacturing cost and even calculation time;
- -
- The accuracy of the proposed method is verified by using the Working Model software.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Length of one scissor’s arm |
| Design parameters | |
| Cylinder’s length | |
| Coefficient of cylinder’s length | |
| Angle between adjacent arms of the double-stage lift | |
| Angle between cylinder and the scissor arm | |
| h | Elevation of the platform |
| Velocity of the platform | |
| Acceleration of the platform | |
| Δh | Height of the platform |
| Lifting ratio | |
| l | Distance between supports A and B on the platform |
| lG | Position of total load PG on the platform |
| Velocity of the cylinder | |
| P | Lift weight of the objects/people |
| Wp | Weight of the platform |
| W | Weight of an scissor arm |
References
- Pan, C.S.; Chiou, S.S.; Kau, T.Y.; Wimer, B.M.; Ning, X.; Keane, P. Evaluation of postural sway and impact forces during ingress and egress of scissor lifts at elevations. Appl. Ergon. 2017, 65, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Paramasivam, V.; Tilahun, S.; Kerebih Jembere, A.; Selvaraj, S.K. Analytical investigation of hydraulic scissor lift for modular industrial plants in Ethiopia. Mater. Today Proc. 2021, 46, 7596–7601. [Google Scholar] [CrossRef]
- Solmazyiğit, İ.; Başkurt, R.C.; Ovalı, İ.; Tan, E. Design and Prototype Production of Scissor Lift Platform 25 Tons Capacity. Eur. J. Res. Dev. 2022, 2, 326–337. [Google Scholar] [CrossRef]
- Soma Raghavendra, C.; Raghunath Reddy, B.; Tech Student, M. Design and Analysis of an Aerial Scissor Lift. Int. J. Eng. Sci. Comput. 2017, 7, 13890–13903. [Google Scholar]
- Hongyu, T.; Ziyi, Z. Design and Simulation Based on Pro/E for a Hydraulic Lift Platform in Scissors Type. Procedia Eng. 2011, 16, 772–781. [Google Scholar] [CrossRef]
- Arunkumar, G.; Kartheeshwaran, R.; Siva, J. Investigation on design, analysis and topological optimization of hydraulic scissor lift. J. Phys. 2021, 2054, 012081. [Google Scholar] [CrossRef]
- Choe, H.; Kwon, Y.; Jo, J.; Ri, K.; Jang, H.; Xing, T. A method to Improve the Stability of Scissor Lifting Platform by using Finite Element Analysis. Int. J. Sci. Res. Sci. Eng. Technol. 2022, 9, 314–322. [Google Scholar]
- Karagülle, H.; Akdağ, M.; Bülbül, İ. Design Automation of a Two Scissors Lift. Eur. J. Res. Dev. 2022, 2, 178–191. [Google Scholar] [CrossRef]
- Spackman, H.M. Mathematical Analysis of Scissor Lifts; Naval Ocean Systems Center: San Diego, CA, USA, 1989. [Google Scholar]
- Kirsanov, M.N. Parallelogram mechanism with any number of sections. Russ. Eng. Res. 2018, 38, 268–271. [Google Scholar] [CrossRef]
- Dong, R.G.; Pan, C.S.; Hartsell, J.J.; Welcome, D.E.; Lutz, T.; Brumfield, A.; Harris, J.R.; Wu, J.Z.; Wimer, B.; Mucino, V.; et al. An investigation on the dynamic stability of scissor lift. Open J. Saf. Sci. Technol. 2012, 2, 8–15. [Google Scholar] [CrossRef]
- Dang, A.T.; Nguyen, D.N.; Nguyen, D.H. A Study of Scissor Lifts Using Parameter Design. In Proceedings of the International Conference on Engineering Research and Applications, ICERA 2020, Thai Nguyen, Vietnam, 1–2 December 2020; pp. 75–85. [Google Scholar]
- Saxena, A. Deriving a Generalized, Actuator Position-Independent Expression for the Force Output of a Scissor Lift. arXiv 2016, arXiv:1611.10182. [Google Scholar]
- Ciupan, C.; Ciupan, E.; Pop, E. Algorithm for Designing a Hydraulic Scissor Lifting Platform. In MATEC Web of Conferences; EDP Sciences: Ulis, France, 2019; Volume 299. [Google Scholar]
- Stawinski, L.; Zaczynski, J.; Morawiec, A.; Skowronska, J.; Kosucki, A. Energy Consumption Structure and Its Improvement of Low-Lifting Capacity Scissor Lift. Energies 2021, 14, 1366. [Google Scholar] [CrossRef]
- Stawinski, L.; Kosucki, A.; Morawiec, A.; Sikora, M. A new approach for control the velocity of the hydrostatic system for scissor lift with fixed displacement pump. Arch. Civ. Mech. Eng. 2019, 19, 1104–1115. [Google Scholar] [CrossRef]
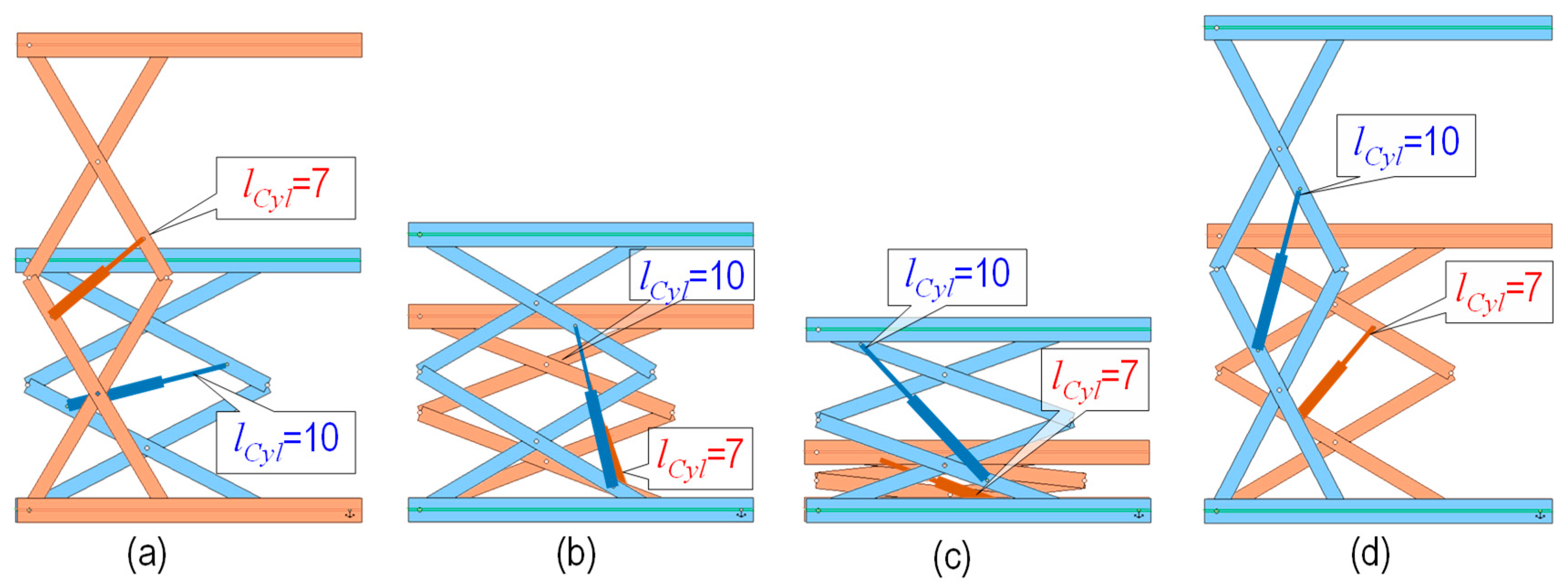

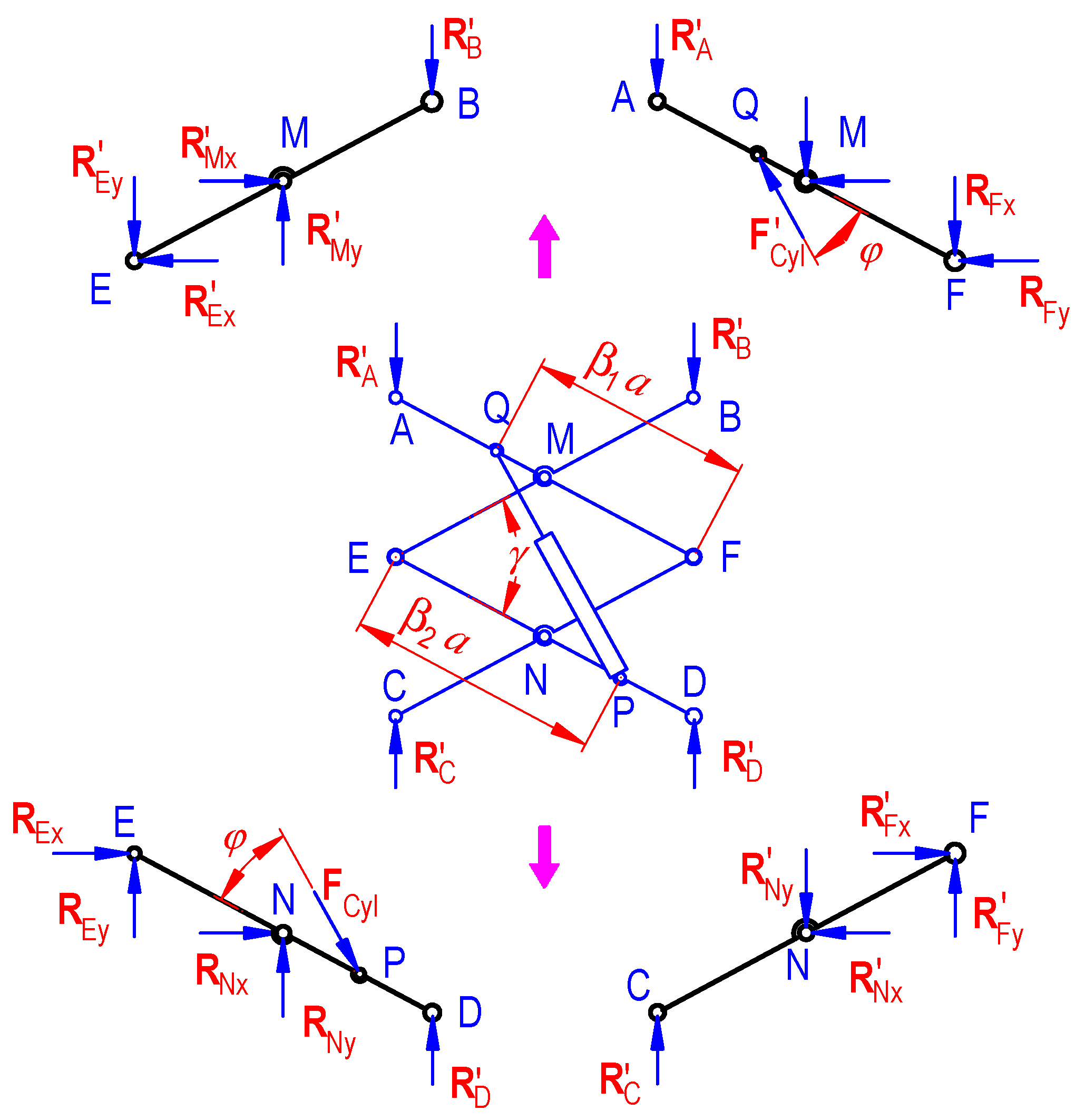
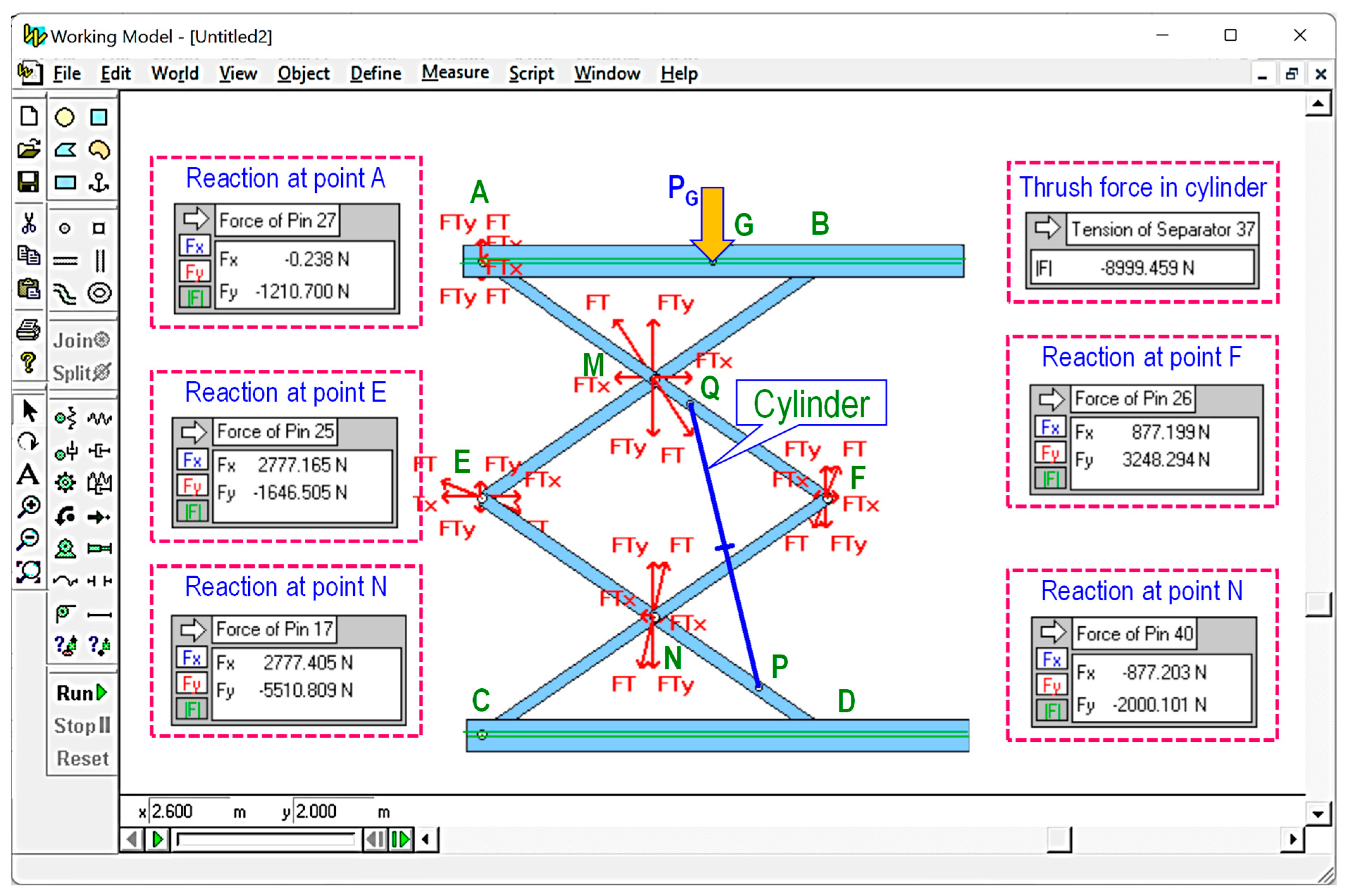
| a = 1 m; W = 75 N PG = 5000 N | lG = 0.1 m | lG = 0.5 m | |||||
|---|---|---|---|---|---|---|---|
| F1 (N) | F2 (N) | F1 (N) | F2 (N) | ||||
| FCyl | 124,566.36 | 124,565.07 | 0.00 | 124,566.36 | 124,566.94 | 0.00 | |
| FMx | 61,127.42 | 61,122.84 | 0.01 | 61,127.42 | 61,112.33 | 0.02 | |
| FMy | 14,268.85 | 14,278.06 | 0.06 | 10,144.26 | 10,161.17 | 0.17 | |
| FNx | 61,723.78 | 61,717.87 | 0.01 | 61,723.78 | 61,708.80 | 0.02 | |
| FNy | 6331.15 | 6346.54 | 0.24 | 10,455.74 | 10,484.27 | 0.27 | |
| FEy | 14,859.43 | 14,873.10 | 0.09 | 12,797.13 | 12,813.08 | 0.12 | |
| FFy | 10,890.57 | 10,931.50 | 0.37 | 12,952.87 | 12,982.33 | 0.23 | |
| FCyl | 26,115.27 | 26,114.77 | 0.00 | 26,115.27 | 26,117.07 | 0.01 | |
| FMx | 7986.74 | 7983.42 | 0.04 | 7986.74 | 7984.82 | 0.02 | |
| FMy | 13,130.70 | 13,129.67 | 0.01 | 4453.48 | 4449.83 | 0.08 | |
| FNx | 8064.66 | 8064.48 | 0.00 | 8064.66 | 8064.90 | 0.00 | |
| FNy | 7469.30 | 7470.02 | 0.01 | 16,146.52 | 16,151.73 | 0.03 | |
| FEy | 14,290.35 | 14,289.76 | 0.00 | 9951.74 | 9950.31 | 0.01 | |
| FFy | 11,459.65 | 11,459.93 | 0.00 | 15,798.26 | 15,801.26 | 0.02 | |
| FCyl | 17,291.62 | 17,297.80 | 0.04 | 17,291.62 | 17,291.80 | 0.00 | |
| FMx | 11,805.09 | 11,805.20 | 0.00 | 11,805.09 | 11,805.20 | 0.00 | |
| FMy | 1632.62 | 1632.74 | 0.01 | 2473.26 | 2473.13 | 0.01 | |
| FNx | 23,260.18 | 23,260.05 | 0.00 | 23,260.18 | 23,306.05 | 0.30 | |
| FNy | 14,585.65 | 14,585.80 | 0.00 | 10,479.77 | 10,480.00 | 0.00 | |
| FEy | 2220.86 | 2220.94 | 0.00 | 167.92 | 168.00 | 0.05 | |
| FFy | 10,023.89 | 10,024.00 | 0.00 | 7970.95 | 7971.08 | 0.00 | |
| FCyl | 8011.80 | 8011.79 | 0.00 | 8011.80 | 8011.80 | 0.00 | |
| FMx | 1000.35 | 1000.37 | 0.00 | 1000.35 | 1000.38 | 0.00 | |
| FMy | 433.85 | 433.80 | 0.01 | 6719.24 | 6719.15 | 0.00 | |
| FNx | 1124.10 | 1124.10 | 0.00 | 1124.10 | 1124.10 | 0.00 | |
| FNy | 7291.15 | 7291.19 | 0.00 | 1005.76 | 1005.85 | 0.01 | |
| FEy | 426.83 | 426.85 | 0.00 | 2715.87 | 2715.82 | 0.00 | |
| FFy | 3001.83 | 3001.84 | 0.00 | 140.87 | 140.83 | 0.03 | |
| FCyl | 18,357.97 | 18,359.20 | 0.01 | 18,357.97 | 18,359.70 | 0.01 | |
| FMx | 2354.19 | 2356.25 | 0.09 | 2354.19 | 2356.10 | 0.08 | |
| FMy | 7734.32 | 7733.72 | 0.01 | 17,471.61 | 17,469.00 | 0.01 | |
| FNx | 1126.41 | 1127.38 | 0.09 | 1126.41 | 1127.48 | 0.09 | |
| FNy | 10,290.68 | 10,291.90 | 0.01 | 553.39 | 554.03 | 0.12 | |
| FEy | 6442.16 | 6442.09 | 0.00 | 11,310.81 | 11,309.70 | 0.01 | |
| FFy | 6432.84 | 6433.57 | 0.01 | 1564.19 | 1566.28 | 0.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, A.-T.; Nguyen, T.T.N. Investigation on the Design of Double-Stage Scissor Lifts Based on Parametric Dimension Technique. Machines 2023, 11, 684. https://doi.org/10.3390/machines11070684
Dang A-T, Nguyen TTN. Investigation on the Design of Double-Stage Scissor Lifts Based on Parametric Dimension Technique. Machines. 2023; 11(7):684. https://doi.org/10.3390/machines11070684
Chicago/Turabian StyleDang, Anh-Tuan, and Thi Thanh Nga Nguyen. 2023. "Investigation on the Design of Double-Stage Scissor Lifts Based on Parametric Dimension Technique" Machines 11, no. 7: 684. https://doi.org/10.3390/machines11070684
APA StyleDang, A.-T., & Nguyen, T. T. N. (2023). Investigation on the Design of Double-Stage Scissor Lifts Based on Parametric Dimension Technique. Machines, 11(7), 684. https://doi.org/10.3390/machines11070684






