Abstract
To satisfy the design requirements for a hydropneumatic spring damper valve, the inlet–outlet pressure drop (ΔP) and the axial force on the spool (FZ) of a valve were investigated using fluid–solid coupling simulations and multi-objective optimization, along with the effects of the diameters of three internal holes (DA, DB, and DC) in the valve on the ΔP and the FZ. First, a meshed computational fluid dynamics model of a damper valve was established based on its geometric structure. Next, the effects of the flow rate (Q) and the diameter of the damping hole in the internal structure on the ΔP and the FZ of the damper valve were investigated. The results showed that the ΔP and the FZ varied nonlinearly with Q. For a given Q, the ΔP decreased as DA, DB, and DC increased. For a given Q, the FZ was not related to DA and DC, but it decreased as DB increased. Finally, the structure of the damper valve was optimized by defining the ΔP and the FZ as the response variables and DA, DB, and DC as the explanatory variables. The results showed that the best configuration of the hole diameters was DA = 8.8 mm, DB = 5.55 mm, and DC = 6 mm. In this configuration, ΔP = 0.704 MPa and FZ = 110.005 N. The ΔP of the optimized valve was closer to the middle value of the target range than that of the initial valve design. The difference between the simulated and target values of the FZ decreased from 0.28% to 0.0045%, satisfying application requirements.
1. Introduction
Hydropneumatic spring suspensions are increasingly being used in off-road vehicles, farm trucks, and racing cars. A suspension system is critical to ensuring the normal operation, maneuverability, and mobility of these vehicles. The performance of the hydropneumatic springs directly affects the ride quality of a vehicle. To ensure the performance of a hydropneumatic spring, the damping characteristics of the damper valve must be considered during its design. Xie et al. [1] highlighted the fact that simple-structure, damping-adjustable damper valves have always been a research topic of interest. A damper valve is a core component of a hydropneumatic spring suspension system. Thus, the improvement of the design of a hydropneumatic spring suspension system necessitates a close examination of this core component.
Giliomee and Els [2] analyzed the rigidity and damping characteristics and the random input responses of a hydropneumatic suspension with a double-gas-chamber spring unit for heavy off-road vehicles and the effects of the damping and rigidity on the overall performance of the hydropneumatic suspension, thereby improving the ride quality and maneuverability of heavy off-road vehicles. Regarding the kinetic characteristics of a semi-active hydropneumatic suspension, Saxon et al. [3] investigated the Bradley Fighting Vehicle of the US Army, established a test system for the hydropneumatic suspension and associated piping, computer controller, and dynamic track tensioner, and proposed a method for the continuous adjustment of the damping of caterpillar vehicles. Theron and Els [4] established a damping model for a semi-active hydropneumatic spring suspension with a two-stage damping system by employing linear fluid mechanics theory, calculating the pressure in the accumulators through the integral calculations of the flow rates to the hydraulic cylinder, and using the damping force of the hydropneumatic suspension unit as the output of the model. The predictions yielded using the model were consistent with the experimental data. Zhuang [5] modeled the nonlinear vertical and lateral dynamics of an active hydropneumatic suspension and analyzed the stability of the model with road surface excitations of different frequencies and magnitudes. The accumulator in the model and the mathematical model of the damper valve were linearized, and the control accuracy of the active hydropneumatic suspension was improved by employing robust control theory and a hierarchical control method. Li et al. [6] established a nonlinear mathematical model of a hydropneumatic suspension based on simulations and tests of hydropneumatic springs. The ride quality of the vehicle was improved with linearization and by employing proportional–integral–derivative control. Zhao et al. [7] established a model of the nonlinear rigidity and damping of a semi-active hydropneumatic suspension and linearized the model using a feedback linearization method. Based on an analysis of the effects of the major parameters on the damping of a damper valve, they proposed a sliding mode control system for semi-active hydropneumatic suspensions. In addition, cavitation is also the focus of many scholars in the research and design of vehicle shock absorbers. For example, Skrickij et al. [8] studied the cavitation effect of single-tube shock absorbers by establishing mathematical models, and proposing a simplified method for evaluating the cavitation process of automotive single-tube shock absorbers. Karpenko et al. [9] explored the adaptive performance of passive control systems based on frequency analysis. However, cavitation and amplitude–frequency characteristics are not studied in this paper. Significant research on the characteristics of damper valves has been conducted using various methods, enriching the theoretical understanding of damper valves. However, most of the existing studies focus on the modeling of the flow in damper valves, and few studies have been conducted on the inlet–outlet pressure drop (ΔP) and axial force on the spool (FZ) that drives the opening of damper valves.
Computational fluid dynamics (CFD) is a useful tool for the in-depth analysis of parameters that are difficult to obtain experimentally, such as flow forces and damping. Numerous studies [10,11,12,13,14] have shown that the flow coefficients of various valves obtained using CFD agree well with experimental data. Morita et al. [15] investigated the unsteady flow in a valve under a partial opening condition and reproduced the unsteady flow phenomenon using CFD. Lisowski et al. [16] proposed a method for calculating the forces associated with the flow in a solenoid-operated directional control valve (pressure and viscous forces). The method was first used to define the surfaces affected by the forces associated with the flow through each path and then to obtain the values of the flow forces using a CFD method. In 2015, Lisowski et al. [17] investigated the pressure compensation problem in a multi-section proportional directional control valve. They obtained the values of the flow resistance through the valve and the axial component of the flow force acting on the valve spool through numerous CFD simulations, established a mathematical model of the flow forces, and examined the possibility of pressure compensation in a three-section control valve based on simulations in the Matlab/Simulink system. Wu et al. [13] described specific CFD simulation methods for fitting the flow–pressure curve of a pressure control valve used in an automotive fuel supply system. Their analysis improved understanding of the coupling mechanism in pressure control valves. Lai et al. [18] investigated the transient characteristics of a dual-disc check valve during the opening period and numerically simulated the transient characteristics and internal flow field of a check valve using an unsteady CFD method. Recent studies [19,20,21,22] have analyzed the dynamic characteristics of various valves using CFD, and the reliability of these CFD results has been widely recognized. In addition, CFD can analyze parameters that are difficult to measure experimentally. However, different relaxation factors are selected for different CFD models, and CFD calculations must be verified against experimental results.
In this study, we analyzed a damper valve that was developed using CFD and a fluid–solid coupling method based on the previous studies reviewed above. This paper first describes the workflow of the hydropneumatic spring damper valve. A CFD model of the initial design of the damper valve was established for finite element verification and analysis, and the verified simulation parameters were used in subsequent multi-parameter model-based simulations and analyses. Finally, to satisfy the engineering application requirements of the damper valve, multi-objective optimization of the damper valve was performed by defining the diameters of three internal holes as the objective of optimization and ΔP and FZ as the response variables.
2. Establishment, Verification, and Analysis of the Damper Valve Model
2.1. Computer-Aided Design (CAD) Model of the Damper Valve
Figure 1a shows the structure of the hydropneumatic spring damper valve. The valve body was fabricated from #45 steel. Kunlun 10 hydraulic oil was used as the working fluid. The spring had an initial back pressure of 110 N and a toughness of 10 N/mm. The flow of the hydraulic oil is indicated by line L1 in the Figure. To improve the quality of the mesh for subsequent calculations, structural components whose effects were negligible [16,17], such as the chamfers, gasket, and spring, were simplified. Figure 1b shows the simplified CAD model. In the paper, DX is the diameter of hole X. DA, DB, and DC have lengths of 10 mm, 6 mm, and 6 mm, respectively. The other structural dimensions are given in Table 1.
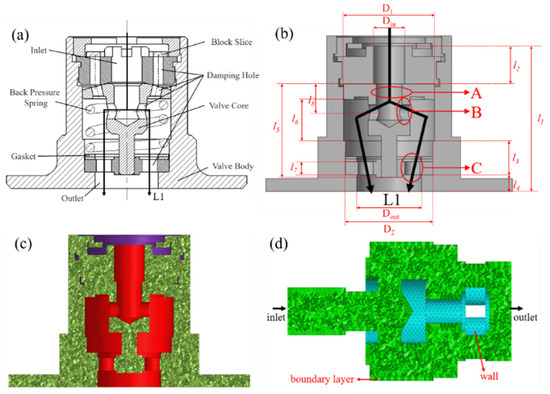
Figure 1.
CAD model and meshed model of damper valve. (a): Illustration of the structure of hydropneumatic spring damper valve; (b): simplified structure of hydropneumatic spring damper valve; (c): meshed model of flow domain; and (d): meshed model of solid domain.

Table 1.
Structural dimensions of the damper valve.
The workflow of the damper valve is as follows. The hydraulic oil flowed in the direction indicated by line L1. When the flow rate reached a certain value, the axial force acting on the spool was larger than the back pressure. Because the initial back pressure of the spring was inadequate to sustain the spool at its initial position, the spool moved toward the outlet. This process is referred to as the valve opening process. When the valve opened, the direction of the flow of the hydraulic oil changed. This study was focused on the effects of the flow rate (Q) and DX (DA, DB, and DC) on ΔP and FZ of the damper valve during the closure stage of the damper valve and the multi-objective optimization of the diameters of the critical holes at the critical flow rate of 70 L/min (representing the transition between the opening and closing of the valve). Therefore, the operation of the valve during the opening stage is not covered here.
2.2. Meshing of Damper Valve Model
Fluid–solid coupling simulations of the damper valve were performed using the Ansys Workbench platform. ΔP in the flow domain was calculated using the Ansys fluent software. The calculation results were imported into the static structural module of the Ansys Workbench platform to calculate FZ.
A mesh independence study of the mesh model of the flow domain established based on the CAD model was performed before it was used for numerical simulations. The study was performed at Q = 22 L/min (the minimum flow rate used in the experiment) and 500 steady iterative step lengths. The residual error was less than 10−4. Figure 2 shows the results. The calculation results stabilized after the number of cells reached 260,000.
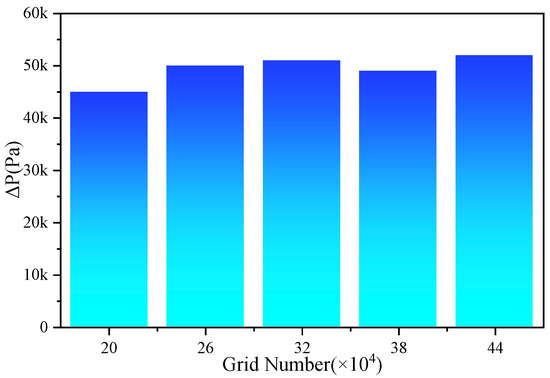
Figure 2.
Mesh independence study.
The wall function, which is usually empirically derived, describes the relationship between a near-wall cell and a wall. In this study, the dimensionless distance between the wall and the first layer of the mesh y+ was configured according to the wall function and the height of the first layer of the mesh. The value of y+ was verified to verify the quality of the mesh. Based on the structural dimensions of the damper valve given above, most of the values of y+ fell in the range of 10–60, which indicated that the standard wall function was acceptable. Based on the structural dimensions of the CAD model and the results of the mesh independence study, and considering the computational complexity and accuracy, the same mesh was used for subsequent simulation calculations. Tetrahedral cells were used that measured 1 mm across. Five boundary layers were defined, and the growth rate was set to 1.2. Figure 1c shows the mesh for the flow domain The solid domain was also meshed using 1 mm tetrahedral cells, as shown in Figure 1d.
2.3. Validation of the Simulation Model
2.3.1. Experimental and Simulation Setups
To verify the reliability of the numerical model, the ΔP values of the initial design of the damper valve at five different steady flow rates (Q = 22 L/min, 41.7 L/min, 51 L/min, 60 L/min, and 70 L/min) were obtained experimentally using a finite element model. Figure 3 shows the experimental setup. Pressure sensors were mounted at the inlet and outlet to measure the inlet and outlet pressures. An electromagnetic flow meter was mounted at the inlet piping to measure the flow rate through the damper valve.
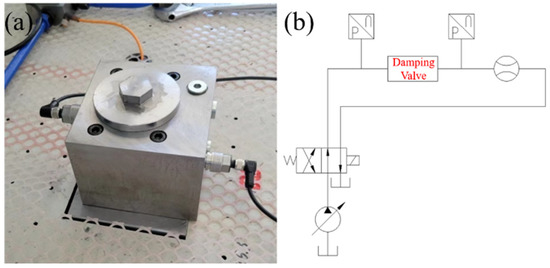
Figure 3.
Test setup and schematic of experimental principle. (a): Test setup; and (b): schematic of experimental principle.
In the CFD simulation, a second-order turbulence model was used to fit the Navier–Stokes equation [23]. The ambient temperature was set to 40 °C. The temperature inside the damper valve did not vary significantly and could be assumed to be constant [13,18,24]. Thus, the energy equation and cavitation were not considered. The governing equations involved are shown in Appendix A. Based on parameter testing, the turbulence was simulated using the k-ε model and the standard wall function. The boundary conditions were the velocity inlet and the pressure outlet. The inlet velocity was calculated from the flow velocity and inlet area using the SIMPLEC algorithm.
2.3.2. Verification and Analysis of Simulation Results
Figure 4a shows a comparison of the simulation and experimental results. ΔP increased quasi-quadratically as the flow rate increased. The simulation and experimental results exhibited similar trends. The maximum, minimum, and mean errors were 8.10%, 0.28%, and 4.10%, respectively. The error might have been due to the simplification of the valve structural components such as the chamfers and spring. Figure 4b shows the nephogram of the pressure distribution in the plane of symmetry of the flow field at Q = 22 L/min. The simulated stress distribution was consistent with the theoretical stress distribution. The simulation error was acceptable, confirming the reliability of the CFD model. Therefore, the same parameters were used in subsequent simulations.
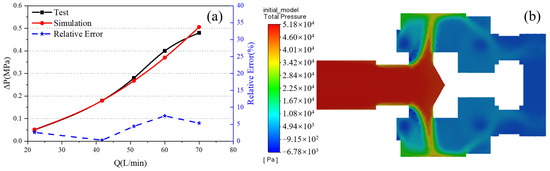
Figure 4.
Simulation results for the initial valve design. (a): Simulation and experimental verification of the initial valve design; and (b): nephogram of the pressure distribution in the plane of symmetry of the flow field in the initial valve design when Q = 22 L/min.
3. Parameter Configuration and Multi-Objective Optimization of Damper Valve
3.1. Parameterized Model Analysis of the Damper Valve
To investigate the effects of DA, DB, and DC on the inlet–outlet pressure drop, the effect of the axial force on the spool of the damper valve, and the effects of the diameters of the internal holes on the opening force of the damper valve, a multi-parameter model of the damper valve was established using different settings for the diameters of the internal holes. First, DA was varied (10 mm, 9 mm, 8 mm, 11 mm, and 12 mm) with both DB and DC held constant at 6 mm. Next, DB was varied (6 mm, 5 mm, 4 mm, 7 mm, and 8 mm), with DA and DC held constant at 10 mm and 6 mm, respectively. Finally, DC was varied (6 mm, 5 mm, and 7 mm), with DA and DB held constant at 10 mm and 6 mm, respectively.
Two indicators of most concern were selected to be analyzed in the subsequent design and optimization of the hydropneumatic spring, which were ΔP and FZ in the flow domain of the damper valve. This was because ΔP was a critical factor that determined the correct opening of the damper valve and ΔP directly affected the stress in the damper valve during the opening process. FZ was a critical factor that affected the service life of the damper valve. ΔP and FZ at the 11 different configurations of DA, DB, and DC as well as five different flow rates were calculated.
3.2. Analysis of the Inlet–Outlet Pressure Drop of the Damper Valve
Overall, ΔP increased quasi-quadratically as Q increased, as shown in Figure 5. Figure 5a–c shows the variations of ΔP with Q at different configurations of DA, DB, and DC. Figure 5d–f shows three-dimensional (3D) representations of the variation trends. In the following, the configuration of DA (x mm), DB (y mm), and DC (z mm) is designated as AxByCz. Figure 5a shows the variations of ΔP with Q and AxByCz with DA varied and DB and DC held constant. ΔP increased as DA or Q increased. Figure 5d shows a 3D representation of the above variation trend. ΔP increased more significantly with Q at a smaller value of DA. ΔP also increased more significantly with Q as DB or DA increased, as shown in Figure 5b,c,e,f. However, DB had a greater effect on ΔP, and DC had an insignificant effect on ΔP. Following this, the variation of ΔP as DA, DB, or DC was varied and the other two diameters were held constant was designated as ΔPxij. For example, ΔPA89 designated the variation of ΔP as DA increased from 8 mm to 9 mm and DB and DC were held constant. As shown in Figure 5a–c, ΔPxij increased quasi-quadratically as Q increased. In particular, DB had the greatest effect on ΔP, while DC had the smallest effect on ΔP. Additionally, ΔP increased insignificantly with DA at a smaller Q but increased more significantly at a larger Q, as shown in Figure 5e. This indicated that the effect of DA on ΔP increased as Q increased. The effect of DB on ΔP also increased as Q increased, as shown in Figure 5e. ΔP was insignificantly affected by DC and was affected mainly by Q, as shown in Figure 5f.
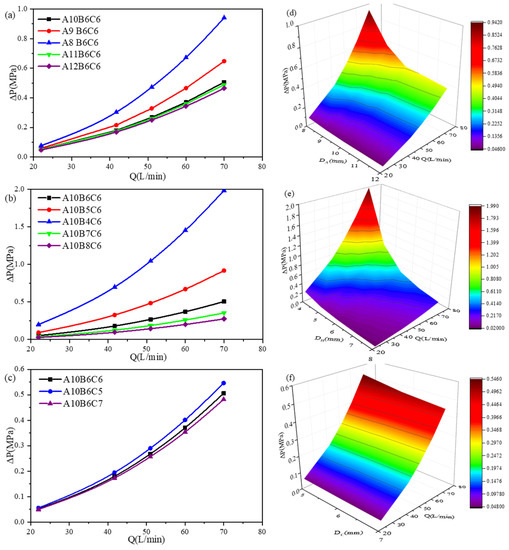
Figure 5.
ΔP-Q curves at different configurations of hole diameters. (a): varying DA while holding DB and DC constant; (b) varying DB while holding DA and DC constant; (c): varying DC while holding DA and DB constant; and (d–f): 3D nephograms of the relationship between ΔP and the Q-hole diameter interaction.
The above results for the variations of ΔP were consistent with those published by Jian et al. [25], who stated that ΔP increased quasi-quadratically as Q increased. In particular, DB had a major effect on ΔP. This was because of the special location and direction of the hole.
3.3. Analysis of the Spool Axial Force of the Damper Valve
Figure 6 shows the variations of FZ with DX and Q. FZ exhibited similar but not identical variations to those of ΔP. Figure 6a–c shows the variations of FZ with Q as DA, DB, and DC were varied. Figure 6d–f shows the 3D representations of the variations. Overall, FZ increased as Q increased, as shown in Figure 6a. However, in contrast to the variations in ΔP (which varied the most significantly with Q at the hole diameter configuration of A8B6C6), FZ increased the most significantly with Q at the hole diameter configuration of A12B6C6. This was because FZ was larger when DA = 12 mm = Din compared with when DA < Din. FZ varied in a manner similar to ΔP as Q increased and DB was varied, as shown in Figure 6b. In addition, at a given Q, FZ increased as DB decreased. DC had an insignificant effect on FZ, and the FZ-Q curves at different values of DC differed insignificantly, with the maximum difference being 1525.6 Pa, as shown in Figure 6c. FZ was insignificantly affected by DA and was mainly affected by Q, as shown in Figure 6d. However, DA had a critical effect on FZ at a higher Q, but only at a higher Q. FZ was significantly affected by both DB and Q, and FZ reached the minimum when DB reached the maximum and Q reached the minimum, as shown in Figure 6e. FZ increased nonlinearly as DB decreased and Q increased. FZ reached the maximum when DB reached the minimum and Q reached the maximum. This indicated the critical effect of DB on FZ because of the location of hole B. FZ was insignificantly affected by DC and was mainly affected by Q, as shown in Figure 6f. Similarly, this was because of the location of hole C, which was located at the outlet and whose effect on the spool axial force was negligible.

Figure 6.
FZ-Q curves at different configurations of hole diameters. (a): varying DA while holding DB and DC constant; (b) varying DB while holding DA and DC constant; (c): varying DC while holding DA and DB constant; and (d–f): 3D nephograms of the relationship between FZ and Q-hole diameter interaction.
The above results showed that DB also had the most significant effect on FZ and the effect of DB on FZ was similar to its effect on ΔP. Both ΔP and FZ increased with Q at various values of DA. However, the effect of DA on FZ was significantly different from its effect on ΔP.
3.4. Multi-Objective Optimization of the Damper Valve
Multi-objective optimization of the damper valve was performed under the condition that it did not open and remained in its initial state when Q ≤ 70 L/min. The initial back pressure of the spring was set to 110 N, and its toughness was set to 10 N/mm. The target value of the ΔP optimization was set to 0.75 MPa, the middle value of the range of ΔP for automobile applications of the damper valve. Therefore, the objective was to optimize ΔP and the maximum spool axial force FZ at Q = 70 L/min. Prior to the optimization of the damper valve, a mathematical model for describing the relationship between the explanatory and response variables was established. The functional relationship between the explanatory and response variables was identified based on massive experimental data. Experimental data were obtained using an orthogonal experimental design because the accuracy of this type of response function is dependent on the quality of the experimental data.
A three-factor (DA, DB, and DC) five-level orthogonal experimental design was adopted. The L25(56) (with “25” indicating the number of tests, “5” indicating the number of levels, and 6 indicating the number of factors) orthogonal table was used. Since only three factors were tested, the last three columns of the table were not used (because there were no parametric values). Table 2 shows the orthogonal experimental design and the test results.

Table 2.
Orthogonal experimental design and test results.
Tests were performed according to the orthogonal experimental design, with test #1 performed using the initial valve designs. Simulations were performed using the corresponding configurations of DA, DB, and DC (designated as x1, x2, and x3, respectively) at Q = 70 L/min. The simulation results for ΔP and FZ are shown in Table 2.
Two functions were established for describing the responses of ΔP and FZ to DA, DB, and DC using response surface methodology. To investigate the overall effects of the explanatory variables on the response variables, the two response variables were weighted to combine the two functions into one function (mathematical model for multi-objective optimization). Based on ΔP and FZ at different levels of the explanatory variables (x1, x2, and x3) obtained from the orthogonal experiment, two functions (Equations (1) and (2)) for describing the responses of ΔP and FZ to the explanatory variables were established.
The response surface functions obtained based on the experimental data shown in Table 2 are as follows:
The closeness of fit of the response functions was verified based on the multiple correlation coefficient R and correction coefficient . Table 3 shows the results. Both R and of the two response functions were greater than 0.85, confirming that the closeness of fit of the response functions for ΔPmax and FZmax was acceptable for subsequent optimization.

Table 3.
Multiple correlation coefficient R and correction coefficient .
Because ΔPmax and FZmax were two major performance indicators of the damper valves, the following objective function was established to investigate the overall effect of the explanatory variables on the two major performance indicators:
where w1 and w2 are the weight factors and w1 + w2 = 1, based on the multiple correlation coefficients for ΔPmax = 0.9672 and FZmax = 0.9549 obtained above. The analytic hierarchy process is used to calculate w1 and w2. Table 4 is the corresponding table of the comparative values of indicator m and indicator n, and emn is the comparative value of the two. According to Table 4, the emn of comparison values between indicators is determined, and the judgment matrix is constructed, as shown in Table 5. ΔP is a key factor in determining whether the damping valve can be opened. ΔP directly affects the stress on the damping valve when it is opened, and its importance is slightly higher than FZ. Therefore, the judgment matrix of this study is shown in Table 6. According to Table 6, w1 = 0.4 and w2 = 0.6; ΔPm and FZm are the means of ΔP and FZ, respectively, with ΔPm = 0.7624 and FZm = 85.8736. ΔPmax and FZmax are as defined in Equations (3) and (4), respectively. With the values of the x1, x2, and x3 limited, the mathematical optimization model can be expressed as:

Table 4.
The comparison value of index m and n.

Table 5.
Theoretical judgment matrix.

Table 6.
Judgment matrix.
Figure 7 shows the nephogram of the relationship between the desirability of the damper valve and the explanatory variables: the effect of the interaction between any pair of explanatory variables on the performance of the damper. Figure 7a shows the nephogram of the effect of the interaction between DA and DB on the desirability. The desirability of the damper valve was high when DB fell in the range of 5–6 mm and DA ≤ 10 mm. Figure 7b shows the nephogram of the effect of the interaction between DA and DC on the desirability. The desirability was high when DC was approximately 6 mm and DA was approximately 9 mm. Figure 7c shows the nephogram of the effect of the interaction between DB and DC on the desirability. The desirability was high when DC was approximately 6 mm and DA was approximately 5.5 mm. Figure 7 reveals the approximate ranges of the optimal solutions of the explanatory variables and the variations of the response variables with the explanatory variables in a straightforward, quantitative manner.

Figure 7.
Nephogram of the explanatory variables–desirability relationship. (a): Desirability at different configurations of DA and DB; (b): desirability at different configurations of DA and DC; and (c): desirability at different configurations of DB and DC.
Table 7 shows the optimum solutions obtained based on the response functions for ΔPmax and FZmax (Equations (3) and (4)) and the optimization model (Equations (5) and (6)) with rounding based on the drill bit sizes used in actual manufacturing.

Table 7.
Optimized hole diameters.
The holes in the damper valves were optimized based on the optimization results. Fluid–solid coupling simulations were performed using the optimized hole sizes. The simulated ΔP and FZ were 0.704 MPa and 110.005 N, respectively. Figure 8 shows a comparison of the simulated ΔP and FZ of the initial and optimized valve designs at Q = 70 L/min. Figure 8 reveals the difference in the performance of the initial and optimized valve designs in a straightforward manner. The simulated ΔP values of the initial and optimized designs of the damper valve were 0.51 and 0.704, respectively, while the target range of ΔP was 0.5–1 MPa. Despite the ΔP of the initial damper valve meeting the design requirements, its value was close to the lower limit of the target range and was less desirable than the value expected by the designers. The ΔP of the optimized damper valve was close to the middle value of the target range. A comparison showed that the ΔP of the optimized valve was better than that of the initial design of the valve. Using ΔP = 0.75 MPa as a reference, the error in ΔP of the initial valve design was 32%, while that of the optimized valve decreased to 6.13%. The simulated FZ values of the initial and optimized valve designs were 116.33 N and 110.005 N, respectively, while the target range was ≤110 N. The FZ of the optimized valve was improved compared with that of the initial valve design. The error in FZ for the initial design was 0.28%, while that of the optimized valve decreased to a negligible level of 0.0045%. It was noteworthy that DA, DB, and DC depended on the drill bit sizes used in actual manufacturing and, thus, could not be designed to the exact dimensions yielded using the multi-objective optimization. This was a major reason for the difference between the simulated and required target values.
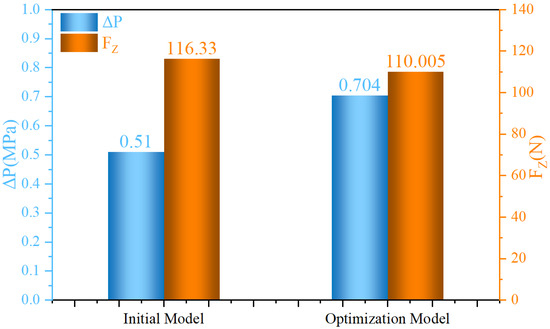
Figure 8.
ΔP and FZ of the initial and optimized valve designs at Q = 70 L/min.
Figure 9 shows the nephogram of the flow field in the optimized damper valve. A comparison of Figure 9a and Figure 4b showed that the numerically simulated ΔP and FZ were closer to the target ΔP and FZ desired for engineering applications. Additionally, the stress distribution in the flow field changed significantly. The reason for this was that the DA and DB of the optimized valve were smaller than those of the initial design. Additionally, as revealed by the simulation results provided in Section 3.2, ΔP increased as DA and DB decreased. It was also noteworthy that significant turbulence occurred at the outlet and in the central chamber of the valve. This was because of the geometric structure of the valve. Figure 9c is highly consistent with Figure 9a,b. The flow velocity near the outlet was low, which indicated that the damper valve had a strong damping effect.

Figure 9.
Nephogram of the flow field of the optimized valve. (a): Nephogram of the stress distribution in the central plane of the flow field; (b): streamlines of the flow field in the damper valve; and (c): path lines of the flow field in the damper valve.
This section describes how an orthogonal simulation experiment was performed using the simulation model to meet the design objective. Next, multi-objective optimization was performed by establishing response surfaces. Finally, a configuration of the hole diameters of the damper valve that met the requirements for actual automobile applications was determined. The optimization results were verified using simulation calculations. Figure 9 displays the results. The optimization results showed that the simulated results of the optimization model were good, the simulated results were largely consistent with the target values, and the numerically simulated flow field was acceptable. This provides an effective reference for the future development of hydropneumatic springs. In addition, we plan to investigate the effects of the parameters not explored in this study (such as the sectional length, length-to-diameter ratio, and number of holes) on the performance of the damper valves.
4. Conclusions
The inlet–outlet pressure drop and spool axial force of a hydropneumatic spring damper valve for heavy vehicle applications were investigated using a fluid–solid coupling method. The objective was to optimize these two parameters to meet design expectations. This work helps lay a foundation for the further design and optimization of damper valves and provides a reference for future redevelopment. Our results are summarized as follows:
(1) With the diameters of the damping holes held constant, the inlet–outlet pressure drop of the damper valve increased quasi-quadratically and nonlinearly with the inlet flow rate. For a given inlet flow rate, the inlet–outlet pressure drop of the damper valve increased nonlinearly with the diameters of the holes. In particular, the diameter of hole B had the greatest effect on the inlet–outlet pressure drop, while DC had the smallest effect on the inlet–outlet pressure drop. The different effects were due to the different locations of the holes.
(2) When the diameters of the damping holes were held constant, the spool axial force increased quasi-quadratically and nonlinearly with the flow rate. For a given inlet flow rate, the spool axial force increased nonlinearly as DA increased, decreased nonlinearly as DB increased, and fluctuated as DC increased. In particular, DB had the greatest effect on the spool axial force, while DC had the smallest effect on the spool axial force. Similarly, the different effects were due to the different locations of the holes.
(3) Multi-objective optimization of the valve was performed against the actual engineering requirements using response surface methodology. The results showed that the design expectations were satisfied when DA, DB, and DC were set to 8.8 mm, 5.55 mm, and 6 mm, respectively. Using an inlet–outlet pressure drop of 0.75 MPa as a reference, the error in ΔP for the initial valve design was 32%, while that of the optimized valve decreased to 6.13%. The error in FZ of the initial valve design was 0.28%, while that of the optimized valve decreased to 0.0045%.
This study had limitations. A small range of Q values was investigated. Overall, this study was focused on low flow-rate, closure operating conditions. The high flow-rate, opening operating conditions, and circulation flow of the damper valve were not investigated. We plan to investigate these topics in future work, especially the flow field in the damper valve in high flow-rate operating conditions and its failure under high flow-velocity operating conditions.
Author Contributions
Formal analysis, C.W.; Methodology, W.N.; Project administration, W.N.; Software, W.N. and L.S.; Validation, W.N. and L.S.; Writing—original draft, W.N. and H.H.; Writing—review and editing, W.N., H.H., L.S., C.W. and F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Interested parties may contact the corresponding author with inquiries.
Acknowledgments
Thanks to all those who made suggestions during the writing stage of this manuscript.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Appendix A
Governing Equation of Flow
In the inertial coordinate system, the conservation of momentum equation in the i-direction can be described as:
where p is the static pressure, ρgi and Fi are the gravitational and other body forces (other body forces may originate from the interaction between the two and may include other model source terms or user-defined source terms), and τij is the stress tensor, which is defined as:
The nonconservative partial differential equation of the continuity equation and the Navier-Stokes equation in the x-direction can be expressed as:
where ∇⋅V is the divergence of the velocity.
The incompressible Navier-Stokes equation can be obtained by designating the density ρ in the above compressive Navier-Stokes equation as a constant. Because ρ is a constant, Equation (A3) can be rewritten as:
For incompressible flow,
Thus,
The following equation can be obtained by deriving the above equation with respect to x:
By adding to both sides of the equation and multiplying both sides with μ, the following equation can be obtained:
By substituting for the second term on the right side of Equation (A4) with Equation (A9) and expanding other terms of Equation (A4), the following equation can be obtained:
By canceling the corresponding positive and negative terms in the above equation, the equation of the momentum in the x-direction of incompressible viscous flow can be simplified as:
which can be further simplified as:
where ∇2u is the Laplacian of the x-direction component of the velocity u.
Thus, the incompressible Navier-Stokes equation can be expressed as:
where j is u, v, or w, and i is x, y, or z.
The standard k-ε model assumes that the flow is completely turbulent and the viscosity between molecules is negligible. The turbulent kinetic energy and dissipation rate of the standard k-ε model are calculated using the following equations:
where Gk is the turbulent kinetic energy produced by the average velocity gradient, Gb is the turbulent kinetic energy produced by the buoyancy, YM is the effect of the pulse expansion of the compressible turbulence on the total dissipation rate, and is the viscosity coefficient of the turbulence.
References
- Xie, F.; Shi, X.; Cao, J.; Ding, Z.; Yu, C.; Gao, Y. Research on Damping Contribution Rate of Key Parameters of Valve-Controlled Damping Adjustable Damper. Front. Energy Res. 2022, 10, 854529. [Google Scholar] [CrossRef]
- Giliomee, C.L.; Els, P.S. Semi-active hydropneumatic spring and damper system. J. Terramech. 1998, 2, 109–117. [Google Scholar] [CrossRef]
- Saxon, N.L.; Meldrum, W.R. Semiactive Suspension: A field Testing Case Study. SAE Tech. Pap. 1998, 107, 23–26. [Google Scholar] [CrossRef]
- Theron, N.J.; Els, P.S. Modelling of a semi-active hydropneumatic spring-damper unit. Int. J. Veh. Des. 2007, 4, 501–521. [Google Scholar] [CrossRef]
- Dejun, Z. Study on Vertical and Lateral Dynamic Performances of Vehicle with Active Hydropneumatic Suspension. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2007. [Google Scholar]
- Xiaowei, L.; Junwu, S.; Jianwu, Z. Feedback Linearization and PID Control for Active Hydro-Pneumatic Suspension. J. Shanghai Jiaotong Univ. 2009, 43, 1521–1525. [Google Scholar]
- Yuzhuang, Z.; Sizhong, C. Investigation of Sliding Mode Control for Semi-Active Hydro-Pneumatic Suspension Based on A Full Vehicle Model. Trans. Beijing Inst. Technol. 2011, 10, 1168–1173. [Google Scholar]
- Skrickij, V.; Savitski, D.; Ivanov, V.; Skačkauskas, P. Investigation of Cavitation Process in Monotube Shock Absorber. Int. J. Automot. Technol. 2018, 19, 801–810. [Google Scholar] [CrossRef]
- Karpenko, M.; Nugaras, J. Vibration Damping Characteristics of the Cork-Based Composite Material in Line to Frequency Analysis. J. Theor. Appl. Mech. 2022, 60, 593–602. [Google Scholar] [CrossRef]
- Vaughan, N.D.; Johnston, D.N.; Edge, K.A. Numerical Simulation of Fluid Flow in Poppet Valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1992, 206, 119–126. [Google Scholar] [CrossRef]
- Sibilla, S.; Gallati, M. Hydrodynamic characterization of a nozzle check valve by numerical simulation. J. Fluids Eng. 2009, 130, 121101–121112. [Google Scholar] [CrossRef]
- Halimi, B.; Kim, S.H.; Suh, K.Y. Engineering of combined valve flow for power conversion system. Energy Convers. Manag. 2013, 65, 448–455. [Google Scholar] [CrossRef]
- Wu, D.; Li, S.; Wu, P. CFD simulation of flow-pressure characteristics of a pressure control valve for automotive fuel supply system. Energy Convers. Manag. 2015, 101, 658–665. [Google Scholar] [CrossRef]
- Asim, T.; Charlton, M.; Mishra, R. CFD based investigations for the design of severe service control valves used in energy systems. Energy Convers. Manag. 2017, 153, 288–303. [Google Scholar] [CrossRef]
- Morita, R.; Inada, F.; Mori, M.; Tezuka, K.; Tsujimoto, Y. CFD Simulations and Experiments of Flow Fluctuations Around a Steam Control Valve. J. Fluids Eng. 2008, 129, 48–54. [Google Scholar] [CrossRef]
- Lisowski, E.; Czyżycki, W.; Rajda, J. Three dimensional CFD analysis and experimental test of flow force acting on the spool of solenoid operated directional control valve. Energy Convers. Manag. 2013, 70, 220–229. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Pressure compensation using flow forces in a multi-section proportional directional control valve. Energy Convers. Manag. 2015, 103, 1052–1064. [Google Scholar] [CrossRef]
- Lai, Z.; Karney, B.; Yang, S.; Wu, D.; Zhang, F. Transient performance of a dual disc check valve during the opening period. Ann. Nucl. Energy 2016, 101, 15–22. [Google Scholar] [CrossRef]
- Saha, B.K.; Chattopadhyay, H.; Mandal, P.B.; Gangopadhyay, T. Dynamic simulation of a pressure regulating and shut-off valve. Comput. Fluids 2014, 101, 233–240. [Google Scholar] [CrossRef]
- Song, X.; Cui, L.; Cao, M.; Cao, W.; Park, Y.; Dempster, W. A CFD analysis of the dynamics of a direct-operated safety relief valve mounted on a pressure vessel. Energy Convers. Manag. 2014, 81, 407–419. [Google Scholar] [CrossRef]
- Ma, Y.; Luo, H.; Zhang, Z.; Zhou, S.; Deng, H. Numerical modeling of dynamic characterics for combined valves in multiphase pump. Eng. Appl. Comput. Fluid Mech. 2017, 11, 328–339. [Google Scholar] [CrossRef]
- Kim, N.-S.; Jeong, Y. An investigation of pressure build-up effects due to check valve’s closing characteristics using dynamic mesh techniques of CFD. Ann. Nucl. Energy 2021, 152, 107996. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Duan, Y.; Jackson, C.; Eaton, M.D.; Bluck, M.J. An assessment of eddy viscosity models on predicting performance parameters of valves. Nucl. Eng. Des. 2019, 342, 60–77. [Google Scholar] [CrossRef]
- Jie, J.; Zhijun, S.; Tao, Y.; Xi, W.; Kexin, R.; Lieyi, D.; Wanyou, L.; Chenxing, J. Research on stability characteristics of a spring-loaded valve with two outlets. Ann. Nucl. Energy 2022, 175, 109250. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).