Logistic Model Tree Forest for Steel Plates Faults Prediction
Abstract
1. Introduction
- (i)
- This article proposes a new ensemble technique, entitled the logistic model tree forest (LMT forest).
- (ii)
- Our work is original in the literature since it contributes to building decision trees based on the LMT method to construct a forest for steel plate fault prediction.
- (iii)
- The study is also original in that it applies the edited nearest neighbor under-sampling approach to the dataset before detecting steel plate faults.
- (iv)
- In the experiments, the proposed LMT forest method with an accuracy of 86.655% outperformed the random forest method with an accuracy of 79.547% on the same dataset.
- (v)
2. Related Works
2.1. Machine Learning-Based Fault Prediction
2.2. Steel Plate Fault Prediction
2.3. The Application of the LMT Algorithm
3. Material and Methods
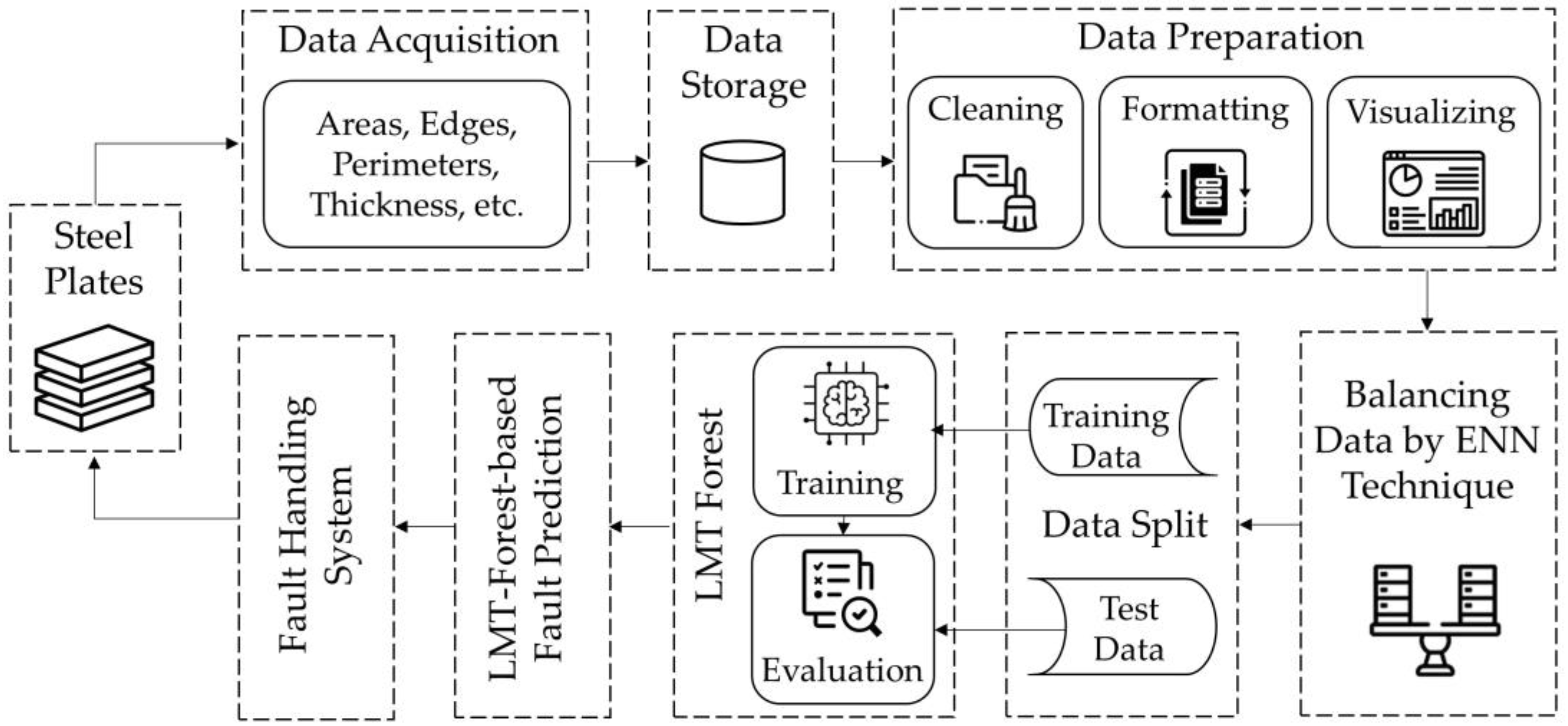
3.1. The Proposed Model Architecture
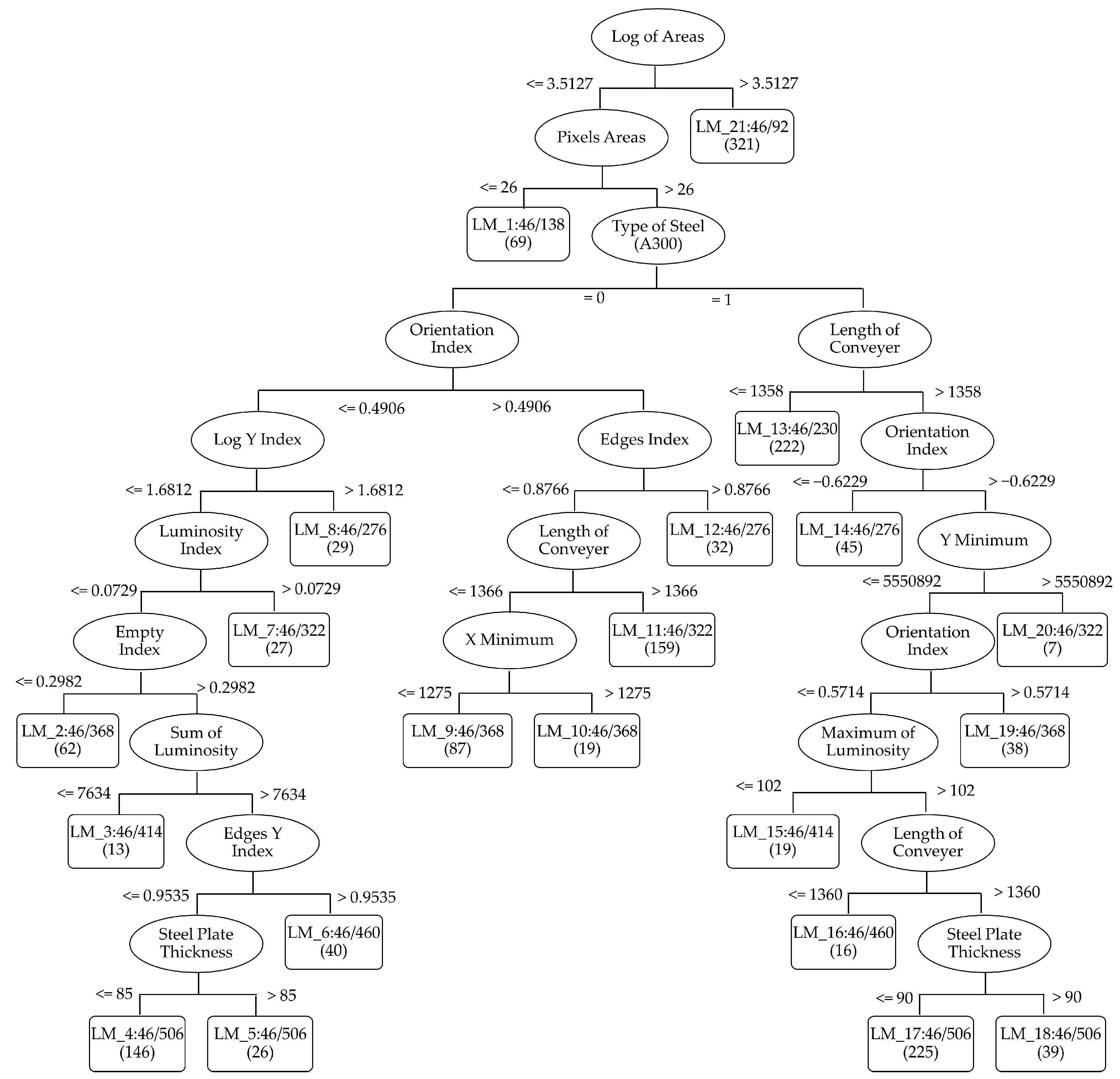
3.2. The Proposed Method: LMT Forest
- Since LMT forest is an ensemble learning approach, it tends to achieve a better accuracy value than a single LMT model. Although some classifiers in the ensemble produce incorrect outputs, other classifiers may have the ability to correct these errors.
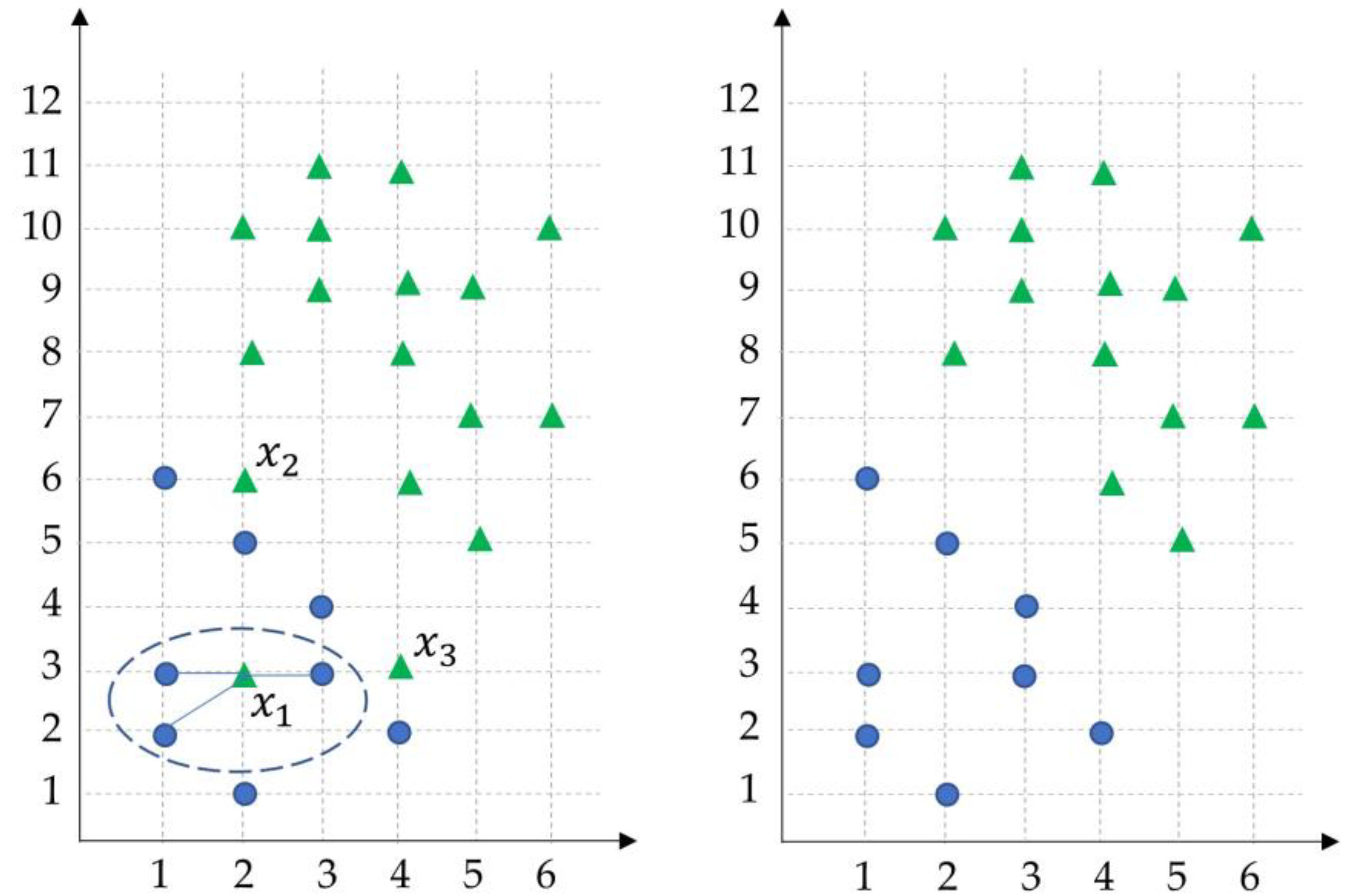
- As it is known, imbalanced datasets refer to classes with unequal observations. In other words, if the number of samples of a class is much higher than the others in a dataset. Imbalanced data make fault prediction models biased toward the majority of cases, resulting in the misclassification of the minority of cases. Our method provides a way to prevent class imbalance by using ENN; thus, it can successfully learn from cases belonging to all classes during the training stage.
- Another advantage of LMT forest is that it can be easily parallelized when it is needed. The algorithm is suitable for parallel and distributed environments.
- The other advantage of LMT forest is its implementation simplicity. It is mainly an ensemble-learning approach that contains several decision trees in a special manner.
- Inspired by the appealing structure of decision tree-based and logistic regression-based models, LMT forest is an interpretable and transparent approach, benefitting from explainable artificial intelligence (XAI). On the other hand, a deep learning (DL) model is difficult to interpret and explain because the composition of layers acts as a black box. In addition, variable selection is not easily possible since DL models solve feature engineering internally in a non-transparent way. Another drawback of DL is the high computational cost required to efficiently learn models since it has a large number of hyperparameters.
- One of the primary advantages of the presented method is that it is designed to apply to any type of data that is appropriate for the classification task. It does not require background or prior information about the given dataset. Therefore, it can be applied to different areas such as health, education, environment, and transportation.
3.3. Theoretical Expression
| Algorithm 1 Logistic Model Tree Forest. |
| Inputs: |
| e: ensemble size |
| k: the number of neighbors |
| T: testing set for classification |
| Output: |
| C: predicted fault types |
| Begin: |
| end if |
| else |
| end if |
| end for |
| for i = 1 to e do |
| Di = Bootstrap(O) |
| Hi = LMT(Di) |
| end for |
| foreach x in T |
| end foreach |
| End Algorithm |
3.4. Dataset Description
4. Experiments
4.1. Experimental Design
- True positive (TP) defines the number of positive classes, which are predicted correctly by the classifier.
- True negative (TN) defines the number of negative classes, which are predicted correctly by the classifier.
- False positive (FP) defines the number of positive classes, which are predicted incorrectly by the classifier.
- False negative (FN) defines the number of negative classes, which are predicted incorrectly by the classifier.
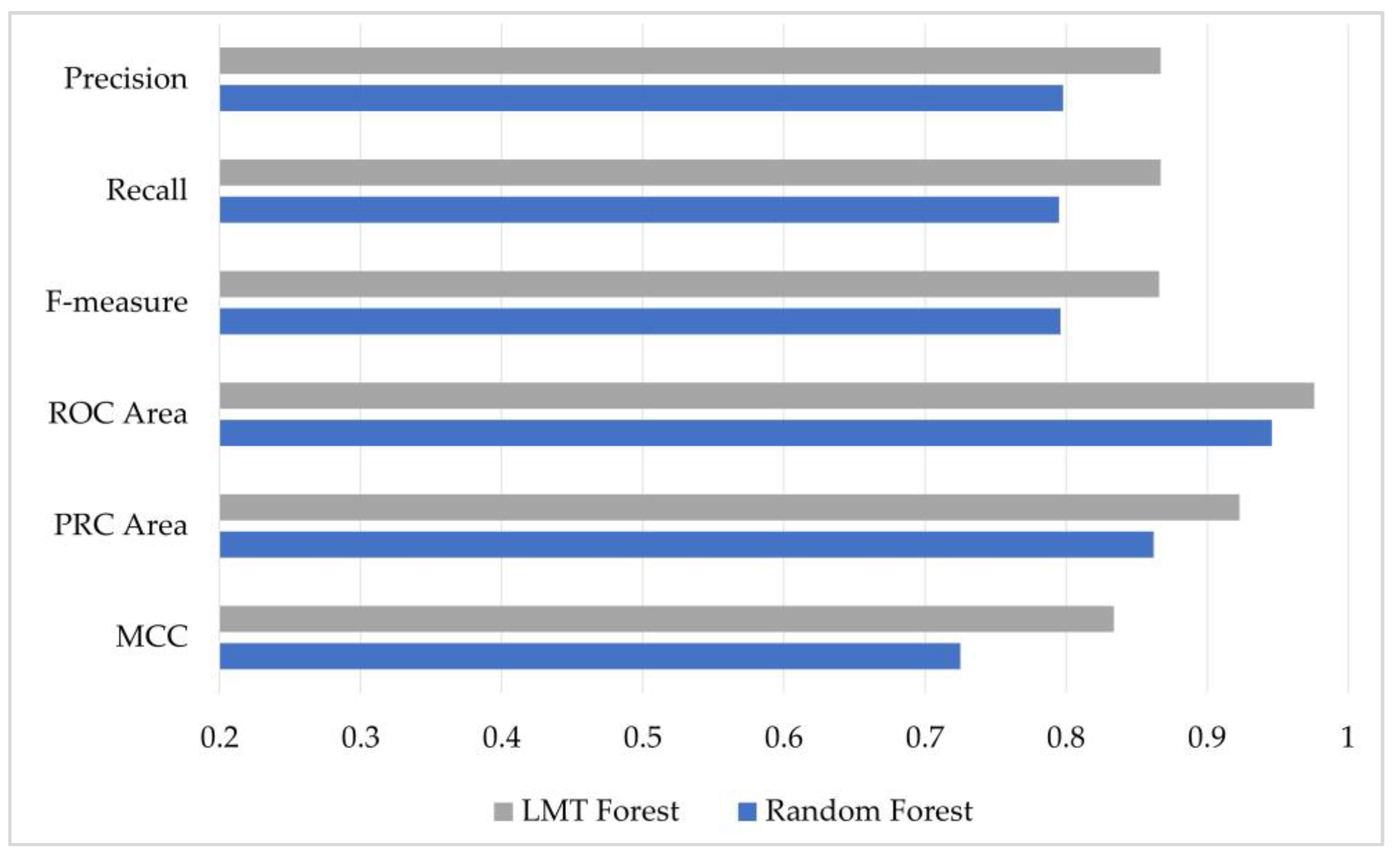
4.2. Experimental Results
4.3. Comparison with the State-of-the-Art Methods
5. Conclusions and Future Works
- LMT forest integrates decision tree and logistic regression approaches to profit from the benefits of both techniques.
- In this study, it was revealed that the ensemble of classifiers instead of a single classifier could attain better performance.
- Different ensemble sizes of 1 to 100 with 10 intervals were tested, and finally, we decided on 60 trees, since after that the accuracy began to decrease slightly.
- The confusion matrix showed that each fault type was distinguished with high accuracy; however, the pastry fault was slightly confused with other fault types by the algorithm.
- According to the results of the Pearson correlation method, the “Log X Index” and “Log of Areas” variables are the most essential features in the decision-making process.
- The superiority of the proposed LMT forest method (86.65%) over the well-known random forest method (79.547%) was approved on the same dataset.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural networks |
| ARIMA | Auto-regressive integrated moving average |
| AUC | Area under curve |
| BSFRS | Bi-selection method based on fuzzy rough sets |
| CART | Classification and regression tree |
| CNN | Convolutional neural networks |
| DAS | Data acquisition system |
| DL | Deep learning |
| DS | Dempster–Shafer |
| ELA | Extended decision label annotation |
| ENN | Edited nearest neighbor |
| FCM-LSE | Fuzzy c-means-least squares estimation |
| GA-BPNN | Genetic algorithm back propagation neural network |
| GBDT | Gradient boosting decision tree |
| GPR | Gaussian process regression |
| IGO | Information gain |
| IoT | Internet of Things |
| KNN | K-nearest neighbors |
| LMT | Logistic model tree |
| LR | Logistic regression |
| LS-SVR | Least squares support vector regression |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MCC | Matthews correlation coefficient |
| MG-SVM | Medium Gaussian support vector machine |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| mRMR | Minimal-redundancy-maximal-relevance |
| NB | Naive Bayes |
| NEC | Neighborhood classifier |
| NMSE | Normalized mean square error |
| NN | Neural network |
| OAO-SVM | One-against-one strategy and support vector machines |
| PCA | Principal component analysis |
| PDTF | Principal component analysis-based decision tree forest |
| PRC | Precision-recall |
| QDC | Quadratic Bayesian classifier |
| QPSO-BP | Quantum particle swarm optimization backpropagation |
| RBFC | Radial basis function classifier |
| RF | Random forest |
| RFE | Recursive feature elimination |
| RMSE | Root mean square error |
| RNN | Recurrent neural networks |
| ROC | Receiver operating characteristic |
| RSRE | Robust sparse feature selection with redundancy elimination |
| RUL | Remaining useful life |
| SCADA | Supervisory control and data acquisition |
| SMOTE | Synthetic minority oversampling technique |
| SN | Sine network |
| SVM | Support vector machine |
| UAV | Unmanned aerial vehicle |
| WEKA | Waikato environment for knowledge analysis |
| XAI | Explainable artificial intelligence |
| XGBoost | Extreme gradient boosting |
References
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef]
- Kamali Maskooni, E.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R. Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sens. 2020, 12, 2742. [Google Scholar] [CrossRef]
- Debnath, P.; Chittora, P.; Chakrabarti, T.; Chakrabarti, P.; Leonowicz, Z.; Jasinski, M.; Gono, R.; Jasińska, E. Analysis of Earthquake Forecasting in India Using Supervised Machine Learning Classifiers. Sustainability 2021, 13, 971. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Optimization of Computational Intelligence Models for Landslide Susceptibility Evaluation. Remote Sens. 2020, 12, 2180. [Google Scholar] [CrossRef]
- Davis, J.D.; Wang, S.; Festa, E.K.; Luo, G.; Moharrer, M.; Bernier, J.; Ott, B.R. Detection of Risky Driving Behaviors in the Naturalistic Environment in Healthy Older Adults and Mild Alzheimer’s Disease. Geriatrics 2018, 3, 13. [Google Scholar] [CrossRef]
- Lee, S.-W.; Kung, H.-C.; Huang, J.-F.; Hsu, C.-P.; Wang, C.-C.; Wu, Y.-T.; Wen, M.-S.; Cheng, C.-T.; Liao, C.-H. The Clinical Application of Machine Learning-Based Models for Early Prediction of Hemorrhage in Trauma Intensive Care Units. J. Pers. Med. 2022, 12, 1901. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Bueno, F.; Loján-Córdova, J. Assessment of Three Machine Learning Techniques with Open-Access Geographic Data for Forest Fire Susceptibility Monitoring—Evidence from Southern Ecuador. Forests 2022, 13, 474. [Google Scholar] [CrossRef]
- Han, J.; Nur, A.S.; Syifa, M.; Ha, M.; Lee, C.-W.; Lee, K.-Y. Improvement of Earthquake Risk Awareness and Seismic Literacy of Korean Citizens through Earthquake Vulnerability Map from the 2017 Pohang Earthquake, South Korea. Remote Sens. 2021, 13, 1365. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Geertsema, M.R.; Kress, V.; Karimzadeh, S.; Valizadeh Kamran, K.; et al. Landslide Detection and Susceptibility Modeling on Cameron Highlands (Malaysia): A Comparison between Random Forest, Logistic Regression and Logistic Model Tree Algorithms. Forests 2020, 11, 830. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J.; et al. Shallow Landslide Susceptibility Mapping: A Comparison between Logistic Model Tree, Logistic Regression, Naïve Bayes Tree, Artificial Neural Network, and Support Vector Machine Algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef]
- Pham, B.T.; Phong, T.V.; Nguyen, H.D.; Qi, C.; Al-Ansari, N.; Amini, A.; Ho, L.S.; Tuyen, T.T.; Yen, H.P.H.; Ly, H.-B.; et al. A Comparative Study of Kernel Logistic Regression, Radial Basis Function Classifier, Multinomial Naïve Bayes, and Logistic Model Tree for Flash Flood Susceptibility Mapping. Water 2020, 12, 239. [Google Scholar] [CrossRef]
- Charton, E.; Meurs, M.-J.; Jean-Louis, L.; Gagnon, M. Using Collaborative Tagging for Text Classification: From Text Classification to Opinion Mining. Informatics 2014, 1, 32–51. [Google Scholar] [CrossRef]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Tan, N.P.; Ismail, M.F. Synthetic Minority Over-Sampling TEchnique (SMOTE) and Logistic Model Tree (LMT)-Adaptive Boosting Algorithms for Classifying Imbalanced Datasets of Nutrient and Chlorophyll Sufficiency Levels of Oil Palm (Elaeis Guineensis) Using Spectroradiometers and Unmanned Aerial Vehicles. Comput. Electron. Agric. 2022, 193, 106646. [Google Scholar] [CrossRef]
- Wang, L.; You, Z.-H.; Chen, X.; Li, Y.-M.; Dong, Y.-N.; Li, L.-P.; Zheng, K. LMTRDA: Using Logistic Model Tree to Predict MiRNA-Disease Associations by Fusing Multi-Source Information of Sequences and Similarities. PLoS Comput. Biol. 2019, 15, e1006865. [Google Scholar] [CrossRef]
- Kabir, E.; Siuly; Zhang, Y. Epileptic Seizure Detection from EEG Signals Using Logistic Model Trees. Brain Inf. 2016, 3, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.-H.; Yang, J.-H.; Liu, P.-C. Rule-Based Classifier Based on Accident Frequency and Three-Stage Dimensionality Reduction for Exploring the Factors of Road Accident Injuries. PLoS ONE 2022, 17, e0272956. [Google Scholar] [CrossRef] [PubMed]
- Jha, S.K.; Ahmad, Z. An Effective Feature Generation and Selection Approach for Lymph Disease Recognition. Comp. Model. Eng. Sci. 2021, 129, 567–594. [Google Scholar] [CrossRef]
- Ayyappan, G.; Babu, R.V. Knowledge Construction on NIV of COVID-19 for Managing the Patients by ML Techniques. Indian J. Comput. Sci. Eng. 2023, 14, 117–129. [Google Scholar] [CrossRef]
- Gorka, M.; Thomas, A.; Bécue, A. Differentiating Individuals through the Chemical Composition of Their Fingermarks. Forensic Sci. Int. 2023, 346, 111645. [Google Scholar] [CrossRef]
- Shu, W.; Yan, Z.; Yu, J.; Qian, W. Information Gain-Based Semi-Supervised Feature Selection for Hybrid Data. Appl. Intell. 2022, 53, 7310–7325. [Google Scholar] [CrossRef]
- Agrawal, L.; Adane, D. Ensembled Approach to Heterogeneous Data Streams. Int. J. Next Gener. Comput. 2022, 13, 1014–1020. [Google Scholar] [CrossRef]
- Ju, H.; Ding, W.; Shi, Z.; Huang, J.; Yang, J.; Yang, X. Attribute Reduction with Personalized Information Granularity of Nearest Mutual Neighbors. Inf. Sci. 2022, 613, 114–138. [Google Scholar] [CrossRef]
- Zhang, X.; Mei, C.; Li, J.; Yang, Y.; Qian, T. Instance and Feature Selection Using Fuzzy Rough Sets: A Bi-Selection Approach for Data Reduction. IEEE Trans. Fuzzy Syst. 2022, 31, 1–15. [Google Scholar] [CrossRef]
- Mohamed, R.; Samsudin, N.A. An Optimized Discretization Approach Using K-Means Bat Algorithm. Turk. J. Comput. Math. Educ. 2021, 12, 1842–1851. [Google Scholar] [CrossRef]
- Nkonyana, T.; Sun, Y.; Twala, B.; Dogo, E. Performance Evaluation of Data Mining Techniques in Steel Manufacturing Industry. Procedia Manuf. 2019, 35, 623–628. [Google Scholar] [CrossRef]
- Srivastava, A.K. Comparison analysis of machine learning algorithms for steel plate fault detection. Int. Res. J. Eng. Technol. 2019, 6, 1231–1234. [Google Scholar]
- Mohamed, R.; Yusof, M.M.; Wahid, N.; Murli, N.; Othman, M. Bat Algorithm and K-Means Techniques for Classification Performance Improvement. Indones. J. Electr. Eng. Comput. Sci. 2019, 15, 1411. [Google Scholar] [CrossRef]
- Mary, D. Constructing optimized Neural Networks using Genetic Algorithms and Distinctiveness. In Proceedings of the 1st ANU Bio-inspired Computing Conference (ABCs 2018), Canberra, Australia, 20 July 2018; pp. 1–8. [Google Scholar]
- Zhang, X.; Mei, C.; Chen, D.; Yang, Y. A Fuzzy Rough Set-Based Feature Selection Method Using Representative Instances. Knowl.-Based Syst. 2018, 151, 216–229. [Google Scholar] [CrossRef]
- Thirukovalluru, R.; Dixit, S.; Sevakula, R.K.; Verma, N.K.; Salour, A. Generating Feature Sets for Fault Diagnosis Using Denoising Stacked Auto-Encoder. In Proceedings of the IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Halawani, S.M. A study of decision tree ensembles and feature selection for steel plates faults detection. Int. J. Tech. Res. Appl. 2014, 2, 127–131. [Google Scholar]
- Buscema, M.; Tastle, W.J. A New Meta-Classifier. In Proceedings of the Annual Meeting of the North American Fuzzy Information Processing Society, Toronto, ON, Canada, 12–14 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Ma, L.; Jiang, H.; Ma, T.; Zhang, X.; Shen, Y.; Xia, L. Fault Prediction of Rolling Element Bearings Using the Optimized MCKD–LSTM Model. Machines 2022, 10, 342. [Google Scholar] [CrossRef]
- Xu, Q.; Jiang, H.; Zhang, X.; Li, J.; Chen, L. Multiscale Convolutional Neural Network Based on Channel Space Attention for Gearbox Compound Fault Diagnosis. Sensors 2023, 23, 3827. [Google Scholar] [CrossRef]
- Pollak, A.; Temich, S.; Ptasiński, W.; Kucharczyk, J.; Gąsiorek, D. Prediction of Belt Drive Faults in Case of Predictive Maintenance in Industry 4.0 Platform. Appl. Sci. 2021, 11, 10307. [Google Scholar] [CrossRef]
- Glowacz, A. Thermographic Fault Diagnosis of Shaft of BLDC Motor. Sensors 2022, 22, 8537. [Google Scholar] [CrossRef] [PubMed]
- Javed, M.R.; Shabbir, Z.; Asghar, F.; Amjad, W.; Mahmood, F.; Khan, M.O.; Virk, U.S.; Waleed, A.; Haider, Z.M. An Efficient Fault Detection Method for Induction Motors Using Thermal Imaging and Machine Vision. Sustainability 2022, 14, 9060. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Zhao, F.; Zhang, E.; Wu, Z.; Shao, L. Surface Defect Detection Methods for Industrial Products: A Review. Appl. Sci. 2021, 11, 7657. [Google Scholar] [CrossRef]
- Çınar, Z.M.; Abdussalam Nuhu, A.; Zeeshan, Q.; Korhan, O.; Asmael, M.; Safaei, B. Machine Learning in Predictive Maintenance towards Sustainable Smart Manufacturing in Industry 4.0. Sustainability 2020, 12, 8211. [Google Scholar] [CrossRef]
- Shim, J.; Kang, S.; Cho, S. Active Inspection for Cost-Effective Fault Prediction in Manufacturing Process. J. Process Control 2021, 105, 250–258. [Google Scholar] [CrossRef]
- Fernandes, M.; Corchado, J.M.; Marreiros, G. Machine Learning Techniques Applied to Mechanical Fault Diagnosis and Fault Prognosis in the Context of Real Industrial Manufacturing Use-Cases: A Systematic Literature Review. Appl. Intell. 2022, 52, 14246–14280. [Google Scholar] [CrossRef] [PubMed]
- Uppal, M.; Gupta, D.; Juneja, S.; Dhiman, G.; Kautish, S. Cloud-Based Fault Prediction Using IoT in Office Automation for Improvisation of Health of Employees. J. Healthcare Eng. 2021, 2021, 8106467. [Google Scholar] [CrossRef]
- Kosuru, V.S.R.; Kavasseri Venkitaraman, A. A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electr. Veh. J. 2023, 14, 101. [Google Scholar] [CrossRef]
- Gong, L.; Liu, B.; Fu, X.; Jabbari, H.; Gao, S.; Yue, W.; Yuan, H.; Fu, R.; Wang, Z. Quantitative Prediction of Sub-Seismic Faults and Their Impact on Waterflood Performance: Bozhong 34 Oilfield Case Study. J. Pet. Sci. Eng. 2019, 172, 60–69. [Google Scholar] [CrossRef]
- Dashti, R.; Daisy, M.; Mirshekali, H.; Shaker, H.R.; Hosseini Aliabadi, M. A Survey of Fault Prediction and Location Methods in Electrical Energy Distribution Networks. Measurement 2021, 184, 109947. [Google Scholar] [CrossRef]
- Carrera, Á.; Alonso, E.; Iglesias, C.A. A Bayesian Argumentation Framework for Distributed Fault Diagnosis in Telecommunication Networks. Sensors 2019, 19, 3408. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Zhao, J. A Novel Transformer-Based Multi-Variable Multi-Step Prediction Method for Chemical Process Fault Prognosis. Process Saf. Environ. Prot. 2023, 169, 937–947. [Google Scholar] [CrossRef]
- Zhang, P.; Cui, Z.; Wang, Y.; Ding, S. Application of BPNN Optimized by Chaotic Adaptive Gravity Search and Particle Swarm Optimization Algorithms for Fault Diagnosis of Electrical Machine Drive System. Electr. Eng. 2021, 104, 819–831. [Google Scholar] [CrossRef]
- Abro, J.H.; Li, C.; Shafiq, M.; Vishnukumar, A.; Mewada, S.; Malpani, K.; Osei-Owusu, J. Artificial Intelligence Enabled Effective Fault Prediction Techniques in Cloud Computing Environment for Improving Resource Optimization. Sci. Program. 2022, 2022, 1–7. [Google Scholar] [CrossRef]
- Doorwar, A.; Bhalja, B.R.; Malik, O.P. Novel Approach for Synchronous Generator Protection Using New Differential Component. IEEE Trans. Energy Convers. 2022, 38, 180–191. [Google Scholar] [CrossRef]
- Tsioumpri, E.; Stephen, B.; McArthur, S.D.J. Weather Related Fault Prediction in Minimally Monitored Distribution Networks. Energies 2021, 14, 2053. [Google Scholar] [CrossRef]
- Shahbazi, Z.; Byun, Y.-C. Smart Manufacturing Real-Time Analysis Based on Blockchain and Machine Learning Approaches. Appl. Sci. 2021, 11, 3535. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Lin, S.-L. Application of Machine Learning to a Medium Gaussian Support Vector Machine in the Diagnosis of Motor Bearing Faults. Electronics 2021, 10, 2266. [Google Scholar] [CrossRef]
- Jiang, F.; Norlund, P. Seismic attribute-guided automatic fault prediction by deep learning. In Proceedings of the EAGE 2020 Annual Conference Exhibition, Online, 8–11 December 2020; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2020; Volume 2020, pp. 1–5. [Google Scholar] [CrossRef]
- Wang, S.; Si, X.; Cai, Z.; Cui, Y. Structural Augmentation in Seismic Data for Fault Prediction. Appl. Sci. 2022, 12, 9796. [Google Scholar] [CrossRef]
- Li, Y. A Fault Prediction and Cause Identification Approach in Complex Industrial Processes Based on Deep Learning. Comput. Intell. Neurosci. 2021, 2021, 6612342. [Google Scholar] [CrossRef]
- Yang, H.-S.; Kim, Y.-S. Design and Implementation of Machine Learning-Based Fault Prediction System in Cloud Infrastructure. Electronics 2022, 11, 3765. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, D.; Dong, A.; Kang, D.; Lv, Q.; Shang, L. Fault Prediction and Diagnosis of Wind Turbine Generators Using SCADA Data. Energies 2017, 10, 1210. [Google Scholar] [CrossRef]
- Yuan, T.; Sun, Z.; Ma, S. Gearbox Fault Prediction of Wind Turbines Based on a Stacking Model and Change-Point Detection. Energies 2019, 12, 4224. [Google Scholar] [CrossRef]
- Wan, L.; Li, H.; Chen, Y.; Li, C. Rolling Bearing Fault Prediction Method Based on QPSO-BP Neural Network and Dempster–Shafer Evidence Theory. Energies 2020, 13, 1094. [Google Scholar] [CrossRef]
- Yang, J.; Li, J.-D. Fault Prediction Algorithm for Offshore Wind Energy Conversion System Based on Machine Learning. In Proceedings of the International Conference on High Performance Big Data and Intelligent Systems (HPBD&IS), Macau, China, 5–7 December 2021; pp. 291–296. [Google Scholar] [CrossRef]
- Fernandes, S.; Antunes, M.; Santiago, A.R.; Barraca, J.P.; Gomes, D.; Aguiar, R.L. Forecasting Appliances Failures: A Machine-Learning Approach to Predictive Maintenance. Information 2020, 11, 208. [Google Scholar] [CrossRef]
- Tsai, M.-F.; Chu, Y.-C.; Li, M.-H.; Chen, L.-W. Smart Machinery Monitoring System with Reduced Information Transmission and Fault Prediction Methods Using Industrial Internet of Things. Mathematics 2020, 9, 3. [Google Scholar] [CrossRef]
- Syafrudin, M.; Alfian, G.; Fitriyani, N.; Rhee, J. Performance Analysis of IoT-Based Sensor, Big Data Processing, and Machine Learning Model for Real-Time Monitoring System in Automotive Manufacturing. Sensors 2018, 18, 2946. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; Yuan, P.; Wang, S.; Wang, L.; Yuan, Y. A Microgrid Alarm Processing Method Based on Equipment Fault Prediction and Improved Support Vector Machine Learning. J. Phys. Conf. Ser. 2020, 1639, 012041. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Tian, H. Spacecraft in Orbit Fault Prediction Based on Deep Machine Learning. J. Phys. Conf. Ser. 2020, 1651, 012107. [Google Scholar] [CrossRef]
- Haneef, S.; Venkataraman, N. Proactive Fault Prediction of Fog Devices Using LSTM-CRP Conceptual Framework for IoT Applications. Sensors 2023, 23, 2913. [Google Scholar] [CrossRef]
- Orrù, P.F.; Zoccheddu, A.; Sassu, L.; Mattia, C.; Cozza, R.; Arena, S. Machine Learning Approach Using MLP and SVM Algorithms for the Fault Prediction of a Centrifugal Pump in the Oil and Gas Industry. Sustainability 2020, 12, 4776. [Google Scholar] [CrossRef]
- Uppal, M.; Gupta, D.; Juneja, S.; Sulaiman, A.; Rajab, K.; Rajab, A.; Elmagzoub, M.A.; Shaikh, A. Elmagzoub; Luige Vladareanu. Cloud-Based Fault Prediction for Real-Time Monitoring of Sensor Data in Hospital Environment Using Machine Learning. Sustainability 2022, 14, 11667. [Google Scholar] [CrossRef]
- Uppal, M.; Gupta, D.; Mahmoud, A.; Elmagzoub, M.A.; Sulaiman, A.; Reshan, M.S.A.; Shaikh, A.; Juneja, S. Fault Prediction Recommender Model for IoT Enabled Sensors Based Workplace. Sustainability 2023, 15, 1060. [Google Scholar] [CrossRef]
- Elanangai, V.; Vasanth, K. An Automated Steel Plates Fault Diagnosis System Using Adaptive Faster Region Convolutional Neural Network. J. Intell. Fuzzy Syst. 2022, 43, 7067–7079. [Google Scholar] [CrossRef]
- Colkesen, I.; Kavzoglu, T. The Use of Logistic Model Tree (LMT) for Pixel- and Object-Based Classifications Using High-Resolution WorldView-2 Imagery. Geocarto Int. 2016, 32, 71–86. [Google Scholar] [CrossRef]
- Nithya, R.; Santhi, B. Decision Tree Classifiers for Mass Classification. Int. J. Signal Imaging Syst. Eng. 2015, 8, 39. [Google Scholar] [CrossRef]
- Wilson, D.L. Asymptotic Properties of Nearest Neighbor Rules Using Edited Data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Alejo, R.; Sotoca, J.M.; Valdovinos, R.M.; Toribio, P. Edited Nearest Neighbor Rule for Improving Neural Networks Classifications. In Proceedings of the 7th International Symposium on Neural Networks (ISNN 2010), Shanghai, China, 6–9 June 2010; pp. 303–310. [Google Scholar] [CrossRef]
- Oyewola, D.O.; Dada, E.G.; Misra, S.; Damaševičius, R. Predicting COVID-19 Cases in South Korea with All K-Edited Nearest Neighbors Noise Filter and Machine Learning Techniques. Information 2021, 12, 528. [Google Scholar] [CrossRef]
- Blachnik, M.; Kordos, M. Comparison of Instance Selection and Construction Methods with Various Classifiers. Appl. Sci. 2020, 10, 3933. [Google Scholar] [CrossRef]
- Buscema, M. MetaNet: The Theory of Independent Judges. Subst. Use Misuse 1998, 33, 439–461. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Cambridge, MA, USA, 2016; pp. 1–664. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fraihat, H.; Almbaideen, A.A.; Al-Odienat, A.; Al-Naami, B.; De Fazio, R.; Visconti, P. Solar Radiation Forecasting by Pearson Correlation Using LSTM Neural Network and ANFIS Method: Application in the West-Central Jordan. Future Internet 2022, 14, 79. [Google Scholar] [CrossRef]
- Nasir, I.M.; Khan, M.A.; Yasmin, M.; Shah, J.H.; Gabryel, M.; Scherer, R.; Damaševičius, R. Pearson Correlation-Based Feature Selection for Document Classification Using Balanced Training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef]
- Jo, I.; Lee, S.; Oh, S. Improved Measures of Redundancy and Relevance for mRMR Feature Selection. Computers 2019, 8, 42. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily Activity Feature Selection in Smart Homes Based on Pearson Correlation Coefficient. Neural Process. Lett. 2020, 51, 1771–1787. [Google Scholar] [CrossRef]
| Dataset Property | Attribute Property | Task | Instance | Feature | Missing Value | Field | Date | Web Hit |
|---|---|---|---|---|---|---|---|---|
| Multivariate | Integer, Real | Classification | 1941 | 27 | N/A | Physical | 2010 | 111,062 |
| No | Variable Name | Min | Mean | Max | Mode | Standard Deviation |
|---|---|---|---|---|---|---|
| 1 | X Maximum | 4 | 617.9645 | 1713 | 212 | 497.6274 |
| 2 | X Minimum | 0 | 571.1360 | 1705 | 41 | 520.6907 |
| 3 | Y Maximum | 6724 | 1,650,738.7053 | 12,987,692 | 28,984 | 1,774,590 |
| 4 | Y Minimum | 6712 | 1,650,684.8681 | 12,987,661 | 1,803,992 | 1,774,578 |
| 5 | Pixels Areas | 2 | 1893.8784 | 152,655 | 52 | 5168.46 |
| 6 | X Perimeter | 2 | 111.8552 | 10,449 | 12 | 301.2092 |
| 7 | Y Perimeter | 1 | 82.9660 | 18,152 | 11 | 426.4829 |
| 8 | Sum of Luminosity | 250 | 206,312.1479 | 1,1591,414 | 7502 | 512,293.6 |
| 9 | Maximum of Luminosity | 37 | 130.1937 | 253 | 127 | 18.69099 |
| 10 | Minimum of Luminosity | 0 | 84.5487 | 203 | 101 | 32.13428 |
| 11 | Length of Conveyer | 1227 | 1459.1602 | 1794 | 1358 | 144.5778 |
| 12 | Type of Steel (A300) | 0 | 0.4003 | 1 | 0 | 0.490087 |
| 13 | Type of Steel (A400) | 0 | 0.5997 | 1 | 1 | 0.490087 |
| 14 | Steel Plate Thickness | 40 | 78.7378 | 300 | 40 | 55.08603 |
| 15 | Empty Index | 0 | 0.4142 | 0.9439 | 0.3333 | 0.137261 |
| 16 | Edges Index | 0 | 0.3317 | 0.9952 | 0.0604 | 0.299712 |
| 17 | Square Index | 0.0083 | 0.5708 | 1 | 1 | 0.271058 |
| 18 | Outside X Index | 0.0015 | 0.0334 | 0.8759 | 0.0059 | 0.058961 |
| 19 | Edges X Index | 0.0144 | 0.6105 | 1 | 1 | 0.243277 |
| 20 | Edges Y Index | 0.0484 | 0.8135 | 1 | 1 | 0.234274 |
| 21 | Outside Global Index | 0 | 0.5757 | 1 | 1 | 0.482352 |
| 22 | Log of Areas | 0.301 | 2.4924 | 5.1837 | 1.716 | 0.78893 |
| 23 | Log X Index | 0.301 | 1.3357 | 3.0741 | 0.9542 | 0.481612 |
| 24 | Log Y Index | 0 | 1.4033 | 4.2587 | 1.0792 | 0.454345 |
| 25 | Luminosity Index | −0.9989 | −0.1313 | 0.6421 | −0.1851 | 0.148767 |
| 26 | Orientation Index | −0.991 | 0.0833 | 0.9917 | 0 | 0.500868 |
| 27 | Sigmoid of Areas | 0.119 | 0.5854 | 1 | 1 | 0.339452 |
| No | Fault Type | Number of Faults | Proportion of Faults (%) | Class Type |
|---|---|---|---|---|
| 1 | Pastry | 158 | 8.14 | Minority |
| 2 | Z-Scratch | 190 | 9.79 | Minority |
| 3 | K-Scratch | 391 | 20.14 | Moderate |
| 4 | Stains | 72 | 3.71 | Minority |
| 5 | Dirtiness | 55 | 2.83 | Minority |
| 6 | Bumps | 402 | 20.71 | Moderate |
| 7 | Other Faults | 673 | 34.67 | Majority |
| Total Number of Samples | 1941 | |||
| Fold Number | Accuracy (%) | |
|---|---|---|
| Random Forest [81] | LMT Forest (Proposed) | |
| 1 | 77.9487 | 85.4545 |
| 2 | 79.8969 | 85.3659 |
| 3 | 78.8660 | 88.4146 |
| 4 | 81.9588 | 88.4146 |
| 5 | 82.4742 | 85.9756 |
| 6 | 80.4124 | 90.2439 |
| 7 | 80.4124 | 87.1951 |
| 8 | 77.3196 | 84.7561 |
| 9 | 78.8660 | 85.9756 |
| 10 | 77.3196 | 84.7561 |
| Average | 79.547 | 86.655 |
| Number of Trees | Accuracy (%) |
|---|---|
| 1 | 74.858 |
| 10 | 84.887 |
| 20 | 86.106 |
| 30 | 86.106 |
| 40 | 86.472 |
| 50 | 86.472 |
| 60 | 86.655 |
| 70 | 86.533 |
| 80 | 86.594 |
| 90 | 86.289 |
| 100 | 86.228 |
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| A | 107 | 0 | 0 | 0 | 2 | 30 | 19 |
| B | 0 | 176 | 2 | 0 | 0 | 7 | 5 |
| C | 0 | 0 | 376 | 2 | 0 | 5 | 8 |
| D | 0 | 0 | 0 | 66 | 0 | 3 | 3 |
| E | 2 | 0 | 0 | 0 | 49 | 3 | 1 |
| F | 20 | 4 | 3 | 3 | 6 | 334 | 32 |
| G | 13 | 2 | 6 | 1 | 1 | 36 | 314 |
| Feature | Score | Feature | Score | Feature | Score |
|---|---|---|---|---|---|
| Log X Index | 0.3064 | Log Y Index | 0.2359 | Orientation Index | 0.1678 |
| Log of Areas | 0.3020 | Minimum of Luminosity | 0.2246 | Empty Index | 0.1569 |
| Type of Steel (A300) | 0.2819 | X Maximum | 0.2190 | Outside Global Index | 0.1368 |
| Type of Steel (A400) | 0.2819 | Length of Conveyer | 0.2144 | Edges X Index | 0.1326 |
| Edges Y Index | 0.2772 | Sigmoid of Areas | 0.2140 | Maximum of Luminosity | 0.1138 |
| Sum of Luminosity | 0.2699 | Edges Index | 0.2009 | Luminosity Index | 0.1065 |
| Outside X Index | 0.2655 | X Perimeter | 0.1938 | Y Perimeter | 0.0868 |
| X Minimum | 0.2475 | Steel Plate Thickness | 0.1823 | Y Maximum | 0.0857 |
| Pixels Areas | 0.2430 | Square Index | 0.1762 | Y Minimum | 0.0857 |
| Reference | Year | Method | Accuracy (%) |
|---|---|---|---|
| Shu et al. [20] | 2023 | Support vector machines with extended decision label annotation (ELA) | 77.53 |
| C4.5 with extended decision label annotation (ELA) | 75.42 | ||
| Agrawal and Adane [21] | 2022 | Long short-term memory (LSTM) | 75.62 |
| Random forest (RF) | 76.11 | ||
| Principal component analysis-based decision tree forest (PDTF) | 75.19 | ||
| Improved PDTF (I-PDTF) | 76.09 | ||
| Ju et al. [22] | 2022 | Radial base function-based support vector machine (RBF-SVM) | 62.80 |
| Classification and regression trees (CARTs) | 62.99 | ||
| Neighborhood classifier (NEC) | 65.68 | ||
| Zhang et al. [23] | 2022 | Bi-selection method based on fuzzy rough sets (BSFRSs) | 69.18 |
| Central density-based instance selection MQRWA (CDIS-MQRWA) | 71.14 | ||
| Edited nearest neighbor MQRWA (ENN-MQRWA) | 73.72 | ||
| Mohamed and Samsudin [24] | 2021 | Naive Bayes | 69.20 |
| K-nearest neighbors (KNNs) | 71.80 | ||
| Decision tree (DT) | 75.10 | ||
| Nkonyana et al. [25] | 2019 | Random forest | 77.80 |
| Support vector machines (SVMs) | 73.60 | ||
| Artificial neural network (ANN) | 69.60 | ||
| Srivastava [26] | 2019 | Decision tree | 76.04 |
| Random forest | 79.39 | ||
| AdaBoost | 78.41 | ||
| K-nearest neighbors | 71.35 | ||
| Support vector machines | 74.90 | ||
| Mohamed et al. [27] | 2019 | Naive Bayes + information gain (IGO) | 66.70 |
| K-nearest neighbor (KNN) + hybrid bat algorithm (BkMDFS) | 72.40 | ||
| Mary [28] | 2018 | Back-propagation neural network | 75.27 |
| Zhang et al. [29] | 2018 | Neural network (NN) | 77.28 |
| Classification and regression trees (CARTs) | 79.08 | ||
| Linear support vector machine | 72.08 | ||
| Minimal-redundancy-maximal-relevance (mRMR)-Wrapper + CART | 79.34 | ||
| Thirukovalluru et al. [30] | 2016 | Support vector machine | 75.27 |
| Random forest | 78.11 | ||
| Halawani [31] | 2014 | AdaBoost.M1 | 81.92 |
| Random forest | 79.96 | ||
| Buscema et al. [32] | 2010 | Meta-consensus | 77.00 |
| ArcX4 | 80.35 | ||
| AdaBoost.M1 | 79.31 | ||
| Quadratic Bayesian classifier (QDC) | 77.20 | ||
| Naive Bayesian combiner (BayesComb) | 71.95 | ||
| Bayesian linear classifier (LDC) | 74.25 | ||
| Sine network (SN) | 74.16 | ||
| Dempster–Shafer combination | 80.58 | ||
| Direct KNN decision dependent (DynDdDirectKnn) | 77.40 | ||
| Proposed Method | Logistic model tree forest | 86.655 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasemkhani, B.; Yilmaz, R.; Birant, D.; Kut, R.A. Logistic Model Tree Forest for Steel Plates Faults Prediction. Machines 2023, 11, 679. https://doi.org/10.3390/machines11070679
Ghasemkhani B, Yilmaz R, Birant D, Kut RA. Logistic Model Tree Forest for Steel Plates Faults Prediction. Machines. 2023; 11(7):679. https://doi.org/10.3390/machines11070679
Chicago/Turabian StyleGhasemkhani, Bita, Reyat Yilmaz, Derya Birant, and Recep Alp Kut. 2023. "Logistic Model Tree Forest for Steel Plates Faults Prediction" Machines 11, no. 7: 679. https://doi.org/10.3390/machines11070679
APA StyleGhasemkhani, B., Yilmaz, R., Birant, D., & Kut, R. A. (2023). Logistic Model Tree Forest for Steel Plates Faults Prediction. Machines, 11(7), 679. https://doi.org/10.3390/machines11070679







