Convolutional-Transformer Model with Long-Range Temporal Dependencies for Bearing Fault Diagnosis Using Vibration Signals
Abstract
1. Introduction
- Novel Deep-Learning Architecture: This method introduces a unique deep-learning architecture that combines CNNs and transformer models to enhance fault diagnosis in rotating machinery. This architecture contributes to this growing area of research by utilising the strengths of both components.
- Sequential Approach: The proposed method offers a systematic and sequential approach to fault diagnosis. It begins with the normalisation of vibration signals, efficiently addressing scale differences. Then, CNNs are employed for feature extraction, capturing important characteristics of the signals. Afterward, transformer models are used to model temporal relationships. This systematic process ensures a comprehensive analysis of the vibration signals.
- Effective Feature Extraction and Temporal Relationship Modelling: Using CNNs, this approach excels at extracting key features from vibration signals, enabling an accurate diagnosis of bearing faults. Incorporating transformer models enables the modelling of long-range temporal dependencies, capturing dynamic patterns, and relationships over extended time intervals for a deeper understanding of fault behaviours and improved diagnosis performance.
- Incorporation of Local and Long-Range Temporal Dependencies: By incorporating both local and long-range temporal dependencies in vibration signals, the method successfully captures the complex patterns and variations associated with bearing faults. This inclusion enhances the diagnostic accuracy and robustness of the model.
- Improvement of CNN and Transformer Model Strengths: The combination of CNNs for feature extraction and transformer models for the modelling of long-range temporal dependencies improves their individual strengths. CNNs efficiently extract discriminative features from the vibration signals, while transformer models excel at modelling long-range temporal relationships. The fusion of these two components enhances the overall performance of the fault diagnosis model, leading to precise fault diagnoses.
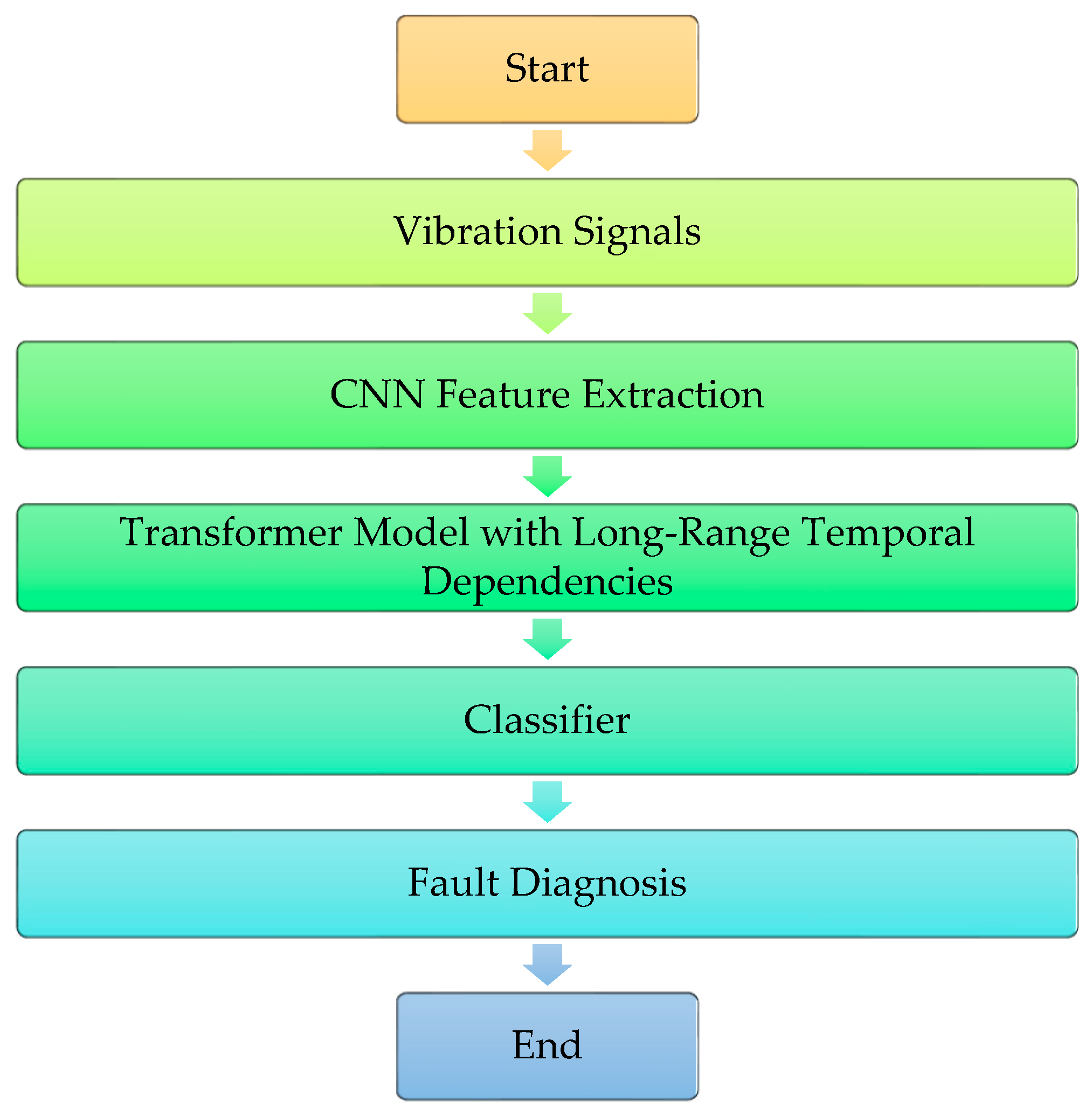
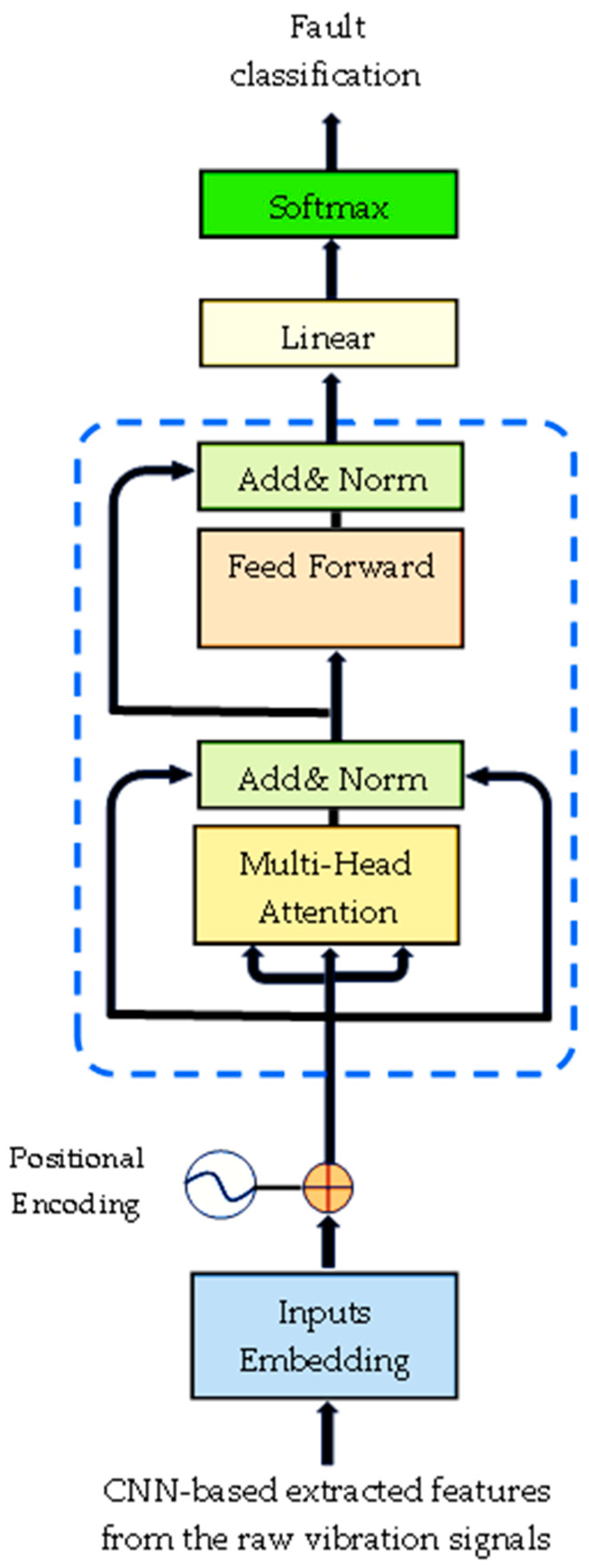
2. The Proposed Method
2.1. CNN Feature Extraction
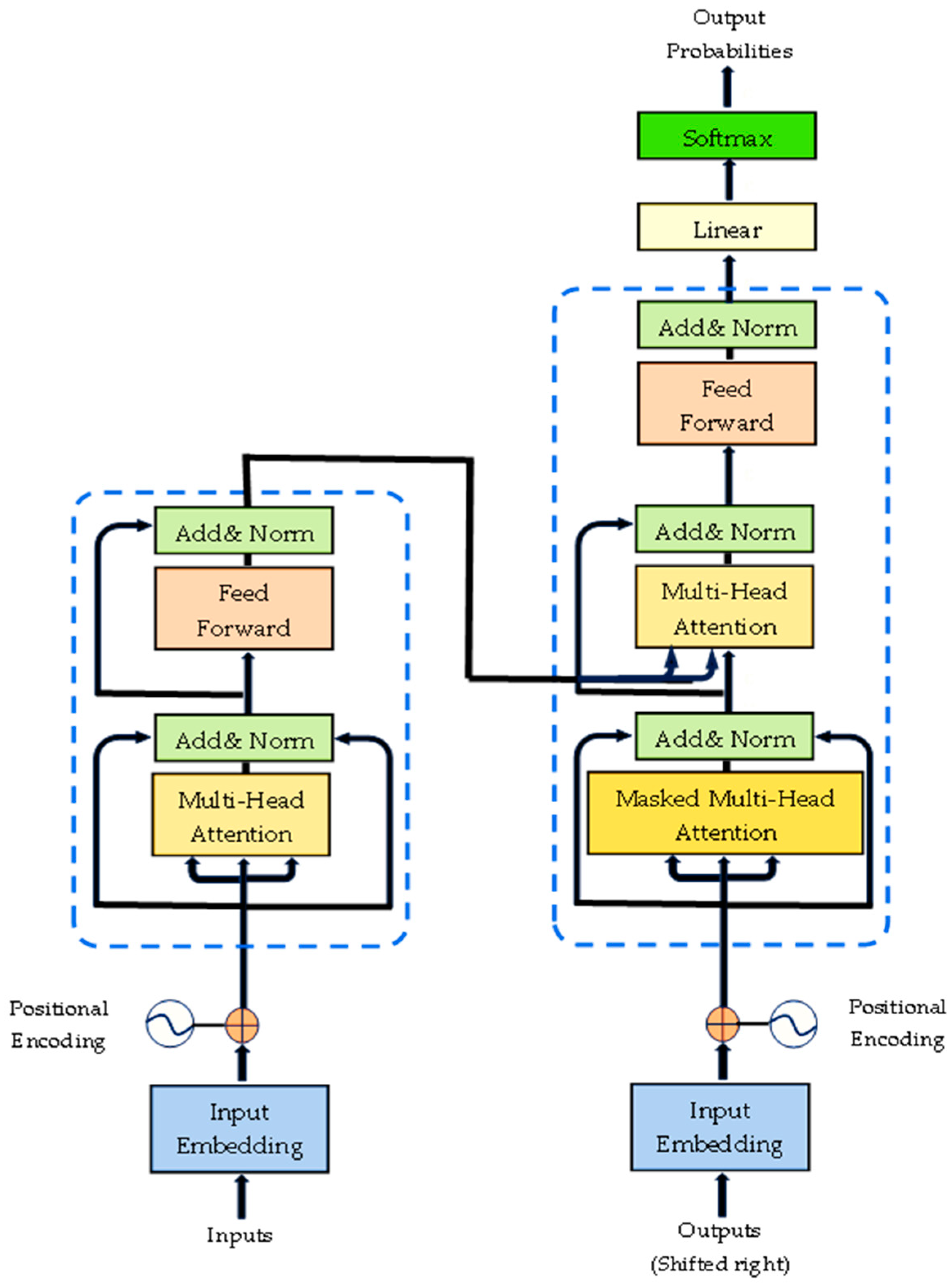
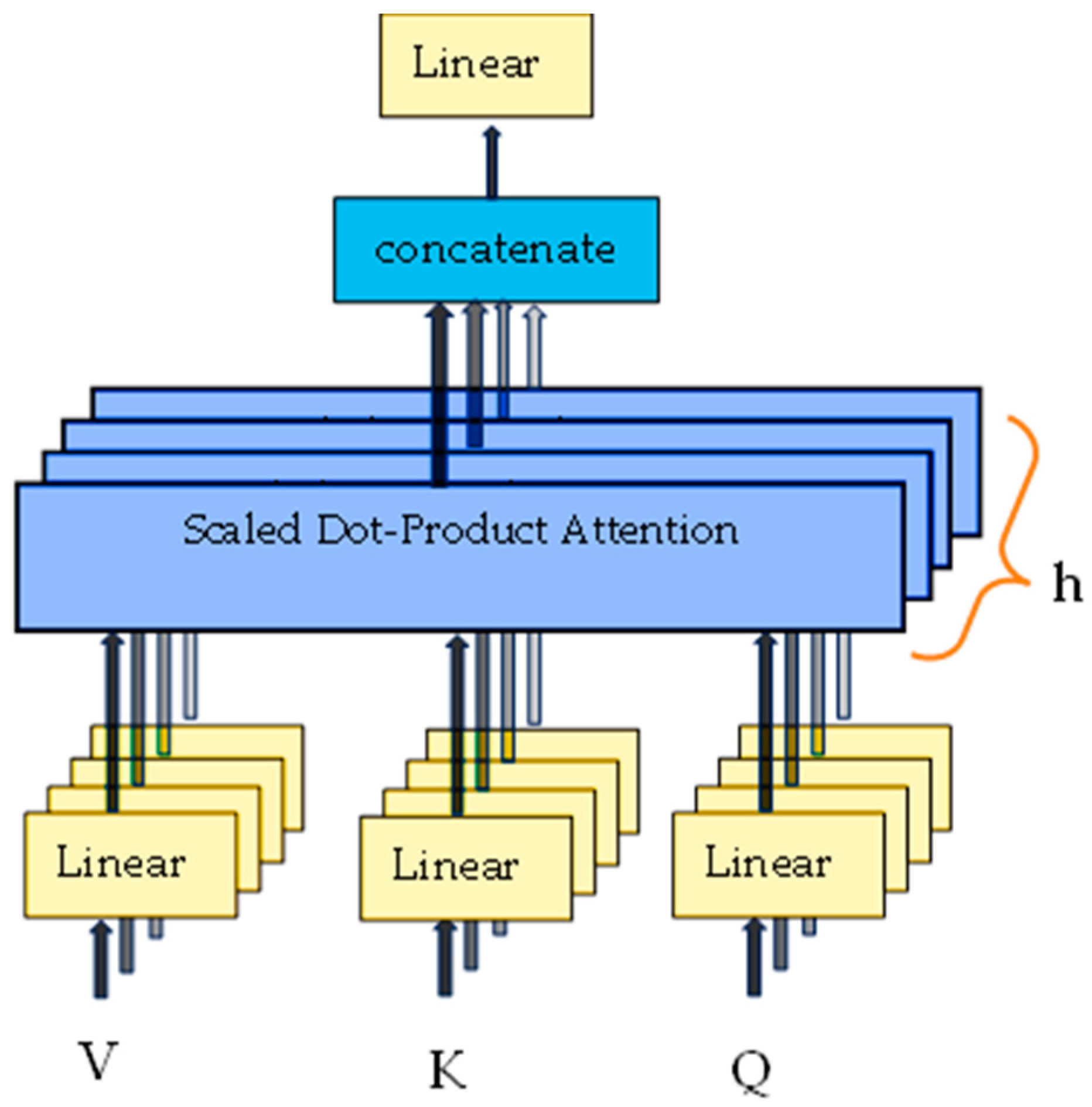
2.2. Temporal Transformer
3. Experimental Study
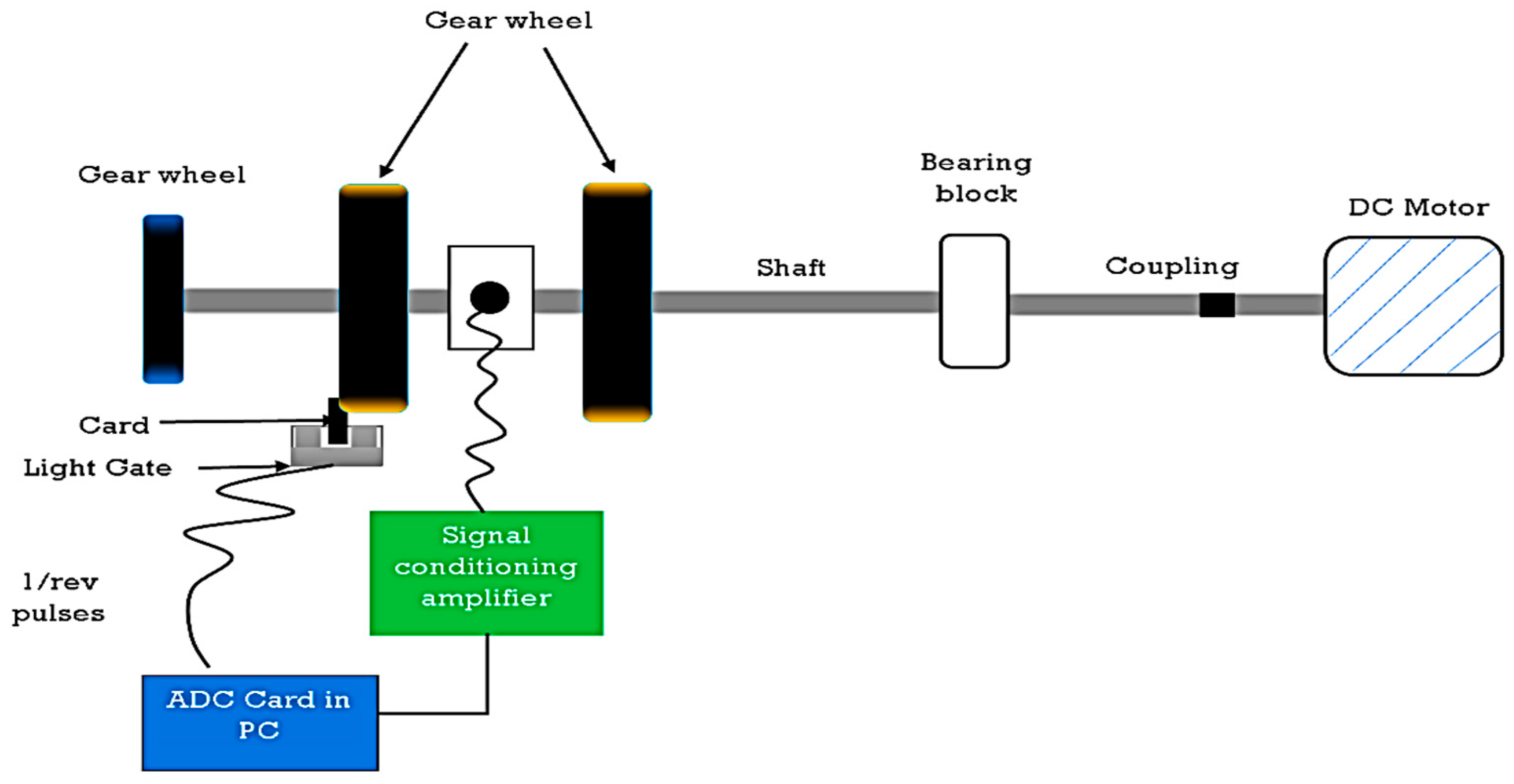
3.1. First Case Study
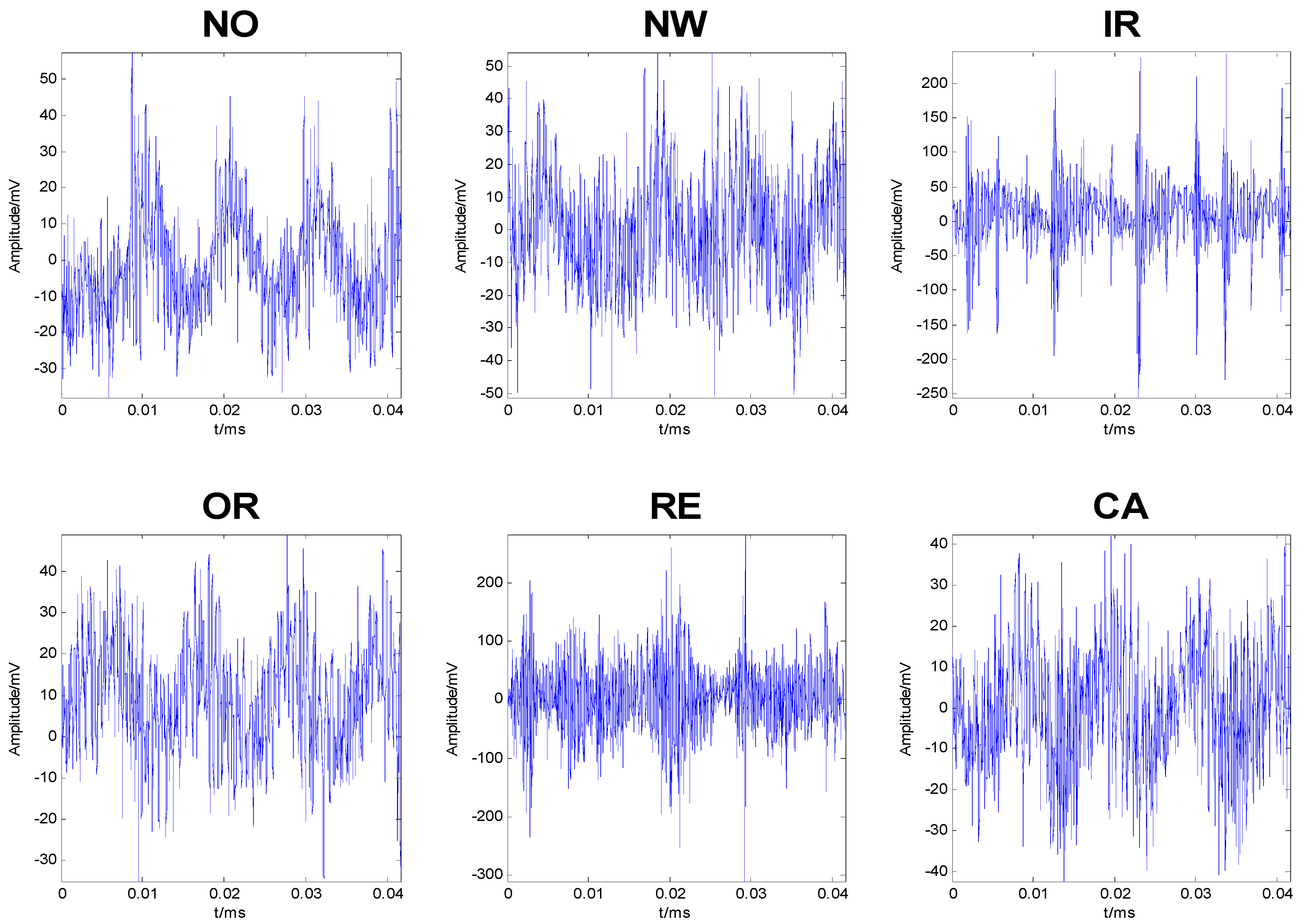
- The NO bearing corresponds to a brand-new bearing in perfect condition.
- The NW bearing has been in service for a certain period but remains in good condition.
- The IR fault is artificially created by removing the cage, shifting the elements to one side, removing the inner race, and subsequently cutting a groove into the raceway of the inner race using a small grinding stone. The bearing is then reassembled.
- The OR fault is artificially created by removing the cage, pushing all the balls to one side, and using a small grinding stone to cut a small groove in the outer raceway.
- The RE fault is simulated by marking the surface of one of the balls using an electrical etcher, imitating corrosion.
- The CA fault is artificially created by removing the plastic cage from one of the bearings and cutting away a section of the cage, thus allowing two of the balls to move freely without being held at a regular spacing, as would normally be the case.
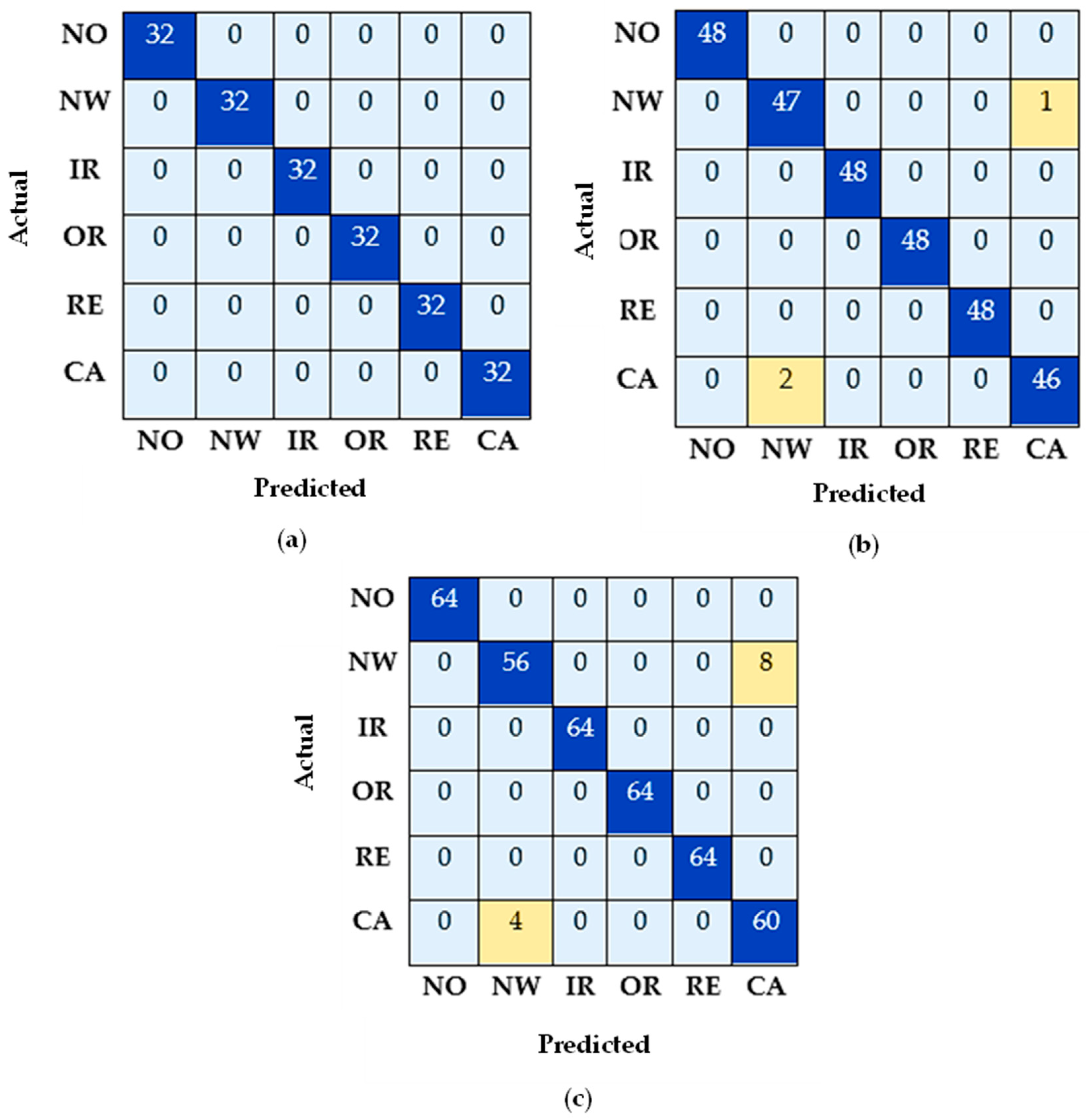
3.1.1. Experimental Results
3.1.2. Comparisons of Results
3.2. Second Case Study
3.2.1. Experimental Results
3.2.2. Comparisons of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, H.O.A.; Nandi, A.K. Condition Monitoring with Vibration Signals: Compressive Sampling and Learning Algorithms for Rotating Machines; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Wang, L.; Chu, J.; Wu, J. Selection of optimum maintenance strategies based on a fuzzy analytic hierarchy process. Int. J. Prod. Econ. 2007, 107, 151–163. [Google Scholar] [CrossRef]
- Higgs, P.A.; Parkin, R.; Jackson, M.; Al-Habaibeh, A.; Zorriassatine, F.; Coy, J. A survey on condition monitoring systems in industry. In Proceedings of the ASME 7th Biennial Conference on Engineering Systems Design and Analysis, Manchester, UK, 19–22 July 2004; Volume 41758, pp. 163–178. [Google Scholar] [CrossRef]
- Kim, J.; Ahn, Y.; Yeo, H. A comparative study of time-based maintenance and condition-based maintenance for optimal choice of maintenance policy. Struct. Infrastruct. Eng. 2016, 12, 1525–1536. [Google Scholar] [CrossRef]
- Ahmed, H.; Wong, M.; Nandi, A. Intelligent condition monitoring method for bearing faults from highly compressed measurements using sparse over-complete features. Mech. Syst. Signal Process. 2018, 99, 459–477. [Google Scholar] [CrossRef]
- Ahmed, H.O.A.; Nandi, A.K. Intrinsic Dimension Estimation-Based Feature Selection and Multinomial Logistic Regression for Classification of Bearing Faults Using Compressively Sampled Vibration Signals. Entropy 2022, 24, 511. [Google Scholar] [CrossRef]
- Tahir, M.M.; Khan, A.Q.; Iqbal, N.; Hussain, A.; Badshah, S. Enhancing Fault Classification Accuracy of Ball Bearing Using Central Tendency Based Time Domain Features. IEEE Access 2016, 5, 72–83. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Analysis of Statistical Time-Domain Features Effectiveness in Identification of Bearing Faults From Vibration Signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Rauber, T.W.; Boldt, F.D.A.; Varejao, F.M. Heterogeneous Feature Models and Feature Selection Applied to Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2014, 62, 637–646. [Google Scholar] [CrossRef]
- Prieto, M.D.; Cirrincione, G.; Espinosa, A.G.; Ortega, J.A.; Henao, H. Bearing Fault Detection by a Novel Condition-Monitoring Scheme Based on Statistical-Time Features and Neural Networks. IEEE Trans. Ind. Electron. 2012, 60, 3398–3407. [Google Scholar] [CrossRef]
- Guo, H.; Jack, L.; Nandi, A. Feature Generation Using Genetic Programming with Application to Fault Classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2005, 35, 89–99. [Google Scholar] [CrossRef]
- Ayaz, E. Autoregressive modeling approach of vibration data for bearing fault diagnosis in electric motors. J. Vibroeng. 2014, 16, 2130–2138. [Google Scholar]
- Lin, H.-C.; Ye, Y.-C. Reviews of bearing vibration measurement using fast Fourier transform and enhanced fast Fourier transform algorithms. Adv. Mech. Eng. 2019, 11, 1687814018816751. [Google Scholar] [CrossRef]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2015, 63, 1793–1803. [Google Scholar] [CrossRef]
- Farokhzad, S. Vibration based fault detection of centrifugal pump by fast fourier transform and adaptive neuro-fuzzy inference system. J. Mech. Eng. Technol. 2013, 1, 82–87. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Time–frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- Yu, J.; Lv, J. Weak Fault Feature Extraction of Rolling Bearings Using Local Mean Decomposition-Based Multilayer Hybrid Denoising. IEEE Trans. Instrum. Meas. 2017, 66, 3148–3159. [Google Scholar] [CrossRef]
- Staszewski, W.; Worden, K.; Tomlinson, G. Time–frequency analysis in gearbox fault detection using the wigner–ville distribution and pattern recognition. Mech. Syst. Signal Process. 1997, 11, 673–692. [Google Scholar] [CrossRef]
- He, Q.; Wang, X.; Zhou, Q. Vibration Sensor Data Denoising Using a Time-Frequency Manifold for Machinery Fault Diagnosis. Sensors 2013, 14, 382–402. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. A comprehensive review on convolutional neural network in machine fault diagnosis. Neurocomputing 2020, 417, 36–63. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.; Li, C.; Sánchez, R.V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Qiao, M.; Yan, S.; Tang, X.; Xu, C. Deep Convolutional and LSTM Recurrent Neural Networks for Rolling Bearing Fault Diagnosis Under Strong Noises and Variable Loads. IEEE Access 2020, 8, 66257–66269. [Google Scholar] [CrossRef]
- Ahmed, H.O.A.; Nandi, A.K. Connected Components-based Colour Image Representations of Vibrations for a Two-stage Fault Diagnosis of Roller Bearings Using Convolutional Neural Networks. Chin. J. Mech. Eng. 2021, 34, 37. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, Q.; Shen, Y.; Qian, C.; Xu, F.; Zhu, Q. Application of recurrent neural network to mechanical fault diagnosis: A review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, B.; Luo, W.; Chen, F. Autoencoder-based representation learning and its application in intelligent fault diagnosis: A review. Measurement 2022, 189, 110460. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset With Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Bhuiyan, R.; Uddin, J. Deep Transfer Learning Models for Industrial Fault Diagnosis Using Vibration and Acoustic Sensors Data: A Review. Vibration 2023, 6, 218–238. [Google Scholar] [CrossRef]
- Ahmed, H.O.A.; Nandi, A.K. Vibration Image Representations for Fault Diagnosis of Rotating Machines: A Review. Machines 2022, 10, 1113. [Google Scholar] [CrossRef]
- Lv, H.; Chen, J.; Pan, T.; Zhang, T.; Feng, Y.; Liu, S. Attention mechanism in intelligent fault diagnosis of machinery: A review of technique and application. Measurement 2022, 199, 111594. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism. Signal Process. 2019, 161, 136–154. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearings using an Improved Multi-Scale Convolutional Neural Network with Feature Attention mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.-B.; Zhang, J.-P.; Zhao, Z.-B.; Zhai, Z.; Chen, X.-F. Interpreting network knowledge with attention mechanism for bearing fault diagnosis. Appl. Soft Comput. 2020, 97, 106829. [Google Scholar] [CrossRef]
- Li, X.; Wan, S.; Liu, S.; Zhang, Y.; Hong, J.; Wang, D. Bearing fault diagnosis method based on attention mechanism and multilayer fusion network. ISA Trans. 2022, 128, 550–564. [Google Scholar] [CrossRef]
- Zhang, X.; Cong, Y.; Yuan, Z.; Zhang, T.; Bai, X. Early Fault Detection Method of Rolling Bearing Based on MCNN and GRU Network with an Attention Mechanism. Shock. Vib. 2021, 2021, 6660243. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, J.; Gu, X.; Ling, D.; Yu, H. Multi-scale attention mechanism residual neural network for fault diagnosis of rolling bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 10615–10629. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, H.; Liu, Z.; Han, H. Multi-scale CNN based on attention mechanism for rolling bearing fault diagnosis. In Proceedings of the Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling (APARM)-IEEE, Vancouver, BC, Canada, 20–23 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Hou, Y.; Wang, J.; Chen, Z.; Ma, J.; Li, T. Diagnosisformer: An efficient rolling bearing fault diagnosis method based on improved Transformer. Eng. Appl. Artif. Intell. 2023, 124, 106507. [Google Scholar] [CrossRef]
- Hou, S.; Lian, A.; Chu, Y. Bearing fault diagnosis method using the joint feature extraction of Transformer and ResNet. Meas. Sci. Technol. 2023, 34, 075108. [Google Scholar] [CrossRef]
- Cen, J.; Yang, Z.; Wu, Y.; Hu, X.; Jiang, L.; Chen, H.; Si, W. A Mask Self-Supervised Learning-Based Transformer for Bearing Fault Diagnosis With Limited Labeled Samples. IEEE Sens. J. 2023, 23, 10359–10369. [Google Scholar] [CrossRef]
- Wu, H.; Triebe, M.J.; Sutherland, J.W. A transformer-based approach for novel fault detection and fault classification/diagnosis in manufacturing: A rotary system application. J. Manuf. Syst. 2023, 67, 439–452. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ahmed, H.; Nandi, A.K. Compressive Sampling and Feature Ranking Framework for Bearing Fault Classification With Vibration Signals. IEEE Access 2018, 6, 44731–44746. [Google Scholar] [CrossRef]
- Seera, M.; Wong, M.D.; Nandi, A.K. Classification of ball bearing faults using a hybrid intelligent model. Appl. Soft Comput. 2017, 57, 427–435. [Google Scholar] [CrossRef]
- Wong, M.L.D.; Zhang, M.; Nandi, A.K. Effects of compressed sensing on classification of bearing faults with entropic features. In Proceedings of the 2015 IEEE 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 27 June 2023).
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- de Almeida, L.F.; Bizarria, J.W.; Bizarria, F.C.; Mathias, M.H. Condition-based monitoring system for rolling element bearing using a generic multi-layer perceptron. J. Vib. Control 2015, 21, 3456–3464. [Google Scholar] [CrossRef]
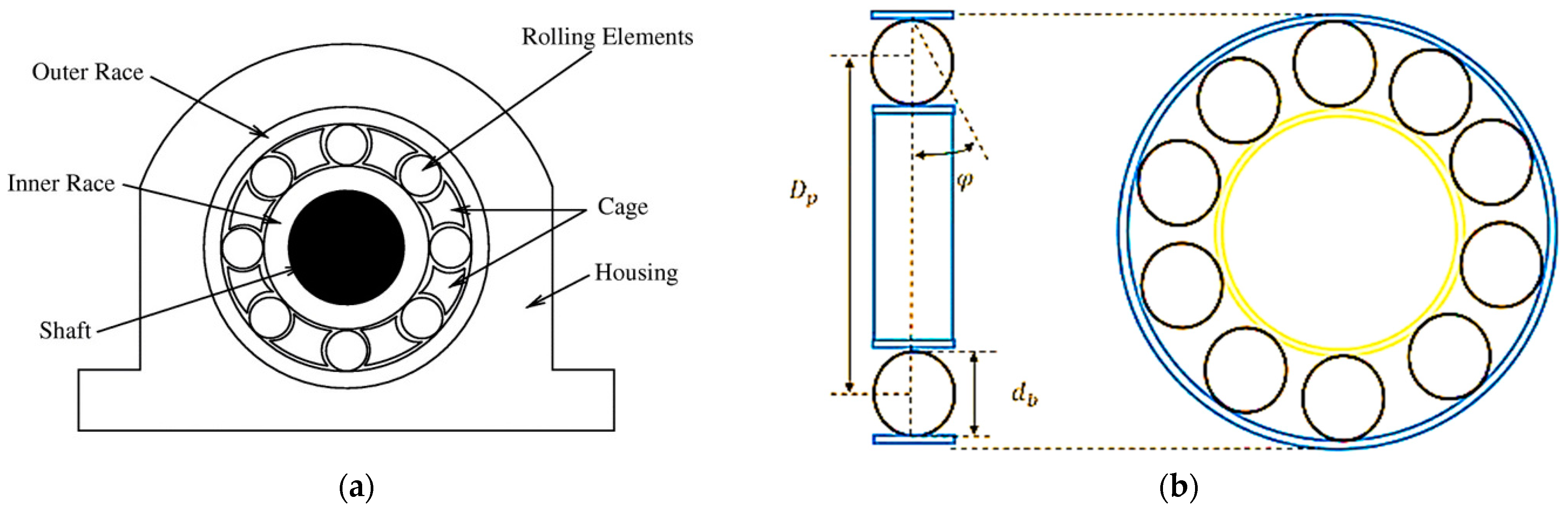

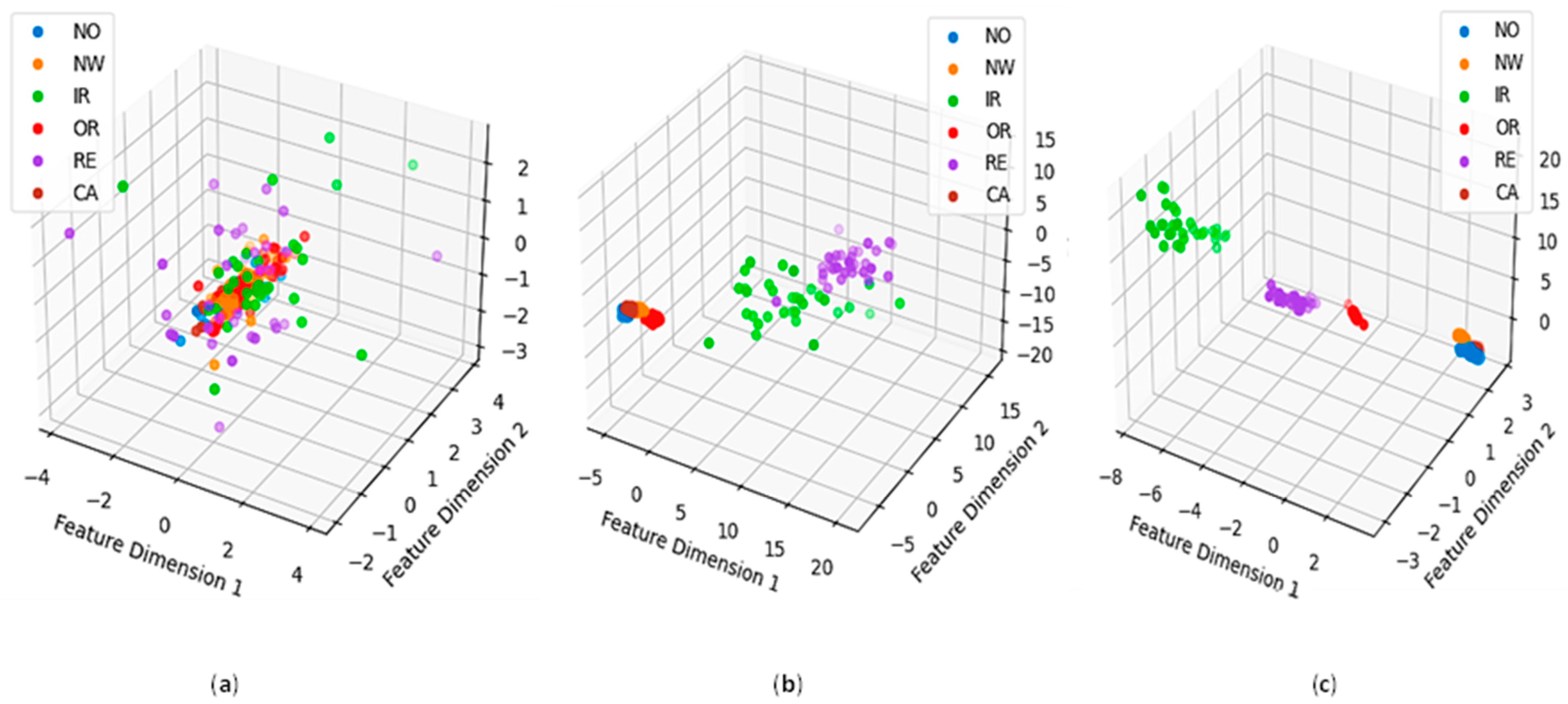

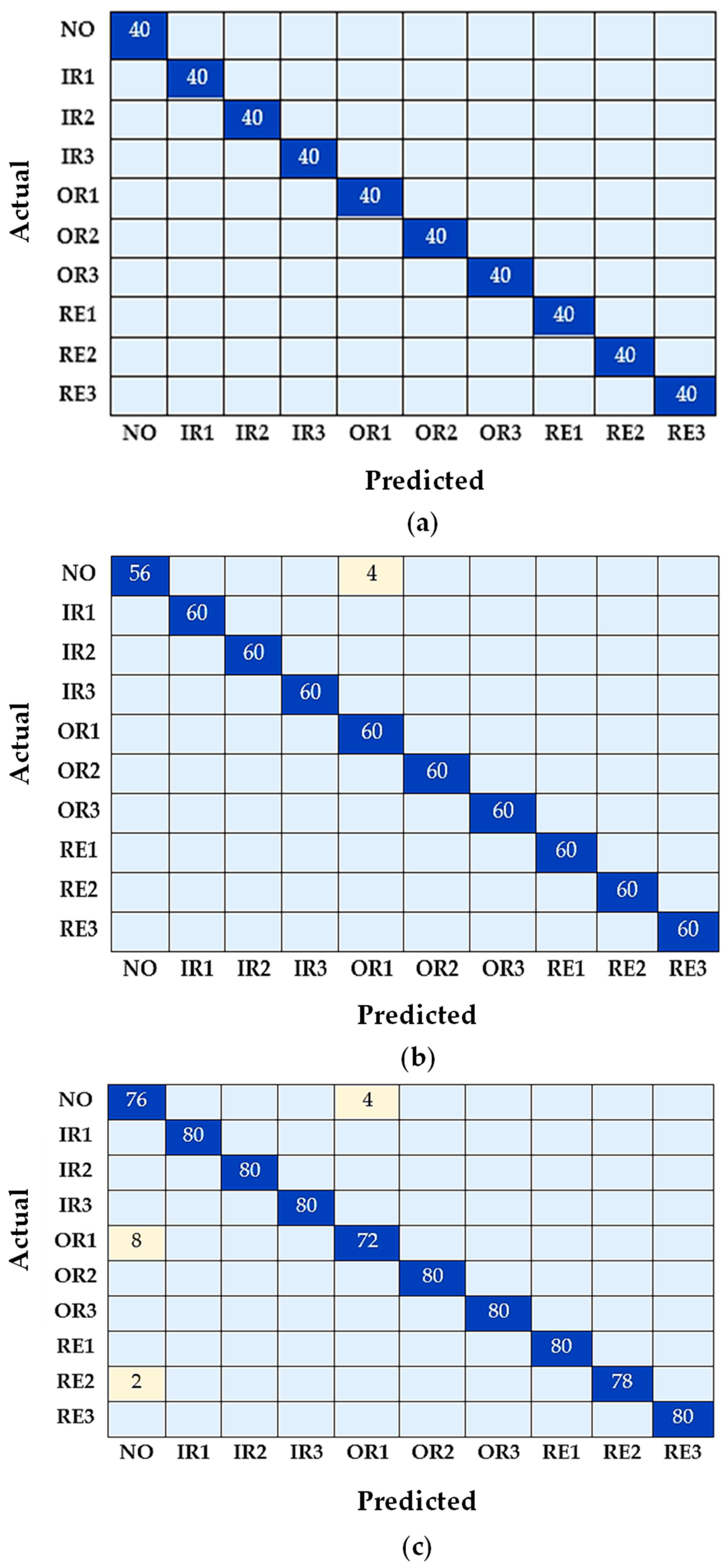
| Bearing Health Condition | Number of Samples | Number of Data Points | |
|---|---|---|---|
| Normal | NO | 160 | 6000 |
| NW | 160 | 6000 | |
| Fault | IR | 160 | 6000 |
| OR | 160 | 6000 | |
| RE | 160 | 6000 | |
| CA | 160 | 6000 |
| Parameter | Value | Description |
|---|---|---|
| Number of convolutional layers | 2 | The number of convolutional layers in the CNN feature extractor. |
| Number of filters per convolutional layer | 64,128 | The number of filters in each convolutional layer. |
| Kernel size | 3 × 3 | The size of the kernels used in the convolutional layers. |
| Stride | 1 | The stride used in the convolutional layers. |
| Padding | 1 | The padding used in the convolutional layers. |
| Number of max pooling layers | 2 | The number of max pooling layers in the CNN feature extractor. |
| Kernel size | 2 × 2 | The size of the kernel used in the max pooling layers. |
| Stride | 2 | The stride used in the max pooling layers. |
| Fully connected layers | 256 | The size of the fully connected layers in the CNN feature extractor. |
| Activation function | ReLU | The activation function used after each convolutional layer. |
| Reduced dimensionality | 2× | The factor by which the dimensionality of the output from the convolutional layers is reduced by the max pooling layer. |
| Parameter | Value | Description |
|---|---|---|
| Hidden size | 128 | The size of the hidden layer. |
| Number of layers | 6 | The number of transformer encoder layers. |
| Number of heads | 8 | The number of heads in the multi-head attention layers. |
| Number of classes | 6 | The number of the output classes in the bearing data of the first case study. |
| Activation function | ReLU | The activation function used after the linear layers. |
| Training Option | Value |
|---|---|
| Loss function | Cross Entropy Loss |
| Optimizer | Adam |
| Learning rate | 0.0001 |
| Number of epochs | 300 |
| Evaluation metrics | Classification accuracy, precision, recall, F1-score, and specificity |
| Metric | Definition | Formula |
|---|---|---|
| Accuracy | The proportion of instances that were correctly classified by the model. | |
| Precision | The proportion of instances that were classified as positive that were positive. | Precision = TP/(TP + FP) |
| Recall | The proportion of positive instances that were correctly classified by the model. | Recall = TP/(TP + FN) |
| F1 score | A weighted average of the precision and recall metrics. | F1 score = 2 ∗ (precision ∗ recall)/(precision + recall) |
| Specificity | The proportion of negative instances that were correctly classified by the model. | Specificity = TN/(TN + FP) |
| Training Size | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) | Std. Dev |
|---|---|---|---|---|---|---|
| 60% | 99.43 | 99.41 | 99.43 | 99.43 | 100 | 0.5 |
| 70% | 99.87 | 99.85 | 99.87 | 99.87 | 100 | 0.1 |
| 80% | 100 | 100 | 100 | 100 | 100 | 0.0 |
| Ref. | Method | Testing Accuracy (%) |
|---|---|---|
| [11] | Genetic programming—based features (unnormalised data) | |
| ANN | 96.5 | |
| SVM | 97.1 | |
| [47] | CS-FS | 99.7 |
| CS-LS | 99.5 | |
| CS-Relief | 99.8 | |
| CS-PCC | 99.8 | |
| CS-Chi-2 | 99.5 | |
| [48] | (FMM-RF) | |
| SampEn | 99.7 | |
| PS | 99.7 | |
| SampEn + PS | 99.8 | |
| [49] | SVM Classifier with: | |
| Entropic features | 98.9 | |
| Compressive sampling followed by signal recovery: | ||
| 92.4 | ||
| 84.6 | ||
| Our proposed method | ||
| Highest average accuracy (with 20% testing data) | 100 | |
| Lowest average accuracy (with 40% testing data) | 99.43 |
| Health Condition | Fault Width (mm) | Classification Label |
|---|---|---|
| NO | 0 | 1 |
| RE1 | 0.18 | 2 |
| RE2 | 0.36 | 3 |
| RE3 | 0.53 | 4 |
| IR1 | 0.18 | 5 |
| IR2 | 0.36 | 6 |
| IR3 | 0.53 | 7 |
| OR1 | 0.18 | 8 |
| OR2 | 0.36 | 9 |
| OR3 | 0.53 | 10 |
| Training Size | Accuracy | Precision | Recall | F1-Score | Specificity | Std. Dev |
|---|---|---|---|---|---|---|
| 60% | 99.18 | 99.14 | 99.18 | 98.98 | 100 | 0.6 |
| 70% | 99.96 | 99.97 | 99.96 | 99.96 | 99.59 | 0.02 |
| 80% | 100 | 100 | 100 | 100 | 100 | 0.0 |
| Ref. | Method | Testing Accuracy (%) |
|---|---|---|
| [5] | 100 | |
| [51] | DNN | 99.74 |
| BPNN | 69.82 | |
| [52] | MLP | 99.4 |
| Our proposed method | ||
| Highest average accuracy (with 20% testing data) | 100 | |
| Lowest average accuracy (with 40% testing data) | 99.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.O.A.; Nandi, A.K. Convolutional-Transformer Model with Long-Range Temporal Dependencies for Bearing Fault Diagnosis Using Vibration Signals. Machines 2023, 11, 746. https://doi.org/10.3390/machines11070746
Ahmed HOA, Nandi AK. Convolutional-Transformer Model with Long-Range Temporal Dependencies for Bearing Fault Diagnosis Using Vibration Signals. Machines. 2023; 11(7):746. https://doi.org/10.3390/machines11070746
Chicago/Turabian StyleAhmed, Hosameldin O. A., and Asoke K. Nandi. 2023. "Convolutional-Transformer Model with Long-Range Temporal Dependencies for Bearing Fault Diagnosis Using Vibration Signals" Machines 11, no. 7: 746. https://doi.org/10.3390/machines11070746
APA StyleAhmed, H. O. A., & Nandi, A. K. (2023). Convolutional-Transformer Model with Long-Range Temporal Dependencies for Bearing Fault Diagnosis Using Vibration Signals. Machines, 11(7), 746. https://doi.org/10.3390/machines11070746







