Winding Pattern Planning and Control of a Filament Winding Machine for Gas-Cylinders

Abstract

Filament winding reinforcement is often applied to fulfill high-pressure resistance and is lightweight for gas cylinder productions. This article analyzes the winding pattern and the corresponding characteristics for filament winding cylinders based on the resulting thickness and strength such that the gas cylinders can be made as light as possible. In order to prevent the sliding between the filament material and the cylinder surface during the winding process, a range of winding angles that do not exceed the maximum static friction at every instant is adopted. The gas cylinder geometric structure formed by a complete round of winding using different winding angles is calculated to find the winding pattern that consumes the least composite filament. The winding pattern can also be determined before production to reduce the cost and time for customized products. By sequential contact points of the winding process, motion planning can be carried out for a four-axis filament winding machine.

1. Introduction

In industrial manufacturing processes, steel cylinders for high-pressure gas are often used to transport all kinds of gases for different purposes. To effectively reduce transportation costs, the weight of the gas cylinders needs to be reduced as much as possible while ensuring the necessary strength requirements. Due to the lightweight and high-strength properties of composite materials, they are widely used in various industries. In terms of the manufacturing of pressure vessels, the early application of glass fiber and the current carbon fiber winding reinforcement process have become an indispensable technology for the aerospace manufacturing of liquid fuel containers and airframes [1].

The filament winding machine was first developed with two motion axes to conduct simple winding of workpieces in the 1950s. With the developments of industry and technology, multi-axis winding mechanisms [2] were proposed. At present, three-axis [3,4], and four-axis are the most commonly used filament winding machines. The current research and development focuses on process optimization and controller design to improve the efficiency and cost reduction of the winding process. Abdalla et al. [5] proposed the use of lathe machine to carry out a wet winding process in 2007. The process achieved uniform winding and a good surface finish. The machine was used to manufacture pipe samples of various sizes and other round products that were used for different mechanical tests and applications. In order to calibrate new filament winding, a study on the effect of winding speed is studied by Hashim et al. [6]. Winding angles are also studied by Ma et al. [7] for the quasi-static behavior of thin-walled carbon fiber-reinforced polymer tubes. In 2018, Lu et al. [8] proposed the adoption of an iterative learning sliding mode controller for tension control and estimated the wire tension using a disturbance observer. A robust H∞ control approach with two-degree of freedom (2DOF) for the winding system was developed to reduce the coupling between winding tension and speed [9,10]. In 2018, Xu et al. [11] proposed a tension control method, which combined fuzzy control and PID control by controlling the output of three different driven rollers to adjust the fiber tension and winding speed during the process. In terms of optimized design, Colombo and Vergani [12] proposed the selection of parameters, such as fiber matrix, fiber volume fraction, and winding angle, in the design phase to obtain the optimal manufacturing parameters for glass-fiber-reinforced composite light tubes. With the development of artificial intelligence, learning-based related methods were also applied to winding machines [13,14]. The improvement of winding quality through sensor integration by machine learning was also discussed in [15]. A recent study has developed using machine vision to measure real-time winding angles [16].

To investigate filament winding reinforced gas cylinder production from design to manufacturing, this research focuses on the filament winding pattern selection according to the resulting strength properties and the amount of material used. In this study, the end cap geometry of a gas cylinder is formed by geodesic winding [17]. The strength of the winding patterns of the composite is also analyzed such that a prespecified pressure resistance can be achieved with the least winding filament. The article is arranged as follows: the second section describes the gas cylinder geometry and winding path analysis in detail; the third section analyzes the stress and strength of the gas cylinders reinforced with composite winding; the fourth section describes the motion path planning and realization of a four-axis filament winding machine; and the last section is the conclusions.

2. Description of Gas Cylinder Geometry and Composite String Winding Path

A.

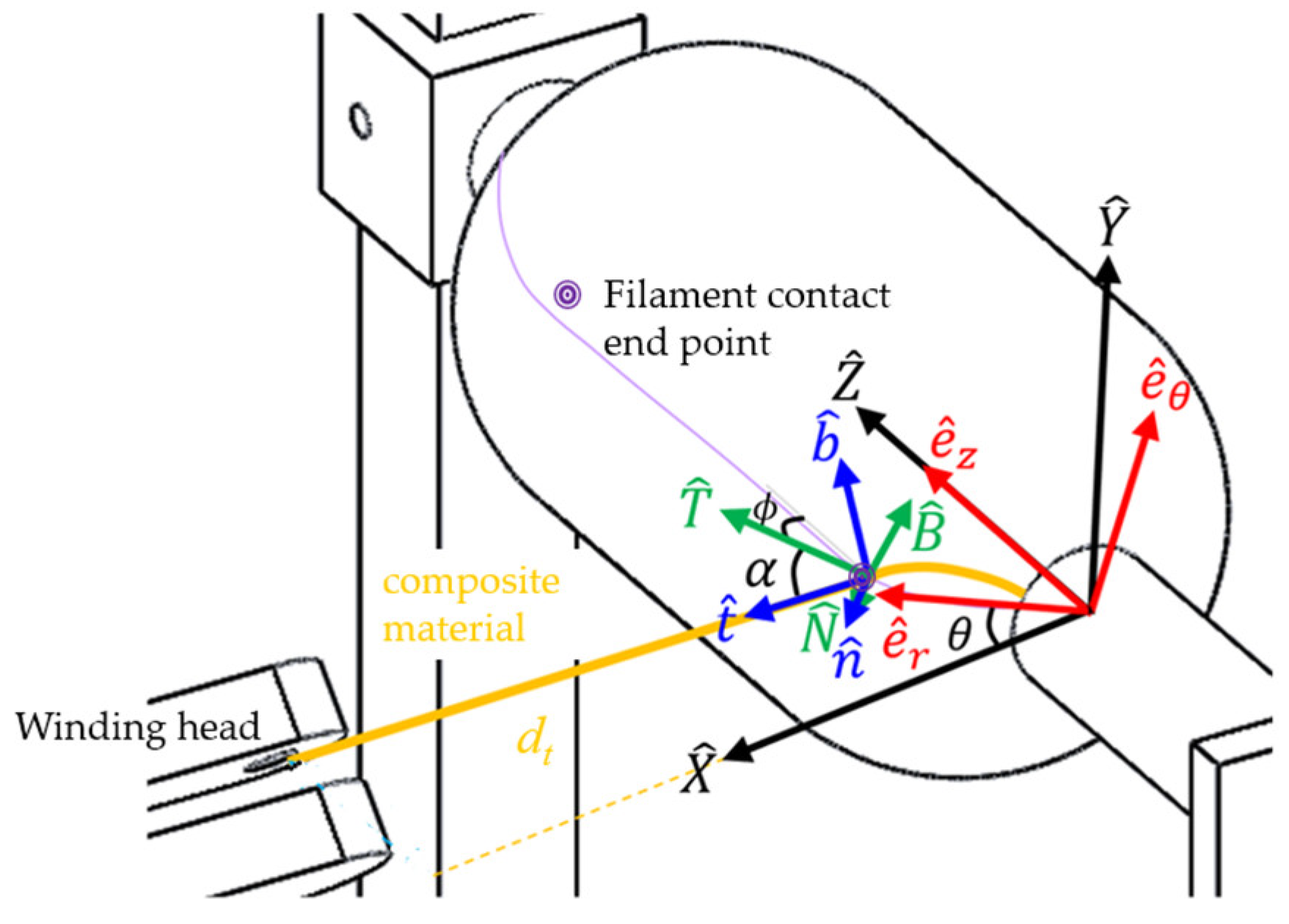
Definition of coordinate axes

In this study, geodesics are used for the winding approach, which provides the shortest paths between two arbitrary points on a surface. Four coordinate systems are introduced as follows based on the longitude and latitude coordinates required by the geodesic system and the relationship between the standard local coordinate system.

(a)

Standard local coordinate system.

The standard local coordinate system ($\widehat{X}, \widehat{Y}, \widehat{Z})$ is fixed on the machine. In general, one vertex of the gas cylinder is selected as the coordinate origin. Then, the $\widehat{\mathit{Z}}$-axis is defined as the axial direction of the gas cylinder directing toward the other vertex. The $\widehat{Y}$-axis is kept perpendicular to the ground and pointing upward. Consequently, the $\widehat{X}$-axis is parallel to the ground, and the direction is toward the side where the filament winding head is located, as shown in Figure 1.

(b)

Cylindrical coordinate system.

The origin of the cylindrical coordinate system $\left({\widehat{e}}_r,{\widehat{e}}_{\theta },{\widehat{e}}_z\right)$ moves according to the $\widehat{Z}$ coordinate value of the instantaneous contact point of the winding filament on the cylinder. The ${\widehat{e}}_z$-axis and the $\widehat{Z}$-axis are in the same direction, and the ${\widehat{e}}_r$-axis is perpendicular to the $\widehat{Z}$-axis and faces toward the instantaneous contact point. The ${\widehat{e}}_{\theta }$-axis is the cross product of the ${\widehat{e}}_z$-axis and the ${\widehat{e}}_r$-axis, and the angle between the ${\widehat{e}}_r$-axis and the $\widehat{X}$-axis is θ. The corresponding coordinate value in the cylindrical coordinate system of a point P at the standard local system can be obtained by:

$$\left[\begin{array}{c}{p}_r\\ p_{\theta }\\ P_z\end{array}\right]=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{p}_X\\ p_Y\\ p_Z\end{array}\right]$$

(1)

(c)

Latitude and longitude coordinate system.

The origin of the latitude–longitude coordinate system $\left(\widehat{T},\widehat{N},\widehat{B}\right)$ moves with the instantaneous contact point of the filament on the cylinder. The $\widehat{N}$-axis is the normal vector of the cylinder surface, which directs outward the cylinder. The $\widehat{T}$-axis is tangent to the meridian direction of the cylinder, and its component along the ${\widehat{e}}_z$-axis is the same as the direction of movement of the winding head. The angle $\varnothing$ is the angle between the $\widehat{T}$-axis and the direction of movement of the winding head, and its sign is the same as the $\widehat{T}$-axis component in the ${\widehat{e}}_r$-axis direction. The $\widehat{B}$-axis is the cross-product of the $\widehat{T}$-axis and the $\widehat{N}$-axis.

For the winding head moving along with the positive and the negative $\widehat{Z}$-axis direction, the relationship between the cylindrical coordinate system and the latitude-longitude coordinate system are shown in Equations (2) and (3), respectively.

$$\left[\begin{array}{c}{p}_T\\ p_N\\ P_B\end{array}\right]=\left[\begin{array}{ccc}sin\varphi & 0& \mathit{cos}\varphi \\ \mathit{cos}\varphi & 0& -sin\varphi \\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{p}_r\\ p_{\theta }\\ p_z\end{array}\right]$$

(2)

$$\left[\begin{array}{c}{p}_T\\ p_N\\ P_B\end{array}\right]=\left[\begin{array}{ccc}sin\varphi & 0& \mathit{cos}\varphi \\ \mathit{cos}\varphi & 0& -sin\varphi \\ 0& -1& 0\end{array}\right]\left[\begin{array}{c}{p}_r\\ p_{\theta }\\ p_z\end{array}\right]$$

(3)

(d)

Winding coordinate system.

The winding coordinate system $\left(\widehat{t},\widehat{n},\widehat{b}\right)$ and the latitude–longitude coordinate system $\left(\widehat{T},\widehat{N},\widehat{B}\right)$ share the same origin, as shown in Figure 1. The direction of the $\widehat{n}$-axis and the $\widehat{N}$-axis are the same, and the $\widehat{t}$-axis is tangent to the winding path. The $\widehat{b}$-axis is the direction of the cross product of the $\widehat{t}$-axis and the $\widehat{n}$-axis, where $\alpha$ is the angle between the $\widehat{t}$-axis and the $\widehat{T}$-axis, and its sign is the same as the $\widehat{t}$-axis component in the $\widehat{B}$-axis direction. For a point P$\left(p_T,p_N,p_B\right)$ in the longitude-latitude coordinate system, the corresponding coordinate value $\left(p_T,p_N,p_B\right)$ in the winding coordinate system can be obtained by:

$$\left[\begin{array}{c}{p}_t\\ p_n\\ P_b\end{array}\right]=\left[\begin{array}{ccc}cos\alpha & 0& sin\alpha \\ 0& 1& 0\\ -sin\alpha & 0& cos\alpha \end{array}\right]\left[\begin{array}{c}{p}_T\\ p_N\\ P_B\end{array}\right]$$

(4)

Based on the definition of coordinates, the winding coordinate and the standard local coordinate of the forward and return winding paths can be obtained by Equations (5) and (6), respectively.

$$\left[\begin{array}{c}{p}_t\\ p_n\\ P_b\end{array}\right]=\left[\begin{array}{ccc}C\alpha S\varphi C\theta +S\alpha S\theta & -C\alpha S\varphi S\theta +S\alpha C\theta & C\alpha C\varphi \\ C\varphi C\theta & -C\varphi S\theta & -S\varphi \\ -S\alpha S\varphi C\theta +C\alpha S\theta & S\alpha S\varphi C\theta +C\alpha S\theta & -S\alpha C\varphi \end{array}\right]\left[\begin{array}{c}{p}_X\\ p_Y\\ p_Z\end{array}\right]$$

(5)

$$\left[\begin{array}{c}{p}_t\\ p_n\\ P_b\end{array}\right]=\left[\begin{array}{ccc}C\alpha S\varphi C\theta -S\alpha S\theta & -C\alpha S\varphi S\theta -S\alpha C\theta & C\alpha C\varphi \\ C\varphi C\theta & -C\varphi S\theta & -S\varphi \\ -S\alpha S\varphi C\theta -C\alpha S\theta & S\alpha S\varphi C\theta -C\alpha S\theta & -S\alpha C\varphi \end{array}\right]\left[\begin{array}{c}{p}_X\\ p_Y\\ p_Z\end{array}\right]$$

(6)

where C and S represent cosine and sine functions, respectively.

B.

Winding path design

The winding mode mainly determines the complete path of the filament on the gas cylinder. However, the path is determined by winding process parameters and the composite material’s parameters, including the geometric shape of the gas cylinder, the winding filament properties, and the winding angle, etc. The winding angle is defined as the intersection angle between the winding filament’s primary axis and the cylinder’s meridian.

(1)

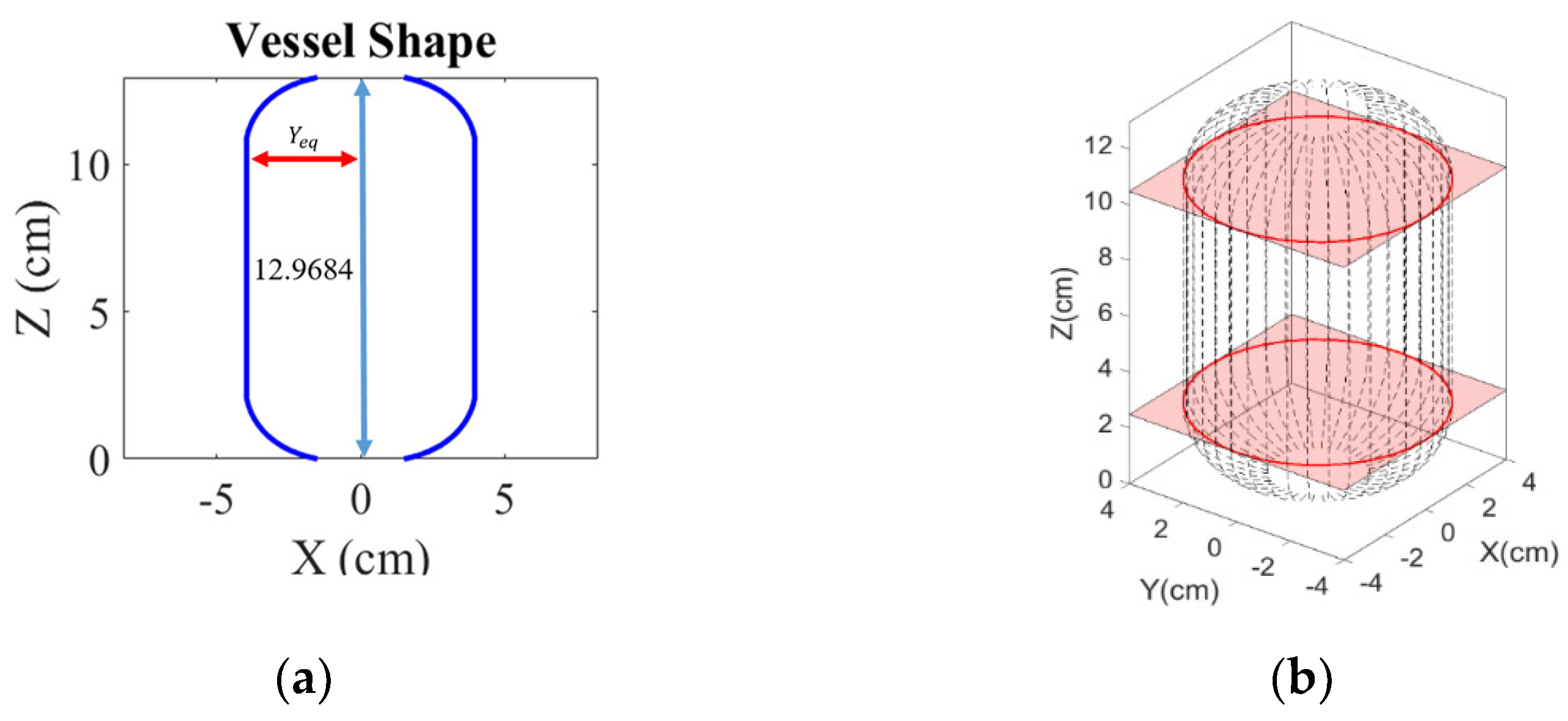
Geometry of cylinder end.

The key feature of the gas cylinder geometry is the shape of the end cap surface, in which the radius of the cylinder body is the radius of the joint ends of the end cap, also known as the equatorial radius ($Y_{eq}$). Based on the static equilibrium and the material properties of the winding strings, an optimal geometry [18] of the gas cylinder end surface can be described by:

$${\mathrm{Z}}^{\prime }\left(Y\right)=\pm \frac{Y\left(Y^2+r{Y}_{eq}^2\right)}{\sqrt{{\left(\frac{k_e+Y^2-1}{k_e+Y_{eq}^2-1}\right)}^{k_e+1}{\left(1+r\right)}^2{Y}_{eq}^6-Y^2{\left(Y^2+r{Y}_{eq}^2 \right)}^2}}$$

(7)

where r is the ratio of the total external force on the end cap to the combined force of the storage pressure exerted on the end cap, Yeq is the equatorial radius, Y and Z are the coordinate value of the end face on the $\widehat{Y}$-axis and the $\widehat{Z}$-axis, respectively. The fiber matrix combination ke is defined as follows.

$${\mathrm{k}}_{\mathrm{e}}=\frac{E_2\left(1+v_{12}\right)}{E_1\left(1+v_{21}\right)}$$

(8)

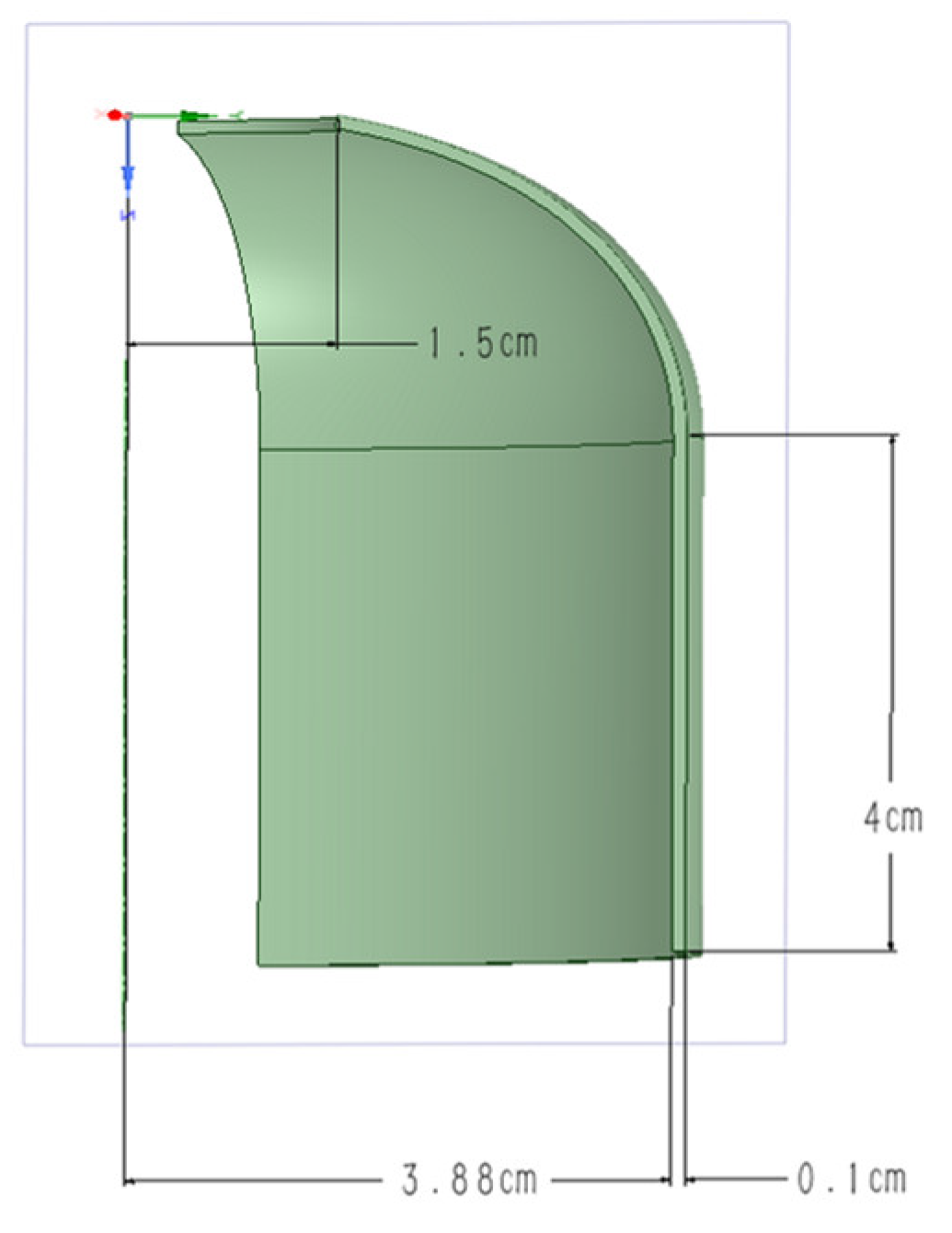
where $E_1$ and $E_2$ are Young’s modulus, and $v_{12}$ and $v_{21}$ are the shear modulus of the composite. The composite material coefficients of carbon fiber strings T700/3234 (carbon fiber/epoxy resin) are referred to [19], where $E_1$ = 132 GPa, $E_2$ = 10.3 GPa, and $v_{12}$ = 0.25, it results $k_e$ = 0.07803. In order to facilitate follow-up practical research, a small gas cylinder is used, where the minimum radius of the end surface is $c=1.5 \mathrm{cm}$, the equatorial radius is Yeq = R = 4 cm and the length of the cylinder is L = 8 cm, According to (7), the gas cylinder geometry is shown in Figure 2.

(2)

Winding path analysis.

Since the winding angle (${\alpha }_c$) of the gas cylinder side−surface is equal to the winding angle at the equatorial radius, determining the cylinder winding angle also determines the winding pattern of the end surface and the cylinder body. However, the friction between the filament and the cylinder must be considered in the end surface winding process to avoid slippage. Therefore, the winding angle ($\alpha$) and the process parameters, such as the cylinder speed ($\omega$), the instantaneous contact point speed ($\dot{\stackrel{\rightharpoonup }{\gamma }}$), are both closely related to the velocity (v_z) on the $\widehat{Z}$-axis. Based on the no-slip consideration for the winding process, the angular velocity ratio can express the static friction coefficient required for the winding process without slippage [20]. For a given static friction coefficient, the following is the no-slip constraint represented by the winding angle and the rotating speed of the gas cylinder.

$${\mu }_{fmax}>{\mu }_f=\left|\frac{\sqrt{1+Y^{’2}}\omega Y^{\prime }}{\sqrt{1+Y^{’2}}\omega sin\alpha -Y^{″}\frac{dZ}{dt}cos\alpha }\right|$$

(9)

In Figure 3, the velocity $\dot{\stackrel{\rightharpoonup }{\gamma }}$ at the instantaneous winding point is divided into two directions $\widehat{t}$ and $\widehat{b}$, as presented in Equation (10) and its differentiation can be obtained by Equation (11).

$$\dot{\stackrel{\rightharpoonup }{\gamma }}={v_t}^{\circ }\times \widehat{t}+v_b\times \widehat{b}$$

(10)

$$\ddot{\stackrel{\rightharpoonup }{\gamma }}=\frac{d_v{}_t}{dt}\times \widehat{t}+\frac{d_v{}_b}{dt}\times \widehat{b}+v_t\times \left(\mathsf{\Omega }\times \widehat{t}\right)+v_b\times \left(\mathsf{\Omega }\times \widehat{b}\right)$$

(11)

For constant winding rate along the $\widehat{t}$ direction, the following conditions are applied.

$$v_b=0$$

(12)

$$\frac{d_v{}_t}{dt}=0$$

(13)

By Equations (10)–(13), the dynamics of the instantaneous winding point can be described by the nonlinear ordinary differential equation as follows.

$$\left(1+Y^{{’}^2}\right)v_z\frac{d{v}_z}{dZ}+Y^{\prime }{Y}^{″}{v}_z^2+Y{Y}^{\prime }{\omega }^2+Y^2\omega \frac{d\omega }{dZ}=0$$

(14)

Based on the winding boundary conditions v_z(0) = 0, Y(0) = Y₀ at Z = 0, and the initial angular velocity $\omega \left(0\right)={\omega }_0$ of the cylinder, the integration of Equation (14) with respect to Z gives.

$$\left(1+Y^{{’}^2}\right)v_z^2+Y^2{\omega }^2=Y_0^2{\omega }_0^2$$

(15)

Subsequently, the rotating speed $\omega$ of the gas cylinder can be represented as:

$$\omega =\pm \frac{\sqrt{Y_0^2{\omega }_0^2-\left(1+Y^{{’}^2}\right)v_z^2}}{Y}$$

(16)

Since $v_b$. keeps zero during the winding process, angle $\alpha$ between the winding filament and the latitude and longitude coordinate system can be obtained by converting $v_t$ to the standard local coordinate system and substituted in Equation (15), where $v_t$ is the component the winding speed $\dot{\stackrel{\rightharpoonup }{\gamma }}$ on the $\widehat{t}$-axis direction.

$$\mathsf{\alpha }={\tan }^{-1}\frac{Y\omega }{v_z\sqrt{1+Y^{’2}}}={\tan }^{-1}\frac{\sqrt{Y_0^2{\omega }_0^2-\left(1+Y^{{’}^2}\right)v_z^2}}{\left(1+Y^{{’}^2}\right)v_z^2}$$

(17)

According to the friction and wear properties of composite [21] and the tribological of carbon fiber composite materials [22], the maximum static friction coefficient between the steel cylinder and the carbon fiber composite is about 0.3. Therefore, the constraint that no winding slippage occurs is rewritten as Equation (18).

$${\mu }_f=\left|\frac{Y^{\prime }}{sin\alpha -\frac{Y^{″}·Yco{s}^2\alpha }{\left(1+Y^{’2} \right)sin\alpha }}\right|\le 0.3$$

(18)

Since $\omega$ and $\alpha$ are real numbers and both Equations (16) and (17) are functions of $v_z$, the upper limit of the reasonable value of $v_z$ can be obtained with a prescribed geometry of the gas cylinder. For winding motion ppurposes $v_z$ can be described as a function of Z, which meets the limit constraints. Figure 4 shows the limit and candidate functions for $v_z$, where $v_z$ is described by the proposed function ${\nu }_Z=k\sqrt{z-z_0}$ with Z₀ = 0. For $k$ = 0.9 and the initial value of the processing Z is considered to be 0, then Z can be a quadratic function of time, as shown in Equation (19), for Z = [0, 2.4842], which covers the path located at the cylinder end cap.

$$Z=0.2025t^2$$

(19)

Consequently, the dynamic response of $v_z$ can be expressed as (20). In this way, $v_z$ = 0 for Z = 0.

$$v_z=0.9\sqrt{0.2025t^2}=0.405t$$

(20)

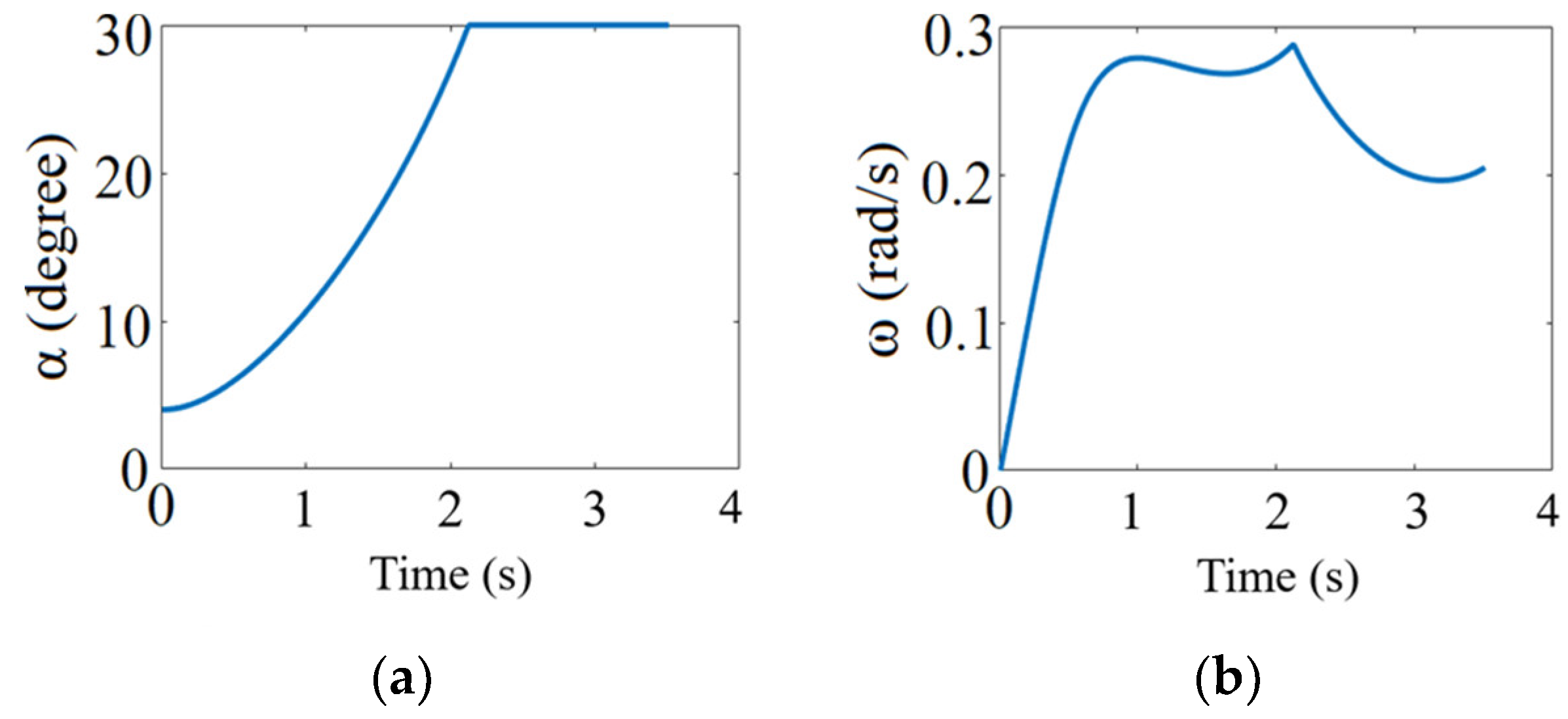
Based on Equation (18) and the geometry of the gas cylinder in Figure 4, the upper limit of the winding angle $\alpha$ at each time instant can be determined. For a smooth winding path from the cylinder end to the cylindrical surface, it is reasonable to set the upper limit of the winding angle for both ends the same as the cylindrical winding angle ${\alpha }_c$. 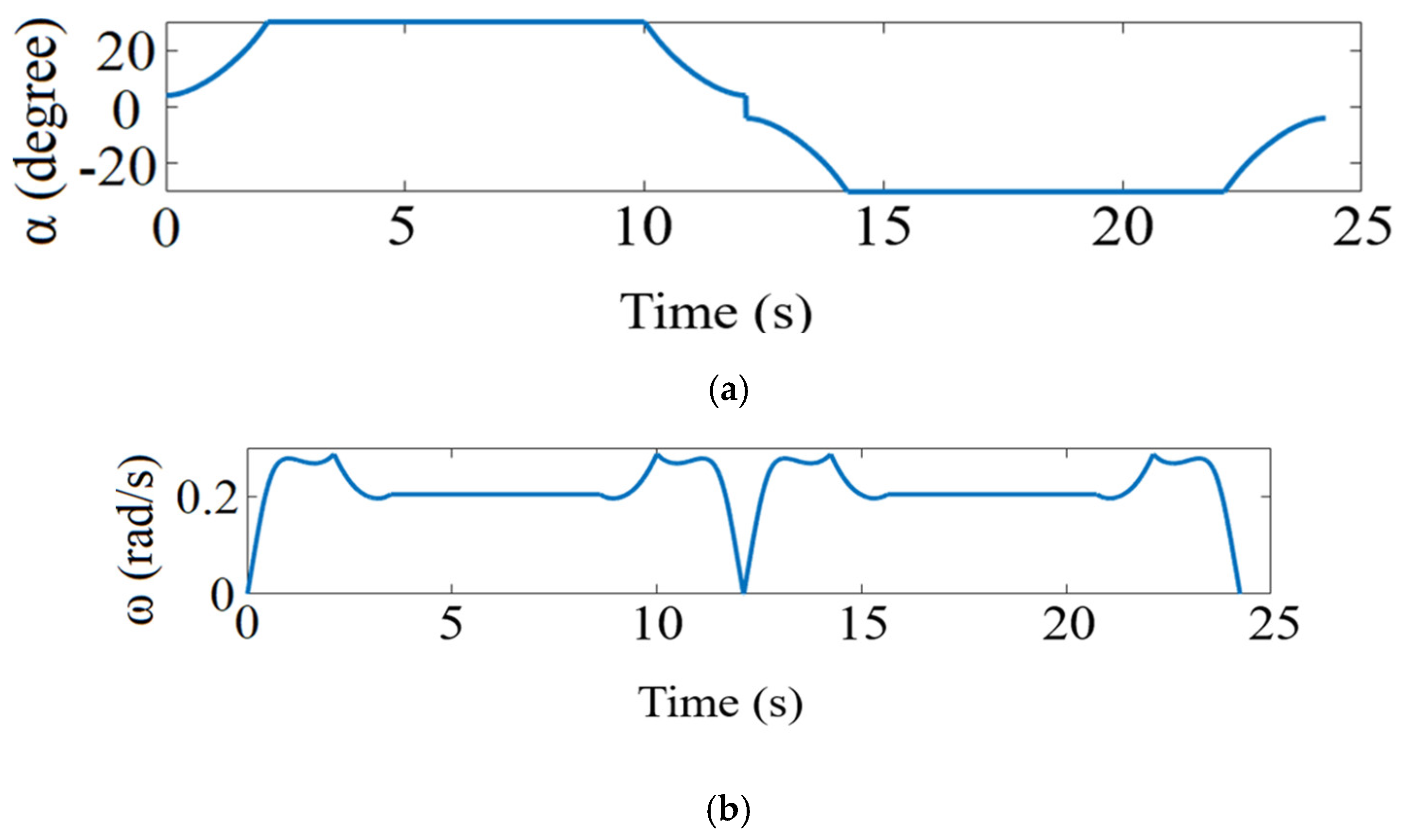Assuming that the tape width of the composite filament is 0.5 cm and ${\alpha }_c={30}^{°}$, the time response of the winding angle $\alpha$ and the cylinder rotating speed $\omega$ on the one cylinder end are shown in Figure 5. Owing to the symmetrical property, the response of $\alpha$ and $\omega$ for a round-trip winding are as illustrated in Figure 6.

C.

Winding path analysis

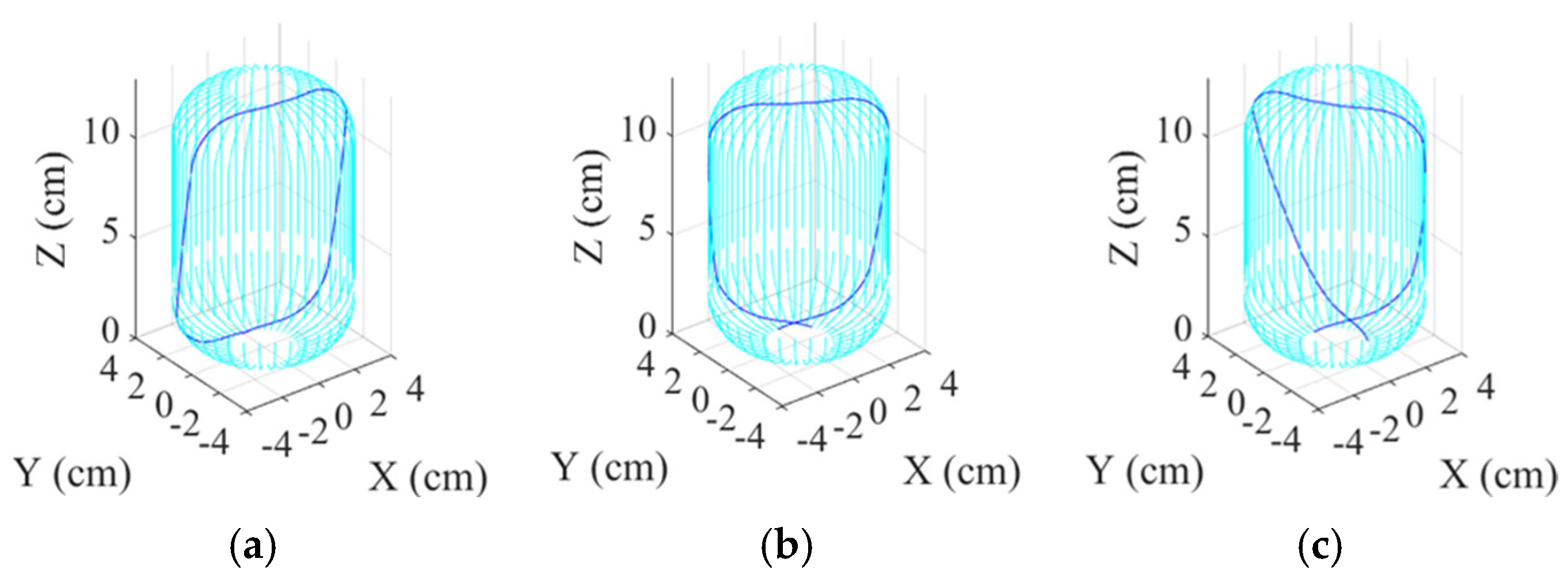
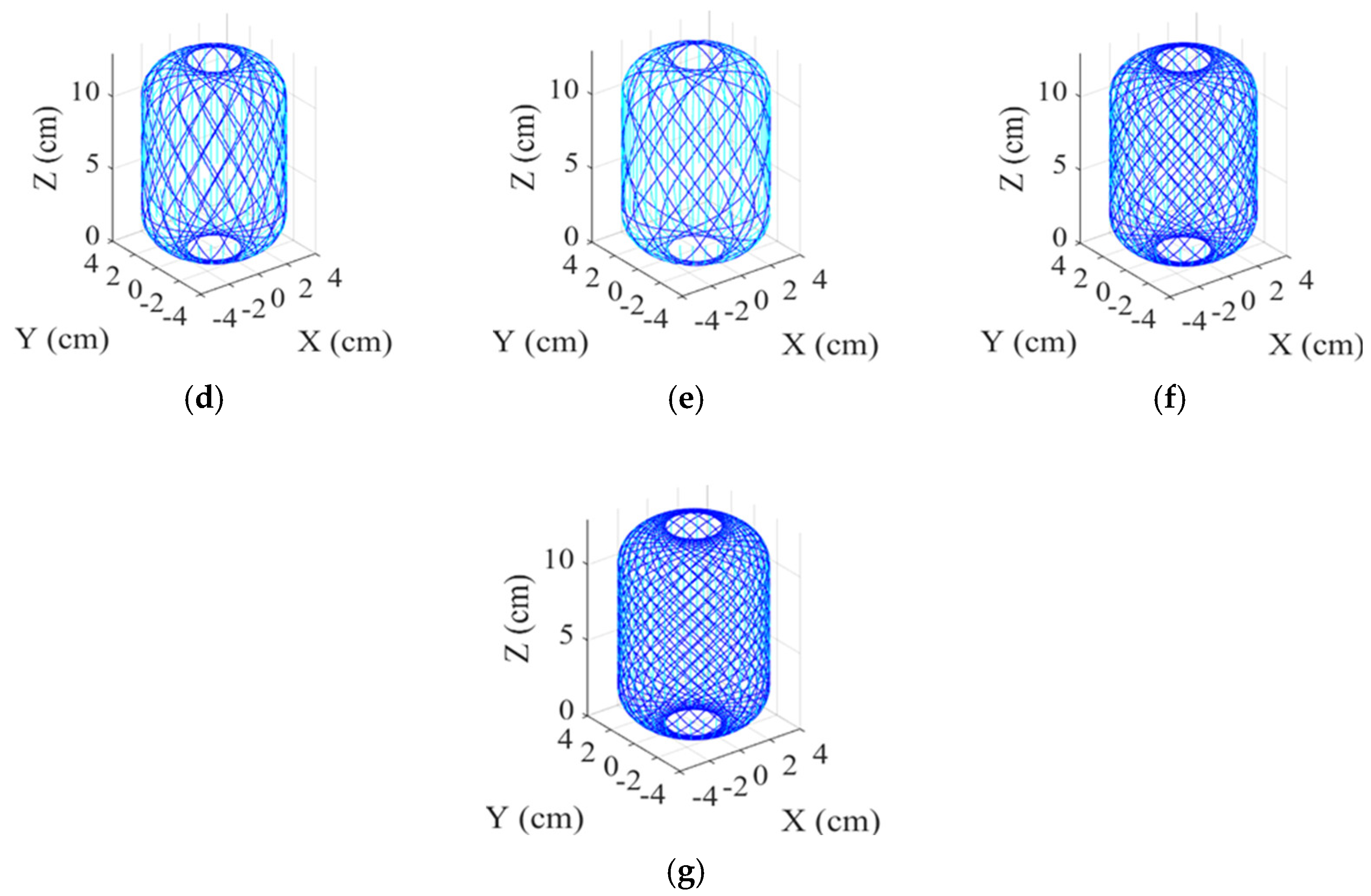
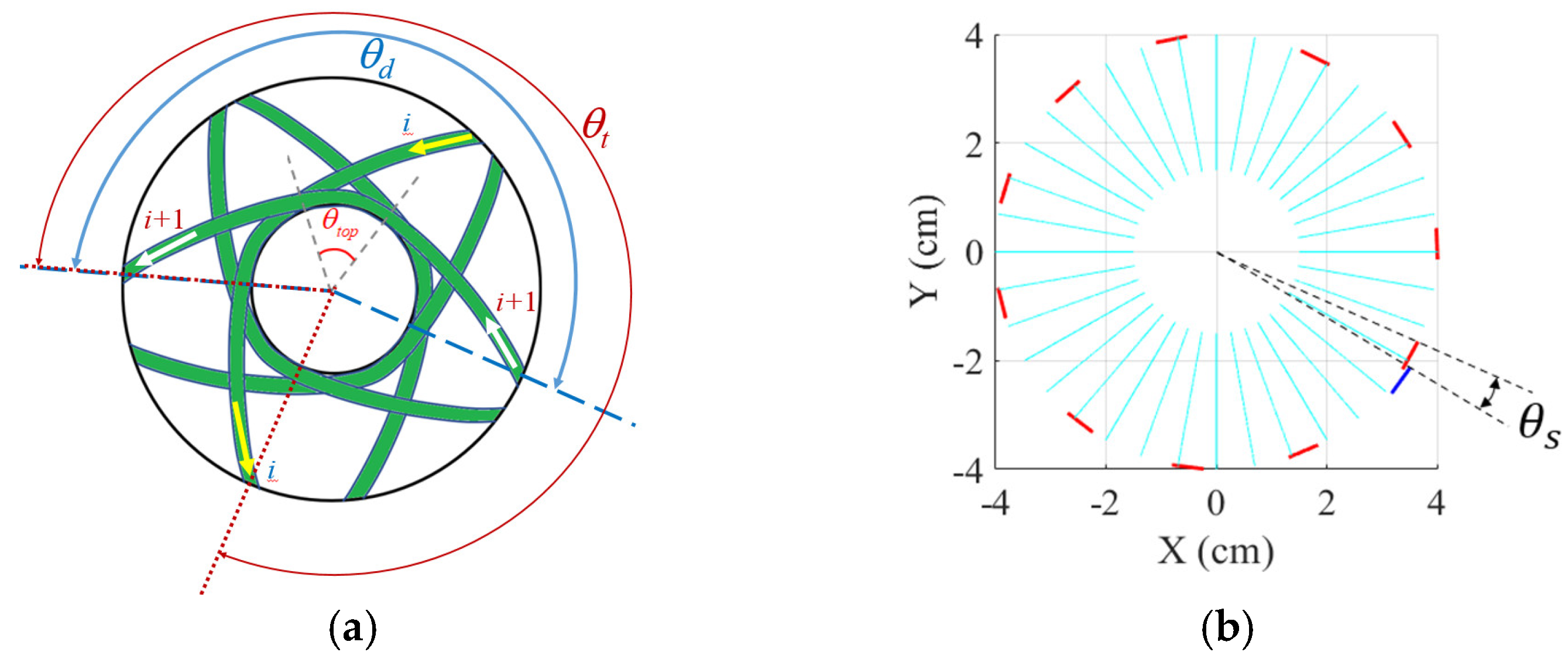
In practical applications, the cylindrical winding angles are between 10° and 40°. For illustrative purposes, the resulting thickness after one complete coverage will be evaluated for each interval of 5°. Based on the cylinder shown in Figure 2, the round-trip winding path of different cylindrical winding angles are shown in Figure 7. Let ${\theta }_d$ denote the angular position difference between the entering and leaving of filament on cylinder end, and ${\theta }_t$ denote the angular position difference after a round trip winding as shown in Figure 8 and Figure 9 It can be obtained that:

$${\mathsf{\theta }}_{\mathrm{t}}=mod\left(\left(\frac{Ltan\alpha }{R}+{\theta }_d\right)\times 2,2\pi \right)$$

(21)

Suppose one complete coverage winding comprises m full-cycle windings and one full-cycle winding consists of i round-trip windings, where i is determined as the maximum number of round-trip windings without parallel overlapping between filaments. Define ${\theta }_s$ as the angular position difference between the i + 1 round-trip winding and the first round-trip winding as shown in Figure 8b, then ${\theta }_s$ can be determined by:

$$\left\{\begin{array}{c}{\theta }_s=mod\left({\theta }_t\times i,2\pi \right)\le \frac{W_f}{Y_{eq}cos{\alpha }_c},for 0<mod\left({\theta }_t\times i,2\pi \right)\le \frac{W_f}{Y_{eq}cos{\alpha }_c}\\ {\theta }_s=2\pi -mod\left({\theta }_t\times i,2\pi \right)\le \frac{W_f}{Y_{eq}cos{\alpha }_c},for mod\left({\theta }_t\times i,2\pi \right)\ge 2\pi -\frac{W_f}{Y_{eq}cos{\alpha }_c}\end{array}\right.$$

(22)

where mod (.) is the remainder calculation. Under relational Equations (21) and (22), the path of one full-cycle winding can be obtained for a given ${\alpha }_c$. The simulation results of the case study are shown in Figure 10. After completion of a full-cycle winding, the maximum angular position difference can be denoted as ${\theta }_m$ and the overlapping angle of the i + 1 and the first round-trip winding is ${\theta }_c$ as shown in Figure 11. Then, the requires number of full-cycle winding to have one full-coverage can be obtained by:

$$s=ceil\left({\theta }_m,\frac{W_f}{\mathit{cos}\alpha }\right)$$

(23)

where ceil (.) is the unconditional carry quotient. Subsequently, the total number of round-trip winding (t_w) for one full coverage is:

$$t_w=i\times s$$

(24)

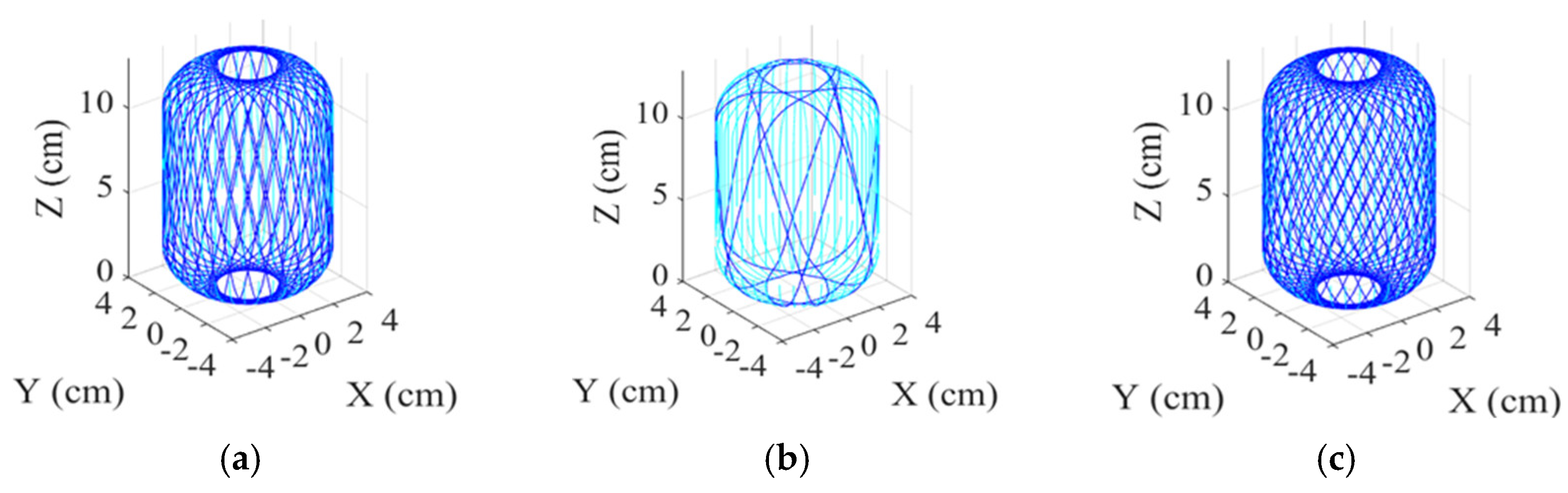
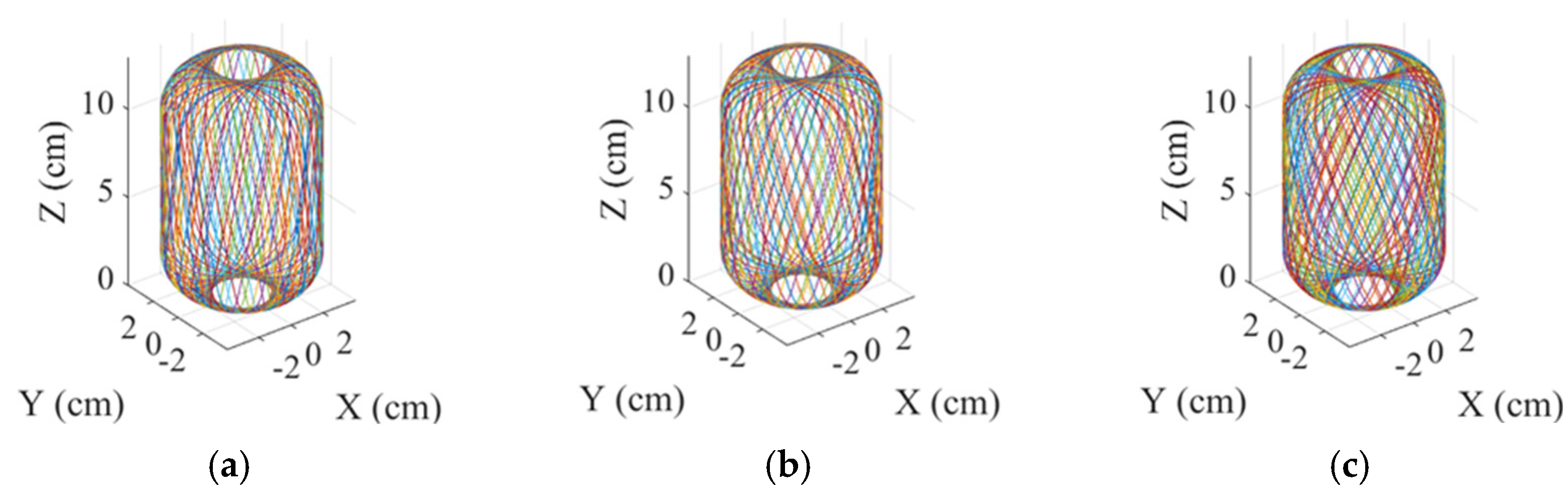
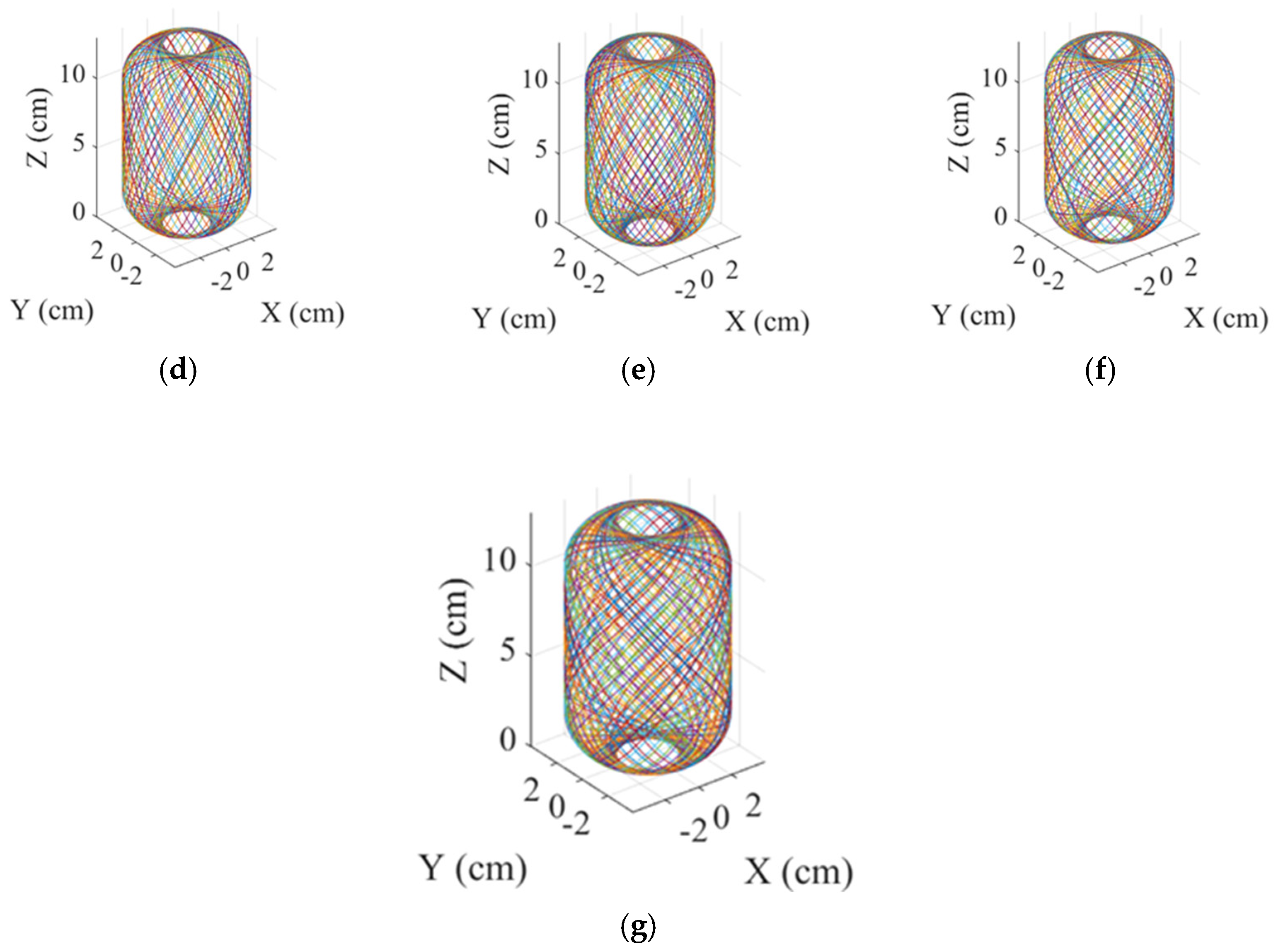
Figure 12 shows paths of one complete winding for different cylindrical winding angles. In

Table 1. Number of round-trip windings to complete one full coverage with different cylindrical winding angles.

V	Number of Times (i) to Wind One Set	Total Number of Winding Sets (s)
10	30	2
15	6	9
20	35	2
25	17	3
30	11	5
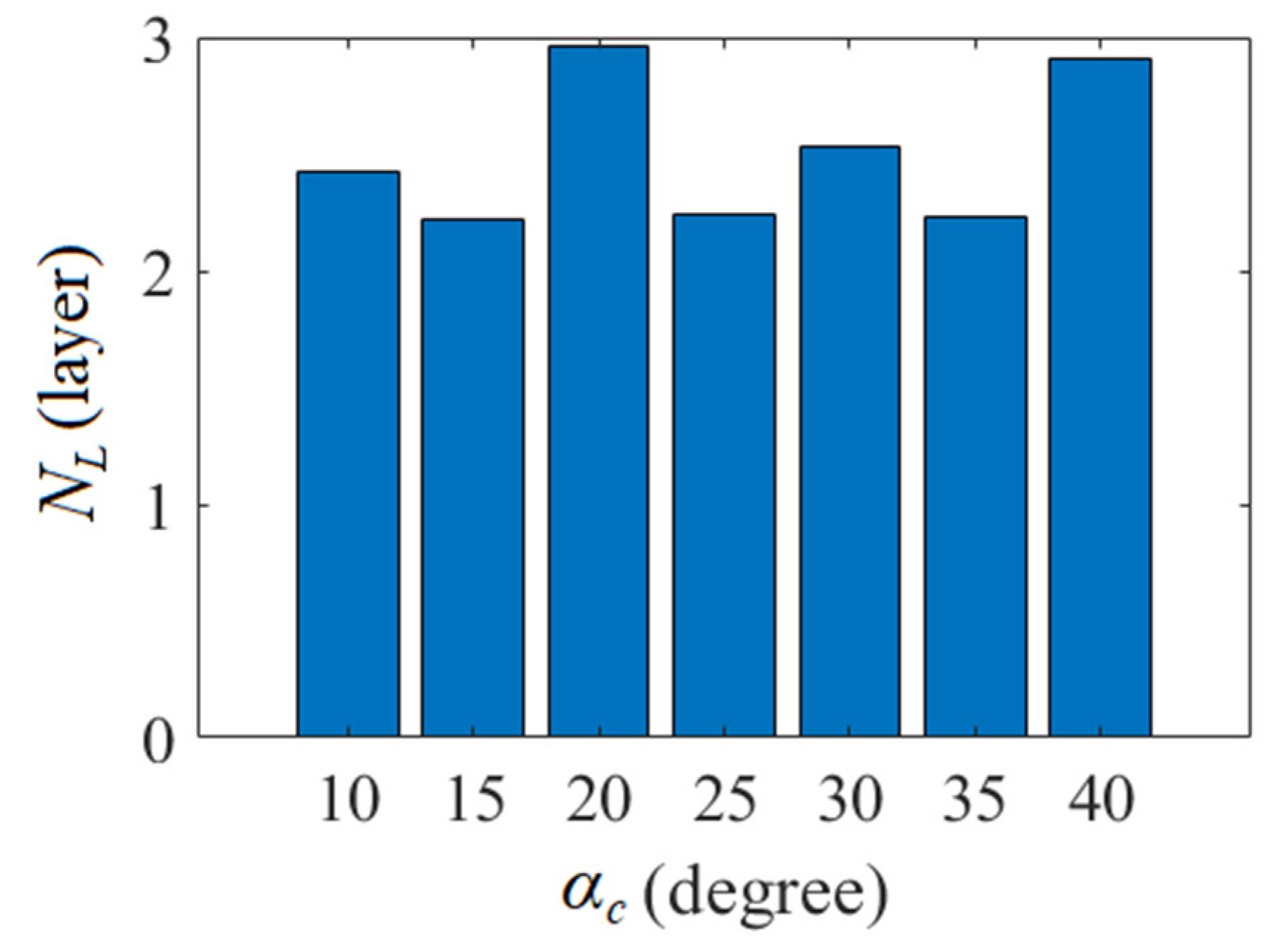
35	23	2
40	28	2

, it shows the Number of round-trip windings to complete one full coverage with different cylindrical winding angles.

Based on the complete winding path obtained, the distribution of filament thickness can then be analyzed to ensure the required strength of the gas cylinder. The average number of filament layers $N_L$ on the cylinder surface with cross-section radius $\rho$ can be determined by:

$$N_L\left(\rho \right)=\frac{\frac{W_f}{cos\alpha }\times t_w\times 2}{2\times \pi \times \rho }$$

(25)

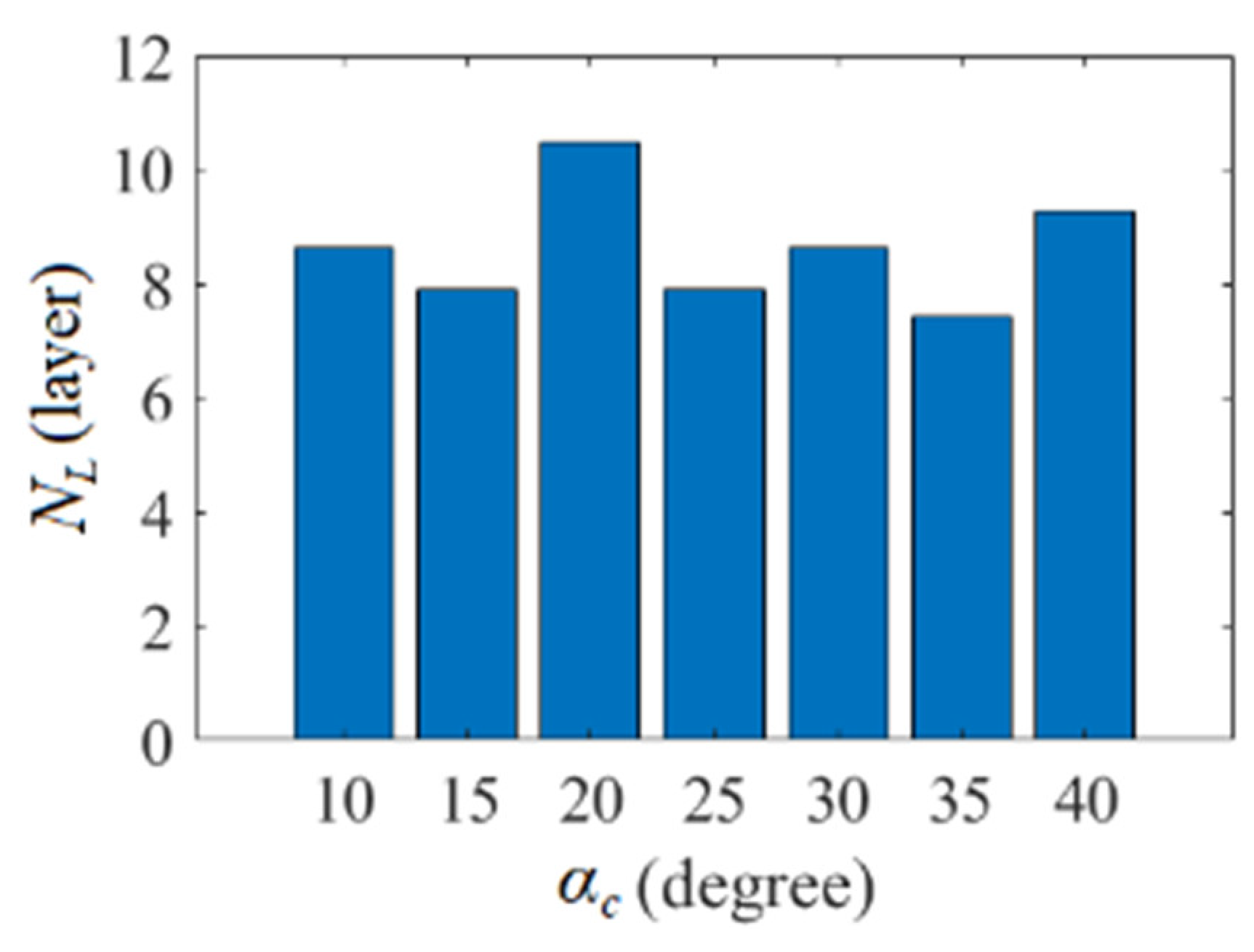
for the case that the gas cylinder has been wound back and forth t_w times. By Equation (25), the average layers of coverage at the joint ends $\rho$ = Y_eq with different ${\alpha }_c$ are shown in Figure 13.

For alignment purposes for subsequent cycles, the last round-trip winding of the prior cycle may require winding extra ${\theta }_c$ at the end circumference with smallest radius; therefore, N_L will be described by

$$N_L\left(\rho \right)=\frac{t_w\times \rho \times {\theta }_{top}+\left(s-1\right)\times \rho \times {\theta }_c}{2\times \pi \times \rho }$$

(26)

For the study case, the average number of layers at the end of the gas cylinder can be estimated and shown as in Figure 14.

3. Stress and Strength Analysis of Reinforced Gas Cylinders Wound with Composite

After completion of a full coverage winding, the stress and strength analysis can be carried out to ensure the specifications of the resulting gas cylinder. This study uses the ANSYS software to analyze the stress distribution of gas cylinders. Regarding the structural system, gas cylinders use the structural steel listed in the ANSYS database as the inner material. Take the gas cylinder in Figure 2 with a thickness of 0.1 cm as an example. A 1/8 model can be used for computational analysis owing to the geometric symmetry of the gas cylinder, as shown in Figure 15.

For the ANSYS Composite PrepPost (ACP) system analysis, T700 carbon fiber produced by Toray of Japan and EPIKURE 3234 resin is used. The materials data is shown in

Table 2. Specifications of hybrid composite made of T700 carbon fiber and EPIKURE 3234 resin.

Composite Carbon Fiber Bundle Tow	6 K	12 K	24 K
Mass per unit length	400 g/1000 m	800 g/1000 m	1650 g/1000 m
Tensile strength	2100 MPa (X)	24 MPa (Y)	65 MPa (Z)
Young’s modulus	132 GPa (X)	10.3 GPa (Y)	10.3 GPa (Z)
Poisson’s ratio	0.25 (XY)	0.38 (YZ)	0.25 (XZ)
String density		$1.57 \mathrm{g}/\mathrm{c}{\mathrm{m}}^3$
Carbon fiber diameter		7 μm
Shear modulus	6500 MPa (XY)	3910 MPa (YZ)	6500 MPa (XZ)
Shear stress	75 MPa (X)	75 MPa (Y)	75 MPa (Z)
Compressive strength	1050 MPa (X)	132 MPa (Y)	132 MPa (Z)

, and the second column of 12 K specifications were used for this study.

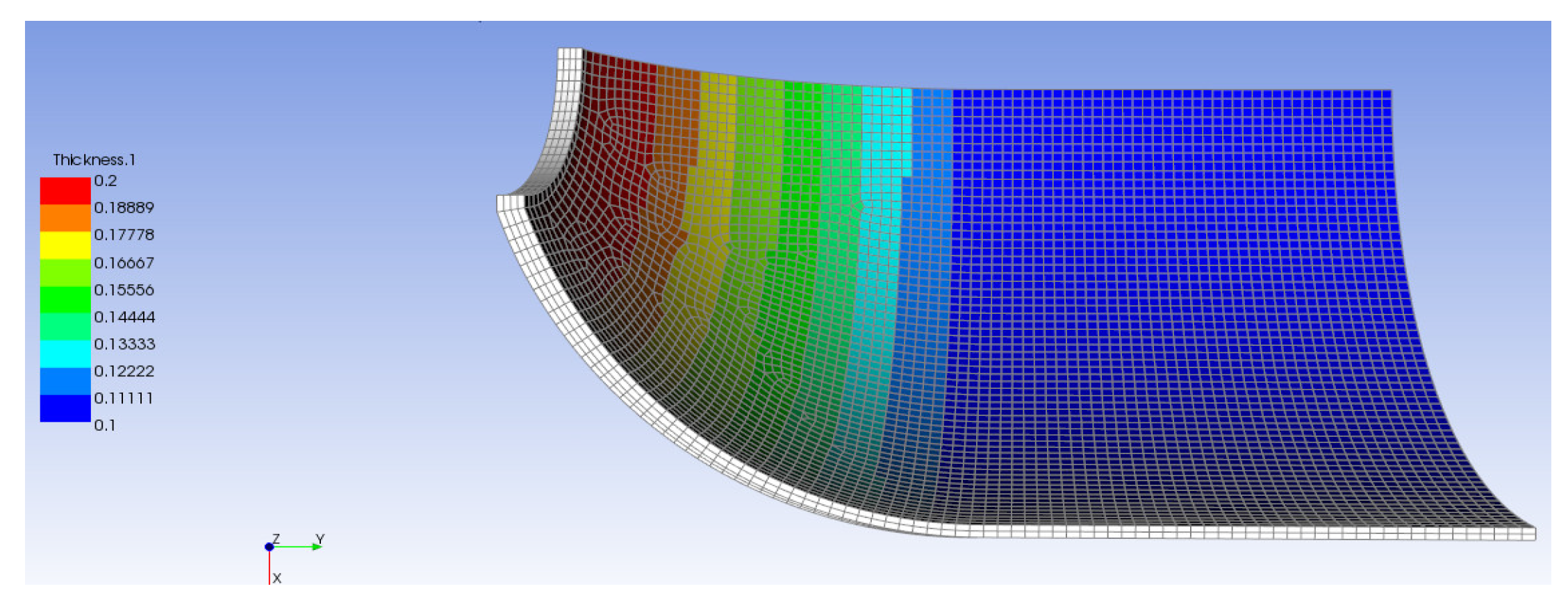
Take the cylindrical winding angle of 30° as an example. For one full coverage winding, the filament will cover the central cylinder surface twice, contributed by one layer with an angle of +30° and the other layer with an angle of −30°. The end cap is also wound at two different angles round-trip, but the winding angles and the number of layers of coverage are determined by Equations (25) and (26). Take the thickness of 0.05 cm for a single layer of composite filament as an example; the thickness distribution of the outer lining by composite materials can be constructed as shown in Figure 16.

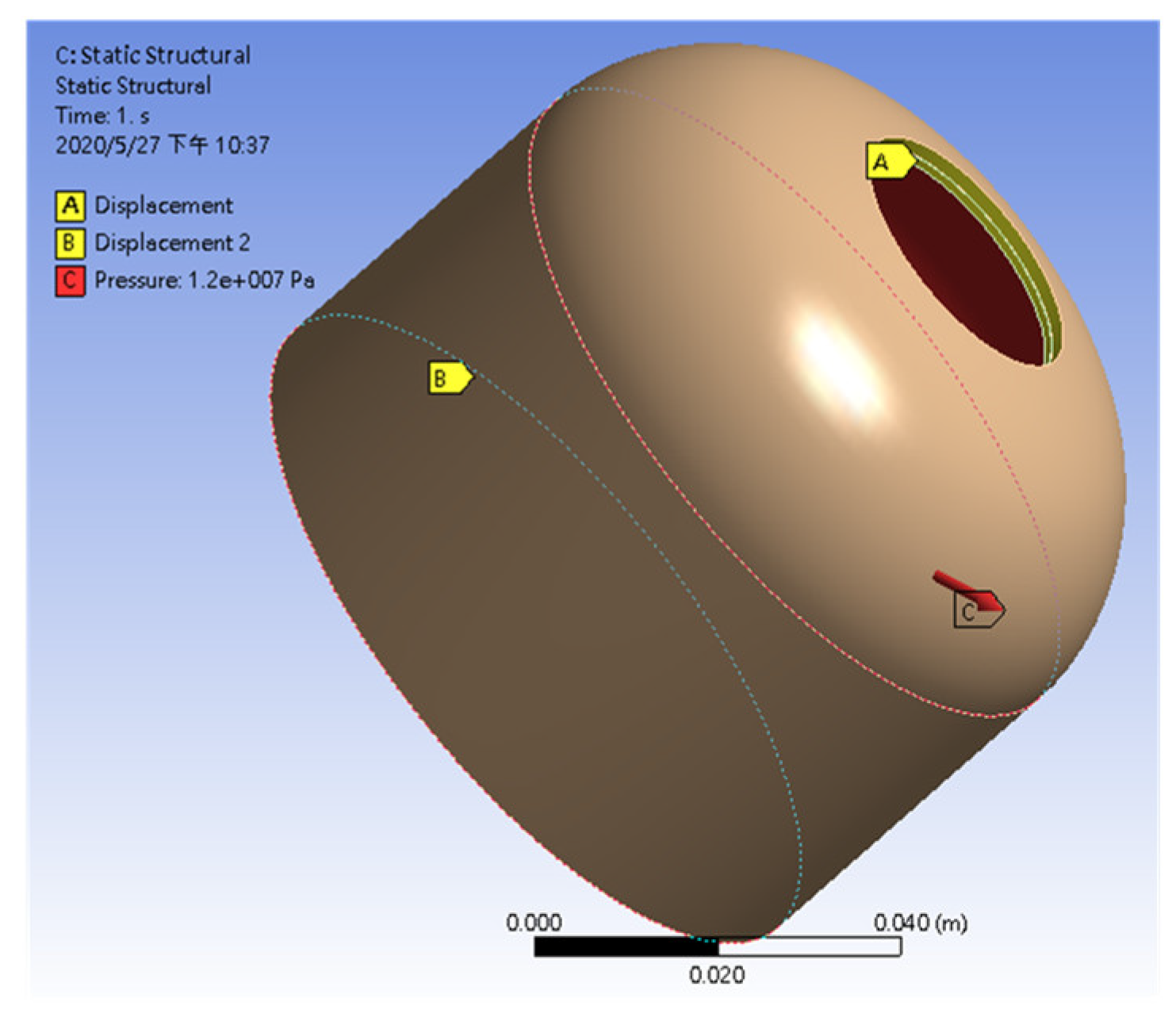
Based on geometric symmetry, the boundary conditions for cross-sections A, B and C, shown in Figure 17, are described as follows. Cross-section A only arrows a displacement along the Z direction, i.e., it is constrained by ΔX = 0 and ΔY = 0. The fact that the membrane thickness of the cylinder end is much larger than that of the cylinder body and the corresponding strength in X and Y direction is very high should be noted. Cross-section B is the symmetry plane of the cylinder, which only arrows displacement in X and Y directions, i.e., it is constrained by ΔZ = 0. For the gas cylinder to withstand a pressure difference of 120 bar, the face C has the pressure boundary condition of 12 MPa outwards.

By adopting the Tsai-Wu failure criterion [23] for failure analysis, it reveals that after completing one full coverage by carbon fiber, the maximum damage value is 0.76157, as shown in Figure 18. As the damage values are all less than 1, the filament reinforcement gas cylinder in this example is capable of withstanding pressure up to 120 bar.

A failure analysis of one complete coverage was conducted for cylindrical winding angles of ${10}^{°}~{40}^{°}$ and the results are shown in

Table 3. Length of material needed to complete one full coverage, and the associated failure criterion index value.

Cylinder Winding Angle °C	Max. Index Value	Min. Index Value	Equatorial Thickness (Layer)	Total Winding Length (cm)
10°	0.8548	0.1598	2.4241	2261.5
15°	0.8264	0.1618	2.2243	2086.8
20°	0.7934	0.1329	2.9639	2792.4
25°	0.7787	0.1172	2.239	2115.5
30°	0.7615	0.1031	2.5269	2388.6
35°	0.7389	0.0938	2.2343	2110.1
40°	0.7124	0.0869	2.9086	2737.6

. It illustrated that all seven winding patterns could withstand the pressure of 120 bar. However, due to the fact that the lateral (secondary axis direction) tensile strength of the carbon fiber composite is much lower than the tensile strength of the primary axis direction, the failure index of the cylindrical winding angle of 10° is closer to 1 than the other.

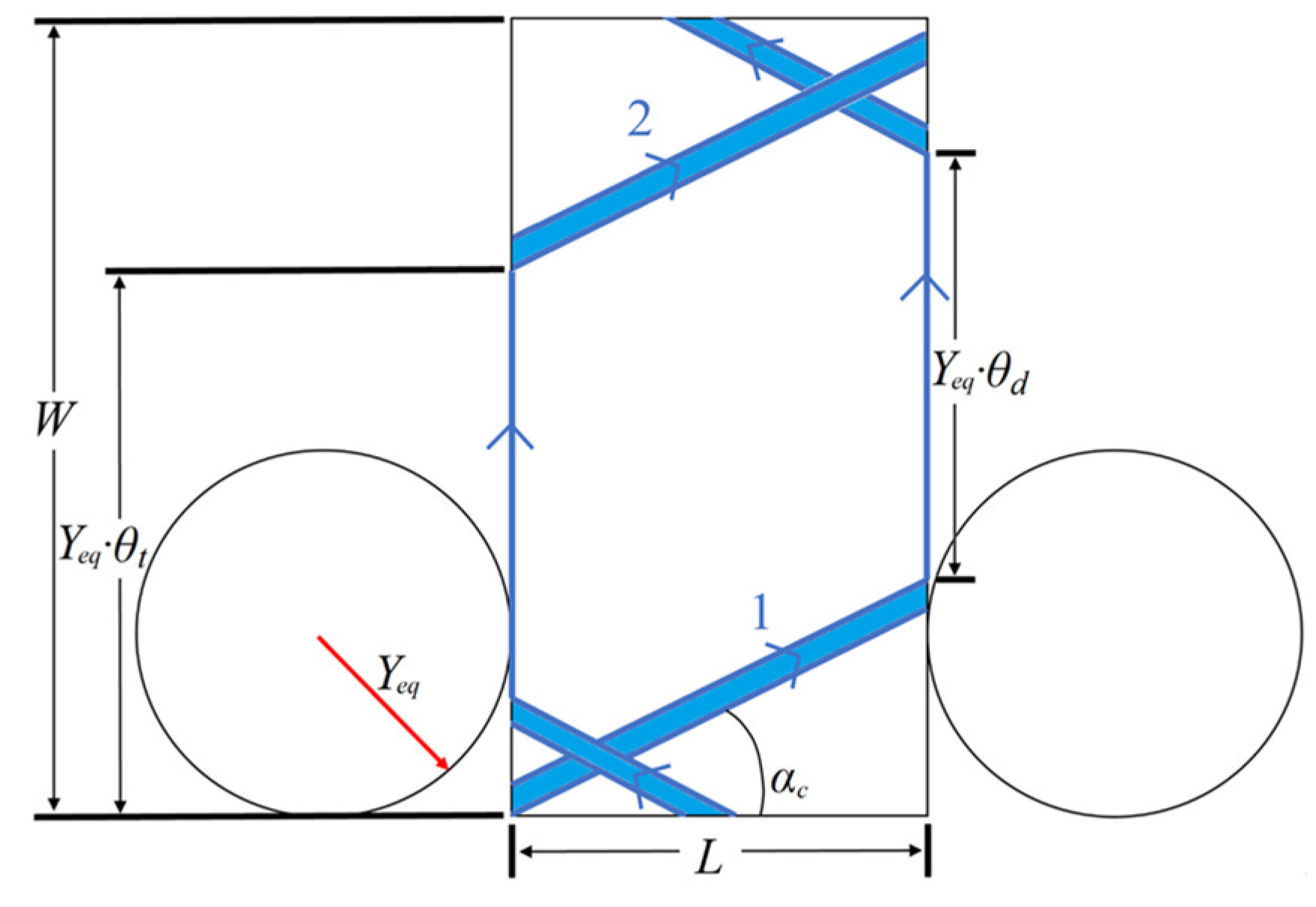
The winding path of the end cap surface is used to calculate the length of the composite materials by piecewise segmented accumulation. Suppose the length of the composite materials used for round-trip winding is $L_t$, the total length $L_{total}$ of composite materials required to complete one full coverage winding can be determined by

$$L_{total}=L_t\times i\times s+c\times {\theta }_C\times \left(s-1\right)$$

(27)

As shown in Table 3, the winding path with cylindrical winding angle ${\alpha }_c$ = 15° can be implemented with the least composite materials with a maximum failure criterion index of 0.8264 for one full coverage among the seven cases. It should be noticed that failure index is useful for the vessels used just once. However, for a rocket launching mission, high-pressure gas cylinders are considered disposable, and for this, the analysis can be used to reduce the costs associated with trial and error.

Based on the study in Section 2 and Section 3, the filament winding reinforcement design procedure for gas cylinders is summarized as follows.

• Determine the geometric parameters of the gas cylinder, including the diameter, the length of the cylinder, and the required withstanding pressure;
• Design the end cap surface geometry based on the withstanding pressure of the cylinder, the geodesic description system, and the composite stress matrix combination;
• According to the maximum static friction conditions, select the cylindrical winding angle ${\alpha }_c$ and determine the number of coverage layers required for the cylinder by stress and strength analysis;
• Realization of path and motion planning based on the winding pattern obtained in step 3. Subsequently, the motion commands for each machine axis can be determined, which will be described in the next section;
• Carry out motion control for each motion axis to complete filament winding.

4. Planning and Realization of Motion Paths of Four-Axis Filament Winding Machine

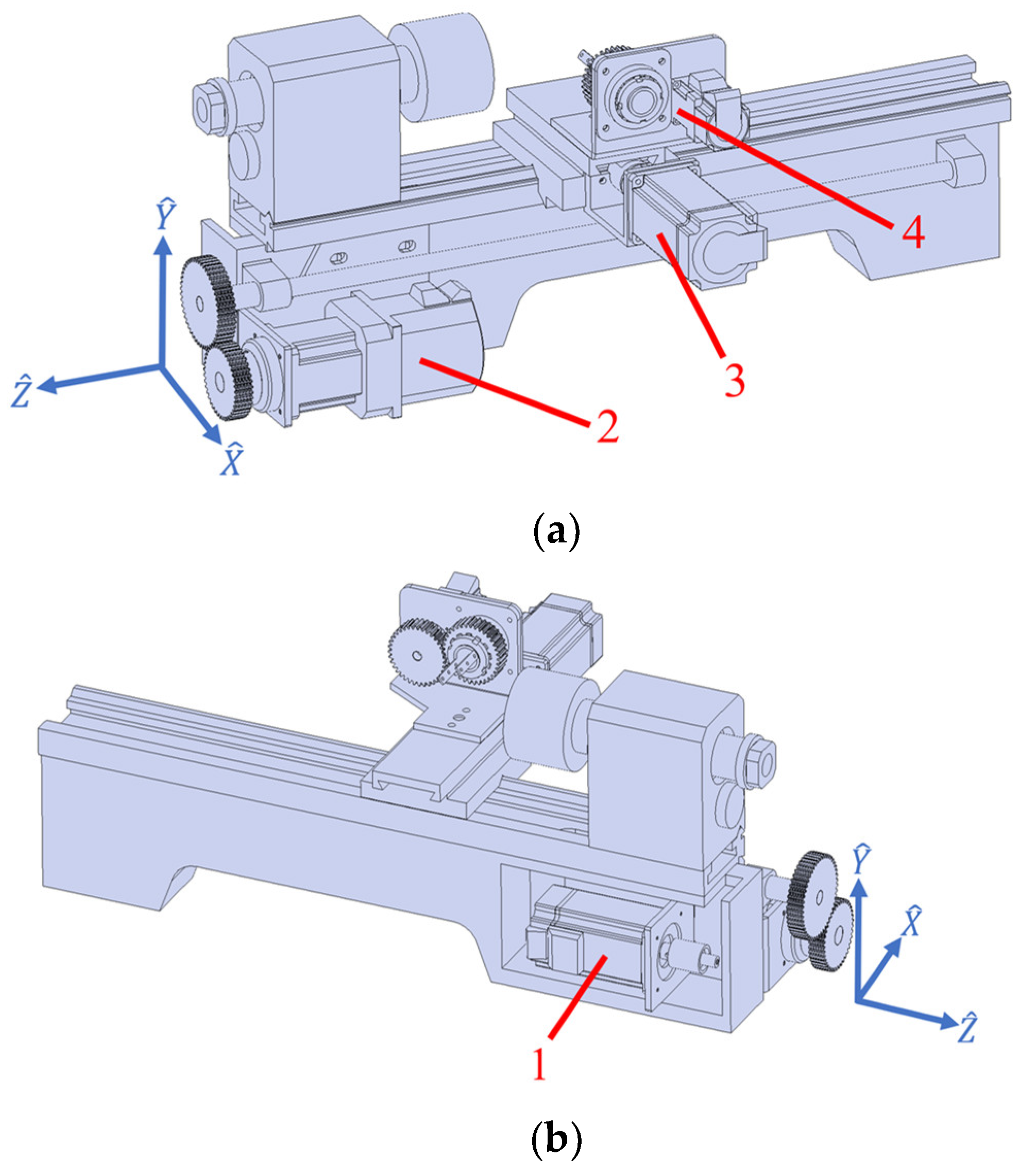
In this section, a four-axis winding machine, as shown in Figure 19, will be applied to perform the winding process. The motion axes geometry and their physical arrangement will be described in association with the winding motion. Implementation of real-time motion control will also be demonstrated to conduct the winding procedure.

The machine is organized to carry out filament winding for gas cylinders by adding an extra motion axis to a three-axis lathe. Translational motions along the $\widehat{X}$ axis (short) and $\widehat{Z}$ axis (long) are performed by motor 3 and 2, respectively. The rotational motions of the $\widehat{X}$ axis are driven by motor 4, and gas cylinder will be mounted along $\widehat{Z}$ axis and driven by motor 1 for the required cylinder rotating speed $\omega$.

A.

Motion control design

Since the $\widehat{Z}$-axis is the primary axis of the gas cylinder, its angle of rotation during the winding is the angle of rotation of the winding coordinate system ${\theta }_Z$. It can be obtained by the integral of the rotational speed $\omega$ of the gas cylinder. During a round-trip winding, the forward and return paths require the same amount of angular motions of ${\theta }_Z$. 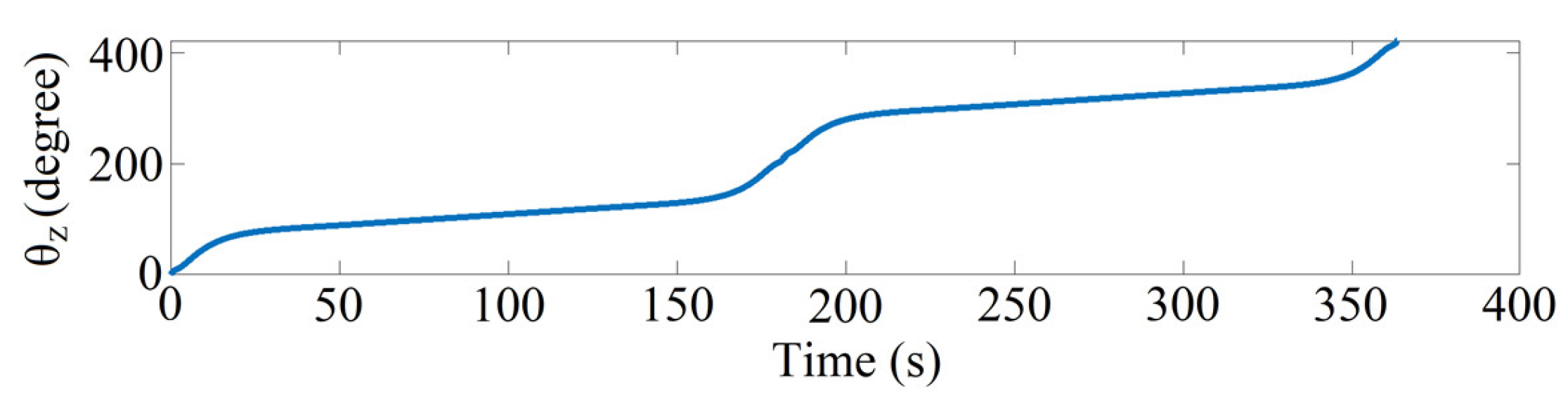Based on the proposed approach in Section 2 (b) and ${\alpha }_c$ = 15°, the time response of ${\theta }_Z$ relative to one round-trip winding can be illustrated as in Figure 20.

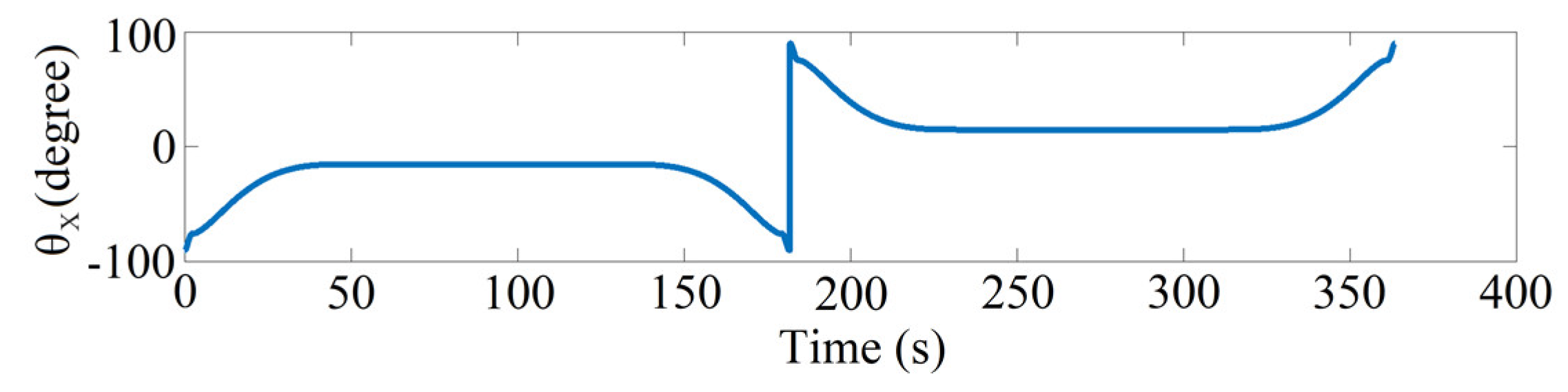
The rotation axis of the $\widehat{X}$-axis (${\theta }_x$) controls the rotation of the winding head. During the winding of the end cap, the angular displacement is obtained through the geodesic principle $R·sin\alpha =c_d$, where $R$ and $c_d$ is the instantaneous radius and geometric constant of the end cap, respectively. For the cylindrical winding angle of 15° and Y_eq = R = 4 cm, c_d = 1.0353 can be obtained, and ${\theta }_x$ for one round-trip winding can be obtained, as shown in Figure 21.

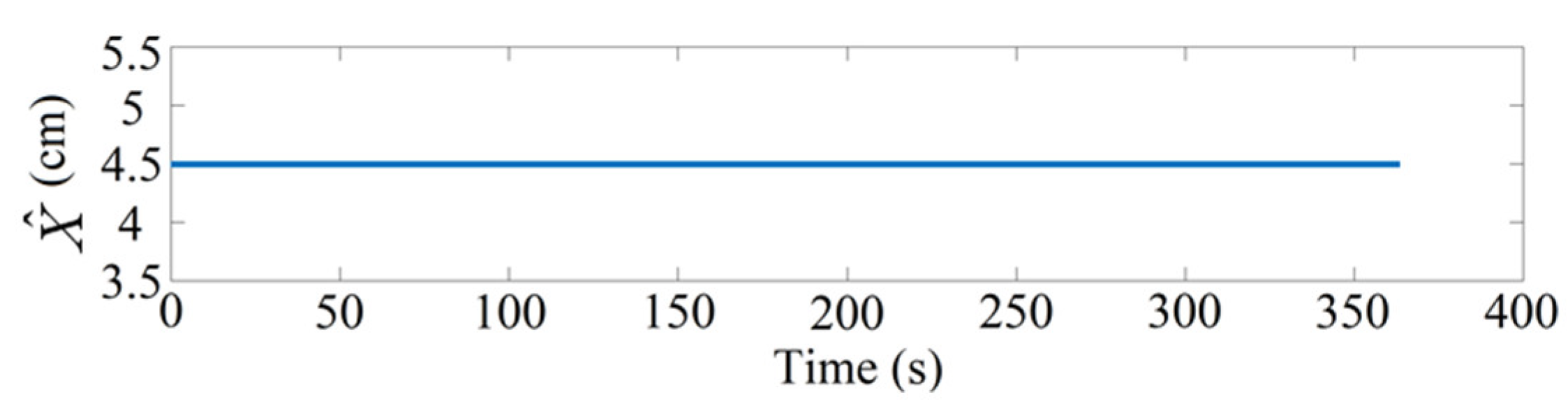
To avoid direct contact with the cylinder surface, the winding head moving in $\widehat{X}-\widehat{Z}$ plane will keep 0.5 cm from the cylinder in this illustration. Under a fixed winding radius, the position of the winding head on the $\widehat{X}$ axis during one complete winding is constant. Since R = 4 cm and thickness incensement is insignificant during one round-trip winding, the time response of the position along $\widehat{X}$-axis will be kept constant as shown in Figure 22.

The relative position from the contact end point to the winding head roller can be represented by $\widehat{t}$, its vector components to the $\widehat{X}$, $\widehat{Y}$, and $\widehat{Z}$ can be obtained by the angle $\theta$ between the ${\widehat{e}}_r$-axis and the $\widehat{X}$-axis, the angle $\varphi$ between the $\widehat{T}$-axis and the ${\widehat{e}}_z$-axis, and the angle $\alpha$ between the $\widehat{T}$-axis and the $\widehat{t}$-axis, as shown in Figure 1. Based on the coordinate transformation described Equations (5) and (6), and assuming that the distance between the instantaneous contact end point on the cylinder and the winding head is of magnitude d_t, and its component in the $\widehat{Z}$ direction is d_z, then the position of the winding head roller in the winding coordinate system $\left(\widehat{t},\widehat{n},\widehat{b}\right)$ can be described in coordinate $\left(\widehat{X},\widehat{Y},\widehat{Z}\right)$ as:

$$\left[\begin{array}{c}{d}_t\\ 0\\ 0\end{array}\right]=\left[\begin{array}{ccc}C\alpha S\varphi C\theta +S\alpha S\theta & -C\alpha S\varphi S\theta +S\alpha C\theta & C\alpha C\varphi \\ C\varphi C\theta & -C\varphi S\theta & -S\varphi \\ -S\alpha S\varphi C\theta +C\alpha S\theta & S\alpha S\varphi C\theta +C\alpha S\theta & -S\alpha C\varphi \end{array}\right]\left[\begin{array}{c}4.5-\rho c\theta \\ -\rho s\theta \\ d_Z\end{array}\right]$$

(28)

$$\left[\begin{array}{c}{d}_t\\ 0\\ 0\end{array}\right]=\left[\begin{array}{ccc}C\alpha S\varphi C\theta -S\alpha S\theta & -C\alpha S\varphi S\theta -S\alpha C\theta & C\alpha C\varphi \\ C\varphi C\theta & -C\varphi S\theta & -S\varphi \\ -S\alpha S\varphi C\theta -C\alpha S\theta & S\alpha S\varphi C\theta -C\alpha S\theta & -S\alpha C\varphi \end{array}\right]\left[\begin{array}{c}4.5-\rho c\theta \\ -\rho s\theta \\ d_Z\end{array}\right]$$

(29)

By the constraint relations, it can be obtained that:

$$d_{\mathrm{Z}}=\frac{4.5cos\varphi cos\theta -\rho cos\varphi {\mathit{cos}}^2\theta \rho cos\varphi {\mathit{sin}}^2\theta }{sin\varphi }$$

(30)

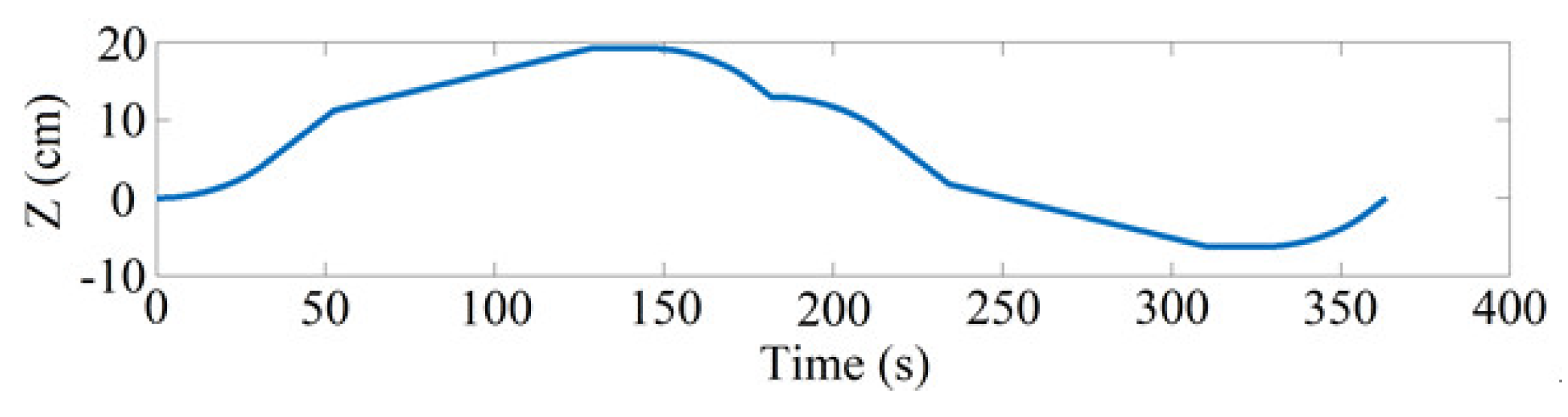
Therefore, the position of the winding head roller that moves along the $\widehat{Z}$-axis direction can be obtained by adding d_z to the $\widehat{Z}$-direction component of the contact endpoint. The time response of the winding head roller can then be obtained, as shown in Figure 23 for the demonstrated case.

B.

Realization of four-axis motion control

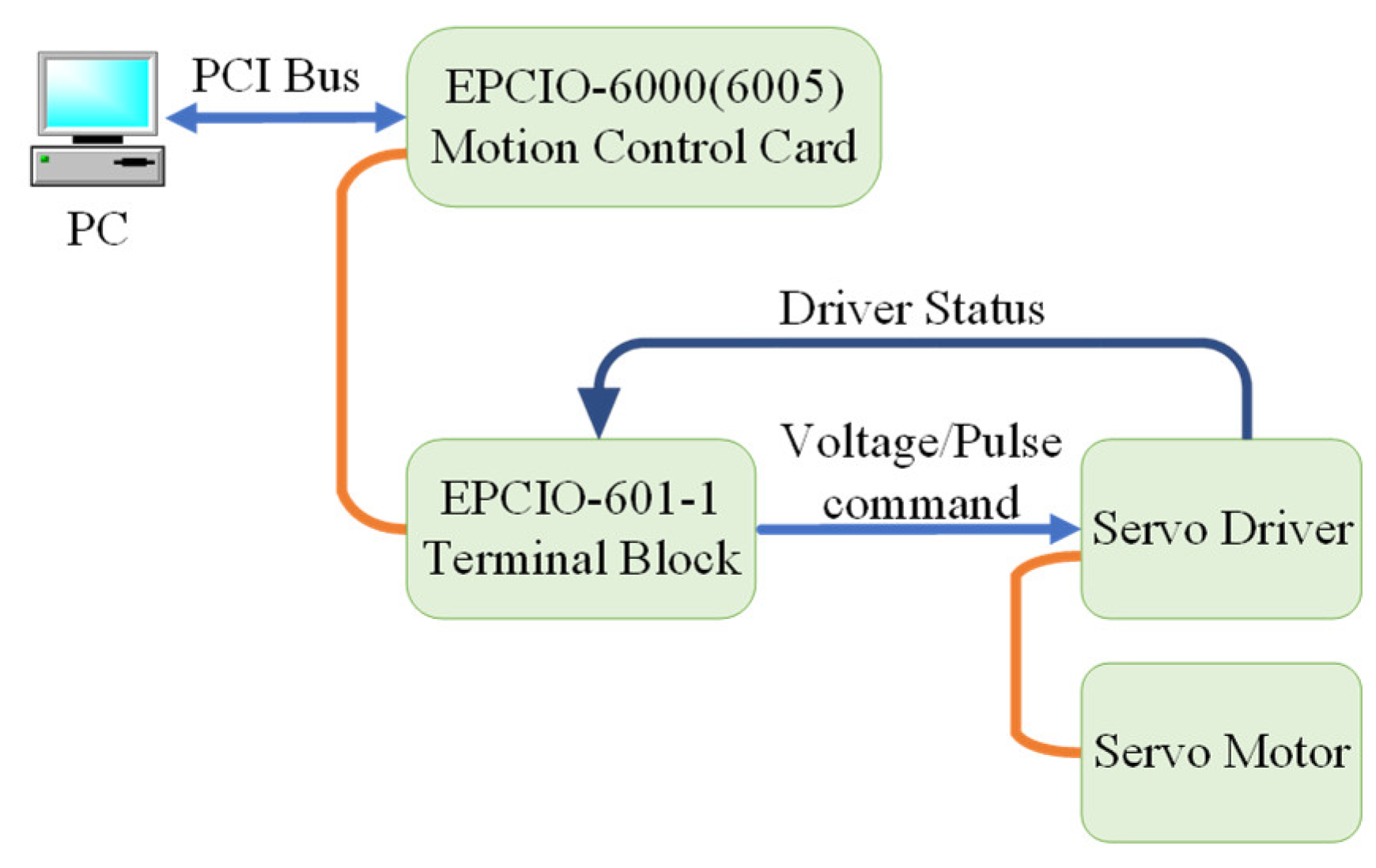
The four-axis motor of the filament winding machine is driven by the motion control interface card through the PCI port of the computer, as shown in Figure 24, such that the motor follows the generated command shown in Section 4 (A).

The Visual Studio C++ was applied as the development environment of the axis motion control interface card and control software. Because the EPCIO driver card can only execute integer pulse commands, continuing to use unconditional carry or round down of the position commands will cause significant cumulative errors. Therefore, in addition to adopting the rounding method, the error caused by rounding up or down must be temporarily stored. When the accumulated value reaches a prescribed threshold, the accumulated integer will be added to the following pulse command of DDA_Time as motion compensation.

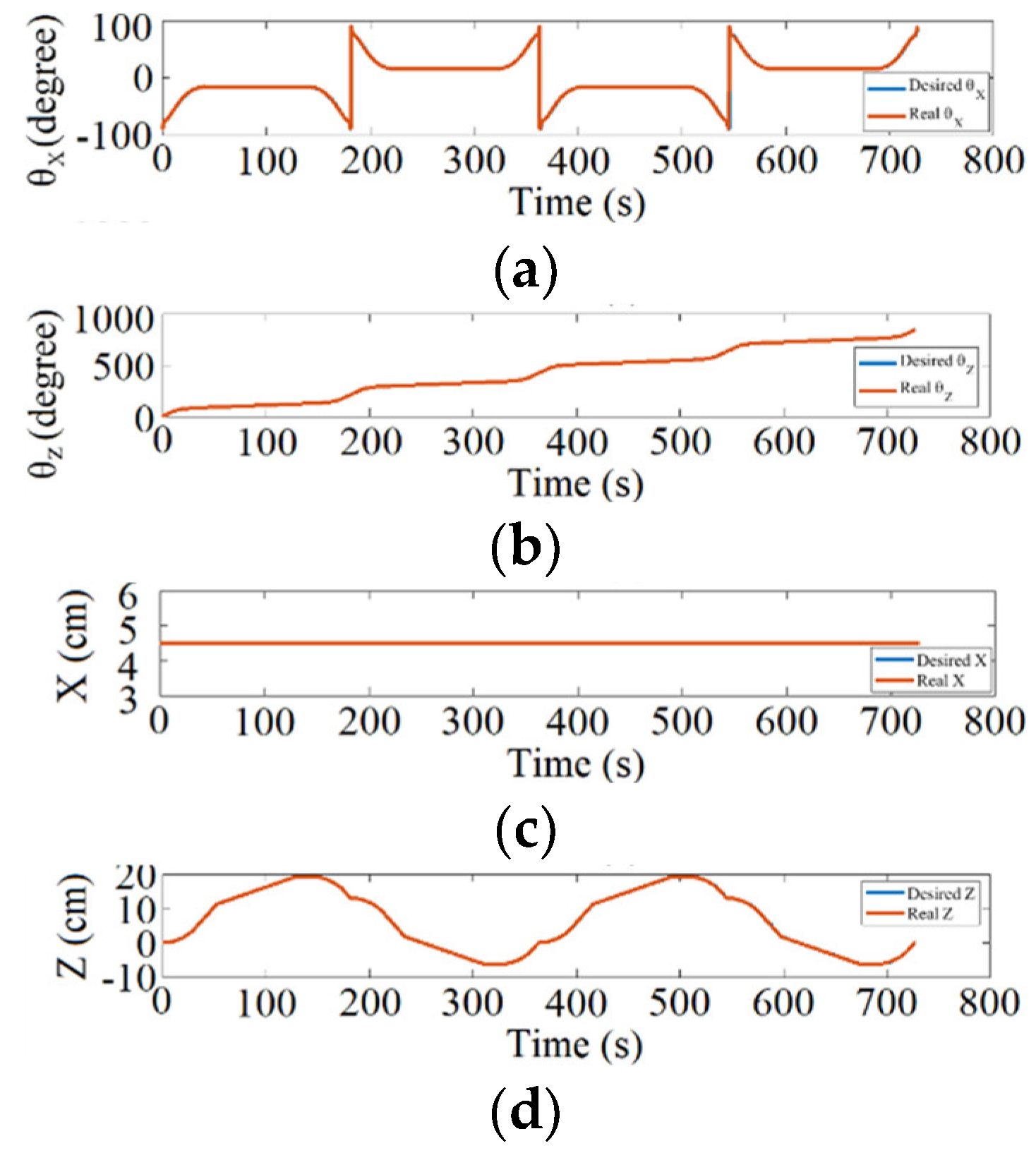
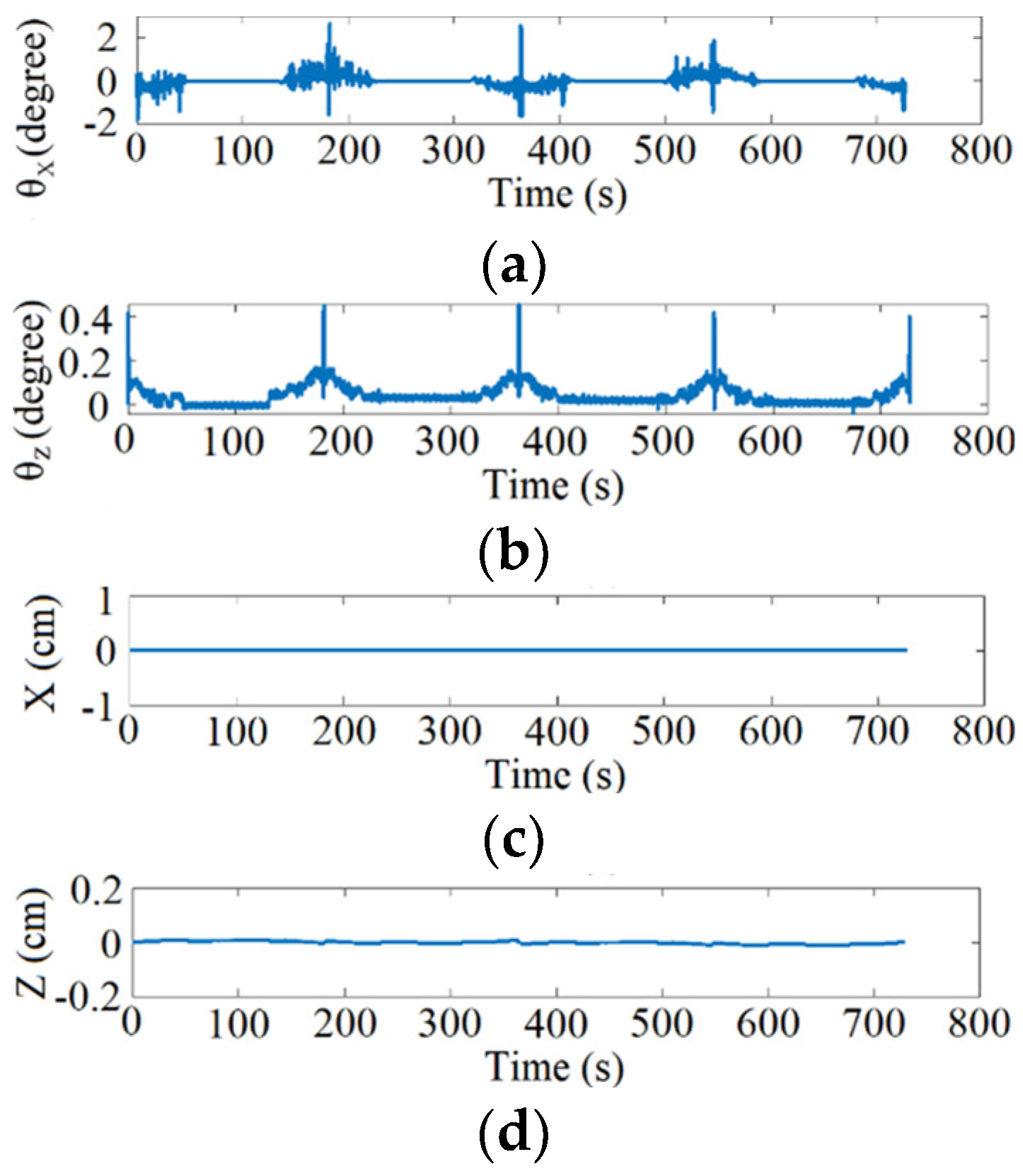
Figure 25 shows the desired and resulting motion response, and Figure 26 shows the error response of the four-axis motion for two round-trip winding. The error can be adjusted by the prescribed threshold and its influence on winding will be limited due to the usage of absolute position reference command instead of incremental type. Figure 27 demonstrates the winding result during two round-trip windings in practice.

5. Conclusions

In this paper, the design of filament winding for gas cylinders under a requested pressure was analyzed based on the cylinder winding angles and cylinders shape. The winding thickness distribution and strength of the pressure vessel were studied according to the winding path and pattern using the least amount of material obtained for the winding process. This article also proposed a procedure to realize motion commands for a four-axis winding machine. Visual Studio carried out implementation with a motion control interface card to confirm the resulting performance. Based on this result, a customized design and development of filament winding for gas cylinders can be systematically conducted.