Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing
Abstract
1. Introduction
2. Methods and Materials
2.1. Lubricants Retention Ability Assessment
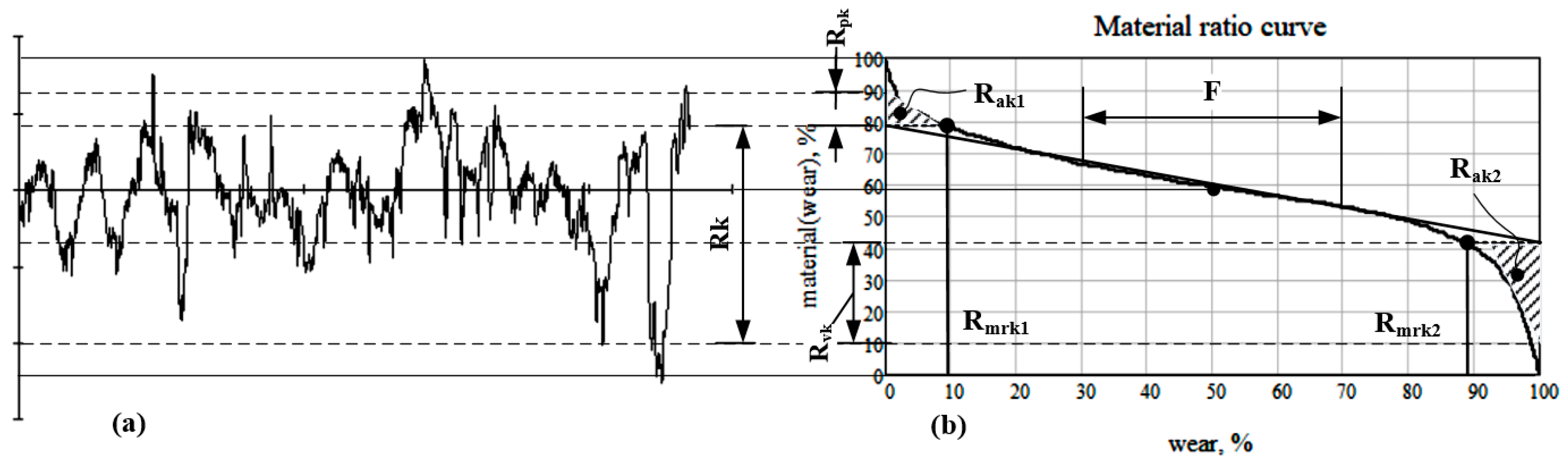
2.2. Methodology for the Build the Material Ratio Curve on the Measured Profilograms Basis, and the Operational Parameters Determination
- –
- —a vector, which contains the calculated material ratios within the RMR total height, in percent;
- –
- —denotes the indexes of the total height levels, and number of the measured values in the evaluation length distance;
- –
- μm—the total height of the R-profile according to the ISO 21920-2 standard;
- –
- mm—the evaluation length of the R-profile;
- –
- Rml, mm—the material length of the R-profile at the given c—level;
- –
- Δ, μm—the discrete’ length along to x-axis of the measured profilogram.
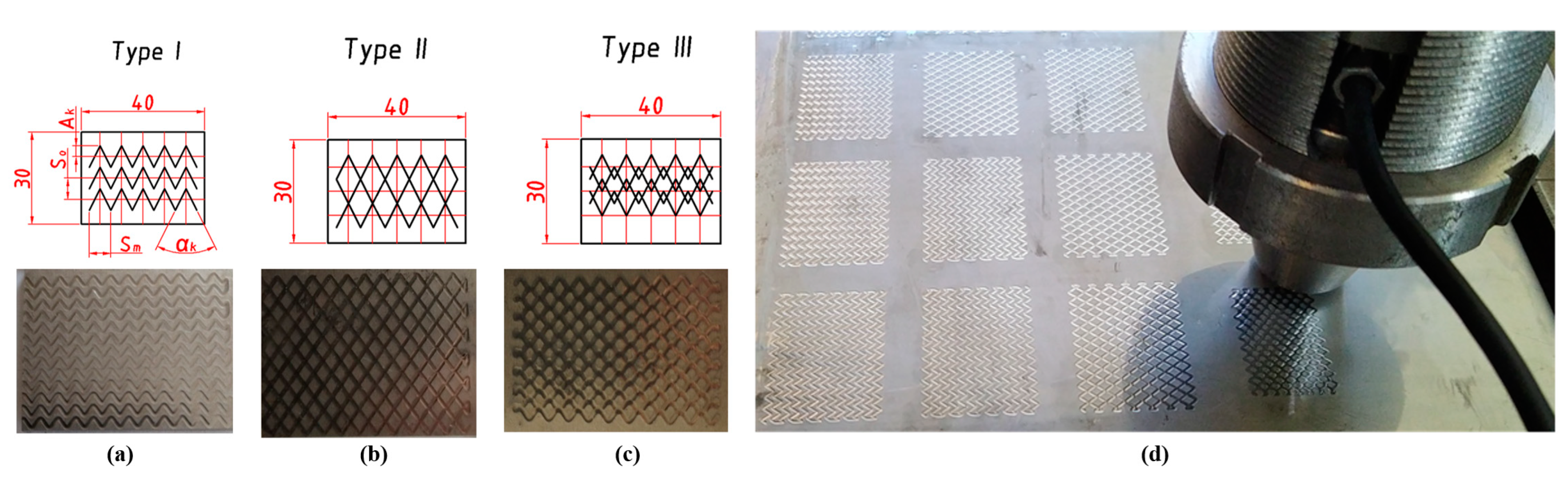
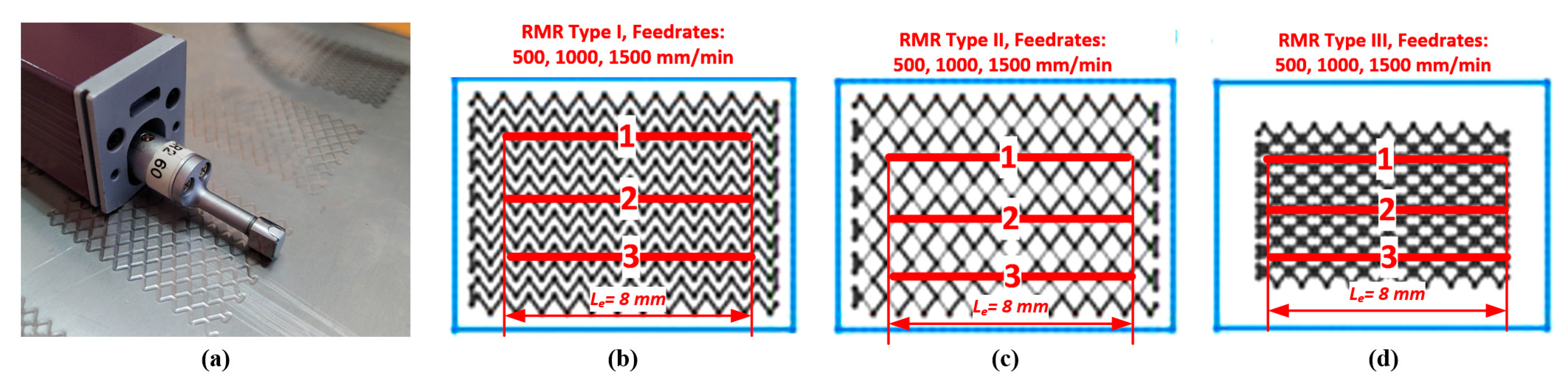
2.3. Materials, Experimental Design, and Equipment for Preparing the Test Specimens
3. Experimentally Obtained Results
4. Results, Analyzes, and Discussion
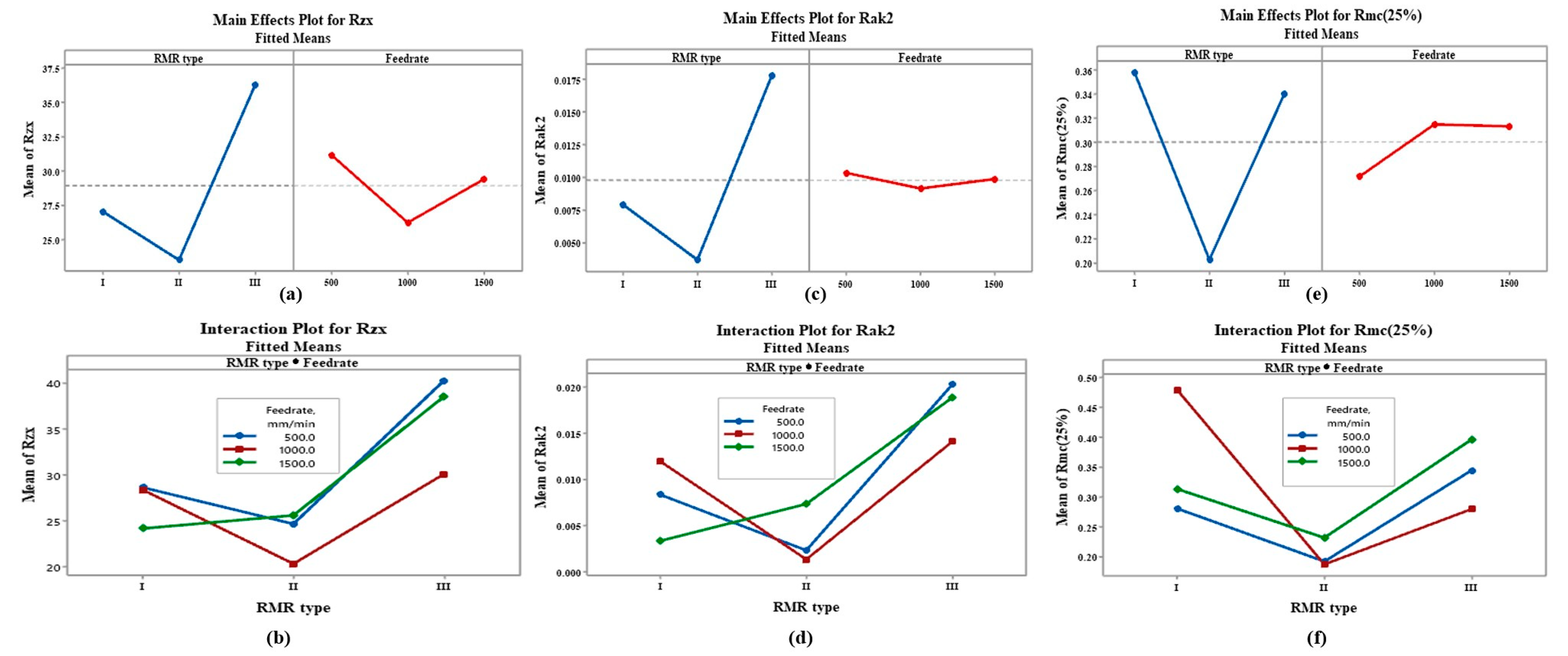
4.1. Influence on the Maximum Height Criteria Rzx
− 0.655·RMRI·F500 + 4.018·RMRI·F1000 − 3.363·RMRI·F1500 − 1.100·RMRII·F500 − 0.506·RMRII·F1000 +
+ 1.606·RMRII·F1500 + 1.755·RMRIII·F500 − 3.512·RMRIII·F1000 + 1.757·RMRIII·F1500
4.2. Influence on the Approximated Valley Area Rak2
+ 0.00009·F1500 −0.00009·RMRI·F500 + 0.00473·RMRI·F1000 − 0.00465·RMRI·F1500 − 0.00191·RMRII·F500 −
− 0.00170·RMRII·F1000 + 0.00361·RMRII·F1500 + 0.00199·RMRIII·F500 − 0.00303·RMRIII·F1000 + 0.00104·RMRIII·F1500
4.3. Influence on the Material Ratio Function Rmc(25%)
+ 0.0133·F1500 − 0.0494·RMRI·F500 + 0.1076·RMRI·F1000 − 0.0581·RMRI·F1500 + 0.0167·RMRII·F500 −
− 0.0317·RMRII·F1000 + 0.0150·RMRII·F1500 + 0.0328·RMRIII·F500 − 0.0759·RMRIII·F1000 + 0.0431·RMRIII·F1500
4.4. Estimation of the Main Effects and Interactions
5. Conclusions
- Partially regular PMRs, regardless of their type, show about a 10 times higher lubricant retaining capacity than those surfaces which do not have patterns with plastically deformed traces. However, this feature reduces their bearing capacity respectively. Therefore, both the required lubricant retaining capacity and bearing capacity of the burnished surface must be considered when designing the parameters of the ball-burnishing operation.
- Among the different types of RMRs investigated, the I st and III rd types of RMR demonstrated a better combination of functional properties than the II nd type of RMR which produced the lowest results in terms of the functional properties. Therefore, future research must be focused mostly on these two types of RMRs.
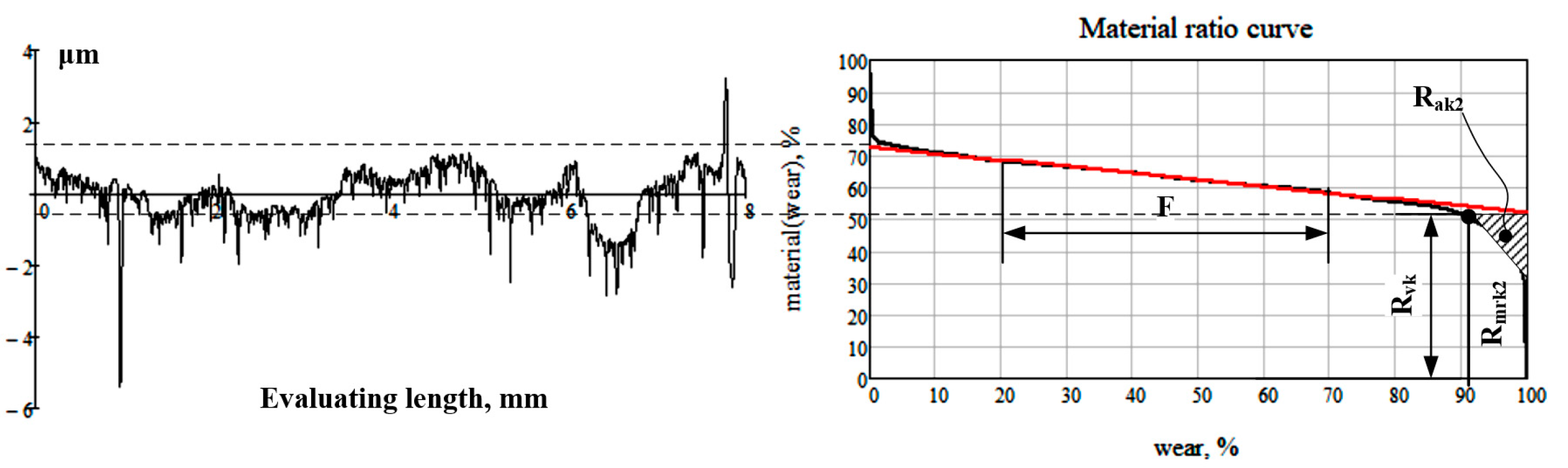
- The standardized methodology for the calculation area of the dales and the Rak2 criterion included in the EN ISO 21902-2 standard are not very suitable to RMRs, due to the difference between the shapes of the MR curves. As shown from the empirically built MR curves of the RMRs (see Figure 7a–c) there was an additional area, which was not taken into account in the determination of the Rak2 criterion, and therefore, the functional parameter for the lubricant retaining capacity of the RMRs had an underestimated value. This gives us reason to research in the future other methods for determining the Rak2 criterion to take into account that additional unused area of the MR curve.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, T.R. Rough Surfaces; Longman: New York, NY, USA, 1982. [Google Scholar]
- Whitehouse, D.J. Handbook of Surface and Nanometrology; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Willis, E. Surface finish in relation to cylinder liners. Wear 1986, 109, 351–366. [Google Scholar] [CrossRef]
- GOST 2789-73; Surface Roughness. Parameters and Characteristics. Gospotrebstandart: Moscow, USSR, 1975. (In Russian)
- Tomanik, E.; El Mansori, M.; Souza, R.; Profito, F. Effect of waviness and roughness on cylinder liner friction. Tribol. Int. 2018, 120, 547–555. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- GOST 24773-81; Surfaces with Regular Microshape. Classification, Parameters and Characteristics. Izdatelstvo Standartov: Moscow, Russia, 1988.
- Mezghani, S.; Demirci, I.; Zahouani, H.; El Mansori, M. The effect of groove texture patterns on piston-ring pack friction. Precis. Eng. 2012, 36, 210–217. [Google Scholar] [CrossRef]
- Hamdi, A. Effect of cutting variables on bearing area curve parameters (BAC-P) during hard turning process. Arch. Mech. Eng. 2020, 67, 73–95. [Google Scholar] [CrossRef]
- Kubatova, D.; Melichar, M. Roughness Evaluation Using Abbott-Firestone Curve Parameters. In Proceedings of the 30th DAAAM International Symposium, 23–26 October 2019, Zadar, Croatia; Katalinic, B., Ed.; DAAAM International: Vienna, Austria, 2019; pp. 0467–0475. ISBN 978-3-902734-22-8. ISSN 1726-9679. [Google Scholar] [CrossRef]
- Cao, C.; Zhu, J.; Tanaka, T. Influence of Burnishing Process on Microstructure and Corrosion Properties of Mg Alloy AZ31. In Advanced Surface Enhancement; Itoh, S., Shukla, S., Eds.; INCASE 2019. Lecture Notes in Mechanical Engineering; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Shneider, Y.G. Service Properties of Parts with Regular Microrelief, 2nd ed.; Revised and Augmented; Mashinostroenie: Leningrad, USSR, 1982; 248p. (In Russian) [Google Scholar]
- Slavov, S.; Dimitrov, D.; Konsulova-Bakalova, M. Advances in burnishing technology. In Advanced Machining and Finishing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 481–525. [Google Scholar]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Reverse Problem in Surface Texture Analysis—One-Process Profile Modeling on the Basis of Measured Two-Process Profile after Machining or Wear. Materials 2019, 12, 4169. [Google Scholar] [CrossRef] [PubMed]
- Nanbu, T.; Ren, N.; Yasuda, Y.; Zhu, D.; Wang, Q.J. Micro-textures in concentrated conformal-contact lubrication: Effects of texture bottom shape and surface relative motion. Tribol. Lett. 2008, 29, 241–252. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, K.; Pawlus, P. Comparing tribological effects of various chevron-based surface textures under lubricated unidirectional sliding. Tribol. Int. 2020, 146, 106205. [Google Scholar] [CrossRef]
- Swirad, S.; Pawlus, P. The Effect of Ball Burnishing on Dry Fretting. Materials 2021, 14, 7073. [Google Scholar] [CrossRef] [PubMed]
- Aftanaziv, I.S.; Kyrychok, P.O.; Melnychuk, P.P. Improving the reliability of machine parts by surface plastic deformation. In Zhytomyr; ZhTI Publishing: New York, NY, USA, 2001; p. 516. (In Ukrainian) [Google Scholar]
- ISO 1302:2002; Geometrical Product Specifications (GPS)—[Indication of Surface Texture in Technical Product Documentation]. 2002. International Organization for Standardization: Geneva, Switzerland. Available online: https://www.iso.org/standard/28089.html (accessed on 12 April 2023).
- Nagit, G.; Slatineanu, L.; Dodun, O.; Ripanu, M.; Mihalache, A. Surface layer microhardness and roughness after applying a vibroburnishing process. J. Mater. Res. Technol. 2019, 8, 4333–4346. [Google Scholar] [CrossRef]
- Dzyura, V.; Maruschak, P.; Kozbur, H.; Kryvyi, P.; Prentkovskis, O. Determining optimal parameters of grooves of partially regular microrelief formed on end faces of rotary bodies. Smart Sustain. Manuf. Syst. 2021, 5, 18–29. [Google Scholar] [CrossRef]
- Dzyura, V.; Maruschak, P.; Kuchvara, I.; Tkachenko, I. Ensuring a stable relative area of burnishing of partially regular microrelief formed on end surfaces of rotary bodies. Stroj. Časopis 2021, 71, 41–50. [Google Scholar] [CrossRef]
- Slavov, S.D.; Iliev, I.V. Design and FEM Static Analysis of An Instrument for Surface Plastic Deformation of Non-Planar Functional Surfaces of Machine Parts. Fiability Durab. 2016, 1, 3–9. Available online: https://doaj.org/article/5d09023126684e709cca46eb394d5573 (accessed on 16 April 2023).
- Banh, Q.-N.; Nguyen, H.-D.; Tran, A.S. Numerical Simulation and Experimental Validation of Surface Roughness by the Smoothing Small Ball-Burnishing Process. Machines 2021, 9, 48. [Google Scholar] [CrossRef]
- Jerez-Mesa, R.; Llumà, J.; Travieso-Rodriguez, J.A. Vibration-Assisted Ball Burnishing. Encyclopedia 2021, 1, 460–471. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Functional Importance of Surface Texture Parameters. Materials 2021, 14, 5326. [Google Scholar] [CrossRef] [PubMed]
- GOST ISO 4287-2014; Geometric Characteristics of Products (GPS). Surface Structure. [Profile Method. Terms, Definitions and Parameters of the Surface Structure]. Federal Technical Regulation and Metrology Agency: Moscow, Russia, 2014. Available online: https://www.russiangost.com/p-141391-gost-r-iso-4287-2014.aspx (accessed on 14 April 2023). (In Russian)
- ISO 13565-2:1996; Geometrical Product Specifications (GPS)—[Surface Texture: Profile Method; Surfaces Having Stratified Functional Properties—Part 2: Height Characterization Using the Linear Material Ratio Curve]. International Organization for Standardization: Geneva, Switzerland, 1996.
- ISO 21920-2:2021; Specifications, Geometrical Product. “Surface Texture: Profile—Part 2: Terms, Definitions and Surface Texture Parameters”. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/72226.html (accessed on 12 May 2023).
- Montgomery, D.C. Design and Analysis of Experiments—Douglas C. Montgomery—Google KHИΓИ. Eight Edition. 2013. Available online: https://www.academia.edu/42781722/Design_and_Analysis_of_Experiments_Eighth_Edition (accessed on 24 April 2023).
- Mathews, P.G. Design of Experiments with MINITAB; ASQ Quality Press: Milwaukee, WI, USA, 2005; Volume 446. [Google Scholar]
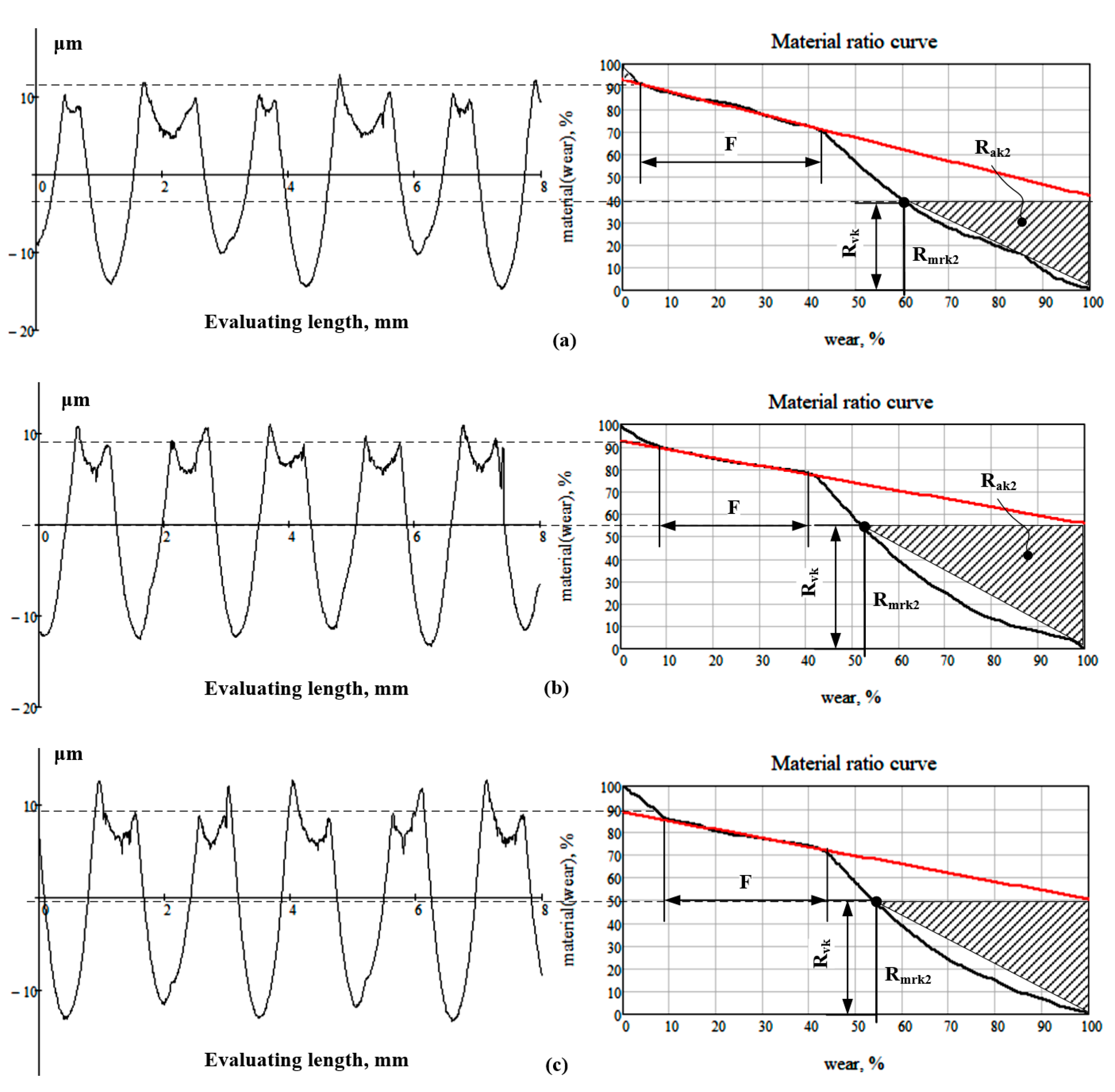
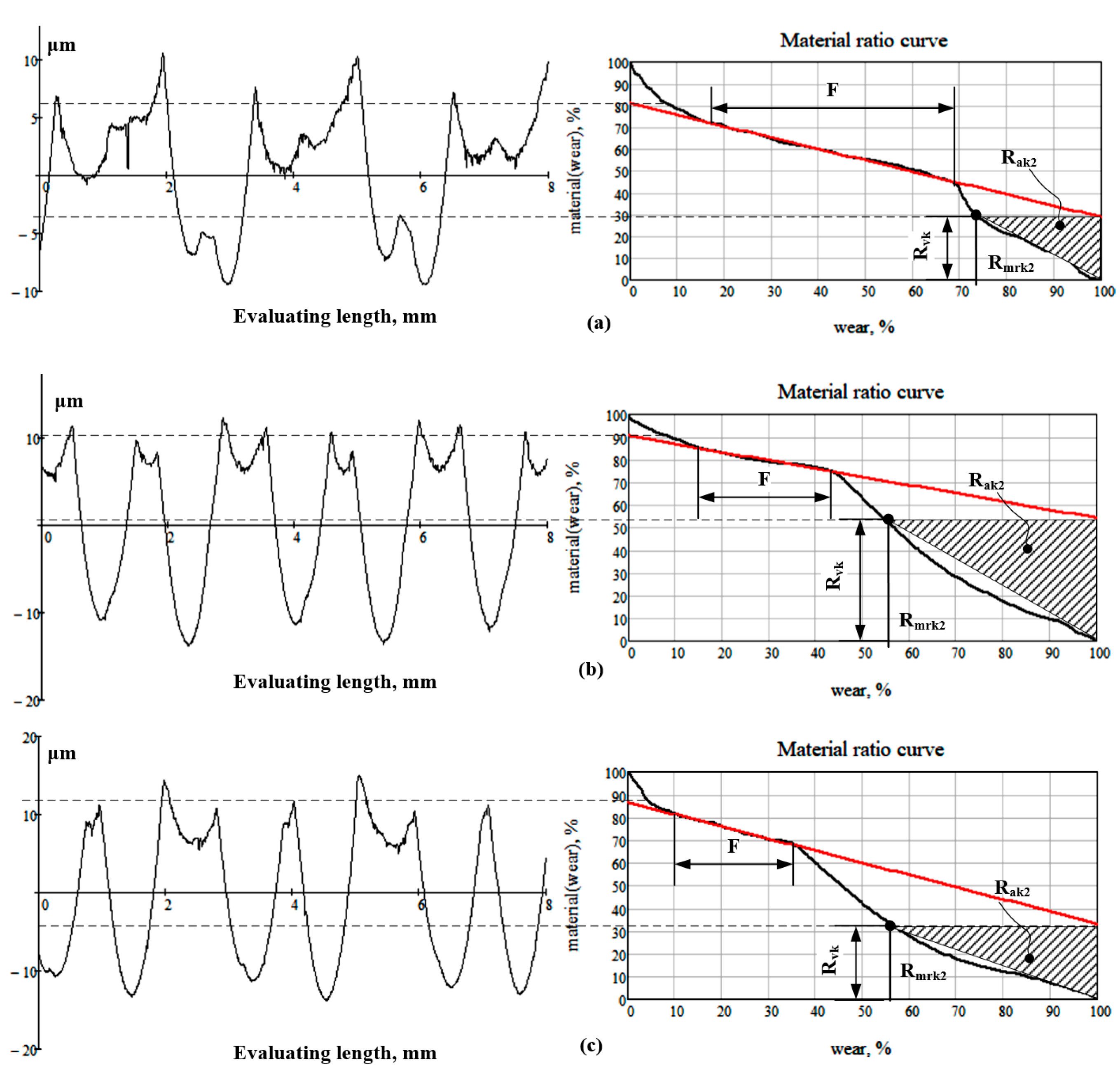
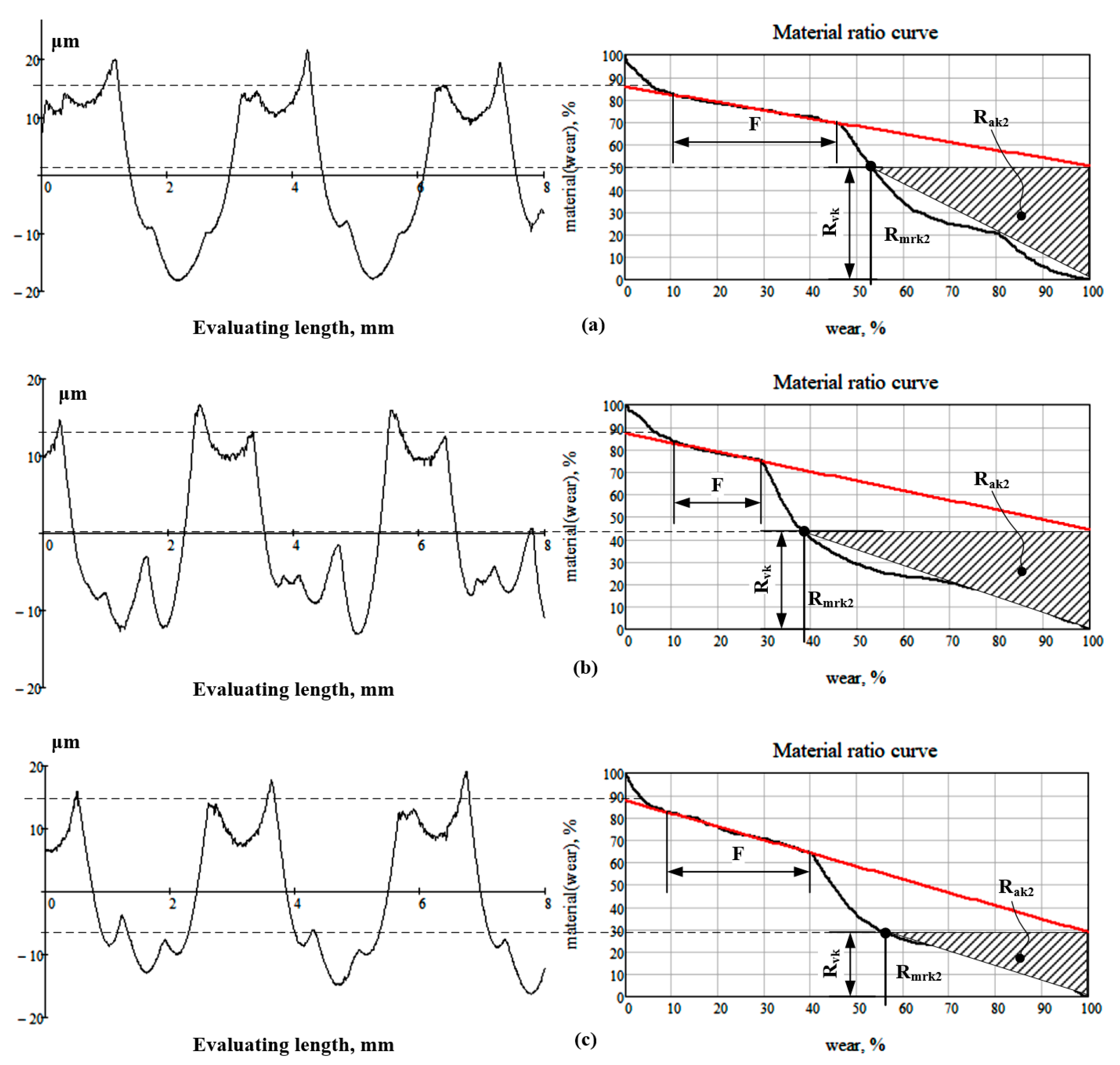
| № | Type of RMR | Feed Rate, fin.i. mm/min | Ra, [µm] | Rzx, [µm] | Rmrk2, [mm] | Rvk, [µm] | Rak2, [mm2] | Rmc(25%), − |
|---|---|---|---|---|---|---|---|---|
| 1 | I | 500 | 8.14 | 32.11 | 2.285 | 8.03 | 0.009171 | 0.291 |
| 2 | I | 500 | 7.54 | 27.56 | 2.135 | 6.89 | 0.007353 | 0.319 |
| 3 | I | 500 | 7.27 | 26.15 | 2.125 | 8.05 | 0.008549 | 0.231 |
| 4 | I | 1000 | 8.86 | 28.80 | 2.255 | 13.90 | 0.015676 | 0.504 |
| 5 | I | 1000 | 8.52 | 28.11 | 1.955 | 11.04 | 0.010794 | 0.469 |
| 6 | I | 1000 | 8.52 | 28.03 | 1.890 | 10.04 | 0.009487 | 0.469 |
| 7 | I | 1500 | 7.64 | 25.11 | 1.595 | 5.02 | 0.004004 | 0.302 |
| 8 | I | 1500 | 5.10 | 23.64 | 1.215 | 4.92 | 0.002992 | 0.319 |
| 9 | I | 1500 | 5.09 | 23.33 | 1.223 | 4.91 | 0.002989 | 0.311 |
| 10 | II | 500 | 6.74 | 27.50 | 1.275 | 2.95 | 0.001879 | 0.171 |
| 11 | II | 500 | 7.37 | 26.41 | 1.230 | 3.05 | 0.001874 | 0.268 |
| 12 | II | 500 | 4.22 | 19.97 | 1.575 | 3.99 | 0.003145 | 0.134 |
| 13 | II | 1000 | 3.31 | 19.41 | 1.290 | 2.04 | 0.001318 | 0.068 |
| 14 | II | 1000 | 5.60 | 21.02 | 0.600 | 1.00 | 0.000300 | 0.232 |
| 15 | II | 1000 | 4.92 | 20.41 | 1.520 | 3.06 | 0.002327 | 0.258 |
| 16 | II | 1500 | 7.87 | 28.74 | 2.875 | 6.93 | 0.009969 | 0.196 |
| 17 | II | 1500 | 7.24 | 24.86 | 2.525 | 7.96 | 0.010044 | 0.338 |
| 18 | II | 1500 | 3.76 | 23.09 | 0.675 | 6.02 | 0.002033 | 0.159 |
| 19 | III | 500 | 11.21 | 39.75 | 2.210 | 11.93 | 0.013177 | 0.297 |
| 20 | III | 500 | 13.42 | 40.21 | 2.460 | 21.12 | 0.025972 | 0.393 |
| 21 | III | 500 | 10.66 | 40.87 | 3.140 | 13.96 | 0.021910 | 0.344 |
| 22 | III | 1000 | 9.41 | 30.22 | 3.250 | 15.11 | 0.024554 | 0.375 |
| 23 | III | 1000 | 8.12 | 29.71 | 3.680 | 7.92 | 0.014578 | 0.233 |
| 24 | III | 1000 | 8.29 | 30.28 | 1.625 | 4.04 | 0.003281 | 0.230 |
| 25 | III | 1500 | 10.73 | 38.30 | 2.275 | 18.15 | 0.020641 | 0.474 |
| 26 | III | 1500 | 10.79 | 39.65 | 2.720 | 17.85 | 0.024272 | 0.413 |
| 27 | III | 1500 | 11.98 | 37.58 | 2.670 | 8.90 | 0.011882 | 0.303 |
| Raw material surface topography parameters: | ||||||||
| 28 | - | - | 0.32 | 3.41 | 0.96 | 1.023 | 0.000491 | 0.861 |
| 29 | - | - | 0.24 | 3.53 | 1.41 | 1.152 | 0.000813 | 0.825 |
| 30 | - | - | 0.28 | 2.84 | 0.56 | 0.64 | 0.000179 | 0.869 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Model Rzx(RMR, F) | 8 | 1049.97 | 93.30% | 1049.97 | 131.247 | 31.35 | 0.000 |
| Linear | 4 | 898.69 | 79.86% | 898.69 | 224.672 | 53.67 | 0.000 |
| RMR type | 2 | 785.92 | 69.84% | 785.92 | 392.961 | 93.88 | 0.000 |
| Feedrate | 2 | 112.77 | 10.02% | 112.77 | 56.383 | 13.47 | 0.000 |
| Two-way Interactions | 4 | 151.29 | 13.44% | 151.29 | 37.821 | 9.04 | 0.000 |
| RMR type · Feedrate | 4 | 151.29 | 13.44% | 151.29 | 37.821 | 9.04 | 0.000 |
| Error | 18 | 75.35 | 6.70% | 75.35 | 4.186 | ||
| Total | 26 | 1125.32 | 100.00% |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Model Rak2(RMR, F) | 8 | 0.001190 | 72.01% | 0.001190 | 0.000149 | 5.79 | 0.001 |
| Linear | 4 | 0.000956 | 57.88% | 0.000956 | 0.000239 | 9.31 | 0.000 |
| RMR type | 2 | 0.000950 | 57.49% | 0.000950 | 0.000475 | 18.49 | 0.000 |
| Feedrate | 2 | 0.000006 | 0.39% | 0.000006 | 0.000003 | 0.13 | 0.882 |
| Two-way Interactions | 4 | 0.000233 | 14.13% | 0.000233 | 0.000058 | 2.27 | 0.102 |
| RMR type · Feedrate | 4 | 0.000233 | 14.13% | 0.000233 | 0.000058 | 2.27 | 0.102 |
| Error | 18 | 0.000462 | 27.99% | 0.000462 | 0.000026 | ||
| Total | 26 | 0.001652 | 100.00% |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Model Rmc(25%) (RMR, F) | 8 | 0.22383 | 71.99% | 0.22383 | 0.027978 | 5.78 | 0.001 |
| Linear | 4 | 0.14106 | 45.37% | 0.14106 | 0.035266 | 7.29 | 0.001 |
| RMR type | 2 | 0.13021 | 41.88% | 0.13021 | 0.065107 | 13.46 | 0.000 |
| Feedrate | 2 | 0.01085 | 3.49% | 0.01085 | 0.005425 | 1.12 | 0.348 |
| Two-way Interactions | 4 | 0.08276 | 26.62% | 0.08276 | 0.020691 | 4.28 | 0.013 |
| RMR type · Feedrate | 4 | 0.08276 | 26.62% | 0.08276 | 0.020691 | 4.28 | 0.013 |
| Error | 18 | 0.08707 | 28.01% | 0.08707 | 0.004837 | ||
| Total | 26 | 0.31090 | 100.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzyura, V.; Maruschak, P.; Slavov, S.; Dimitrov, D.; Semehen, V.; Markov, O. Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines 2023, 11, 633. https://doi.org/10.3390/machines11060633
Dzyura V, Maruschak P, Slavov S, Dimitrov D, Semehen V, Markov O. Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines. 2023; 11(6):633. https://doi.org/10.3390/machines11060633
Chicago/Turabian StyleDzyura, Volodymyr, Pavlo Maruschak, Stoyan Slavov, Diyan Dimitrov, Volodymyr Semehen, and Oleksandr Markov. 2023. "Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing" Machines 11, no. 6: 633. https://doi.org/10.3390/machines11060633
APA StyleDzyura, V., Maruschak, P., Slavov, S., Dimitrov, D., Semehen, V., & Markov, O. (2023). Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines, 11(6), 633. https://doi.org/10.3390/machines11060633







