Parameter Identification of Switched Reluctance Motor SRM Using Exponential Swept-Sine Signal
Abstract
1. Introduction
- -
- The Hammerstein model, which is constituted by a nonlinear block flowed by a linear block. In [10], the authors present an identification method using an input excitation, designed to decouple the linear subsystem from the nonlinear element. Therefore, the system parameter identification is coped using a least squares estimator enjoying the consistency property.
- -
- Wiener model is a linear block followed by a nonlinear block. In [11] the authors present an identification method without requiring any prior knowledge of the nonlinearity. Using sine excitations and getting benefit from model plurality, the initial identification problem is made equivalent to two tractable (though still nonlinear) prediction-error problems.
- -
- Hammerstein-Wiener model is constituted by a linear block surrounded by two nonlinearities. In [12], the authors suggested a system identification approach. The input nonlinearity is considered the backlash type.
- -
- Wiener-Hammerstein model is obtained when two linear blocks surround a nonlinear block. In [13], a technique, based on random-phase multi-sine, for identifying Wiener and Hammerstein models is developed [8]. Then, identification techniques, based on frequency methods, have been proposed in the literature for Hammerstein models [14]. The review about the SRM identification is summarized in Table 1.
- A generalized Hammerstein model (GHM), describing the nonlinear behavior of SRM, is developed.
- The SRMs model can be simplified to a set of cascading nonlinear and linear blocks, called GHM.
- It is shown that the linear parts of the model can be identified using only the input and output signals.
- An analytical model describing accurately the switched reluctance machine is developed. Then, an identification method is proposed allowing us to determine the model parameters.
- Using the identified parameters, the inductance, and the flux linkage characteristics can be obtained.
2. Switched Reluctance Motor Modeling
2.1. Electrical Model
2.2. Mechanical Modeling of SRM
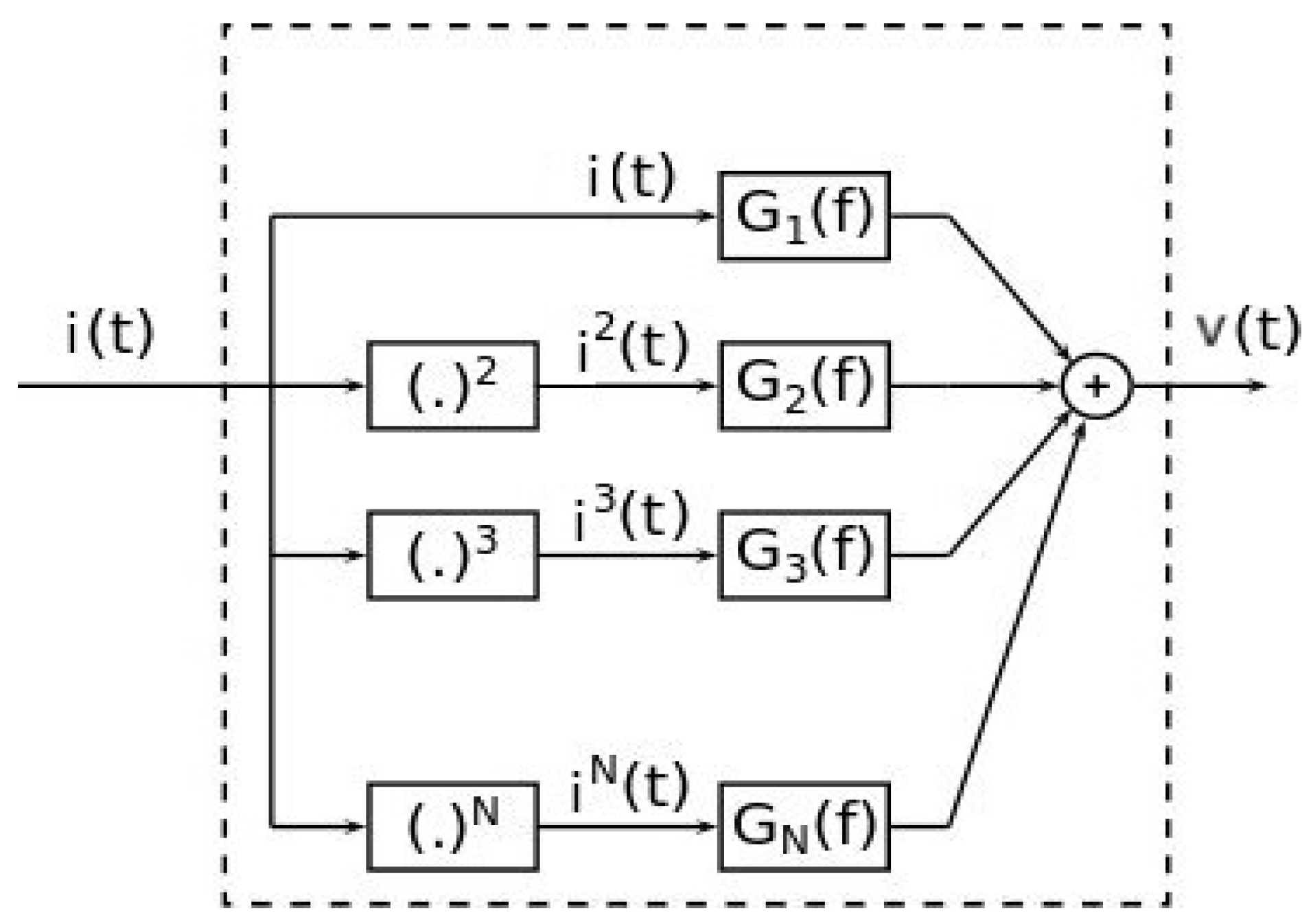
3. Swept Sine Identification Method for GHM
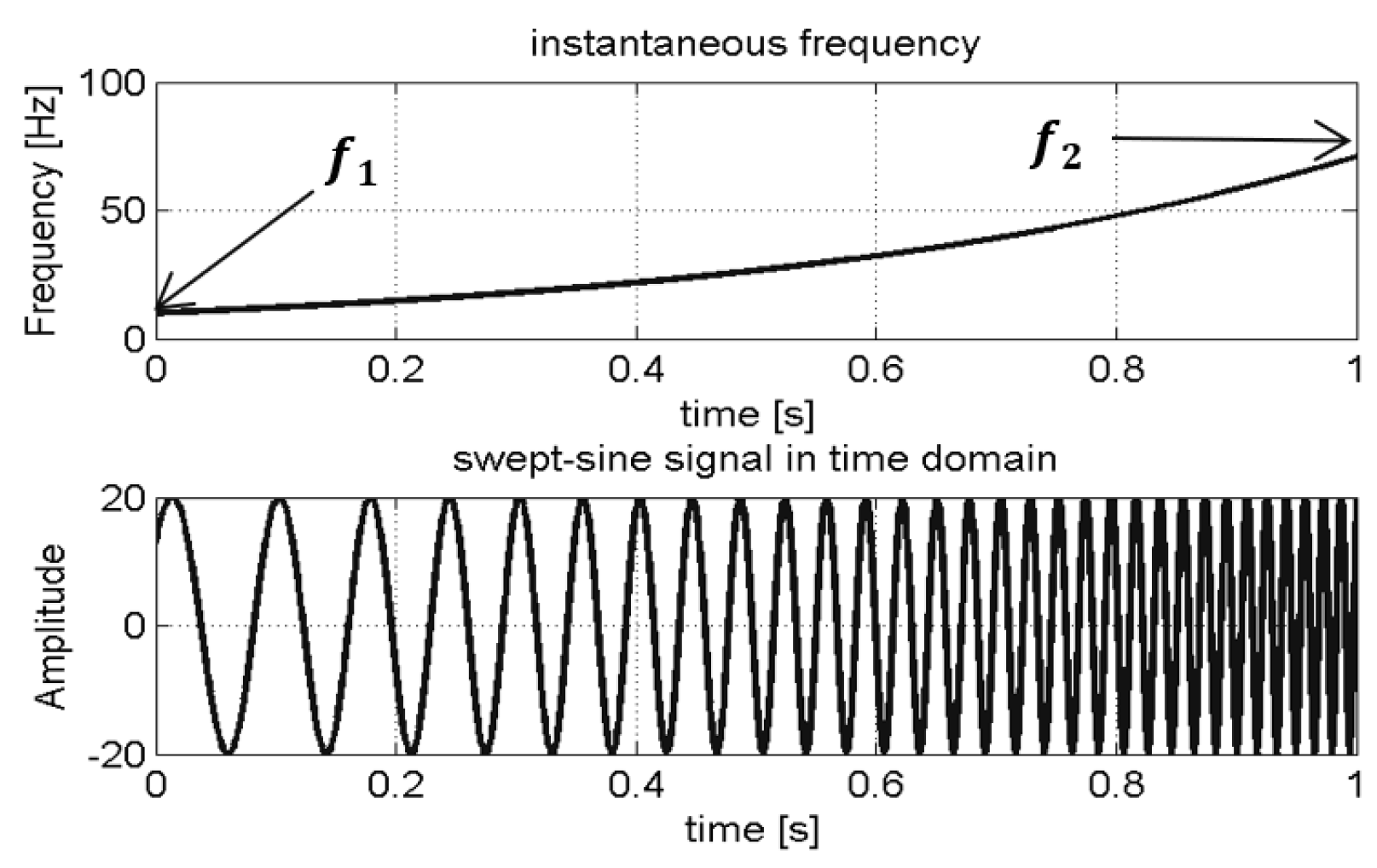
Swept-Sine Wave
- is the output of the system at time t,
- is the input of the system at time t,
- represents the Volterra kernel coefficients for a specific set of time delays , denotes the order of the Volterra model, and the represents the summation over all possible combinations of delays .
4. Simulation Results and Discussion
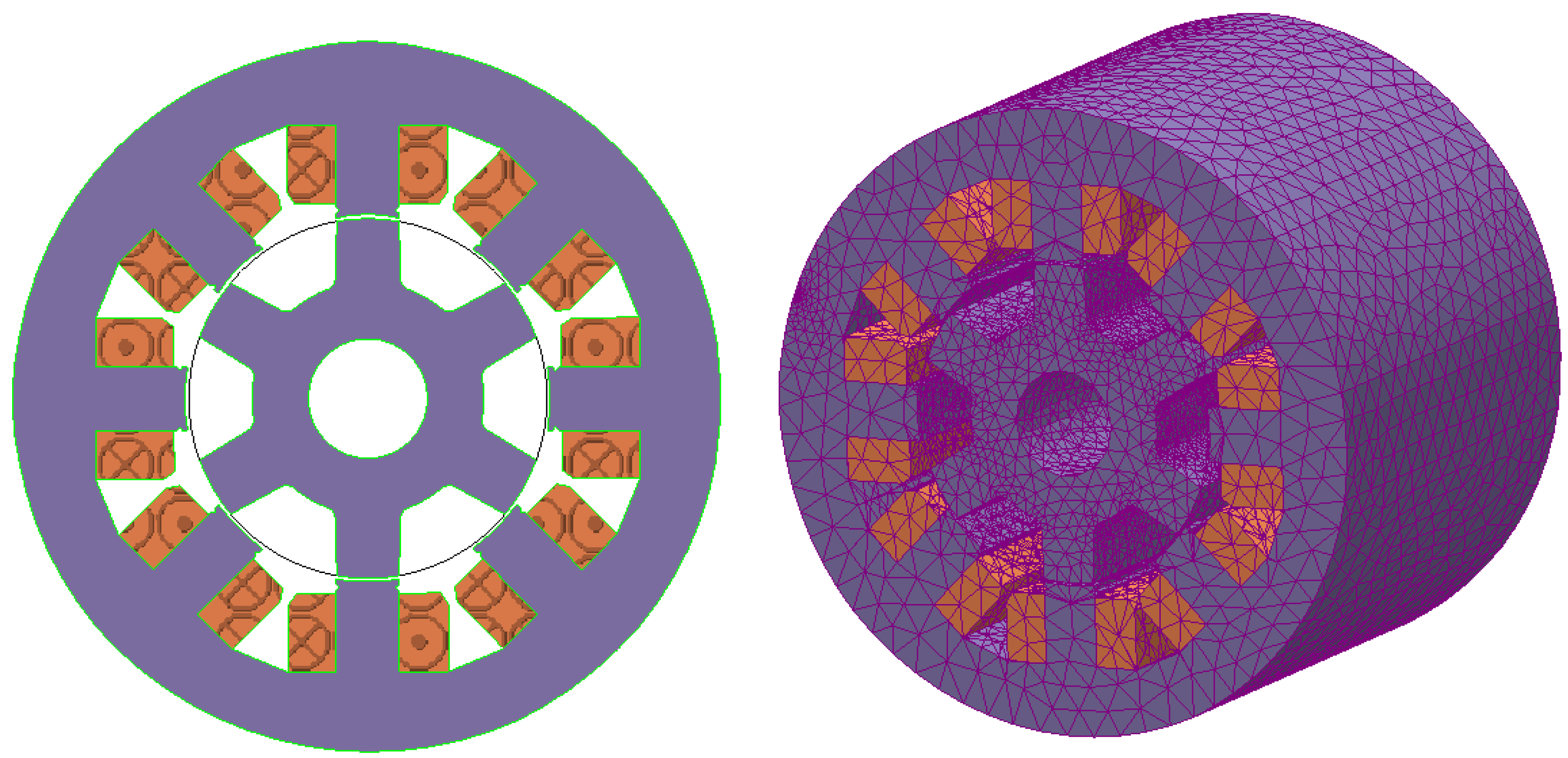
- Create the geometry of the SRM.
- Assign material properties to the components (coils, stator, rotor, air gap…).
- Generate a mesh grid.
- Define boundary conditions, including the applied current as an input.
- Configure the solver settings for accurate results.
- Run the model to solve the electromagnetic field equations and calculate the magnetic flux.
- Extract the magnetic flux distribution from the simulation results (Table 2).
- Divide the obtained magnetic flux by the applied current to obtain the value of the actual inductance.
5. Parameter Identification Procedure
- Reading the data obtained by FEM analyses, initialization of calculation parameters
- Calculates the impulse response from the furrier transforms of the input signals and output we took into account the peaks of a time interval
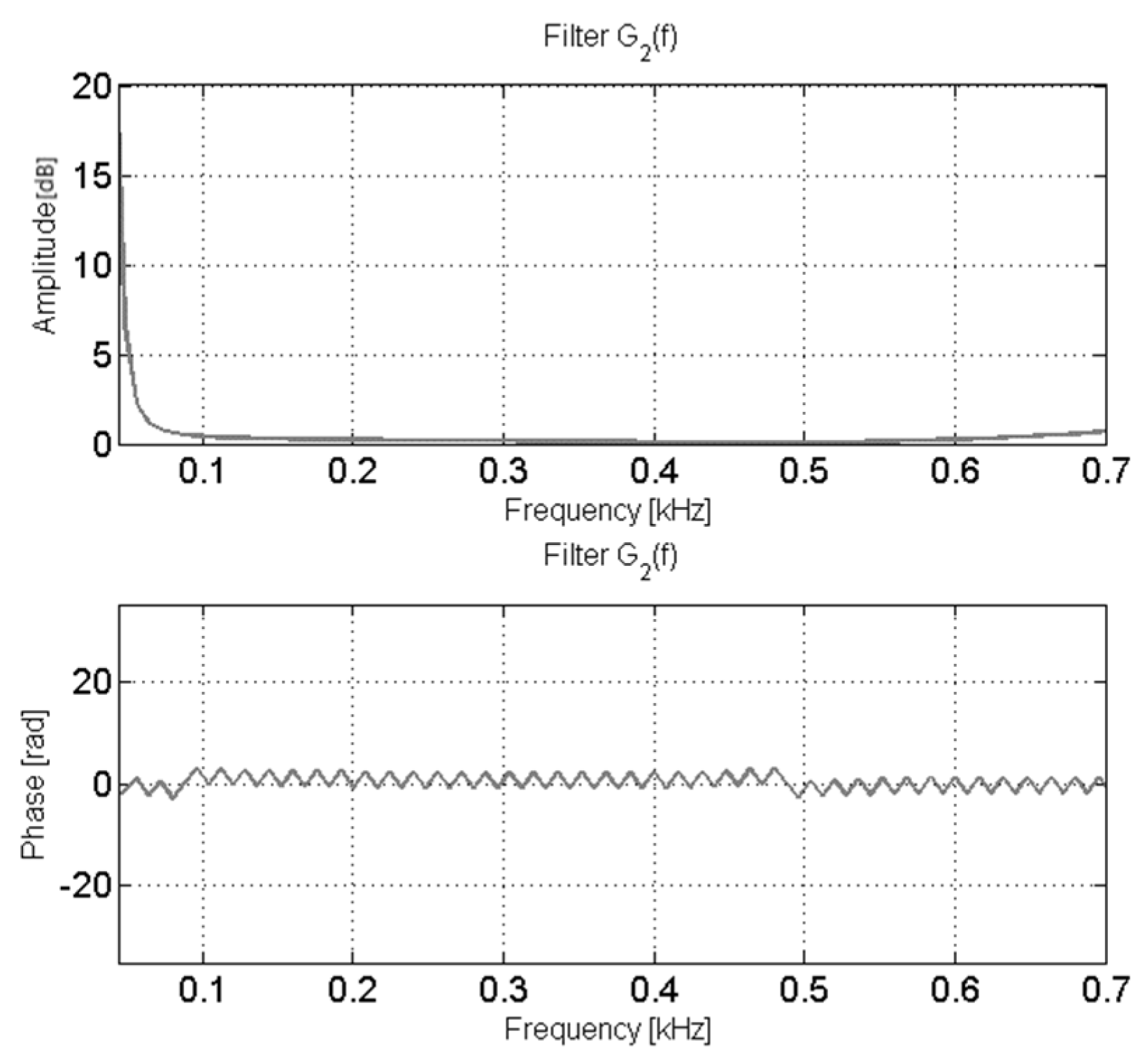
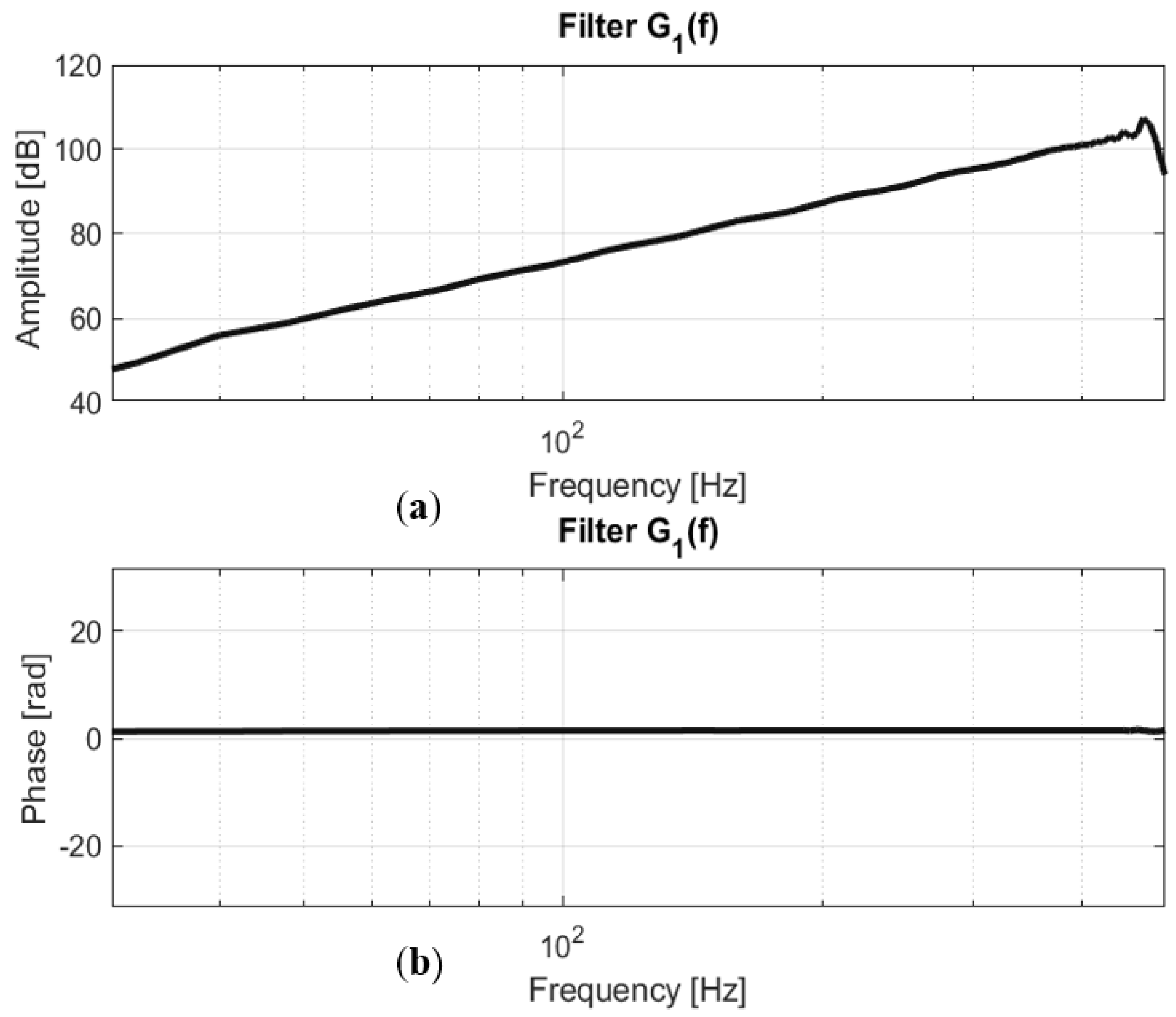
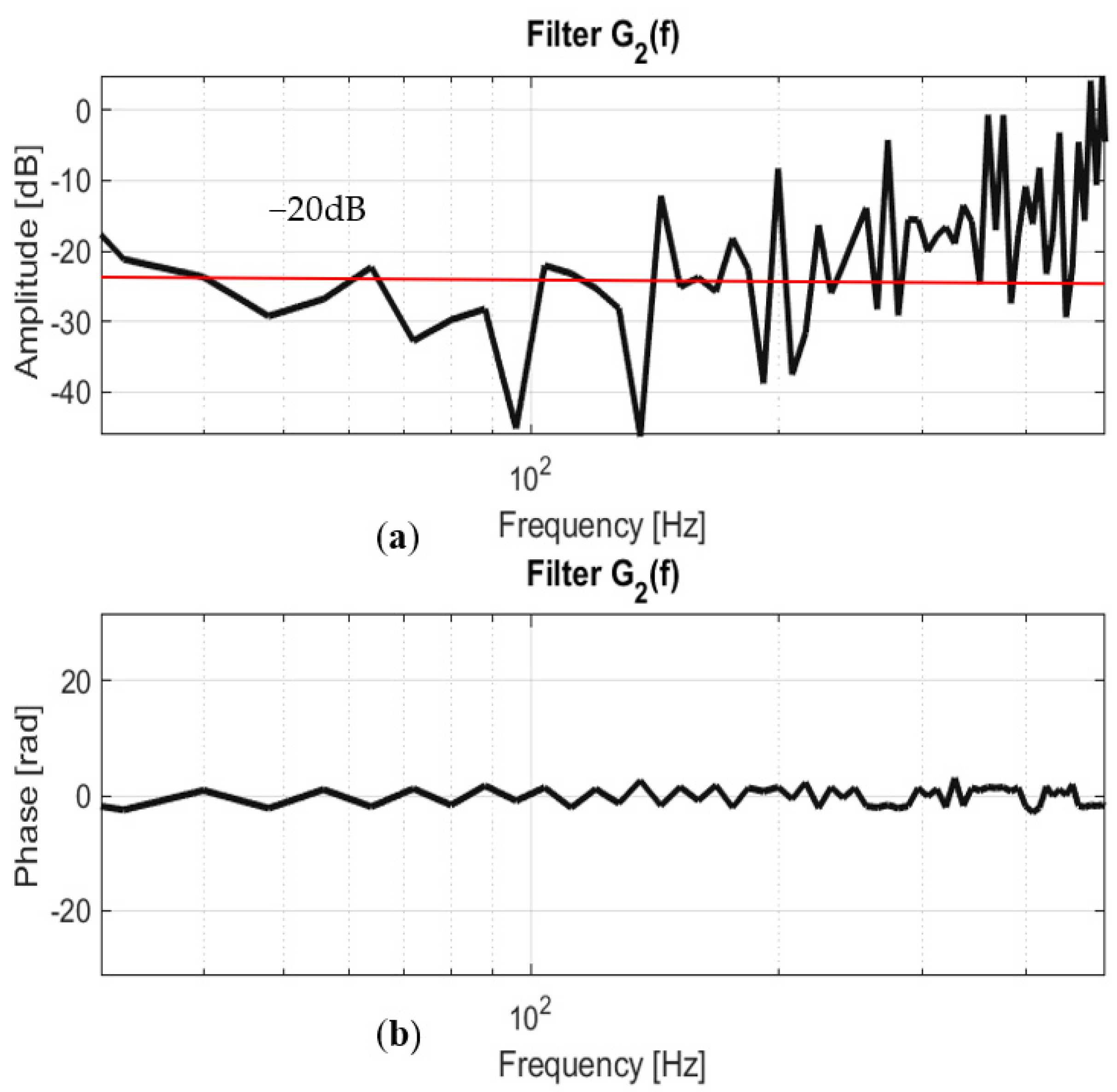
- The harmonics were separated in order to calculate the values of the filters.
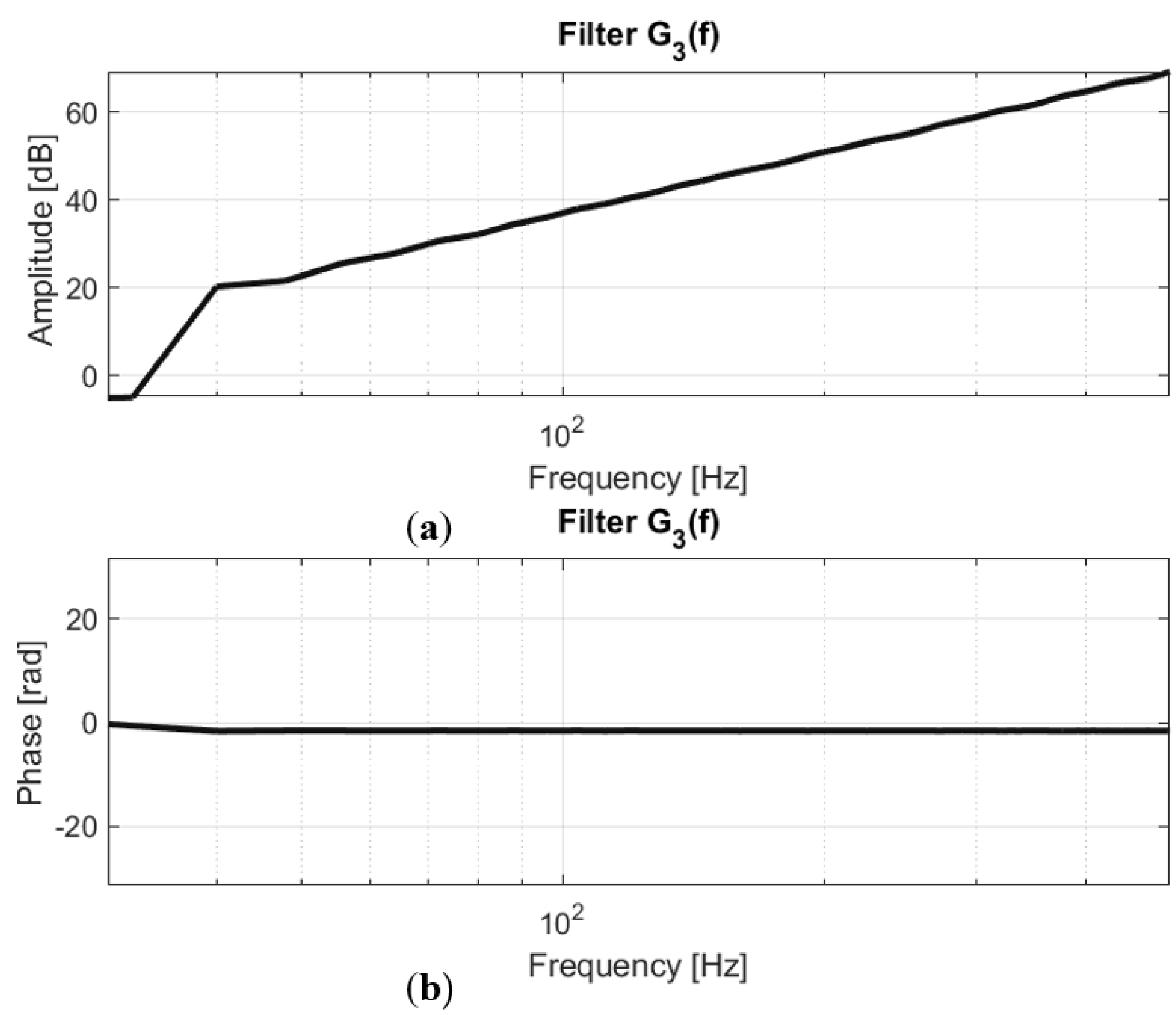
- Calculation of the trigonometric matrix , we calculated this value from Equation (16).
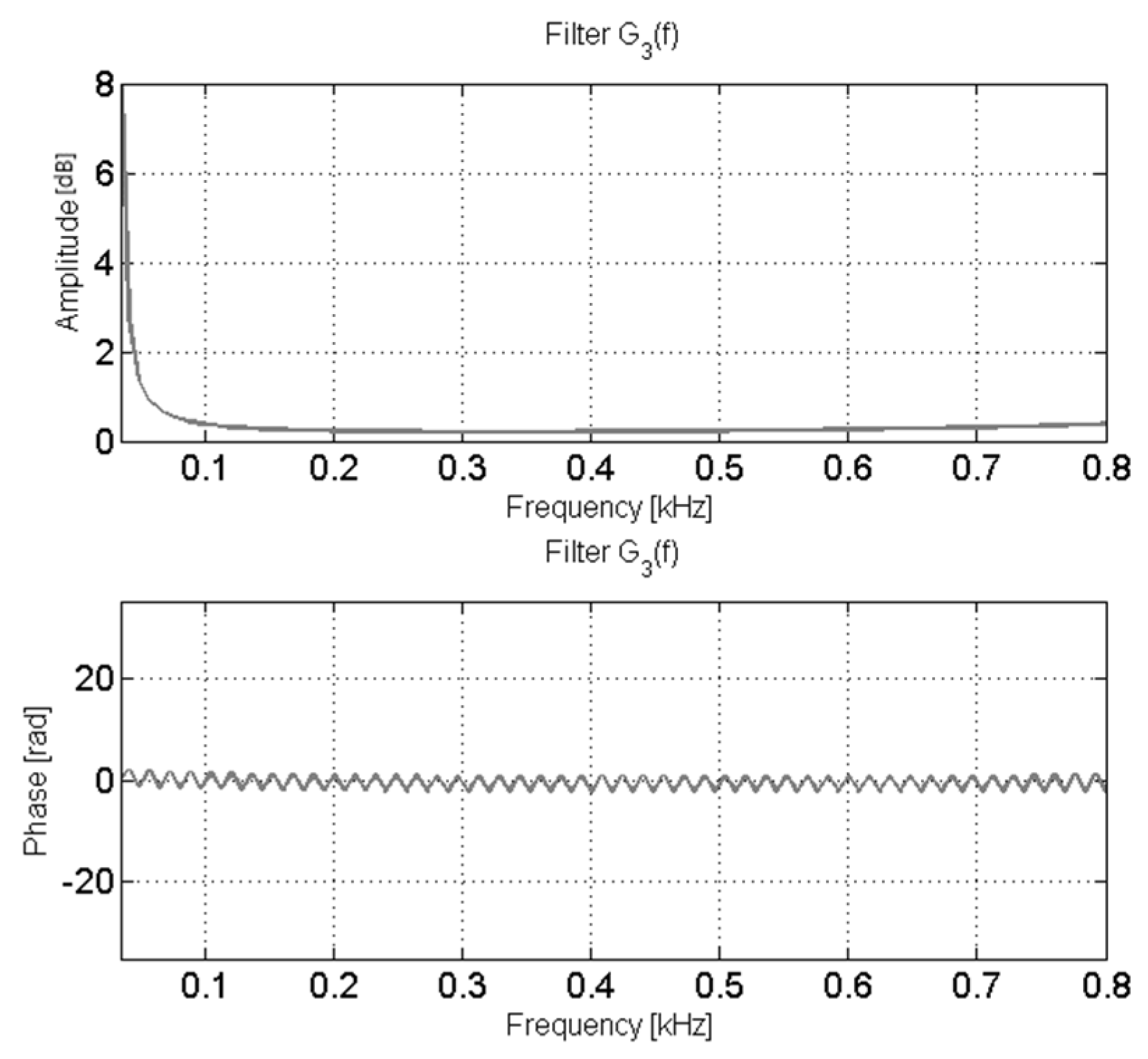
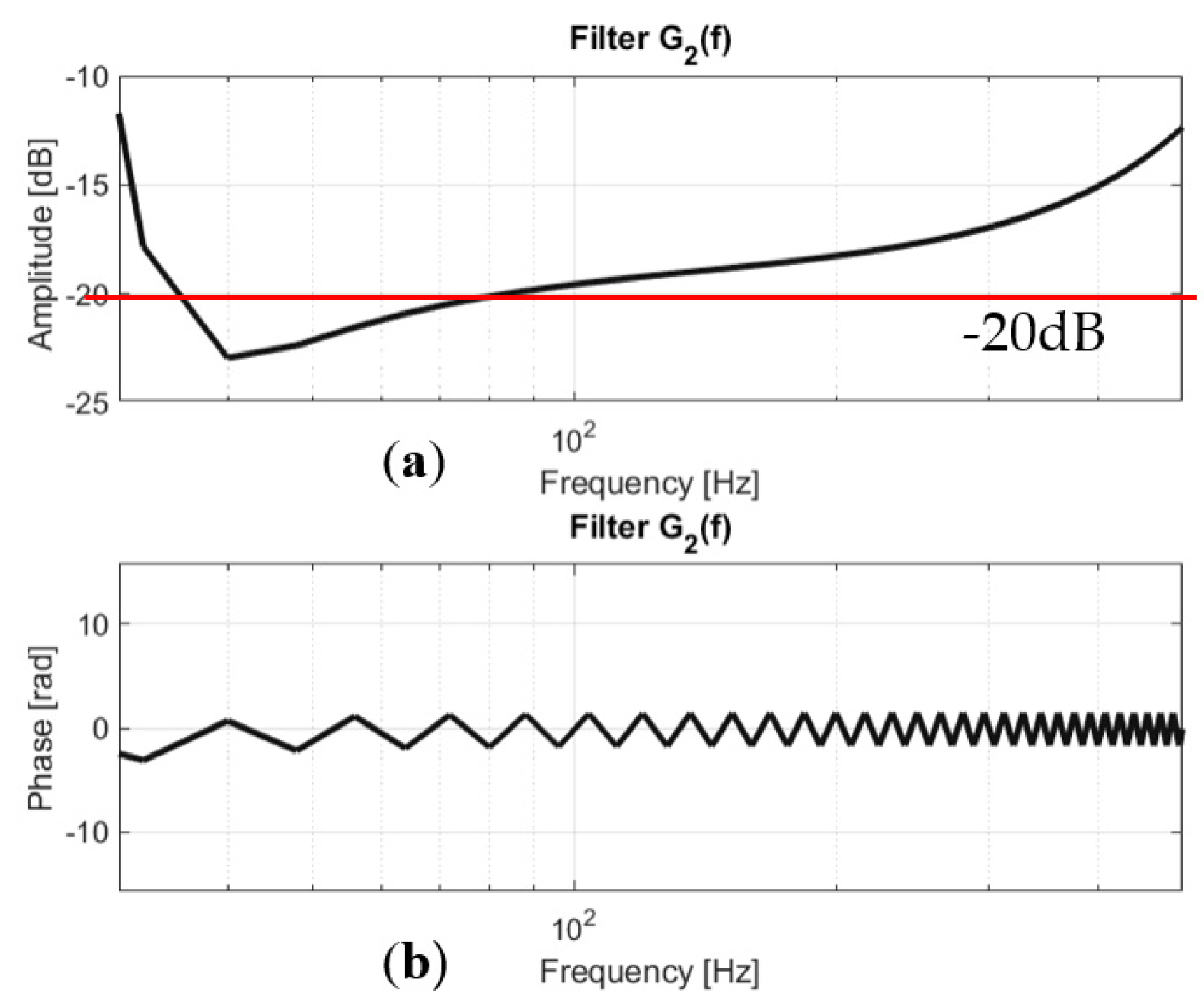
- The value of the filters Gm was calculated from the following fraction .
- Extraction of parameters of first-order systems .
- Construction of the inductors (for the 3 positions of the SRM rotor) from the GHM obtained in step 6.
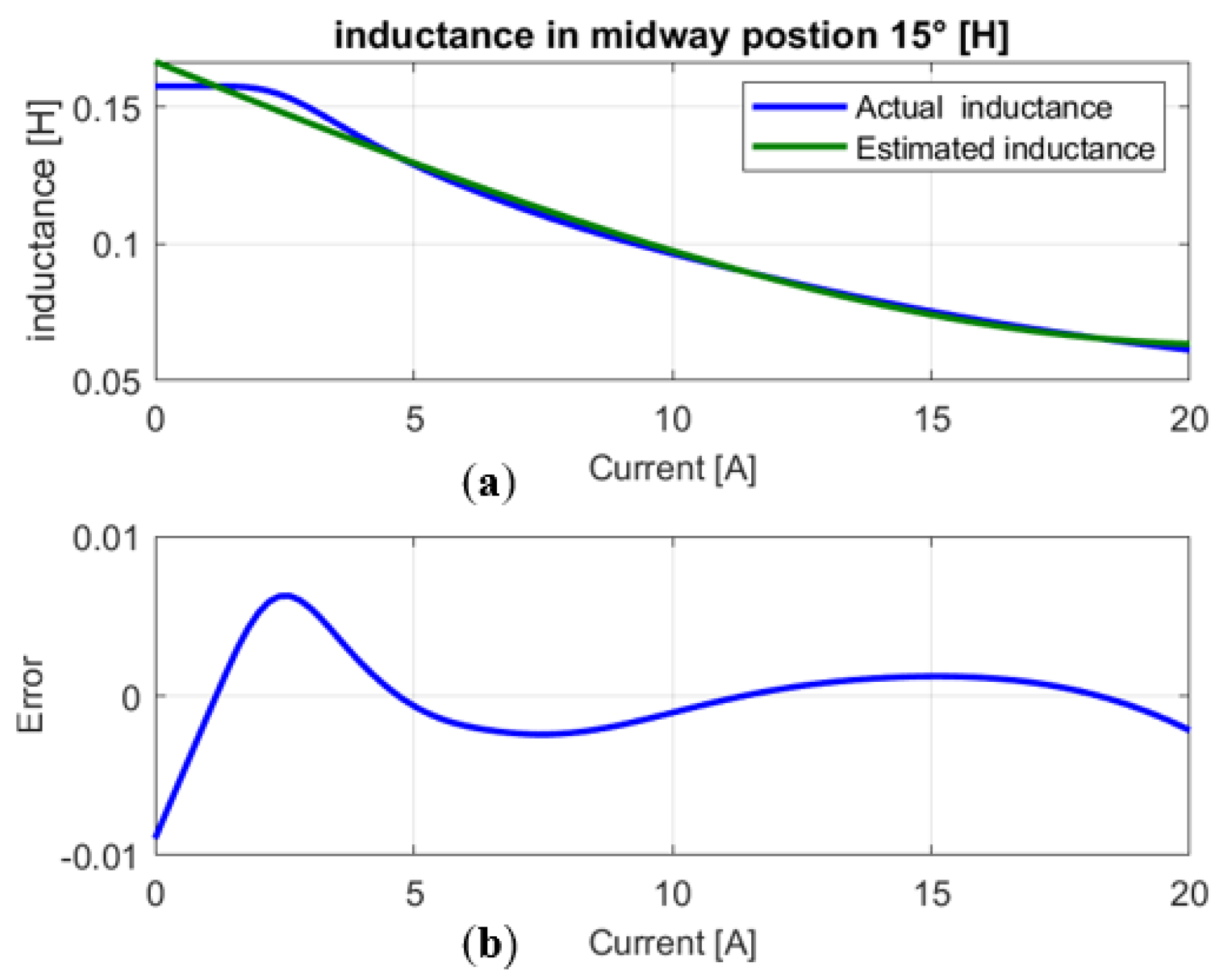
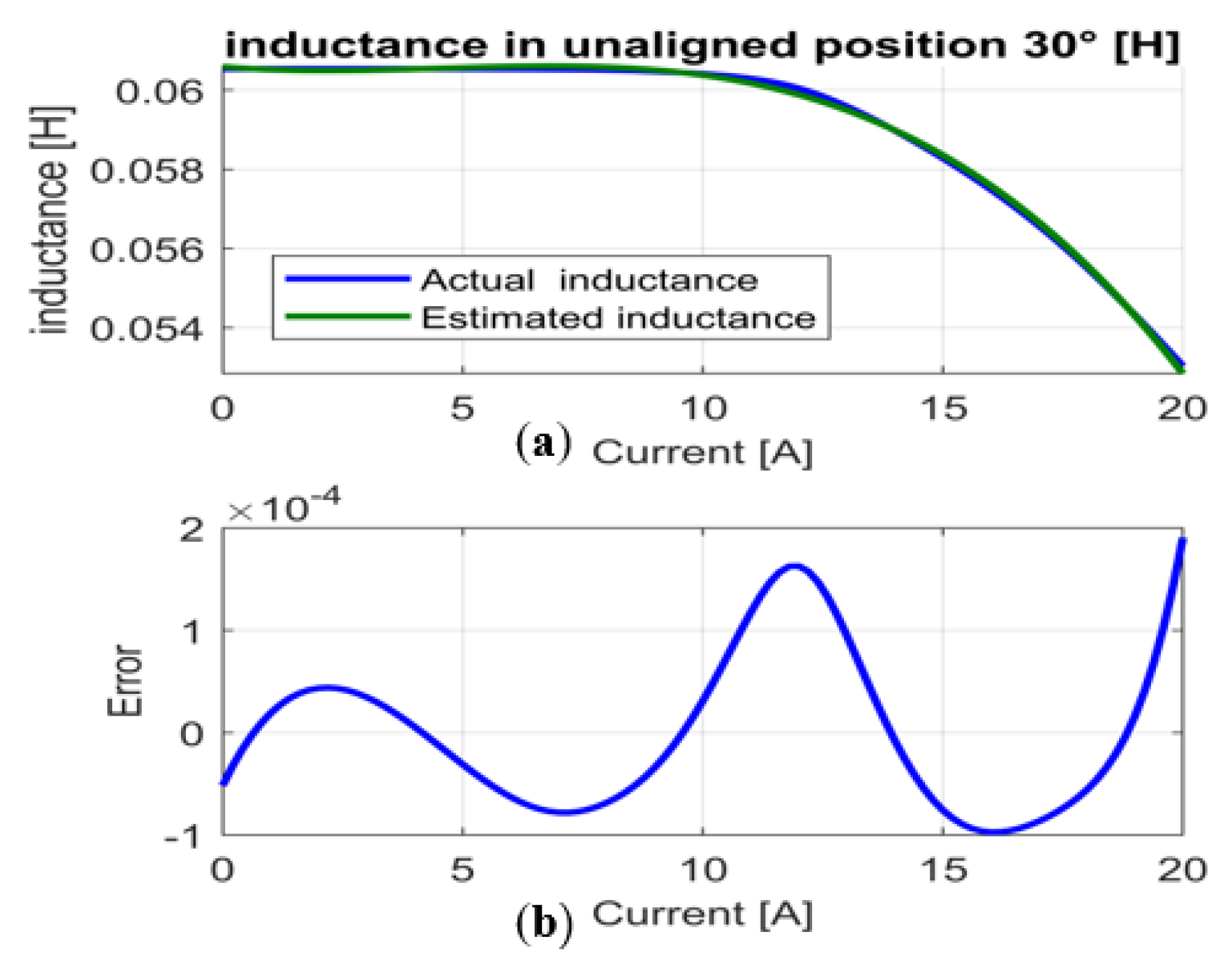
- Construction of the inductance curve estimate and extraction of the parameters of the inductance (see Table 2).
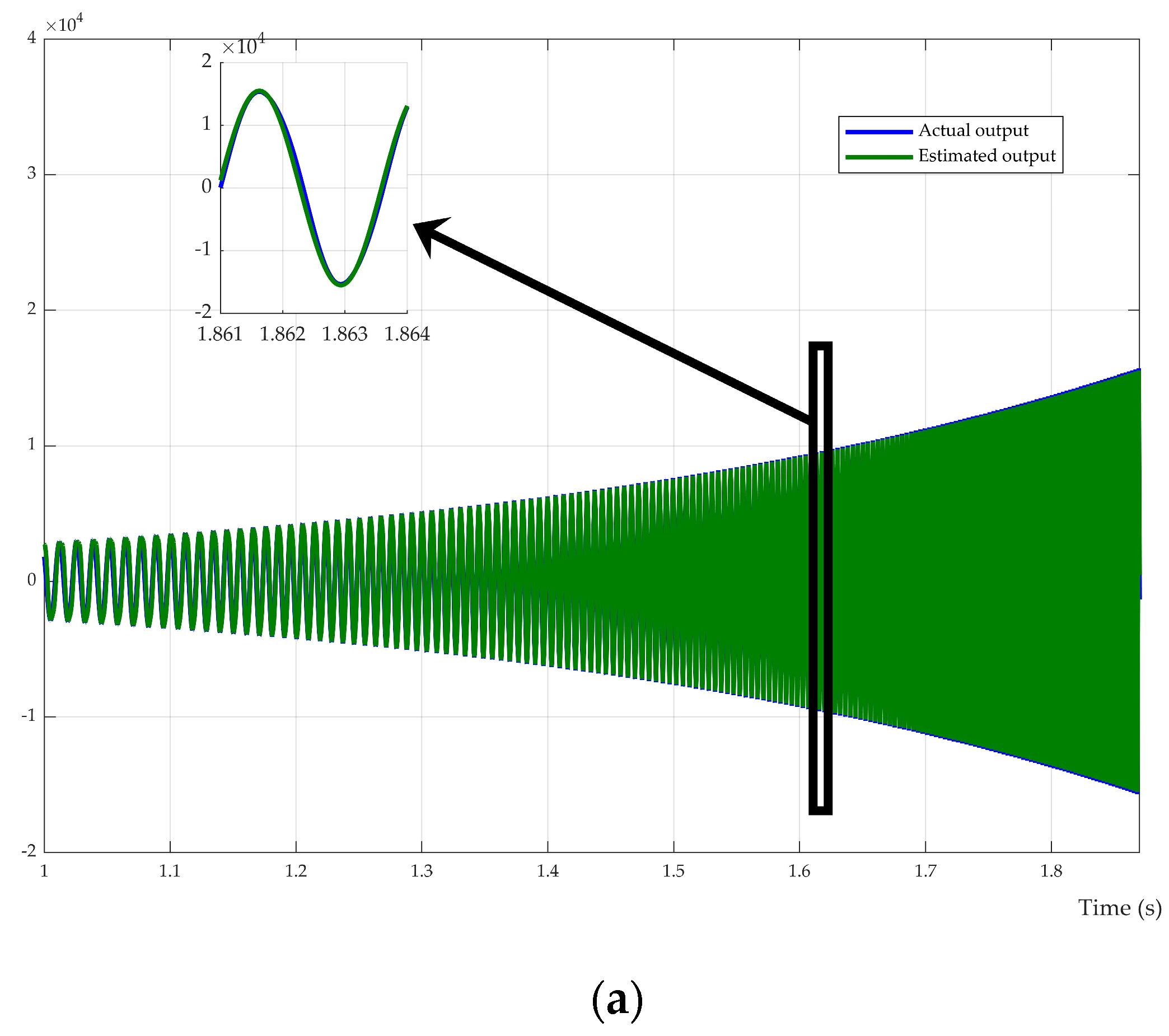
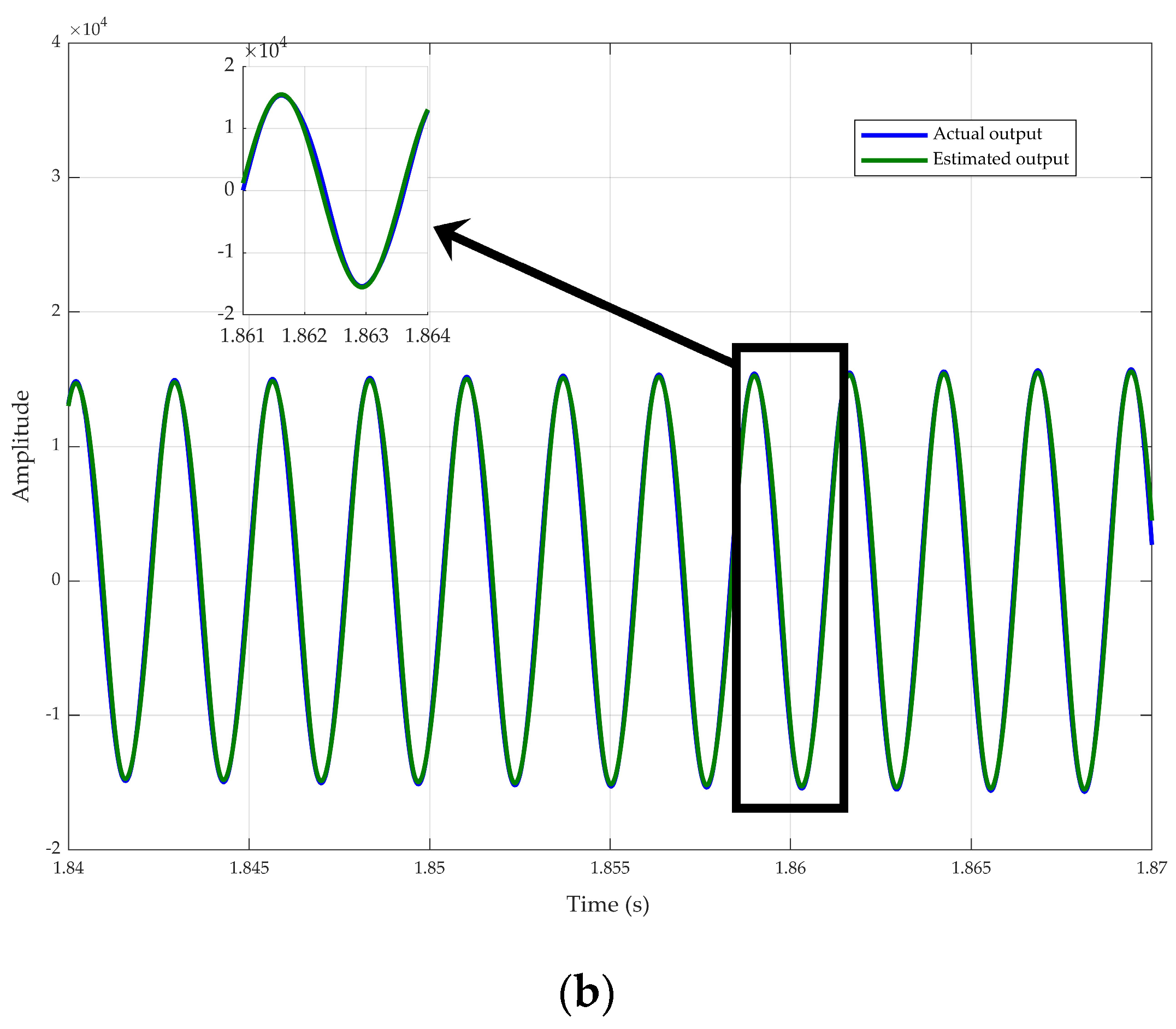
- Calculates the identification error for each rotor position.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, H.; Chen, S.; Xiao, Z.; Hu, J.; Liu, J.; Dustdar, S. Pa-Count: Passenger Counting in Vehicles Using Wi-Fi Signals. IEEE Trans. Mob. Comput. 2023, 1–14. [Google Scholar] [CrossRef]
- Ding, W.; Fu, H.; Hu, Y. Characteristics Assessment and Comparative Study of a Segmented-Stator Permanent-Magnet Hybrid-Excitation SRM Drive with High-Torque Capability. IEEE Trans. Power Electron. 2018, 33, 482–500. [Google Scholar] [CrossRef]
- Mosaad, M.I. Direct Power Control of SRG-Based WECSs Using Optimised Fractional-Order PI Controller. IET Electr. Power Appl. 2020, 14, 409–417. [Google Scholar] [CrossRef]
- Chumacero, E.; Loría, A.; Espinosa-Pérez, G. Velocity-Sensorless Tracking Control and Identification of Switched-Reluctance Motors. Automatica 2014, 50, 3123–3130. [Google Scholar] [CrossRef]
- Tang, H.; Di, J.; Wu, Z.; Li, W. Temperature analysis for the asymmetric six-phase permanent magnet synchronous motor in healthy and fault-tolerant modes. IEEE Trans. Ind. Electron. 2022, 17, 1–12. [Google Scholar] [CrossRef]
- Krishnan, R. Switched Reluctance Motor Drives: Modeling, Simulation, Analysis, Design, and Applications; CRC Press LLC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Farina, A. Simultaneous Measurement of Impulse Response and Distortion with a Swept-Sine Technique. In Proceedings of the 1999 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 20 October 1999; pp. 1–15. [Google Scholar] [CrossRef]
- Crama, P.; Schoukens, J. Initial Estimates of Wiener and Hammerstein Systems Using Multisine Excitation. IEEE Trans. Instrum. Meas. 2001, 50, 1791–1795. [Google Scholar] [CrossRef]
- Schoukens, J.; Pintelon, R.; Rolain, Y. identification of Nonlinear and Linear Systems, Similarities, Differences, Challenges. IFAC Proc. Vol. 2006, 39, 122–124. [Google Scholar] [CrossRef]
- Brouri, A.; Kadi, L.; Slassi, S. Frequency Identification of Hammerstein-Wiener Systems with Backlash Input Nonlinearity. Int. J. Control. Autom. Syst. 2017, 15, 2222–2223. [Google Scholar] [CrossRef]
- Giri, F.; Radouane, A.; Brouri, A.; Chaoui, F.Z. Combined Frequency-Prediction Error Identification Approach for Wiener Systems with Backlash and Backlash-Inverse Operators. Automatica 2014, 50, 768–783. [Google Scholar] [CrossRef]
- Brouri, A.; Amdouri, O.; Chaoui, F.Z.; Giri, F. Frequency Identification of Hammerstein-Wiener Systems with Piecewise Affine Input Nonlinearity. IFAC Proc. Vol. 2014, 47, 10030–10035. [Google Scholar]
- Brouri, A.; Kadi, L.; Lahdachi, K. Identification of Nonlinear System Composed of Parallel Coupling of Wiener and Hammerstein Models. Asian J. Control 2021, 24, 1152–1164. [Google Scholar] [CrossRef]
- Schoukens, M.; Pintelon, R.; Rolain, Y. Parametric Identification of Parallel Hammerstein Systems. IEEE Trans. Instrum. Meas. 2011, 60, 3931–3938. [Google Scholar] [CrossRef]
- Radun, A. Analytically computing the flux linked by a switched reluctance motor phase when the stator and rotor poles overlap. IEEE Trans. Magn. 2000, 36, 1996–2003. [Google Scholar] [CrossRef]
- Aguado-Rojas, M.; Maya-Ortiz, P.; Espinosa-Pérez, G. On-Line Estimation of Switched Reluctance Motor Parameters. Int. J. Adapt. Control. Signal Process. 2018, 32, 950–966. [Google Scholar] [CrossRef]
- Kadi, L.; Brouri, A.; Ouannou, A. Frequency-Geometric Identification of Magnetization Characteristics of Switched Reluctance Machine. Adv. Syst. Sci. Appl. 2020, 20, 11–26. [Google Scholar] [CrossRef]
- Ouannou, A.; Giri, F.; Brouri, A.; Oubouaddi, H.; Abdelaali, C. Parameter Identification of Switched Reluctance Motor Using Exponential Swept-Sine Signal. IFAC-PapersOnLine 2022, 55, 132–137. [Google Scholar] [CrossRef]
- Emadi, A. (Ed.) Handbook of Automotive Power Electronics and Motor Drives, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Peng, F.; Ye, J.; Emadi, A. An Asymmetric Three-Level Neutral Point Diode Clamped Converter for Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2017, 32, 8618–8631. [Google Scholar] [CrossRef]
- Bilgin, B.; Jiang, J.W.; Emadi, A. Switched Reluctance Motor Drives: Fundamentals to Applications, 1st ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2019; ISBN 9781787284395. [Google Scholar]
- Emadi, A.; Young Joo, L.; Rajashekara, K. Power Electronics and Motor Drives in Electric, Hybrid Electric, and Plug-In Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Ouannou, A.; Brouri, A.; Kadi, L.; Oubouaddi, H. Identification of Switched Reluctance Machine Using Fuzzy Model. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 2833–2846. [Google Scholar] [CrossRef]
- Sofiane, Y.; Tounzi, A.; Piriou, F. A Non Linear Analytical Model of Switched Reluctance Machines. Appl. Phys. 2002, 172, 163–172. [Google Scholar] [CrossRef]
- Zwerger, T.; Mercorelli, P. Using a Bivariate Polynomial in an EKF for State and Inductance Estimations in the Presence of Saturation Effects to Adaptively Control a PMSM. IEEE Access 2022, 10, 111545–111553. [Google Scholar] [CrossRef]
- Zwerger, T.; Mercorelli, P. Combining SMC and MTPA Using an EKF to Estimate Parameters and States of an Interior PMSM. In Proceedings of the 2019 20th International Carpathian Control Conference (ICCC), Krakow-Wieliczka, Poland, 26–29 May 2019; pp. 1–6. [Google Scholar]
- Barros, T.A.D.S.; Neto, P.J.D.S.; Filho, P.S.N.; Moreira, A.B.; Filho, E.R. An Approach for Switched Reluctance Generator in a Wind Generation System with a Wide Range of Operation Speed. IEEE Trans. Power Electron. 2017, 32, 8277–8292. [Google Scholar] [CrossRef]
- Diao, K.; Sun, X.; Bramerdorfer, G.; Cai, Y.; Lei, G.; Chen, L. Design Optimization of Switched Reluctance Machines for Performance and Reliability Enhancements: A Review. Renew. Sustain. Energy Rev. 2022, 168, 112785. [Google Scholar] [CrossRef]
- Garcia-Amoros, J.; Andrada, P.; Blanque, B.; Marin Genesca, M. Influence of Design Parameters in the Optimization of Linear Switched Reluctance Motor under Thermal Constraints. IEEE Trans. Ind. Electron. 2017, 46, 1. [Google Scholar] [CrossRef]
- Novak, A.; Lotton, P.; Simon, L. Synchronized Swept-Sine: Theory, Application, and Implementation. J. Audio Eng. Soc. 2015, 63, 786–798. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, L. System Identification and Online Equalization Technique Based Swept Sine Vibration Testing Control. In Proceedings of the 2014 Sixth International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2014. [Google Scholar] [CrossRef]
- Glentis, G.O.; Koukoulas, P.; Kalouptsidis, N. Efficient Algorithms for Volterra System Identification. IEEE Trans. Signal Process. 1999, 47, 3042–3057. [Google Scholar] [CrossRef]
- Liu, C.; Deng, Z.; Xie, L.; Li, K. The Design of the Simple Structure-Specified Controller of Magnetic Bearings for the High-Speed SRM. IEEE/ASME Trans. Mechatron. 2015, 20, 1798–1808. [Google Scholar] [CrossRef]




| Refs | Overview | Contribution | Drawbacks |
|---|---|---|---|
| [15] | Identification method is developed online, but it fails to include the saturation effect. This hypothesis is not suitable for this type of electrical machine. Indeed, a highly saturated magnetic circuit features the latter, as the co-energy increases with the saturation level. Therefore, it works mainly in the magnetically saturated region. | This model can be used to obtain the machine characteristics without requiring data measurement., it simply requires information on the geometry, flux density, iron saturation, and unsaturated iron permeability. | This approach is not suitable for other positions. It is preferable to repeat this experiment for several rotor positions. |
| [7] | An inexpensive method is introduced for measuring the transfer function of systems that are weakly non-linear and approximately time-invariant. The technique employs novel measurement techniques. | There is no need to maintain tight synchronization between the sampling clock of the excitation signal and the system response. | This technique works reliably if the system includes parts that exhibit non-linear behavior, and in these cases, the measurement results include the quantification of the harmonic distortion at various orders. |
| [14] | The aim of this study is to introduce a new technique for identifying the parameters of parallel Hammerstein systems. In this approach, the linear dynamic aspects of the system are described by a parametric rational function in the z-domain, while the static nonlinear components are modeled using a linear combination of basic functions. | The time required by this method to obtain the parameters is notably shorter. Unlike other algorithms, the main advantage of this approach is that the number of physical signal paths determines the number of parallel branches. | The root mean square (RMS) error ratio between the parallel Hammerstein model and the single Hammerstein model is of value 10%. |
| [15] | A three stages identification technique is developed. This solution gives the phase and modulus estimates of the linear part, as well as the estimates of the input and output nonlinearities. | It is not necessary to have knowledge about the type of nonlinearity. | To employ this approach, a significant quantity of data is required, which requires a slightly long computation time and large memory usage. Furthermore, this method has local convergence characteristics. |
| [10] | A piecewise constant signal is utilized to detect the nonlinearities present in the system. | A non-static nonlinearity (backlash or backlash-inverse). | The dynamic nonlinearity is bordered by straight lines. |
| [16] | The proposed approach by the authors involves a linear parametric model using a 2-stage identification process. In this solution, a recursive least-squares algorithm with a forgetting factor is used. This method assumes the availability of measurements for stator voltages and currents, as well as rotor position and speed. | The identification method is developed online. | The identification method does not take into account the saturation effect of the switched reluctance machine. |
| [17] | In this work, the authors proposed an analytical modelling and identification method of magnetization characteristics of a SRM. In this method, a Hammerstein model is excited by a signal having rich frequency spectrum. Its parameters can then be estimated using data acquisition and recursive least square (RLS). | The technic is based on frequency technics is developed allowing the identification of SRM nonlinearities (considering the saturation and the hysteresis effects). This approach enjoys the simplicity of implementation, good convergence properties, and very fast computing time. | Identification scheme requires a less computational load and low memory usage. the hysteresis effect is not considered. A filtering algorithm of the current at the winding terminal is suggested. Accordingly, the system nonlinearities can be easily identified using the recording of the phase current. |
| Proposed | The proposed technique is based on a parallel connection of several Hammerstein models that have polynomial nonlinearity. The model is driven by a swept-sine signal then finite element method analysis is performed to estimate the SRM parameters. | This method can be performed easily allowing to obtain the flux-linkage characteristics with good accuracy. It also offers significant advantages in terms of signal-to-noise ratio and immunity to changes over time in the system being tested. | Phase noise in linear blocks |
| Current (A) | Flux Linkage (Wb) 0° | Inductance (H) 0° | Flux Linkage (Wb) 15° | Inductance (H) 15° | Flux Linkage (Wb) 30° | Inductance (H) 30° |
|---|---|---|---|---|---|---|
| 0.200 | 0.066 | 0.328 | 0.032 | 0.158 | 0.012 | 0.061 |
| 0.400 | 0.131 | 0.328 | 0.063 | 0.158 | 0.024 | 0.061 |
| 0.600 | 0.197 | 0.328 | 0.095 | 0.158 | 0.036 | 0.061 |
| 0.800 | 0.262 | 0.328 | 0.126 | 0.158 | 0.048 | 0.061 |
| 1.000 | 0.328 | 0.328 | 0.158 | 0.158 | 0.061 | 0.061 |
| 1.200 | 0.393 | 0.327 | 0.189 | 0.158 | 0.073 | 0.061 |
| 1.400 | 0.458 | 0.327 | 0.221 | 0.158 | 0.085 | 0.061 |
| 1.600 | 0.523 | 0.327 | 0.252 | 0.158 | 0.097 | 0.061 |
| 1.800 | 0.586 | 0.326 | 0.283 | 0.157 | 0.109 | 0.061 |
| 2.000 | 0.648 | 0.324 | 0.313 | 0.157 | 0.121 | 0.061 |
| Parameter Description | Symbol | Value | Unit |
|---|---|---|---|
| Number of stator teeth | Ns | 8 | −− |
| Number of rotor teeth | Nr | 6 | −− |
| Number of phases | q | 4 | −− |
| Number of turns/phases | N | 250 | |
| Bore diameter | D | 46.02 | mm |
| Outer diameter | D0 | 89.1 | mm |
| Air gap thickness | E | 0.8 | mm |
| Stator tooth height | hs | 11.267 | mm |
| Rotor tooth height | hr | 7.498 | mm |
| Rotor tooth width | Wr | 8.287 | mm |
| Stator tooth width | Ws | 7.912 | mm |
| Rotor cylinder head thickness | Yr | 6.263 | mm |
| Machine length | L | 50 | mm |
| Position | ||||
|---|---|---|---|---|
| Aligned position 0° | ||||
| Midway position 15° | ||||
| Unaligned position 30° |
| Position | |||
|---|---|---|---|
| Aligned position 0° | |||
| Midway position 15° | |||
| Unaligned position 30° |
| Parameter | Actual | Estimated | % Error |
|---|---|---|---|
| 0.8493 | 0.86 | 1.07 | |
| 0.3893 H | 0.4 H | 1.07 | |
| 0.1393 H | 0.15 H | 7.75 | |
| 0.0499 H | 0.0606 H | 4.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouannou, A.; Brouri, A.; Giri, F.; Kadi, L.; Oubouaddi, H.; Hussien, S.A.; Alwadai, N.; Mosaad, M.I. Parameter Identification of Switched Reluctance Motor SRM Using Exponential Swept-Sine Signal. Machines 2023, 11, 625. https://doi.org/10.3390/machines11060625
Ouannou A, Brouri A, Giri F, Kadi L, Oubouaddi H, Hussien SA, Alwadai N, Mosaad MI. Parameter Identification of Switched Reluctance Motor SRM Using Exponential Swept-Sine Signal. Machines. 2023; 11(6):625. https://doi.org/10.3390/machines11060625
Chicago/Turabian StyleOuannou, Abdelmalek, Adil Brouri, Fouad Giri, Laila Kadi, Hafid Oubouaddi, Shimaa A. Hussien, Norah Alwadai, and Mohamed I. Mosaad. 2023. "Parameter Identification of Switched Reluctance Motor SRM Using Exponential Swept-Sine Signal" Machines 11, no. 6: 625. https://doi.org/10.3390/machines11060625
APA StyleOuannou, A., Brouri, A., Giri, F., Kadi, L., Oubouaddi, H., Hussien, S. A., Alwadai, N., & Mosaad, M. I. (2023). Parameter Identification of Switched Reluctance Motor SRM Using Exponential Swept-Sine Signal. Machines, 11(6), 625. https://doi.org/10.3390/machines11060625








