Degradation-Sensitive Control Algorithm Based on Phase Optimization for Interleaved DC–DC Converters
Abstract
1. Introduction
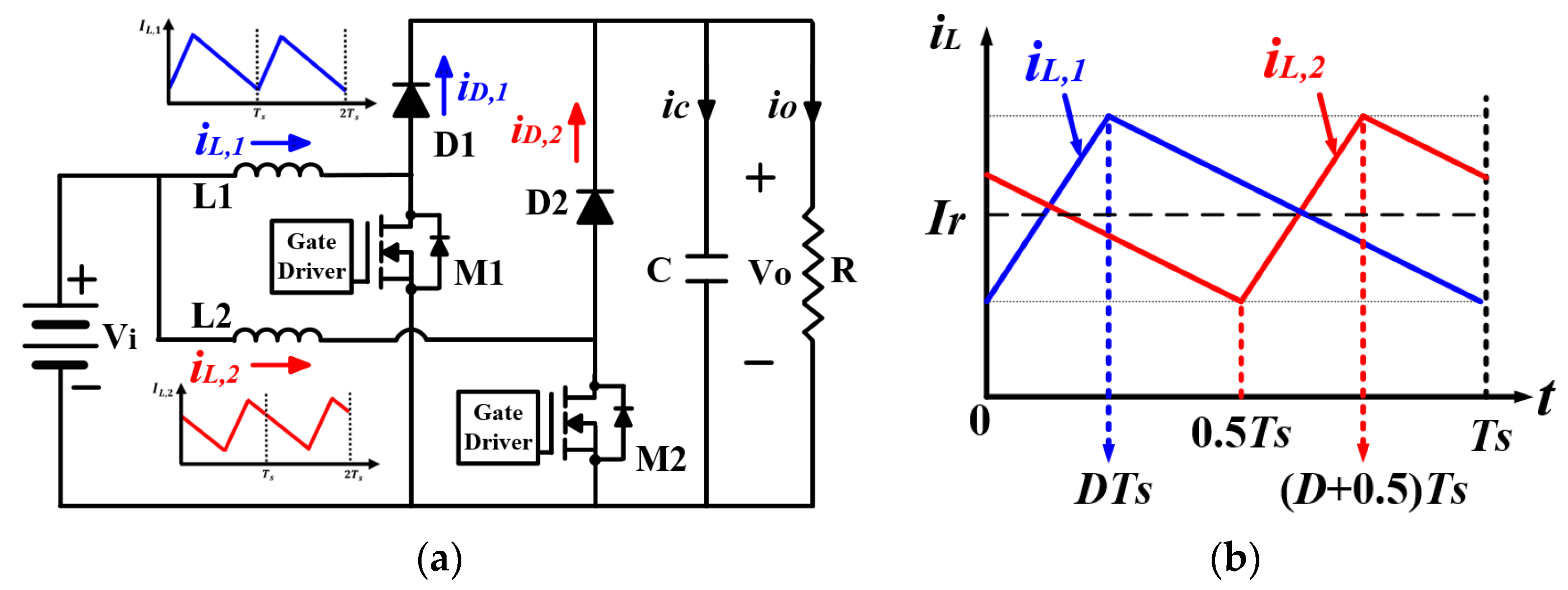
2. Conventional Interleaved DC–DC Boost Converter
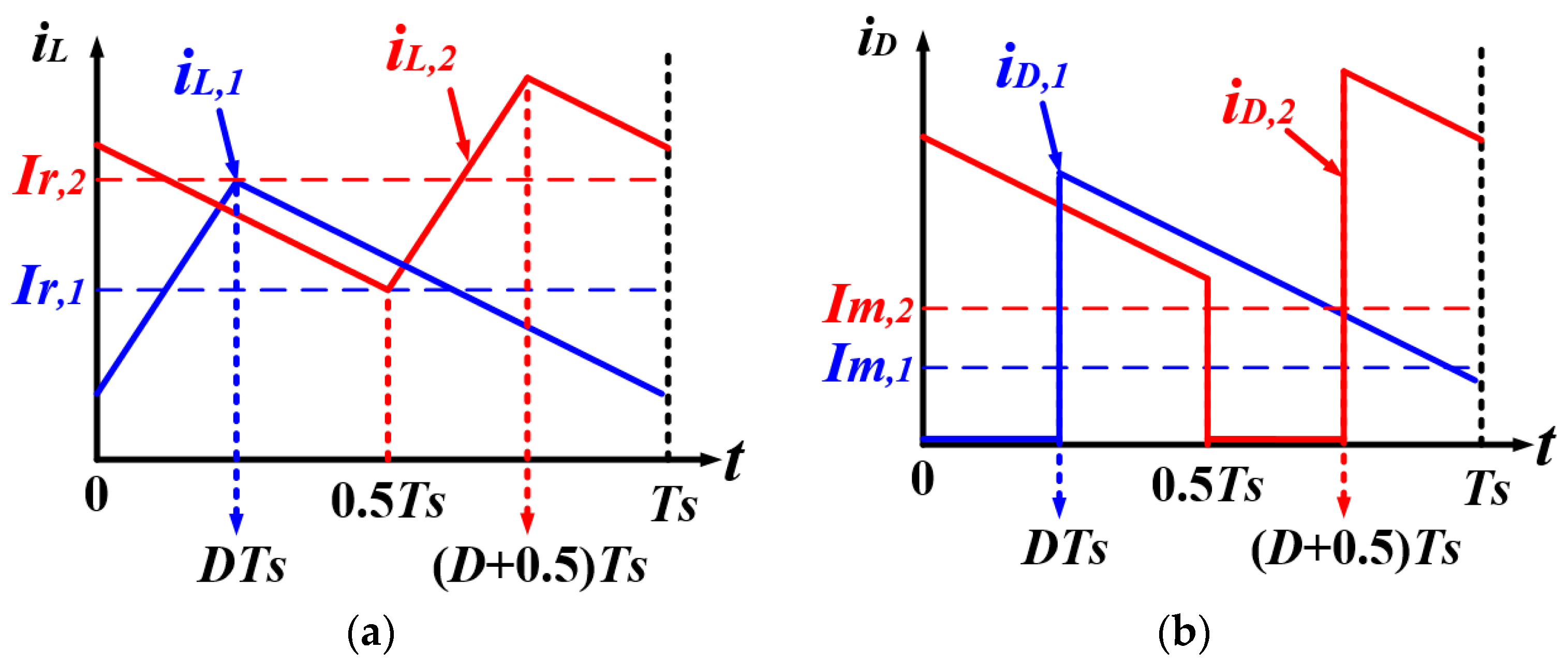
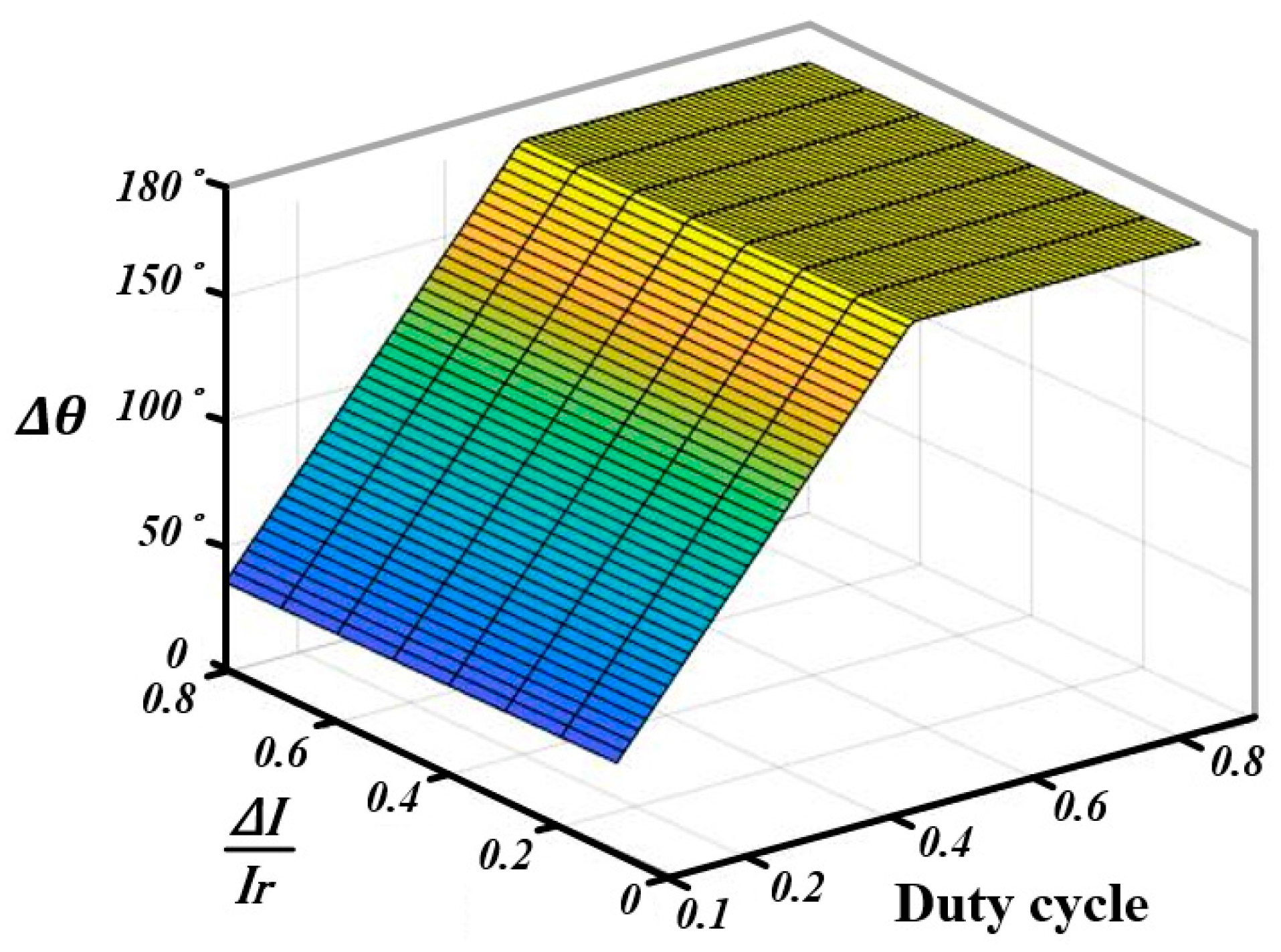
3. Mathematical Analysis of Proposed Phase Optimization Algorithm
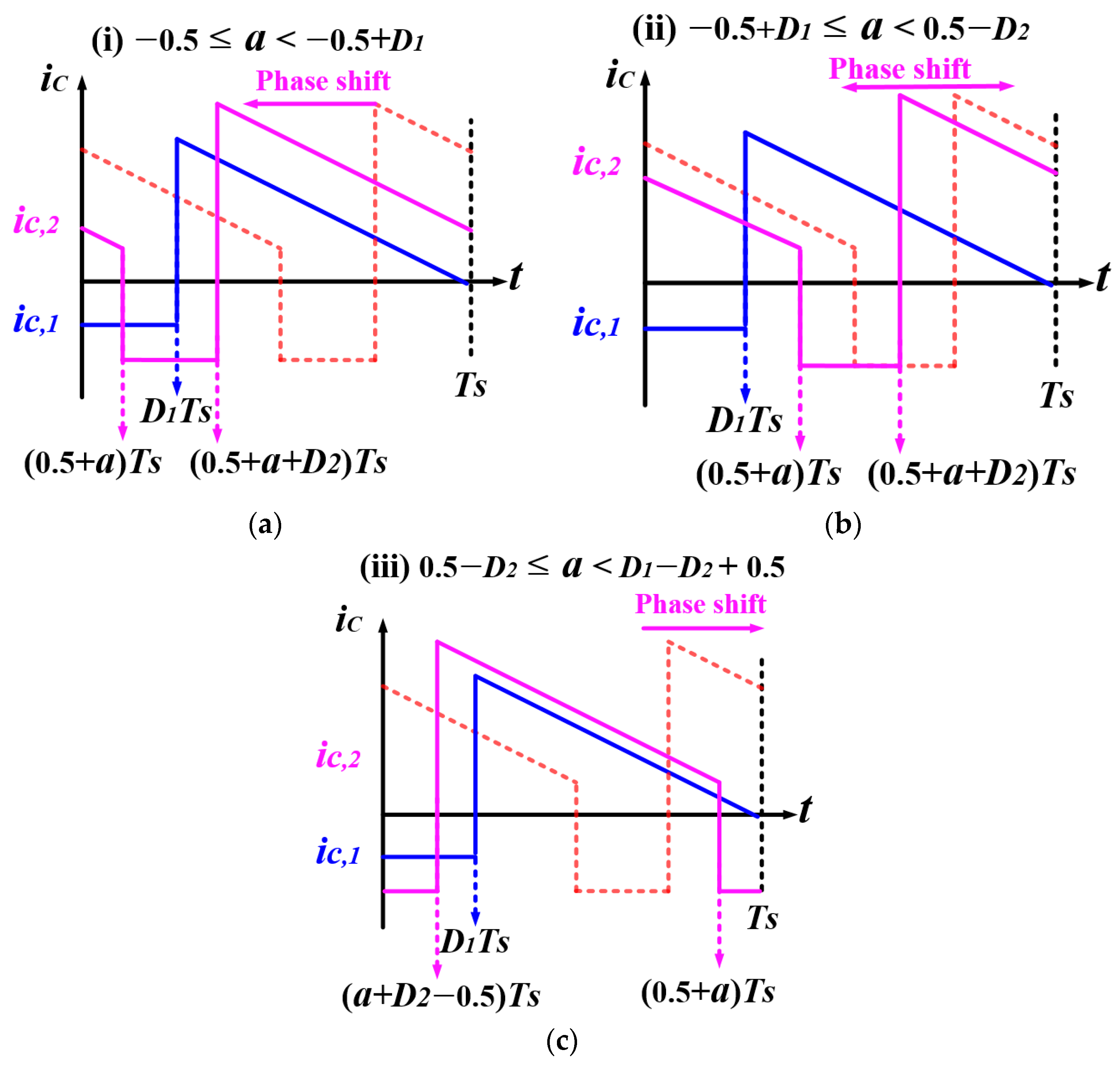
- (i)
- −0.5 −0.5 +
- (ii)
- −0.5 + 0.5 −
- (iii)
- 0.5 – 0.5
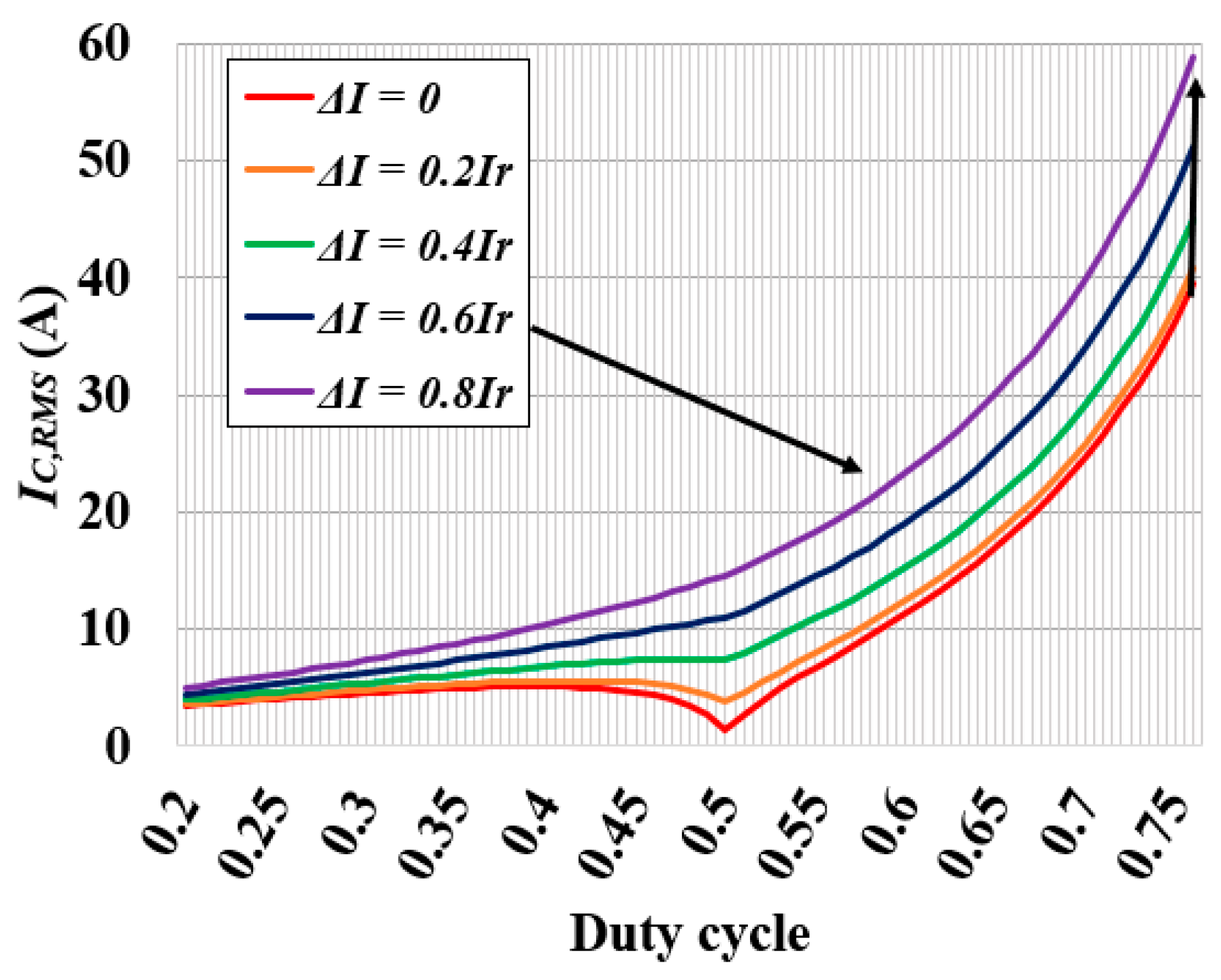
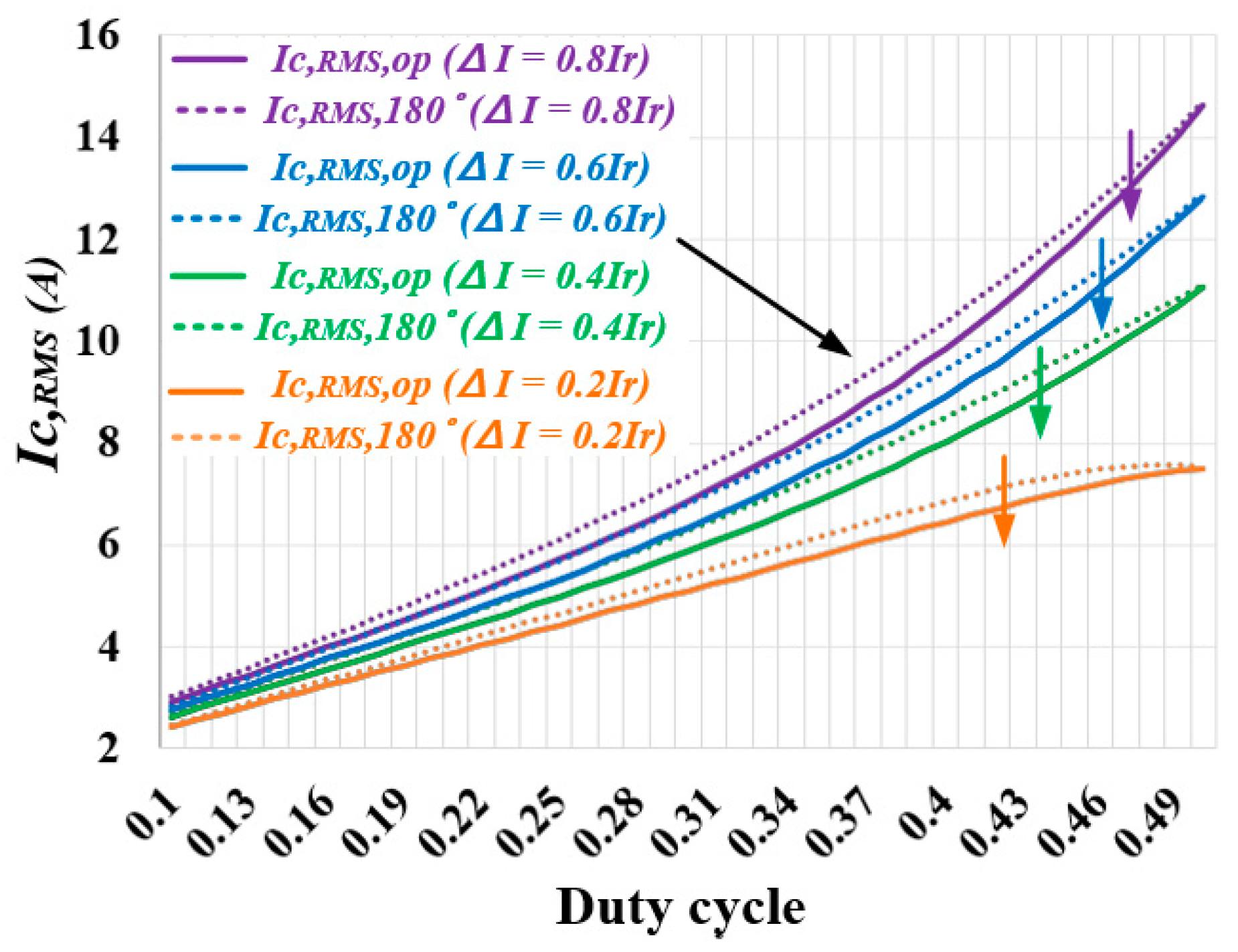
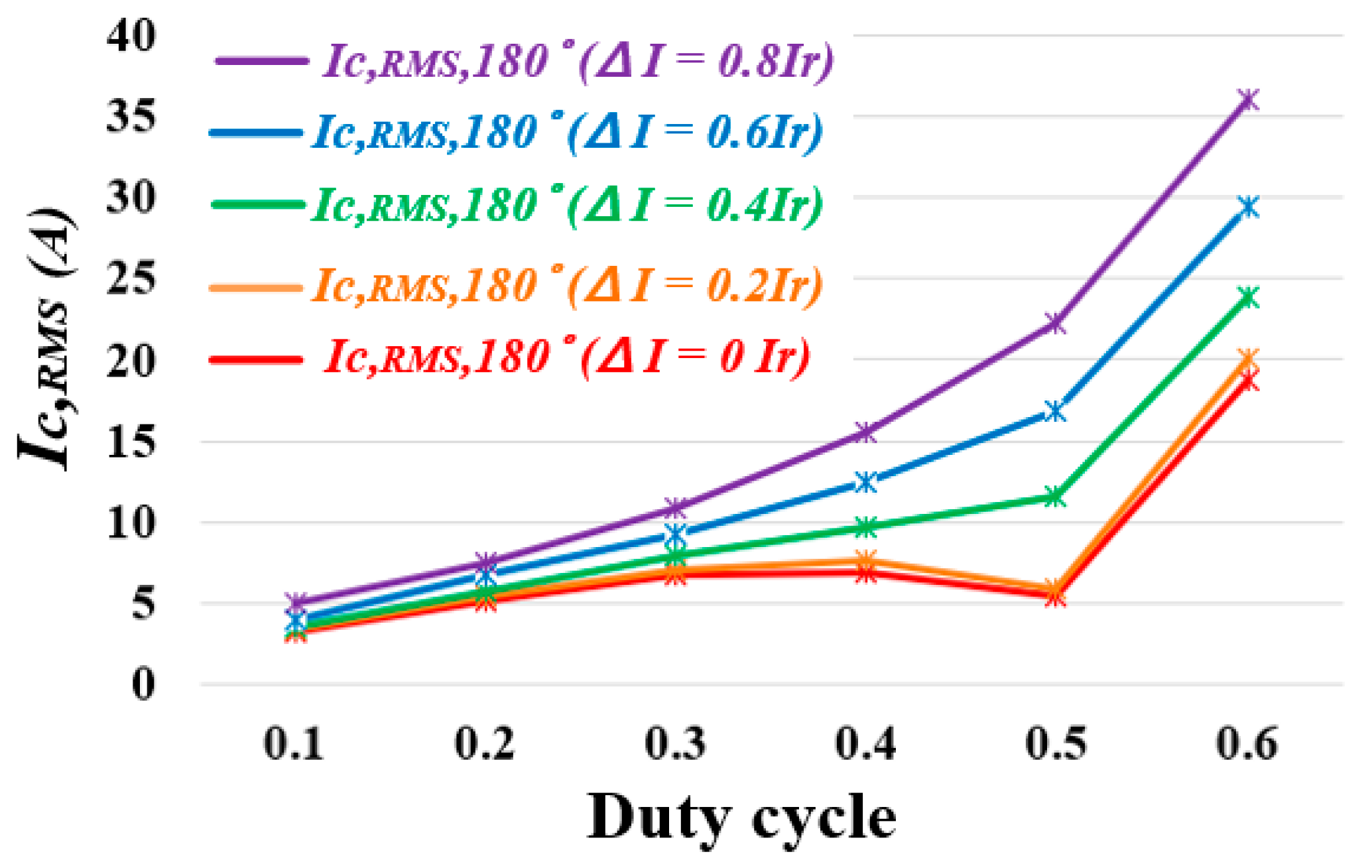
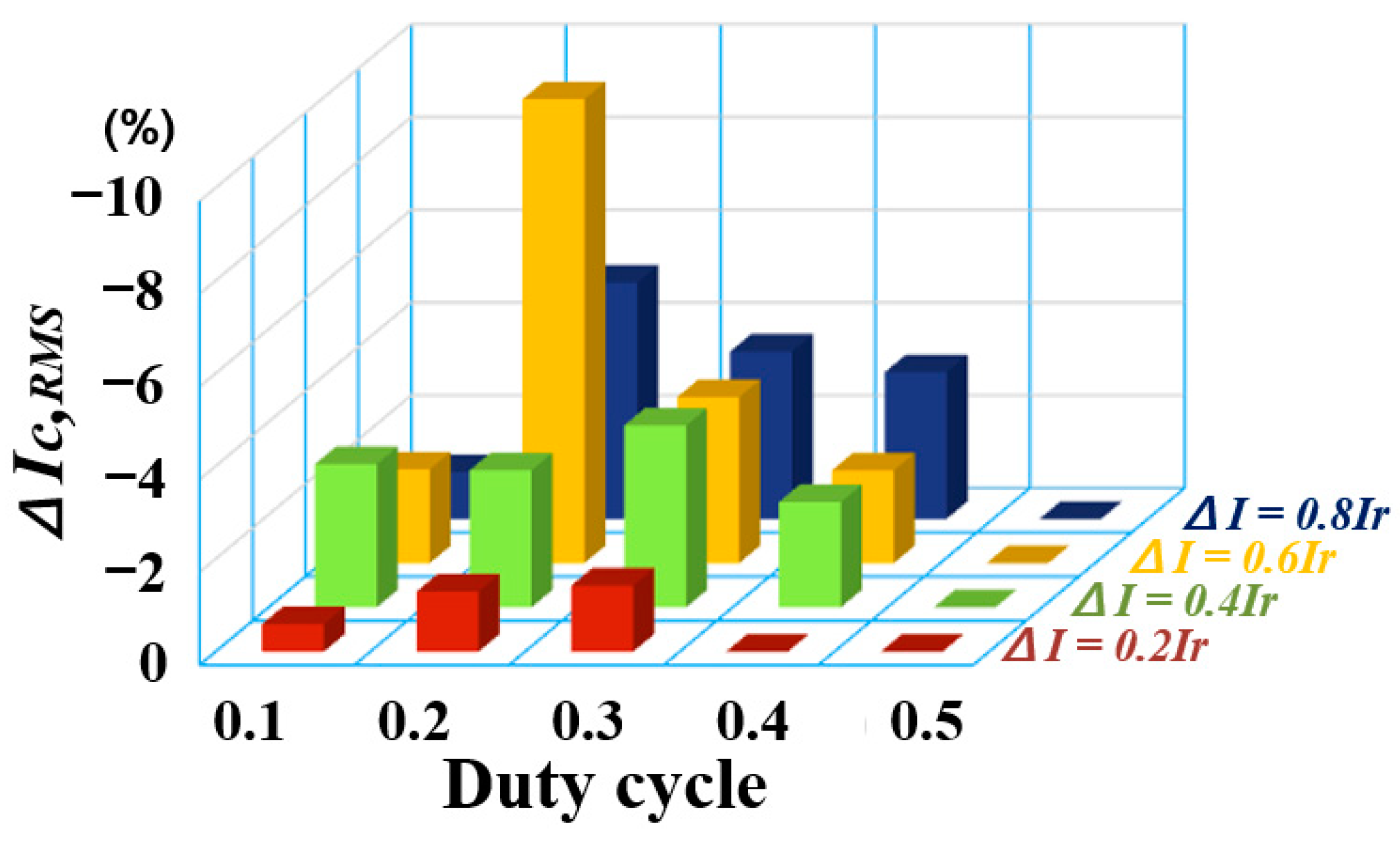
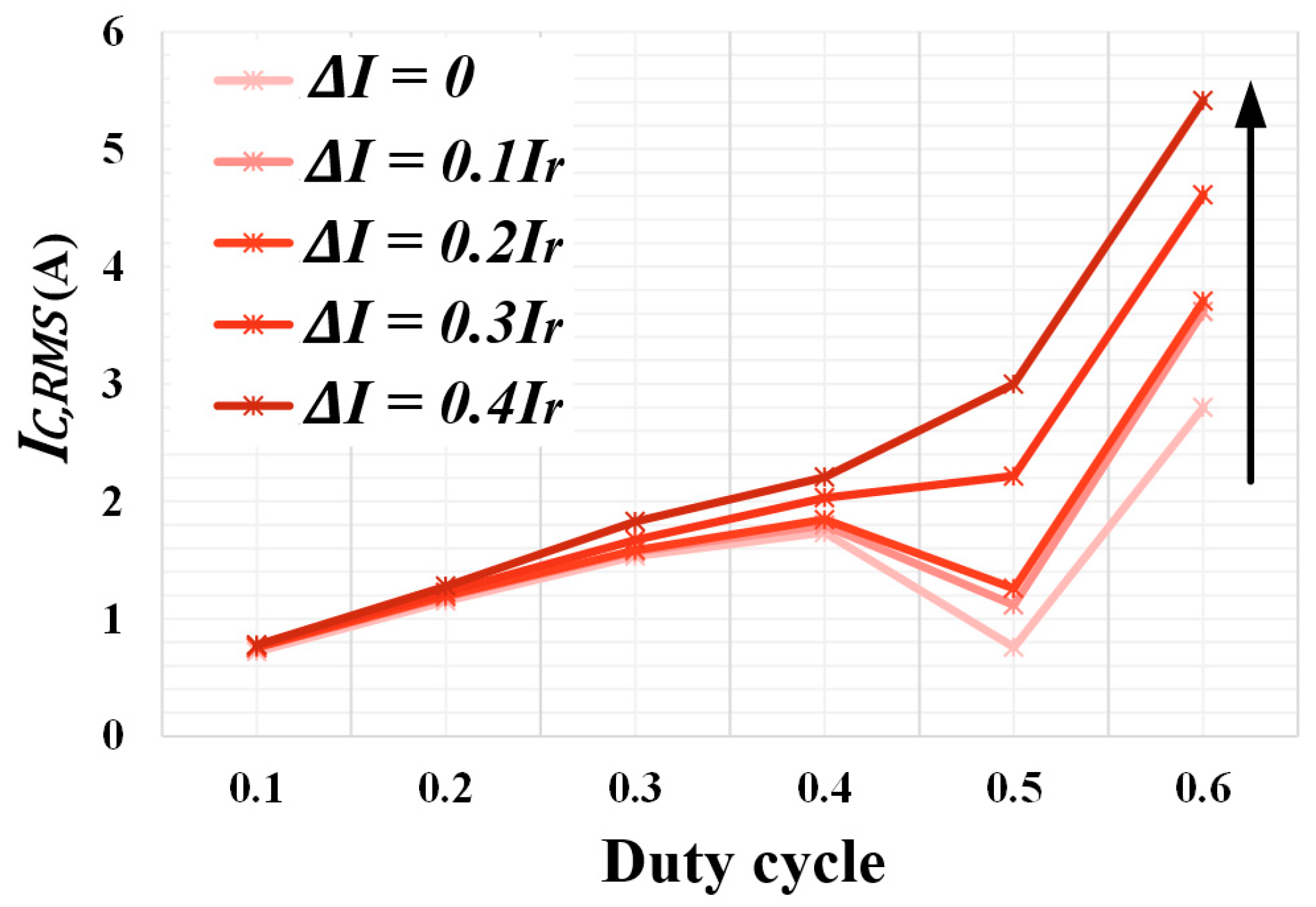
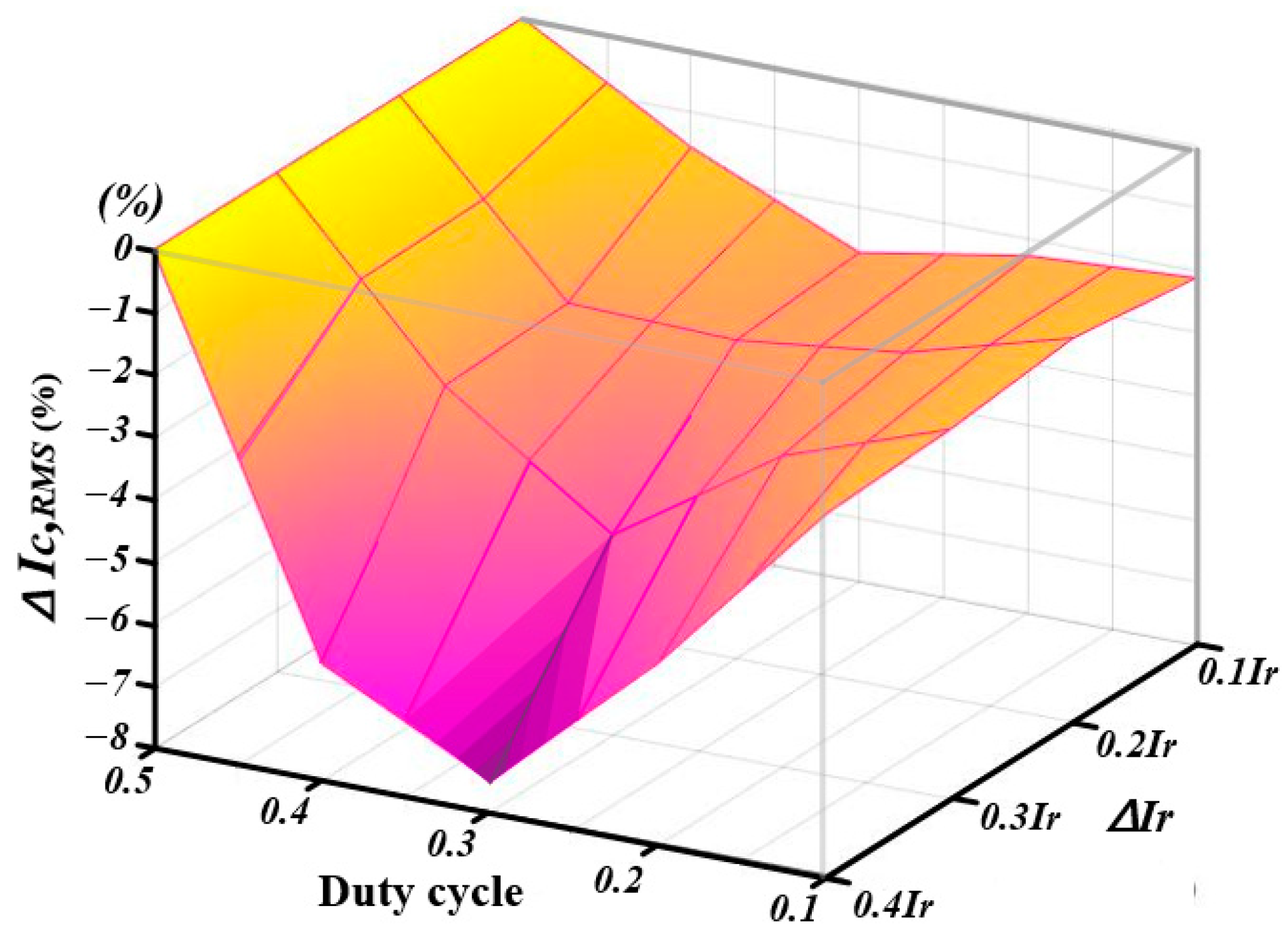
4. Simulation Results of Proposed Phase Optimization Algorithm
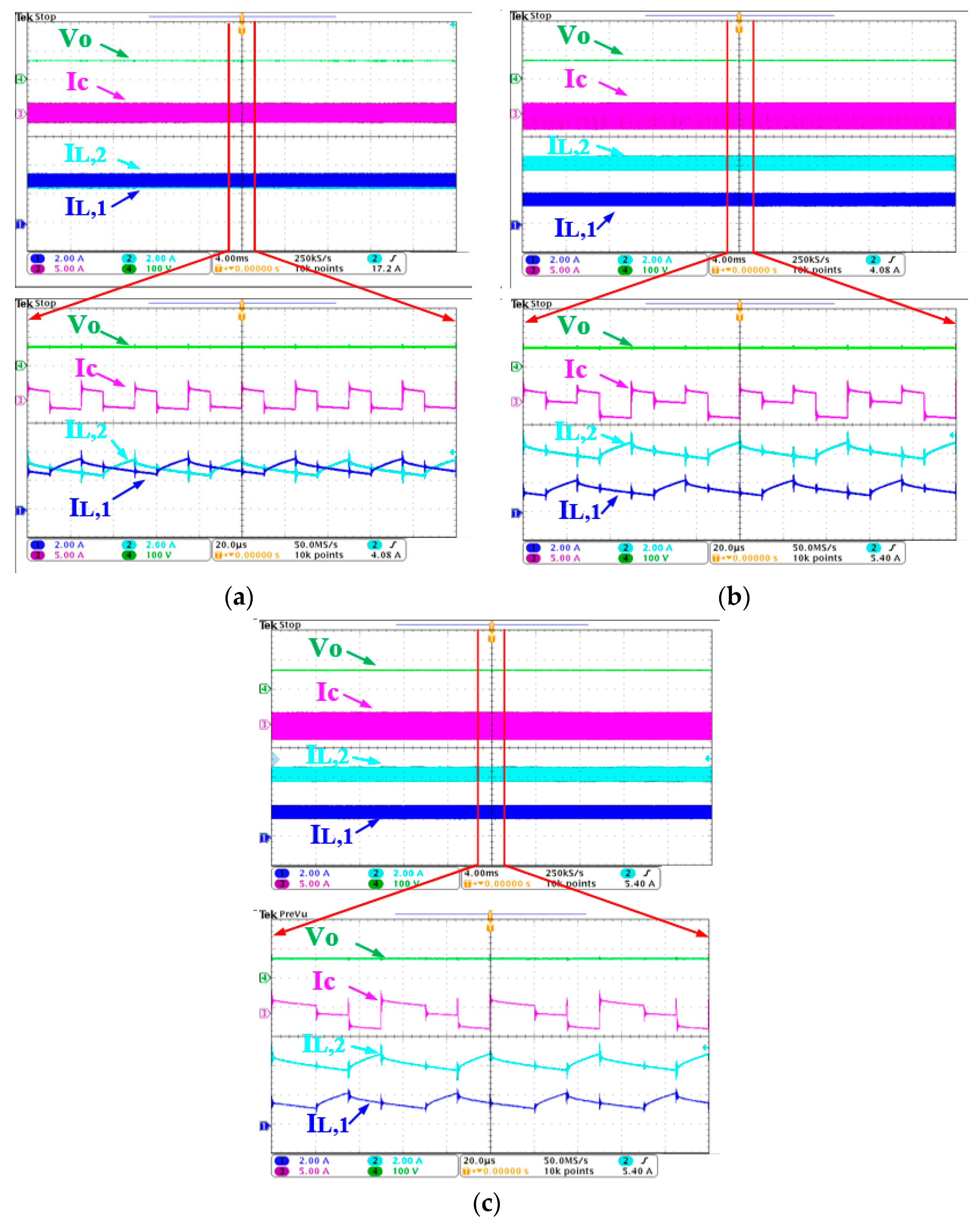
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ravi, D.; Letha, S.S.; Samuel, P.; Reddy, B.M. An Overview of Various DC-DC Converter Techniques used for Fuel Cell based Applications. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 16–21. [Google Scholar]
- Syah, M.N.; Firmansyah, E.; Utomo, D.R. Interleaved Bidirectional DC-DC Converter Operation Strategies and Problem Challenges: An Overview. In Proceedings of the 2022 IEEE International Conference in Power Engineering Application (ICPEA), Shah Alam, Malaysia, 7–8 March 2022; pp. 1–6. [Google Scholar]
- Aranda, E.D.; Litrán, S.P.; Prieto, M.B.F. Combination of interleaved single-input multiple-output DC-DC converters. CSEE Power Energy Syst. 2022, 8, 132–142. [Google Scholar]
- Rahimpour, S.; Tarzamni, H.; Kurdkandi, N.V.; Husev, O.; Vinnikov, D.; Tahami, F. An Overview of Lifetime Management of Power Electronic Converters. IEEE Access 2022, 10, 109688–109711. [Google Scholar] [CrossRef]
- Chakraborty, S.; Hasan, M.M.; Paul, M.; Tran, D.; Geury, T.; Davari, P.; Blaabjerg, F.; Baghdadi, M.E.; Hegazy, O. Real-Life Mission Profile-Oriented Lifetime Estimation of a SiC Interleaved Bidirectional HV DC/DC Converter for Electric Vehicle Drivetrains. IEEE Emerg. Sel. Topics Power Electron. 2022, 10, 5142–5167. [Google Scholar] [CrossRef]
- Givi, H.; Farjah, E.; Ghanbari, T. A Comprehensive Monitoring System for Online Fault Diagnosis and Aging Detection of Non-Isolated DC–DC Converters’ Components. IEEE Trans. Power Electron. 2019, 34, 6858–6875. [Google Scholar] [CrossRef]
- Khosroshahi, A.; Abapour, M.; Sabahi, M. Reliability Evaluation of Conventional and Interleaved DC–DC Boost Converters. IEEE Trans. Power Electron. 2015, 30, 5821–5828. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry-Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Song, Y.; Wang, B. Quantitative evaluation for reliability of hybrid electric vehicle powertrain. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 1404–1409. [Google Scholar]
- Murken, M.; Gratzfeld, P. Reliability Comparison of Bidirectional Automotive DC/DC Converters. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–7. [Google Scholar]
- Ni, Z.; Lyu, X.; Yadav, O.P.; Singh, B.N.; Zheng, S.; Cao, D. Overview of Real-Time Lifetime Prediction and Extension for SiC Power Converters. IEEE Trans. Power Electron. 2020, 35, 7765–7794. [Google Scholar] [CrossRef]
- Hannonen, J.; Honkanen, J.; Ström, J.-P.; Kärkkäinen, T.; Silventoinen, P.; Räisänen, S. Capacitor aging detection in DC-DC converter output stage. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 5538–5545. [Google Scholar]
- Laadjal, K.; Sahraoui, M.; Cardoso, A.J.M. On-Line Fault Diagnosis of DC-Link Electrolytic Capacitors in Boost Converters Using the STFT Technique. IEEE Trans. Power Electron. 2021, 36, 6303–6312. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters—An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef]
- Samavatian, V.; Fotuhi-Firuzabad, M.; Dehghanian, P.; Blaabjerg, F. Reliability Modeling of Multistate Degraded Power Electronic Converters With Simultaneous Exposure to Dependent Competing Failure Processes. IEEE Access 2021, 9, 67096–67108. [Google Scholar] [CrossRef]
- Andresen, M.; Buticchi, G.; Liserre, M. Active thermal control of isolated soft switching DC/DC converters. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6818–6823. [Google Scholar]
- Dusmez, S.; Akin, B. An Active Life Extension Strategy for Thermally Aged Power Switches Based on the Pulse-Width Adjustment Method in Interleaved Converters. IEEE Trans. Power Electron. 2016, 31, 5149–5160. [Google Scholar] [CrossRef]
- Marquez, A.; Leon, J.I.; Hahn, F.; Merchan, R.G.; Buticchi, G.; Vazquez, S.; Gerada, C.; Liserre, M.; Franquelo, L.G. Power Devices Aging Equalization of Interleaved DC–DC Boost Converters via Power Routing. IEEE. Emerg. Sel. Topics Ind. Electron. 2020, 1, 91–101. [Google Scholar] [CrossRef]
- Karki, U.; Gonzalez-Santini, N.S.; Peng, F.Z. Effect of gate-oxide degradation on electrical parameters of silicon carbide MOSFETs. IEEE Trans. Electron. Devices 2020, 67, 2544–2552. [Google Scholar] [CrossRef]
- Jensen, W.R.; Foster, S.N. Online detection of MOSFET gate oxide degradation in a three-phase inverter-drive application. IEEE Trans. Transp. Electrif. 2021, 7, 50–57. [Google Scholar] [CrossRef]


| Circuit Parameters | |
|---|---|
| L1 | 1 mH |
| L2 | 1 mH |
| Switching Frequency | 20 kHz |
| R | 22 Ω |
| C | 680 µF |
| Vi | 200 V |
| A | B | C | D | |
|---|---|---|---|---|
| 0.107 Ω | 0.154 Ω | 0.523 Ω | 1.23 Ω | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, J.; Kwak, S.; Choi, S. Degradation-Sensitive Control Algorithm Based on Phase Optimization for Interleaved DC–DC Converters. Machines 2023, 11, 624. https://doi.org/10.3390/machines11060624
Jeong J, Kwak S, Choi S. Degradation-Sensitive Control Algorithm Based on Phase Optimization for Interleaved DC–DC Converters. Machines. 2023; 11(6):624. https://doi.org/10.3390/machines11060624
Chicago/Turabian StyleJeong, Jaeyoon, Sangshin Kwak, and Seungdeog Choi. 2023. "Degradation-Sensitive Control Algorithm Based on Phase Optimization for Interleaved DC–DC Converters" Machines 11, no. 6: 624. https://doi.org/10.3390/machines11060624
APA StyleJeong, J., Kwak, S., & Choi, S. (2023). Degradation-Sensitive Control Algorithm Based on Phase Optimization for Interleaved DC–DC Converters. Machines, 11(6), 624. https://doi.org/10.3390/machines11060624






