A Non-Integer High-Order Sliding Mode Control of Induction Motor with Machine Learning-Based Speed Observer
Abstract
1. Introduction
- We propose a new control scheme called ST-FOSMC that combines Fractional-Order Sliding Mode Control (FOSMC) and Super-Twisting (ST) algorithms. We use FOSMC to shape the error dynamics of the system for robustness against disturbances and uncertainties, while ST is used for fast convergence and high-performance tracking. We evaluate the stability of the proposed control system by analyzing the ST and FOSMC error dynamics, which represent the difference between desired and actual states of the system and the deviation from the sliding surface defined by FOSMC, respectively. By studying the behavior of both error dynamics, we ensure the stability of the closed-loop system. Our proposed ST-FOSMC scheme achieves a robust and high-performance control with guaranteed stability.
- Our work proposes a machine learning-based method, specifically GPR, to estimate the speed of an Induction Motor (IM). The proposed GPR utilize an autoregressive (AR) GPR method that incorporates the estimated speed, voltage, and current from the previous discrete time to improve the accuracy of speed estimation. GPR is a non-parametric probabilistic model that is capable of accurately estimating the speed of an IM. By using an autoregressive approach, we are able to leverage the previously estimated speed, voltage, and current values to further enhance the accuracy of the estimation. Our proposed GPR-based method offers a reliable and accurate means of speed estimation for IM, which is crucial for effective motor control. This method has the potential to improve the efficiency and performance of IM control systems, especially in applications where precise speed control is critical.
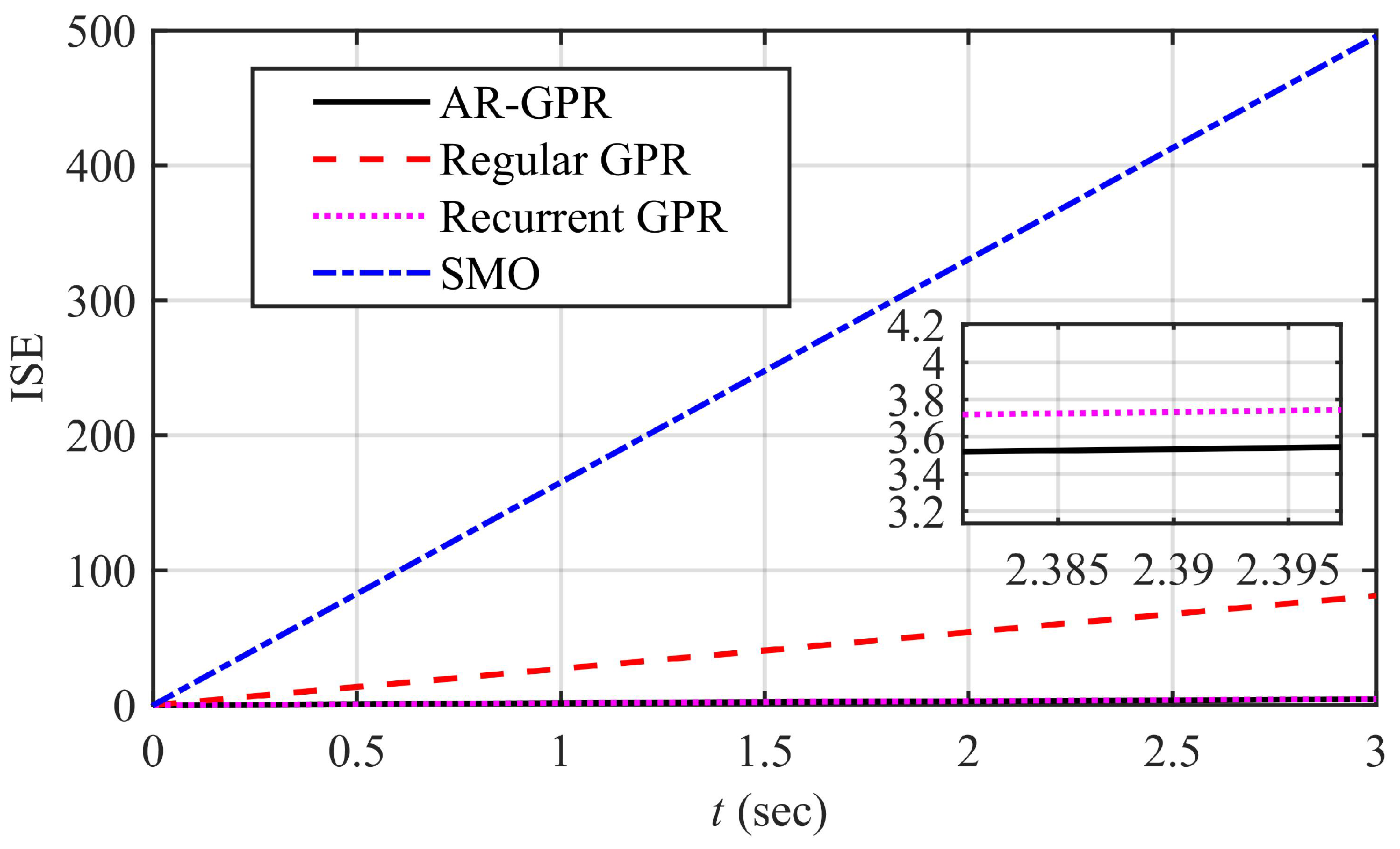
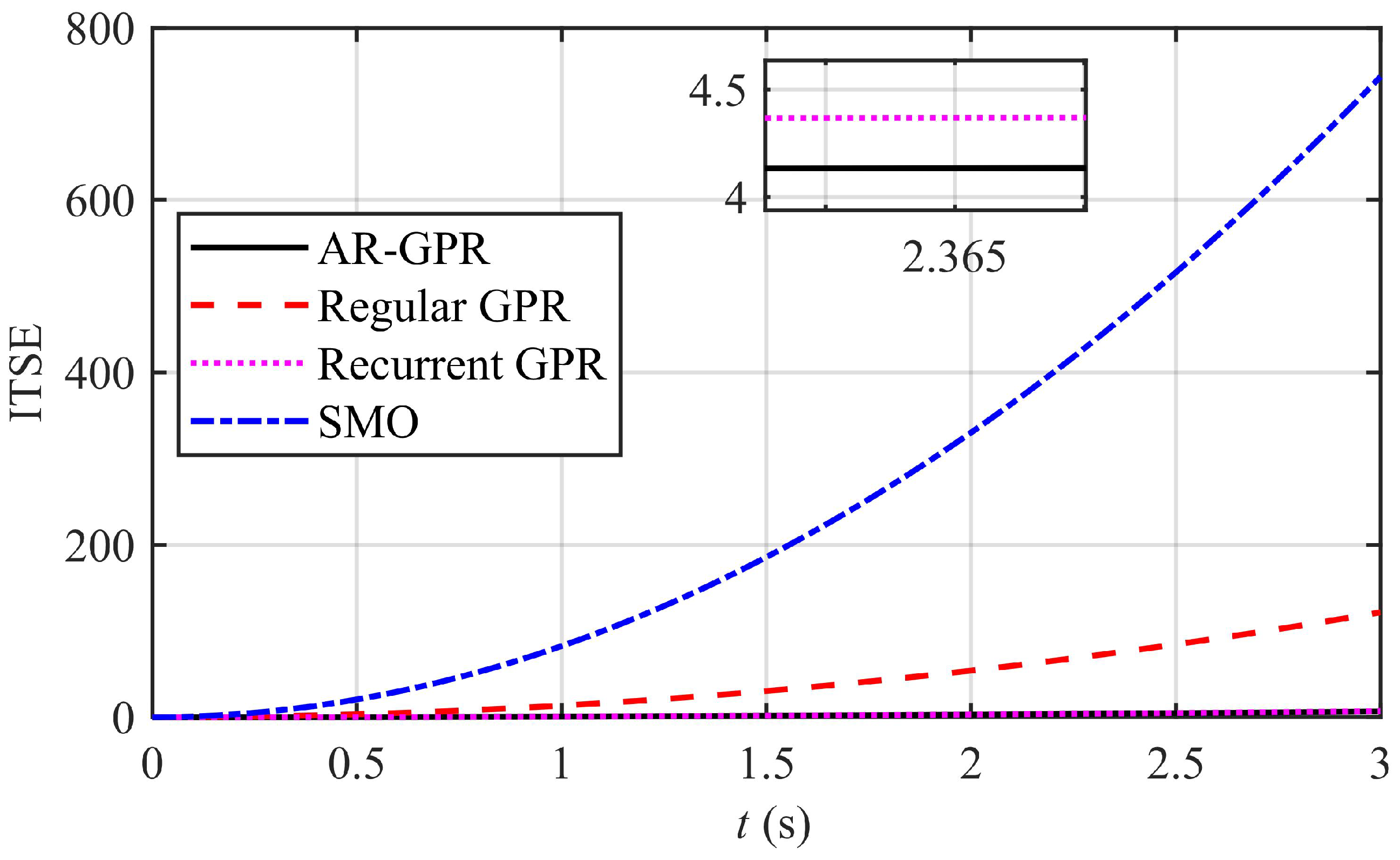
- Comparative analysis of the GPR framework with a state-of-the-art SMO is also performed. Both the observers are evaluated through different performance indices, including integral square error, integral time square error, and root mean square error. The superiority of the proposed GPR framework-based ST-FOSMC scheme are also verified using various performance indices, stability, and robustness test, and comparisons with existing control methods.
2. Basic Definitions for Fractional Calculus
3. Induction Motor Modeling
4. Model Predictive Torque Control Modeling
5. Super-Twisting Fractional-Order Sliding Mode Control Design
6. Gaussian Process Regression-Based IM Modeling
6.1. Lyapunov Stability of GPR
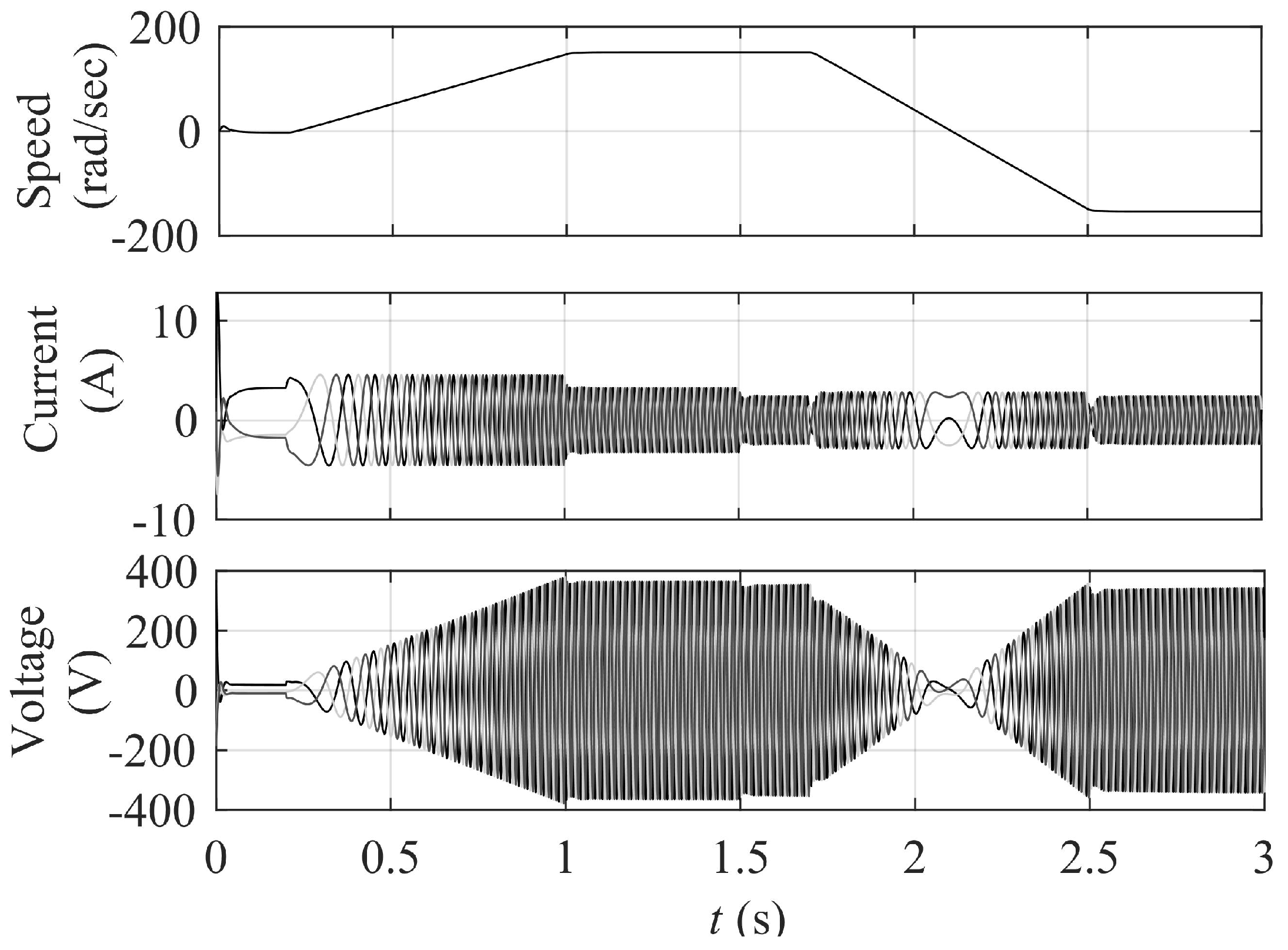
7. Performance Evaluation
7.1. Performance Evaluation Parameters
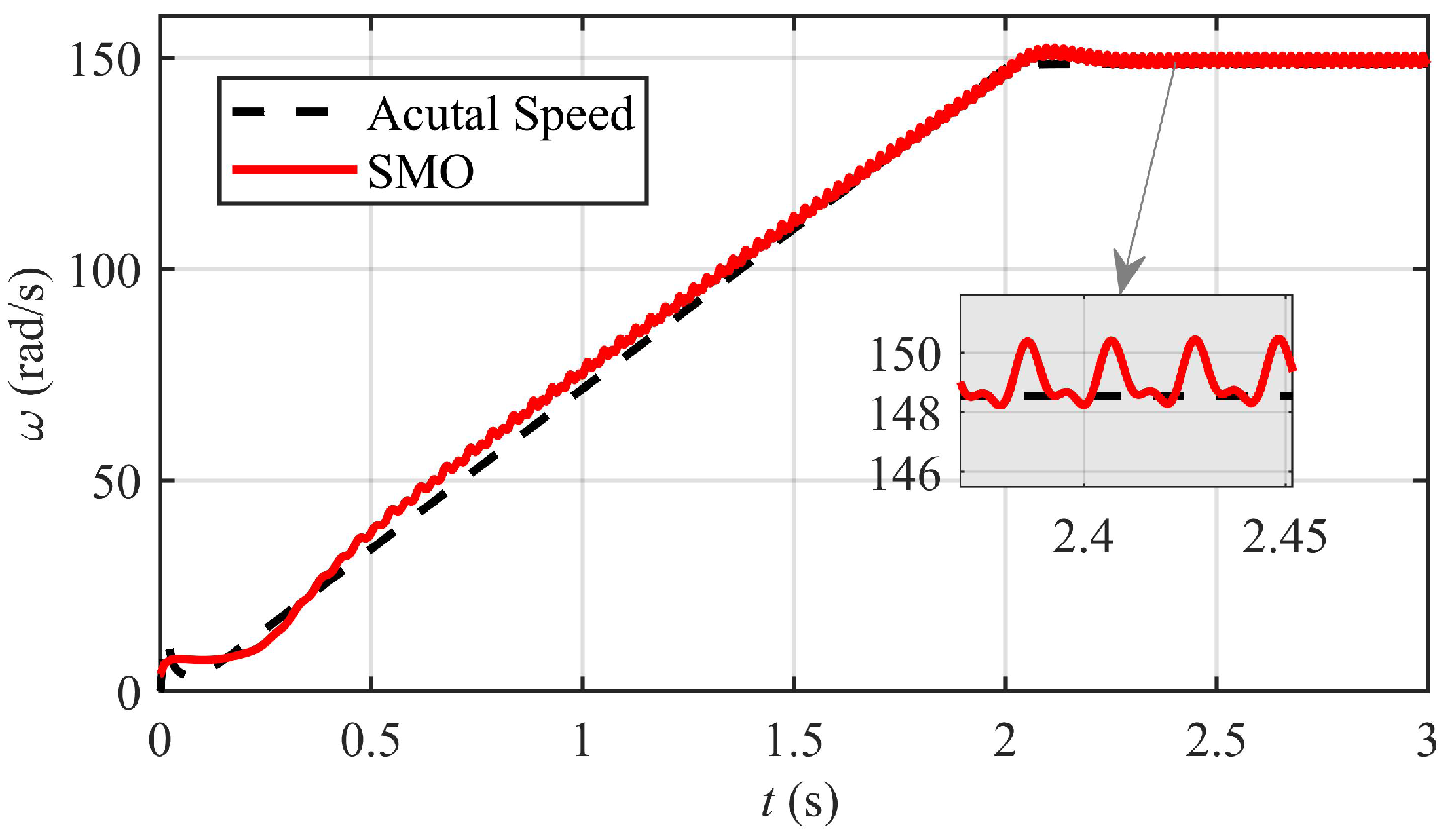
7.2. Sliding Mode Observer
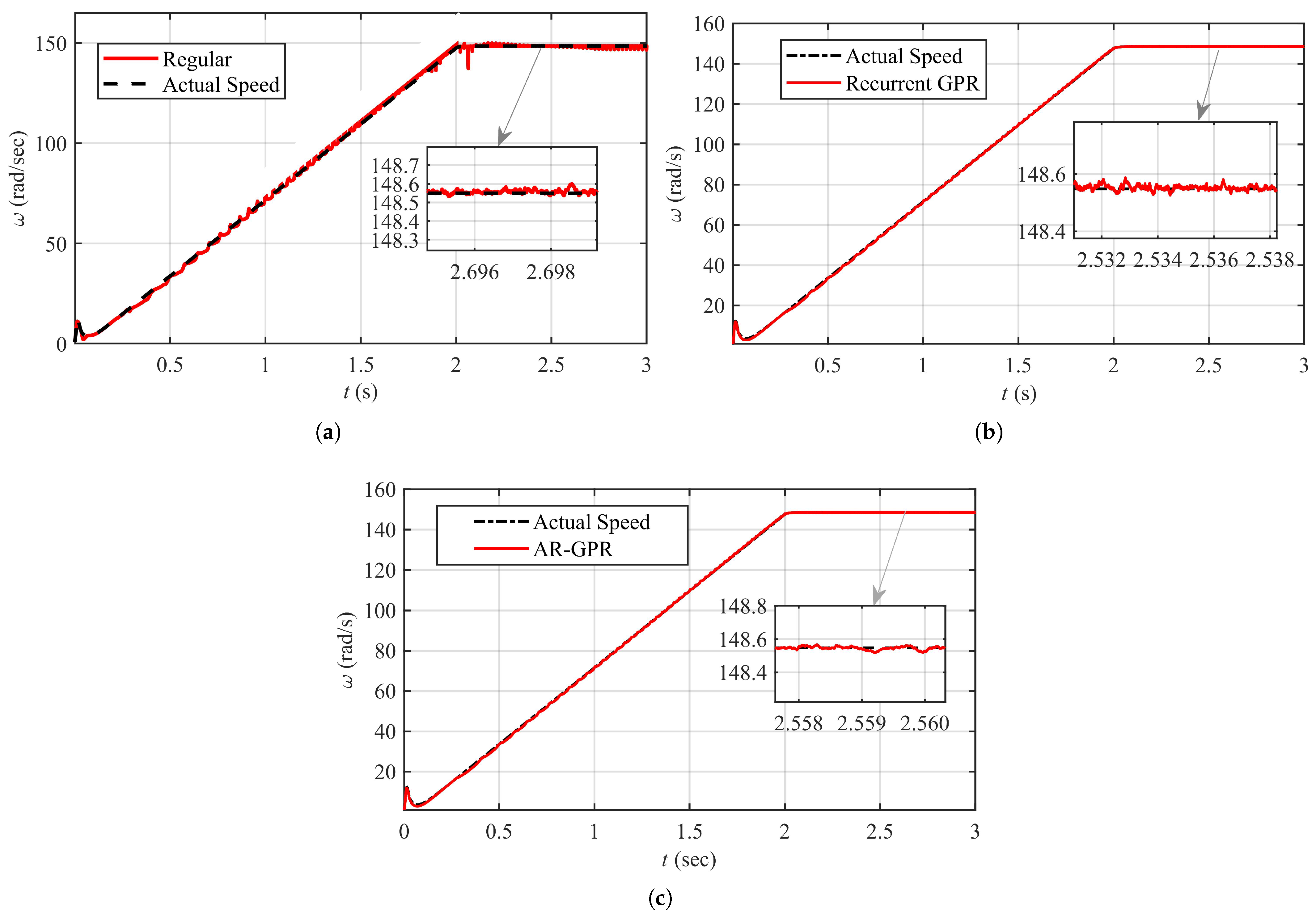
7.3. GPR Model-Based Speed Estimation
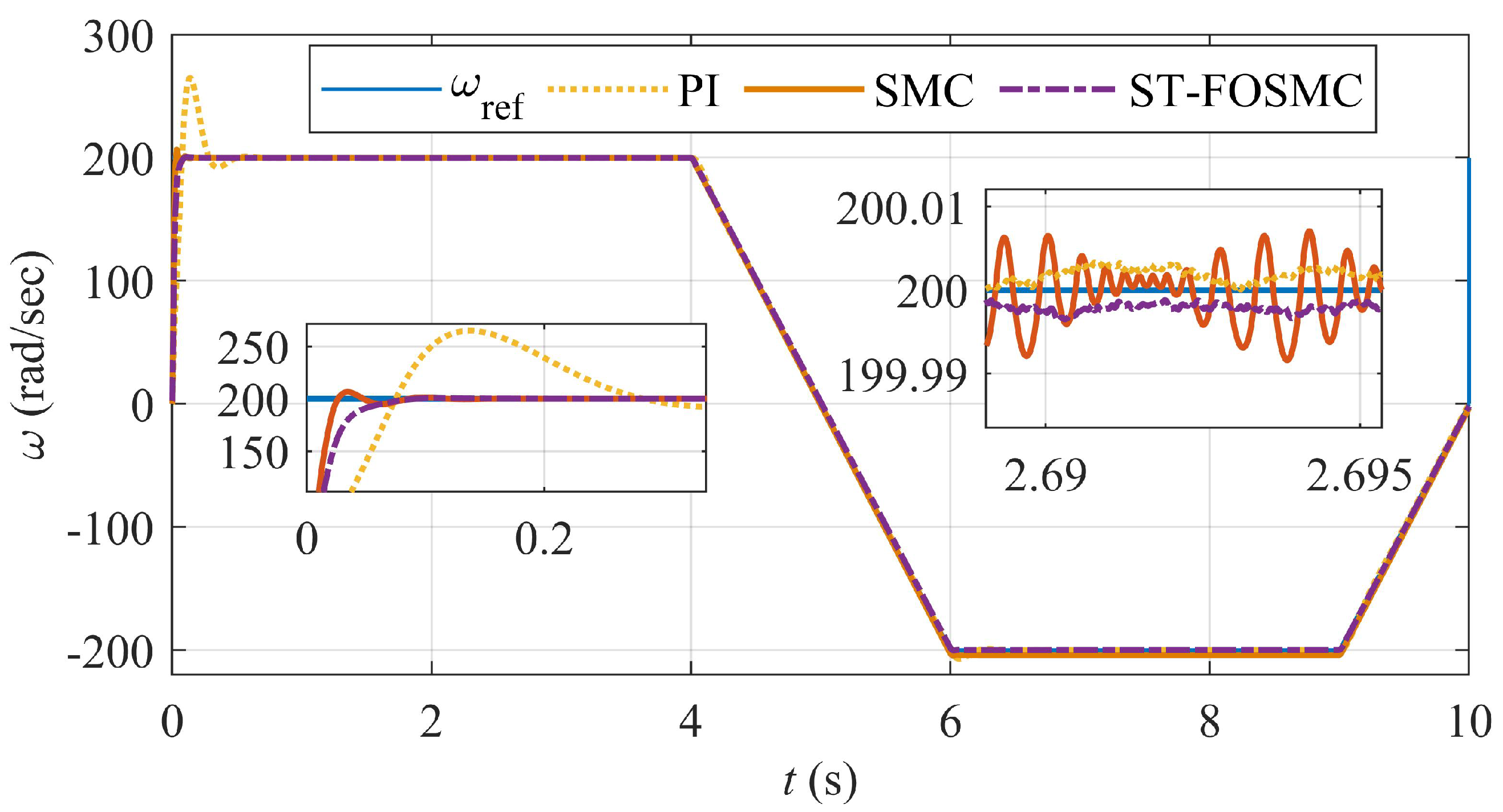
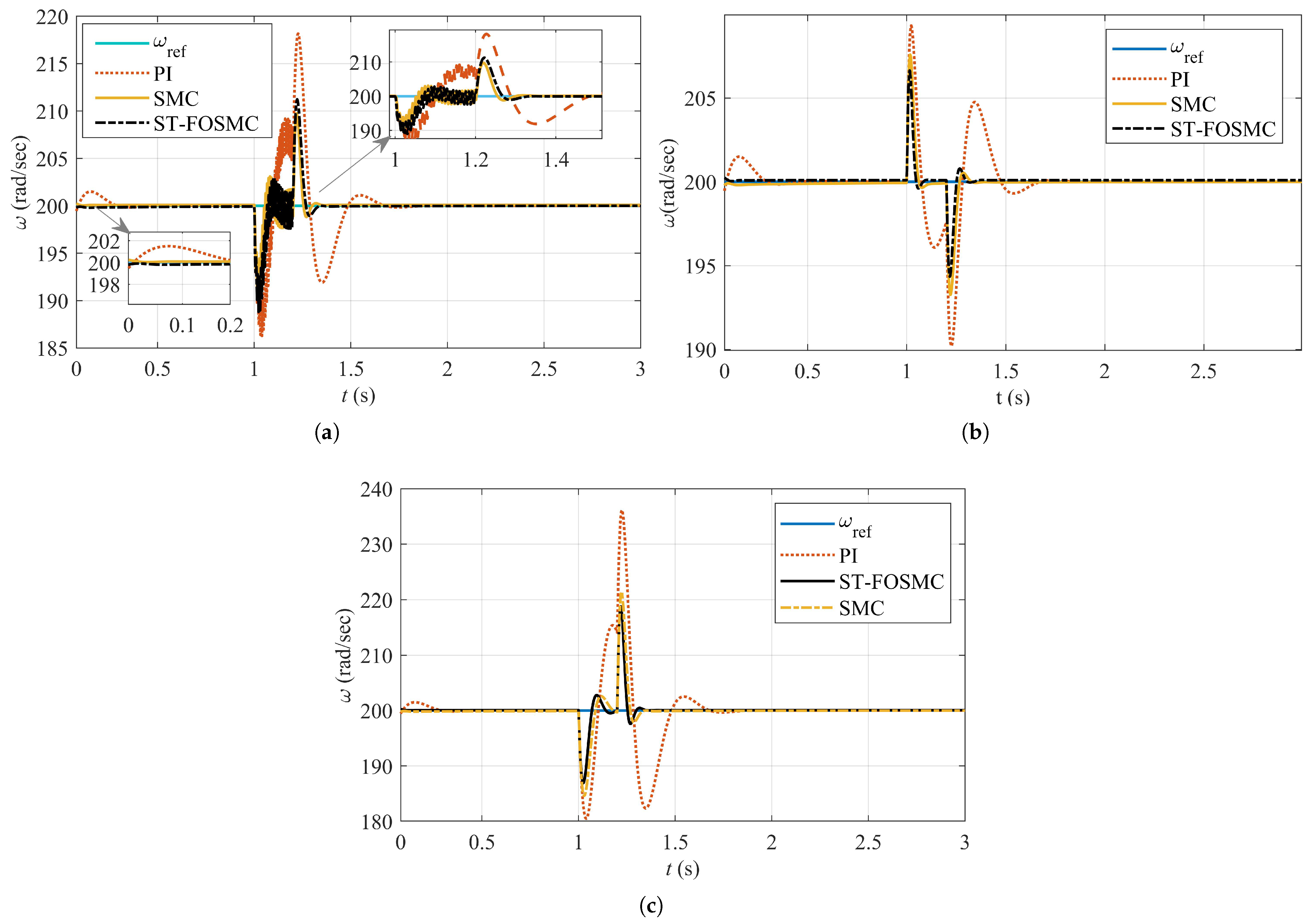
7.4. Performance Evaluation of ST-FOSMC under Various Test Cases
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lanusse, P.; Oustaloup, A.; Sabatier, J. Robust factional order PID controllers: The first generation CRONE CSD approach. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, Catania, Italy, 23–25 June 2014; pp. 1–6. [Google Scholar]
- Zhang, B.; Pi, Y. Robust fractional order proportion-plus-differential controller based on fuzzy inference for permanent magnet synchronous motor. IET Control Theory Appl. 2012, 6, 829–837. [Google Scholar] [CrossRef]
- Viola, J.; Angel, L.; Sebastian, J. Design and robust performance evaluation of a fractional order PID controller applied to a DC motor. IEEE/CAA J. Autom. Sin. 2017, 4, 304–314. [Google Scholar] [CrossRef]
- Efe, M.Ö. Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 1561–1570. [Google Scholar] [CrossRef]
- Ladaci, S.; Charef, A. On fractional adaptive control. Nonlinear Dyn. 2006, 43, 365–378. [Google Scholar] [CrossRef]
- Calderon, A.J.; Vinagre, B.M.; Feliu, V. Fractional order control strategies for power electronic buck converters. Signal Process. 2006, 86, 2803–2819. [Google Scholar] [CrossRef]
- Delavari, H.; Ghaderi, R.; Ranjbar, A.; Momani, S. Fuzzy fractional order sliding mode controller for nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 963–978. [Google Scholar] [CrossRef]
- Abdelhamid, D.; Bouden, T.; Boulkroune, A. Design of fractional-order sliding mode controller (FSMC) for a class of fractional-order non-linear commensurate systems using a particle swarm optimization (PSO) algorithm. J. Control Eng. Appl. Inform. 2014, 16, 46–55. [Google Scholar]
- Cao, D.; Fei, J. Adaptive fractional fuzzy sliding mode control for three-phase active power filter. IEEE Access 2016, 4, 6645–6651. [Google Scholar] [CrossRef]
- Zhong, X.; Shao, X.; Li, X.; Ma, Z.; Sun, G. Fractional order adaptive sliding mode control for the deployment of space tethered system with input limitation. IEEE Access 2018, 6, 48958–48969. [Google Scholar] [CrossRef]
- Sami, I.; Khan, B.; Asghar, R.; Mehmood, C.A.; Ali, S.M.; Ullah, Z.; Basit, A. Sliding Mode-Based Model Predictive Torque Control of Induction Machine. In Proceedings of the 2019 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 21–22 February 2019; pp. 1–5. [Google Scholar]
- Song, S.; Zhang, B.; Song, X.; Zhang, Y.; Zhang, Z.; Li, W. Fractional-order adaptive neuro-fuzzy sliding mode H∞ control for fuzzy singularly perturbed systems. J. Frankl. Inst. 2019, 356, 5027–5048. [Google Scholar] [CrossRef]
- Xu, D.; Wang, B.; Zhang, G.; Wang, G.; Yu, Y. A review of sensorless control methods for AC motor drives. CES Trans. Electr. Mach. Syst. 2018, 2, 104–115. [Google Scholar] [CrossRef]
- Ullah, N.; Ali, M.A.; Ibeas, A.; Herrera, J. Adaptive fractional order terminal sliding mode control of a doubly fed induction generator-based wind energy system. IEEE Access 2017, 5, 21368–21381. [Google Scholar] [CrossRef]
- Singh, S.; Tiwari, A. Various techniques of sensorless speed control of PMSM: A review. In Proceedings of the 2017 Second International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 22–24 February 2017; pp. 1–6. [Google Scholar]
- Yan, Z.; Jin, C.; Utkin, V. Sensorless sliding-mode control of induction motors. IEEE Trans. Ind. Electron. 2000, 47, 1286–1297. [Google Scholar]
- Cherifi, D.; Miloud, Y. Technology, Online Stator and Rotor Resistance Estimation Scheme Using Sliding Mode Observer for Indirect Vector Controlled Speed Sensorless Induction Motor. Am. J. Comput. Sci. 2019, 2, 1–8. [Google Scholar] [CrossRef]
- Guezmil, A.; Berriri, H.; Pusca, R.; Sakly, A.; Romary, R.; Mimouni, M.F. High order sliding mode observer-based backstepping fault-tolerant control for induction motor. Asian J. Control 2019, 21, 33–42. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Basit, A.; Ullah, N.; Ro, J.S. Integral super twisting sliding mode based sensorless predictive torque control of induction motor. IEEE Access 2020, 8, 186740–186755. [Google Scholar] [CrossRef]
- Rasmussen, H.; Vadstrup, P.; Borsting, H. Full adaptive backstepping design of a speed sensorless field oriented controller for an induction motor. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No. 01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 4, pp. 2601–2606. [Google Scholar]
- Alonge, F.; D’Ippolito, F.; Sferlazza, A. Sensorless control of induction-motor drive based on robust Kalman filter and adaptive speed estimation. IEEE Trans. Ind. Electron. 2013, 61, 1444–1453. [Google Scholar] [CrossRef]
- Yin, Z.; Li, G.; Zhang, Y.; Liu, J.; Sun, X.; Zhong, Y. A speed and flux observer of induction motor based on extended Kalman filter and Markov chain. IEEE Trans. Power Electron. 2016, 32, 7096–7117. [Google Scholar] [CrossRef]
- Yu, H.X.; Hu, J.T. Speed and load torque estimation of induction motors based on an adaptive extended Kalman filter. In Advanced Materials Research; Trans Tech Publ.: Stafa-Zurich, Switzerland, 2012; Volume 433, pp. 7004–7010. [Google Scholar]
- Yildiz, R.; Barut, M.; Zerdali, E.; Inan, R.; Demir, R. Load torque and stator resistance estimations with unscented Kalman filter for speed-sensorless control of induction motors. In Proceedings of the 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & 2017 Intl Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Brasov, Romania, 25–27 May 2017; pp. 456–461. [Google Scholar]
- Jannati, M.; Idris, N.; Aziz, M. Speed sensorless fault-tolerant drive system of 3-phase induction motor using switching extended kalman filter. TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 7640–7649. [Google Scholar] [CrossRef]
- Bogosyan, S.; Barut, M.; Gokasan, M. Braided extended Kalman filters for sensorless estimation in induction motors at high-low/zero speed. IET Control Theory Appl. 2007, 1, 987–998. [Google Scholar] [CrossRef]
- Zerdali, E.; Barut, M. Novel version of bi input-extended Kalman filter for speed-sensorless control of induction motors with estimations of rotor and stator resistances, load torque, and inertia. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 4525–4544. [Google Scholar] [CrossRef]
- Silva, W.L.; Lima, A.M.N.; Oliveira, A. Speed estimation of an induction motor operating in the nonstationary mode by using rotor slot harmonics. IEEE Trans. Instrum. 2014, 64, 984–994. [Google Scholar] [CrossRef]
- Karanayil, B.; Rahman, M.F.; Grantham, C. Online stator and rotor resistance estimation scheme using artificial neural networks for vector controlled speed sensorless induction motor drive. IEEE Trans. Ind. Electron. 2007, 54, 167–176. [Google Scholar] [CrossRef]
- Jahangir, M.; Afzal, H.; Ahmed, M.; Khurshid, K.; Nawaz, R. An expert system for diabetes prediction using auto tuned multi-layer perceptron. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 722–728. [Google Scholar]
- Jahangir, M.; Afzal, H.; Ahmed, M.; Khurshid, K.; Amjad, M.F.; Nawaz, R.; Abbas, H. Auto-MeDiSine: An auto-tunable medical decision support engine using an automated class outlier detection method and AutoMLP. Neural Comput. Appl. 2019, 32, 2621–2633. [Google Scholar] [CrossRef]
- Ayyaz, S.; Qamar, U.; Nawaz, R. HCF-CRS: A Hybrid Content based Fuzzy Conformal Recommender System for providing recommendations with confidence. PLoS ONE 2018, 13, e0204849. [Google Scholar] [CrossRef]
- Brandstetter, P.; Kuchar, M. Sensorless control of variable speed induction motor drive using RBF neural network. J. Appl. Log. 2017, 24, 97–108. [Google Scholar] [CrossRef]
- Song, S.; Zhang, B.; Xia, J.; Zhang, Z. Adaptive backstepping hybrid fuzzy sliding mode control for uncertain fractional-order nonlinear systems based on finite-time scheme. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 1559–1569. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Xu, Z.; Ye, L. Seasonal streamflow forecasts using mixture-kernel GPR and advanced methods of input variable selection. Hydrol. Res. 2019, 50, 200–214. [Google Scholar] [CrossRef]





| IM Parameters | Values |
|---|---|
| Rated Power | |
| Phases | 3 |
| Line Voltage | |
| System Frequency | |
| Full Load Slip | |
| Number of Poles | 4 |
| Switching Frequency | |
| Stator Resistance | |
| Stator Leakage Resistance | |
| Rotor Resistance | |
| Rotor Leakage Resistance | |
| Moment of Inertia | |
| Mutual Inductance | |
| Full Load Current | |
| Full Load Speed |
| Parameters | Values | RMSE (%) |
|---|---|---|
| 0.9 | ||
| 1.1 | ||
| c5 | 0.1 | |
| c6 | 4 | |
| for Regular GPR | 2.5 for V(k), 160 for I(k) | 0.3808 |
| 4.5 for V(k), 260 for I(k), | ||
| for AR-GPR | 2.1 for V(k-1), 200 for I(k-1), | 0.14 |
| 300 for | ||
| K | 10 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sami, I.; Ullah, S.; Ullah, S.; Bukhari, S.S.H.; Ahmed, N.; Salman, M.; Ro, J.-S. A Non-Integer High-Order Sliding Mode Control of Induction Motor with Machine Learning-Based Speed Observer. Machines 2023, 11, 584. https://doi.org/10.3390/machines11060584
Sami I, Ullah S, Ullah S, Bukhari SSH, Ahmed N, Salman M, Ro J-S. A Non-Integer High-Order Sliding Mode Control of Induction Motor with Machine Learning-Based Speed Observer. Machines. 2023; 11(6):584. https://doi.org/10.3390/machines11060584
Chicago/Turabian StyleSami, Irfan, Shafaat Ullah, Shafqat Ullah, Syed Sabir Hussain Bukhari, Naseer Ahmed, Muhammad Salman, and Jong-Suk Ro. 2023. "A Non-Integer High-Order Sliding Mode Control of Induction Motor with Machine Learning-Based Speed Observer" Machines 11, no. 6: 584. https://doi.org/10.3390/machines11060584
APA StyleSami, I., Ullah, S., Ullah, S., Bukhari, S. S. H., Ahmed, N., Salman, M., & Ro, J.-S. (2023). A Non-Integer High-Order Sliding Mode Control of Induction Motor with Machine Learning-Based Speed Observer. Machines, 11(6), 584. https://doi.org/10.3390/machines11060584











