Yard Crane Rescheduling under the Influence of Random Fault

Abstract

In the operation of the imported container area of the container yard, the fault of the yard crane often occurs, and the fault is random and unpredictable, which greatly affects the operational efficiency of the container yard. To improve the operation efficiency of the container yard, this paper studies the rescheduling optimization problem of the multi-container area and multi-yard crane when random faults occur in container lifting operations in the container import area. Considering the different impacts of different fault conditions on the container yard operation, the fault impact judgment mechanism is established. The waiting time of external container trucks and customer satisfaction is considered for yard crane rescheduling. Yard crane rescheduling model after the fault is constructed, aiming at the minimum deviation from the original scheduling scheme. And the AEA (annealing evolution algorithm) algorithm is used to solve it. The effectiveness of magic and the specificity of the algorithm are verified by the analysis of numerical examples in different scales. The research data of Dalian Port is used to carry out experiments, and the experimental analysis of examples in different scales verifies the effectiveness of the model and the scientific nature of the algorithm. Compared with the existing scheme, this scheme is more practical, which can not only give the treatment scheme immediately when the fault occurs but also effectively improve the working efficiency of the container yard and provide a reference for the port to enhance customer satisfaction.

1. Introduction

With the rapid development of the shipping industry, the port also has a new demand for container handling. The world’s largest terminal operator handled 65.4 million 20-foot equivalent units (TEUs) in 2014, an increase of 5.5 per cent over the previous year (UNCTAD (2015)) [1]. According to the survey of Tianjin port, Dalian port, and other ports, to better transform the service-oriented port, the focus of container terminals has gradually changed from effectiveness to efficiency in recent years. Terminal container work’s top priority is coordinating the overall situation and improving operation efficiency and customer satisfaction. Since there will be many emergencies in port work, spreader fault is one of them. When it occurs, using the original YC scheduling scheme may have a particular impact on the original plan of the container yard, and the total completion time of pick-up operation and waiting time of container trucks in the whole period will increase. Therefore, considering the waiting limit of external container trucks, it is necessary to study further how to determine whether rescheduling is necessary after a fault occurs.

Among the existing literature on YC scheduling, Li et al., 2022 [2] developed a YC scheduling model considering no crossing constraints and dynamic deadlines. To improve the flexibility of container yard handling, a joint scheduling method (LRPSO) based on particle swarm optimization and local rescheduling strategy is proposed to solve the problem faster and more efficiently. Chu et al., 2019 [3] conducted a study on the issue of considering transitions of three YCs in two adjacent container box areas. For this problem, a 0–1 mixed integer planning (MIP) model is constructed to minimize the total process time and thus reduce the total container storage time in the container YC, which helps to save container yard resources and improve productivity. For small-scale instances, the proposed model can be solved optimally by CPLEX. Since the problem is an NP-hard problem, a fast heuristic algorithm and an improved genetic algorithm are designed to generate approximate optimal solutions for large-scale instances. Most papers on YC scheduling problems are designed linear models and solved by exact algorithms. In addition to individual YC scheduling studies, more YC scheduling problems for collector trucks are considered. Yu et al., 2019 [4] studied the YC scheduling problem for mixed-stack terminals and proposed a mixed integer linear programming (MILP) model that jointly optimizes the waiting cost of trucks and the penalty cost caused by exceeding the waiting time threshold. Considering the NP-complete nature of this scheduling problem, they developed an efficient rolling horizon algorithm based on some heuristics to reduce the computational time. Hsu et al., 2021 [5] investigated the problem of optimizing the cooperative operation of a yard crane (YC) and yard truck (YT) for export containers in a terminal container yard area. Four hybrid methods dealt with the yard bridge scheduling problem (YCSP) and the yard truck scheduling problem (YTSP).

Zhou et al., 2020 [6] developed a mixed integer programming model and proposed a two-stage heuristic algorithm to simultaneously determine the scheduling of YCs and the parking position of vehicles for efficient operations. Torbi et al., 2022 [7] studied the sequencing of YCs and YTs, considering the impact of potential interference and shift problems between YCs on the performance of YCs. The study innovatively considered interference and shifting problems between YCs in a mathematical model and proposed a hybrid linear programming model to solve the scheduling problem of loading operations with the objective function of minimizing the completion time of stacker operations. Gao et al., 2022 [8] developed a multi-objective optimization model with a novel truck-based partitioning strategy aimed at minimizing the total longitudinal distance of the field bridge and the total waiting time of internal and external trucks. The effectiveness of the integrated truck-based and block-based scheduling strategies is verified by comparing them with existing strategies. Numerical experiments show that the integrated scheduling policy balances the two conflicting objectives better than the priority and first-come-first-served scheduling policies. Zhu et al., 2022 [9] use a two-loop strategy combined with a hybrid storage policy to focus on the dockyard YC scheduling problems. The scheduling plan of YTs and the storage location of inbound containers are considered. Based on the above factors, a mixed integer planning model is developed to minimize the vessel berthing time to complete all tasks. The proposed model is solved using a particle swarm optimization algorithm. Ma et al., 2022 [10] proposed a mixed integer two-layer programming model to optimize ship-related time Windows and YC deployment for inbound trucks. A hybrid genetic algorithm based on collective decision optimization is proposed.

In addition to considering the influence of internal gathering cards on YC scheduling, the influence of uncertainty on YC scheduling has been gradually raised in recent years. Liu et al., 2020 [11] developed a stochastic programming model that considers the fluctuations of external truck arrival time and yard crane handling capacity and derived a fixed scheme that minimizes the expected crane completion time and task waiting time values. Meanwhile, two rule-based algorithms are proposed for crane operation schemes in deterministic environments, and a genetic algorithm is used to find the optimal solution to adapt to the uncertainty. Yang et al., 2022 [12] considered the influence of uncertain container demand, studied the comprehensive optimization of storage yard resources, and established a stochastic optimization model to improve the robustness of daily storage yard management. Due to the complexity of the model, a harmonious search algorithm based on a two-stage decomposition strategy is designed to solve the proposed model. To speed up the solution, a scoring method was developed to generate an initial space allocation plan, and a tabu list was added to improve the quality of the solution. He et al., 2019 [13] considered how to conduct YC scheduling under the uncertainties of ship arrival time and handling capacity, external truck arrival time and container number. A mathematical model is proposed to optimize the total delay and additional loss of the estimated end time of the task group under all uncertain conditions. In addition, a framework based on a genetic algorithm is proposed to solve this problem by combining three—stage algorithms. Lei et al., 2020 [14] set up a stochastic programming model from the perspective of active strategy, considering the fluctuation of external truck arrival time and the different operation volumes of the YC, to obtain a fixed scheme that has the minimum expected value of the YC completion time and the total task waiting time in all cases. This solution does not require rescheduling in the face of different situations.

Zheng et al., 2019 [15] proposed a two-stage stochastic programming model aimed at minimizing tasks’ expected total lag time and focusing on the uncertainty of the retrieval tasks’ release time. For small-scale problems, the sample mean approximation (SAA) method is used. For large-scale problems, genetic algorithms (GA) and rule-based heuristic algorithms are developed. Feng et al., 2022 [16] proposed a YC scheduling modeling method based on deep reinforcement learning for uncertain task scenarios in the case of multi-YC scheduling, Iris et al., 2019 [17] proposed a mixed integer linear planning model to address integrated operational planning and energy management for seaports with smart grids without considering uncertain renewable energy generation. They use an integrated way obtains an optimal operations plan, demand response (including energy arbitrage) and optimal power flow to solve the problem. Most of the above literature considering the uncertainty is solved by modeling.

The summary is shown in

Table 1. Literature summary of YC scheduling.

Citation	YC	YT	Uncertainty	Optimization Objective	Model	Solution Method
Li et al. (2022) [2]	√			Min-YCoperation time	SOSM	LRPSO
Chu et al. (2019) [3]	√			Min-YCoperation time	MIP	CPLEX IQGA
Yu et al. (2019) [4]	√	√		Min-YCoperation time & YTwaiting time	MILP	Rolling horizon algorithm
Hsu et al. (2021) [5]	√	√		Min-YCoperation time & YTwaiting time	Simulation model	SGPSO
Liu et al. (2020) [11]	√	√	√	Min-YCoperation time & YTwaiting time	SPM	Tailored GA
Zhou et al. (2020) [6]	√	√		Min-YC finish time	MIP	Two-stage TSA
Torbi et al. (2022) [7]	√	√		Min-YCoperation time	MILP	CPLEX
Gao et al. (2022) [8]	√	√		Min-YCMoving length & YTwaiting time	MMOE	Comprehensive scheduling strategy
Zhu et al. (2022) [9]	√	√		Min-Operation time	MIP	PSO
Ma et al. (2022) [10]	√	√		Min-YCoperation time & YTwaiting time	MIP	HGA
Yang et al. (2022) [12]	√		√	Min-operation cost	SOSM	HSA
He et al. (2019) [13]	√	√	√	Min-uncertainty delay time	SOSM	GA Three-stage algorithm
Lei et al. (2020) [14]	√	√	√	Min-YCoperation time & YTwaiting time	SPM	active strategy
Zheng et al. (2019) [15]	√	√	√	Min-uncertainty delay time	SPM	SAA GA
Feng et al. (2022) [16]	√		√	Min-Operation time	SOSM	Deep reinforcement learning

Note: SOSM: stochastic optimal scheduling model; SPM: Stochastic Programming Models; MIP: Mixed Integer Programming; MILP: Mixed Integer Linear Program; MMOE: multi-objective optimization model; HSA: Harmonious search algorithm.

.

In the existing rescheduling literature, the rescheduling of yard cranes is relatively less considered, and most focus on rescheduling the railway or production process with interference. In the literature on Railway rescheduling considering interference, Zhou et al., 2022 [18] studied the increasingly significant impact of interference on the train control and scheduling of the current line and related lines, focusing on the timetable cooperative rescheduling of HSR multiple scheduling areas under large-scale interference. The problem is formulated as a mixed integer linear programming (MILP) model to minimize the weighted sum of the arrival delay time of trains, the departure delay time of trains at the handover station and the number of train delays at all stations. The rescheduling scheme is generated by the strategy of retiming and reordering. Liu et al., 2022 [19] studied that high-speed railway (HSR) is vulnerable to interference, and the duration of interference is usually highly uncertain and unpredictable. He proposed a rescheduling model based on the event activity network, which uses a two-stage stochastic programming method to minimize the end time as the optimization goal and formulate a conflict-free rescheduling scheme for all possible scenarios. Kumar et al., 2021 [20] proposed an effective train rescheduling method based on multi-objective and dictionary-based inspection. Firstly, the constraints are extracted to explain the mcmigp index, and gkaco is used to optimize the constraints for optimal rescheduling.

The optimization objective is to minimize train delay, dwell time, schedule deviation and operation cost and increase service reliability. Zhu et al., 2019 [21] studied the problem that railway operation is vulnerable to accidental interference and proposed to deal with it in an efficient and passenger-friendly manner. They proposed a mixed integer linear programming model for rescheduling by scheduling. The weight of each decision is estimated separately according to the time-dependent passenger demand, and the optimization objective is to minimize passenger delay. Peng et al., 2023 [22] studied the problem of speed management under uncertain interference in the high-speed railway system, which led to the temporary speed limit (TSR) and the need to reschedule trains. A mixed integer linear programming model is established to reduce train travel time and improve passenger comfort. Considering the uncertainty of interference, the rolling horizon algorithm is used to solve it. Zhu et al., 2020 [23] studied that during railway interference, to provide better alternatives to passengers, a novel passenger-oriented timetable rescheduling model was proposed, which integrated timetable rescheduling and passenger rescheduling into a mixed integer linear programming model, to minimize generalized travel time. An adaptive fixed sum optimization (AFAO) algorithm is developed. In the research of railway rescheduling considering interference, researchers will establish a mathematical model according to the characteristics of the problem. However, the solutions are divided into two types: rescheduling based on a certain realistic strategy and giving an algorithm based on the optimization objective.

In the production rescheduling with interference, Caldeira et al., 2022 [24] considered the flexible job shop rescheduling problem with new job insertion (fjsrp) to minimize the completion time. An improved discrete backtracking search algorithm and an insertion rescheduling strategy based on relaxation are proposed to solve this problem. Chakraborty et al., 2020 [25] studied the problem of resource-constrained project rescheduling. In this study, two discrete-time models are proposed to deal with two types of interference, and a solution is proposed which can deal with single and a series of independent interference in the way of reactive rescheduling. Ning et al., 2020 [26] studied the optimization of interference management and job shop scheduling and proposed a multi-objective optimization model of interference management and rescheduling strategy. An improved quantum bacterial optimization algorithm (iqbfo) based on prospect theory was designed to solve the proposed model. Chakraborty et al., 2021 [27] studied the resource-constrained project scheduling problem (RCPSP) and designed a mathematical model of the reactive scheduling method, the event-based reactive method (ebra). In addition to the precise method using LINGO software, this study proposes an enhanced iterative greedy algorithm (ENIG). In the production rescheduling problem, researchers almost choose to establish a rescheduling model and design an algorithm to solve it.

In addition to the above two rescheduling problems, Iris et al., 2019 [28] have developed a recoverable robust optimization method to solve weekly berth and quay crane planning problems. Considering the uncertainty of ship arrival time and the fluctuation of container handling rate on the quay crane, a rescheduling model was established with cost as the optimization objective. And an adaptive large neighborhood heuristic framework was proposed to solve this problem. Zheng et al., 2023 [29] studied the comprehensive rescheduling problem of berth assignment and quay crane assignment with vessel delays and unplanned vessel arrivals. The first step is to use the rolling time domain method to determine the rescheduling time. The second step is to establish a rescheduling model and design an improved genetic algorithm (IGA) to obtain a rescheduling solution at the rescheduling time using various rescheduling strategies. Finally, Lv et al., 2020 [30] studied the problem of disturbance recovery in berth allocation in transfer terminals. A mixed integer linear programming model was established to adjust the original berth allocation plan, to minimize the recovery cost caused by deviation from the original plan. The squeaky wheel optimization heuristic algorithm is proposed to find the approximate optimal solution in large-scale problems. The above three berthing rescheduling problems with uncertainty are also solved by modeling and design algorithms. Therefore, modeling and algorithm solving are also selected in this paper.

In the existing literature, there are relatively few rescheduling problems considering the impact of failures. Zhao et al., 2019 [31] studied common machine failures in production scheduling and proposed a new rescheduling decision model based on random forest, an effective machine learning method for learning the optimal rescheduling strategy under different machine failures. A genetic algorithm (GA) generates the initial scheduling scheme. Sang et al., 2021 [32] studied the interference events, such as equipment failures that often occur in the production process of the processing workshop, because the existing rescheduling strategy is difficult to effectively reduce the deviation between the rescheduling plan and the initial scheduling plan. This study proposes a new interference management method, including an interference management model and multi-objective optimization algorithm (NSA-III-RPE). Bhongade et al., 2023 [33] studied the problem that the original flow shop plan needs to be modified and/or rearranged for interference, such as machine failure. A rescheduling method based on right shift rescheduling and affected operation rescheduling is established to solve the problem. According to the above literature, faults can affect the original scheduling plan, which is common in bridge scheduling. The existing fault and rescheduling literature also consider the characteristics of randomness and uncertainty of fault. Some use machine learning to determine different fault rescheduling strategies, while others give different rescheduling strategies according to different fault characteristics. However, the above research takes the minimum deviation from the original scheme as the optimization goal.

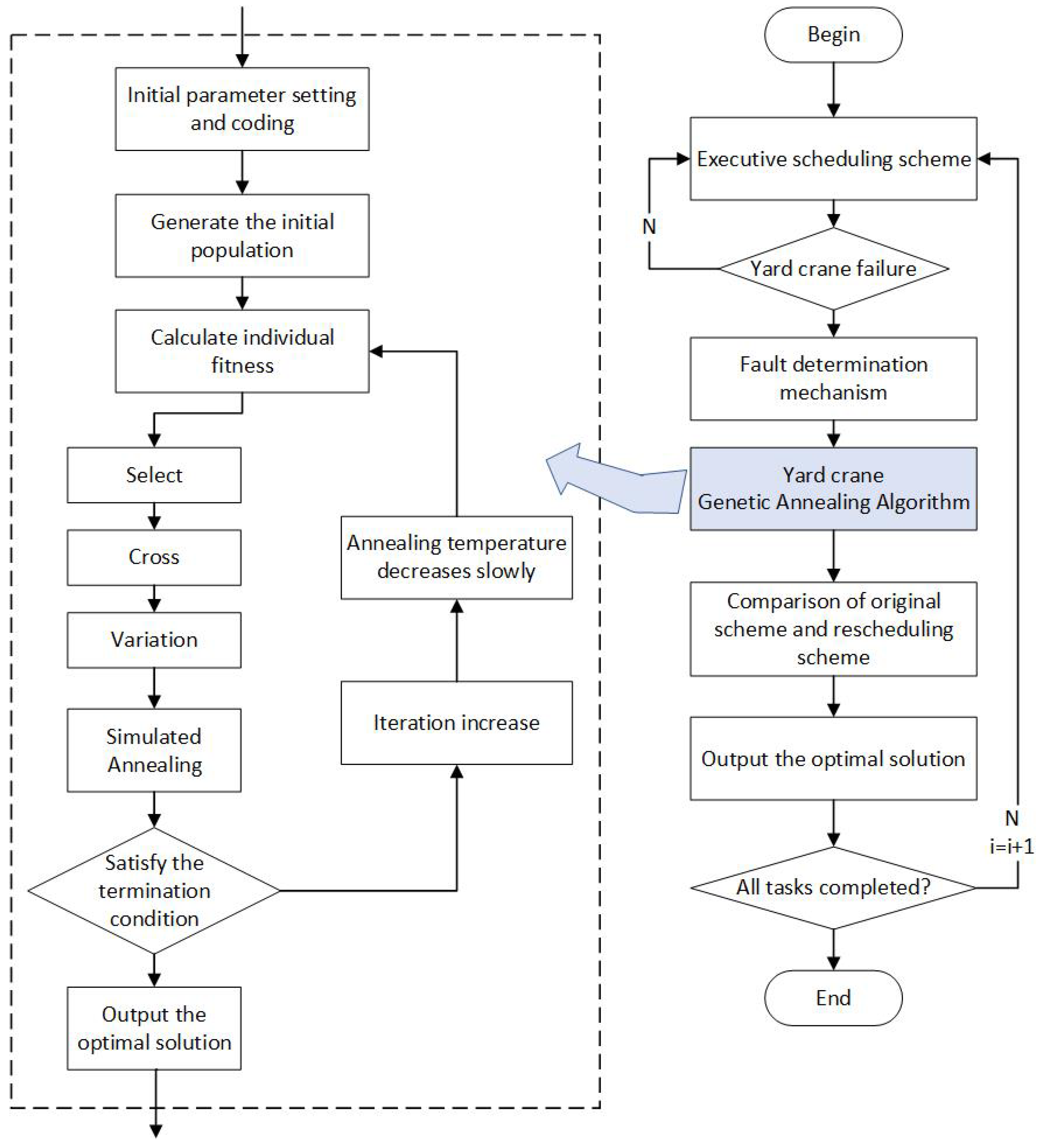
In the mentioned literature on YC scheduling, the existing literature focuses on the joint scheduling of container trucks and YCs. In recent years, some research has gradually begun to consider the impact of uncertainty on container yards and yard crane scheduling. But most of the uncertainty is general and not specific enough. Therefore, this paper gives the impact of specific uncertainty (random fault impact) on the YC scheduling in the import container yard and provides the rolling fault impact judgment mechanism. As shown in Table 1, most studies take the shortest time as the optimization goal, the general scheduling problem considers the shortest operation time, and some studies evaluating the uncertainty will optimize the shortest delay time simultaneously. Because few papers consider yard crane fault and rescheduling, we refer to some papers on rescheduling caused by interruption and find that most of them use the combination of modeling and algorithm to solve the problem. At the same time, some papers that consider machine fault and rescheduling mostly have the goal of minimum deviation from the original scheduling scheme. So, we establish the rescheduling model, minimizing the deviation from the original scheduling scheme as the hybrid optimization target and using the AEA algorithm to solve it, and further verify the effectiveness of the model and algorithm through numerical experiments. Unfortunately, the existing YC scheduling literature does not consider the effect of yard crane fault on schedule, probably because the fault as an uncertainty factor is taken as an external force influence condition. But, through the investigation in the port, we know that faults are similar to the common yard crane dispatching factors, such as uncrossing between YCs, which are both influencing factors that cannot be ignored in real operation. Therefore, the biggest contribution of this paper is to consider the fault of the yard crane, an unavoidable factor in the actual operation, and to give a more practical dispatching scheme for the dispatching work of ports.

2. Problem Description and Model

2.1. Problem Description

In the container terminal, it is generally necessary to make an appointment to pick up imported containers, and the external container truck will arrive within the scheduled time. Then the container yard will give a operation plan according to the appointment on that day. However, in actual operation, the spreader of the YC will have different degrees of fault at varying times of operation due to mechanical fault, damaged parts, or improper operation. When the spreader fails during the container pick-up and cannot be untied, the task container is connected with the spreader at this time, and the workers can only go forward for inspection after the YC is moved to a safe position to land the container. Except in this case, once the fault is found, the workers can go forward to check and judge the faulty situation quickly. Generally, the maintenance time is less than one hour, and the staff will carry out the maintenance in place and continue the operation after the maintenance is completed. Considering the upper limit of waiting time of the external container truck, the task container of the failed YC is redistributed during the maintenance time, and the rescheduling scheme of other YCs is given. When the time of fault maintenance exceeds one hour after the YC is removed, considering the upper waiting time limit of the external container truck and the idle situation of the container yard equipment, the YC rescheduling scheme is given after adjusting the number of YCs in this container area. Therefore, this problem can be described as follows: as Figure 1 shows, when the spreader of the YC fails during the operation in the import container area of the container terminal, the rescheduling scheme of the YC is given with the shortest total operation time and the slightest difference from the original scheduling scheme as the goal, considering the different influence degree of different fault conditions on the container yard operation, As shown in Figure 2 of the fault judgment flow chart taking into account the waiting time of the external container truck and customer satisfaction.

2.2. Fault Diagnosis and Rescheduling Optimization Model

2.2.1. Assumed Condition

• During the planning period, the number of tasks in the container block is known, and the container blocks, bays and arrival time of container trucks of each task are randomly generated.
• During the simultaneous operation of two YCs, the YCs cannot be crossed and keep a certain safe distance, which is called safety rules for short.
• Each YC has the same working efficiency and walking speed.
• The YC fault that makes the YC unable to move is not considered.
• When the YC fails, the degree of fault can be known immediately, and maintenance can be carried out without waiting time.
• The YC that has been repaired can be put into use immediately, and there are enough YCs in the container yard to replace the fault YC.

2.2.2. Parameters and Variables

(1)

Input Parameter

• $m$: YC fault serial number in the planning period;
• $T_m$: The occurrence time of the m^th fault (unit: s).
• $t_m$: Maintenance time of the m^th fault (unit: s).
• $YCQ$: Original YC dispatching scheme.
• $t_{origin}$: Working time of original YC dispatching scheme (unit: s);
• $y{t}_{i_{\left(i+1\right)}^n}^n$: Sum of the time for moving the YC n from the i^th task position to the i + 1^th: task position and the time for loading and unloading the i + 1^th task in the original scheduling scheme (unit: s).

(2)

Scene Parameters

• n = 1, 2, …, N, N is the number of YCs in the container block, and n is the serial number of YCs;
• i = 1, 2, …, I, I is the number of tasks, and i is the serial number of tasks;
• a = 1, 2, …, A, A is the total number of container stacks;
• b = 1, 2, …, B, B is the total number of bay in the multi-container blocks;
• c = 1, 2, …, C, C is the number of tiers, and ${\mathrm{c}}_{\mathrm{i}}$ is the tier serial number of the i^th container; $C_i$ is the highest number of levels at which the $i_{\mathrm{th}}$ the task is located and $c_i$ is the tier serial number of the $i_{\mathrm{th}}$ container
• slot{a,b,c}, Container position of layer c, b bay, a stack;
• ${\mathrm{A}}_{}$: The number of container stacks;
• $A^{\prime }$: The number of virtual container stacks;
• ${\mathrm{B}}_{}$: The number of container bays;
• $B^{\prime }$: The number of virtual container bays;
• ${\mathrm{A}}_i^{\mathrm{n}}$: the stack of i^th task of YC n; ${\mathrm{A}}_0^{\mathrm{n}}$: Initial stack of YC n;
• ${\mathrm{B}}_i^{\mathrm{n}}:\mathrm{the} \mathrm{bay} \mathrm{of} \mathrm{ith} \mathrm{task} \mathrm{of} \mathrm{YC} \mathrm{n};{ \mathrm{B}}_0^{\mathrm{n}}$: Initial bay of YC n;
• ${\mathrm{T}}_{\mathrm{i}}^{\mathrm{truck}}$: Arrival time of container truck i (unit: s);
• ${\mathrm{t}}_{\mathrm{wait}}$: Upper limit of waiting time for container truck (unit: s);
• ${\mathrm{L}}_{\mathrm{boxl}}$: Length of container (unit: m);
• ${\mathrm{L}}_{\mathrm{boxw}}$: Width of container (unit: m);
• ${\mathrm{v}}_0$: Walking speed of YC (unit: m/s);
• ${\mathrm{t}}_{\mathrm{F}}$: Time for lifting and releasing containers (unit: s);
• $△{\mathrm{B}}_{\mathrm{safe}}$: Safety distance to be maintained between the YCs (unit: m);

(3)

Intermediate variables

• ${\mathrm{T}}_{\mathrm{i}}^{\mathrm{begin}}$: Begin time of the i^th task (unit: s);
• ${\mathrm{T}}_{\mathrm{i}}^{\mathrm{end}}$: Completion time of the i^th task (unit: s);
• ${\mathrm{i}}_0^{\mathrm{m}}$: The first task number corresponding to the YC when the m^th fault occurs.
• ${\mathrm{i}}_{\mathrm{w}0}^{\mathrm{m}}$: The first task number corresponding to the end of the m^th maintenance.
• ${\mathrm{Q}}_{\mathrm{n}}^{\mathrm{m}}$: The number of tasks of the YC n operation after the occurrence of the m^th fault;
• ${\mathrm{I}}_{\mathrm{i}}^{\mathrm{n}}$: Task index number corresponding to the i^th task of YC n,$1\le {\mathrm{I}}_{\mathrm{n}}^{\mathrm{i}}\le \mathrm{I},1\le \mathrm{i}\le {\mathrm{Q}}_{\mathrm{n}}$;
• ${\mathrm{t}}_{{\mathrm{I}}_{\mathrm{i}}^{\mathrm{n}}}^{\mathrm{n}}$: operation time of i^th task of YC n (unit: s);
• ${\mathrm{wt}}_{{\mathrm{I}}_{\mathrm{i}}^{\mathrm{n}}}^{\mathrm{n}}$: Time for the YC n to move from the i^th task position to the I + 1st task position (unit: s);
• ${\mathrm{ft}}_{{\mathrm{I}}_{\mathrm{i}}^{\mathrm{n}}}^{\mathrm{n}}$: Loading and unloading time of the i^th task of YC n (unit: s);
• ${\mathrm{t}}_{{\mathrm{i}}_{\mathrm{o}}^{\mathrm{m}}}^{\mathrm{before}}$: operation time of task before the occurrence of the m^th fault (unit: s);
• ${\mathrm{rt}}_{{\mathrm{i}}_{\mathrm{o}}^{\mathrm{m}}}^{\mathrm{during}}$: operation time of task after rescheduling during the m^th fault maintenance period (unit: s);
• ${\mathrm{rt}}_{{\mathrm{i}}_{\mathrm{o}}^{\mathrm{m}}}^{\mathrm{after}}$: Working time of task after rescheduling after the completion of the m^th fault maintenance (unit: s);
• ${\mathrm{t}}_{\mathrm{schedule}}$: Total working time of operation task (unit: s);
• ${\mathrm{t}}_{\mathrm{reschedule}}$: Working time of rescheduling scheme (unit: s);

(4)

Decision Variable

• $X_{in}^m$: 0–1 variable, indicates after fault m whether task i is completed by YC n.
• $G_{ij}^{mn}$: 0–1 variable, indicates after fault m whether task i operate before task j.

2.2.3. Mathematical Model

(1)

Objective Function

$$f=\mathit{min}\{{\displaystyle \sum }_{n=i}^N{\displaystyle \sum }_{i=1}^{Q_n^m}|X_{in}^m{t}_{I_i^n}^n-y{t}_{I_i^n}^n|\}$$

The objective function represents the minimum deviation between the total working time, the rescheduling scheme, and the original scheduling scheme.

(2)

Constraints of scheduling schemes

$$\begin{gathered} I_{i_1}^n=I_{i_2}^n;I_i^{n_1}=I_i^{n_2}\left(i_1\ne i_2;i_1,i_2=1,2,3,\dots ,{\mathrm{Q}}_n^m;n_1\ne n_2\in \left\{1,2,3,\dots ,N\right\}\right) \\ {\displaystyle \prod }_{n=1}^N{\displaystyle \prod }_{i=1}^{{\mathrm{Q}}_{\mathrm{n}}^{\mathrm{m}}}{X}_{in}^m=1\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right) \\ {G}_{ij}^{mn}\le X_{in}^m+X_{jn}^m\left(i,j=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right) \end{gathered}$$

(1)

$$t_{I_i^n}^n=w{t}_{I_i^n}^n+f{t}_{I_i^n}^n\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(2)

$$T_{I_i^n}^{end}\ge T_{I_i^n}^{truck}+t_{I_i^n}^n\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(3)

$$\begin{gathered} T_{I_i^n}^{end}=\mathit{max}\{T_{I_{i-1}^n}^{end}+t_{I_{i-1}^n}^n,T_{I_i^n}^{truck}\}+t_{I_i^n}^n, T_{I_i^n}^{begin}\le T_{I_j^n}^{begin} \\ {T}_{I_j^n}^{begin}\le T_{I_i^n}^{end}+\left(1-G_{ij}^{mn}\right)M \left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right) \end{gathered}$$

(4)

$$\begin{gathered} w{t}_{I_i^n}^n=\frac{\left[B\left(I_i^n\right)-B\left(I_{i-1}^n\right)\right]\ast L_{boxl}+\frac{\left[A\left(I_i^n\right)-A\left(I_{i-1}^n\right)\right]}{A_x+A_f}\ast L_{boxw}}{v_0} \\ \left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right) \end{gathered}$$

(5)

$$\left[B\left(I_i^n\right)-B\left(I_{i-1}^n\right)\right]\le △B_{safe}\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(6)

$$T_{I_i^n}^{end}-T_{I_i^n}^{begin}\le t_{wait}\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(7)

$$Q_n^m\ge 0\left(m=1,2,3,\dots ;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(8)

$$t_{i_o^m}^{before}={\displaystyle \sum }_{i=1}^{i_0^m-1}\left(T_i^{end}-T_i^{begin}\right)\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m; m=1,2,3,\dots ;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(9)

$$r{t}_{i_o^m}^{during}={\displaystyle \sum }_{i=i_0^m}^{i_{w0}^m-1}\left(T_i^{end}-T_i^{begin}\right)\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m; m=1,2,3,\dots ;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(10)

$$r{t}_{i_o^m}^{after}={\displaystyle \sum }_{i=i_{wo}^m}^I\left(T_i^{end}-T_i^{begin}\right)\left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m; m=1,2,3,\dots ;n\in \left\{1,2,3,\dots ,N\right\}\right)$$

(11)

$$\begin{gathered} t_{reschedule}=min\left\{\begin{array}{c}{t}_{origin}\\ t_{i_0^m}^{before}+r{t}_{i_0^m}^{after}{i}_0^m=i_{w0}^m\\ t_{i_0^m}^{before}+r{t}_{i_0^m}^{during}+r{t}_{i_0^m}^{after}{i}_0^m\ne i_{w0}^m\end{array}\right. \\ \left(i=1,2,3,\dots ,{\mathrm{Q}}_n^m; m=1,2,3,\dots ;n\in \left\{1,2,3,\dots ,N\right\}\right) \end{gathered}$$

(12)

Equation (1) indicates that a task can only be operated by a one-YC and only once. Equation (2) shows the equal constraints of task working time, YC walking time, and loading and unloading time. Equation (3) indicates that the completion time of the i^th task of YC n is the sum of the corresponding container truck’s arrival and working times. Equation (4) indicates the equality constraint among task completion time, task start time, and working time. Equation (5) suggests the equality constraint of the time required for the YC to walk from one task to the next. Equation (6) indicates the constraint of safe working distance during the YC operation; Equation (7) ensures that the waiting time of each task cannot exceed the upper limit of the waiting time of the container truck. Equation (8) is that after the ${\mathrm{m}}^{\mathrm{th}}$ fault if the number of tasks in the subsequent YC n operation is 0, the original scheduling scheme is still used; otherwise, the judgment continues. Equation (9) is the equality constraint of the working time of the yard task before the fault. Equation (10) is an equality constraint of the working time of yard tasks during maintenance. Equation (11) is the equality constraint of the working time of the yard task after the maintenance. Equation (12) indicates the total working time of the task operation obtained by the rescheduling scheme.

3. Solution Method for Model

3.1. Fault Determination Mechanism

In the actual operation process of the container terminal inlet area, mechanical aging, overuse, operation errors, and so on may lead to the breakdown of the YC. Maintenance can also solve these faults. However, the fault’s degree, time, and location may affect the original scheduling scheme. Therefore, when a fault occurs, it is the key to improving the efficiency of container yard operation to immediately judge the impact of the fault on the original scheduling scheme.

After each fault occurs, we must first judge the fault situation. This paper gives the following judgment mechanism (as shown in Figure 2):

3.2. Multi-Stage Rolling Mechanism

In the process of YC dispatching, faults occur randomly, and the timing, frequency, location, and degree of faults are different, which brings many difficulties to the task of container pick-up. After the fault occurs, the YC rescheduling scheme should be made in time to ensure the completion of the YC task on time. This paper adds the multi-stage rolling mechanism to the rescheduling optimization algorithm to realize the cyclic analysis of the fault situation in the YC scheduling process. The principles are as follows:

STEP1: i is the task stage, and the initial stage i = 1. At this time, the yard executes the initial scheduling scheme without considering faults;

STEP2: In the i stage of the task, if a random fault occurs, the “fault Determination Mechanism “ is used to judge the occurrence of the fault.

STEP3: Determine the remaining tasks, the number of YCs, and their position parameters;

STEP4: The YC rescheduling scheme uses the “SAGA Algorithm for YC Scheduling”.

STEP5: Comparing the rescheduling scheme with the original scheme, the scheme with a shorter working time of the YC and satisfying the above constraints is selected;

STEP6: Judge whether all tasks are completed; if so, jump to STEP7, otherwise, i = i + 1, and return to STEP2 to wait for the next fault;

STEP7: The optimal scheduling scheme is given, and the algorithm calculation is finished.

The specific process is shown in the following Figure 3:

3.3. SAGA Algorithm for YC Scheduling

3.3.1. Coding Mode and the Generation of Initial Population

There are N YC operations, and I tasks in the container yard, and the chromosome length is S. The ith coding number in the chromosome is the YC operation number of the ith task. As the Figure 4 shows.

The chromosome length is the same as the number of containers to be operated on in a period. All the coding numbers on the chromosome are YC numbers, so any coding number on the chromosome is less than the total number of YCs. An initial population is generated according to this principle. At the same time, in the initial stage, the location of each container pick-up task will be randomly generated, including container block, bay, stack, and layer. As Figure 5 shows.

3.3.2. Calculating Fitness

The fitness value is designed according to the objective function f. For the solution corresponding to any given chromosome, the fitness value is Fitness(i) = Cmax − f(i), where the value of Cmax is infinite.

For example, the No.1 YC’s walking time, container turning time, and container pick-up time is calculated in sequence according to the order of primary target containers. The search starts from the bay of the target container to locate its stack. The shortest container turning time is obtained using the container turning algorithm for this target container. The walking time, container turning time, and container pick-up time of the No.1 YC are obtained by analogy. Thus, the total operation time of the No.1 YC period is obtained. Similarly, the total operation time of the remaining YCs is obtained, and the sum is the objective function value. Finally, the objective function value of each individual is obtained by iteration, and the fitness is obtained.

3.3.3. Selection Mechanism

In this paper, the roulette mechanism is adopted for parent selection, and the selection principles are as follows:

• For each YC, If the tasks are assigned to container blocks that are too far apart, the walking time of the YC will be too long, so it is not suitable to keep the chromosome. Therefore, this algorithm stipulates that the task arrangement that requires the single walking distance of the YC to exceed two container areas is not selected;
• The objective functions of chromosomes that meet the above requirements are sorted, and the roulette wheel selection mechanism is used for parent selection (allowing the same individuals).

3.3.4. Crossover Operation

The crossover operation is a single-point crossing (Figure 6). Firstly, a crossing point is randomly selected in the parent, and the parent chromosome is divided into the left and correct parts. Then, the gene and sequence of the left part in parent A are reserved in offspring A, and the genes missing in the right part in offspring A are arranged according to the gene sequence in parent B. Finally, the gene arrangement of offspring B is obtained by the same method (as shown in Figure 6).

3.3.5. Variation Operation

To satisfy the constraints: (1) The YCs cannot cross each other while moving. (2) The waiting time for each task can be, at most, the upper limit of the container truck waiting time. Therefore, we chose to use variation operation on chromosomes that did not meet the above constraints. The specific operation rules are as follows: generate a random number from 0 to 1, and if it is greater than the variation probability, adopt the conventional variation method, that is, randomly generate two points from 1 to N, and exchange the job numbers on this gene bit in the chromosome (as shown in the Figure 7); If it is greater than the variation probability, the gene sequence of the chromosome is traversed, the positions of the YCs crossing each other during the movement of the YCs are exchanged, and the YCs whose waiting time of the task exceeds the upper limit of the waiting time of the container truck are randomly replaced. This increases the population diversity and ensures the satisfaction of the constraints. As shown in Figure 7.

3.3.6. SA Operation

This paper adds SA operation to improve the optimal solution selection. The last optimal solution is saved in the search process of the algorithm and compared with the current optimal solution, which ensures optimal and improves detection efficiency. Set the threshold ${\mathrm{Y}}_0$ and the number of terminating steps ${\mathrm{L}}_0$ for the new solution not to be accepted and carry out an SA sampling search on the individuals ${\mathrm{P}}_{\mathrm{i}}$ of the population at the temperature ${\mathrm{T}}_{\mathrm{k}}$. The process is as follows:

STEP1: Initial state S = ${\mathrm{P}}_{\mathrm{i}}$. Initial optimal solution S* = ${\mathrm{P}}_{\mathrm{i}}$. Unaccepted times uc = 0. Iteration times it = 0;

STEP2: A new state S’ is generated from the current state S. Calculation increment $△\mathrm{f}=\mathrm{f}\left({\mathrm{S}}^{\prime }\right)-\mathrm{f}\left(\mathrm{S}\right)$;

STEP3: Calculate acceptance probability $\mathrm{P}=\left\{\begin{array}{c}1,△\mathrm{f}<0\\ {\mathrm{e}}^{-\frac{△\mathrm{f}}{{\mathrm{T}}_{\mathrm{k}}}},△\mathrm{f}\ge 0\end{array}\right.$;

STEP4: If S’ is accepted, let S = S’ and $\mathrm{uc}$ = 0; Otherwise $\mathrm{uc}$ = $\mathrm{uc}$ + 1.

STEP5: Judging whether the number of times the new solution is not accepted reaches a threshold ${\mathrm{Y}}_0$, and if $\mathrm{uc}\ge {\mathrm{Y}}_0$, terminating the loop.

STEP6: Determine whether the number of iterations reaches the number of terminating steps ${\mathrm{L}}_0$. If $\mathrm{it}\ge {\mathrm{L}}_0$, terminating the loop; otherwise, it = it + 1.

STEP 7: If the termination condition is not met, the temperature is slowly lowered according to the temperature reduction formula, and the iteration times are reset. The formula of temperature reduction is:${ \mathrm{T}}_{\mathrm{it}}={\mathsf{\alpha }\ast \mathrm{T}}_{\mathrm{it}-1}$. In the formula, $\mathsf{\alpha }$ is 0.95 is the number of cooling (iterations), ${\mathrm{T}}_0$ is the initial temperature.

STEP8: If the termination condition is satisfied, the current optimal solution S* is assigned to ${\mathrm{P}}_{\mathrm{i}}$;

STEP9: Repeat STEP1- STEP8 until SA sampling is carried out for each individual in the population.

3.3.7. Compared with The Original Scheduling Scheme

After calculating the rescheduling scheme, we must compare it with the original scheme and choose a better one. The selection principles are as follows:

• Analyze the container truck waiting time of the scheme. If the original scheme continues to be used after the fault, it will make the container truck waiting time exceed the upper limit of the container truck waiting time, then use the rescheduling scheme. Otherwise, continue to judge.
• The final objective function values of the two schemes are compared, and the scheme with smaller function values is selected as the final rescheduling scheme.

4. Experiments Analysis

4.1. Scene Parameter Setting

According to the investigation of Tianjin Port, Yantai Port, Dalian Port, and other places, there will be random faults of YCs in a container yard within 24 h of the working cycle. They took the actual data of a port as an example; the specific scene parameters are shown in Table 1. The number of containers to be picked up is 100, and the positions of these 100 containers in each container block are given randomly. Each container task corresponds to a container truck; the arrival time is immediate. According to the investigation, the moving speed of the center bridge in the field is between 0.42 m/s and 1.08 m/s. According to the specific data of Dalian Port, we set the moving speed of the center bridge at 0.83 m/s. The number of YCs in the yard is 12, and it is assumed that the random YC will fail in a 24-h working cycle, and the number of faults is three times. Fault occurrence time and YC maintenance time are given randomly. As shown in

Table 2. Scene parameter setting.

Parameter	Numerical Value	Parameter	Numerical Value
Stack A	6	Work Cycle/h	24
Bay B	15	YC	12
Layer C	4	Walking Speed of YC m/s	0.83
Container Yard D	9	Number of Tasks	100
Container Length/m	11.8	Container Height/m	2.18
Container Width/m	2.13

.

At present, it is stipulated that the population size of the genetic algorithm is 100, and the maximum number of iterations is 300. Therefore, the number of YCs corresponding to the containers picked up in the imported container block is randomly generated. MATLAB R2020a programmed the solution on the 11th Gen Intel(R) Core (TM) i7-11800H @ 2.30 GHz processor and PC with 32 GB memory. After 20 times solving, the solution with the smallest objective function value and the best convergence result graph was selected. Thus, the corresponding task number of each YC is obtained.

4.2. Algorithm Parameter Determination

To determine the optimal value of the model algorithm parameters in this paper, we set the initial values of the selection probability, crossover probability and mutation probability to 0.5. Then, by changing the probability, 20 comparative experiments were carried out, and the average value of the results was taken. The specific results are as follows as shown in the

Table 3. Results of comparative experiments for determining the selection probability.

Selection Probability	Objective Function Value	Convergence Rounds
0.3	1385.3012	20
0.5	2539.6386	21
0.6	2090.6024	25
0.7	1904.3976	48
0.8	3412.7711	43
0.9	2374.9398	51

,

Table 4. Results of comparative experiments for determining the crossing probability.

Crossing Probability	Objective Function Value	Convergence Rounds
0.3	2492.8313	29
0.5	2539.6386	21
0.6	2391.9277	38
0.7	1985.1807	51
0.8	2189.3716	41
0.9	2762.9518	38

and

Table 5. Results of comparative experiments for determining the variation probability.

Variation Probability	Objective Function Value	Convergence Rounds
0.3	1968.1928	20
0.5	2539.6386	21
0.6	3205.4217	37
0.7	2474.4579	41
0.8	2081.9277	47
0.9	2049.3374	59

:

Comprehensively considering the size of the objective function and the convergence round, we select the result with a smaller and larger objective function values. We determine that the selection probability is 0.7, the crossover probability is 0.7, and the mutation probability is 0.9. Follow-up algorithm characteristic analysis. The specific results are as follows as shown in the

Table 6. Sensitivity analysis of the walking speed of the yard crane.

Working Speed	Working Time	Objective Function Value
0.42	18,792.1687	1824.31
0.5	18,739.3373	1901.37
0.65	18,679.3341	1879.45
083	18,655.4819	1876.98
1.08	17,164.8193	1894.33

.

We conducted a sensitivity analysis on the walking speed of the yard crane in the input parameters and changed the data between 0.42 m/s and 1.08 m/s. It can be seen that with the increase of the yard crane speed, the working time of the yard area becomes shorter, which is consistent with the actual situation. At the same time, the results of the algorithm’s objective function are not different, so it can be seen that the proposed algorithm has good stability while maintaining sensitivity.

4.3. Algorithm Validity Analysis

To verify the algorithm’s effectiveness, the algorithm proposed in this paper is compared with the results of Cplex. Because there is no nonlinear constraint in the model constraint, Cplex can be used as the lower bound of this problem. As shown in

Table 7. Comparison of algorithm results.

Number of Tasks	Number of Fault	Objective Function Value			GPA/%	CPU Time
		Algorithm in This Paper	Lower Bound	Upper Bound		The Algorithm in This Paper/s	Lower Bound/s	Upper Bound
10	3	612.17	612.09	-	0.01	12.74	3.142	-
20	3	600.41	597.31	-	0.52	38.12	9.58	-
50	3	752.11	749.34	-	0.37	59.97	41.33	-
100	3	513.19	498.07	-	2.95	162.48	61.78	-
150	3	897.64	874.97	-	2.53	181.97	754.63	-
100	1	622.87	609.88	-	2.09	52.41	30.49	-
100	2	634.84	620.17	-	2.31	110.07	106.47	-
200	1	986.71	-	1749.68	43.61	176.34	-	5319.64
200	2	1067.09	-	1897.11	43.75	216.37	-	5689.31
200	3	1123.19	-	2046.74	45.12	274.39	-	5760.19
300	3	1649.73	-	3198.26	48.42	367.18	-	9134.17

.

Select the data in the above example and compare and analyze the results by changing the number of tasks and taking the average value of multiple results. When the number of tasks is small, the scale of the example is small, and there is almost no deviation between the algorithm and Cplex. As the number of tasks increases, the deviation also increases slowly; When the number of tasks remains constant, the number of specified faults changes, and with the increase of the number of faults, the deviation of the objective function will also increase when more than 200 tasks are performed. However, none exceed 3%, which is within the acceptable range. When Cplex solves the results of 150 tasks, the CPU running time is much longer than this algorithm. When there are more than 200 tasks in the field area, the solving time of Cplex is too long, and the result obtained by the final solution is quite different from that obtained by the algorithm in this paper, which can be used as the upper bound of the algorithm. In contrast, the proposed algorithm can solve the results stably in small-scale tasks and quickly in large-scale tasks. Thus, the effectiveness of the algorithm in this paper is verified.

4.4. Superiority Analysis of Algorithm

To further verify the superiority of the algorithm in this paper, the traditional genetic algorithm (GA) and tabu search algorithm (TS) is used to solve the bay of different scales, and the experimental results are shown in

Table 8. Comparison of algorithms.

Number of Bay	Number of Fault	Objective Function Value					CPU Time
		AEA	GA	TS	GAP1	GAP2	AEA	GA	TS	GAP1	GAP2
		/min	/min	/min	/%	/%	/s	/s	/s	/%	/%
8	2	259.76	261.14	265.19	0.53	2.09	7.15	7.25	7.36	1.40	2.94
10	2	309.75	314.88	319.33	1.66	3.09	8.24	8.51	8.45	3.28	2.55
15	2	431.51	445.01	446.71	3.13	3.52	11.81	11.95	11.93	1.19	1.02
20	2	634.84	639.18	641.87	0.68	1.11	11.79	12.01	12.05	1.87	2.21
25	2	547.66	558.11	571.93	1.91	4.43	14.27	14.58	14.42	2.17	1.05
30	2	507.64	519.13	524.17	2.26	3.26	14.44	14.91	14.51	3.25	0.48
30	3	513.19	528.43	530.19	2.97	3.31	17.19	17.51	17.52	1.86	1.92
30	4	649.07	660.19	662.18	1.71	2.02%	18.84	19.02	19.83	0.96	5.25
Average Value		-	-	-	1.86	2.8	-	-	-	2.00	2.18

.

As can be seen from Table 8, the number of faults remains constant. Under the task number of different scales, the objective function value calculated by this algorithm is better than the GA algorithm by 1.86% and the VQA algorithm by 2.85% on average, and the advantage is more evident with the increase of the scale. Regarding CPU time consumption, the solution time is positively related to the scale—the more tasks, the longer the solution time. The algorithm in this paper takes the shortest time, and the GA algorithm takes the longest. Among them, the algorithm in this paper is better than the GA algorithm by 2%, and the VQA algorithm by 2.18%, and the advantages become more evident with the increase of the scale. Therefore, the superiority of this algorithm is verified.

4.5. Comparative Analysis of Schemes

To further verify the scheme’s effectiveness, the rescheduling scheme and the original scheme are compared and analyzed, and the results are compared and analyzed with the above example data as reference, as shown in

Table 9. Comparison of schemes.

	Waiting Time Limit of Container Truck		Yard Crane Operation Time
	Original Scheduling Scheme	Rescheduling Scheme	Original Scheduling Scheme	Rescheduling Scheme	Objective Function	The Selected Scheme
The first fault occurs	Not exceed√	Not exceed√	18,655.48	18,788.73	133.253	Original scheduling scheme
The second fault occurs	Not exceed√	Not exceed√	18,655.48	18,655.48	0	Original scheduling scheme
The third fault occurs	Exceed×	Not exceed√	18,655.48	16,122.47	940.06	Rescheduling scheme

.

It can be seen from Table 9 that the fault judgment and rescheduling optimization model in this paper is reasonable and effective in arranging scheme rescheduling. For the fault that causes the waiting time of the container truck to exceed the upper limit of the waiting time, such as the third fault, the rescheduling scheme should be directly selected in the actual scenario, and the calculation result of this algorithm also shows that the rescheduling scheme should be selected. For the faults that meet the waiting time limit of the container truck, if the working time of the yard crane after the calculation is longer than that of the original scheme, the original scheme is selected; otherwise, the rescheduling scheme is selected. The algorithm effectively realizes this judgment.

4.6. Case Study

According to the scene parameters and algorithm parameter settings, we calculate the original scheduling scheme of the field area for the randomly generated task box positions and collection card arrival time, as shown in

Table 10. Task number corresponding to each YC in the original scheduling scheme.

YC	Original Scheduling Scheme
1	5  6  10  22  35  43  51  61  65  69  74  84  90
2	3  9  11  12  13  46  72  76  83  93
3	23  27  40  60  62  75  88  99
4	8  19  41  47  57  78  86  91  98
5	33  52  58  66  97
6	26  53  54  67  82  100
7	4  14  16  20  28  29  30  34  45  79  89
8	36  44  49  56  64  70  71  94  96
9	1  7  15  18  55  68
10	38  73  92  95
11	21  24  25  31  32  37  39  42  50  59  63  77  80  81  87
12	2  17  48  85
Working time	18,655.4819 s

. The algorithm iteration diagram is shown in the Figure 8.

The fault and maintenance time can be manually input into the system. The situation of three faults is artificially specified, and the rescheduling results after faults occur are shown in the following

Table 11. Comparison of scheduling schemes after the first fault.

The First Fault Occurs
Time of Fault	16,708 s
Breakdown maintenance time	4521 s
Number of failed YC	3
YC	Original scheduling scheme	Rescheduling scheme
1	5  6  10  22  35  43  51  61  65  69  74  84  90	5  6  10  19  24  33  35  36  48  49  57  59  60  69
2	3  9  11  12  13  46  72  76  83  93	3  9  11  12  13  14  17  22  29  30  34  39  52  53  58  79  85  94
3	23  27  40  60  62  75  88  99	-
4	8  19  41  47  57  78  86  91  98	8  16  18  20  38  47  54  82  91
5	33  52  58  66  97	50  71  75  88
6	26  53  54  67  82  100	55  65  74  86
7	4  14  16  20  28  29  30  34  45  79  89	4  21  23  67  73  77  83  90  92
8	36  44  49  56  64  70  71  94  96	15  46  63  66  72  76  80  87  95
9	1  7  15  18  55  68	1  7  41  61  84  97  99
10	38  73  92  95	25  26  27  28  31  32  42  43  44  45  51  56  62  68  70  81
11	21  24  25  31  32  37  39  42  50  59  63  77  80  81  87	37  40  89  93
12	2  17  48  85	2  64  100
Working time	18,655.4819 s	18,788.7349 s
Objective function value	133.253 s
conclusion	If the YC is removed for maintenance, it is necessary to add another YC and use the original scheduling scheme.

,

Table 12. Comparison of scheduling schemes after the second fault.

The Second Fault Occurs
Time of fault	47,049 s
Breakdown maintenance time	1521 s
Number of failed YC	7
YC	scheduling scheme
1	5  6  10  22  35  43  51  61  65  69  74  84  90
2	3  9  11  12  13  46  72  76  83  93
3	23  27  40  60  62  75  88  99
4	8  19  41  47  57  78  86  91  98
5	33  52  58  66  97
6	26  53  54  67  82  100
7	4  14  16  20  28  29  30  34  45  79  89
8	36  44  49  56  64  70  71  94  96
9	1  7  15  18  55  68
10	38  73  92  95
11	21  24  25  31  32  37  39  42  50  59  63  77  80  81  87
12	2  17  48  85
Working time	18,655.4819 s
Objective function value	0
conclusion	When the YC is repaired in situ, there is no new task in the maintenance process, which will not affect the work in the yard, so the original dispatching scheme is used.

and

Table 13. Comparison of scheduling schemes after the third fault.

The Third Fault Occurs
Time of fault	72,446 s
Breakdown maintenance time	3472 s
Number of failed YC	11
YC	Original scheduling scheme	Rescheduling scheme
1	5  6  10  22  35  43  51  61  65  69  74  84  90	5  6  10  22  35  43  51  61  65  69  74  94
2	3  9  11  12  13  46  72  76  83  93	3  9  11  12  13  46  72  76  83  85  89  90  93
3	23  27  40  60  62  75  88  99	23  27  40  60  62  75  97
4	8  19  41  47  57  78  86  91  98	8  19  41  47  57  78  87  99
5	33  52  58  66  97	33  52  58  66  92  97
6	26  53  54  67  82  100	26  53  54  67  82  95
7	4  14  16  20  28  29  30  34  45  79  89	4  14  16  20  28  29  30  34  45  79  88
8	36  44  49  56  64  70  71  94  96	36  44  49  56  64  70  71  98
9	1  7  15  18  55  68	1  7  15  18  55  68  86  91  96
10	38  73  92  95	38  73  83
11	21  24  25  31  32  37  39  42  50  59  63  77  80  81  87	21  24  25  31  32  37  39  42  50  59  63  77  80  81  84
12	2  17  48  85	2  17  48  100
Working time	18,655.4819 s	17,715.4217 s
Objective function value	940.0602 s
conclusion	When the YC is repaired in situ, it is necessary to reschedule and use a new scheme.

. The algorithm iteration comparison diagram is shown in the Figure 9 and Figure 10.

5. Conclusions

This paper studies the YC rescheduling problem of multi-container areas under the influence of random faults in the import container yard of container terminals, proposes the judgment mechanism of the impact of random faults on existing operations, establishes a rolling optimization model considering the waiting time of external container trucks and the influence of random faults, and designs a hybrid genetic simulated annealing algorithm to solve the problem according to the characteristics of the problem. Furthermore, this paper considers the fault of the yard crane, an unavoidable factor in the actual operation, and gives a more practical dispatching scheme for the dispatching work of ports. Therefore, the contribution of this paper is to consider the fault of the yard crane, an unavoidable factor in the actual operation, and to give a more practical dispatching scheme for the dispatching work of ports.

About limitation, this paper considers the problem of yard crane rescheduling under the influence of random faults, but the faults in actual operation are various. Some faults are related to the durable years of the yard crane and maintenance frequency, etc. This paper does not consider the above factors. At the same time, this paper assumes that there are enough yard cranes to replace fault yard cranes, but in practice, it is difficult to replace them due to the low idle rate of equipment or insufficient personnel. For ports, the fault is a kind of uncertain event.

In future research, as Iris et al., 2019 [34] said, ports invest in harvesting renewable energy. The power generated by clean energy can be used in the port or injected into the utility grid. “Using clean energy is becoming increasingly common in today’s ports. The fault mode of the electric yard crane and the oil yard crane mentioned here is not similar. Therefore, we could study the problem of electric drive yard cranes in the future.

Meanwhile, as shown by the limitations discussed above, the types of faults are diverse. Some are uncertain, but others can also be predicted and analyzed. You can refer to the mechanism proposed by Ghasemi et al., 2019 [35], which uses fuzzy inference system demand prediction as the output. In subsequent research, fault prediction and YC rescheduling research can be combined.