Regularities of Changes in the Motion Resistance of Wheeled Vehicles along a Curvilinear Trajectory

Abstract

The value of the motion resistance is one of the important characteristics that determines the technical and operational properties of the vehicle, in particular its fuel economy under operating conditions. This article summarizes the approaches to determining the rolling resistance of a wheeled vehicle in straight motion, which is a separate case from curved motion. The value of this parameter is one of the vehicle components of the motion resistance along a curved path. The regularities of changes in the motion resistance of a two-axle wheeled vehicle along a curvilinear trajectory are determined based on the determination of the motion resistance of individual wheels, which considers resistance to rectilinear motion and additional resistance along a curved path caused by the twisting and lateral displacement of the wheel disc relative to the tire patch. Analytical dependences of changes in the motion resistance along a curvilinear trajectory of two-axle vehicles with the design features of transmission, placement of tires, and their characteristics were obtained. It was found that reducing the radius of curvature of the trajectory to the minimum turning radius increases the motion resistance coefficient for the investigated vehicles by 1.68−2.04 times in relation to the rolling resistance coefficient in straight motion.

1. Introduction

The choice of vehicle should be based on a comparison of the efficiency of possible alternatives. Complex performance indicators are used to take into account as many factors as possible. Their structure may contain economic, technical, and environmental components [1]. The technical component allows for the assessment of the degree of adaptability of the vehicle to given operating conditions. Within its limits, efficiency criteria are distinguished according to the absolute and specific energy consumption of the vehicle. In most countries, the ratio of actual fuel consumption to completed transport work is used to evaluate the efficiency of transport work [2]. In references [3,4], the authors evaluate the mechanical efficiency of large-class city buses using the ratio of the useful work performed on the sections of a given route in the city of Rzeszów (Poland) to the energy consumption of the studied bus model. The relevant analytical dependencies, presented in [2,3,4], take into account the speed, acceleration, and modes of movement of the vehicle, the gradient of the road, and the weather conditions, and require the determination of the total resistance of the road. In [2], only the general methodology for evaluating the efficiency of the vehicle according to various indicators of fuel efficiency is described. In [3,4], the efficiency of the bus under the conditions of rectilinear movement is studied on a given segment. In these works, examples of the evaluation of the technical efficiency of vehicles moving along a curvilinear trajectory were not considered.

Usually, the driving route contains slopes and curved sections. Therefore, both the longitudinal and transverse dynamics of connected automated vehicles were taken into account in [5]. The results of the computer simulation in [5] show that the strategy of integrated planning of traffic modes based on the complex dynamics of the vehicle provided an acceleration of the vehicle by less than 2 m∙s⁻², and demonstrate the advantages of this strategy in terms of transverse stability and energy efficiency on continuous curved roads compared to the longitudinal strategy. The developed models took into account total road resistance and road topography; however, they were implemented only for vehicles of the same type with the same set of technical and operational characteristics. The authors of [6] evaluate the energy efficiency of vehicles for given categories and types of power plants on city roads, for which the resistance of the road and the level of curvature of the road are determined. However, these parameters contain unclear information. The level of curvature of the road is described by a linguistic variable that can take the same value for different trajectories of movement within a given range of radii. The results of study [7] revealed that the speed and transverse location of vehicles on the carriageway under the conditions of curved traffic depend on the place of interaction between vehicles in front of the center of the curve.

In references [8,9], the parameters of curvilinear movement of a tracked vehicle were investigated. Within the framework of study [8], the position of the longitudinal axis and the angle of the deviation vector of the speed of movement were determined as the main parameters. Additionally, the turning resistance coefficient is taken into account, which is determined based on the length of the track, angular velocity, normal, and tangential acceleration of the vehicle body. The presence of significant noise in the acceleration values during measurement by inertial sensors significantly limits the accuracy of determining the kinematic and force parameters that characterize the change in the direction of movement of the car. The exponential dependence of the turning resistance coefficient is proposed, taking into account its maximum value and the ratio of the coefficient of curvature to the curvature, at which the force of lateral sliding of the lower rollers is equal to the force of friction. However, the resulting models describe the movement of tracked vehicles with the discrete properties of the steering system on dry sandy soil. Equations of the curvilinear trajectory of a four-wheeled tractor were obtained in [9], simulating the tractor’s entry into a turn, the exit of a turn, and the rotation of its body. The deviation of the wheels of both axles under the action of lateral forces is taken into account. The correlation dependence between the radius of curvature and the turning angle of the machine frame is constructed. The obtained equations allow for the calculation of the coordinates of the center of mass of the vehicle depending on the turning angle and the intensity of the change in the course angle. The results of this study are the basis for the development of new methods to reduce fuel consumption and maintain the stability of vehicles under operating conditions. However, the obtained models do not take into account such factors as terrain, weather conditions, and the sliding and skidding of wheels during curvilinear movement.

The authors of [10] investigated the influence of the design of inter-wheel differentials on the resistance to curvilinear movement on paved roads. The study was carried out on the example of an all-wheel drive car with a wheel formula of 8 × 8. As one of the criteria for the analysis of the resistance to curvilinear movement, the relative increase in the actual turning radius of the car, taking into account the slip of the tire at the point of contact compared with the theoretical turning radius calculated without taking into account the slip, was chosen. Among the three self-locking high-friction differentials considered, the models characterizing the operation of inter-wheel differentials, in which the degree of locking depends on the square of the difference in the angular velocities of the half-axles, turned out to be the most rational in terms of the degree of influence on the resistance to curvilinear movement. The authors did not take into account the peculiarities of the operating conditions of the vehicle and the parameters of stability during acceleration.

In [11], the analytical dependence of the total coefficient of road resistance of special wheeled vehicles on vehicle acceleration, the angular velocity, the angular acceleration, and the distance between the sensors in the lateral plane are presented. The use of the model is limited by the given conditions. The obtained results made it possible to study the dynamics of the change in the coefficient of the road resistance depending on the speed of movement of the vehicles with a 6 × 6 wheel formula.

In [12], the authors provide data according to which, among all resistance forces in a modern passenger car, 20–30% of the total fuel consumption is due to rolling resistance (depending on driving conditions and tire characteristics). The author claims that reducing its value by 10% will provide a reduction in fuel consumption from 1% to 2%. Taking into account the ranges of values of the rolling resistance coefficient, its accurate assessment will allow determining the optimal driving modes, reducing rolling resistance and harmful emissions into the atmosphere. Rolling resistance cannot be physically measured. Its value strongly depends on the speed of the vehicle, the type of road surface, tire pressure, and tire temperature.

Special attention was paid to the rolling resistance coefficient on an undeformed support surface in the work of Soltus A.P., Wong J.Y., Ilarionov V.A., Sakhno V.P., Petrushov V.A., Jazar R.N., Gillespie T., Suntsov N.V., Knoros V.I., Falkevych B.S. and others; special attention was paid to the determination of the rolling resistance coefficient on an undeformed support surface because, as shown by the results of statistical studies, wheeled vehicles move mainly along a trajectory close to a straight line, and the turning angles of the steered wheels are within 1.5° [13].

To determine the coefficient f when driving a car on roads with good quality asphalt or cement concrete, reference [14] recommends an empirical dependence that takes into account only the speed of the car, and after equivalent transformations, takes the form:

$$f=0.0114\left(1+\frac{V}{32}\right)$$

(1)

where V is the speed of the vehicle, m/s.

In [15], it is recommended that this coefficient is determined by the expression:

$$f=0.0115\left(1+\frac{V}{31.94}\right)$$

(2)

where V is the speed of the vehicle, m/s.

In reference [16], it is stated that for traction calculations, it is sometimes sufficient to submit the coefficient of rolling resistance in the form of linear dependence on the speed of movement. According to [16], for the most common range of air pressure in the tire (about 0.179 MPa) at speeds of up to 130 km/h, it is recommended that the average value of the rolling resistance coefficient is determined using the following expression:

$$f=0.01\left(1+\frac{V}{44.44}\right)$$

(3)

where V is the speed of the vehicle, m/s.

The analysis of Dependencies (1)–(3) shows that they are functions of the speed of movement of the first order; accordingly, these dependencies will be depicted in the form of straight lines on graphs. If we take speed V = 0 in these dependencies, then we will obtain the values of the rolling resistance coefficient at the low speeds of 0.0114, 0.0115 and 0.01, respectively. At the same time, the value of the coefficient f will also be influenced by the values of indicators 32, 31.94, and 44.44, into which the speed V is divided. Therefore, at a speed of movement V = 15 m/s, the rolling resistance coefficients, calculated according to Expressions (1)–(3), will acquire the following values: 0.0167, 0.0169, and 0.0134. The difference in calculations is 20.7%.

At the same time, Dependencies (1)–(3) were obtained experimentally for specific tires on an undistorted surface, so they cannot be used to determine the rolling resistance coefficient for other tires, and even more so on different support surfaces.

In contrast to the above dependencies, in reference [17], to determine the coefficient f, the authors recommend a dependency in which, in addition to the speed of movement, the experimentally obtained values of the rolling resistance coefficient at low speed of movement and they also recommend a coefficient that takes into account the air pressure, the type of tire, and its dimensions:

$$f=f_0{k}_{f}V$$

(4)

where f₀ is the rolling resistance coefficient of the tire at low speed, which is determined experimentally, taking into account the supporting surface and pressure in the tire; k_f is a coefficient, the value of which is recommended in [17], to be determined experimentally for each type and size of tire depending on the internal pressure of the tire; V is vehicle speed, km/h.

Paper [17] gives experimental values of coefficient f₀ for cement–concrete, gravel or crushed stone pavement cobblestones in dry, wet, dirty, snowy, and icy conditions. So, for a dry asphalt concrete coating, the coefficient f₀ is within 0.012–0.025, for a dry crushed stone or gravel coating it is within 0.02–0.025, and for dry paving stones, 0.025–0.035. It can be determined from the analysis of the data presented in the work which types of tire the value of coefficient f₀ is given. The value of coefficient k_f is not given in this paper.

In references [17,18,19], for the calculation of the rolling resistance coefficient f at the nominal air pressure in the tire depending on the speed of movement, empirical second-order dependencies are recommended, taking into account the experimental values of this coefficient at low speed.

Thus, in reference [14], the following dependence is given:

$$f=f_0\left(1+\frac{V^2}{1500}\right)$$

(5)

where f₀ is the rolling resistance coefficient of the tire at low speed, which is recommended that it is determined experimentally; V is the speed of the car, m/s.

In references [13,17], the dependence is recommended for determining coefficient f:

$$f=f_0\left(1+\frac{V^2}{2143}\right)$$

(6)

where f₀ is the rolling resistance coefficient of the tire at low speed; V is the speed of the car, m/s.

At the same time, Dependencies (5) and (6) differ from each other only by coefficients 1/1500 and 1/2143. In this case, the difference in the calculations of coefficient f is based on these dependencies at the speed of movement V = 15 m/s is 3.9%.

According to references [18,19], the following dependence is recommended to determine the rolling resistance coefficient f:

$$f=f_0\left(1+\frac{k_f}{f_0}{V}^2\right)$$

(7)

where f₀ is the rolling resistance at low speed; k_f is the speed influence coefficient, the value of which, in the absence of experimental data, is recommended to take k_f = 7·× 10⁻⁶ s²/m²; V is the speed of the vehicle, m/s.

In reference [19], it is stated that during calculations according to Dependence (7), the coefficients f₀ and k_f should be determined experimentally for each individual tire. For most car tires, it is recommended that they take f₀ = 0.015, k_f = 7·× 10⁻⁶ s²/m².

In references [20,21,22], dependences to determine the rolling resistance coefficient are given, in which the air pressure in the tire is additionally taken into account. For example, in references [20,21], the following dependence is given for passenger car tires on roads with a concrete surface:

$$f=f_0+f_s{\left(3.6\frac{V}{100}\right)}^{2.5}$$

(8)

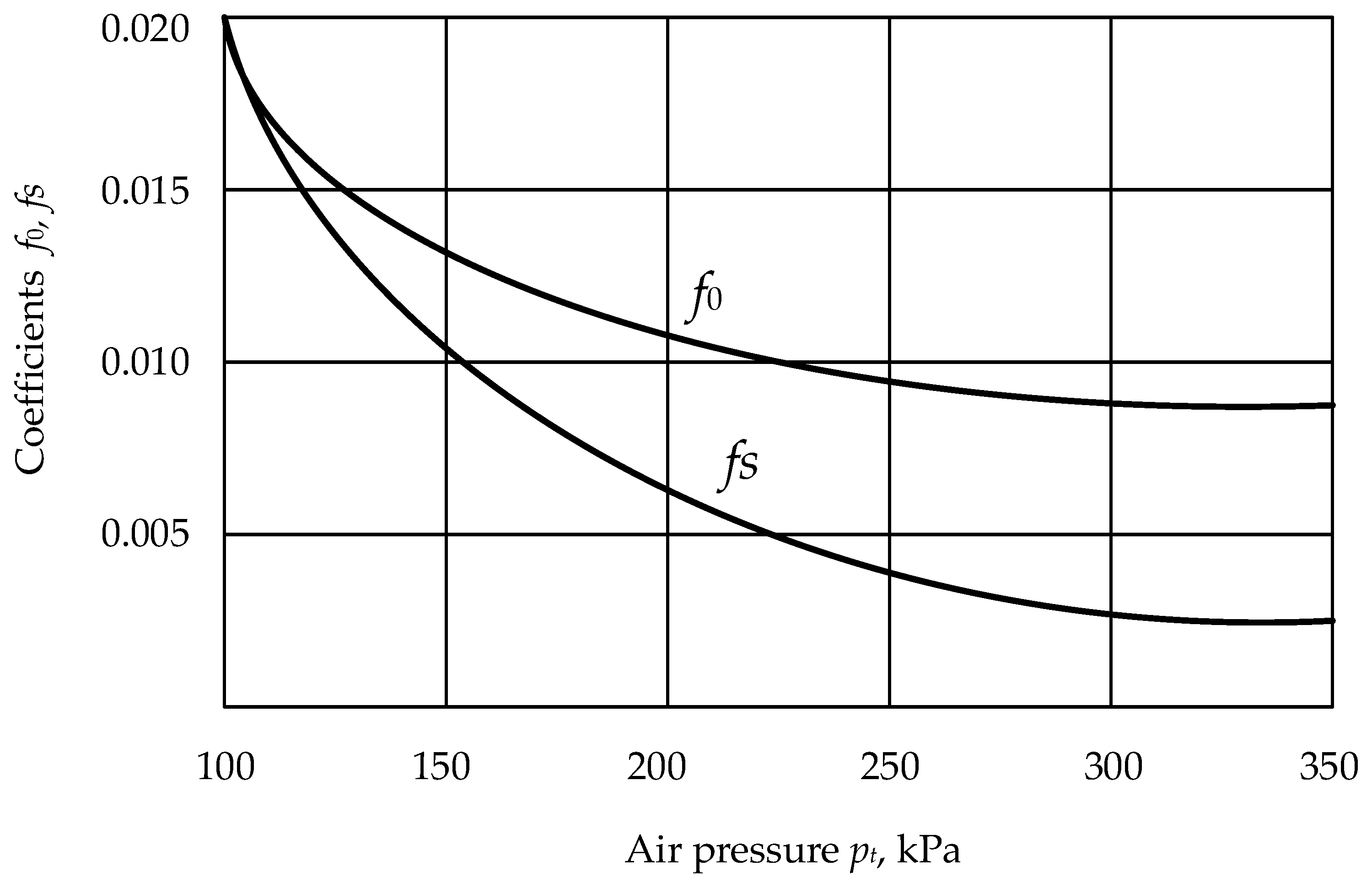
where V is the speed of the car; m/s; f₀, f_s are coefficients depending on the air pressure in the tire.

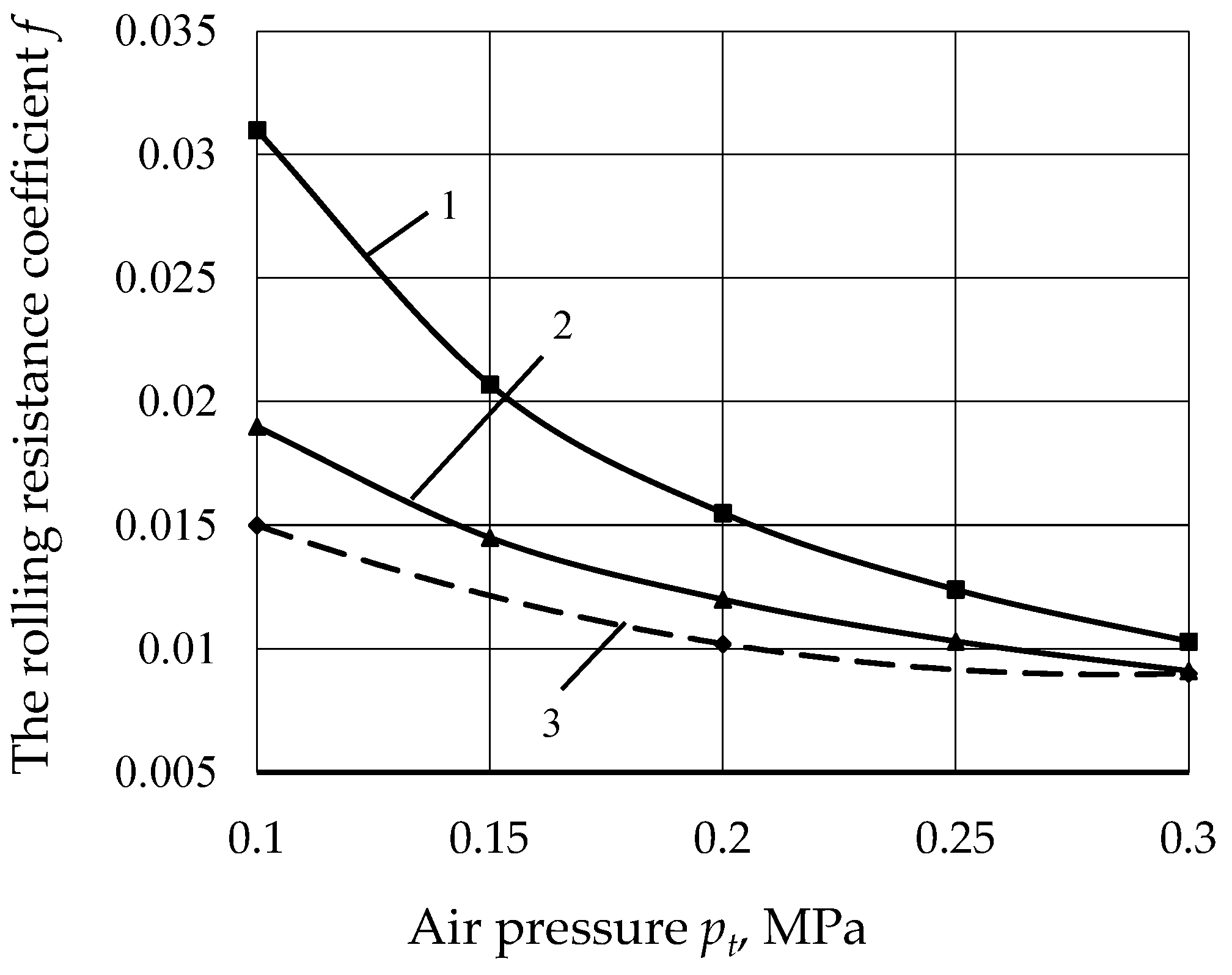
The coefficients f₀, f_s in references [20,21] are recommended to be determined according to the graphs shown in Figure 1.

In reference [22], an empirical dependence is given for the determination of the coefficient of rolling resistance f on an asphalt concrete surface, which takes into account the speed of movement and the air pressure in the tire (9). At the same time, experimental studies of the coefficient of rolling resistance of a car wheel were carried out at a speed of 30–170 km/h and an air pressure of 100–500 kPa in the tire.

$$f=k_0{e}^{cV}$$

(9)

where k₀ and c are coefficients depending on the air pressure in the tire, the values of which are given in

Table 1. The value of coefficients k₀ and c depending on the tire air pressure p_t [22].

pt, kPa	k0	c, s/m	pt, kPa	k0	c, s/m	pt, kPa	k0	c, s/m
100	0.015	0.0224	250	0.011	0.0202	400	0.008	0.0184
150	0.0136	0.0218	300	0.010	0.0199	450	0.0077	0.0178
200	0.012	0.0208	350	0.009	0.0193	500	0.0071	0.0168

; V is the speed of the vehicle, m/s.

If we take speed V close to 0, then in Dependence (9), coefficient k₀ is the rolling resistance coefficient f₀, taking into account that e^cV ≈ 1. At the same time, reference [22] does not indicate for which type of tire the value of coefficient k₀ is given.

Paper [23] gives an empirical relationship between the force of rolling resistance, air pressure in the tire, and the speed of the car on a paved road.

$$P_f=G_w\left(\frac{20.2}{{0.64p}_t}+\frac{V^{3.7}}{0.778·{10}^6{p}_t^{2.03}}\right)$$

(10)

where G_w is the load, tnf; P_f is the rolling resistance force, kgf; p_t is the air pressure in the tire, kgf/cm²; V is the speed of the vehicle, km/h.

From Dependence (10), after simple transformations, the following expression can be obtained to determine the rolling resistance coefficient f, depending on the air pressure in the tire and the speed of movement in terms of SI units:

$$f=\frac{0.0031}{p_t}+1.371954·{10}^{-9}\frac{V^{3.7}}{p_t^{2.03}}$$

(11)

where p_t is the air pressure in the tire, MPa; V is the speed of the vehicle, m/s.

The first component of Dependence (11) determines the coefficient of rolling resistance at a speed close to zero, and the second component determines the influence of speed on its value. This dependence makes it possible to determine the influence of the air pressure in tire p_t on each component of coefficient f.

Analysis of references [13,17,19] showed that lower values of the rolling resistance coefficient are typical of passenger car tires with a metal-cord cover, and higher values are typical of truck tires with adjustable air pressure. For specific tires, this coefficient is determined experimentally.

If we take into account that the coefficient of rolling resistance does not exceed 0.008 under the best conditions, then from the analysis of Dependence (11), it can be seen that it is valid under the condition that f = 0.0031/p_t > 0.008. Under this condition, p_t < 0.3872 MPa. It is obvious that Dependence (11) is typical of tires in which the air pressure does not exceed 0.3872 MPa.

In [24], an empirical dependence in the form of a polynomial of the third degree is recommended for determining the rolling resistance coefficient on paved roads. If in this dependence we express the variables in terms of SI units, then we obtain the following expression:

$$f=\frac{0.00409}{\sqrt[3]{p_t^2}}+\frac{0.001}{\sqrt{p_t}}{\left(\frac{V}{100}\right)}^2+\frac{0.0091}{\sqrt[3]{p_t^4}}{\left(\frac{V}{100}\right)}^3$$

(12)

where p_t is the air pressure in the tire, MPa; V is the speed of the car, m/s.

Similar to the above, Dependence (12) is valid under the condition that $f=0.00409/\sqrt[3]{p_t^2}>0.008$. Under these conditions, the dependence is typical of tires with air pressure p_t < 0.3655 MPa.

Therefore, Dependencies (11) and (12) are valid for determining the rolling resistance coefficient of tires in which the air pressure does not exceed 0.3872 MPa and 0.3655 MPa, respectively. Under other conditions, the obtained values of this coefficient are beyond the possible values obtained experimentally.

At the same time, the number of works dedicated to the study of the resistance of the wheel movement along a curved path is limited, which is explained, on the one hand, by the movement of vehicles on trajectories that are almost straight-line movements, and on the other hand, by the complexity of the phenomena associated with such movements. Therefore, the purpose of this paper is to study the regularities of changes in the motion resistance along a curvilinear trajectory using the example of typical models of two-axle vehicles.

The paper consists of four sections. In Section 1, the results of the research of other scientists on the motion resistance along a curvilinear trajectory and the rolling resistance on a straight line as its component are analyzed. In Section 2, the methodology for analytically determining the increase in the motion resistance along a curvilinear trajectory, taking into account the slip angle of the wheel, is presented. Section 3 presents the results of determining the rolling resistance coefficient using different methods, including taking into account the air pressure in the tires, as well as the results of the experiment on determining the motion resistance coefficient along a curvilinear trajectory. An analytical dependence of the increase in the motion resistance was obtained for typical two-axle vehicles with different design structures and types of tires. The discussion and conclusions are presented in Section 4.

2. Materials and Methods

The elastic wheel is considered to be a complete and complex mechanism that converts the rotational movement of the wheel relative to the axis of rotation into its translational movement on the support surface. It includes the hard disc, the elastic body of the tire (the tire) and the contact patch of the tire, which belong to both the wheel and the supporting surface. Its integrity is determined by external and internal connections. External connections form the integrity of its design, and the internal ones represent requirements for it, which in the future, will form the technical and economic indicators of the wheeled vehicle. At the same time, one of the main requirements for the wheel is the provision of minimal resistance to its movement, which directly determines the fuel economy of the vehicle [25,26].

When an elastic wheel moves in a straight line along an undeformed support surface, it is necessary to overcome the friction in the rubber–metal–fabric cover, the tread rubber, and the friction formed when the tire comes in contact with the support surface, which, during the movement of the wheel, causes a displacement of the uniform normal reactions relative to the center of the tire patch by the amount d. This displacement of the uniform relative to the center of the contact patch causes the moment of rolling resistance of the elastic wheel. In the theory, displacement d is taken into account by the coefficient of rolling resistance f, which is understood as the ratio of displacement d to the dynamic radius of wheel r_d, and it is determined by the expression:

$$f=\frac{d}{r_d}.$$

(13)

To move the wheel, it is necessary to overcome this moment of resistance. If the wheel is driven, the pushing force is supplied from the frame of the vehicle to the axle of the wheel, and if the wheel is not driven, the torque is supplied directly to the disc from the transmission of the vehicle. The force and torque applied to the hard disc from the vehicle frame and transmission cause reactions when the tire comes in contact with the bearing surface, causing the vehicle to move [25,26].

Therefore, in order to ensure the rectilinear movement of an elastic wheel on an undeformed support surface, it is necessary to overcome the rolling resistance, which depends on the value of the rolling resistance coefficient f. Therefore, determining the rolling resistance of an elastic wheel along a straight path is reduced to the calculation of the coefficient of rolling resistance, which is one of the main characteristics of an elastic wheel, as it directly affects the technical and economic properties of the wheel. At the same time, we consider the rectilinear motion of an elastic wheel to be a special case of curvilinear motion when the radius of curvature of the wheel’s trajectory moves towards infinity.

In the future, when studying the resistance of the wheel movement along a curved trajectory, we will adopt the following:

• The supporting surface is a road with an asphalt concrete surface;
• Only adhesion zones are present in the contact patch;
• When the wheel rolls in a circle, the wheel twists and moves sideways while traveling on a path equal to half the length of the longitudinal axis of the tire contact patch;
• When moving in a circle, the energy supplied to the wheel is distributed equally between the turning and lateral displacement of the disc relative to the tire contact patch;
• The relationship between the lateral force and the slip angle is linear.

During the wheel motion along a curved trajectory, the tire contact patch takes part in the transfer and relative motion [25,27]. The center of transfer motion is the center of the turning of the vehicle, which is formed by the angle of turning of the steered wheels and the base of the vehicle. As for the center of relative motion, it is located within the contact patch of the tire, and as the radius of curvature increases, it shifts to the edge of the patch [25,27]. According to reference [25], when rolling an elastic wheel along a curved trajectory with a radius of curvature R > 1 m, with sufficient accuracy for practice, it can be assumed that the center of the relative turning of the contact patch shifts to the edge of the patch. The trajectory of the curvilinear movement of the elastic wheel can be determined by the trajectory of the center of relative rotation of the contact patch. At the same time, during rectilinear movement, the trajectory is determined by the movement of the geometric center of the tire contact patch.

Analysis of the results of the conducted research [25,27] proved that when moving along a curved trajectory, in the absence of sliding in the contact of the wheel with the support surface, there is simultaneous turning and lateral displacement of the disc relative to the contact patch of the tire when the elastic wheel passes a distance equal to half the length of the longitudinal axis of the contact patch of the tire.

Given that the trajectory of the wheel movement will be determined by the center of the relative turning of the contact patch of the tire, the relative turning of the disc and its lateral displacement will be determined by the relative positions of the contact patch of the tire before and after the elastic wheel passes a distance equal to half the length of the longitudinal axis of the contact patch.

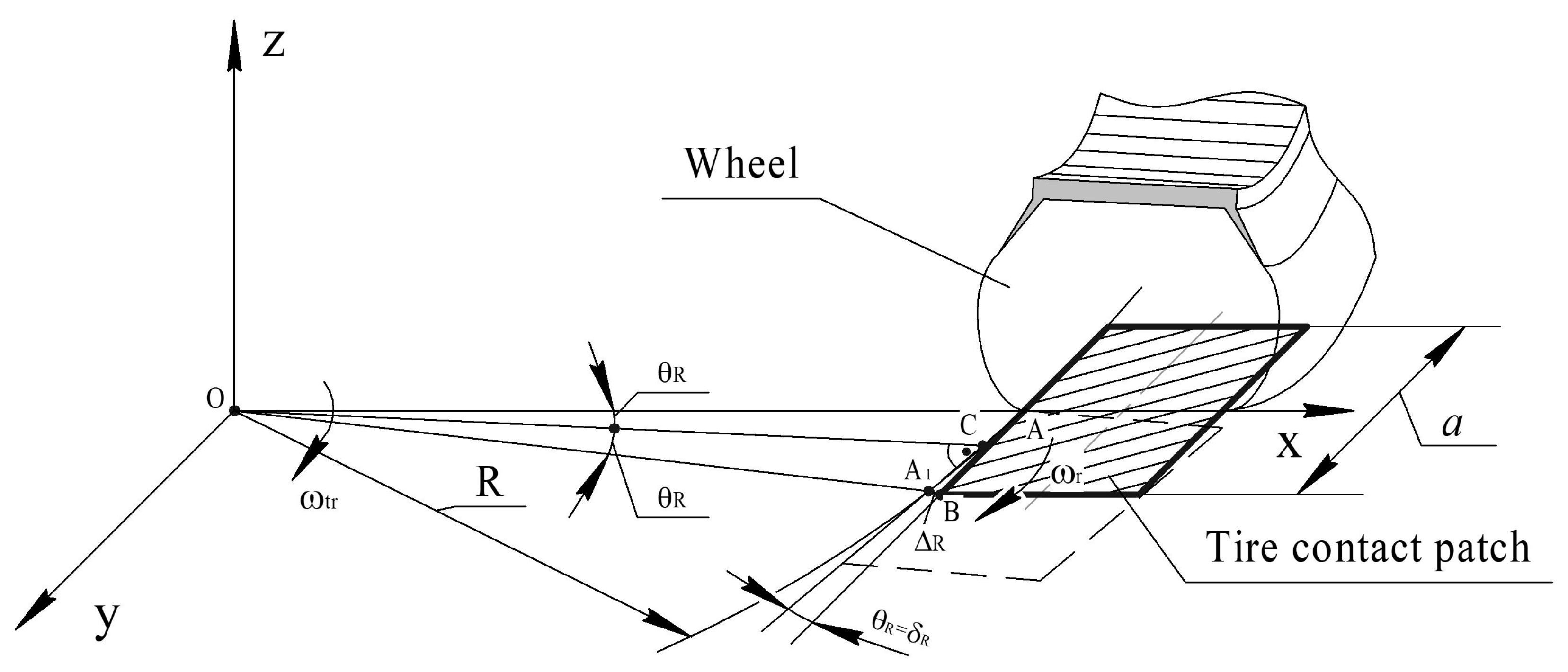
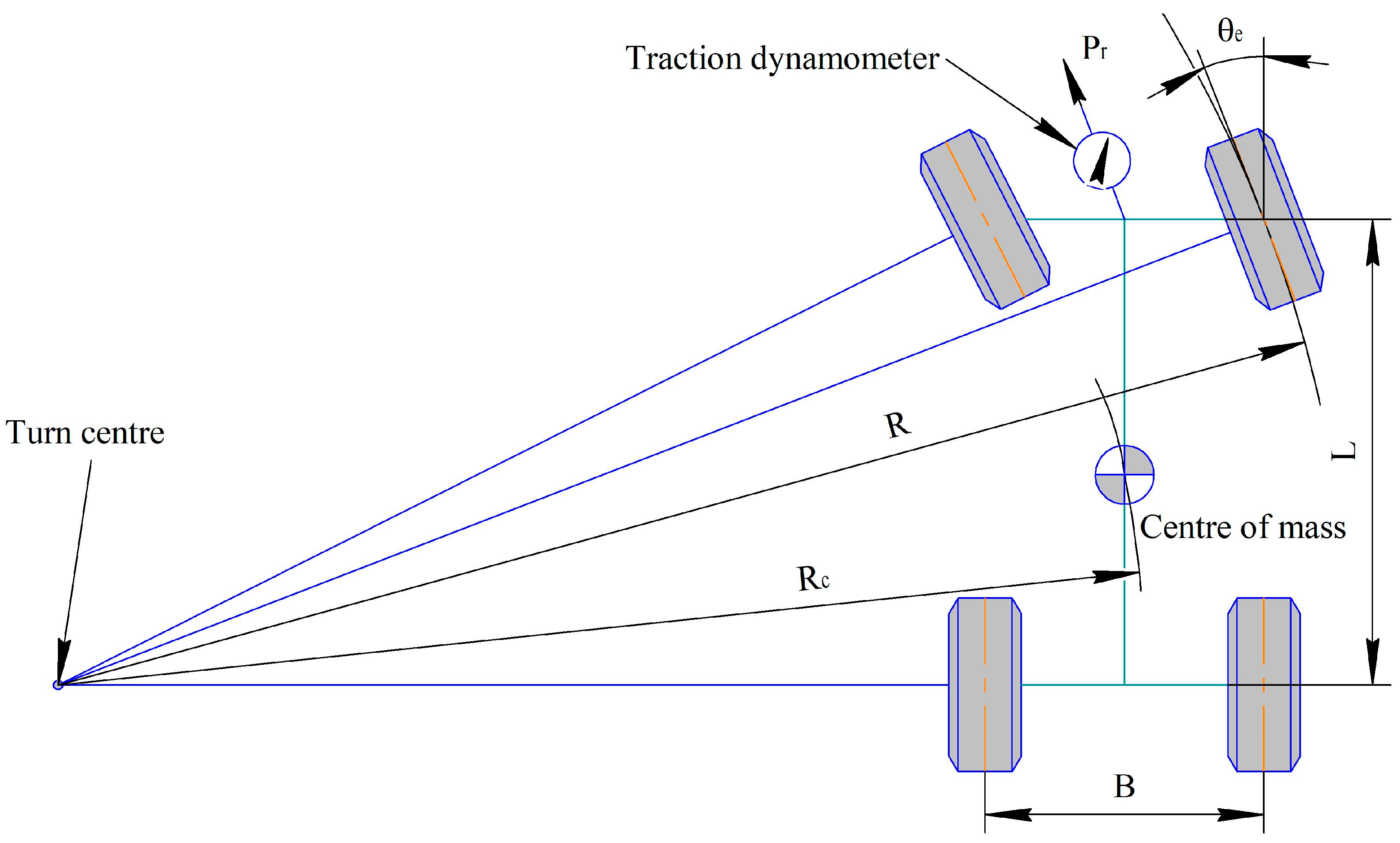
Taking into account the above, Figure 2 presents a scheme for determining the angle of relative rotation of the contact patch of the tire and its lateral displacement relative to the wheel disc during the movement of the elastic wheel along a curvilinear trajectory.

The contact tire patch of the elastic wheel has the shape of a rectangle, the same size as the tire patch with the longitudinal axis, as can be seen in the analysis in Figure 2. Point O is the center of the transfer movement of the contact tire patch, relative to which the center of relative rotation of the patch, point A, moves in a circle with a radius R, with an angular velocity of ω_tr. At the same time, the tire patch turns relative to the center of relative turning, point A, with an angular velocity of ω_r. After passing through the center of the wheel of distance a/2, the center of relative rotation will take position A₁, and the contact tire patch will take the position shown in Figure 2 by a dashed line. Angle θ_R between these two positions will be the twisting angle of the disc with respect to the tire patch during the movement of the wheel along a curved path of radius R.

Because $\angle$ A₁AB = $\angle$ AOC, as angles with mutually perpendicular sides, then their values are determined by the expression:

$${\theta }_R=\frac{a}{4R}$$

(14)

where θ_R is the twisting angle of the disc relative to the tire patch while the passing through the center of the wheel by the distance S = a/2, rad; a is the tire patch length, m; R is the radius of the trajectory of the center of relative turning of the tire patch, point A, m.

The turning of the disc relative to the tire patch by an angle θ_R will cause a moment of turning resistance relative to the vertical axis passing through the center of the relative turning of the tire patch, point A. We define this moment as follows:

$$M_{\theta }=C_{\theta }{\theta }_R$$

(15)

where M_θ is the moment of turning resistance of the disc, N·m; C_θ is the angular stiffness of the tire relative to the vertical axis of the wheel passing through the center of the tire patch, N·m/rad. In the absence of experimental data, it is recommended to determine the angular stiffness of the tire according to empirical dependence C_θ = (0.51-0.63) G_w, N·m/rad, where G_w is the load on the wheel, N. At the same time, lower values refer to high-pressure tires and larger ones to wide-profile tires with adjustable air pressure.

At the same time, after passing through the center of the wheel by the distance S = a/2, point A will shift in a lateral direction relative to the initial position of the tire patch by Δ_R = A₁B. By this amount, the disc of the elastic wheel will shift in a lateral direction relative to the initial position. The value of this displacement is determined by the following expression:

$${\mathsf{\Delta }}_R=\frac{a}{2}{\theta }_R.$$

(16)

The lateral displacement of the disc by the amount Δ_R will cause the wheel to roll with slip angle δ_R, which, according to Figure 2, is equal to angle θ_R, and cause the appearance of a lateral force, which, taking into account the accepted assumptions, we write as follows:

$$P_s=K_s{\delta }_R$$

(17)

where P_S is the lateral force that occurs when the disc is displaced laterally during its passage through the center of the wheel along the circle of the path S = a/2, N; δ_R is the slip angle, which is caused by the rolling characteristics of an elastic wheel along a curved path with a radius of R, rad. This slip angle is usually called “kinematic”; K_S is the coefficient of lateral deflection, N/rad.

As for the lateral force, it is located in a plane perpendicular to the rolling plane of the wheel. The analysis of the research results presented in references [25,27] proved that when the wheel moves along a curved path, the energy supplied to the wheel disc due to the pushing force from the vehicle frame or due to the torque from the transmission is distributed equally to the twisting of the disc and its lateral displacement relative to the tire patch. In this case, if the angles θ_R = δ_R = a/4R, the coefficient of lateral displacement, according to [25], is determined by the following expression:

$$K_s=\frac{2C_{\theta }}{a}.$$

(18)

It follows from this that the movement of an elastic wheel along a curved path will cause, in addition to rolling resistance along a straight path, resistance due to the twisting of the tire body between the hard disc and the patch and the lateral displacement of the disc relative to the patch. The twisting of the tire body will cause a moment of the vertical axis passing through the center of relative turning of the tire patch, and the lateral displacement will cause a lateral force. Evidently, in order to ensure the movement of an elastic wheel along a curved path with a radius R, it is necessary to supply energy to the wheel disc to overcome the rolling resistance and ensure the turning of the disc by the angle θ_R and its lateral displacement by the amount Δ_R relative to the tire patch. At the same time, the pushing force of the car frame and the torque applied to the wheel disc act in the plane of its rolling.

The presence of an amorphous body of the tire and different planes of action of these three dynamic factors indicate the peculiarity of the phenomena occurring in the body of the tire when moving along a curved path, and cause difficulties in calculating the motion resistance coefficient of the wheel along a curved path.

The movement of the wheel along a curved path in the absence of an inclination to the support surface, which is typical of non-steered wheels of vehicles, was considered above. However, the presence of steered wheels, which turn relative to the axis of the kingpins with a transverse and longitudinal inclination, causes them to roll with an inclination relative to the support surface. As a result of the research carried out in [27], it was determined that when an elastic wheel with an inclination towards the road moves along a curved path, the phenomena caused by the rolling of the inclined wheel are additionally superimposed on the phenomena occurring in the pneumatics (tire bodies) during movement along the curved path. With an unchanged trajectory in the elastic wheel, they cause a change in the slip angle of the pneumatic tire and a lateral displacement of the disc relative to the tire patch.

To determine the influence of the inclination of the wheel to the road during movement along a curved trajectory, according to [27], the concept of “reduced” radius of curvature of the trajectory of the elastic wheel is introduced. It is understood as the conditional radius of the trajectory of the wheel movement, with which the wheel would move without tilting along a curved trajectory, but with the twisting angle and lateral displacement, which take into account the phenomena accompanying the rolling of the wheel along a curved trajectory and with an inclination to the road.

At the same time, the direction of the inclination of the wheel relative to the center of its turning is of significant importance, and the dependencies obtained in [27] make it possible to determine the value of the twisting angle of the tire body and the lateral displacement when the wheel moves with an inclination to the road along a curved trajectory.

If the wheel has an inclination, then the kinematic slip angle, according to [27], is determined by the following expression:

$$\sum {\delta }_R=\frac{a}{4R}\pm \frac{asin\gamma }{4r_w}$$

(19)

where Σδ_R is the kinematic slip angle when rolling the wheel, with an inclination (with camber) to the road, rad; r_w is the rolling radius of the wheel, m; γ is the current camber angle, deg.

Note that in Expression (19), the “plus” sign is used for the case when the wheel is tilted away from the center of rotation, and the “minus” sign is used when it is tilted toward the center of rotation. In this case, a “plus” sign is used with the camber angle γ.

As for the current camber angle of the wheel, it is a function of the transverse and longitudinal inclination of the kingpin and the camber angle in the position of the straight-line movement of the vehicle, and is determined by the following expression [27]:

$$\gamma \left(\theta \right)={\gamma }_0+{\alpha }_t\left(1-cos\theta \right)\pm {\beta }_{t}sin\theta$$

(20)

where γ₀ is the camber angle of the wheel in the position of rectilinear movement, rad; α_t, β_t are angles of transverse and longitudinal inclination of the kingpin, rad.; θ is the current angle of the turning of the wheel in degrees.

In Expression (20), the “plus” sign must be used when the left-steered wheel is turned to the left from the position of the car’s straight-line motion, and the right wheel is turned to the right. If otherwise, the “minus” sign should be used.

If the wheel with an inclination to the road moves along a curved path with a kinematic slip angle Σδ_R, then, taking into account the Expression (14) and the above, we write:

$$\frac{a}{4R_r}=\frac{a}{4R}\pm \frac{asin\gamma }{4r_w}.$$

(21)

Using Expression (21), we have determined the “reduced” radius of curvature of the trajectory of the wheel with an inclination (camber) to the road:

$$R_r=\frac{R{r}_w}{r_w\pm R}$$

(22)

where R_r is the “reduced” radius of the wheel’s trajectory in the presence of the camber angle γ, m; R is the radius of the trajectory of the wheel in the absence of a camber angle, m.

If the vehicle is equipped with paired wheels on the rear axles, then the patches of the two tires of these paired wheels are reduced to a rectangle of equal size.

It follows from the above that the wheel motion resistance along a curvilinear trajectory consists of the resistance along a straight path, which will be determined by the rolling resistance coefficient f and the resistance caused by the simultaneous twisting and lateral displacement of the disc relative to the tire patch. This additional resistance will be determined by an increase in the wheel motion resistance coefficient along a curvilinear trajectory Δf.

Given that the curvilinear motion is characterized by the twisting angle of the disc and the kinematic slip angle, which are equal in absolute value to each other, we will look for a functional relationship between an increase in the motion resistance coefficient along a curvilinear trajectory and the kinematic slip angle, taking into account the shape of the contact patch and the angular stiffness of the tire. The motion resistance coefficient along a curvilinear trajectory will be determined by the following expression:

$$f_R=f+\mathsf{\Delta }f$$

(23)

where f_R is the motion resistance coefficient along a curvilinear trajectory; f is the rolling resistance coefficient along a straight line; Δf is the increase in the motion resistance coefficient along a curvilinear trajectory.

Taking into account that the moment of the motion resistance exists along a straight line, the lateral force and the moment from twisting the body of the tire when moving along a curvilinear trajectory act in different planes; the increase in the motion resistance coefficient along a curvilinear trajectory Δf can only be determined experimentally.

3. Results

3.1. Analytical Determination of the Rolling Resistance Coefficient

To evaluate the above dependencies, calculations were made of the rolling resistance coefficient of a radial tire at the nominal air pressure in the tire on a horizontal concrete surface with a speed change from 0 to 50 m/s. The results of the calculations are given in

Table 2. Calculated values of the rolling resistance coefficient f from the vehicle speed V.

N	Formula	Vehicle Speed V, m/s						Δ at V = 50 m/s, %
		0	10	20	30	40	50
1	$f=0.0114\left(1+\frac{V}{32}\right)$	0.0114	0.0150	0.0185	0.0221	0.0257	0.0292	37.46
2	$f=0.0115\left(1+\frac{V}{31.94}\right)$	0.0115	0.0151	0.0187	0.0223	0.0259	0.0295	38.83
3	$f=0.01\left(1+\frac{V}{44.44}\right)$	0.0100	0.0123	0.0145	0.0168	0.0190	0.0213	0.00
4	$f=f_0\left(1+\frac{V^2}{1500}\right)$, at f0 = 0.01	0.0100	0.0107	0.0127	0.0160	0.0207	0.0267	25.48
5	$f=f_0\left(1+\frac{V^2}{2143}\right)$, at f0 = 0.01	0.0100	0.0105	0.0119	0.0142	0.0175	0.0217	1.95
6	$f=f_0\left(1+\frac{k_f}{f_0}{V}^2\right)$, at f0 = 0.01; kf = 7 × 10−6	0.0100	0.0107	0.0128	0.0163	0.0212	0.0275	29.40
7	$f=f_0+f_s{\left(3.6\frac{V}{100}\right)}^{2.5}$, at f0 = 0.01; fs = 0.005	0.0115	0.0151	0.0187	0.0223	0.0259	0.0295	38.83
8	$f=f_0{e}^{cV}$, at f0 = 0.01; c = 0.0199	0.0100	0.0123	0.0145	0.0168	0.0190	0.0213	0.00

. Additionally, Table 2 shows the relative error Δ% at V = 50 m/s. A comparison was made with Dependence (3).

The values of coefficient f, calculated according to the corresponding dependencies, differ from each other, as can be seen in the analysis in Table 2. At the same time, the maximum error in the calculation of the rolling resistance coefficient at a speed of 50 m/s does not exceed 49.33%.

Table 2 plots the dependence of the rolling resistance coefficient f on the speed of motion V at f₀ = 0.01 (Figure 3). Shown in Figure 3 are the dependency numbers that correspond to the number of the formula in Table 2.

The graphs differ both in the nature of the change in coefficient f and in terms of values, as can be seen in the analysis in Figure 3. According to Figure 3, Graphs 1–3, constructed according to Expressions (1)–(3), are linear dependencies. At the same time, all other graphs represent dependencies that approach parabolas.

The above studies are related to the determination of the rolling resistance coefficient at nominal load and nominal pressure. At the same time, its value is significantly affected by the air pressure in the tire.

3.2. Determination of the Rolling Resistance Coefficient Taking into Account the Air Pressure in the Tire

Empirical dependencies to determine the rolling resistance the coefficient of tires, which additionally take into account air pressure, which is important for tires with adjustable air pressure, were analyzed. According to Formulas (11) and (12), the rolling resistance coefficient was calculated, taking into account the air pressure in the tire and the speed of the vehicle. The results of the calculations are given in

Table 3. Calculated values of the rolling resistance coefficient based on Dependencies (11) and (12).

Formula	Pressure pt, MPa	Vehicle Speed V, m/s
		0	10	20	30	40	50
$f=\frac{0.0031}{p_t}+1.371954·{10}^{-9}\frac{V^{3.7}}{p_t^{2.03}}$	0.1	0.031	0.0317	0.0406	0.074	0.1557	0.316
	0.2	0.0155	0.0157	0.0178	0.026	0.046	0.085
	0.3	0.0103	0.01038	0.0113	0.0149	0.0237	0.0409
$f=\frac{0.00409}{\sqrt[3]{p_t^2}}+\frac{0.001}{\sqrt{p_t}}{\left(\frac{V}{100}\right)}^2+\frac{0.0091}{\sqrt[3]{p_t^4}}{\left(\frac{V}{100}\right)}^3$	0.1	0.019	0.0195	0.0218	0.0256	0.0366	0.0514
	0.2	0.012	0.0123	0.0135	0.0161	0.0206	0.043
	0.3	0.009	0.0092	0.01	0.0119	0.0148	0.0192

.

The calculated values differ significantly from each other, as can be seen in the analysis in Table 3. Thus, with an air pressure in the tire of 0.1 MPa and a speed close to zero, the estimated values of the coefficient f, according to Dependencies (11) and (12), are 0.031 and 0.019, respectively, and at V = 50 m/s, they acquire values of 0.316 and 0.0514.

At an air pressure of 0.3 MPa in the tire, the calculated values of the coefficient f at a speed close to zero are 0.0103 and 0.009, and at V = 50 m/s—0.0409 and 0.0192, respectively. This significant difference in the values of the coefficient f confirms that for specific tires, the real values of the rolling resistance coefficient can be determined experimentally, taking into account the importance of the influence of the values of this coefficient on the fuel economy of the car and, in general, on its operational characteristics.

To analyze the effect of motion speed and air pressure on the value of f, Figure 4 shows the graphs of the dependence of the rolling resistance coefficient f on the speed of motion at an air pressure in the tire of 0.1, 0.2, 0.3 MPa, calculated according to Expressions (11) and (12), respectively.

The analysis in Figure 4a shows that the decrease in the air pressure in the tire leads to the increase in the calculated value of coefficient f. Thus, at a speed of motion close to zero, the decrease in air pressure from 0.3 to 0.1 MPa leads to the increase in the coefficient f from 0.0103 to 0.031. Regarding the influence of speed, it does not have a significant effect on its value before reaching a speed of 15 m/s. At the same time, starting from a speed of 15 m/s, this effect is significant, especially at low air pressure.

The analysis in Figure 4b shows that the decrease in air pressure in the tire also leads to the increase in the calculated value of the coefficient f according to Expression (12). Therefore, with a change in air pressure in the tire from 0.3 to 0.1 MPa and a speed close to zero, the value of the coefficient f increases from 0.009 to 0.019. As for the influence of speed, it is insignificant up to a motion speed of 15 m/s, and with a further increase in motion speed, this influence is significant.

From the analysis of the above, it follows that a decrease in air pressure in the tire and an increase in speed always cause an increase in coefficient f. The lack of sufficient experimental data does not allow us to draw a conclusion about the possibility of using the absolute values of coefficient f.

Experimental studies on coefficient f were carried out on a two-seater passenger front-wheel drive car with a curb weight of 930 kg. The total weight of the car included two additional passengers weighing 156 kg and a metal ballast of 50 kg placed in the luggage compartment. The car was equipped with Nokian 185/60 R14 82 T M+S tires with a maximum allowable tire pressure of 0.32 MPa. During the experimental investigation, the air pressure in the tires varied discretely and was 0.1, 0.2, 0.3 MPa, and the ambient temperature was within (20–25) °C. A research was carried out on a road with an asphalt concrete surface. A force was applied to the car through a dynamometer, and its value was determined when it was moving uniformly at a speed close to zero. At the same time, the forces of rolling resistance and friction in the car’s transmission were overcome.

The rolling resistance coefficient of the car wheels was determined using the following expression:

$$f_0=\frac{P-P_{fr}}{G_v}$$

(24)

where P is the force applied to the car, N; P_fr is the resistance force in the vehicle transmission nodes, N; G_v is the weight of the car, N.

In Figure 5, experimental and calculated by Expressions (11) and (12) dependencies of the rolling resistance coefficient on the air pressure in the tire at a speed close to zero are shown.

As the air pressure in the tire decreases, the experimental and calculated values of the rolling resistance coefficient f increase, as can be seen in the analysis in Figure 5. Therefore, according to experimental data, with a decrease in tire pressure from 0.3 to 0.1 MPa, the rolling resistance coefficient increased from 0.009 to 0.015. At the same time, the values of the rolling resistance coefficient f, calculated according to Dependencies (11) and (12), differ from each other and differ from the experimental ones.

Therefore, at a tire air pressure of 0.3 MPa, the values of the rolling resistance coefficient calculated by Expressions (11) and (12) are 0.0103 and 0.009, respectively (experiment 0.009). When the air pressure in the tire is 0.1 MPa, the calculated values of the rolling resistance coefficient are 0.031 and 0.019, respectively (experiment 0.015). Such a discrepancy between calculated and experimental data regarding the effect of pressure on the value of the rolling resistance coefficient indicates that the elastic wheel is a complex mechanism with non-holonomic properties, and the determination of the rolling resistance coefficient as a result of analytical calculations is impossible.

It is obvious that the empirical dependences (11) and (12) given in references [23,24] refer to specific tires with their characteristic structural, elastic, and damping properties, which ultimately form the value of coefficient f.

From the analysis of the above, it follows that determining the coefficient of rolling resistance for a real tire, taking into account the air pressure and the speed of motion, is only possible experimentally, since the tires are structurally different. The difference lies in the presence of a metal cord in the tire shell, operational pressure changes (adjustable air pressure tires), cord type (radial and bias-play), tread features (height, saturation, summer, winter, and presence of metal spikes), presence of tube (tube and tubeless), profile height, etc. These design factors directly affect the value of the rolling resistance coefficient, and their influence can only be determined experimentally. At the same time, the analysis of references [2,16] shows that at the nominal air pressure in the tire and the nominal load at a motion speed close to zero, the rolling resistance coefficient for most tires when driving on an asphalt concrete surface is within 0.008-0.015. At the same time, lower values are typical of tires with a metal cord, and higher values are typical of tires with adjustable air pressure.

3.3. Experimental Determination of the Motion Resistance Coefficient along a Curvilinear Trajectory

The cars were used as research objects, front-wheel drive Lada Kalina (AvtoVAZ, Tolyatti, Russia), all-wheel drive Mitsubishi Outlander (NAGOYA PLANT, Okadzaki, Japan) and rear-wheel drive GAZ–330210 (GAZ, Nizhny Novgorod, Russia), which made it possible to take into account the characteristics of the transmission, the type of tires, and paired wheels.

An electronically controlled clutch was installed in the Mitsubishi Outlander transmission, which caused a significant increase in force on the dynamometer. To determine the friction in the transmission of the Mitsubishi Outlander, special studies were conducted; the wheels were suspended and torque was alternately applied to the wheels of the car with the rest of the wheels locked and unlocked. As a result of the processing of experimental data, it was established that to overcome friction in the transmission of this car, it is necessary to apply an additional force of up to 30 N to the dynamometer when moving in a straight line, and when moving along a curved path, this force increases to 115 N.

As for the friction in the other two cars, the analysis of the results of similar studies showed that it did not exceed the force necessary to overcome it on the dynamometer of 6 N and it did not depend on the curvature of the motion trajectory.

The initial and experimental data of the cars are given in

Table 4. Initial data of research objects.

Parameter	Lada Kalina	Mitsubishi Outlander	GAZ–330210
Base, mm	2470	2670	2900
Wheel track, mm:
front	1430	1540	1700
rear	1410	1540	1560
Weight on wheels, kg:
front	684	875	1062
rear	501	755	1422
Tire:
model,	Sava 175/65 R14	Goodyear Eagle 225/55 R18	Rosava 185/75 R16C
air pressure, MPa	0.2	0.23	0.3
The dimensions of the tire patches, mm
Steered wheels:
longitudinal axis, a	160	125	147
transverse axis, b	140	170	128
Non-steered wheels:			paired
longitudinal axis, a	120	124	106 (ex) 115 (in)
transverse axis, b	125	160	121 (ex) 129 (in)
The force of friction in the transmission, N	3–5	30–115	4–6
The rolling resistance coefficient f	0.0081	0.0092	0.0094

.

During experimental research, force P_R was applied to cars through a dynamometer, and its value was determined when it was moving uniformly at parking speed. Figure 6 shows a schematic representation of the determination of the traction force P_R.

The trajectory of the car was determined by the turning angles of the steered wheels. At the same time, the radius of the car’s trajectory was determined by the track of the outer steered wheel. The turning angles and camber angles of the steered wheels were determined for each radius of the motion trajectory.

First, the effort was determined when the car was moving in a straight line. At the same time, the forces of rolling resistance and friction in the car’s transmission were overcome. During rectilinear motion, the coefficient of the rolling resistance of the car wheels was determined according to Expression (24) according to the data of the experimental studies. The forces applied to the dynamometer during the straight-line motion are as follows: Lada Kalina car—100 N; Mitsubishi Outlander—180 N; GAZ–330210—240 N. The friction forces in the transmission during straight-line motions were as follows: Lada Kalina—4 N; Mitsubishi Outlander—30 N; GAZ–330210—6 N. The rolling resistance coefficients determined by Expression (24) were as follows: Lada Kalina—0.0081; Mitsubishi Outlander—0.0092; GAZ–330210—0.0094.

Taking into account the load, the total length of the contact patches of the tires brought to the center of mass was determined using the expression

$$\sum a=a_{si}\frac{G_{si}}{G_v}+a_{se}\frac{G_{se}}{G_v}+a_{ni}\frac{G_{ni}}{G_v}+a_{ne}\frac{G_{ne}}{G_v}$$

(25)

where Σa is the total length of the contact patches of the tires brought to the center of mass; a_si, a_se, a_ni, a_ne are the lengths of contact patches of wheel tires, steered internal and external, non−steered internal and external, respectively, which were determined experimentally; G_si, G_se, G_ni, G_ne are the load on the wheels of steered internal and external, non-steered internal and external, respectively.

The radius of the trajectory of the center of mass of the car is determined using the expression

$$R_c=\sqrt{\left[{\left(\sqrt{R^2-L^2}-\frac{B}{2}\right)}^2+{\left(L\frac{G_r}{G_v}\right)}^2\right]}$$

(26)

where R_c is the radius of the trajectory of the center of mass of the car, m; R is the radius of the trajectory of the external steered wheel, which is determined experimentally, m; L is the base of the vehicle, m; B is the track of steered wheels; G_v is car weight, N; G_r is the weight on the rear axle.

The increase in force on the dynamometer in relation to the straight-line motion of the car is determined as follows:

$$\mathsf{\Delta }{P}_R=P_R-P_f-P_{fr}$$

(27)

where ΔP_R is the increase in force on the dynamometer when moving along a curved path, N; P_R is the force on the dynamometer when moving along a curved trajectory, N; P_f is the force of rolling resistance, N; P_fr is the force of friction resistance in the transmission, N.

The increase in the resistance coefficient when moving along a curved trajectory is determined by the following expression:

$$\mathsf{\Delta }{f}_{exp}=\frac{{\mathsf{\Delta }P}_R}{G_v}.$$

(28)

The results of the experimental studies are given in

Table 5. Results of the experimental studies for Lada Kalina G_v = 11,850 N.

Parameter	Radius, m
	5.1	6.1	9.0	12.0
PR, N	190–200	145–150	120–122	110–112
ΔPR, N	90–100	50–55	20–22	10–12
Δfexp = ΔPR/Gv	0.00759–0.00844	0.00422–0.00464	0.00168–0.00186	0.00084–0.001
Σa, m	0.143	0.143	0.143	0.143
Rc, m	3.892	4.977	8.009	11.078
Σa/Rc	0.0367	0.0288	0.0179	0.0129
$\mathsf{\Delta }f=\frac{102.6}{p}{\left(\frac{\sum a}{R_c}\right)}^2$ at p = 17.5	0.0081	0.00486	0.00187	0.000975

,

Table 6. Results of the experimental studies for Mitsubishi Outlander G_v = 16,300 N.

Parameter	Radius, m
	5.25	6.25	10.02	14.88	33.29
PR, N	390–400	320–330	290–295	275–280	212–213
ΔPR, N	130–140	60–70	20–25	5–10	2–3
Δfexp = ΔPR/Gv	0.00797–0.0085	0.00368–0.0043	0.0012–0.0015	0.0003–0.0006	0.00012–0.00018
Σa, m	0.124	0.124	0.124	0.124	0.124
Rc, m	3.9	5.024	8.967	13.92	32.65
Σa/Rc	0.0318	0.0247	0.0138	0.0089	0.0038
$\mathsf{\Delta }f=\frac{102.6}{p}{\left(\frac{\sum a}{R_c}\right)}^2$ at p = 13	0.00797	0.00482	0.00149	0.000624	0.00011

and

Table 7. Results of the experimental studies for GAZ−330210 G_v = 24,860 N.

Parameter	Radius, m
	5.355	5.815	8.03	15.1
PR, N	380–400	330–350	280–290	250–260
ΔPR, N	140–160	90–110	40–50	10–20
Δfexp = ΔPR/Gv	0.00563–0.00643	0.0036–0.0044	0.0016–0.00201	0.0004–0.0008
Σa, m	0.129	0.129	0.129	0.129
Rc, m	4.011	4.506	6.84	14.067
Σa/Rc	0.0322	0.0286	0.0189	0.00917
$\mathsf{\Delta }f=\frac{102.6}{p}{\left(\frac{\sum a}{R_c}\right)}^2$ at p = 17.5	0.00608	0.00479	0.00209	0.00049

.

In accordance with the results of the experimental studies, Figure 7 presents graphs of the increase in the motion resistance coefficient depending on Σa/R_c.

The analysis of the obtained experimental data given in Table 5, Table 6 and Table 7 and Figure 7 testifies that the increase in the motion resistance coefficient along a curvilinear trajectory is proportional to the kinematic slip angle. At the same time, the characteristics of the curves are approximated by a parabolic dependence with sufficient accuracy for practice

$$\mathsf{\Delta }f=\frac{102.6}{p}{\left(\frac{\sum a}{R_c}\right)}^2$$

(29)

where Δf is the calculated value of the increase in the motion resistance coefficient along a curvilinear trajectory; p is the parabola parameter, which is determined experimentally and takes into account the stiffness of the tire relative to the vertical axis of the ratio between the axes of the contact patches. For the considered tires, the parabola parameter is within 13–17.5.

At the same time, the analysis of the experimental data conducted on a Mitsubishi Lancer car with Nokian WR 205/60 R16 tires, in which the transverse axis of the contact patches is 1.5 times greater than the longitudinal one, showed that the parabola parameter decreased to 12. Therefore, an increase in the transverse axis of the tire contact patches in relation to the longitudinal leads to a decrease in the parabola parameter.

The results of the calculations of Δf according to Dependence (29) are given in Table 5, Table 6 and Table 7.

Figure 8 shows the graphs of the experimental and calculated dependencies of the increase in the motion resistance coefficient on the kinematic slip angle for the Lada Kalina car.

The analysis in Figure 8 and Table 5 shows the co-occurrence of the experiment with the calculation, and the error does not exceed 7%. At the same time, when moving along a curvilinear trajectory with a minimum radius of curvature, the motion resistance for two-axle cars increases by 1.68−2.04 times in relation to the straight-line motion. Empirical Dependence (29) was obtained to determine the increase in the motion resistance coefficient along a curved trajectory, which is a function of the kinematic slip angle and changes according to the parabolic law. At the same time, the parabola parameter takes into account the stiffness of the tire relative to the vertical axis and the ratio between the transverse and longitudinal axes of the tire contact patch. An increase in this ratio leads to a decrease in the parabola parameter.

Thus, the motion resistance coefficient of a two-axle car along a curvilinear trajectory takes into account the rolling resistance coefficient and the increase in the motion of the resistance coefficient caused by the lateral displacement and twisting of the disc relative to the contact patch, and it is expressed by the following dependence:

$$f_R=f+\frac{102.6}{p}{\left(\frac{\sum a}{R_c}\right)}^2$$

(30)

For the considered tires, this parameter is in the range of 12−17.5 and requires the coordination for other types of tires.

4. Discussion

Motion resistance is a significant factor that affects the fuel economy of vehicles. Total motion resistance along a curvilinear trajectory consists of the resistance along a straight path, which is determined by the rolling resistance coefficient, and an additional resistance caused by the simultaneous twisting and lateral displacement of the disc relative to the tire patch. The determining characteristics that form the value of the coefficient of rolling resistance when moving in a straight line on an asphalt concrete surface are the design features of tires, which include: the presence of a metal cord in the tire shell, the number of layers of the cord and its material, the type of tread (summer, winter, and presence of metal spikes), the height and saturation of the tread pattern, the construction of the cord (diagonal and radial), the presence of tubes, the area and shape of the tire’s contact patch, etc.

According to Empirical Dependences (1)–(3), the influence of speed on the coefficient of rolling resistance is determined by a linear law. These dependencies do not take into account the experimental value of the rolling resistance coefficient at low speed. The given empirical dependences for determining the rolling resistance coefficients (7), (8), (11), and (12) contain their experimental values at a movement speed close to zero, and the influence of movement speed is described by a parabolic law.

It was established that smaller values of the rolling resistance coefficient are typical of tubeless tires with a metal cord shell, and larger values are typical of tires with adjustable air pressure.

As research shows, the resistance in curvilinear motion mainly depends on the vehicle layout and the characteristics of the installed tires. The characteristics of tires differ in the elastic properties, shape, and size of tire contact patches. The experimental study was carried out using such vehicles as example: two front-wheel drive vehicles, rear-wheel drive vehicle with dual wheels on the rear axle, and a four-wheel drive vehicle. The following types of tires were installed in the mentioned vehicles: Nokian WR 205/60 R16 tires (NOKIAN TIRES, Vsevolzhsk, Russia), with the dimensions of the contact patches of the front wheels being a = 0.109 m, b = 0.151 m, and the dimensions of the rear wheels being a = 0.102 m, b = 0.150 m; Sava 175/65 R14 tires (T.C. DEBICA S.A., Debica, Poland), with the dimensions of the contact patches of front wheels being a = 0.16 m, b = 0.14 m, and the dimensions of the rear wheels being a = 0.122 m, b = 0.125 m; Goodyear Eagle 225/55 R18 tires (SUMITOMO RUBBER INDUSTRIES, LTD, Toyota, Japan), with the dimensions of the contact patches of the front wheels being a = 0.125 m, b = 0.17 m, and the dimensions of the rear wheels being a = 0.124 m, b = 0.16 m. The vehicle with dual wheels on the rear axle was equipped with Rosava 185/75 R16C tires (ROSAVA, Bila Tserkva, Ukraine), with the dimensions of the contact patches of the front wheels being a = 0.147 m, b = 0.128 m. For the paired rear wheels, the internal dimensions were as follows: a = 0.115 m, b = 0.129 m. The external dimensions were as follows: a = 0.106 m, b = 0.121 m. Thus, the selected vehicles, as research objects, take into account typical two-axle vehicle layouts and different types of tires.

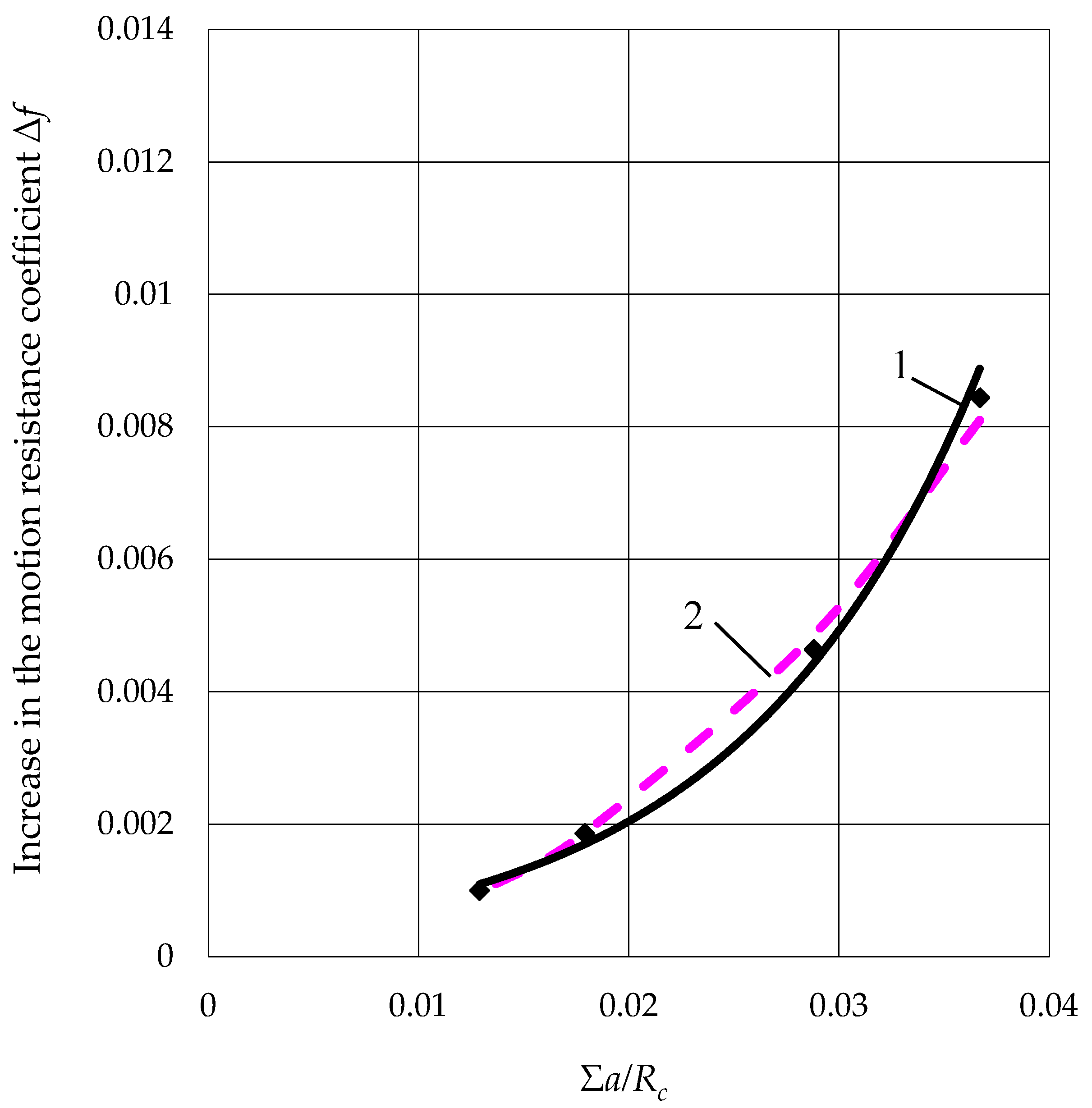
During the motion of the wheel along a curved path, there is simultaneous twisting and lateral displacement of the disc relative to the tire patch, which cause a twisting moment and a lateral force. These dynamic factors lie in planes perpendicular to the rolling plane of the wheel and cause additional resistance to the motion of the wheel, which is characterized by the increase in the motion resistance coefficient. An empirical dependence was obtained for its determination, whose value is directly proportional to the dimensions of the tire contact patch, the angular stiffness of the tire, and is inversely proportional to the radius of curvature of the trajectory. At the same time, this coefficient is a function of the kinematic slip angle and changes according to the parabolic law, and the parabola parameter takes into account the stiffness and the shape of the tire’s contact patch. Its value is affected by the ratio between the transverse and longitudinal axes of the tire contact patch. An increase in this ratio causes a decrease in the parabola parameter. The obtained experimental values of the parabola parameter for the considered tires are within 12–17.5.

It has been established that for two-axle wheeled vehicles with sufficient accuracy for practice, it is recommended to determine the increase in the motion resistance coefficient based on the trajectory of the wheel brought to the center of mass of the wheeled vehicle. When moving along a curvilinear trajectory with a minimum radius, the motion resistance coefficient increases by 1.68–2.04 times in relation to the straight-line motion.

Further research will be directed towards the study of three-axle vehicles with a tandem axle group, which leads to a significant increase in the motion resistance along a curved trajectory. The results of these studies on the total resistance of curvilinear movement will be useful for specialists in the field of improving the energy efficiency of vehicles.