Abstract
As a temporary means of water transportation, floating bridges play an important role in the military and other fields. However, traditional floating bridges have limitations such as large size, heavy weight, and slow construction time. In this paper, we propose a rigid-flexible composite folding floating bridge. The main structure of the floating bridge consists of three layers: the bridge deck, airbag, and water bag. The floating bridge units are connected by flexible connectors to allow for pre-connection and folding of the bridge, reducing storage and transportation space, and improving construction efficiency. The proposed floating bridge also has a complete engineering application design and has been checked for safety and reliability (including the strength, buoyancy, and bearing capacity of the connections). We used AQWA software to simulate and analyze the anchorage scheme of the floating bridge and its response to wave loads and conducted a ballast test on a floating bridge model to verify its feasibility as a main bearing body. The results show that the floating bridge we designed has the advantages of being lightweight, having fewer consumables, having a small storage and transportation space, and being able to be constructed quickly.
1. Introduction
As a common transportation facility for crossing rivers, floating bridges are widely used in both military and civilian fields due to their low construction cost, ease of use, and convenient storage. In military logistics, they play a crucial role in ensuring the effective delivery of materials, soldiers, and baggage from the front of combat forces, and are of great strategic significance for crossing deep rivers, landing on shores, and passing through land gullies [1]. Traditional floating bridges are categorized based on their structural forms, which can be broadly divided into three types: split floating bridges, belt floating bridges, and self-propelled floating bridges.
The split floating bridge relies on the lower leg boat to provide buoyancy for the bridge body, and the upper part is generally laid with a steel truss bridge deck for carrying traffic (e.g., the floating bridge can arrange ships horizontally or longitudinally equidistantly). The belt floating bridge integrates the whole pontoon by continuous immersion. Compared with the separated pontoon equipment, the structure is simpler, and the erection and withdrawal speeds are faster. Additionally, fewer operators and less additional equipment for pontoon transportation are required. The clearance is greatly reduced, which makes the traffic of the belt pontoon more stable; the corresponding traffic speed is also greatly improved. The self-propelled floating bridge is pontoon equipment that integrates the chassis, floating body, and bridge deck structure. It can achieve land and water mobility without other equipment (e.g., the self-propelled pontoon jointly developed by Britain and Germany has a maximum bearing capacity of tons of military load). However, this kind of floating bridge has a complex structure, high cost, and is difficult to maintain, making it challenging to use widely.
Compared with the research on existing floating bridges, it is found that military floating bridges play an irreplaceable role in the military field. Among them, the technology development trend is mobile concealment, fast and stable, and will develop in the direction of motorization, being lightweight, modularization, informatization, and systematization. However, its modular and multi-functional development is not mature, which limits its range of use and application scenarios. In addition, civil floating bridges have shown great vitality in economically developed, densely populated areas, areas with numerous rivers and lakes, and coastal areas. Their technical development is especially focused on high traffic capacity and strong bearing capacity, and they will develop in the direction of large-scale production, standardization, and high weight bearing strength. Under these circumstances, the floating bridge needs to adapt to the different water environments and meteorological conditions, including seas, lakes, rivers, and various water conditions and be safely and stably usable. However, the traditional pontoon module is generally a concrete or steel structure, characterized by large volume, heavy weight, complex box movement, large storage space, and high storage cost. Moreover, the assembly of the traditional floating bridge is not flexible, often reducing the efficiency of construction on water due to the limitations of the floating bridge itself.
To overcome these major issues, many scholars have conducted in-depth research. Zhou et al. [2] proposed a highly maneuverable ocean-intelligent floating bridge system to address the problems of large volume, heavy weight, difficult transportation, insufficient maneuverability, and low intelligence level in traditional floating bridges. The floating bridge uses modular technology and a lightweight floating body main structure, consisting of an inflatable airbag, steel frame, and upper and lower plates. However, further performance improvements are needed for rapid construction. Lee et al. [3] proposed a solution based on a control system design and automatic installation to address the problem of difficult installation of floating bridges under combat or natural disaster conditions. The automatic control system is connected to the power system of the floating unit to achieve control and positioning. The use of an automatic control system can improve assembly speed. Liu et al. [4] proposed a refitted floating container structure for emergency floating bridge assembly to ensure traffic safety in the event of a river collapse. Through finite element simulation analysis and optimization, the load requirements of the improved floating container structure were demonstrated. However, there are still deficiencies in rapid construction and space utilization. Minoretti et al. [5] proposed a submerged floating tube bridge (SFTB) that is underwater in a designated location, which optimizes the use of the water surface to a certain extent. However, it is obviously not suitable for emergencies. Moan et al. [6] proposed three design concepts for floating bridges, including curved, end-anchored floating bridges; straight, side-anchored floating bridges with mooring systems; and floating suspension bridges with pylons supported by TLP or spar floating bodies. They also proposed submerged tunnel-type concepts, to provide a research basis for future floating bridge designs. They addressed the problems of transportation efficiency, land use, and construction difficulty.
To address the aforementioned issues, this paper explores and designs a foldable floating bridge based on a combination of rigidity and flexibility. It features lightweight construction, low material consumption, convenient assembly, safe and stable operation, and ease of transportation. The foldable pontoon employs a composite folding structure that consists primarily of a bridge deck, airbag, and water bag. The structure of the pontoon capsule belongs to the category of membrane structures, which have long been in use in the fields of architecture and aerospace. This structure utilizes internal pressure to provide the mechanical properties of the overall structure.
Our main contributions are as follows:
- We have designed a rigid-flexible combination folding structure, which ingeniously combines the advantages of the two materials, greatly improving the load capacity and trafficability compared with the current rigid-flexible composite floating bridge;
- We have improved the design of the flexible connector, allowing for pre-connection and folding. This approach enables storage and transportation space savings and rapid erection;
- We have adopted a reliable and stable structural design, which can be used in various scenarios (e.g., military shoal landing, emergency rescue, and disaster relief);
- We have conducted a series of calculations and analyses to evaluate the safety and reliability of the floating bridge (e.g., buoyancy calculation, strength check of the connections, and bearing capacity calculation). Additionally, we have used AQWA software to calculate and verify the anchoring scheme of the floating bridge and its motion response under wave loads. Finally, we used a physical model to conduct a ballast test to confirm the feasibility of the inflatable capsule as the primary bearing structure of the floating bridge.
The remaining chapters of this paper are structured as follows: Section 2 introduces the overall structural design of the rigid-flexible folding floating bridge; Section 3 presents the calculations for the floating bridge’s buoyancy, strength at connection points, and bearing capacity; Section 4 utilizes simulation analysis to study the floating bridge’s motion response and anchoring system check; Section 5 uses a physical model to conduct ballast tests to verify the feasibility of the inflatable capsule as the primary bearing structure of the floating bridge. In Section 6, we discuss and summarize the research content of this paper and outline future research plans to address the limitations of our study.
2. The Structural Design
2.1. The Overall Structural Design of the Rigid-Flexible Folding Floating Bridge
The main body of the new rigid-flexible composite folding floating bridge proposed in this paper is a three-layer structure consisting of a bridge deck, airbag, and water bag. The scheme adopts a longitudinal distribution of airbags and a staggered arrangement of the bridge deck and middle protruding airbags. The bridge deck at the upper part of the pontoon unit is integrally formed by aluminum alloy stamping, which provides good mechanical properties and anti-skid properties. Meanwhile, the cylindrical fixed shaft set at the side of the bridge deck is connected by flexible connectors, enabling the pre-connection and folding of the pontoon. The airbag under the bridge deck is the main bearing body that reduces the weight of the pontoon. Four bottom water sacs, connected with the upper high-pressure airbag, are longitudinally arranged under the airbag. The outer parts of the airbag and water bag are wrapped by a woven outer net, which acts as a fixed support. The overall structure design of the rigid-flexible folding floating bridge is shown in Figure 1.
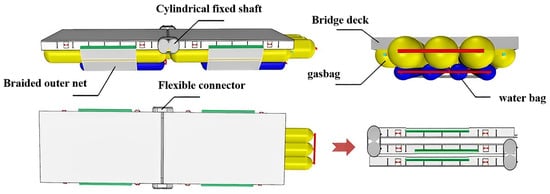
Figure 1.
The overall structural design of the rigid-flexible folding floating bridge.
2.2. Structure Design of Airbag and Water Bag
The capsule is made of seven layers of laminated composite materials, including an anti-aging layer, adhesive layer, air barrier layer, adhesive layer, woven load-bearing layer, and adhesive layer. The material has strong tensile resistance, which makes the capsule hard to tear under the action of large surface tension. The main airbag is composed of five sub-airbag bodies. The middle three airbags are staggered with the bridge deck and share the inflation pipe to improve inflation efficiency. The remaining airbag ends are equipped with control valves, and local reinforcement is carried out around the valves. The longitudinally staggered water bladder at the bottom of the main bladder can reduce the center of gravity of the pontoon, ensure its stability, and increase overall reliability. The water bag shares the water injection pipeline to improve water injection efficiency. The surface of each airbag and water bag is covered by a woven net made of nylon flat belts, which limits their relative displacement and ensures the orderly deployment of each structure during the application of the floating bridge. The overall structure of the airbag is shown in Figure 2.
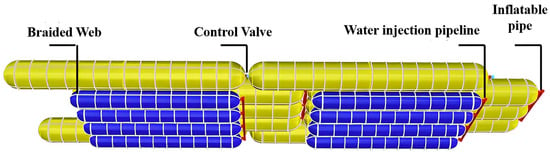
Figure 2.
The overall structure of the airbag.
2.3. Structural Design of the Connection
The vertical connection [7] of the floating bridge is shown in Figure 3. The middle-stiffened air cushion needs to be inflated during use. When the air cushion is inflated, the folding rods on both sides of the bridge deck are supported and remain vertical. During the straightening process of the rotatable folding bar, the folding bar slider squeezes the slide track movable bullet, pressing it down, and the slider continues to move. When the rotatable folding bar is fully straightened, the movable bullet pops up to constrain the folding bar, supporting the upper and lower frames, so that the folding bar does not fold when the buoyancy tank is loaded.
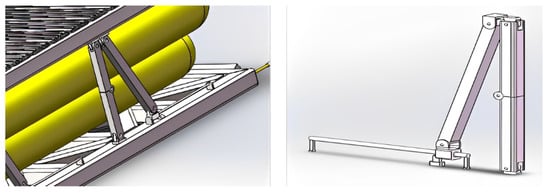
Figure 3.
The vertical connection of the floating bridge.
The floating bridge unit in this paper is connected to the upper bridge deck by flexible connectors, which are longitudinal connections, as shown in Figure 4. The flexible connector consists of an inner high-strength flexible connection belt and an outer steel ring [8]. The inner high-strength connection belt is woven with high-tensile wire. This material is a high-strength polyethylene fiber with a low friction coefficient and strong corrosion resistance. It can reduce the deformation of the outer steel ring and the cylinder fixed shaft by using its elastic deformation when squeezed. The outer steel ring makes the connection between the two pontoon units more reliable. Lifting lugs are set at the eccentric part of the column to facilitate lifting construction. The steel chain between the lifting lugs can limit the relative rotation between the two pontoon units after the pontoon is deployed. The inner high-strength flexible connecting belt and the outer steel ring have less friction resistance when rotating relative to the fixed axis of the cylinder. Therefore, the folding of the floating bridge can be achieved through the relative rotation of the cylinder, saving the storage and transportation space of the floating bridge. The flexible connector can achieve the pre-connection of the floating bridge on land, eliminating the steps of connecting the floating bridge unit in the water and improving the efficiency of the floating bridge assembly operation. The damping effect of the flexible elastomer material is used to effectively reduce the impact of the wave load, avoid obvious depression when the floating bridge is under pressure, and enhance the overall reliability of the floating bridge. Therefore, it has strong resistance to the shear stress and torque generated by waves on the floating bridge [9].
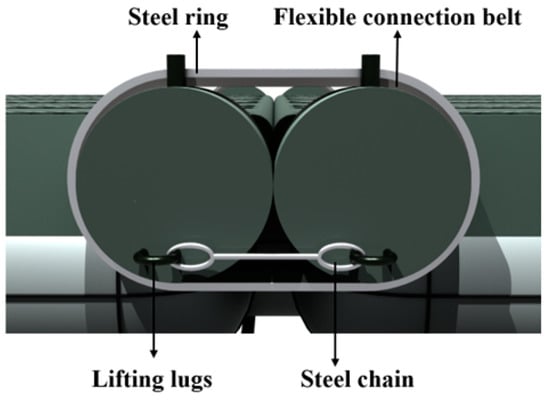
Figure 4.
Longitudinal connection of the floating bridge.
2.4. Bridge Deck Design
The upper surface of the bridge deck: The bridge deck is formed by stamping aluminum alloy. The section is a cavity structure that reduces weight while ensuring mechanical properties. The unit cross-section is strengthened to improve the bearing capacity of the bridge deck [10]. A small hole is located on the bridge deck, which can drain water promptly after a wave on the bridge deck to ensure the buoyancy of the floating bridge [11]. In addition, an anti-skid coating is sprayed on the upper surface of the bridge deck, an anti-skid welding rod is added, and the rubber strip inlay groove is stamped on both sides of the anti-skid welding rod using stamping technology [12]. A rubber strip with high wear resistance of the corresponding size is then inlaid in the groove. The connection between the bridge deck and the rubber strip uses the joint fixation method of adhesive bonding and bolt bolting to achieve a better anti-slip effect [13]. The unit of the upper surface of the bridge deck is shown in Figure 5, which is located on top of the topmost steel frame structure of the model in Figure 4.
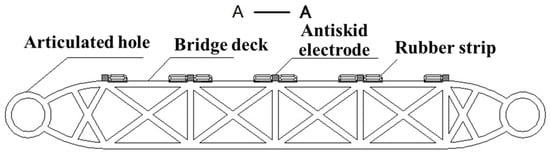
Figure 5.
The unit of the upper surface of the bridge deck.
Internal surface of bridge deck: The interior of the bridge deck adopts a transverse skeleton structure, which saves material consumption and ensures sufficient strength. Its internal contour fits the airbag surface, which gives the airbag better contact and fit with the bridge panel [14]. At the same time, the contact surface is coated with a surface coating, which can reduce the abrasion of the bridge panel against the airbag and extend the service life of the airbag. A built-in partition plays a limiting role in the airbag to prevent the airbag from longitudinal displacement [15]. An anchor ring is set at the side of the bridge deck to connect the anchor chain with the pontoon [16]. After the airbag water bag is retracted, it can be placed in the skeleton of the bridge deck to reduce the wear and accidental damage of the pontoon during transportation and storage, and reduce the unit storage space [17,18]. The internal structure of the bridge deck is shown in Figure 6.
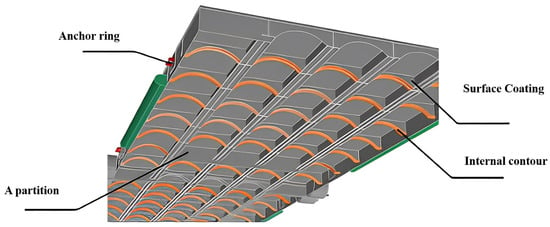
Figure 6.
The internal structure of the bridge deck.
2.5. Implementation Plan
Floating bridge deployment: The deployment process of the floating bridge is shown in Figure 7. When erecting, the air compressor should be used to inflate and form the airbags at both ends of the first pontoon unit [19]. After inflation, the pontoon unit will have a certain buoyancy, and then it can be overturned and lifted to the water surface with lifting equipment. The following steps would be: Repeat the above process, overturn and lift the second pontoon unit to the water surface in the same way, use the tugboat to pull the first pontoon unit, and inflate the three airbags in the middle to provide greater buoyancy. Repeat the above process until the entire pontoon is spread on the water’s surface. Open the valve of the bottom water bag to inject water into the bottom water bag, reduce the center of gravity of the pontoon to improve its stability, and close the valve after the water bag is filled to complete the deployment of the pontoon. After the pontoon is deployed, the anchor chain should be connected to the anchor rings on both sides of the pontoon, and the gravity anchor should be anchored by tugboats [20]. At the same time, the lifting lugs between two adjacent pontoon units should be connected with steel chains to prevent the relative rotation of the pontoon units.

Figure 7.
The deployment process of the floating bridge.
Floating bridge withdrawal: During the withdrawal of the pontoon, the anchor chain should be withdrawn first, and the pontoon should be moved to the shore by a tugboat. All the flexible connectors should be removed, the pontoon unit should be separated, and the water bag should be drained by the water pump. The middle three airbags should be deflated to retain a certain buoyancy; then they should be lifted to the shore by lifting equipment. The airbags at both ends of the pontoon unit should be deflated, and the airbag water bag should be retracted to the bridge deck. The same operation should be performed on all pontoon units, and the pontoon should be lifted to the shore and folded for recycling.
3. Ballast Numerical Calculation
In this paper, the calculation of buoyancy, strength check of the connection of the floating bridge, and calculation of the bearing capacity of the floating bridge are carried out [21].
3.1. Floating Calculation
From a statics standpoint, the floating bridge experiences draft and bending under the load [22,23]. Since the bending deformation of the bridge span is typically negligible compared to the draft, the pontoon can be treated as a rigid body with a rigid load-bearing structure [24,25]. As an example, we will calculate the buoyancy required for a Type 15 light tank, with parameters as shown in Table 1.

Table 1.
Parameters of Type 15 Light Tank.
According to the buoyancy requirements of the floating bridge, the draft of the floating bridge is given by the equation:
where is the total weight of the bridge span and load, is the weight of the pontoon, and is the weight of the load. The symbol denotes the allowable draft of the floating bridge.
For the rigid and flexible combined floating bridge: , but the freeboard shall not be less than 10 cm. Draft due to dead load :
Live load without draft caused by eccentricity:
where is the volume of water, and is the calculated waterplane area of the floating bridge.
In this paper, the new rigid-flexible composite folding pontoon is 10 m long, 5 m wide, and 1.334 m high, with a diameter of 1m. Each pontoon unit is horizontally arranged with five airbags, and the dead weight of the bridge span is gf = 0.1 t/m. To ensure safe distance on the bridge deck, there is at most one tank on each of the two pontoon units. To simplify the draft calculation, the circular section of the airbag is approximated by a square, which is a safety simplification.
After calculation, , . It can be seen that < and the freeboard height is greater than 0.1 m, so the pontoon can carry a 36 t Type 15 light tank.
The above calculation is conservative and safe, so the design parameters of the pontoon are shown in Table 2.

Table 2.
Design parameters of the floating bridge.
3.2. Strength Check of the Floating Bridge Connection
The floating bridge adopts the structure of a flexible connector to connect adjacent units. The main body of the flexible connector is a high-strength polyethylene fiber connection belt. The strength check of the connection of adjacent units is the strength check of the connection belt. As the load moves towards the joint on the bridge deck, longitudinal displacement will occur at this point under the action of the load, resulting in a huge tensile stress on the connecting belt. When the load moves directly above the joint, the longitudinal displacement of the joint will reach the maximum, and the tensile stress of the connecting belt will also reach the maximum. To ensure the safety of the structure, the connecting belt must still have sufficient tensile strength under this working condition.
3.2.1. Establishment of the Abstract Model
The floating bridge adopts the structure of an “airbag and bridge deck”. The airbag provides buoyancy to support the bridge deck. When the load moves to point B between the two units, point B will experience a downward displacement, while the displacement at points A and C is quite small and can be almost ignored. The abstract model is shown in Figure 8. Considering its action mechanism, we take two adjacent elements as the research object and abstract it as an elastic foundation beam with fixed hinge supports at both ends and elastic hinge support at the connection. The flexibility coefficient of the elastic hinge support is the same as that of the elastic foundation. At the same time, the load, a “Type 15 light tank”, is abstracted as a distributed load acting symmetrically on the joint.
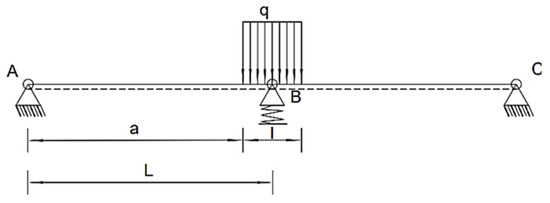
Figure 8.
Abstract model of the floating bridge.
3.2.2. Determination of Stiffness Coefficient k and Distributed Load q of Elastic Foundation
We equate the airbag to a cuboid with a square section and the same cross-sectional area and length as the airbag. The side length of the square, d, can be calculated as:
where is the radius of the airbag.
The stiffness coefficient, , of the elastic foundation beam (buoyancy increased by unit length and unit depth of airbag sinking) can be calculated as:
where is the density of water, is the acceleration due to gravity, and is the side length of the square.
The distributed load, , can be calculated as:
3.2.3. Deflection at Point B
According to the deflection curve equation of the elastic foundation beam:
where:
The final calculated deflection as: .
3.2.4. Internal Force Model of the Connecting Ring
Since the bridge deck itself hardly undergoes tensile deformation, while the connecting ring undergoes tensile deformation, here we simplify the whole structure as a rod structure. Taking the connecting ring as the research object:
According to the static balance principle, the internal force of the connecting ring is obtained:
The tensile stress of connecting ring:
The high-strength connecting belt on the inner layer of the flexible connector is woven with high-tensile wire. The material used is a high-strength polyethylene fiber, which has the following performance characteristics: (i) twice the strength of carbon fiber, which is one of the three strongest fibers in the world, (ii) a smooth surface, low friction coefficient, and not prone to fuzz, and (iii) strong corrosion resistance, good radiation resistance, and stable under ultraviolet radiation.
Considering various factors such as elongation at break and ultimate settlement, the allowable stress of the material can be obtained through conservative calculation, where the safety factor is 5:
The tensile stress at the connection is less than the allowable stress of the material, indicating that the structure is safe.
3.3. Formatting of Mathematical Components
3.3.1. Establishment of a Simplified Model
Because the midstream part of the continuous beam system pontoon is a continuous superstructure supported by a series of pontoon airbags, it should be viewed as a continuous beam supported by elastic supports (double elastic support) from the standpoint of structural mechanics. It is a statically indeterminate structure with a high degree of redundancy, requiring the solution of simultaneous equations with many unknowns during calculation. For the continuous beam system floating bridge with the same pontoon airbag and equidistant configuration, when the rigidity of the upper bridge span structure is large and the airbag configuration is dense, it can be simplified as an elastic foundation beam (referred to as an elastic foundation beam). In other words, the bridge is supported by a continuous elastic foundation.
3.3.2. Calculation of Pontoon Parameters
Generally, the floating bridge is long, and its middle part can be regarded as an elastic foundation beam with infinite length at both ends while ignoring its boundary effect. The load of the floating bridge mainly comes from its gravity. The length of the floating vehicle is far less than the length of the floating bridge. At this time, the load can be simplified as a concentrated load. The problem can be simplified as follows: a concentrated load P is applied at the center of an infinite beam, and the point of action of the P force is taken as the origin. Since both sides are infinite and symmetrical, only the right half needs to be studied.
According to Equation (14) and the boundary conditions of the right half beam, four integral constants are solved:
The boundary conditions are:
- When x approaches infinity, the displacement and bending moment of the beam are zero. The bending moment equation of the beam is:
- At x = 0, due to the left-right symmetry, θ = 0, Q = P/2. The rotation equation of the beam is:
The shear equation of the beam is:
The deflection formula for the floating bridge is:
Considering that the airbag will wrinkle under the load, and that the material and working pressure conditions selected for this pontoon, the final calculated axial, and circumferential strains are (See Appendix A for the specific verification process):
The axial strain is less than 15%, and the circumferential strain is slightly more than 15%, but both are less than the tensile elongation at the material’s break. To sum up, the main technical parameters and indicators of the pontoon are shown in Table 3.

Table 3.
Main technical parameters and indicators of the floating bridge.
4. Simulation Analysis of Motion Response and Mooring
Motion Response and Mooring Check
As a floating structure, the floating bridge is required to have good stability in traffic and generally has to perform normally under Class III and IV sea conditions. Therefore, when checking the performance of the floating bridge, it is necessary to not only check whether the bearing capacity meets the requirements, but also to focus on the anchoring scheme of the floating bridge and the motion response under the wave load [26]. The general hydrodynamic software AQWA [27,28] is used to establish the model of the floating bridge anchorage coupling system under the action of three or four sea states, and the coupling dynamic response of the system in the time domain is obtained. The floating bridge motion response and dynamic tension change of the anchor chain under the action of transverse and longitudinal waves are emphatically analyzed [29,30,31,32,33].
For the sake of safety, this paper selects only one pontoon element for finite element numerical simulation [34], ignoring the motion constraints of adjacent pontoon elements. Because the structure of the floating bridge designed in this paper is too complex, to reduce the amount of data processing during finite element simulation, the floating bridge unit is simplified into a shell with a length of 30 m, a width of 8 m, and a height of 3 m. The center of gravity is defined as X: 4 m, Y: 15 m, and Z: 1.3 m.
The anchoring form adopts four cable-stayed anchors perpendicular to the length direction of the pontoon. The included angle between the anchor chain and the water bottom is 30°. The spacing between the anchor points on the same side is 15 m, 7.5 m from the end of the pontoon unit, the draft of the pontoon is 1m, and the water depth is 15 m. The anchoring form is shown in Figure 9.
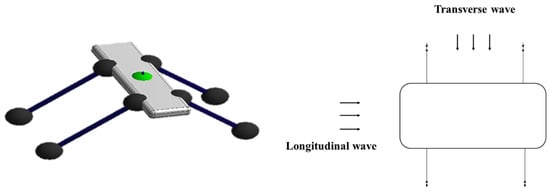
Figure 9.
Floating bridge unit anchorage and wave position.
To simulate the motion response of the floating bridge and the dynamic change of the anchor chain tension under the third and fourth sea conditions [35], the wave parameters entered in the AQWA software calculation are the wave height H = 1.25 m, the initial period T = 5 s, and the end period T = 2 s. The wave direction is used to simulate the two working conditions of the floating bridge unit-transverse wave and longitudinal wave, as shown in Figure 9.
The dynamic response of the floating bridge under wave action is shown in Figure 10. When the pontoon unit is facing transverse waves, the roll angle fluctuates within a range of plus or minus 15°. When the pontoon unit is facing longitudinal waves, the pitch angle fluctuates within a range of plus or minus 2°. Compared to the size of the floating bridge, the amplitude of motion is very small, which does not affect the stability of the floating bridge.
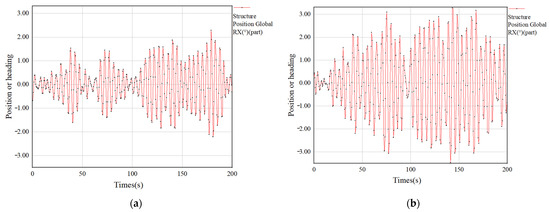
Figure 10.
Dynamic response of buoy movement. (a) Transverse wave buoy, (b) Longitudinal wave buoy.
Under wave action, the mooring force of each of the four anchor chains and the dynamic change rule of the mooring forces of the floating bridge are not consistent. Under the wave parameters set above [36], the dynamic change of the mooring forces of each anchor chain is shown in Figure 11.

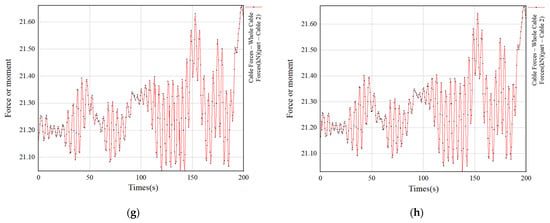
Figure 11.
Dynamic change of mooring force of each anchor chain. (a) Dynamic change of anchor chain mooring force of floating bridge crosswise upstream No.1. (b) Dynamic change of anchor chain mooring force of pontoon bridge crosswise upstream No.2. (c) Dynamic Change of Mooring Force of No.3 Anchor Chain of Floating Bridge Transverse Upward Wave. (d) Dynamic Change of Mooring Force of No. 4 Anchor Chain of Floating Bridge Transverse Upward Wave. (e) Dynamic change of anchor chain mooring force of pontoon bridge longitudinal upstream No.1. (f) Dynamic Change of Mooring Force of Anchor Chain No.2 Longitudinal Upward Wave of Floating Bridge. (g) Dynamic Change of Mooring Force of Longitudinal Upward Wave No.3 Anchor Chain of Floating Bridge. (h) Dynamics of Mooring Force of No. 4 Anchor Chain Longitudinal Upward Wave of Floating Bridge.
It can be seen from the figure that the maximum mooring force of the No. 1 and No. 3 anchor chains on the wave side is about 27 kN, and the maximum mooring force of the No. 2 and No. 4 anchor chains is about 22 kN when the pontoon is facing the waves transversely. When the pontoon is facing the waves longitudinally, the maximum mooring forces of the four anchor chains are equal, all of which are 21 kN. The transverse wave mooring force of the pontoon is large, but it is also within the normal range.
According to the AQWA finite element numerical simulation, the mooring force of the anchor chain is relatively small, regardless of whether the pontoon is facing waves horizontally or longitudinally, and the mooring scheme is reasonable.
The AQWA software is used to carry out numerical simulations of the motion response and mooring force of the floating bridge unit under the action of wave load. The results show that under the action of sea conditions of Class III and IV, the rolling and pitching angles of the floating bridge are relatively small, and the floating bridge has good stability when fully loaded. The mooring force of the anchor chain is also within the normal range, and the mooring scheme is reasonable.
5. Experiments
5.1. Experiment 1: Bearing Reliability Test of the Floating Bridge
To explore the reliability of using inflatable airbags as the main ballast bearing device of the floating bridge [37], we created a solid floating bridge model based on the model presented in this paper and verified the feasibility of using airbags as the main bearing device through a floating bridge ballast experiment [38,39,40].
To collect the relevant technical parameters of the inflatable pontoon, we produced an experimental scale model of the inflatable pontoon (with a scale ratio of 1:5). The model was composed of airbags and water bags made of PVC material, with a diameter of 20 cm and a length of 10 m. The inflatable pontoon combines an airbag and water bag to ensure buoyancy and stability and is covered with a layer of steel plate to allow for vehicle passage and storage of goods. The combined structure of the water bag and the airbag is used to provide fixed ballast, reduce the center of gravity of the pontoon, and improve its stability, as shown in Figure 12.
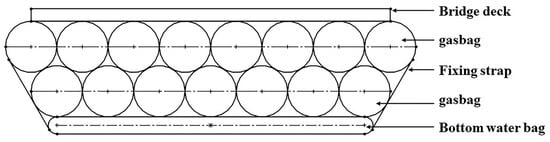
Figure 12.
Equipment schematic.
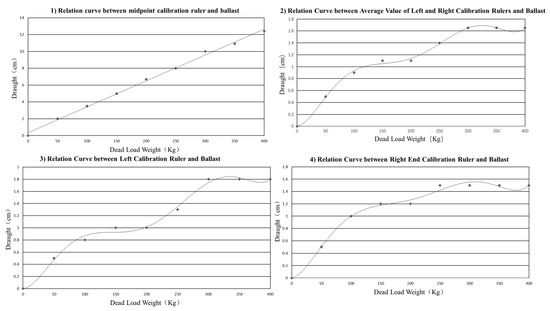
The experimental environment is shown in Figure 13 (see Appendix A for the specific experimental process). The experimental phenomenon is presented in Figure 14a. The data obtained from the experiment were analyzed using an Excel table, and the results were processed to fit the relationship curve between the load under various working conditions and the pontoon draft. The Excel table for data statistics, experimental results, and analysis results are presented below:

Figure 13.
Experimental environment.

Figure 14.
Experimental phenomenon: (a) Experiment 1; (b) Experiment 2.
The draft record of the pontoon in the Ballast Test with a Water Bag is shown in Table 4.

Table 4.
Ballast Test with Water Bag pontoon draft record.
The relationship curve between scale and ballast is shown in Figure 14.
Through the chart, it is found that the draft at the midpoint of the pontoon varies linearly with the ballast weight [41], and the linear equation is y = 0.032x. The draft at both ends of the pontoon follows the ballast change curve. From the slope angle K, it can be observed that the process first involves an increase in K, followed by a decrease, then an increase again, and finally, a decrease.
After analysis, it was found that this change rule is directly related to the shape of the airbag. The cross-section of a single airbag is circular. When the load is applied, the airbag will sink to increase buoyancy. To achieve the same buoyancy, the increased draft of the airbag is different [42]. At the beginning and the end, the draft increases faster, and near the maximum waterline of the airbag, the draft increases more slowly. This experiment is a control experiment.
5.2. Experiment 2: Relationship between Lateral Eccentric Load and Transverse Inclination of Pontoon
We conducted experiments in an open-air test pool to explore the relationship between the lateral deflection and transverse inclination of the pontoon (see Appendix A for the specific experimental process) and fitted the relationship curve between the ballast and draft based on the different draft values obtained under different ballast conditions. The ballast diagram is shown in Figure 16, and the experimental phenomenon is shown in Figure 14b.
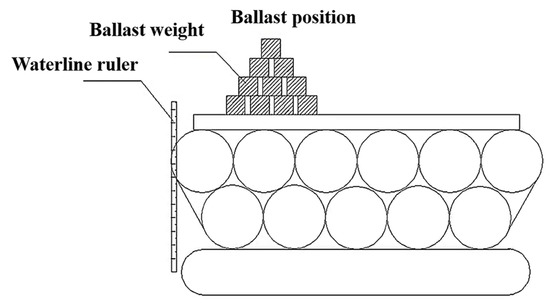
Figure 16.
Ballast Diagram.
The data obtained from the experiment were statistically analyzed using an Excel table, and a relationship curve was fitted between the change of load under different working conditions and the change of pontoon draft. The Excel table with the data statistics, experimental results, and analysis results are presented below. The relationship between partial load and the draft are summarized in Table 5.

Table 5.
Record of the relationship between partial load and draft.
The draft relation curve between eccentric load and position is shown in Figure 17.
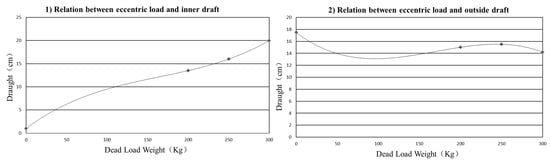
Figure 17.
The draft relation curve between eccentric load and position.
To describe the deformation of the pontoon more intuitively under an eccentric load, we assume that the draft at the centerline of the pontoon does not change when the pontoon is under an eccentric load. Based on this assumption, the general situation of the transverse bending of the pontoon can be described by analyzing the draft record of the scale at the left and right ends, as well as the actual geometric parameters of the model, including the pontoon’s width of 1200 mm and the length of the scale extending out of the side of 200 mm. This is shown in Figure 18.
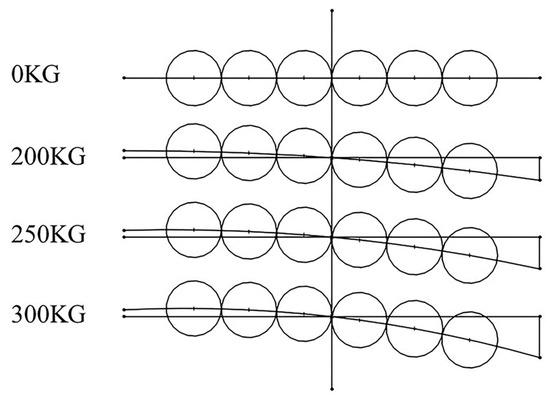
Figure 18.
Schematic diagram of pontoon transverse bending.
It can be seen from the figure that with the increase of the ballast weight, the draft of the pressure side of the floating bridge change is relatively large, while the change on the other side is not obvious. This phenomenon indicates that the lateral stiffness of the pontoon model needs to be strengthened. Properly adding lateral airbags or rigid structures to the floating bridge to improve the lateral stiffness should be considered. To sum up, through the recording and analysis of the experimental data, it is found that the airbag has a certain bearing capacity, and the idea of using the airbag as the main bearing device is highly feasible [43].
6. Discussion and Conclusions
In this paper, we have studied the structure and performance of traditional floating bridges and proposed a rigid-flexible combination folding floating bridge that can be quickly erected, convenient for transportation, safe, and stable. This innovative design addresses the problems of large volume, weight, difficult transportation, low construction efficiency, and other issues that traditional floating bridges face.
To improve the overall continuity and reliability of the floating bridge, a rigid-flexible combination floating bridge is proposed in the form of a staggered arrangement of longitudinal airbags and rigid frames, which ingeniously combine the advantages of the two materials (utilizing the compressibility and buoyancy of the airbag and the expansion of the airbag to form an extrusion with the steel frame after being filled with air, to provide pretension for the steel frame structure, and using the longitudinal strength of the full airbag to share the stress of the steel frame structure). To improve reliability and stability, the longitudinal strength of the inflatable airbags is used to resist the shear force and torque at the connection of the two pontoon units. To further improve portability while meeting the strength and rigidity requirements, this design proposes an aluminum alloy stamping integrated forming bridge deck, which has an internal structure of transverse skeleton type. Woven mesh is used to fix the airbag and water bag to limit their relative displacement. A buffer material is used at the contact between the bridge deck and the airbag to avoid pressure concentration and improve anti-wear performance and space utilization. The design of the floating bridge is checked, calculated, simulated, and verified by experiments, demonstrating the scientific feasibility of the rigid-flexible combination floating bridge.
For military purposes, this floating bridge can quickly traverse and move military personnel, vehicles, and other combat materials when inland rivers or roads are damaged. It can also be used for offshore landing operations, connecting ships and coasts, and realizing the rapid landing of troops and vehicles. For civilian use, it can be used in emergency rescue and disaster relief, traffic emergencies, and other occasions where it is not necessary or impossible to build a permanent bridge to meet traffic needs. It can also be used as a temporary transition for inland water conservancy projects or offshore projects to facilitate the passage and work of workers, vehicles, and equipment. It can be widely used in disaster relief, water rescue engineering construction, and other fields. It is excellent equipment that can meet traffic emergency needs.
The disadvantage of this floating bridge is that it takes time to inflate during erection, and there is room for improvement in erection speed. In the future, it is necessary to study the inflating method and inflating equipment of this floating bridge.
Author Contributions
Conceptualization, J.G. and C.W.; methodology, J.G.; software, C.W.; validation, C.W. and H.H.; formal analysis, C.W.; investigation, C.W.; resources, J.G.; data curation, H.H.; writing—original draft preparation, C.W.; writing—review and editing, J.G.; visualization, C.W.; supervision, C.W.; project administration, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. The Detailed Calculation Process of Pontoon Parameters Is as Follows
From Formulas (14)–(16):
The formula for calculating the midspan deflection and midspan bending moment of the floating bridge can be obtained by substituting x = 0 into Formula (18):
Because the airbag folds under load, the calculated bending moment of the fold is:
The bending moment in the midspan of the floating bridge is smaller than the theoretical folded bending moment, that is, ≤ . Since the actual ultimate bending moment of the inflatable membrane is about 1.5~2 times the theoretical folded bending moment, the value here is relatively safe.
Where:
If the maximum draft of the pontoon is times the pontoon height:
Therefore, when is the smallest, the internal pressure is the smallest. We can bring the design parameters of the pontoon into Formula (A5), where , , .
The material selected for this pontoon has an elastic modulus E = 474.8 MPa, and the minimum thickness of the membrane material is = 3.5 mm. According to the literature [44], the working elongation of the membrane should not exceed 15%. Therefore, it is necessary to check the elongation of the membrane material under the current air pressure. With a minimum internal pressure of , we can calculate the axial and circumferential stresses as follows:
The axial and circumferential strains are:
Appendix A.2. Specific Experimental Verification Process
Appendix A.2.1. Experiment 1 Implementation Plan
Preparation stage:
- Confirm that the weather is good and that the wind will not affect the test.
- Determine the maximum load allowed by the deflection of the floating bridge.
- Observe the pontoon for damage. If damage is present, replace the affected airbag immediately.
- Ensure that all instruments are functioning correctly.
Test stage:
- Connect the air pump and inflate the airbag until the air pressure reaches the specified value. Disconnect the air pump interface, lift the pontoon with four people, and slowly put it into the water (near the edge of the pool).
- Model water injection: Connect the pontoon water inlet to the water pump, put the water pump into the water, connect the power supply, and inject water until the corresponding pressure value is reached. Then disconnect the water pump interface.
- Record the no-load draft reading. After the model is stable, record the draft depth d of the floating bridge when it is empty with the bottom water bag.
- Conduct the ballast test: Perform the ballast test at 2 calibration scales on the pontoon deck, place 50 kg weights, and read the readings of the three calibration scales on the pontoon after the pontoon is stable. Then increase the ballast weight with a gradient of 50 kg until the ballast reaches 400 kg and record the corresponding scale readings.
- Data summary: Fit a curve of the relationship between the ballast and draft of the floating bridge with the bottom water pocket based on the different draft values obtained under different ballast conditions.
Appendix A.2.2. Experiment 2 Implementation Plan
Test stage:
- Airbag Inflation: Connect the air pump and inflate the airbag until the air pressure reaches the specified value, then disconnect the air pump interface.
- Water Injection: Connect the water pump to fill the pontoon water bag.
- Record the No-load Draft Reading: After the model stabilizes, read the draft of the floating bridge when it is not loaded.
- Carry out the Ballast Test: Place a 50 kg weight at the pontoon position and conduct a partial load test. After the pontoon stabilizes, read the scale reading in the middle of the pontoon. Then increase the ballast weight with a gradient of 50 kg until the ballast reaches 400 kg and record the corresponding scale readings.
Appendix A.3. The Source of Formula (7) and the Description of This Formula Variables
The differential equation of the deflection curve of the elastic foundation beam is:
Solve the parameter in Formula (A7):
where is the bending characteristic coefficient of the beam:
According to the bending moment formula, Angle formula, and shear formula:
Set the equations together and replace A1, A2, A3, and A4 with other parameters, then we get the Formula (7):
where is the deflection at , is the corner at , is the bending moment at , is the shearing force at , is the length of the uniform load. , , , are four functions of :
References
- Lwin, M. Floating bridges. In Bridge Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2019; pp. 2201–2221. [Google Scholar]
- Zhou, J.; Liang, H. An intelligent floating bridge system with strong maneuverability on the sea. In Proceedings of the 2022 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2022. [Google Scholar]
- Lee, D.; Kim, Y. Control system for installation and position keeping of interconnected flexible floating bridge. Meas. Control 2020, 53, 2092–2100. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, H.; Geng, B.; Zhou, J.; Li, Y. FE analyses and structural optimization on refitted floating container. J. Phys. Conf. Ser. 2019, 1303, 012039. [Google Scholar] [CrossRef]
- Minoretti, A.; Xiang, X.; Johansen, I.; Eidem, M. The future of the tunnel crossing: The submerged floating tube bridge. Struct. Eng. Int. 2020, 30, 493–497. [Google Scholar] [CrossRef]
- Moan, T.; Eidem, M. Floating bridges and submerged tunnels in Norway—The history and future outlook. In WCFS2019: Proceedings of the World Conference on Floating Solutions, Singapore, 22–23 April 2019; Springer: Singapore, 2019. [Google Scholar]
- Silva, A.L.L.; Correia, J.A.; Xin, H.; Lesiuk, G.; De Jesus, A.M.; Fernandes, A.A.; Berto, F. Fatigue strength assessment of riveted details in railway metallic bridges. Eng. Fail. Anal. 2021, 121, 105120. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Castro, J.M.; Calcada, R.; Soares, J.M.; Coelho, H.; Pacheco, P. Probabilistic numerical evaluation of dynamic load allowance factors in steel modular bridges using a vehicle-bridge interaction model. Eng. Struct. 2021, 226, 111316. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Zheng, S.X.; Ding, Z.H.; Zhang, J.; Tai, Y.J. Seismic reliability evaluation of bridges under spatially varying ground motions using a four-parameter distribution. Eng. Struct. 2021, 247, 113157. [Google Scholar] [CrossRef]
- Somala, S.; Karthik, K.; Mangalathu, S. Diaphragm abutment Californian bridges subjected to UCERF2 rupture scenarios: Complete damage state evolution with improvements to seismic codes. Soil Dyn. Earthq. Eng. 2022, 155, 107204. [Google Scholar] [CrossRef]
- Fenerci, A.; Kvåle, K.A.; Xiang, X.; Øiseth, O. Hydrodynamic interaction of floating bridge pontoons and its effect on the bridge dynamic responses. Mar. Struct. 2022, 83, 103174. [Google Scholar] [CrossRef]
- Thomas, J.; Van, A. An exact solution for inflated orthotropic membrane tubes. Thin Wall Struct. 2013, 67, 116–120. [Google Scholar] [CrossRef]
- Cheng, Z.; Gao, Z.; Moan, T. Extreme responses and associated uncertainties for a long end-anchored floating bridge. Eng. Struct. 2020, 219, 110858. [Google Scholar] [CrossRef]
- Thomas, J.; Jiang, Z.; Wielgosz, C. Continuous and finite element methods for the vibrations of inflatable beams. Int. J. Steel Struct. 2006, 21, 197–222. [Google Scholar] [CrossRef]
- Viuff, T.; Leira, B.; Xiang, X.; Øiseth, O. Effects of wave directionality on extreme response for a long end-anchored floating bridge. Appl. Ocean Res. 2019, 90, 101843. [Google Scholar] [CrossRef]
- Xu, Y.; Øiseth, O.; Moan, T.; Naess, A. Prediction of long-term extreme load effects due to wave and wind actions for cable-supported bridges with floating pylons. Eng. Struct. 2018, 172, 321–333. [Google Scholar] [CrossRef]
- Skorpa, L. Developing new methods to cross wide and deep Norwegian fjords. Procedia Eng. 2010, 4, 81–89. [Google Scholar] [CrossRef]
- Xu, Y.; Øiseth, O.; Moan, T. Time domain simulations of wind- and wave-induced load effects on a three-span suspension bridge with two floating pylons. Mar. Struct. 2018, 58, 434–452. [Google Scholar] [CrossRef]
- Cheng, Z.; Svangstu, E.; Moan, T.; Gao, Z. Long-term joint distribution of environmental conditions in a Norwegian fjord for design of floating bridges. Ocean Eng. 2019, 191, 106472. [Google Scholar] [CrossRef]
- Martins, A.; Simões, L.; Negrão, J. Optimization of extradosed concrete bridges subjected to seismic action. Comput. Struct. 2021, 245, 106460. [Google Scholar] [CrossRef]
- Salman, N.; Issa, M. Calibration and parametric investigation of integral abutment bridges. Eng. Struct. 2021, 227, 111381. [Google Scholar] [CrossRef]
- Broch, E. Planning and utilisation of rock caverns and tunnels in Norway. Tunn. Undergr. Space Technol. 2016, 55, 329–338. [Google Scholar] [CrossRef]
- Wang, H.; Jin, X. Dynamic analysis of maritime gasbag-type floating bridge subjected to moving loads. Int. J. Nav. Arch. Ocean Eng. 2016, 8, 137–152. [Google Scholar] [CrossRef]
- Seo, J.; Kidd, B. Parametric study of deteriorating precast concrete double-tee girder bridges using computational models. Eng. Struct. 2021, 230, 111714. [Google Scholar] [CrossRef]
- Zhu, D.; Yuan, P.; Dong, Y. Probabilistic performance of coastal bridges under hurricane waves using experimental and 3D numerical investigations. Eng. Struct. 2021, 242, 112493. [Google Scholar] [CrossRef]
- Farvizi, F.; Melville, B.W.; Shamseldin, A.Y.; Shafiei, S.; Hendi, E. Experimental investigation of tsunami bore-induced forces and pressures on skewed box section bridges. Ocean Eng. 2021, 224, 108730. [Google Scholar] [CrossRef]
- Van, A.; Wielgosz, C. Finite element formulation for inflatable beams. Thin Wall Struct. 2007, 45, 221–236. [Google Scholar] [CrossRef]
- Viuff, T.; Xiang, X.; Leira, B.; Øiseth, O. Software-to-software comparison of end-anchored floating bridge global analysis. J. Bridge Eng. 2020, 25, 04020022. [Google Scholar] [CrossRef]
- Bertolesi Elisa Buitrago, M.; Adam, J.; Calderon, P.A. Fatigue assessment of steel riveted railway bridges: Full-scale tests and analytical approach. J. Constr. Steel Res. 2021, 182, 106664. [Google Scholar] [CrossRef]
- Rajeeth, T.; Ravi, G. Fatigue reliability evaluation of aged railway steel bridges based on probabilistic fracture mechanics. Trans. Tianjin Univ. 2022, 7, 593–599. [Google Scholar] [CrossRef]
- Xu, Z.; Melville, B.; Nandasena, N.A.K.; Whittaker, C.; Shamseldin, A.; Farvizi, F. Tsunami loads on slab bridges. Coast. Eng. 2021, 165, 103853. [Google Scholar] [CrossRef]
- Razzaq, M.; Sennah, K.; Ghrib, F. Live load distribution factors for simply-supported composite steel I-girder bridges. J. Constr. Steel Res. 2021, 181, 106612. [Google Scholar] [CrossRef]
- Qu, K.; Sun, W.Y.; Kraatz, S.; Deng, B.; Jiang, C.B. Effects of floating breakwater on hydrodynamic load of low-lying bridge deck under impact of cnoidal wave. Ocean Eng. 2020, 203, 107217. [Google Scholar] [CrossRef]
- He, Y.; Ji, W.; Ying, J.; Han, B. Hydrodynamic performance of a continuous floating bridge with heave plates. Appl. Ocean Res. 2021, 108, 102442. [Google Scholar] [CrossRef]
- Hou, W.; Zheng, Y.; Guo, W.; Pengcheng, G. Piezoelectric vibration energy harvesting for rail transit bridge with steel-spring floating slab track system. J. Clean. Prod. 2020, 291, 125283. [Google Scholar] [CrossRef]
- Viuff, T.; Xiang, X.; Øiseth, O.; Leira, B.J. Model uncertainty assessment for wave- and current-induced global response of a curved floating floating bridge. Appl. Ocean Res. 2020, 105, 102368. [Google Scholar] [CrossRef]
- Jun, Z.; Wei, L. Dynamic model of a hinged-girder floating bridge subjected by moving loads. Appl. Ocean Res. 2021, 114, 102804. [Google Scholar] [CrossRef]
- Manisha; Kaligatla, R.; Sahoo, T. Effect of bottom undulation for mitigating wave-induced forces on a floating bridge. Wave Motion 2019, 89, 166–184. [Google Scholar] [CrossRef]
- Kar, P.; Sahoo, T.; Meylan, M. Bragg scattering of long waves by an array of floating flexible plates in the presence of multiple submerged trenches. Phys. Fluids 2020, 32, 096603. [Google Scholar] [CrossRef]
- Vernon, A. Squire. Ocean wave interactions with sea ice: A reappraisal. Annu. Rev. Fluid Mech. 2020, 5, 37–60. [Google Scholar]
- Fu, S.; Cui, W.; Chen, X.; Cong, W. Hydroelastic analysis of a nonlinearly connected floating bridge subjected to moving loads. Mar. Struct. 2005, 18, 85–107. [Google Scholar]
- Dai, J.; Leira, B.; Moan, T.; Kvittem, M.I. Inhomogeneous wave load effects on a long, straight and side-anchored floating floating bridge. Mar. Struct. 2020, 72, 102763. [Google Scholar] [CrossRef]
- Cheng, Z.; Gao, Z.; Moan, T. Wave load effect analysis of a floating bridge in a fjord considering inhomogeneous wave conditions. Eng. Struct. 2018, 163, 197–214. [Google Scholar] [CrossRef]
- Gutiérrez-Romero, J.E.; García-Espinosa, J.; Serván-Camas, B.; Zamora-Parra, B. Non-linear dynamic analysis of the response of moored floating structures. Mar. Struct. 2016, 49, 116–137. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).