Study on the Engagement Characteristics and Control Strategy of High Speed Difference Dry Friction Clutch
Abstract
1. Introduction
2. Materials and Methods
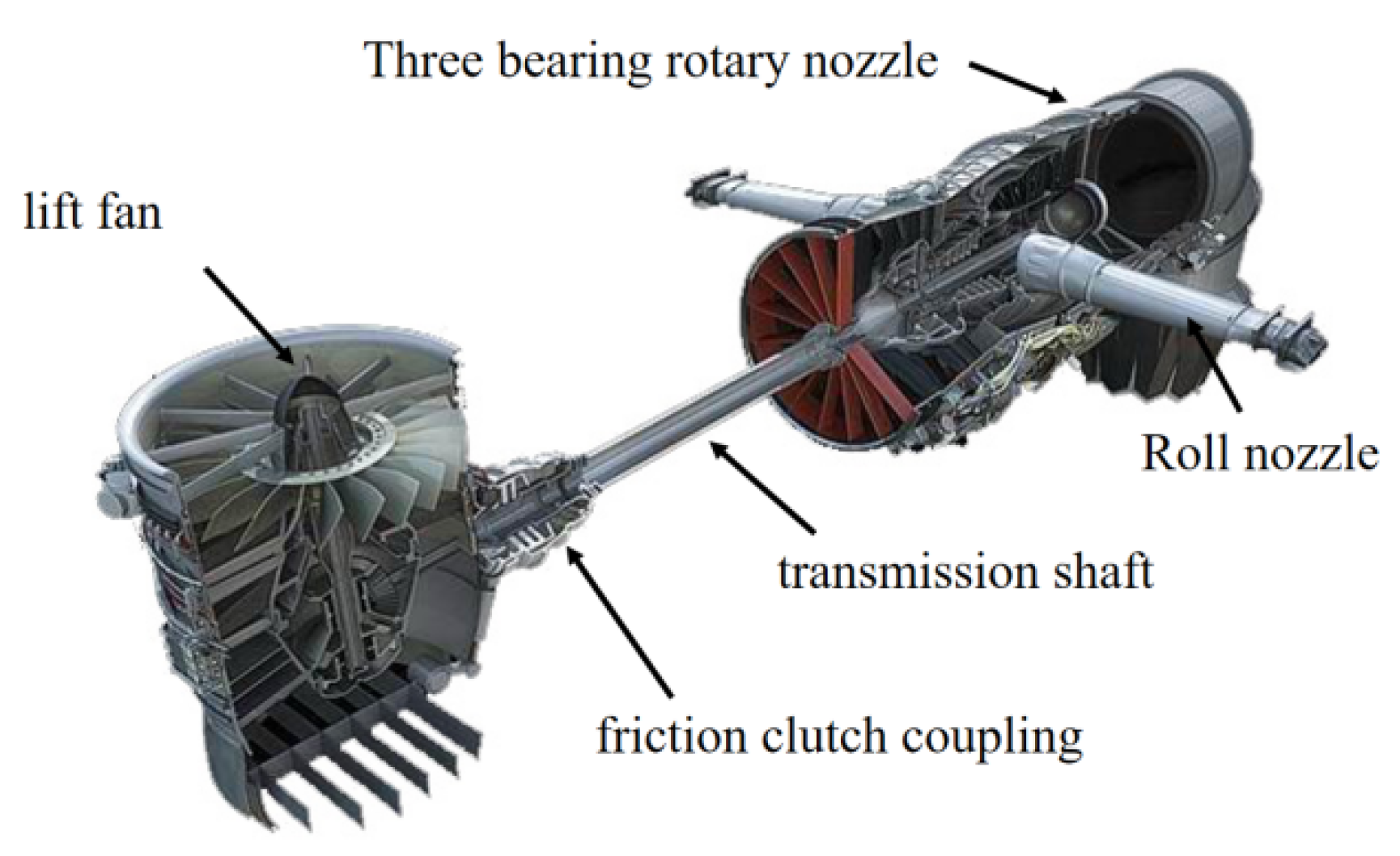
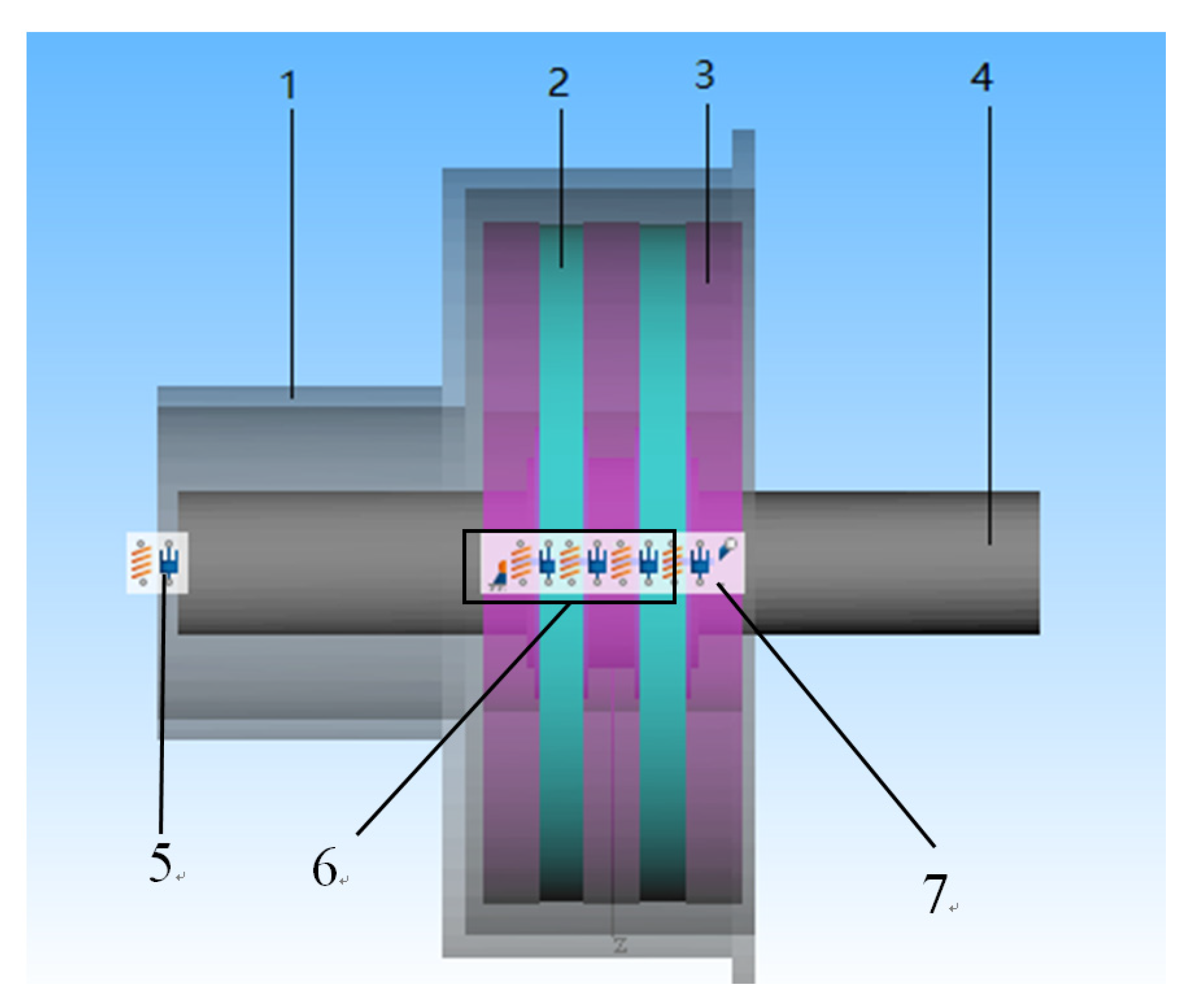
2.1. Short Range/Vertical Aircraft Propulsion System
2.1.1. Principle of Short Range/Vertical Aircraft Propulsion System
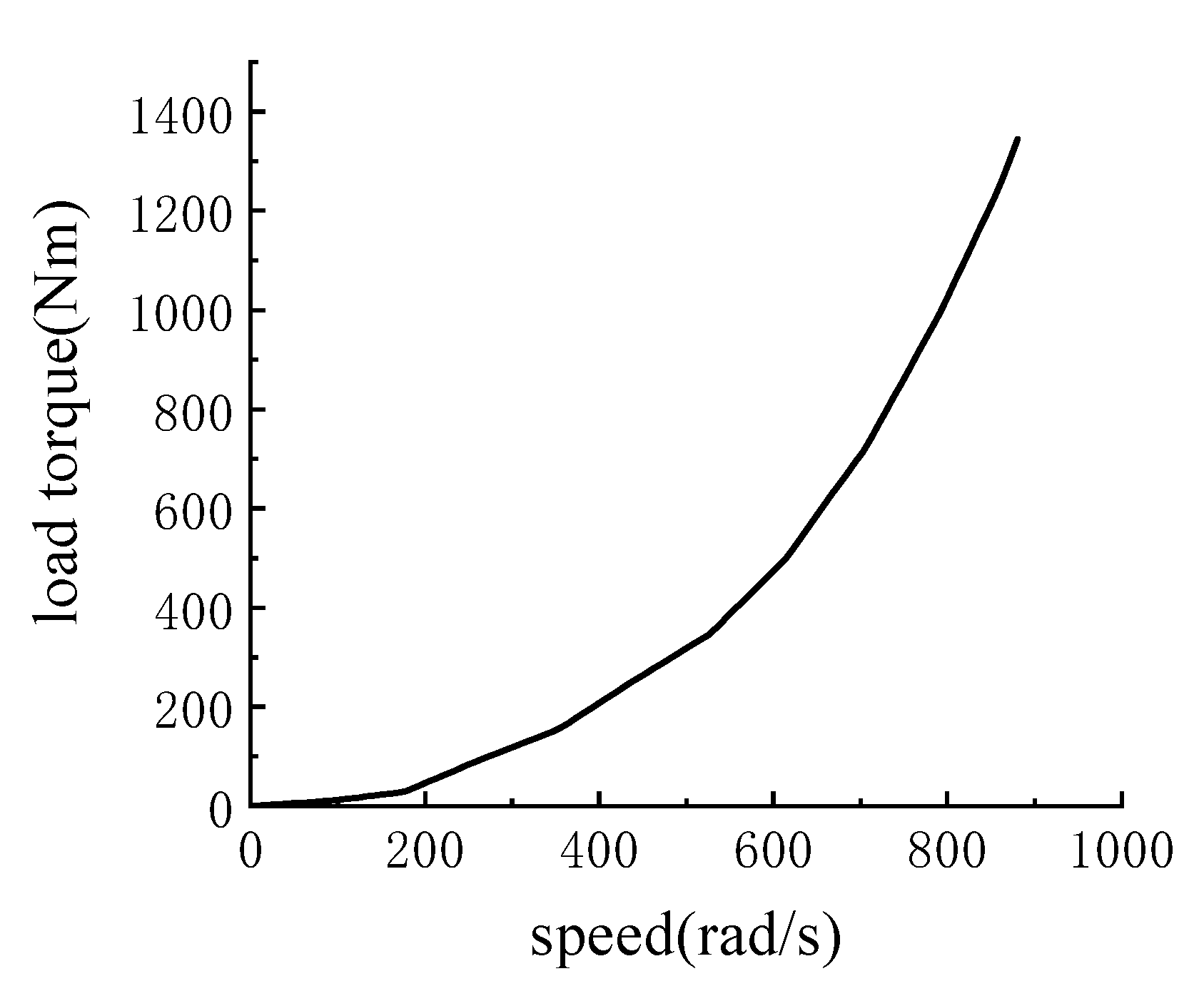
2.1.2. Test Equipment and Methods
- Turn on the input motor, push the input speed to the corresponding speed, and the stable running time is not less than 5 s.
- Start the friction plate actuator, and the pressure starts to load.
- After the speed of both ends of the clutch is the same, keep it for 5 s, and then retract the mechanical locking actuator.
- Confirm that the mechanical locking continues for 10 s.
- Reduce the input speed.
- Extend the mechanical lock actuator and stabilize for 5 s.
- Unload the friction plate actuator, the pressure is unloaded.
- After the output end stops under the action of inertia, after confirming that the clutch is disengaged, turn off the input end motor so that the motor speed decays to 0 within 10 s.
2.2. Model of Engagement Characteristics of Dry Friction Clutches
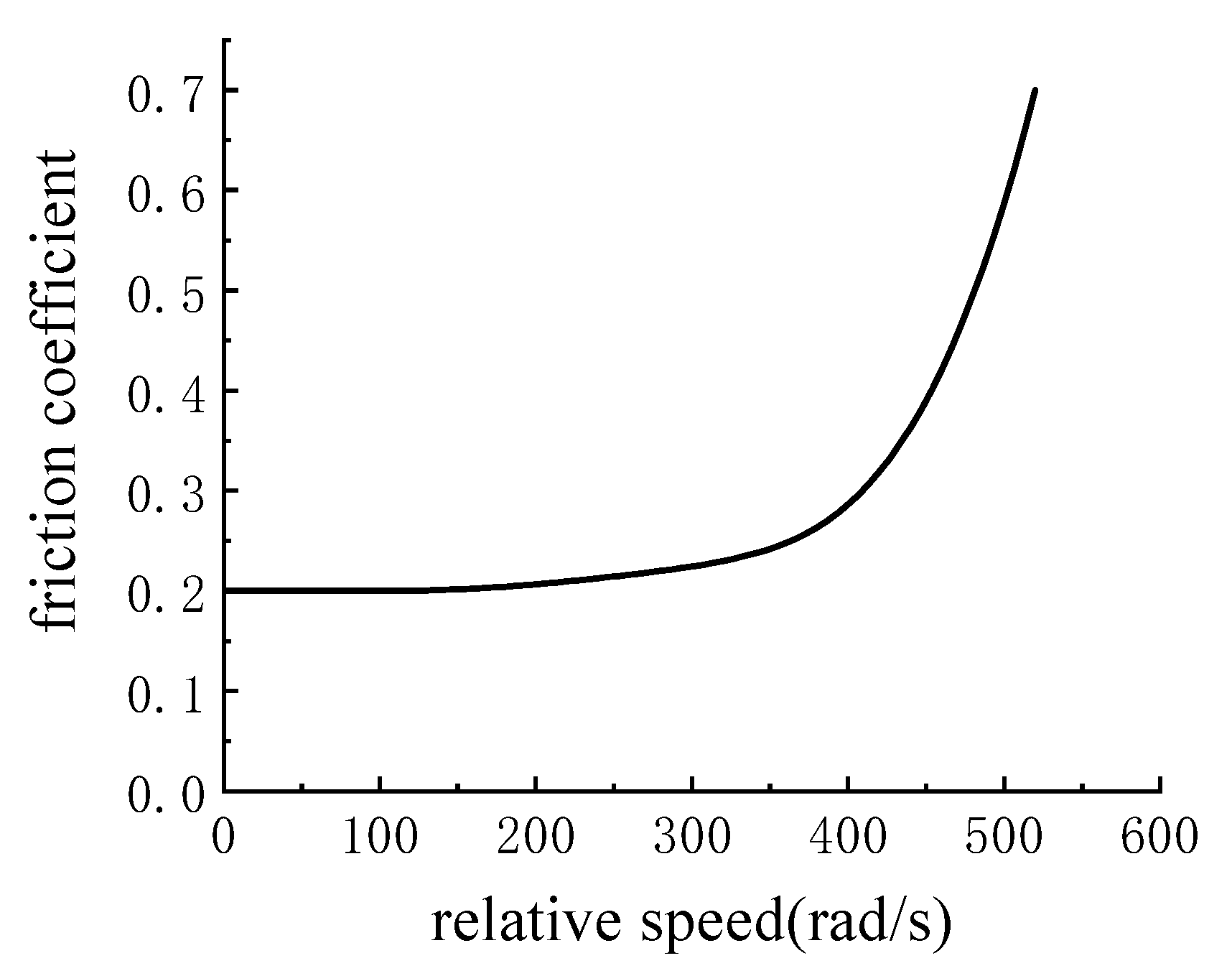
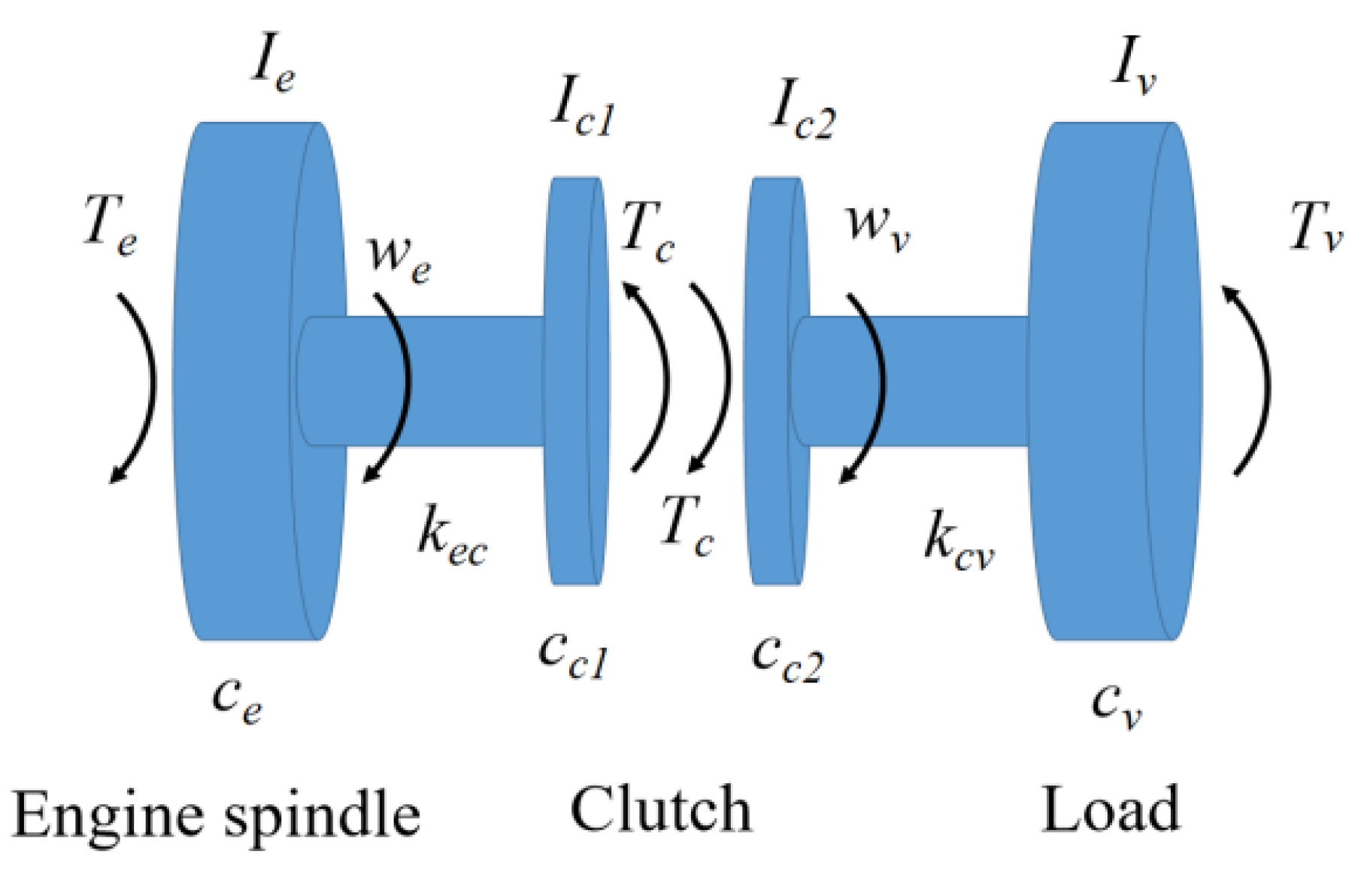
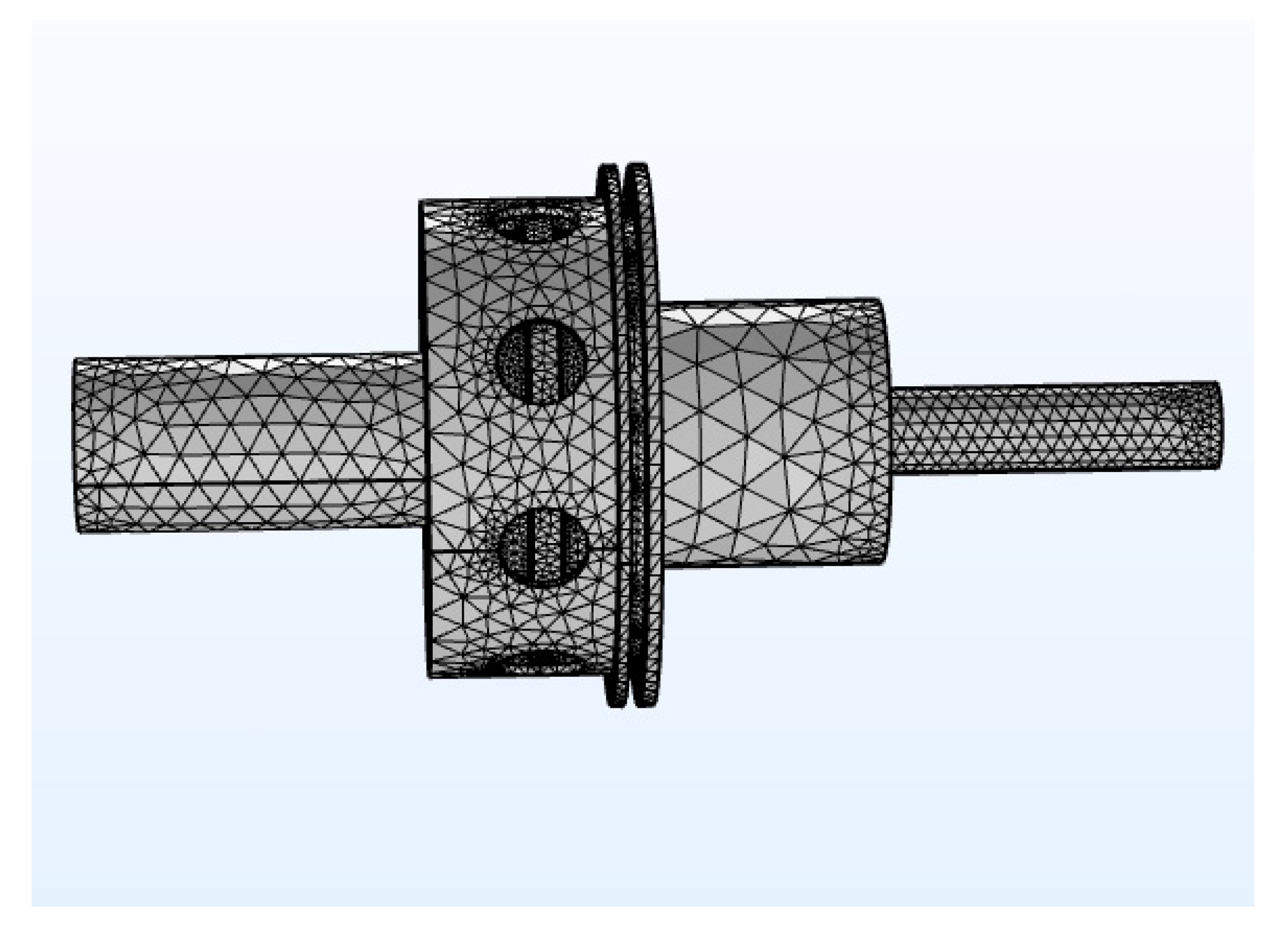
2.2.1. Modeling of the Friction Clutch Dynamics
2.2.2. Modeling of the Friction Clutch Temperature Field
3. Results and Verification
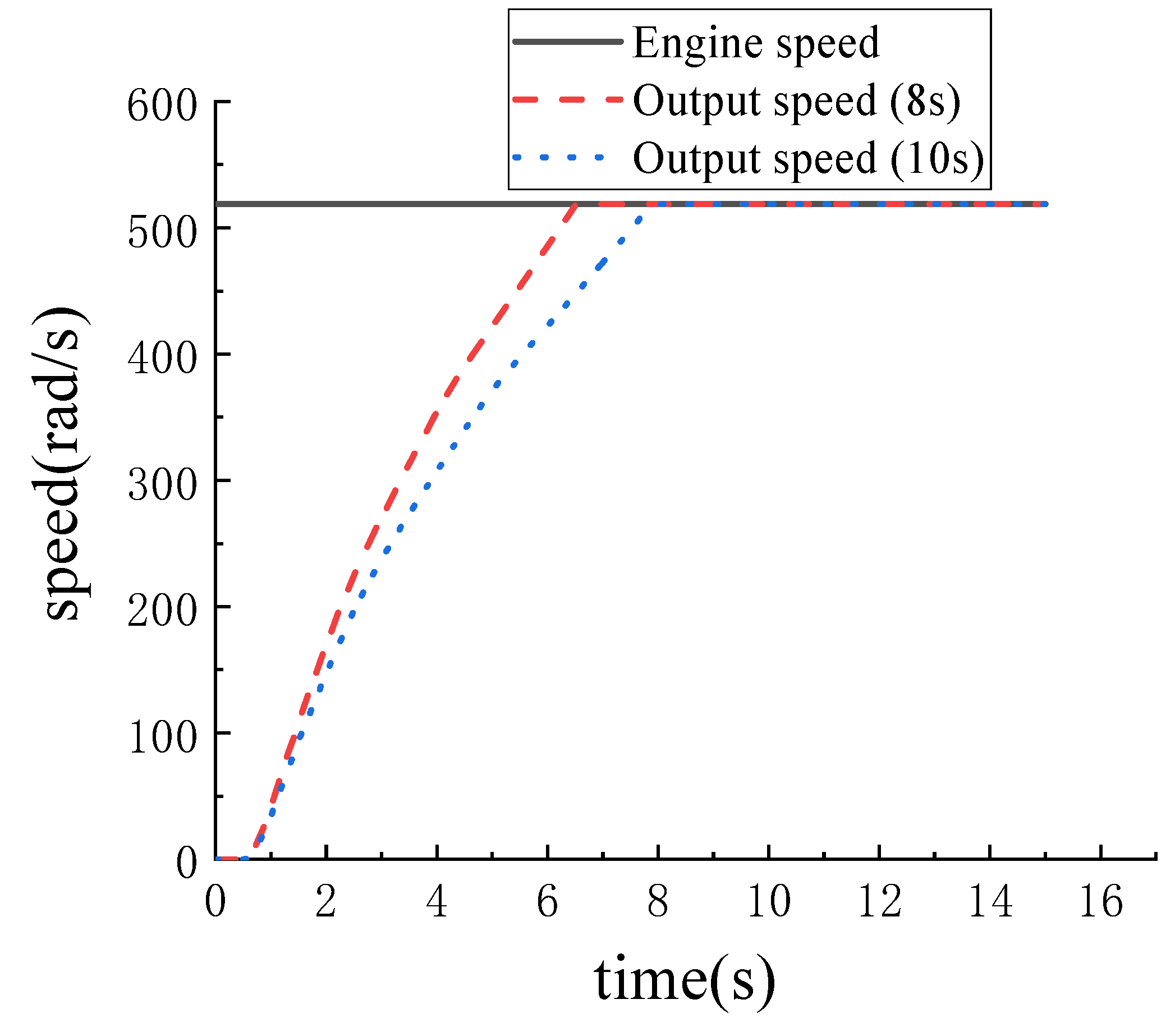
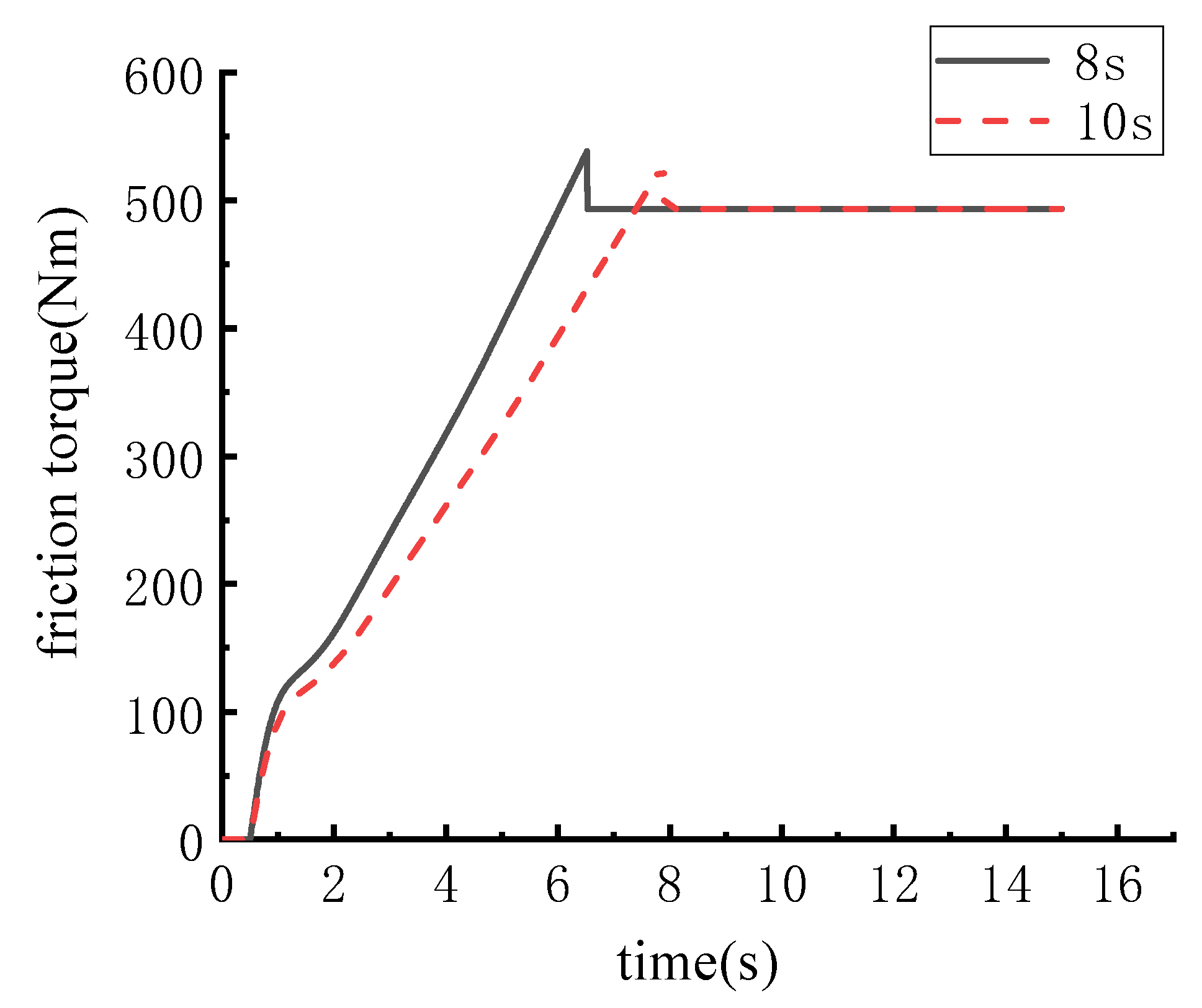
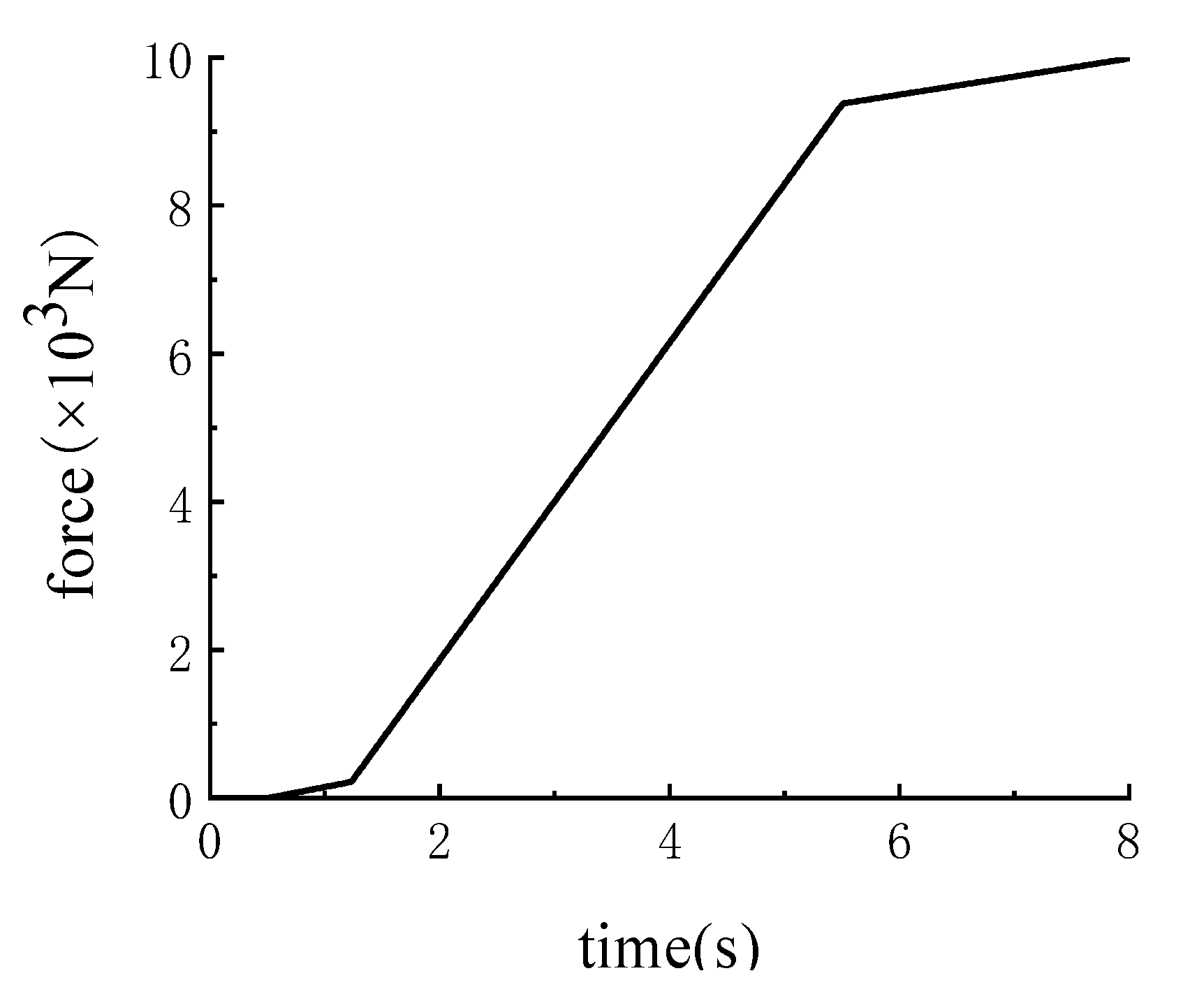
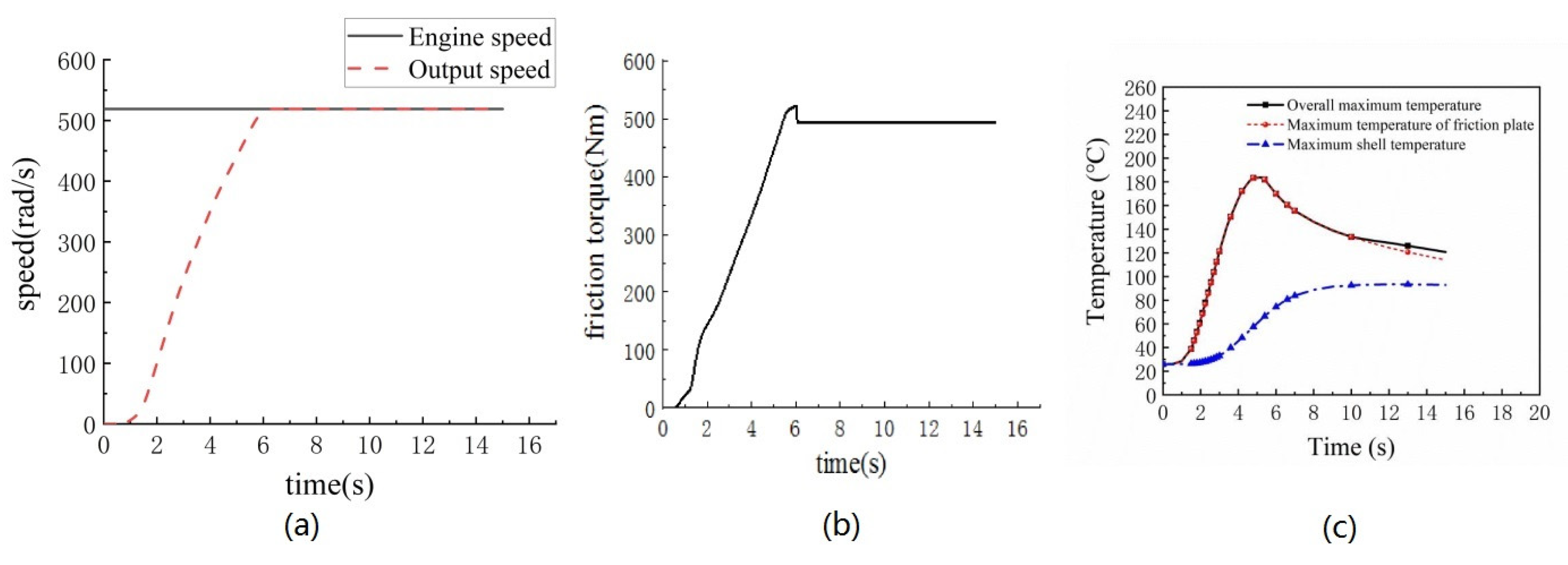
3.1. The Simulation Results of the Engagement Characteristics of Dry Friction Clutch
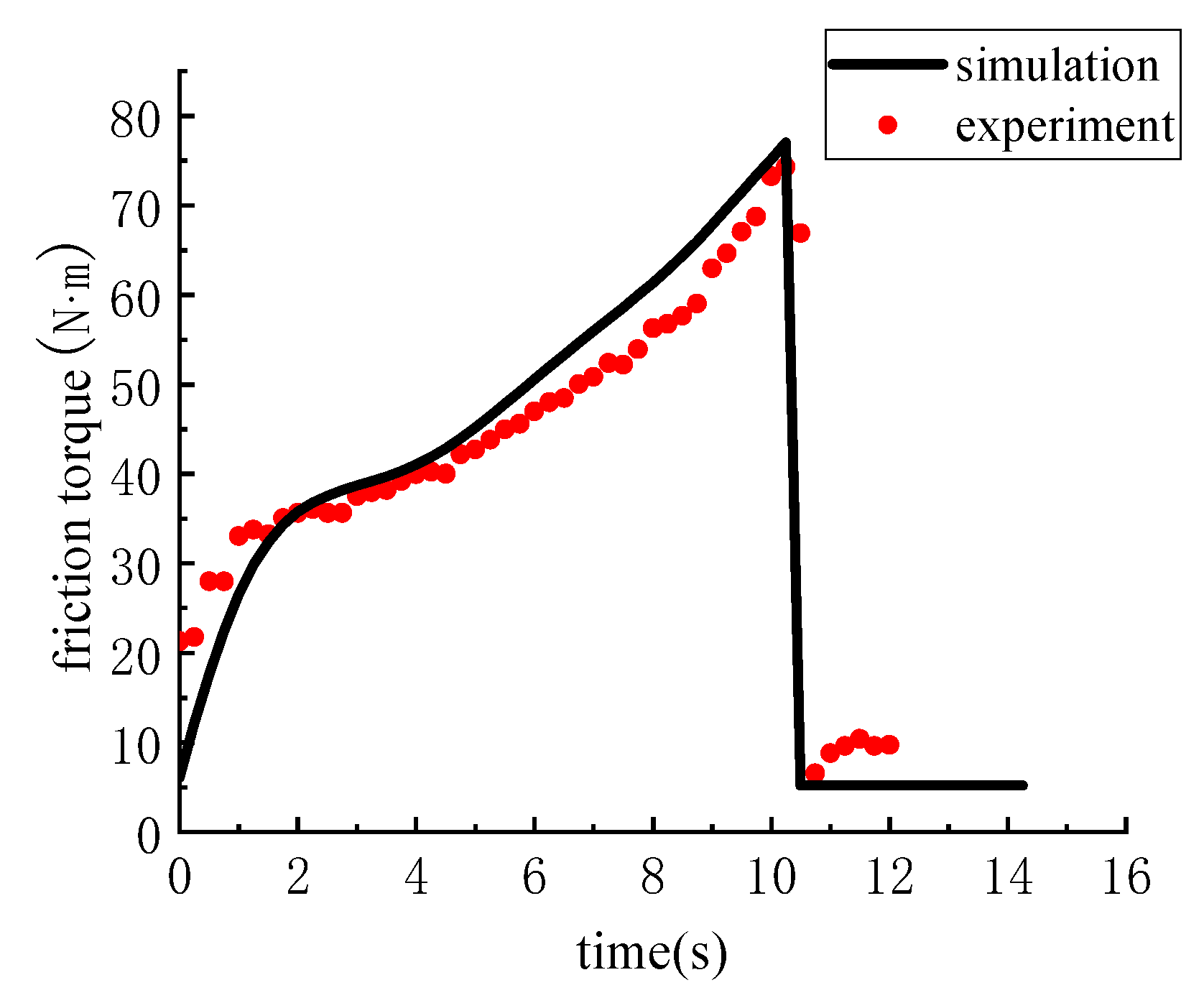
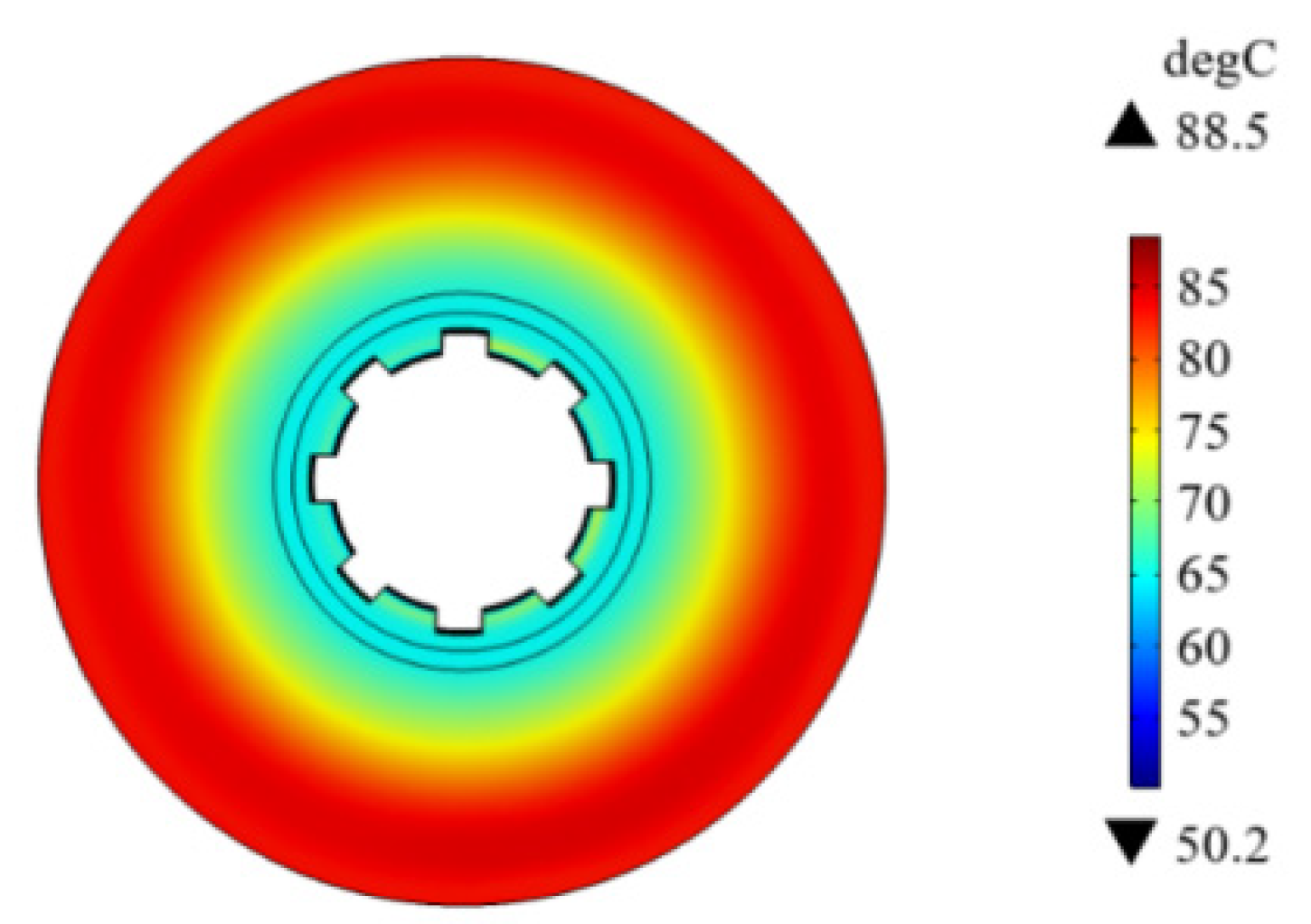
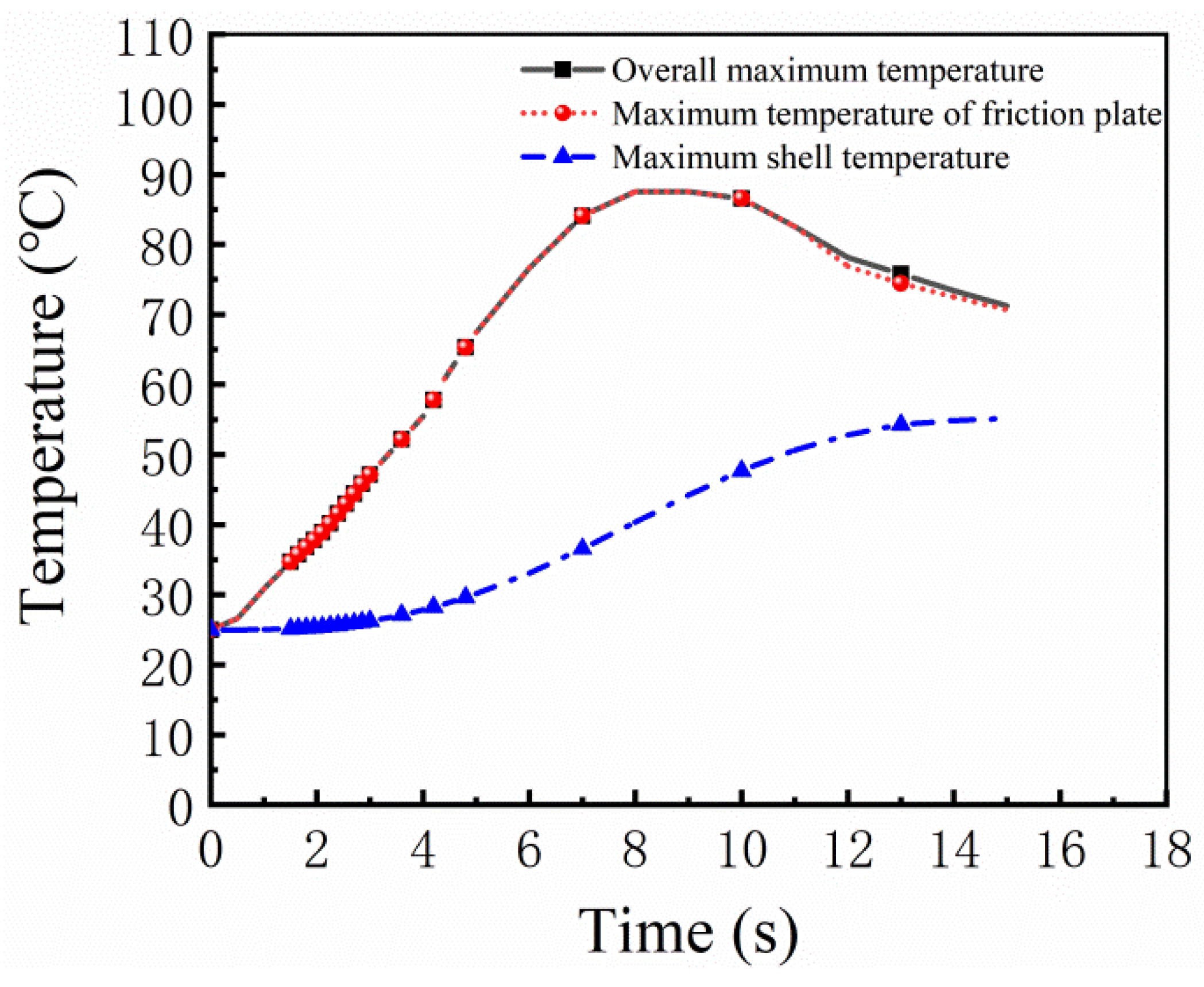
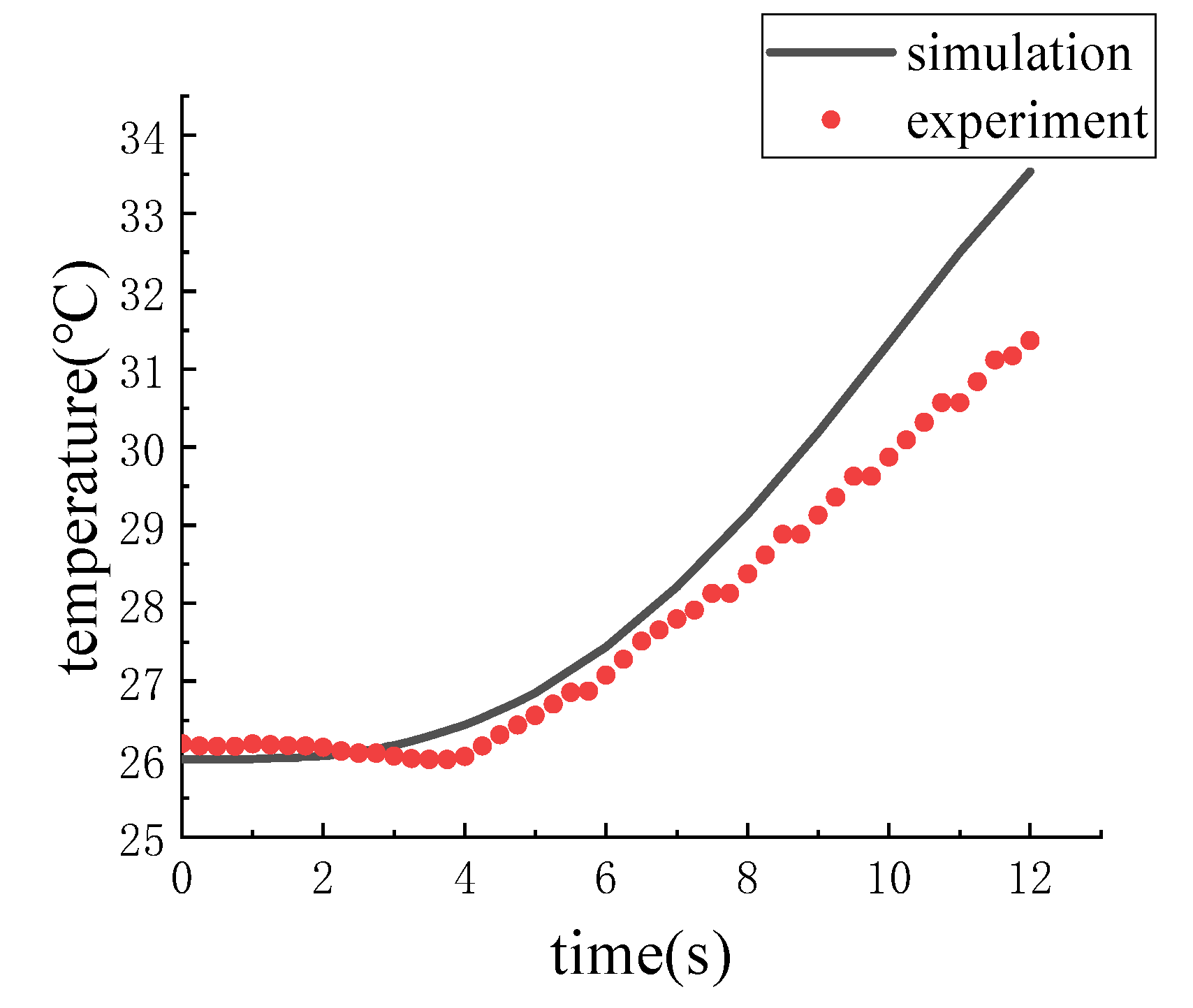
3.2. The Verification of Dynamics Model and Temperature Model
3.2.1. Dynamic Model
3.2.2. Temperature Model
4. Discussion
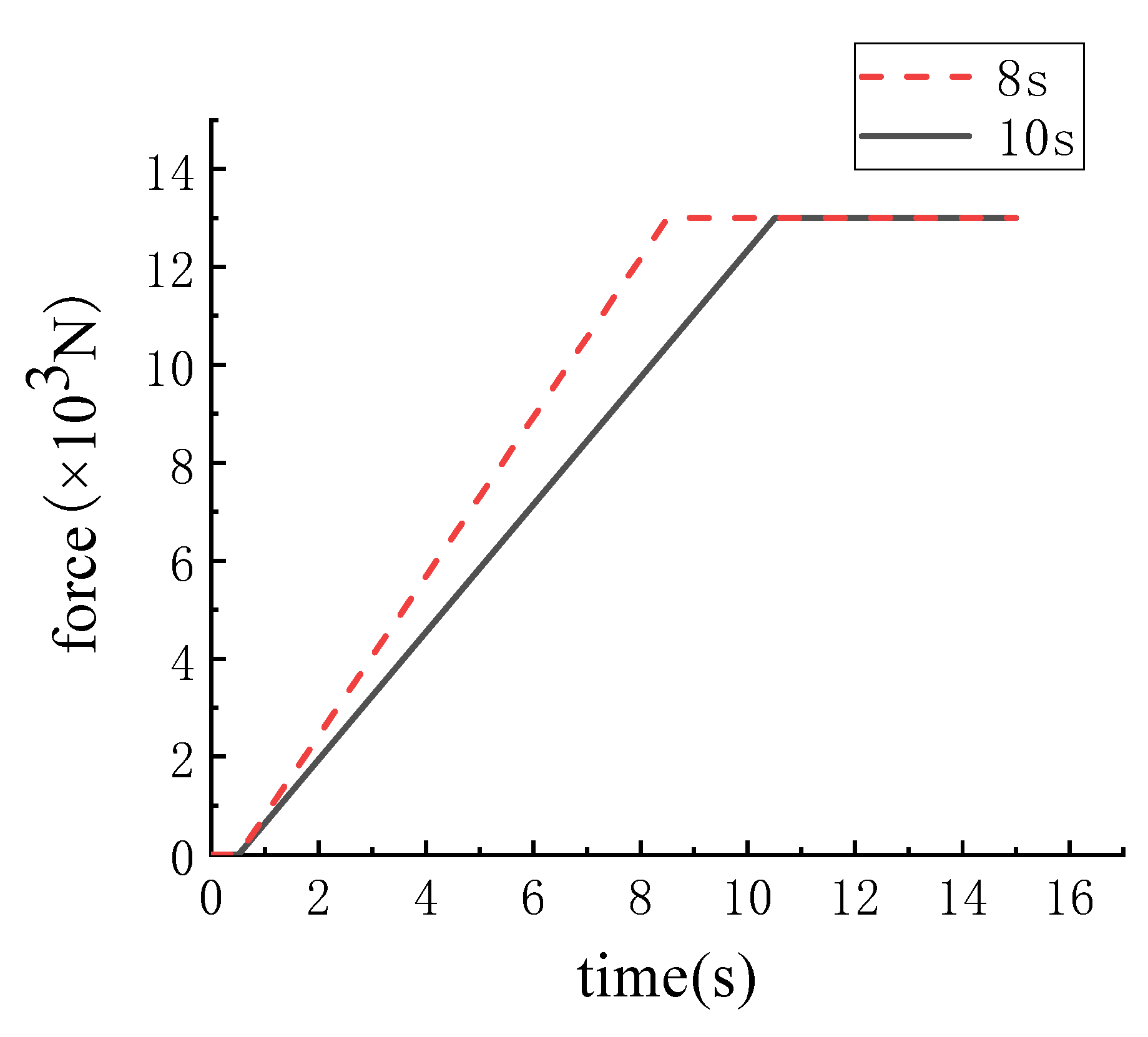
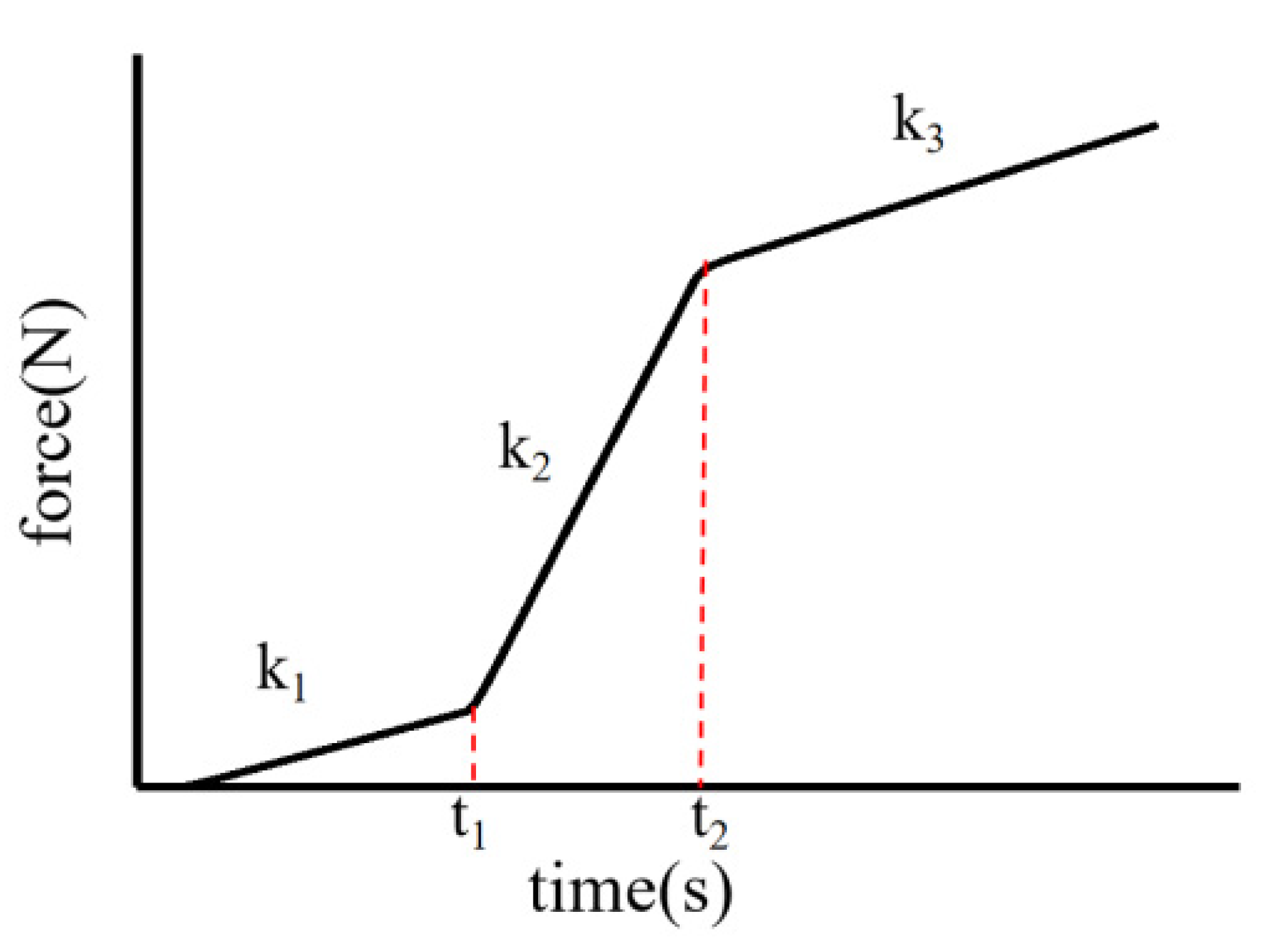
4.1. The Engagement Characteristics of the Traditional Fixed Slope Engagement Pressure
4.2. The Variable Slope Engagement Pressure Loading
4.2.1. The Engagement Characteristics of the Variable Slope Engagement Pressure Loading
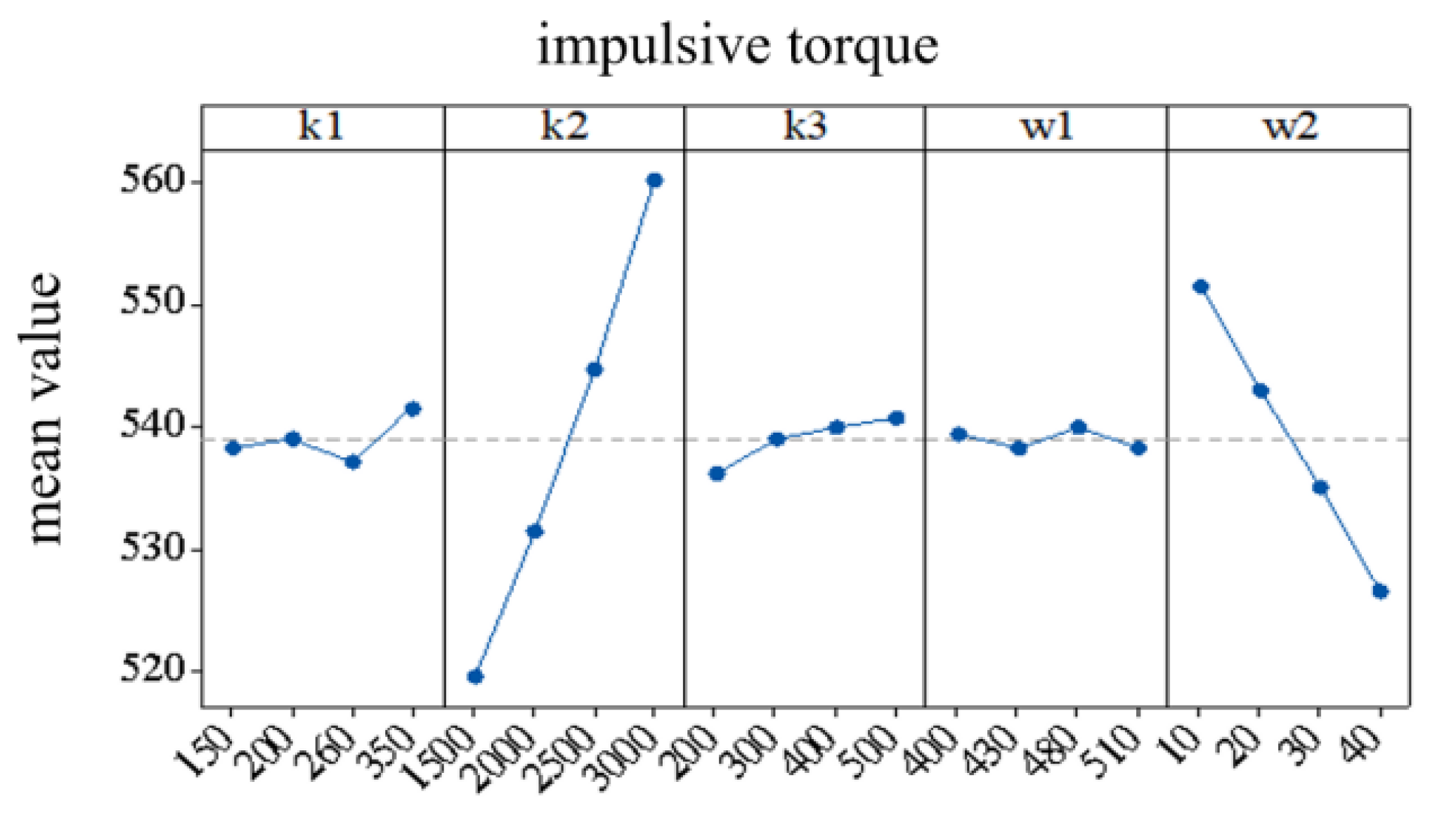
4.2.2. The Optimization of the Control Strategy for Variable Slope Pressure Loading
- (1)
- Orthogonal design
- (2)
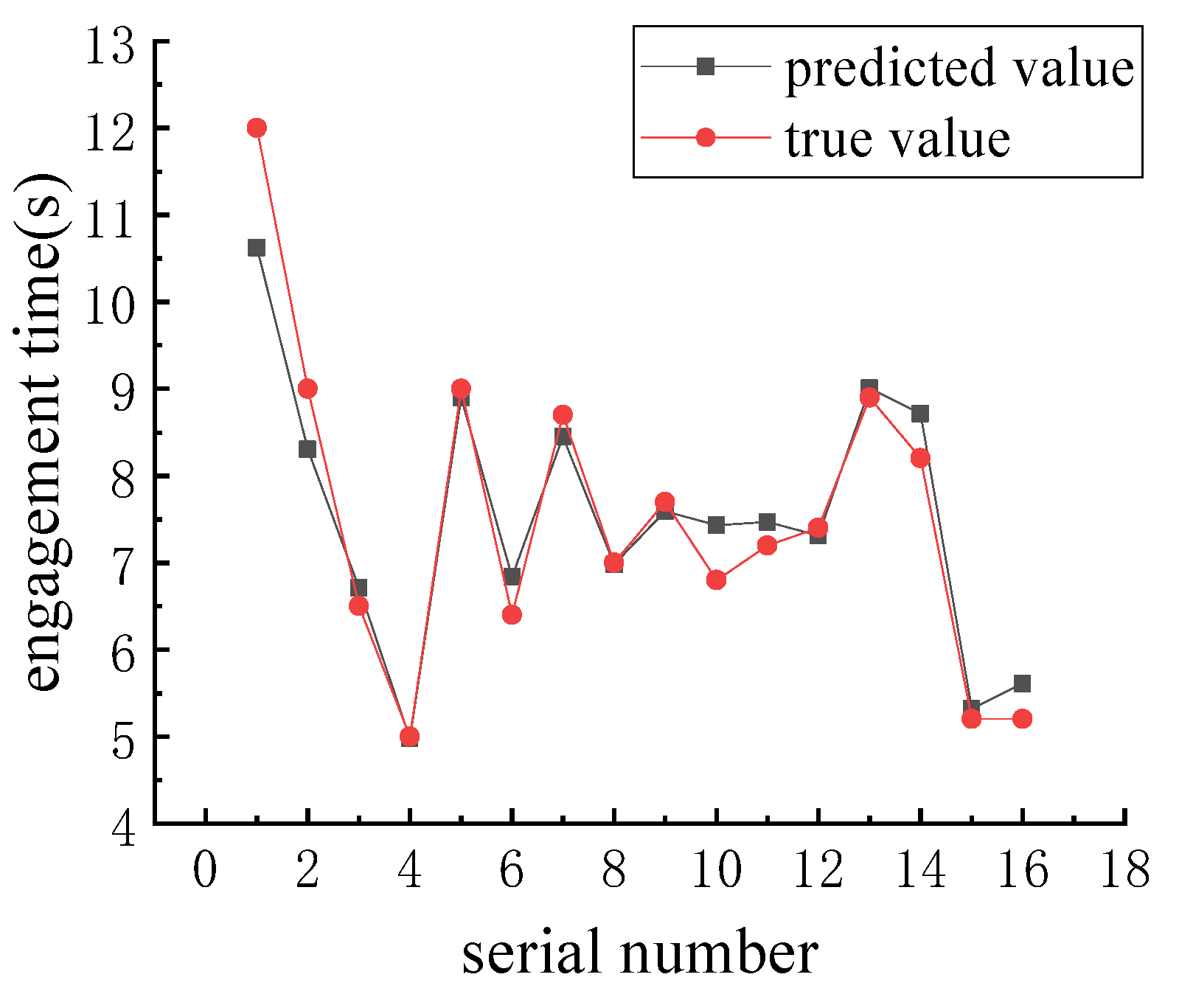
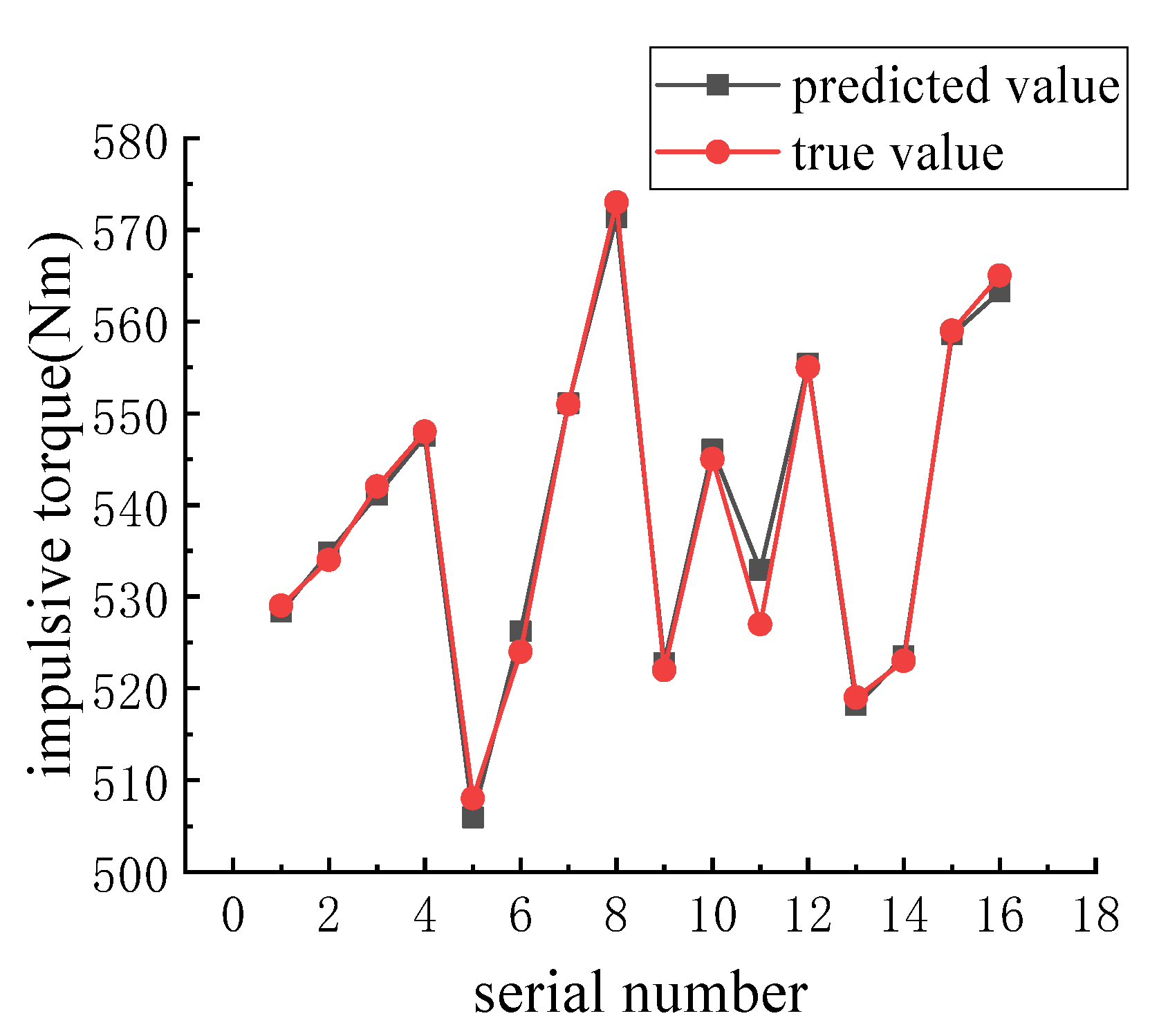
- SVR-PSO multi-objective optimization algorithm and results
5. Conclusions
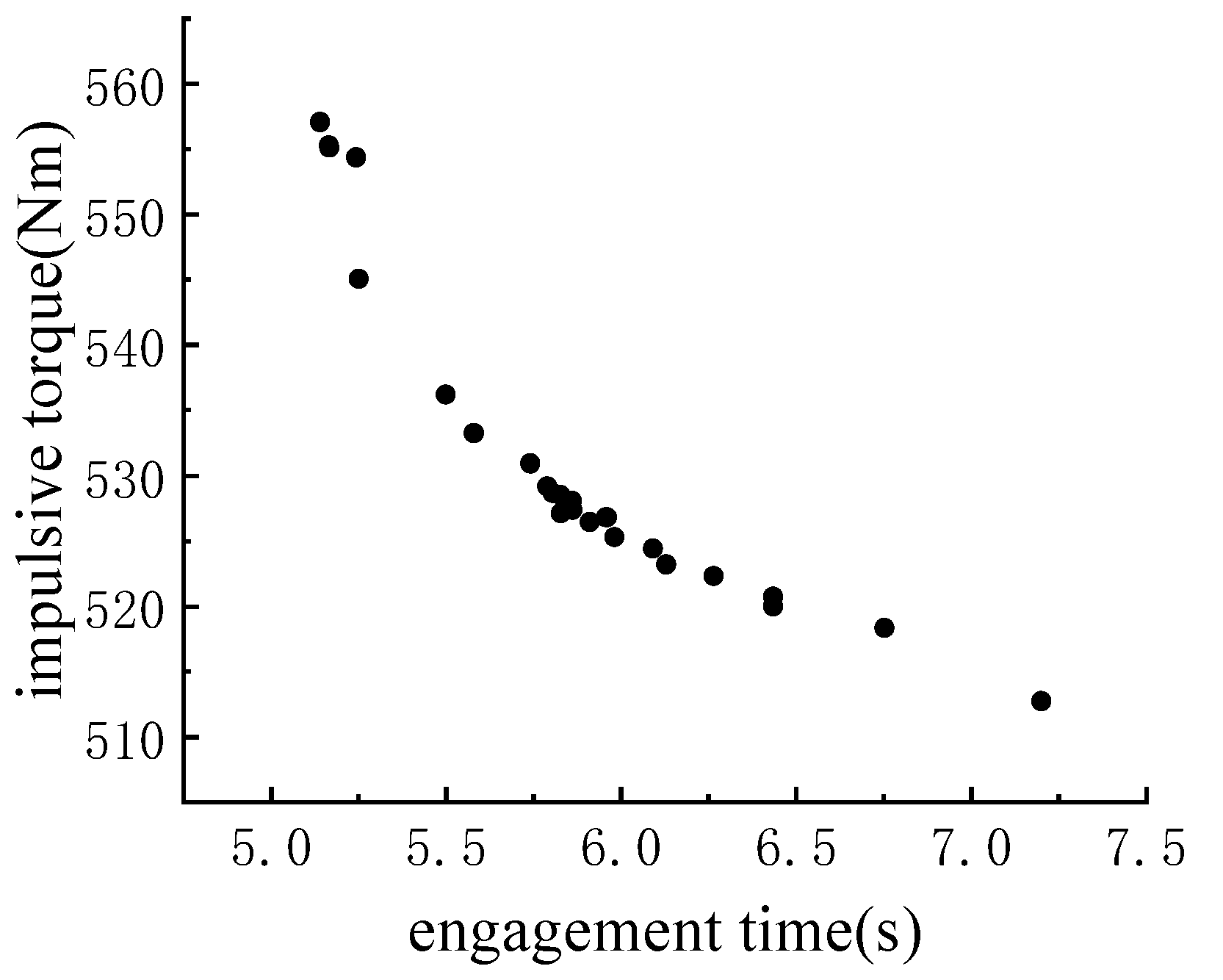
- It is found that the faster engagement pressure loading occurs along with the shorter engagement time, the larger impact torque, and the higher temperature. How to decrease simultaneously engagement time and impact torque is important to the high speed difference friction clutch.
- Compared with the traditional fixed-slope engagement pressure loading method, the pro-posed variable-slope engagement pressure loading method can reduce simultaneously the engagement time, temperature rise, and impact torque, which has good application and spread value.
- The proposed SVR-PSO optimization algorithm can obtain the best parameters of the variable-slope pressing force strategy. The optimized Pareto solution can be applied to different working conditions.
- The simulational data show good agreement with the experimental result. It means that the simulation models have high precision and application value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoggarth, R.; Mange, R. Highlights of the Lockheed Martin F-35 STOVL jet effects programme. Aeronaut. J. 2009, 113, 119–127. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, H.; Liu, Y. An evaluative review of the VTOL technologies for unmanned and manned aerial vehicles. Comput. Commun. 2020, 149, 356–369. [Google Scholar] [CrossRef]
- Zhao, L.; Lin, Y.; Li, Z.; Huang, C. Optimal starting control of zero-synchronous shock AMT based on torque compensation. Sci. Prog. 2020, 103, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhao, X.X.; Sun, J.N. Optimal Clutch Pressure Control in Shifting Process of Automatic Transmission for Heavy-Duty Mining Trucks. Math. Probl. Eng. 2020, 2020, 8618759. [Google Scholar] [CrossRef]
- Liu, Z.J.; Wang, L.; Ren, C.B. Accurate Calculation and Control of Dry Dual-Clutch Torque during Shifting Process. Adv. Mater. Res. 2012, 490, 1913–1919. [Google Scholar] [CrossRef]
- Crowther, A.; Zhang, N.; Liu, D.K.; Jeyakumaran, J.K. Analysis and simulation of clutch engagement judder and stick-slip in automotive powertrain systems. Drive Syst. Tech. 2008, 218, 1427–1446. [Google Scholar] [CrossRef]
- Crowther, A.R.; Zhang, N. Torsional finite elements and nonlinear numerical modelling in vehicle powertrain dynamics. J. Sound Vib. 2004, 284, 825–849. [Google Scholar] [CrossRef]
- Negrean, I.; Crisan, A.V.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 065301. [Google Scholar] [CrossRef]
- Lai, V.V.; Paszkiewicz, I.; Brunel, J.F.; Dufrenoy, P. Squeal occurrence related to the tracking of the bearing surfaces on a pin-on-disc system. Mech. Syst. Signal Process. 2021, 165, 108364. [Google Scholar] [CrossRef]
- Mouffak, E.; Bouchetara, M. Transient thermal behavior of automotive dry clutch discs by using Ansys software. Mechanika 2017, 22, 562–570. [Google Scholar] [CrossRef]
- Pisaturo, M.; Senatore, A. Simulation of engagement control in automotive dry-clutch and temperature field analysis through finite element model. Appl. Therm. Eng. 2016, 93, 958–966. [Google Scholar] [CrossRef]
- Wenbin, L.; Jianfeng, H.; Jie, F.; Liyun, C.; Chunyan, Y. Simulation and application of temperature field of carbon fabric wet clutch during engagement based on finite element analysis. Int. Commun. Heat Mass Transf. 2016, 71, 180–187. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Grzes, P. Mutual influence of the sliding velocity and temperature in frictional heating of the thermally nonlinear disc brake. Int. J. Therm. Sci. 2016, 102, 254–262. [Google Scholar] [CrossRef]
- Jian, Q.F.; Shui, Y. Numerical and experimental analysis of transient temperature field of ventilated disc brake under the condition of hard braking. Int. J. Therm. Sci. 2017, 122, 115–123. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, G.P.; Xia, C. Analysis of fixed-wing VTOL aircraft with gas-driven fan propulsion system. Aerosp. Sci. Technol. 2020, 104, 105984. [Google Scholar] [CrossRef]
- Li, L.; Lu, Z.; Liu, X.L.; Sun, T.; Jing, X.; Shangguan, W.B. Modeling and analysis of friction clutch at a driveline for suppressing car starting judder. J. Sound Vib. 2018, 424, 335–351. [Google Scholar] [CrossRef]
- Rao, J.G.; Selvam, P.; Sinnur, K.H. Effect of Type of Carbon Matrix on Tribological Properties of C C Aircraft Brake Discs. Def. Sci. J. 2019, 69, 585–590. [Google Scholar] [CrossRef]
- Shu, Y.; Jie, C.; Qizhong, H.; Xiang, X.; Tong, C.; Yunping, L. Effect of Braking Speeds on the Tribological Properties of Carbon/Carbon Composites. Mater. Trans. Jim 2010, 51, 1038–1043. [Google Scholar] [CrossRef]


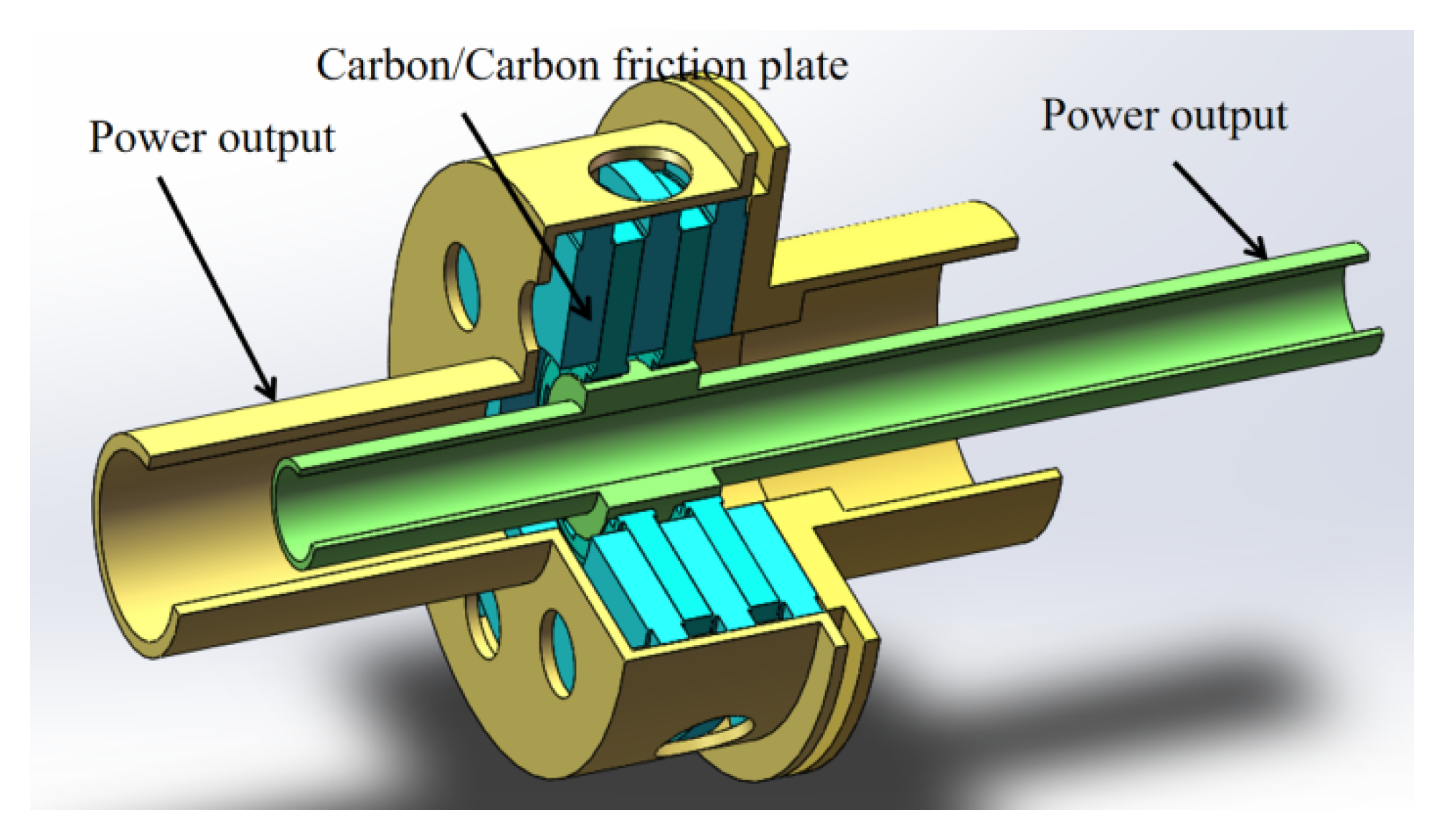






| Physical and Mechanical Properties | Numeric Value |
|---|---|
| density/(g·cm−3) | 1.76 |
| tensile strength/MPa | 55.7 |
| compressive strength/MPa | 68.8 |
| bending strength/MPa | 72.9 |
| Interlayer shear strength/MPa | 7.6 |
| Thermal conductivity W/(m·K) | 100 |
| Properties | Friction Plate | Steel |
|---|---|---|
| Thermal conductivity | 100 W/(m·K) | 46 W/(m·K) |
| Specific heat capacity | 1800 J/(kg·K) | 300 J/(kg·K) |
| Density | 753 kg/m3 | 7800 kg/m3 |
| Loading Mode | Engagement Time (s) | Impact Torque (Nm) | Maximum Temperature (°C) |
|---|---|---|---|
| up time is 8 s | 6.5 | 539 | 215 |
| up time is 10 s | 8 | 529 | 234 |
| variable-slope | 5.9 | 523 | 184 |
| Factor | Horizontal | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| k1 (N/s) | 150 | 200 | 260 | 350 |
| k2 (N/s) | 1500 | 2000 | 2500 | 3000 |
| k3 (N/s) | 200 | 300 | 400 | 500 |
| w1 (rad/s) | 400 | 430 | 480 | 510 |
| w2 (rad/s) | 10 | 20 | 30 | 40 |
| Order Number | k1 (N/s) | k2 (N/s) | k3 (N/s) | w1 (Rad/s) | w2 (Rad/s) | T (s) | M (N·m) |
|---|---|---|---|---|---|---|---|
| 1 | 150 | 1500 | 200 | 400 | 10 | 12 | 529 |
| 2 | 150 | 2000 | 300 | 430 | 20 | 9 | 534 |
| 3 | 150 | 2500 | 400 | 480 | 30 | 6.5 | 542 |
| 4 | 150 | 3000 | 500 | 510 | 40 | 5 | 548 |
| 5 | 200 | 1500 | 300 | 480 | 40 | 9 | 508 |
| 6 | 200 | 2000 | 200 | 510 | 30 | 6.4 | 524 |
| 7 | 200 | 2500 | 500 | 400 | 20 | 8.7 | 551 |
| 8 | 200 | 3000 | 400 | 430 | 10 | 7 | 573 |
| 9 | 260 | 1500 | 400 | 510 | 20 | 7.7 | 522 |
| 10 | 260 | 2000 | 500 | 480 | 10 | 6.8 | 545 |
| 11 | 260 | 2500 | 200 | 430 | 40 | 7.2 | 527 |
| 12 | 260 | 3000 | 300 | 400 | 30 | 7.4 | 555 |
| 13 | 350 | 1500 | 500 | 430 | 30 | 8.9 | 519 |
| 14 | 350 | 2000 | 400 | 400 | 40 | 8.2 | 523 |
| 15 | 350 | 2500 | 300 | 510 | 10 | 5.2 | 559 |
| 16 | 350 | 3000 | 200 | 480 | 20 | 5.2 | 565 |
| Order Number | k1 (N/s) | k2 (N/s) | k3 (N/s) | w1 (Rad/s) | w2 (Rad/s) | Time (s) | Actual Time (s) | Fractional Error (%) | Impulsive Torque (N·m) | Actual Impact Torque (N·m) | Fractional Error (%) | Maximum Temperature (°C) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 260 | 1635 | 412 | 489 | 40 | 7.2 | 7.9 | 8.9 | 513 | 512 | 0.2 | 202 |
| 2 | 300 | 2639 | 249 | 510 | 15 | 5.1 | 5 | 2 | 557 | 560 | 0.5 | 181 |
| 3 | 287 | 2486 | 229 | 503 | 36 | 5.5 | 5.5 | 0 | 536 | 534 | 0.4 | 175 |
| 4 | 279 | 1847 | 253 | 485 | 38 | 6.8 | 7.3 | 6.8 | 518 | 514 | 0.8 | 198 |
| 5 | 303 | 1896 | 247 | 492 | 36 | 6.4 | 6.9 | 7.2 | 521 | 514 | 1.4 | 201 |
| 6 | 300 | 2141 | 244 | 505 | 35 | 5.9 | 6 | 1.7 | 528 | 523 | 1 | 188 |
| average error | 4.4 | average error | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Chen, Z.; Shi, Z.; Zhang, Y. Study on the Engagement Characteristics and Control Strategy of High Speed Difference Dry Friction Clutch. Machines 2023, 11, 407. https://doi.org/10.3390/machines11030407
Zhu C, Chen Z, Shi Z, Zhang Y. Study on the Engagement Characteristics and Control Strategy of High Speed Difference Dry Friction Clutch. Machines. 2023; 11(3):407. https://doi.org/10.3390/machines11030407
Chicago/Turabian StyleZhu, Chu, Zhi Chen, Zongcai Shi, and Yingdong Zhang. 2023. "Study on the Engagement Characteristics and Control Strategy of High Speed Difference Dry Friction Clutch" Machines 11, no. 3: 407. https://doi.org/10.3390/machines11030407
APA StyleZhu, C., Chen, Z., Shi, Z., & Zhang, Y. (2023). Study on the Engagement Characteristics and Control Strategy of High Speed Difference Dry Friction Clutch. Machines, 11(3), 407. https://doi.org/10.3390/machines11030407