Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation
Abstract
1. Introduction
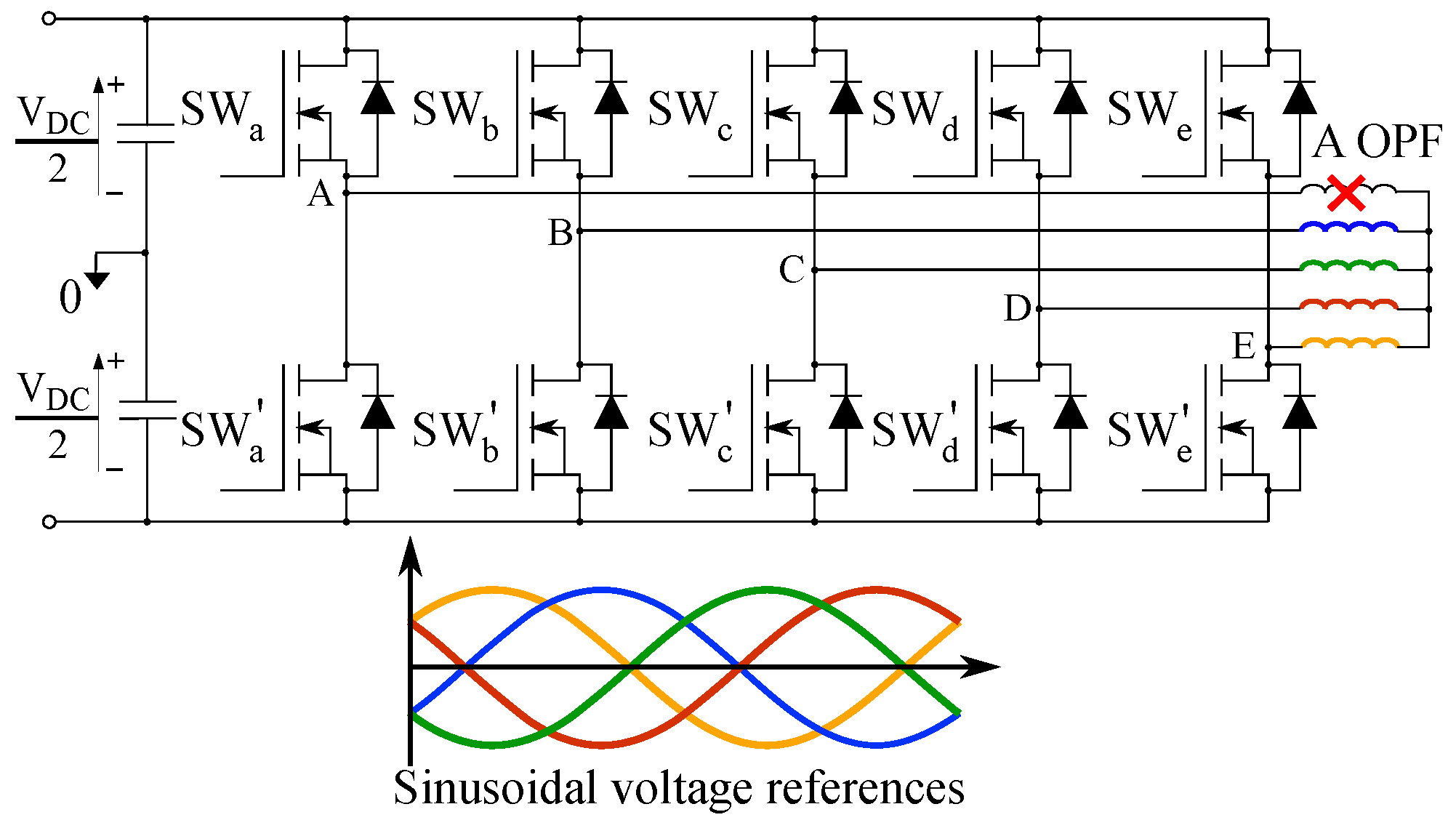
2. Fault-Tolerant Control
3. Proposed Hybrid Discontinuous Modulation
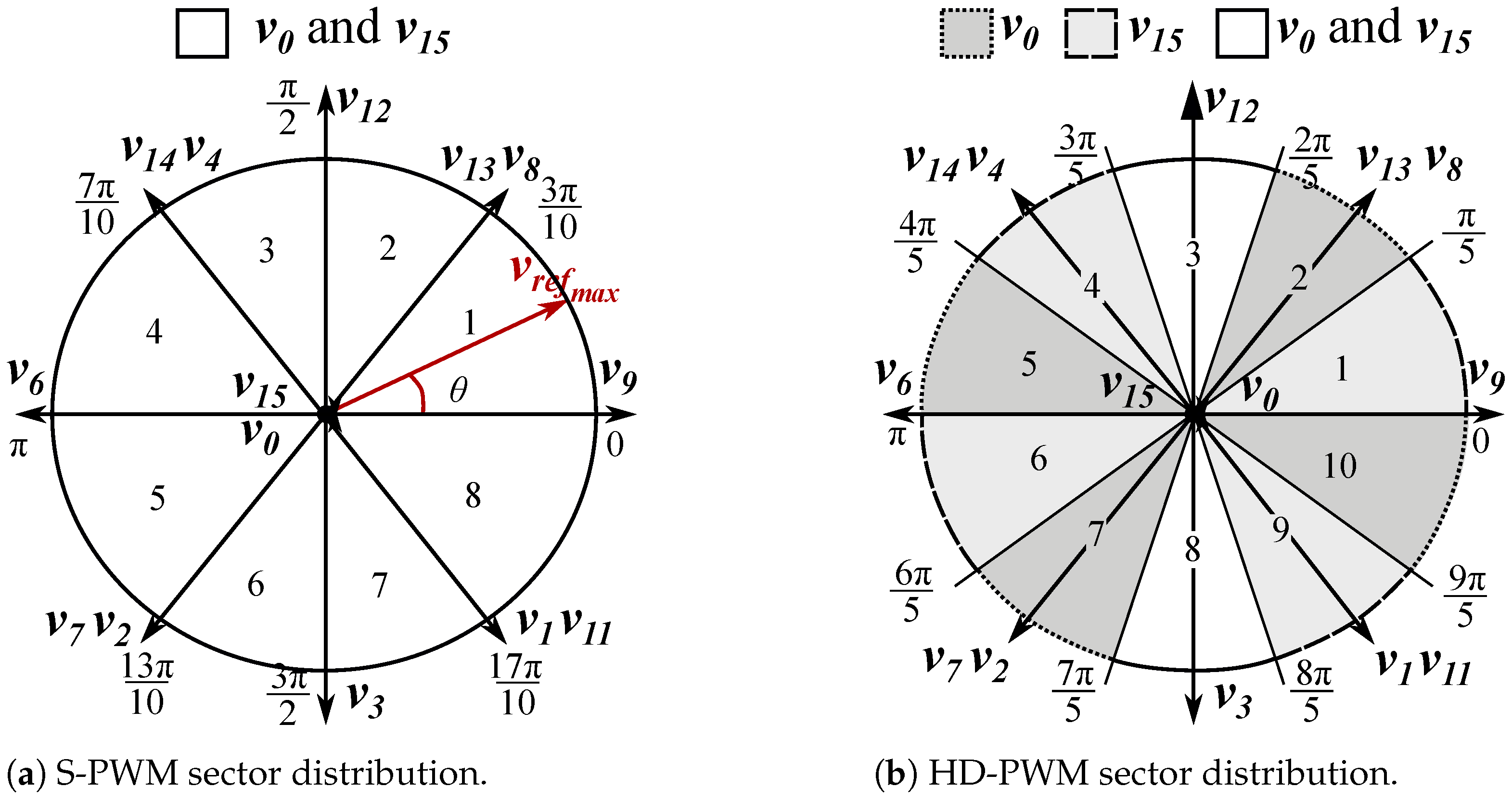
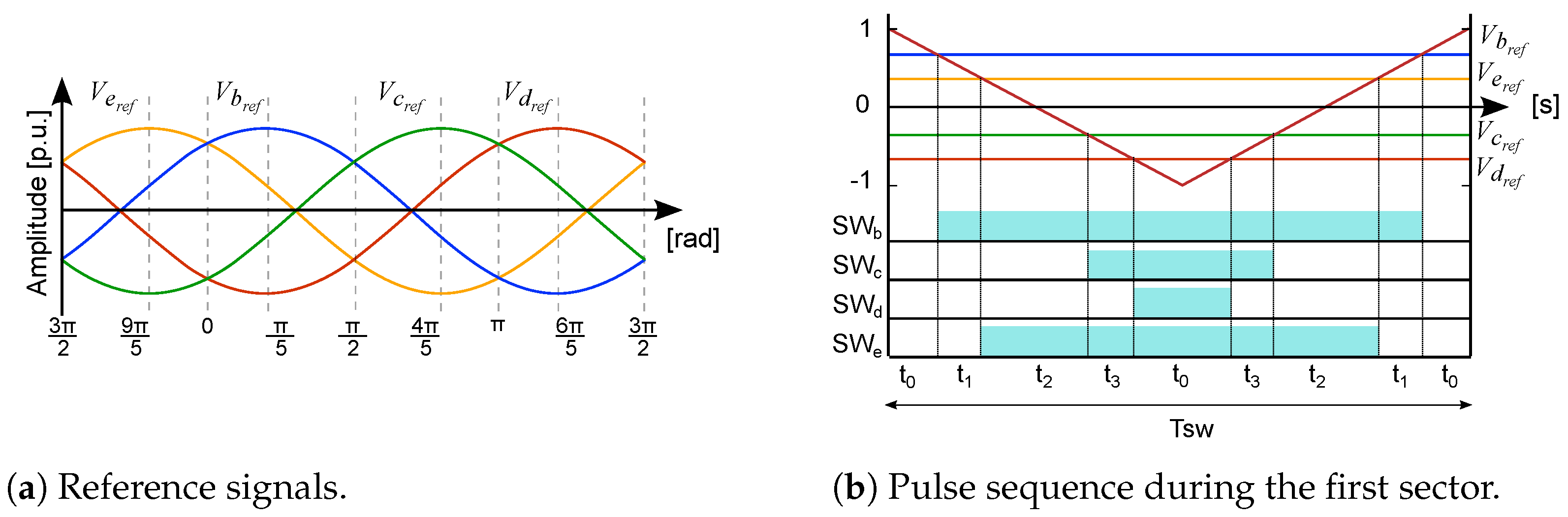
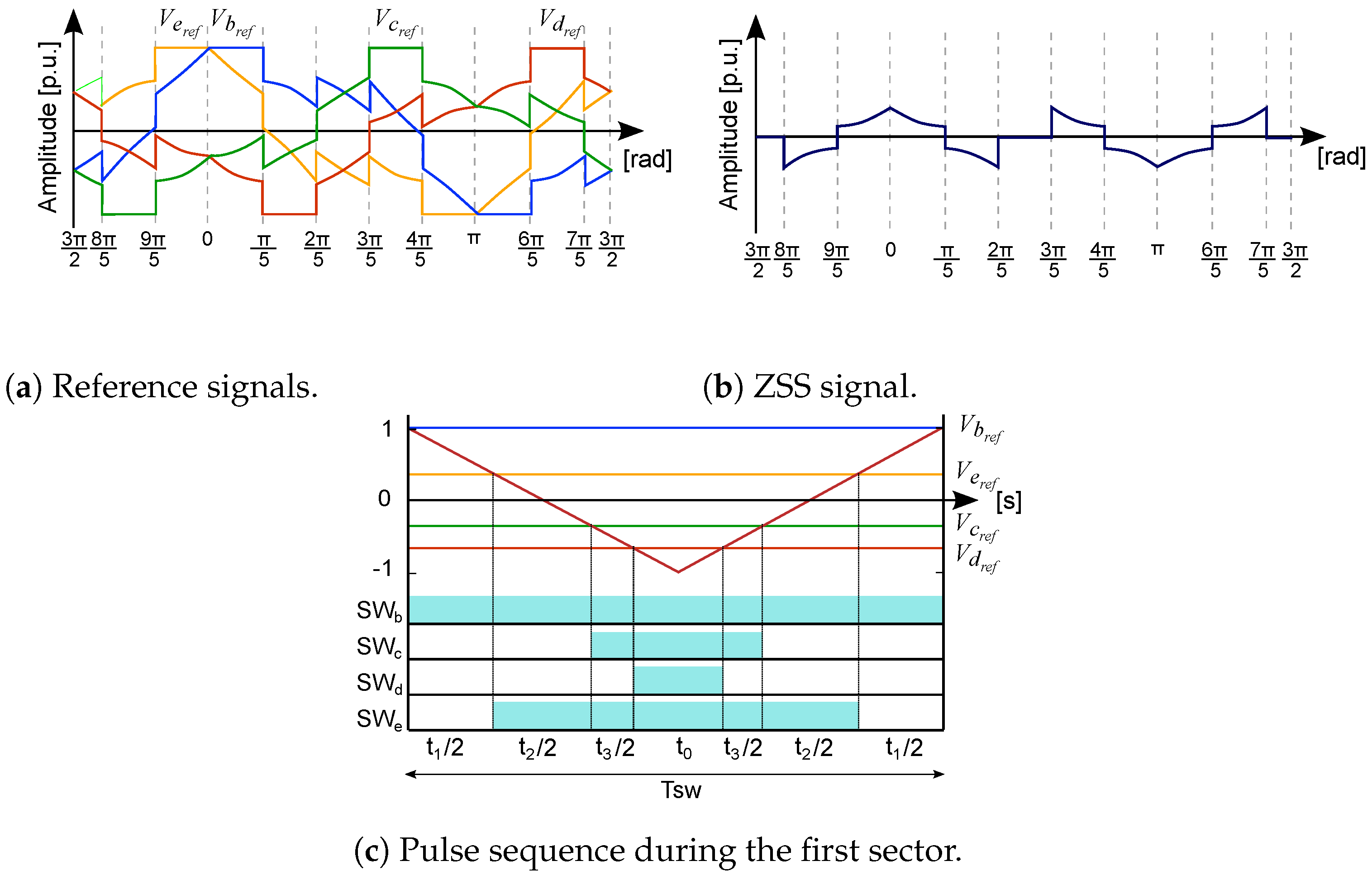
3.1. Principle of the HD-PWM
3.2. HD-PWM Harmonic Distortion Factor
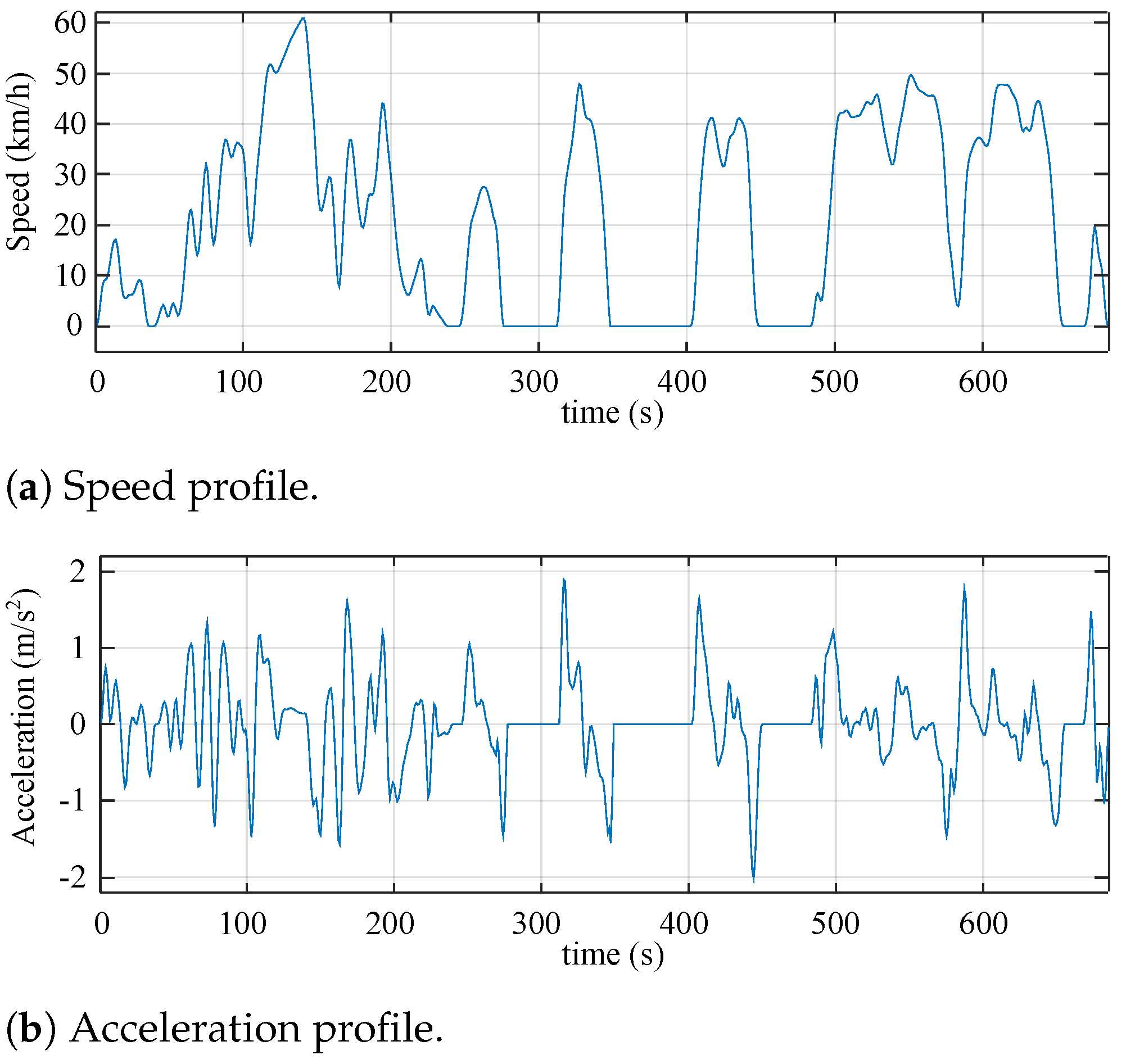
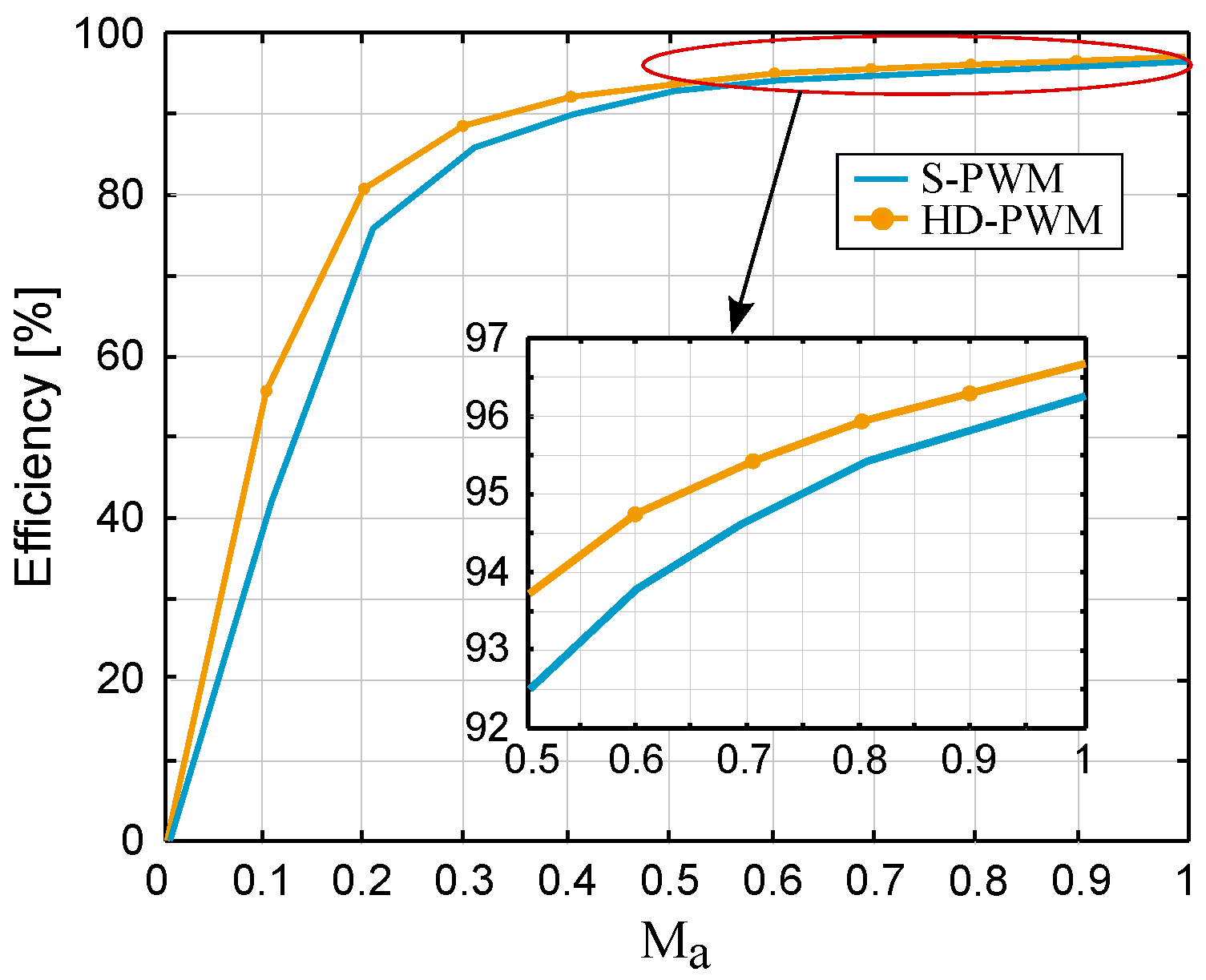
4. Simulation-Based Switching Loss Analysis of the Proposed HD-PWM
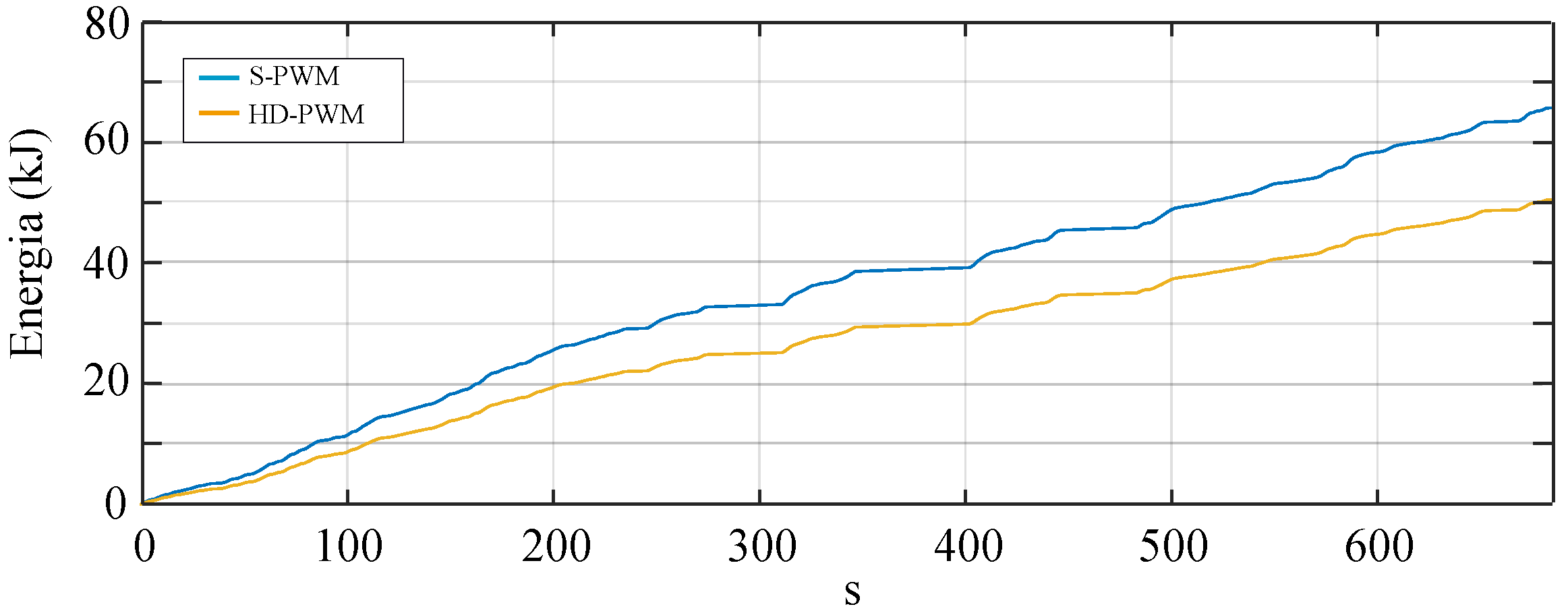
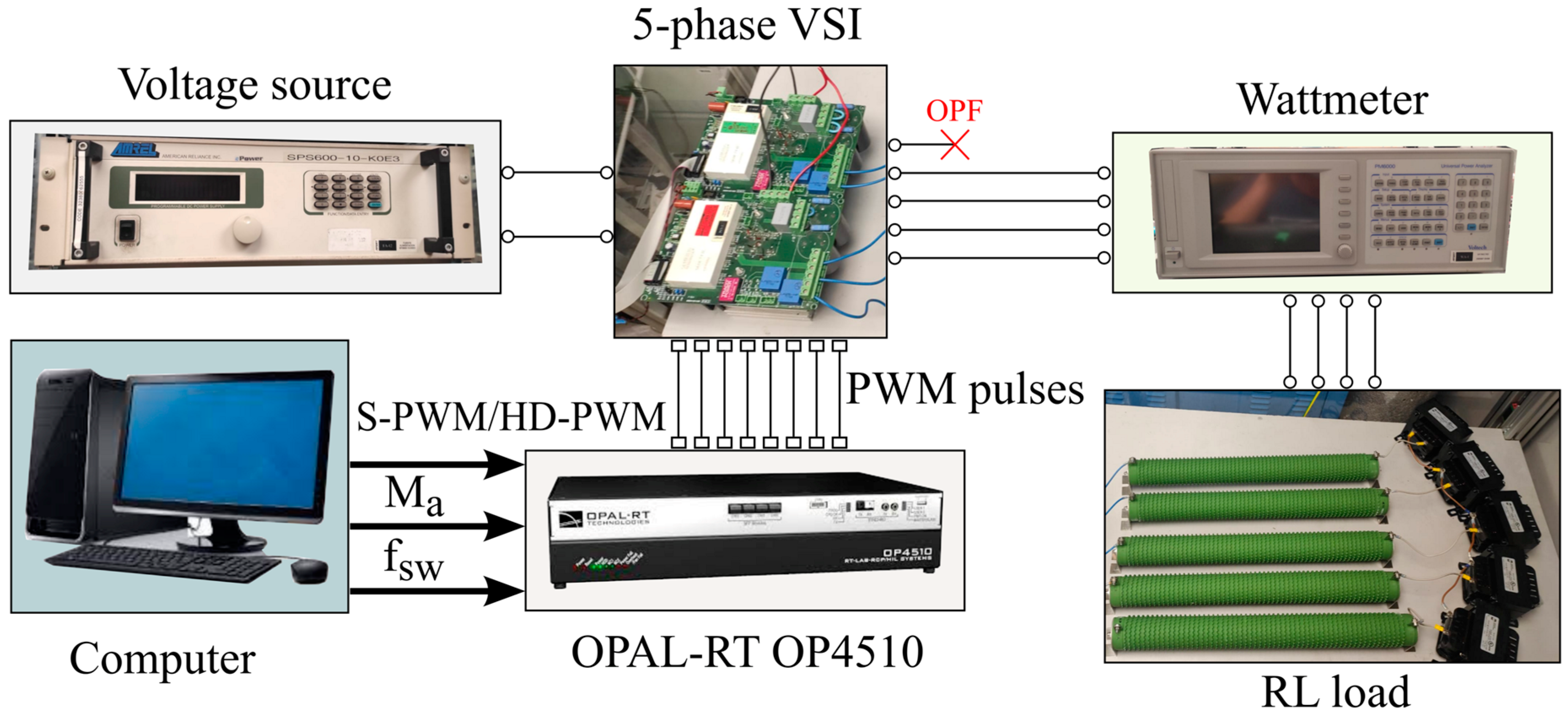
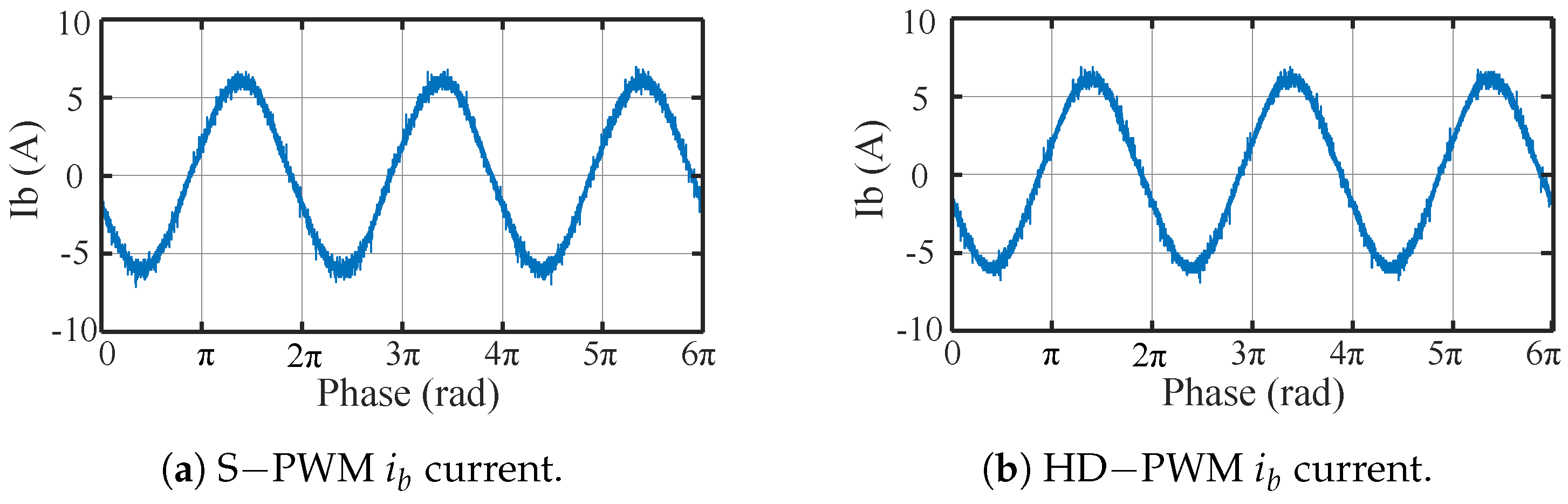
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Switching frequency | |
| Angular frequency | |
| Commutation period | |
| Neutral-point voltage mean value | |
| Motor flux | |
| Angular position | |
| Maximum modulation index | |
| Maximum phase-to-neutral voltage | |
| Modulation index | |
| Zero-vector application time | |
| Modulation signal | |
| Zero-sequence signal | |
| Clamping time | |
| DC voltage level |
References
- Liu, H.; Wang, D.; Yi, X.; Meng, F. Torque Ripple Suppression Under Open-Phase Fault Conditions in a Five-Phase Induction Motor With Harmonic Injection. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 274–288. [Google Scholar] [CrossRef]
- Chikondra, B.; Muduli, U.R.; Behera, R.K. An Improved Open-Phase Fault-Tolerant DTC Technique for Five-Phase Induction Motor Drive Based on Virtual Vectors Assessment. IEEE Trans. Ind. Electron. 2021, 68, 4598–4609. [Google Scholar] [CrossRef]
- Tong, M.; Hua, W.; Su, P.; Cheng, M.; Meng, J. Investigation of a Vector-Controlled Five-Phase Flux-Switching Permanent-Magnet Machine Drive System. IEEE Trans. Magn. 2016, 52, 1–5. [Google Scholar] [CrossRef]
- Kumar, M.S.; Revankar, S.T. Development scheme and key technology of an electric vehicle: An overview. Renew. Sustain. Energy Rev. 2017, 70, 1266–1285. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Shen, Y.; Mao, J. A Nine-Phase Permanent Magnet Electric-Drive-Reconstructed Onboard Charger for Electric Vehicle. IEEE Trans. Energy Convers. 2018, 33, 2091–2101. [Google Scholar] [CrossRef]
- Yin, Z.; Sui, Y.; Xing, L.; Zheng, P.; Cheng, L.; Liu, J. Comparative Investigations of Inverter Short-Circuit Fault and Winding Terminal Short-Circuit Fault in Open-End Winding Five-Phase PM Machine System. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Robles, E.; Fernandez, M.; Andreu, J.; Ibarra, E.; Zaragoza, J.; Ugalde, U. Common-mode voltage mitigation in multiphase electric motor drive systems. Renew. Sustain. Energy Rev. 2022, 157, 111971. [Google Scholar] [CrossRef]
- Prieto, B. Design and Analysis of Fractional-Slot Concentrated-Winding Multiphase Fault-Tolerant Permanent Magnet Synchronous Machines. Ph.D. Thesis, Tecnum Universidad de Navarra, Gipuzkoa, Spain, 2015. [Google Scholar]
- Smet, V.; Forest, F.; Huselstein, J.J.; Richardeau, F.; Khatir, Z.; Lefebvre, S.; Berkani, M. Ageing and Failure Modes of IGBT Modules in High-Temperature Power Cycling. IEEE Trans. Ind. Electron. 2011, 58, 4931–4941. [Google Scholar] [CrossRef]
- Bahman, A.S.; Iannuzzo, F. 8—Computer-aided engineering simulations. In Wide Bandgap Power Semiconductor Packaging; Suganuma, K., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Cambridge, UK, 2018; pp. 199–223. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Lefebvre, S.; Joubert, P.Y.; Labrousse, D.; Bontemps, S. Estimating Current Distributions in Power Semiconductor Dies Under Aging Conditions: Bond Wire Liftoff and Aluminum Reconstruction. IEEE Trans. Components Packag. Manuf. Technol. 2015, 5, 483–495. [Google Scholar] [CrossRef]
- Guzman, H.; Gonzalez, T.; Barrero, F.; Durán, M. Open-Phase Fault Operation on Multiphase Induction Motor Drives. In Induction Motors—Applications, Control and Fault Diagnostics; IntechOpen: London, UK, 2015. [Google Scholar] [CrossRef]
- Sen, B.; Wang, J. Stationary Frame Fault-Tolerant Current Control of Polyphase Permanent-Magnet Machines Under Open-Circuit and Short-Circuit Faults. IEEE Trans. Power Electron. 2016, 31, 4684–4696. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.; Liu, G.; Cheng, R.; Xie, Y. Remedial Field-Oriented Control of Five-Phase Fault-Tolerant Permanent-Magnet Motor by Using Reduced-Order Transformation Matrices. IEEE Trans. Ind. Electron. 2017, 64, 169–178. [Google Scholar] [CrossRef]
- Epstein, A.H.; O’Flarity, S.M. Considerations for Reducing Aviation’s CO2 with Aircraft Electric Propulsion. J. Propuls. Power 2019, 35, 572–582. [Google Scholar] [CrossRef]
- Qi, X.; Holtz, J. Modeling and Control of Low Switching Frequency High-Performance Induction Motor Drives. IEEE Trans. Ind. Electron. 2020, 67, 4402–4410. [Google Scholar] [CrossRef]
- Tian, B.; Sun, L.; Molinas, M.; An, Q. Repetitive Control Based Phase Voltage Modulation Amendment for FOC-Based Five-Phase PMSMs Under Single-Phase Open Fault. IEEE Trans. Ind. Electron. 2020, 68, 1949–1960. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A. Fault-Tolerant Interior-Permanent-Magnet Machines for Hybrid Electric Vehicle Applications. IEEE Trans. Veh. Technol. 2007, 56, 1546–1552. [Google Scholar] [CrossRef]
- Tian, B.; Molinas, M.; An, Q. PWM Investigation of a Field-Oriented Controlled Five-Phase PMSM Under Two-Phase Open Faults. IEEE Trans. Energy Convers. 2020, 36, 580–593. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, X.; Cui, R.; Han, S. A Generalized Open-Circuit Fault-Tolerant Control Strategy for FOC and DTC of Five-Phase Fault-Tolerant Permanent-Magnet Motor. IEEE Trans. Ind. Electron. 2022, 69, 7825–7836. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Hu, M.; Zhu, J. Model Predictive Torque Control with SVM for Five-Phase PMSM Under Open-Circuit Fault Condition. IEEE Trans. Power Electron. 2020, 35, 5531–5540. [Google Scholar] [CrossRef]
- Liu, G.; Qu, L.; Zhao, W.; Chen, Q.; Xie, Y. Comparison of Two SVPWM Control Strategies of Five-Phase Fault-Tolerant Permanent-Magnet Motor. IEEE Trans. Power Electron. 2016, 31, 6621–6630. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, W.; Liu, G.; Lin, Z. Extension of Virtual-Signal-Injection-Based MTPA Control for Five-Phase IPMSM Into Fault-Tolerant Operation. IEEE Trans. Ind. Electron. 2019, 66, 944–955. [Google Scholar] [CrossRef]
- Tian, B.; An, Q.T.; Duan, J.D.; Sun, D.Y.; Sun, L.; Semenov, D. Decoupled Modeling and Nonlinear Speed Control for Five-Phase PM Motor Under Single-Phase Open Fault. IEEE Trans. Power Electron. 2017, 32, 5473–5486. [Google Scholar] [CrossRef]
- Chen, Q.; Gu, L.; Lin, Z.; Liu, G. Extension of Space-Vector-Signal-Injection-Based MTPA Control Into SVPWM Fault-Tolerant Operation for Five-Phase IPMSM. IEEE Trans. Ind. Electron. 2020, 67, 7321–7333. [Google Scholar] [CrossRef]
- Cheng, L.; Sui, Y.; Zheng, P.; Wang, P.; Wu, F. Implementation of Postfault Decoupling Vector Control and Mitigation of Current Ripple for Five-Phase Fault-Tolerant PM Machine Under Single-Phase Open-Circuit Fault. IEEE Trans. Power Electron. 2018, 33, 8623–8636. [Google Scholar] [CrossRef]
- Depenbrock, M. Pulse width control of a 3-phase inverter with nonsi-nusoidal phase voltages. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988; pp. 399–403. [Google Scholar]
- Dujic, D.; Jones, M.; Levi, E. Analysis of Output Current Ripple rms in Multiphase Drives Using Space Vector Approach. IEEE Trans. Power Electron. 2009, 24, 1926–1938. [Google Scholar] [CrossRef]
- Prieto, J.; Jones, M.; Barrero, F.; Levi, E.; Toral, S. Comparative Analysis of Discontinuous and Continuous PWM Techniques in VSI-Fed Five-Phase Induction Motor. IEEE Trans. Ind. Electron. 2011, 58, 5324–5335. [Google Scholar] [CrossRef]
- Fernandez, M.; Ibarra, E.; Robles, E.; Cuñado, O.; Aranguren, M.; Kortabarria, I.; Bouzid, Y. FPGA and CPU based real-time simulation platform for EV propulsion system analysis under driving cycles. In Proceedings of the Conference on Design of Circuits and Integrated Systems (DCIS), Bilbao, Spain, 20–22 November 2019. [Google Scholar]
- Ko, J.; Jin, D.; Jang, W.; Myung, C.L.; Kwon, S.; Park, S. Comparative investigation of NOx emission characteristics from a Euro 6-compliant diesel passenger car over the NEDC and WLTC at various ambient temperatures. Appl. Energy 2017, 187, 652–662. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Lee, H.H. Development of a Three-to-Five-Phase Indirect Matrix Converter with Carrier-Based PWM Based on Space-Vector Modulation Analysis. IEEE Trans. Ind. Electron. 2016, 63, 13–24. [Google Scholar] [CrossRef]
- Lemmens, J.; Vanassche, P.; Driesen, J. Optimal Control of Traction Motor Drives Under Electrothermal Constraints. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 249–263. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mascarella, D.; Joos, G. Space-Vector-Based Generalized Discontinuous Pulsewidth Modulation for Three-Level Inverters Operating at Lower Modulation Indices. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 912–924. [Google Scholar] [CrossRef]
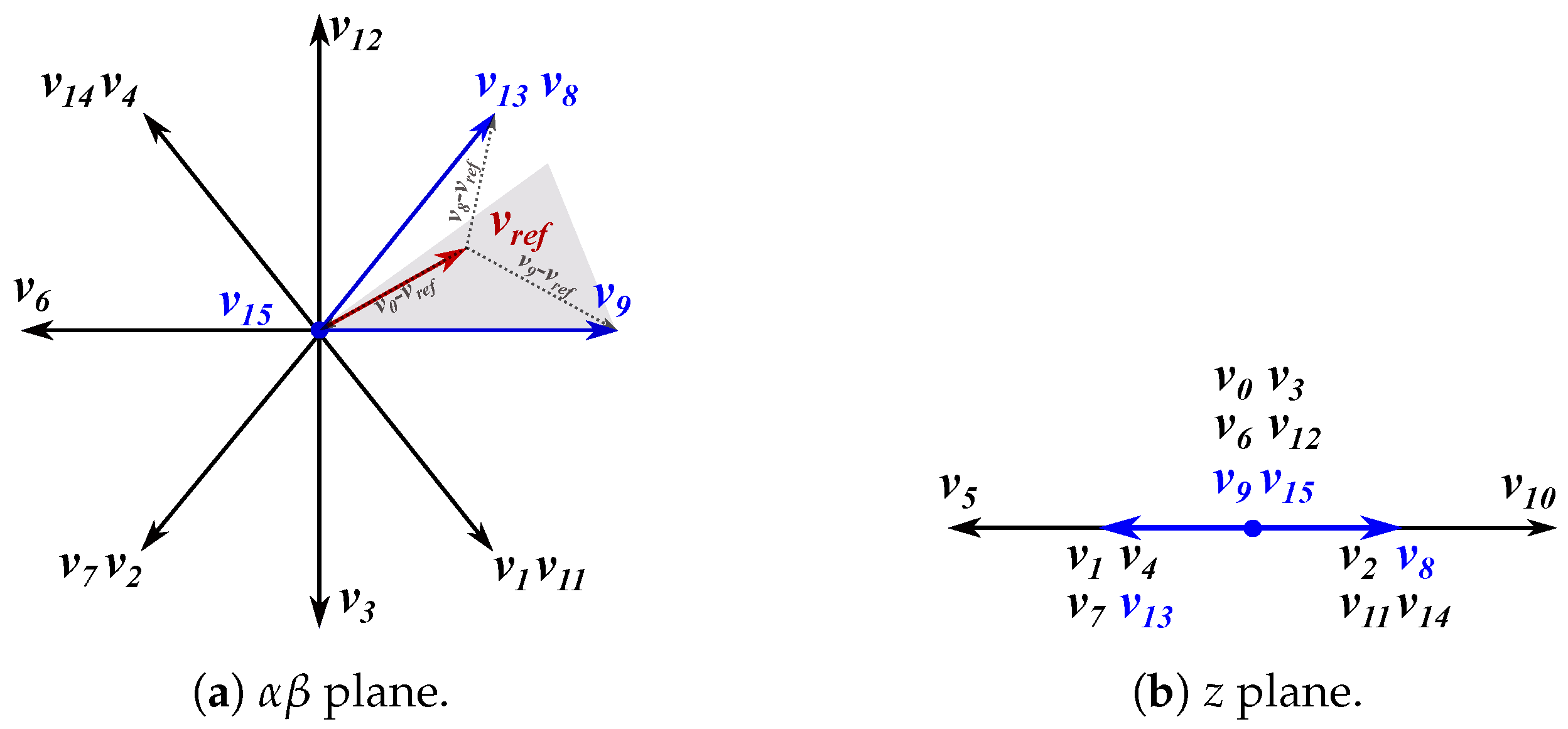
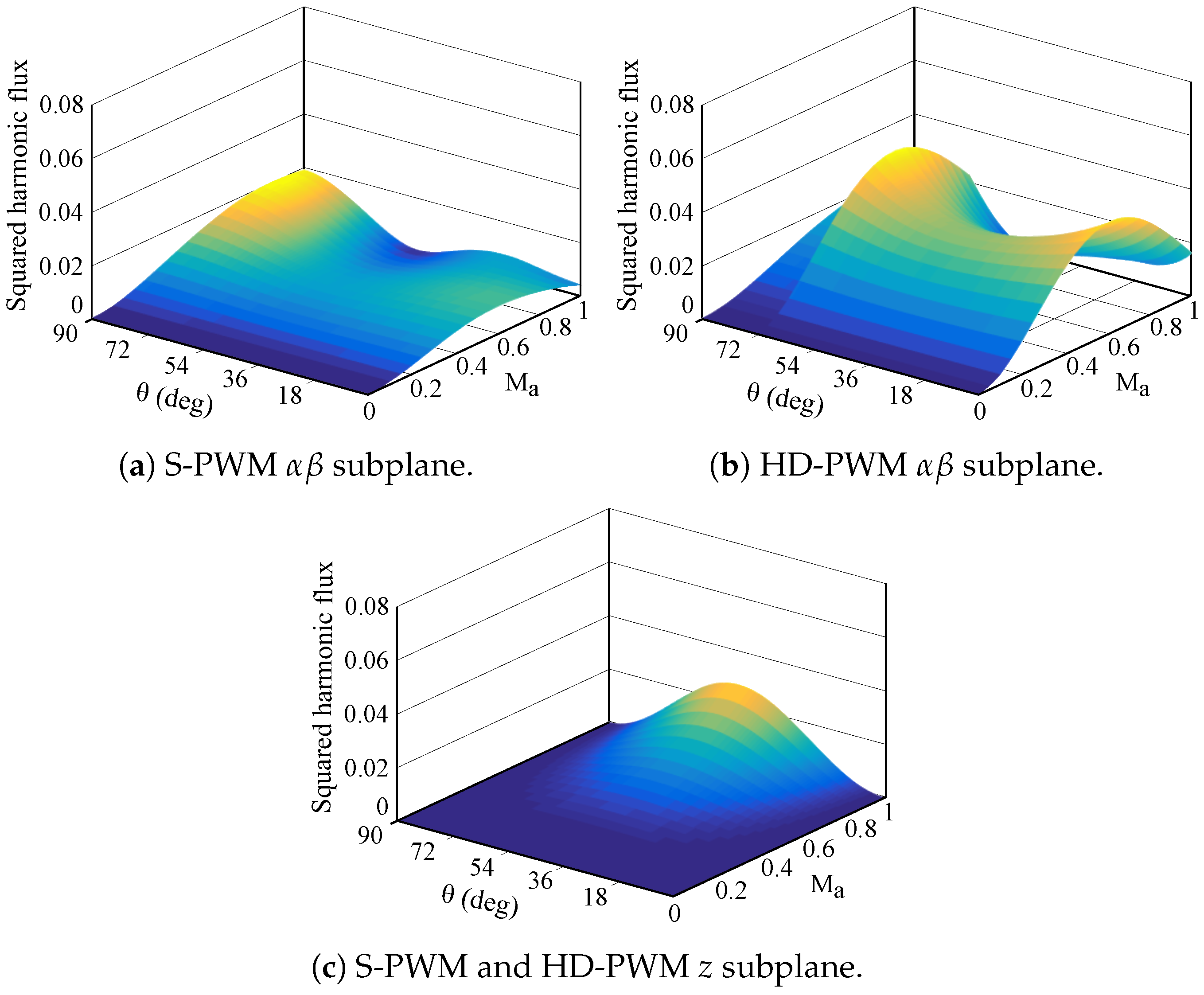
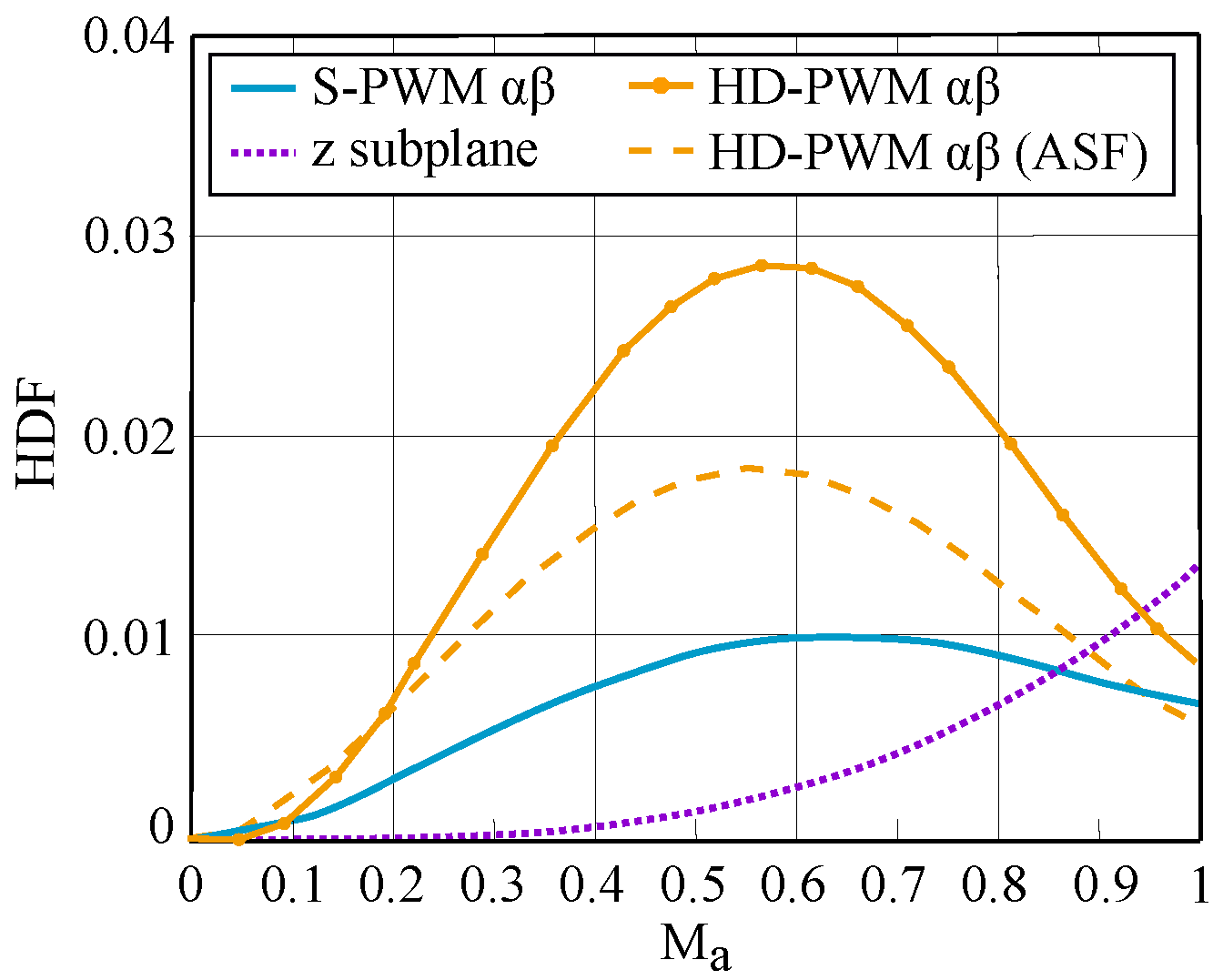
| Sectors 1 and 5 | Sectors 2 and 6 | Sectors 3 and 7 | Sectors 4 and 8 | |
|---|---|---|---|---|
| = | ||||
| 1st Harm. | 3rd Harm. | 5th Harm. | 7th Harm. | 9th Harm. | |
|---|---|---|---|---|---|
| S−PWM | 100 | 1.94 | 0.83 | 0.13 | 0.07 |
| HD−PWM | 100 | 1.75 | 0.95 | 0.24 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandez, M.; Robles, E.; Aretxabaleta, I.; Kortabarria, I.; Martín, J.L. Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation. Machines 2023, 11, 404. https://doi.org/10.3390/machines11030404
Fernandez M, Robles E, Aretxabaleta I, Kortabarria I, Martín JL. Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation. Machines. 2023; 11(3):404. https://doi.org/10.3390/machines11030404
Chicago/Turabian StyleFernandez, Markel, Endika Robles, Iker Aretxabaleta, Iñigo Kortabarria, and José Luis Martín. 2023. "Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation" Machines 11, no. 3: 404. https://doi.org/10.3390/machines11030404
APA StyleFernandez, M., Robles, E., Aretxabaleta, I., Kortabarria, I., & Martín, J. L. (2023). Proposal of Hybrid Discontinuous PWM Technique for Five-Phase Inverters under Open-Phase Fault Operation. Machines, 11(3), 404. https://doi.org/10.3390/machines11030404






