Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles
Abstract
1. Introduction
- This paper proposes new measures for PTC. With the measures, path tracking controllers are compared with one another. From comparison, it is known which controller is superior to another in terms of path tracking, steering effort and lateral stability.
- This paper verifies that most path tracking controllers are effective for path tracking on low-μ roads if it is finely tuned. Differently from previous works adopting a switching or coordination method between path tracking and lateral stability on low μ roads, most of controllers can improve the path tracking performance while preserving lateral stability on low-μ roads. Moreover, the controllers tuned on low-μ roads can be directly used for path tracking on high-μ ones.
- This paper investigates the effect of 4WS on path tracking performance on low-μ roads. In the area of vehicle stability control, 4WS has been recommended for lateral stability. However, in this paper, it is shown that it is not desirable to use 4WS for path tracking on low-μ roads because it provides little improvement over FWS.
2. Design of Path Tracking Controllers
2.1. Pure Pursuit Method
2.2. Stanley Method
2.3. LQR
2.4. PID Control
2.5. SMC
2.6. MPC
2.7. Yaw Rate Tracking Control Method
3. Performance Measures for Path Tracking Control
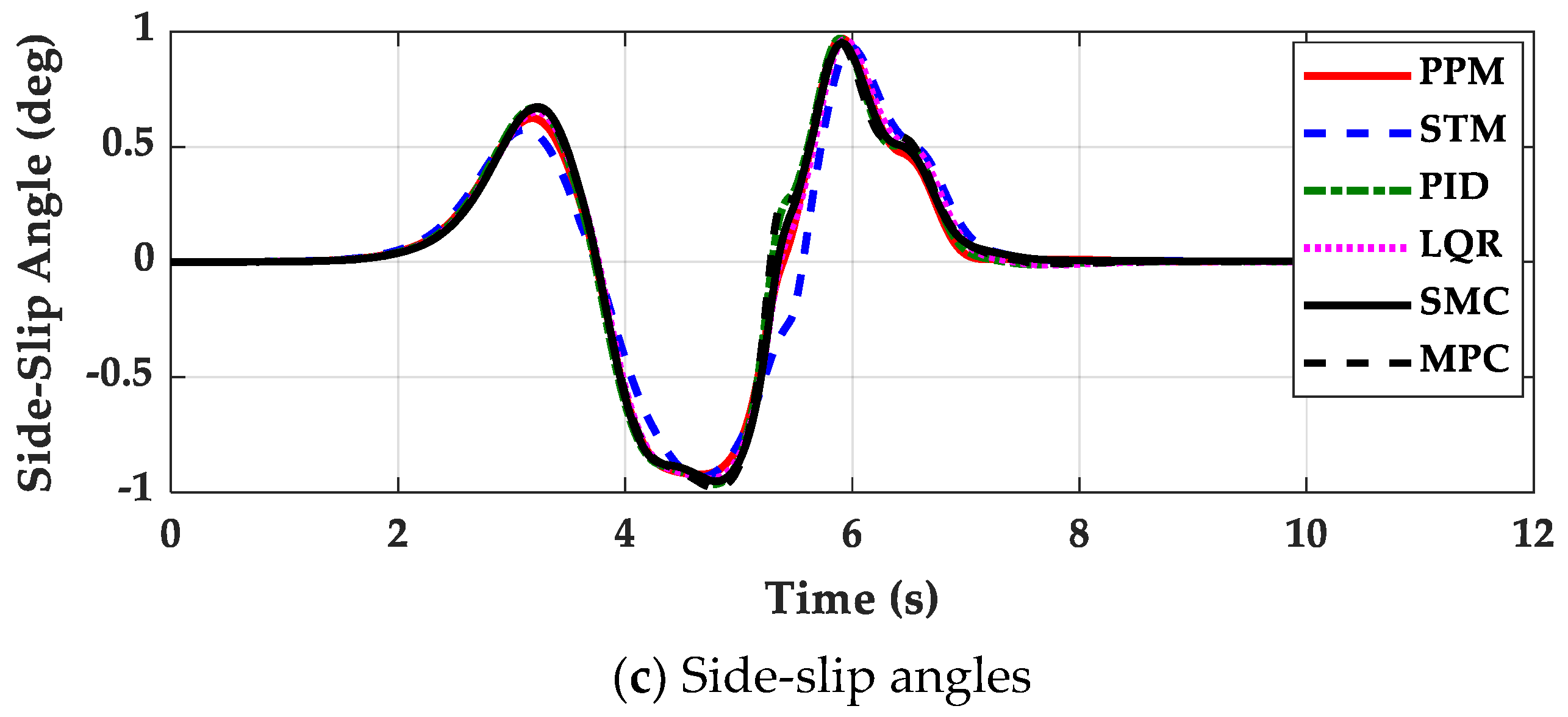
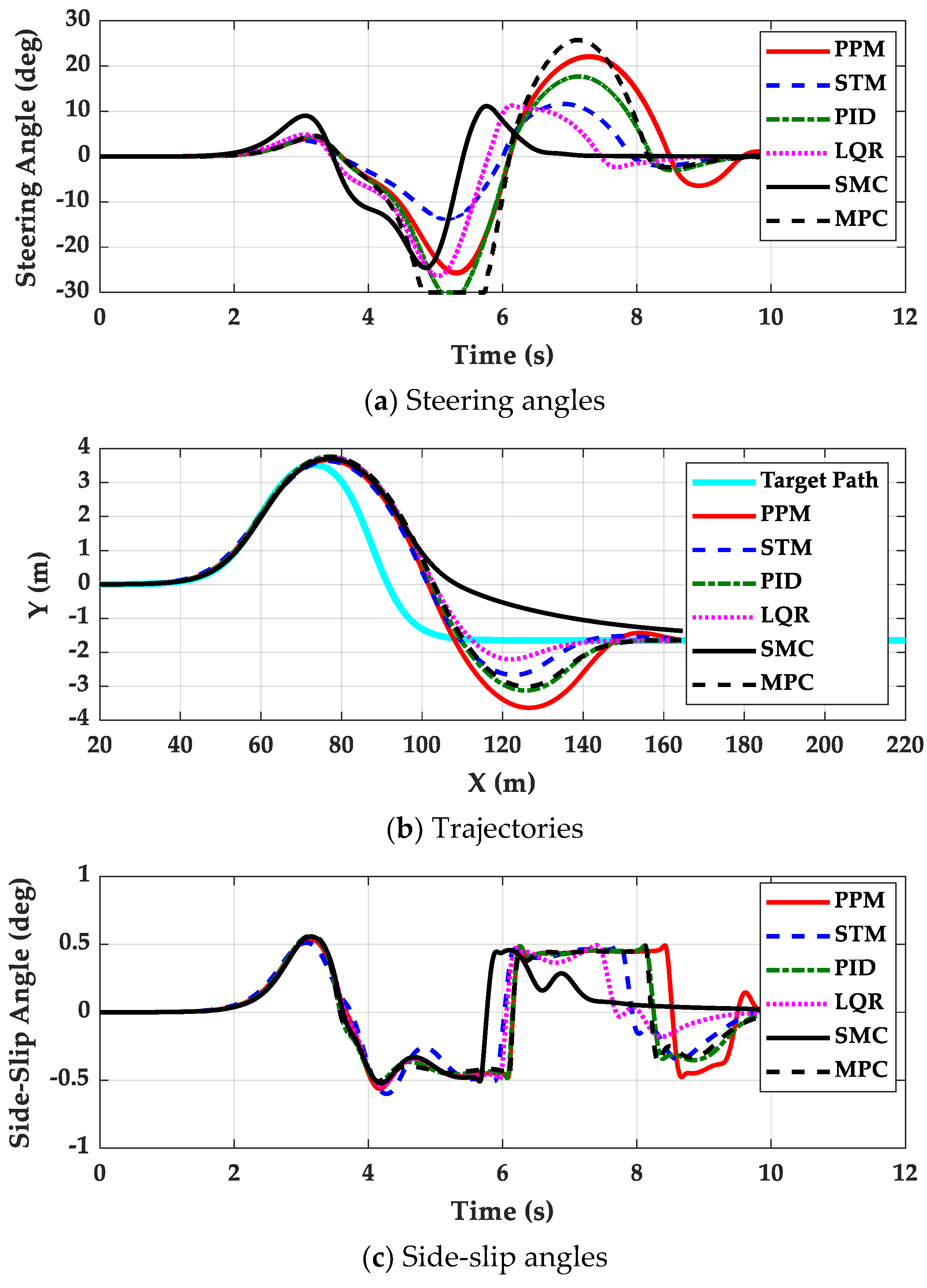
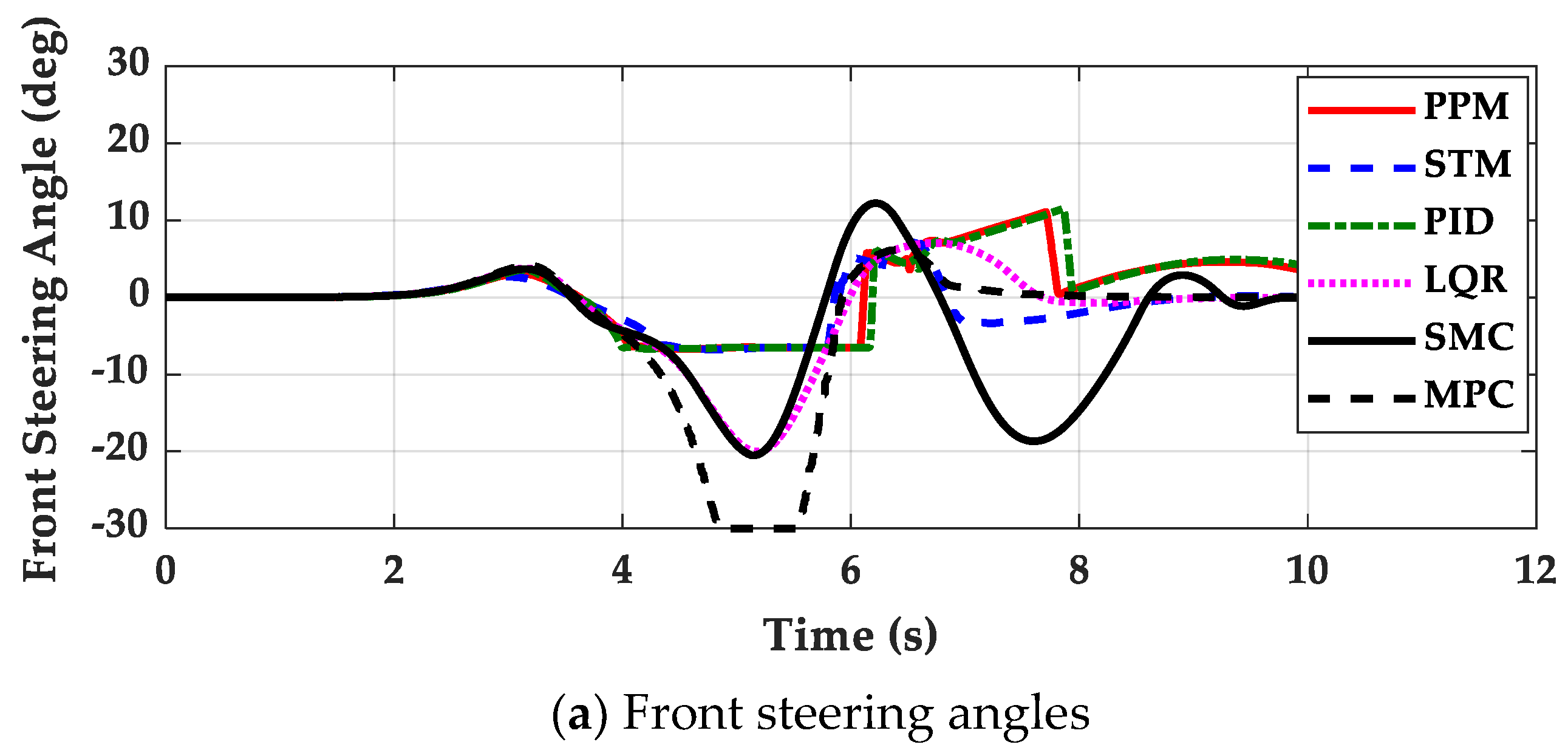
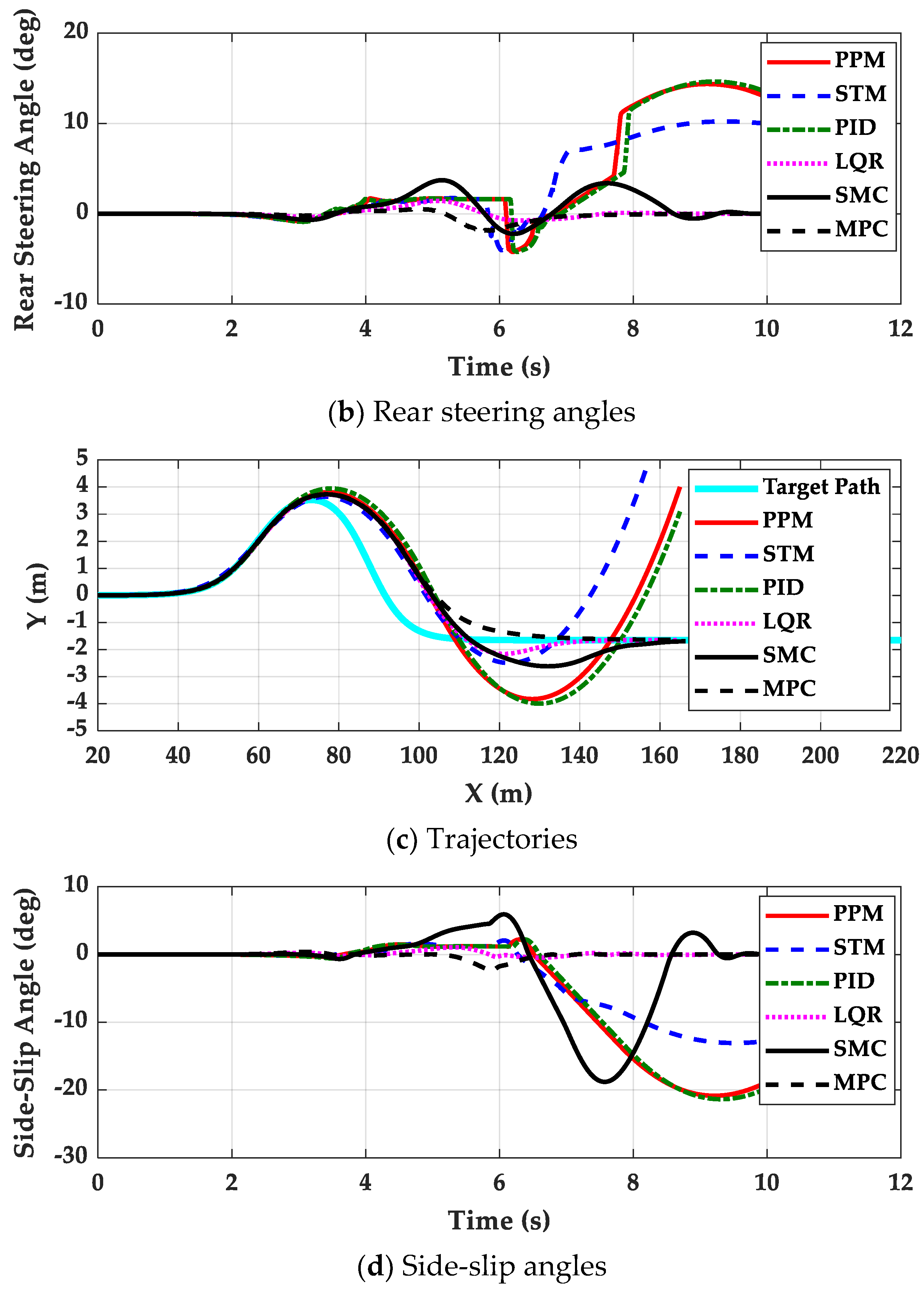
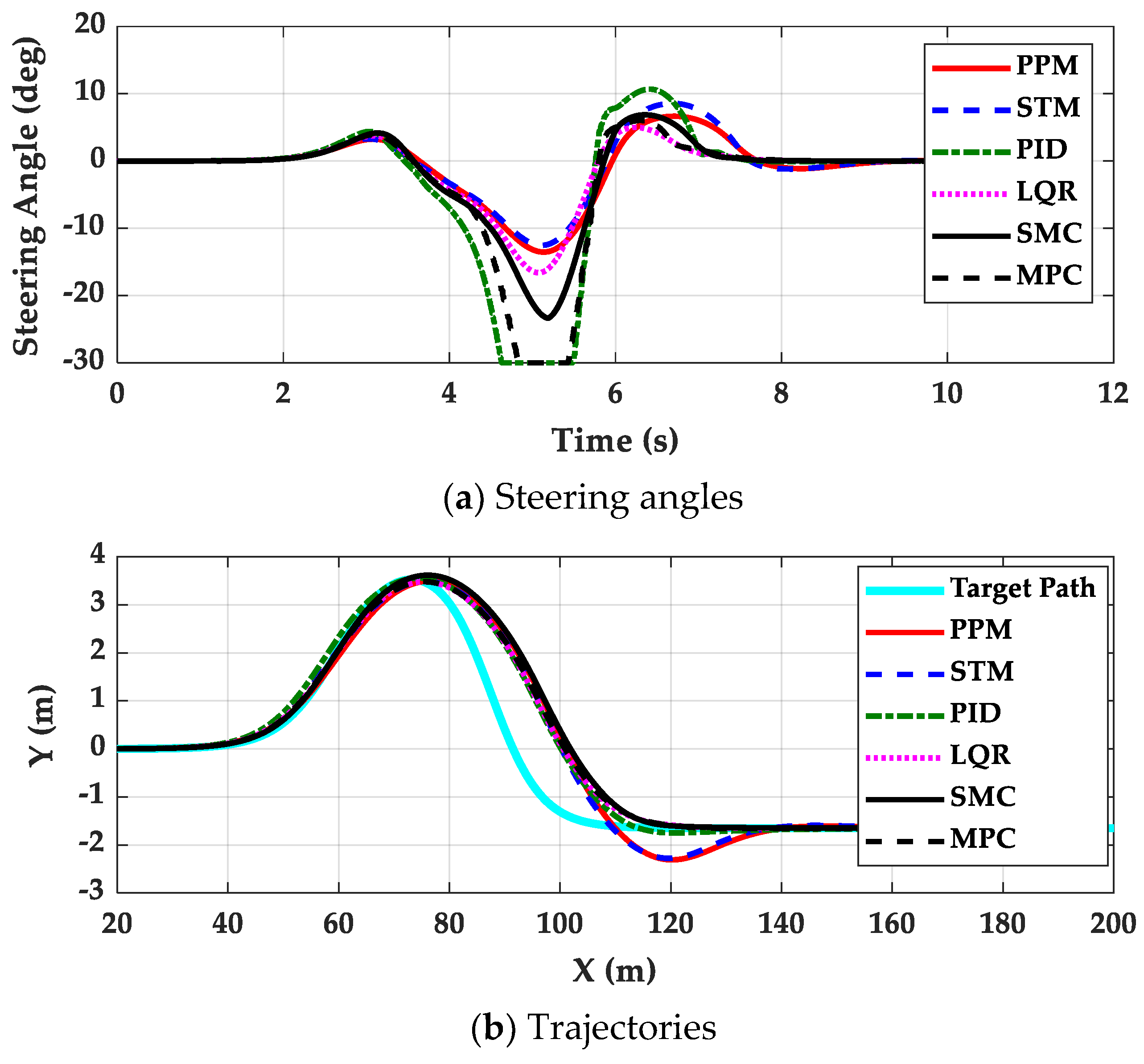
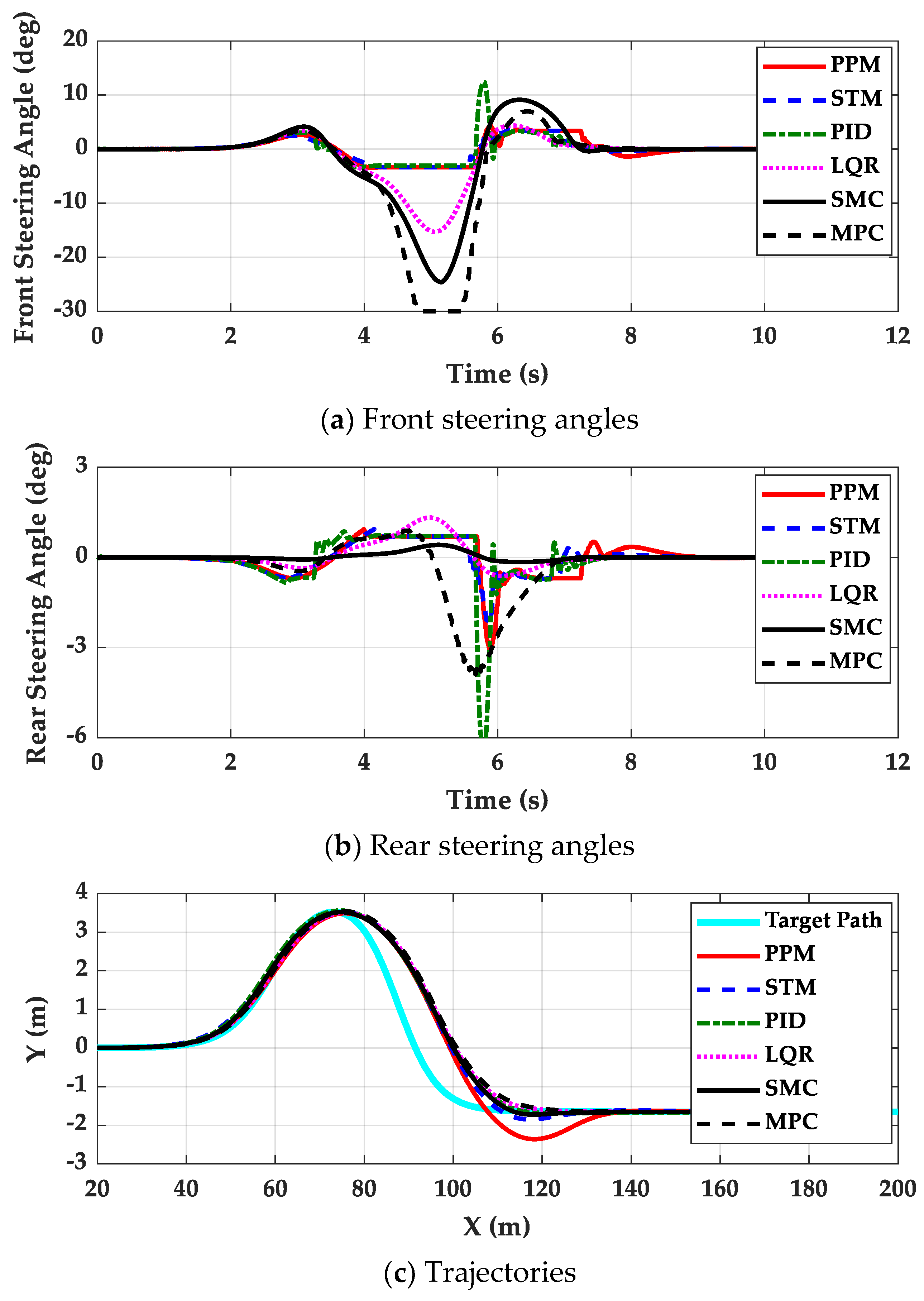
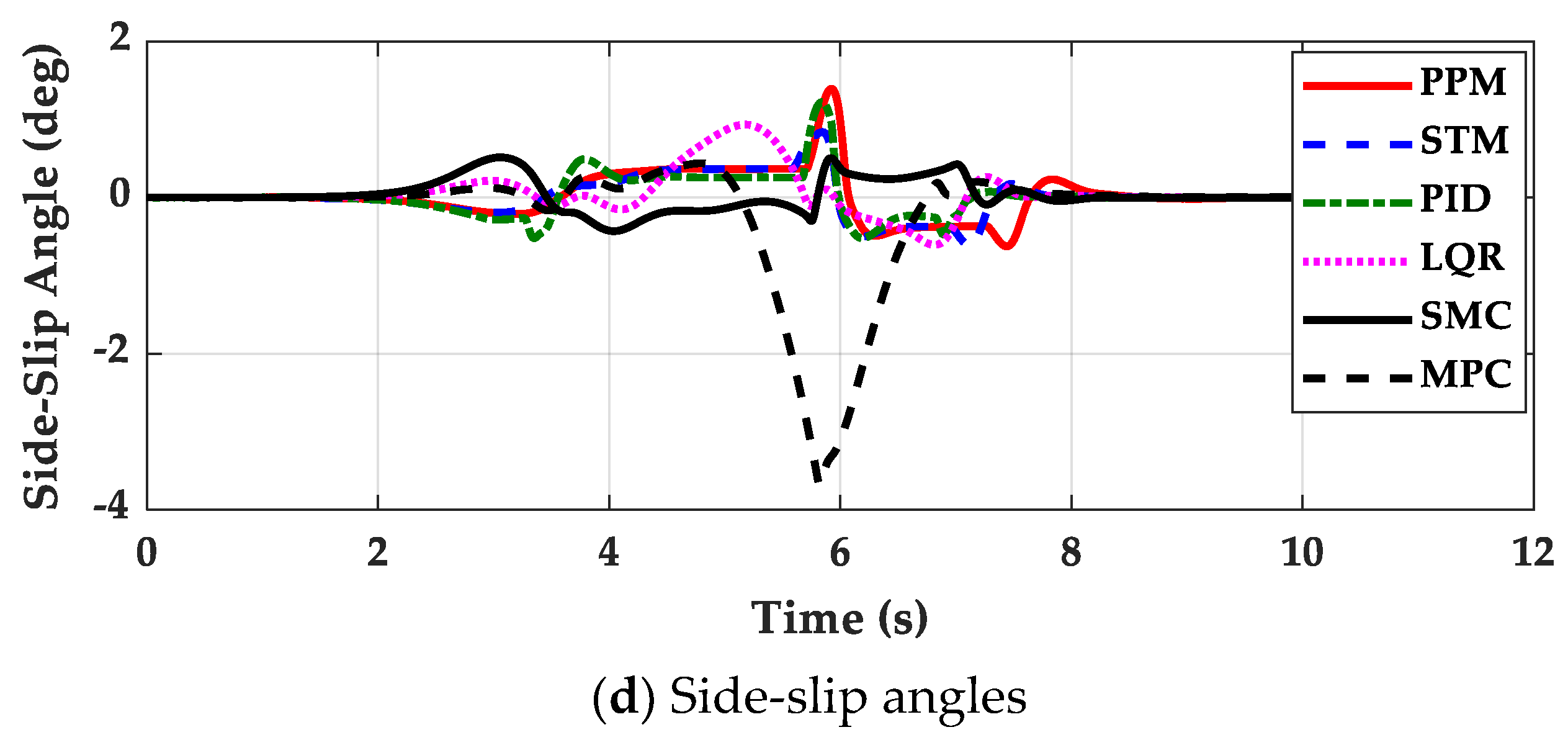
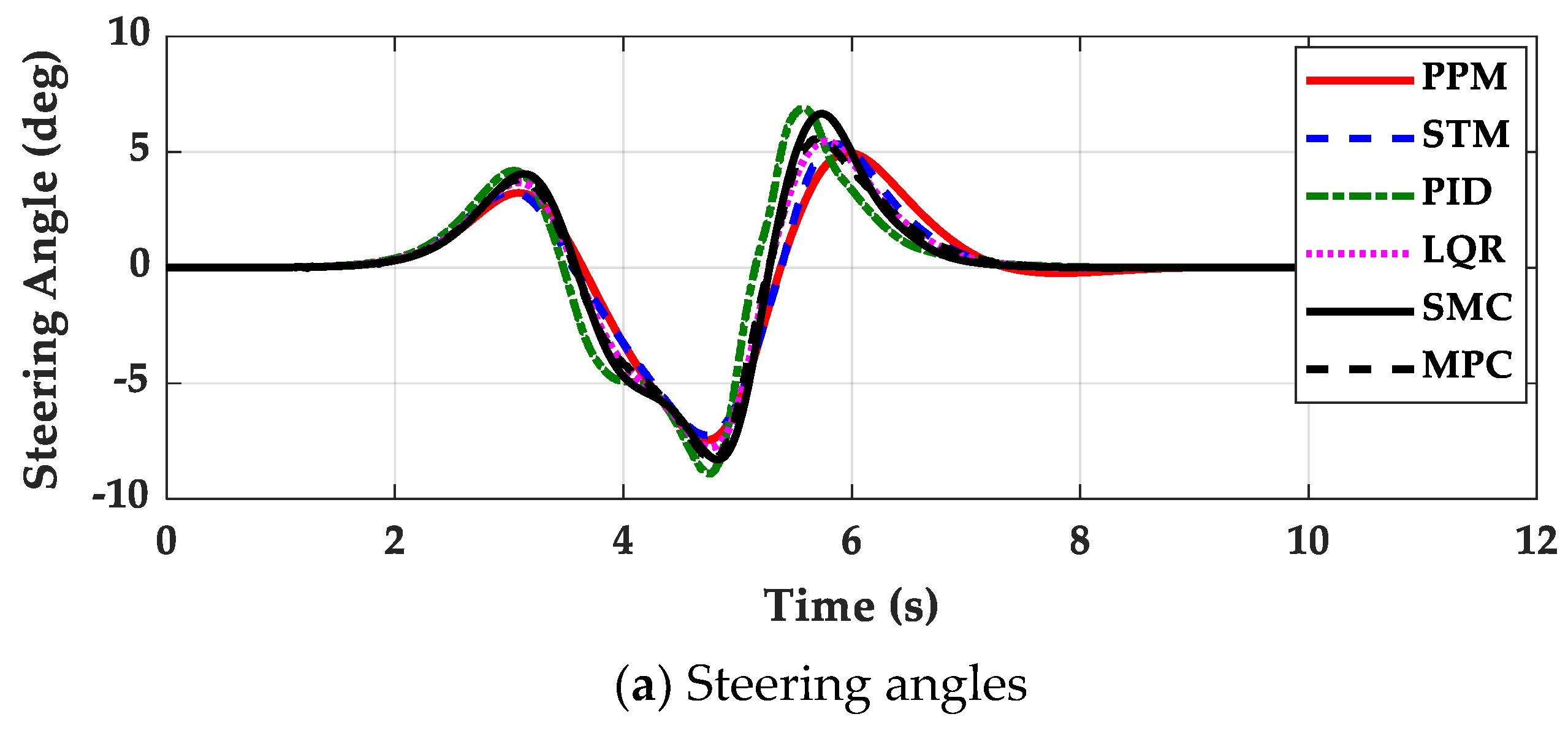
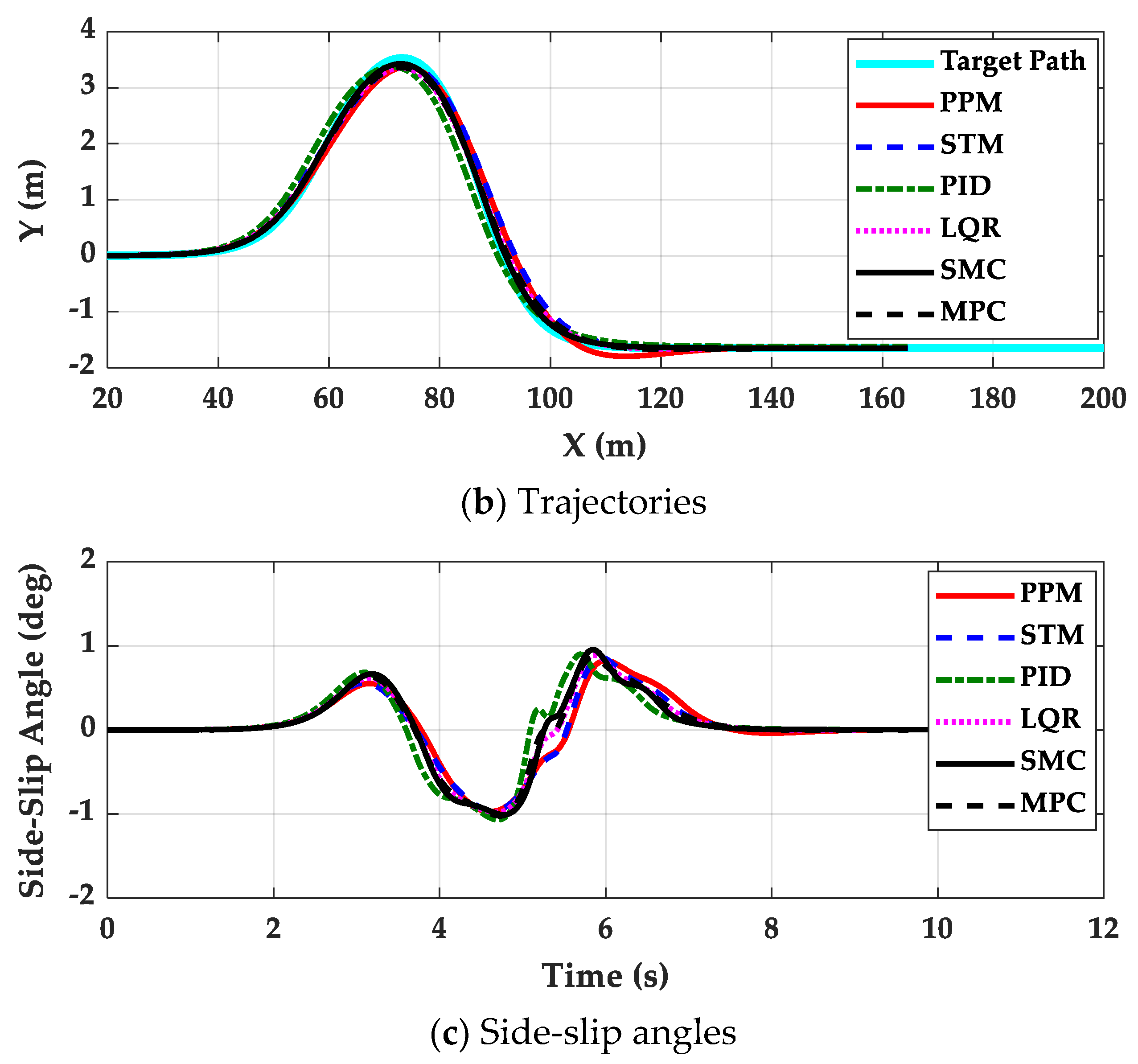
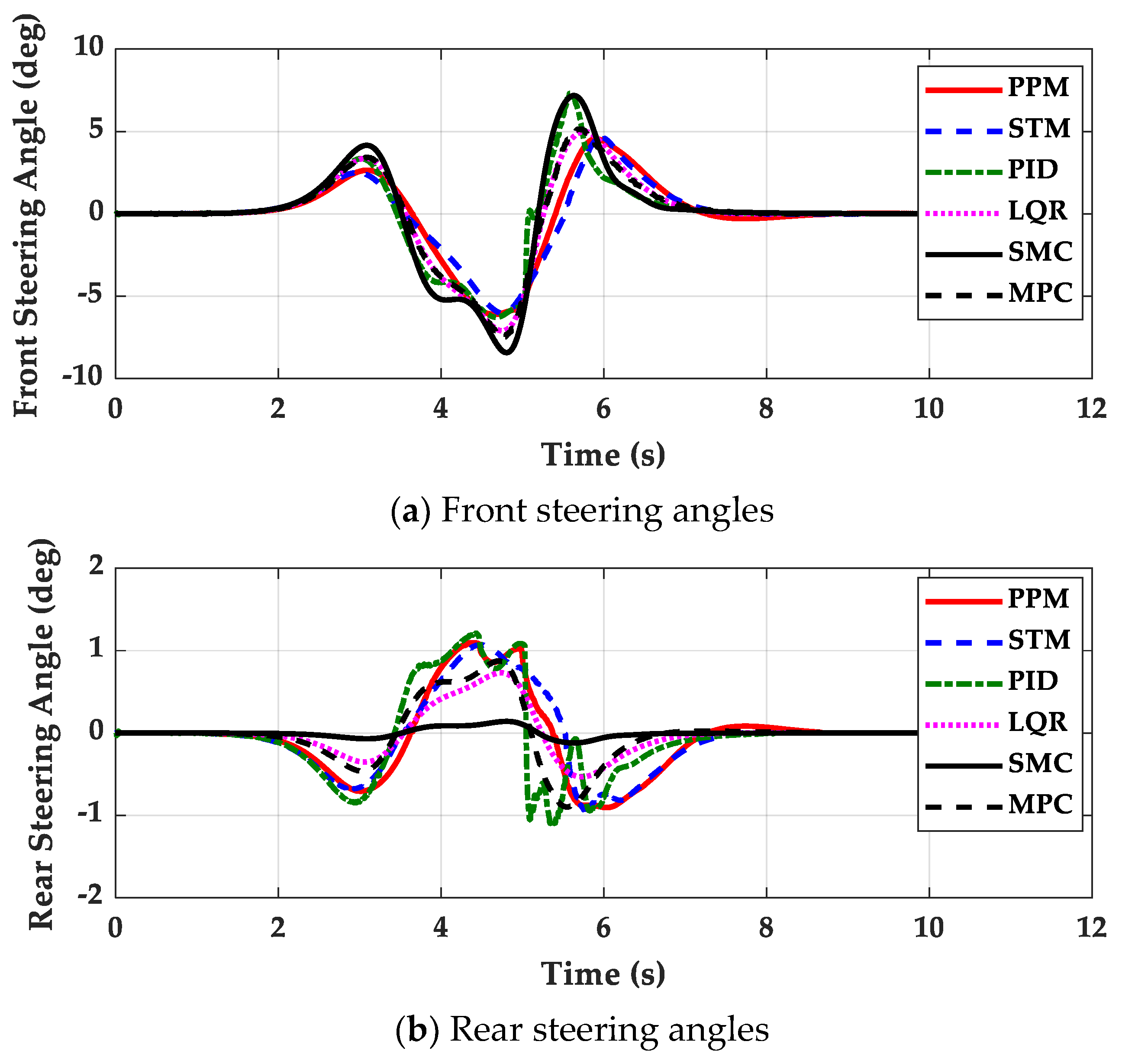
4. Simulation and Validation
5. Conclusions
- The controllers presented in this paper are effective for path tracking on low-μ roads because those gave good path tracking performance while maintaining lateral stability. This means that a switching or coordination scheme between path tracking and lateral stability is not needed for path tracking on low-μ roads.
- The controllers designed on low-μ roads can be used on high-μ ones, except the emergency maneuver for collision avoidance. However, the reverse does not hold. For this reason, it is desirable that the path tracking controller should be designed for low-μ roads.
- The 4WS or RWS vehicle is not recommend for path tracking because there are few particular advantages in using 4WS or RWS. If 4WS is used with LQR, SMC and MPC, it is desirable that the steering angles of rear wheels for these controllers should be limited to very small values. However, this will make the performance of these controllers with 4WS nearly identical to those with FWS.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| 4WS | 4-wheel steering |
| 4WIS | 4-wheel independent steering |
| 4WIB | 4-wheel independent braking |
| 4WID | 4-wheel independent drive |
| FWS | front wheel steering |
| LQR | linear quadratic regulator |
| MPC | model predictive control |
| PID | proportional-integral-derivative |
| PPM | pure pursuit method |
| PTC | path tracking control |
| RWS | rear wheel steering |
| SMC | sliding mode control |
| STM | Stanley method |
| Cf, Cr | cornering stiffness of front/rear tires (N/rad) |
| Ci | cornering stiffness of each wheel (N/rad) |
| ey, eφ | lateral offset error (m) and heading error (rad) |
| Fx, Fy, Fz | longitudinal, lateral and vertical tire forces (N) |
| Fyf, Fyr | lateral forces of front and rear wheels (N) |
| g | gravitational acceleration constant (=9.81 m/s2) |
| Iz | yaw moment of inertial (kg·m2) |
| Kc | gain of sliding mode control for yaw rate tracking |
| Kpy, Kiy, Kdy | P-, I- and D-gain on lateral offset error in PID controller |
| Kpφ, Kiφ, Kdφ | P-, I- and D-gain on heading error in PID controller |
| KSMC | gain of sliding mode control for path tracking |
| ks | distance gain in Stanley method |
| kv | velocity gain |
| Kγ | steady−state yaw rate gain |
| L | wheel base (m) |
| Lp | lookahead distance (m) |
| lf, lr | distance from C.G. to front and rear axles (m) |
| m | vehicle total mass (kg) |
| N | prediction horizon of MPC |
| Ts | sampling time of the discrete-time model used in MPC |
| v | vehicle speed (m/s) |
| vx, vy | longitudinal and lateral velocities of a vehicle (m/s) |
| y | lateral displacement (m) |
| yd | target displacement (m) |
| Yref | reference lateral displacement of the target path (m) |
| αf, αr | tire slip angles of front and rear wheels (rad) |
| β | side-slip angle (rad) |
| δf, δr | front and rear steering angles (rad) |
| δmax | maximum steering angle (rad) |
| ΔFyi | control tire force obtained from WPCA (N) |
| ΔMc | control yaw moment (Nm) |
| ΔX | center offset (m) |
| ΔY | lateral offset (m) |
| OS% | percentage overshoot |
| ΔDX | response delay (m) |
| ΔSX | settling delay (m) |
| γ, γd | real and reference yaw rates (rad/s) |
| κ | curvature of a path at a particular point (1/m) |
| ξi | maximum allowable value of weight in LQ objective function |
| ϕi | derived slip angle (rad) |
| φ | heading angle (rad) |
| φd | target heading angle (rad) |
| Ψref | reference heading angle of the target path (m) |
| ρi | weight in LQ objective function |
| σ | equivalent slip ratio |
| μ | tire-road friction coefficient |
References
- Montanaro, U.; Dixit, S.; Fallaha, S.; Dianatib, M.; Stevensc, A.; Oxtobyd, D.; Mouzakitisd, A. Towards connected autonomous driving: Review of use-cases. Veh. Syst. Dyn. 2019, 57, 779–814. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Omeiza, D.; Webb, H.; Jirotka, M.; Kunze, M. Explanations in autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10142–10162. [Google Scholar] [CrossRef]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Sorniotti, A.; Barber, P.; De Pinto, S. Path tracking for automated driving: A tutorial on control system formulations and ongoing research. In Automated Driving; Watzenig, D., Horn, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Amer, N.H.; Hudha, H.Z.K.; Kadir, Z.A. Modelling and control strategies in path tracking control for autonomous ground vehicles: A review of state of the art and challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and comparison of path tracking based on model predictive control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef]
- Yao, Q.; Tian, Y.; Wang, Q.; Wang, S. Control strategies on path tracking for autonomous vehicle: State of the art and future challenges. IEEE Access 2020, 8, 161211–161222. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2022, in press. [Google Scholar] [CrossRef]
- Yakub, F.; Mori, Y. Comparative study of autonomous path-following vehicle control via model predictive control and linear quadratic control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 1695–1714. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Output constraint control on path following of four-wheel independently actuated autonomous ground vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4033–4043. [Google Scholar] [CrossRef]
- Hang, P.; Luo, F.; Fang, S.; Chen, X. Path tracking control of a four-wheel-independent-steering electric vehicle based on model predictive control. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar]
- Hang, P.; Chen, X.; Luo, F. Path-Tracking Controller Design for a 4WIS and 4WID Electric Vehicle with Steer-by-Wire System; SAE 2017-01-1954; SAE: Warrendale, PN, USA, 2017. [Google Scholar]
- Guo, J.; Luo, Y.; Li, K. An adaptive hierarchical trajectory following control approach of autonomous four-wheel independent drive electric vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2482–2492. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Li, F. A Robust Path Tracking Control Method for Intelligent Vehicle; SAE 2018-01-1582; SAE: Warrendale, PN, USA, 2018. [Google Scholar]
- Hang, P.; Chen, X.; Luo, F. LPV/H∞ controller design for path tracking of autonomous ground vehicles through four-wheel steering and direct yaw-moment control. Int. J. Automot. Technol. 2019, 20, 679–691. [Google Scholar] [CrossRef]
- Ren, Y.; Zheng, L.; Khajepour, A. Integrated model predictive and torque vectoring control for path tracking of 4-wheeldriven autonomous vehicles. IET Intell. Transp. Syst. 2019, 13, 98–107. [Google Scholar] [CrossRef]
- Zhang, B.; Zong, C.; Chen, G.; Li, G. An adaptive-prediction-horizon model prediction control for path tracking in a four-wheel independent control electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 3246–3262. [Google Scholar] [CrossRef]
- Chen, X.; Peng, Y.; Hang, P.; Tang, T. Path tracking control of four-wheel independent steering electric vehicles based on optimal control. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5436–5442. [Google Scholar]
- Wang, Y.; Shao, Q.; Zhou, J.; Zheng, H.; Chen, H. Longitudinal and lateral control of autonomous vehicles in multi-vehicle driving environments. IET Intell. Transp. Syst. 2020, 14, 924–935. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.; Yue, M.; Li, J. Trajectory tracking algorithm in a hierarchical strategy for electric vehicle driven by four independent in-wheel motors. J. Chin. Inst. Eng. 2020, 43, 807–818. [Google Scholar] [CrossRef]
- He, Z.; Nie, L.; Yin, Z.; Huang, S. A two-layer controller for lateral path tracking control of autonomous vehicles. Sensors 2020, 20, 3689. [Google Scholar] [CrossRef]
- Wu, H.; Si, Z.; Li, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control. IEEE Access 2020, 8, 73071–73081. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.; Si, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control and sliding mode control. Adv. Mech. Eng. 2021, 13, 16878140211045142. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X. Path tracking control of 4-wheelsteering autonomous ground vehicles based on linear parameter-varying system with experimental verification. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 411–423. [Google Scholar]
- Liang, Y.; Li, Y.; Zheng, L.; Yu, Y.; Ren, Y. Yaw rate tracking-based path-following control for four-wheel independent driving and four-wheel independent steering autonomous vehicles considering the coordination with dynamics stability. Proc IMechE Part D J. Automob. Eng. 2021, 235, 260–272. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Wang, F.; Tang, Z.; Chen, L. Coordinated control based path following of distributed drive autonomous electric vehicles with yaw-moment control. Cont. Eng. Prac. 2021, 106, 104659. [Google Scholar] [CrossRef]
- Xiang, C.; Peng, H.; Wang, W.; Li, L.; An, Q.; Cheng, S. Path tracking coordinated control strategy for autonomous four in-wheel-motor independent-drive vehicles with consideration of lateral stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1023–1036. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Model predictive control with learned vehicle dynamics for autonomous vehicle path tracking. IEEE Access 2021, 9, 128233–128249. [Google Scholar] [CrossRef]
- Yang, K.; Tang, X.; Qin, Y.; Huang, Y.; Wang, H.; Pu, H. Comparative study of trajectory tracking control for automated vehicles via model predictive control and robust H-infinity state feedback control. Chin. J. Mech. Eng. 2021, 34, 74. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Meng, Y.; Gu, Q.; Bai, G. Integrated path tracking control of steering and braking based on holistic MPC. IFAC PapersOnLine 2021, 54, 45–50. [Google Scholar] [CrossRef]
- Tong, Y.; Jing, H.; Kuang, B.; Wang, G.; Liu, F.; Yang, Z. Trajectory tracking control for four-wheel independently driven electric vehicle based on model predictive control and sliding model control. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021. [Google Scholar]
- Jeong, Y.; Yim, S. Model predictive control-based integrated path tracking and velocity control for autonomous vehicle with four-wheel independent steering and driving. Electronics 2021, 10, 2812. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Hu, W.; Cai, Y.; Huang, C.; Chen, L. Path tracking control strategy for the intelligent vehicle considering tire nonlinear cornering characteristics in the PWA form. J. Frankl. Inst. 2022, 359, 2487–2513. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Path tracking control with four-wheel independent steering, driving and braking systems for autonomous electric vehicles. IEEE Access 2022, 10, 74733–74746. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Integrated path tracking and lateral stability control with four-wheel independent steering for autonomous electric vehicles on low friction roads. Machines 2022, 10, 650. [Google Scholar] [CrossRef]
- Hu, H.; Bei, S.; Zhao, Q.; Han, X.; Zhou, D.; Zhou, X.; Li, B. Research on trajectory tracking of sliding mode control based on adaptive preview time. Actuators 2022, 11, 34. [Google Scholar] [CrossRef]
- Barari, A.; Afshari, S.S.; Liang, X. Coordinated control for path-following of an autonomous four in-wheel motor drive electric vehicle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6335–6346. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Meng, Y.; Gu, Q.; Bai, G. Integrated path tracking control of steering and differential braking based on tire force distribution. Int. J. Control Autom. Syst. 2022, 20, 536–550. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Yang, C.; Qie, T.; Ma, M. Adaptive model predictive control-based path following control for four-wheel independent drive automated vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14399–14412. [Google Scholar] [CrossRef]
- Wong, H.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley and Sons, Inc.: NewYork, NY, USA, 2001. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: NewYork, NY, USA, 2006. [Google Scholar]
- Katsuyama, E.; Yamakado, M.; Abe, M. A state-of-the art review: Toward a novel vehicle dynamics control concept taking the driveline of electric vehicles into account as promising control actuators. Veh. Syst. Dyn. 2021, 59, 976–1025. [Google Scholar] [CrossRef]
- Yim, S. Coordinated control with electronic stability control and active steering devices. J. Mech. Sci. Technol. 2015, 29, 5409–5416. [Google Scholar] [CrossRef]
- Yim, S. Comparison among active front, front independent, 4-wheel and 4-wheel independent steering systems for vehicle stability control. Electronics 2020, 9, 798. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Jing, H.; Chen, N. Coordinated active steering and four-wheel independently driving/braking control with control allocation. Asian J. Control 2016, 18, 98–111. [Google Scholar] [CrossRef]
- Nah, J.; Yim, S. Vehicle stability control with four-wheel independent braking, drive and steering on in-wheel motor-driven electric vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K.; Dai, Y. Coordinated path-following and direct yaw-moment control of autonomous electric vehicles with sideslip angle estimation. Mech. Syst. Signal Process. 2018, 105, 183–199. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Yim, S.; Kim, S.; Yun, H. Coordinated control with electronic stability control and active front steering using the optimum yaw moment distribution under a lateral force constraint on the active front steering. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 581–592. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA grand challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Sharp, R.S.; Casanova, D.; Symonds, P. A mathematical model for driver steering control, with design, tuning and performance results. Veh. Syst. Dyn. 2000, 33, 289–326. [Google Scholar]
- Son, Y.S.; Kim, W.; Lee, S.-H.; Chung, C.C. Robust multi-rate control scheme with predictive virtual lanes for lane-keeping system of autonomous highway driving. IEEE Trans. Veh. Technol. 2015, 64, 3378–3391. [Google Scholar] [CrossRef]
- Kang, C.M.; Lee, S.-H.; Chung, C.C. On-road path generation and control for waypoint tracking. IEEE Intell. Transp. Syst. Mag. 2016, 9, 36–45. [Google Scholar] [CrossRef]
- Kim, D.J.; Kang, C.M.; Lee, S.H.; Chung, C.C. Discrete-time integral sliding model predictive control for dynamic lateral motion of autonomous driving vehicles. In Proceedings of the American Control Conference, Milwaukee, WI, USA, 27–29 June 2018; pp. 4757–4763. [Google Scholar]
- Choi, W.Y.; Kim, D.J.; Kang, C.M.; Lee, S.H.; Chung, C.C. Autonomous vehicle lateral maneuvering by approximate explicit predictive control. In Proceedings of the American Control Conference, Milwaukee, WI, USA, 27–29 June 2018; pp. 4739–4744. [Google Scholar]
- Xu, S.; Peng, H. Design, analysis and experiments of preview path tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 48–58. [Google Scholar] [CrossRef]
- Lee, K.; Jeon, S.; Kim, H.; Kum, D. Optimal path tracking control of autonomous vehicle: Adaptive full-state linear quadratic gaussian (LQG) control. IEEE Access 2019, 7, 109120–109133. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- Guldner, J.; Utkin, V.I.; Ackermann, J. A sliding mode control approach to automatic car steering. In Proceedings of the American Control Conference, Baltimore, MD, USA, 29 June–1 July 1994; pp. 1969–1973. [Google Scholar]
- Yim, S. Active roll stabilization with disturbance feedforward control. IEEE Access 2021, 9, 19788–19799. [Google Scholar] [CrossRef]
- Yoon, J.; Yim, S.; Cho, W.; Koo, B.; Yi, K. Design of an unified chassis controller for rollover prevention, manoeuvrability and lateral stability. Veh. Syst. Dyn. 2010, 48, 1247–1268. [Google Scholar] [CrossRef]
- Yim, S.; Choi, J.; Yi, K. Coordinated control of hybrid 4WD vehicles for enhanced maneuverability and lateral stability. IEEE Trans. Veh. Technol. 2012, 61, 1946–1950. [Google Scholar] [CrossRef]
- Cho, W.; Yoon, J.; Kim, J.; Hur, J.; Yi, K. An investigation into unified chassis control scheme for optimised vehicle stability and maneuverability. Veh. Syst. Dyn. 2008, 46, 87–105. [Google Scholar] [CrossRef]
- Kim, H.H.; Ryu, J. Sideslip angle estimation considering short-duration longitudinal velocity variation. Int. J. Automot. Technol. 2011, 12, 545–553. [Google Scholar] [CrossRef]
- Mechanical Simulation Corporation. VS Browser: Reference Manual, The Graphical User Interfaces of BikeSim, CarSim, and TruckSim; Mechanical Simulation Corporation: Ann Arbor, MI, USA, 2009. [Google Scholar]
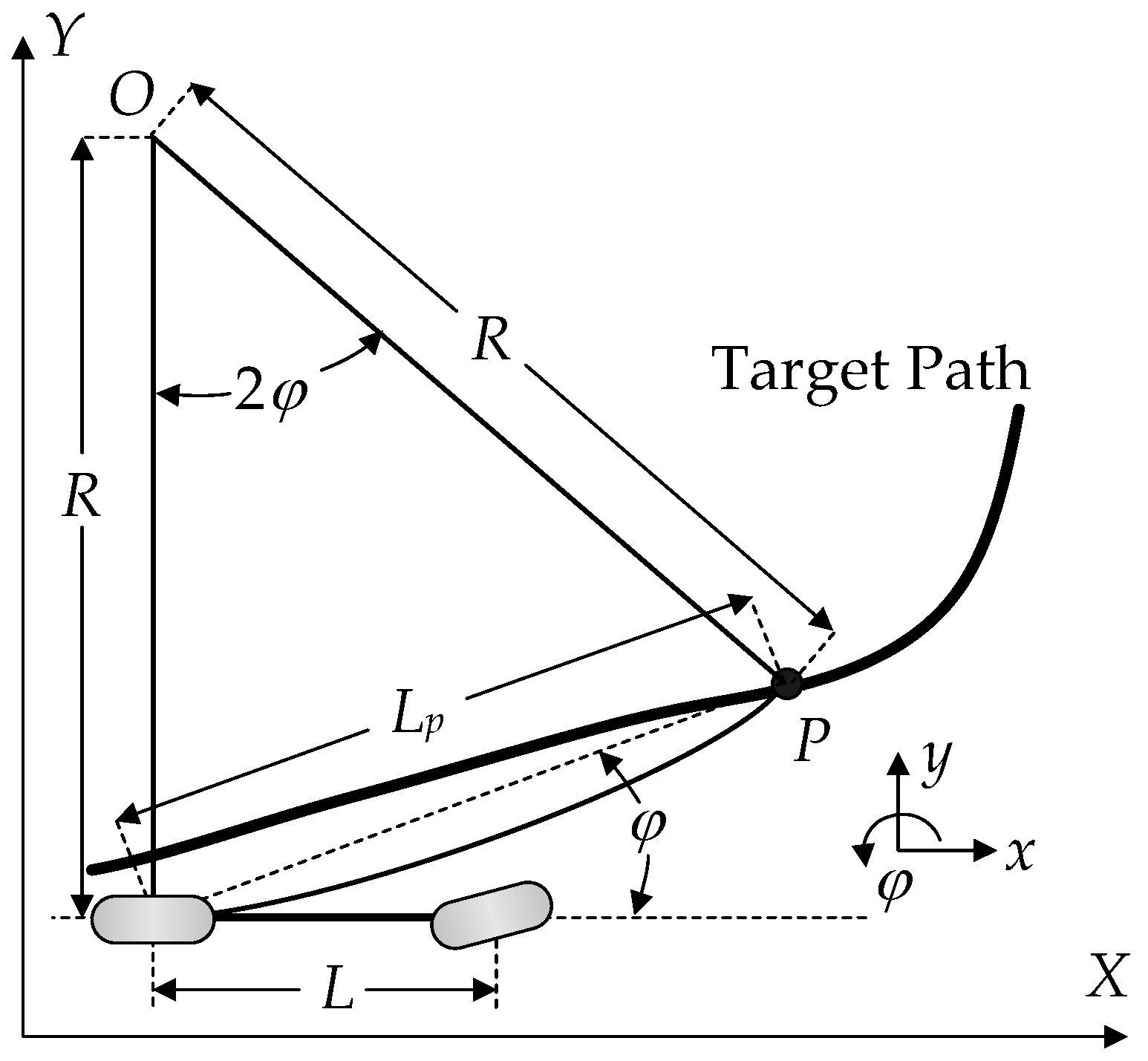
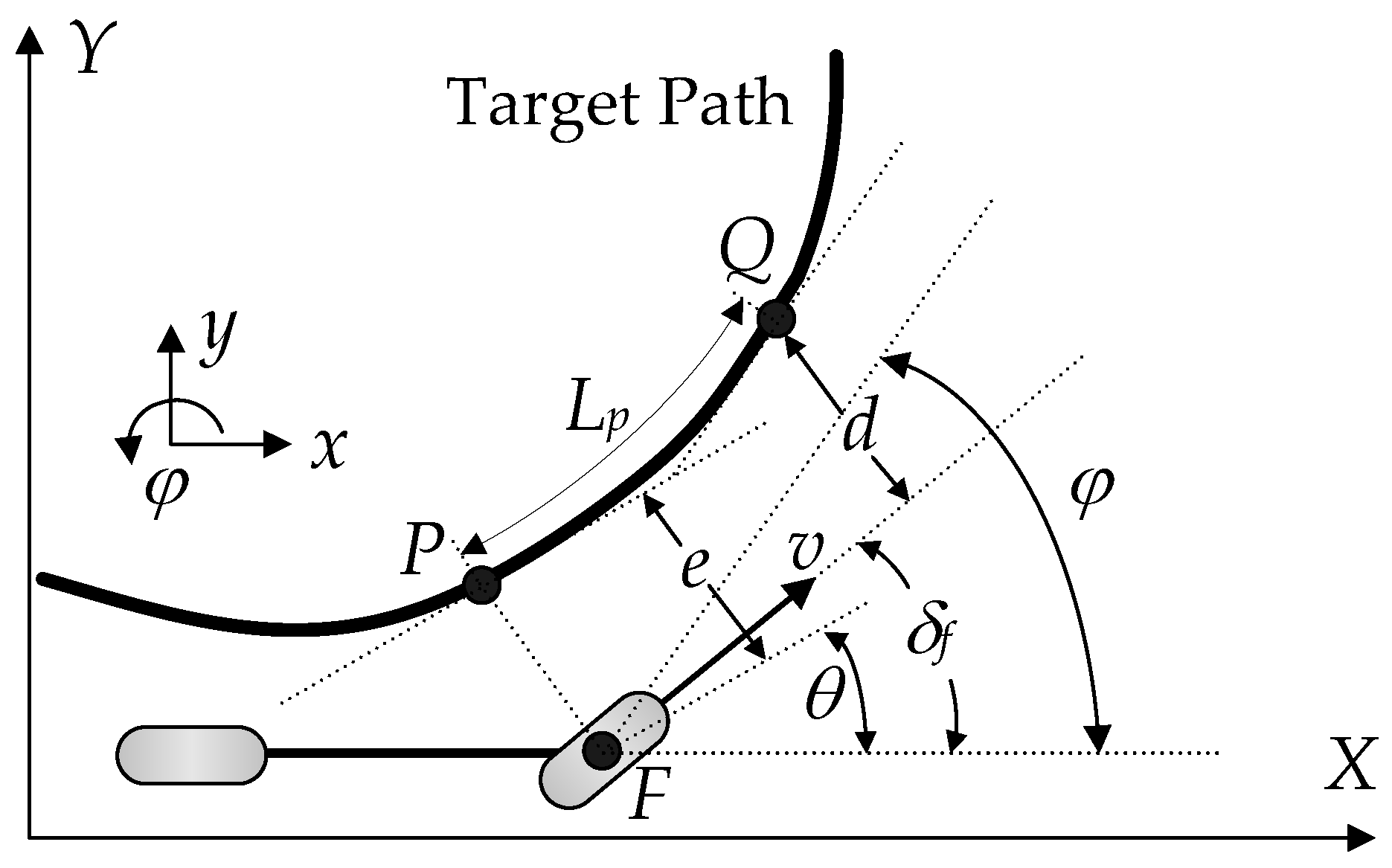
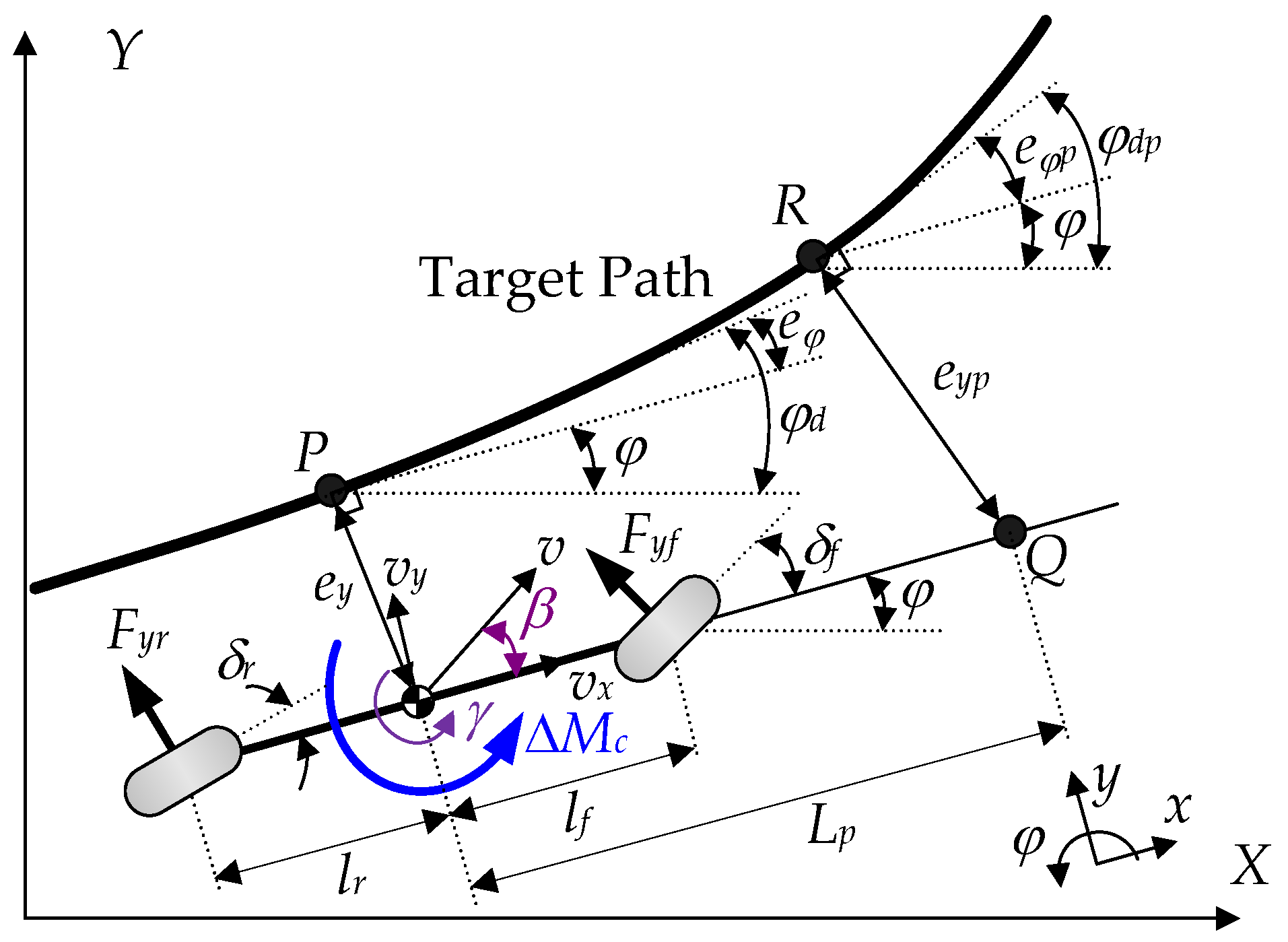

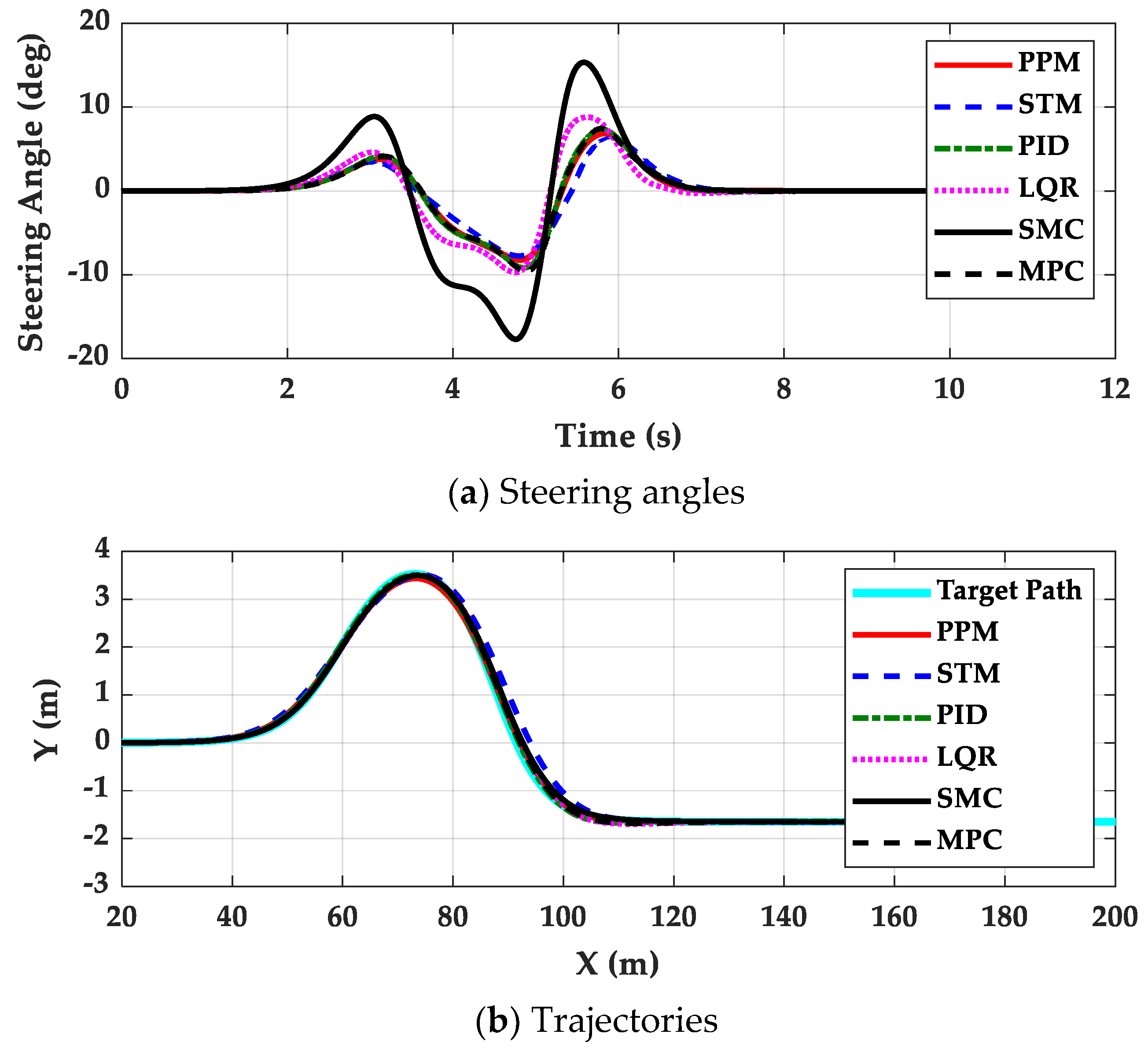


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ms | 1823 kg | lf | 1.27 m |
| Iz | 6286 kg⋅m2 | lr | 1.90 m |
| Cf | 42,000 N/rad | Cr | 62,000 N/rad |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 0.01 | −0.093 | 0.0 | 0.60 | −0.07 | 0.97 | 2.87 |
| STM | 1.14 | −0.016 | 0.2 | 2.49 | 1.84 | 0.94 | 3.38 |
| PID | 0.08 | −0.016 | 0.4 | 0.46 | −4.55 | 0.97 | 4.29 |
| LQR | 0.53 | −0.022 | 0.9 | 1.03 | −4.43 | 0.96 | 3.36 |
| SMC | 0.41 | −0.029 | 0.0 | 1.14 | 1.92 | 0.95 | 3.67 |
| MPC | 0.45 | −0.028 | 0.6 | 0.76 | −3.63 | 0.98 | 4.90 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 0.03 | −0.037 | 0.0 | 0.49 | −2.76 | 0.46 | 3.09 |
| STM | 0.90 | −0.024 | 0.2 | 2.10 | 0.22 | 0.39 | 1.84 |
| PID | 0.15 | 0.013 | 0.0 | 0.28 | −2.86 | 0.49 | 5.57 |
| LQR | 0.48 | −0.021 | 0.8 | 0.83 | −4.11 | 0.41 | 2.75 |
| SMC | 0.08 | −0.021 | 0.0 | 0.41 | −1.20 | 0.97 | 6.79 |
| MPC | 0.43 | −0.033 | 0.7 | 0.78 | −1.83 | 0.69 | 3.55 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 3.47 | 0.136 | 39.2 | 10.02 | 54.78 | 0.56 | 8.90 |
| STM | 3.49 | 0.109 | 19.7 | 9.96 | 51.73 | 0.60 | 4.86 |
| PID | 3.87 | 0.241 | 28.5 | 11.00 | 39.99 | 0.56 | 8.76 |
| LQR | 4.18 | 0.218 | 10.7 | 11.46 | 32.33 | 0.55 | 6.49 |
| SMC | 3.95 | 0.186 | 0.0 | 17.11 | 55.64 | 0.56 | 6.45 |
| MPC | 4.23 | 0.232 | 26.3 | 11.44 | 41.27 | 0.57 | 10.94 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 91.97 | 0.479 | 42.0 | 62.49 | 55.92 | 20.86 | 17.78 |
| STM | 90.30 | 4.514 | 16.4 | 51.11 | 54.43 | 13.07 | 19.13 |
| PID | 4.88 | 0.423 | 45.3 | 12.35 | 55.94 | 21.37 | 17.80 |
| LQR | 4.46 | 0.240 | 10.0 | 11.43 | 31.43 | 1.09 | 4.40 |
| SMC | 3.65 | 0.207 | 18.7 | 11.69 | 55.39 | 18.81 | 32.01 |
| MPC | 4.08 | 0.206 | 0.0 | 12.41 | 33.35 | 2.43 | 8.89 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 3.35 | −0.031 | 12.7 | 9.53 | 28.57 | 0.62 | 5.15 |
| STM | 2.58 | −0.035 | 12.2 | 8.70 | 41.14 | 0.62 | 4.94 |
| PID | 1.25 | 0.031 | 1.9 | 8.64 | 23.99 | 0.59 | 11.71 |
| LQR | 2.26 | −0.045 | 0.0 | 9.02 | 12.50 | 0.61 | 6.00 |
| SMC | 2.91 | 0.090 | 0.0 | 10.36 | 10.98 | 0.58 | 7.39 |
| MPC | 2.31 | −0.045 | 0.2 | 9.36 | 11.54 | 0.59 | 10.89 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 2.42 | −0.032 | 14.3 | 7.73 | 26.07 | 1.41 | 16.51 |
| STM | 2.33 | −0.004 | 3.9 | 8.06 | 17.87 | 0.84 | 12.24 |
| PID | 1.44 | 0.034 | 0.8 | 8.63 | 5.48 | 1.22 | 20.47 |
| LQR | 2.46 | −0.018 | 0.0 | 8.94 | 11.71 | 0.93 | 4.09 |
| SMC | 1.65 | −0.008 | 1.4 | 8.51 | 13.15 | 0.51 | 7.68 |
| MPC | 2.56 | 0.012 | 0.0 | 9.24 | 13.23 | 3.67 | 8.22 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 0.83 | −0.159 | 2.77 | 1.94 | 16.33 | 0.97 | 3.00 |
| STM | 0.60 | −0.127 | 0.0 | 2.14 | 3.45 | 0.96 | 3.28 |
| PID | −1.77 | −0.153 | 0.0 | −1.05 | 12.14 | 1.07 | 5.71 |
| LQR | −0.11 | −0.172 | 0.2 | 0.84 | 1.31 | 0.98 | 2.29 |
| SMC | −1.92 | −0.100 | 0.0 | 0.38 | 2.60 | 1.01 | 3.93 |
| MPC | −0.01 | −0.166 | 0.4 | 0.80 | 1.18 | 1.02 | 3.74 |
| ΔX (m) | ΔY (m) | OS% | ΔDX (m) | ΔSX (m) | MASSA (deg) | MASSAR (deg/s) | |
|---|---|---|---|---|---|---|---|
| PPM | 1.05 | −0.073 | 4.1 | 2.07 | 16.47 | 0.37 | 2.13 |
| STM | 2.02 | 0.049 | 0.3 | 4.46 | 3.72 | 0.36 | 1.45 |
| PID | −1.61 | −0.152 | 0.0 | −0.77 | 6.56 | 0.71 | 9.07 |
| LQR | −0.03 | −0.151 | 0.3 | 0.81 | 0.62 | 0.37 | 2.56 |
| SMC | −1.15 | −0.180 | 0.0 | −0.45 | 15.31 | 0.91 | 4.17 |
| MPC | −0.12 | −0.138 | 0.2 | 0.55 | 2.06 | 0.56 | 5.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Yim, S. Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles. Machines 2023, 11, 403. https://doi.org/10.3390/machines11030403
Lee J, Yim S. Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles. Machines. 2023; 11(3):403. https://doi.org/10.3390/machines11030403
Chicago/Turabian StyleLee, Jaepoong, and Seongjin Yim. 2023. "Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles" Machines 11, no. 3: 403. https://doi.org/10.3390/machines11030403
APA StyleLee, J., & Yim, S. (2023). Comparative Study of Path Tracking Controllers on Low Friction Roads for Autonomous Vehicles. Machines, 11(3), 403. https://doi.org/10.3390/machines11030403








