Optimizing Cascaded Control of Mechatronic Systems through Constrained Residual Reinforcement Learning

Abstract

Cascaded control structures are prevalent in industrial systems with many disturbances to obtain stable control but are cumbersome and challenging to tune. In this work, we propose cascaded constrained residual reinforcement learning (RL), an intuitive method that allows to improve the performance of a cascaded control structure while maintaining safe operation at all times. We draw inspiration from the constrained residual RL framework, in which a constrained reinforcement learning agent learns corrective adaptations to a base controller’s output to increase optimality. We first revisit the interplay between the residual agent and the baseline controller and subsequently extend this to the cascaded case. We analyze the differences and challenges this structure brings and derive some principle insights from this into the stability and operation of the cascaded residual architecture. Next, we propose a novel actor structure to enable efficient learning under the cascaded setting. We show that the standard algorithm is suboptimal for application to cascaded control structures and validate our method on a high-fidelity simulator of a dual motor drivetrain, resulting in a performance improvement of 14.7% on average, with only a minor decrease in performance occurring during the training phase. We study the different principles constituting the method and examine and validate their contribution to the algorithm’s performance under the considered cascaded control structure.

1. Introduction

Cascaded control structures are indispensable for the operation of various industrial systems, providing stable control for applications where a single controller fails to stabilize a control variable that is subject to non-trivial disturbances. By introducing a second, inner controller that stabilizes the secondary influence according to the needs of the primary control loop, the overall system can be rendered stable. Examples of cascaded control include valve positioning [1], electrical motor control [2], industrial drying processes [3], steam boiler feedwater control [4] and motion control in robotic systems [5]. Due to the interplay between the different controllers resulting from the nested structure, however, cascaded controllers are cumbersome and challenging to tune in order to obtain the desired system response [6,7]. As mechatronic systems and drivetrains face an increasing need to become more performant and autonomous while operating in varying environments, the tuning of cascaded control structures is still an active research area [8,9,10], studying, amongst others, methods such as genetic algorithms [11] or Bayesian optimization [12] to obtain the appropriate control parameters.

Opposed to conventional control structures, in recent years, reinforcement learning (RL) [13] has emerged as a promising alternative for challenging systems or environments. RL is a rapidly developing research field, with several algorithms that have sparked a wide range of applications and research paths, notable examples being soft actor critic [14], proximal policy optimization [15], maximum a posteriori policy optimization [16] and more recently temporal difference learning for model predictive control [17]. By optimizing a feedback policy directly from observations of the controlled system’s behavior under the given task, RL algorithms provide a framework to learn control policies tailored to the system at hand, while requiring no underlying assumptions about the system or its environment. While RL has achieved successes in challenging problems over the recent years [18,19,20], its adoption in industry has been limited. A first reason impeding its integration is the frequent gap between applications of RL research and commonly occurring control structures, such as cascaded controllers.

Recent work exists in this area for the altitude and attitude control of an airplane [21], where a cascaded structure is obtained by training two RL algorithms sequentially. In [22], a similar approach is followed for the position and attitude control of quadrotors. The difficulty of such architectures is further illustrated by the offline training requirement due to unstable behavior, as noted in [21]. In [23], a framework is proposed to align the terminology of cascaded control with that of hierarchical RL [24]. Related to cascaded control, in hierarchical RL a challenging task is tackled by decomposing it into subtasks. As this subdivision to different tasks results in a similarly nested architecture, some recent examples of applications to cascaded structures exist in [25], where hierarchical RL is used to control the water level in connected canals and [26] to optimize fuel cell use and degradation in a fuel cell hybrid electrical vehicle. Next to hierarchical RL, multi-agent RL [27], in which the simultaneous control of RL agents is studied, finds applications in systems with a degree of cascaded structure, such as smart grids and industrial production energy balancing [28] or wake control of wind farms [29], by considering all controlled variables as distinct subsystems. Though the challenge of a cascaded control structure has surfaced in a number of works on reinforcement learning, to the best of our knowledge, the potential of RL for such systems has not been studied distinctly.

A second main reason inhibiting the integration of RL into industrially used devices and drivetrains is the lack of safety guarantees. As RL fashions new insights through trial and error, potentially dangerous situations can occur for safety-critical applications, especially during the early exploration phases during training or when faced with unseen conditions after convergence. This lack of safety guarantees may be prohibitive for its application, especially—but not exclusively—in industrial environments. As such, the need for safe RL is one of the current grand challenges in reinforcement learning research [10] and has led to an emerging research field in the recent years. A particularly interesting branch of research into robust learning control covers combining (deep) learning methods with conventional controller structures. Notable examples include neuroadaptive learning, using neural networks as extended state observers and virtual control law approximators in backstepping-based control [30], combining RL with robust MPC [31] or employing a safe fallback policy for the RL agent in unknown states [32]. Specifically for industrial applications, constrained residual RL (CRRL) [33] takes a control engineering point of view by using RL methods to optimize the performance of a stabilized system. A robust base controller is used to guide and constrain the RL policy, which is added residually to the outputs of the conventional controller. As such, the conventional controller provides the bulk of the control action and ensures robustness at all times, while the RL agent learns a residual output to optimize performance for the current operating conditions. The performance of this method was demonstrated in [33] both experimentally and theoretically. As one of its main drawbacks, however, the method was only validated for single-input-single-output (SISO) systems, providing no guarantees on the more complex situation of multiple-input-multiple-output (MIMO) systems, as can be encountered in cascaded control structures.

In this contribution, we aim to bridge this gap in the current literature by studying the potential of safe reinforcement learning for cascaded control problems in an industrial setting. We propose cascaded CRRL, a method allowing to optimize MIMO control systems in a cascaded setting. We show that the standard CRRL framework is suboptimal for these systems and study the impact of the cascaded structure of the base controllers on the proposed algorithm and its different components. The contributions of this work are as follows:

• We study the generalization of the CRRL method to MIMO, cascaded systems and propose a novel CRRL architecture for such systems.
• We deepen the theoretical understanding of the standard CRRL control architecture and extend this to principle insights into the operation and stability of the cascaded CRRL architecture.
• We consider the practical design considerations required to enable the efficient training of a cascaded CRRL agent operating at different levels of a control structure. We propose a dedicated architecture for the residual agent and validate its performance and different assumptions through ablation studies on a high fidelity simulator of a dual motor drivetrain.

The manuscript is structured as follows. Section 2 first lays out the necessary background knowledge before detailing the developed method. Section 3 describes the system on which the method is validated. Section 4 presents the performed experiments and discusses their results. Finally, Section 5 concludes the study and gives an outlook to future research based on the work in this contribution.

2. Method

2.1. Preliminaries: Reinforcement Learning

Reinforcement learning aims to solve a Markov decision process (MDP). An MDP is a tuple $M=(\mathcal{S},\mathcal{A},r,p)$, with $s\in \mathcal{S}$ the states, $a\in \mathcal{A}$ the actions, $r(s,a)$ the reward function that values taking action a in state s, and $p\left(s_{t+1}\right|s_t,a_t)$ the probability of transitioning to state $s_{t+1}$ at the next timestep. The return or objective is defined as the infinite discounted sum of rewards $R\left(\tau \right)={lim}_{T\to \infty }{\sum }_{t=0}^T{\eta }^{t}r(s_t,a_t)$ with $\tau =(s_0,a_0,s_1,a_1,\dots )$ being a progressive sequence of states and actions and $0\le \eta \le 1$ being a temporal discount factor. The resulting goal of any RL method is to find an optimal policy ${\pi }^{*}\left(a_t\right|s_t)$ that maximizes the expected return [34]

$$\begin{array}{cc}\hfill J\left(\pi \right)& ={\mathbb{E}}_{\tau \sim p\left(\tau \right|\pi )}\left[R\left(\tau \right)\right]\hfill \\ \hfill {\pi }^{*}& =arg\underset{\pi }{max}J\left(\pi \right)\hfill \end{array}$$

(1)

with $p\left(\tau \right|s_0,\pi )={\mathsf{\prod }}_{t=0}^{T-1}p\left(s_{t+1}\right|s_t,a_t)\pi \left(a_t\right|s_t)$.

In this work, we employ the soft actor–critic (SAC) algorithm for all experiments. SAC is a state-of-the-art RL method that combines a state-action-value estimate, i.e., the critic, with a separate policy, i.e., the actor, both approximated by a neural network. These estimates are updated iteratively through temporal differencing until they satisfy the Bellman equation. The main characteristic of SAC is the use of a stochastic policy, the entropy of which is actively steered so as to accommodate the exploration–exploitation dichotomy [35]. The stochastic policy outputs a mean and variance in response to an input state, and actions are realized by sampling according to the corresponding Gaussian distribution. By actively steering this, exploration is encouraged during training, and a higher stability after convergence is reached. For further details, we refer to [14,35].

2.2. Constrained Residual Reinforcement Learning

Residual reinforcement learning (RRL) refers to a learning control architecture that merges classical control principles with ideas from reinforcement learning. The main idea is straightforward [33]. The plant is controlled by the superposition of a stabilizing base controller and a residual agent. The agent has access to the same state as the stabilizing base controller, possibly augmented with additional system information and is trained using standard learning methods from RL. With constrained RRL (CRRL), the contribution of the agent is constrained between a fixed lower and upper bound. During training, the agent learns to adapt the base controller’s output to increase the overall optimality, directly from observed system behavior.

More formally, in CRRL, the total control input to the system $u_{\theta }\left(s\right)$ is the sum of the conventional controller’s output, $u\left(s\right)$, and the RL algorithm’s constrained output, ${\pi }_{\theta }(s,y)$. Here, y represents any information that the agent can access but the base controller cannot. Two variants were studied in [33]: absolute and relative CRRL. Absolute CRRL is defined as a residual agent whose actions are constrained by a uniform, absolute bound irrespective of the base controller’s output

$$u_{\theta }\left(s\right)=u\left(s\right)+{\beta }_A{\pi }_{\theta }(s,y)$$

(2)

where ${\beta }_A$ is the parameter that determines the scale of the residual actions. For relative CRRL, the residual actions are constrained to a fraction of the conventional controller’s output and therefore scale with the latter. $u_{\theta }\left(s\right)$ is then given by

$$u_{\theta }\left(s\right)=u\left(s\right)(1+{\beta }_R{\pi }_{\theta }(s,y))$$

(3)

with ${\beta }_R>0$ as a parameter constraining the actions of the neural network relative to the actions of the base control algorithm.

CRRL topologies were proposed in an attempt to realize a version of safe RL. Indeed, a simple argument can be put forth to assure that the overall architecture respects some definition of safety. During the operation of a CRRL architecture, we can distinguish between two phases: An exploration phase is where the agent’s actions are random and explorative. During this phase, the agent is trained and is characterized by a performance decrease. The second and final exploitation phase deploys the trained agent and is characterized by a performance increase.

During the exploration phase, there is no way to assure that the residual agent’s actions are helpful. In the most pessimistic case, this implies that in the initial phases of training, the (random) agent’s action has the same effect as a destabilizing disturbance. However, after some number of iterations, the randomness injected by the learning framework will eventually cool down and the agent should converge to its optimal policy. In turn, this should result in a performance increase. Then, because there is formally no difference between natural exogenous input disturbances and the artificially injected agent’s actions, the performance is maintained by the efforts of the base controller. If we tune the base controller assuming a superposition of any natural input disturbances and the agent’s actions, we can avoid any disastrous performance decrease during training. Here, one may recognize two conflicting design criteria. On the one hand, we want to design the controller so that the input disturbances are not amplified beyond a certain safety value. On the other hand, we want to design the controller so that the injected disturbances are not filtered out entirely, which would prevent the agent from learning anything except that its actions are pointless. We come back to this later.

In conclusion, we may note that the relative CRRL topology was empirically shown to maintain safety better during training [33]. An increased performance improvement after convergence could be observed for an equal performance decrease during exploration, compared to the absolute CRRL topology. We argue this is a direct result of the non-uniformity of the absolute bounds. Note, nonetheless, that the relative bounds imply that when the base control signal is zero, the residual agent’s action is constrained to zero as well. Though it might not be possible to express a more optimal control signal like this for just any application, for those cases where this is true, one obtains a natural scaling of the exploration, resulting in accelerated and improved learning.

This work pursues a practical generalization of the CRRL approach to MIMO systems. Intuitively, the same reasoning applies as was detailed in Section 2.2. If the base controller is capable of attenuating input disturbances, the safety of the learning controller is guaranteed. A precise analysis dedicated to the control and system at hand should deliver some practical bounds to consider when balancing the robustness and learning capacity. In this work, we further consider the special case of cascaded control structures as is common in MIMO contexts. Simply put, a residual agent is superposed on any cascaded control output resulting into N agents for N-state cascades.

Consider the block diagram of a generic N-stage MIMO cascaded control architecture in Figure 1. Note that all signals are vector quantities considering the present MIMO context. The closed-loop system exists of N controllers, $C_n$, and N subsystems, $P_n$ so that the n-th controller generates the $(n-1)$-th reference $x_{n-1}^{*}$, and the $(n-1)$-th process variable is used as the input of the n-th subsystem, $P_n$. In normal operation, the system may be affected by input disturbances $\left\{d_n\right\}$, modeling exogenous excitations. Conveniently, we also include N disturbances, $d_n^{*}$, that affect the intermediate reference signals, $x_n^{*}$. Note that $d_1^{*}=d_1$. These reference disturbances are not a part of any natural control operation provided that the left branch of Figure 1 usually represents a deterministic computation. Instead, they represent the input from the cascaded CRRL agents. This situation is different from the standard CRRL topology, where $N=1$ so that the notion of reference disturbances does not apply.

In the following subsections, we concretize this general idea of a cascaded CRRL structure, where a residual agent is superposed on the conventional controller at each cascade level. In Section 2.3, we first derive some general principles, giving insight into the operation and stability of such a structure. In Section 2.4, we consider the practical implementation details and propose the dedicated actor structure required to efficiently train under the considered cascaded control architecture. In Section 4, the performance of this method is validated in simulation, and its different assumptions are tested.

2.3. Stability Considerations Based on Linear System Analysis

As mentioned in the previous section, the operating principle of a CRRL learning architecture relies entirely on the stability and robustness of the base controller. From a traditional control perspective, the residual agent(s) can be treated as exogenous input disturbances. If the base controller is capable of effectively attenuating the disturbances, there will be a limited decrease in performance, even with the additional artificial exploration noise. This analysis holds for the training phase. During the exploitation phase, when the residual agent’s actions are supposedly beneficial, the base controller should not filter out the agent’s actions. This discussion implies that it is important to keep two design criteria in mind when tuning the base controller knowing that it will be augmented into a CRRL architecture afterwards. One should try to limit the performance degradation during training on the one hand, whilst allowing sufficient maneuverability to enjoy a performance improvement during the exploitation phase.

It is hard to develop bounds for the residual agent(s) that guarantee stable operation irrespective to the field of application and the standard base controller specific to that field. Therefore, in this section, we first lay out a number of design principles that may be applied when adopting a CRRL architecture. Next, as the present analysis attempts an extension to cascaded architectures, we extend this discussion to a cascaded structure and employ these to derive some principle insights into the stability of the cascaded CRRL structure. Note that this extension to a cascaded structure will require some additional precautions since now the input of the different agents, which can be considered as a disturbance during the exploration phase, may be amplified by the various cascades. On the other hand, when we alter our perspective, the cascaded outputs can be interpreted as reference signals for the succeeding levels, except for the final output. That way, we want good tracking performance of the first cascaded layers to avoid completely filtering out the actions of the residual agents on those levels such that the exploration signals would not reach the system.

The analysis in this section is limited to linear systems and is a frequency domain analysis. We argue that the principles transfer to nonlinear systems as long as the non-linearity is limited. We discuss design principles that aim to minimize the performance ${\parallel e\parallel }_2^2$ for natural white noise disturbances, d, and low-frequency reference signals. This description follows the definition of input–output controllability. The following discussion relies on ideas taken from the book [36].

2.3.1. Standard Feedback Controller

Let us first consider a standard feedback controller with system and control frequency response matrices, P, and, C, and control disturbance d. Then the closed loop dynamics are governed by

$$x=T{x}^{*}+S{d}^{*}$$

(4)

with

$$\begin{array}{cc}\hfill S& ={(I+PC)}^{-1}P\hfill \\ \hfill T& =SC\hfill \end{array}$$

(5)

which implies that

$${\parallel x\left(j\omega \right)\parallel }_2\le \overline{\sigma }\left(T\right)\parallel x^{*}{\left(j\omega \right)\parallel }_2+\overline{\sigma }\left(S\right){\parallel d^{*}\left(j\omega \right)\parallel }_2$$

(6)

or with $G=T-I$

$${\parallel e\left(j\omega \right)\parallel }_2\le \overline{\sigma }\left(G\right)\parallel x^{*}{\left(j\omega \right)\parallel }_2+\overline{\sigma }\left(S\right){\parallel d^{*}\left(j\omega \right)\parallel }_2$$

(7)

with $\overline{\sigma }(.)$ corresponding to the maximum singular value. The analysis in this section is based on the consideration that the satisfactory gain for a matrix transfer function is determined by the singular values of the transfer function [36]. As such, the former allows to derive some high-level reasonings about the influence of the residual agent at different frequencies when we apply it on the signal d or $x^{*}$. The superposition of the residual agent on d corresponds with the standard topology, which we will refer to as the control topology. Superposition on $x^{*}$ corresponds with an until now unstudied reference topology. Consideration of this topology is useful for the analysis of cascaded controllers.

We may identify the following design objectives:

1.

For good input–output controllability, we want $\overline{\sigma }\left(T\right)\approx \underline{\sigma }\left(T\right)\approx 1$, preferably for all frequencies but certainly for lower frequencies corresponding to common reference signals. For most physical closed-loop response functions, $\overline{\sigma }\left(T\right)\to 0$ for $\omega \to \infty$. The analysis is largely the same for the control or reference topology. Except for the reference topology, it might be beneficial to have $\overline{\sigma }\left(T\right)\approx 1$ for a slightly higher frequency range at the expense of $\overline{\sigma }\left(T\right)>1$ at lower frequencies. This to make sure that the exploration noise is not filtered out entirely, in the context of slightly nonlinear systems.

2.

For disturbance attenuation, we want $\overline{\sigma }\left(S\right)$ small at high frequencies. At lower frequencies, however, a distinction with conventional design objectives appears, as we then want $\overline{\sigma }\left(S\right)$ to have the same order of magnitude as $\overline{\sigma }\left(T\right)$. As such, high-frequency disturbances are filtered out whilst low-frequency disturbances continue to have a measurable effect on the output. The order of magnitude determines the decrease in performance during the exploration phase, but at the same time the performance increases during the exploitation phase. For the reference topology, we can adopt the same design objective as for any conventional control topology.

We refer to [36] for a discussion on how these design objectives translate into actionable design principles on the open loop gain $PC$.

2.3.2. Cascaded Feedback Controller

Let us now also consider the cascaded feedback control architecture. Consider therefore the following closed-loop dynamics of a generic cascaded system, as shown in Figure 1:

$$x_n=T_n{x}_n^{*}+\sum _{i=1}^n\prod _{j=1}^{n-i}{S}_{n-j}{T}_{i-1}{d}_i^{*}+\sum _{i=2}^n\prod _{j=1}^{n-i}{S}_{n-j}{d}_i$$

(8)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_n& ={(I+P_n{T}_{n-1}{C}_n)}^{-1}{P}_n\hfill \\ \hfill T_n& =S_n{T}_{n-1}{C}_n\hfill \end{array}\end{array}$$

(9)

with $T_0=I$. These expressions resemble those of the standard topology with the exception that in the computation of the outer loop dynamics, we have to take into account the inner loop dynamics $T_{n-1}$. Usually, cascaded controllers are therefore tuned starting from the inner loop and working our way out to the final outer loop. In fact, this is exactly the use of cascaded control such that with $T_{n-1}\approx I$, each loop can be considered a conventional control design problem.

It follows that

$$\begin{array}{c}\parallel x_n{\left(j\omega \right)\parallel }_2\le \overline{\sigma }\left(T_n\right){\parallel x_n^{*}\left(j\omega \right)\parallel }_2\hfill \\ +{\displaystyle \sum _{i=1}^n}{\displaystyle \prod _{j=1}^{n-i}}\overline{\sigma }\left(S_{n-j}\right)\overline{\sigma }\left(T_{i-1}\right){\parallel d_i^{*}\left(j\omega \right)\parallel }_2\hfill \\ \hfill +{\displaystyle \sum _{i=2}^n}{\displaystyle \prod _{j=1}^{n-i}}\overline{\sigma }\left(S_{n-j}\right){\parallel d_i\left(j\omega \right)\parallel }_2\end{array}$$

(10)

or likewise that

$$\begin{array}{c}\parallel e_n{\left(j\omega \right)\parallel }_2\le \overline{\sigma }\left(G_n\right){\parallel x_n^{*}\left(j\omega \right)\parallel }_2\hfill \\ +{\displaystyle \sum _{i=1}^n}{\displaystyle \prod _{j=1}^{n-i}}\overline{\sigma }\left(S_{n-j}\right)\overline{\sigma }\left(T_{i-1}\right){\parallel d_i^{*}\left(j\omega \right)\parallel }_2\hfill \\ \hfill +{\displaystyle \sum _{i=2}^n}{\displaystyle \prod _{j=1}^{n-i}}\overline{\sigma }\left(S_{n-j}\right){\parallel d_i\left(j\omega \right)\parallel }_2\end{array}$$

(11)

These expressions further give rise to the following worst case scenario:

$$\begin{array}{c}\parallel x_n{\left(j\omega \right)\parallel }_2\le \hfill \\ \hfill \alpha \parallel x_n^{*}{\left(j\omega \right)\parallel }_2+\frac{\beta -{\beta }^{n+1}}{1-\beta }\alpha \parallel d^{*}{\left(j\omega \right)\parallel }_2+\frac{\beta -{\beta }^n}{1-\beta }{\parallel d\left(j\omega \right)\parallel }_2\end{array}$$

(12)

or

$$\begin{array}{c}\parallel e_n{\left(j\omega \right)\parallel }_2\le \hfill \\ \hfill \gamma \parallel x_n^{*}{\left(j\omega \right)\parallel }_2+\frac{\beta -{\beta }^{n+1}}{1-\beta }\alpha \parallel d^{*}{\left(j\omega \right)\parallel }_2+\frac{\beta -{\beta }^n}{1-\beta }{\parallel d\left(j\omega \right)\parallel }_2\end{array}$$

(13)

so that $\alpha =\underset{n}{max}\overline{\sigma }\left(T_n\right)$, $\beta =\underset{n}{max}\overline{\sigma }\left(S_n\right)$, $\gamma =\underset{n}{max}\overline{\sigma }\left(G_n\right)$, ${\parallel d\left(j\omega \right)\parallel }_2=\underset{n}{max}{\parallel d_n\left(j\omega \right)\parallel }_2$ and $\parallel d^{*}{\left(j\omega \right)\parallel }_2=\underset{n}{max}{\parallel d_n^{*}\left(j\omega \right)\parallel }_2$. Note that this expression reduces trivially to Equation (6).

To give a first analysis, assume that the cascaded controller was designed successfully according to conventional principles so that $\alpha \approx 1$, $\beta <1$ and $\gamma \approx 0$ in the frequency ranges of practical interest. It follows that the outer control loops are affected by the inner loop disturbances; however, the effect diminishes with each iteration. The analysis above also allows to give some frequency-dependent bounds on the noise amplitudes $d_n^{*}$. In case that the system’s performance cannot be guaranteed using a conventional control architecture and design and a CRRL approach is adopted, we can adopt the design principles from the standard case and extrapolate them control layer by control layer when designing the CRRL approach.

This section gives some superficial design objectives and principles related to CRRL control architectures. The aim of this analysis was to provide some deeper insights in the operating principles of CRRL architectures. We recognize that these principles are still far from practical, but we believe that they already grasp some essential aspects of standard and cascaded CRRL approaches. Overall, it is a very interesting prospect to consider the use of a learning method in the lifetime of the system already during its initial control design. For now though, we leave this conceptual direction for future research.

2.4. Practical Implementation

The considered cascaded architecture poses both challenges and opportunities in terms of the specific design required to enable a residual agent to optimize the baseline controller at each level. In this section, we propose a novel structure for the RL agent to realize the cascaded CRRL architecture and detail the different elements of this structure. In Section 4, these are validated through ablation studies on a simulated system.

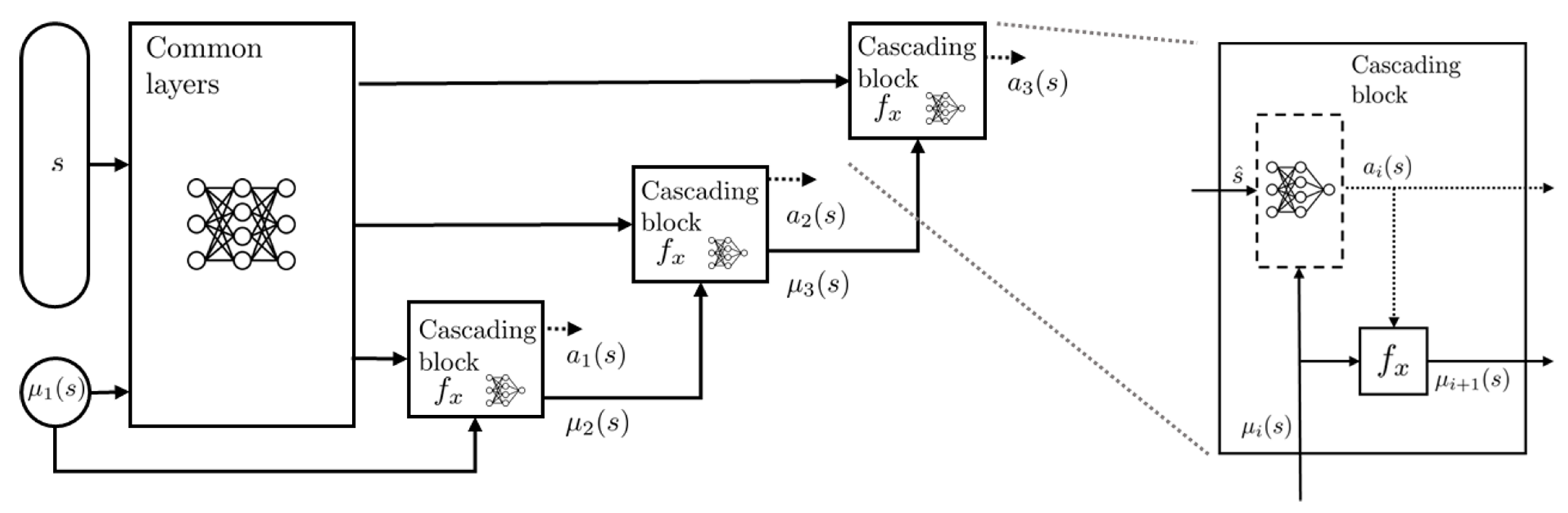
(a) Actor: Figure 2 shows the structure of the cascaded CRRL actor network. The network consists of a separate output head for each cascade level in the form of a cascading block, as well as a common part that forms a common state representation, passed to all cascade output heads. Through the cascading block, the cascaded structure of the system is reflected in the policy network. Each cascading block calculates the residual output for its respective level. As the objective of these residual actions is to optimize their base controller’s outputs, which can commonly not be derived from the current system’s state only (e.g., due to the integration effect in a PI controller), the base controller’s action is a necessary input for each output head. Since the lower-levels’ base controller outputs are not known beforehand, as these depend on the residual actions of the preceding output heads, the base controllers are included as non-trainable network layers in the policy, represented as $f_x$ in the cascading blocks. In each block, the base controller’s output for the next level is calculated from the current residual action and the previous level’s base input, along with any necessary state information. This is passed together with the representation of the state and top level base action, calculated by the common layers, to the next level’s output head, which calculates the level’s residual action through its block-specific network layers. This is continued until the residual for the lowest level is calculated.

While this structure for the actor network, including the base controllers as non-trainable layers, is necessary for training, during deployment, the residual policy can be reduced to its neural network layers only (i.e., discarding the $f_x$ blocks and cascaded connections) and executed in parallel with the base controllers’ cascaded structure. After execution of the first cascade level, the first level’s residual and the state representation of the common layers is calculated. The residual is applied and execution of the second output head is halted until the second level’s base controller’s output is calculated. This is passed together with the common state representation to the second head, after which the second level’s residual is calculated. This is again continued until the residual action for the lowest level is calculated.

Formally, the total control action $u_{\theta ,i}\left(s\right)$ for the i-th cascade level is given by

$$u_{\theta ,i}\left(s\right)=u(s,u_{\theta ,i-1}\left(s\right))(1+{\beta }_R{\pi }_{\theta ,i}\left(y(s,u_{\theta ,i-1}\left(s\right))\right)).$$

(14)

(b) Critic: The objective of the critic is to estimate the state–action–value estimate of the current action in the given state. Similar to [33], we found that passing the total action applied to the system, i.e., the vector combining $u_{\theta ,i}\left(s\right)$ for $i=1\cdots n$ with n the number of cascade layers and $u_{\theta ,i}$ the corresponding level’s residual action multiplied by the base controller action and ${\beta }_R$, along with the state s provides enough information for the critic to learn an appropriate estimate.

In the following sections, the performance of the method is validated, and the requirement and influence of the different elements are studied.

3. Simulation Environment

3.1. System Overview

In this contribution, we study the cascaded CRRL methodology on a simulated dual-drive drivetrain. In a dual-drive configuration, two motors actuate a single load. This topology has been proposed as an alternative to single-drive systems in varying configurations for different applications such as electric vehicles [37], robot actuation [38] and haptic feedback [39]. For our simulation experiments, we employ a high fidelity simulator, designed through a dedicated study on the dual-motor drivetrain architecture for electrical vehicles [40]. In this section, we provide a high level overview of the simulated system, its operation and parameters. As a detailed description of its implementation particularities is out of scope for this paper, we refer to [40] for further info.

The considered drivetrain and its load consists of two different induction motors, connected to and driving a single axis. A load, e.g., the vehicle, is attached to the drivetrain that is required to track a varying velocity setpoint. A velocity controller tracks the velocity reference, determining the overall torque setpoint. A second supervisory controller subsequently determines the power split between the two drives. Within each drive, a flux controller determines a flux setpoint given the motor’s torque setpoint, after which field-oriented control [41] is employed to determine the necessary phase currents and subsequently the voltages of the motors. In this work, we limit ourselves to the velocity, power split and flux controllers, resulting in a three-level cascaded structure, in which the third level is present in parallel for both motors.

The load and reference velocity of the drivetrain are based on a vehicular load and a modal driving cycle. Nonetheless, note that we consider the system as a general industrial drivetrain as we include the velocity controller in our analysis, considering the load to be representative for a general application. The vehicular-based load is divided in the powertrain load $F_{\mathrm{powertrain}}$ as the motor transfers power to the wheels through the drivetrain, a drag force $F_{\mathrm{drag}}$ due to the air resistance and a force $F_{\mathrm{roll}}$ due to the rolling resistance of the tires:

$$\begin{array}{cc}\hfill F_{\mathrm{powertrain}}& =\frac{i_f(T_{{\mathrm{IM}}_1}+i_t{T}_{{\mathrm{IM}}_2})}{r_w},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill F_{\mathrm{drag}}& =\frac{1}{2}{\rho }_{\mathrm{air}}{c}_{d}A{v}^2,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill F_{\mathrm{roll}}& =c_{r}mg,\hfill \end{array}$$

(17)

where $i_t$ and $i_f$ are the transmission and differential gear ratio; $T_{{\mathrm{IM}}_1}$ and $T_{{\mathrm{IM}}_2}$ are the delivered torque by the first and second induction machines, respectively; $r_w$ is the wheel radius; ${\rho }_{\mathrm{air}}$ is the air density; $c_d$ is the drag coefficient; A is the cross sectional area of the vehicle; v is the absolute speed of the vehicle, as the wind speed is not taken into account; and $c_r$ is the rolling resistance coefficient given by $c_r=c_{r,1}+c_{r,2}{v}^2$. The total mass of the system, including the longitudinal and rotational inertia, is given by

$$m_t=m+\frac{J_w}{r_w^2}+\frac{J_d{i}_f^2}{r_w^2}+\frac{i_f^2(J_{{\mathrm{IM}}_1}+i_t^2{J}_{{\mathrm{IM}}_2})}{r_w^2},$$

(18)

with m as the vehicle’s mass, and $J_w$, $J_d$, $J_{{\mathrm{IM}}_1}$ and $J_{{\mathrm{IM}}_2}$ as the inertia of the wheels, drivetrain and the induction machines, respectively. Through Newton’s second law, the change of load velocity v is then given by

$$\dot{v}=\frac{1}{m_t}(F_{\mathrm{powertrain}}+F_{\mathrm{drag}}+F_{\mathrm{roll}}).$$

(19)

For the simulation of the induction machines, we refer to the in-depth description given in [40]. The employed parameter values can be found in Appendix A.

3.2. Base Controllers

For each cascade level, the following base controller is implemented:

3.2.1. Velocity

As is common, a PI controller with $K_P=110$, $K_I=8$ and sample frequency 50 Hz is employed to track the velocity setpoint.

3.2.2. Power Split

The power split between the motors is given by $\eta \in [0,1]$, with $T_{{\mathrm{IM}}_1}=\eta T$ and $T_{{\mathrm{IM}}_2}=(1-\eta )T$ with T the overall torque setpoint determined by the velocity controller. To determine the power split between the motors, we employ a feedforward model-based controller that minimizes the total estimated steady state losses of the two motors. The loss in each motor is estimated as

$$\begin{array}{cc}\hfill P_{\mathrm{loss}}& =k_1{\psi }_{rd}^2+k_4\frac{T^2}{{\psi }_{rd}^2},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill k_1& =\frac{3}{2}(\frac{R_s}{L_m^2}+\frac{N_P^2{\omega }^2{L}_m^2}{R_m{L}_r^2}),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill k_4& =\frac{2}{3N_P^2}(\frac{R_s{L}_r^2}{L_m^2}+R_r),\hfill \end{array}$$

(22)

as described in [42]. When $\eta$ is either 1 or 0, i.e., one of the motors delivers the full power, the other motor can be either left on or turned off (i.e., the motor’s inverter switches remain open). This is implemented by ranging $\eta$ from $-0.1$ to $1.1$, with ${\mathrm{IM}}_1$ turned off if $\eta <0$ and ${\mathrm{IM}}_2$ turned off if $\eta >1$.

3.2.3. Flux

As with gamma, the base flux controller of each motor is a feedforward model-based controller that minimizes the steady-state losses [42]:

$${\psi }_{\mathrm{set},\mathrm{IM}}=\sqrt{T_{\mathrm{set},\mathrm{IM}}}\sqrt{\frac{2}{3}\frac{L_r}{N_P}\sqrt{\frac{R_s{L}_r^2+R_r{L}_m^2}{R_s{L}_r^2+L_m^4\frac{N_P^2{\omega }_M^2}{R_m}}}}$$

(23)

4. Simulation Experiments and Results

In this section, a series of simulation experiments are performed aimed at testing the performance of the proposed method (Section 4.1, Section 4.2, Section 4.4 and Section 4.5) and studying the assumptions and operation of the method (Section 4.1 and Section 4.3). We first provide the necessary general, point-by-point information of the performed simulation experiments. Next, we detail each experiment and discuss the results.

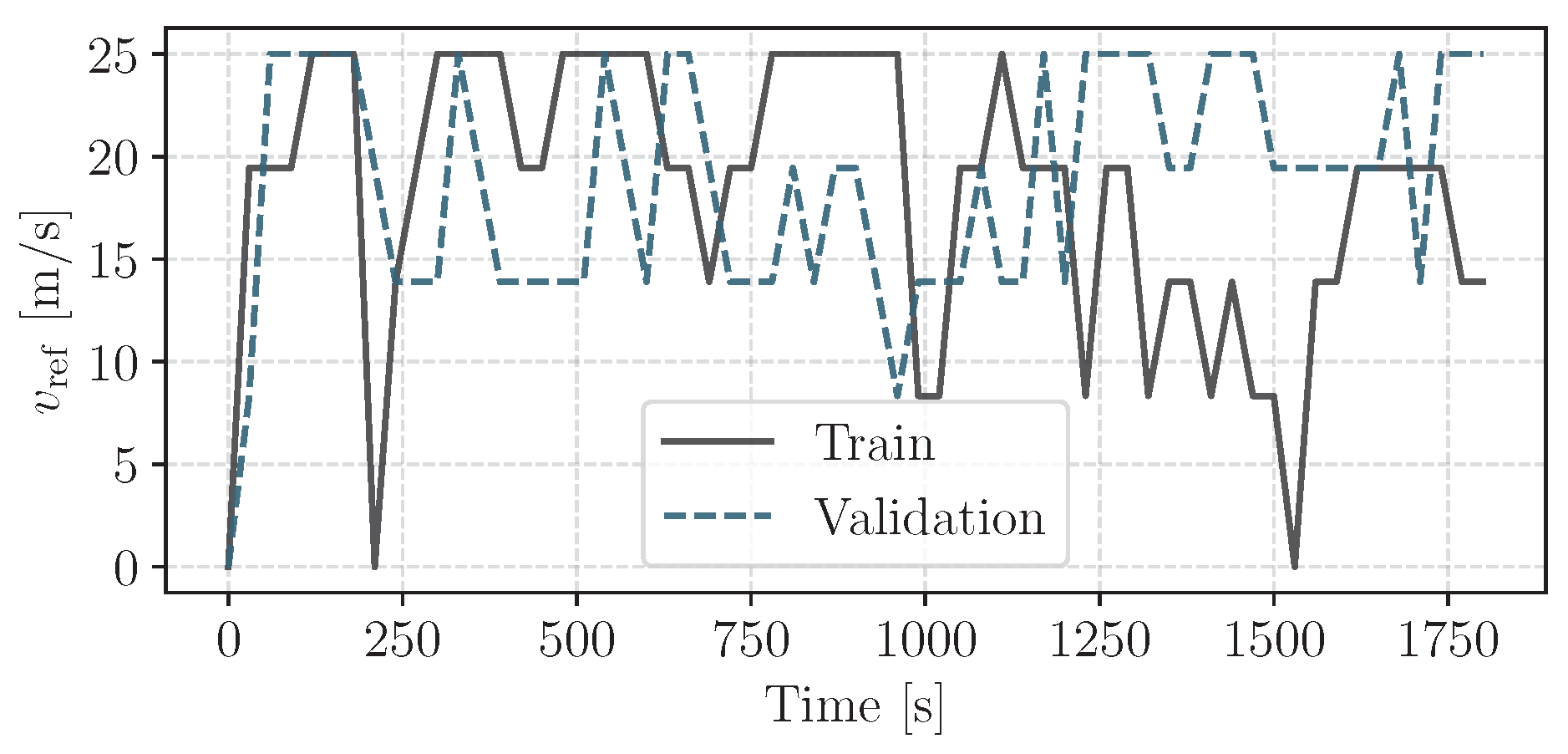
All results in this section are generated by training an agent on the training trajectory, whose total length is 5 h 30, and subsequently deploying it deterministically, i.e., by taking the mean value of the actor’s output distribution [35] instead of sampling an action, on the test trajectory of length 1h. The trajectories, based on modal driving cycles, are visualized in Figure 3. Unless stated otherwise, the results shown are the performance on the test trajectory, averaged over 20 independent train/evaluation runs. The employed reward for the cascaded CRRL algorithm is the mean absolute error (MAE) of the linear velocity of the vehicular load and its reference. The hyperparameters for the single and multiple output configurations as defined later are given in

Table 1. SAC parameters.

Parameter	Single	Multiple
	Output	Output
Optimizer (all networks)	Adam	Adam
Learning rate—Actor	3 × 10${}^{-5}$	3 × 10${}^{-5}$
Learning rate—Critic	3 × 10${}^{-3}$	3 × 10${}^{-4}$
Discount $\left(\eta \right)$	0.91	0.91
Batch size (randomly sampled from replay buffer)	256	256
Replay buffer size	1 × 10${}^6$	1 × 10${}^6$
Number of hidden layers—Actor	2	2
Number of actor head-specific layers	-	1
Number of hidden layers—Critic	3	3
Number of neurons per hidden layer—Actor	128	64
Number of neurons per hidden layer—Critic	256	128
Nonlinearity	ReLU	ReLU
Target smoothing coefficient	0.005	0.005

. The relative allowed deviation ${\beta }_R$ for each CRRL agent is 0.2 over all experiments, unless stated otherwise. The CRRL agents read the state and apply an action to the system every 1.5 s. An epoch is defined as 75 s. The state of the system, passed to the agents, consists of the current and previous overall torque setpoint, the previous torque setpoint of both induction motors, a flag indicating if each motor is currently on or off, the actual and current reference velocity and the current estimated stator flux of both induction motors. For the multiple output configuration, the total calculation time for the training of 1 epoch is 3.3 s on an Intel i9-12900K CPU. Note that this is only necessary for training the network. During deployment, only a forward pass of the actor network is needed, which consists of only 135 680 FLOPS with the current network parameters.

4.1. Cascaded CRRL Performance

As described in Section 2.2, the training and deployment of a CRRL architecture consists of two phases: the exploration phase and the exploitation phase. During the exploration phase, the residual agent’s actions have a significant degree of randomness as the agent is learning to optimize the overall system. As this corresponds to a disturbance on the base controller’s output, this phase might result in temporarily decreased performance of the overall system. During the exploitation phase on the other hand, the residual agent has converged to its (possibly local) optimal policy, improving the overall system performance given a successful training phase. As such, the performance of the cascaded CRRL controller needs to be evaluated both after convergence and during training.

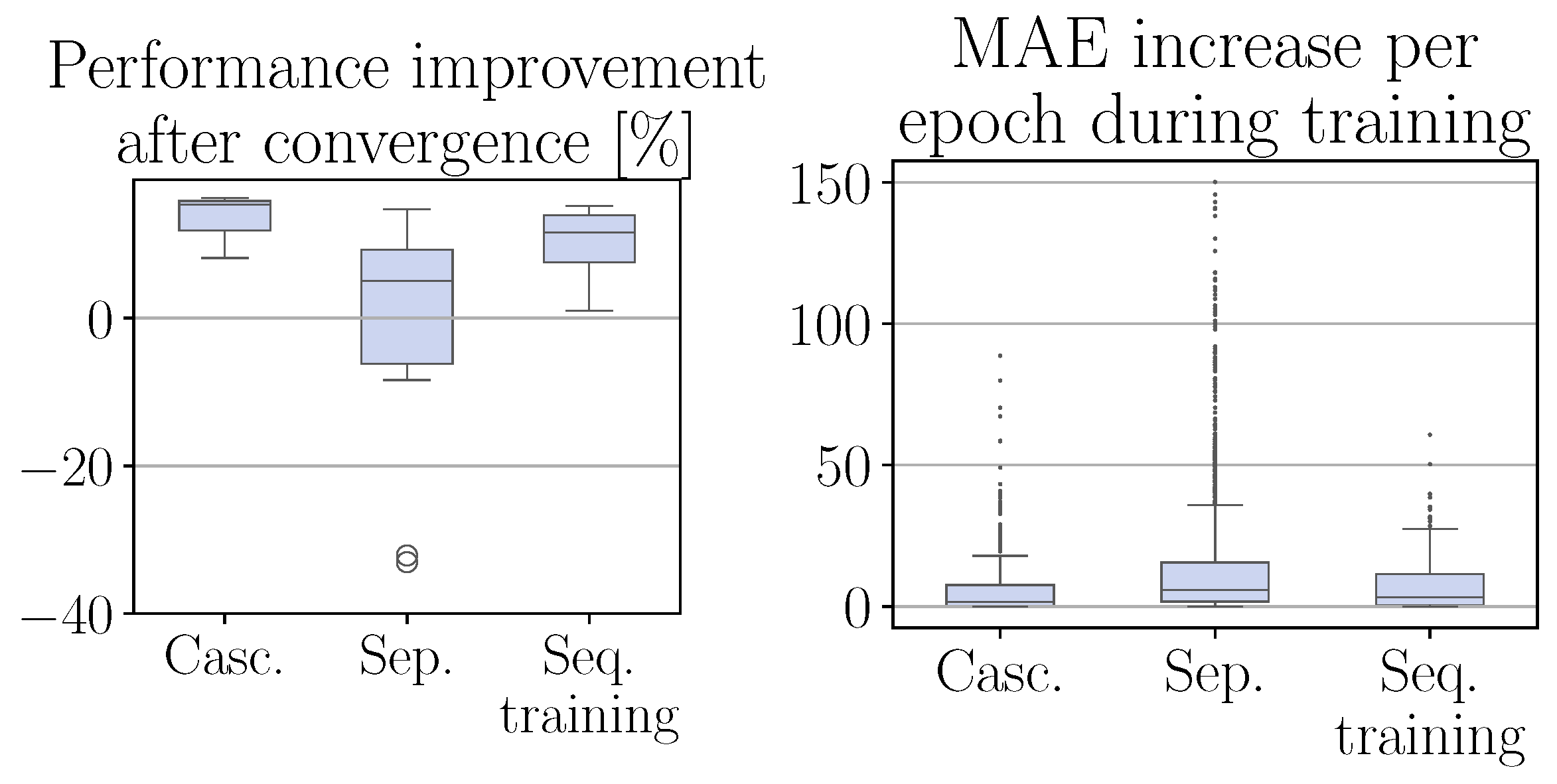
(a)

Exploitation phase: Figure 4 on the left shows the overall performance increase after convergence of the cascaded CRRL controller (Casc.) on the test trajectory, i.e., the total MAE on this trajectory, relative to the overall performance when deploying the base controllers only. On the test trajectory, the cascaded CRRL consistently results in a significant improvement through its system-specific corrective adaptations over the different runs, with an average improvement of 14.7%.

(b)

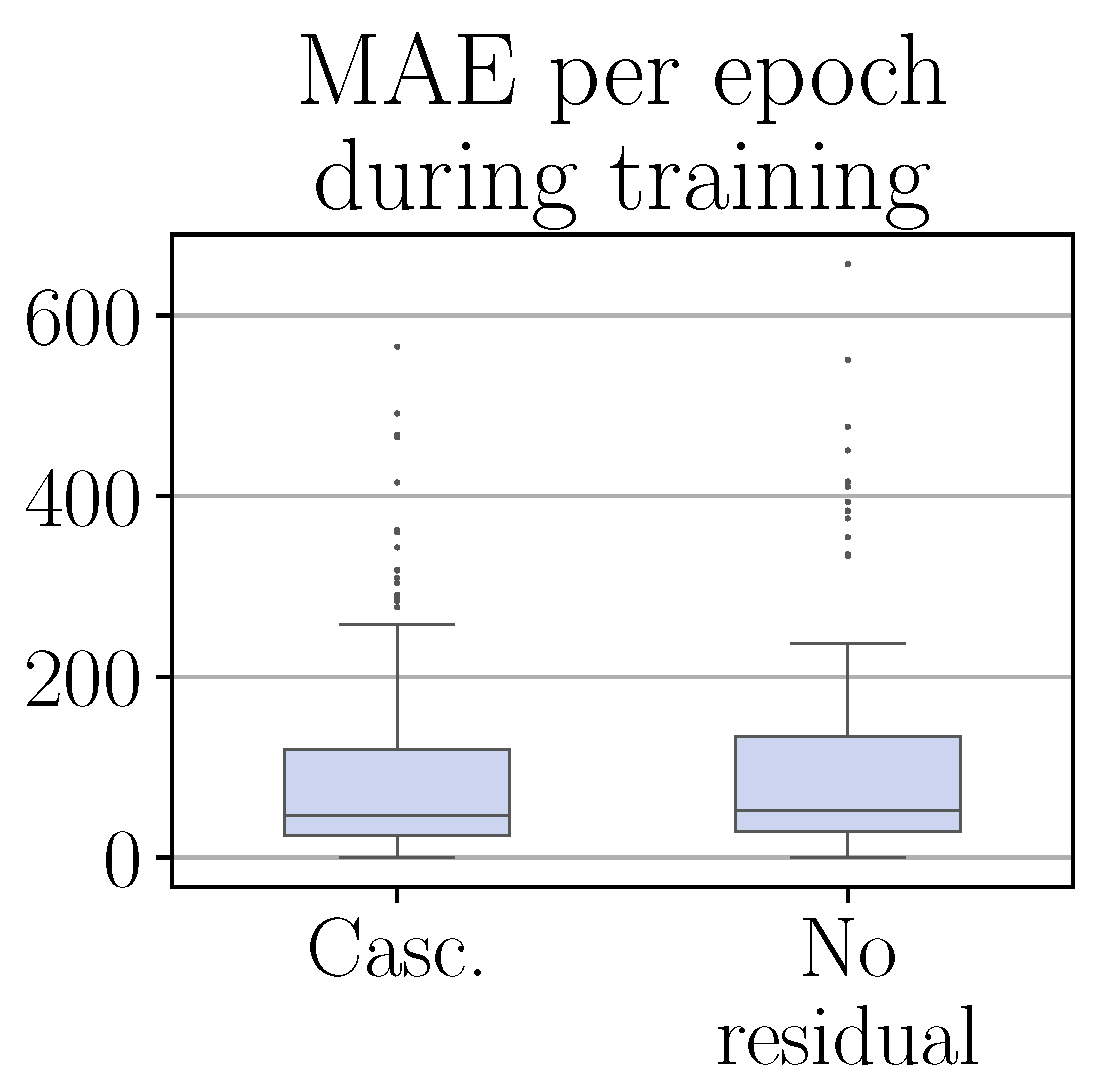
Exploration phase: Figure 4 on the right and Figure 5 compare the performance of the cascaded CRRL controller during training with that of the baseline controller. Figure 5 shows the MAE per epoch during training for both cascaded CRRL (Casc.) and with only the base controllers acting (no residual). Figure 4 on the right shows a more detailed view, giving the increase in MAE per epoch during training for each epoch, where the performance with the cascaded CRRL agent was decreased compared to when only the base controllers are deployed. This relative representation allows to compare the different forms of CRRL controllers, as studied in the following experiments, more accurately. In Figure 5, we can see that due to the CRRL structure that is maintained, the final improvement of 14.7% on average is obtained with only minimal performance decrease during the exploration phase. This shows that the cascaded CRRL algorithm maintains the main property of the CRRL framework, leveraging the robustness of the base controller to maintain safe operation at all times during training, as opposed to standard RL algorithms, where the initial exploration phase may result in unsafe situations before a performance improvement is attained.

4.2. Comparison to Standard CRRL

To compare the performance of the cascaded CRRL to the standard CRRL, we first compare our method to a naive application of the standard concept, where a distinct CRRL controller is added to each base controller and all four resulting CRRL controllers are trained simultaneously, denoted as the separate configuration in Figure 4. With a mean improvement after convergence of only 0.5% due to various runs, where the algorithm did not converge to a beneficial policy as well as a higher decrease in performance occurring during training, the resulting performance is significantly worse. This does not come as a surprise, as, due to the cascaded structure, this configuration suffers from non-stationarity, which is a well-known issue in hierarchical RL [24] where the observed state–action–next state transitions vary over time due to the changing lower-level policies.

To mitigate this, we train each standard CRRL controller sequentially until convergence, starting from the top level. After training of the first agent, it is deployed deterministically, and the second agent is trained. This is repeated until all agents are trained. In Figure 4, where this configuration is denoted as sequential training, we can see that the performance, both during training as on the test trajectory, significantly improved over the concurrent training, reaching a mean improvement of 10.9%. However, the performance of cascaded CRRL is not reached. This indicates that the ability to optimize all residual actions concurrently is advantageous for reaching a better overall performance, as studied further in the following experiment.

4.3. Influence of the Elements of Cascaded CRRL

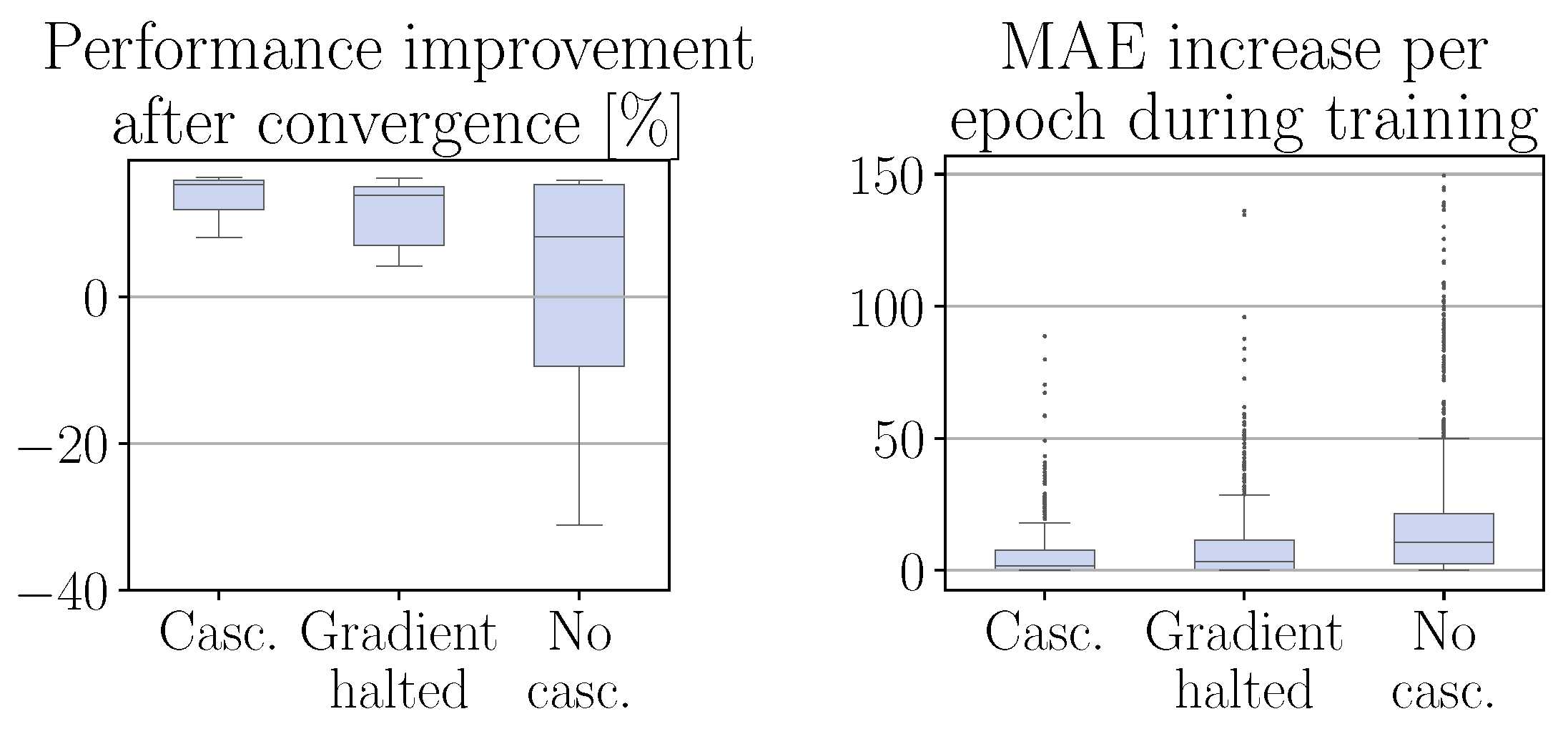
In the previous experiments, it was observed that the performance of cascaded CRRL is better than when different standard CRRL agents are optimized sequentially. This indicates that the concurrent information flow of the effect of each action on the estimated Q-value during training may be beneficial for the agent to learn to improve the overall system performance.

To test this, we train a configuration in which only the gradients of the output head of the first level flow through to the common layers. Of the other heads, the gradients are interrupted after the head-specific layers in the cascading block when moving backwards through the network. As such, the common layers, which pass their output state representation to all output heads, are trained through the information of the top cascade level only. Note that the information flow is not completely interrupted, as the other output heads still influence the gradient through the common forward pass of all actions through the critic network. The result is shown in Figure 6, denoted as the gradient-halted configuration. We see that the performance, though still better than in the separate case, is worse than for the original method, both after deployment and during training, reaching an average improvement of 11.3%. This confirms that the agent benefits from the improved information flow due to the joint training.

Next, we check the influence of the cascading structure of the actor network. We apply standard CRRL as if the system was a non-cascaded MIMO system: the actor has an output layer of four neurons, i.e., the four residual actions, and all base actions, i.e., calculated as if no residual actions are applied, are passed to the actor together with the state as input to the first layer. The result is shown in Figure 6, denoted as the no cascading configuration. We can see that the performance, with a mean improvement of only 1.1%, as several runs do not converge to a beneficial policy, is significantly worse than for the cascaded structure, resembling the performance of the separate configuration of Section 4.1. By not including the base controllers in the actor network and cascading the calculated residuals through them, the agent does not have access to the full information of the system on which it acts, which leads to a strongly decreased performance over the cascaded CRRL method. Note that the no cascading configuration is still given the original base actions as input to its first layer.

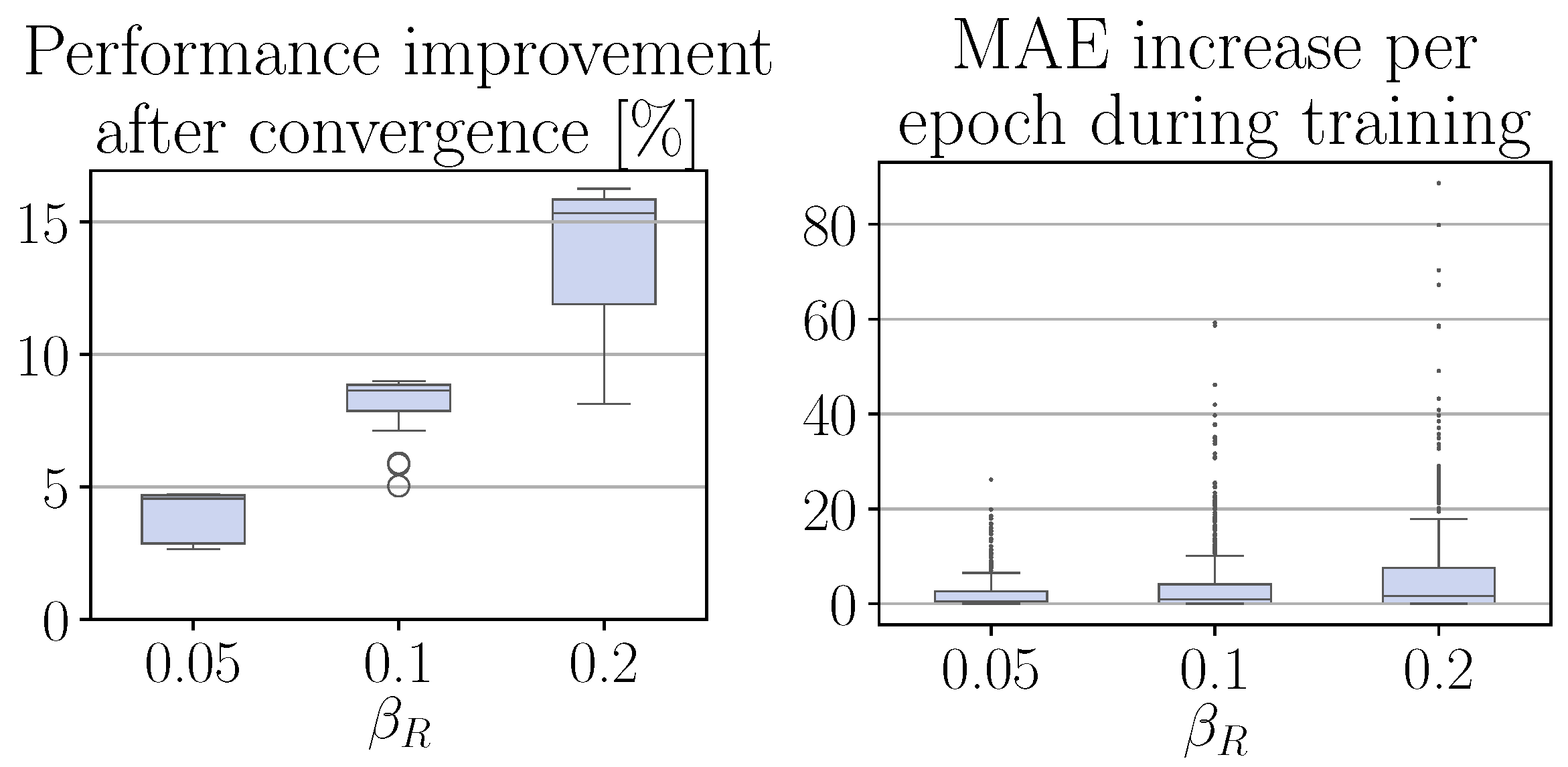
4.4. Effect of Varying the Residual Agent Bounds

The residual RL agent in cascaded CRRL requires no extra parameters to tune compared to the standard hyperparameters of the SAC algorithm [35], except for the bound of the residual agent, determined by ${\beta }_R$. In Figure 7, the effect of varying this bound is studied for different values of ${\beta }_R$. We can see that the freedom allowed by the residual agent is a trade-off between the potential performance improvement after convergence and the possible, though at all times limited, performance decrease during training. As such, ${\beta }_R$ is an intuitive parameter to tune that can be increased iteratively while observing system performance in practice.

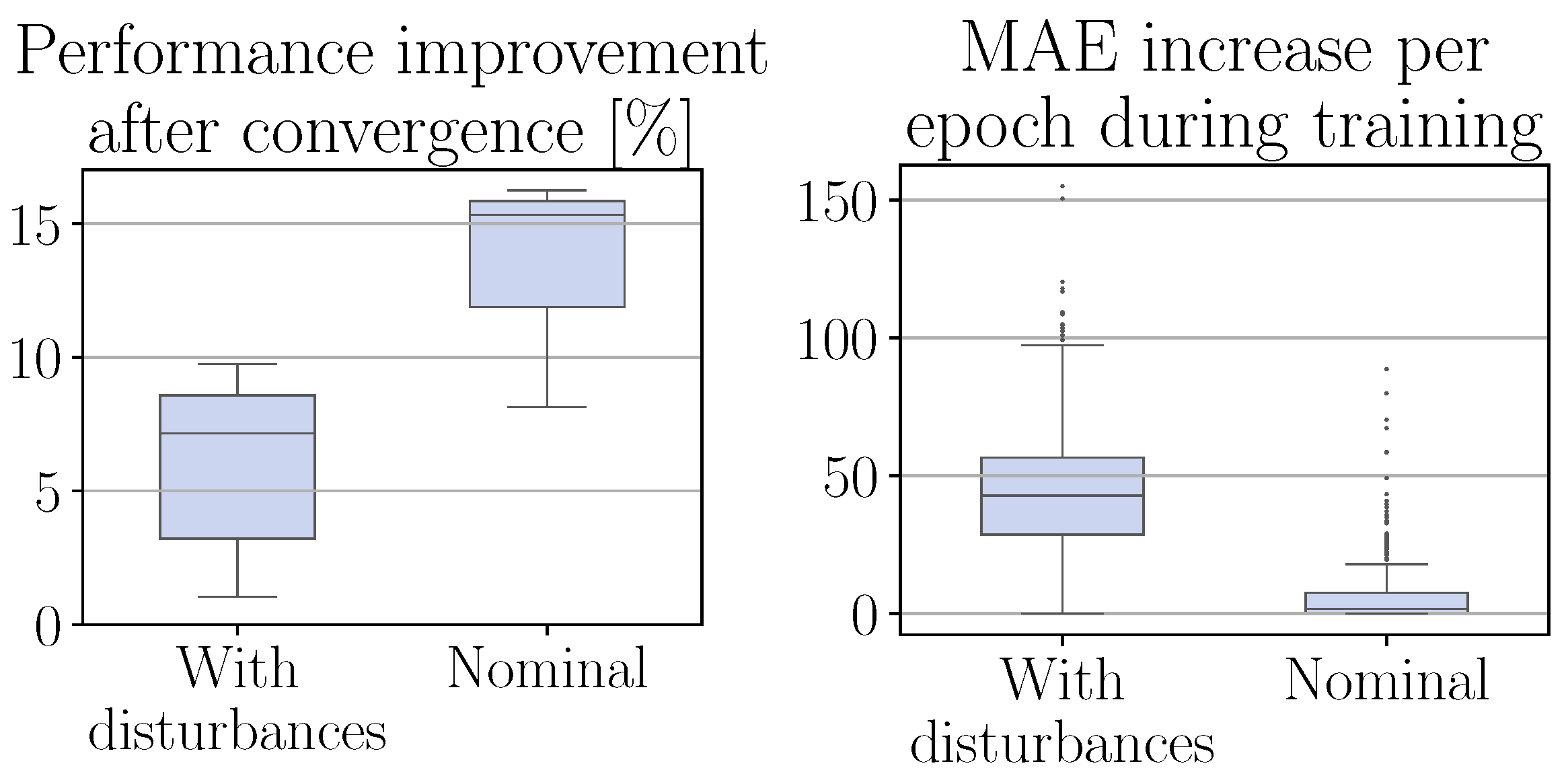
4.5. Effect of Measurement Disturbances

Finally, we study the influence of measurement disturbances on the performance of the cascaded CRRL controller. For this, we perform an experiment where measurement noise, sampled from $\mathcal{N}(0,0.02x)$ with $\mathcal{N}$ the normal distribution and x the nominal value of the measurement, is added to all measurements. Note that this is a severe disturbance with a variance of 2% of the nominal value, well out of the accuracy range of common commercially available encoders and current sensors. The results are shown in Figure 8. As can be seen, even though the performance unavoidably drops due to the significant disturbances, the residual agent continues to succeed in finding a policy that further optimizes the baseline controller significantly.

5. Conclusions and Future Work

In this article, we presented cascaded constrained residual reinforcement learning, a method to optimize the performance of a cascaded control architecture while maintaining safe operation at all times. We drew inspiration from the constrained residual RL framework, where a reinforcement learning agent is used as an add-on to a conventional controller to optimize its performance while leveraging its robustness to guarantee safe operation. We first revisited the interaction between the residual agent and the baseline controller and discussed the inherent differences between the standard output-based residual agent topology and the reference topology, which surfaces in a cascaded structure. Subsequently, we employed this to derive some principle insights in the operation and stability of a cascaded residual structure. Next, in simulation experiments, we showed that a naive application of standard CRRL to the cascaded control structure of a dual motor drivetrain results in unstable performance due to the non-stationarity of the resulting observations for the higher level agents. We proposed a novel actor structure, reflecting the cascaded structure of the system and incorporating the base controllers during training to ensure full system information for the residual agent. We validated the resulting cascaded CRRL method’s performance in the simulated environment and showed that it results in a stable improvement of 14.7% on average of the base controller structure, with limited decreases in performance during the training phase, maintaining the robustness of the CRRL framework. In a series of ablation studies, we validated its assumptions and studied the different principles leading to the efficient optimization of the cascaded, residual agent.

Based on the work in this contribution, a novel research path that will be studied is to consider the use of a residual agent already in the initial design of the baseline controller, studying design principles for tuning the base controller for the conflicting objectives of, for example, noise attenuation, while allowing sufficient exploration of the residual agent. A second research path that can be discerned and that will be pursued in the following work is the optimization of cascaded systems with large differences in response time between the different levels, as often encountered in practical applications.