Abstract
This work proposes a solution for redundant nonholonomic mobile manipulator control with corridor constraints on base motion. The proposed control strategy applies an artificial potential field for base navigation to achieve joint control with desired trajectory tracking of the end effector. The overall kinematic model is created by describing the nonholonomic mobile platform and the kinematics of the manipulator. The objective function used consists of a primary control task that optimizes the joint variables to achieve the desired pose or trajectory of the end effector and a secondary control task that optimizes the joint variables for the base to support the arm and stay within the corridor. As a last priority, an additional optimization is introduced to optimize the maneuverability index. The proposed baseline navigation has global convergence without local minima and is computationally efficient. This is achieved by an optimal grid-based search on a coarse discrete grid and a bilinear interpolation to obtain a continuous potential function and its gradient. The performance of the proposed control algorithm is illustrated by several simulations of a mobile manipulator model derived for a Pal Tiago mobile base and an Emiko Franka Panda robotic manipulator.
1. Introduction
In cases where the working range of industrial manipulators is insufficient, mobile manipulators are used, where the manipulator is attached to a mobile platform. The latter requires a more advanced localization and control algorithm. To achieve any pose of the end effector, a manipulator with at least 6 DOF (degrees of freedom) is required. However, in practice, manipulators and biological systems are usually equipped with more than six actuated joints to achieve redundancy. This allows them to circumvent motion constraints due to joint limits, avoid singularities, optimize the manipulability index, avoid obstacles, or introduce other tasks such as the mobile base preference path. For example, in this work, a redundant mobile manipulator system with 10 independent generalized coordinates (defining the configurations of the mobile platform and manipulator joints) is used to achieve an end-effector pose with 6 DOF. Due to the high degree of redundancy, the computation of inverse kinematics for such a robotic system becomes computationally intensive and complex. In general, there is no analytical solution, and we may be faced with an infinite number of different joint configurations that solve the inverse kinematics problem.
Usually, redundancy resolution in velocity space is achieved by the generalized Moore–Penrose inverse (pseudo-inverse), which minimizes the quadratic norm of joint rates for a desired translational and angular velocity of the end effector. The complexity of the pseudo-inverse of a manipulator Jacobian matrix is O(3) [1], which can become inefficient for hyper-redundant systems, such as snake-like robots or continuum robots [2]. Nevertheless, velocity pseudo-inverse approaches are popular because they provide universal, robot-independent, and well-documented solutions [3,4,5,6]. The approach relies on differentiable objective functions to obtain gradient joint velocities for redundancy resolution [7,8] and thus do not directly address the geometry of the redundancy degree, but instead address it at the velocity level. The latter becomes important when nonholonomic systems with wheels are used to achieve mobility. This leads to the distinction between kinematic redundancy and velocity redundancy [4], where the number of feasible velocities, and thus velocity redundancy, is reduced by the number of nonholonomic (velocity) constraints. Instead of a regular base with wheels, an omnidirectional base could be used that utilizes the unconstrained velocity space of the base, resulting in a holonomic system with simpler control design and higher velocity redundancy [9,10].
Various approaches that extend or replace the classical pseudo-inverse velocity approaches include reinforcement learning, particle swarm optimization [8,11,12]; nonlinear optimization approaches [7]; genetic algorithms [13], the model predictive approach [14,15]; neural networks [8], adaptive control [16]; the robust control approach [14,17]; graph search approaches, such as A star or rapidly exploring random tree [18,19]; potential field, and the like. A more detailed overview of planning and control approaches for mobile manipulators is presented in [5,20].
To achieve the desired performance of a mobile manipulator, the base and end effector must be planned and controlled together. Typically, this is achieved through pseudo-inverse velocity approaches, where the configuration of the base supports the desired performance of the end effector in tracking the trajectory [4]. In addition, a separate trajectory for the base can be provided as a second priority task [6,10,21], or the priorities between the base and the end-effector tracking can change depending on the nature of the task [22]. The position of the base can also be optimized by time relaxation along the intended path to better support the manipulator [23]. In [24], joint control of the base and end effector is proposed, with the arm also being nonholonomic. To deal with the uncertainties of base motion, an effective decoupling of the end effector and base motion is proposed in [25] using real-time control of the arm by fast visual inertial sensing.
In the literature, the main task of the mobile manipulator is to follow the desired effector trajectory. This can be achieved with decentralized control, where the mobile base and arm are separate controlled systems or with centralized systems where a single joint control system is used. The mobile base can be moved first in the arm’s work area before joint control begins, or the arm starts moving even before it is within the reaching area of the arm. The movement of the base may be free, moving only in the direction of the end-effector’s target, or it may attempt to optimize its own objective function, such as avoiding obstacles, but is not constrained to a path or trajectory. On the other hand, the base may be controlled to follow the reference trajectory, which may be a second priority task. The latter solution is very common in the literature [4,6,10,21] and requires planning of both the trajectories of the end effector and the base. In the presence of disturbances [26] or inadequate planning, the desired pose of the end effector may not be within the range of the mobile manipulator when the base is optimally following the trajectory or vice versa. This problem was explored in [23] with ways to relax the timing constraints on the mobile base, which can optimize its position along a fixed reference path.
Potential field approaches are widely used in mobile robotics for path planning and motion control. A common problem with potential field approaches is local minima, since a repulsive field is typically generated locally for an obstacle and can nullify attractive target behaviors. Full or partial obstacle information can be used to modify the potential field around obstacles to avoid local minima, as in [27,28,29] or by geometrically modeling obstacles through envelopes [30]. The desired change in the potential field to overcome local minima could be achieved by including multiple attractive points instead of just one point in the target [31] or by adding virtual obstacles to move away from local minima [32]. In addition, the artificial potential field can be enhanced by introducing a potential density along the obstacles for path planning using a quasi-geodesic curve, as presented in [33]. Strategies for bypassing local minima could also include behavioral strategies, such as wall tracking in [34].
Some approaches also combine global grid-based search algorithms with artificial potential fields to improve performance. A partial artificial potential field and a three-neighbor A* algorithm to address irregular obstacles is proposed in [35]. In [36], a combination between the probabilistic roadmap with A* search and the artificial potential field method is proposed to improve the roadmap construction. In [37], the authors combine intermediate goal points obtained by the A* algorithm and the improved potential field to obtain a global optimal path. The potential field can also be interpolated from a discrete cost map obtained from an optimal grid-based search [38,39].
Potential field approaches are also common in manipulators and mobile manipulators for path planning and control [5,40]. Redundant manipulator path planning is proposed in [41,42], where separate potential fields are proposed for translational and rotational motions. In [43], a deep reinforcement learning algorithm is combined with an artificial potential field to improve the convergence of 7 DOF manipulator planning. In [44], virtual targets and obstacles are added to avoid detected local minima in manipulator planning. Examples of collision-proof trajectory planning for mobile manipulators with artificial potential field can be found in [45,46].
This paper addresses the trajectory tracking problem for redundant mobile robots. The robot has 10 independent generalized coordinates that define the configuration of the mobile platform and joints to position the end effector in the global coordinate system with 6 DOF. The joint control of the end effector and the mobile base is implemented in velocity space using the classical pseudo-inverse Jacobian approach, which combines the coordinated action of the arm and the base considering the corridor-constrained motion of the base. The main idea is to allow free movement of the base within the given corridor so that the primary task of tracking the end-effector can be performed as efficiently as possible. In industry, such corridors are a common solution to enable efficient material flow of automated guided vehicles and other mobile transporters. The corridors are also usually marked with lines on the ground to prevent other participants from interfering with the operation of the autonomous transporters. To achieve the desired control behavior of the base, a navigation function is proposed. The navigation function is constructed from a known environment layout and enables convergent navigation of the base without problems with local minima.
The main contribution of this work is the following. We have derived a trajectory tracking controller for a redundant mobile platform with 9 DOF, consisting of a Pal Tiago Base and an Emika Franka Panda robotic manipulator. A velocity-based inverse kinematic approach is formulated and extended to account for the joint trajectory of the end effector and the mobile base for potential field navigation in a corridor-constrained environment. The proposed navigation function has no local minima because it applies an optimal discrete E*-graph-based search to compute the discrete cost-to-goal potential. To be efficient, a coarse discrete grid can be used since an additional interpolation using bilinear interpolation is provided to obtain a smooth potential and its gradient. Furthermore, several known approaches are integrated into a final solution applied to a redundant mobile manipulator. The performance is validated and compared using several simulations.
2. Problem Specification
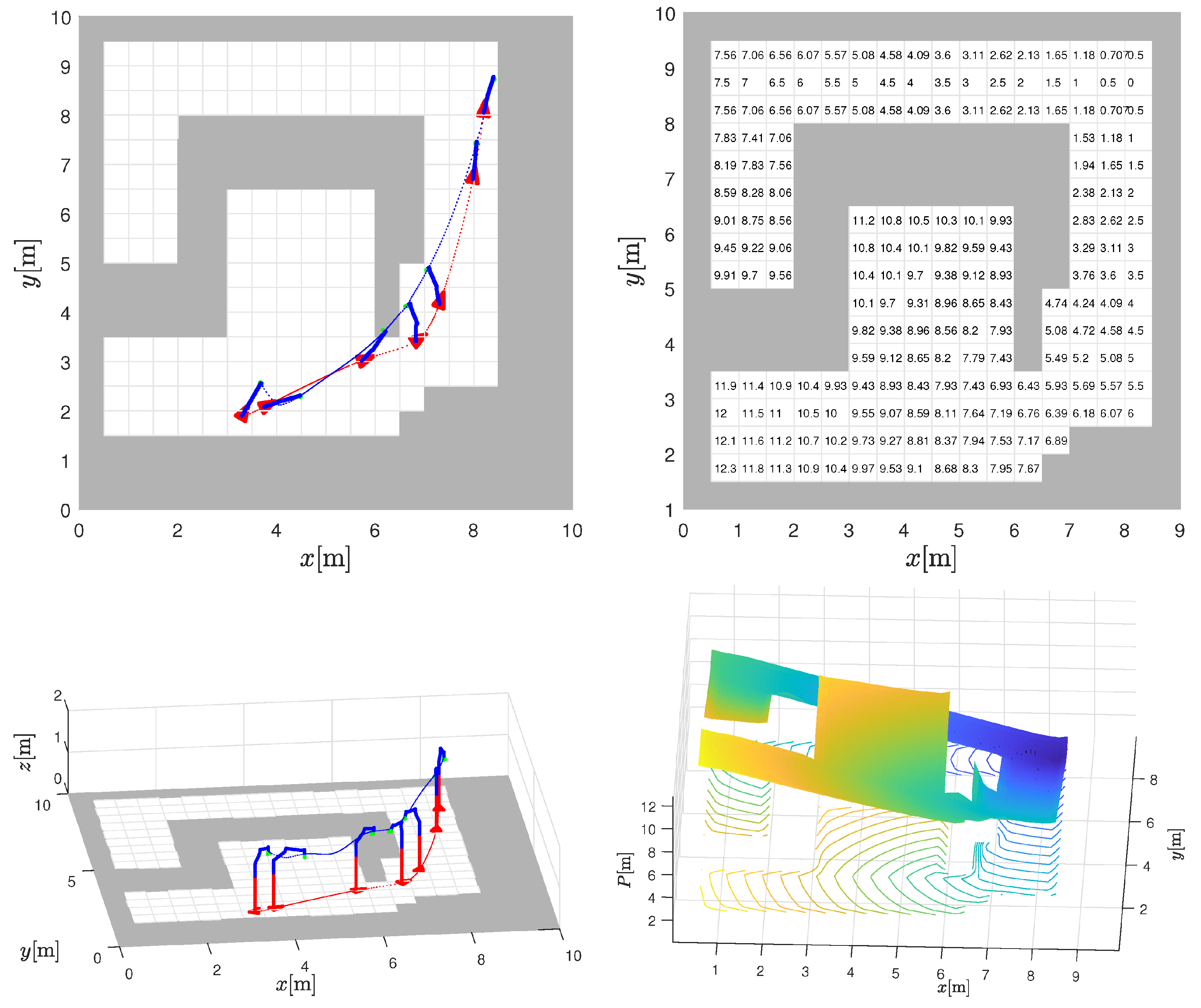
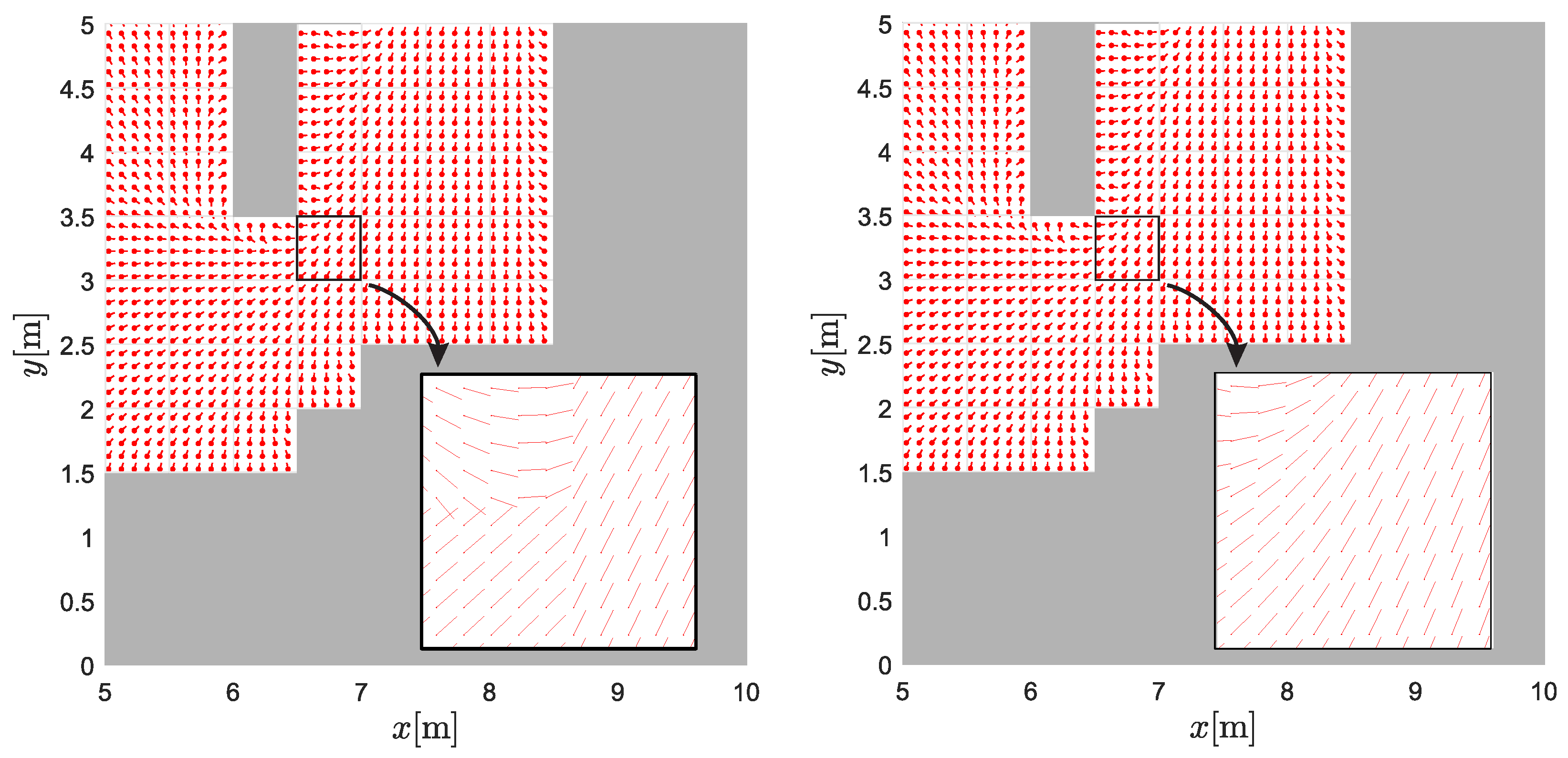
The main task of the mobile manipulator is to follow the desired trajectory of the end effector, while the movement of the base is restricted by a corridor. It can move freely within the corridor so that optimal tracking of the end effector is achieved. In industry, such corridors are a common solution to achieve efficient material flow of automated guided vehicles and other mobile transporters. The basic idea is shown in Figure 1, in which the base can move freely between the forbidden gray areas at ground level ( m) to best support the tracking of the end effector’s trajectory.
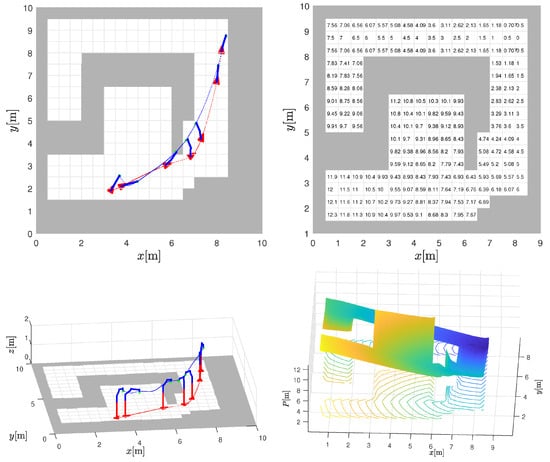
Figure 1.
The desired trajectory of the end effector is marked with a blue dotted line, and the achieved path of the base is marked with a red dotted line. The movement of the mobile base is restricted to a free corridor marked by white square cells (top left and bottom left). The discrete potential field for the distance to the target (top right) is obtained by the graph-based search to the target location at m. A smooth interpolated potential field navigation function (bottom-right) is used to control the mobile base to support tracking of the desired end-effector trajectory.
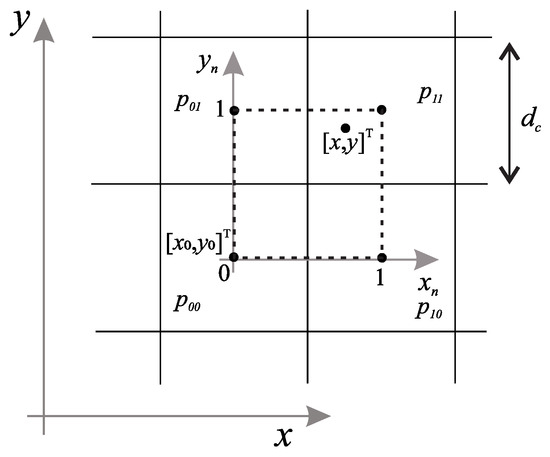
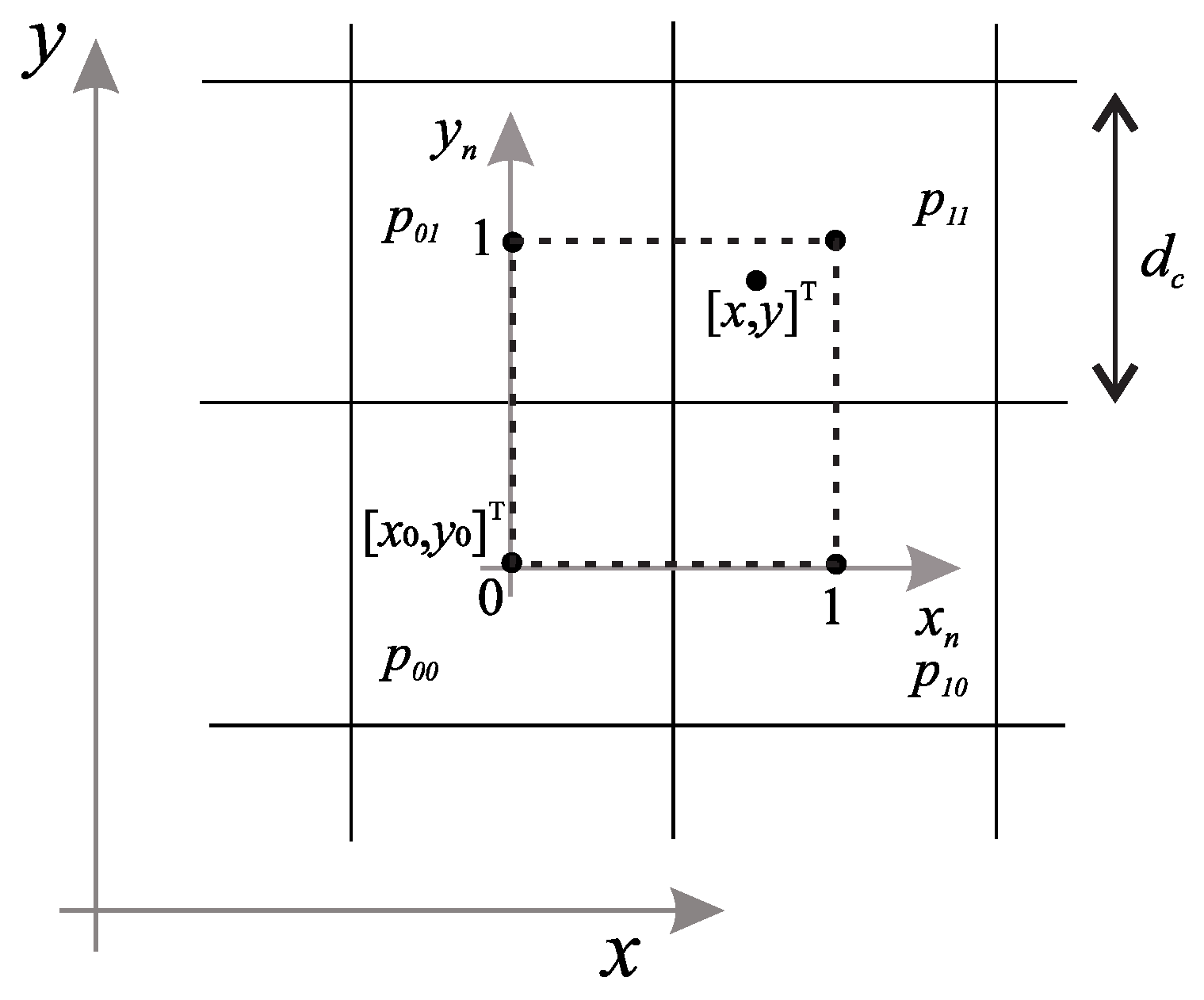
In this work, we propose potential field navigation for the base to stay within the designated corridor. The potential field is automatically computed based on the given layout and the known target position of the end effector (at the end of its reference trajectory) so that the base can be safely navigated. Note that the layout may also contain dead ends (e.g., the concave shape of the corridor in the top-left image in Figure 1), which can typically lead to local minima if the potential field is not properly designed. To obtain a feasible navigation (without local minima), the potential field is estimated using a graph-based search on a discrete grid, such as Dijstra’s, A*, E*, or a similar algorithm. This yields a discrete potential where each free cell contains unique distance-to-target values, and occupied cells have infinite values (gray cells in Figure 1 where base motion is not allowed). The values of the discrete potentials in Figure 1 (top right) were calculated using the E* algorithm [47], which extends the A* algorithm by adding two orthogonal parent nodes to obtain a better cost-to-goal estimate for each cell. Such a discrete potential field is computationally efficient because a relatively coarse discrete grid is used (e.g., 0.5 m cell border in Figure 1 top left), but it is not suitable for basic navigation because any position within the cell would have the same potential. To obtain a smooth potential field with unique values for any position, an interpolation approach could be used that takes into account the potential of the neighboring cells. Following the negative gradient (steepest descent), the mobile base can be safely and optimally navigated in the constrained space to support the end-effector’s movement without providing an explicit reference path for it. For known targets, the navigation functions can even be precomputed and easily used during operation. The following provides details on the construction of the potential field and simple gradient following control for the base.
4. Mobile Manipulator Model
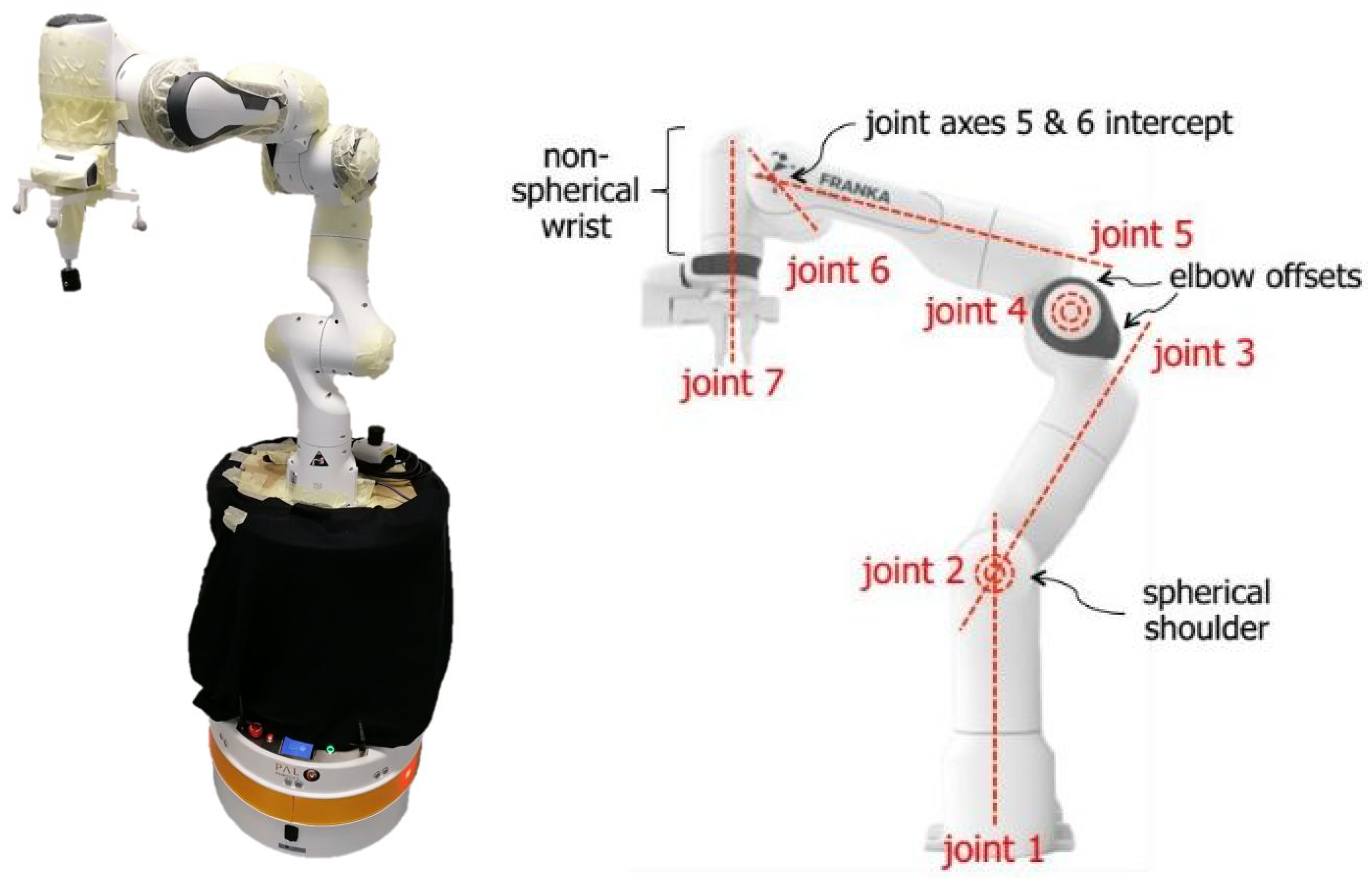
The proposed joint trajectory tracking control of the end effector and mobile base corridor navigation using a potential field is illustrated by simulations on a nonholonomic and redundant mobile platform with 9 DOF. The platform consists of a Pal Tiago base and an Emika Franka Panda robotic manipulator (Figure 4). The manipulator is attached to the mobile base at a height of 0.833 m.
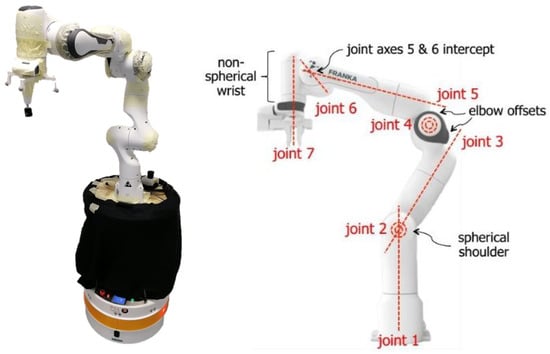
Figure 4.
Mobile manipulator with Emika Franka Panda robot manipulator and Pal Tiago base.
4.1. System Model
Denavit–Hartenberg (DH, with parameters in Table 1) notation is used to obtain direct kinematics of the manipulator
where is the end effector pose expressed in local coordinates of the mobile base, is the configuration variable of the n-th DOF manipulator, and is a nonlinear mapping. The mobile base is constrained to move in a plane and has pose , so the configuration variable of the entire mobile platform extends to . Thus, the pose of the end effector , expressed in global coordinates, depends nonlinearly on

Table 1.
Denavit-Hartenberg (DH) for Emika Franka Panda manipulator.
The mobile base is assumed to have ideal rotation of the wheels, which prevents the base from moving in a lateral direction. This is a nonholonomic motion constraint that does not restrict the reachable space of , only its velocity space , and will be considered in Section 4.2.
4.2. Velocity Kinematic Model
The time derivative of (5) yields the velocity dependence
where is the analytically determined Jacobian. Note that although the dimension of is ( for our manipulator), the whole system has degrees of freedom (DOF) in velocity space because the mobile base has a nonholonomic constraint (the base cannot slide laterally on the wheels). Therefore, the velocity of the end effector cannot be arbitrary but must take into account the differential drive kinematics of the base
where v and are the command velocity for the base. Introducing pseudo-velocity of configuration variable and taking into account the relations (6), (7), we obtain a feasible end-effector velocity taking into account the kinematic constraint of the base
where is a constrained Jacobian of dimension and
5. Inverse Kinematic in Velocity Space
Inverse kinematics are defined in velocity space and applied to the trajectory tracking control of the end effector.
5.1. Controller for the End Effector of the Mobile Manipulator
The mobile manipulator is redundant when . The mobile manipulator in Figure 4 has degrees of freedom, which means that there are infinitely many solutions to the pseudo-velocities of the joints that lead to the desired velocity of the end effector. This allows the mobile manipulator to achieve secondary objectives in addition to the desired velocities .
The pseudo-velocities of the configuration vector are obtained from the velocities of the end effector
where is the right pseudo-inverse of , is the null space of , and are pseudo-joint velocities for the lower priority task. The end-effector velocities are made proportional to the tracking error, and the feed-forward velocity of the reference trajectory is included to provide zero-error tracking of the reference trajectory
where is the reference pose for the end-effector, and is a positive definite matrix of control gains.
Robust pseudo-inverse is used to mitigate kinematic singularity problems [3,22] with the proximity to the singularity limit estimated by the manipulability measure as follows
where is the threshold value of the manipulability index, and is the scale constant.
Since the system is redundant, a lower priority task can also be provided where any could be assigned. Given a scalar objective function that depends on the configuration , can be defined to minimize . To achieve a decrease of , must be chosen such that . The derivative of is
where , and relation is considered (see (8)). A possible choice for , as suggested by [4], is
where is a positive scalar. The choice for defined in (13) gives
5.2. Secondary Task and Objective Function
In addition to the primary task in (9), a secondary task can also be provided to ensure that the base follows its desired planar trajectory. This can be achieved by a priority scheme [3,22] in which tracking the base’s reference trajectory has a lower priority than tracking the end effector
where is the desired velocity of the end effector as the primary task, is the desired base velocity vector of the secondary task, and is the desired pseudo-velocities projected into the remaining orthogonal space. For the secondary task Jacobians , , the pseudo-inverse Jacobian and the null space hold: , , , and .
Finally, the last priority task is projected onto the remaining orthogonal subspace in (9) or (14), where system operation can be optimized according to an objective function. For the objective function, the manipulability measure (15) is used
Note that lower priority tasks can only be executed if the system has sufficiently high redundancy.
5.3. Mobile Base Corridor-Constrained Control
The base can move freely in a defined corridor while assisting the end effector in tracking the reference trajectory. To achieve the desired movement of the base, the potential field navigation computed for the corridor is used. This defines the second priority task that guides the base away from the corridor boundaries and to the desired destination. Together with the primary task (end-effector tracking), this defines the joint control (14) where the overall commands for the base are defined.
For the base, we propose a negative gradient following control obtained from the proposed interpolated potential field and the interpolated gradient vector field (defined by (3)). Following the negative gradient guarantees safe motion toward the target with the base approaching the target in each control sample. Note that the potential function described in Section 3 has no local minima.
For current base state , the reference driving direction is defined by the negative gradient
the orientation error of the base reads
and the control law then defines the base velocities as follows
where is a positive constant defining the closed loop dynamics of the orientation, and is the translational base velocity computed by the first priority task (the first element of in Equation (14)). The thus obtained is applied to joint control (14).
6. Simulation Analysis and Validation
In the following, the control performance of the mobile manipulator is validated through several simulated scenarios. The control algorithm from Section 5 is implemented with a sampling time of s. Other constants used in the control are as follows. The gain matrix in (10) is , the parameters in (11) are , , and the gain in (18) is . The results of trajectory tracking and pose control of mobile manipulator’s end effector are shown.
6.1. Joint Arm Trajectory Tracking and Base Potential Field Navigation
The arm must follow a predetermined reference trajectory that defines position and orientation (6 DOF). This is achieved as the first priority task in (14). The mobile base is navigated to the desired corridor using the potential field as a secondary task. Any remaining freedom in the redundancy is used to optimize the operation for manipulability. In the control law, the limits for velocities and accelerations are set to and , respectively.
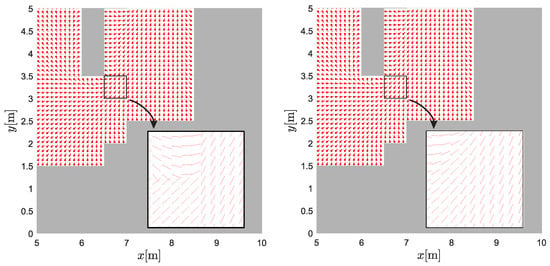
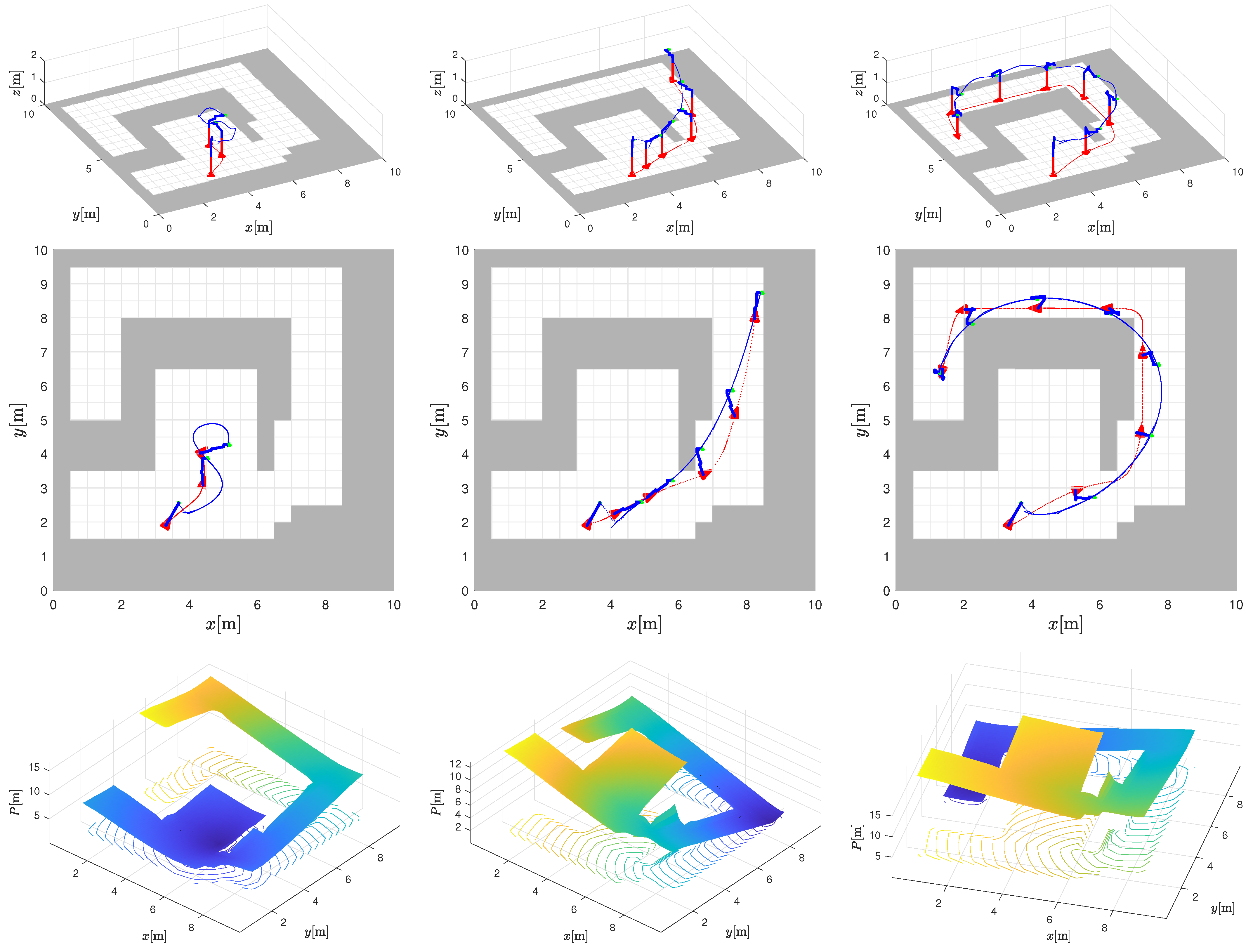
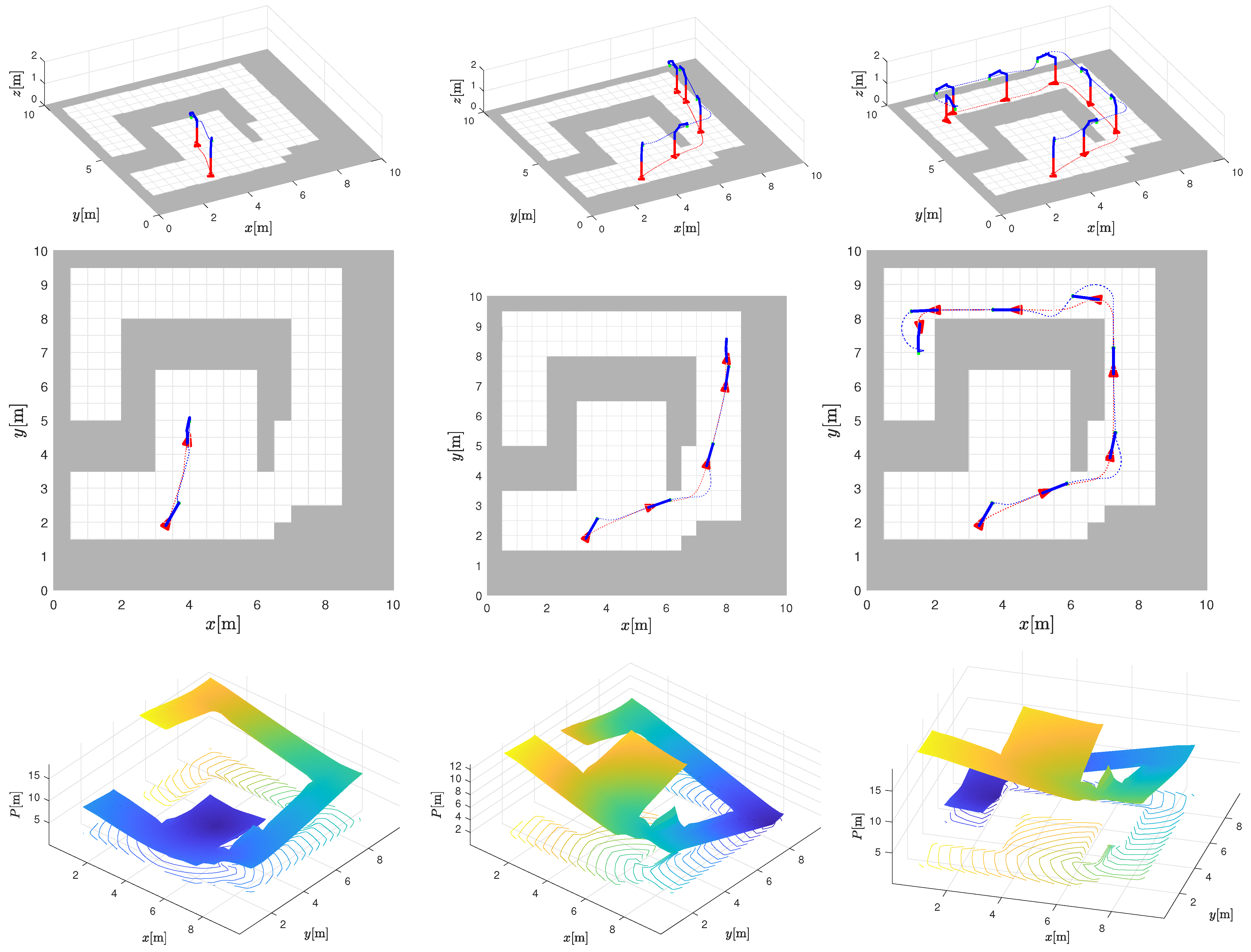
In Figure 5, three different scenarios are shown: arm tracking in a free space where the base motion is not affected by tight corridor constraints (Figure 5, left column) and two cases of arm tracking where base motion must adapt to corridor constraints (Figure 5, middle and right columns). In Figure 6, the control velocities and tracking errors of the end effector are shown for scenarios in Figure 5.
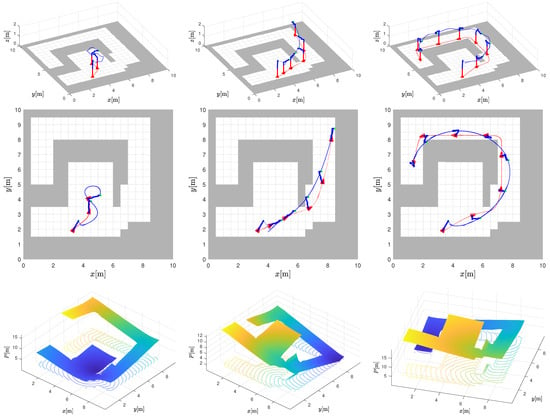
Figure 5.
Trajectory tracking: three scenarios (shown in columns) of joint arm trajectory tracking and the base potential field navigation. The first and second rows show the reference trajectory of the arm (solid blue line), the obtained motion (dotted blue line), and the base trajectory (dotted red line). The third row shows the calculated potential navigation with the displayed contours of the same potential.
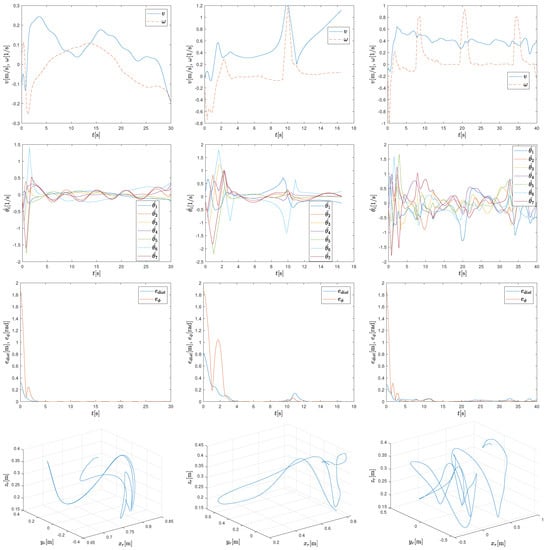
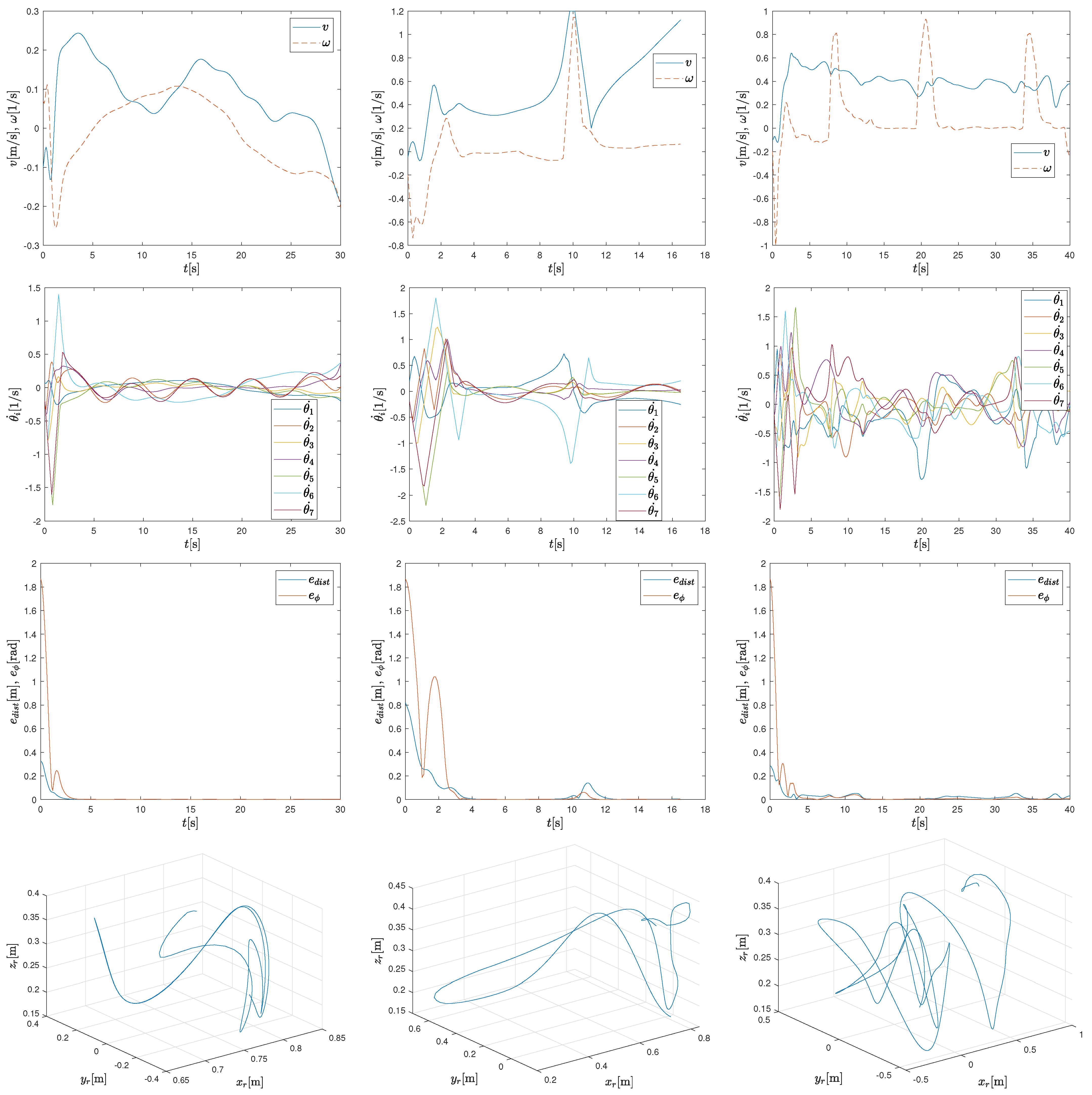
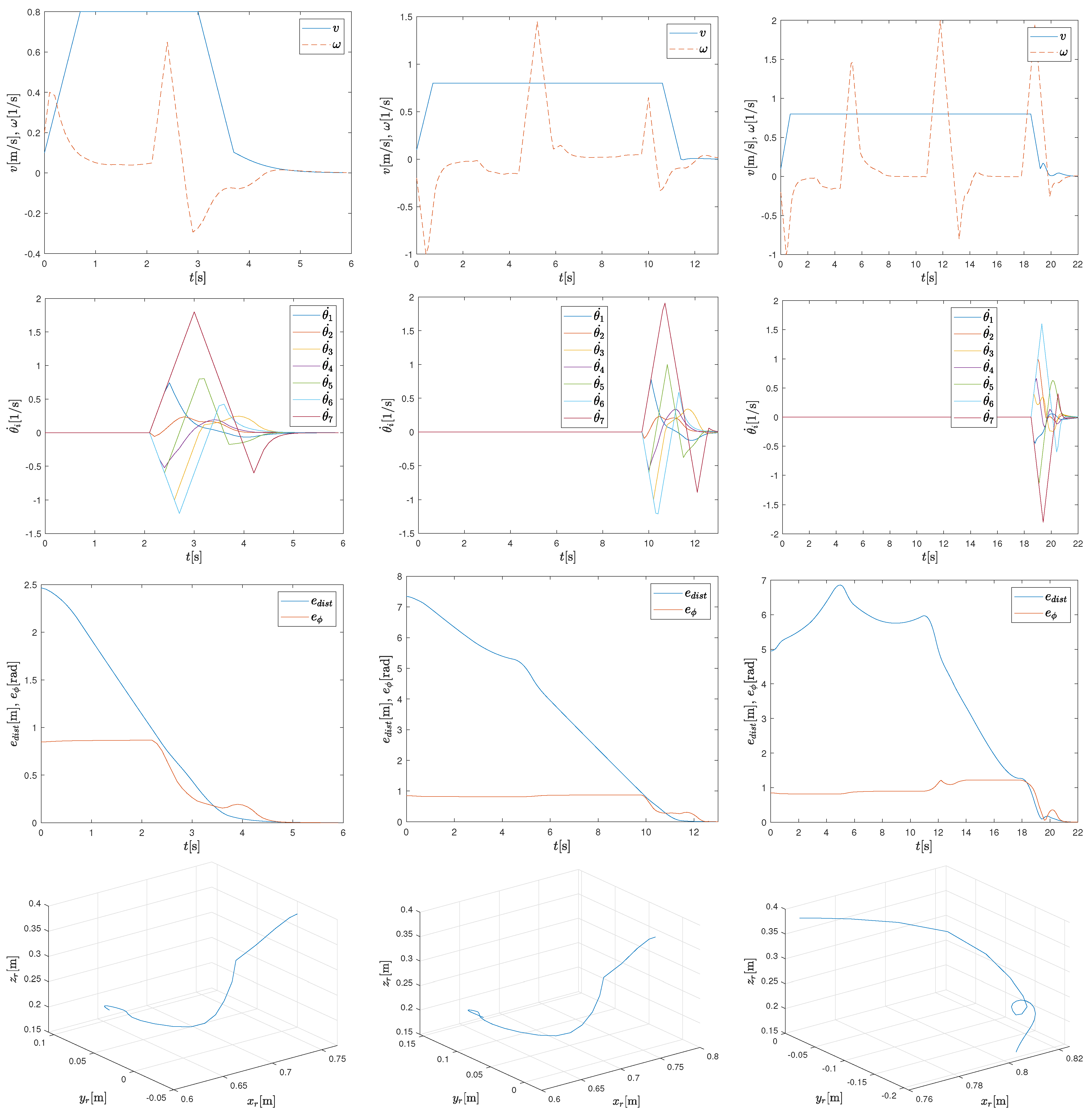
Figure 6.
Mobile base velocities (first row), arm joint velocities (second row), tracking distance error and orientation error norm (third row), and relative position of the end effector with respect to the mobile base (fourth row) for the scenarios in Figure 5.
In the last two scenarios, the reference trajectory intersects the corridor defined for the base. This is allowed since the corridor is constrained only for the base. However, the base and the arm must then find an appropriate configuration to allow the base to stay within the corridor and still support reference tracking of the end effector. Note how the base approaches the edge of the corridor and how the arm must extend toward the reference trajectory. At these moments, a slight increase in the velocities of the base and arm joints can be observed. As the working range of the arm is close to its limits, tracking errors also increase significantly.
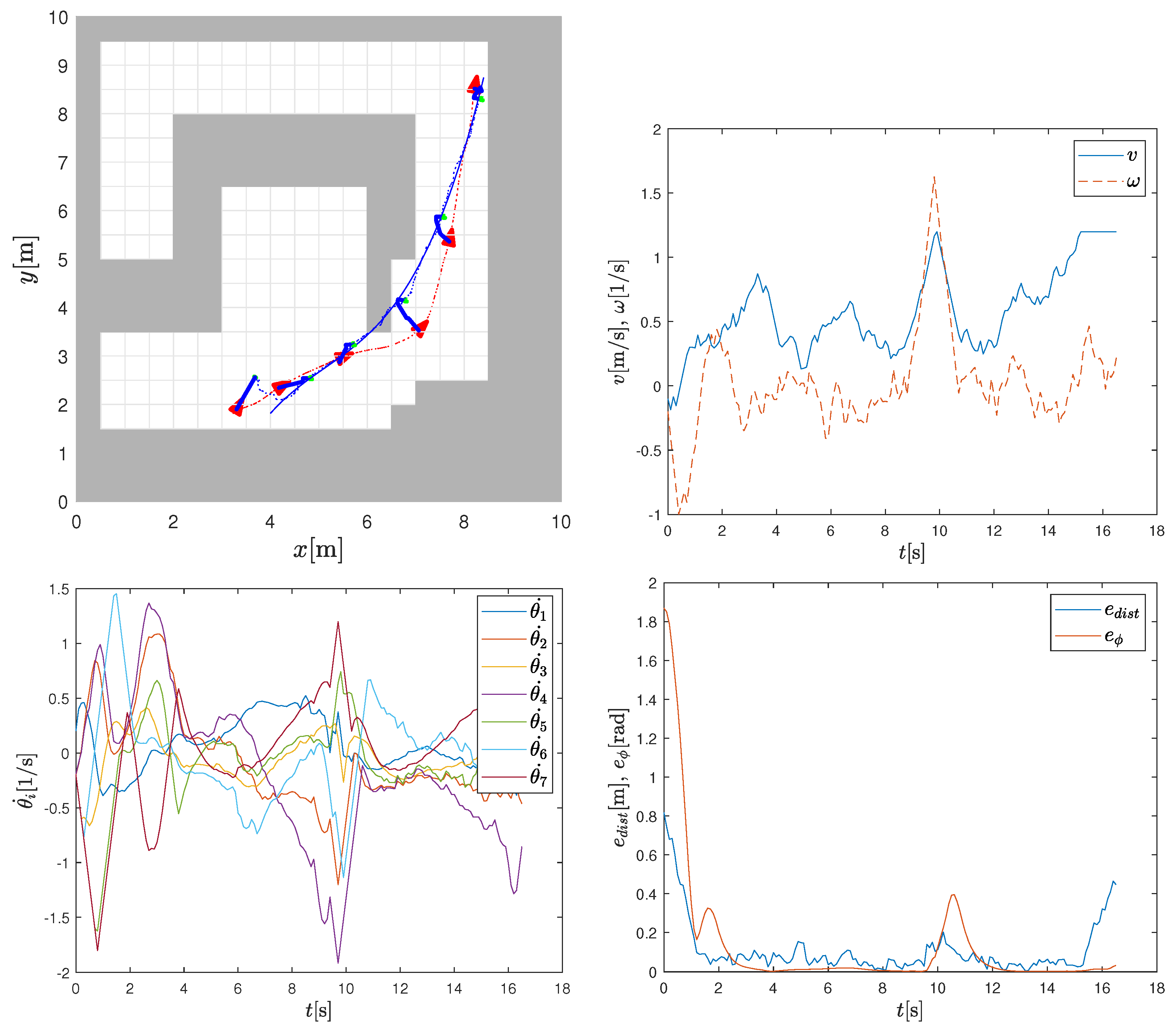
To obtain a more realistic simulation, the scenario in the second column in Figure 5 is repeated in Figure 7 with added non-deterministic effects simulating noise and wheels slipping. Whenever the wheels of the mobile base slip, the end effector moves less or more than desired by the controller. The slippage also affects the accuracy of the sensor system (e.g., wheel odometry), leading to errors in the estimated system configuration [26]. In the simulation, the calculated command velocities are corrupted with additional randomly distributed normal noise. This results in disturbed motion of the base. The standard deviation for translation velocity noise is m/s, and the standard deviation for angular velocity noise is rad/s. To mimic slip effects, the standard deviation for angular velocity increases linearly with angular velocity. The simulated slippage of the base causes a larger tracking error of the end effector. This is reflected in more aggressive control actions calculated to compensate for the tracking error, as shown in Figure 7. Despite the additional noise, the end effector reliably follows the reference trajectory.
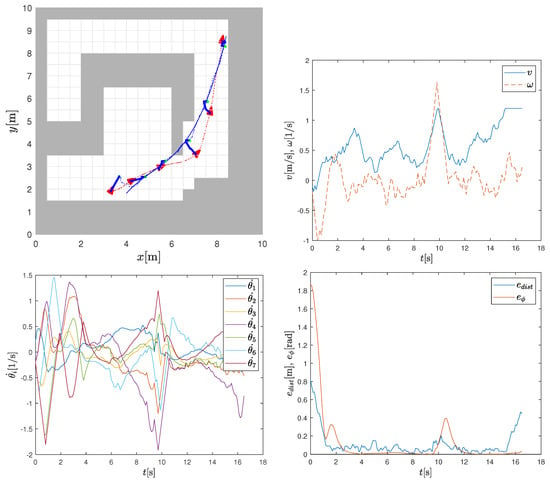
Figure 7.
Trajectory tracking with added noise in actions (top left) showing reference trajectory of arm (solid blue line), the obtained motion (dotted blue line), and base trajectory (dotted red line); velocities of the mobile base (top right), velocities of the arm joints (bottom left), and tracking distance error and orientation error norm (bottom right).
6.2. Joint Arm Pose Control and Base Potential Field Navigation
The same control strategy can be used to reach the reference pose of the end effector without specifying an explicit trajectory to that reference pose. The mobile base is navigated similarly to Section 6.1 by the presented potential field navigation, which is used as a secondary task to support the arm. In control law, limits for velocities and accelerations are set to and , respectively.
In Figure 8, three different scenarios are shown: arm pose control in a free space where base motion is not affected by tight corridor constraints (Figure 8 left column) and two cases of arm pose control where base motion must adapt to corridor constraints (Figure 8 middle and right columns). To avoid unnecessary movements of the arm joints in Figure 8 and Figure 9 when the distance to the target position is large (e.g. larger than 1 m), the joint velocities are set to zero as shown in Figure 9.
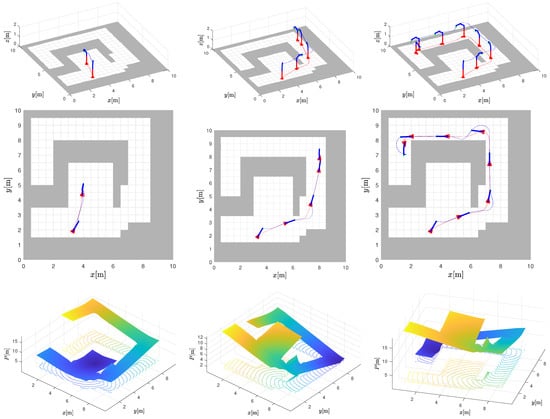
Figure 8.
Pose control: three scenarios (shown in columns) of joint arm pose control and base potential field navigation. The first and second rows show the movement of the arm (dotted blue line) and the trajectory of the base (dotted red line). The third row shows the calculated potential navigation with the contours of the same potential.
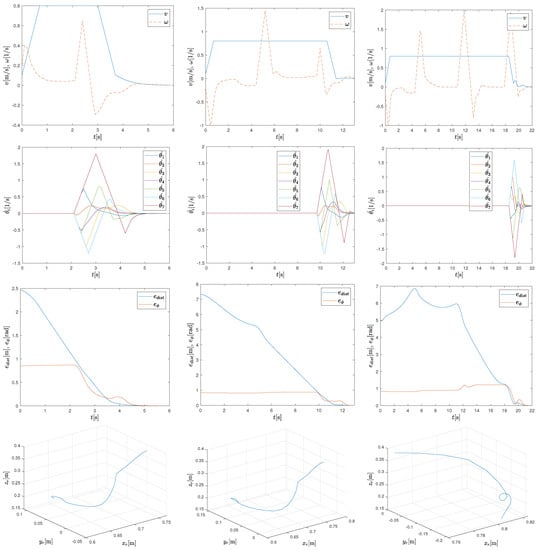
Figure 9.
Velocities of the base (first row), velocities of the arm joints (second row), distance error and norm of the orientation error to the target pose (third row), and relative position of the end effector with respect to the mobile base (fourth row) for the scenarios in Figure 8.
7. Discussion
The discrete potential field (distance to-goal) can be precomputed for a known static environment and goal. If a mobile manipulator delivers between multiple known destinations (e.g., pickup and drop-off locations), a separate potential field is computed for each destination. Since a coarse discretization is possible (due to the interpolation used), this is a moderate memory requirement. At runtime, bilinear interpolation is performed only for the cells along the current path, resulting in a computationally efficient implementation. However, if the environment is dynamic (e.g., with moving obstacles), the discrete potential function can be updated at runtime. In this case, the version of E* with dynamic replanning should be used to achieve higher efficiency [47].
To compute the navigation function, the goal position for the base must be known. However, we only define corridor constraints for the base and have no explicit requirements for the path of the base or its goal. Therefore, the goal can be chosen the same as for the end effector. The actions for the base and the arm are then defined such that the end effector follows the reference trajectory (first priority task), and the base simultaneously travels along the current negative gradient of the navigation function (second priority task). The coordination of the tasks is implicitly archived since the secondary task lies in the orthogonal space of the primary one. However, this is only true as long as the reference trajectory can be reached from the corridor, taking into account the working range of the arm. If this is not the case, the fully extended arm cannot satisfy both control tasks (the primary and the secondary). This causes the manipulability index to approach zero, and thus the pseudo-inverse would have a singularity problem. With the robust pseudo-inverse (11), these singularity problems are mitigated, while at the same time accuracy is compromised, leading to increased end-effector tracking error.
8. Conclusions
In this work a solution is proposed for a redundant nonholonomic mobile manipulator with joint arm and base control, where corridor constraints are considered for the movement of the base. The base can move freely within the given corridor. A novel navigation function for base motion that has no local minima and optimally steers the base within the corridor is proposed. The navigation is computationally efficient and can be computed in advance for static environments. It applies optimal grid-based search to generate a discrete potential and online bilinear interpolation to obtain smooth potential and gradient fields.
In the future, we plan to extend the mobile base-gradient-following controller with model predictive capabilities to further improve the end-effector tracking. We will validate the proposed approach on a real system. It is also worthwhile to explore the possibility of extending the proposed potential field navigation to 3D corridors and also use it for arm navigation to avoid obstacles.
Author Contributions
Conceptualisation, methodology and software, J.B. and G.K.; writing—original draft preparation, J.B. and G.K.; writing—review and editing, J.B., T.P. and G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was founded by the Slovenian Research Agency under Grants P2-0219 and L2-3168.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Slovenian Research Agency under Grants P2-0219 and L2-3168.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Householder, A.S. Unitary Triangularization of a Nonsymmetric Matrix. J. ACM 1958, 5, 339–342. [Google Scholar] [CrossRef]
- Ghosal, A. Resolution of redundancy in robots and in a human arm. Mech. Mach. Theory 2018, 125, 126–136. [Google Scholar] [CrossRef]
- Nakamura, Y. Advanced Robotics: Redundancy and Optimization, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1990. [Google Scholar]
- Bayle, B.; Renaud, M.; Fourquet, J.Y. Nonholonomic Mobile Manipulators: Kinematics, Velocities and Redundancies. J. Intell. Robot. Syst. 2003, 36, 45–63. [Google Scholar] [CrossRef]
- Sandakalum, T.; Ang, M.H. Motion Planning for Mobile Manipulators—A Systematic Review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, H.; Cheong, J.; Kim, W. Virtual Joint Method for Kinematic Modeling of Wheeled Mobile Manipulators. Int. J. Control Autom. Syst. 2014, 12, 1059–1069. [Google Scholar] [CrossRef]
- Ancona, R. Redundancy modelling and resolution for robotic mobile manipulators: A general approach. Adv. Robot. 2017, 31, 706–715. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S.; Chen, D.; Liao, L. Tracking control of redundant mobile manipulator: An RNN based metaheuristic approach. Neurocomputing 2020, 400, 272–284. [Google Scholar] [CrossRef]
- Ram, R.; Pathak, P.; Junco, S. Trajectory control of a mobile manipulator in the presence of base disturbance. Simulation 2019, 95, 529–543. [Google Scholar] [CrossRef]
- Sorour, M.; Cherubini, A.; Fraisse, P. Motion Control for Steerable Wheeled Mobile Manipulation. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ram, R.; Pathak, P.; Junco, S. Inverse kinematics of mobile manipulator using bidirectional particle swarm optimization by manipulator decoupling. Mech. Mach. Theory 2019, 131, 385–405. [Google Scholar] [CrossRef]
- Shyh Chyan, G.; Ponnambalam, S. Obstacle avoidance control of redundant robots using variants of particle swarm optimization. Robot. Comput. Integr. Manuf. 2012, 28, 147–153. [Google Scholar] [CrossRef]
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Z.; Yang, C.; Zhang, L.; Yuan, P.; Ding, L.; Wang, T. Robust Stabilization of a Wheeled Mobile Robot Using Model Predictive Control Based on Neurodynamics Optimization. IEEE Trans. Ind. Electron. 2017, 64, 505–516. [Google Scholar] [CrossRef]
- Spahn, M.; Brito, B.; Alonso-Mora, J. Coupled Mobile Manipulation via Trajectory Optimization with Free Space Decomposition. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 12759–12765. [Google Scholar] [CrossRef]
- Brahmi, A.; Saad, M.; Gauthier, G.; Zhu, W.H.; Ghommam, J. Adaptive Control of Mobile Manipulator Robot based on Virtual Decomposition Approach. In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics, Lisbon, Portugal, 29–31 July 2016; pp. 254–261. [Google Scholar] [CrossRef]
- Mailah, M.; Pitowarno, E.; Jamaluddin, H. Robust Motion Control for Mobile Manipulator Using Resolved Acceleration and Proportional-Integral Active Force Control. Int. J. Adv. Robot. Syst. 2005, 2, 14. [Google Scholar] [CrossRef]
- Connell, D.; Manh La, H. Extended rapidly exploring random tree–based dynamic path planning and replanning for mobile robots. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418773874. [Google Scholar] [CrossRef]
- Castaman, N.; Pagello, E.; Menegatti, E.; Pretto, A. Receding Horizon Task and Motion Planning in Changing Environments. Robot. Auton. Syst. 2021, 145, 103863. [Google Scholar] [CrossRef]
- Sereinig, M.; Werth, W.; Faller, L.M. A review of the challenges in mobile manipulation: Systems design and RoboCup challenges. Elektrotechnik Informationstechnik 2020, 137, 1–12. [Google Scholar] [CrossRef]
- Chu, B. Modeling of a Mobile Manipulator for Redundancy Resolution. In Proceedings of the 29th ISARC, Eindhoven, The Netherlands, 26–29 June 2012. [Google Scholar] [CrossRef]
- Mashali, M.; Alqasemi, R.; Dubey, R. Task priority based dual-trajectory control for redundant mobile manipulators. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 1457–1462. [Google Scholar] [CrossRef]
- Mashali, M.; Wu, L.; Alqasemi, R.; Dubey, R. Controlling a Non-Holonomic Mobile Manipulator in a Constrained Floor Space. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 725–731. [Google Scholar] [CrossRef]
- Mazur, A.; Szakiel, D. On path following control of nonholonomic mobile manipulators. Appl. Math. Comput. Sci. 2009, 19, 561–574. [Google Scholar] [CrossRef]
- Sandy, T.; Buchli, J. Dynamically decoupling base and end-effector motion for mobile manipulation using visual-inertial sensing. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6299–6306. [Google Scholar] [CrossRef]
- Mohamed, S.A.S.; Haghbayan, M.H.; Westerlund, T.; Heikkonen, J.; Tenhunen, H.; Plosila, J. A Survey on Odometry for Autonomous Navigation Systems. IEEE Access 2019, 7, 97466–97486. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Fixed-Wing UAV Formation Control Design with Collision Avoidance Based on an Improved Artificial Potential Field. IEEE Access 2018, 6, 78342–78351. [Google Scholar] [CrossRef]
- Lyu, H.; Yin, Y. Fast Path Planning for Autonomous Ships in Restricted Waters. Appl. Sci. 2018, 8, 2592. [Google Scholar] [CrossRef]
- Weerakoon, T.; Ishii, K.; Nassiraei, A.A.F. An artificial potential field based mobile robot navigation method to prevent from deadlock. J. Artif. Intell. Soft Comput. Res. 2015, 5, 189–203. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, G.; Feng, L.; Wu, J.; Liu, S. Collision avoidance for mobile robots based on artificial potential field and obstacle envelope modelling. Assem. Autom. 2016, 36, 318–332. [Google Scholar] [CrossRef]
- Cosio, F.A.; Castaneda, M.P. Autonomous robot navigation using adaptive potential fields. Math. Comput. Model. 2004, 40, 1141–1156. [Google Scholar] [CrossRef]
- Park, M.; Lee, M.C. A new technique to escape local minimum in artificial potential field based path planning. KSME Int. J. 2003, 17, 1876–1885. [Google Scholar] [CrossRef]
- Agirrebeitia, J.; Avilés, R.; de Bustos, I.F.; Ajuria, G. A new APF strategy for path planning in environments with obstacles. Mech. Mach. Theory 2005, 40, 645–658. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Y.; Song, J. Real-time motion planning for mobile robots by means of artificial potential field method in unknown environment. Ind. Robot. Int. J. 2010, 37, 384–400. [Google Scholar] [CrossRef]
- Chen, J.; Tan, C.; Mo, R.; Zhang, H.; Cai, G.; Li, H. Research on path planning of three-neighbor search A* algorithm combined with artificial potential field. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211026449. [Google Scholar] [CrossRef]
- Raheem, F.A.; Abdulkareem, M.I. Development of a* algorithm for robot path planning based on modified probabilistic roadmap and artificial potential field. J. Eng. Sci. Technol. 2020, 15, 3034–3054. [Google Scholar]
- Pan, H.; Guo, C.; Wang, Z. Research for path planning in indoor environment based improved artificial potential field method. In Proceedings of the 2017 Chinese Intelligent Automation Conference, Tianjin, China, 25 October 2017; pp. 273–281. [Google Scholar]
- Ogren, P.; Leonard, N.E. A convergent dynamic window approach to obstacle avoidance. IEEE Trans. Robot. 2005, 21, 188–195. [Google Scholar] [CrossRef]
- Klančar, G.; Seder, M. Coordinated Multi-Robotic Vehicles Navigation and Control in Shop Floor Automation. Sensors 2022, 22, 1455. [Google Scholar] [CrossRef] [PubMed]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. In Autonomous Robot Vehicles; Cox, I.J., Wilfong, G.T., Eds.; Springer: New York, NY, USA, 1990; pp. 396–404. [Google Scholar] [CrossRef]
- Soodmand, I.; Kebbach, M.; Herrmann, S.; Bader, R.; Woernle, C. An Artificial Potential Field Algorithm for Path Planning of Redundant Manipulators Based on Navigation Functions. In Proceedings of the Advances in Robot Kinematics 2022, Bilbao, Spain, 26–30 June 2022; Altuzarra, O., Kecskeméthy, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 470–477. [Google Scholar]
- Badawy, A. Manipulator trajectory planning using artificial potential field. In Proceedings of the 2014 International Conference on Engineering and Technology (ICET), Cairo, Egypt, 19–20 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Li, D.; Zhu, W.; Sun, J.; Zhang, X.; Li, S. Constrained Motion Planning of 7-DOF Space Manipulator via Deep Reinforcement Learning Combined with Artificial Potential Field. Aerospace 2022, 9, 163. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, L.; Shao, Z. Path Planning for Obstacle Avoidance of Manipulators Based on Improved Artificial Potential Field. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 2991–2996. [Google Scholar] [CrossRef]
- Hargas, Y.; Mokrane, A.; Hentout, A.; Hachour, O.; Bouzouia, B. Mobile manipulator path planning based on artificial potential field: Application on RobuTER/ULM. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Barros Viturino, C.C.; de Melo Pinto Junior, U.; Gustavo Scolari Conceição, A.; Schnitman, L. Adaptive Artificial Potential Fields with Orientation Control Applied to Robotic Manipulators. IFAC-PapersOnLine 2020, 53, 9924–9929. [Google Scholar] [CrossRef]
- Philippsen, R. E* Interpolated Graph Replanner. In Proceedings of the Workshop Proceedings on Algorithmic Motion Planning for Autonomous Robots in Challenging Environments, Held in Conjunction with the IEEE International Conference on Intelligent Robots and Systems (IROS), San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Klančar, G.; Zdešar, A.; Krishnan, M. Robot Navigation Based on Potential Field and Gradient Obtained by Bilinear Interpolation and a Grid-Based Search. Sensors 2022, 22, 3295. [Google Scholar] [CrossRef] [PubMed]
- Bilinear Interpolation. Available online: https://en.wikipedia.org/wiki/Bilinear_interpolation (accessed on 15 February 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).