Measuring Methods of Radius of Curvature and Tread Circle-Fitting Studies for Railway Wheel Profiles
Abstract
:1. Introduction
2. Radius of Curvature Determination of Wheel Profile
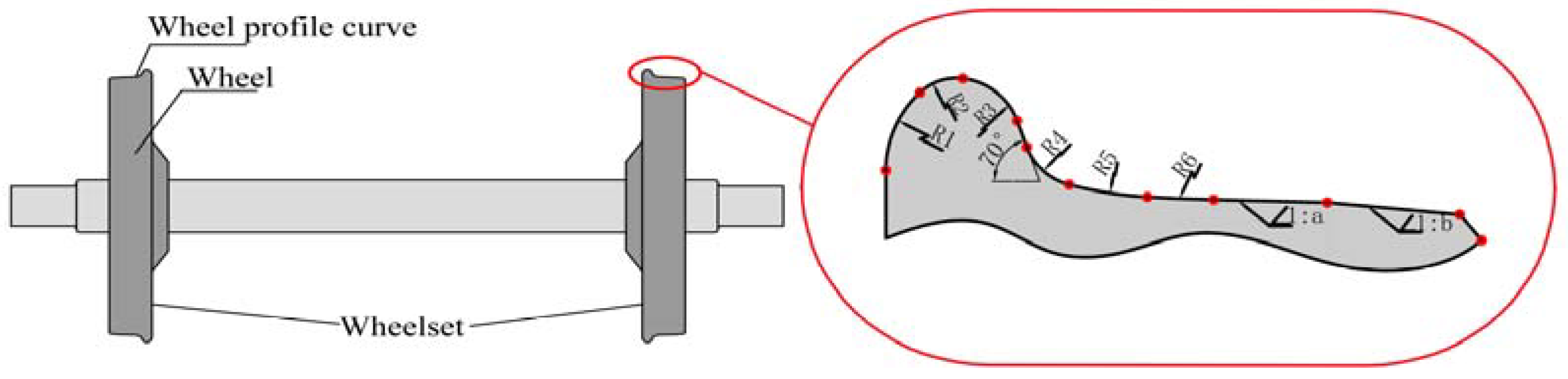
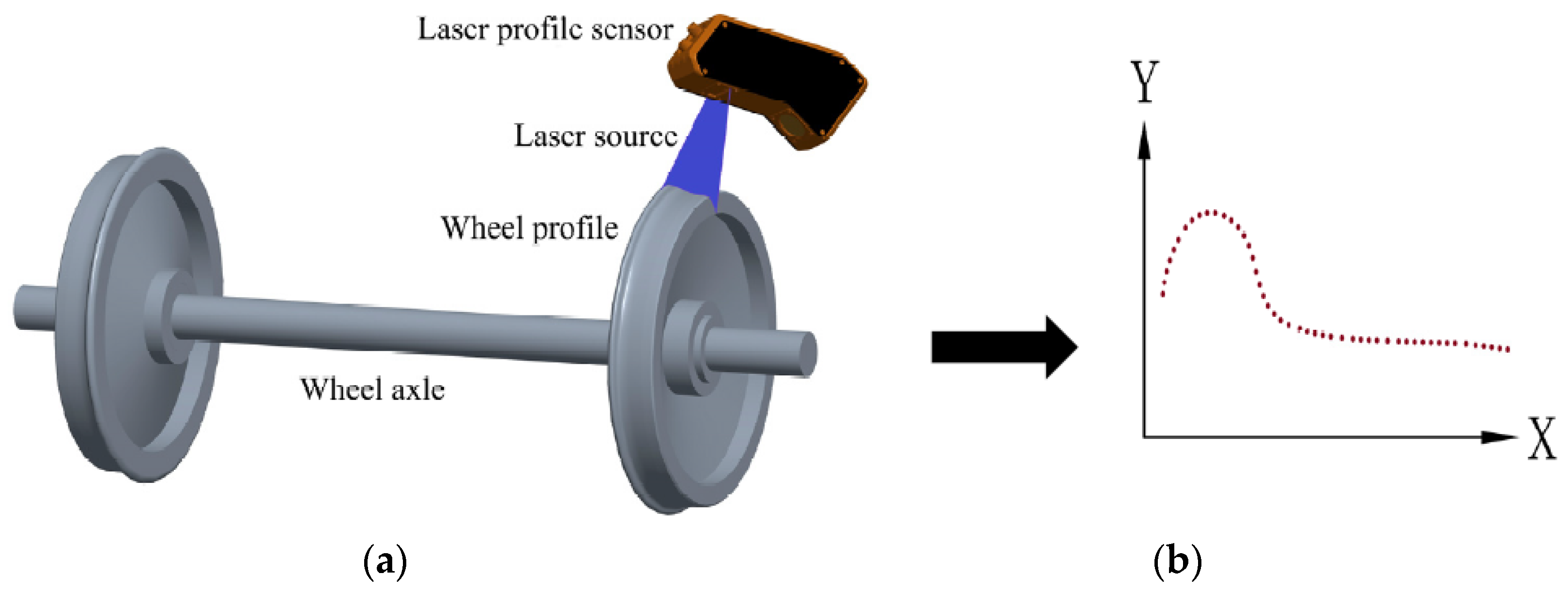
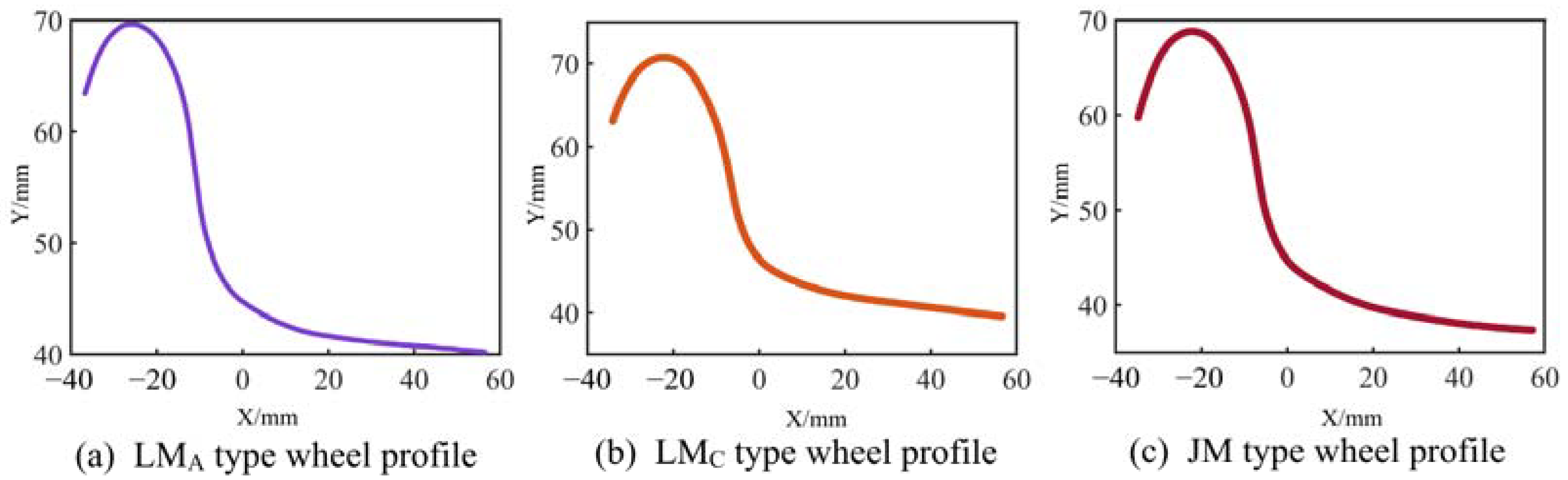
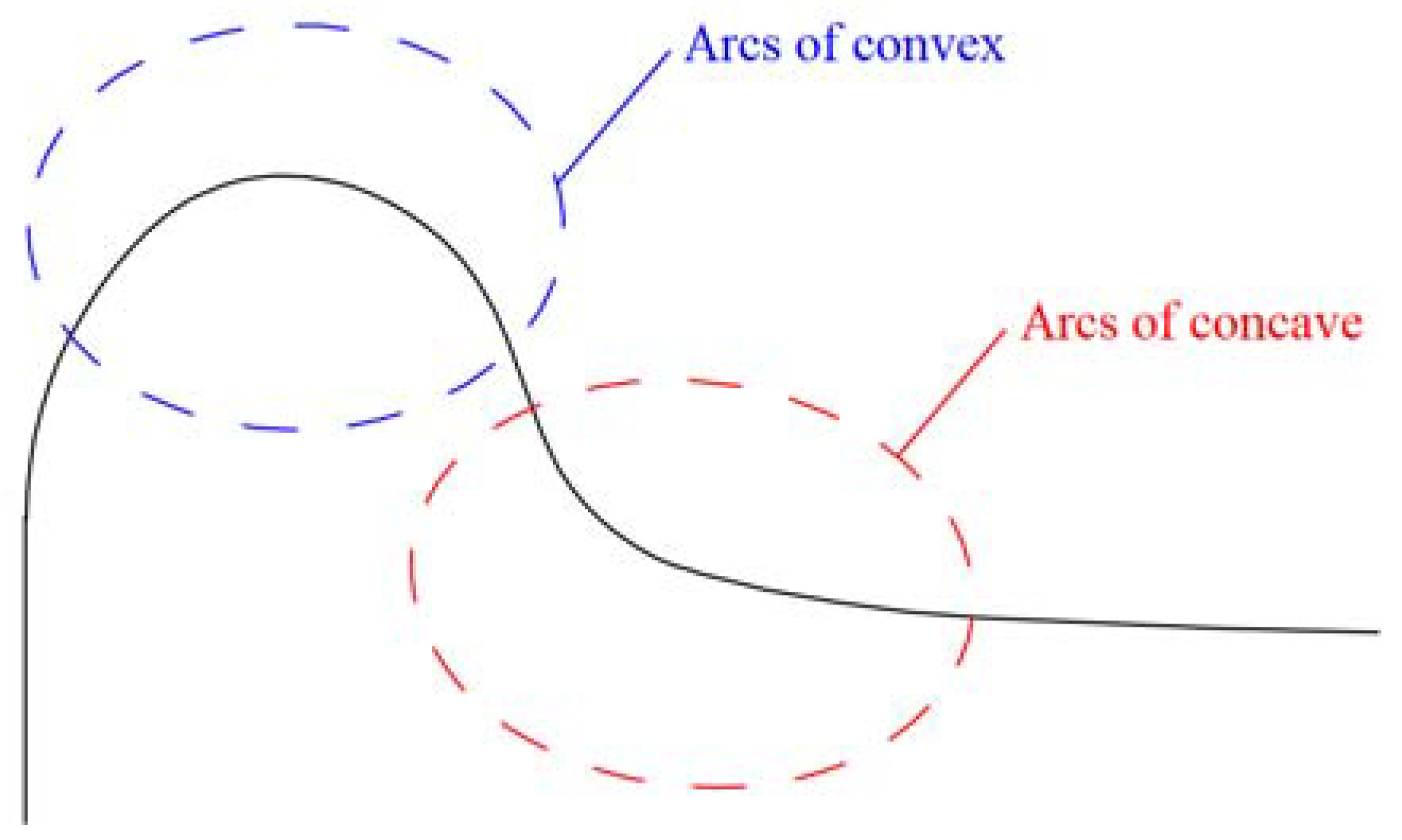
2.1. Composition of Wheel Profile Curve and Analysis Interests
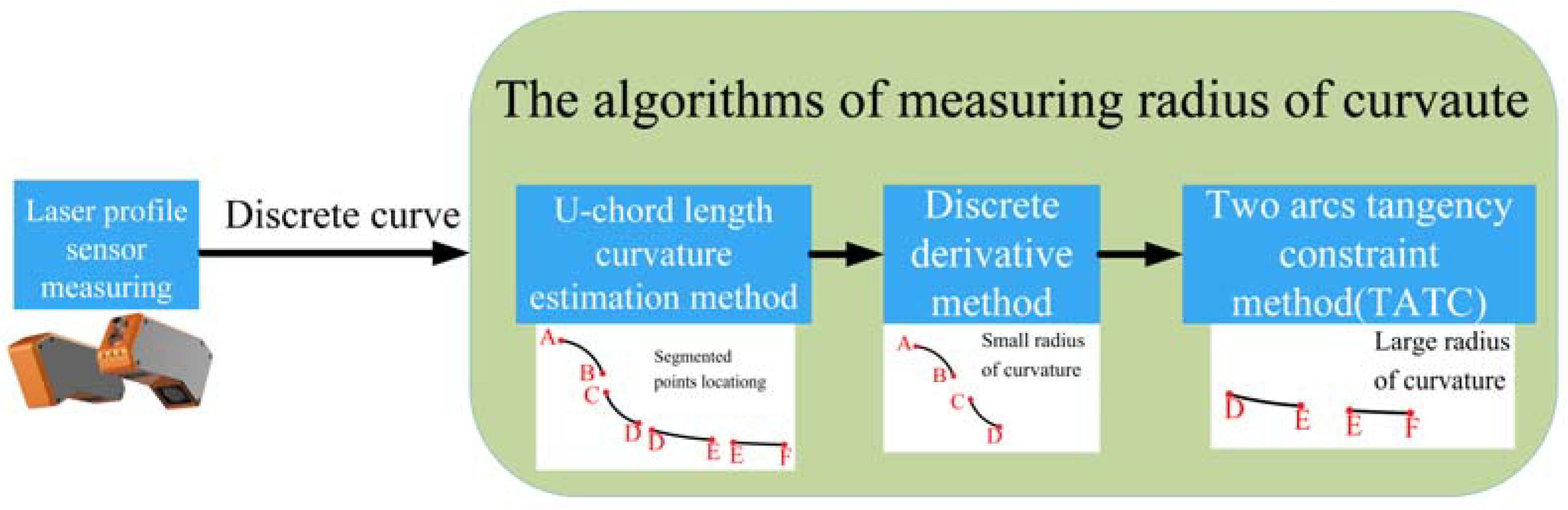
2.2. Methods of Measuring the Radius of Curvature from the Discrete Curve of a Wheel Profile
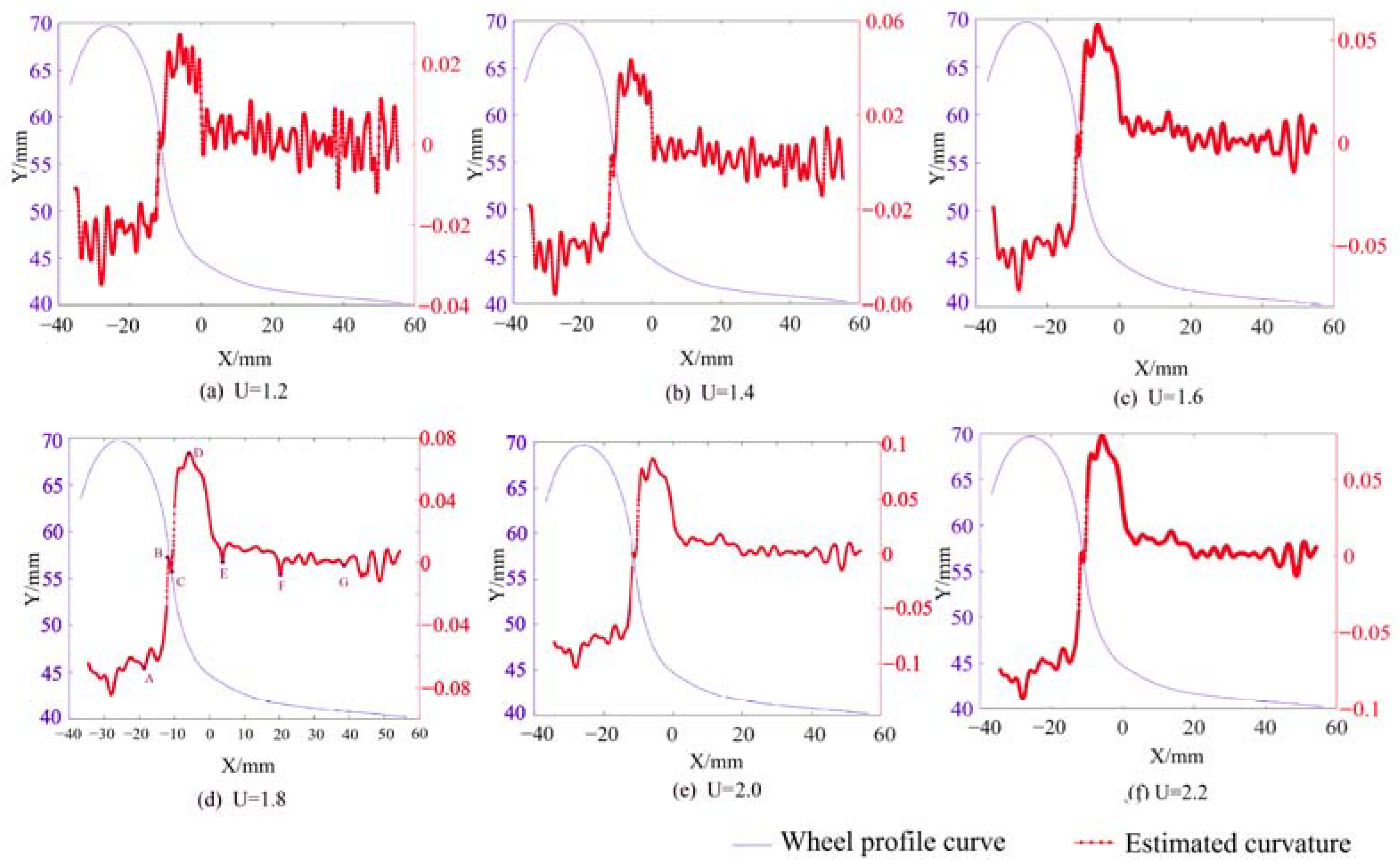
2.2.1. U-Chord Curvature Estimation Method
| Algorithm 1. U-chord curvature method of discrete curve. | ||
| Input: | U: the constraint-supported domain. | |
| Pi (xi, yi): points’ coordinates of the discrete curve. | ||
| imax: the maximum number of points in one discrete curve. | ||
| Output: | Ui: the estimated curvature value of each point in the profile curve. | |
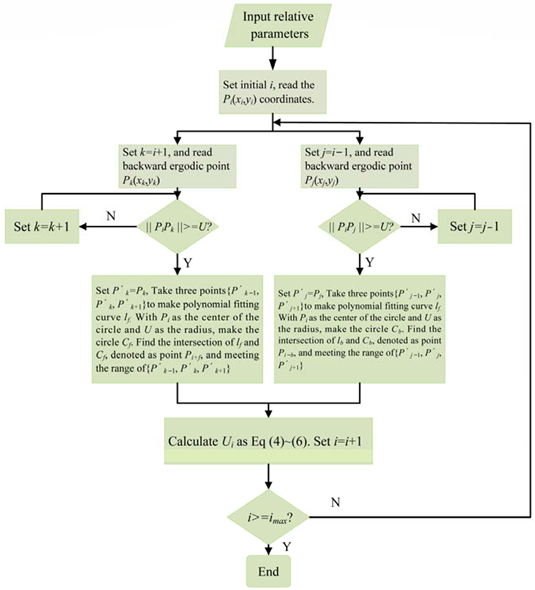 | ||
| (4) | ||
| (5) | ||
| (6) | ||
2.2.2. Discrete Derivative Method Analysis for Wheel Profile Discrete Curve
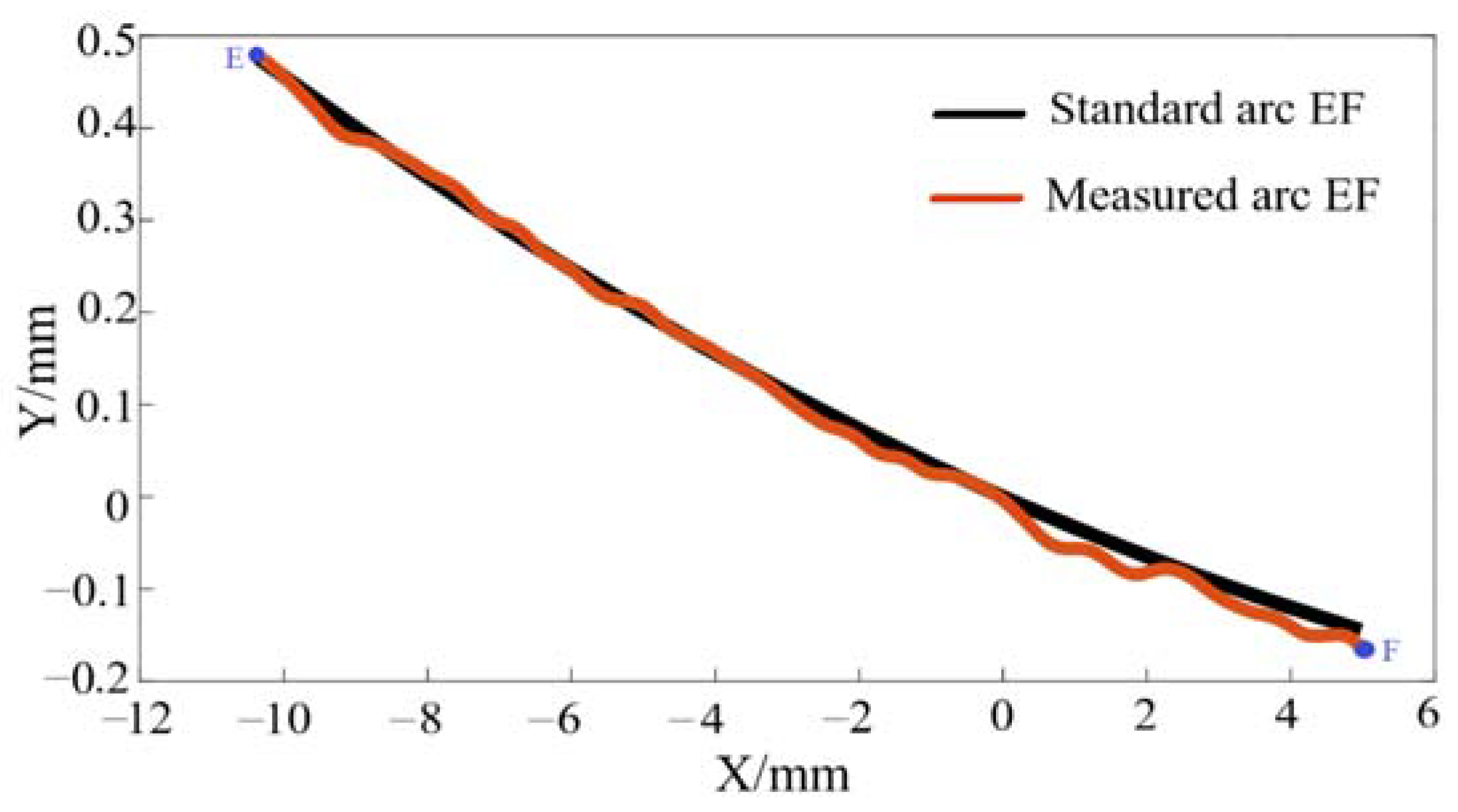
2.2.3. The Circle-Fitting Method of TATC
| Algorithm 2. Two-Arcs Tangency Constraint (TATC) method | |
| Input: | P1i (x1i, y1i): data points of arc EF. |
| P2i (x2i, y2i): data points of arc DE. | |
| [a2, b2, r2]: circle O2 parameters [27]. | |
| w0: initial weight matrix. | |
| qmax: the maximum number of iteration times. | |
| Δq: the minimum precision. | |
| Output: | [a1, b1, r1]: circle O1 parameters. |
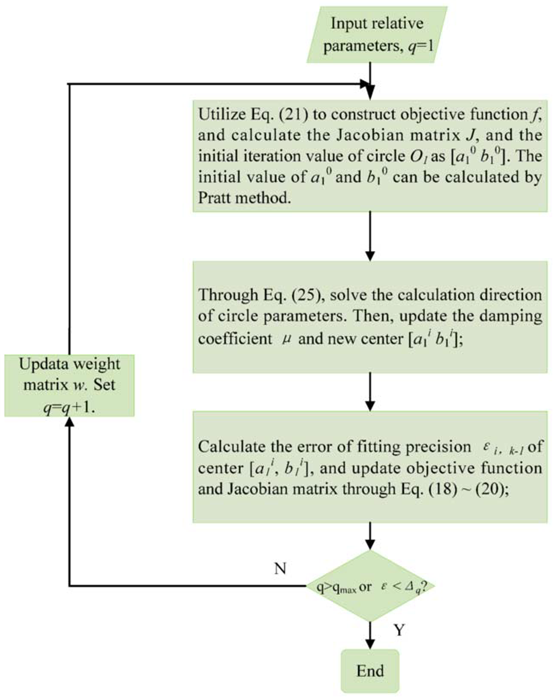 | |
3. Experimental Testing and Analysis
3.1. Experimental Equipment and Test Objectives
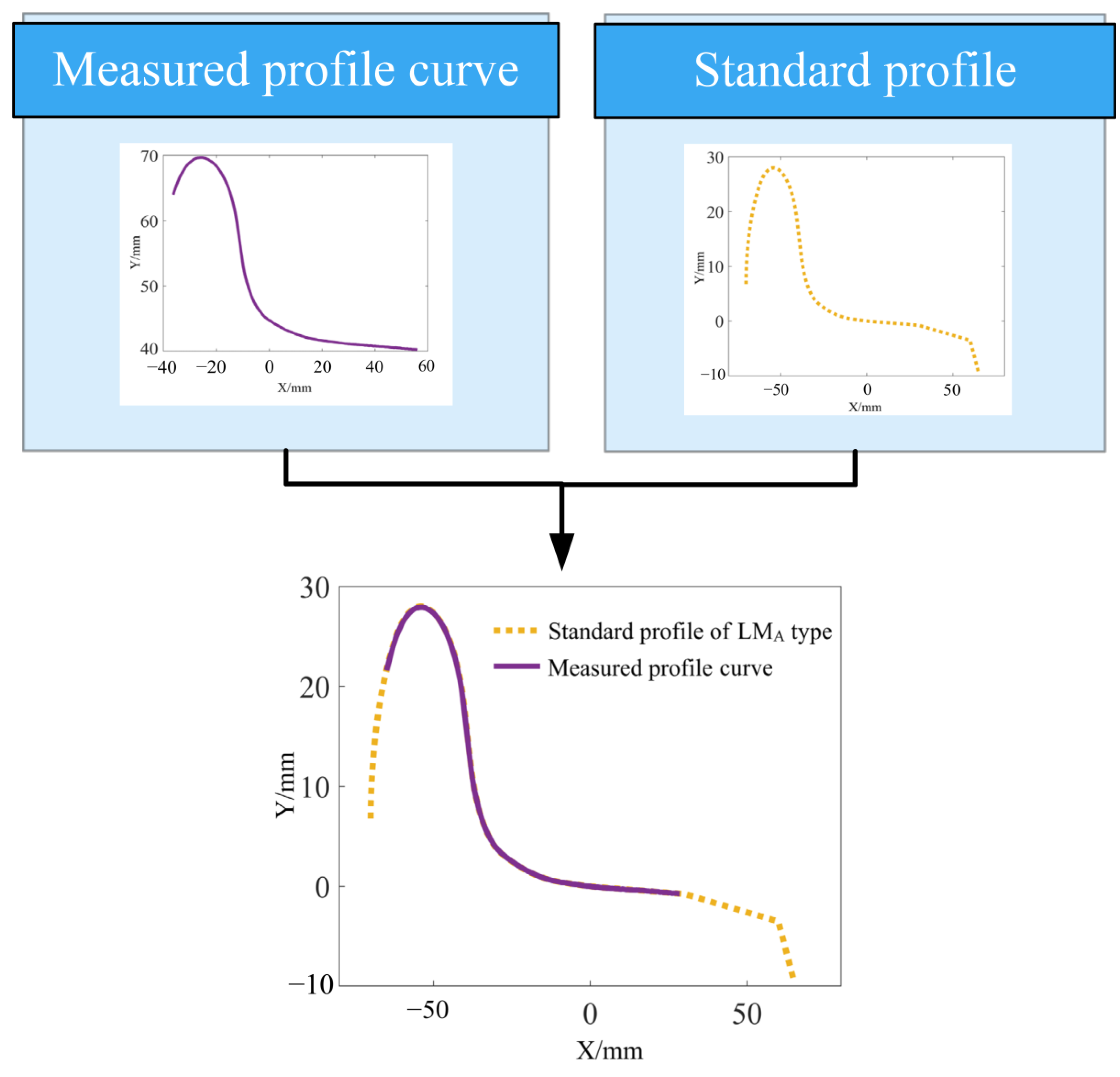
3.2. Segmentation Point Experiments Based on U-Chord Curvature Estimation
3.3. The Radius of Curvature Calculation Based on Discrete Derivative Method
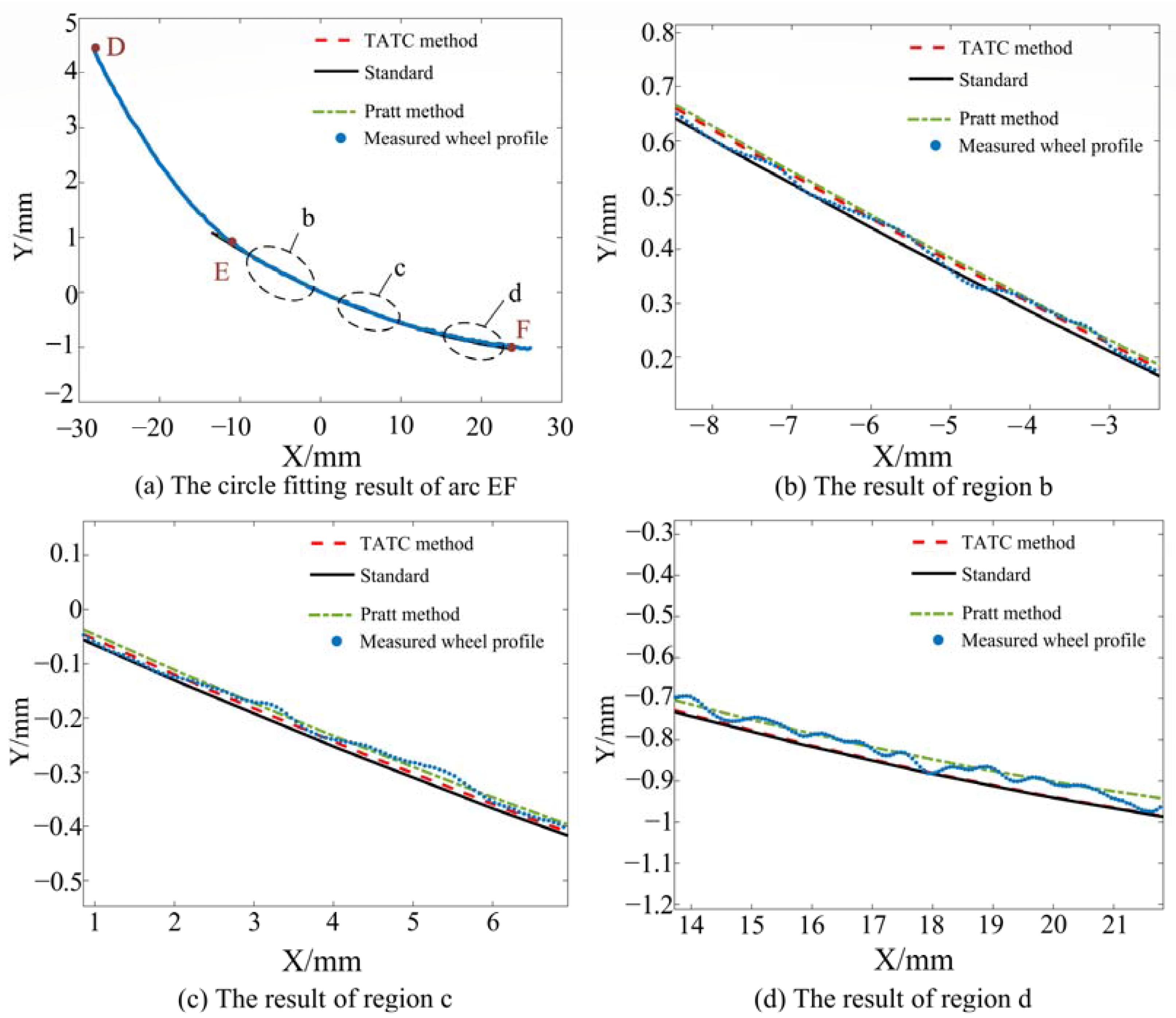
3.4. The Fitting Circle Experiment of the Circle of the Connection Tread and the Circle of the Central Tread
4. The Measurement Analysis of Uncertainty Evaluation
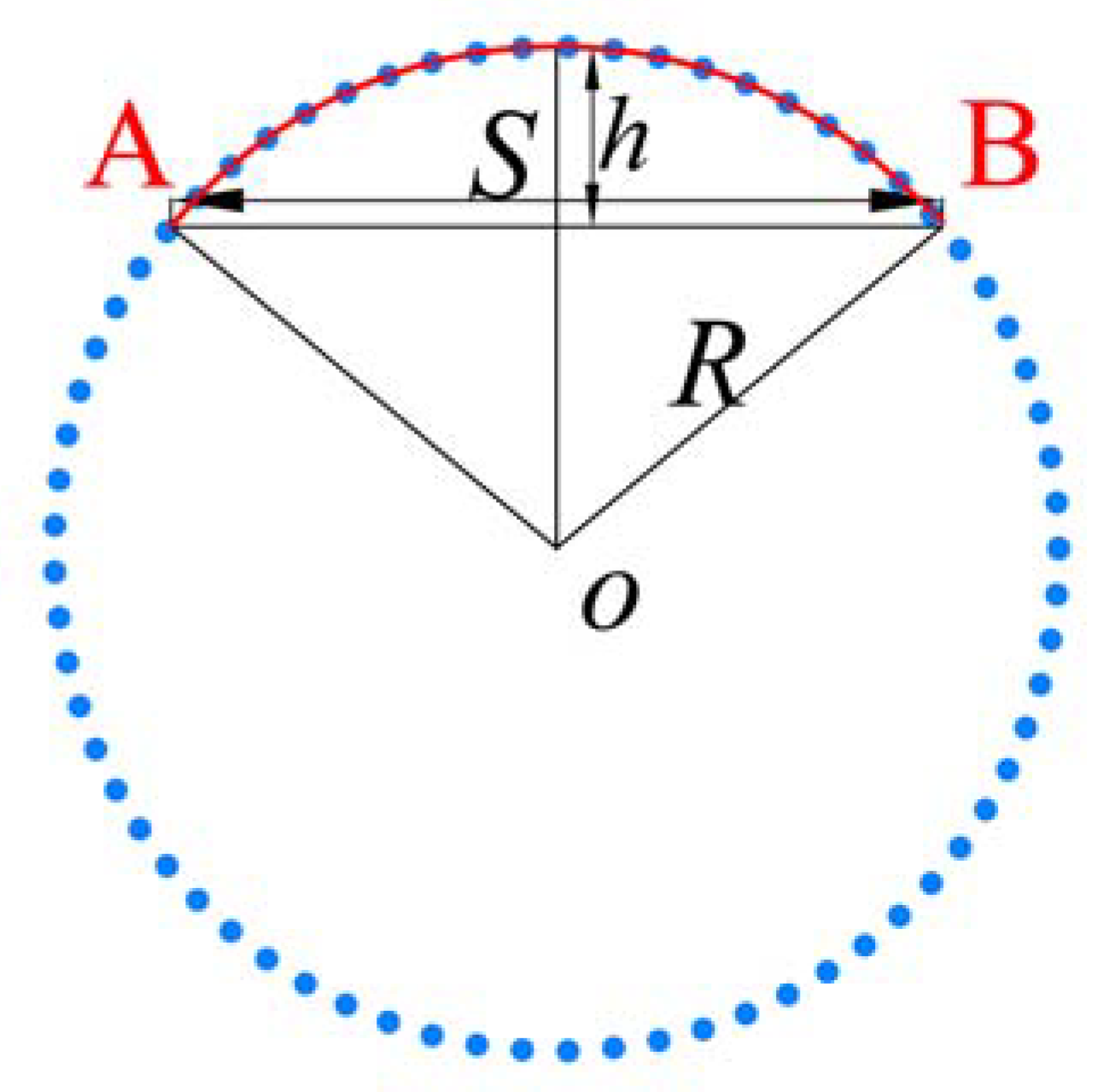
4.1. The Uncertainty Analysis in arc AB
4.1.1. Type-A Standard Uncertainty of arc AB
4.1.2. Type-B Uncertainty of arc AB
4.2. The Uncertainty Analysis in arc EF
4.2.1. Type-A Uncertainty Analysis of arc EF
4.2.2. Type-B Uncertainty Analysis of arc EF
5. Conclusions
- (1)
- The U-chord curvature method fairly met the demand of the precision of segmented points, and the segmented points’ position errors were less than 0.790 mm in the LMA type.
- (2)
- By the pre-experiment and the discrete derivative calculations in the small radius of curvature segments, the radii of curvature of the three wheel profile types were measured. In arc AB, the relative errors were 1.83%, 1.85%, and 0.60% for the LMA, LMc, and JM types, respectively. In arc CD, the relative errors were 2.19%, 2.5%, and 2.22%, respectively.
- (3)
- In the large radius of curvature segments, the discrete derivative calculation results occurred with large errors; this was because the discrete derivative method, which was based on a limiting approach method, did not work, and the noise points affected this method’s accuracy. For the continuous two short arcs EF of the wheel profile, the proposed TATC method and solution method accurately calculated the radius of curvature of arc EF, and the maximum relative errors were 0.40% and 1.51% for the LMA and JM types, respectively.
- (4)
- With the LMA-type profile as an example, the uncertainty evaluation results of arc AB and arc EF showed that the radius curvature confidence intervals were ±0.19 mm and ±2.1 mm, respectively, with a 95% confidence probability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hou, M.; Chen, B.; Cheng, D. Study on the Evolution of Wheel Wear and Its Impact on Vehicle Dynamics of High-Speed Trains. Coatings 2022, 12, 1333. [Google Scholar] [CrossRef]
- Liao, B.; Luo, Y. Study on the Factors Affecting the Wheel–Rail Lateral Impact of the Forepart of the Curved Switch Rail. Machines 2022, 10, 676. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, S. Polygonal Wear Mechanism of High-Speed Train Wheels Based on Lateral Friction Self-Excited Vibration. Machines 2022, 10, 608. [Google Scholar] [CrossRef]
- Yamashita, H.; Feldmeier, C.; Yamazaki, Y.; Kato, T.; Fujimoto, T.; Kondo, O.; Sugiyama, H. Wheel profile optimization procedure to minimize flange wear considering profile wear evolution. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2022, 236, 672–683. [Google Scholar] [CrossRef]
- Ren, W.; Li, L.; Cui, D.; Chen, G. An Improved Parallel Inverse Design Method of EMU Wheel Profile from Wheel Flange Wear Viewpoint. Shock. Vib. 2021, 2021, 8895536. [Google Scholar] [CrossRef]
- Ikeuchi, K.; Handa, K.; Lundén, R.; Vernersson, T. Wheel tread profile evolution for combined block braking and wheel–rail contact: Results from dynamometer experiments. Wear 2016, 366, 310–315. [Google Scholar] [CrossRef]
- Mokhtarian, F.; Suomela, R. Robust image corner detection through curvature scale space. In Curvature Scale Space Representation: Theory, Applications, and MPEG-7 Standardization; Springer: Dordrecht, The Netherlands, 2003; pp. 215–242. [Google Scholar]
- He, X.C.; Yung, N.H. Curvature Scale Space Corner Detector with Adaptive Threshold and Dynamic Region of Support. In Proceedings of the 17th International Conference on Pattern Recognition 2004, Cambridge, UK, 26 August 2004; Volume 2. [Google Scholar]
- Zhang, X.; Lei, M.; Yang, D.; Wang, Y.; Ma, L. Multi-scale curvature product for robust image corner detection in curvature scale space. Pattern Recognit. Lett. 2007, 28, 545–554. [Google Scholar] [CrossRef]
- Zhong, B.; Liao, W. Direct Curvature Scale Space: Theory and Corner Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 508–512. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, D.; Huang, S.; Tu, L.; Zhang, X. Corner detection using Chebyshev fitting-based continuous curvature es-timation. Electron. Lett. 2015, 51, 24. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Hong, M.; Xu, L.; Yang, D.; Lovell, B.C. Robust image corner detection based on scale evolution difference of planar curves. Pattern Recognit. Lett. 2009, 30, 4. [Google Scholar] [CrossRef]
- Guo, J.; Yang, J. An iterative procedure for robust circle fitting. Commun. Stat.-Simul. Comput. 2018, 48, 1872–1879. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, X.; Qin, Y.; Akyilmaz, O. Weighted geometric circle fitting for the Brogar Ring: Parameter-free approach and bias analysis. Measurement 2022, 192, 110832. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, F.Q.; Zhang, G.J. Radius Constraint Least-square Circle Fitting Method and Error Analysis. J. Optoelectron.·Laser 2006, 5, 604–607. (In Chinese) [Google Scholar]
- Zhu, J.; Li, X.F.; Tan, W.B.; Xiang, H.B.; Chen, C. Measurement of short arc based on centre constraint least-square circle fitting. Opt. Precis. Eng. 2009, 17, 10. [Google Scholar]
- Tao, W.; Zhong, H.; Chen, X.; Selami, Y.; Zhao, H. A new fitting method for measurement of the curvature radius of a short arc with high precision. Meas. Sci. Technol. 2018, 29, 075014. [Google Scholar] [CrossRef]
- Song, Z.; Sun, C.; Cheng, D.; Wang, H.; Hu, X. Research on Arc Parameters of Wheel Profile and Its Influence on Wheel-Rail Contact and Vehicle Dynamics. China Railw. Sci. 2019, 40, 10. (In Chinese) [Google Scholar]
- Zhang, S. On-line Inspection Key Technology Research for the Train Wheelset Geometric Parameters. Ph.D. Dissertation, Jilin University, Changchun, China, 2017. (In Chinese). [Google Scholar]
- Lin, F. Research on Wheel Wear and Wheel Profile Optimization of High Speed Train. Ph.D. Dissertation, China Academy of Railway Sciences, Beijing, China, 2014. (In Chinese). [Google Scholar]
- Piao, M. Five Evaluating Principles for Optimal Wheel/Rail Match. J. Dalian Jiaotong Univ. 2010, 31, 3. (In Chinese) [Google Scholar]
- Pan, J.; Song, A.; Huang, J.; Yan, C. Precise Measurement and Visual Expression of Gear Overall Deviation. Machines 2022, 10, 158. [Google Scholar] [CrossRef]
- Guo, J.J.; Zhong, B.J. U-Chord Curvature: A Computational Method of Discrete Curvature. Pattern Recognit. Artif. Intell. 2014, 27, 8. (In Chinese) [Google Scholar]
- Zhong, B.J.; Liao, W.H. Enhanced Corner Detection Based on the Topology Boundary of Refined Digital Curves. Pattern Recognit. Artif. Intell. 2005, 18, 2. (In Chinese) [Google Scholar]
- Zhong, B.J. On the Stability of Refined L-Curvature under Rotation Transformations. Appl. Mech. Mater. 2010, 20, 401–406. [Google Scholar] [CrossRef]
- An, Y.; Wang, L.; Ma, R.; Wang, J. Geometric Properties Estimation from Line Point Clouds Using Gaussian-Weighted Discrete Derivatives. IEEE Trans. Ind. Electron. 2020, 68, 1. [Google Scholar] [CrossRef]
- Pratt, V. Direct least-squares fitting of algebraic surfaces. ACM SI-GGRAPH Comput. Graph. 1987, 21, 145–152. [Google Scholar] [CrossRef]
- Bergström, P.; Edlund, O. Robust registration of point sets using iteratively reweighted least squares. Comput. Optim. Appl. 2014, 58, 543–561. [Google Scholar] [CrossRef]
- National Rallway Administration of the People’s Republic of China. Locomotive Vehicle Wheel Geometric Parameter Measuring Machine; TB/T 3476-2017; National Rallway Administration of the People’s Republic of China: Beijing, China, 2017. (In Chinese)
- Wang, Y.; Luo, R.; Hu, J. Research on Wheel Rail Wear under Different Registration Strategy. China Railw. 2017, 9, 83–90. (In Chinese) [Google Scholar]
- Huang, M.C.; Tai, C.C. The Pre-Processing of Data Points for Curve Fitting in Reverse Engineering. Int. J. Adv. Manuf. Technol. 2000, 19, 6. [Google Scholar] [CrossRef]
- Yang, H. Study on CAD Modeling Techniques Based on Variation Design in Reverse Engineering. Ph.D. Dissertation, Shandong University, Jinan, China, 2007. (In Chinese). [Google Scholar]
- Shi, C.; Zhu, J.; Sun, G.; Guo, X.; Wang, J.; Bao, H. Insitu measuring method and experimental research on key circular arc profile parameters of form grinding wheel. China Meas. Test 2021, 47, 3. (In Chinese) [Google Scholar]








| Parameters | Value |
|---|---|
| Maximum sample points in one line point cloud | 1920 |
| Repeatability of x-axis | 40 μm |
| Repeatability of z-axis | 20 μm |
| Linearity | ±0.01 %FS |
| Temperature drift | ±0.01 %FS·°C−1 |
| Wheel Profile Type | Radius of Outside of Flange Circle (arc AB)/mm | Radius of Throat Root Circle (arc CD)/mm | Radius of Connection Tread Circle (arc DE)/mm | Radius of Central Circle (arc EF)/mm | Outside of Connection to Tread |
|---|---|---|---|---|---|
| LMA | 15 | 14 | 90 | 450 | 1:40 |
| LMC | 25.05 | 13 | The curve of a set of points | 5.5:100 | |
| JM | 20 | 14 | 100 | 500 | R200 |
| Segmented Points | Index | Coordinates after Registration/mm | Coordinates of Standard/mm | Errors/mm |
|---|---|---|---|---|
| A | 155 | (−55.629, 27.834) | (−55.557, 27.913) | 0.106 |
| B | 448 | (−40.305, 17.980) | (−40.265, 18.152) | 0.278 |
| C | 492 | (−38.089, 11.849) | (−38.026, 12.295) | 0.450 |
| D | 663 | (−28.076, 3.244) | (−28.471, 3.327) | 0.474 |
| E | 953 | (−10.245, 0.473) | (−10.750, 0.499) | 0.506 |
| F | 1206 | (4.492, −0.163) | (4.254, −0.127) | 0.790 |
| Segments | Standard Value of the Radius of Curvature/mm | DD Method/mm | Huang Method/mm | Yang Method/mm |
|---|---|---|---|---|
| The left side of point A | 12 | 12.210 | 16.357 | 14.796 |
| AB | 15 | 15.274 | 18.844 | 18.248 |
| CD | 14 | 14.307 | 17.397 | 17.781 |
| DE | 90 | 119.038 | 131.042 | 121.004 |
| EF | 450 | 251.714 | 230.625 | 247.846 |
| Segments | Standard Value of the Radius of Curvature/mm | DD Method/mm | Huang Method/mm | Yang Method/mm |
|---|---|---|---|---|
| The left side of point A | 12 | 12.336 | 16.127 | 16.819 |
| AB | 25.05 | 24.586 | 21.091 | 27.334 |
| CD | 13 | 13.325 | 17.751 | 16.764 |
| Segments | Standard Value of the Radius of Curvature/mm | DD Method/mm | Huang Method/mm | Yang Method/mm |
|---|---|---|---|---|
| The left side of point A | 12 | 12.430 | 14.893 | 14.971 |
| AB | 20 | 19.881 | 24.295 | 22.501 |
| CD | 14 | 14.311 | 16.348 | 15.084 |
| DE | 100 | 131.746 | 152.082 | 144.659 |
| EF | 500 | 449.522 | 421.574 | 312.472 |
| Radius of Curvature/mm | Arc AB | Arc EF | Arc AB | Arc EF | Arc AB | Arc EF |
|---|---|---|---|---|---|---|
| Position | Set 1 | Set 2 | Set 3 | |||
| 1 | 15.271 | 452.088 | 15.213 | 451.701 | 15.271 | 451.751 |
| 2 | 14.956 | 452.518 | 14.896 | 452.582 | 15.026 | 452.677 |
| 3 | 15.021 | 451.914 | 14.953 | 452.218 | 14.936 | 451.751 |
| 4 | 14.952 | 451.913 | 15.044 | 452.506 | 15.103 | 452.441 |
| 5 | 15.038 | 452.629 | 15.128 | 452.551 | 15.092 | 452.462 |
| 6 | 15.175 | 449.924 | 15.073 | 449.372 | 15.126 | 449.214 |
| 7 | 15.215 | 449.534 | 15.151 | 450.063 | 15.174 | 449.160 |
| 8 | 15.041 | 448.036 | 15.034 | 447.981 | 15.085 | 447.831 |
| 9 | 15.194 | 449.075 | 15.208 | 449.057 | 15.172 | 449.061 |
| 10 | 15.109 | 451.980 | 15.121 | 452.399 | 15.125 | 451.895 |
| Component of Uncertainty | Symbol | Calculation | Confidence Coefficient | Value/mm |
|---|---|---|---|---|
| Type-A standard uncertainty | Equations (30) and (31) | —— | 0.0211 | |
| Repeatability and linearity of x-axis direction | 0.0240 | |||
| Temperature drift of x-axis direction | 0.0133 | |||
| Type-B uncertainty about x-axis direction component | —— | 0.0274 | ||
| Repeatability and linearity of z-axis direction | 0.0117 | |||
| Temperature drift of z-axis direction | 0.0018 | |||
| Type-B uncertainty about z-axis direction component | —— | 0.0118 | ||
| Type-A standard uncertainty | —— | 0.0896 | ||
| The combine standard uncertainty | —— | 0.0920 |
| Component of Uncertainty | Symbol | Calculation | Confidence Coefficient | Value/mm |
|---|---|---|---|---|
| Type-A standard uncertainty | Equations (30) and (31) | —— | 1.0945 | |
| Type-B standard uncertainty | Equations (37)–(39) | 0.2377 | ||
| Combined standard uncertainty | —— | 1.1200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Bao, S.; Zhou, C.; Sun, J.; He, X. Measuring Methods of Radius of Curvature and Tread Circle-Fitting Studies for Railway Wheel Profiles. Machines 2023, 11, 181. https://doi.org/10.3390/machines11020181
Gao C, Bao S, Zhou C, Sun J, He X. Measuring Methods of Radius of Curvature and Tread Circle-Fitting Studies for Railway Wheel Profiles. Machines. 2023; 11(2):181. https://doi.org/10.3390/machines11020181
Chicago/Turabian StyleGao, Chunfu, Siyuan Bao, Chongqiu Zhou, Jianfeng Sun, and Xinsheng He. 2023. "Measuring Methods of Radius of Curvature and Tread Circle-Fitting Studies for Railway Wheel Profiles" Machines 11, no. 2: 181. https://doi.org/10.3390/machines11020181
APA StyleGao, C., Bao, S., Zhou, C., Sun, J., & He, X. (2023). Measuring Methods of Radius of Curvature and Tread Circle-Fitting Studies for Railway Wheel Profiles. Machines, 11(2), 181. https://doi.org/10.3390/machines11020181





