On the Use of a Genetic Algorithm for Determining Ho–Cook Coefficients in Continuous Path Planning of Industrial Robotic Manipulators
Abstract
1. Introduction
2. Materials and Methods
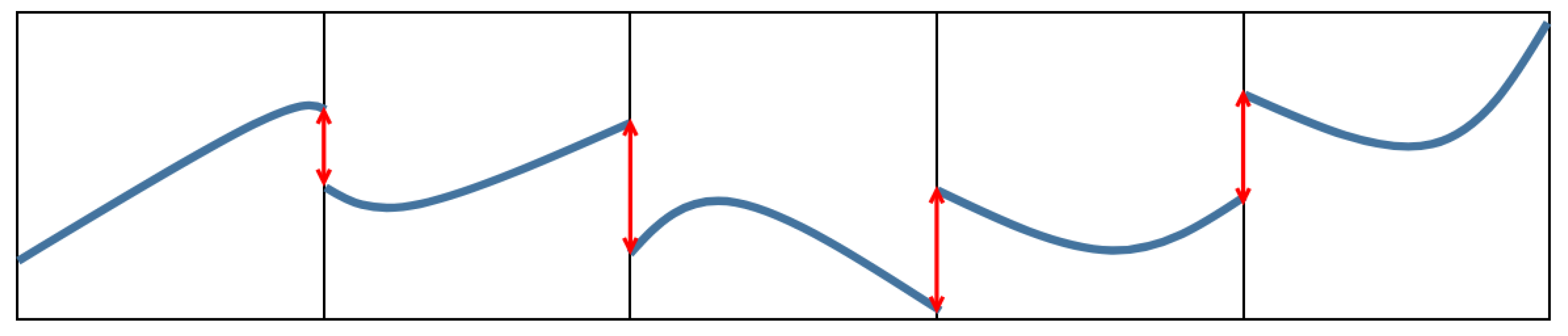
2.1. Ho–Cook Path Planning
- k—the trajectory point;
- m—the total number of trajectory points, and
- B—coefficients of the interpolation polynomials.
2.2. Genetic Algorithm
- Shape of the potential solutions;
- The way in which the crossover and mutation will be applied;
- The probabilities with which the evolutionary operations will occur;
- The fitness function that will evaluate the solutions;
- The number of iterations (generations) of the algorithm;
- The number of candidate solutions in the algorithm;
- The manner of the solution selection for the operations.
2.2.1. Solution Construction
2.2.2. Application of Evolutionary Computing Operations
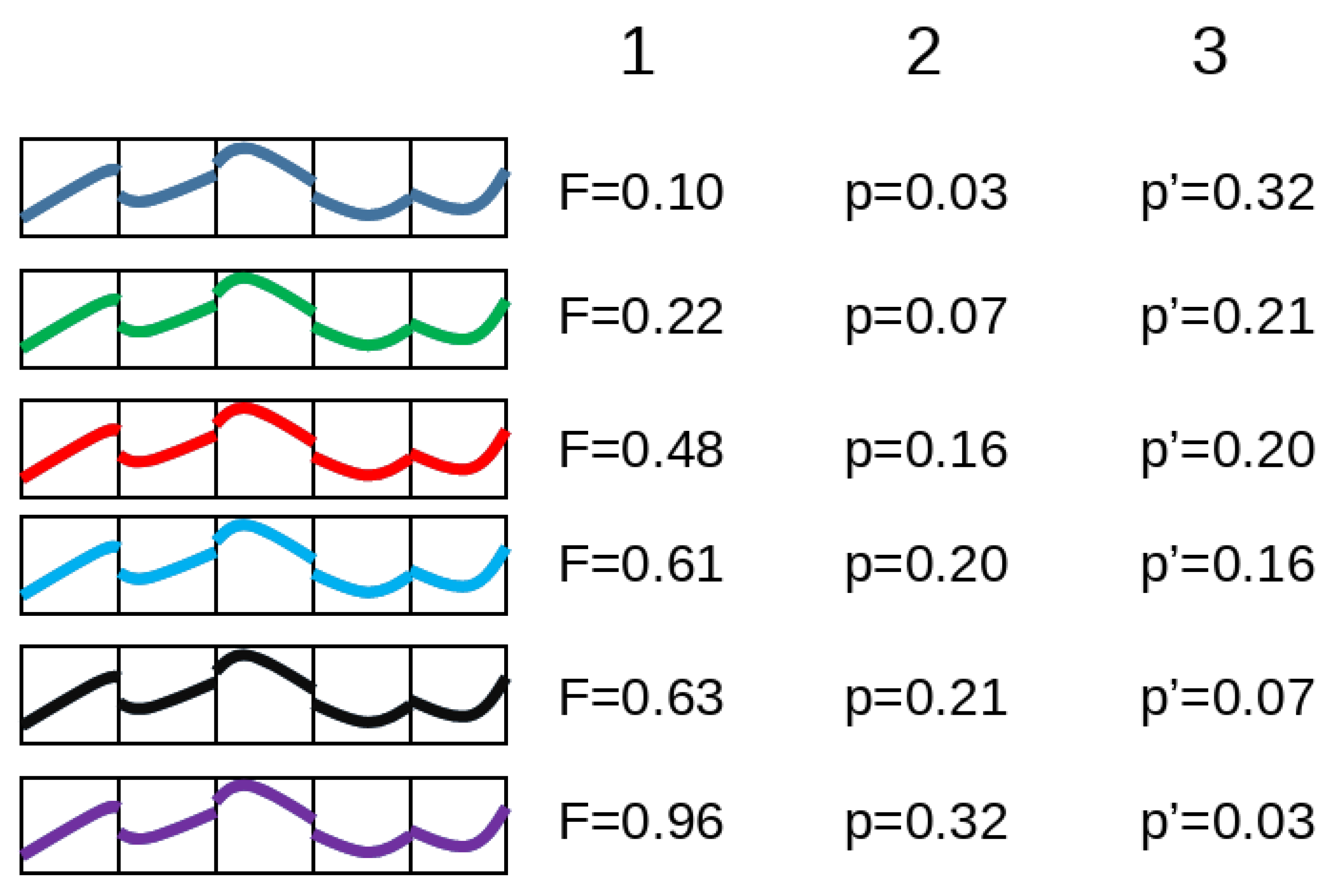
2.2.3. The Fitness Function
2.2.4. Candidate Solution Selection
2.3. Interpolation
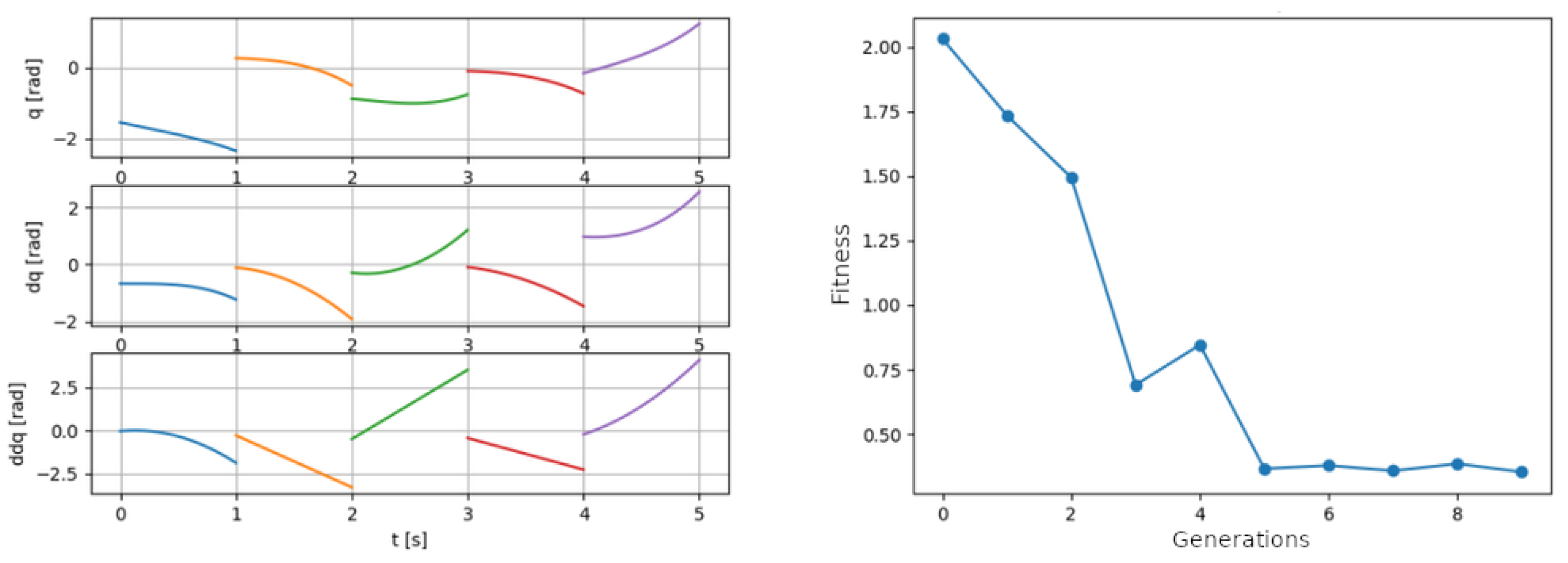
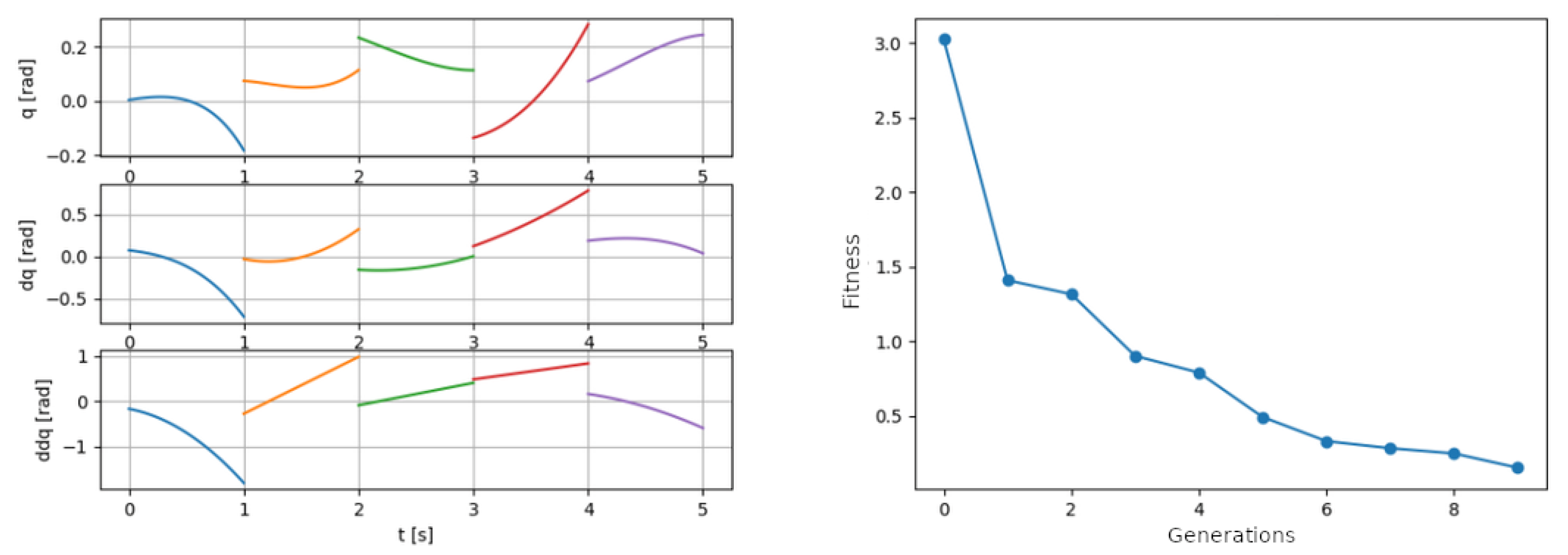
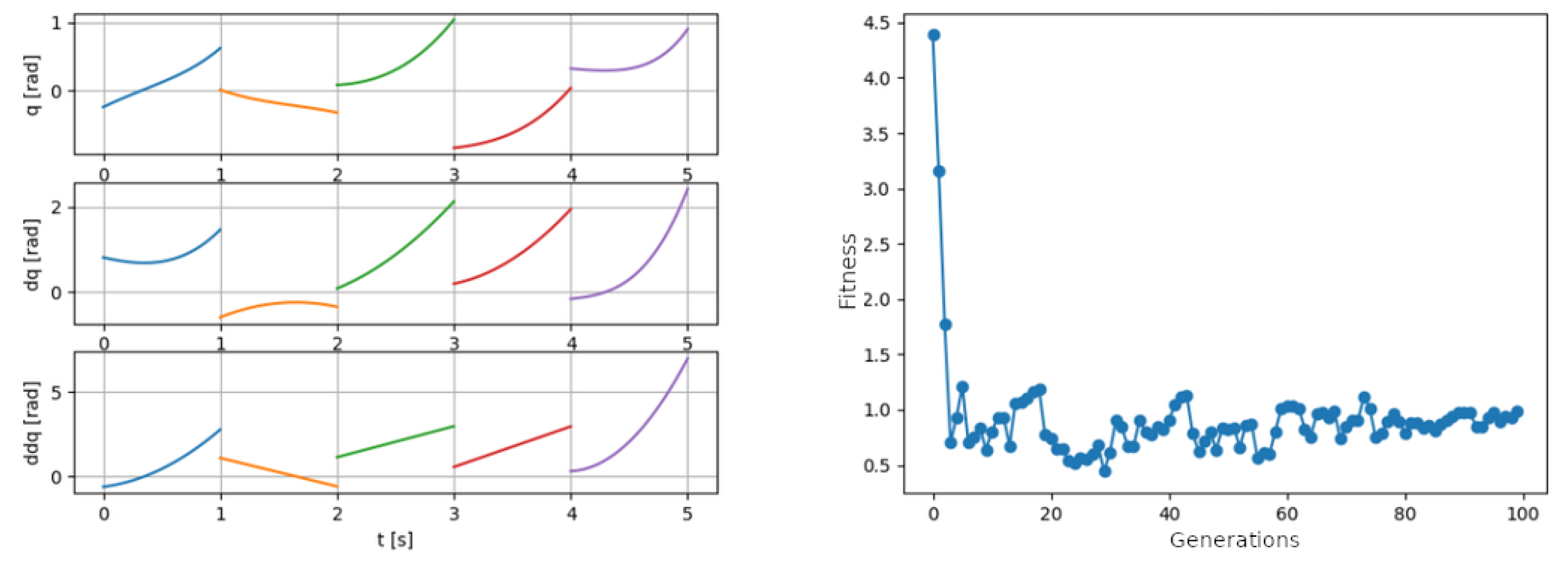
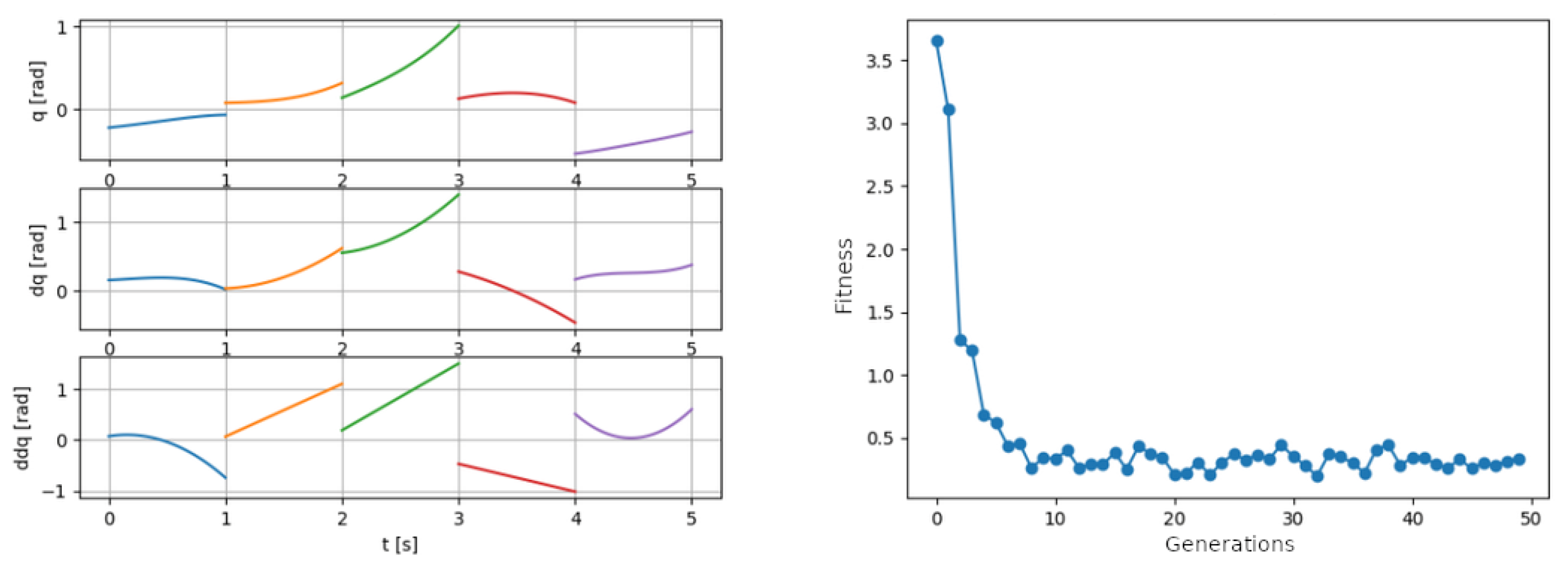
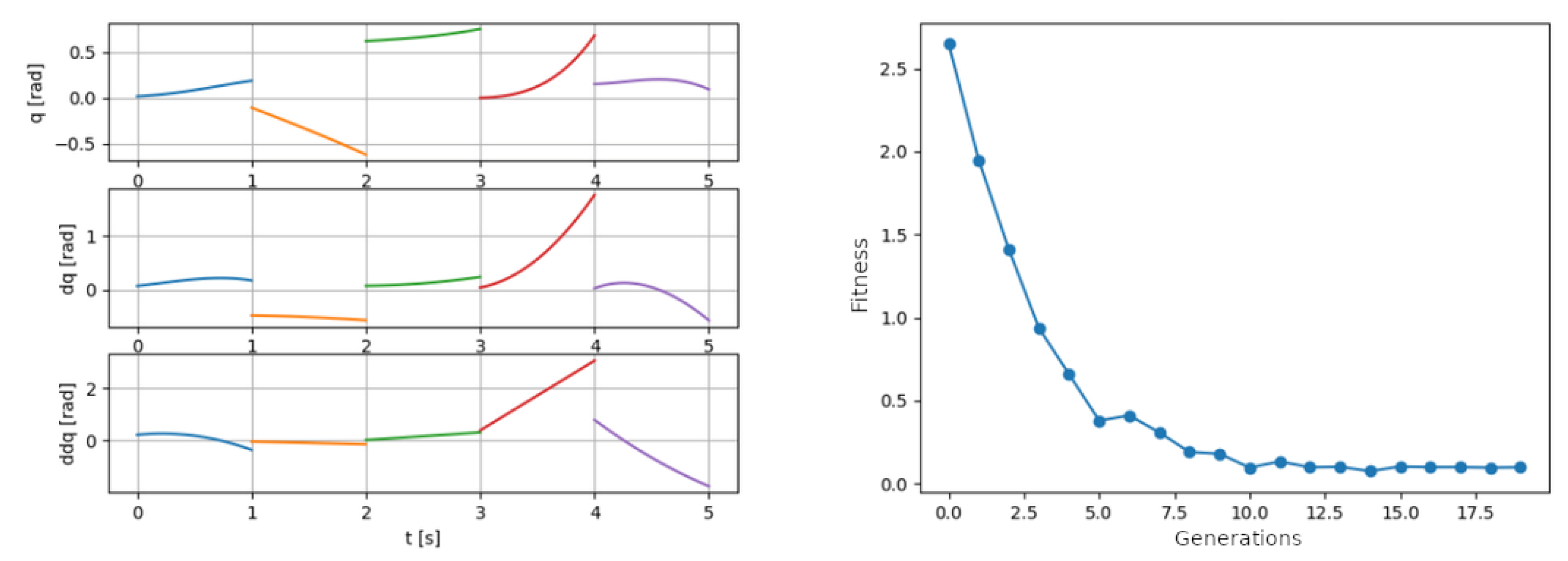
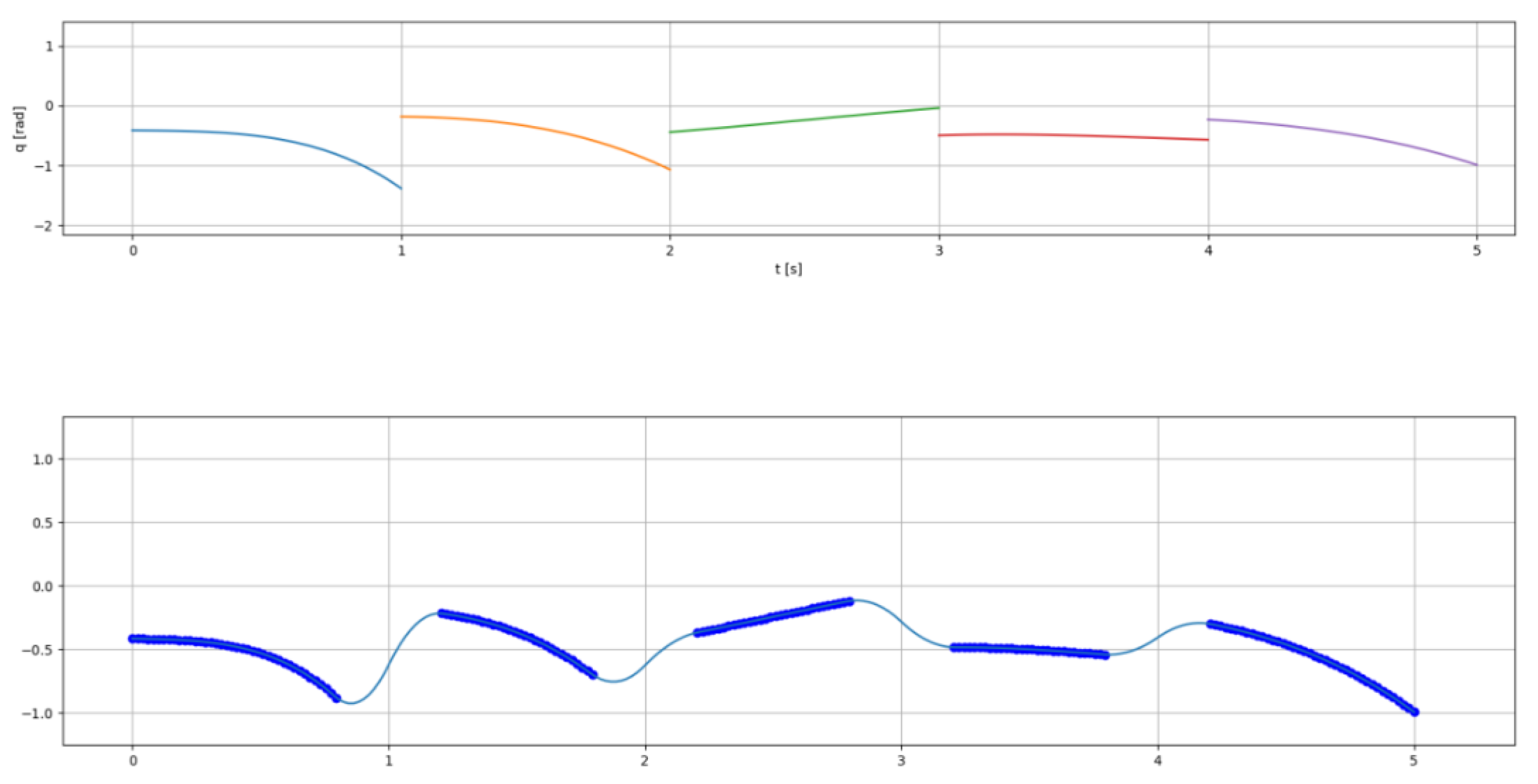
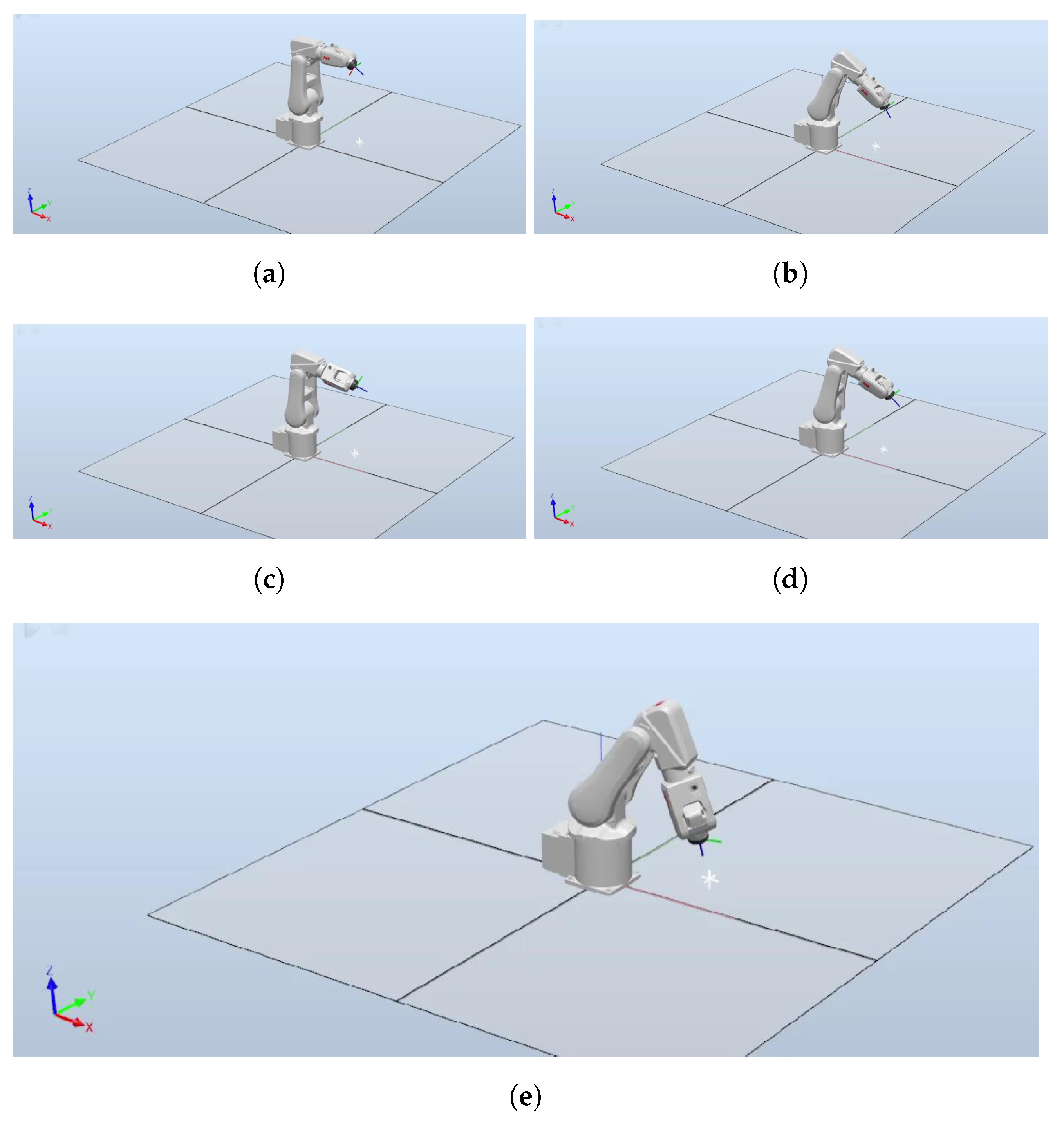
3. Results and Discussion
3.1. Determining the Optimal Boundary Condition
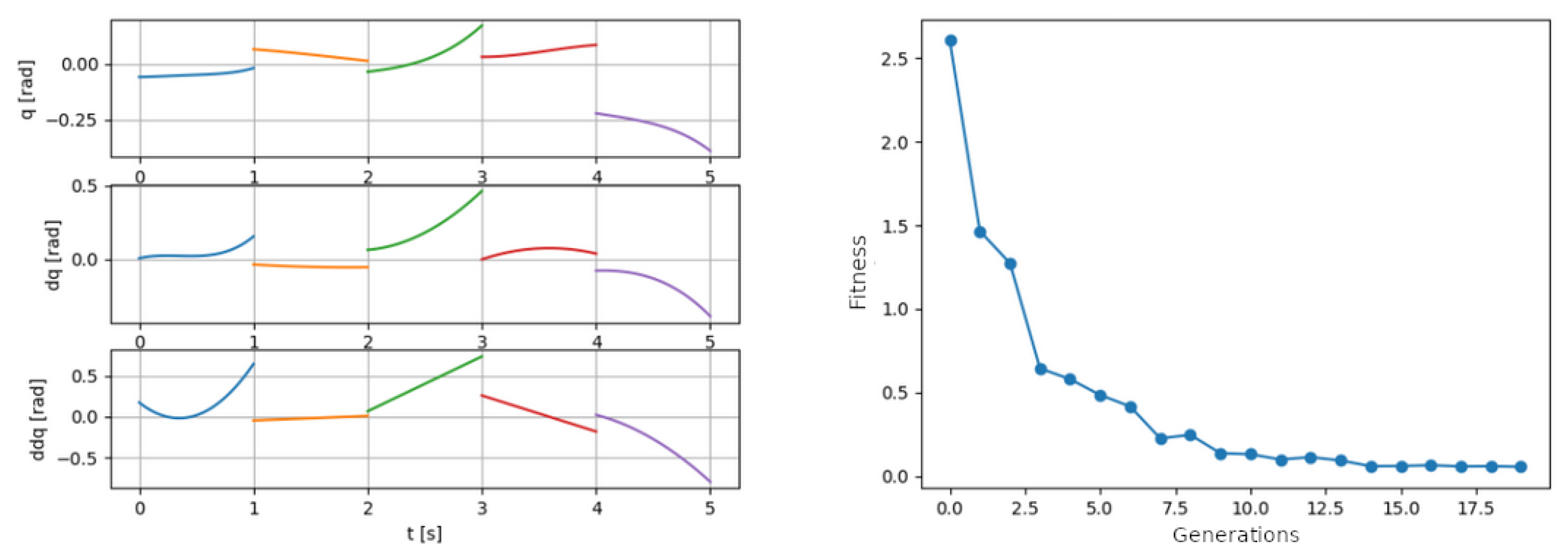
3.2. Determining the GA Parameters
- Population size of 100 executed for 100 generations;
- Population size of 1000 executed for 50 generations;
- Population size of 10,000 executed for 20 generations.
Execution Time
3.3. Result Illustration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Fuhlbrigge, T.; Li, X. Automated industrial robot path planning for spray painting process: A review. In Proceedings of the 2008 IEEE International Conference on Automation Science and Engineering, Washington, DC, USA, 23–26 August 2008; pp. 522–527. [Google Scholar]
- Raja, P.; Pugazhenthi, S. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- Angeles, J.; Rojas, A.; Lopez-Cajun, C.S. Trajectory planning in robotic continuous-path applications. IEEE J. Robot. Autom. 1988, 4, 380–385. [Google Scholar] [CrossRef]
- Chettibi, T. Smooth point-to-point trajectory planning for robot manipulators by using radial basis functions. Robotica 2019, 37, 539–559. [Google Scholar] [CrossRef]
- Cowley, A.; Cohen, B.; Marshall, W.; Taylor, C.J.; Likhachev, M. Perception and motion planning for pick-and-place of dynamic objects. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 816–823. [Google Scholar]
- Khan, A.T.; Cao, X.; Li, Z.; Li, S. Evolutionary Computation Based Real-time Robot Arm Path-planning Using Beetle Antennae Search. EAI Endorsed Trans. AI Robot. 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Draganjac, I.; Sesar, V.; Bogdan, S.; Kovacic, Z. An internet-based system for remote planning and execution of SCARA robot trajectories. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 3485–3490. [Google Scholar]
- Lengagne, S.; Mathieu, P.; Kheddar, A.; Yoshida, E. Generation of dynamic motions under continuous constraints: Efficient computation using b-splines and taylor polynomials. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 698–703. [Google Scholar]
- Lian, J.; Yu, W.; Xiao, K.; Liu, W. Cubic spline interpolation-based robot path planning using a chaotic adaptive particle swarm optimization algorithm. Math. Probl. Eng. 2020, 2020, 1849240. [Google Scholar] [CrossRef]
- Carrasco, J.; García, S.; Rueda, M.; Das, S.; Herrera, F. Recent trends in the use of statistical tests for comparing swarm and evolutionary computing algorithms: Practical guidelines and a critical review. Swarm Evol. Comput. 2020, 54, 100665. [Google Scholar] [CrossRef]
- Bansal, J.C.; Singh, P.K.; Pal, N.R. Evolutionary and Swarm Intelligence Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; Volume 779. [Google Scholar]
- Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Saga, M.; Car, Z. Path planning optimization of six-degree-of-freedom robotic manipulators using evolutionary algorithms. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420908076. [Google Scholar] [CrossRef]
- Shukla, P.; Kumar, H.; Nandi, G.C. Robotic grasp manipulation using evolutionary computing and deep reinforcement learning. Intell. Serv. Robot. 2021, 14, 61–77. [Google Scholar] [CrossRef]
- Ferigo, A.; Iacca, G.; Medvet, E. Beyond body shape and brain: Evolving the sensory apparatus of voxel-based soft robots. In Proceedings of the International Conference on the Applications of Evolutionary Computation (Part of EvoStar), Virtual Event, Germany, 20–22 April 2021; Springer: Berlin/Heidelberg, Germany; pp. 210–226. [Google Scholar]
- Kim, J.; Ba, D.X.; Yeom, H.; Bae, J. Gait optimization of a quadruped robot using evolutionary computation. J. Bionic Eng. 2021, 18, 306–318. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Tong, X.; Zhao, G.; Chen, B. Genetic algorithm-based trajectory optimization for digital twin robots. Front. Bioeng. Biotechnol. 2022, 9, 1433. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Tan, K.C.; Zhang, J. A meta-knowledge transfer-based differential evolution for multitask optimization. IEEE Trans. Evol. Comput. 2021, 26, 719–734. [Google Scholar] [CrossRef]
- Martin, J.G.; Frejo, J.R.D.; García, R.A.; Camacho, E.F. Multi-robot task allocation problem with multiple nonlinear criteria using branch and bound and genetic algorithms. Intell. Serv. Robot. 2021, 14, 707–727. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Wang, B.; Liu, Y.; Wang, C. The application of an adaptive genetic algorithm based on collision detection in path planning of mobile robots. Comput. Intell. Neurosci. 2021, 2021, 5536574. [Google Scholar] [CrossRef]
- Rahmaniar, W.; Rakhmania, A.E. Mobile Robot Path Planning in a Trajectory with Multiple Obstacles Using Genetic Algorithms. J. Robot. Control (JRC) 2022, 3, 1–7. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Li, H.; Zhao, T.; Dian, S. Forward search optimization and subgoal-based hybrid path planning to shorten and smooth global path for mobile robots. Knowl.-Based Syst. 2022, 258, 110034. [Google Scholar] [CrossRef]
- García, E.; Villar, J.R.; Tan, Q.; Sedano, J.; Chira, C. An efficient multi-robot path planning solution using A* and coevolutionary algorithms. Integr. Comput.-Aided Eng. 2023, 30, 41–52. [Google Scholar] [CrossRef]
- Yu, Z.; Duan, P.; Meng, L.; Han, Y.; Ye, F. Multi-objective path planning for mobile robot with an improved artificial bee colony algorithm. Math. Biosci. Eng. 2023, 20, 2501–2529. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Lou, J.; Yu, X.; Chen, Y.; Sun, Z.; Zheng, P. Robot Welding Path Planning and Application Based on Graphical Computing. In Proceedings of the Seventh International Congress on Information and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2023; pp. 597–605. [Google Scholar]
- Li, J.; Zou, L.; Luo, G.; Wang, W.; Lv, C. Enhancement and evaluation in path accuracy of industrial robot for complex surface grinding. Robot. Comput.-Integr. Manuf. 2023, 81, 102521. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, X.; Zhou, Y.; Liu, Y.; Zhou, X.; Chen, H.; Zhao, H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022, 585, 441–453. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Zhou, T.; Armaghani, D.J.; Qiu, Y. Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Artif. Intell. Rev. 2022, 55, 5673–5705. [Google Scholar] [CrossRef]
- Budi, H.S.; Elveny, M.; Zhuravlev, P.; Jalil, A.T.; Al-Janabi, S.; Alkaim, A.F.; Saleh, M.M.; Shichiyakh, R.A. Development of an adaptive genetic algorithm to optimize the problem of unequal facility location. Found. Comput. Decis. Sci. 2022, 47, 111–125. [Google Scholar] [CrossRef]
- Orsag, M.; Poropat, M.; Bogdan, S. Hybrid fly-by-wire quadrotor controller. Automatika 2010, 51, 19–32. [Google Scholar] [CrossRef]
- Konjević, B.; Kovačić, Z. CONTINUOUS JERK TRAJECTORY PLANNING ALGORITHMS. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, SCITEPRESS, Noordwijkerhout, The Netherlands, 28–31 July 2011; Volume 2, pp. 481–489. [Google Scholar]
- Konjević, B.; Punčec, M.; Kovačić, Z. Two approaches to bounded jerk trajectory planning. In Proceedings of the 2012 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia and Herzegovina, 25–27 March 2012; pp. 1–7. [Google Scholar]
- Močnik, G.; Kačič, Z.; Šafarič, R.; Mlakar, I. Capturing Conversational Gestures for Embodied Conversational Agents Using an Optimized Kaneda–Lucas–Tomasi Tracker and Denavit–Hartenberg-Based Kinematic Model. Sensors 2022, 22, 8318. [Google Scholar] [CrossRef]
- Shim, S.; Lee, S.; Joo, S.; Seo, J. Denavit-Hartenberg Notation-Based Kinematic Constraint Equations for Forward Kinematics of the 3–6 Stewart Platform. J. Mech. Robot. 2022, 14, 054505. [Google Scholar] [CrossRef]
- Baressi Šegota, S.; Anđelić, N.; Šercer, M.; Meštrić, H. Dynamics Modeling of Industrial Robotic Manipulators: A Machine Learning Approach Based on Synthetic Data. Mathematics 2022, 10, 1174. [Google Scholar] [CrossRef]
- Milenkovic, P.; Wang, Z.; Rodriguez, J.I. Encountering singularities of a serial robot along continuous paths at high precision. Mech. Mach. Theory 2023, 181, 105224. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Han, S.; Xiao, L. An improved adaptive genetic algorithm. SHS Web Conf. 2022, 140, 01044. [Google Scholar] [CrossRef]
- Wang, B.; Yao, X.; Jiang, Y.; Sun, C.; Shabaz, M. Design of a real-time monitoring system for smoke and dust in thermal power plants based on improved genetic algorithm. J. Healthc. Eng. 2021, 2021, 7212567. [Google Scholar] [CrossRef]
- Ibrahim, M.; Nurhakiki, F.; Utama, D.; Rizaki, A. Optimised genetic algorithm crossover and mutation stage for vehicle routing problem pick-up and delivery with time windows. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sanya, China, 12–14 November 2021; Volume 1071, p. 012025. [Google Scholar]
- Damia, A.; Esnaashari, M.; Parvizimosaed, M. Adaptive Genetic Algorithm Based on Mutation and Crossover and Selection Probabilities. In Proceedings of the 2021 7th International Conference on Web Research (ICWR), Tehran, Iran, 19–20 May 2021; pp. 86–90. [Google Scholar]
- Saadaoui, D.; Elyaqouti, M.; Assalaou, K.; Lidaighbi, S. Parameters optimization of solar PV cell/module using genetic algorithm based on non-uniform mutation. Energy Convers. Manag. X 2021, 12, 100129. [Google Scholar] [CrossRef]
- Sohail, A. Genetic algorithms in the fields of artificial intelligence and data sciences. Ann. Data Sci. 2021, 1–12. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Jana, R.K.; Bhattacharya, S. A Comparative Study of Dynamic Approaches for Allocating Crossover and Mutation Ratios for Genetic Algorithm-based Optimization of Wind Power Generation Cost in Jafrabad Region in India. In Proceedings of the International Conference on “Recent Advancements in Science, Engineering & Technology, and Management, Nagpur, India, 25–26 March 2021. [Google Scholar]
- Avdeenko, T.; Serdyukov, K. Genetic Algorithm Fitness Function Formulation for Test Data Generation with Maximum Statement Coverage. In Proceedings of the International Conference on Swarm Intelligence, Qingdao, China, 17–21 July 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 379–389. [Google Scholar]
- Fogel, D.B. Evolutionary algorithms in theory and practice. Complexity 1997, 2, 26–27. [Google Scholar] [CrossRef]
- Liu, J.; Jin, B.; Yang, J.; Xu, L. Sea surface temperature prediction using a cubic B-spline interpolation and spatiotemporal attention mechanism. Remote Sens. Lett. 2021, 12, 478–487. [Google Scholar] [CrossRef]
- Tayebi, S.; Momani, S.; Arqub, O.A. The cubic B-spline interpolation method for numerical point solutions of conformable boundary value problems. Alex. Eng. J. 2022, 61, 1519–1528. [Google Scholar] [CrossRef]
- Gigras, Y.; Gupta, K. Artificial intelligence in robot path planning. Int. J. Soft Comput. Eng. (IJSCE) 2012, 2, 2231–2307. [Google Scholar]
- Liu, M. Robotic online path planning on point cloud. IEEE Trans. Cybern. 2015, 46, 1217–1228. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, Q.; Jiang, Z.; Liu, H. Robot learning from demonstration for path planning: A review. Sci. China Technol. Sci. 2020, 63, 1325–1334. [Google Scholar] [CrossRef]
- Bonny, T.; Kashkash, M. Highly optimized Q-learning-based bees approach for mobile robot path planning in static and dynamic environments. J. Field Robot. 2022, 39, 317–334. [Google Scholar] [CrossRef]
- Anđelić, N.; Car, Z.; Šercer, M. Neural Network-Based Model for Classification of Faults During Operation of a Robotic Manipulator. Teh. Vjesn. 2021, 28, 1380–1387. [Google Scholar]
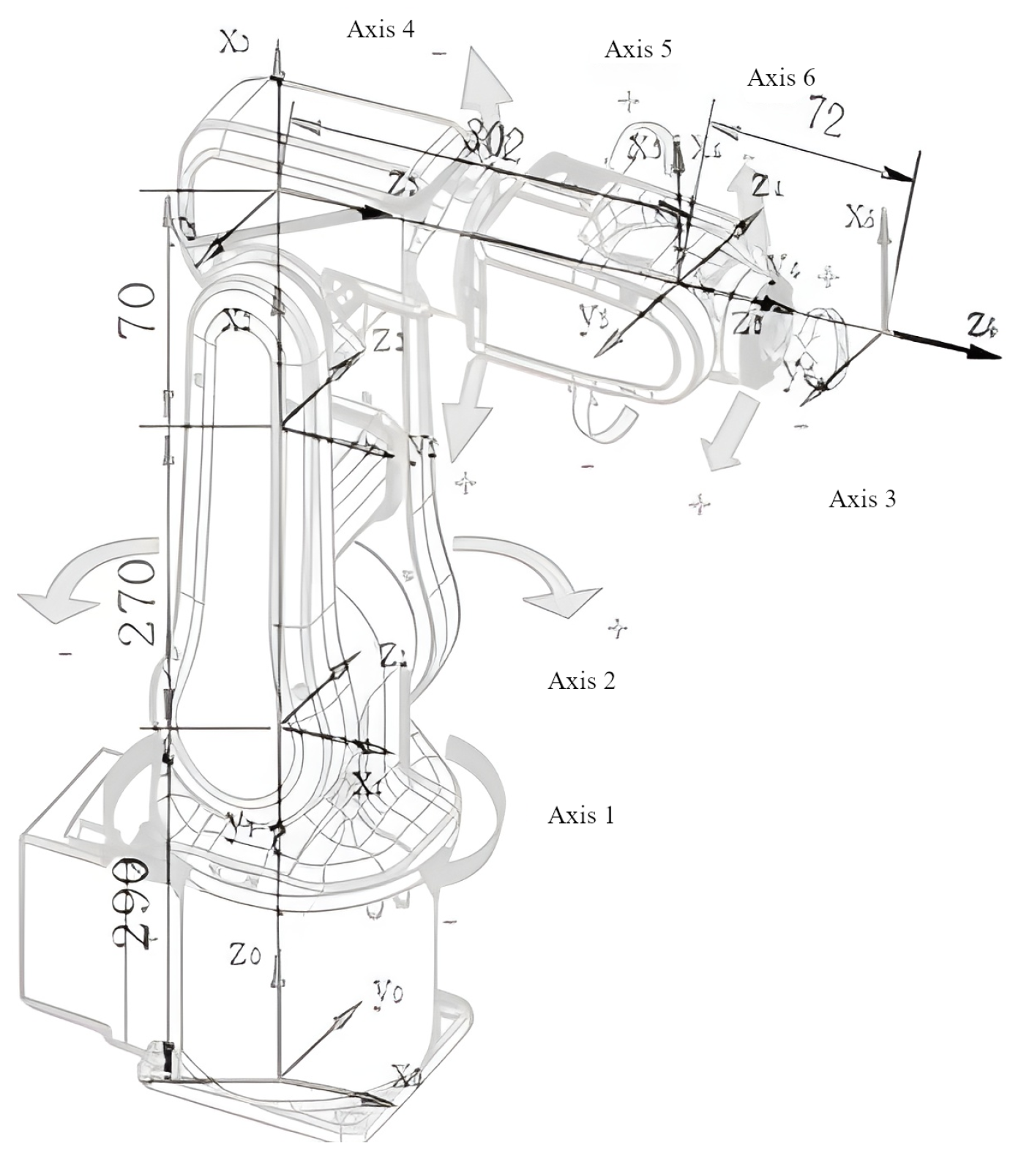




| [rad] | d [mm] | a [mm] | [rad] |
|---|---|---|---|
| Population | Generations | Total Time [s] | Average Time per Generation [s] |
|---|---|---|---|
| 100 | 100 | 23.4 | 0.234 |
| 1000 | 50 | 119.5 | 2.39 |
| 10,000 | 20 | 403.4 | 20.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grenko, T.; Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Štifanić, D.; Štifanić, J.; Glučina, M.; Franović, B.; Car, Z. On the Use of a Genetic Algorithm for Determining Ho–Cook Coefficients in Continuous Path Planning of Industrial Robotic Manipulators. Machines 2023, 11, 167. https://doi.org/10.3390/machines11020167
Grenko T, Baressi Šegota S, Anđelić N, Lorencin I, Štifanić D, Štifanić J, Glučina M, Franović B, Car Z. On the Use of a Genetic Algorithm for Determining Ho–Cook Coefficients in Continuous Path Planning of Industrial Robotic Manipulators. Machines. 2023; 11(2):167. https://doi.org/10.3390/machines11020167
Chicago/Turabian StyleGrenko, Teodor, Sandi Baressi Šegota, Nikola Anđelić, Ivan Lorencin, Daniel Štifanić, Jelena Štifanić, Matko Glučina, Borna Franović, and Zlatan Car. 2023. "On the Use of a Genetic Algorithm for Determining Ho–Cook Coefficients in Continuous Path Planning of Industrial Robotic Manipulators" Machines 11, no. 2: 167. https://doi.org/10.3390/machines11020167
APA StyleGrenko, T., Baressi Šegota, S., Anđelić, N., Lorencin, I., Štifanić, D., Štifanić, J., Glučina, M., Franović, B., & Car, Z. (2023). On the Use of a Genetic Algorithm for Determining Ho–Cook Coefficients in Continuous Path Planning of Industrial Robotic Manipulators. Machines, 11(2), 167. https://doi.org/10.3390/machines11020167













