Experimental Study of Robotic Polishing Process for Complex Violin Surface
Abstract
1. Introduction
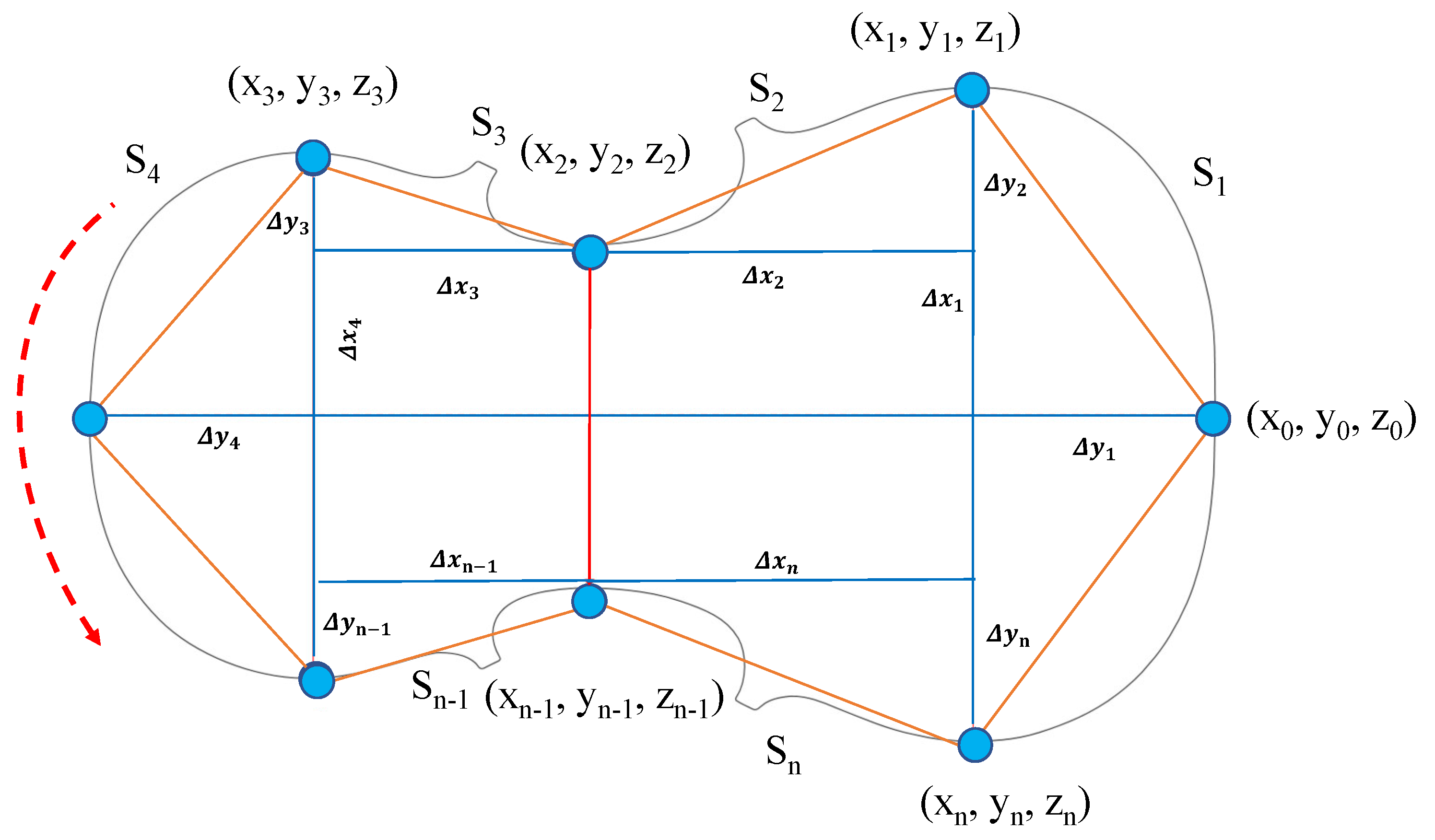
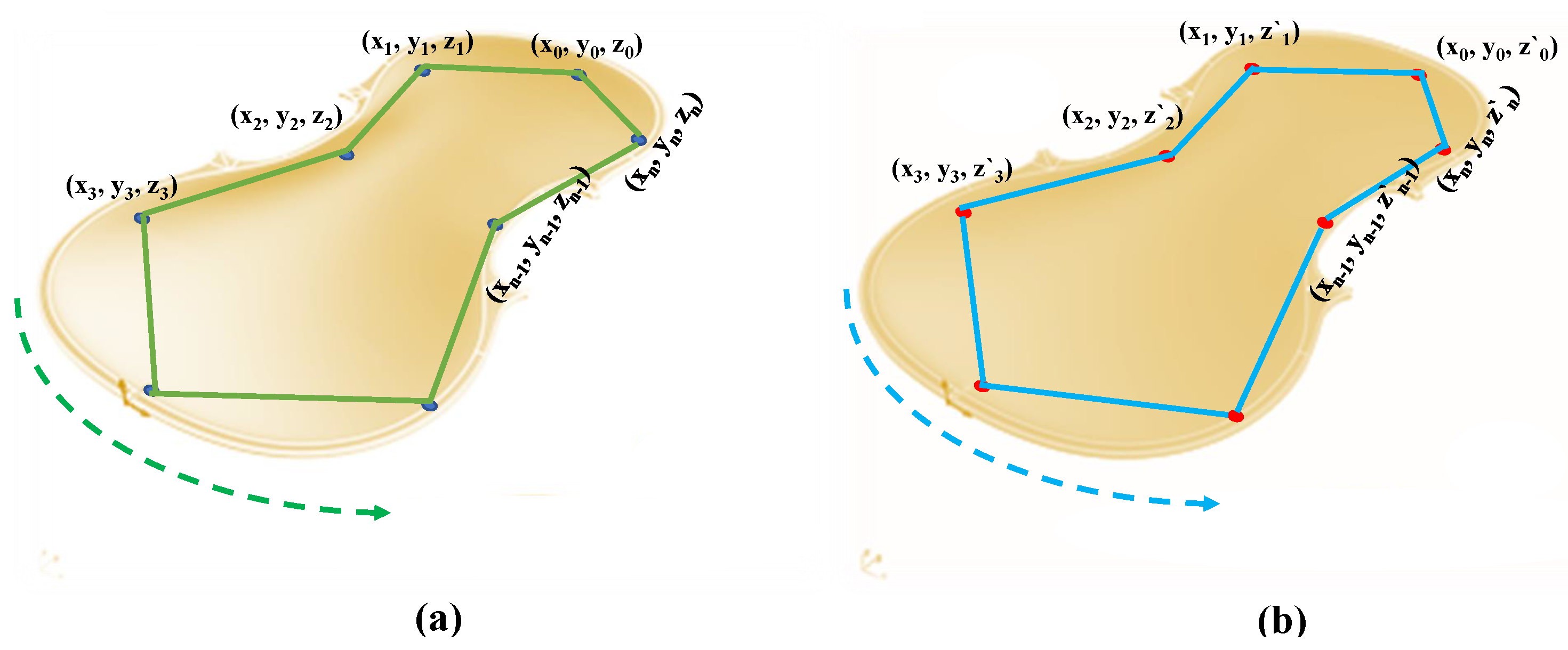
2. Smooth Polishing Path
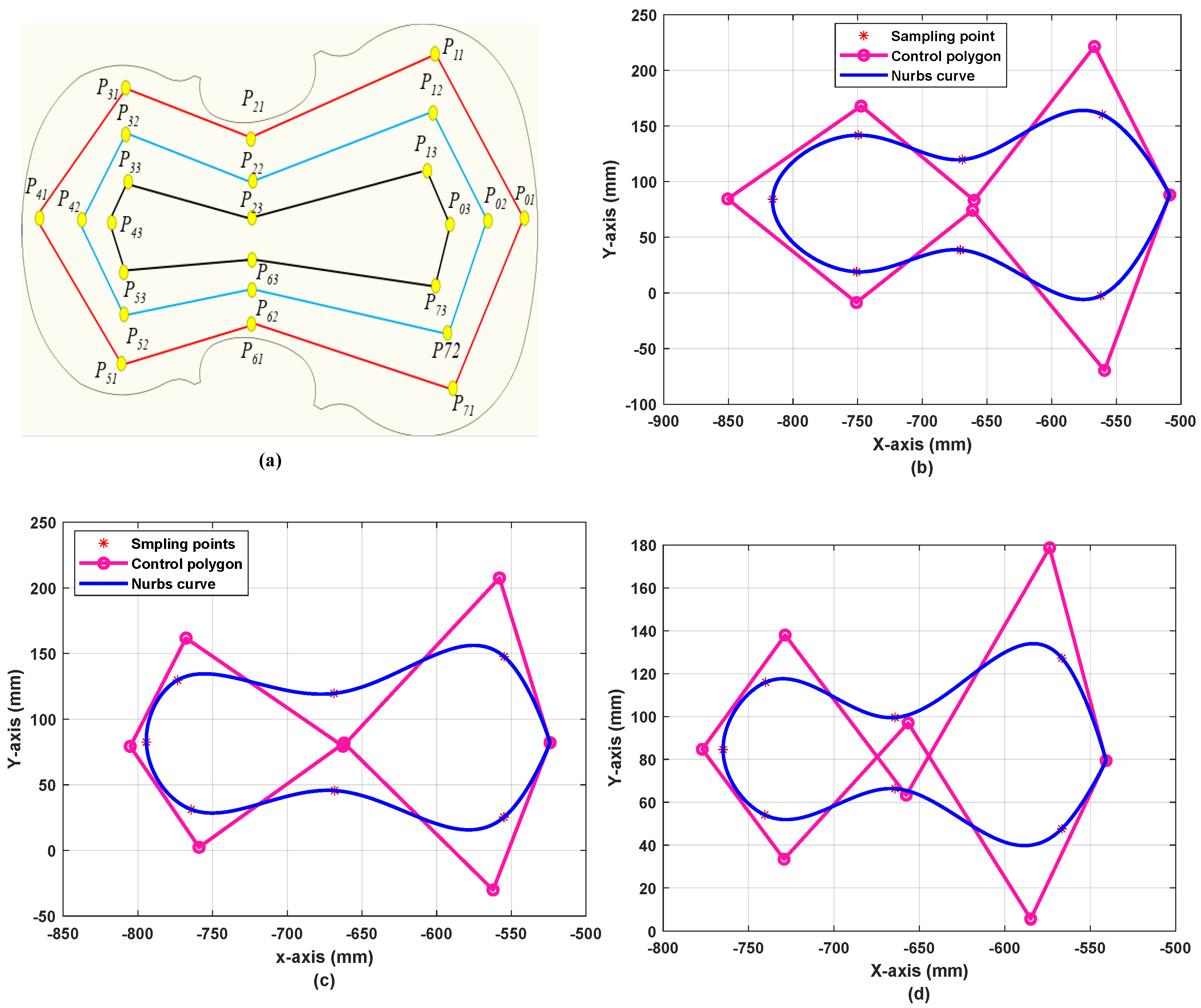
2.1. Nurbs Interpolation Curve
2.1.1. S-Curve Velocity Planning
2.1.2. S-Shape Speed Curve Algorithm Steps
- First, the total displacement between any two points according to [42] should be calculated bywhere h is the total displacement, which is equal to . From Equation (6), the peak velocity can be described asIn this casewhen is actually reached and maintained during the constant velocity phase, ; otherwise, , where according to [42] can be described as
- Next, we calculate the length of the acceleration/deceleration periods and total time; so, in the case of ; then,
- Then, we determine the formula of each stage of the S-shaped speed curve as
2.2. Quaternion Pose Squad Interpolation Method
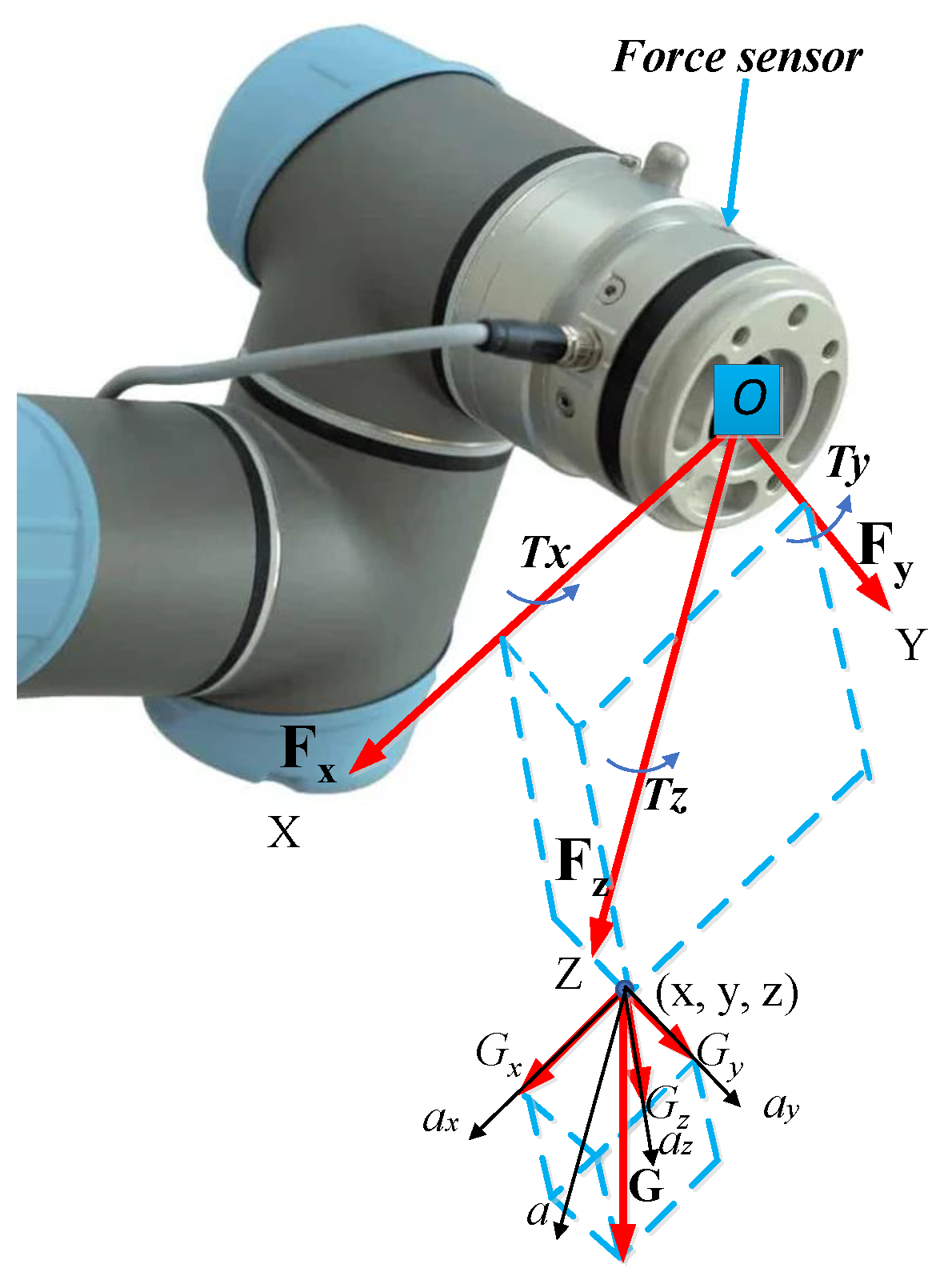
3. Admittance Force Control Method with Gravity Compensation
3.1. Controlled Contact Force
3.2. Gravity Compensation
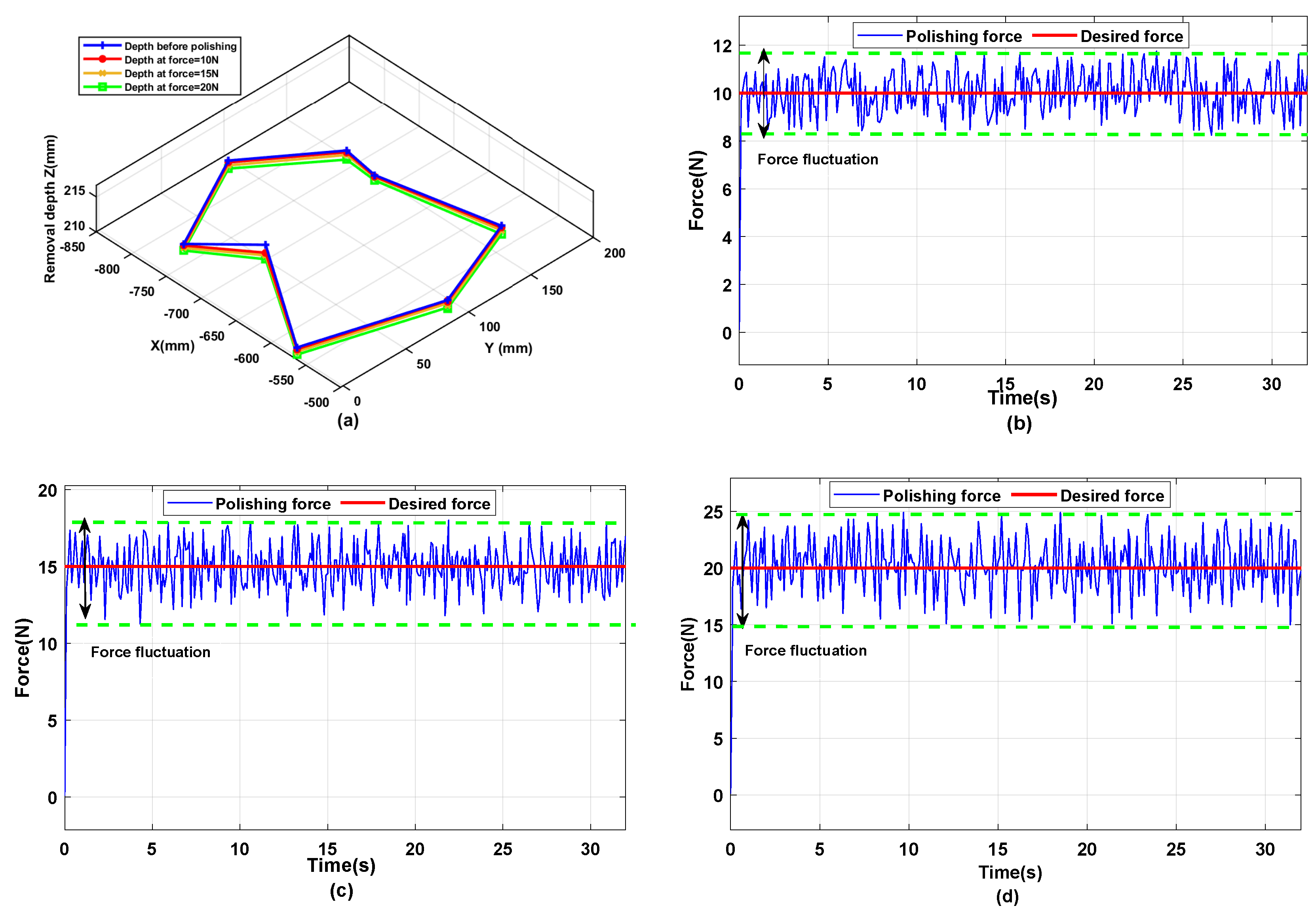
4. Removal Depth
Removal Depth of Violin Surface
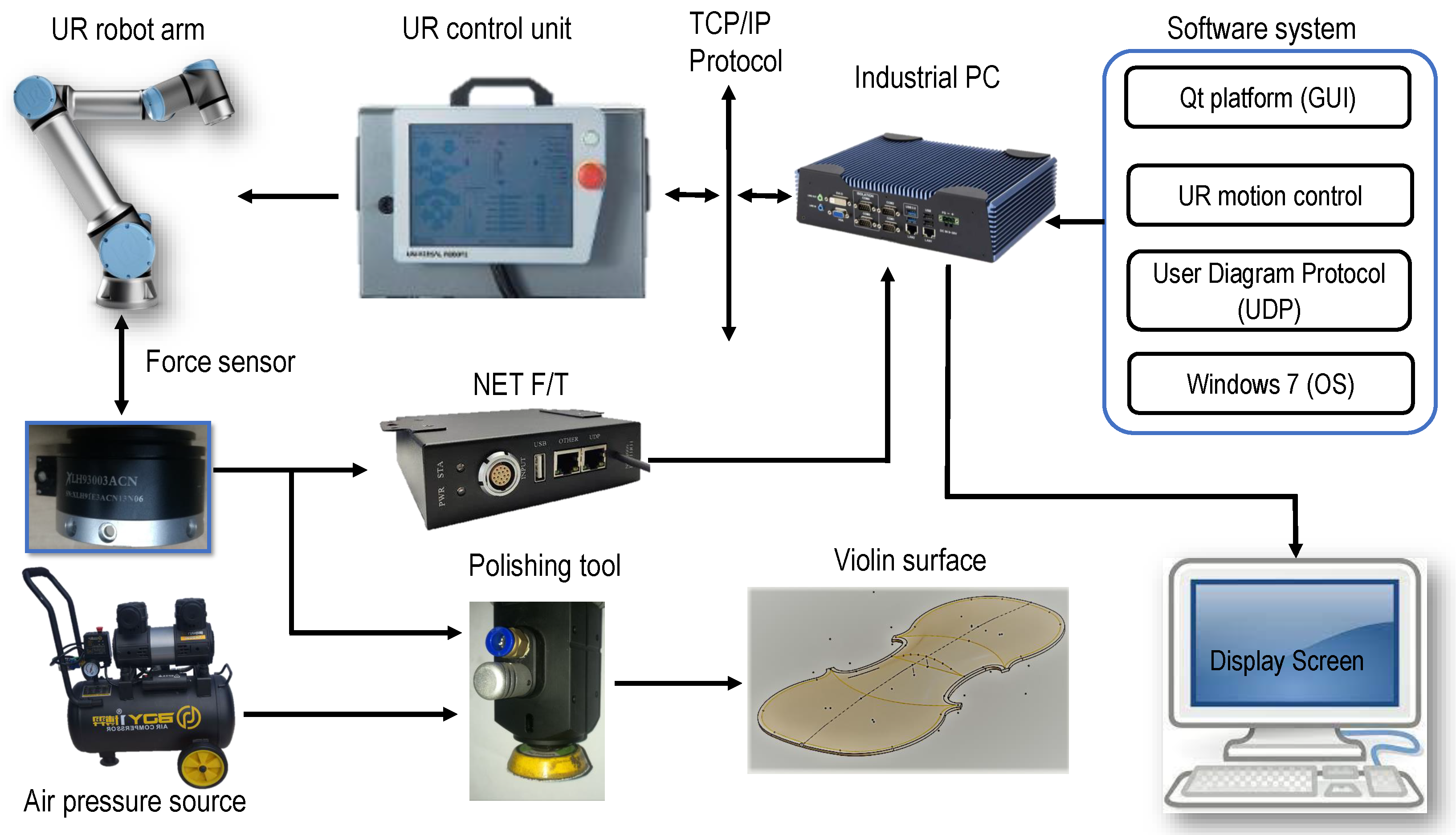
5. Experimental Study
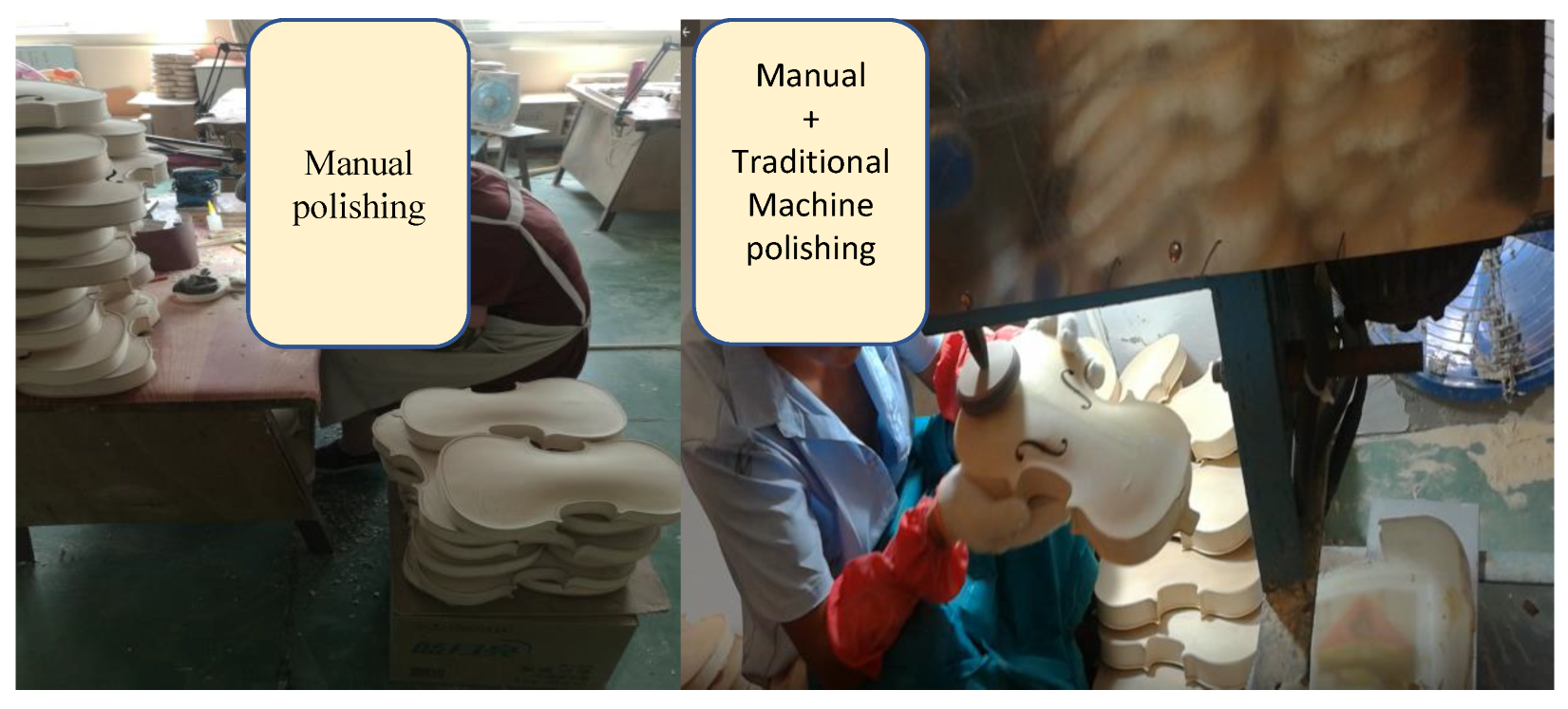
5.1. Experimental Setup
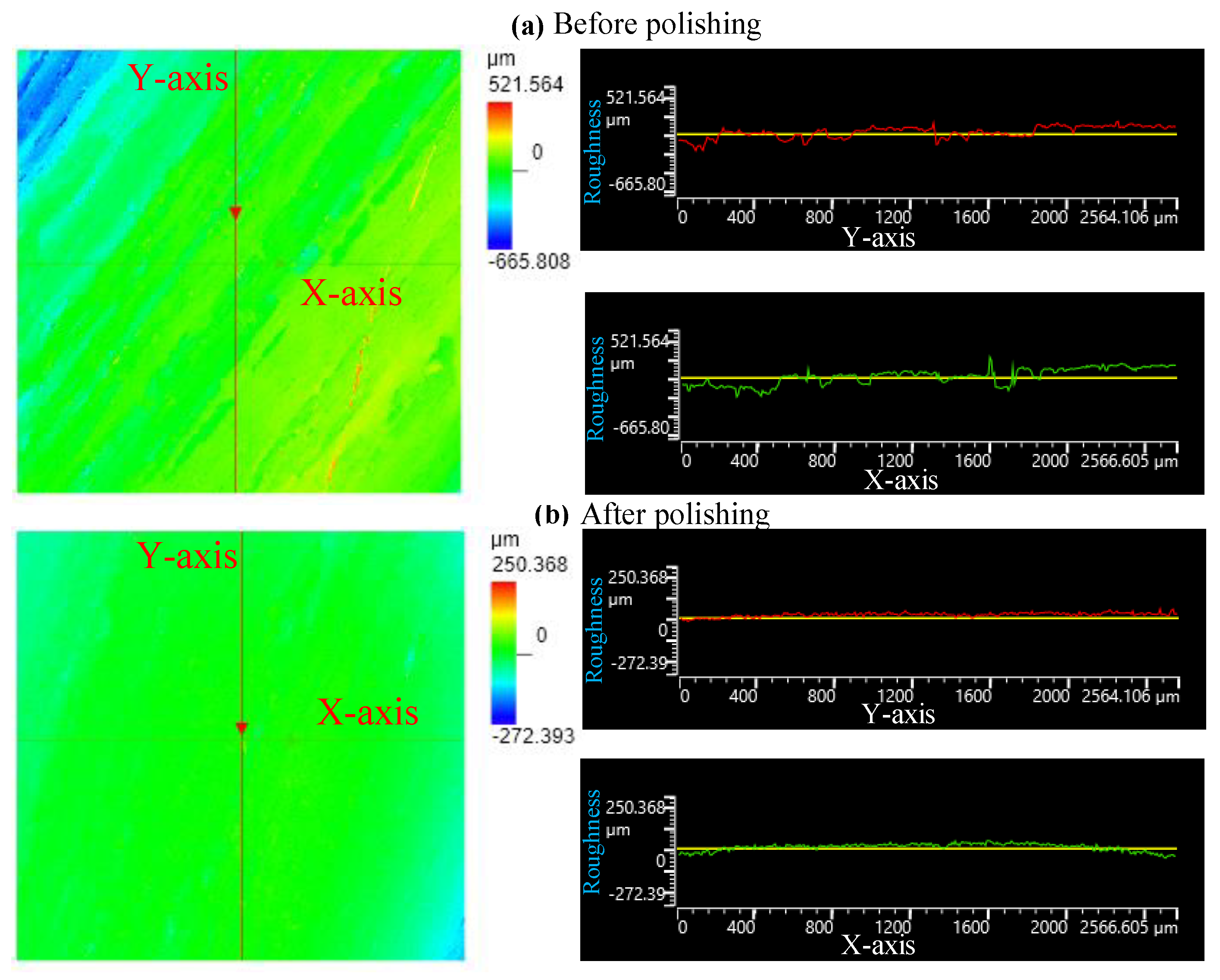
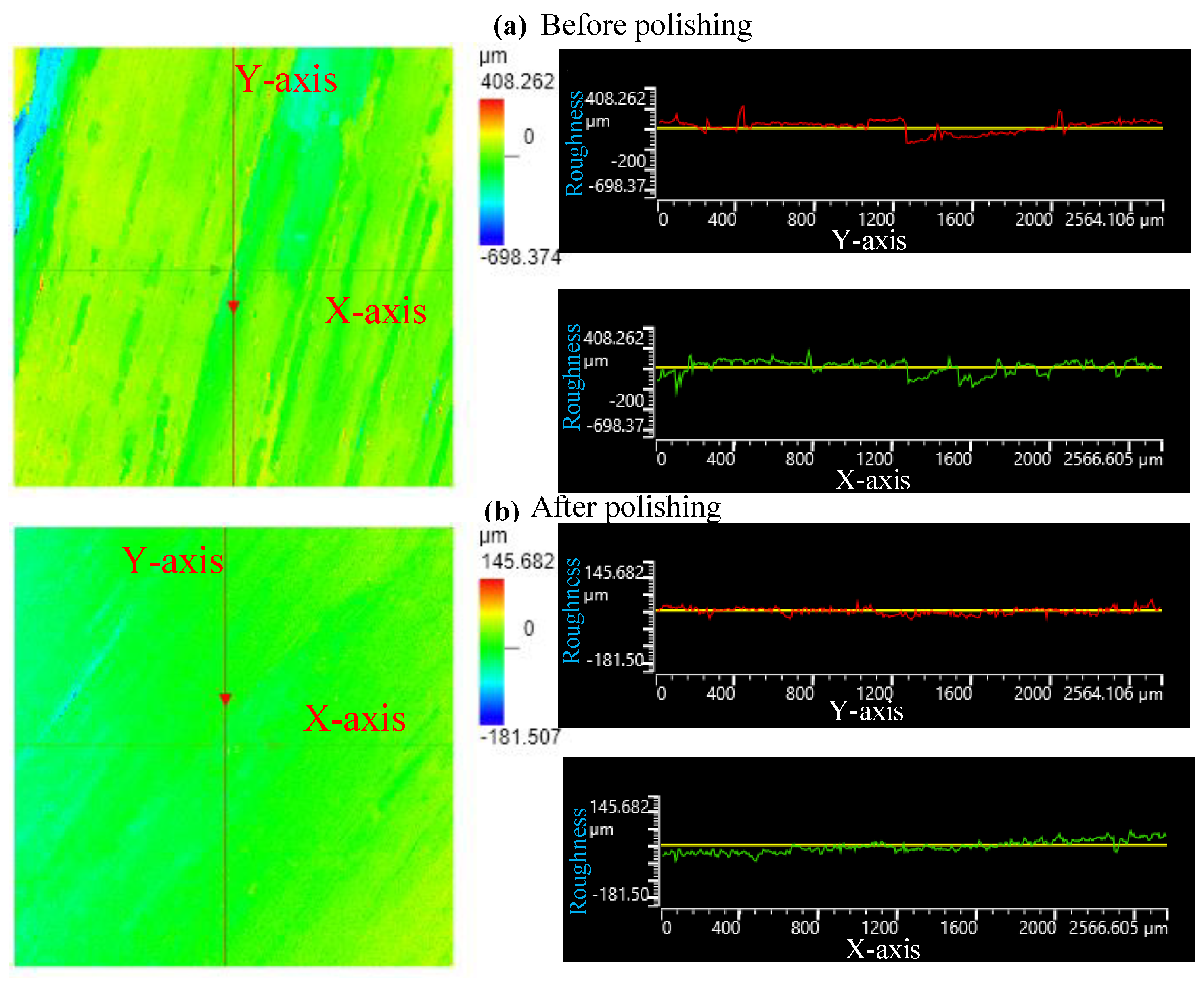
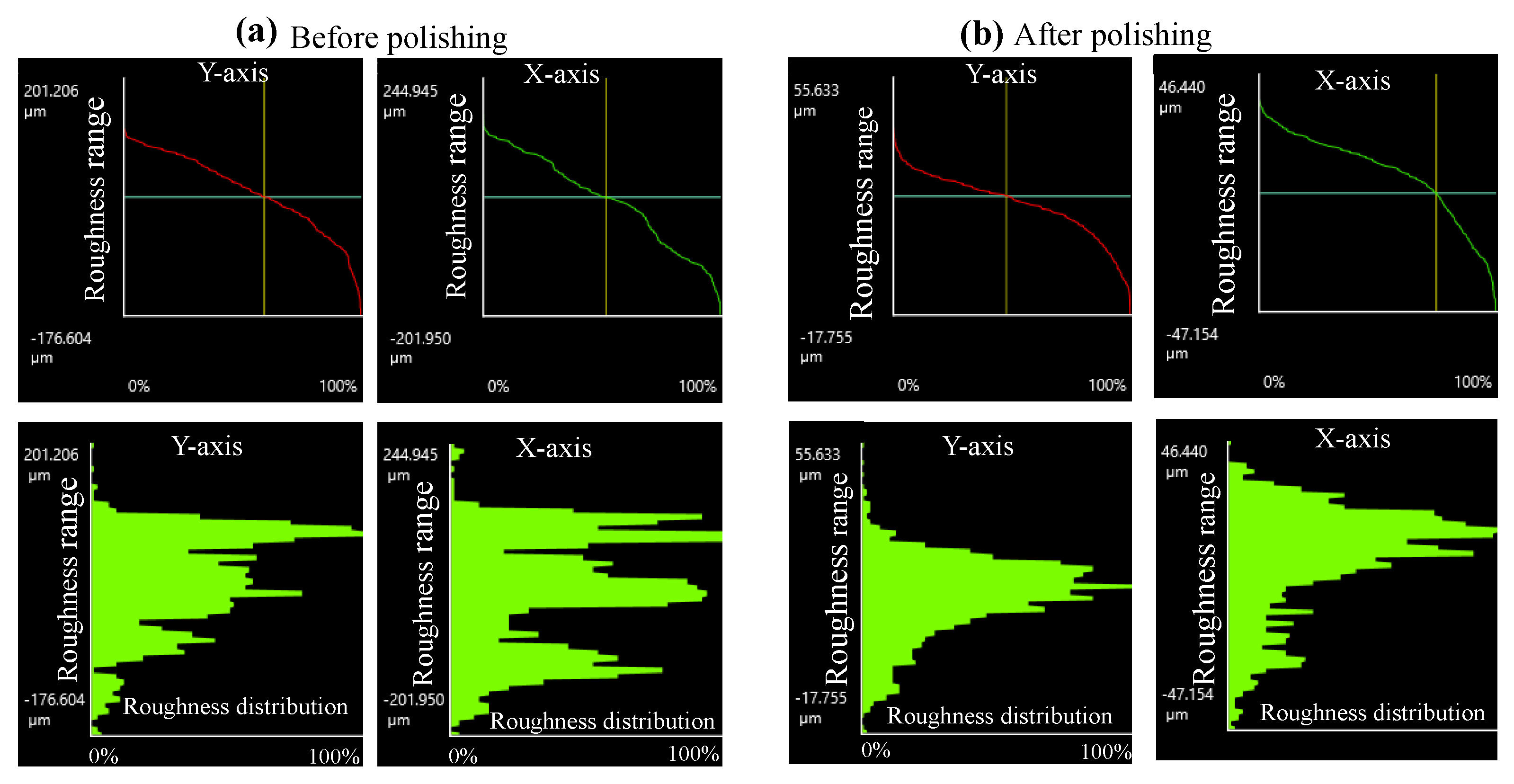
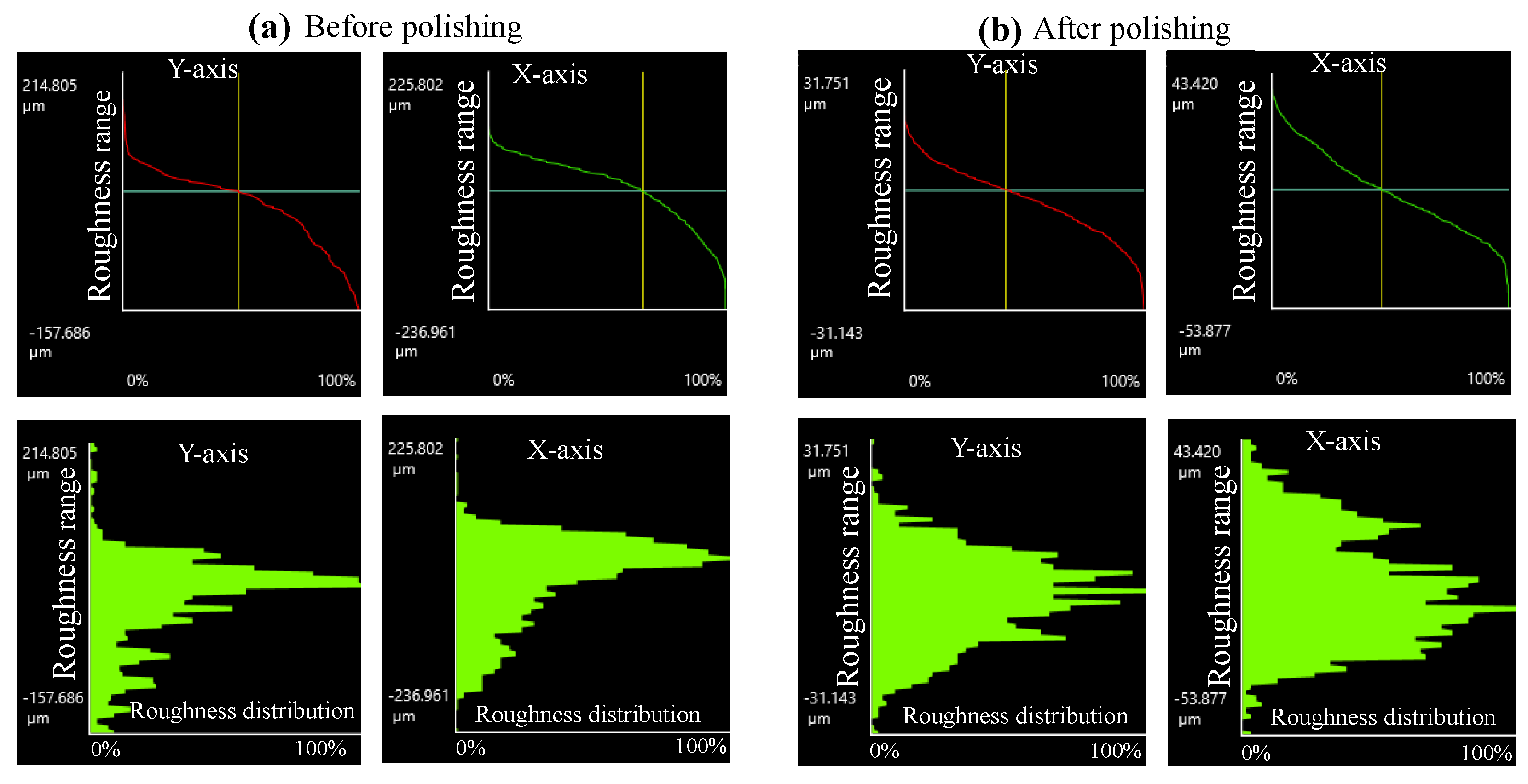
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Guan, Y.; Chen, H.; Wang, B.; Zhang, T.; Liu, X.; Hong, J.; Wang, D.; Zhang, H. A high-bandwidth end-effector with active force control for robotic polishing. IEEE Access 2020, 8, 169122–169135. [Google Scholar] [CrossRef]
- Mohsin, I.; He, K.; Li, Z.; Zhang, F.; Du, R. Optimization of the polishing efficiency and torque by using Taguchi method and ANOVA in robotic polishing. Appl. Sci. 2020, 10, 824. [Google Scholar] [CrossRef]
- Xie, X.; Sun, L. Force control based robotic grinding system and application. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 2552–2555. [Google Scholar]
- Lin, W.; Xu, P.; Li, B.; Yang, X. Path planning of mechanical polishing process for freeform surface with a small polishing tool. Robot. Biomim. 2014, 1, 24. [Google Scholar] [CrossRef]
- yczkowska-Widłak, E.; Lochyński, P.; Nawrat, G. Electrochemical polishing of austenitic stainless steels. Materials 2020, 13, 2557. [Google Scholar] [CrossRef] [PubMed]
- Mohammad, A.E.K.; Hong, J.; Wang, D.; Guan, Y. Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications. Robot. Comput.-Integr. Manuf. 2019, 55, 65–75. [Google Scholar]
- Cui, Z.; Meng, F.; Liang, Y.; Zhang, C.; Wang, Z.; Qu, S.; Yu, T.; Zhao, J. Sub-regional polishing and machining trajectory selection of complex surface based on K9 optical glass. J. Mater. Process. Technol. 2022, 304, 117563. [Google Scholar] [CrossRef]
- Su, J.B.; Liao, H.Y.; Su, Q.S. The current status and development trend in research of robotic polishing system for die and mould. Moju Gongye (Die Mould. Ind.) 2012, 38, 63–66. [Google Scholar]
- Tian, F.; Lv, C.; Li, Z.; Liu, G. Modeling and control of robotic automatic polishing for curved surfaces. CIRP J. Manuf. Sci. Technol. 2016, 14, 55–64. [Google Scholar] [CrossRef]
- Feng, D.; Sun, Y.; Du, H. Investigations on the automatic precision polishing of curved surfaces using a five-axis machining centre. Int. J. Adv. Manuf. Technol. 2014, 72, 1625–1637. [Google Scholar] [CrossRef]
- Kalt, E.; Monfared, R.; Jackson, M. Towards an automated polishing system: Capturing manual polishing operations. Int. J. Res. Eng. Technol. 2016, 5, 182–192. [Google Scholar]
- Liao, L.; Xi, F. A linearized model for control of automated polishing process. In Proceedings of the 2005 IEEE Conference on Control Applications, Toronto, ON, Canada, 28–31 August 2005; pp. 986–991. [Google Scholar]
- Fan, C.; Hong, G.S.; Zhao, J.; Zhang, L.; Zhao, J.; Sun, L. The integral sliding mode control of a pneumatic force servo for the polishing process. Precis. Eng. 2019, 55, 154–170. [Google Scholar] [CrossRef]
- Márquez, J.; Pérez, J.; Rıos, J.; Vizán, A. Process modeling for robotic polishing. J. Mater. Process. Technol. 2005, 159, 69–82. [Google Scholar] [CrossRef]
- Kharidege, A.; Ting, D.T.; Yajun, Z. A practical approach for automated polishing system of free-form surface path generation based on industrial arm robot. Int. J. Adv. Manuf. Technol. 2017, 93, 3921–3934. [Google Scholar] [CrossRef]
- Ye, J.; Niu, Z.; Zhang, X.; Wang, W.; Xu, M. In-situ deflectometic measurement of transparent optics in precision robotic polishing. Precis. Eng. 2020, 64, 63–69. [Google Scholar] [CrossRef]
- Dong, J.; Shi, J.; Liu, C.; Yu, T. Research of pneumatic polishing force control system based on high speed on/off with PWM controlling. Robot. Comput.-Integr. Manuf. 2021, 70, 102133. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, W.; Chen, Y.; Xu, M. In-Situ Inspection for Robotic Polishing of Complex Optics. Int. J. Robot. Autom. Technol. 2022, 9, 26–32. [Google Scholar] [CrossRef]
- Ge, J.; Deng, Z.; Li, Z.; Li, W.; Lv, L.; Liu, T. Robot welding seam online grinding system based on laser vision guidance. Int. J. Adv. Manuf. Technol. 2021, 116, 1737–1749. [Google Scholar] [CrossRef]
- Li, J.; Zhang, T.; Liu, X.; Guan, Y.; Wang, D. A survey of robotic polishing. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2125–2132. [Google Scholar]
- Zhu, D.; Feng, X.; Xu, X.; Yang, Z.; Li, W.; Yan, S.; Ding, H. Robotic grinding of complex components: A step towards efficient and intelligent machining—Challenges, solutions, and applications. Robot. Comput.-Integr. Manuf. 2020, 65, 101908. [Google Scholar] [CrossRef]
- Mohammad, A.E.K.; Wang, D. A novel mechatronics design of an electrochemical mechanical end-effector for robotic-based surface polishing. In Proceedings of the 2015 IEEE/SICE International Symposium on System Integration (SII), Nagoya, Japan, 11–13 December 2015; pp. 127–133. [Google Scholar]
- Xiao, G.; Huang, Y.; Yin, J. An integrated polishing method for compressor blade surfaces. Int. J. Adv. Manuf. Technol. 2017, 88, 1723–1733. [Google Scholar] [CrossRef]
- Zhu, D.; Xu, X.; Yang, Z.; Zhuang, K.; Yan, S.; Ding, H. Analysis and assessment of robotic belt grinding mechanisms by force modeling and force control experiments. Tribol. Int. 2018, 120, 93–98. [Google Scholar] [CrossRef]
- Lv, Y.; Peng, Z.; Qu, C.; Zhu, D. An adaptive trajectory planning algorithm for robotic belt grinding of blade leading and trailing edges based on material removal profile model. Robot. Comput.-Integr. Manuf. 2020, 66, 101987. [Google Scholar] [CrossRef]
- Wahballa, H.; Duan, J.; Dai, Z. Constant force tracking using online stiffness and reverse damping force of variable impedance controller for robotic polishing. Int. J. Adv. Manuf. Technol. 2022, 121, 5855–5872. [Google Scholar] [CrossRef]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robot. Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, H.; Xie, Q.; Li, X.; Ding, H. A Path Planning Method Under Constant Contact Force for Robotic Belt Grinding. In Intelligent Robotics and Applications, Proceedings of the 12th International Conference, ICIRA 2019, Shenyang, China, 8–11 August 2019; Springer: Cham, Switzerland, 2019; pp. 35–49. [Google Scholar]
- Zhang, J.; Wang, H.; Kumar, A.S.; Jin, M. Experimental and theoretical study of internal finishing by a novel magnetically driven polishing tool. Int. J. Mach. Tools Manuf. 2020, 153, 103552. [Google Scholar] [CrossRef]
- Xiaohu, X.; Dahu, Z.; Zhang, H.; Sijie, Y.; Han, D. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades. Chin. J. Aeronaut. 2019, 32, 2368–2382. [Google Scholar]
- Mohsin, I.; He, K.; Li, Z.; Du, R. Path planning under force control in robotic polishing of the complex curved surfaces. Appl. Sci. 2019, 9, 5489. [Google Scholar] [CrossRef]
- Zhu, D.; Luo, S.; Yang, L.; Chen, W.; Yan, S.; Ding, H. On energetic assessment of cutting mechanisms in robot-assisted belt grinding of titanium alloys. Tribol. Int. 2015, 90, 55–59. [Google Scholar] [CrossRef]
- Yang, Y.; Ruoqi, W.; Yingpeng, W.; Yuwen, S. Contact force controlled robotic polishing for complex PMMA parts with an active end-effector. J. Adv. Manuf. Sci. Technol. 2021, 1, 2021012. [Google Scholar]
- Tian, F.; Li, Z.; Lv, C.; Liu, G. Polishing pressure investigations of robot automatic polishing on curved surfaces. Int. J. Adv. Manuf. Technol. 2016, 87, 639–646. [Google Scholar] [CrossRef]
- Ding, Y.; Min, X.; Fu, W.; Liang, Z. Research and application on force control of industrial robot polishing concave curved surfaces. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1674–1686. [Google Scholar] [CrossRef]
- Feng-yun, L.; Tian-sheng, L. Development of a robot system for complex surfaces polishing based on CL data. Int. J. Adv. Manuf. Technol. 2005, 26, 1132–1137. [Google Scholar] [CrossRef]
- Hähnel, S.; Pini, F.; Leali, F.; Dambon, O.; Bergs, T.; Bletek, T. Reconfigurable robotic solution for effective finishing of complex surfaces. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Turin, Italy, 4–7 September 2018; Volume 1, pp. 1285–1290. [Google Scholar]
- Huang, T.; Li, C.; Wang, Z.; Liu, Y.; Chen, G. A flexible system of complex surface polishing based on the analysis of the contact force and path research. In Proceedings of the 2016 IEEE Workshop on Advanced Robotics and Its Social Impacts (ARSO), Shanghai, China, 8–10 July 2016; pp. 289–293. [Google Scholar]
- Mohsin, I.; He, K.; Du, R. Robotic Polishing of Free-Form Surfaces with Controlled Force and Effective Path Planning. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; Volume 52064, p. V005T07A003. [Google Scholar]
- Ochoa, H.; Cortesão, R. Impedance control architecture for robotic-assisted mold polishing based on human demonstration. IEEE Trans. Ind. Electron. 2021, 69, 3822–3830. [Google Scholar] [CrossRef]
- Li, Y. Arc-Length Parameterized NURBS Tool Path Generation and Velocity Profile Planning for Accurate 3-Axis Curve Milling. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2012. [Google Scholar]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Amersdorfer, M.; Kappey, J.; Meurer, T. Real-time freeform surface and path tracking for force controlled robotic tooling applications. Robot. Comput.-Integr. Manuf. 2020, 65, 101955. [Google Scholar] [CrossRef]
- Duan, J.; Liu, Z.; Bin, Y.; Cui, K.; Dai, Z. Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach. Sensors 2022, 22, 439. [Google Scholar] [CrossRef]





| Point | Point | Point | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| P01 | −508.72 | 88.12 | 212.35 | P02 | −524.10 | 82.09 | 219.05 | P03 | −546.72 | 79.40 | 221.70 |
| P11 | −560.85 | 160.33 | 212.01 | P12 | −554.81 | 147.57 | 218.48 | P13 | −556.53 | 120.20 | 221.44 |
| P21 | −669.15 | 119.84 | 216.67 | P22 | −663.76 | 119.60 | 222.83 | P23 | −664.31 | −99.54 | 226.69 |
| P31 | −749.56 | 141.78 | 212.74 | P32 | −773.46 | 129.72 | 219.33 | P33 | −767.00 | 115.97 | 221.54 |
| P41 | −815.76 | 84.26 | 213.18 | P42 | −794.32 | 82.50 | 220.70 | P43 | −764.94 | 84.60 | 223.66 |
| P51 | −762.77 | 19.06 | 211.56 | P52 | −764.33 | 31.20 | 217.62 | P53 | −750.53 | 54.10 | 222.15 |
| P61 | −680.64 | 38.68 | 214.55 | P62 | −668.29 | 45.57 | 220.59 | P63 | −7663.47 | 66.33 | 226.12 |
| P71 | −561.96 | −2.43 | 211.79 | P72 | −546.95 | 25.30 | 218.13 | P7 | −542.65 | 47.62 | 219.74 |
| P81 | −508.72 | 88.12 | 212.52 | P82 | −524.10 | 82.09 | 219.05 | P83 | −546.72 | 79.40 | 221.70 |
| Point | ||||||
|---|---|---|---|---|---|---|
| P01 | 212.11 | 0.24 | 211.87 | 0.36 | 211.15 | 0.72 |
| P11 | 211.76 | 0.25 | 211.36 | 0.40 | 210.82 | 0.54 |
| P21 | 216.45 | 0.22 | 216.17 | 0.28 | 215.72 | 0.45 |
| P31 | 212.50 | 0.24 | 212.11 | 0.39 | 211.45 | 0.66 |
| P41 | 212.92 | 0.26 | 212.50 | 0.42 | 212.04 | 0.46 |
| P51 | 211.33 | 0.23 | 210.98 | 0.35 | 210.61 | 0.37 |
| P61 | 214.34 | 0.21 | 213.97 | 0.37 | 213.42 | 0.55 |
| P71 | 211.54 | 0.25 | 211.19 | 0.35 | 210.77 | 0.42 |
| P81 | 212.26 | 0.26 | 211.90 | 0.36 | 211.30 | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahballa, H.; Duan, J.; Wang, W.; Dai, Z. Experimental Study of Robotic Polishing Process for Complex Violin Surface. Machines 2023, 11, 147. https://doi.org/10.3390/machines11020147
Wahballa H, Duan J, Wang W, Dai Z. Experimental Study of Robotic Polishing Process for Complex Violin Surface. Machines. 2023; 11(2):147. https://doi.org/10.3390/machines11020147
Chicago/Turabian StyleWahballa, Hosham, Jinjun Duan, Wenlong Wang, and Zhendong Dai. 2023. "Experimental Study of Robotic Polishing Process for Complex Violin Surface" Machines 11, no. 2: 147. https://doi.org/10.3390/machines11020147
APA StyleWahballa, H., Duan, J., Wang, W., & Dai, Z. (2023). Experimental Study of Robotic Polishing Process for Complex Violin Surface. Machines, 11(2), 147. https://doi.org/10.3390/machines11020147








