Abstract
Excavation load prediction is of great importance for the prior design and latter performance evaluation of tunnel boring machines (TBMs). In this paper, an improved load prediction model is developed based on classical Colorado school of mines model for TBMs equipped with constant cross-sectional disc cutters. The typical structure and principle are introduced to predict the single cutter force, and the total cutter group load is calculated by defining the equivalent diameter and cutter spacing. Subsequently, the improved model of a more brief and acceptable type is established via summation. Some novel performance indexes, including the reformed field penetration index, torque/thrust penetration index, and specific energy are, respectively, derived in formulaic form. By field data verification in the borehole zones of two cases, the proposed model is proven to be more accurate in the total load prediction. The single-factor regression results show that the reformed field penetration index reveals the nonlinear relationship between TBM load and penetration rate, and the torque/thrust penetration index is a new TBM inherent index to evaluate the working conditions. Specific energy, used to evaluate the excavation efficiency, is positive with rock strength and proved negative with penetration rate via a normalization analysis. Finally, suggestions on the cutter group configuration against abominable stratum are discussed.
1. Introduction
Because of the advantages of safety, efficiency and low interference to the surrounding environment, full-face tunnel boring machines (TBMs) have been applied to various rock tunnel projects, such as water delivery, transportation and mine tunnelling [1,2]. However, TBM is particularly sensitive to geological conditions during the excavation. A slight change in the geological conditions may result in a dramatic decline in the TBM’s performance [3]. Hence, proper operation planning of TBMs should be carried out based on an excavation performance prediction and monitoring during parameter configuration and operational processing. Specifically, for a TBM equipped with disc cutters to break rock, a load model related to the TBM configuration and excavation parameters with corresponding stratum conditions is at the heart of excavation predictions. In addition, the load thrust force and torque are also the most important performance monitoring indexes for TBM drivers.
In self-stable hard rock stratum, the extrusion and shear action of the cutterhead is the main source of thrust and torque load, and rock fragmentation under cutter press is the theoretical basis. Plenty of work has been conducted to investigate the interactions between rock and the cutter, and various estimation models have been developed [4], which can be categorized into two main groups. Firstly, the fully empirical type, represented by the classical Norwegian University of Science and Technology (NTNU) model obtained by regression analysis and is still developing with new projects [5]. Secondly, the empirical–theoretical type [6], represented by the Colorado school of mines (CSM) model based on the linear cutting test and impact power, summarized by the regression method [7]. The NTNU model may fit data from similar sites well and is well-accepted by drivers; however, its reliance on historical data has limited its generalization forecasting abilities in new projects. Oppositely, the CSM model studies the specific interaction mechanisms between rock properties and the cutter group configuration (CGC), and multiple-target regression is carried out on lab test data with high reliability. The CSM model could be suitable for different stratum and CGC conditions, impelling it as the most popular model of TBM load and performance prognosis [8,9,10]. However, the CSM model has its disadvantages in its fast application: the impact of the penetration rate (PR) is not evidently addressed and the calculation form is complex. Furthermore, the CSM model does not present a direct vision between the TBM total load and configuration parameters, much less the principle for the TBM design and operation, and until now it is still an experience-guided strategy.
With the development of various machine learning algorithms, numerous data-driven models have been established for load and performance predictions. The random forest-based predictors for the driving forces of earth pressure balance shield tunnel boring machines [11] were proposed to predict the thrust and torque in a soil-rock mixed-face ground with more accurate results. The adaptive neuro-fuzzy inference system (ANFIS) and support vector regression (SVR) [12] were employed to predict the TBM advance rate, and the results of the analysis showed that the artificial intelligence-based methods can effectively be implemented for the prediction of TBM performance. A dynamic load prediction approach [13] was proposed based on heterogeneous in situ data and a data-driven technique. A long short-term memory model [14] was developed and the variation in the total thrust and cutterhead torque with various geological conditions can be well reflected. The studies mentioned above demonstrate how data-driven technology can be used to develop and analyze intricate engineering systems. However, the current load modeling approach, which relies on machine learning and engineering data is still essentially an “end-to-end” black box training approach [15,16]. It would help to make prediction models more workable and serve as a guide for construction excavation if it were possible to generate an explicit model that could accurately depict the causal relationship between parameters under the assumption of a particular level of prediction accuracy.
TBM performance evaluation is closely related to load prediction. By using a reliable load prediction and proper performance indexes, drivers can evaluate the goodness of the current TBM working condition and adjust the operating parameters accordingly. Relationships between the load and operating parameters have been investigated by various researchers. For example, the field penetration index (FPI) was first proposed by Nelson and aimed to eliminate the effect of PR under specific ground condition [17]. The torque/thrust index (TFI) represented that the ratio of torque to thrust was proportional with PR to the power of 0.5 via statistical analysis [18]. However, these indicators are mostly defined by experience, and the correlation between the parameters may be improper. On the other hand, the energy consumed in the TBM tunneling process was investigated to improve the excavation efficiency. The specific energy (SE) is defined as the energy cost of thrust and torque to break a unit volume of rock and is an important index of excavation efficiency. Numerous physical experiments have been conducted for SE optimization studies [19,20]. However, most of them are based on a single cutter, making the results difficult to represent the full-scale operation of TBM cutterheads. The rock property and TBM configuration are hardly taken into consideration by the empirical or statistical models based on case study [21], which are only applicable to projects that are identical.
To address these problems, a novel improved TBM load prediction (ILP) model is established in this paper based on the classical CSM model, and some reformed indexes for performance prediction and evaluation are proposed. These improvements are easier for drivers to use and interpret, and enable field personnel to better monitor and manage a TBM, as well as reduce the maintenance time and costs. The remainder of this paper is organized as follows. The proposed ILP model and performance indexes are derived in Section 2. The accuracy of the proposed ILP model, feasibility and effectiveness of the indexes are validated in Section 3 with field data extracted from two TBM projects. Section 4 provides suggestions on the CGC in extreme stratums. Finally, conclusions are drawn in Section 5.
2. Methods
The whole load of a TBM working in hard rock consists of the thrust along the axial direction and the torque around the tunnel axis. Considering the rock–machine interaction, the thrust can be decomposed into the axial force of the cutter group, the frictional force between the equipment and rock, and the buildup force generated by the crushed surrounding rock on the cutterhead face. In addition, the torque includes the circumferential torque of the cutter group and the frictional moment. The above components show that the calculation of the cutter group force is key to the whole load prediction.
2.1. Improved Load Prediction Model Based on the Classical CSM Model
The CSM model has been widely used and its accuracy has been proven to be acceptable in numerous tunneling projects for its ability to adapt to different stratum and cutter specifications. In the CSM model, the axial force of the cutter group is the accumulation of the normal force of all cutters, and the circumferential torque is the accumulation of the product between the rolling force and the installation radius. Obviously, the force analysis of a single cutter is the basis for load prediction.
There exist two kinds of disc cutter geometry: V-shaped type and constant cross-section (CSS) type, the latter is mainly used in recent projects for its high tolerance against abrasion [22,23]. Figure 1 depicts the configuration of the whole cutterhead and the simplified assembly structure of a CSS disc cutter, where R is the cutter radius and T is the cutter tip width. The cutter ring is settled axially on the cutter seat, which is equipped on the cutter shaft through bearing pairs with rotational freedom, and the cutter shaft can be adjusted along the tunnel axis direction to be suitable for cutter rings of different radius and wear condition. It is worth noting that only the cutter ring interacts with the rock directly.
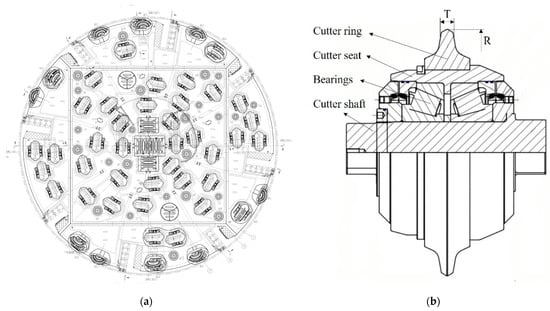
Figure 1.
(a) Configuration of the whole cutterhead; (b) simplified assembly structure of a constant cross-section disc cutter.
The CSM model assumes the existence of a circular crushed zone along the periphery of the cutter tip under the hydrostatic push force of the propelling cylinders, as shown in Figure 2.
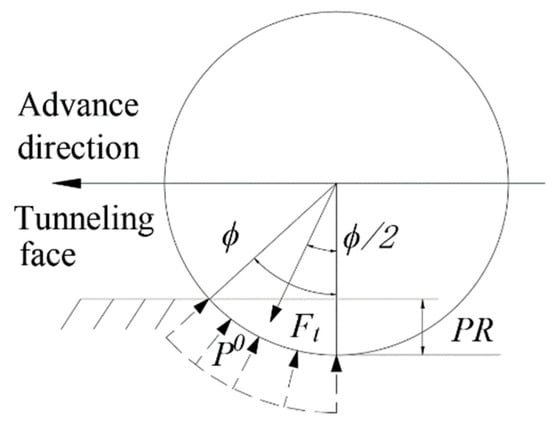
Figure 2.
Pressure distribution along the disc cutter periphery.
This pressure is supposed to be distributed uniformly within the crushed zone and the distribution region can be specified by angle ϕ, which is decided by the penetration rate p and R as:
and the total force (combination of rolling and normal force) is defined as:
where ψ is the pressure distribution function constant, which is typically valued between −0.2 to 0.2 and decreases with an increase in T; P0 is the basis pressure of the crushed zone and expressed in the following formula under the multi-factors nonlinear regression method [7]:
where σc and σt are the uniaxial compressive strength (UCS) and the tensile strength (TS) of the rock mass, respectively; C denotes the dimensionless parameter (approximately equals to 2.12); and S is the radial spacing between the adjacent disc cutters, as shown in Figure 3. Cutters on the cutterhead plane are classified into three types: center cutters in the central region, edge cutters in the transition area and face cutters between them in dominating amount. Commonly, cutters are located separately along concentric circles, and the edge and face cutters are always of the same scale, while the center cutter is of a smaller type and used in pairs.
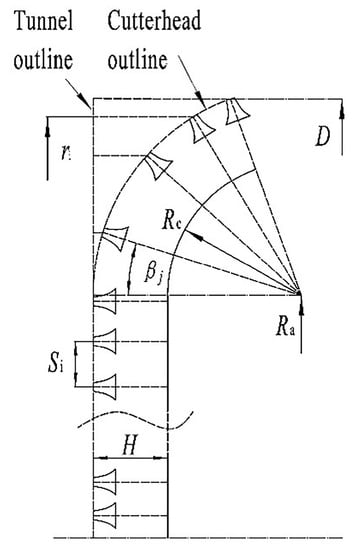
Figure 3.
Cutter distribution on the cutterhead plane.
For simplification, the cutter spacing of the ith face and center cutters can be defined as:
where ri is the installment radius of the ith cutter, nc and nf are the amount of center and face cutters, respectively.
For edge cutters, their cutter spacing should be the average value of the arc length between the ith cutter tip along the cutterhead outline, instead of the reflected distance on the tunnel outline in Figure 3, which is:
where ne is the amount of edge cutters, Rc is the radius of the transition curve at the edge of the cutterhead plane, and βi is the distribute angle of the ith cutter. Obviously, for the center and face cutters, βi = 0, and for edge cutters βi = arcsin((ri − Ra)/(Rc + H)), where H is the assembly height between the cutter tips and the cutterhead outline, and Ra is the radial position of the transition curve center.
For cutters in the transition positions of the three groups, their cutter spacing should be treated as the distance against the previous or next cutter of the same group.
The normal and rolling force can be derived by the orthogonal decomposition of Ft as:
The thrust and torque load (Fth, Tt) for a TBM can be calculated as:
where is the total normal force of all the cutters, is the total number of cutters; Fp is the build-up force with the crushed surrounding rock on the cutterhead face; is the frictional force between the base shield and the surrounding rock, us is the sliding friction coefficient, Gc is the gravity of the excavation part; is the frictional force between the other shield and the surrounding rock, Ftc is the force of the torque cylinders; is the friction between the rollers in subsequent equipment and the guideway, uh is the rolling friction coefficient, Gh is the gravity of the subsequent equipment; is the circumferential torque of all cutters; and Tp is the friction moment generated by Fp.
Combining Equations (6)–(9), the thrust and torque load for a TBM based on the CSM model can be represented as:
The above formula form is complex and difficult to be used by drivers, and the summation procedure is lengthy as the ϕ and β of each cutter are different, especially for the edge cutters. For further discussion, the impact of PR should be revealed first in Equation (1) by replacing the inverse trigonometric form. Note a TBM’s actual penetration in hard stratum, within 20 mm, is quite small in contrast to a cutter radius of no less than 216 mm (17 inch cutter). Based on the fundamental mathematical approximation:
The approximate form of ϕ can be specified as:
For PR within 20 mm and a 17 inch cutter, the simplification error ratio is less than 7 × 10−3. Subsequently, we can obtained the simplified new form of Equation (2) as:
and Equations (6) and (7) can be rewritten as:
Now the quantitative relationship between PR and cutter force is derived, together with the power of the cutter geometry and geographical parameters. The rolling force is independent from the cutter radius but is severely affected by PR, while the normal force is related with both the cutter radius and PR. Meanwhile, the geographical parameters, cutter spacing and tip thickness have the same impact power on the thrust force and torque.
As mentioned before, cutters of different groups have inconsistent spacing, radius, tip width and assemble angle, their quick summation still remains to be solved for their fast application. Note that the length of the cutterhead outline is the summation of the cutter spacing, and we define the equivalent diameter as:
where D is the TBM diameter, βmax is the position angle of the last edge cutter, and D is denoted as:
Obviously, De is larger than D, and the ratio diminishes with the increase in D as (Rc + H) and βmax are fixed value. In general, (Rc + H) = 0.5 m and βmax = 1.22. Subsequently, the average cutter spacing Sa can be described as:
To reveal the relationship between the load and parameters of a TBM in an easier and clearer manner, we propose an improved load prediction model (ILP). The model assumes that the cutter group consists of N face cutters with uniform forces and the same cutter spacing Sa, which means that and the equivalent installment radius . Thus, the total normal force and the circumferential torque of all the cutters can be converted to:
and the thrust and torque load of Equations (8) and (9) for the TBM can be specified as:
where is the total friction force as Fp and Tp are negligible in the case of stable surrounding rock. In contrast to the CSM model, the proposed ILP model is easier to understand, and the influence of the geographical condition, CGC, TBM diameter and PR is expressed in a more apparent manner. Moreover, Equations (22) and (23) are consistent with dimensional homogeneity.
2.2. TBM Performance Evaluation Indexes Based on the ILP Model
The torque and thrust force are two important design indexes of the TBM driving system, and are also key monitoring parameters during excavation. Most TBM performance indexes, such as FPI, TFI and SE, are formed by these parameters. Their mathematical formulas are derived based on the ILP model, and some reformed indexes are presented in this section.
2.2.1. Reformed Field Penetration Index
The concept of FPI [24] is defined as
where Fthr is the actual thrust force. However, the relationship between thrust and PR in the construction site is not linear, and it is essential to find the appropriate form of FPI.
A similar concept was proposed by Sundin [25] as the rock mass boreability index (BI) to express the excavation difficulty degree of the rock, which is expressed as the ratio of the single cutter normal force to the PR:
Likewise, Laughton [26] indicated that a linear relationship between PR and Fn does not exist. Meanwhile, according to the research by Gong [27], BI is not isolated from PR but in the approximate form of , where BI(1) is the specific rock mass boreability index (SRMBI), defined as the BI at a penetration of 1 mm/r and only related to the rock mass property and TBM configuration. However, it cannot be expressed by a specific formula, and its value is often obtained statistically from actual construction data.
Hence, combining the index form of Gong and the ILP model, we reformed the traditional form of the FPI. According to Equation (15), the predicted cutter normal force is proportionally related to the cubic root of PR, and the reformed field penetration index (RFPI) and can be specified as:
2.2.2. Torque/Thrust Penetration Index
The RFPI index is still correlated with the geographical conditions and cannot give exact indications to the drivers on a TBM working condition. It makes sense to seek an inherent index of a specified TBM. The ratio of torque and thrust has been proven to be proportional with PR to the power of 0.5, but the coefficient has not been studied [18], and the power of PR to thrust force and torque may be improper. Based on Equations (22) and (23), TFI under the ILP model can be expressed as:
Equation (27) shows that the TFI is only related to the cutterhead diameter, cutter radius and PR. Note that the total friction force, which may be 40% of total thrust load, is removed as a fixed value to achieve a relatively independent analysis of the load introduced during the rock-breaking process. Further, we define a new torque/thrust penetration index (TFP) in this paper described as:
Referring to the guidelines of a 19-inch cutter provided by Robbins, despite the fact that the normal cutter wear reduces the cutter radius, it does not affect the TFI at a rate of more than 7%. Similarly, R in the TFP is not affected during the tunneling process. Therefore, it can be considered that the TFP is the relationship between the normal force and torque of the cutter group that should be satisfied under different geological conditions and PR, which means that the normal conditions of a TBM can be judged by the real-time TFP.
2.2.3. Specific Energy
SE is an important index of excavation efficiency, which can be expressed as [19]:
Based on the ILP model, SE can be specified as:
It is clear that UCS and TS have a significant impact on SE, which proves that the existing statistical analysis without the classification of geological parameters is unreliable. For the given stratum conditions and TBM parameters, SE is monotonically decreases with respect to PR, with the minimal value occurring at . This value apparently exceeds the available range in common excavation. Therefore, during the tunneling process, PR should be set to reduce SE as much as possible while also increasing the advance speed. Noting also that the propulsion system is characterized by a large load but low speed, so the power consumption (hundreds of kilowatts) is much smaller than that (Megawatt) of the cutterhead drive system. Equation (30) can be rewritten without the propulsion system power consumption as:
3. Validation and Analysis
The experiments based on a linear cutting machine (LCM) equipped with only one or two cutters is not suitable to examine the load model of an entire TBM. Inversely, in field sites e generating reliable data, the geographical parameters are hard to assessed because the span of vertical boreholes in mountain areas is much bigger in contrast to urban subway tunnel sites, mainly caused by the larger depth and cost. Online testing is such a waste of time that it may never be done unless an unexpected abominable stratum is encountered. Hence, the work date when an TBM excavates through prior-drilling zones is of great value and is always saved by field engineers for further research [28]. In this section, the data sampled around the boreholes of different stratum types at two construction sites, respectively located in northwest and northeast China, is used to verify the ILP model and the performance evaluation indexes. The results are compared with the classical CSM model.
3.1. Validation of the ILP Model
Some basic parameters of the two TBMs used for validation are listed in Table 1. The diameter of 1# TBM and 2# TBM are 7.93 m and 6.53 m, while the radii of the transition curve center are 3.46 m and 2.80 m, respectively. The face and edge cutters used in the two TBMs are all of 19-inch type with a radius of 241 mm and a tip width of 19 mm, while the center cutter is a 17-inch cutter with a radius of 216 mm and a tip width of 12.5 mm. Since the PR, rock character and real-time thrust and torque load are almost identical for the data sampled from these two construction sites, the average values of data around the boreholes are taken as the parameter values.

Table 1.
Some basic parameters of the TBMs in the two construction sites.
This section is divided by subheadings. It provides a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn. The cutter group configuration parameters and the total friction force Ff are set according to the design drawings and cutter change records. As seen in Table 1, the amount of center and edge cutters (nc and ne) is the same, both 8 and 12. However, the number of face cutters nf are 36 and 24, and the total friction forces Ff are set as 4.1 MN and 3.0 MN. In the CSM model, the pressure distribution function constants ψ for the 17-inch and 19-inch cutters are −0.05 and −0.1, respectively. The difference in the ILP model is that all the cutters are 19-inch cutters with a ψ of 0.01.
The root mean squared error (RMSE) and mean absolute percentage error (MAPE) were used to measure the prediction accuracy of the model. A larger RMSE or MAPE value indicates the difference between the predicted and true values is greater. RMSE and MAPE are, respectively defined as:
where yi is the actual extent of cutter wear, is the predicted extent of cutter wear, and n denotes the number of instances in the dataset.
The predicted force and torque using the different models are compared separately with actual values, as shown in Figure 4 and Figure 5. The following findings were observed: (1) The MAPE of the two models are both within 10%, meaning that the approximation process is acceptable. (2) The prediction errors of the proposed ILP model for both thrust and torque are less than 5%, which outperforms the CSM model. Meanwhile, the mean errors in the predictions of the latest studies [11,12,14] are about 10% to 15%. Obviously, the prediction results of the ILP model are acceptable. (3) The prediction results of the thrust are almost identical for the ILP and CSM models, while in terms of torque prediction, the ILP model poses a significant improvement. The main reason is that the total friction force Ff is set to a fixed value without taking into account the changing surrounding rock, resulting in similar prediction results for thrust. This is not the case in the torque calculation, so the results are greatly improved.
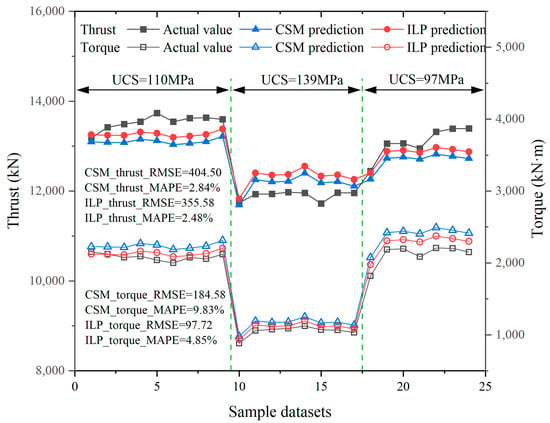
Figure 4.
Comparison between the actual and predicted load of 1# TBM.
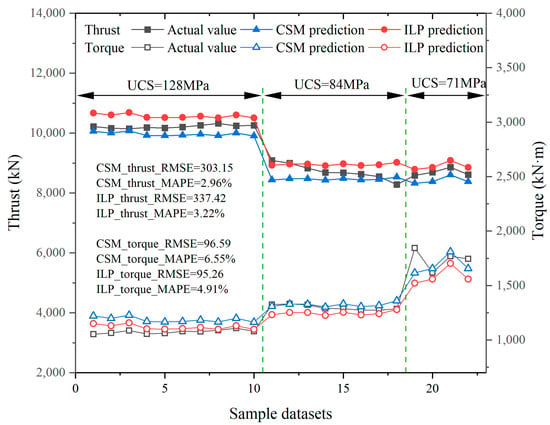
Figure 5.
Comparison between the actual and predicted load of 2# TBM.
To further validate the performance of the ILP model with specific parameters, we selected the continuous filed data near the No.70686 borehole in 1# TBM. The geological parameters UCS and TS sampled in the area are 100 MPa and 7 MPa, respectively. Both of the results are plotted in Figure 6 with the MAPE = 2.64% in thrust and MAPE = 7.36% in torque, which demonstrate the excellent performance of the proposed ILP model in load prediction. In addition, the RMSE values of the same order of magnitude as in Figure 4 also illustrate the effectiveness of the ILP model.
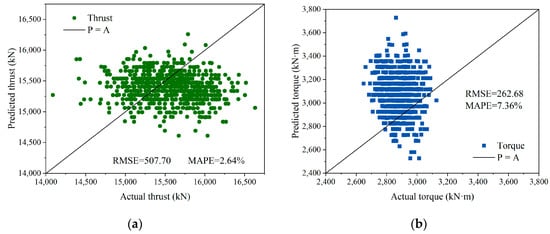
Figure 6.
Performance of the ILP model on datasets around No.70686 borehole: (a) Thrust; (b) Torque.
3.2. Analysis of TBM Performance Evaluation Indexes
3.2.1. RFPI
The proportionate relationship between thrust and PR is one that TBM drivers commonly use as operating experience, which has been corrected with the FPI based on the ILP model. The nonlinear relationship is validated with field data by the single-factor regression method. Ordinary least squares is the most common approach for estimating the coefficient, used to minimize the residual sum of squares between the observed targets in the dataset. The datasets from the No.65900 (UCS = 43.2 MPa, TS = 2.62 MPa) and No.70545 (UCS = 34.2 MPa, TS = 6.4 MPa) boreholes were selected, which are in the work region of the excavation. Meanwhile, the PR in the two datasets gradually increased with the excavation. The fitting results are shown in Figure 7. The regression equation of the No.65900 data are in the form of 34,616.64p1/3, R-square = 0.60, while similar result of the No.70545 data are in the form of TFI = 36,456.47p1/3, R-square = 0.48. The theoretical coefficient values are 32,367.57 and 35,498.86, which is evidence that the total normal force of the cutter group is proportional to the cube root of PR. In terms of the RFPI based on the actual data, the normal distributions are presented in Figure 8. Considering that the RFPI is not a standard non-dimension number, dimensionless processing has been carried out. The corresponding mean value μ and standard deviation σ of the No.65900 data are equal to 0.81 and 0.07, respectively, while μ and σ of No.70545 are0.84 and 0.07, respectively. The theoretical RFPI is in the interval [μ − σ = 0.74, μ + σ = 0.88], also supporting the validity of the ILP model.
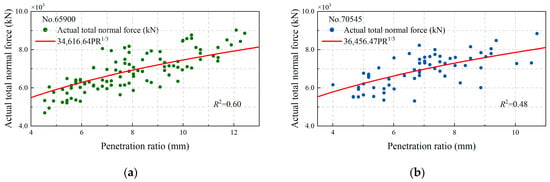
Figure 7.
Regression analysis of thrust and PR of the data around boreholes: (a) No.65900; (b) No.70545.
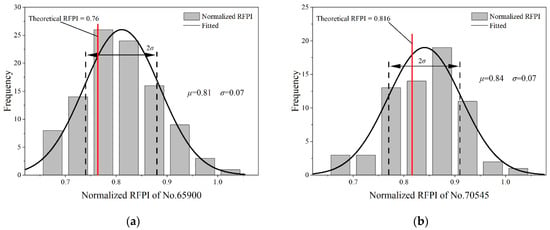
Figure 8.
Distribution of the RFPI of the data around boreholes: (a) No.65900; (b) No.70545.
3.2.2. TFI and TFP
TFI was proposed and analyzed to be theoretically isolated from the geographical condition and most cutter group configuration parameters except for cutter radius. Equation (27) demonstrates that the stratum conditions have no effect on the TFI. The same single-factor regression method and the same datasets from the No.65900 and N0.70545 boreholes were utilized for validation. The finally fitting results are shown in Figure 9. The regression equation of the No.65900 data are in the form of TFI = 2.92p0.5, R-square = 0.64, while the similar result of the No.70545 data are in the form of TFI = 2.97p0.5, R-square = 0.63. On the other hand, the ideal theoretical model according to Equation (27) is TFI = 2.95p0.5, which means that the power of PR equals 0.5 and the coefficient errors are 0.05 and 0.02. Hence, the TFI in Equation (27) can describe the correlation between the torque and thrust of a TBM with a fixed diameter and cutter radius in a common range of PR and stratum with an acceptable error ratio.
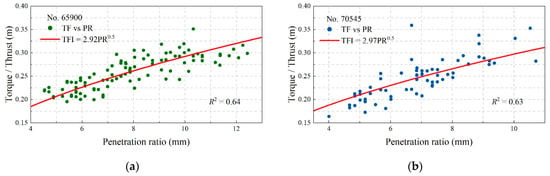
Figure 9.
Regression analysis of torque/thrust and PR around the boreholes: (a) No.65900; (b) No.70545.
TFP is determined by dividing the TFI by p0.5, and can be treated as an inherent parameter of a specified TBM for its correlation with diameter and cutter radius. Caused by the dynamic character of the TBM driving system and cutter wear, TFP in the field should be maintained within the proper range. For field applications, the suggested upper and lower bounds should be designed to build a workspace instead of a fixed value. As mentioned in Section 3.1, the prediction error of the thrust force and torque is 5%, and the change ratio of R−0.5 with the maximum permitted abrasion length of 30 mm for a 19-inch cutter is 7% [29]. Thus, a reasonable work space based on the theoretically predicted formula of TFP can be derived considering the TBM dynamic error and cutter wear. To be exact, for the datasets from the No.65900 and No.70545 boreholes, the upper and lower bounds are TFPup = 3.26 and TFPlow = 2.67, while the theoretical TFP is 2.95. As shown in Figure 10, the upper and lower bounds are transformed into straight horizontal lines. Field data can be classified and data points with a TFP over the upper bound are noted as failure points with potential cutter wear, while data points under the lower bound are specified as ideal points where the cutter group is well maintained. Most data points are located between the bounds, representing the majority of normal conditions. Therefore, TBM performance can be evaluated by calculating the real-time TFP and compare this with the boundary values TFPup and TFPlow.
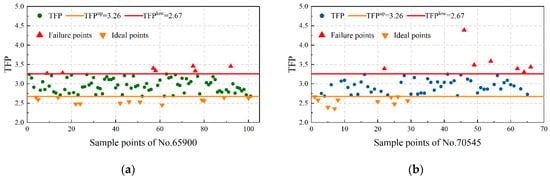
Figure 10.
Working conditions evaluation based on the TFP: (a) No.65900; (b) No.70545.
3.2.3. SE
In order to better evaluate the TBM excavation efficiency with SE, Equations (29) and (31) were validated by data sampled around the boreholes in 1# TBM and 2# TBM. As mentioned in Section 2.2.3, the advancing speed of the TBM is quite small and the energy consumed by the propelling system could be neglected in contrast to the cutterhead driving system. This can be reflected in the assembled power, 1# TBM equips 10 electric motors of 350 kW, and the thrust hydraulic system is driven by an electric motor of 132 kW. The comparison of power proves the feasibility of Equation (31). The final validation results are displayed in Figure 11. The trend in SE for both the actual and predicted results of 1# TBM and 2# TBM in different geographical conditions confirm the effectiveness of Equation (31). The prediction error is caused by the torque prediction deviation explained before. The diversity in SE also validates the strong positive correlation between UCS and SE, which should be considered when exploring the correlation between SE and PR.
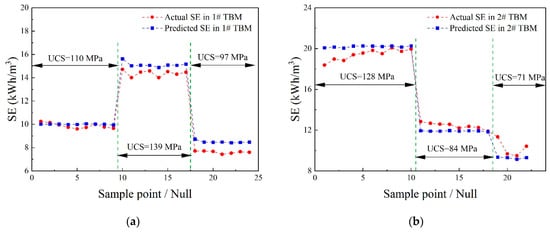
Figure 11.
Comparison between the actual and predicted specific energy: (a) 1# TBM; (b) 2# TBM.
To avoid the influence of different UCS, SE and PR of 1# or 2# TBMs, TBMs at different stratum should be normalized separately by dividing their average values in corresponding stratum types. The normalized relationship between SE and PR of 1# and 2# TBM is shown in Figure 12. The outliers, especially the normalized PR at points 14 and 18 in (a) and points 18 and 21 in (b), are generated by untimely driver adjustments for the sudden change in geological conditions. Further, both the actual and predicted SE change oppositely with PR in most conditions UCS and the SE amplitude deviation is always smaller than PR for the theoretical power exponent of −1/6.
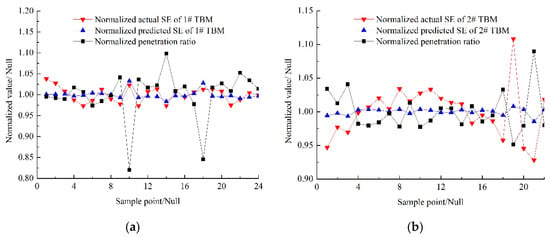
Figure 12.
Correlation between the normalized specific energy and PR: (a) 1# TBM; (b) 2# TBM.
4. Discussion
As analyzed in Section 3, the investigation of the correlations between TBM load and PR based on the ILP model gives the exact indications to drivers to monitor the working conditions. In the same way, the relationship between TBM load, SE and cutter group configuration parameters can provide recommendations for cutter layout in specific stratum, especially in extreme stratum. Cutter failure frequently occurs due to overload caused by an improper configuration, which can be categorized into two types: bearing damage with the overload of cutter force described in Equation (14) and cutter ring damage with stress exceeding extremities, while the basic contact pressure of the cutter ring under the ILP model could be transformed as:
According to Equations (14), (22), and (34), parameters such as cutter spacing, cutter radius and tip thickness have a significant influence on the cutter stress, force and even the whole TBM load. In a specific project, the TBM diameter is first determined. Then, cutter amount would be ensured based on the cutter spacing design. Optimal cutter spacing research is carried out by numerical simulation and LCM tests, always set between 75 to 90 mm considering the small range of PR [30]. In the analysis of this paper, the cutter spacing played an opposite role in the single cutter force in Equation (14) and total thrust force in Equation (22). To be exact, the Sa was smaller resulting in a smaller cutter force and basic pressure but made more cutters and a bigger final thrust load. Cutter load capacity is constrained by material strength which has little space for improvement in the short term, at the same time, the propelling force is always adequate for a normal scale TBM. Therefore, in the case of extremely hard stratum (UCS > 200 MPa), it is recommended to choose the layout of a smaller Sa, with more cutters and a bigger propelling force, which can effectively reduce the force and damage of a single cutter under the same PR and avoid frequent cutter replacement. It is worth noting that SE becomes larger in this situation, which means that the excavation efficiency is reduced.
Cutter radius and tip thickness are the following parameters that must be ensured. R has no effect on P0 but is positively related with , thus the exchange of a smaller cutter, such as using a 17-inch cutter to replace a 19-inch cutter would bring a smaller thrust load and decrease the damage risk to a bearing at same PR and UCS. This change would not help the basic pressure, but rather reduce the abrasion tolerance and remaining useful life. Thus, unless the bearing is damaged in a very large proportion, it is not suggested to employ a smaller cutter. T has the opposite influence on the basic pressure and cutter force, where a thinner cutter will decrease the load of the bearing but improve the risk of cutter ring damage, so T should be disposed according to the specific failure type in extremely hard stratum.
Oppositely in soft stratum, according to the concept of TFI, torque exceeds more rapidly with PR in contrast to thrust force, meaning the equipped torque capacity is the mainly limitation of higher excavation speeds in the stratum of a lower UCS, instead of cutter assemble strength. This deduction is consistent with the study of Liu [8] on a TB880SE TBM used in the Qinling tunnel. A bigger cutter spacing with fewer cutters should be used to decrease the torque load and SE. Meanwhile, a larger and thinner cutter should be selected to reduce the frequency of cutter changes.
5. Conclusions
To reveal the correlation between TBM load and rock–machine interaction parameters and further evaluate TBM performance, an improved load prediction model has been established based on the approximate linearization of the classical CSM model, and the following conclusions can be drawn via mathematical derivation and field data validation.
- (1)
- Compared to the classical CSM model, the proposed ILP model turned out to have a better prediction accuracy via field data verification. In addition, the proposed ILP model is easier to use and interpreted by drivers.
- (2)
- FPI should be defined as the quotient between the thrust force and the cubic root of PR, which reveals a nonlinear relationship between TBM load and PR.
- (3)
- TFI with a fixed CGC is proportional with the square root of PR and independent with geographical parameters, new index TFP is further developed with upper and lower bounds considering the TBM dynamic error and cutter abrasion to constrain a proper work space for the TBM. Excavation parameter adjustments and further shutdown inspections are needed when the TFP remains over the upper bound.
- (4)
- In hard stratum, cutter damage should be firstly concerned instead of SE, and a smaller cutter spacing should be used. A smaller cutter radius and tip width may be helpful against bearing damage, while for cutter ring failure a bigger cutter radius and tip width is a suggested configuration.
- (5)
- In soft stratum, a bigger cutter spacing and thinner cutters should be used to decrease the torque load.
In this paper, the equations in the proposed prediction model are related only to the UCS and TS of the geological parameters, whose values around the boreholes are considered to not change drastically. Future work will be focused on more geological parameters and their variation values to describe the complex conditions encountered by TBM.
Author Contributions
Conceptualization, X.Z.; methodology, X.Z.; software, X.Z. and W.W.; writing—original draft preparation, X.Z.; writing—review and editing, G.G., Y.Z. and Y.C.; supervision, Y.Z.; project administration, G.G. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China, grant no. 2020YFF0218004, National Natural Science Foundation of China, grant no. 52105074, Open Project of State Key Laboratory of Shield Machine and Boring Technology, grant no. SKLST-2021-K02.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ebrahim, F.; Jamal, R. Correlation of tunnel convergence with TBM operational parameters and chip size in the Ghomroud tunnel, Iran. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2008, 23, 700–710. [Google Scholar] [CrossRef]
- Bilgin, N.; Algan, M. The performance of a TBM in a squeezing ground at Uluabat, Turkey. Tunn. Undergr. Space Technol. 2012, 32, 58–65. [Google Scholar] [CrossRef]
- Ramoni, M.; Anagnostou, G. Tunnel boring machines under squeezing conditions. Tunn. Undergr. Space Technol. 2010, 25, 139–157. [Google Scholar] [CrossRef]
- Farrokh, E.; Rostami, J.; Laughton, C. Study of various models for estimation of penetration rate of hard rock TBMs. Tunn. Undergr. Space Technol. 2012, 30, 110–123. [Google Scholar] [CrossRef]
- Zare, S.; Bruland, A.; Rostami, J. Evaluating D&B and TBM tunnelling using NTNU prediction models. Tunn. Undergr. Space Technol. 2016, 59, 55–64. [Google Scholar] [CrossRef]
- Xia, Y.; OuYang, T.; Zhang, X.; Luo, D. Mechanical model of breaking rock and force characteristic of disc cutter. J. Cent. South Univ. 2012, 19, 1846–1852. [Google Scholar] [CrossRef]
- Rostami, J. Development of a Force Estimation Model for Rock Fragmentation with Disc Cutters through Theoretical Modeling and Physical Measurement of Crushed Zone Pressure. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 1997. [Google Scholar]
- Jianqin, L.; Jiabao, R.; Wei, G. Thrust and torque characteristics based on a new cutter-head load model. Chin. J. Mech. Eng. 2015, 28, 801–809. [Google Scholar] [CrossRef]
- Zhang, K.; Yu, H.; Liu, Z.; Lai, X. Dynamic characteristic analysis of TBM tunnelling in mixed-face conditions. Simul. Model. Pract. Theory: Int. J. Fed. Eur. Simul. Soc. 2010, 18, 1019–1031. [Google Scholar] [CrossRef]
- Liao, J.; Chen, Z.; Yao, B. High-performance adaptive robust control with balanced torque allocation for the over-actuated cutter-head driving system in tunnel boring machine. Mechatron. Sci. Intell. Mach. 2017, 46, 168–176. [Google Scholar] [CrossRef]
- Kong, X.X.; Ling, X.Z.; Tang, L. Random forest-based predictors for driving forces of earth pressure balance (EPB) shield tunnel boring machine (TBM). Tunn. Undergr. Space Technol. 2022, 122, 104373. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 2016, 58, 236–246. [Google Scholar] [CrossRef]
- Sun, W.; Shi, M.L.; Zhang, C. Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Autom. Constr. 2018, 92, 23–24. [Google Scholar] [CrossRef]
- Li, J.H.; Li, P.X.; Guo, D. Advanced prediction of tunnel boring machine performance based on big data. Geosci. Front. 2021, 12, 331–338. [Google Scholar] [CrossRef]
- Zhang, L.T.; Zhang, Q.; Zhou, S.Y. Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm. Appl. Sci. 2021, 11, 5671. [Google Scholar] [CrossRef]
- Fattahi, H.; Babanouri, N. Applying Optimized Support Vector Regression Models for Prediction of Tunnel Boring Machine Performance. Geotech. Geol. Eng. 2017, 35, 2205–2217. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Khamehchiyan, M.; Bruland, A. Developing new equations for TBM performance prediction in carbonate-argillaceous rocks: A case history of Nowsood water conveyance tunnel. Geomech. Geoengin. Int. J. 2009, 4, 287–297. [Google Scholar] [CrossRef]
- Fukui, K.; Okubo, S. Some Attempts for Estimating Rock Strength and Rock Mass Classification from Cutting Force and Investigation of Optimum Operation of Tunnel Boring Machines. Rock Mech. Rock 2006, 39, 25–44. [Google Scholar] [CrossRef]
- Cho, J.; Jeon, S.; Jeong, H.; Chang, S. Evaluation of cutting efficiency during TBM disc cutter excavation within a Korean granitic rock using linear-cutting-machine testing and photogrammetric measurement. Tunn. Undergr. Space Technol. 2013, 35, 37–54. [Google Scholar] [CrossRef]
- Cardu, M.; Iabichino, G.; Oreste, P.; Rispoli, A. Experimental and analytical studies of the parameters influencing the action of TBM disc tools in tunnelling. Acta Geotech. Int. J. Geoengin. 2017, 12, 293–304. [Google Scholar] [CrossRef]
- Balci, C. Correlation of rock cutting tests with field performance of a TBM in a highly fractured rock formation: A case study in Kozyatagi-Kadikoy metro tunnel, Turkey. Tunn. Undergr. Space Technol. 2009, 24, 423–435. [Google Scholar] [CrossRef]
- Acaroglu, O.; Ozdemir, L.; Asbury, B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction. Tunn. Undergr. Space Technol. 2008, 23, 600–608. [Google Scholar] [CrossRef]
- She, L.; Zhang, S.R.; Wang, C. A cutting mechanics model of constant cross-section type disc cutter and its application based on dense core theory. Int. J. Rock Mech. Min. Sci. 2022, 150, 105025. [Google Scholar] [CrossRef]
- Burkhardt, M.; Kim, E.; Nelson, P.P. EMI database analysis focusing on relationship between density and mechanical properties of sedimentary rocks. Geomech. Eng. 2018, 14, 491–498. [Google Scholar] [CrossRef]
- Sundin, N.O.; Wanstedt, S. A boreability model for TBM’s. In Proceedings of the 1st North American Rock Mechanics Symposium, The University of Texas, Austin, TX, USA, 1 June 1994. [Google Scholar]
- Laughton, C. Evaluation and Prediction of Tunnel Boring Machine Performance in Variable Rock Masses; The University of Texas: Austin, TX, USA, 1998. [Google Scholar]
- Gong, Q.M.; Jiao, Y.Y.; Zhao, J. Numerical modelling of the effects of joint spacing on rock fragmentation by TBM cutters. Tunn. Undergr. Space Technol. 2006, 21, 46–55. [Google Scholar] [CrossRef]
- Gong, Q.M.; Zhao, J. Development of a rock mass characteristics model for TBM penetration rate prediction. Int. J. Rock Mech. Min. Sci. 2009, 46, 8–18. [Google Scholar] [CrossRef]
- Roby, J.; Sandell, T.; Kocab, J.; Lindbergh, L. Current state of disc cutter design and development directions. Mining Engineering 2009, 61, 26–34. [Google Scholar]
- Han, D.; Cao, P.; Liu, J.; Zhu, J. An Experimental Study of Dependence of Optimum TBM Cutter Spacing on Pre-set Penetration Depth in Sandstone Fragmentation. Rock Mech. Rock Eng. 2017, 50, 3209–3221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).