Conversion of a Small-Size Passenger Car to Hydrogen Fueling: Simulation of CCV and Evaluation of Cylinder Imbalance
Abstract
1. Introduction
2. Materials and Methods
2.1. 0D/1D Model Overview
2.2. PID Controllers
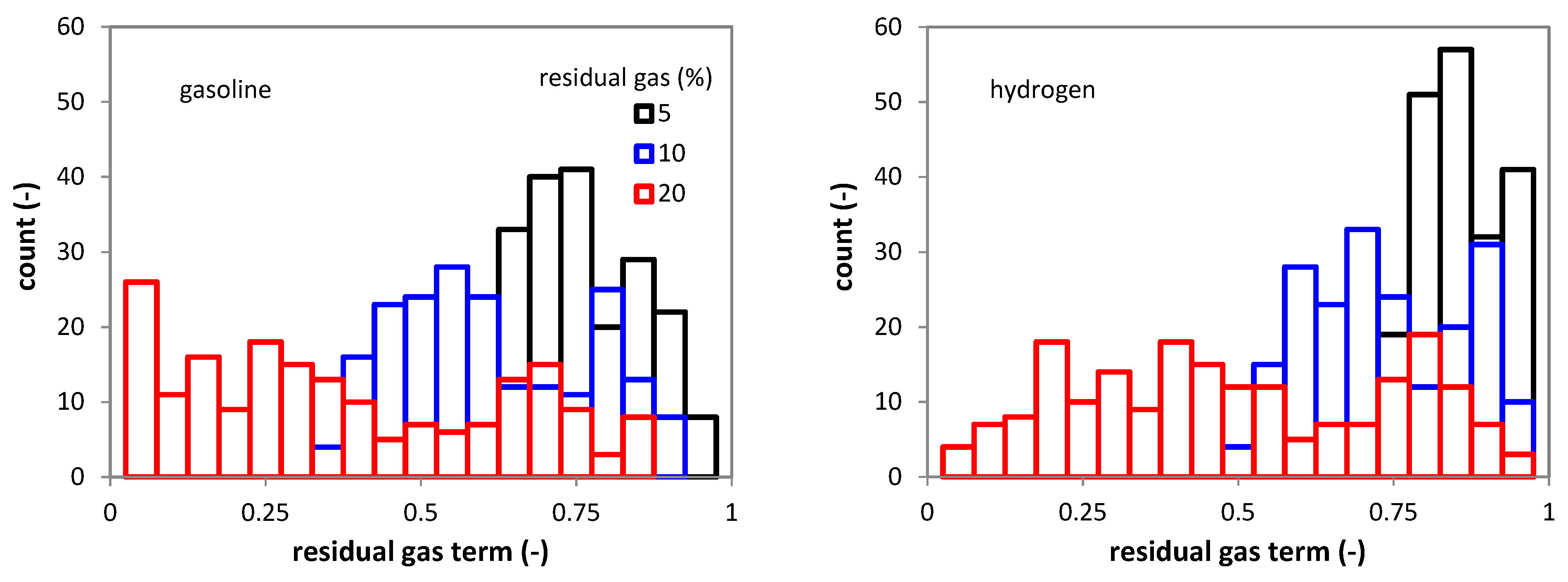
2.3. Cyclic Variability Sub-Model
3. Results and Discussion
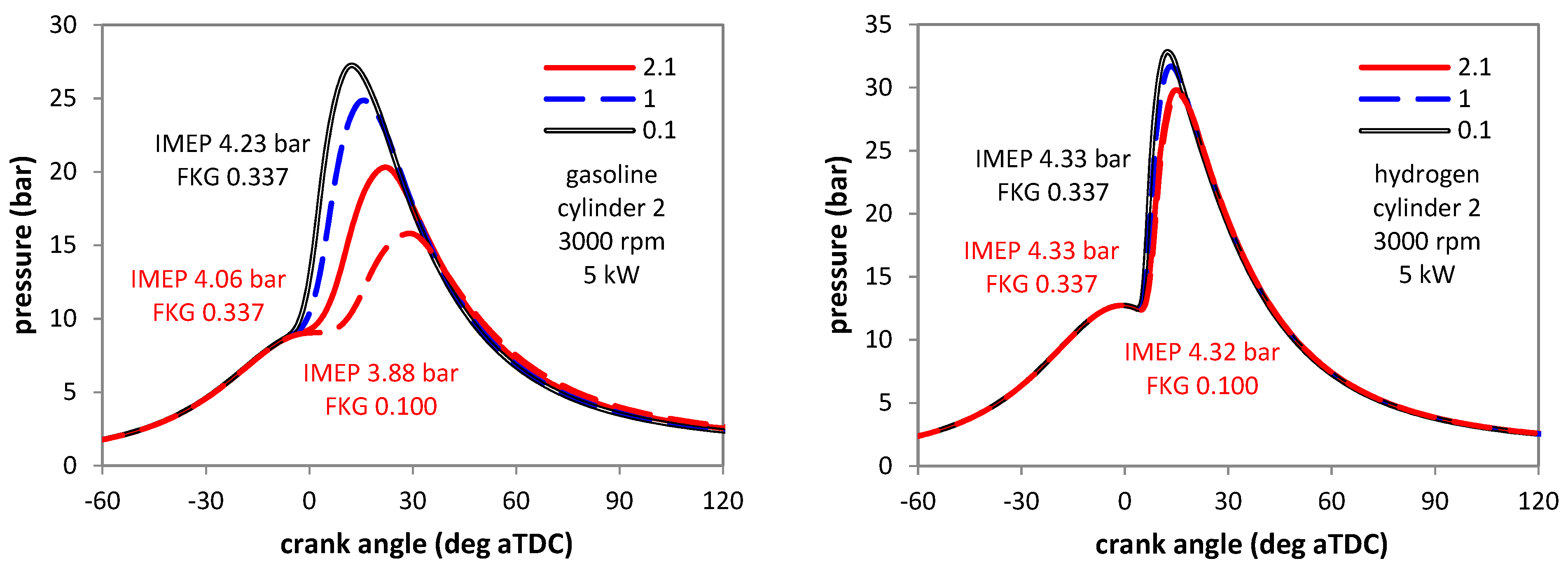
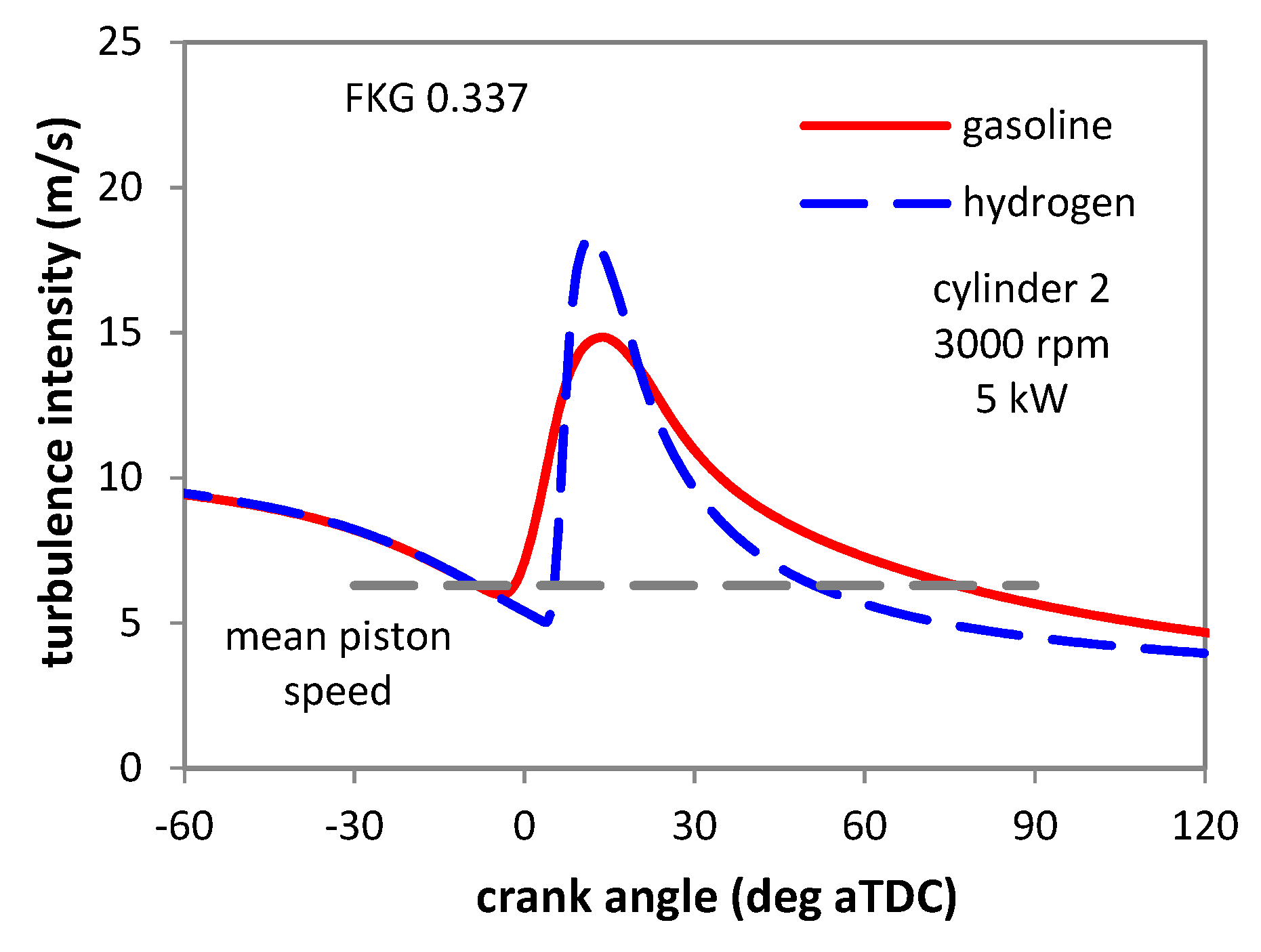
3.1. CCV Effects on In-Cylinder Pressure
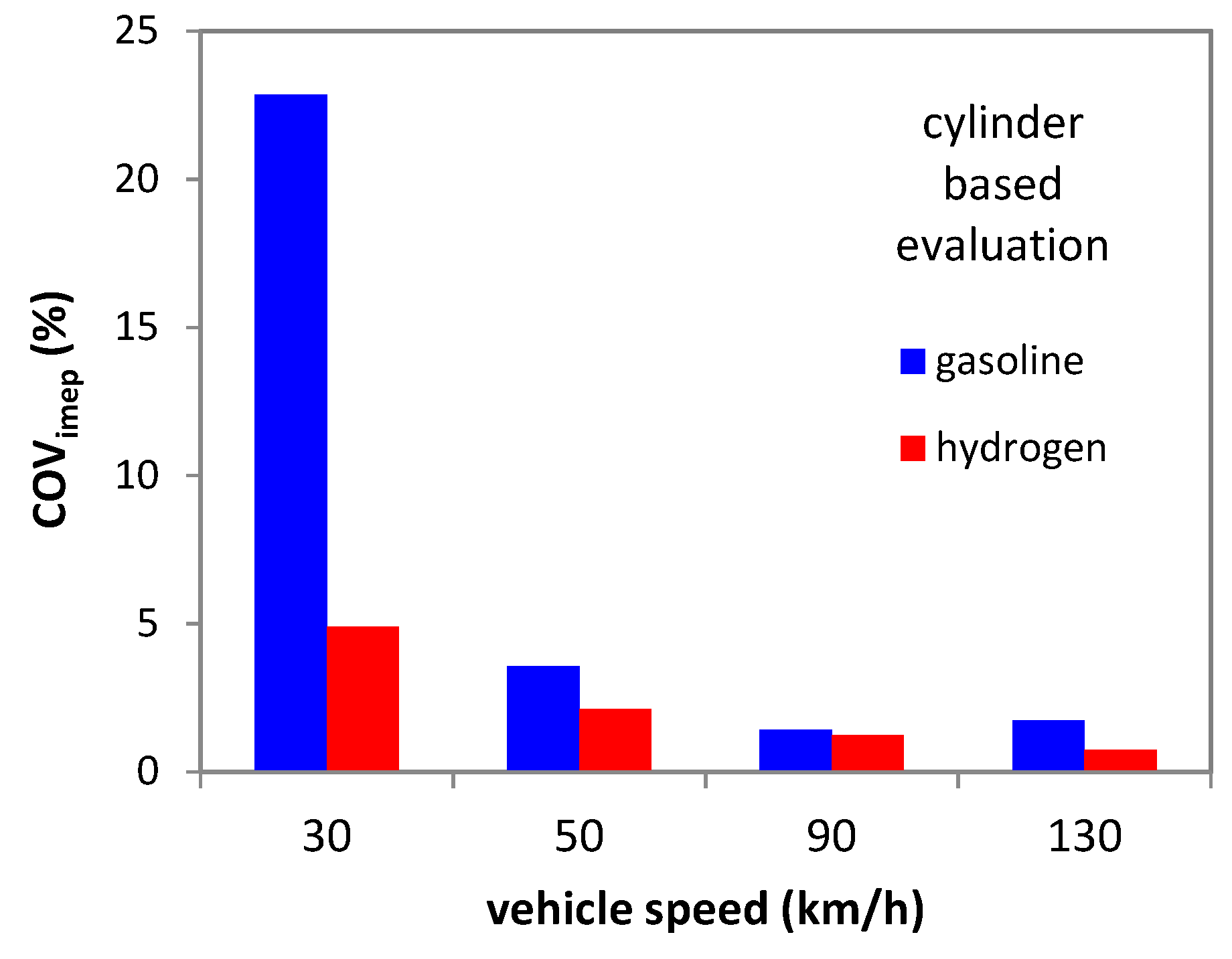
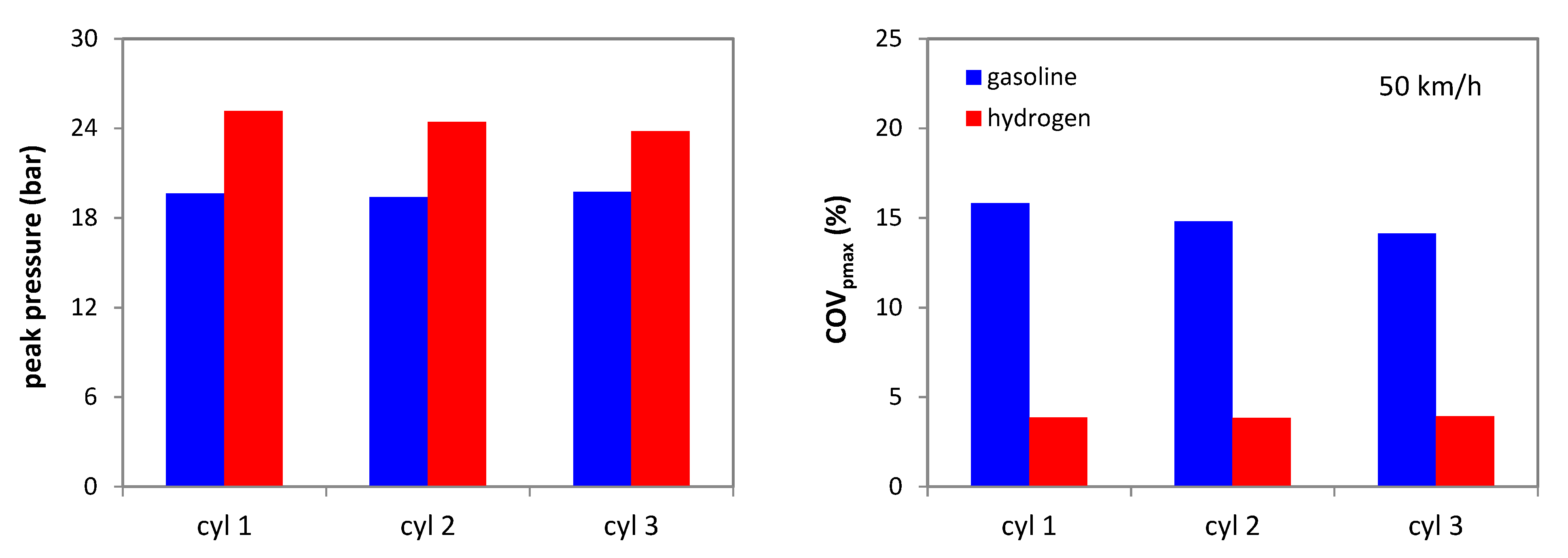
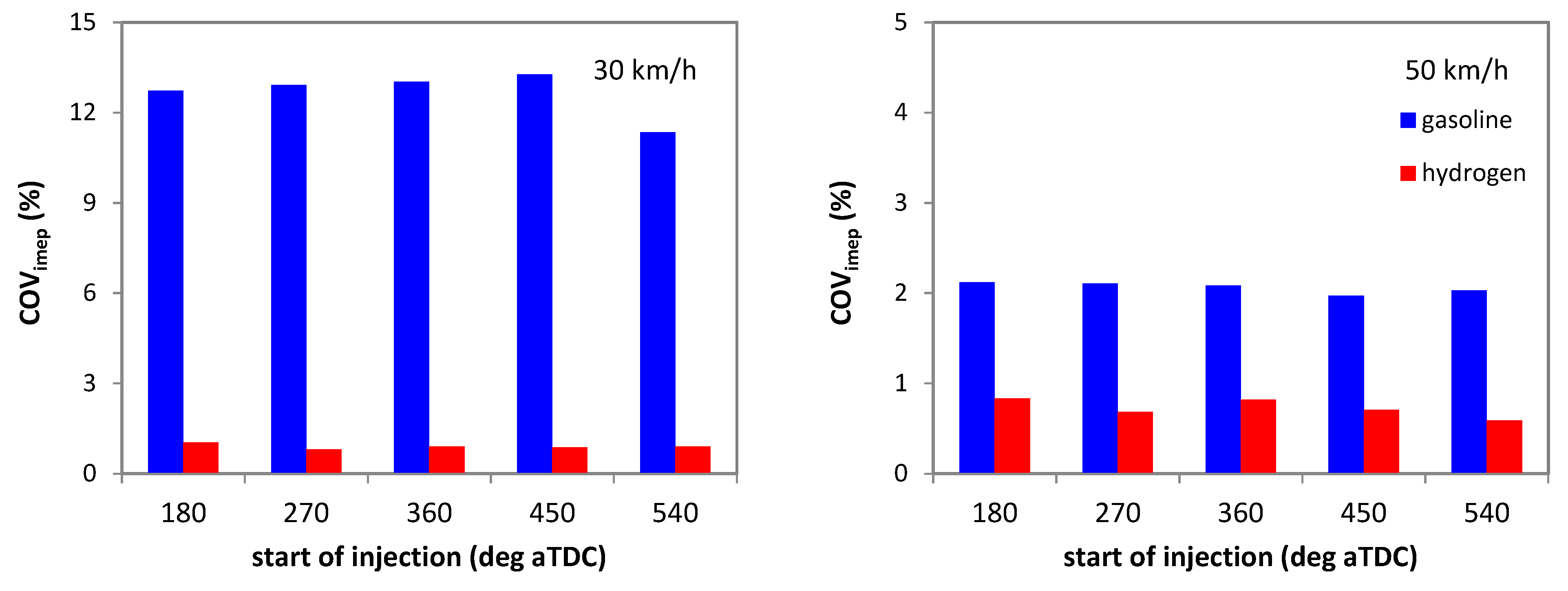
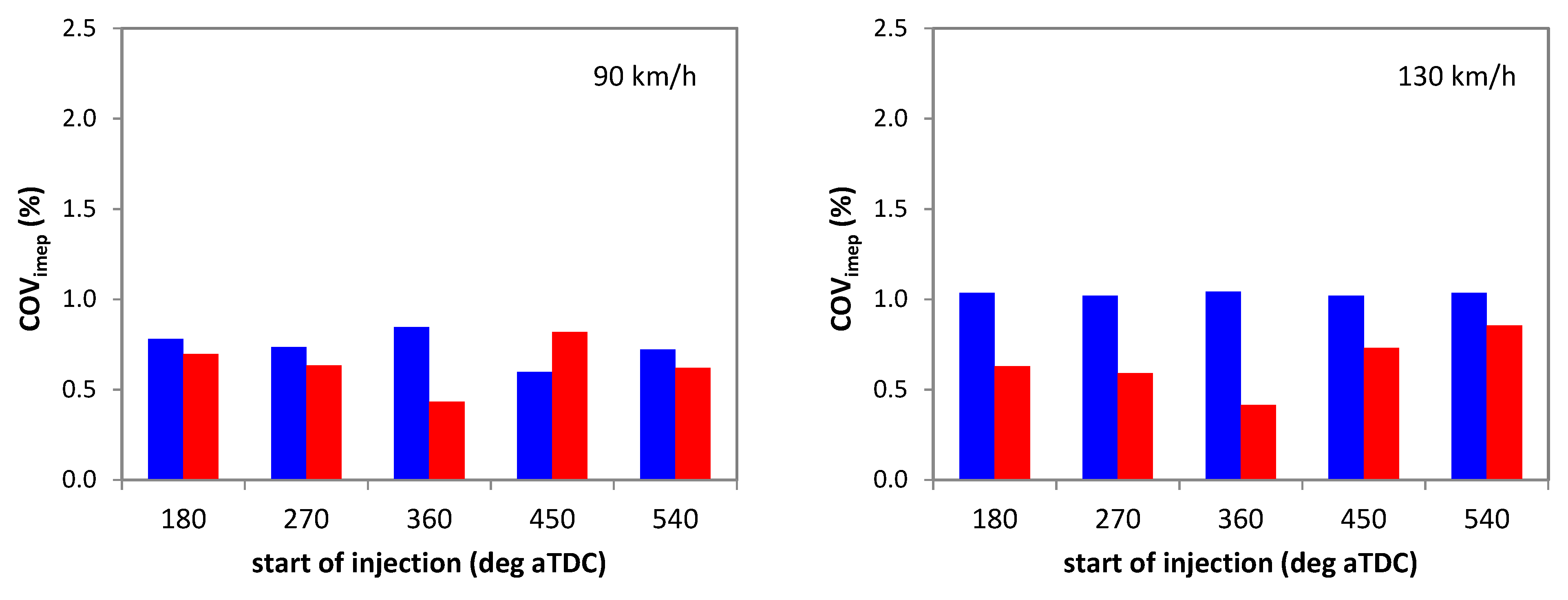
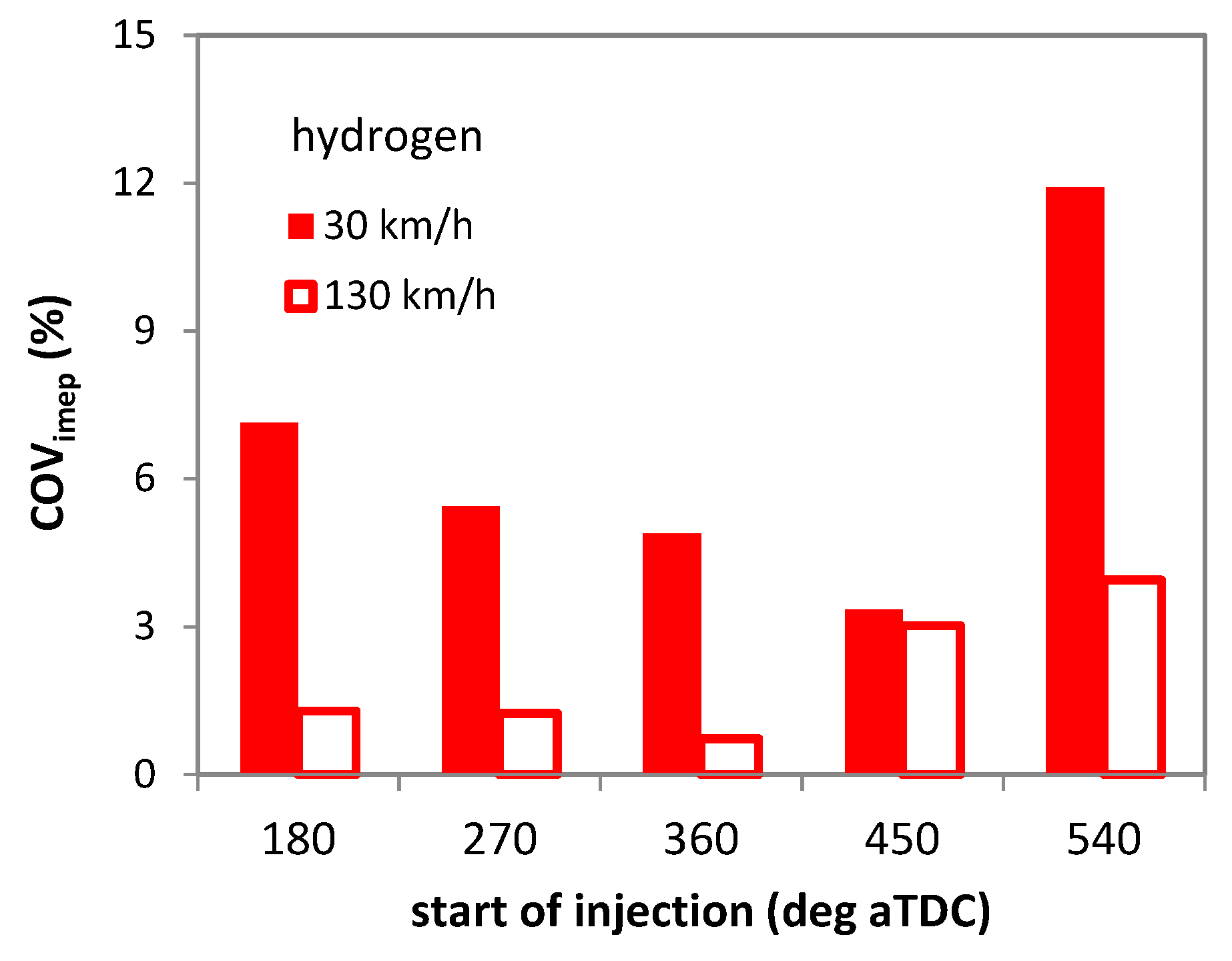
3.2. CCV Effects for Different Vehicle Speed Values
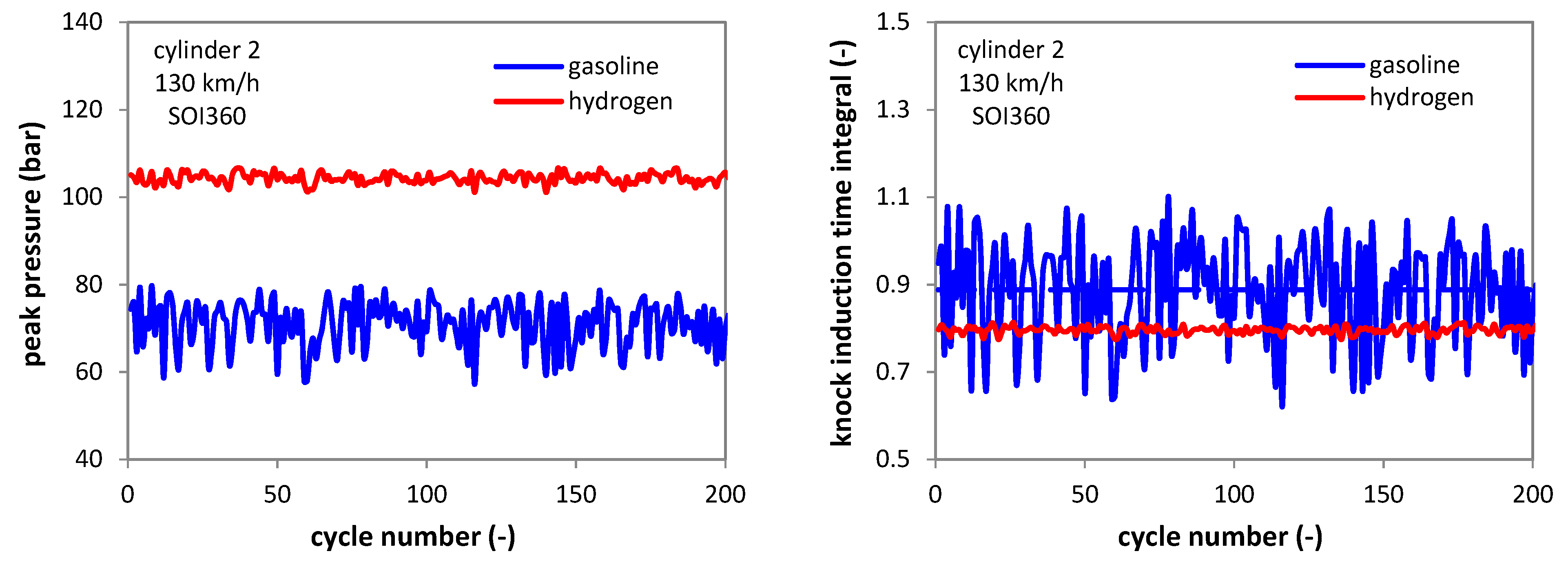
3.3. Start of Injection Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sacchi, R.; Bauer, C.; Cox, B.; Mutel, C. When, where and how can the electrification of passenger cars reduce greenhouse gas emissions? Renew. Sustain. Energy Rev. 2022, 162, 112475. [Google Scholar] [CrossRef]
- Hydrogen Council, Roadmap towards Zero Emission: BEVs and FCEVs, 10/21. Available online: www.hydrogencouncil.com (accessed on 10 December 2022).
- Mills, S.J. Heavy Duty Hydrogen ICE: Production Realization by 2025 and System Operation Efficiency Assessment. In Powertrain Systems for Net-Zero Transport, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021; ISBN 9781003219217. [Google Scholar]
- Edwards, R.L.; Font-Palm, C.; Howe, J. The status of hydrogen technologies in the UK: A multi-disciplinary review. Sust. Energy Technol. Assess. 2021, 43, 100901. [Google Scholar] [CrossRef]
- IRENA. Green Hydrogen Cost Reduction: Scaling up Electrolysers to Meet the 1.5 °C Climate Goal; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; ISBN 978-92-9260-295-6. [Google Scholar]
- Saccani, C.; Pellegrini, M.; Guzzini, A. Analysis of the Existing Barriers for the Market Development of Power to Hydrogen (P2H) in Italy. Energies 2020, 13, 4835. [Google Scholar] [CrossRef]
- Sebastian Oliva, H.; Matias Garcia, G. Investigating the impact of variable energy prices and renewable generation on the annualized cost of hydrogen. Int. J. Hydrogen Energy, 2023; in press, corrected proof. [Google Scholar] [CrossRef]
- Jones, J.; Genovese, A.; Tob-Ogu, A. Hydrogen vehicles in urban logistics: A total cost of ownership analysis and some policy implications. Renew. Sust. Energy Rev. 2020, 119, 109595. [Google Scholar] [CrossRef]
- Rout, C.; Li, H.; Dupont, V.; Wadud, Z. A comparative total cost of ownership analysis of heavy duty on-road and off-road vehicles powered by hydrogen, electricity, and diesel. Heliyon 2022, 8, e12417. [Google Scholar] [CrossRef]
- Onorati, A.; Payri, R.; Vaglieco, B.M.; Agarwal, A.K.; Bae, C.; Bruneaux, G.; Canakci, M.; Gavaises, M.; Günthner, M.; Hasse, C.; et al. The role of hydrogen for future internal combustion engines. Int. J. Engine Res. 2022, 23, 529–540. [Google Scholar] [CrossRef]
- Janusz-Szymańska, K.; Grzywnowicz, K.; Wiciak, G.; Remiorz, L. Reduction of carbon footprint from spark ignition power facilities by the dual approach. Arch. Thermodyn. 2021, 42, 171–192. [Google Scholar] [CrossRef]
- Krishna Addepalli, S.; Pei, Y.; Zhang, Y.; Scarcelli, R. Multi-dimensional modeling of mixture preparation in a direct injection engine fueled with gaseous hydrogen. Int. J. Hydrogen Energy 2022, 47, 29085–29101. [Google Scholar] [CrossRef]
- Villante, C.; Pede, G.; Genovese, A.; Ortenzi, F. Hydrogen-CNG Blends as Fuel in a Turbo-Charged SI Ice: ECU Calibration and Emission Tests; SAE Technical Paper 2013-24-0109; SAE International: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Bao, L.; Sun, B.; Luo, Q. Optimal control strategy of the turbocharged direct-injection hydrogen engine to achieve near-zero emissions with large power and high brake thermal efficiency. Fuel 2022, 325, 124913. [Google Scholar] [CrossRef]
- Thawko, A.; Tartakovsky, L. The Mechanism of Particle Formation in Non-Premixed Hydrogen Combustion in a Direct-Injection Internal Combustion Engine. Fuel 2022, 327, 125187. [Google Scholar] [CrossRef]
- Maio, G.; Boberic, A.; Giarracca, L.; Aubagnac-Karkar, D.; Colin, O.; Duffour, F.; Deppenkemper, K.; Virnich, L.; Pischinger, S. Experimental and numerical investigation of a direct injection spark ignition hydrogen engine for heavy-duty applications. Int. J. Hydrog. Energy 2022, 47, 29069–29084. [Google Scholar] [CrossRef]
- Janarthanam, S.; Blankenship, J.; Soltis, R.; Szwabowski, S.; Jaura, A.K. Architecture and Development of a Hydrogen Sensing and Mitigation System in H2RV—Ford’s Concept HEV Propelled with a Hydrogen Engine; SAE Technical Paper 2004-01-0359; SAE International: Warrendale, PA, USA, 2004. [Google Scholar] [CrossRef]
- Verhelst, S.; Wallner, T. Hydrogen-fueled internal combustion engines. Progress Energy Combust. Sci. 2009, 35, 490–527. [Google Scholar] [CrossRef]
- Stępień, Z.A. Comprehensive Overview of Hydrogen-Fueled Internal Combustion Engines: Achievements and Future Challenges. Energies 2021, 14, 6504. [Google Scholar] [CrossRef]
- Kosmadakis, G.M.; Rakopoulos, D.C.; Rakopoulos, C.D. Assessing the cyclic-variability of spark-ignition engine running on methane-hydrogen blends with high hydrogen contents of up to 50%. Int. J. Hydrogen Energy 2021, 46, 17955–17968. [Google Scholar] [CrossRef]
- Irimescu, A.; Cecere, G.; Sementa, P. Combustion Phasing Indicators for Optimized Spark Timing Settings for Methane-Hydrogen Powered Small Size Engines; SAE Technical Paper 2022, 2022-01-0603; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Wallner, T.; Lohse-Busch, H.; Gurski, S.; Duoba, M.; Thiel, W.; Martin, D.; Korn, T. Fuel economy and emissions evaluation of BMW Hydrogen 7 Mono-Fuel demonstration vehicles. Int. J. Hydrogen Energy 2008, 33, 7607–7618. [Google Scholar] [CrossRef]
- Irimescu, A.; Vaglieco, B.M.; Merola, S.; Zollo, V.; De Marinis, R. Conversion of a Small Size Passenger Car to Hydrogen Fueling: Focus on Rated Power and Injection Phasing Effects; SAE Technical Paper 2022, 2022-24-0031; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Irimescu, A.; Vaglieco, B.M.; Merola, S.S.; Zollo, V.; De Marinis, R. Conversion of a small size passenger car to hydrogen fueling: Simulation of full load performance. In Proceedings of the The 17th European Automotive Congress, The 32nd SIAR International Congress of Automotive and Transport Engineering, Timisoara, Romania, 26–28 October 2022. [Google Scholar]
- Fit for 55: Towards more Sustainable Transport: Proposal for a Regulation of the European Parliament and of the Council on the Deployment of Alternative Fuels Infrastructure, and Repealing Directive 2014/94/EU of the European Parliament and of the Council, Document 9111/22, May 2022, Article 6 Targets for Hydrogen Refuelling Infrastructure of Road Vehicle. Available online: https://www.consilium.europa.eu (accessed on 10 December 2022).
- Gamma Technologies. GT-SUITE Flow Theory Manual, version 7.4; Gamma Technologies: Westmont, IL, USA, 2013. [Google Scholar]
- Capata, R.; Sciubba, E. Use of Modified Balje Maps in the Design of Low Reynolds Number Turbocompressors. In Proceedings of the ASME 2012 International Mechanical Engineering Congress & Exposition IMECE2012, Houston, TX, USA, 9–15 November 2012. [Google Scholar]
- Cuturi, N.; Sciubba, E. Design of a Tandem Compressor for the Electrically-Driven Turbocharger of a Hybrid City Car. Energies 2021, 14, 2890. [Google Scholar] [CrossRef]
- Irimescu, A.; Merola, S.S.; Vaglieco, B.M. Towards better correlation between optical and commercial spark ignition engines through quasi-dimensional modeling of cycle-to-cycle variability. Therm. Sci. 2022, 26, 1685–1694. [Google Scholar] [CrossRef]
- Huang, D.; Lai, M.C. Experimental investigation of characteristics of pressure modulation in a fuel injection system. Int. J. Automot. Technol. 2009, 10, 9–16. [Google Scholar] [CrossRef]
- Heo, H.S.; Bae, S.J.; Lee, H.K.; Park, K.S. Analytical study of pressure pulsation characteristics according to the geometries of the fuel rail of an MPI engine. Int. J. Automot. Technol. 2012, 13, 167–173. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, H.; Kita, K.; Ogata, Y.; Nishida, K. Statistical variation analysis of fuel spray characteristics under cross-flow conditions. Fuel 2022, 307, 121887. [Google Scholar] [CrossRef]
- Irimescu, A. Comparison of combustion characteristics and heat loss for gasoline and methane fueling of a spark ignition engine. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2013, 14, 161–168. [Google Scholar]
- Kaneko, Y.; Nagashima, T.; Tomidokoro, T.; Matsuda, M.; Yokomori, T. Experimental Investigation of the Effects of Fuel Injection on the Cycle-to-Cycle Variation of the In-Cylinder Flow in a Direct-Injection Engine Using High-Speed Particle Image Velocimetry Measurement. SAE Int. J. Engines 2022, 15, 791–805. [Google Scholar] [CrossRef]
- Verhelst, S.; Woolley, R.; Lawes, M.; Sierens, R. Laminar and Unstable Burning Velocities and Markstein Lengths of Hydrogen-Air Mixtures at Engine-Like Conditions. Proc. Combust. Inst. 2005, 30, 209–216. [Google Scholar] [CrossRef]
- Gerke, U.; Steurs, K.; Rebecchi, P.; Boulouchos, K. Derivation of Burning Velocities of Premixed Hydrogen/Air Flames at Engine-Relevant Conditions Using a Single-Cylinder Compression Machine with Optical Access. Int. J. Hydrogen Energy 2010, 35, 2566–2577. [Google Scholar] [CrossRef]
- Singotia, P.K.; Saraswati, S. Cycle-by-cycle variations in a spark ignition engine fueled with gasoline and natural gas. IOP Conf. Ser. Mater. Sci. Eng. 2019, 691, 012061. [Google Scholar] [CrossRef]
- Irimescu, A.; Mihon, L.; Pãdure, G. Automotive transmission efficiency measurement using a chassis dynamometer. Int. J. Automot. Technol. 2011, 12, 555–559. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw Hill: New York, NY, USA, 1988; ISBN 9780070286375. [Google Scholar]
- Fischer, M.; Sterlepper, S.; Pischinger, S.; Seibel, J.; Kramer, U.; Lorenz, T. Operation principles for hydrogen spark ignited direct injection engines for passenger car applications. Int. J. Hydrogen Energy 2022, 47, 5638–5649. [Google Scholar] [CrossRef]
- Qiao, N.; Krishnamurthy, C.; Moore, N. Determine Air-Fuel Ratio Imbalance Cylinder Identification with an Oxygen Sensor. SAE Int. J. Engines 2015, 8, 1005–1011. [Google Scholar] [CrossRef]
- Cavina, N.; Ranuzzi, F.; de Cesare, M.; Bnignoni, E. Individual cylinder air-fuel ratio control for engines with unevenly spaced firing order. SAE Int. J. Engines 2017, 10, 614–624. [Google Scholar] [CrossRef]
- Wang, T.; Chang, S.; Liu, L.; Zhu, J.; Xu, Y. Individual cylinder air–fuel ratio estimation and control for a large-bore gas fuel engine. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719833629. [Google Scholar] [CrossRef]
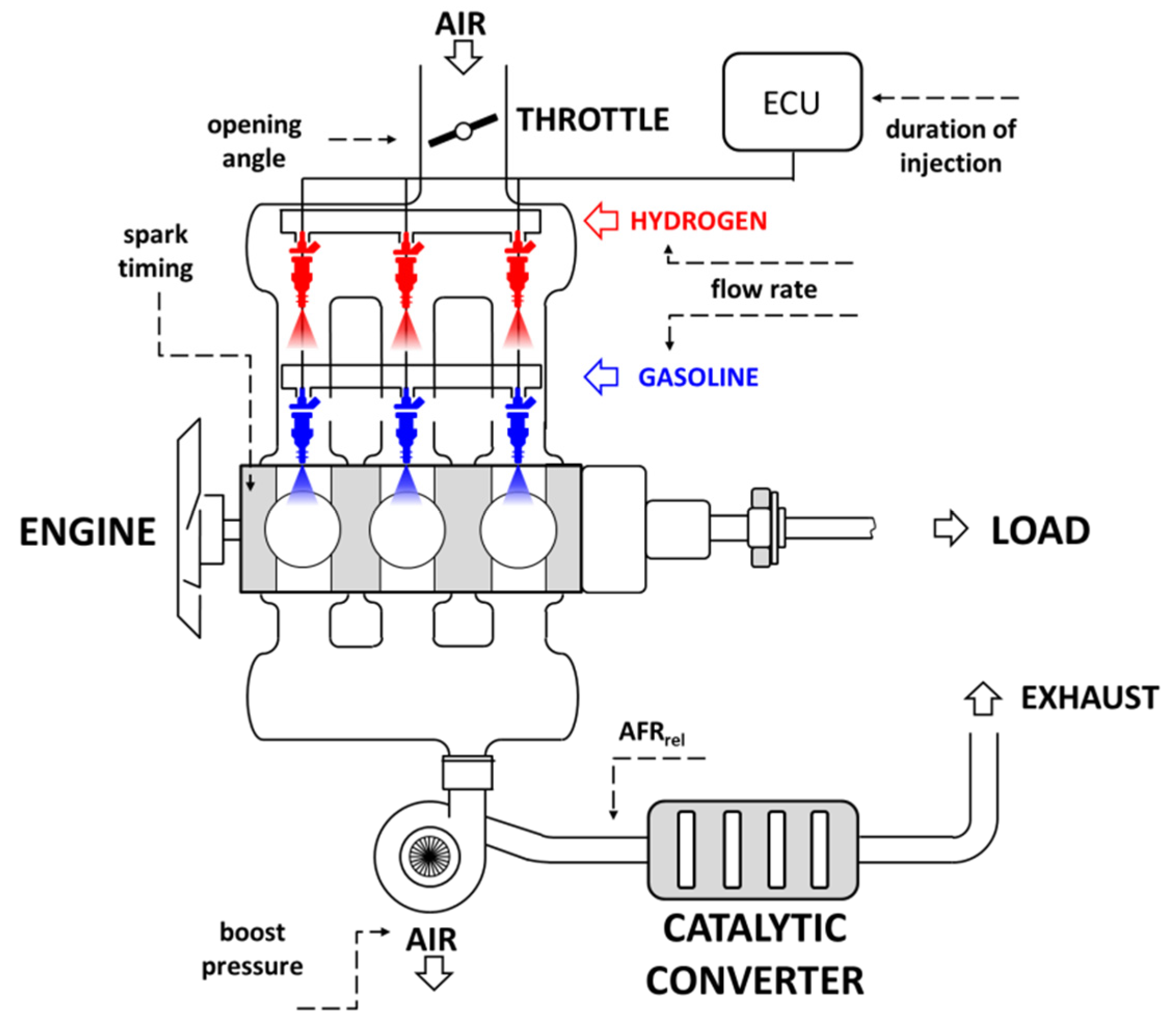
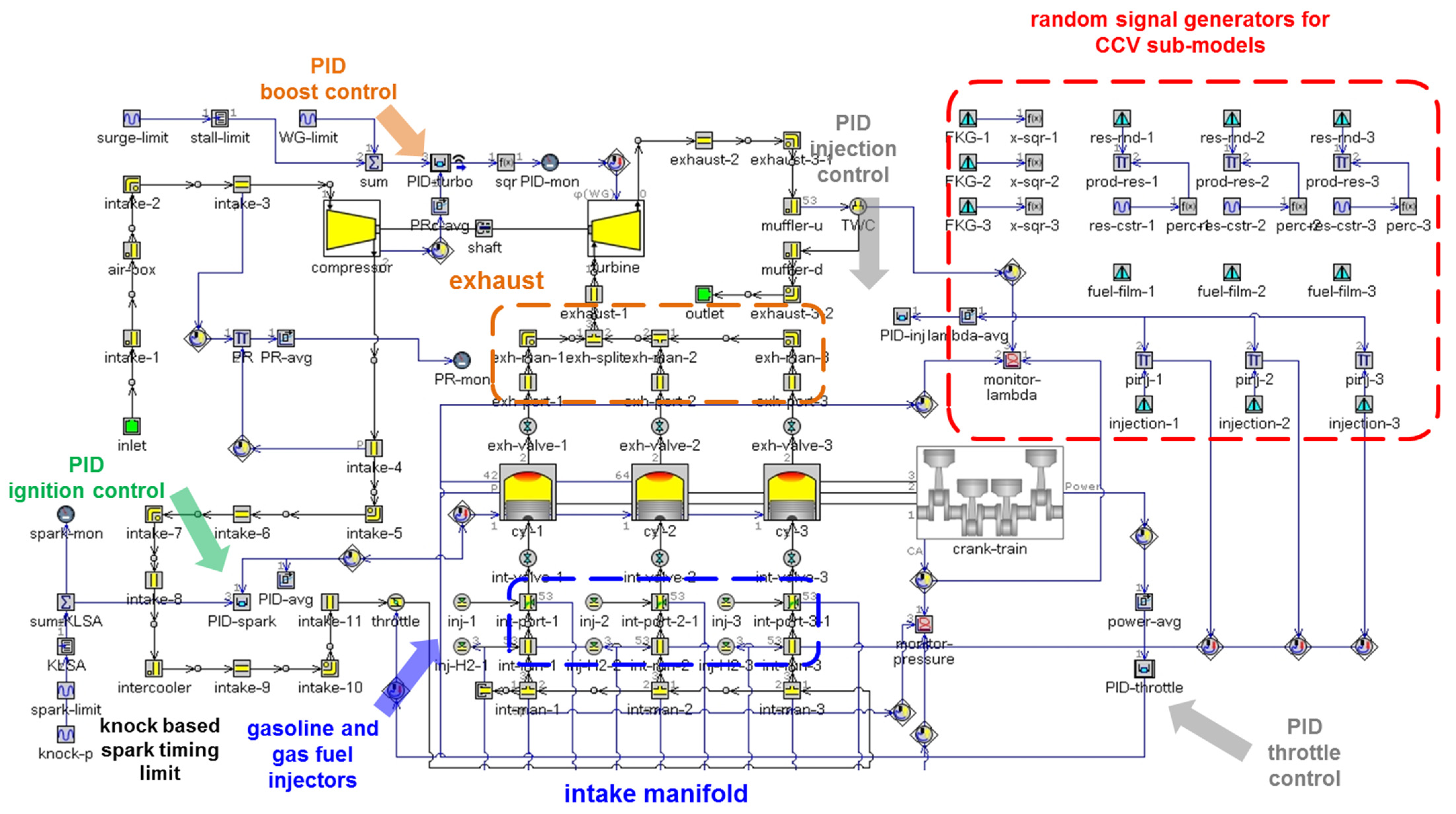





| Description | |
|---|---|
| Displacement | 599 cm3 |
| Number of cylinders | 3 |
| Rated power | 40 kW @ 5250 rpm |
| Rated torque | 80 Nm @ 2000–4400 rpm |
| Bore x Stroke | 63.5 mm × 63.0 mm |
| Connecting rod length | 114 mm |
| Compression ratio | 9.5:1 |
| Number of valves | 2 per cylinder |
| Intake valves opening/closure | 363/164 deg bTDC |
| Exhaust valves opening/closure | 157/349 deg a/bTDC |
| Fuel system | port fuel injection at 3.5 bar for gasoline and 5 bar for hydrogen |
| Ignition | inductive discharge, 2 spark plugs per cylinder |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irimescu, A.; Vaglieco, B.M.; Merola, S.S.; Zollo, V.; De Marinis, R. Conversion of a Small-Size Passenger Car to Hydrogen Fueling: Simulation of CCV and Evaluation of Cylinder Imbalance. Machines 2023, 11, 135. https://doi.org/10.3390/machines11020135
Irimescu A, Vaglieco BM, Merola SS, Zollo V, De Marinis R. Conversion of a Small-Size Passenger Car to Hydrogen Fueling: Simulation of CCV and Evaluation of Cylinder Imbalance. Machines. 2023; 11(2):135. https://doi.org/10.3390/machines11020135
Chicago/Turabian StyleIrimescu, Adrian, Bianca Maria Vaglieco, Simona Silvia Merola, Vasco Zollo, and Raffaele De Marinis. 2023. "Conversion of a Small-Size Passenger Car to Hydrogen Fueling: Simulation of CCV and Evaluation of Cylinder Imbalance" Machines 11, no. 2: 135. https://doi.org/10.3390/machines11020135
APA StyleIrimescu, A., Vaglieco, B. M., Merola, S. S., Zollo, V., & De Marinis, R. (2023). Conversion of a Small-Size Passenger Car to Hydrogen Fueling: Simulation of CCV and Evaluation of Cylinder Imbalance. Machines, 11(2), 135. https://doi.org/10.3390/machines11020135







