Design of Quasi-Halbach Permanent-Magnet Vernier Machine for Direct-Drive Urban Vehicle Application
Abstract
1. Introduction
2. Machine Principle
- -
- The integral of the two first terms leads to a constant value. The latter is independent of θ, and thus, is without any torque generation. In fact, this constitutes the magnetizing energy of the machine.
- -
- Terms that are cosine functions of θs whose integrals range from 0 to 2π are equal to zero.
- -
- The three terms that are functions of θs and θ can potentially generate torque. As the energy conversion is such machine should be based on the interaction between the two fields, the integrals of these terms are canceled by choosing:
- -
- For the last three terms that are functions of θs and θ, each of them can generate an electromagnetic torque through the interaction of both magnetic fields. This can be achieved by choosing the following relationship between pr to ps and Ns [30]:
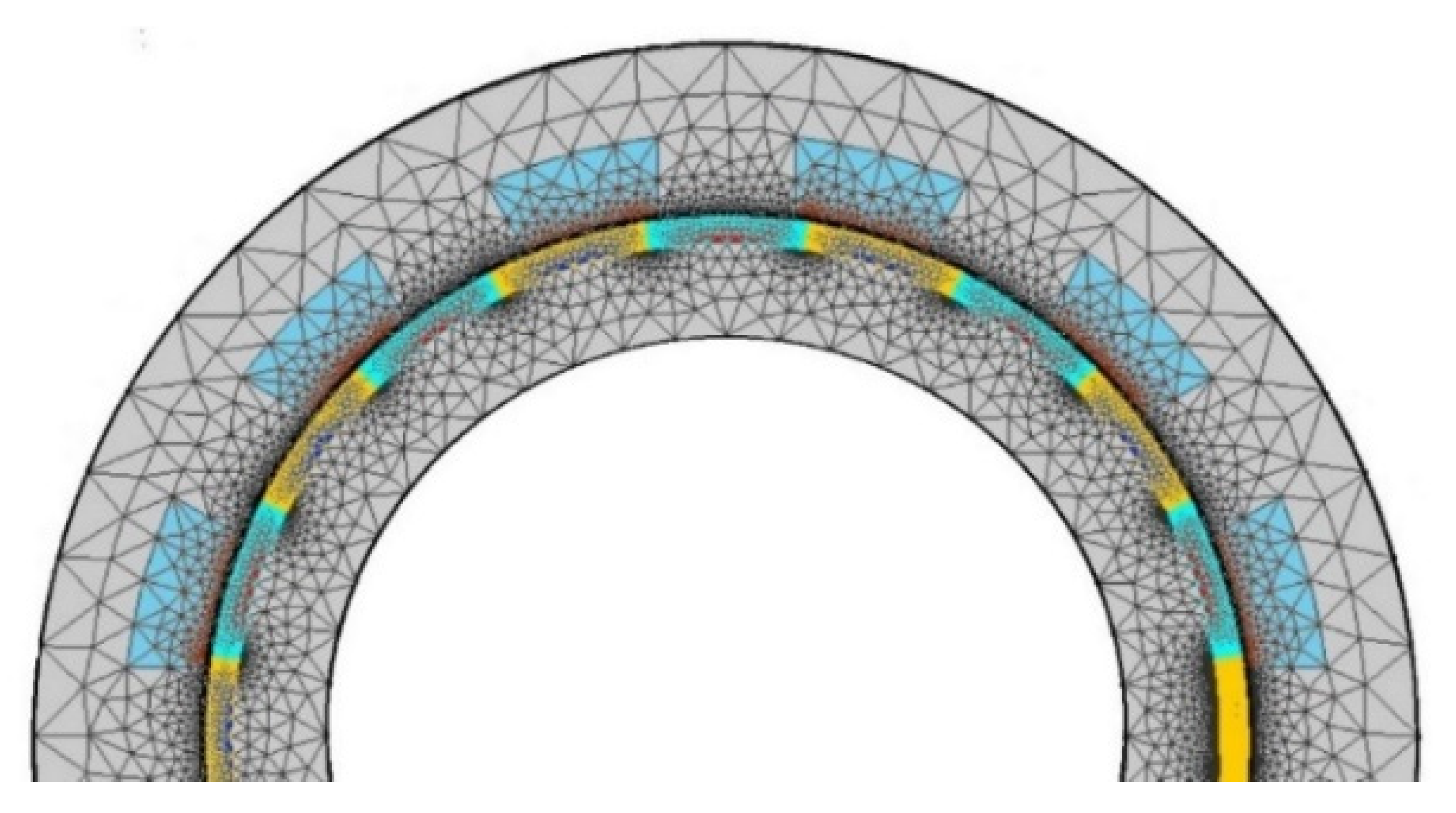
3. Motor Design
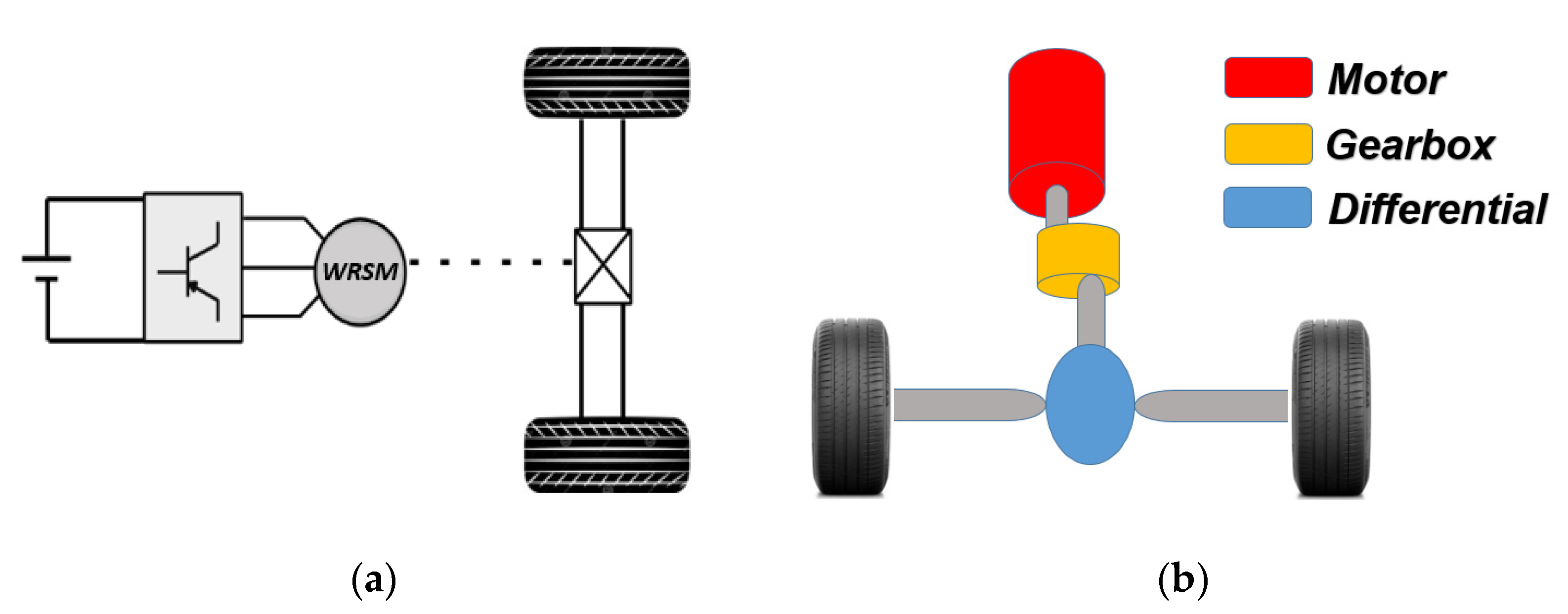
3.1. Specifications of the Application
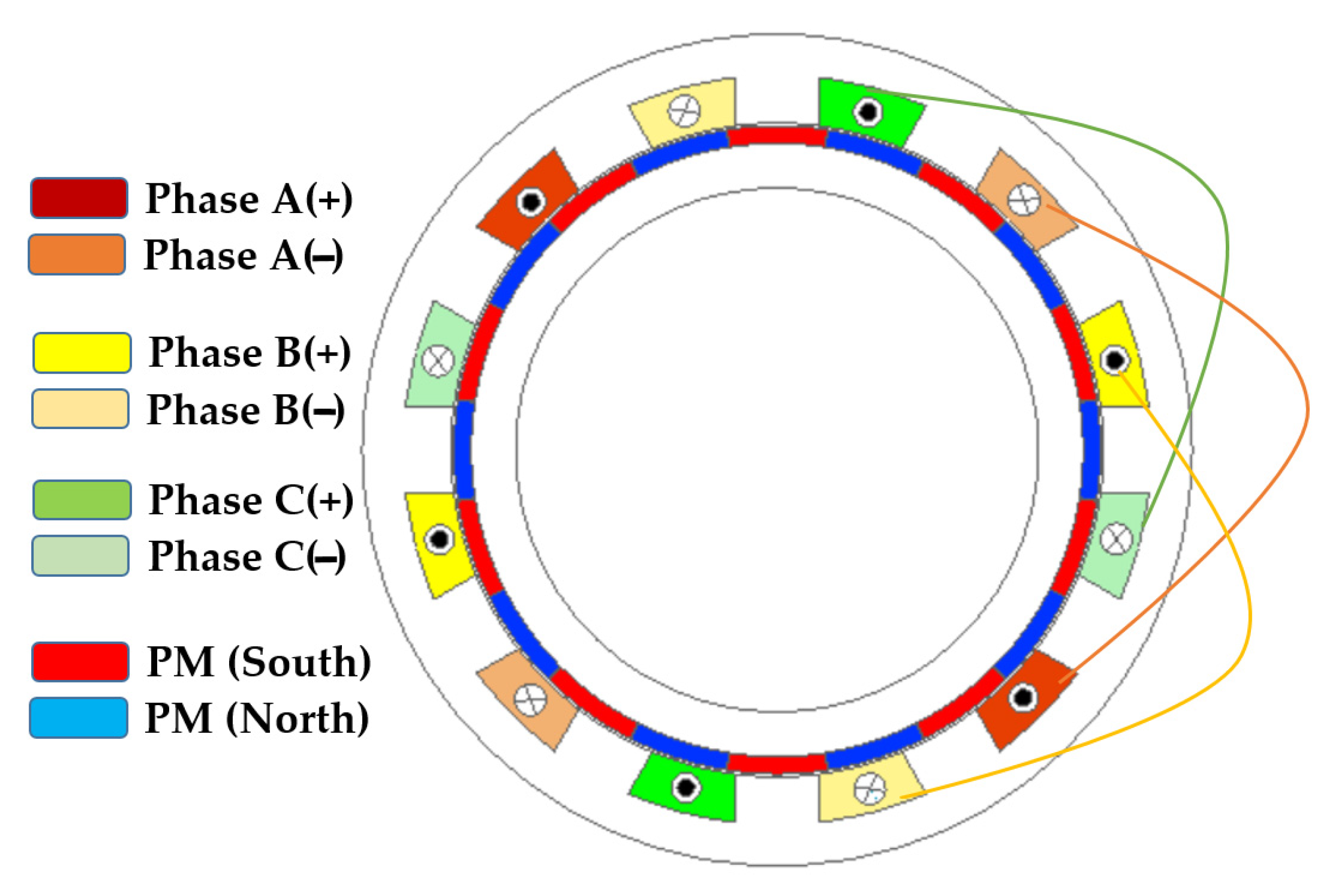
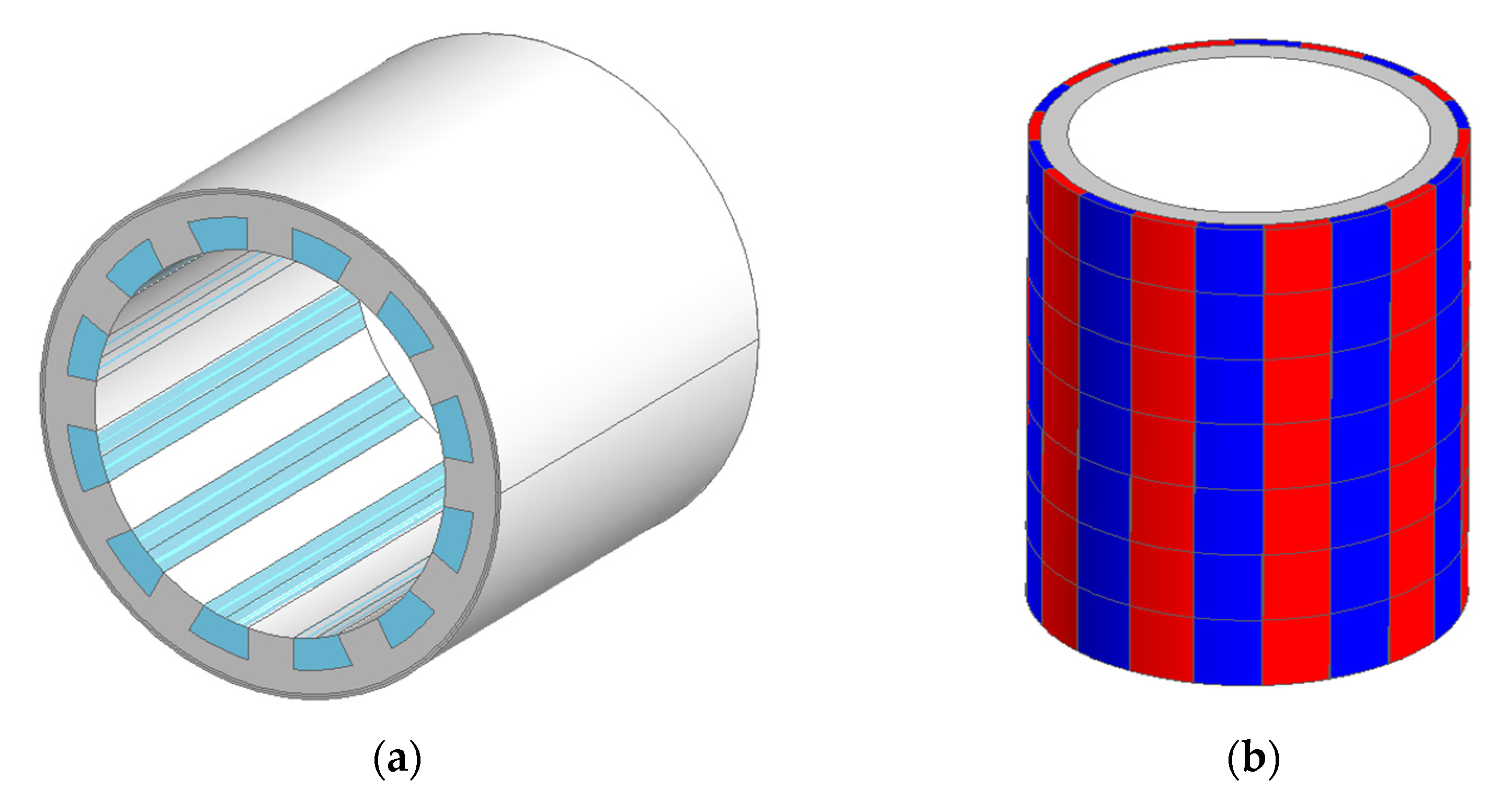
3.2. Design of the Prototype
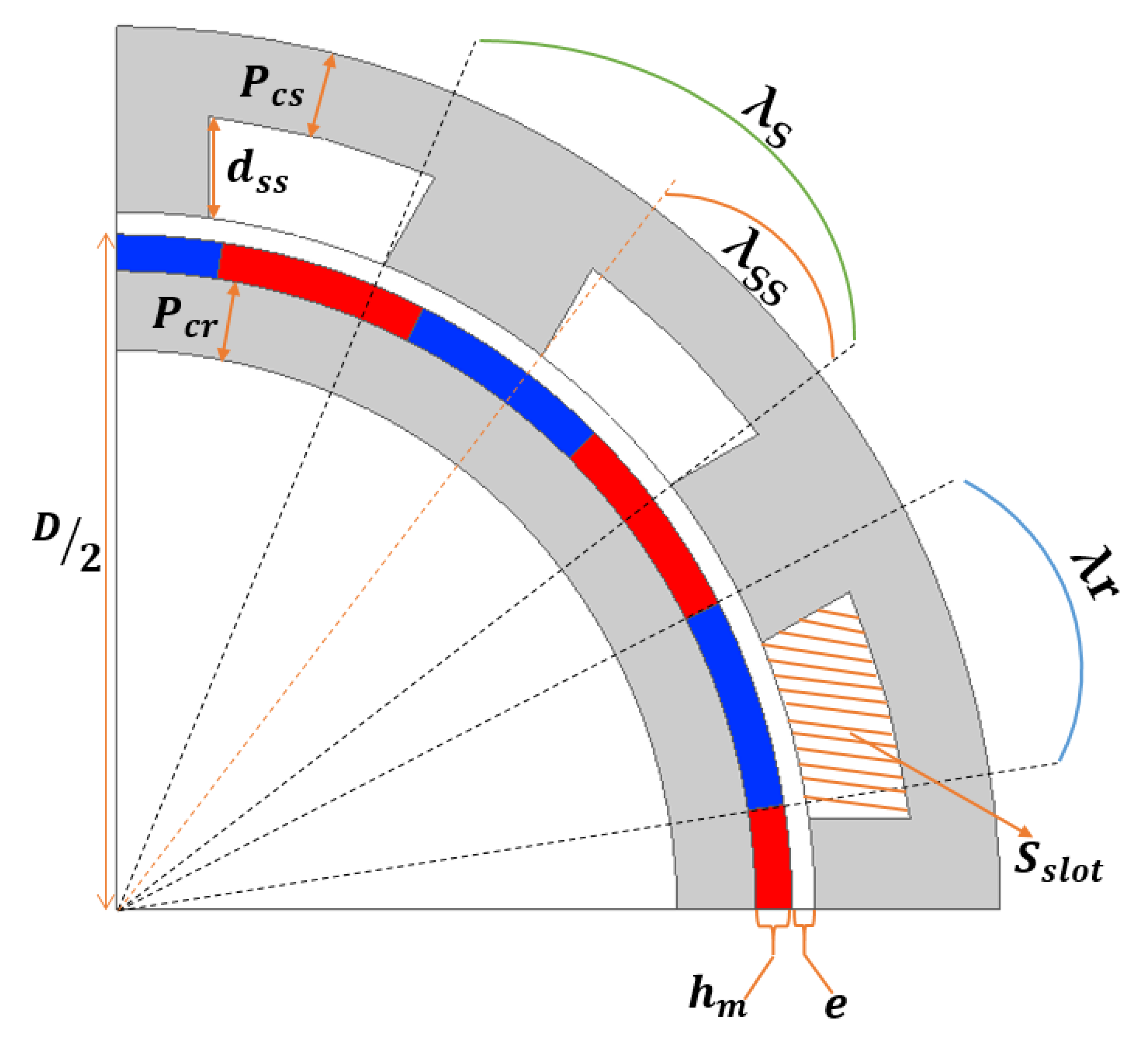
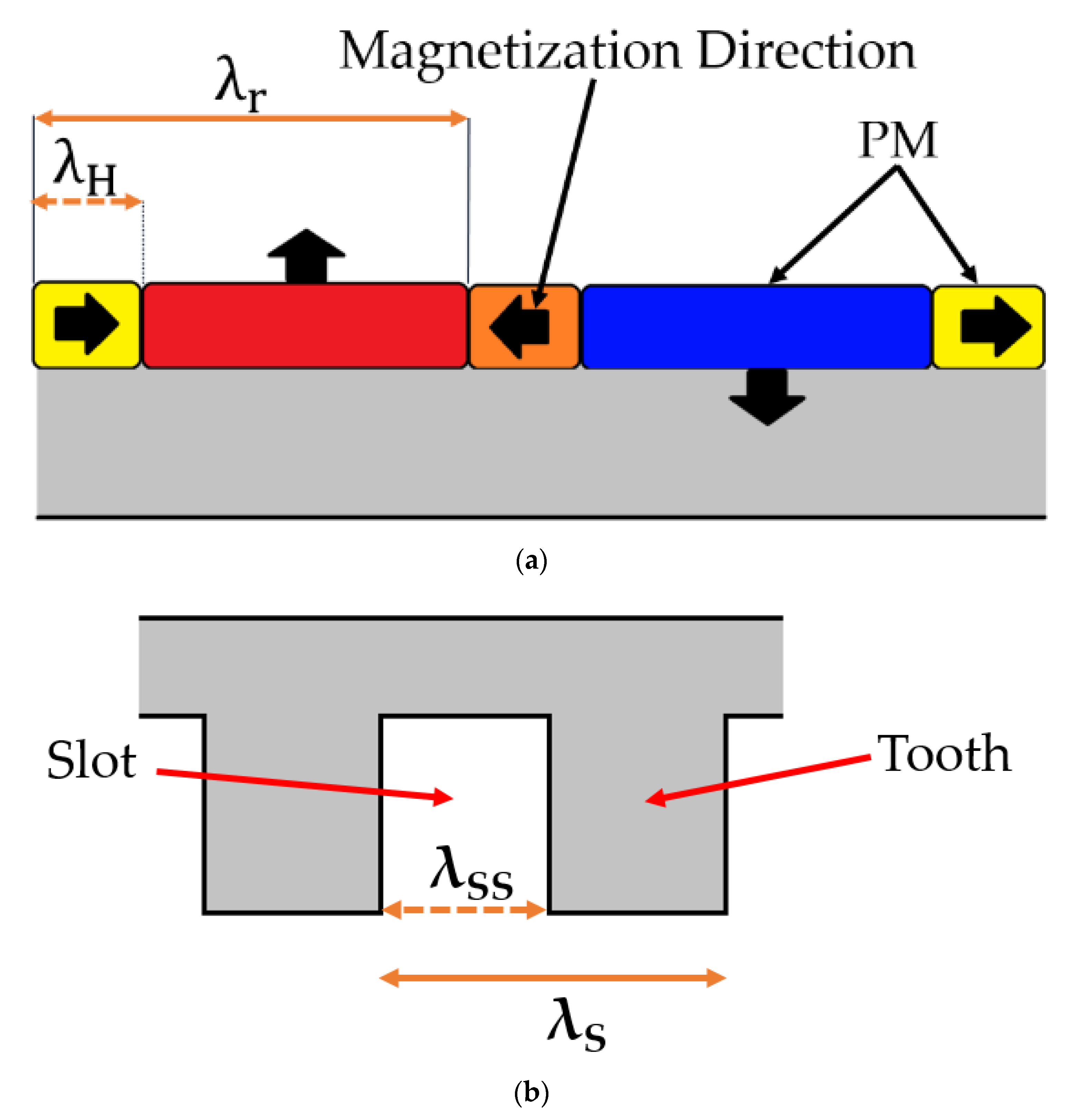
3.3. Parameters to Optimize the PMVM
4. Sensitivity Analysis of the Design Parameters
5. Study at No Load
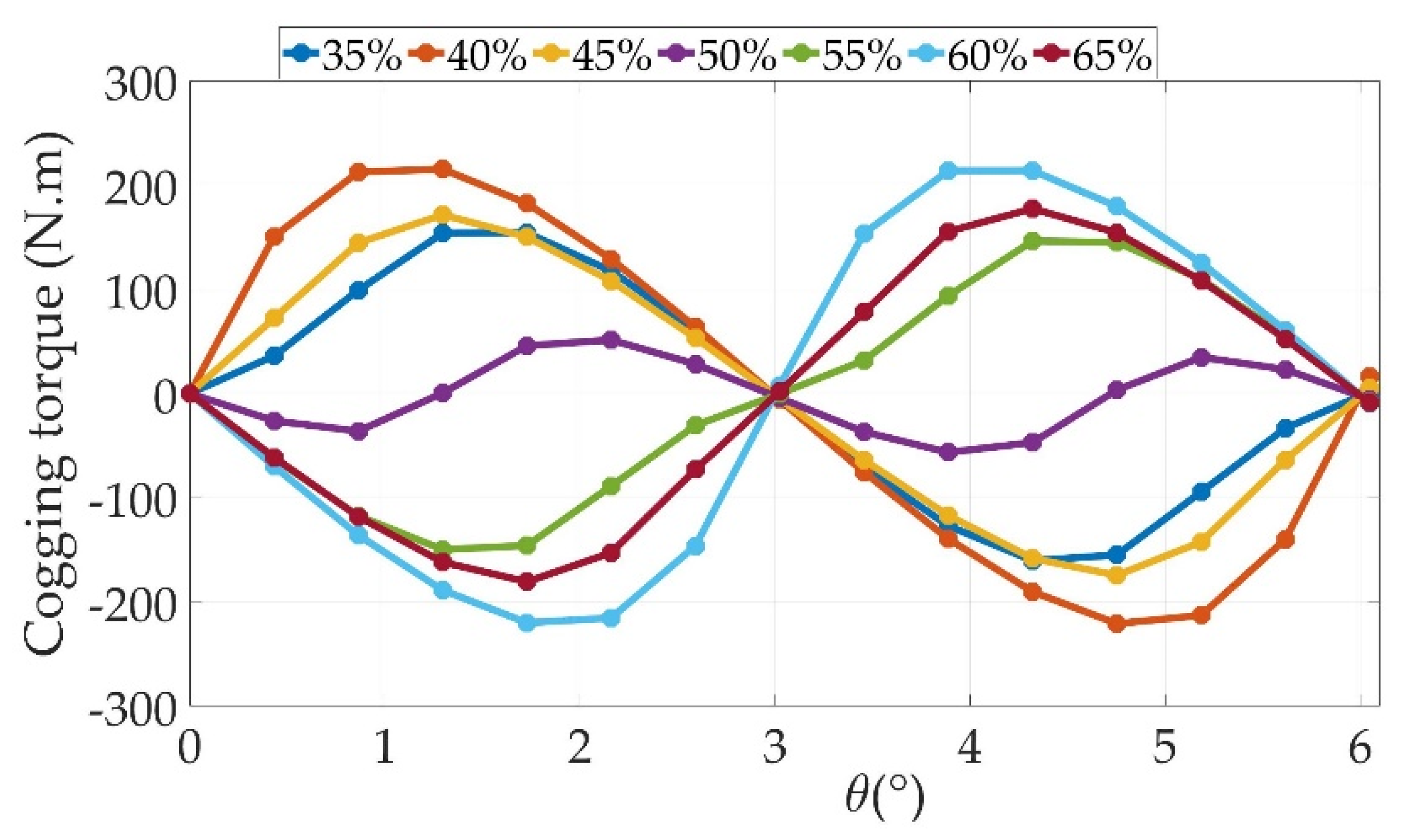
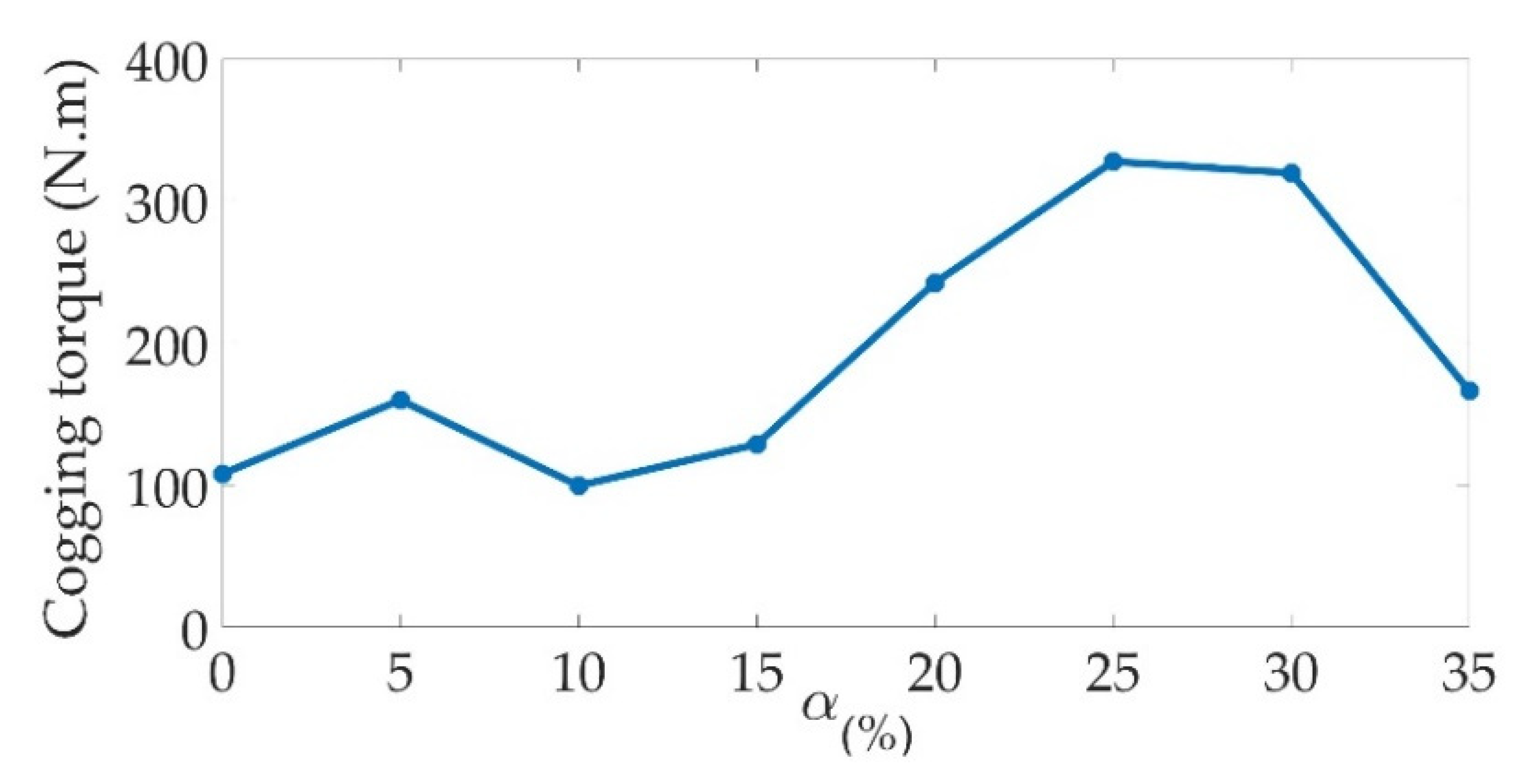
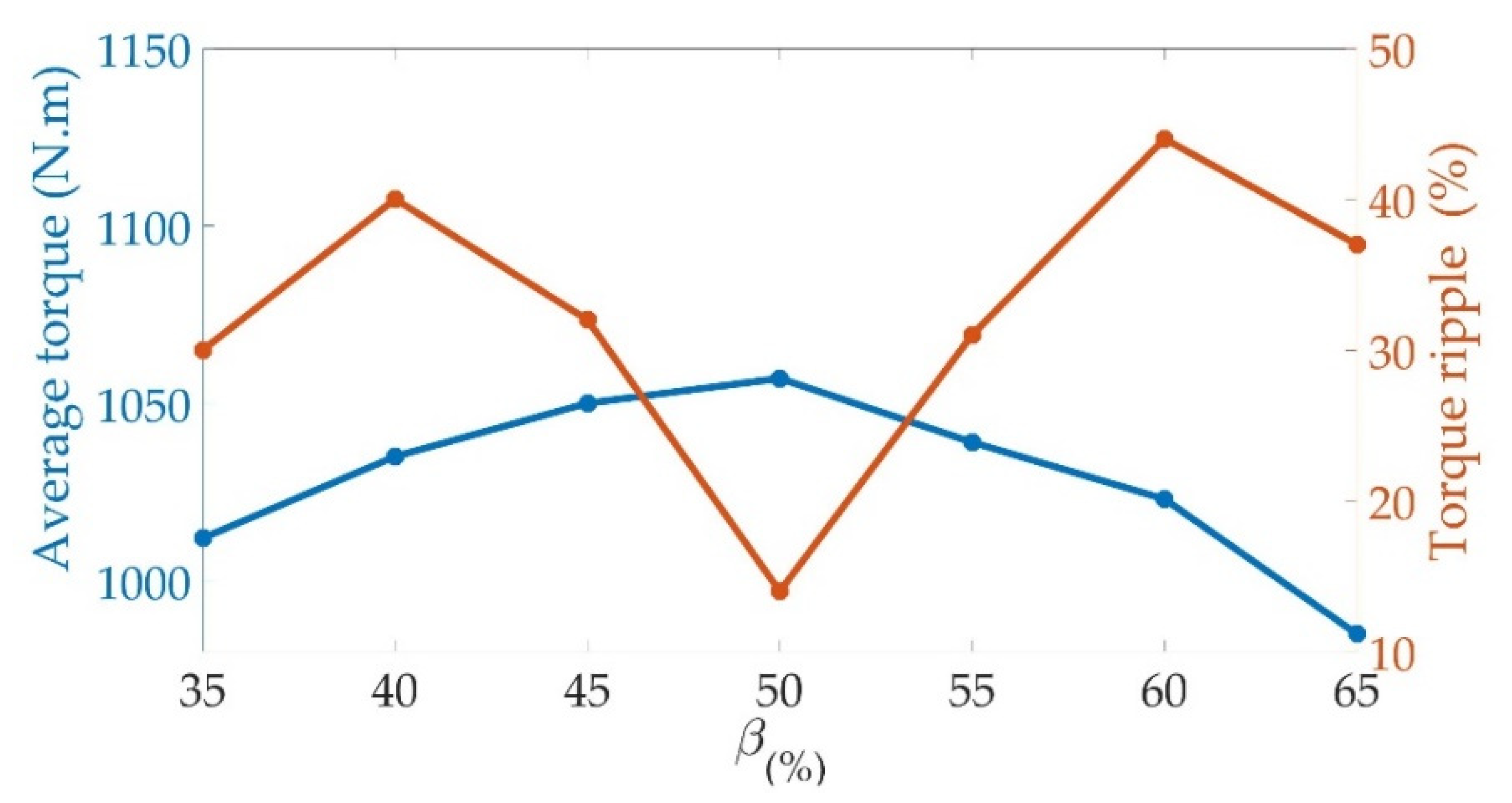
5.1. Impact of Ratio Slot Opening
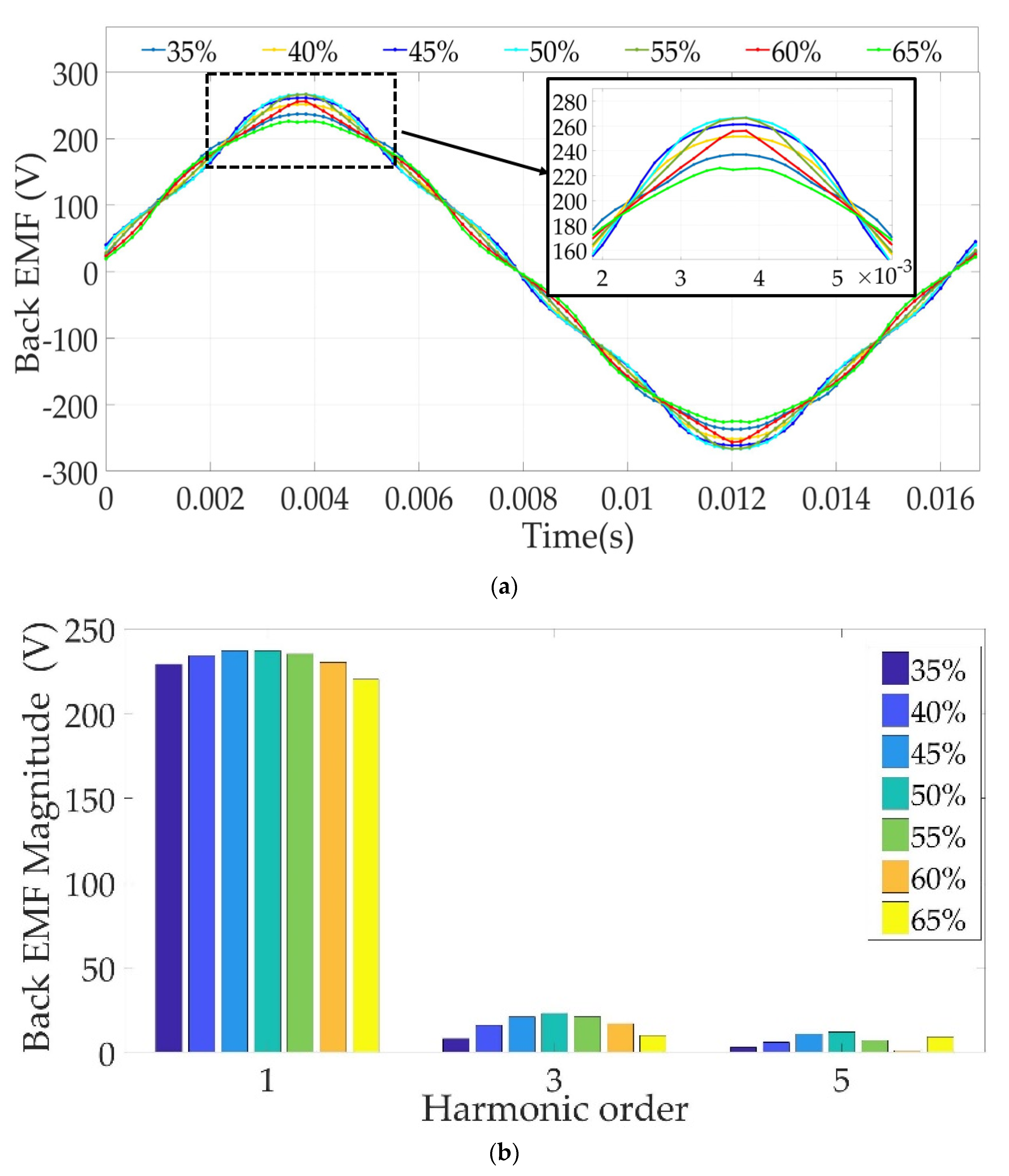
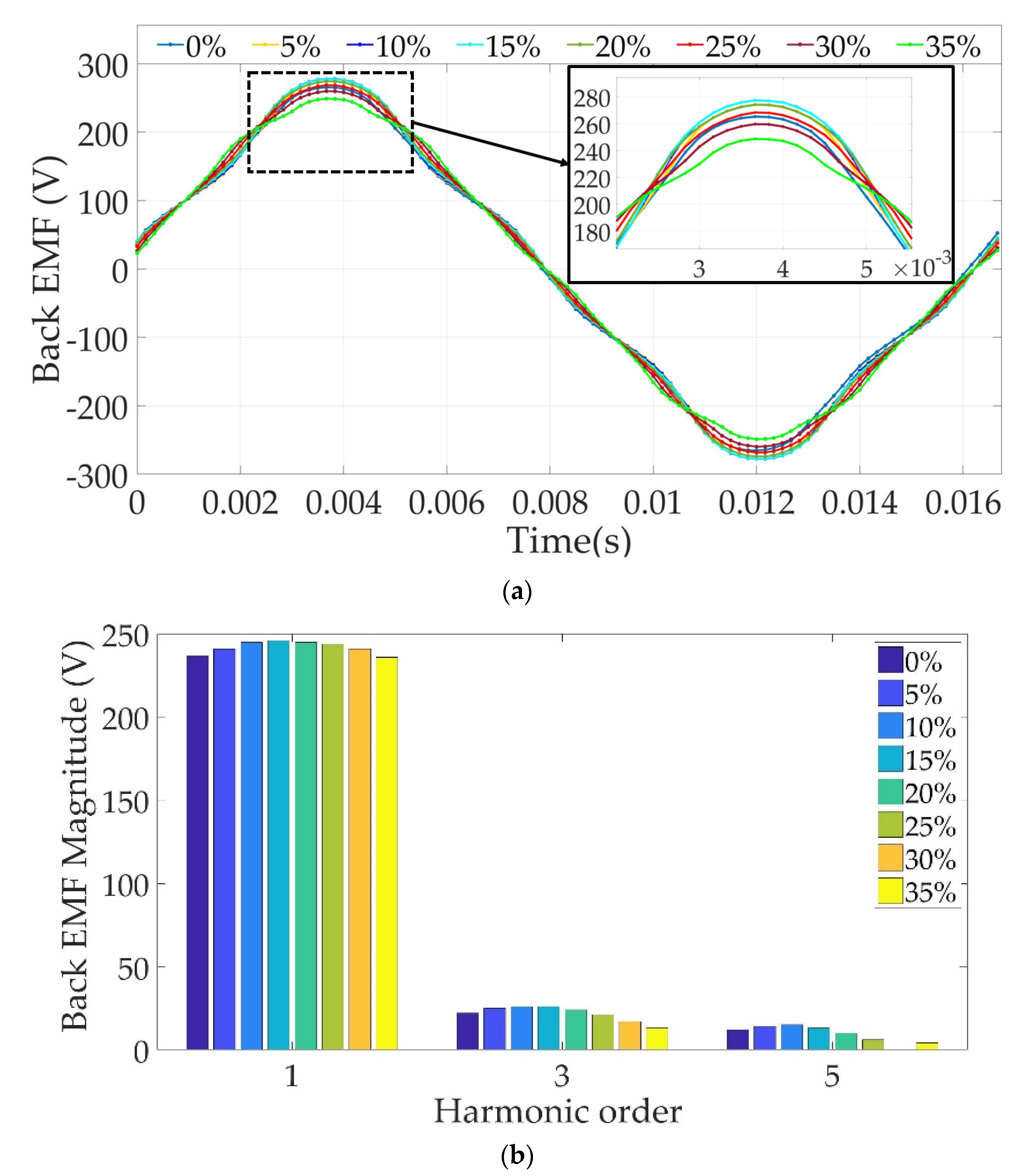
5.2. Impact of Permanent-Magnet (PM) Halbach Arrangement
6. Study at Load
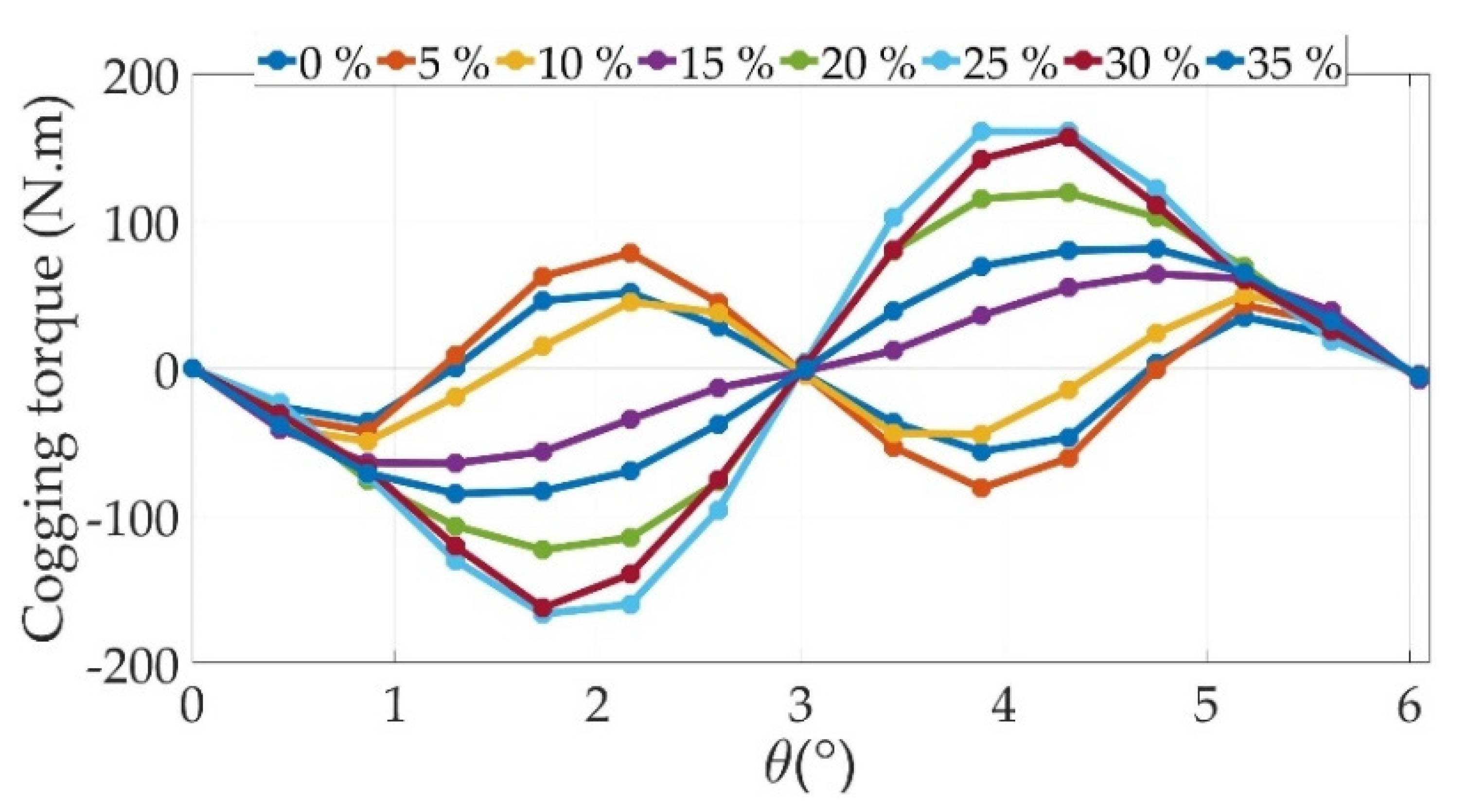
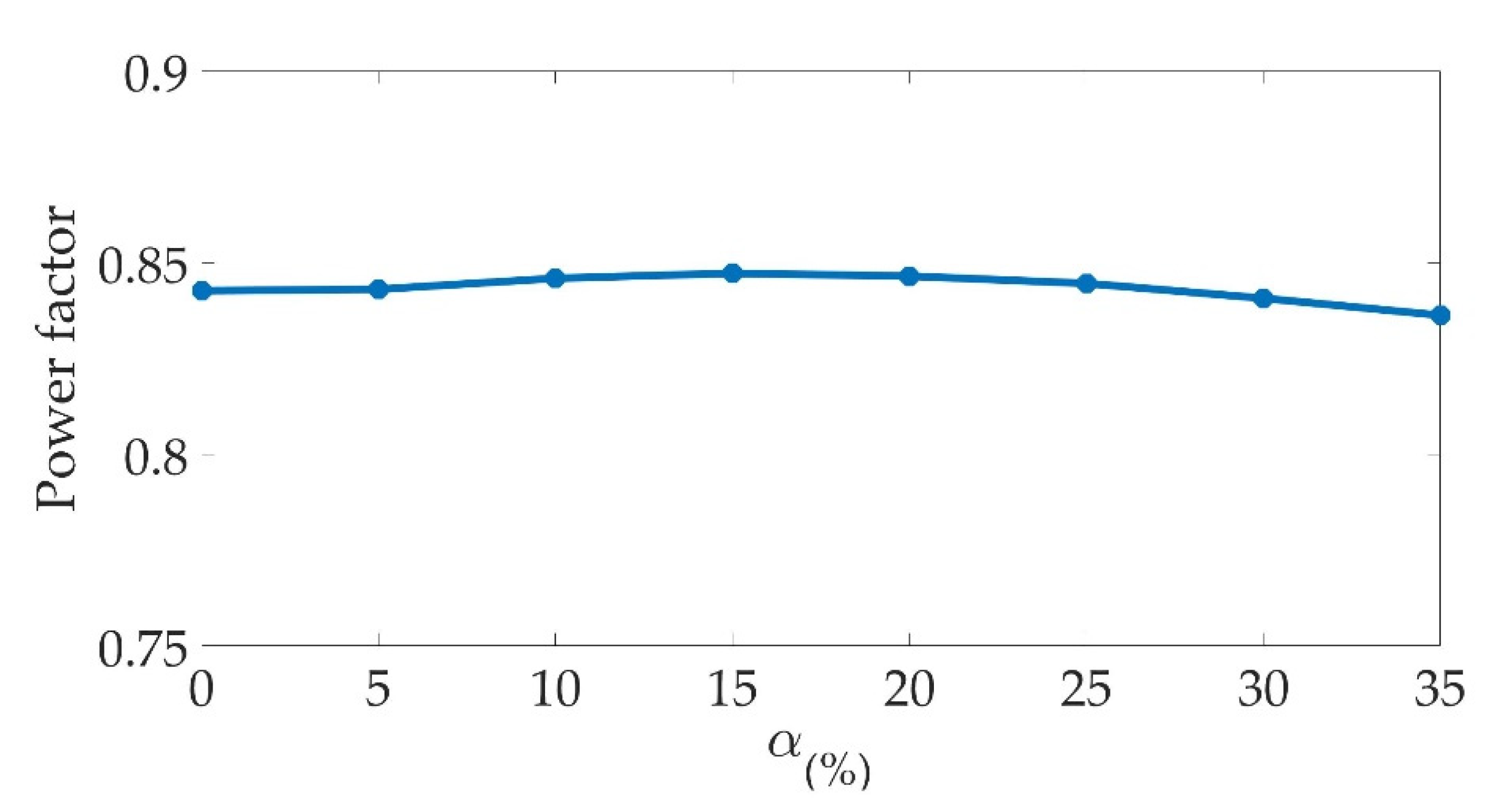
6.1. Impact of Ratio Slot Opening
6.2. Impact of Permanent-Magnet (PM) Halbach Arrangement
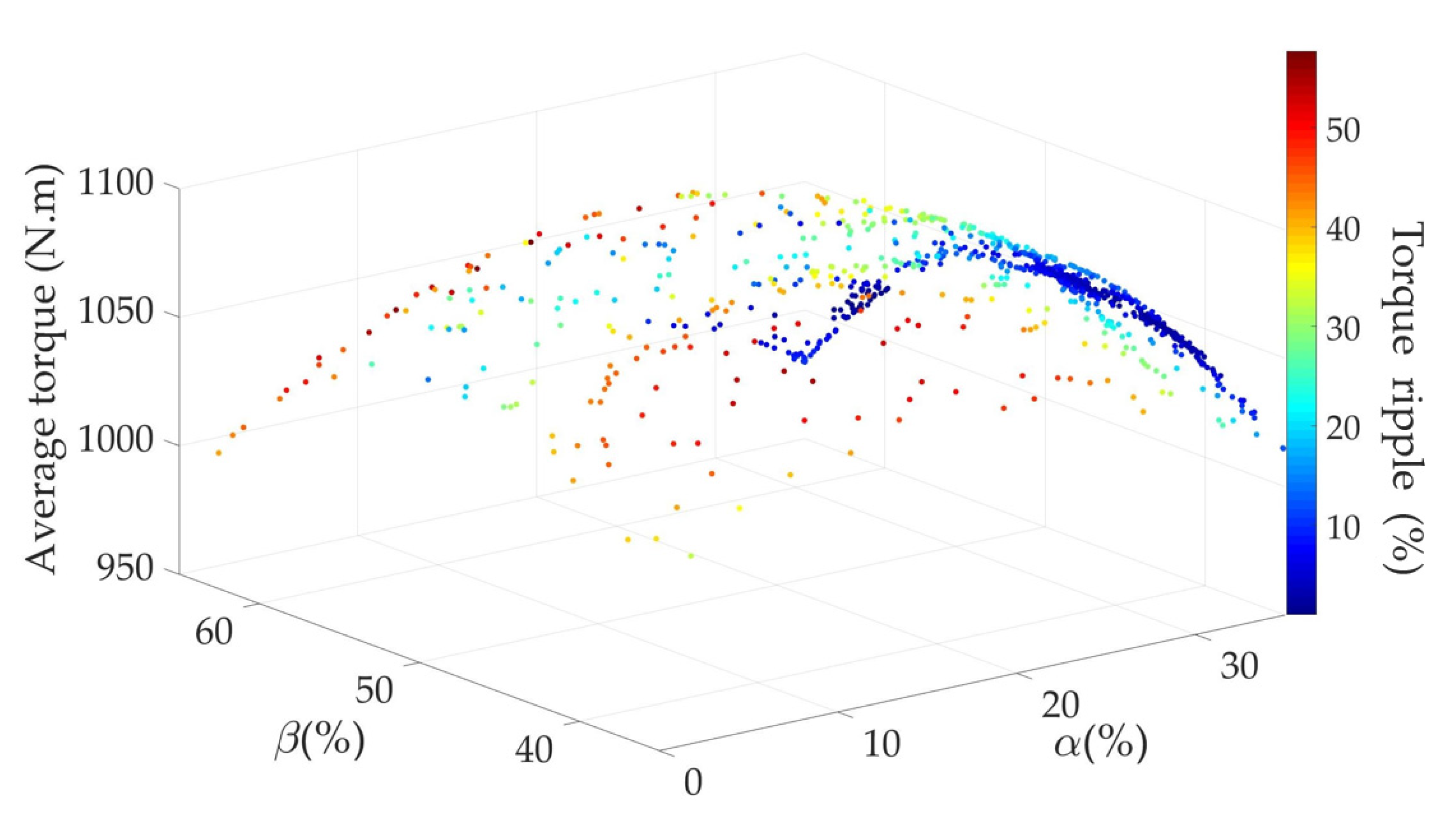
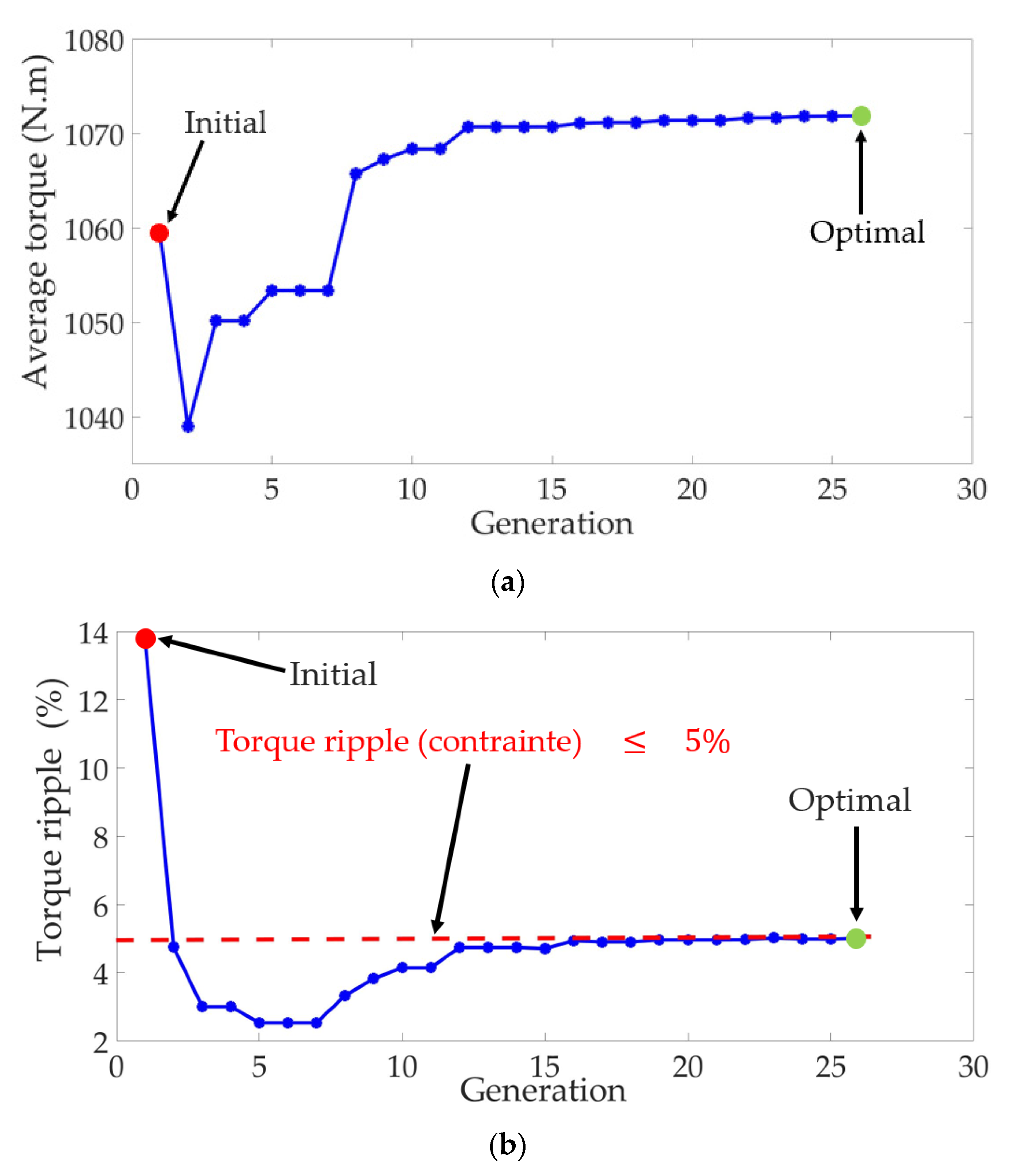
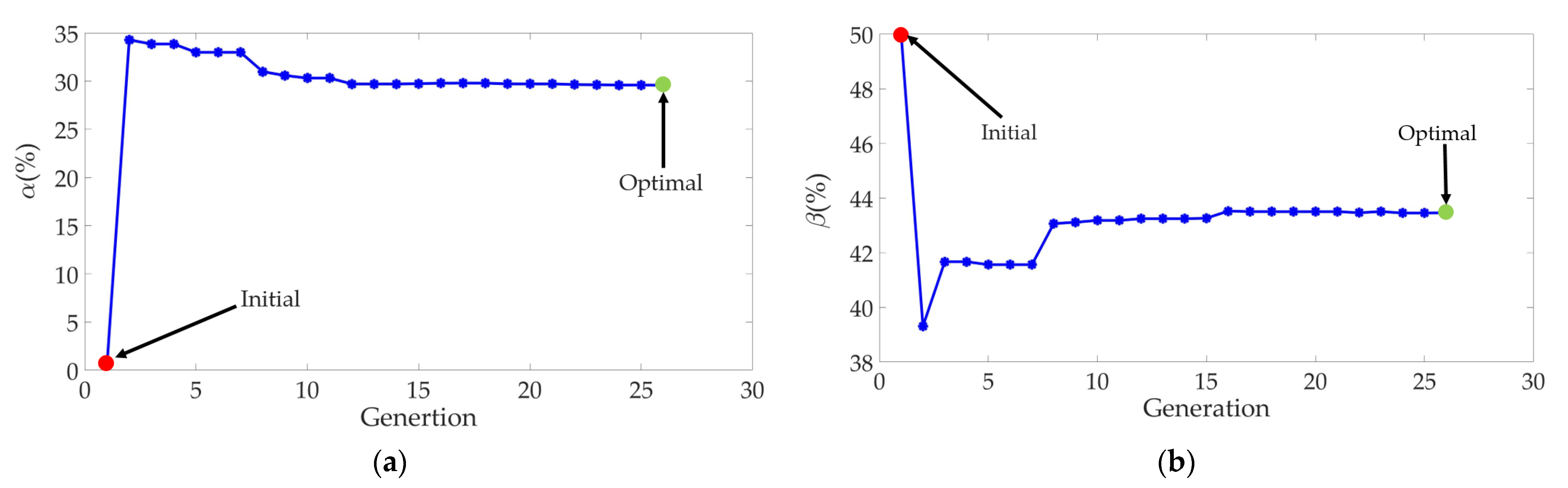
7. Optimization of the Prototype
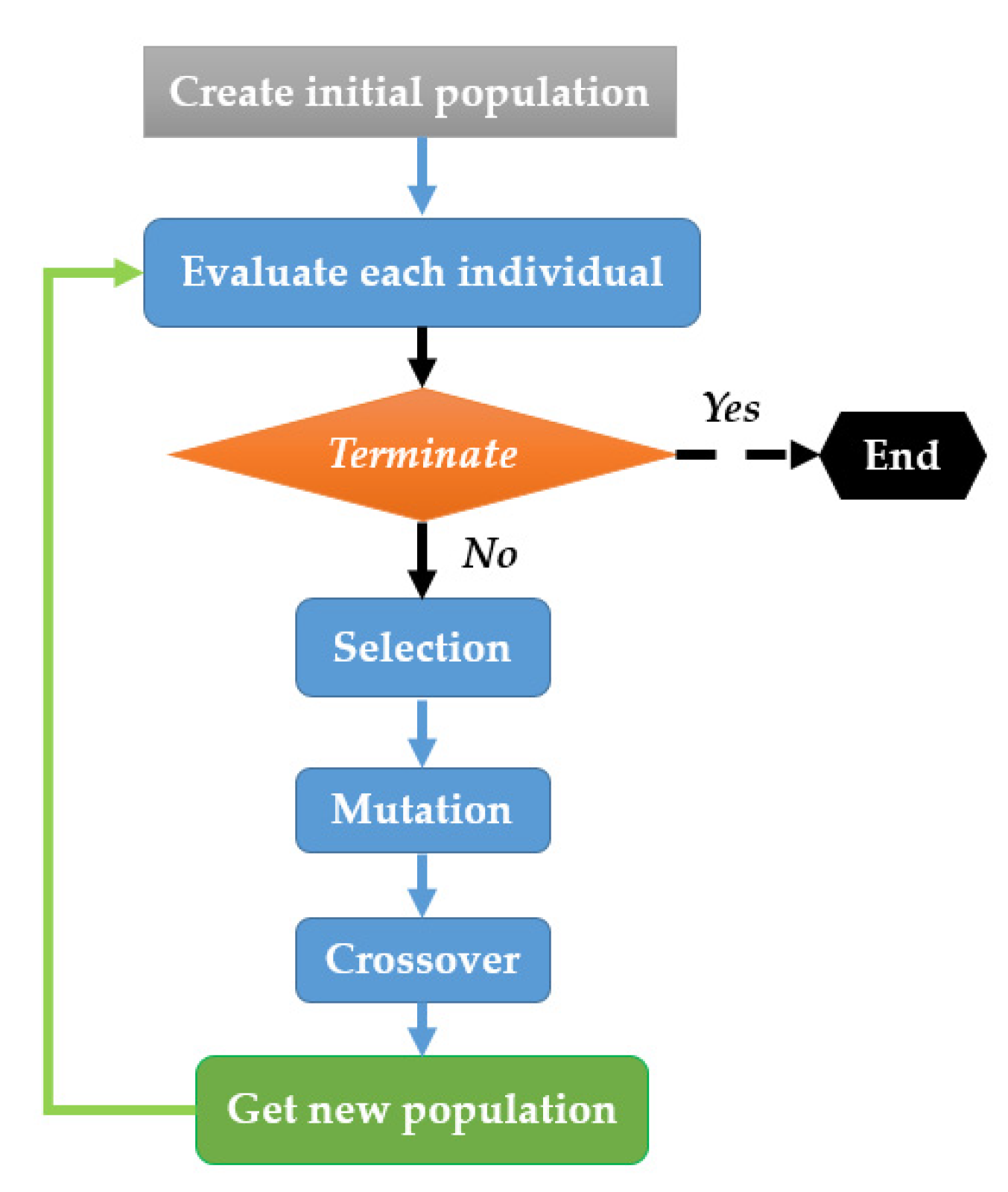
Design and Optimization Method
- -
- Randomly generate the base population.
- -
- Evaluate each individual and score it according to its adaptation to the problem.
- -
- Select the individuals that will give offspring. Several methods exist, some of which are probabilistic.
- -
- The selected individuals have a probability of interbreeding and mutating so that the new generation is better adapted to the problem at hand.
- Objective function
- Constraint
- Design variables
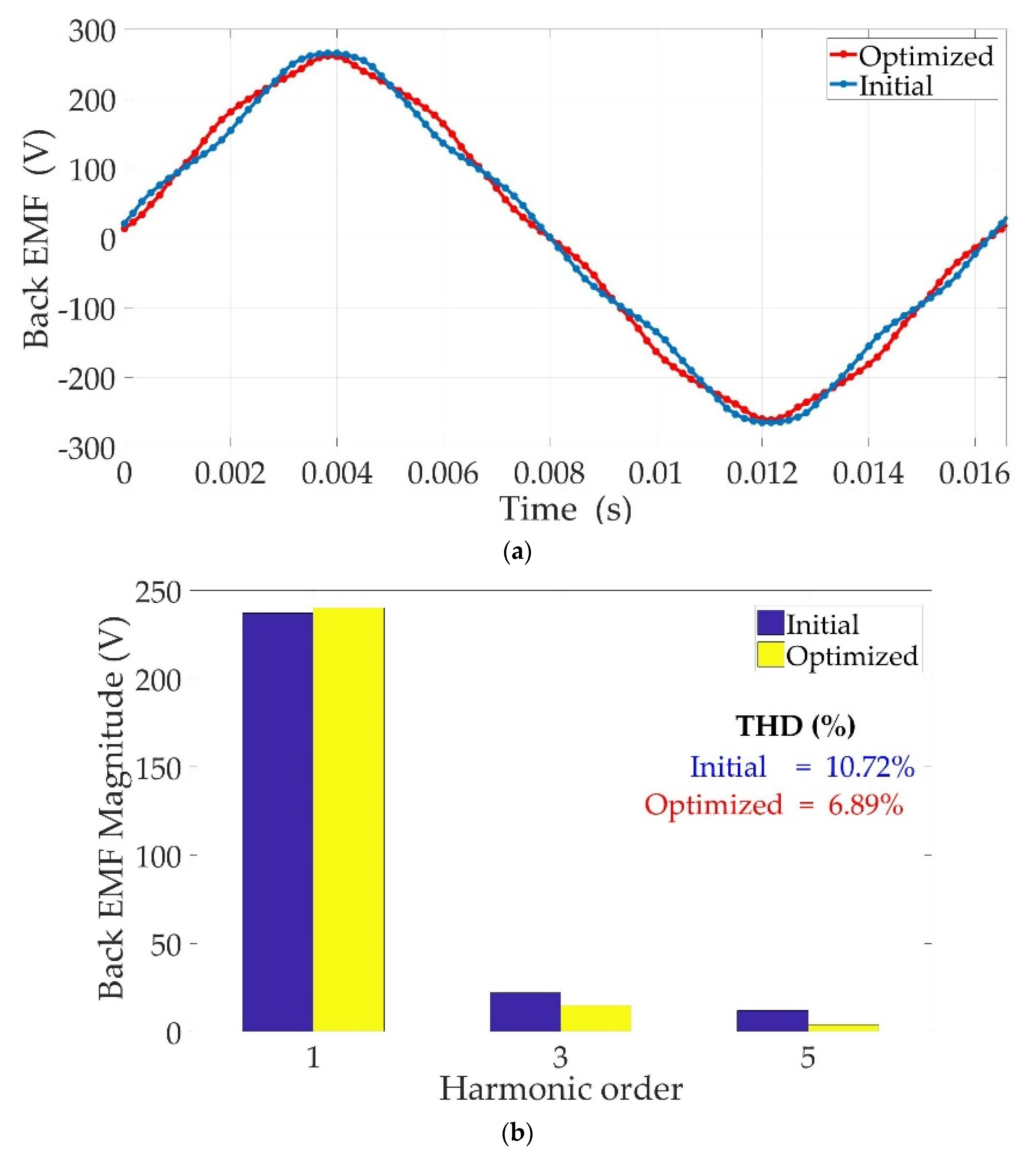
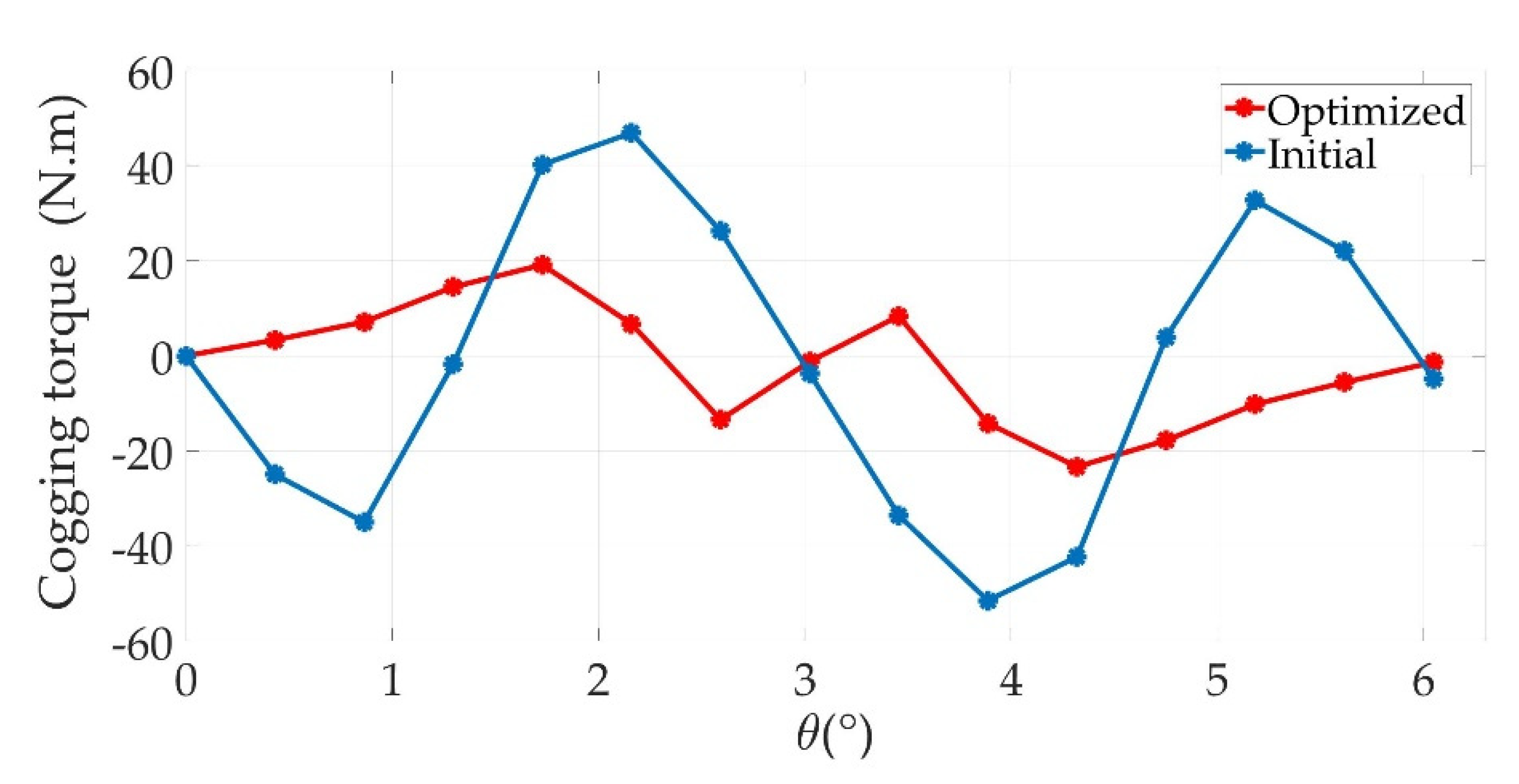
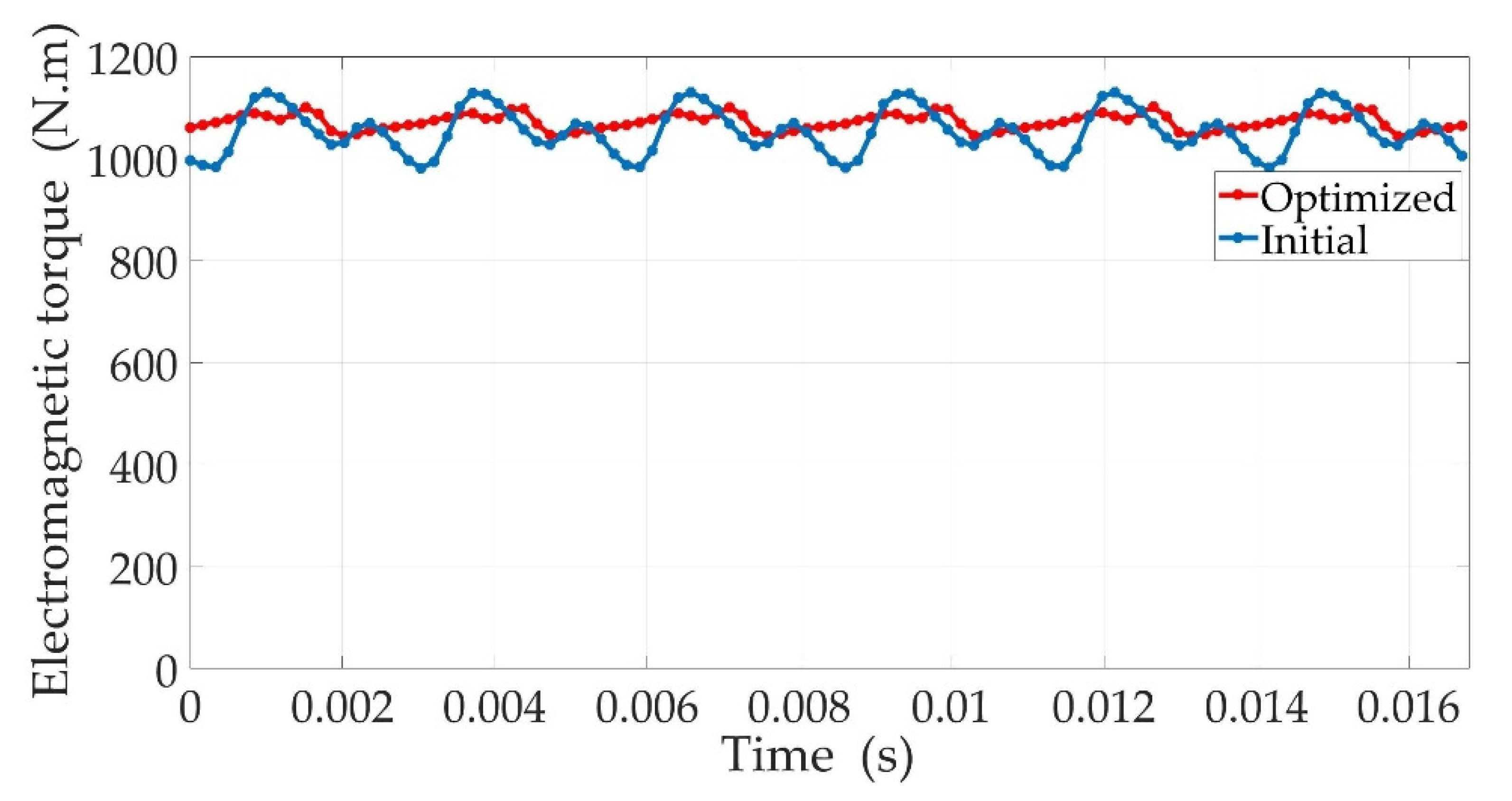
8. Results and Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Chan, C.C. The state of the art of electric, hybrid, and fuel cell vehicles. Proc. IEEE 2002, 90, 247–275. [Google Scholar] [CrossRef]
- El Hadraoui, H.; Zegrari, M.; Chebak, A.; Laayati, O.; Guennouni, N. A Multi-Criteria Analysis and Trends of Electric Motors for Electric Vehicles. World Electr. Veh. J. 2022, 13, 65. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Al Sakka, M.; Geury, T.; El Baghdadi, M.; Dhaens, M.; Al Sakka, M.; Hegazy, O. Review of Fault Tolerant Multi-Motor Drive Topologies for Automotive Applications. Energies 2022, 15, 5529. [Google Scholar] [CrossRef]
- Cai, W.; Wu, X.; Zhou, M.; Liang, Y.; Wang, Y. Review and Development of Electric Motor Systems and Electric Powertrains for New Energy Vehicles. Automot. Innov. 2021, 4, 3–22. [Google Scholar] [CrossRef]
- Chau, K.T. Electric Vehicle Machines and Drives: Design, Analysis and Application; John Wiley & Sons: Solaris South Tower, Singapore, 2015. [Google Scholar]
- Chasiotis, I.D.; Karnavas, Y.L. Designing High Power Density In-Wheel PMSM for Sustainable Hybrid Electric Vehicles. In Proceedings of the 2019 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Athens, Greece, 22–23 April 2019. [Google Scholar]
- Iyer, L.V.; Minaker, B.; Mukherjee, K.; Tjong, J.; Kar, N.C. On-board direct-drive surface permanent magnet synchronous machine with fractional-slot concentrated windings for electric vehicles. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016. [Google Scholar] [CrossRef]
- Xu, S.; Wei, L.; Zhang, X.; Bai, Z.; Jiao, Y. Research on Multi-Mode Drive Optimization Control Strategy of Four-Wheel-Drive Electric Vehicles with Multiple Motors. Sustainability 2022, 14, 7378. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, B.; Huang, Y.; Semail, E.; Nguyen, N.K. Quantitative Comparisons of Outer-Rotor Permanent Magnet Machines of Different Structures/Phases for In-Wheel Electrical Vehicle Application. Energies 2022, 15, 6688. [Google Scholar] [CrossRef]
- Watts, A.; Vallance, A.; Whitehead, A.; Hilton, C.; Fraser, A. The Technology and Economics of In-Wheel Motor. SAE Intern. J. Passeng. Cars-Electron. Electr. Syst. 2010, 3, 37. [Google Scholar]
- Jung, Y.-H.; Park, M.-R.; Kim, K.-O.; Chin, J.-W.; Hong, J.-P.; Lim, M.-S. Design of High-Speed Multilayer IPMSM Using Ferrite PM for EV Traction Considering Mechanical and Electrical Characteristics. IEEE Trans. Ind. Appl. 2020, 57, 327–339. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, B.; Qu, R.; Li, D.; Li, J.; Huo, Y. Comparative Thermal Analysis of IPMSMs With Integral-Slot Distributed-Winding (ISDW) and Fractional-Slot Concentrated-Winding (FSCW) for Electric Vehicle Application. IEEE Trans. Ind. Appl. 2019, 55, 3577–3588. [Google Scholar] [CrossRef]
- Aiso, K.; Kan, A. Performance Comparison of High-Speed Motors for Electric Vehicle. World Electr. Veh. J. 2022, 13, 57. [Google Scholar] [CrossRef]
- Jahns, T.M. The expanding role of PM machines in direct-drive applications. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar] [CrossRef]
- Kabasawa, A.; Takahashi, K. Development of the IMA Motor for the V6 Hybrid Midsize Sedan. In Proceedings of the SAE World Congress, Detroit, MI, USA, 11–14 April 2005. [Google Scholar]
- Toba, A.; Lipo, T.A. Novel dual-excitation permanent magnet vernier machine. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999. [Google Scholar]
- Liu, C.; Zhong, J.; Chau, K.T. A Novel Flux-Controllable Vernier Permanent-Magnet Machine. IEEE Trans. Magn. 2011, 47, 4238–4241. [Google Scholar] [CrossRef]
- Qu, R.; Li, D.; Wang, J. Relationship between magnetic gears and vernier machines. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar]
- Zhang, J.; Tounzi, A.; Delarue, P.; Piriou, F.; Leontidis, V.; Dazin, A.; Caignaert, G.; Libaux, A. Quantitative Design of a High Performance Permanent Magnet Vernier Generator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Kim, B.; Lipo, T.A. Operation and Design Principles of a PM Vernier Motor. IEEE Trans. Ind. Appl. 2014, 50, 3656–3663. [Google Scholar] [CrossRef]
- Moldovan, D.V.; Jurca, F.N.; Marţiş, C.S.; Minciunescu, P.; Vărăticeanu, B. The Influence of Permanent Magnets’ Position in the Double Stator Vernier Machine’s Performances. In Proceedings of the 2019 Electric Vehicles International Conference (EV), Bucharest, Romania, 3–4 October 2019. [Google Scholar]
- Liu, C.; Chau, K.T.; Zhang, Z. Novel Design of Double-Stator Single-Rotor Magnetic-Geared Machines. IEEE Trans. Magn. 2012, 48, 4180–4183. [Google Scholar] [CrossRef]
- Guendouz, W.; Tounzi, A.; Rekioua, T. Analysis of PM Vernier machine prototypes aimed at a direct drive operating of EV. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022. [Google Scholar]
- Jia, L.; Lin, M.; Le, W.; Li, N.; Kong, Y. Dual-Skew Magnet for Cogging Torque Minimization of Axial Flux PMSM With Segmented Stator. IEEE Trans. Magn. 2020, 56, 1–6. [Google Scholar] [CrossRef]
- Cao, L.; Zuo, Y.; Xie, S.; Hoang, C.C.; Han, B.S.; Lee, C.H.T. A Comparison of Permanent-Magnet Vernier Motor and Interior Permanent-Magnet Motor for Hybrid Electric Vehicles. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022. [Google Scholar]
- Wu, D.; Xiang, Z.; Zhu, X.; Quan, L.; Jiang, M.; Liu, Y. Optimization Design of Power Factor for an In-Wheel Vernier PM Machine From the Perspective of Air-Gap Harmonic Modulation. IEEE Trans. Ind. Electron. 2020, 68, 9265–9276. [Google Scholar] [CrossRef]
- Adnani, K.; Shafiei, S.; Millimonfared, J.; Moghani, J.S. Modified Unipolar Hybrid Permanent Magnet Vernier Machine Using Halbach Array Configuration. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019. [Google Scholar]
- Altair Engineering Flux 2D & HyperStudy 2022 Software Documentation. Available online: http://fluxmotordoc.altair.com/webroot/uploads/helponline/Documentation/2022/Installation%20guide/Installation_guide_en.pdf (accessed on 1 November 2022).
- Li, Q.; Fan, T. Torque Improvement of External-Rotor Permanent Magnet Machine Using Flux Concentrated Rotor. In Proceedings of the 2018 IEEE International Magnetics Conference (INTERMAG), Singapore, 23–27 April 2018. [Google Scholar]
- Liu, Y.; Li, H.Y.; Zhu, Z.Q. A High-Power Factor Vernier Machine With Coil Pitch of Two Slot Pitches. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Huang, J.; Fu, W.; Niu, S.; Zhao, X. Comparative Analysis of Different Permanent Magnet Arrangements in a Novel Flux Modulated Electric Machine. IEEE Access 2021, 9, 14437–14445. [Google Scholar] [CrossRef]






| Symbol | Parameters (Unit) | Value |
|---|---|---|
| Autonomy NEDC (km) | 370 | |
| Battery Capacity (kw/h) | 42 | |
| Battery voltage (V) | 430 | |
| L/W/H | Length/width/height (mm) | 4084/1730/1562 |
| Vehicle mass (kg) | 1480 | |
| Payload (kg) | 486 | |
| Wheel radius (m) | 0.2 | |
| Gear transmission efficiency (%) | 90 | |
| Gear box ratio | 9.3 | |
| Top speed (km/h) | 135 | |
| Acceleration time (0–100 km/h) (s) | 13.2 |
| Symbol | Parameters (Unit) | Value |
|---|---|---|
| FWD | Forward locomotion | / |
| Peak power (kW) | 65 | |
| Rated power (kW) | 40 | |
| Peak torque (N.m) | 220 | |
| Maximum speed (rpm) | 11,300 | |
| Base speed (rpm) | 3000 | |
| Efficiency (%) | 95 |
| Symbol | Parameters (Unit) | Value |
|---|---|---|
| Peak power (kW) | 58.5 | |
| Rated power (kW) | 36 | |
| Peak torque (N.m) | 1840 | |
| Rated torque (N.m) | 1060 | |
| Maximum speed (rpm) | 1215 | |
| Base speed (rpm) | 322 |
| Symbol | Parameters (Unit) | Value |
|---|---|---|
| m | Phase number - | 3 |
| Number of turns per slot - | 18 | |
| D | Outer rotor diameter (mm) | 240 |
| Thickness of stator yoke (mm) | 20 | |
| Thickness of rotor yoke (mm) | 20 | |
| L | Active length (mm) | 350 |
| Thickness of PM (mm) | 6.5 | |
| e | Thickness of air gap (mm) | 1 |
| Rated current (A) | 80 |
| Formula | Symbol | Terminals Low | Terminals High |
|---|---|---|---|
| / | β | 35% | 65% |
| / | α | 0% | 35% |
| Variable/Objective | Initial | Optimal |
|---|---|---|
| α | 0% | 29.57% |
| β | 50% | 43.46% |
| 1055 N.m | 1073 N.m | |
| 14.08% | 5% | |
| 0.84 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guendouz, W.; Tounzi, A.; Rekioua, T. Design of Quasi-Halbach Permanent-Magnet Vernier Machine for Direct-Drive Urban Vehicle Application. Machines 2023, 11, 136. https://doi.org/10.3390/machines11020136
Guendouz W, Tounzi A, Rekioua T. Design of Quasi-Halbach Permanent-Magnet Vernier Machine for Direct-Drive Urban Vehicle Application. Machines. 2023; 11(2):136. https://doi.org/10.3390/machines11020136
Chicago/Turabian StyleGuendouz, Walid, Abdelmounaim Tounzi, and Toufik Rekioua. 2023. "Design of Quasi-Halbach Permanent-Magnet Vernier Machine for Direct-Drive Urban Vehicle Application" Machines 11, no. 2: 136. https://doi.org/10.3390/machines11020136
APA StyleGuendouz, W., Tounzi, A., & Rekioua, T. (2023). Design of Quasi-Halbach Permanent-Magnet Vernier Machine for Direct-Drive Urban Vehicle Application. Machines, 11(2), 136. https://doi.org/10.3390/machines11020136





