Exponential Local Fisher Discriminant Analysis with Sparse Variables Selection: A Novel Fault Diagnosis Scheme for Industry Application
Abstract
:1. Introduction
- The SELFDA can maximize the between-class separability and reserve the within-class local structure simultaneously through the localization factor. That is means, the multimodality of operating data has been preserved from sample dimension.
- The least absolute shrinkage and selection operator (LASSO) is used to select the responsible variables for SELFDA model effectively. Then the sparse discriminant optimization problem is formulated and solve by minimization-maximization method. Thus, the data characteristics can be well exploited from the variable dimension.
- Besides, the matrix exponential strategy is integrated into the framework of LFDA. As a consequence, the SELFDA method can function well when encountering the common SSS problem in despite of the dimensions of the input samples.
- Although SELFDA is an LFDA-based method, it is able to jointly overcome the two limitations of conventional LFDA. Thus, SELFDA is more feasible and universal in engineering practices. To our best knowledge, this paper is also the first time to leverage the SELFDA for fault classification of real-world diesel engine.
2. Revisit of LFDA
3. Methodology
3.1. Problem Statement and Motivation
3.2. SELFDA
3.3. Discriminant Power of SELFDA
| Algorithm 1 SELFDA |
| Input: Training data Output: The data matrix projection
|
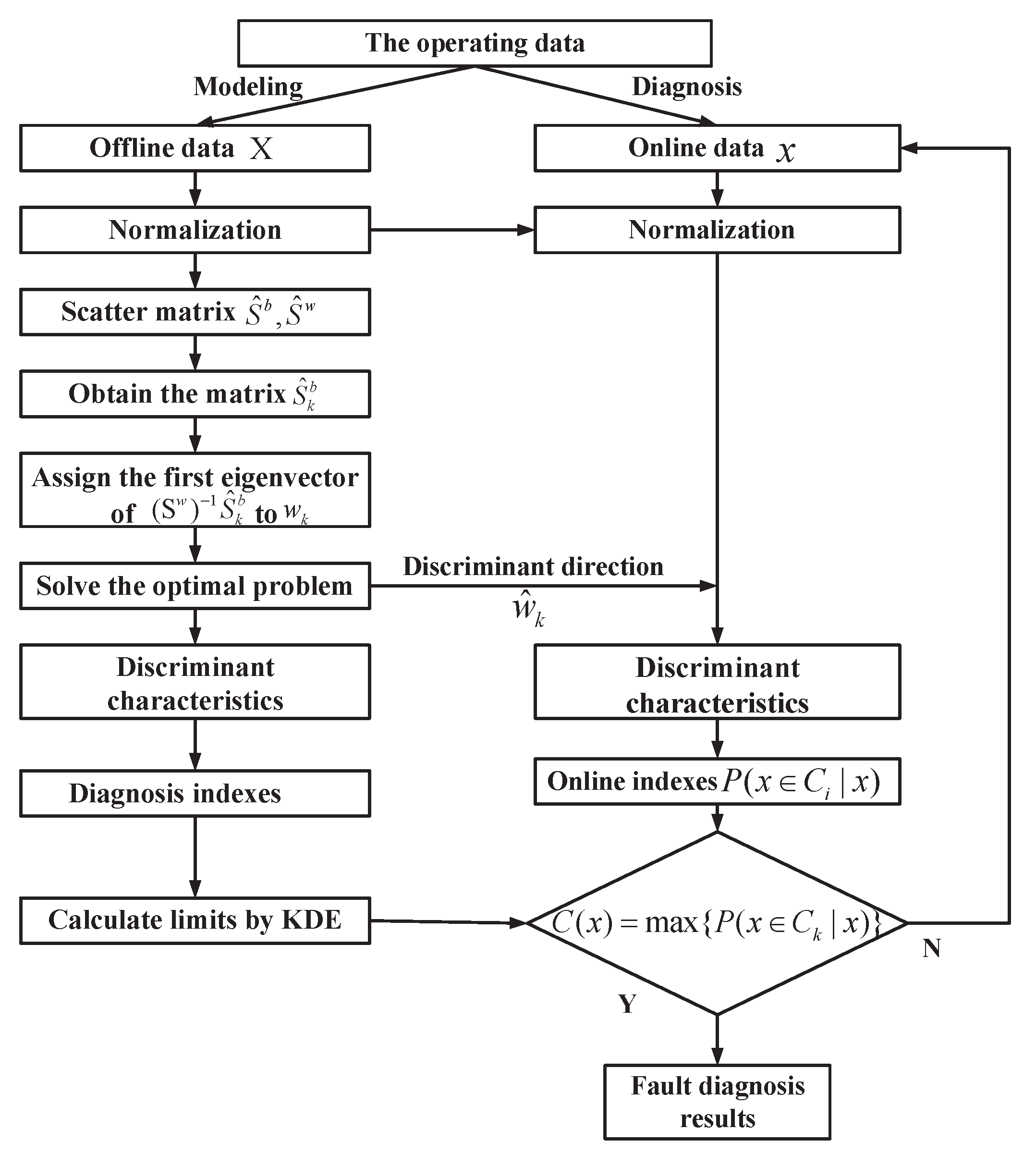
3.4. SELFDA-Based Fault Diagnosis Scheme
4. Experimental Results and Discussion
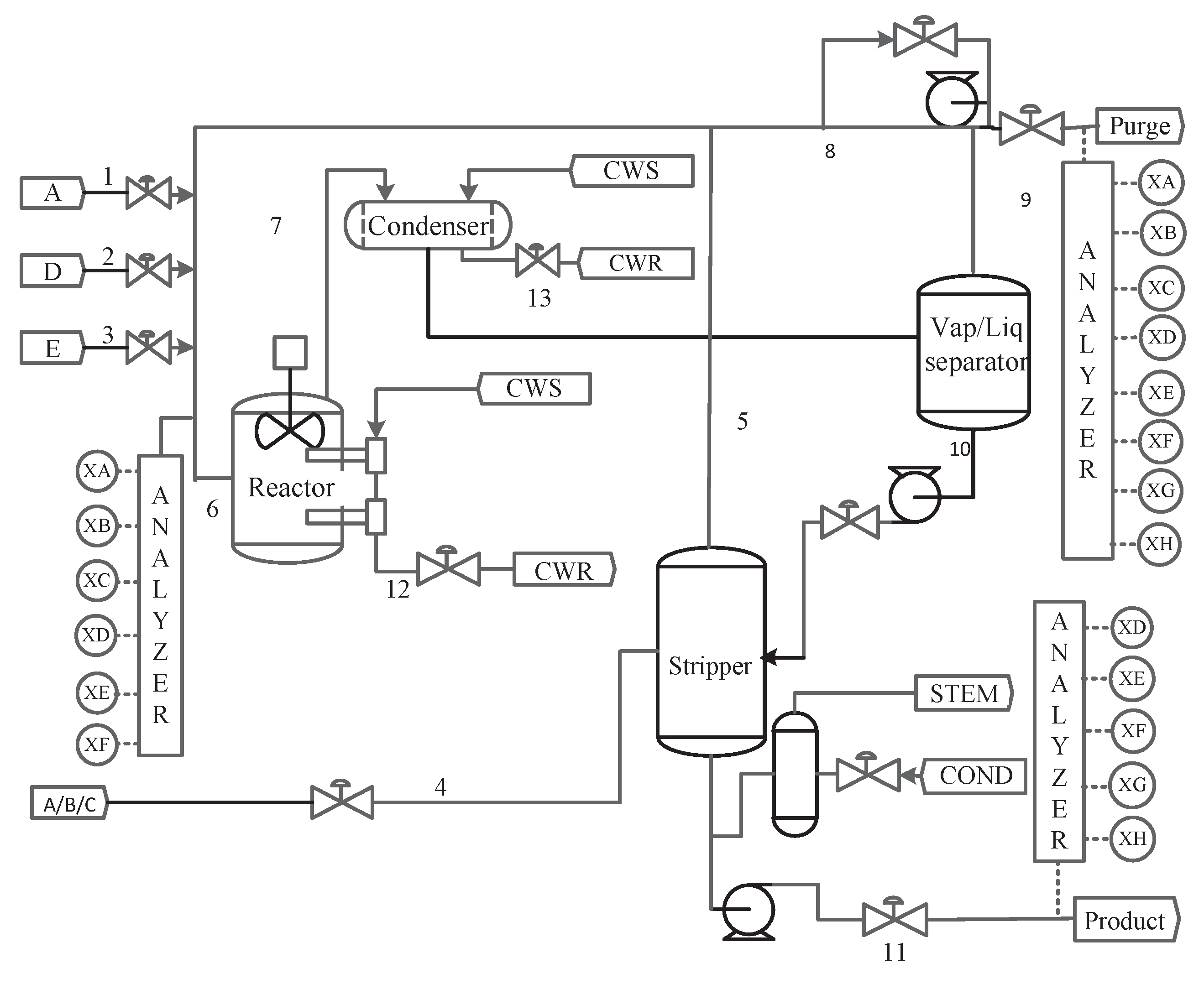
4.1. TE Process
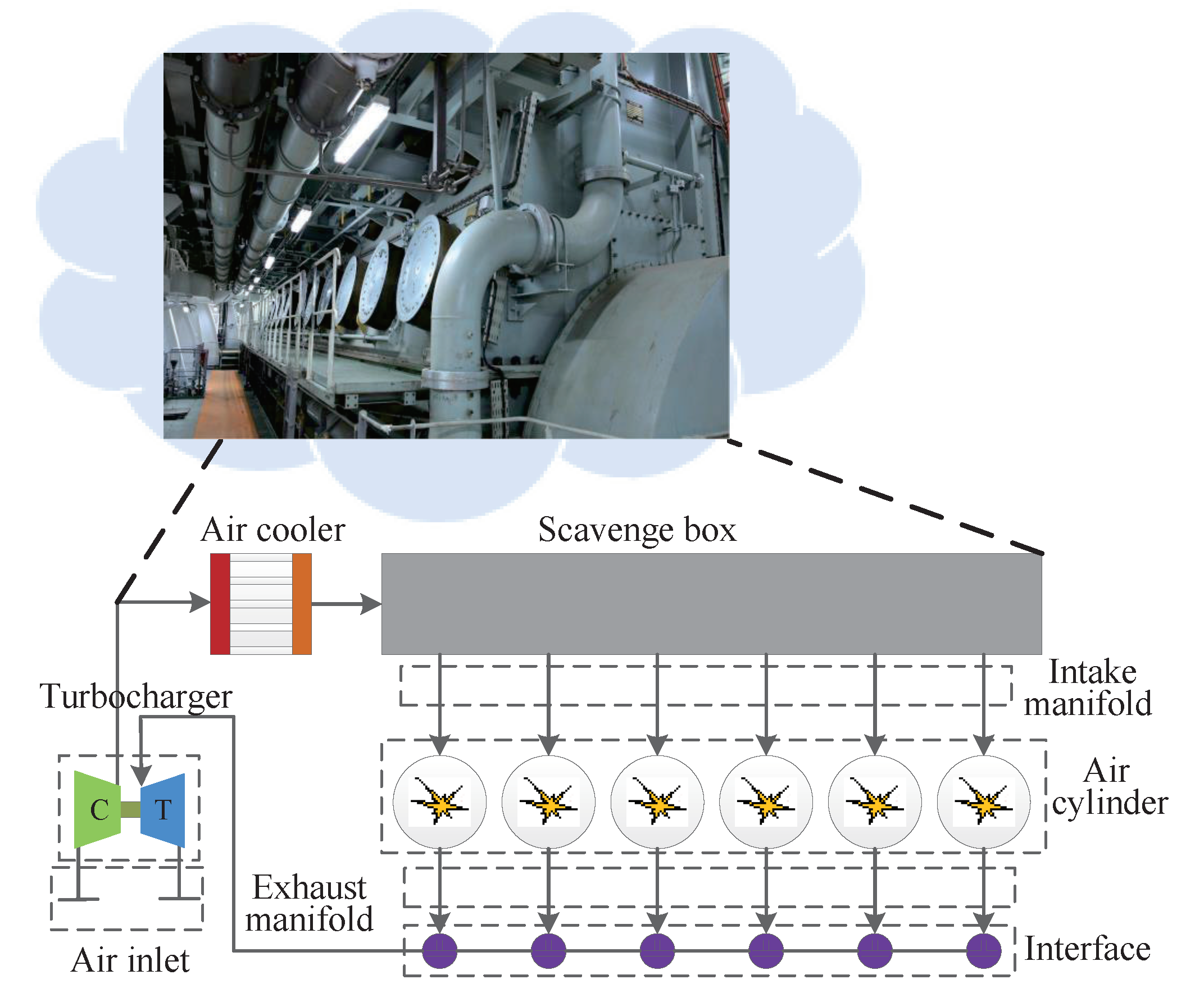
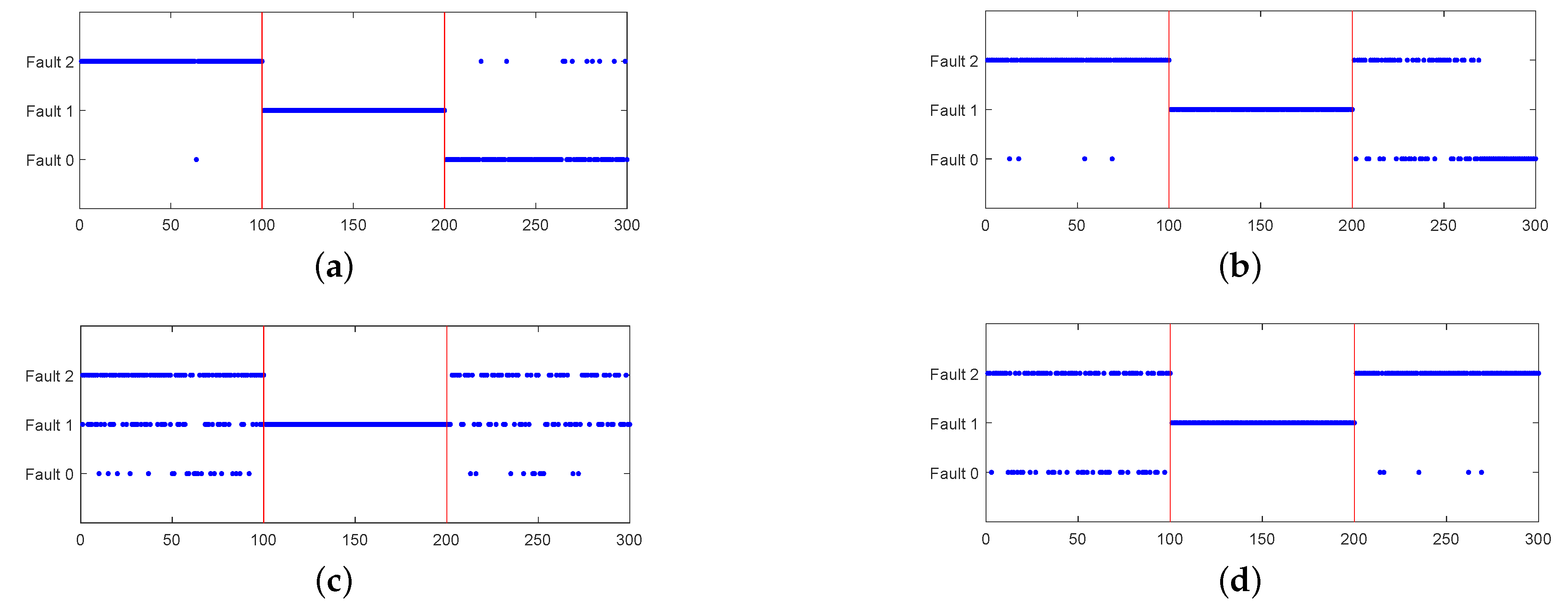
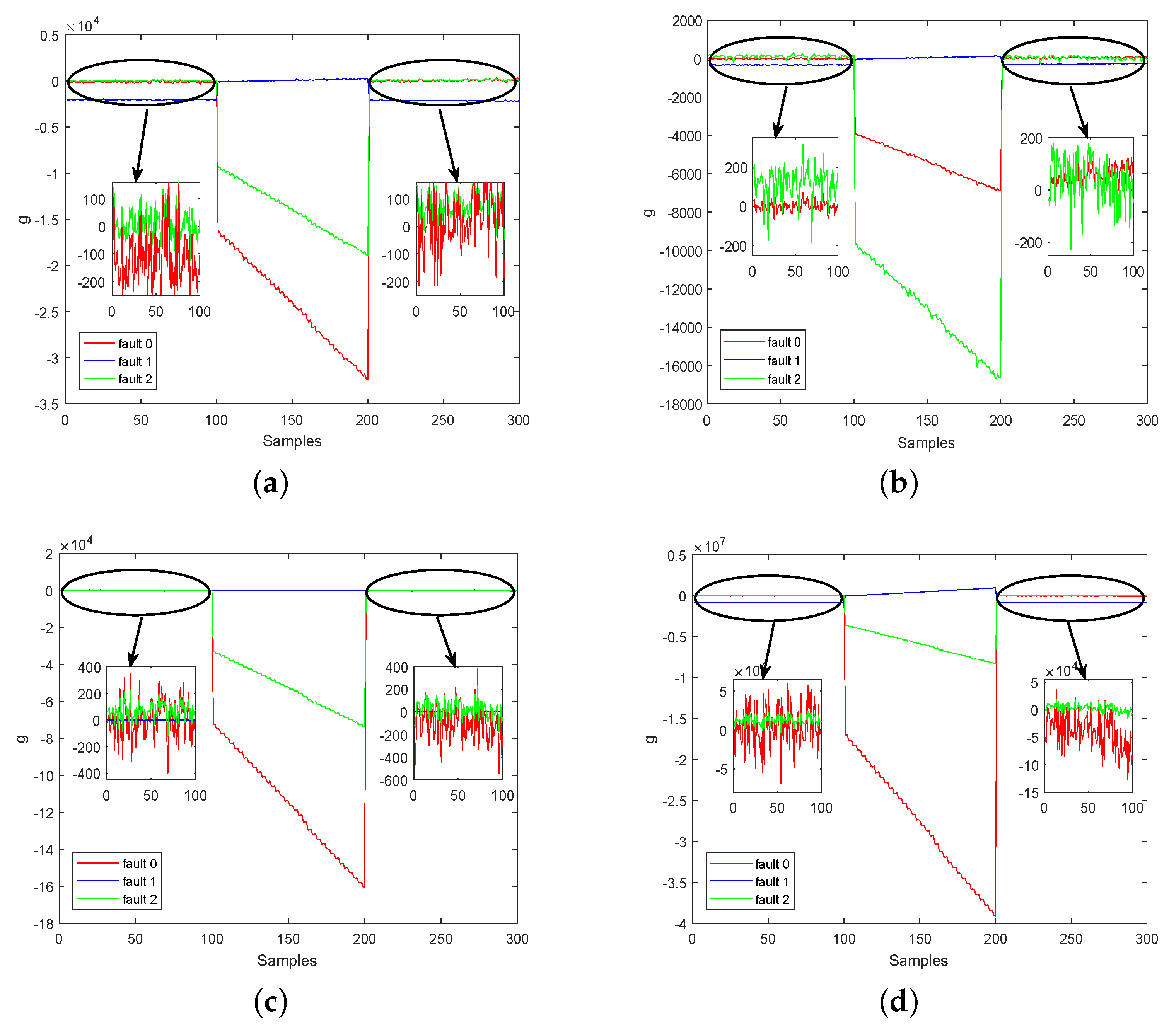
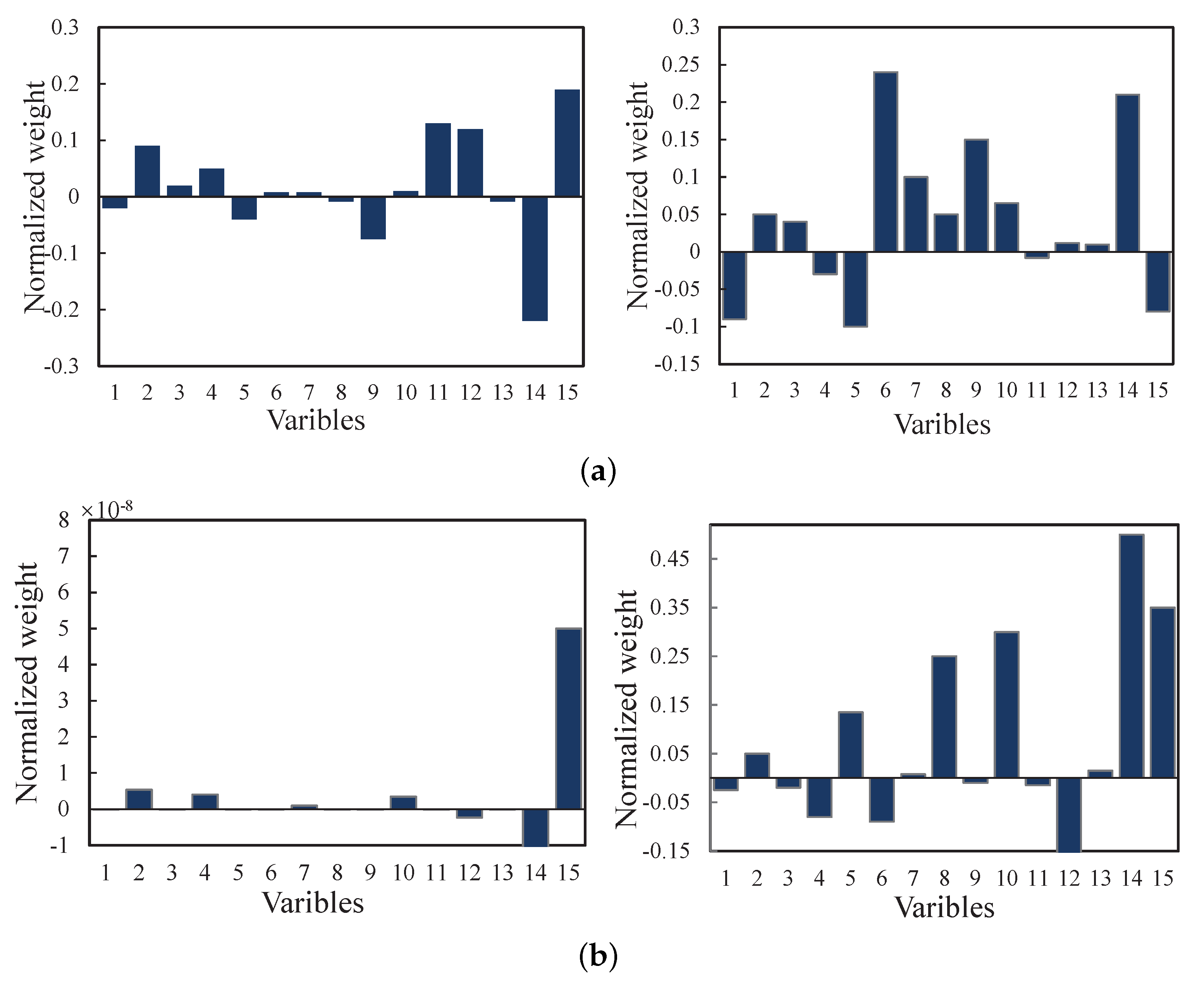
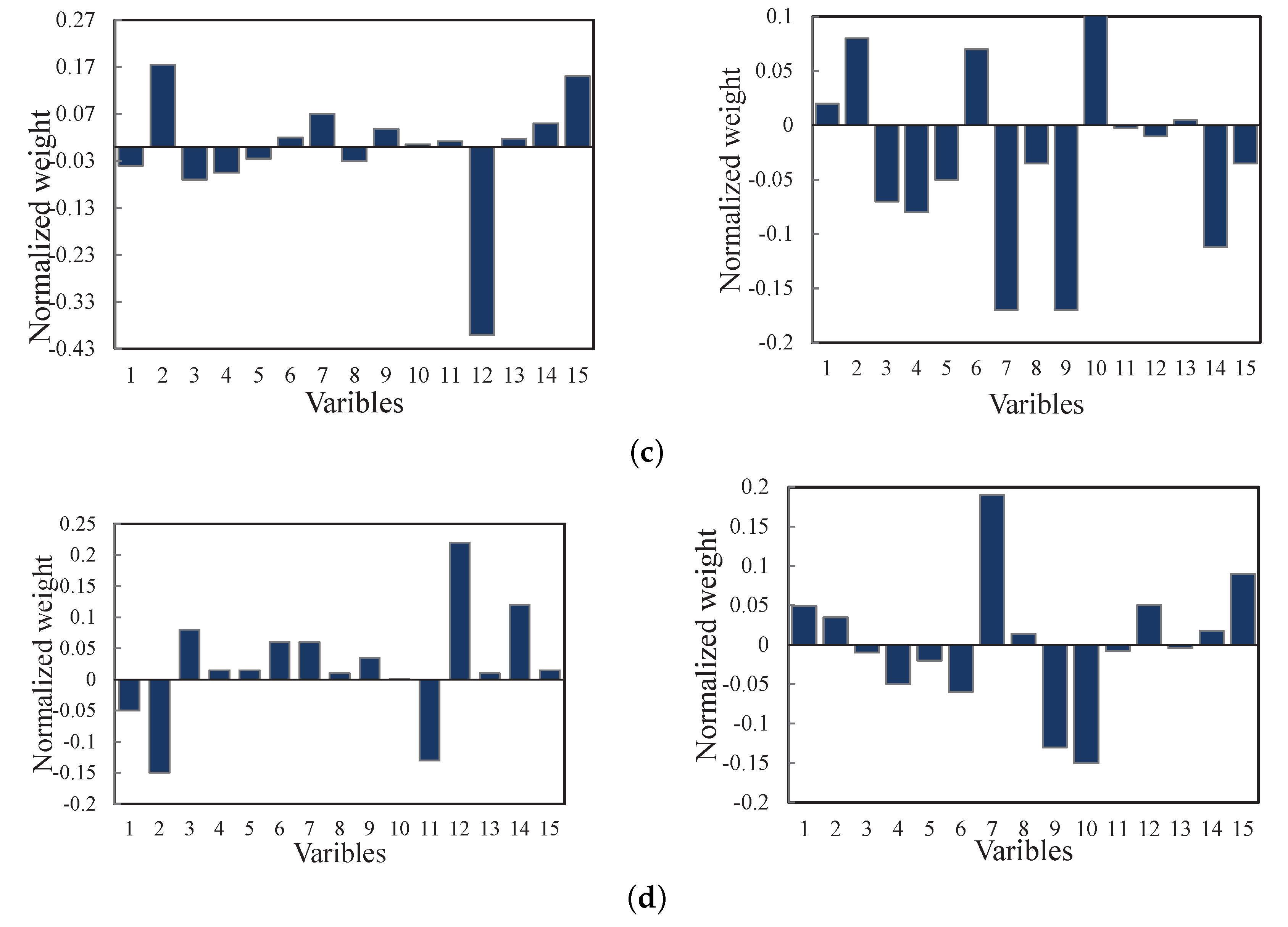
4.2. Real-World Diesel Working Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| FDA | Fisher discriminant analysis |
| LFDA | Local Fisher discriminant analysis |
| SSS | Small sample size |
| FDI | Fault detection and isolation |
| PCA | Principal component analysis |
| LPP | Local preserving projection |
| TE | Tennessee Eastman process |
| CVA | Canonical variable analysis |
| SMDA | Semi-supervised mixture discriminant analysis |
| SFA | Slow feature analysis |
| LASSO | Least absolute shrinkage and selection operator |
| SLFDA | Sparse local Fisher discriminant analysis |
| Probability density function | |
| SELFDA | Sparse variables selection based exponential local Fisher discriminant analysis |
References
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-Based Techniques Focused on Modern Industry: An Overview. IEEE Trans. Ind. Electron. 2015, 62, 657–667. [Google Scholar] [CrossRef]
- Subrahmanya, N.; Shin, Y.C. A data-based framework for fault detection and diagnostics of non-linear systems with partial state measurement. Eng. Appl. Artif. Intell. 2013, 26, 446–455. [Google Scholar] [CrossRef]
- Chiang, L.H.; Russell, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer Science & Business Media: Berlin, Germany, 2000. [Google Scholar]
- Wang, H.; Cai, Y.; Fu, G.; Wu, M.; Wei, Z. Data-driven fault prediction and anomaly measurement for complex systems using support vector probability density estimation. Eng. Appl. Artif. Intell. 2018, 67, 1–13. [Google Scholar] [CrossRef]
- Tidriri, K.; Tiplica, T.; Chatti, N.; Verron, S. A generic framework for decision fusion in Fault Detection and Diagnosis. Eng. Appl. Artif. Intell. 2018, 71, 73–86. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S. Recent Advances in Key-Performance-Indicator Oriented Prognosis and Diagnosis with a MATLAB Toolbox: DB-KIT. IEEE Trans. Ind. Inform. 2018, 15, 2849–2858. [Google Scholar] [CrossRef]
- Nor, N.M.; Hassan, C.R.C.; Hussain, M.A. A review of data-driven fault detection and diagnosis methods: Applications in chemical process systems. Rev. Chem. Eng. 2019, 36, 513–553. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X.; Huang, B. Performance-Driven Distributed PCA Process Monitoring Based on Fault-Relevant Variable Selection and Bayesian Inference. IEEE Trans. Ind. Electron. 2016, 63, 377–386. [Google Scholar] [CrossRef]
- Tong, C.; Lan, T.; Zhu, Y.; Shi, X.; Chen, Y. A missing variable approach for decentralized statistical process monitoring. ISA Trans. 2018, 81, 8–17. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, F. Critical-to-fault-degradation variable analysis and direction extraction for online fault prognostic. IEEE Trans. Control Syst. Technol. 2017, 25, 842–854. [Google Scholar] [CrossRef]
- Sugiyama, M. Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Yu, J. Localized Fisher discriminant analysis based complex chemical process monitoring. AIChE J. 2011, 57, 1817–1828. [Google Scholar] [CrossRef]
- Yu, J. Nonlinear bioprocess monitoring using multiway kernel localized Fisher discriminant analysis. Ind. Eng. Chem. Res. 2011, 50, 3390–3402. [Google Scholar] [CrossRef]
- Feng, J.; Wang, J.; Zhang, H.; Han, Z. Fault Diagnosis Method of Joint Fisher Discriminant Analysis Based on the Local and Global Manifold Learning and Its Kernel Version. IEEE Trans. Autom. Sci. Eng. 2016, 13, 122–133. [Google Scholar] [CrossRef]
- Zhong, K.; Han, M.; Qiu, T.; Han, B. Fault Diagnosis of Complex Processes Using Sparse Kernel Local Fisher Discriminant Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1581–1591. [Google Scholar] [CrossRef]
- Liang, M.; Jie, D.; Kaixiang, P.; Chuanfang, Z. Hierarchical Monitoring and Root Cause Diagnosis Framework for Key Performance Indicator-Related Multiple Faults in Process Industries. IEEE Trans. Ind. Inform. 2018, 15, 2091–2100. [Google Scholar]
- Adeli, E.; Thung, K.H.; An, L.; Wu, G.; Shi, F.; Wang, T.; Shen, D. Semi-supervised discriminative classification robust to sample-outliers and feature-noises. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 515–522. [Google Scholar] [CrossRef]
- Zhong, S.; Wen, Q.; Ge, Z. Semi-supervised Fisher discriminant analysis model for fault classification in industrial processes. Chemom. Intell. Lab. Syst. 2014, 138, 203–211. [Google Scholar] [CrossRef]
- Yan, Z.; Huang, C.C.; Yao, Y. Semi-supervised mixture discriminant monitoring for chemical batch processes. Chemom. Intell. Lab. Syst. 2014, 134, 10–22. [Google Scholar] [CrossRef]
- Liu, J.; Song, C.; Zhao, J. Active learning based semi-supervised exponential discriminant analysis and its application for fault classification in industrial processes. Chemom. Intell. Lab. Syst. 2018, 180, 42–53. [Google Scholar] [CrossRef]
- Chen, L.F.; Liao, H.Y.M.; Ko, M.T.; Lin, J.C.; Yu, G.J. A new LDA-based face recognition system which can solve the small sample size problem. Pattern Recognit. 2000, 33, 1713–1726. [Google Scholar] [CrossRef]
- Ye, J.; Li, Q. A two-stage linear discriminant analysis via QR-decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 929–941. [Google Scholar]
- Zhang, T.; Fang, B.; Tang, Y.Y.; Shang, Z.; Xu, B. Generalized discriminant analysis: A matrix exponential approach. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 40, 186–197. [Google Scholar] [CrossRef]
- Adil, M.; Abid, M.; Khan, A.Q.; Mustafa, G.; Ahmed, N. Exponential discriminant analysis for fault diagnosis. Neurocomputing 2016, 171, 1344–1353. [Google Scholar] [CrossRef]
- Dornaika, F.; Bosaghzadeh, A. Exponential local discriminant embedding and its application to face recognition. IEEE Trans. Cybern. 2013, 43, 921–934. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Recursive Exponential Slow Feature Analysis for Fine-Scale Adaptive Processes Monitoring With Comprehensive Operation Status Identification. IEEE Trans. Ind. Inform. 2019, 15, 3311–3323. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Tong, C.; Lan, T.; Shi, X. Double-layer ensemble monitoring of non-gaussian processes using modified independent component analysis. ISA Trans. 2017, 68, 181–188. [Google Scholar] [CrossRef]
- Ahmed, R.; Sayed, M.E.; Gadsden, S.A.; Tjong, J.; Habibi, S. Automotive Internal-Combustion-Engine Fault Detection and Classification Using Artificial Neural Network Techniques. IEEE Trans. Veh. Technol. 2015, 64, 21–33. [Google Scholar] [CrossRef]
- Ruiz, F.A.; Isaza, C.V.; Agudelo, A.F.; Agudelo, J.R. A new criterion to validate and improve the classification process of LAMDA algorithm applied to diesel engines. Eng. Appl. Artif. Intell. 2017, 60, 117–127. [Google Scholar] [CrossRef]
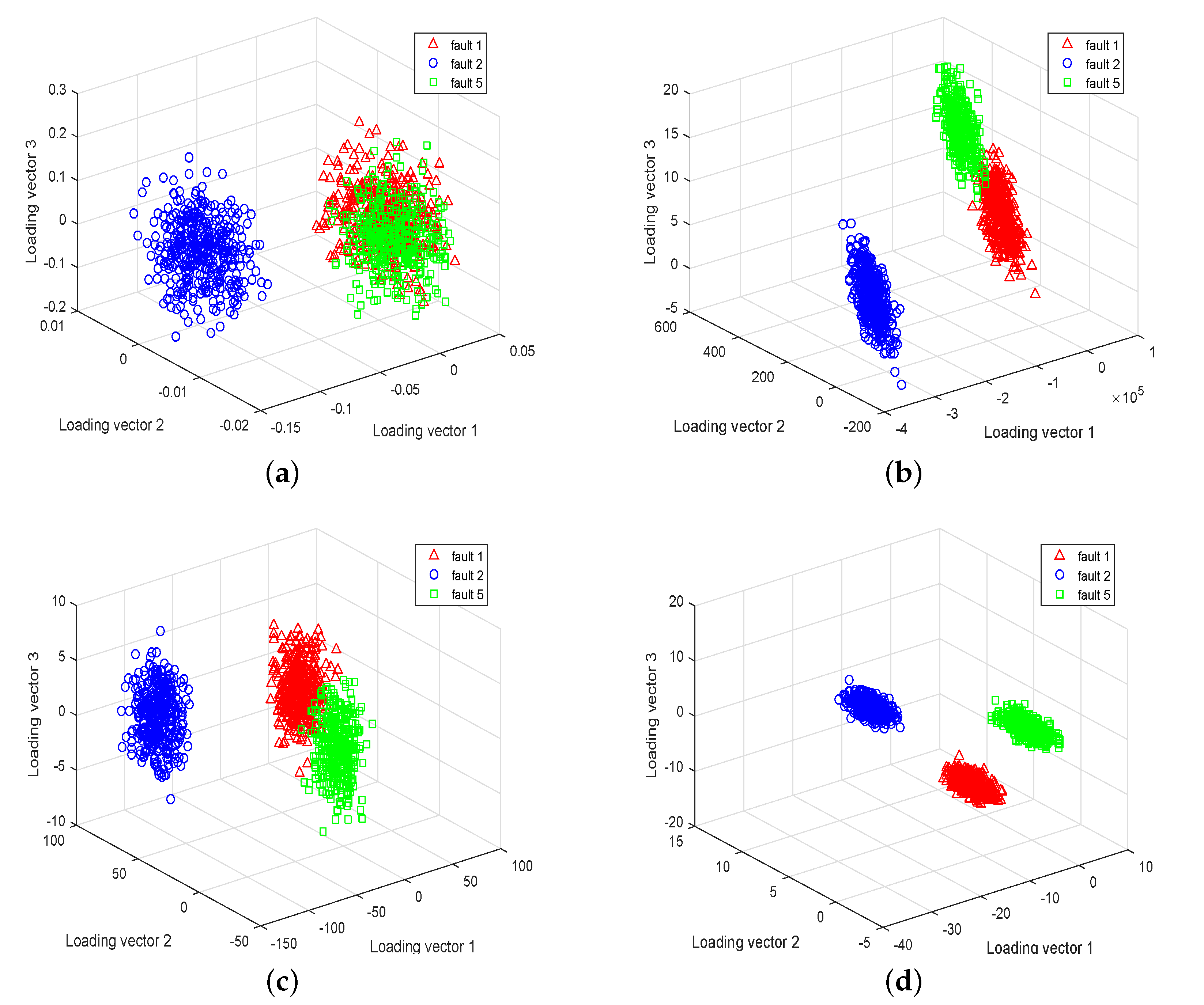
| No | Description | Type |
|---|---|---|
| Fault 1 | A/C feed ratio B composition constant | Step |
| Fault 2 | B composition, A/C ration constant | Step |
| Fault 5 | Condenser cooling water inlet temperature | Step |
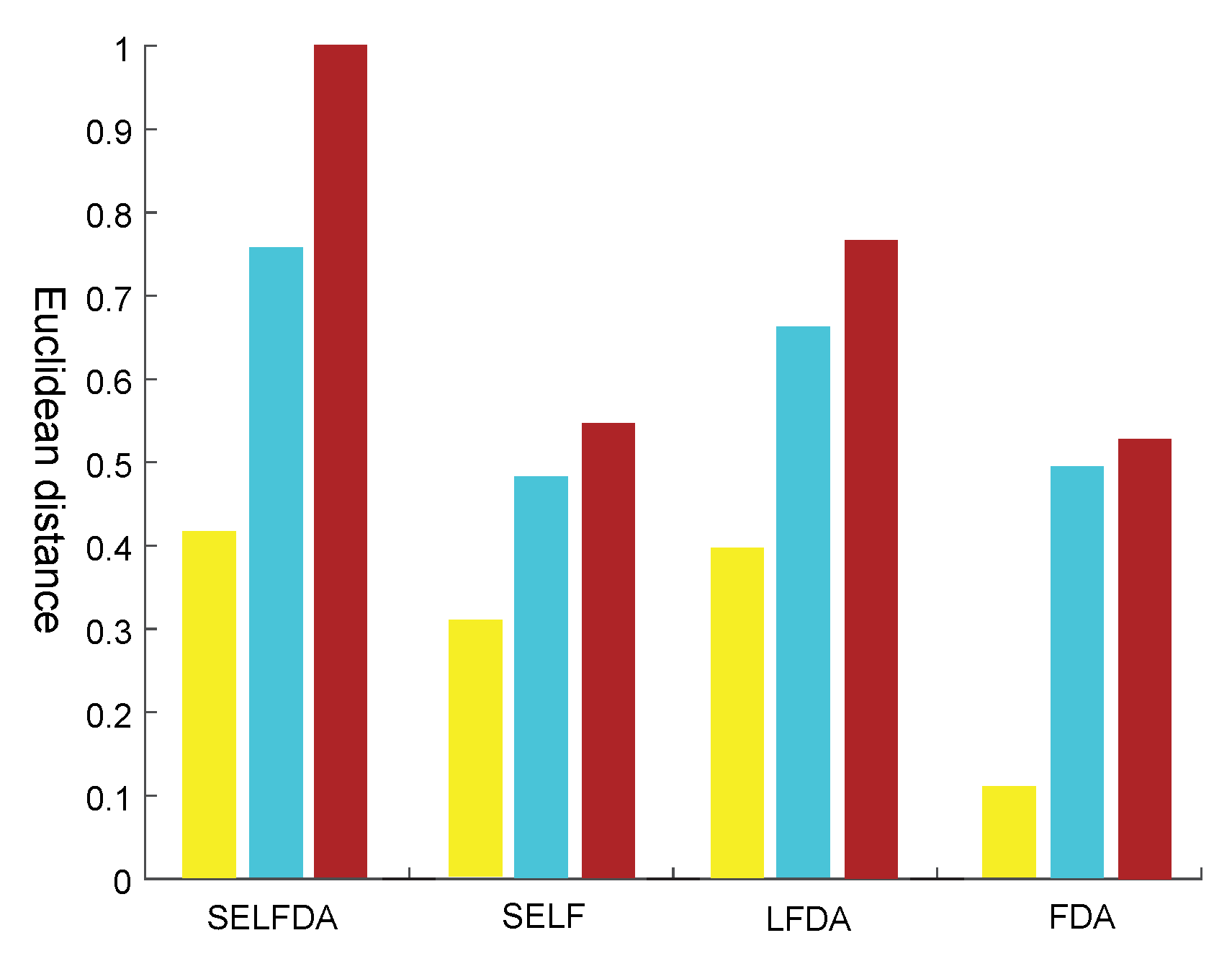
| FDA | LFDA | SELF | SELFDA | |
|---|---|---|---|---|
| Fault 1 | 83.25% | 83.25% | 64% | 100% |
| Fault 2 | 39.5% | 0.95% | 100% | 100% |
| Fault 5 | 63.75% | 69.5% | 66.5% | 96.25% |
| Average | 62.17% | 54.08% | 76.83% | 98.75% |
| Parameter | Value | Unit |
|---|---|---|
| Rated power | 3570 | Kw |
| Rated speed | 142 | r/min |
| Cylinders | 6 | N |
| Fuel consumption | 174.36 | g/kw·h |
| Stroke | 2 | t |
| Oil | MGO | - |
| Viscosity | 3–5 at 100 °C | cSt |
| Density | ≤0.887 at 15 °C | g/cm |
| No. | Variable Description | Units | No. | Variable Description | Units |
|---|---|---|---|---|---|
| 1 | Diesel power | kW | 9 | Scavenge air pressure | Bar |
| 2 | Exhaust manifold pressure | Bar | 10 | Scavenge air temp | |
| 3 | Press flow | kg/c | 11 | Pressure difference | Bar |
| 4 | Outlet temp of press | 12 | Exhaust gas tempe | ||
| 5 | Outlet pressure of press | Bar | 13 | Exhaust pipe pressure | Bar |
| 6 | Intercooler post temp | 14 | Turbocharger inlet tempe | ||
| 7 | Fuel consumption | g/kw·h | 15 | Turbocharger outlet tempe | |
| 8 | Intercooler post pressure | Bar |
| FDA | LFDA | SELF | SELFDA | |
|---|---|---|---|---|
| Fault 0 | 1% | 4% | 20% | 35% |
| Fault 1 | 100% | 100% | 100% | 100% |
| Fault 2 | 10% | 43% | 49% | 95% |
| Average | 37% | 49% | 56.33% | 76.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Xu, Y.; Zhong, K. Exponential Local Fisher Discriminant Analysis with Sparse Variables Selection: A Novel Fault Diagnosis Scheme for Industry Application. Machines 2023, 11, 1066. https://doi.org/10.3390/machines11121066
Ding Z, Xu Y, Zhong K. Exponential Local Fisher Discriminant Analysis with Sparse Variables Selection: A Novel Fault Diagnosis Scheme for Industry Application. Machines. 2023; 11(12):1066. https://doi.org/10.3390/machines11121066
Chicago/Turabian StyleDing, Zhengping, Yingcheng Xu, and Kai Zhong. 2023. "Exponential Local Fisher Discriminant Analysis with Sparse Variables Selection: A Novel Fault Diagnosis Scheme for Industry Application" Machines 11, no. 12: 1066. https://doi.org/10.3390/machines11121066
APA StyleDing, Z., Xu, Y., & Zhong, K. (2023). Exponential Local Fisher Discriminant Analysis with Sparse Variables Selection: A Novel Fault Diagnosis Scheme for Industry Application. Machines, 11(12), 1066. https://doi.org/10.3390/machines11121066






